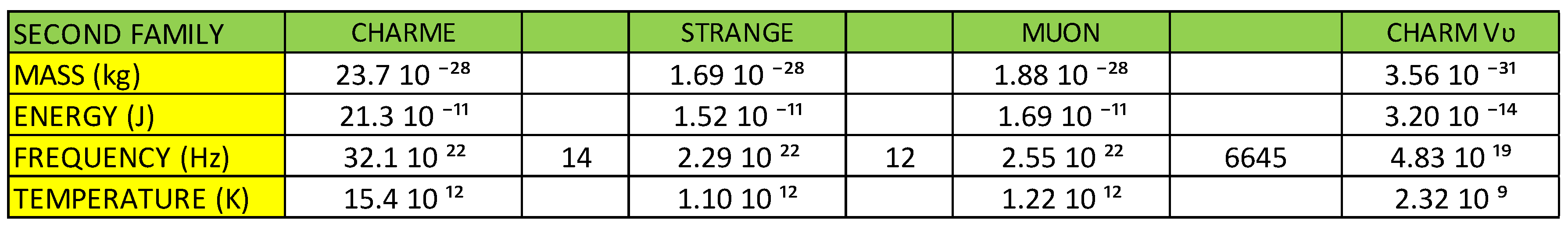1. Introduction: Capacitive Property of Matter, Correspondence ADS/CFT

In figure 1, we observe that the neutron is a clear example that represents the capacitive property of matter, we see through the interactions of quarks, antiquarks and gluons how the neutron is formed.

Figure 1. Capacitive property of matter, mass distribution in interactions 1 & 2.

Figure 1. Capacitive property of matter, mass distribution in interactions 1 & 2.

1.2. Space-Time Torsion Mechanism

In the paper: Theory of the Generalization of the Boltzmann’s Constant in Curved Space-Time. Shannon-Boltzmann Gibbs Entropy Relation and the Effective Boltzmann’s Constant [2], we have determined that we can quantify the curvature of space-time through the effective Boltzmann constant which varies from:

1.38 10ˉ²³ J/K > Kʙe > 1.78 10ˉ⁴³ J/K

(2)

Now we are going to determine that there is a mechanism that generates a torsional force in the Space-time structure that adds to the contraction force. The contraction force is inward, towards the centre of mass of the body in question and the torsion force is a tangent force that lags the contraction force by 90 degrees. It is similar to the phasor diagrams that occur in an RC electrical circuit.

We can represent it in the following diagram:

Figure 2. Vector representation of the forces in a black hole. Fc = f, represents the force towards the interior of the black hole generated by the mass m and Ft = -iφ, is a tangential force that retards Fc by 90 degrees, generated by the mass δ.

Figure 2. Vector representation of the forces in a black hole. Fc = f, represents the force towards the interior of the black hole generated by the mass m and Ft = -iφ, is a tangential force that retards Fc by 90 degrees, generated by the mass δ.

From the following equation:

$${\mathrm{d}\mathrm{s}}^2=-\left(1-\left(\frac{2\mathrm{M}\mathrm{G}}{{\mathrm{R}\mathrm{c}}^2}\right)\right){\mathrm{c}}^2{\mathrm{d}\mathrm{t}}^2+\left(1/\left(1–\frac{2\mathrm{M}\mathrm{G}}{{\mathrm{R}\mathrm{c}}^2}\right)\right){\mathrm{d}\mathrm{R}}^2+{\mathrm{R}}^2\mathrm{d}{\mathsf{\theta }}^2+{\mathrm{R}}^2{\mathrm{s}\mathrm{i}\mathrm{n}}^2\mathrm{d}\mathsf{\phi }²$$

(3)

We will analyse the Schwarzschild solution for a punctual object in which mass and gravity are introduced.

$$Rs=2GM/c²,istheSchwarzschild´sradius.$$

(4)

Where M is the mass of a black hole, c is the speed of light, and G is the gravitational constant.

if we consider dθ = 0; and dφ = 0; that is, we move in the direction of dR.

(5)

R = Rs, ds = 0, let's analyse this specific situation.

(6)

Replacing the conditions given in (13), (14) and (15) in equation (12), we have:

(dR / dt) ² = v² = c² (1 - (2MG/Rc²) ²

R = Rs, v = 0; ds² = 0; Rs is the Schwarzschild´s radius.

(7)

R > Rs, v < c; ds < 0, time type trajectory.

(8)

R < Rs, v > c; ds > 0, space type trajectory.

(9)

Condition (9) is very important because to the extent that R < Rs, v > c is fulfilled, it is precisely this speed difference that generates the imaginary mass in a black hole given by $-i\delta .$

Planck length equation:

$$Lp=\surd (hG/c³)$$

(10)

where h is Planck's constant, G is the gravitational constant, and c is the speed of light.

If we consider condition (9) and equation (10), to the extent that R < Rs and v > c, are fulfilled, we deduce that the Planck length decreases in value.

We define the following:

Lpɛ = Lp = 1.616199 10⁻³⁵ m; electromagnetic Planck length.

Lpɢ = gravitational Planck length.

(11)

Lpɢ < Lpɛ

(12)

Always holds:

This is telling us that as the black hole grows, the Planck length inside a black hole decrease, this mechanism generates a torsional force or tangential force, which delays the force of gravitational attraction by 90 degrees, this mechanism is what generates dark matter.

A more rigorous explanation is given in the paper: Rlc Electrical Modelling of Black Hole and Early Universe. Generalization of Boltzmann’s Constant in Curved Space-Time [3].

Up to this point we have explained that there are two forces that act in the structure of space-time. As we place mass in a given space-time, a gravitational force of attraction acts, which curves and contracts space-time until a black hole is formed. As the black hole grows, in addition to the force of gravitational attraction or contraction of space-time, a tangential or torsion force of space-time begins to act, which delays the force of gravitational attraction by 90 degrees.

The behaviour of the system is analogous to an RC circuit. We can say that an RC Circuit stores electrical energy and a black hole stores gravitational potential energy.

1.3. Theory of the Generalization of the Boltzmann’s Constant in Curved Space-Time. Shannon-Boltzmann Gibbs Entropy Relation and the Effective Boltzmann’s Constant

This theory proposes the quantification of the curvature of space-time considering the Boltzmann constant variable; Thus, the concept of effective Boltzmann constant was born. This allows us to measure the curvature of space-time.

The Boltzmann constant varies between the following limits:

1.38 10⁻²³ J/K > Kв effective > 1.78 10⁻⁴³ J/K

The curvature of space-time is a direct function of temperature, the higher the temperature, the greater the curvature of space-time.

1.38 10⁻²³ J/K => flat space-time

1.38 10⁻²³ J/K > Kв effective > 1.78 10⁻⁴³ J/K => curved space-time

1.3.1. Calculation of the Curvature of Space-Time for Different States of Matter

In the paper: Theory of the Generalization of the Boltzmann’s Constant in Curved Space-Time. Shannon-Boltzmann Gibbs Entropy Relation and the Effective Boltzmann’s Constant [2], we have calculated the curvature of space-time for different states of matter.

In the following table, we show these calculations:

In table 1, for different states of matter, we have calculated the curvature of space-time with respect to flat space-time, for a Boltzmann constant corresponding to Kʙ = 1.38 10ˉ²³ J/K.

Table 1. We can observe in table 1, according to the state of matter, how the KB, frequency, wavelength, etc, vary; according to whether we are in a flat space-time or in a curved space-time.

Table 1. We can observe in table 1, according to the state of matter, how the KB, frequency, wavelength, etc, vary; according to whether we are in a flat space-time or in a curved space-time.

Earth	Flat space-time	Curved space-time	units
Kʙ (Boltzmann´s constant)	1.38 10ˉ²³	2.97 10ˉ²⁸	(J/K)
f (frequency)	1.25 10¹⁴	2.69 10⁹	Hz
λ (wavelength)	2.4 10ˉ⁶	0.11	m
second of arc	1.85 10ˉ¹²	8.49 10ˉ⁸	m
Cv (curvature)	1	4.58 10⁴	times
F (gravity)		9.81	N
Sun	Flat space-time	Curved space-time	units
Kʙ (Boltzmann´s constant)	1.38 10ˉ²³	3.59 10ˉ³⁷	(J/K)
f (frequency)	3.12 10¹⁷	8.1 10³	Hz
λ (wavelength)	9.61 10ˉ¹⁰	3.7 10⁴	m
second of arc	7.41 10ˉ¹⁶	0.0285	m
Cv (curvature)	1	3.84 10¹³	times
F (gravity)		2.73 10²	N
White dwarf star	Flat space-time	Curved space-time	units
Kʙ (Boltzmann´s constant)	1.38 10ˉ²³	1.97 10ˉ³⁷	(J/K)
f (frequency)	4.12 10¹⁷	5.74 10³	Hz
λ (wavelength)	0.72 10ˉ⁹	5.224 10³	m
second of arc	5.55 10ˉ¹⁶	0.0403	m
Cv (curvature)	1	7.2 10¹³	times
F (gravity)		4.7 10⁶	N
Neutron star	Flat space-time	Curved space-time	units
Kʙ (Boltzmann´s constant)	1.38 10ˉ²³	2.42 10ˉ⁴²	(J/K)
f (frequency)	2.084 10²²	3.655 10³	Hz
λ (wavelength)	1.43 10ˉ¹⁴	8.207 10⁴	m
second of arc	1.1 10ˉ²⁰	0.0633	m
Cv (curvature)	1	5.75 10¹⁸	times
F (gravity)		2.0 10¹²	N
Black hole	Flat space-time	Curved space-time	units
Kʙ (Boltzmann´s constant)	1.38 10ˉ²³	1.78 10ˉ⁴³	(J/K)
f (frequency)	2.084 10²³	2.688 10³	Hz
λ (wavelength)	1.439 10ˉ¹⁵	1,11 10⁵	m
second of arc	1.108 10ˉ²¹	0.0856	m
Cv (curvature)	1	7.72 10¹⁹	times
F (gravity)		5.0 10¹²	N

For a black hole, whose space-time curvature, Cv = 7.72 10¹⁹ times with respect to flat space-time, corresponds to a gravitational force of F = 5 10¹² N.

2. Standard Model of Elementary Particles

Now that we have finished the introduction, we are going to work with the table that represents the standard model of elementary particles. Let's transform the characteristics of elementary particles into parameters that are easy to work with as shown in Table 2.

Figure 3. Standard Model.

Figure 3. Standard Model.

Table 2. particles of the standard model as a function of mass in kg, energy in Joules, frequency in Hz and temperature in K.

Table 2. particles of the standard model as a function of mass in kg, energy in Joules, frequency in Hz and temperature in K.

3. New Physical Model Proposed for Photons, Quarks and Gluons

Example 1:

Figure 4. Representation of ℓs and T₀ of interaction 1, proton.

Figure 4. Representation of ℓs and T₀ of interaction 1, proton.

Example 2:

Figure 5. Representation of ℓs and T₀ of interaction 1, neutron.

Figure 5. Representation of ℓs and T₀ of interaction 1, neutron.

Proposed physical model for photons:

Figure 6. Physical model of photon.

Figure 6. Physical model of photon.

Proposed physical model for quarks up:

Figure 7. Physical model of quarks up.

Figure 7. Physical model of quarks up.

Proposed physical model for quarks down:

Figure 8. Physical model of quarks down.

Figure 8. Physical model of quarks down.

Proposed physical model for gluons:

Figure 9. Physical model of gluons.

Figure 9. Physical model of gluons.

4. Analysis of the Origin of Elementary Particles Using the Theory of the generalization of the Boltzmann Constant in curved Space-Time

I) First family of elementary particles

Figure 10. first family of elementary particles.

Figure 10. first family of elementary particles.

In figure 11, the ball represented moves with respect to the vertical axis. If this displacement is small with respect to λ/2, we can consider that the movement is that of a harmonic oscillator and if we have several balls, they will all move with the same frequency or period, this is an important characteristic of the motion of a harmonic oscillator, as shown in Figure 11.

Figure 11. harmonic oscillator.

Figure 11. harmonic oscillator.

II) Second family of elementary particles

Figure 12. second family of elementary particles.

Figure 12. second family of elementary particles.

III) Third family of elementary particles

Figure 13. Third family of elementary particles.

Figure 13. Third family of elementary particles.

5. Application of the Model and Results

5.1. Comparison between Stellar Bodies and Elementary Particles Considering the Theory of the Generalization of the boltzmann Constant in Curved Space-Time

In table 3, for a gravitational force Fg = 10¹⁰ N, we can divide the elementary particles into two groups; in blue, the stable elementary particles correspond to a gravitational force less than 10¹⁰ N; in orange, unstable elementary particles, correspond to a gravitational force greater than 10¹⁰ N.

Table 3. Compare the gravitational force between stellar bodies and elementary particles.

Table 3. Compare the gravitational force between stellar bodies and elementary particles.

Fg = 10¹⁰ N, it is an inflection point, between the gravitational forces Fg and the coulomb force Fq; below 10¹⁰ N, Fg > Fq, the elementary particles are stable; above 10¹⁰ N, Fq > Fg, the elementary particles are unstable.

However, this inflection point only exists for elementary particles, for pure energy type E, according to the Einstein equation E = mc².

For stellar bodies, in which the energy is given by the mass m, from the equation E = mc², there is no inflection point.

If we analyse Table 2, we see that the temperature corresponding to the top quark is slightly lower than the temperature of the Higgs potential.

Temperature Q-top = 2.00 10¹⁵ K

Temperature Higgs = 2.97 10¹⁵ K

Taking into account that the decay time of the top quark is of the order of 10ˉ²⁵ s.

Here we are going to propose the following, for a temperature higher than the temperature of the Higgs potential, T Higgs = 2.97 10¹⁵ K, the coulomb force is much greater than the gravitational force, Fq >>Fg, under these conditions, the coulomb force is so great that it does not allow the gravitational force field to encapsulate matter in the pure energy state E, consequently breaking the inverse symmetry of the electroweak force.

Above the Higgs temperature, the gravitational force field cannot encapsulate matter in the form of pure energy, the electromagnetic force field, the energy of the electromagnetic field moves freely independent of the force of gravity; below the Higgs temperature, the gravitational force field interacts with the electromagnetic force field, this interaction allows the formation of elementary particles.

If we look at table 3, the gravitational force of a black hole is 5 10¹² N and the force of the Top quark is 2 10¹³ N, we see that the gravitational force of the top quark is greater than the force of a black hole, this is because a top quark does not have the critical mass to form a black hole, even though its temperature reaches 10¹⁵ K.

Another very important deduction that we can make is the following, it is the gravitational field together with the Higgs field that give rise to elementary particles. It is the Higgs potential that determines the temperature that causes the gravitational field to encapsulate elemental energy to form elemental particles.

In conclusion, to form elementary particles we need:

1) gravitational field, gives us gravitons.

2) electric field, provides us with the quanta of elemental energy.

3) The Higgs field, gives us the temperature for the gravitons to unite with the quanta of elementary energies to form elementary particles.

Let us remember that the Higgs H field has a value of 246 GeV (2.85 10¹⁵ K) in a vacuum.

The Higgs potential is the value of energy that the Higgs field stores at a given moment, it is a scalar field, it is a temperature field.

The Higgs boson is the excitation of the Higgs field and is produced in a particle accelerator.

The potential of the Higgs field has a maximum at the origin and falls to its minimum, which is the current vacuum that corresponds to 246 GeV, the value of the Higgs field.

5.2. Mass-Temperature Relationship in Elemental and Non-Elemental Particles

In Table 4, it is observed that the mass-temperature relationship is constant for all the particles of the standard model, including the W (+/-) bosons, z⁰ Boson, Higgs boson, protons and neutrons.

In figure 14, we represent the mass-temperature relationship, which gives us a straight line whose slope is 1.53 10ˉ⁴⁰ kg/k.

Table 4. Mass-temperature relationship for elemental and non-elemental particles. It is observed for all situations that the mass-temperature relationship is 1.53 10ˉ⁴⁰ kg / k.

Table 4. Mass-temperature relationship for elemental and non-elemental particles. It is observed for all situations that the mass-temperature relationship is 1.53 10ˉ⁴⁰ kg / k.

Figure 14. The mass-temperature relationship is a straight line whose slope takes the value of 1.53 10ˉ⁴⁰ kg/k.

Figure 14. The mass-temperature relationship is a straight line whose slope takes the value of 1.53 10ˉ⁴⁰ kg/k.

Figure 15. Gravitational force vs temperature for elementary particles and stellar bodies.

Figure 15. Gravitational force vs temperature for elementary particles and stellar bodies.

In red, the elementary particles are represented and in blue, the stellar bodies are represented.

In figure 15, we can see that elementary particles have a gravitational attraction force of the order of stellar bodies; for example, electrons have a gravitational force on the order of white dwarf stars and the bottom quark has a gravitational force on the order of neutron stars.

Let us remember that 2.97 10¹⁵ K is the temperature at which the symmetry break occurs. Above that temperature, the electroweak repulsion force Fq is much greater than the gravitational attraction force Fg, Fq >> Fg, therefore which makes the formation of elementary particles impossible.

In figure 15, the yellow line marks the boundary between stable and unstable elementary particles, below the yellow line, the elementary particles are stable, above the yellow line, the elementary particles are unstable.

According to the models proposed for the quarks in Figure 7 and 8, the instability of the particles occurs because for Fg = 10¹⁰ N, the force Fq of repulsion or electrostatic disintegration exceeds the force Fg of gravitational attraction.

Up to this point we have carried out an intuitive analysis of why some elementary particles are stable and why other elementary particles are unstable.

Now we are going to analyse intuitively, why the first family of quarks can form hadrons and why the second and third families of quarks cannot form hadrons.

In the paper: Electrical-Quantum Modelling of the Neutron and Proton as a Three-Phase Alternating Current Electrical Generator. Determination of the Number of Quarks-Antiquarks-Gluons and Gravitons, inside a Neutron [1], we have modelled a neutron and a proton as a three-phase alternating current generator.

In the following graph, we are going to bring the figures that represent the neutron as a reminder example:

Figure 16. Neutron.

Figure 16. Neutron.

Figure 17. Neutron phasor diagram.

Figure 17. Neutron phasor diagram.

If we analyse table 2, we observe that there is a relationship of 2 between the parameters of the up and down quark.

It is also important to consider that the up and down quarks are in the stable zone of figure 15; These two combinations are very important and are what gives the first family of quarks the ability to form hadrons.

For the second family of Charme and strange quarks, the relationship between the parameters of the quarks is 14 and in addition both quarks are in the unstable zone of figure 15, these two combinations mean that the second family of quarks does not have the ability to form hadrons. It would be very difficult to form a phasor diagram analogous to that of the neutron, figure 17, with the charme and strange quarks.

For the third family of top and bottom quarks, the relationship between the parameters of the quarks is 41 and in addition both quarks are in the unstable zone of figure 15, these two combinations mean that the third family of quarks does not have the ability to form hadrons. It would be very difficult to form a phasor diagram analogous to that of the neutron, figure 17, with the top and bottom quarks.

At this point we wonder, if the gravitational force of the stellar bodies is of the order of the gravitational force of the elementary particles, why the stellar bodies move at a speed v << c and the elementary particles move at a speed approximate to the speed of the light?

The answer to this question can be related to the capacitive property of matter, to the extent that matter forms complex bodies, gravity mixes with energy and this manifests itself in our daily life, in which we perceive that the bodies are they move slowly, that is, v << c, our classical world, deterministic. For elementary particles, in which the gravity-energy relationship is minimal, we see that the speed of the elementary particles is approximately the speed of light, v approximately c, quantum world, probabilistic.

We are going to try to find a relationship between the sun-earth and proton-electron model.

First relationship

Ms / Mp = 1.98 10³⁰ / 1.67 10ˉ²⁷ = 1.18 10⁵⁷

Mt / Me = 5.97 10²⁴ / 9.1 10ˉ³¹ = 0.656 10⁵⁵

(Ms / Mp) / (Mt / Me) = 1.18 10⁵⁷ / 0.656 10⁵⁵ = 1.79 10²

Where Ms is the mass of the sun, Mt is the mass of the earth, Mp is the mass of the proton and Me is the mass of the electron.

Second relationship

Ms / Mt = 1.98 10³⁰ / 5.97 10²⁴ = 3.31 10⁵

Mp / Me = 1.673 10ˉ²⁷ / 9.1 10ˉ³¹ = 1.83 10³

(Ms / Mt) / (Mp / Me) = 3.31 10⁵ / 1.83 10³ = 1.80 10²

Where Ms is the mass of the sun, Mt is the mass of the earth, Mp is the mass of the proton and Me is the mass of the electron.

Third relationship

Dts = 1.5 10¹¹ m, earth-sun distance

Dpe = 5.3 10ˉ¹¹ m, proton-electron distance

If we consider zero (0) as a reference and measure to the left the distance Dpe = 5.3 10ˉ¹¹ m, now if we change the reference to the left then the distance Dpe = 5.3 10¹¹ m.

With this we want to demonstrate that the distance Dpe and Dts are equivalent in relation to the size of the bodies Ms/Mt vs Mp/Me.

We apply the Bohr model to calculate the speed of the electron around the nucleus of the atom, proton:

Ve = n h / (r me 2 π)

Ve = 1 x 6.62 10ˉ³⁴ / 5.3 10ˉ¹¹ x 9.1 10ˉ³¹ x 2 x 3,14

Ve = 2.18 10⁵ m/s, electron velocity

Ve = 218,000 m/s

We are going to calculate the speed of the earth around the sun:

Vt = ꙍ x Rt

Vt = (2π /T) x Rt

Vt = (2 x 3,14 x 1.5 10¹¹ m) / 3.15 10⁷ s

Vt = 2.99 10⁴ m/s

Vt = 29,900 m/s

Where Ve is electron velocity and Vt is earth velocity.

We have shown that the difference between the speed of the electron Ve and the speed of the earth with respect to the sun Vt is one order of magnitude; this is due to the difference between the mass ratio Ms/Mt vs Mp/Me, 1.8 10², if an equal mass ratio existed, surely Vt would be the same as the speed of the electron Ve. Therefore, the sun-earth model is equivalent to the proton-electron model.

To conclude, we have demonstrated that gravity is fundamental in determining the parameters that elementary particles acquire when they are formed. Furthermore, we have shown that the attractive force of elementary particles is similar to that of stellar bodies.

In the next section, we will analyse β ˉ decay, to emphasize how electrons, antineutrinos and photons are produced.

5.3. Origin of the Electron and Antineutrino - β ˉ Decay

In the paper: Electrical-Quantum Modelling of the Neutron and Proton as a Three-Phase Alternating Current Electrical Generator. Determination of the Number of Quarks-Antiquarks-Gluons and Gravitons, inside a Neutron [1]; we have analysed β ˉ decay, considering the electrical model of the proton and the neutron as a three-phase alternating current electrical generator.

Figure 18. β ˉ decay.

Figure 18. β ˉ decay.

Figure 19. Neutron.

Figure 19. Neutron.

Figure 20. Proton.

Figure 20. Proton.

Figure 21. Vector diagram of the neutron in black and vector diagram of the proton in red.

Figure 21. Vector diagram of the neutron in black and vector diagram of the proton in red.

We are going to develop the vector diagrams of the neutron and the proton, considering the interactions 1 & 2, let's divide them into parts to facilitate vector interpretation.

Figure 22. Vector diagram of the interactions in βˉ decay, Neutron → Proton: R(DD)R & R(DD)R, B(DD)B & B(DD)B, G(UU)G & G(UU)G, B(DD)R & B(UD)R and B(DU)G & B(UU)G.

Figure 22. Vector diagram of the interactions in βˉ decay, Neutron → Proton: R(DD)R & R(DD)R, B(DD)B & B(DD)B, G(UU)G & G(UU)G, B(DD)R & B(UD)R and B(DU)G & B(UU)G.

Figure 23. Vector diagram of the interactions in βˉ decay, Neutron → Proton: R(DD)B & R(DU)B, R(DU)G & R(DU)G, G(UD)R & G(UD)R and G(UD)B & G(UU)B.

Figure 23. Vector diagram of the interactions in βˉ decay, Neutron → Proton: R(DD)B & R(DU)B, R(DU)G & R(DU)G, G(UD)R & G(UD)R and G(UD)B & G(UU)B.

Analysing the interactions, we have:

Figure 24. interactions βˉ, neutron → proton.

Figure 24. interactions βˉ, neutron → proton.

If we look at figure 22 & 23, we have:

E1, E2 and E3; they are vectors that indicate the same direction.

E4 and E5; they are vectors that indicate the same direction.

We are going to assume that E1 and E5 are equal, then we are going to graphically represent E2, E3 and E4.

We know that E4 is equal to D, down quark.

We also know that E2 + E3 = 1.0625 D

Graphically we are going to represent it as follows:

Figure 25. Vector representation of: E2 + E3 + E4 = E.

Figure 25. Vector representation of: E2 + E3 + E4 = E.

E (yellow), corresponds approximately to 0.5 on the graphic scale and this gives a value of 0.29 MeV/c², compared to the value of D = 4.7 MeV/c².

E = 0.29 MeV/c²

To finish, we apply the last conversion factor:

When we apply the conversion factor to calculate the mass involved in interactions 1 & 2 of the proton, we obtained:

Fc = 12.89

Therefore, applying the conversion factor we have:

E = 12.89 x 0.29 MeV/c² = 3.73 MeV/c²

When we apply the conversion factor to calculate the mass involved in interactions 1 & 2 of the neutron, we obtained:

Fc = 10.70

Therefore, applying the conversion factor we have:

E = 10.70 x 0.29 MeV/c² = 3.10 MeV/c²

In this way, we conclude the following:

Taking into account that E = mc²

The energy released in Beta decay corresponds, according to our calculation, to the value between 3.10 MeV and 3.73 MeV

ΔE = 0.63 MeV

Conclusion, in our analysis we calculate that the decay of a neutron into a proton has a Q value that varies between the following values:

Q = Δmc² = 3.10 MeV to 3.73 MeV

Q = (3.10 + ΔE) MeV

Let's compare these values with a typical decay like the one shown in figure 23, bismuth decays into polonium.

$${ }_{83}^{214}\mathit{Bi}\to { }_{84}^{214}\mathit{Po}+{\beta }^{-}+\overline{v_e}+3.26\mathit{MeV}$$

Comparing both decays, we observe that the energy values, Q, are in the order, taking into account that we work with vectors.

Another important conclusion to highlight, the Wˉ boson, is an ideal boson, the result of interactions between quarks, antiquarks and gluons; Phasor diagrams show that the Wˉ boson represents a black box for experimental physicists, that is, we have no way of determining the Wˉ boson through a theory, so we postulate its existence through practical experiments, because that is how it was determined its existence, because in this way we were able to measure it, until now.

Let the experts in this matter analyse carefully and draw the correct conclusions.

5.3.1. Analysis of the Wˉ Boson

Here we are going to hypothesize that the Wˉ boson is the result of the interactions of quarks, antiquarks and gluons when a neutron decays into a proton.

In the following table we are going to quantify these interactions.

Table 5. βˉ decay and the calculation of the Wˉ boson.

Table 5. βˉ decay and the calculation of the Wˉ boson.

βˉ DECAY
NEUTRO N	PROTO N	INTERACTI ON	PSF = 12.89 (MeV/c²)	NSF = 10.70 (MeV/c²)
R(DD)R	R(DD)R	E = 0
B(DD)B	B(UU)B	E1	32.18	26.66
G(UU)G	G(UU) G	E = 0
B(DD)R	B(UD)R	E2	32.09	26.66
B(DU)G	B(UU)G	E3	32.09	26.66
R(DD)B	R(DU)B	E4	60.58	50.29
R(DU)G	R(DU) G	E = 0
G(UD)R	G(UD) R	E = 0
G(UD)B	G(UU)B	E5	32.18	26.66
			193.04	160.3
			Δ MeV/ c² = 160.3 + 33.01 = 193.04

If we look at table 5, the vectors E1, E2, E3, E4 and E5; represent the interactions that occur in βˉ decay.

The value of the total interaction is of the order of:

ΔMeV/c² = 160.3 + 33.01 = 193.04 MeV/c²;

However, E1 is equal to E5:

E1 = E5

The mass or energy of E1 cancels with the mass or energy of E5

The second interaction that we are going to analyse is the following:

E2+E3 ≈ E4

(64.18 + 53.32) ≈ (60.58 + 50.29)

The net resulting energy will be:

E2 + E3 = (53.32 + 10.86) MeV/c²

E4 = (50.29 + 10.29) MeV/c²

En = (3.03 + 0.57)

En = (3.03+ 0.57) MeV/c²

Taking into account that E = mc²

En = (3.03 + 0.57) MeV

Let's compare with the calculation given above:

Q = Δmc² = 3.10 MeV to 3.73 MeV

Q = (3.10 + 0.63) MeV

To conclude, the total interaction that results from the decay of a neutron into a proton, given by the vectors E1, E2, E3, E4 and E5 is:

ΔMeV/c² = 160.3 + 33.01 = 193.04 MeV/c²

Taking into account that E = mc²

ΔMeV´ = 160.3 + 33.01 = 193.04 MeV

However, there are vectors that cancel each other, that is, the net interaction resulting in the decay of the neutron into a proton is given by:

En = (3.03+ 0.57) MeV/c²

En´ = (3.03+ 0.57) MeV

which is an approximate calculation given by:

Q = (3.10 + ΔE) MeV/c²

Q´ = (3.10 + ΔE) MeV

According to our calculation, the mass of the Wˉ boson calculated in the decay of the neutral into a proton using the theory of quantum electrical modelling of a neutron and proton as a three-phase alternating current generator, is of the order 0.0001 of the maximum value of the Wˉ, 80.3 GeV/c².

Figure 26. βˉ decay.

Figure 26. βˉ decay.

If we look at figure 26, in my opinion, it does not represent the interactions of quarks, antiquarks and gluons.

Figure 22 and 23, are much more representative of the quark, antiquark and gluon interactions that occur in βˉ decay.

Generalizing, just as the βˉ decay, represented by figure 22 and 23, is the result of interactions between quarks, antiquarks and gluons, in other words, the Wˉ boson is an ideal boson, it would represent a black box, given the impossibility of a physical-mathematical definition that would describe such an interaction. We could extrapolate this for the W⁺ bosons and Z bosons, they are ideal bosons, they are the result of quark, antiquark and gluon interactions.

The βˉ decay described in the paper: Electrical-Quantum Modelling of the Neutron and Proton as a Three-Phase Alternating Current Electrical Generator. Determination of the Number of Quarks-Antiquarks-Gluons and Gravitons, inside a Neutron [1], is the first theory that proposes a vector model to describe the quarks, antiquarks and gluons interactions that occur in βˉ decay. It is important to emphasize that the electroweak field theory (QED) is simplified and transformed into an electric field theory (EQFT). The EQFT theory is an alternative and complementary theory to the QED theory.

5.3.2. Fine Structure Constant

Using the βˉ decay, we will determine the origin and meaning of the fine structure constant

If we look at figure 22 & 23, we have:

E1, E2 and E3; they are vectors that indicate the same direction.

E4 and E5; they are vectors that indicate the same direction.

We are going to assume that E1 and E5 are equal, then we are going to graphically represent E2, E3 and E4.

We know that E4 is equal to D.

We also know that E2 + E3 = 1.0625 D

E (yellow, figure 25), corresponds approximately to 0.5 on the graphic scale.

Normalizing, we divide 0.5 cm by 1.0625 cm, this gives us:

Fn = 0.5 cm / 1.0625 = 0.47, dimensionless

We divide the normalization factor Fn by the neutron scaling factor NSF, we have:

Fn / NSF = 0.47 / 10.70 = 0.04392

Fn / NSF = 0.04392

We divide the normalization factor Fn by the proton scaling factor PSF, we have:

Fn / PSF = 0.47 / 12.89 = 0.03646

Fn / PSF = 0.03646

We subtract (Fn / NSF) minus (Fn / PSF), we have:

(Fn / NSF) – (Fn / PSF) = 0.0074

We call this result the fine structure constant

α´ = 0.0074, calculated fine structure constant

1/ α´ = 135.13

α = 0.0073, theoretical fine structure constant

1/α = 137

We are going to calculate the difference in %:

% = ((137 – 135.13) / 137) x 100 = 1.36

% = 1.36

Our calculations differ 1.36% from the theoretical value, not bad if we consider that we work with vectors.

We have determined how the fine structure constant originates, now we are going to try to explain its true meaning.

In βˉ decay the following occurs:

Neutron -> proton + eˉ + ṽ + ΔE

However, we must remember that there is a coupling energy between the proton and the electron that allows the electron to rotate in a stable orbit around the proton.

In reality, they are two stable orbits, as is a difference in energy, one orbit corresponds to the minimum energy and the other orbit corresponds to the maximum energy.

The difference between the two orbits is what determines the fine structure constant.

When the electron is in one orbit and jumps to the second orbit it emits a photon, and if it returns to the original orbit, it absorbs a photo, that difference between the energy levels of the orbitals is what is known as fine structure, that distance is a multiple of a certain number given by the following equation:

α = e²/ 4 π ε h c, fine structure constant

Electrons move within regions called orbitals. In each of these, up to a maximum of two electrons can be located. With this in mind, the table tells us that there are energy levels starting at n=1 and advancing one at a time. Also, if we look at the columns, we will see that there are four groups. The s, p, d and f orbitals. We have one s orbital per level, three p orbitals, five d orbitals and seven f orbitals. Some levels have this collection incomplete while others have it complete. All this information is summarized in the table 6.

So, atoms can have at most as many electrons as fit in the energy levels they occupy. For hydrogen, this would be two, since this element has only one s orbital available to accommodate its electrons.

Table 6. atomic orbitals.

Table 6. atomic orbitals.

5.4. Analysis of the Proposed Models for the Photon

First analysis:

Figure 27. Physical model of photon.

Figure 27. Physical model of photon.

Figure 28. Feynmann diagram, (a) emission of a photon by an electron (b) absorption of a photon by an electron.

Figure 28. Feynmann diagram, (a) emission of a photon by an electron (b) absorption of a photon by an electron.

In figure 28, we see the Feynmann diagram of an electron that absorbs (b) or emits (a) a photon. The electron has a negative charge (-), therefore for this condition we propose for the photon `` the physical model of photon 3´´, which adjusts to the negative charge of the electron.

Second analysis:

Figure 29. (c) emission of a photon by a positron (d) absorption of a photon by a positron.

Figure 29. (c) emission of a photon by a positron (d) absorption of a photon by a positron.

In figure 29, we see the Feynmann diagram of a positron that absorbs (d) or emits (c) a photon. The positron has a negative charge (+), therefore for this condition we propose for the photon `` the physical model of photon 1´´, which adjusts to the positive charge of the positron.

Third analysis:

Figure 30. Feynmann diagram, (e) a photon creates an electron and positron, (f) an electron and a positron create a photon.

Figure 30. Feynmann diagram, (e) a photon creates an electron and positron, (f) an electron and a positron create a photon.

In figure 30, it is observed (e) a photon creates an electron and positron, (f) an electron and a positron create a photon, therefore, for these conditions we propose for the photon ``physical model of photon 2´´, which adjusts to the positive charge of the positron and the negative charge of the electron.

Let us remember that the photon has the following characteristics:

Mass = 0

Electric charge = 0

Spin = 1

All these conditions are met in the models proposed for the photon in Figure 26.

It is also important to remember that space-time depends on temperature, the higher the temperature, the greater the curvature of the space-time fabric.

Taking into account the statement, just as neutrinos with a temperature of the order of 2.55 10⁴ K, a mass of the order of 3.92 10ˉ³⁶ Kg, have a gravitational force similar to that of the Earth, we can be certain that as the temperature increases, photons are also affected by the curvature of space-time, as is the case with all elementary particles.

At low temperatures, photons move at the speed of light and their mass is negligible. As the temperature increases, the curvature of space-time affects the photons, slowing them down relative to the speed of light and increasing their mass.

We can propose for x-rays and gamma rays, high-energy photons, traveling at a speed slightly lower than the speed of light c = 3 10⁸ m/s.

We can state it another way, in our theory quantum electric modelling of the neutron and proton as a three-phase alternating current electric generator, photons are a particular case of gluons. Just as the mass of neutrons and protons is given by gluons, at high energies 10¹² K; It is to be expected that at high energies photons also acquire mass, in the same way that gluons do inside protons and neutrons.

5.5. Analysis of the Proposed Models for the Gluons

When we develop the electrical model of a proton and neutron as a three-phase alternating current electrical generator, we observe that photons are a particular case of gluons.

Let us remember that the gluon has the following characteristics:

Mass = 0

Electric charge = 0

Colour charge = yes

Spin = 1

Figure 31. Physical model of gluons.

Figure 31. Physical model of gluons.

Figure 32. Proton.

Figure 32. Proton.

Figure 33. Cross-gluon interaction in a proton.

Figure 33. Cross-gluon interaction in a proton.

If we look at interaction 2 in Figure 32 and 33, we see that the main difference between gluons and photons is that in some gluons the interaction is carried out with the same frequency, while in other gluons the interaction is carried out with different frequencies. In photons, the interaction always takes place with the same frequency.

If we look at figure 32, the interaction 1 of gluons always takes place at the same frequency.

It is for this reason that we say that photons are a particular case of gluons.

We are going to represent the gluons for the interaction 1 and 2, in the proton:

Interaction 1:

Figure 34. Interaction 1, The interaction of gluons takes place at the same frequency.

Figure 34. Interaction 1, The interaction of gluons takes place at the same frequency.

Let's analyse figure 32:

The RR gluon exchange takes place at the D-quark frequency.

The BB gluon exchange takes place at the U quark frequency.

The GG gluon exchange takes place at the U quark frequency.

RR gluons have a different frequency from BB and GG gluons.

The exchange of RB, RG, BR and GR gluons is carried out with different frequencies.

The exchange of BG and GB gluons occurs with the same frequency.

Interaction 2:

Figure 35. Interaction 2, The interaction of gluons takes place at different frequencies: RB, RG and BR.

Figure 35. Interaction 2, The interaction of gluons takes place at different frequencies: RB, RG and BR.

Figure 36. Interaction 2, The interaction of gluons takes place at different frequencies: GR and at the same frequency: BG and GB.

Figure 36. Interaction 2, The interaction of gluons takes place at different frequencies: GR and at the same frequency: BG and GB.

5.6. We Will Demonstrate the Existence of a Force Tangential to the Repulsive Force in Subatomic Disintegrations, This Force Advances the Repulsive Force by 90 Degrees

We will analyse the following equation:

E² = m²c⁴ + P²c²

where E is energy, m is mass, and c is the speed of light in a vacuum.

If we consider 0 the moment P of a particle, P = 0, we have:

E² = m²c⁴

E = (+/-) mc²

If we consider mass as a fundamental property of matter we have:

E = + mc², positive energy, (+ m), gravitational attraction

E = - mc², negative energy (- m), gravitational repulsion

According to the equation E = (+/-) mc², we have that gravity acts in two ways, (+m) as an attractive force or (-m) as a repulsive force.

METRIC FOR TIME TYPE TRAJECTORIES.

Figure 37. Time-like trajectory, light cone, ds < 0.

Figure 37. Time-like trajectory, light cone, ds < 0.

Let's write the metric:

$$d\tau ²=dt²-(dx/c²+dy/c²+dz/c²)>0$$

This metric is defined for speeds less than light, v < c.

We skip the mathematical steps and with this metric we calculate the moment P and the energy E.

$$\begin{gathered} P=mv/\surd (1-\left(\frac{v^2}{c^2}\right)),moment of aparticle. \\ E=mc²/\surd (1-\left(\frac{v^2}{c^2}\right)),energy of aparticle. \end{gathered}$$

If we analyse the energy, we see that when the particle is at rest the energy corresponds to E = mc²; when the speed tends to c, the energy tends to infinity.

v = 0, E = mc²

v → c, E → ∞

Now we are going to perform the following mathematical trick, although the metric does not allow us to do this because it is not defined for speeds greater than light, v > c, we are going to see the consequences of the following mathematical operation.

E = mc² / √-1 √(v²/c²) – 1

multiplying the numerator and denominator by the imaginary number i:

$$E=-imc²/\left(\sqrt{\left(\frac{v^2}{c^2}\right)–1}\right)$$

we see that the terms – i appear.

If we compare with the mass of a black hole:

$M=m-i\delta$

m, baryonic mass.

$-imc²/\left(\sqrt{\left(\frac{v^2}{c^2}\right)–1}\right)$ = $-i\delta$, for v > c; mass of dark matter.

How can we interpret this, what meaning does it have?

Although the metric we use is not defined for particles that move at a speed greater than that of light, there are massless, tachyonic particles that can cross this barrier and travel at a speed greater than that of light.

These tachyonic particles produce a tangential force Ft to the attractive force Fc of gravity and as the speed increases with respect to the speed of light, they generate dark matter. It must be made clear that these particles are inside the black hole.

METRIC FOR SPACE TYPE TRAJECTORIES

Figure 38. Space-like trajectory, light cone, ds > 0.

Figure 38. Space-like trajectory, light cone, ds > 0.

Let's write the metric:

$$d\tau ²=-dt²+(dx/c²+dy/c²+dz/c²)<0$$

We skip the mathematical steps and with this metric we calculate the moment P and the energy E.

$$P=-mv/\surd (v²/c²)–1$$

$$E=-mc²/\surd (v²/c²)–1$$

These equations for momentum P and energy E are valid for speeds greater than light and can never reach speeds of light.

v → ∞, E = 0

v → c, E = -∞

How can we interpret this, what does it mean?

We are going to relate the equations of P and E with the electrical model RLC of the universe, at the moment that the black hole explodes, let us remember that the space-time that was compressed begins to expand and generates a well of gravitational potential of negative energy analogous to the equation E = - mc² / √(v²/c²) – 1, in other words, a spectrum of gravitational waves is produced that produce a repulsive force that gives rise to the expansion of space-time. In this case, tachyons are related to gravitons and particles of elemental energy, in which, during the period of cosmic inflation, they travel at a speed greater than that of light.

Now we are going to perform the following mathematical trick, although the metric does not allow us to do this because it is not defined for speeds less than light, v < c, we are going to see what happens if a particle exceeds the limit for speeds less than c.

E = - mc² / √(v²/c²) – 1

E = - mc² / √-1 √ (1 - v²/c²)

Multiplying and dividing by the imaginary number i.

$$E=imc²/(\surd (1-(v²/c²))$$

If we compare with the mass of a black hole:

$$M=m-i\delta$$

m, baryonic mass.

$$-M=-m+i\delta$$

$$imc²/\surd (1-v²/c²)=i\delta$$

where M represents the total mass, the minus sign indicates that the mass M generates a repulsive force, - m represents the baryonic mass, the minus sign indicates that the mass m generates a repulsive force and iδ is a mass that generates a tangential force the force generated by the mass - m and advance 90 degrees to the force generated by the mass - m.

The subatomic disintegrations that occur in particle accelerators represent a clear example.

Here we put forward the hypothesis that, for v < c, there is an additional force that corresponds to the mass iδ that leads 90 degrees to the force given by the mass - m, in other words, when the subatomic disintegration of particles occurs, two forces act, a repulsive force given by the mass - m and a tangential force that leads 90 degrees to the force given by - m, resulting from the mass iδ.

In the following tables we will define the statement.

Table 7. From left to right represented by the numbers 1,2 and 3; We describe the forces that act on matter. In phase 1, for v < c, only an attractive force acts; in phase 2, for v = c, only an attractive force acts; in phase 3, for v > c, inside a black hole, we can see that two forces act, an attractive force and a tangential force that delays the attractive force by 90 degrees.

Table 7. From left to right represented by the numbers 1,2 and 3; We describe the forces that act on matter. In phase 1, for v < c, only an attractive force acts; in phase 2, for v = c, only an attractive force acts; in phase 3, for v > c, inside a black hole, we can see that two forces act, an attractive force and a tangential force that delays the attractive force by 90 degrees.

TIME TYPE PATH	LIGHT TYPE PATH	SPACE TYPE PATH
1	2	3
ds < 0	ds = 0	ds > 0
v < c	v = c	v > c
$m$	$m$	$M=m-i\delta$
attraction	attraction	attraction
Lp = Lpɛ	Lpɢ = Lpɛ = Lp	Lpɢ < Lpɛ
E = $m$ c² / √1 - (v²/c²)	Phase change	E = - i $\delta$ c² / √(v²/c²) – 1

Table 8. From right to left, represented by the numbers 1,2 and 3, we will describe the forces that act on matter. In phase 1, for v > c, we see that a repulsive force acts, in phase 2, for v = c, we see that a repulsive force acts; in phase 3, for v < c, we see that two forces act, a repulsive force and a tangential force that leads the repulsive force by 90 degrees.

Table 8. From right to left, represented by the numbers 1,2 and 3, we will describe the forces that act on matter. In phase 1, for v > c, we see that a repulsive force acts, in phase 2, for v = c, we see that a repulsive force acts; in phase 3, for v < c, we see that two forces act, a repulsive force and a tangential force that leads the repulsive force by 90 degrees.

TIME TYPE PATH	LIGHT TYPE PATH	SPACE TYPE PATH
3	2	1
ds < 0	ds = 0	ds > 0
v < c	v = c	v > c
$-M=-m+i\delta$	$-m$	$-m$
Repulsion	Repulsion	Repulsion
Lp = Lpɛ	Lpɢ = Lpɛ = Lp	Lpɢ < Lpɛ
E = $i\delta$ c² / √1 - (v²/c²)	Phase change	E = - m c² / √(v²/c²) – 1

Figure 39. Diagram of forces that act in the disintegration of subatomic particles.

Figure 39. Diagram of forces that act in the disintegration of subatomic particles.

In conclusion, two forces act inside a black hole, a force of attraction towards the interior of the black hole and a tangent or torsion force that delays the force of attraction by 90 degrees. Two forces also act in the disintegration of elementary particles, a repulsion force and a tangential or torsion force that advances the repulsion force by 90 degrees.

5.8. Generalization of the ADS/CFT Correspondence

In theoretical physics, the ADS/CFT correspondence is a conjectured relationship between two kinds of physical theories. On one side are anti-de Sitter spaces (ADS) which are used in theories of quantum gravity, formulated in terms of string theory or M-theory. On the other side of the correspondence are conformal field theories (CFT) which are quantum field theories, including theories similar to the Yang–Mills theories that describe elementary particles.

It also provides a powerful toolkit for studying strongly coupled quantum field theories. Much of the usefulness of the duality results from the fact that it is a strong–weak duality: when the fields of the quantum field theory are strongly interacting, the ones in the gravitational theory are weakly interacting and thus more mathematically tractable. This fact has been used to study many aspects of nuclear and condensed matter physics by translating problems in those subjects into more mathematically tractable problems in string theory.

Quantum gravity is the branch of physics that seeks to describe gravity using the principles of quantum mechanics. Currently, a popular approach to quantum gravity is string theory, which models elementary particles not as zero-dimensional points but as one-dimensional objects called strings. In the ADS/CFT correspondence, one typically considers theories of quantum gravity derived from string theory or its modern extension, M-theory.

The application of quantum mechanics to physical objects such as the electromagnetic field, which are extended in space and time, is known as quantum field theory. In particle physics, quantum field theories form the basis for our understanding of elementary particles, which are modelled as excitations in the fundamental fields. Quantum field theories are also used throughout condensed matter physics to model particle-like objects called quasiparticles.

In the ADS/CFT correspondence, one considers, in addition to a theory of quantum gravity, a certain kind of quantum field theory called a conformal field theory. This is a particularly symmetric and mathematically well-behaved type of quantum field theory. Such theories are often studied in the context of string theory, where they are associated with the surface swept out by a string propagating through spacetime, and in statistical mechanics, where they model systems at a thermodynamic critical point.

5.8.1. Quantization of Space-Time (DST) and Matter (EQFT)

DST, Dynamic space-time with quantum gravity, with negative, positive and flat curvature.

EQFT, Electrical Quantum field theory is a generalization of conformal quantum field theories, this theory is the result of uniting the field theory of electromagnetic interactions, the field theory of weak interactions and the field theory of strong interactions in a single field theory of electrical interactions.

In order to carry out the quantization of matter and space-time, we are going to need the following table:

Table 9. Represents values of ImI, baryonic mass; IδI, dark matter mass; IMI, mass of baryonic matter plus the mass of dark matter; IEmI, energy of baryonic matter; IEδI, dark matter energy; IEI, Sum of the energy of baryonic matter plus the energy of dark matter and Rs, Schwarzschild´s radius, as a function of, c, speed of light; Cɢ, speed greater than the speed of light; T, temperature in Kelvin; using the parametric equations.

Table 9. Represents values of ImI, baryonic mass; IδI, dark matter mass; IMI, mass of baryonic matter plus the mass of dark matter; IEmI, energy of baryonic matter; IEδI, dark matter energy; IEI, Sum of the energy of baryonic matter plus the energy of dark matter and Rs, Schwarzschild´s radius, as a function of, c, speed of light; Cɢ, speed greater than the speed of light; T, temperature in Kelvin; using the parametric equations.

Planck´s length equation:

$$Lp=\surd (hG/C³)$$

(19)

If we look at table 9, we see that Cɢ varies between the following limits:

10⁸ m/s < Cɢ < 3 10²¹ m/s

(20)

Replacing (20) into (19), we have:

Cɢ = 3 x 10⁸ m/s to 3 x 10²¹ m/s

Lp = 1.61 10⁻³⁵ m to 1.28 10⁻⁵⁴ m

To quantify gravity, we will use the principle of minimal action:

The action we call S has the following dimensions:

S = {M} x {T} x C², C = L/T

S = Energy involved in a process x Time the process lasts

S = {M} x {L} x C, C speed of light.

S = momentum x spatial size

Now we ask ourselves, what is the minimum value of the action?

Quantum mechanics postulates that there is a minimum value for the action and it is defined by h (Planck's constant) and is non-zero. If we consider S = h, we have:

Lg = h / (M x C), we call this length quantum size, minimum gravitational length.

This tells us that a mass M cannot be located in a region smaller than Lg.

Let's calculate the quantum size Lg:

For a black hole of 3 solar masses, 6 10³⁰ kg, we have:

Lg = 6.63 10⁻³⁴ / 6 10³⁰ x 3 10⁸ = 6.63 10⁻³⁴ / 18 10³⁸

Lg = 0.368 10⁻⁷²

Lg = 3.68 10⁻⁷³ m

For a black hole of 1.20 10⁸² kg, we have:

Lg = h / M x C

Lg = 6.63 10⁻³⁴ / 1.20 10⁸² x 3 10⁸

Lg = 6.63 10⁻³⁴ / 3.6 10⁹⁰ = 1.84 10⁻¹²⁴

Lg = 1.84 10⁻¹²⁴ m

Taking into account the calculations just carried out and the values in table 5, we generate the following table:

Table 10. represents the quantization of matter Lp and the quantization of space-time Lg.

Table 10. represents the quantization of matter Lp and the quantization of space-time Lg.

According to calculations, in a black hole we see that the quantization of space-time is different from the quantization of matter and varies as the black hole grows.

We can also infer that column 1 would correspond to the quantization of matter and space-time outside a black hole, in the domain of the 4 fundamental forces.

Inside a black hole the following is true:

The quantization values of the matter would vary in the following range:

1.61 10⁻³⁵ m to 1.27 10⁻⁵⁴ m

(21)

The space-time quantization values would vary in the following range:

3.68 10⁻⁷³m to 1.84 10⁻¹²⁴ m

(22)

Comments:

When we talk about quantizing matter, we mean that ordinary matter as we know it needs a minimum space-time that is given by the Planck length Lp, which is different from Lg, which represents the quantization value of the space-time. The Planck length, Lp, determines the limiting space in which matter below this value becomes a black hole, that is, it loses the properties of the electromagnetic force field, the weak and strong force field.

Lp = Lpɛ = 1.61 10⁻³⁵ m, electromagnetic Planck longitude.

Lɢ < Lpɛ

Lɢ = gravitational Planck length.

Lɢ varies from 1.61 10⁻³⁵ m to 1.27 10⁻⁵⁴ m

Lp >> Lg

Lg varies from 3.68 10ˉ⁷³ m to 1.84 10ˉ¹²⁴ m

Up to this point we have shown that the DST space-time is quantized in values of Lg between:

3.68 10ˉ⁷³ m to 1.84 10ˉ¹²⁴ m

We have also shown that the matter/energy, represented by the EQFT quantum fields, are also quantized in values of Lp between:

1.61 10⁻³⁵ m to 1.27 10⁻⁵⁴ m

Now that we have demonstrated that space-time and matter are quantized, in a brief comment we are going to explain the quantization of the curvature of space-time.

5.8.2. Quantization of the Curvature of Space-Time

In the paper: Theory of the Generalization of the Boltzmann’s Constant in Curved Space-Time. Shannon-Boltzmann Gibbs Entropy Relation and the Effective Boltzmann’s Constant [2], we have demonstrated the quantization of the curvature of space-time.

Here, we are going to make a brief summary of the quantization of space-time curvature.

The quantization of the curvature of space-time is carried out through the effective Boltzmann constant.

Let us remember that the effective Boltzmann constant varies between the following limits:

1.38 10⁻²³ J/K > Kв effective > 1.78 10⁻⁴³ J/K

The curvature of space-time is a direct function of temperature, the higher the temperature, the greater the curvature of space-time.

1.38 10⁻²³ J/K => flat space-time

1.38 10⁻²³ J/K > Kв effective > 1.78 10⁻⁴³ J/K => curved space-time

Up to this point, we analyse the quantization of space-time and matter, and in a brief summary, we describe the quantization of the curvature of space-time through the effective Boltzmann constant.

5.8.3. Electrical Modelling of a Neutron as a Three-Phase Alternating Current Generator. Origin of Mass and Gravity

In the paper: Electrical-Quantum Modelling of the Neutron and Proton as a Three-Phase Alternating Current Electrical Generator. Determination of the Number of Quarks-Antiquarks-Gluons and Gravitons, inside a Neutron [1], we have calculated the number of quarks, antiquarks, gluons and gravitons inside a neutron.

Here, we are going to carry out a summary of those calculations, to determine how the mass and gravity in a neutron are originated and quantified.

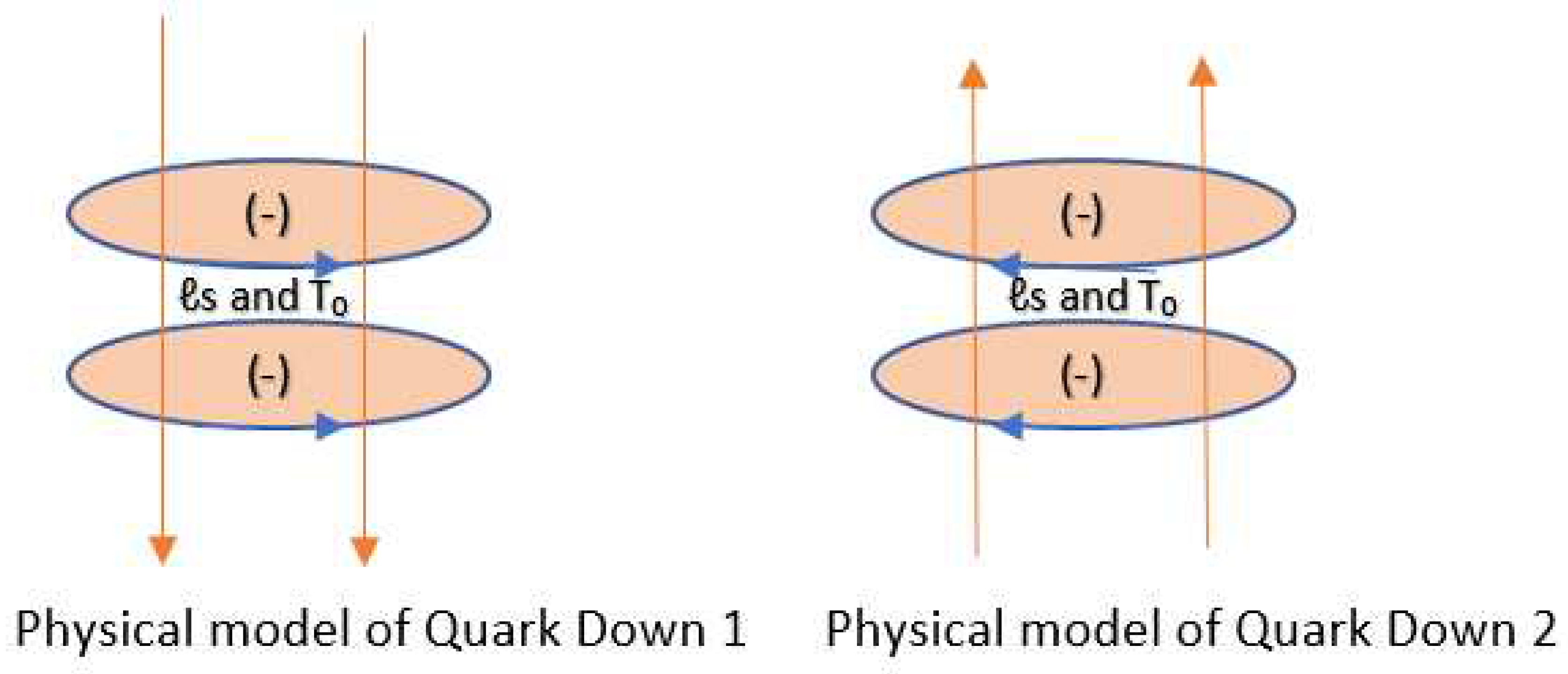
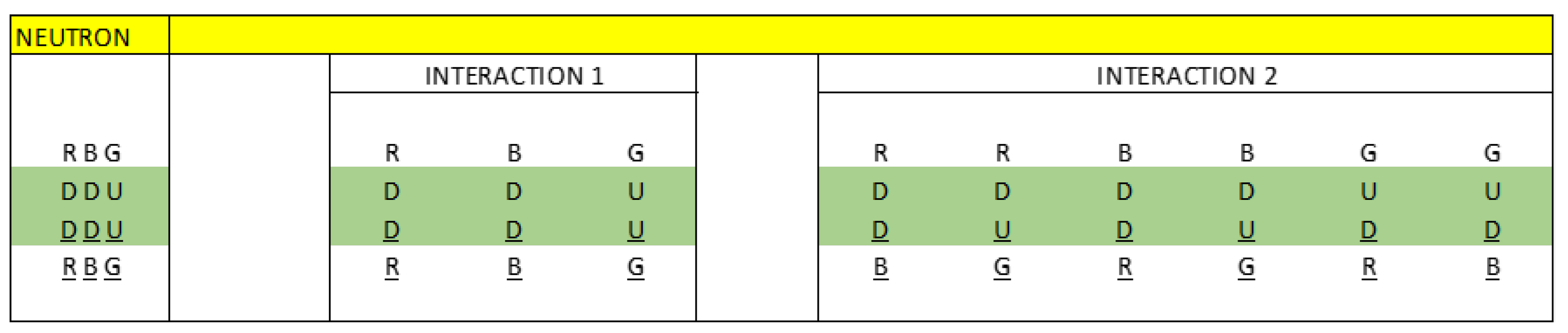
Electrical-Quantum Modelling of the Neutron as a Three-Phase Alternating Current Electrical Generator

Figure 40. Neutron.

Figure 40. Neutron.

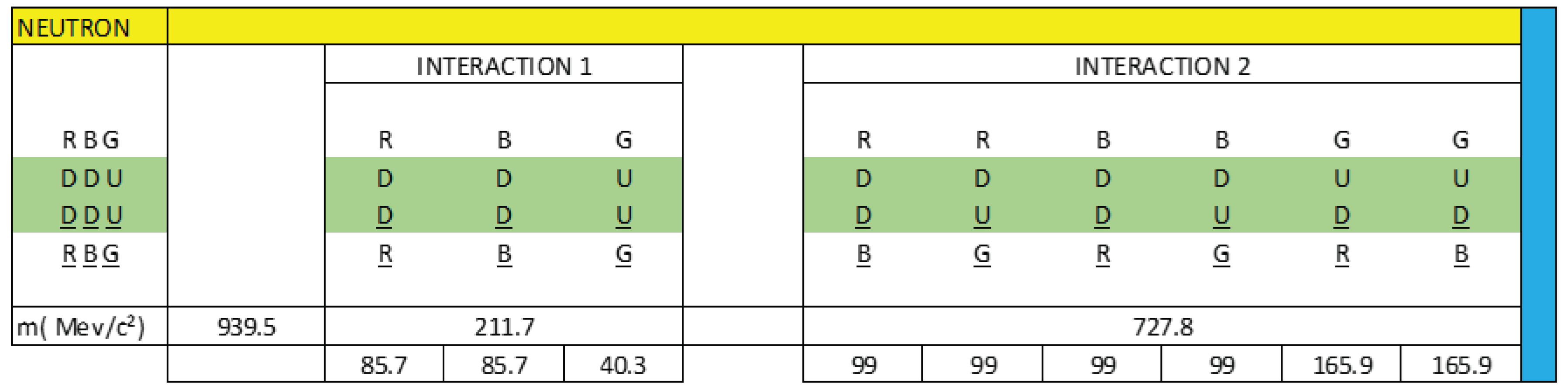
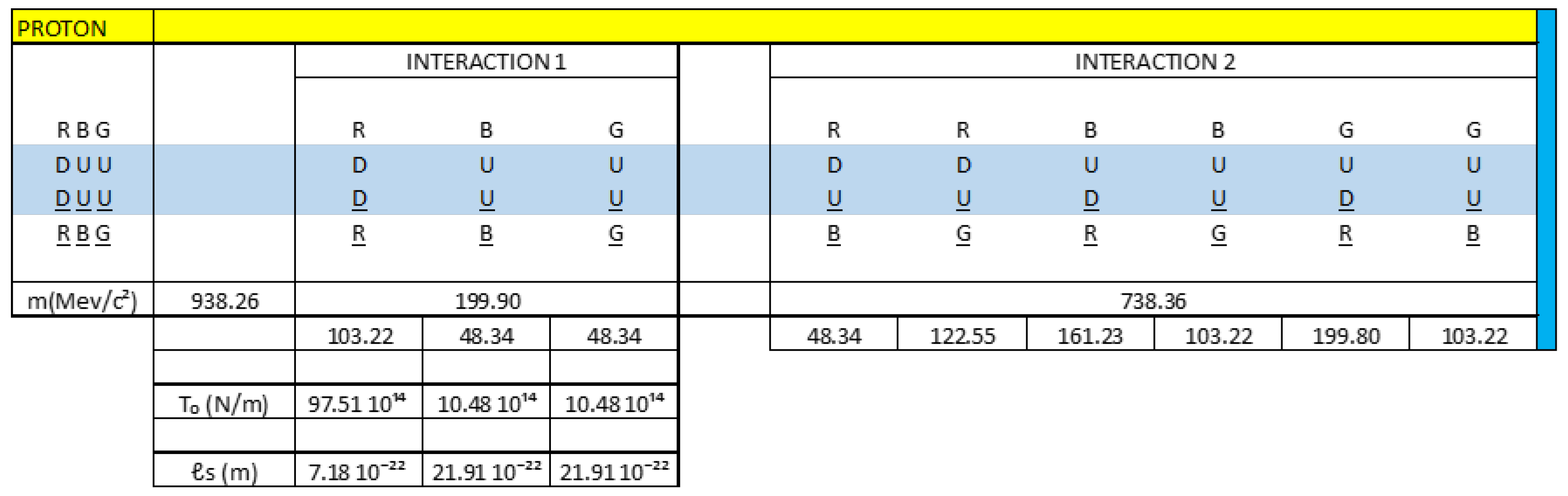
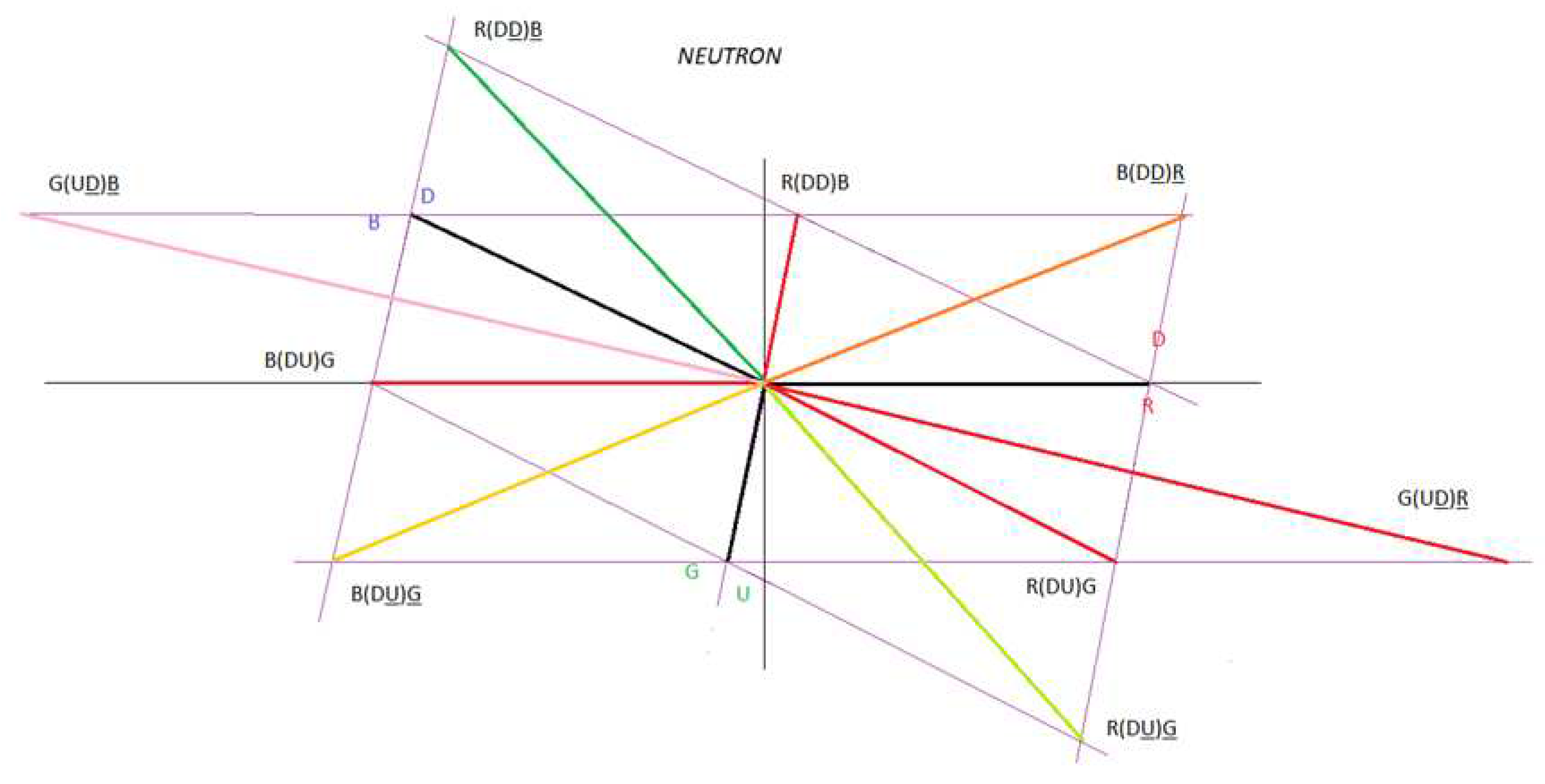
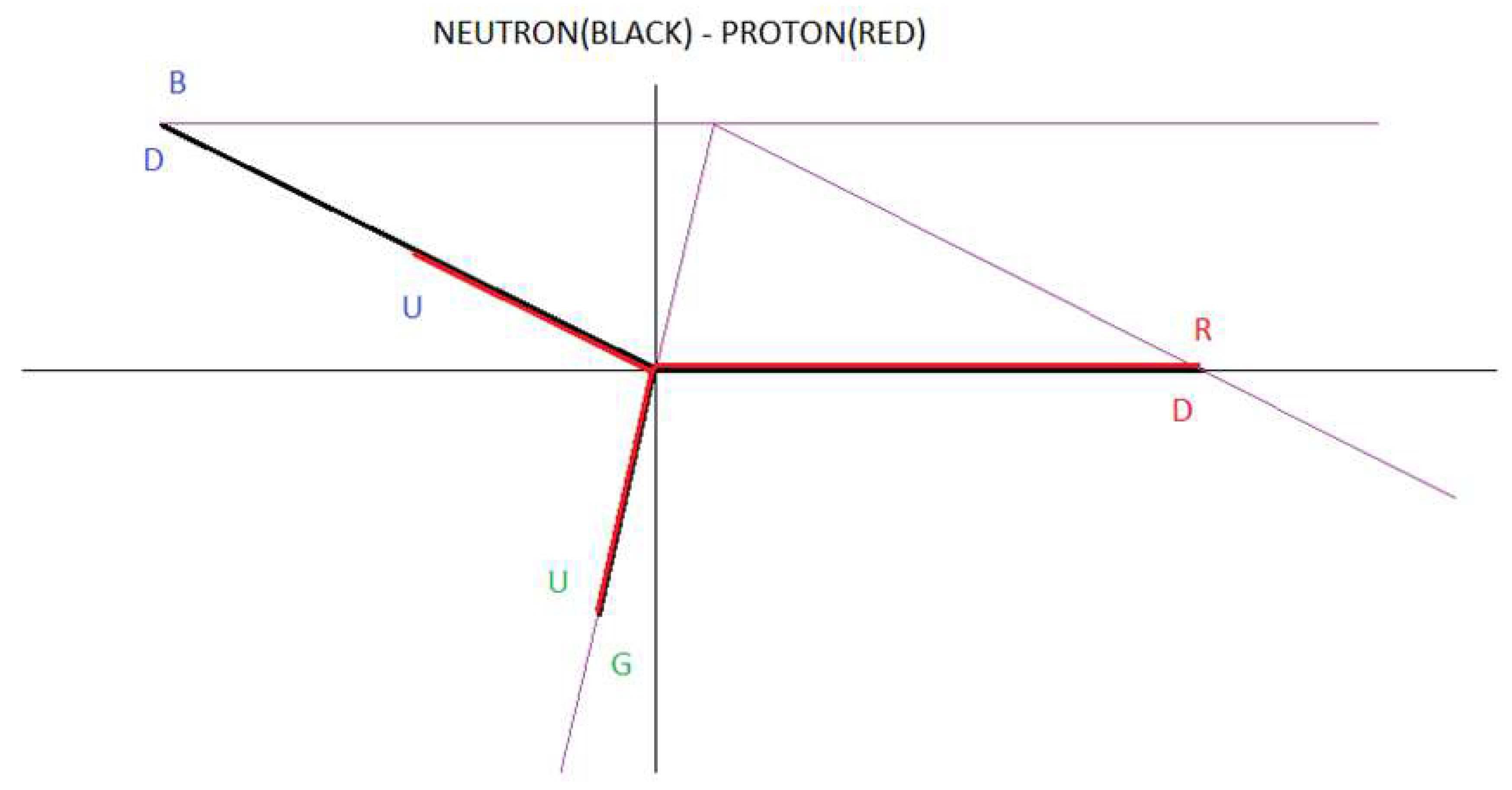
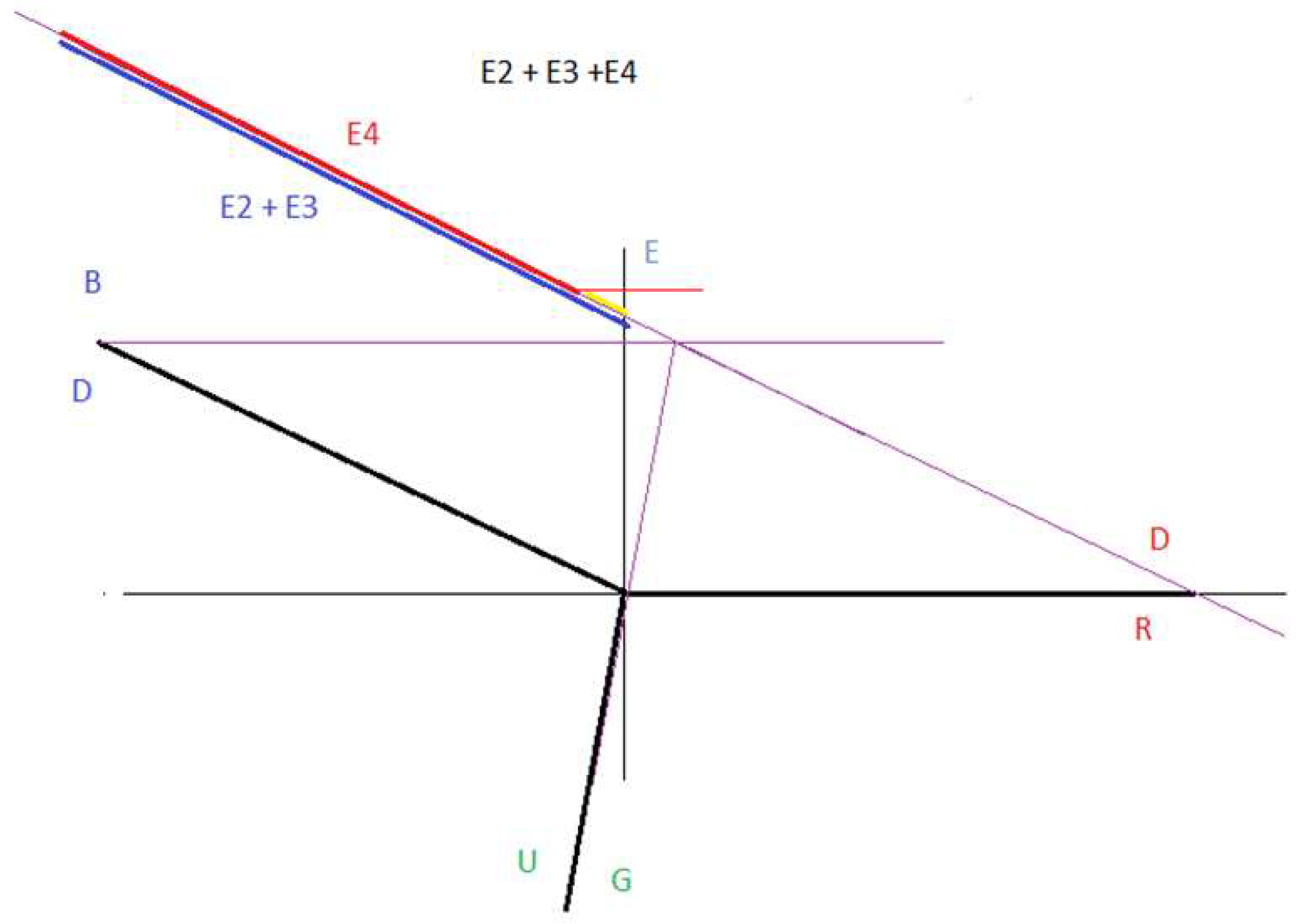
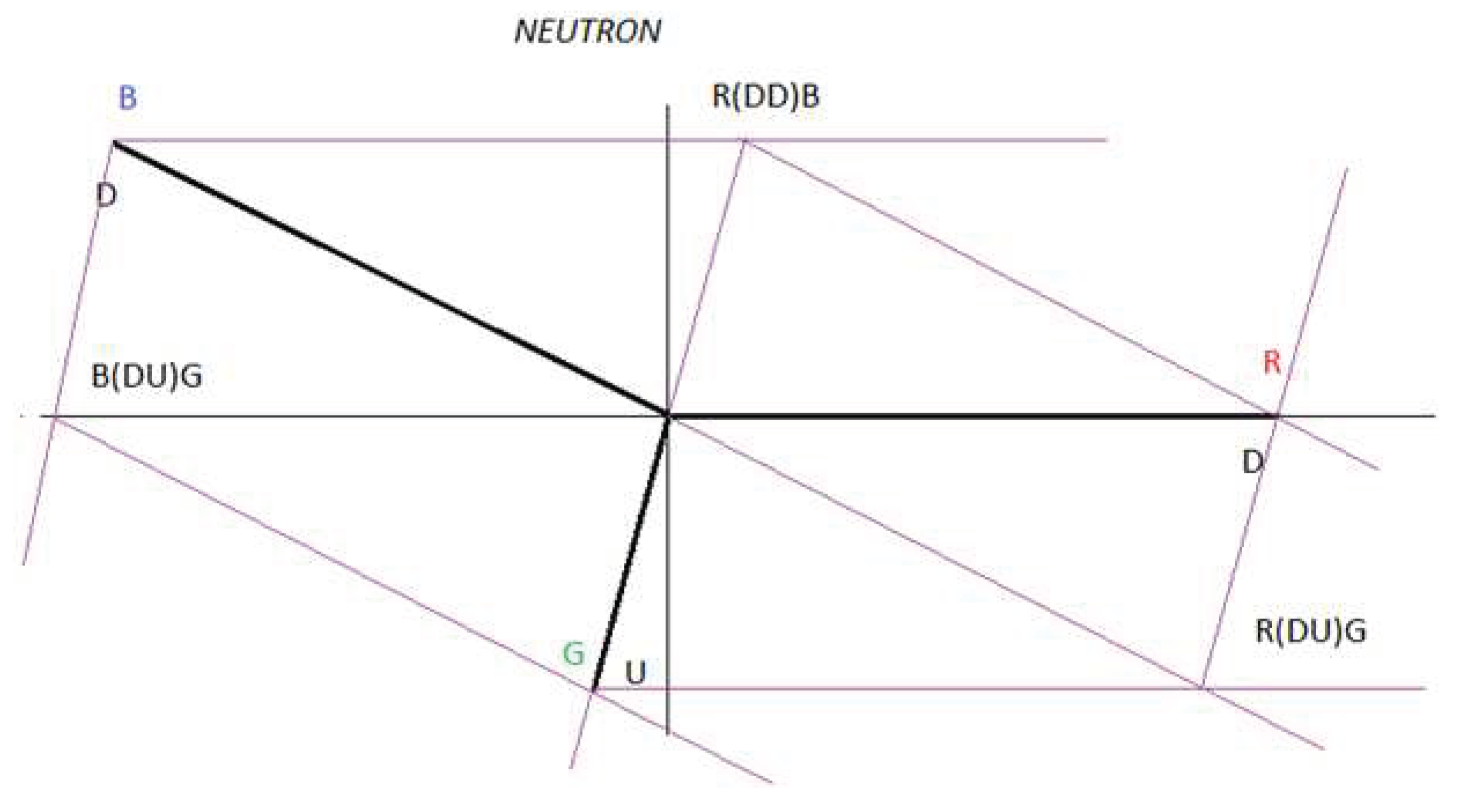
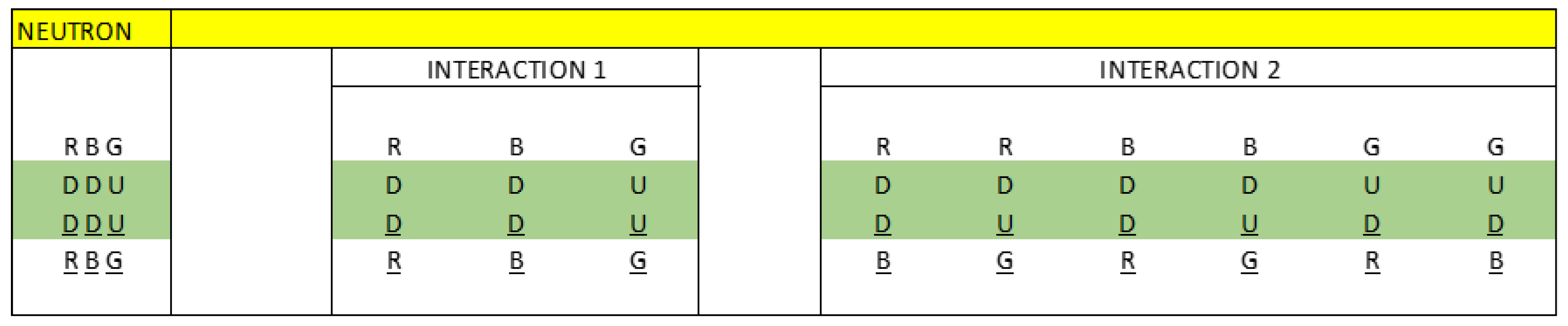
We are going to work with figure 40 to create our electrical model of the neutron as a three-phase alternating current electrical generator.

The dipole DD is analogous to L1 and RR is analogous to the current flowing through L1.

The dipole DD is analogous to L2 and BB is analogous to the current flowing through L2.

The dipole UU is analogous to L3 and GG is analogous to the current flowing through L3.

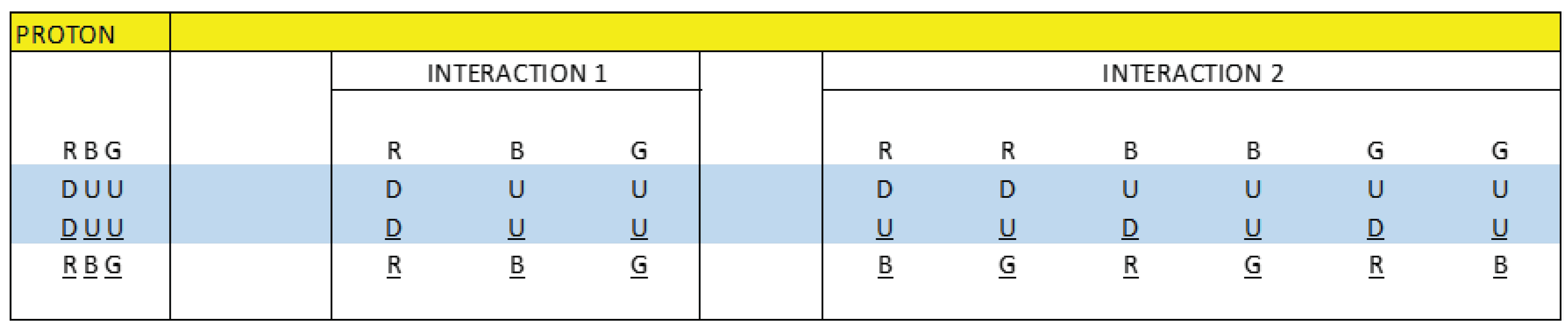
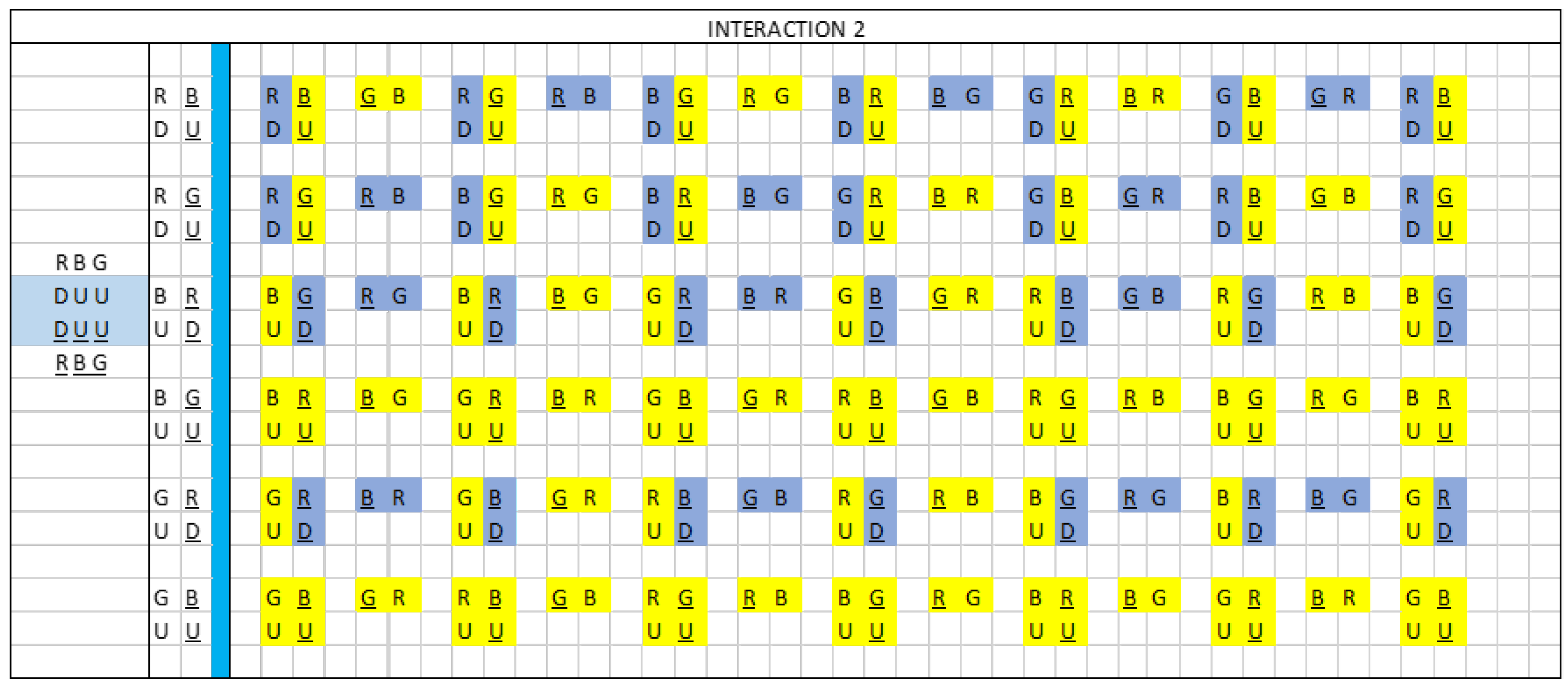
We see that there are two types of interactions.

Interaction 1 or direct interaction and interaction 2 or cross interaction.

We said that down quarks have one frequency and up quarks have another frequency; Thanks to gluons, vector or phasor operations cease to be a problem, making it possible for a quark to transform into another quark, of the same frequency, thanks to the exchange of gluons. It is an amazing mechanism.

In analogy to a three-phase alternating current electric generator, we are going to represent interaction 1 and interaction 2, using vectors whose resulting vector is null. In this way, we are going to simulate a neutron as a three-phase alternating current electrical generator.

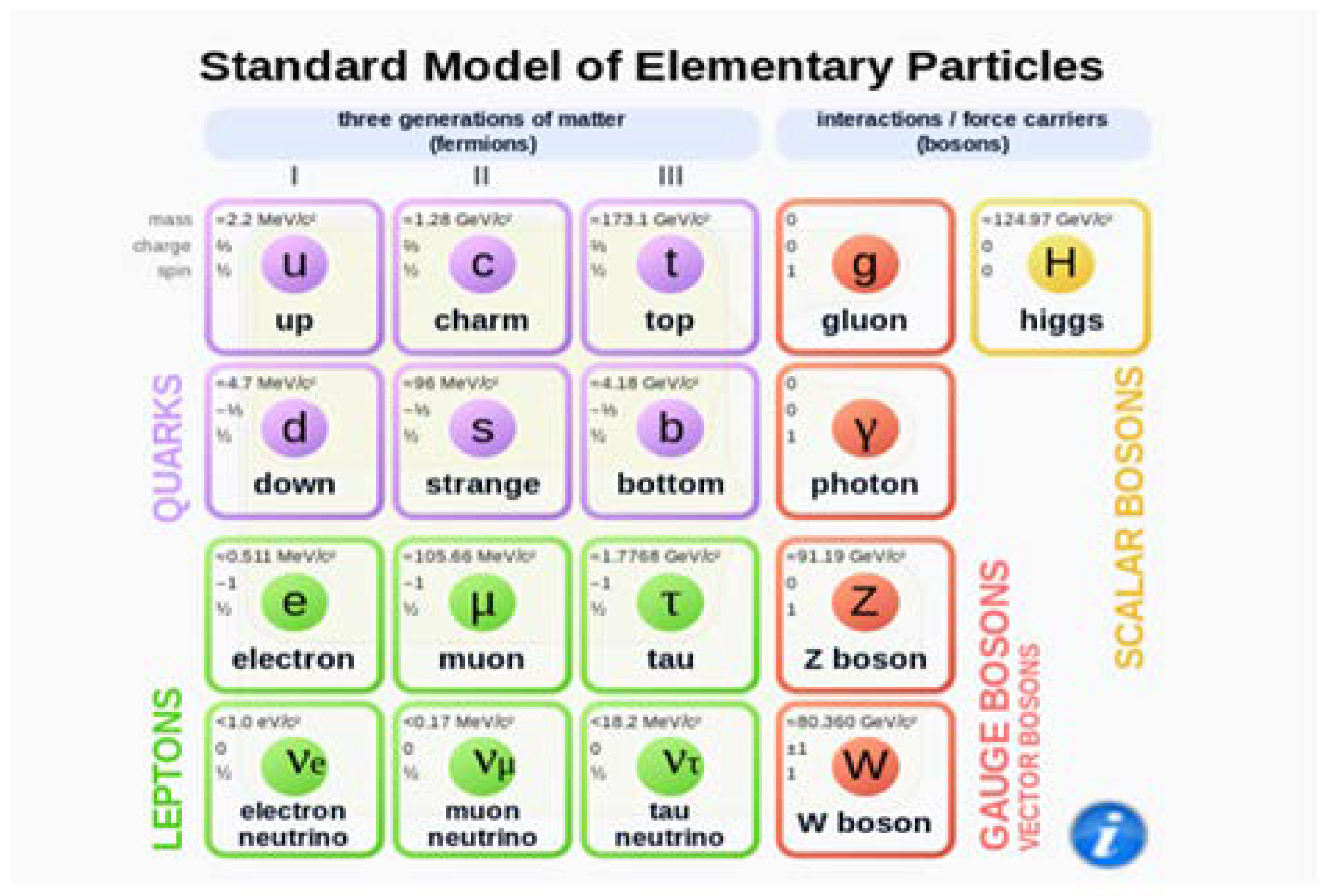
In Figure 3 of the standard model, we see that the up quark has a mass of 2.2 MeV/c² and the down quark has a mass of 4.7 MeV/c².

Taking these values as reference we are going to make our vector diagram of the neutron.

Quark Down = 4.7 MeV/c²

Quark up = 2.2 MeV/c²

It is important to make it clear that all interactions are vector, although we do not represent them as such in the figures.

Figure 41. interaction 1 of the neutron.

Figure 41. interaction 1 of the neutron.

Interaction 1:

If we analyse figure 40, star connection, we see that the following vector sum is null:

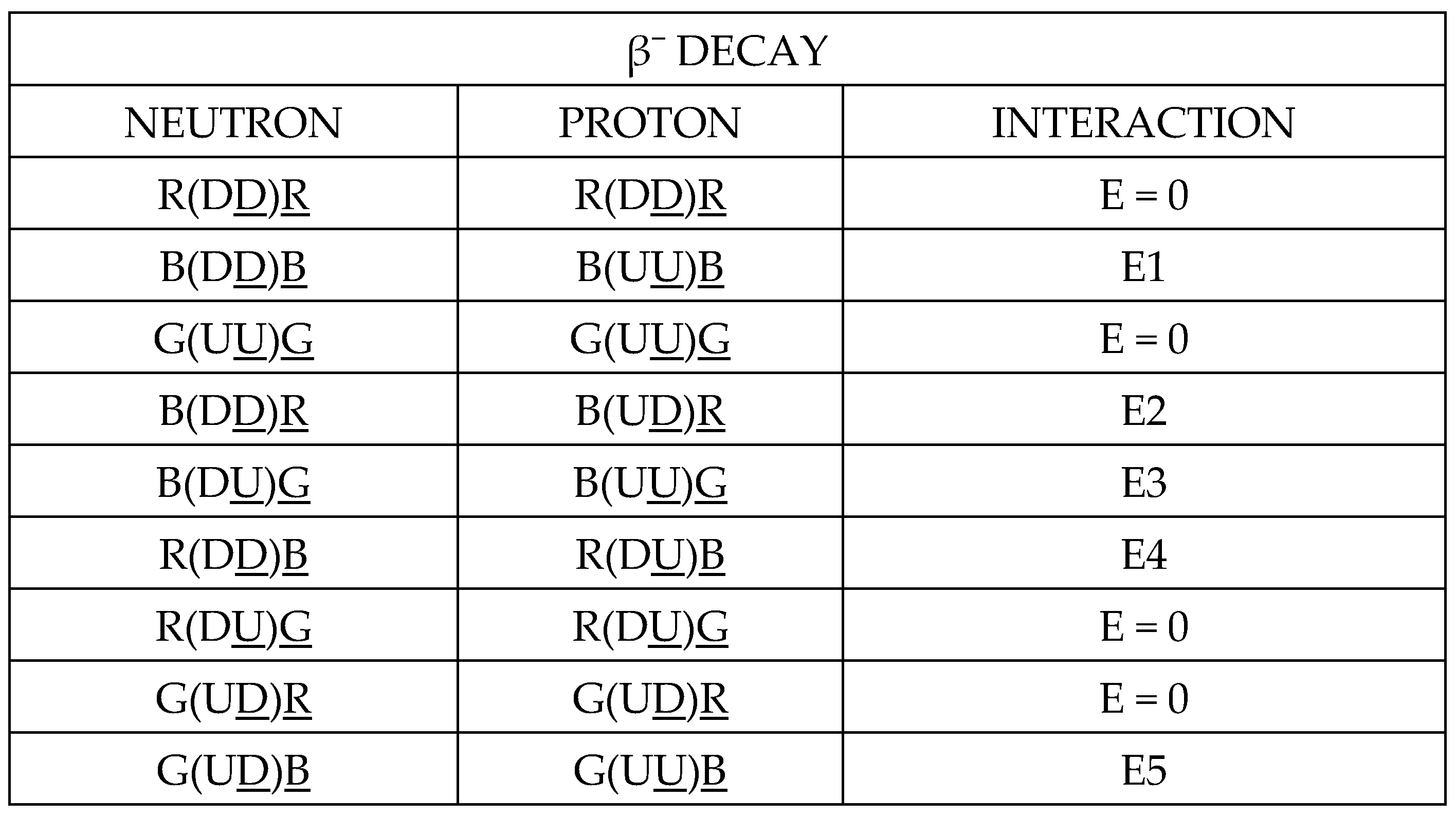
R(DD)R + B(DD)B + G(UU)G = 0

If we analyse figure 40, triangle connection, we see that the following vector sum is null:

R(DD)B + B(DU)G + R(DU)G = 0

This is telling us that the net charge in interaction 1 is zero.

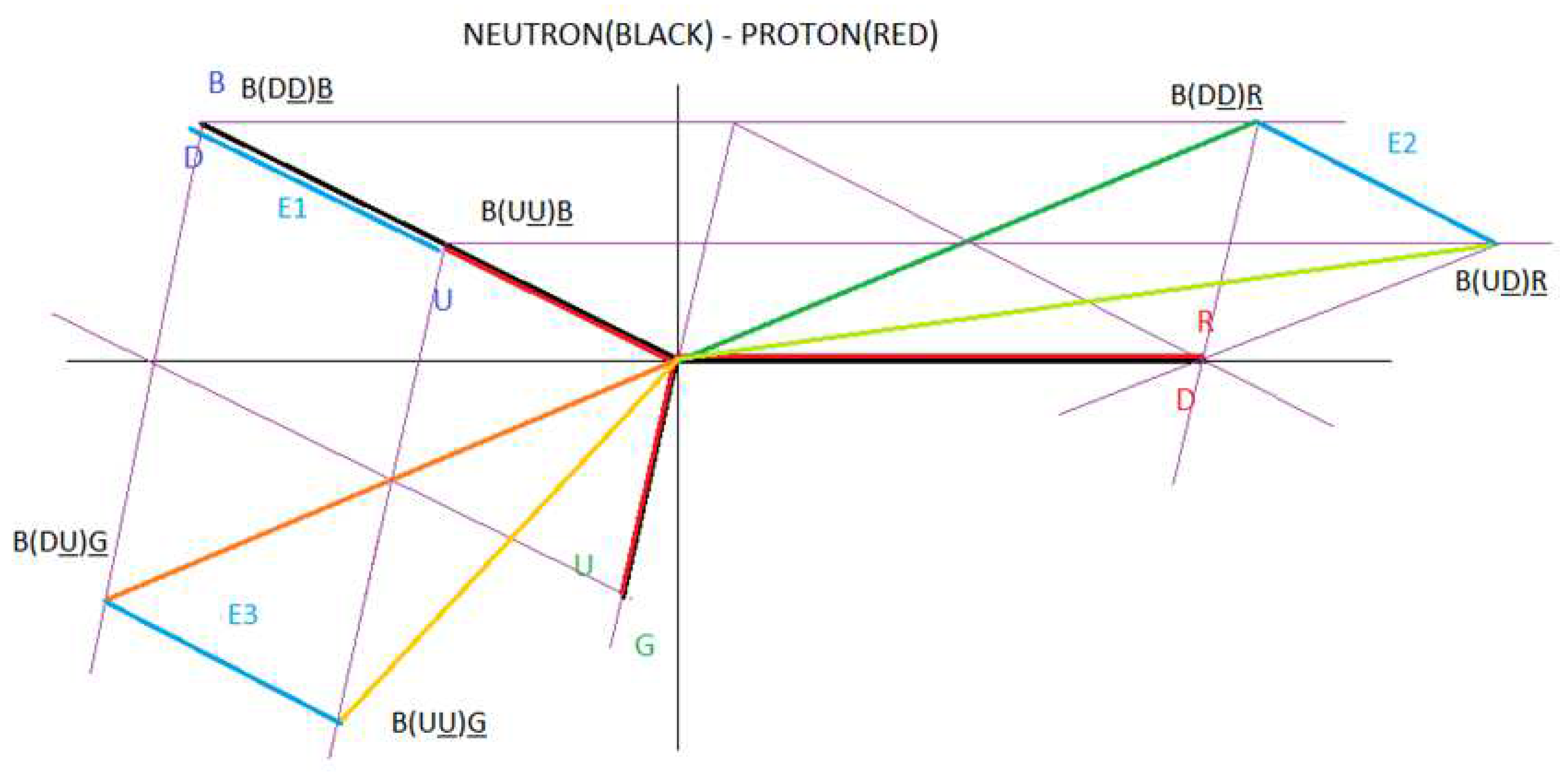
Figure 42. Interaction 1 & 2 of the neutron.

Figure 42. Interaction 1 & 2 of the neutron.

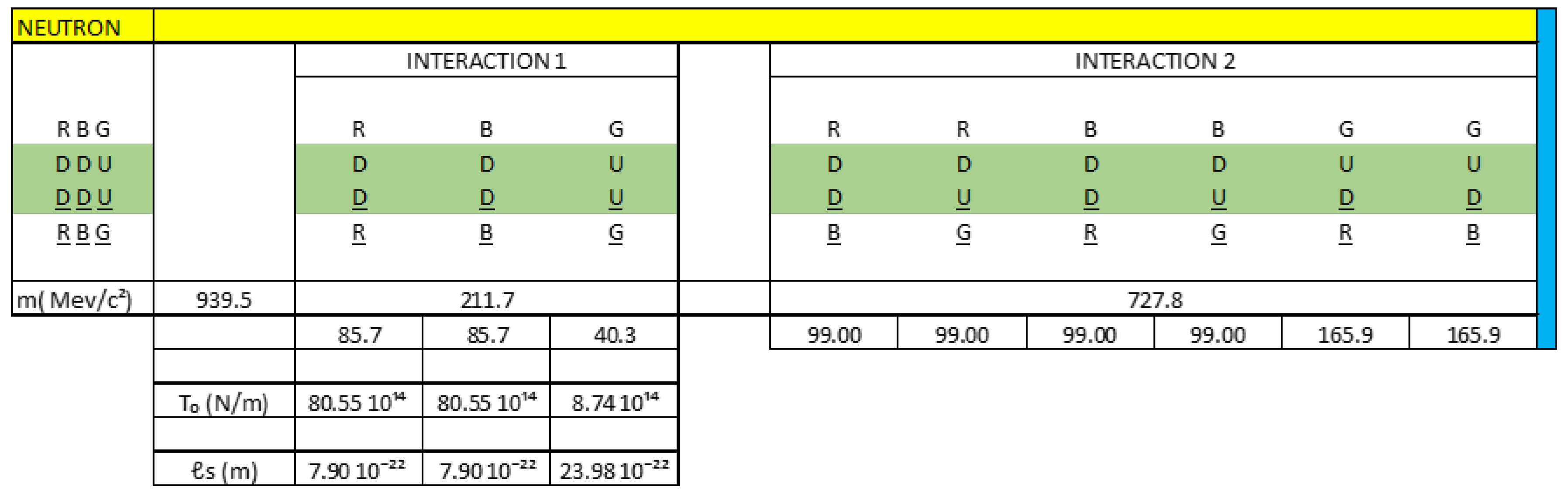
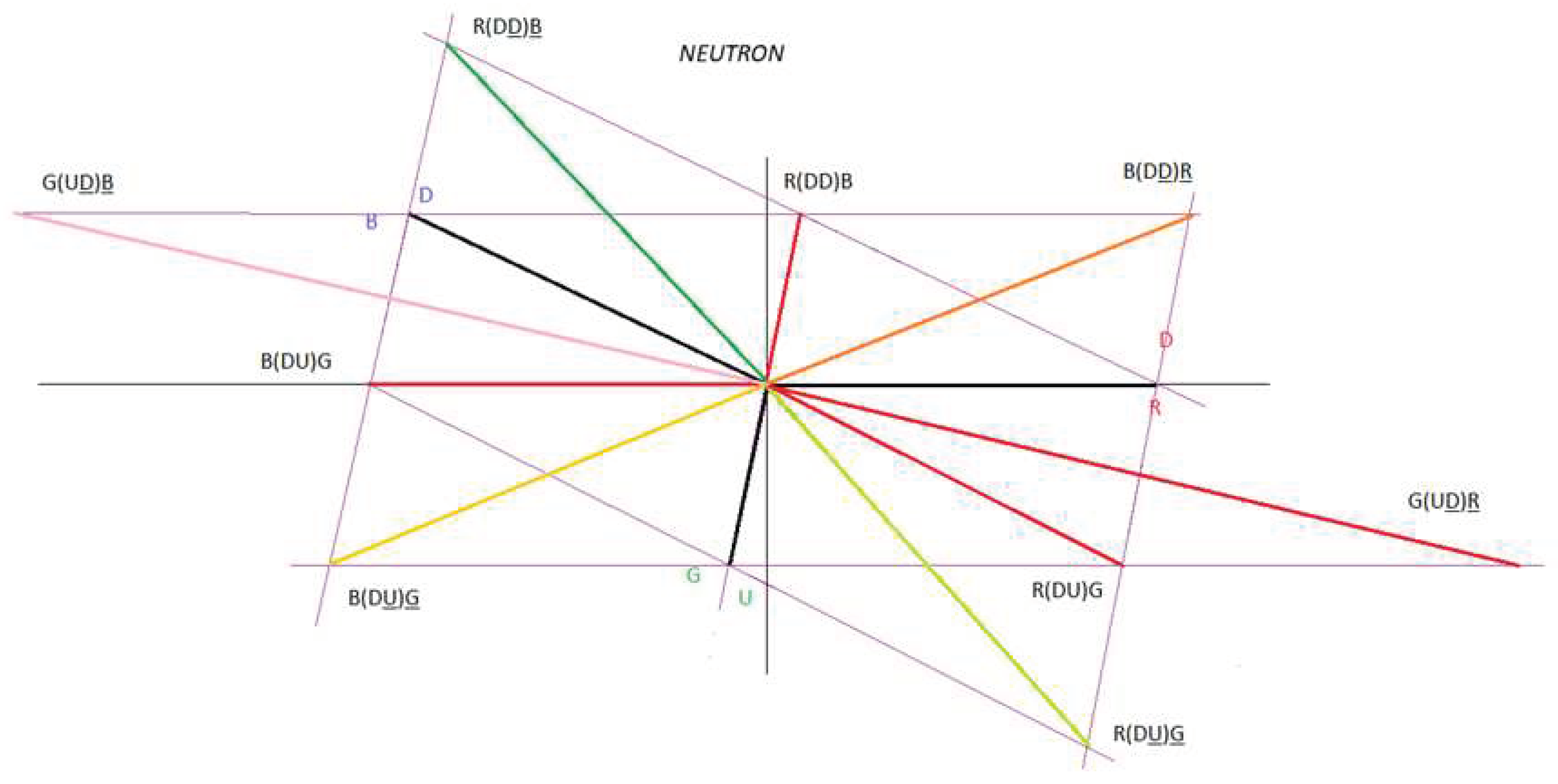
Interaction 2:

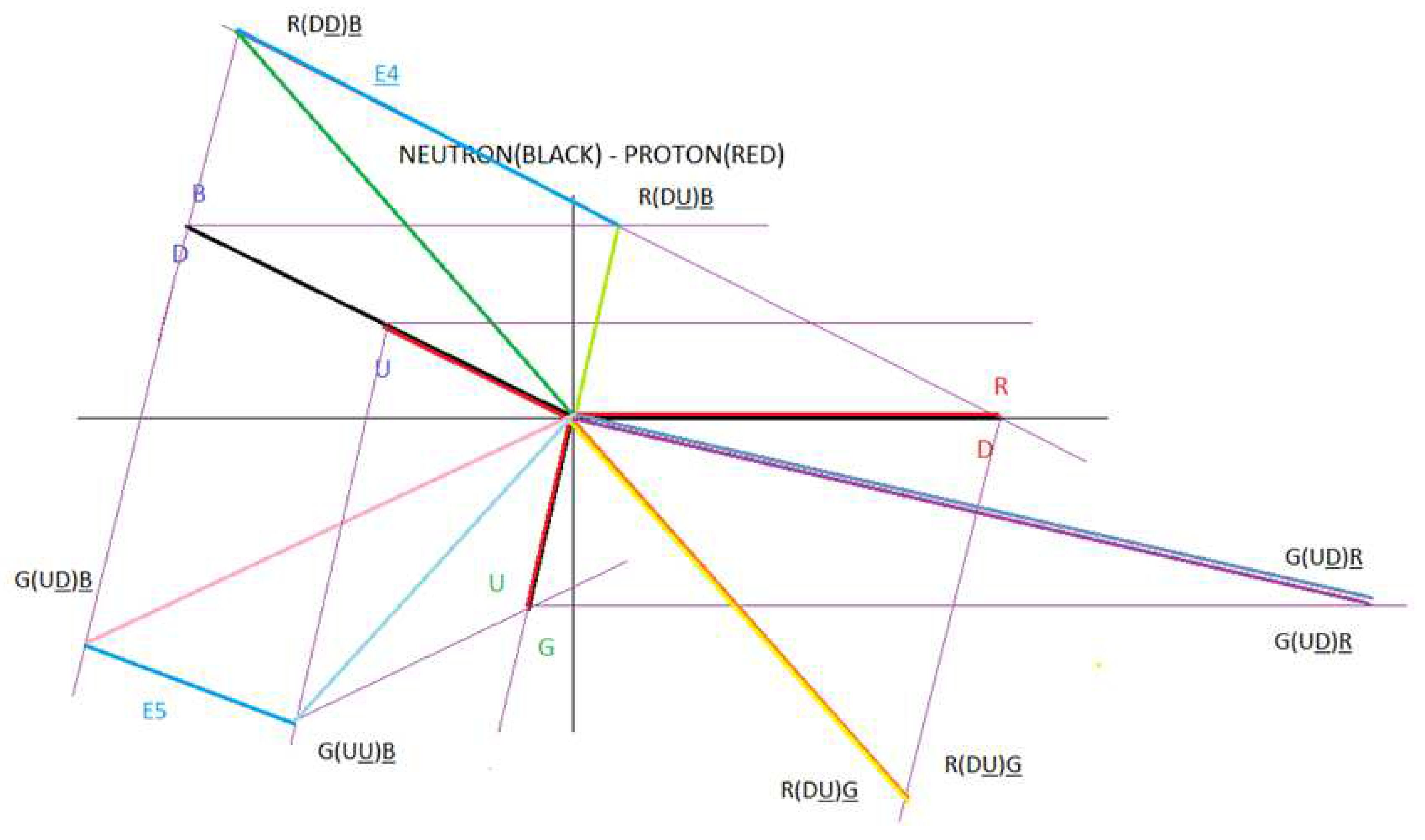
If we analyse figure 42, we observe that the following vector sum is also null:

R(DD)B + R(DU)G + B(DD)R + B(DU)G + G(UD)R + G(UD)B = 0

This is telling us that the net charge in interaction 2 is zero.

Taking into account interaction 1 and interaction 2, the total net charge of the neutron is zero, as appropriate.

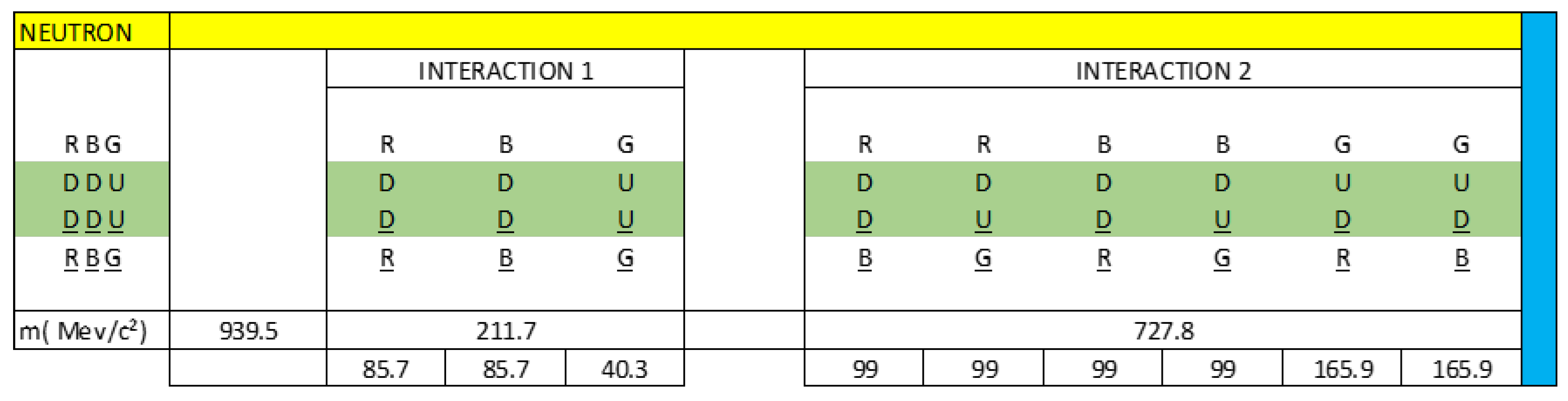
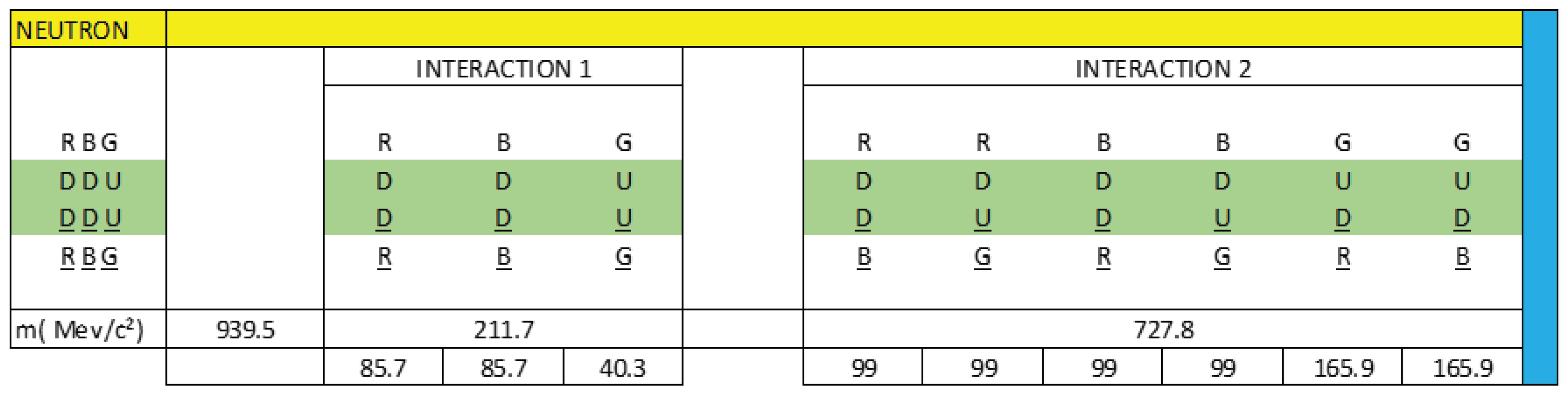
Knowing that the total mass of the neutral is 939.5 MeV/c², we are going to calculate the mass content in each interaction:

R(DD)R = 85.7 MeV/c²

B(DD)B = 85.7 MeV/c²

G(UU)G = 40.2 MeV/c²

R(DD)B = 99 MeV/c²

R(DU)G = 99 MeV/c²

B(DD)R = 99 MeV/c²

B(DU)G = 99 MeV/c²

G(UD)R = 165.9 MeV/c²

G(UD)B = 165.9 MeV/c²

We are going to represent these values in figure 42:

Figure 43. Mass distribution in interactions 1 & 2.

Figure 43. Mass distribution in interactions 1 & 2.

The electrical modelling of a neutral as a three-phase alternating current electrical generator allows us to assign a mass value to interactions 1 & 2, which we represent using a phasor diagram, as shown in figure 42. It also allows us to verify that the sum of net charge in interactions 1 & 2 is zero, as appropriate.

Analysing the vector diagrams in Figure 41 and 42, we see that the degrees of freedom of the vectors are practically zero, there is no possibility of deviations, the hypothesis that the charge has to be zero restricts any possibility of changes in the position of the vectors, that is, the vectors have a unique configuration, given in Figure 41 and 42.

Conclusions: It is important to keep in mind that the relationship between the interactions of quarks, anti-quarks and gluons is vector-type, that is, each interaction will be represented by a module and an angle.

In the neutron, if we add the phasors of interaction 1 and interaction 2 vector-wise, we see that the resulting vector is zero, in other words, the net charge is zero; but if we add the module of each vector in MeV/c² scalarly, the sum gives us 939.5 MeV/c², we represent this in figure 42 and 43, which corresponds to the neutron.

Definitely, we can assure that neutrons are true generators of energy, mass and gravity; We have verified how with three quarks that add up to approximately 10 MeV/c², we can generate a mass of 939.5 MeV/c² through the interactions of quarks, anti-quarks and gluons.

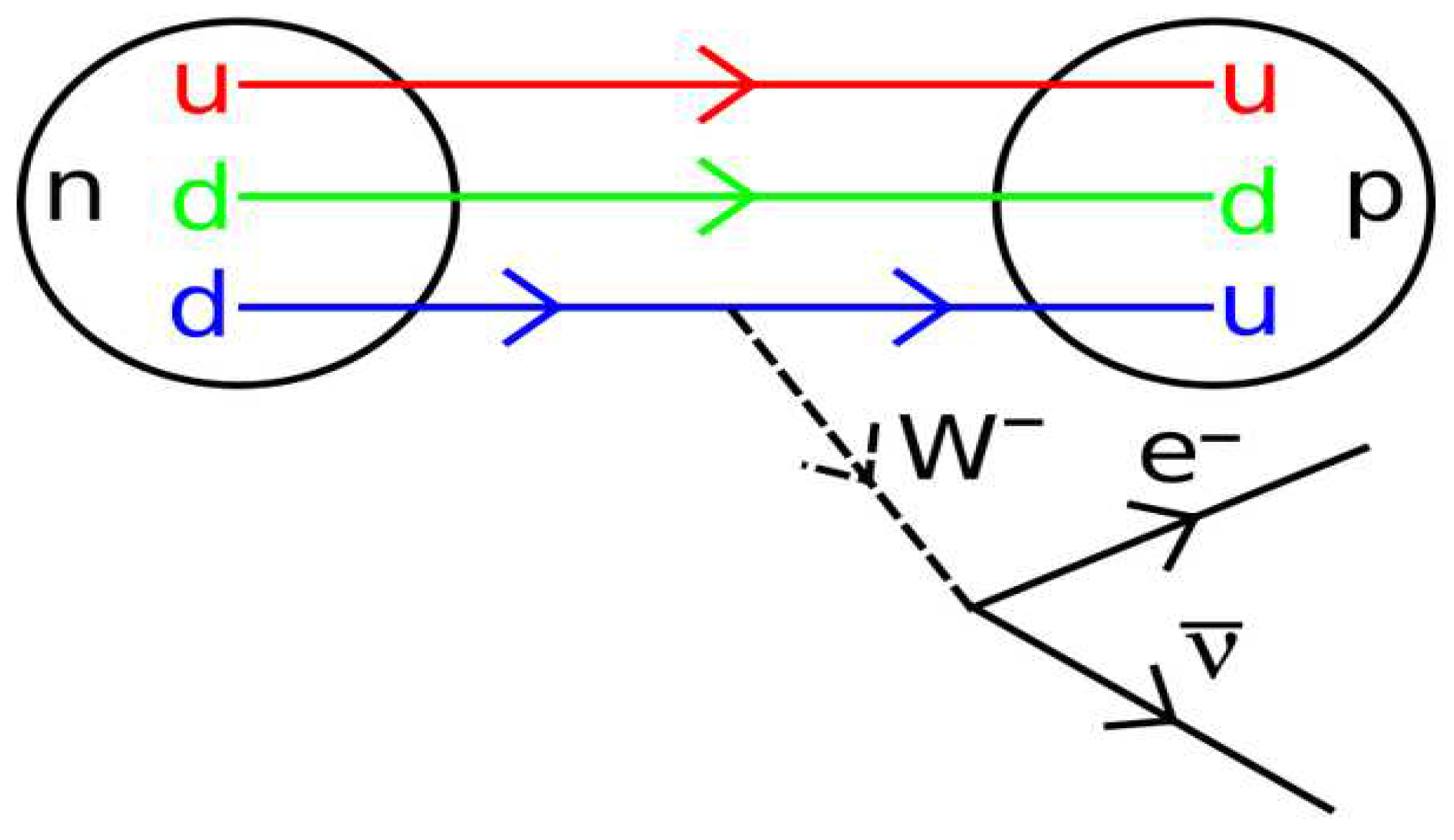
When we analysed Beta minus decay, we said that the W (+/-) bosons and the Z boson are ideal bosons, they are bosons that are born as a black box of the experimentation, due to the lack of a physical-mathematical theory that describes them.

When we analysed Beta minus decay, we determined that the W+ boson is the result of quark, antiquark and gluon interactions. This became evident when we used the Electrical-Quantum Modelling of the Neutron and Proton as a Three-Phase Alternating Current Electrical Generator.

In conclusion, when we use the Electrical-Quantum Modelling of the Neutron and Proton as a Three-Phase Alternating Current Electrical Generator, the weak electrode field interactions (QED) and the strong field interactions (QCD), are simply reduced to interactions of electromagnetic field (EQFT).

In the strong force, the gluons RBG and R B G are markers to indicate that the interactions between quark, antiquark and gluons are vectors that have a magnitude and an angle.

Mechanism that Generates Mass in Neutrons, Calculation of the Number of Quarks-Antiquarks-Gluons Inside a Neutron

If we look at figure 43, we see that the neutron has a mass of 939.5 MeV/c², if we add the mass of the two D Quark and the mass of the U quark it gives us approximately 10 MeV/c²; We ask ourselves, how is the mass of 929 MeV/c² generated? That is precisely what we want to answer in this section.

If we look at figure 43, we see that we can represent the neutron by dipoles of matter and antimatter formed by quark and anti-quark. Interaction 1 can be represented by 3 dipoles and interaction 2 can be represented by 6 dipoles.

If we analyse any dipole, we see that at one end it is formed by matter and at the other end by antimatter, opposite charges of the opposite sign.

These dipoles behave like electrical antennas, if we consider that these dipoles move in one direction, they vibrate, they are polarized, they generate an electromagnetic field in analogy to the dipoles of antennas.

The variation of the electric field in the antennas produces a variation in the electric potential and this in turn produces a flow of current, thus generating an electromagnetic wave.

In analogy to dipole antennas, polarized vibrations in one direction produce a flow of gluons that carry charge, producing a current that would generate an electromagnetic field. This flow of charge-carrying gluons would be analogous to a flow of current and this would produce an electromagnetic field generated by the matter-antimatter dipole.

We know through the equation E = mc², that energy is related to mass and precisely that energy that results from gluonic exchange is the energy that generates the mass 928 MeV/c² in a neutron.

Neutron mass = 939.56 MeV/c²

2md + mu = 11.6 MeV/c²

where md is the mass of the D quark and mu is the mass of the U quark.

Gluon exchange mass = 928 MeV/c²

We are going to perform the following calculations:

We are going to work with the bond energy that keeps the electron attached to the proton, in the hydrogen atom.

13.6 eV = 2.17 10⁻¹⁸ Joules

E = h x f; f = E/h = 2.17 10⁻¹⁸ / 6.63 10⁻³⁴

f = 3.2 10¹⁵ Hz

E = K x T; T = E/K = 2.17 10⁻¹⁸ / 1.38 10⁻²³

T = 1.57 10⁵ K

M(photon) = h / (λ x C)

c = λ x f; λ = c/f = 3 10⁸ / 3.210¹⁵ = 0.937 10⁻⁷

λ = 9.37 10⁻⁸ m

M(photon) = h / (λ x C) = 6.63 10⁻³⁴ / 9.37 10⁻⁸ x 3 10⁸

M(photon-gluon) = 2.35 10⁻³⁵ kg

That would be the mass of the photon-gluon that holds the electron to the proton in the hydrogen atom.

Let's assume that the binding energy is 136,000 eV:

136,000 eV = 2.17 10⁻¹⁴ Joules

E = h x f; f = E/h = 2.17 10⁻¹⁴ / 6.63 10⁻³⁴

f = 3.2 10²⁰ Hz

E = K x T; T = E/K = 2.17 10⁻¹⁴ / 1.38 10⁻²³

T = 1.57 10⁹ K

M(photon) = h / (λ x C)

c = λ x f; λ = c/f = 3 10⁸ / 3.2 10²⁰ = 0.937 10⁻¹²

λ = 9.37 10⁻¹³ m

M(photon) = h / (λ x C) = 6.63 10⁻³⁴ / 9.37 10⁻¹³ x 3 10⁸

M(photon-gluon) = 2.35 10⁻³⁰ kg

Let's assume that the binding energy is 1,360,000,000 eV:

1,360,000,000 eV = 2.17 10⁻¹⁰ Joules

E = h x f; f = E/h = 2.17 10⁻¹⁰ / 6.63 10⁻³⁴

f = 3.2 10²³ Hz

E = K x T; T = E/K = 2.17 10⁻¹⁰ / 1.38 10⁻²³

T = 1.57 10¹³ K

M(photon-gluon) = h / (λ x C)

c = λ x f; λ = c/f = 3 10⁸ / 3.2 10²³ = 0.937 10⁻¹⁵

λ = 9.37 10⁻¹⁶ m

M(photon) = h / (λ x C) = 6.63 10⁻³⁴ / 9.37 10⁻¹⁶ x 3 10⁸

M(photon-gluon) = 2.35 10⁻²⁷ kg

Let's assume that in a hydrogen atom the electron is linked to the proton through the BB gluons, which are analogous to photons and can escape confinement, in addition, the rest of the gluons have colour charge other than zero, they cannot escape confinement. We can consider that in general from the point of view of energy, for the same temperature conditions all gluons have equivalent energies of the same order.

When we analyse βˉ decay, we show that a neutron decays into a proton and if the released electron is trapped forming the hydrogen atom, we will see that the BB gluons would be the linked photons in the electromagnetic theory, which unites the proton with the electron

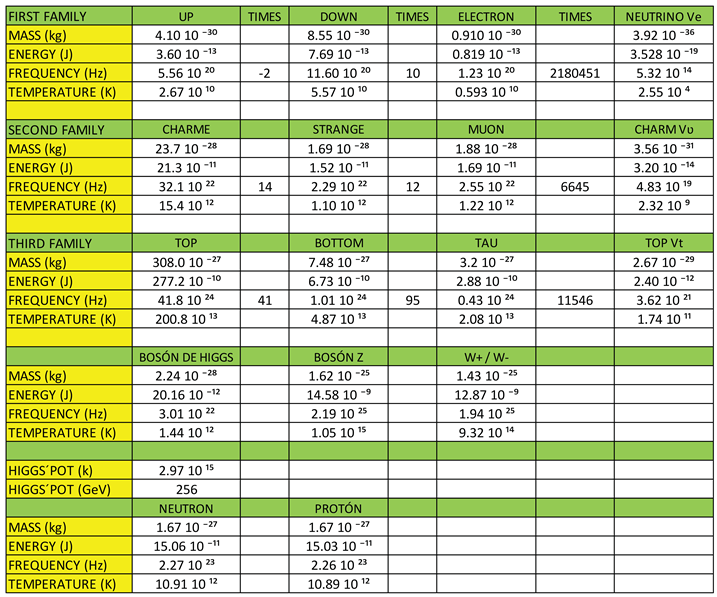
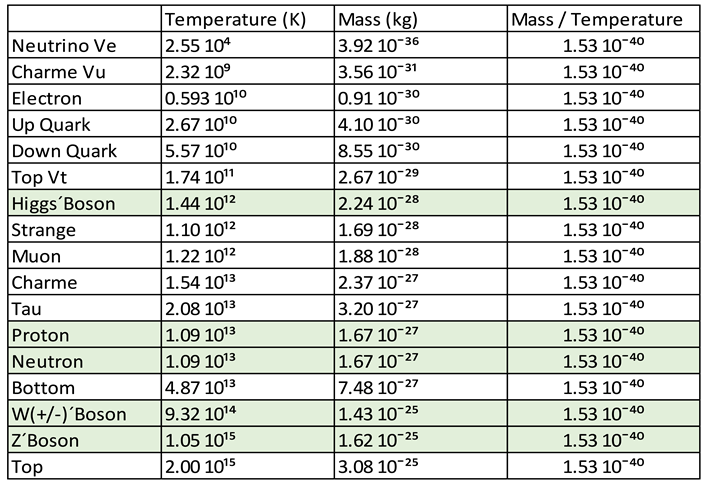
With the calculations carried out, we are going to generate the following table:

Table 11. Gluon Mass.

Table 11. Gluon Mass.

In table 11, we observe that as the energy increases, the frequency increases, the temperature increases and consequently the mass of the gluon increases.

If we remember what we said that neutrons and protons are formed by dipoles of matter and antimatter (quark and anti-quark), which oscillate in a certain direction similar to the electric dipoles in antennas, if we analyse table 11, we see that as the dipoles increase their vibration frequency, their energy increases, their temperature increases and the mass of the gluon also increases as predicted.

If we look at table 11, for T = 1.57 10⁹ K, we see that the mass of the gluons is approximate to the mass of the U quark and D quark, shown in figure 6. This is telling us that if we consider the correct temperature, the mass of the gluons will coincide with the mass of the U quark and D quark.

mu = 4.10 10ˉ³⁰ kg, T = 2.67 10¹⁰ K

md = 8.55 10ˉ³⁰ kg, T = 5.57 10¹⁰ K

Gluon mass = 2.35 19ˉ³⁰ kg, T = 1.57 10⁹ K

Taking into account the statement:

We are going to perform the following calculation:

Neutron mass = 939.56 MeV/c²

2md + mu = 11.6 MeV/c²

Number of gluons = neutron mass / unit mass of a gluon

For T = 1.57 10⁵ K:

Approximate number of gluons per neutron = 1.67 10⁻²⁷ / 2.35 10⁻³⁵

Approximate number of gluons per neutron = 0.71 10⁸

QTY g = 7.1 10⁷ = 71,000,000.00

71 million gluons in a neutron, for T = 1.57 10⁵ K.

Where QTY g, is the number of gluons inside a neutron.

When we talk about gluons, we refer to quarks-antiquarks and gluons as a whole, as long as the interaction relationship 1 & 2 is fulfilled, as shown in figure 43.

According to table 11, we see that the number of gluons in a neutron depends on the temperature (energy) at which the calculation is carried out.

Looking at table 11, we see that as the temperature increases, the mass of the quark-gluons increases, for example, for a temperature of 10⁹ K, the mass of a quark-gluon is in the order 10ˉ³⁰ kg. Now, for a temperature of 10¹³ K, the mass of the quark-gluons is on the order of 10ˉ²⁷ kg.

Next, we are going to calculate the quantity of quarks-antiquarks-gluons existing, in a discriminated manner, in the dipoles of the interaction 1 & 2.

Interaction 1:

QTY g INT 1: = 0.376 10ˉ²⁷ kg / 2.35 10ˉ³⁵ kg = 1.6 10⁷ Q-Gluons

Qty g R(DD)R = 0.152 10ˉ²⁷ kg / 2.35 10ˉ³⁵ kg = 0.648 10⁷ Q-Gluons

Qty g B(DD)B = 0.152 10ˉ²⁷ kg / 2.35 10ˉ³⁵ kg = 0.648 10⁷ Q-Gluons

Qty g G(UU)G = 0.072 10ˉ²⁷ kg / 2.35 10ˉ³⁵ kg = 0.306 10⁷ Q-Gluons

Interaction 2:

QTY g INT 2 = 1.293 10ˉ²⁷ kg / 2.35 10ˉ³⁵ kg = 5.50 10⁷ Q-Gluons

QTY g R(DD)B = 0.1759 10ˉ²⁷ kg / 2.35 10ˉ³⁵ = 0.748 10⁷ Q-Gluons

QTY g R(DU)G = 0.1759 10ˉ²⁷ kg / 2.35 10ˉ³⁵ = 0.748 10⁷ Q-Gluons

QTY g B(DD)R = 0.1759 10ˉ²⁷ kg / 2.35 10ˉ³⁵ = 0.748 10⁷ Q-Gluons

QTY g B(DU)G = 0.1759 10ˉ²⁷ kg / 2.35 10ˉ³⁵ = 0.748 10⁷ Q-Gluons

QTY g G(UD)R = 0.294 10ˉ²⁷ kg / 2.35 10ˉ³⁵ = 1.254 10⁷ Q-Gluons

QTY g G(UD)B = 0.294 10ˉ²⁷ kg / 2.35 10ˉ³⁵ = 1.254 10⁷ Q-Gluons

Where Q-Gluons, it means quarks-antiquarks-gluons.

It is very important to be clear that the mass of quark-antiquarks-gluons varies with temperature.

These calculations were carried out for a temperature T = 1.57 10⁵ K.

Calculation of the Number of Gluons by Dividing the Volume of the Neutron by the Volume of the Quark

Rn = 0.4 10ˉ¹⁵ m

Where Rn is radius of the neutron

Vn = (4/3) ᴨ R³ = (4/3) x 3.14 x (0.4 10ˉ¹⁵) ³

Vn = 0.267 10ˉ⁴⁵ m³

Rq = 0.43 10⁻¹⁸ m

Where Rq is quark radius.

Vq = (4/3) ᴨ R³ = (4/3) x 3.14 x (0.43 10⁻¹⁸) ³ =

Vq = 0.33 10⁻⁵⁴ mᶾ

Where Vq is volume of the quark

D = Vn / Vq = 0.267 10ˉ⁴⁵ m³ / Vq = 0.33 10⁻⁵⁴ mᶾ

D = 0.80 10⁹ = 8.0 10⁸

D = 80 10⁷ gluons

Where D is the number of quark-antiquarks-gluons

According to our calculations, we have:

D ≈ 10 QTY g

We said that the mass of gluons decreases with temperature, see table 11, if we calculate the number of quarks-antiquarks-gluons for a temperature lower than T = 10⁵ K, we will achieve the equality D = QTY g.

D = QTY g

Mechanism that Generates Gravity in Neutrons, Calculation of the Number of Gravitons Inside a Neutron

From the point of view of charge, we said that interaction 1 and interaction 2 of quarks represent electric dipoles (Spin 1). We also said that these dipoles are polarized and vibrate in one direction, producing an electromagnetic field that gives rise to a flow of gluons that generates an electric current and through this mechanism we manage to produce mass in Hadrons (proton, neutron, etc).

From the point of view of mass, if we consider quark and anti-quark dipoles as point masses that vibrate, we can idealize it as a quark linked to an anti-quark by a spring (Gravitons with spin 2), these two masses vibrating together by a spring, they would produce disturbances in space-time that would propagate in the form of gravitational waves.

This would be the mechanism by which gravitational waves are generated, gravitons that would propagate in space-time.

In conclusion, it is the charge and mass properties in the quark and anti-quark dipoles represented in interaction 1 and interaction 2, which produce 100% of the mass in protons and neutrons and also originate the gravitational waves (gravitons), that propagate in space-time, what we call gravity.

Neutron mass = 939.56 MeV/c²

2md + mu = 11.6 MeV/c²

where md, is the mass of the D quark and mu, is the mass of the U quark.

We are going to perform the following calculations using the effective Boltzmann constant to quantize and quantify gravity.

Kʙl = 9.15 10⁻²⁶ J/K,

Where Kʙl is approximate effective Boltzmann constant of the moon.

El = Kʙl x T

El = 9.15 10⁻²⁶ x 1.6 10³ = 14.64 x 10⁻²³

El = 14.64 10⁻²³ Joules

El = h x fl; fl = El / h = 14.64 10⁻²³ / 6.63 10⁻³⁴ = 2.34 10¹¹

fl = 2.34 10¹¹ Hz

M(graviton) = h / (λl x c)

c = λl x fl; λl = c / fl = 3 10⁸ / 2.34 10¹¹ = 1.28 10⁻³

λl = 1.28 10⁻³ m

M(graviton) = h / (λl x c) = 6.63 10⁻³⁴ / 1.28 10⁻³ x 3 10⁸ = 1.72 10⁻²⁹

M(graviton)l-eff = 1.72 10⁻²⁹ kg

Kʙt = 2.68 10⁻²⁸ J/K

Where Kʙt is approximate effective Boltzmann constant of the earth.

Et = Kʙt x T

Et = 2.68 10⁻²⁸ x 6.7 10³ = 17.95 x 10⁻²⁵

Et = 17.95 10⁻²⁵ Joules

Et = h x ft; ft = Et / h = 17.95 10⁻²⁵ / 6.63 10⁻³⁴ = 2.70 10⁹

Ft = 2.70 10⁹ Hz

M(graviton) = h / (λ x C)

c = λt x ft; λt = c/ft = 3 10⁸ / 2.70 10⁹ = 1.11 10⁻¹

λt = 11.1 10⁻¹ m

M(graviton) = h / (λt x c) = 6.63 10⁻³⁴ / 1.11 10⁻¹ x 3 10⁸

M(graviton)t-eff = 1.99 10⁻⁴¹ kg

Kʙs = 3.58 10⁻³⁷ J/K

Where Kʙs is approximate effective Boltzmann constant of the sun.

Es = Kʙs x T

Es = 3.58 10⁻³⁷ x 15 10⁶ = 53.7 x 10⁻³¹

Es = 53.7 10⁻³¹ Joules

Es = h x fs; fs = Es / h = 53.7 10⁻³¹ / 6.63 10⁻³⁴ = 8.09 10³

fs = 8.09 10³ Hz

M(graviton) = h / (λs x c)

c = λs x fs; λs = c / fs = 3 10⁸ / 8.09 10³ = 0.37 10⁵

λs = 3.7 10⁴ m

M(graviton) = 6.63 10⁻³⁴ / (3.7 10⁴ x 3 10⁸) = 0.59 10⁻⁴⁶

M(graviton)s-eff = 5.9 10⁻⁴⁷ kg

Kʙe = 1.9 10⁻³⁷ J/K

Where Kʙe is approximate effective Boltzmann constant of a star white dwarf.

Ee = Kʙe x T

Ee = 1.9 10⁻³⁷ x 20 10⁶ = 38 x 10⁻³¹

Ee = 38 10⁻³¹ Joules

Ee = h x fe; fe = Ee / h = 38 10⁻³¹ / 6.63 10⁻³⁴ = 5.73 10³

fe = 5.73 10³ Hz

M(graviton) = h / (λe x c)

c = λe x fe; λe = c / fe = 3 10⁸ / 5.73 10³ = 0.52 10⁵

λe = 5.2 10⁴ m

M(graviton) = h / (λe x c) = 6.63 10⁻³⁴ / 5.2 10⁴ x 3 10⁸ = 0.425 10⁻⁴⁶

M(graviton)e-eff = 4.25 10⁻⁴⁷ kg

Kʙn = 2.42 10⁻⁴² J/K

Where Kʙn is approximate effective Boltzmann constant of a neutron star.

En = Kʙn x T

En = 2.42 10⁻⁴² x 10¹² = 2.42 x 10⁻³⁰

En = 2.42 10⁻³⁰ Joules

En = h x fn; fn = En / h = 2.42 10⁻³⁰ / 6.63 10⁻³⁴ = 0.36 10⁴

fn = 3.6 10³ Hz

M(graviton) = h / (λn x c)

c = λn x fn ; λn = c / fn = 3 10⁸ / 3.6 10³ = 0.83 10⁵

λs = 8.3 10⁴ m

M(graviton) = h / (λn x c) = 6.63 10⁻³⁴ / 8.3 10⁴ x 3 10⁸ = 0.266 10⁻⁴⁶

M(graviton)n-eff = 2.66 10⁻⁴⁷ kg

Kʙq = 1.78 10⁻⁴³ J/K

Where Kʙq is approximate effective Boltzmann constant of a black hole.

Eq = Kʙq x T

Eq = 1.78 10⁻⁴³ x 10¹³ = 1.78 x 10⁻³⁰

Eq = 1.78 10⁻³⁰ Joules

Eq = h x fq; fq = Eq / h = 1.78 10⁻³⁰ / 6.63 10⁻³⁴ = 0.26 10⁴

fq = 2.6 10³ Hz

M(graviton) = h / (λq x c)

c = λq x fq ; λq = c / fq = 3 10⁸ / 2.6 10³ = 1.15 10⁵

λq = 1.15 10⁵ m

M(graviton) = h / (λq x c) = 6.63 10⁻³⁴ / 1.15 10⁵ x 3 10⁸ = 1.76 10⁻⁴⁷

M(graviton)q-eff = 1.76 10⁻⁴⁷ kg

We are going to represent all these calculations in table 12:

Table 12. Calculation of the mass of the graviton as a function of temperature.

Table 12. Calculation of the mass of the graviton as a function of temperature.

It is important to clarify that the mass of the calculated graviton is an effective mass or equivalent that is related to the definition that was used to calculate the effective Boltzmann constant, for example, in a neutron star the minimum particle considered to calculate the effective mass is a neutron and the effective graviton equivalent mass calculated for a neutron star is related to the mass of the neutron, that is, the graviton equivalent or effective mass calculated for a neutron star is a mass resulting from an unimaginable amount of individual gravitons.

In analogy with the calculations carried out for gluons, we are going to carry out similar calculations for gravitons using the mass of the effective graviton.

For a neutron star, we have:

Let's assume the mass of the neutron for T= 10¹² K:

Neutron mass = 939.56 MeV/c²

2md + mu = 11.6 MeV/c²

QTY gr = Neutron mass / unit mass of a graviton.

QTY gr = 1.67 10⁻²⁷ / 2.66 10⁻⁴⁷

m gr = 2.66 10ˉ⁴⁷ kg

Where m gr, is the unit mass of the graviton for T = 10¹² K.

QTY gr = 0.627 10²⁰

QTY gr = 6.27 10¹⁹

Where QTY gr, is number of gravitons in a neutron, for T = 10¹² K.

Why do we use the mass of the neutron, mn = 939.56 MeV/c², to calculate the number of gravitons in a neutron!

This question, in my opinion, would have 2 answers:

First answer, from the point of view of mass, if we consider quark and anti-quark dipoles as point masses that vibrate, we can idealize it as a quark linked to an anti-quark by a spring (Gravitons with spin 2), these two masses vibrating together by a spring, they would produce disturbances in space-time that would propagate in the form of gravitational waves. This would be the mechanism by which gravitational waves are generated, gravitons that would propagate in space-time.

Second answer, if we consider the Maldacena correspondence ADS = CFT, the right side of the equation, CFT, tells us that there is a mass that corresponds to the neutron and is mn = 939.56 MeV/c²; The left side tells us that there must be a gravitational mass equivalent to mn = 939.56 MeV/c², which must be equivalent to the CFT mass, for the equation ADS = CFT to be fulfilled.

These are the two answers, for which we use the mass of the neutron to calculate the number of gravitons inside a neutron.

We will calculate the number of corresponding gravitons, for interactions 1 & 2:

Interaction 1:

QTY gr INT 1: = 0.376 10ˉ²⁷ kg / 2.66 10ˉ⁴⁷ kg = 1.41 10¹⁹ Graviton

Qty gr R(DD)R = 0.152 10ˉ²⁷ kg / 2.66 10ˉ⁴⁷ kg = 0.571 10¹⁹ Graviton

Qty gr B(DD)B = 0.152 10ˉ²⁷ kg / 2.66 10ˉ⁴⁷ kg = 0.571 10¹⁹ Graviton

Qty gr G(UU)G = 0.072 10ˉ²⁷ kg / 2.66 10ˉ⁴⁷ kg = 0.270 10¹⁹ Graviton

Interaction 2:

QTY gr INT 2 = 1.293 10ˉ²⁷ kg / 2.66 10ˉ⁴⁷ kg = 4.86 10¹⁹ Graviton

QTY gr R(DD)B = 0.1759 10ˉ²⁷ kg / 2.66 10ˉ⁴⁷ = 0.661 10¹⁹ Graviton

QTY gr R(DU)G = 0.1759 10ˉ²⁷ kg / 2.66 10ˉ⁴⁷ = 0.661 10¹⁹ Graviton

QTY gr B(DD)R = 0.1759 10ˉ²⁷ kg / 2.66 10ˉ⁴⁷ = 0.661 10¹⁹ Graviton

QTY gr B(DU)G = 0.1759 10ˉ²⁷ kg / 2.66 10ˉ⁴⁷ = 0.661 10¹⁹ Graviton

QTY gr G(UD)R = 0.294 10ˉ²⁷ kg / 2.66 10ˉ⁴⁷ = 1.105 10¹⁹ Graviton

QTY gr G(UD)B = 0.294 10ˉ²⁷ kg / 2.66 10ˉ⁴⁷ = 1.105 10¹⁹ Graviton

It is important to make it clear that the number of gravitons calculated inside a neutron corresponds to the temperature T = 10¹² K.

If we look at table 12, we see that as the temperature increases the mass of the graviton decreases.

M-theory, Extra Dimensions and the Theory of the Generalization of Boltzmann's Constant in Curved Spacetime

In the paper: RLC Electrical Modelling of Black Hole and Early Universe. Generalization of Boltzmann’s Constant in Curved Space-Time [3], we developed this topic, now we are going to give a short introduction.

Considering these two theories, the M-theory and the theory of the generalization of Boltzmann's constant in curved space-time, we will make the following comparison, in 3 stages.

Here we put forward the following hypothesis:

First stage: Corresponds to the (3 + 1) dimensions in which we live, the three spatial dimensions plus time. In the theory of the generalization of the Boltzmann constant in curved space-time, it corresponds to the regime in which the Boltzmann constant is equal to Kʙ = 1.38 10⁻²³ J/K. We are in a perturbative regime, that is, small gs, dominated by the strings. This regime is characterized by the fact that the space-time structure does not undergo modifications, flat space-time.

Second stage: matter undergoes the first compaction process. This would be represented by the 10-dimensional superstring theory, that is, by the dimensions (3 + 1) plus 6 additional dimensions that arise from the first compaction process. In the theory of the generalization of the Boltzmann constant in curved space-time, this regime would be characterized because the Boltzmann constant varies between 1.38 10⁻²³ J/K > Kʙ > 1.78 10⁻⁴³ J/K. We are in a perturbative to non-perturbative transition regime, that is, gs tends to a large value. This regime is characterized by the fact that the structure of space-time undergoes modifications. An example of this regime would be white dwarf stars and neutron stars. This is a regime in which spacetime is curved.

Third stage: In this stage of M-Theory, the second compaction process occurs, that is, the decompression of dimension 11 occurs, the radius R becomes infinitely large. In the theory of the generalization of the Boltzmann constant in curved space-time, in this regime, the Boltzmann constant assumes the value of Kʙ = 1.78 10⁻⁴³ J/k. We are in the non-perturbative regime, that is, gs is infinite. In this regime, the structure of space-time undergoes great changes, a concrete example would be the creation of black holes. The decompression of dimension 11 in M-theory is equivalent to creating a black hole. In this stage the maximum curvature of space-time occurs. At this stage, as the black hole grows, inside a black hole, it is true that the gravitational Planck length Lpɢ is less than the electromagnetic Planck length Lpɛ.

Decompactification of dimension 11

It is important to understand that the concept of dimension depends on the scale of energies or distances. We are used to the four dimensions of everyday life (x, y, z, t), now when we work at high energies in the LHC, at small distances we introduce 6 more dimensions, that is, we would be working in 10 dimensions, which is the case of the plasma of quarks and gluons. In the theory of the generalization of the Boltzmann constant in curved spacetime, we can represent this by varying the Boltzmann constant in the range of 1.38 10⁻²³ J/K > Kʙ > 1.78 10⁻⁴³ J/ K.

If we imagine dimension 11 as a circle, unroll the circle to represent it as an interval, then all particles have a wave function in on that interval, which must be periodic. This type of wave is characterized by a number K and we can represent it as follows, k = 0, (+/-) 1, (+/-) 2, (+/-) 3, etc.

The momentum or energy that the particles possess does not reside in the 10 dimensions, it is hidden in the dimension 11. This internal energy manifests as additional mass in the dimension 11.

Using equations, we can represent it as follows:

λ = (2 π R) / K

λ = h / p

p = (h k) / 2 π R = m c

p² = (h k / 2 π R) ² = m² c²

The energy can be written as:

E = √ {(m² c⁴) + (Px² + Py² +Pz²) C² + (h k / 2 π R) ² C²}

Where the rest mass seen by an observer is equal to:

M² = m² + (h k / 2 π R c) ²

This is the general formula that tells us how to detect an extra dimension.

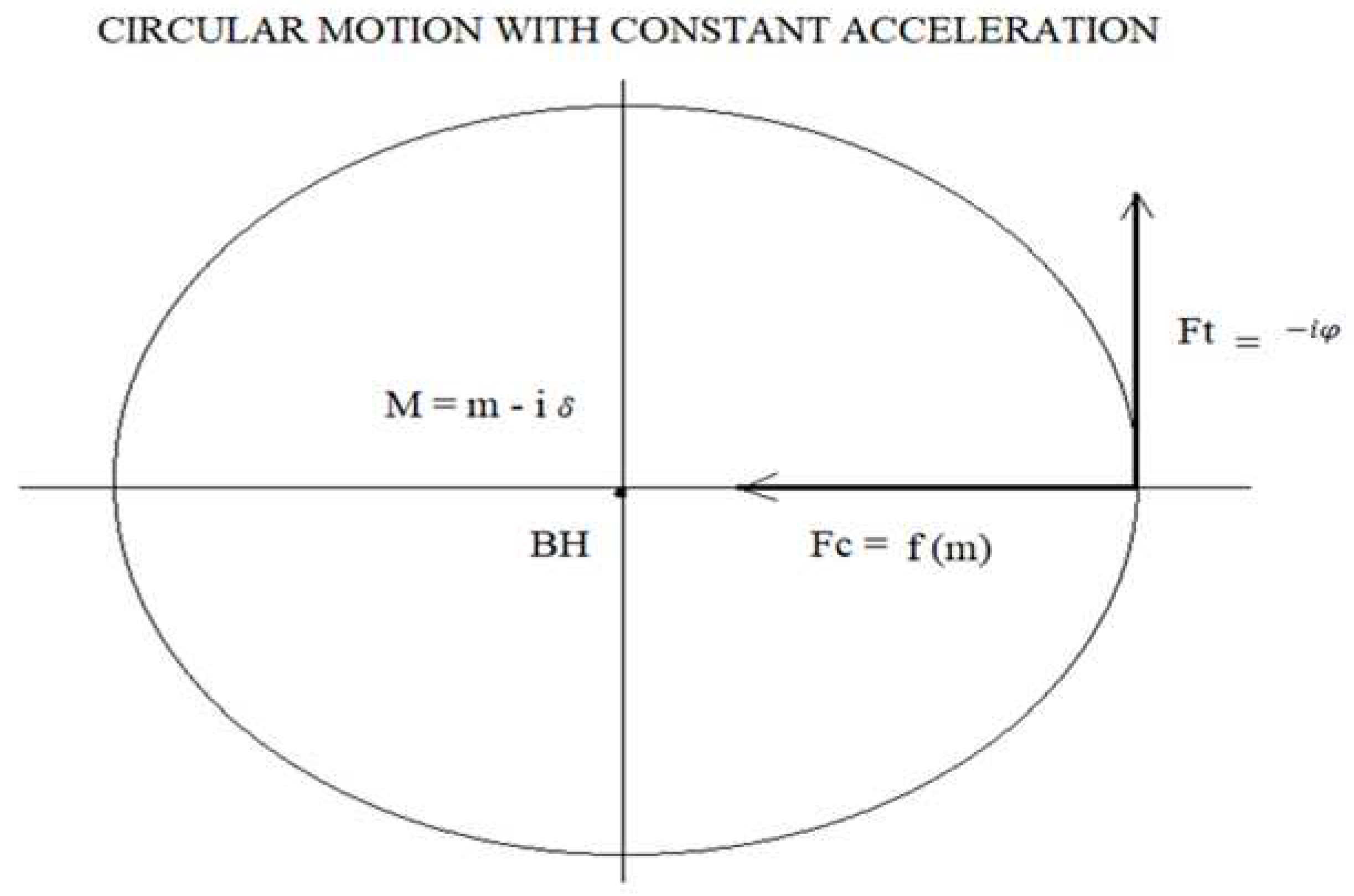
We define that the mass of a black hole is equal to:

$$M=m-i\delta$$

$$M^2=m^2+\delta ²$$

$$\delta ²=(hk/2\pi Rc)²$$

Where $\delta$ represents the imaginary mass of a black hole that results from decompactification of dimension 11 of the M theory and m represents the baryonic mass.

We can complement all the development presented with the analysis carried out in section 3. COSMIC INFLATION, of the paper: RLC Electrical Modelling of Black Hole and Early Universe. Generalization of Boltzmann’s Constant in Curved Space-Time [3].

Specifically, in (18):

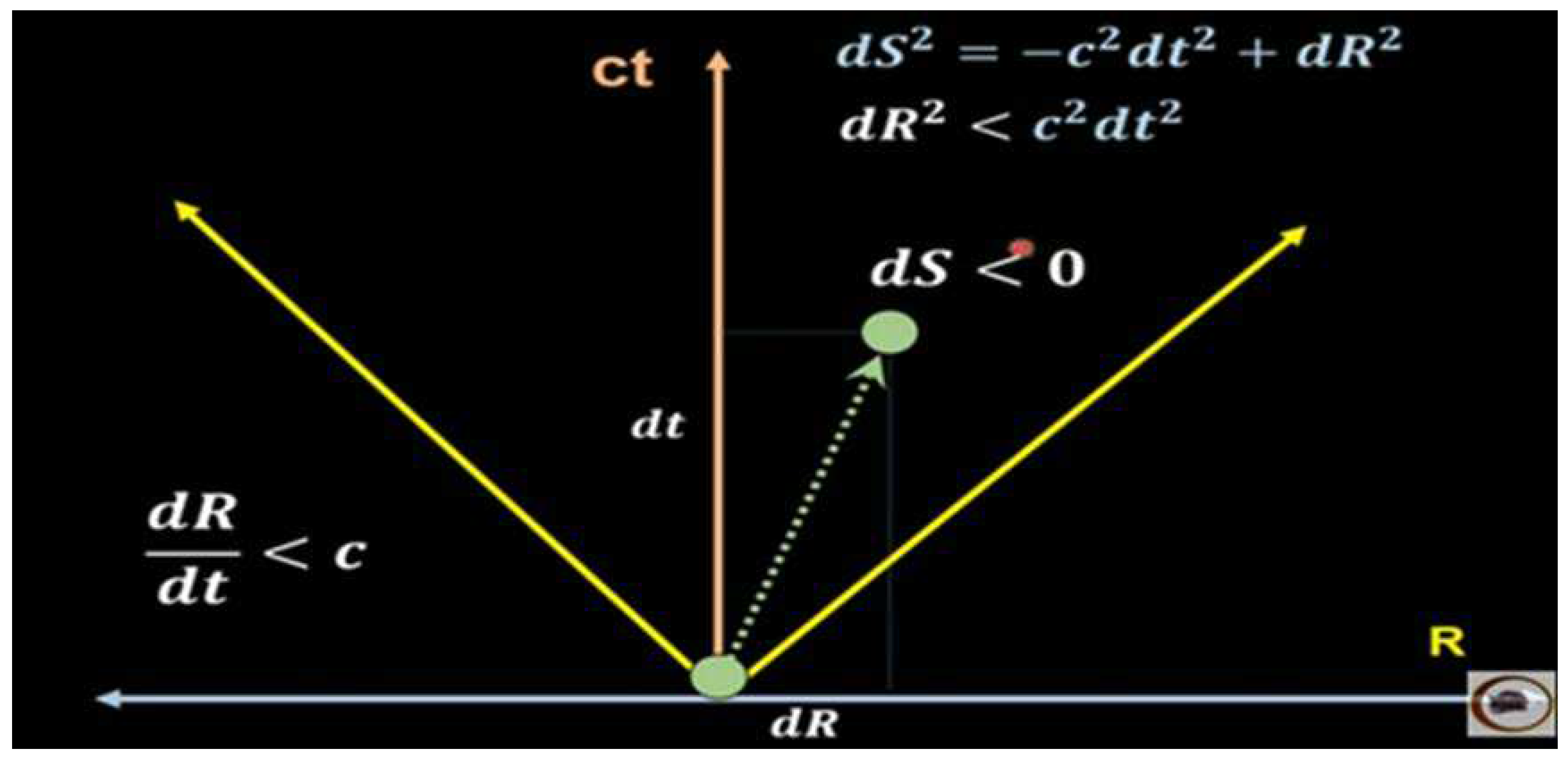
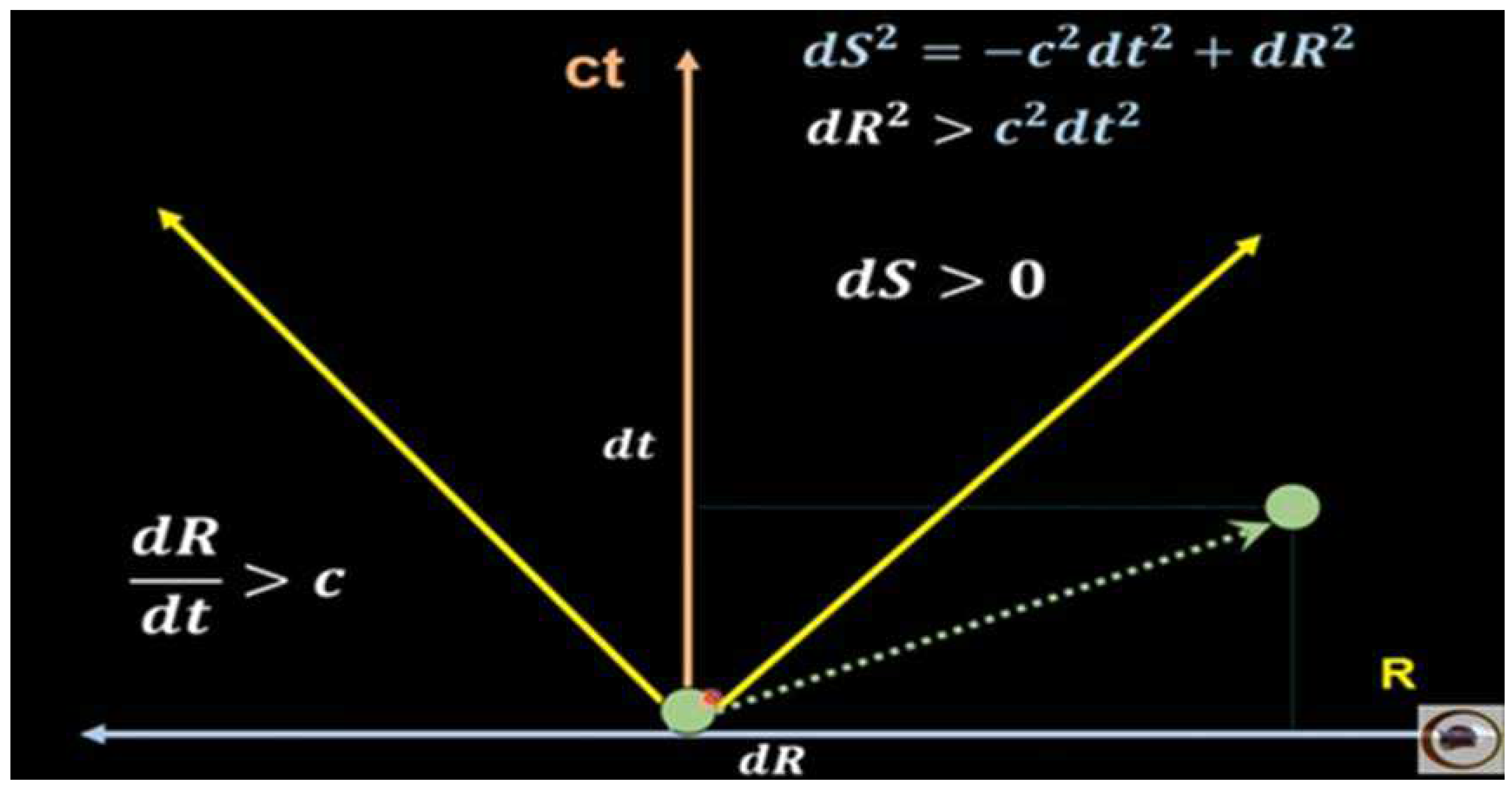
R < Rs, v > c; ds > 0, space type trajectory.

Condition (18) is very important because to the extent that R < Rs, v > c is fulfilled, it is precisely this speed difference that generates the imaginary mass in a black hole given by -iδ.

ADS/CFT correspondence and the theory of the generalization of Boltzmann's constant in curved spacetime

When analysing M-theory and the theory of the generalization of the Boltzmann constant in curved space-time, it is inevitable to make a comparison with the ADS/CFT correspondence.

According to the analysis carried out in M-theory and the theory of the generalization of Boltzmann's constant in curved space-time, in a non-perturbative regime, when gs is infinitely large, we can equate a theory of gravity in anti-de Sitter space ADS n+1-dimensional, with a field theory according to CFT n-dimensional.

We wonder why we can do this? And the answer lies in the value that the Boltzmann constant takes.

We will give the answer with an example where the plasma viscosity of quarks and gluons is calculated. For the non-perturbative regime, for very large gs tending to infinity, we are comparing two theories in which the Boltzmann constants are approximately equal.

For the case of the 11-dimensional ADS theory, where we introduce a black hole, Boltzmann's constant is equal to Kʙ = 1.38 10⁻⁴³ J/K. For the 10-dimensional CFT theory, in which we want to calculate the plasma viscosity of quarks and gluons, the Boltzmann constant is of the order of 0.76 10⁻⁴¹ J/K > Kʙ > 1.78 10⁻⁴³ J/ K.

This tells us that we can use the ADS and CFT theories to calculate the plasma viscosity of quarks and gluons because both theories work in an almost identical non-perturbative regime, which is why whichever of the theories we use to calculate the answer will be practically the same.

In strong coupling, in the limit where gs tends to infinity, that is, in the non-perturbative regime, we can reduce superstring theory to general relativity and with that we can simply use a theory of gravity in anti-de Sitter space ADS, to describe the strong coupling regime of a particle theory, we call dual QCD. This becomes a very useful duality.

In other words, whenever we use a CFT theory that works with a Boltzmann constant close to Kʙ = 1.78 10⁻⁴³ J/K, we can say that the duality ADS = CFT is fulfilled.

Up to this point, we have analysed superstring theory and M theory. I consider it very important to make a small summary of the first bosonic string theory.

Bosonic string theory

Describes the behaviour of both open strings and closed strings. However, the theory has several problems, three being the main ones: absence of fermions, existence of tachyons and the number of dimensions.

The name bosonic string theory is a consequence of the fact that theory is only capable of describing bosons and therefore does not include to ordinary matter that is composed of fermions.

Furthermore, when developing the theory, a particle emerges that has a speed greater than that of light, and therefore, according to relativity, an imaginary mass. This particle is known as Tachyon and has been tried to eliminate it from the theory, although without result.

Finally, for this theory to have quantum consistency, it is necessary to consider that the background space-time has 26 dimensions: 1 temporal and the rest spatial.

If we analyse the interior of a black hole or the beginning of the Big Bang, we can hypothesize that space-time is dominated by bosonic strings, that is, space-time is in the domain of the inverse symmetry break of the electro-weak theory, dominated only by elementary bosons.

Let us remember that the dimensions are a function of the energy, therefore at high temperatures, high energies correspond and this implies that the dimensions are high.

Finally, there is the tachyon, a bosonic particle whose speed v >> c, let us remember that in the inside a black hole or at the beginning of the big bang with the expansion of the universe, it is true that gravitons as well as particles of elementary matter move at a speed v greater than c, in accordance with space-time.

Here we are postulating the following hypothesis in which we say that the bosonic string theory applies only to the interior of a black hole and to the beginning of the big bang.

When we say that the speed of tachyons is greater than the speed of light inside black holes, this does not contradict Einstein's theories.

Let's explain it, according to the theory of the RLC electrical model of the universe, it happens that inside a black hole as it grows following the law of the constant Tau of the RC circuit, the Planck length Lp decreases.

If we consider that the speed is equal to V = e/t, as the Planck length decreases, time also decreases, now if we consider that the Planck length is constant, as time decreases the speed increases.

This is what makes us think that the speed increases inside a black hole, but in reality, if we combine the correct variation of the gravitational Planck length Lpɢ with the correct time variations, the speed really remains c, the speed of light.

That is why we say that inside a black hole the trajectories are of the time type, while on the outside of a black hole the trajectories are of the space type.

Inside a black hole, the gravitational Planck length Lpɢ is smaller than the electromagnetic Planck length Lpɛ.

Generalizing, inside black holes and at the beginning of the Big Bang, they are under the domain of bosonic string theory. Outside of black holes, it is under the domain of superstring theory and M-theory.

Both theories are complementary to the theory proposed in this paper, DST = EQFT duality.

Gauge Symmetries

The idea of Gauge theory is the following, we take a field that has a symmetry s, from that, we extract the fundamental characteristics of the field, which in the case of gauge theory are the interactions, that is, a force field.

Adding a field to restore the invariance of physics is the basis of all fundamental interactions in particle physics.

This is the basic idea, of which the interactions of electromagnetic force fields, weak force field interactions and strong force field interactions are born.

The study of the symmetries of the universe allows us to understand in a deeper way the origin of the laws that govern it.

Standard Model

The standard model is the unification of three different symmetry, the symmetry of electromagnetism, the symmetry of isospin and the symmetry of colours.

We can represent this in the following way:

SU(3) x SU(2) x U(1)

U(1) Symmetry and electromagnetic interaction field

The quantum field of the electrons has a global symmetry when we shift all the complex numbers in the same way, but if we locally shift the different parts of the field in a different way, the laws that describe the electrons seem to change, this change of reference does not obey to symmetry, if we want to re-establish the absolute nature of the laws of physics, whatever the reference level we choose, we must introduce a force field with which it interacts with the field of electrons, called the electromagnetic field, which has particles that interact with electrons called photons.

SU(2) symmetry and the weak force interaction field

interaction between protons and neutrons.

SU(2)

W(+/-) bosons and Z boson are excitations of the SU(2) field

SU(3) ) symmetry and the strong force interaction field

Interactions between quarks.

SU(3)

Gauge field: gluons

We will analyse and compare the theory of the standard model and the theory proposed in this paper.

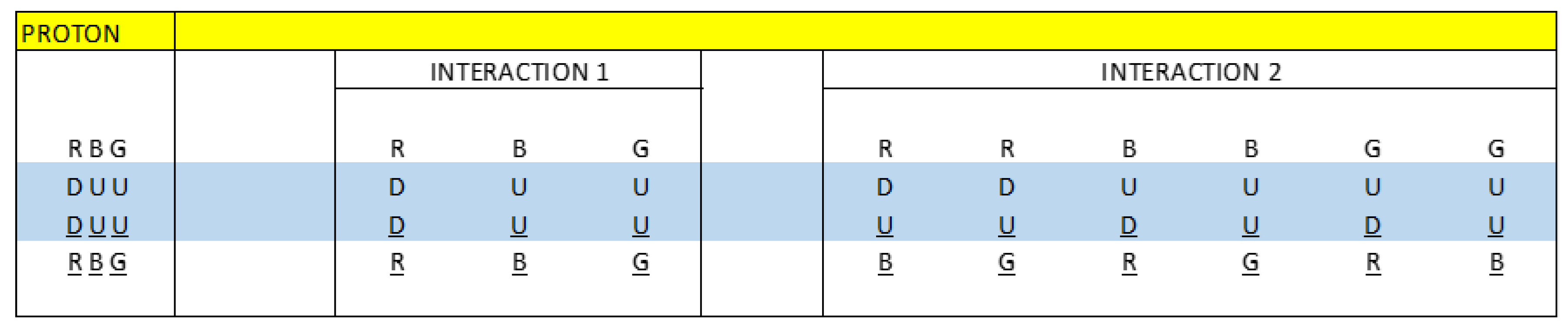
In the paper: Electrical-Quantum Modelling of the Neutron and Proton as a Three-Phase Alternating Current Electrical Generator. Determination of the Number of Quarks-Antiquarks-Gluons and Gravitons [1], inside a Neutron, we develop a model for the neutron and proton, equivalent to a three-phase electric generator.

This model uses quarks and antiquarks, gluons are the charge carriers between quarks and antiquarks interactions.

We define two types of interactions, interaction 1 or direct interaction and interaction 2 or cross interaction.

The markers, R B G and R B G, are used to remind us that interactions 1 and interaction 2 are vectors and have an angle.

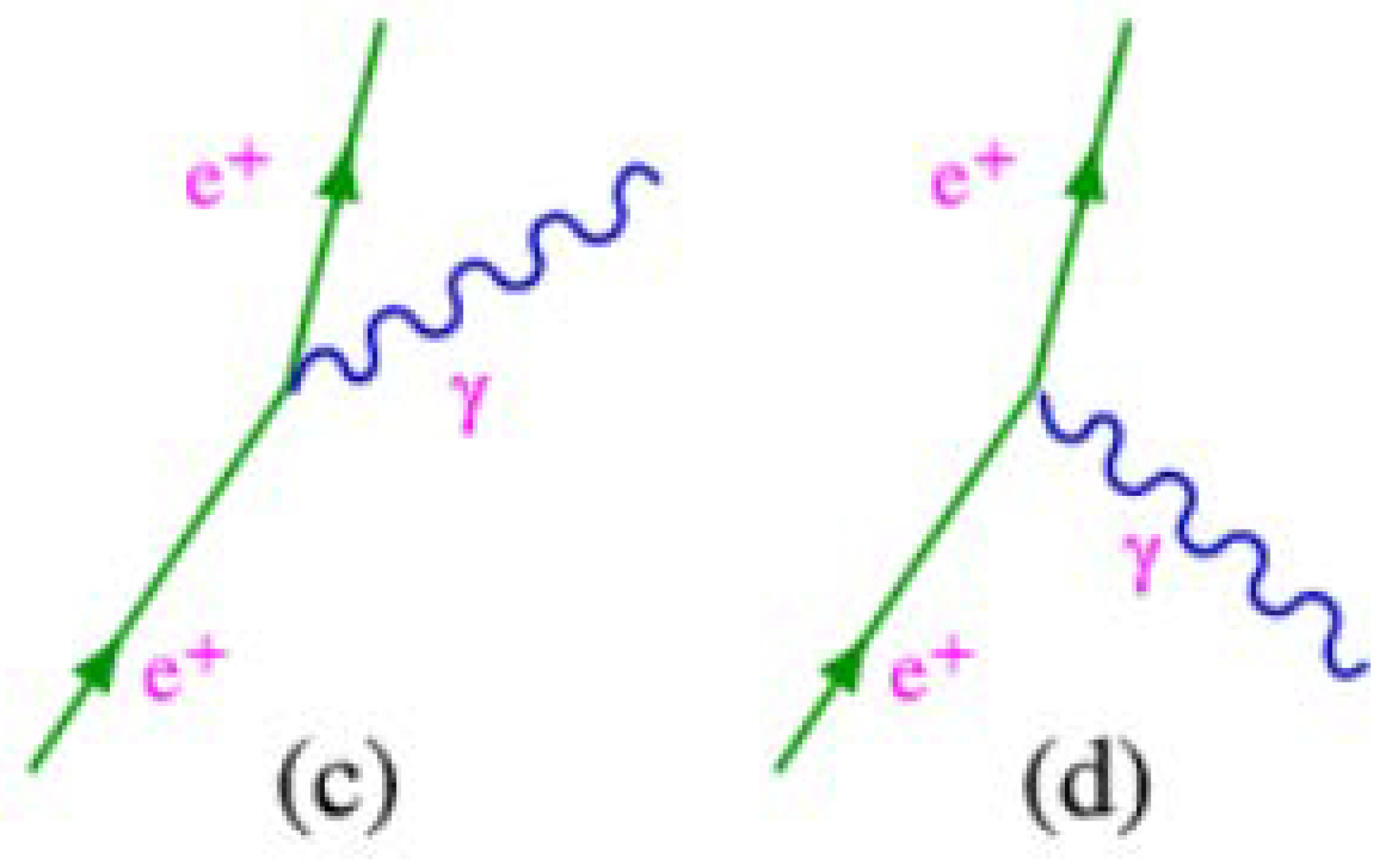
When we analyse β ˉ decay, we discover that photons are a particular case of gluons that can escape confinement.

When we analyse β ˉ decay, we show that the Wˉ boson is the result of quarks-antiquarks-gluons interactions, they are ideal bosons, which originate when a neutron transforms into a proton. This allowed us to generalize for the W+ and Z⁰ bosons, which are also ideal bosons, the result of quarks-antiquarks-gluon interactions.

When we analyse the models proposed for photons and gluons, we observe that they are composed of sub-particles or elementary electric quanta.

To conclude, i want to say that in our model, all force interactions are reduced to a single electrical or electromagnetic interaction.

In our model, the weak interaction is reduced to an electrical interaction given by the quarks-antiquarks-gluons interactions.

In our model, the strong interaction is reduced to an electrical interaction given by the quarks-antiquarks-gluons interactions.

In other words:

SU(3) x SU(2) x U(1), standard model

is reduced to:

U(1), proposed model

Finally, our proposed model simplifies the three interactions that exist in the standard model to a single electromagnetic or electrical interaction.

5.8.4. DST = EQFT, Theory of Everything (T.O.E.)

Based on the development of the following items:

Quantization of space-time (DST) and matter (EQFT)

Quantization of the curvature of space-time

Electrical modelling of a neutron as a three-phase alternating current generator. Origin of mass and gravity.

Electrical-quantum modelling of the neutron as a three-phase alternating current electrical generator

Mechanism that generates mass in neutrons, calculation of the number of quarks-antiquarks-gluons inside a neutron

Calculation of the number of gluons by dividing the volume of the neutron by the volume of the quark.

Mechanism that generates gravity in neutrons, calculation of the number of gravitons inside a neutron.

M-theory, extra dimensions and the theory of the generalization of Boltzmann's constant in curved spacetime

Gauge Symmetries

We will propose a generalization of the ADS/CFT correspondence. Here we hypothesize that we replace the ADS/CFT correspondence with a general equation given by DST = EQFT duality.

ADS is replaced by DST; DST represents a theory of quantum gravity associated with the theory of the generalization of the Boltzmann constant in curved space-time.

CFT is replaced by EQFT, EQFT represents a unique electric quantum field theory, which unites the electromagnetic field theory, the weak field theory and the strong field theory and is associated with the theory: Electrical-Quantum Modelling of the Neutron and Proton as a Three-Phase Alternating Current Electrical Generator [1].

DST = EQFT, theory of everything (T.O.E.)

Here we put forward the hypothesis that the equation DST = EQFT, represents the theory of everything, is the equation that unites gravity and quantum mechanics, this fact is achieved through the theory of the generalization of the constant of Boltzmann in a curved space-time and electrical-quantum modelling of the neutron and proton as a three-phase alternating current electrical generator

We can represent it using the following general equations:

We will describe simple equations that represent the electromagnetic wave spectrum.

Eε = h x fε

Cε = λε x fε

Eε = h x Cε / λε

Eε = Kʙε x Tε

Kʙε = 1.38 10⁻²³ J/K

We will describe simple equations that represent the gravitational wave spectrum.

Eɢ = h x fɢ

Cɢ = λɢ x fɢ

Eɢ = h x Cɢ / λɢ

Eɢ = Kʙɢ x Tɢ

Kʙɢ = 1.38 10⁻²³ J/K > Kв ef > 1.78 10⁻⁴³ J/K

In the paper: RLC Electrical Modelling of Black Hole and Early Universe. Generalization of Boltzmann’s Constant in Curved Space-Time, we explain the origin of the universe, the origin of cosmic inflation, the origin of dark matter and the origin of dark energy [3].

In the paper: Theory of the Generalization of the Boltzmann’s Constant in Curved Space-Time. Shannon-Boltzmann Gibbs Entropy Relation and the Effective Boltzmann’s Constant, we explain how we can quantify the curvature of space-time and show using the Shannon-Boltzmann-Gibbs entropy relation that information is conserved [2].

In the paper: RC Electrical Modelling of Black Hole. New Method to Calculate the Amount of Dark Matter and the Rotation Speed Curves in Galaxies, we explain how we can calculate the amount of dark matter in a galaxy and how we can model the rotation curves of a galaxy using a new method [4].

In the paper: Electrical-Quantum Modelling of the Neutron and Proton as a Three-Phase Alternating Current Electrical Generator. Determination of the Number of Quarks-Antiquarks-Gluons and Gravitons, inside a Neutron, considering a neutron and a proton as three-phase alternating current energy generators, we explain how the mass is generated (we calculate the number of quarks-antiquarks-gluons) and the gravity (we calculate the number of gravitons) in a neutron [1].

In this paper, using the theory of the generalization of the Boltzmann constant in curved space-time, we proposed a method to determine the origin of elementary particles and how matter/energy is related to gravity, this allowed us to generalize the correspondence ADS/CFT, for a general theory or theory of everything.

The theory of the generalization of the Boltzmann constant and the quantum-electrical modelling of the neutron and the proton as a three-phase alternating current electrical generator, are the fundamental basis or pillar that allows us to unite the theory of general relativity and quantum mechanics.

This theory allows us to quantify space-time, it allows us to quantify the curvature of space-time, it does not allow us to unite the field theory of electromagnetic interactions, weak interaction and strong interaction in a single quantum field theory of electrical interactions EQFT.

Finally, it allows us to generalize the Maldacena ADS/CFT correspondence. It allows us to propose a universal theory or theory of everything, represented by the equation DST = EQFT.

Thoughts and reflections:

Higgs mechanism versus conformal mechanism

Gauge symmetry demands massless particles. The Higgs mechanism, on the other hand, is a technique for determining particle mass. In this case, the symmetry is broken at the price of providing particles with mass. This interaction occurs in a flat space. However, in curved space, particle mass may violate a symmetry known as conformal symmetry.

Breaking this symmetry is proven to give gravitons, photons, scalar fields (bosons), and Dirac particles mass in flat space. This mass is directly proportional to the conformal factor's (field) temporal derivative. The equation of motion of a particle in conformal space in curved space looks to be moving in a fluid (viscous), which may be the cause of inertia. There appears to be a background (conformal) field present with which particles and fields interact.

This text was posted by Arbab Ibrahim (Abdus Salam Intentional Centre for Theoretical Physics (ICTP)- Trieste-Italy), in QUANTUM PHYSICS [5].

This text, highlights the essence of this paper, shows us how the breakdown of symmetry in curved space-time provides mass to fermionic and bosonic particles as a function of temperature, as the temperature increases, the curvature of space-time increases, the fermionic and bosonic particles of the standard model acquire mass, it includes photons and gravitons to be clear.

It is precisely this reasoning that led us to generalize the Maldacena ADS/CFT correspondence, where conformal quantum fields CFT, a particular case of quantum field theory, are generalized to the entire quantum field theory EQFT.

DST represents dynamic space-time, which we have shown is quantized, is on a plane of equality with EQFT, represented by electrical quantum field theory; this duality, DST = EQFT, represents the equation of the theory of everything.

To conclude our work, we are going to perform the following examples:

Example 1:

Quantification of space-time curvature

In the paper: RLC Electrical Modelling of Black Hole and Early Universe. Generalization of Boltzmann’s Constant in Curved Space-Time [3], we perform this example.

The observation of the 1919 solar eclipse in Brazil and Africa provided the first experimental proof of the validity of Albert Einstein's theory of relativity. We will calculate the Boltzmann constant for the sun and show how it adjusts to the deviation found.

No solar eclipse has had as much impact in the history of science as that of May 29, 1919, photographed and analysed at the same time by two teams of British astronomers. One of them was sent to the city of Sobral, Brazil, in the interior of Ceará; the other to the island of Principe, then a Portuguese territory off the coast of West Africa. The goal was to see if the path of starlight would deviate when passing through a region with a strong gravitational field, in this case the surroundings of the Sun, and by how much this change would be if the phenomenon was measured.

Einstein introduced the idea that gravity was not a force exchanged between matter, as Newton said, but a kind of secondary effect of a property of energy: that of deforming space-time and everything that propagates over it, including waves like light. “For Newton, space was flat. For Einstein, with general relativity, it curves near bodies with great energy or mass”, comments physicist George Matsas, from the Institute of Theoretical Physics of the São Paulo State University (IFT-Unesp). With curved space-time, Einstein's calculated value of light deflection nearly doubled, reaching 1.75 arcseconds.

The greatest weight should be given to those obtained with the 4-inch lens in Sobral. The result was a deflection of 1.61 arc seconds, with a margin of error of 0.30 arc seconds, slightly less than Einstein's prediction.

Demonstration:

Let us calculate the Boltzmann´s constant for the Sun, Kʙs, curved space-time.

Hawking's temperature equation:

Kʙs = (h x c³) / (8 x π x Ts x G x Ms)

Where Kʙs is the Boltzmann constant for the sun, Ts is the temperature of the sun's core, G is the universal constant of gravity, and Ms is the mass of the sun.

Kʙs = (6.62 10⁻³⁴ x 27 10²⁴) / (8 x 3.14 x 1.5 10⁷ x 6.67 10⁻¹¹ x 1.98 10³⁰)

Kʙs = 3.59 10⁻³⁷ J/K, Boltzmann's constant of the sun.

We use the following equation:

Es = Kʙs x Ts

Es = 3.59 10⁻³⁷ x 1.5 10⁷

Es = 5.38 10⁻³⁰ J/K

We use the following equation:

Es = h x fs

fs = Es / h

fs = 5.38 10⁻³⁰ / 6.62 10⁻³⁴ = 0.81 10⁴ = 8.1 10³ Hz

fs = 8.1 10³ Hz

We use the following equation:

c = λs x fs

λs = c / fs

λs = 3 10⁸ / 8.1 10³

λs = 3.7 10⁴ m

We use the following equation:

Degree = λs / 360

Degree =102.77 m

We use the following equation:

Arcsecond = degree / 3600

Arcsecond = 102.77 m / 3600 = 0.0285 m

1.61 arcsecond = 0.0458 m

1 inch = 0.0254 m

4 inch = 0.1016 m

With a 4-inch lens, we can measure the deflection produced by the 1.61 arcsecond curvature of space-time, which was predicted by Albert Einstein's theory of general relativity, and corresponds to a wavelength λs = 3.7 10⁴ m, a frequency fs = 8.1 10³ Hz, for an effective Boltzmann constant of the sun Kʙs = 3.59 10⁻³⁷ J/K.

We will carry out the same calculations for Kʙ = 1.38 10⁻²³ J/K, flat space-time.

Kʙ = 1.38 10⁻²³ J/K

We use the following equation:

E = Kʙ x Ts

E = 1.38 10⁻²³ x 1.5 10⁷

E = 2.07 10⁻¹⁶ J/K

We use the following equation:

E = h x f

f = E / h = 2.07 10⁻¹⁶ / 6.62 10⁻³⁴

f = 3.12 10¹⁷ Hz

We use the following equation:

c = λ x f

λ = c / f

λ = 3 10⁸ / 0.312 10¹⁸

λ = 9.61 10⁻¹⁰ m

We use the following equation:

Degree = λ / 360

Degree = 0.02669 10⁻¹⁰ m

We use the following equation:

Arcsecond = degree / 3600

Arcsecond = 7.41 10⁻¹⁶ m

Using the Boltzmann constant Kʙ = 1.38 10⁻²³ J/K, we cannot correctly predict by mathematical calculations the deflection of light given by Albert Einstein's general theory of relativity, to be measured in the telescope at Sobral.

Through the example given, we can conclude that the Boltzmann´s constant Kʙs = 3.59 10⁻³⁷ J/K fits the calculations of the deflection of light in curved space-time.

Example 2:

Quark-gluon viscosity

We ask ourselves, why do we use the Boltzmann constant of a black hole to calculate the viscosity of a quark-gluon plasma?

We will give the answer with an example where the plasma viscosity of quarks and gluons is calculated. For the non-perturbative regime, for very large gs tending to infinity, we are comparing two theories in which the Boltzmann constants are approximately equal.

For the case of the 11-dimensional ADS theory, where we introduce a black hole, Boltzmann's constant is equal to Kʙ = 1.38 10⁻⁴³ J/K. For the 10-dimensional CFT theory, in which we want to calculate the plasma viscosity of quarks and gluons, the Boltzmann constant is of the order of 0.76 10⁻⁴¹ J/K > Kʙ > 1.78 10⁻⁴³ J/ K.

This tells us that we can use the ADS(DST) and CFT(EQFT) theories to calculate the plasma viscosity of quarks and gluons because both theories work in an almost identical non-perturbative regime, which is why whichever of the theories we use to calculate the answer will be practically the same.

In strong coupling, in the limit where gs tends to infinity, that is, in the non-perturbative regime, we can reduce superstring theory to general relativity and with that we can simply use a theory of gravity in anti-de Sitter space ADS, to describe the strong coupling regime of a particle theory, we call dual QCD. This becomes a very useful duality.

In other words, whenever we use a CFT theory that works with a Boltzmann constant close to Kʙ = 1.78 10⁻⁴³ J/K, we can say that the duality ADS = CFT is fulfilled.

Using the formulas found in the scientific article [6], we have:

ɲ, shear viscosity.

VQGP, Kinematic viscosity.

VQGP = 3 x h x c² / (4 x π x Kʙ x T)

ɲ/S = VQGP x T, viscosity entropy ratio

Calculation of the viscosity of quark-gluon plasma:

Considering that a quark-gluon plasma has a Boltzmann constant given by:

Kʙ = 1.78 10⁻⁴³ J/K

VQGP = 3 x h x c² / (4 x π x Kʙ x T), ħ = h / (2π)

c = 3 10⁸ m/s

T = 10¹³ K

h = 6,62 10⁻³⁴ (m² x kg)/s

VQGP = (3 x 6.62 10⁻³⁴ x 9 10¹⁶) / (4 x 3.14 x 1.78 10⁻⁴³ x 10¹³ x (2 x 3.14))

VQGP = (178.74 10⁻¹⁸) / (140.40 10⁻³⁰)

VQGP = 1.27 10¹²

ɲ/s = VQGP x T; Applying the following formula we have:

ɲ/s = 1.27 10¹² x 10¹³ = 1.27 10²⁵

ɲ/s = 1.27 10²⁵; viscosity-entropy relationship.

Figure 44. QGP plasma viscosity applying the Maldacena correspondence.

Figure 44. QGP plasma viscosity applying the Maldacena correspondence.

If we look at Figure 44, we will see that the viscosity of the QGP plasma, by the holographic method, is ɲ/s = 0.1, less than liquid helium (superfluid) and less than water. We ask ourselves, is this value correct? Could it be that a black hole with a density of approximately 10²¹ kg/m³, a density similar to that of QGP plasma, behaves like a superfluid whose viscosity is lower than that of liquid helium?

In the paper: RLC Electrical Modelling of Black Hole and Early Universe. Generalization of Boltzmann's Constant in Curved Space-Time [3], the critical temperature for the Bose-Einstein condensate of rubidium atoms was calculated for the following values of the Boltzmann constants, Kʙ = 1.38 10⁻²³ J/K and Kʙ = 1.78 10⁻⁴³ J/K, both values of the Boltzmann constant indicate that there are two types of temperatures that allow the creation of a Bose-Einstein condensate:

• Tc, min = 170 10⁻⁹ K, minimum critical temperature of the Bose-Einstein condensate for low temperatures, with rubidium atoms.

• Tc, max = 1.01 10¹³ K, maximum critical temperature of the Bose-Einstein condensate for high temperatures with rubidium atoms.

At this point, we have to clarify that a black hole is a QGP plasma, a high-temperature Bose-Einstein condensate in which the quarks behave as if they were free, generating a cascade of gluons of infinite energy, forming the state most energetic that exists in the universe.

If we look again at Figure 44, we see that the viscosity ɲ/s = 10¹¹ for brea. In our calculation, for a black hole of 3 solar masses, a density of approximately 10²¹ kg/mᶾ, the value of the viscosity is of the order of ɲ/s = 10²⁵; i interpret that this value is more in line with reality, it is the correct value, taking into account the density.

Let's try to understand why the behaviour of the quark-gluon plasma resembles that of a superfluid. If we remember how we generate the scale factor of the Boltzmann constant, as matter gains energy and goes through the states of a white dwarf star, neutron star, until forming a QGP plasma; we see that the Boltzmann constant changes from Kʙ = 1.38 10⁻ ²³ J/K to 1.78 10⁻⁴³ J/K; This gives us an idea of how compacted or concentrated the mass is (gains energy) and how curved space-time is. This curvature of space-time is proportional to the amount of energy that the mass gains and we can compare it to a spring that compresses.

When we produce the QGP in a particle accelerator, the quark-gluon plasma has stored energy but this state is not stable and at this point the QGP has an approximate Boltzmann constant Kʙ = 1.78 10⁻⁴³ J/K. For curved space-time and matter to return to their stable state, the Boltzmann constant must go from Kʙ = 1.78 10⁻⁴³ J/K to 1.38 10⁻²³ J/K, that is, in this point all the energy stored in the compressed spring is released until it reaches its natural state, that is, until the Boltzmann constant reaches the value of Kʙ = 1.38 10⁻²³ J/K. It is this energy that makes QGP look like a superfluid, but in reality, if we consider the scale factor of the Boltzmann constant, we will see that ɲ/s = 1.27 10²⁵ (viscosity-entropy relationship). The energies involved in this process are very great.

I can't imagine how something that has a density on the order of 10²¹ kg/mᶾ behaves like a superfluid with a lower viscosity than liquid helium.

Possibly, in the Boltzmann constant Kʙ is the response to the erroneous value given by the holographic method to calculate the viscosity of the QGP, ɲ/s = 0.1; I leave it to the reader to draw their own conclusions.

Example 3:

The two states of the Higgs field

By studying the Higgs field, theoretical physicists have discovered that the Higgs field, which permeates all of spacetime, exists in two states, in addition to the state known today; There is a second state thousands of times denser called the ultra-dense state of the Higgs field. This creates a potential problem, which is the possibility of a transition between the two states. We will analyse that this transition is almost impossible to happen.

First state of the Higgs field:

The Higgs field that we know today fills the entire space-time of our universe and together with the gravitational field, gives mass to the particles, for example, when the elemental energy corresponding to the electron moves in the Higgs field and the field gravitational, its interaction with the two fields gives the mass to the electron as we know it in the standard model table.

The Higgs boson is the excitation of the Higgs field; the Higgs field should not be confused with the Higgs boson.

The Higgs field has a value in vacuum and corresponds to:

H = 246 GeV (2.85 10¹⁵ K), this corresponds to a minimum potential energy V that gives stability to our current universe.

Second state of the Higgs field - Ultra dense state

Hypothesis: I propose that the ultra-dense state of the Higgs field occurs inside black holes.

In the paper: Electrical-Quantum Modelling of the Neutron and Proton as a Three-Phase Alternating Current Electrical Generator. Determination of the Number of Quarks-Antiquarks-Gluons and Gravitons, inside a Neutron [1]; We proposed a model for black holes which we are going to represent in the following figure:

Figure 45. Equivalent Neutron / Black Hole.

Figure 45. Equivalent Neutron / Black Hole.

The explosion of a supernova goes beyond chemical energy or nuclear energy; that is why we propose that a supernova when it explodes separates matter m (+) from antimatter m (-), in other words, the black hole that remains would be made up of matter and the antimatter expands in the space-time that surrounds the black hole.

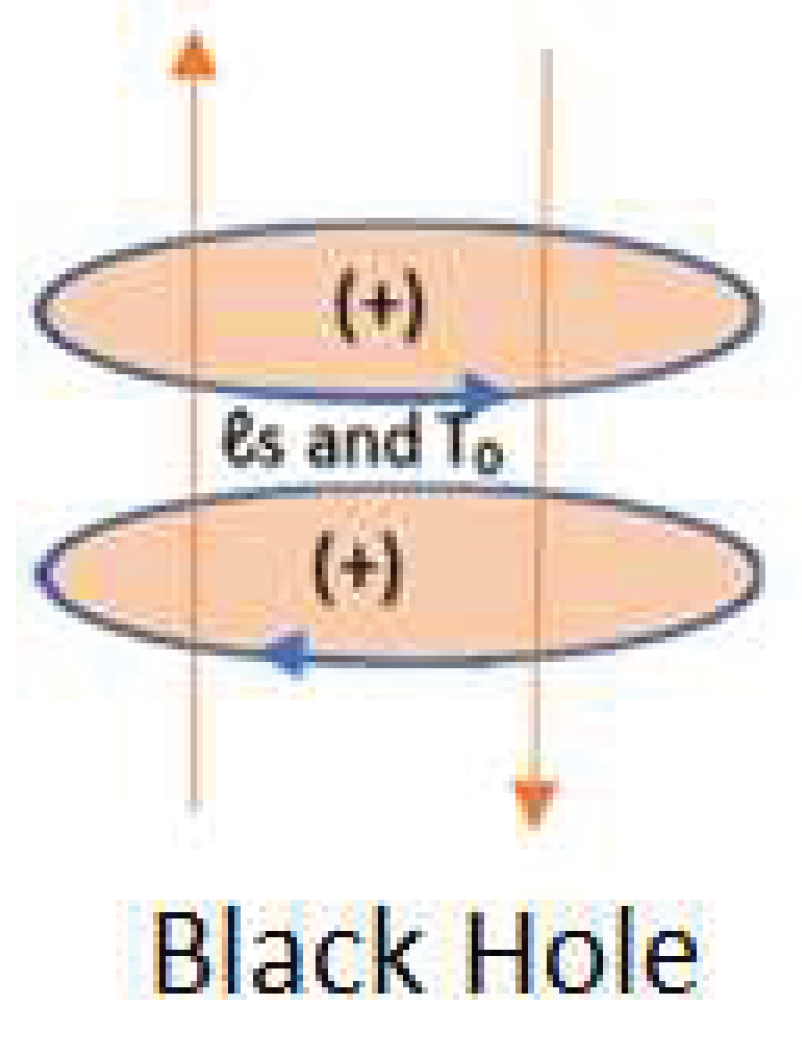
With this we are proposing that inside a black hole there is no antimatter m (-), that is, the interior of a black hole is made up only of matter m (+). This is represented in figure 45 and 46.

Figure 46. Black Hole, the orange arrows represent magnetic fields, the blue arrows represent electric fields.

Figure 46. Black Hole, the orange arrows represent magnetic fields, the blue arrows represent electric fields.

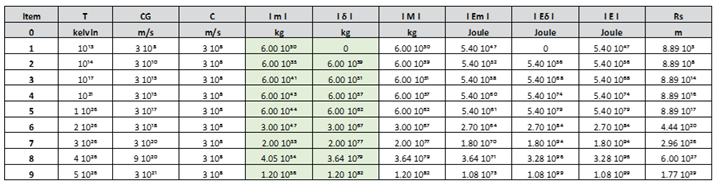
To conclude, let's consider the following table:

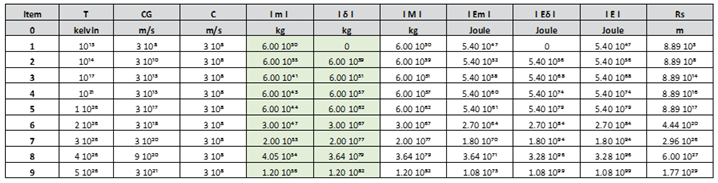
Table 13. Represents values of ImI, baryonic mass; IδI, dark matter mass; IMI, mass of baryonic matter plus the mass of dark matter; IEmI, energy of baryonic matter; IEδI, dark matter energy; IEI, Sum of the energy of baryonic matter plus the energy of dark matter and Rs, Schwarzschild´s radius, as a function of, c, speed of light; Cɢ, speed greater than the speed of light; T, temperature in Kelvin; using the parametric equations.

Table 13. Represents values of ImI, baryonic mass; IδI, dark matter mass; IMI, mass of baryonic matter plus the mass of dark matter; IEmI, energy of baryonic matter; IEδI, dark matter energy; IEI, Sum of the energy of baryonic matter plus the energy of dark matter and Rs, Schwarzschild´s radius, as a function of, c, speed of light; Cɢ, speed greater than the speed of light; T, temperature in Kelvin; using the parametric equations.

Conclusion:

The ultra-dense Higgs field inside a black hole is not constant and varies between the following extremes:

H1 = 8.6 GeV (10¹³ K), minimum value of the ultra-dense Higgs field, occurs when a stellar black hole of three solar masses forms. See table 13.

H2 = 4.4 10¹⁵ GeV (5 10²⁶ K), maximum value of the ultra-dense Higgs field, is the value that the Higgs field takes inside a black hole at the moment it explodes and produces a white hole or Big Bang. See table 13.

The ultra-dense state of the Higgs field varies between the values of H1 = 8.6 GeV (10¹³ K) < ultra-dense Higgs field < H2 = 4.4 10¹⁵ GeV (5 10²⁶ K); and only occurs inside black holes.

The first state of the Higgs field is associated with the false vacuum, domain of the four fundamental forces; The ultra-dense state of the Higgs field is associated with the true vacuum, domain of the gravitational force field.

Figure 47. The two states of the Higgs field.

Figure 47. The two states of the Higgs field.

Example 4:

Calculation of the entropy of a black hole, neutron star and white dwarf star

To perform entropy calculations for stellar bodies such as white dwarf stars and neutron stars or possibly any stellar body, we will first calculate the equivalent black hole of the body of interest and then using the entropy formula of a black hole, we will calculate the entropy value for that body in question; As a final result, the entropy of the body of interest will be less than or equal to the entropy of its counterpart black hole. Using this mechanism, we can estimate the approximate entropy value of any stellar body knowing that it cannot be greater than the entropy of its equivalent black hole.

We will calculate the entropy value for the following situations:

A) Calculation of the entropy of a black hole of three solar masses.

B) Calculation gives the entropy of a black hole at the moment of the Big Bang.

C) Calculation of entropy for a neutron star.

D) Calculation of entropy for a white dwarf star.

We are going to use the following entropy equations:

S = (4 π Kʙ x G² x M²) / Lp² x C⁴

(23)

S = (π x Kʙ x Rs²) / Lp²

(24)

Kʙ = Boltzmann constant, G = Universal gravitational constant, M = mass of a body to calculate entropy, Lp = Planck length, C = Speed of light and Rs = Schwarzschild radius.

Comments:

When applying the formula to calculate the entropy of a black hole, it is important to clarify that the Boltzmann constant used corresponds to the Boltzmann constant of a black hole and assumes the following value, Kʙ = 1.78 10⁻⁴³ J/K.

The values from table 9 and 10 were used.

A) Calculation of the entropy of a black hole of three solar masses

M = 3ϴ = 6 10³⁰ kg

Kʙ = 1.78 10⁻⁴³ J/K

C = 3 10⁸ m/s

Lp = 1.61 10⁻³⁵ m

S = (4 π Kʙ x G² x M²) / Lp² x C⁴

Replacing the values,

S = 4 x 3.14 x 1.78 10⁻⁴³ x 36 10⁶⁰ x 44.48 10⁻²² / (2.59 10⁻⁷⁰ x 81 10³²)

S = 35799.49 10⁻⁵ / 209.79 10⁻³⁸

S = 1.70 10³⁵ J/K

B) Calculation gives the entropy of a black hole at the moment of the Big Bang

M = 1.20 10⁸² kg

Kʙ = 1.78 10⁻⁴³ j/k

C = 3 10²¹ m/s

Lp = 1.27 10⁻⁵⁴ m

Rs = 1.59 10³⁰ m

S = 4 π Kʙ x G² x M² / (Lp² x C⁴)

Replacing the values,

S = 4 x 3.14 x 1.78 10⁻⁴³ x 1.44 10¹⁶⁴ x 44.48 10⁻²² / (1.61 10⁻¹⁰⁸ x 81 10⁸⁴)

S = 1431.97 10⁹⁹ / 130.41 10⁻²⁴

S = 1.098 10¹²⁴ J/K

S = π Kʙ x Rs² / Lp²

S = 3.14 x 1.78 10⁻⁴³ x 2.52 10⁶⁰ / 1.61 10⁻¹⁰⁸

S = 14.08 10¹⁷ / 1.61 10⁻¹⁰⁸

S = 8.74 10¹²⁵ J/K

C) Calculation of entropy for a neutron star

M = 2.2Mϴ = 4.4 10³⁰ kg

Calculation of the Schwarzschild radius.

Rs = 2 x G x M/C²

Rs = 2 x 6.67 10⁻¹¹ x 4.4 10³⁰ / 9 10¹⁶ = 58.69 10³⁰ / 9 10¹⁶ = 6.52 10³ m

Rs = 6.52 10³ m

Entropy calculation:

S = π Kʙ x Rs² / Lp²

S = 3.14 x 1.78 10⁻⁴³ x 42.51 10⁶ / 2.59 10⁻⁷⁰

S = 237.59 10⁻³⁷ / 2.59 10⁻⁷⁰

S = 9.173 10³⁴ J/K

D) Calculation of entropy for a white dwarf star

M = 1.2 Mϴ = 2.4 10³⁰ kg

Calculation of the Schwarzschild radius:

Rs = (2 x G x M) / C²

Rs = 2 x 6.67 10⁻¹¹ x 2.4 10³⁰ / 9 10¹⁶ = 32.016 10³⁰ / 9 10¹⁶ = 3.55 10³ m

Rs = 3.55 10³ m

Entropy calculation:

S = π Kʙ x Rs² / Lp²

S = 3.14 x 1.78 10⁻⁴³ x 12.60 10⁶ / 2.59 10⁻⁷⁰

S = 70.43 10⁻³⁷ / 2.59 10⁻⁷⁰

S = 2.719 10³⁴ J/K

Finally, in Table 14, we will represent a summary of the entropy calculations for different stellar bodies.

Table 14. Entropy values for white dwarf stars, neutron stars, and black holes.

Table 14. Entropy values for white dwarf stars, neutron stars, and black holes.

Example 5:

Analysis of the equations of the electromagnetic and gravitational wave spectrum

We will describe simple equations that represent the electromagnetic wave spectrum.

Eε = h x fε

Cε = λε x fε

Eε = h x Cε / λε

Eε = Kʙε x Tε

Kʙε = 1.38 10⁻²³ J/K

We will describe simple equations that represent the gravitational wave spectrum.

Eɢ = h x fɢ

Cɢ = λɢ x fɢ

Eɢ = h x Cɢ / λɢ

Eɢ = Kʙɢ x Tɢ

Kʙɢ = 1.38 10⁻²³ J/K > Kв ef > 1.78 10⁻⁴³ J/K

We are going to carry out our analysis from the point of view of temperature, we are going to consider the following equations:

Eε = Kʙε x Tε

(25)

Eɢ = Kʙɢ x Tɢ

(26)

T = 170 nK, temperature of the Bose-Einstein condensate for Rubidium atoms.

Eε = Kʙε x Tε

Eε = Kʙε x Tε = 1.38 10⁻²³ J/K x 170 10⁻⁹ K = 234.6 10⁻³² = 2.34 10⁻³⁴ J

Eε = 2.34 10⁻³⁴ J

Eε = h x fε

fε = Eε / h = 2.34 10⁻³⁴ J / 6.62 10⁻³⁴ = 0.353

fε = 0.353 Hz

C = λε x fε

λε = C / fε = 3 10⁸ / 0.353 = 8.49 10⁸ m

Eɢ = Kʙɢ x Tɢ

Eɢ = Kʙɢ x Tɢ = 1.38 10⁻²³ J/K x 170 10⁻⁹ K = 234.6 10⁻³² = 2.34 10⁻³⁴ J

Eɢ = 2.34 10⁻³⁴ J

Eɢ = h x fɢ

fɢ = Eɢ / h = 2.34 10⁻³⁴ J / 6.62 10⁻³⁴ = 0.353

fɢ = 0.353 Hz

C = λɢ x fɢ

λɢ = C / fɢ = 3 10⁸ / 0.353 = 8.49 10⁸ m

λɢ = 8.49 10⁸ m

T = 2 10⁷ K, temperature of a white dwarf star

Eε = Kʙε x Tε

Eε = 1.38 10ˉ²³ x 2 10⁷

Eε = 2.76 10ˉ¹⁶ J

Eε = h x fε

fε = Eε / h = 2.76 10ˉ¹⁶ / 6.62 10ˉ³⁴ = 0.4123 10¹⁸

fε = 4.12 10¹⁷ Hz

C = λε x fε

λε = C / fε = 3 10⁸ / 4.12 10¹⁷ = 0.72 10ˉ⁹ m

Eɢ = Kʙɢ x Tɢ

Eɢ = 1.9 10ˉ³⁷ x 2 10⁷

Eɢ = 3.8 10ˉ³⁰ J

Eɢ = h x fɢ

fɢ = Eɢ / h = 3.8 10ˉ³⁰ / 6.62 10ˉ³⁴ = 0.5740 10⁴ = 5.74 10³

fɢ = 5740 Hz = 5.74 10³ Hz

C = λɢ x fɢ

λɢ = C / fɢ = 3 10⁸ / 5.740 10³

λɢ = 0.5226 10⁵ m = 52264 m = 5.224 10⁴ m

T = 10¹³ K, temperature of a black hole of three solar masses

Eε = Kʙε x Tε

Eε = 1.38 10⁻²³ J/K x 10¹³ K = 1.38 10⁻¹⁰

Eε = 1.38 10⁻¹⁰ J

Eε = h x fε

fε = Eε / h = 1.38 10⁻¹⁰ / 6.62 10⁻³⁴ = 0.208 10²⁴ = 2.08 10²³

fε = 2.08 10²³ Hz

C = λε x fε

λε = C / fε = 3 10⁸ / 2.08 10²³ = 1.44 10⁻¹⁵ m

Eɢ = Kʙɢ x Tɢ

Eɢ = 1.78 10⁻⁴³ J/K x 10¹³ K = 1.78 10⁻³⁰ J

Eɢ = 1.78 10⁻³⁰ J

Eɢ = h x fɢ

fɢ = Eɢ / h = 1.78 10⁻³⁰ J / 6.62 10⁻³⁴ = 0.268 10⁴

fɢ = 2.68 10³ Hz

C = λɢ x fɢ

λɢ = C / fɢ = 3 10⁸ / 2.68 10³ = 1.11 10⁵ m

λɢ = 1.11 10⁵ m

T = 10²⁷ K, black hole decay temperature

Eε = Kʙε x Tε

Eε = 1.38 10⁻²³ J/K x 10²⁷ K = 1.38 10⁴

Eε = 1.38 10⁴ J

Eε = h x fε

fε = Eε / h = 1.38 10⁴ / 6.62 10⁻³⁴ = 0.208 10³⁸ = 2.08 10³⁷

fε = 2.08 10³⁷ Hz

C = λε x fε

λε = C / fε = 3 10⁸ / 2.08 10³⁷ = 1.44 10⁻²⁹ m

λε = 1.44 10⁻²⁹ m

Eɢ = Kʙɢ x Tɢ

Eɢ = 1.78 10⁻⁴³ J/K x 10²⁷ K = 1.78 10⁻¹⁶

Eɢ = 1.78 10⁻¹⁶ J

Eɢ = h x fɢ

fɢ = Eɢ / h = 1.78 10⁻¹⁶ J / 6.62 10⁻³⁴ = 0.268 10¹⁸

fɢ = 2.68 10¹⁷ Hz

C = λɢ x fɢ

λɢ = C / fɢ = 3 10⁸ / 2.68 10¹⁷ = 1.11 10⁻⁹ m

λɢ = 1.11 10⁻⁹ m

T = 10³² K, Planck temperature

Eε = Kʙε x Tε

Eε = 1.38 10⁻²³ J/K x 10³² K = 1.38 10⁹

Eε = 1.38 10⁹ J

Eε = h x fε

fε = Eε / h = 1.38 10⁹ / 6.62 10⁻³⁴ = 0.208 10⁴³ = 2.08 10⁴²

fε = 2.08 10⁴² Hz

C = λε x fε

λε = C / fε = 3 10⁸ / 2.08 10⁴² = 1.44 10⁻³⁴ m

λε = 1.44 10⁻³⁴ m

Eɢ = Kʙɢ x Tɢ

Eɢ = 1.78 10⁻⁴³ J/K x 10³² K = 1.78 10⁻¹¹

Eɢ = 1.78 10⁻¹¹ J

Eɢ = h x fɢ

fɢ = Eɢ / h = 1.78 10⁻¹¹ J / 6.62 10⁻³⁴ = 0.268 10²³

fɢ = 2.68 10²² Hz

C = λɢ x fɢ

λɢ = C / fɢ = 3 10⁸ / 2.68 10²² = 1.11 10⁻¹⁴ m

λɢ = 1.11 10⁻¹⁴ m

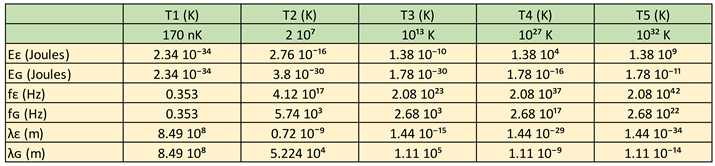
Table 15. Energy, frequency and wavelength as a function of temperature.

Table 15. Energy, frequency and wavelength as a function of temperature.

If we analyse the lower temperature limit, it corresponds to the Bose-Einstein condensate for rubidium atoms.

In my opinion, if we continue to lower the temperature, we will reach a critical point, an inflection point, in which a transition or phase change of matter will occur.

In item 4. ANALYSIS OF THE ORIGIN OF ELEMENTARY PARTICLES USING THE THEORY OF THE GENERALIZATION OF THE BOLTZMANN CONSTANT IN CURVED SPACE-TIME, we analyse how important temperature is in the formation of elemental particles.

For low temperatures, the reverse process occurs, we will reach a critical inflection point Tc, in which the disintegration of the elementary particles occurs, separating the gravitons from the elemental electrical content.

The critical temperature, or inflection point, is the temperature at which the matter reaches (0) Kelvin.

This separation produces a repulsive force, which causes the temperature to reach negative values below zero (0) kelvin.

In a simple analysis we are going to justify why the temperature reaches negative values, in an environment of repulsive gravity.

Let's consider the ideal gas equation:

PV = n KB T

V = constant, repulsive forces act

ΔP V = n KB ΔT

(Pf – Pi) V = n KB (Tf – Ti)

In an environment in which repulsive gravity act, the final pressure will be lower than the initial pressure, therefore the value of (Pf - Pi) will be negative; this implies that the final temperature will be lower than the initial temperature.

In conclusion, in an environment in which repulsive gravity act, disintegration of matter, the temperature is below zero (0) Kelvin.

The lower limit of temperature below zero (0) kelvin corresponds when the graviton and the elemental energy levels (strings) remain still, without moving.

Example 6:

Quantum entanglement and the Bose-Einstein condensate

In the paper: RLC Electrical Modelling of Black Hole and Early Universe. Generalization of Boltzmann’s Constant in Curved Space-Time [3], we write the equation that defines the temperature of the Bose Einstein condensate:

According to the information of [7], Cauê Muraro - Agência USP - 10/30/2007, the temperature of a Bose-Einstein condensate for 100,000 rubidium atoms corresponds to Tcmin = 180 nK.

Where Tcmin, low temperature Bose-Einstein condensate.

For KB = 1.38 10⁻²³ J/K and rubidium atoms corresponds:

Tcmin = 180 nk

Approximate critical temperature of the Bose-Einstein condensate for low temperatures, with rubidium atoms.

Let's calculate Tcmax, for Kʙ = 1.78 10⁻⁴³ J/K

Where Tcmax, High temperature Bose-Einstein condensate.

Tcmax, we are going to calculate considering the relationship between the Boltzmann constant Kʙ = 1.38 10⁻²³ J/K, for flat space-time and KB = 1.78 10⁻⁴³ J/K for curved space-time.

For Kʙ = 1.78 10⁻⁴³ J/K and rubidium atoms corresponds:

Tcmax = 180 nk / 1.78 10⁻²⁰ = 1.01 10¹³ K

Tcmax = 1.01 10¹³ K

Critical temperature of the Bose-Einstein condensate for high temperatures with rubidium atoms.

Here we put forward the hypothesis that for an effective Boltzmann´s constant Kʙ = 1.78 10⁻⁴³ J/K, there is a temperature Tcmax, that corresponds to a high temperature Bose Einstein condensate.

For a temperature of approximately 1.01 10¹³ K, in a plasma of quarks and gluons, a phase transition occurs that gives rise to a Bosonic condensate, at high temperatures, which is characterized by being very energetic.

We can interpret it as follows, when a star collapses and a black hole is formed, we can affirm that a high-temperature Bode-Einstein condensate exists inside a black hole.

In analogy with the properties of materials at very low temperatures, super fluids and superconductivity; quark-gluon plasma achieves similar exotic properties, but not with atoms and molecules as we normally know.

these properties are achieved for the quark-gluon plasma, a superfluid or super solid, the main property of which makes this liquid or solid behave like isolated quarks, allowing the gluons to stack up neatly in an infinite cascade of energy, making it the most energetic matter in the universe.

We also said that quarks are fermions and gluons are bosons, but in black holes, by analogy with what happens with superconducting materials, and super fluids and super solids, the plasma of quarks and gluons as a whole act as a Bose-Einstein condensate, as a single atom whose macroscopic properties are unique.

Here we hypothesize that quantum entanglement is related to the Bose-Einstein condensate, that is, there is quantum entanglement for a Bose-Einstein condensate of low temperature Tcmin and there is also quantum entanglement for a Bose-Einstein condensate of high temperature Tcmax.

We are familiar with low temperature quantum entanglement, Tcmin, in quantum computers, for Kʙ = 1.38 10⁻²³ J/K.

At high temperatures, Tcmax, for Kʙ = 1.78 10⁻⁴³ J/K, quantum entanglement is given to calculate the viscosity of the quark-gluon plasma.

Using duality DST = EQFT

We can use the Boltzmann constant of the quark-gluon plasma or eventually the Boltzmann constant for a black hole, interchangeably, to calculate the viscosity of the quark-gluon plasma, which will give us the same result.

Boltzmann constant for quark-gluon plasma: Kʙ = 0.76 10⁻⁴¹ J/K.

Boltzmann constant for black hole: Kʙ = 1.78 10⁻⁴³ J/K.

5.8.5. Harshit Jain – Comment on

It seems like your text touches on several complex concepts related to the Boltzmann constant, string theory, particle formation, and their relationship with temperature. Here's a restructured version to make it more coherent:

"Within our paper, a key focus was leveraging the Boltzmann constant as a foundational element for constructing a more accurate model of the universe. Utilizing temperature as a distinguishing factor between flat and curved space-time structures was pivotal in this pursuit.

In our exploration, we delved into the Vlasov Equations, particularly emphasizing the role of the Boltzmann constant in interactions, such as the Debye electron interaction. This interaction aids in delineating temperature variations, contributing to our understanding of the overall wave function of the universe.

Another significant aspect of our paper revolved around string theory. We addressed the deep damping of interaction Maxwell state equations, specifically examining the formation of strings with varying constants (Homotropy). This exploration led us to consider the application of the Boltzmann Hagedorn conjecture, particularly in understanding how different temperatures contribute to the formation of various particles, such as mesons and bosons.

Our investigation into the interaction between temperature, matter, and space-time fabrics was fundamental in establishing a coherent understanding, aligning with your previously considered stability of different particle generations through the Boltzmann-derived energy capacity.

Furthermore, in the realm of string theory, where entities are viewed as strings at the Planck scale, the relationship between these strings and temperature (represented by the Boltzmann constant) becomes crucial. Here, we delve into the implications of Boltzmann interaction fields and other relevant factors.

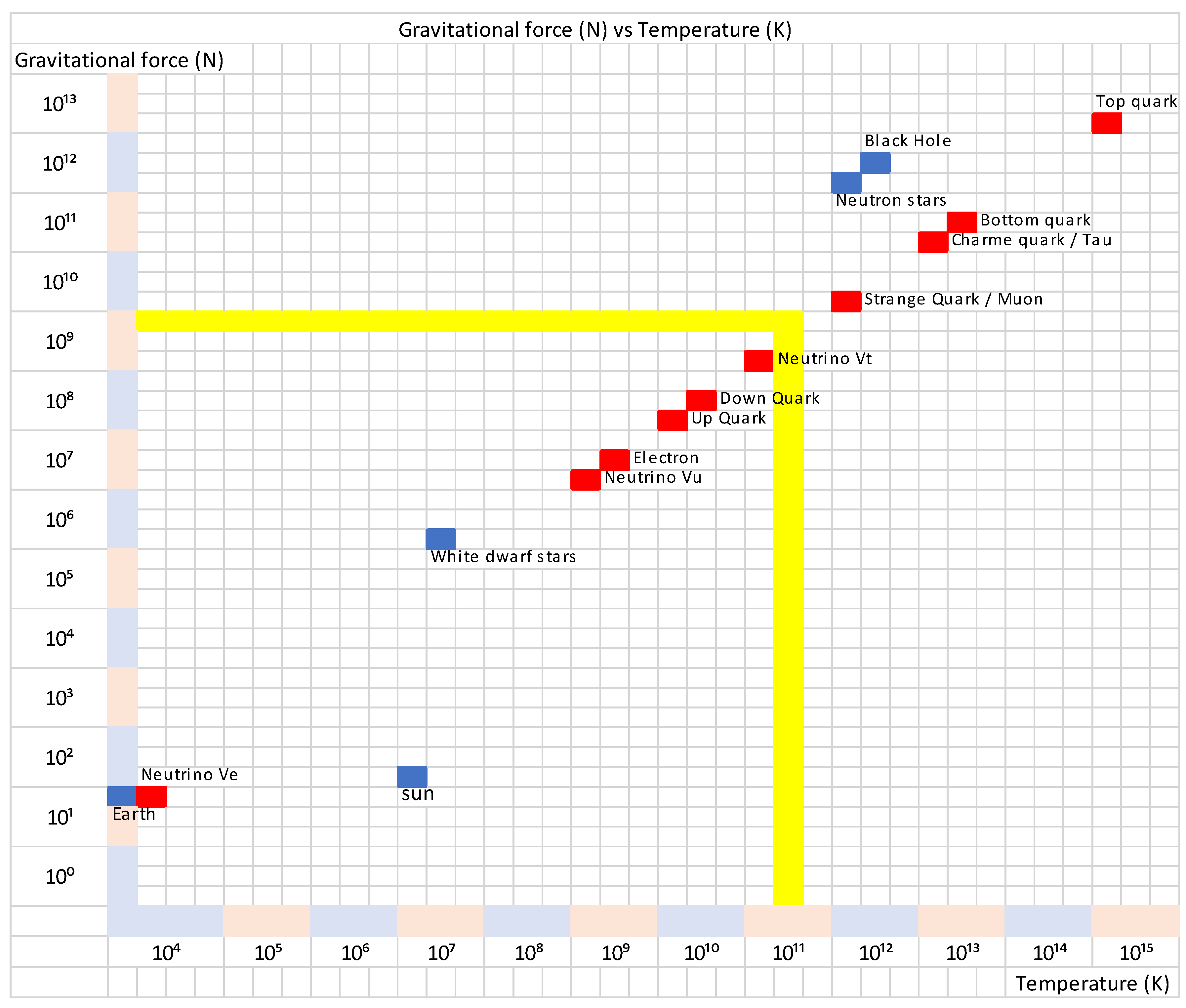
Specifically discussing gluons and leptons, your classification based on stability is noteworthy. However, our paper strives to connect this stability classification with temperature within the quantum scenario. For instance, considering the RLC modelling you've previously provided, we explore the nexus between stability and temperature, especially when two entities are mixed our work aims to bridge the gap between fundamental constants like the Boltzmann constant, string theory, particle stability, and their interrelation with temperature in the complex fabric of the universe." Energy, as understood through the lens of stability classes determined by the hyperfine structure constant (group theory), Quantum Field Theory (QFT), and conformal field theory, plays a pivotal role in quantum-level interactions with help of Boltzmann constant. These interactions manifest in stable clusters and the Zeno interaction during quark formation in the event horizon of a black hole (phasor interaction) in one form of formation.

By introducing new models for photons, quarks, and gluons and extending the Boltzmann constant theory to curved space-time, our work demonstrates the generalization of the standard model. This extension incorporates gravity as a fundamental component, influencing the properties governing elementary particles through Einsteinian Hamiltonian interactions within their fields. Our aim in generalizing the standard model is to unify quantum field theory (as represented by the standard model) and gravity. Our calculations indicate that the gravitational forces acting on elementary particles approximate those acting on stellar bodies like white dwarf stars, neutron stars, and black holes.

The Higgs potential, a mass internal interaction, and its associated temperature are directly related to the curvature of space-time. Observing the temperatures of quarks reveals their proximity to those of these stellar bodies, hence the similarity in gravitational effects on elementary particles and stellar bodies. Our model describing quarks posits two opposing forces within them: a repulsive/disintegrative force (Fq) and a gravitational attractive force (Fg), offering insight into different modes of bubble formation in their interactions.

Our calculations elucidate the stability of the first quark family and the instability of the second and third quark families. The critical point occurs at the gravitational force Fg = 10¹⁰ N; below this value, elementary particles remain stable (Fg > Fq), whereas above this threshold, they become unstable (Fg < Fq).

In section 5.5, we have demonstrated the existence of a force tangential to the repulsive force in the disintegration of subatomic particles interaction. This tangential or torsion force precedes the repulsive force by 90 degrees. Analogously, within a black hole, two forces operate: a gravitational force drawing inward and a tangential or torsional gravitational force delaying the gravitational force by 90 degrees.

Finally, we propose the equation DST = EQFT as representative of the Theory of Everything (TOE), serving as a generalization of the Maldacena ADS/CFT correspondence, in our research, we have showcased the quantization of both space-time and matter. 'DST' signifies dynamic space-time and is associated with the theory that expands the Boltzmann constant concept into curved space-time.

On the other hand, 'EQFT' represents electromagnetic quantum field theory. Our focus lies in understanding quantum complexity in electrodynamics and its influence on the formation of various elementary particles.

The theory extending the Boltzmann constant into curved space-time unifies general relativity and quantum mechanics. Evidence of this convergence is visible in CP interactions within string theory, entanglement, and other disintegration functions or may be integration function inherent to these interactions. Utilizing vector interactions becomes crucial across various scenarios. However, detailing its importance everywhere would require extensive additional formulations, as these interactions permeate numerous scenarios.

For instance, in calculating the entropy of celestial bodies like white dwarf stars and neutron stars, we calculate their equivalent black hole entropy. This method allows us to estimate the approximate entropy of any stellar body, understanding that it cannot surpass the entropy of its equivalent black hole. When we generate Quark-Gluon Plasma (QGP) in particle accelerators, it initially stores energy but remains an unstable state. At this stage, the QGP exhibits an approximate Boltzmann constant Kʙ = 1.78 10⁻⁴³ J/K. To revert space-time and matter to their stable state, the Boltzmann constant needs to transition from Kʙ = 1.78 10⁻⁴³ J/K to 1.38 10⁻²³ J/K. This release of energy causes the QGP to resemble a superfluid, despite the substantial energy involved (ɲ/s = 1.27 10²⁵, depicting the viscosity-entropy relationship).

The viscosity of a quark-gluon plasma utilizes the Boltzmann constant of a black hole for calculation. For instance, comparing theories like 11-dimensional ADS theory (Kʙ = 1.38 10⁻⁴³ J/K) and 10-dimensional CFT theory (with a collision Boltzmann constant around 0.76 10⁻⁴¹ J/K > Kʙ > 1.78 10⁻⁴³ J/K) allows for nearly identical calculations, reflecting the non-perturbative regime's similarity in both theories.

In the strong coupling regime, utilizing superstring theory in the limit where gs tends to infinity approximates general relativity, facilitating the use of anti-de Sitter space ADS as a tool to describe the strong coupling regime of a particle theory (dual QCD). Our research emphasizes the breakdown of symmetry in curved space-time, attributing mass to fermionic and bosonic particles concerning temperature. As temperature rises, space-time curvature increases, affecting particles in the standard model, including photons and gravitons. This reasoning led us to generalize the Maldacena ADS/CFT correspondence, extending conformal quantum fields CFT to the entire quantum field theory EQFT.

The equation DST = EQFT symbolizes the duality between dynamic space-time and quantum field theory, representing the theory of everything. In conclusion, our work elucidates complex interactions between space-time, matter, and various fields, showcasing how their interplay leads to the emergence of mass and fundamental forces in the universe, quantifying space-time curvature was a pivotal aspect explored in the paper 'RC Electrical Modelling of Black Hole: New Method to Calculate the Amount of Dark Matter and the Rotation Speed Curves in Galaxies.' The 1919 solar eclipse observed in Brazil and Africa provided crucial experimental validation for Albert Einstein's theory of relativity. In this context, we aim to calculate the Boltzmann constant for the Sun and demonstrate how it aligns with the observed deviation. No solar eclipse in history impacted science as profoundly as the one on May 29, 1919. Photographed and analysed simultaneously by two British astronomer teams—one in Sobral, Brazil, and the other on Principe, a Portuguese territory—the goal was to measure the deviation of starlight passing through the Sun's gravitational field. Einstein's theory of general relativity proposed that space-time curved around bodies with high energy or mass, altering the trajectory of light.

Einstein's predicted light deflection nearly doubled, reaching 1.75 arcseconds due to curved space-time. The most significant results emerged from observations made in Sobral, using a 4-inch lens, indicating a deflection of 1.61 arcseconds with a 0.30 arcsecond margin of error—slightly less than Einstein's forecast. Our calculations for the number of gravitons within a neutron equate to a temperature of T = 10¹² K. As per Table 12, the graviton's mass decreases with rising temperature for particular interaction.

The culmination of various aspects in our research leads to the proposition of a theory of everything (TOE), symbolized by the equation DST = EQFT:

Quantization of space-time (DST) and matter and its interaction (EQFT)

Quantization of space-time curvature

Electrical modelling of a neutron as a three-phase alternating current generator, revealing the origin of mass and gravity in particles as double Boltzmann understanding

Mechanisms generating mass and gravity within neutrons, calculating the constituent particles and gravitons

Proposed generalization of the ADS/CFT correspondence with the equation DST = EQFT, unifying gravity and quantum mechanics across space-time scenarios—negative, positive, or flat curvature

This equation, DST = EQFT, symbolizes the theory of everything, representing an interaction field unifying gravity and quantum mechanics. It extends from the generalization of the Boltzmann constant in curved space-time

In the paper 'RLC Electrical Modelling of Black Hole and Early Universe: Generalization of Boltzmann’s Constant in Curved Space-Time,' we delve into the origins of the universe, cosmic inflation, dark matter, and dark energy. And this paper also 'Theory of the Generalization of the Boltzmann’s Constant in Curved Space-Time: Shannon-Boltzmann Gibbs Entropy Relation and the Effective Interacted Boltzmann’s Constant,' having to we quantify space-time curvature and demonstrate, using the Shannon-Boltzmann-Gibbs entropy relation, the conservation of information.

The paper 'RC Electrical Modelling of Black Hole: New Method to Calculate the Amount of Dark Matter and the Rotation Speed Curves in Galaxies' details how we quantify dark matter in a galaxy and model its rotation curves using an innovative approach and a newly introduced constant in interactive work.

In the paper 'Electrical-Quantum Modelling of the Neutron and Proton as a Three-Phase Alternating Current Electrical Generator: Determination of the Number of Quarks-Antiquarks-Gluons and Gravitons inside a Neutron,' we elucidate the generation of mass (calculating the number of quarks-antiquarks-gluons) and gravity (calculating the number of gravitons) within a neutron, treating it as a three-phase alternating current energy generator.

Utilizing the theory of the generalization of the Boltzmann constant in curved space-time, this paper proposes a methodology to elucidate the origin of elementary particles and their relation to gravity. This allowed us to generalize the ADS/CFT correspondence, extending it into a general theory or theory of everything.

The theory of the generalization of the Boltzmann constant serves as the fundamental pillar uniting general relativity and quantum mechanics, enabling the quantification of space-time and its curvature. Ultimately, it facilitates the generalization of the Maldacena ADS/CFT correspondence, leading to the proposal of a universal theory represented by the equation 'entangled DST = EQFT.'

Reflections: Comparing the Higgs mechanism with the conformal mechanism reveals their distinctions. Gauge symmetry necessitates massless particles, but the Higgs mechanism confers mass by breaking symmetry. While this interaction occurs in flat space, in curved space, it might disrupt conformal symmetry.

In curved space, breaking this symmetry could endow particles like gravitons, photons, scalar fields (bosons), and Dirac particles with mass through interaction. This mass appears proportional to the conformal factor's temporal derivative. In a conformal space within curved space, a particle's motion resembles movement through a fluid (viscous), potentially accounting for inertia.

Regarding mass, envisioning quark and anti-quark dipoles as vibrating point masses linked by a spring (Gravitons with spin 2), these vibrating masses interact together, causing disturbances in space-time propagating as gravitational waves.

This could elucidate the generation of gravitational waves through gravitons' propagation within space-time interaction in my view, the equation ADS = CFT holds paramount significance in physics, paving the way toward the sought-after Theory of Everything (TOE) in science. Extending the Maldacena ADS/CFT correspondence, considering the generalization of the Boltzmann constant, leads us to the equation DST = EQFT, where DST symbolizes space-time with negative, positive, or plane curvature, while EQFT encompasses Electromagnetic Quantum Field Theory, comprising electromagnetic field theory linked to weak field theory (QED) and strong field theory (QCD) for formulating various functions.

In your paper 'Electrical-Quantum Modelling of the Neutron and Proton as a Three-Phase Alternating Current Electrical Generator: Determination of the Number of Quarks-Antiquarks-Gluons and Gravitons inside a Neutron,' we explore gravity quantification, specifically exemplifying it for the neutron. We've demonstrated that DST space-time quantization aligns with the quantization of EQFT field theory, representing a theory of quantum gravity associated with the generalization of the Boltzmann constant in curved space-time. This understanding assists in comprehending interactions within both curved and flat space-time.

The equation DST = EQFT elucidates an intrinsic, direct relationship between matter and space-time, revealing quantized space-time and its curvature. It's important to note that conformal field theory is not utilized in this context. This equation holds broader implications than the ADS/CFT correspondence, especially within different regions of self and inner interactions forming ADS/CFT. Building upon DST = EQFT, we propose that fundamental particles originate due to the relationship between space-time curvature, elemental matter, and temperature.

Essentially, it's the curvature of space-time and gravity associated with temperature that accounts for elementary particle genesis, a topic we will delve into extensively later.

In Figure 21 - Vector diagram of the neutron in black and vector diagram of the proton in red you included it is same as vector interaction.

In our paper 'Theory of the Generalization of the Boltzmann’s Constant in Curved Space-Time: Shannon-Boltzmann Gibbs Entropy Relation and the Effective Boltzmann’s Constant,' we analyse the space-time contraction factor for various celestial bodies, incorporating Shannon-Gibbs energy within its interaction. Let's briefly recap the calculation of the space-time contraction factor for a black hole: Assuming a black hole comprises a plasma of quarks and gluons based on the Maldacena correspondence ADS = CFT, we calculate the space-time contraction factor and its effective Boltzmann constant. For instance, considering a black hole's mass at 3.0 solar masses (Mϴ), and its formation temperature at 10¹³ K, aligning with the temperature at which matter forms a soup of quarks and gluons in particle collisions Boltzmann understanding.

This paper concludes by emphasizing the significance of these analyses in our research, contributing comprehensively to various analytical aspects by which we take whole interaction to formation of particle by generalization.

6. Conclusions

References

1. Flores, H.G.; Gonçalves de Souza, M.I. Electrical-Quantum Modelling of the Neutron and Proton as a Three-Phase Alternating Current Electrical Generator. Determination of the Number of Quarks-Antiquarks-Gluons and Gravitons, Inside a Neutron. Preprints 2023, 2023102076. [CrossRef]
2. Flores, H.G.; Gonçalvez de Souza, M.I. Theory of the Generalization of the Boltzmann’s Constant in Curved Space-Time. Shannon-Boltzmann Gibbs Entropy Relation and the Effective Boltzmann’s Constant. Preprints 2023, 2023090301. [CrossRef]
3. Flores, H.G. Rlc Electrical Modelling of Black Hole and Early Universe. Generalization of Boltzmann’s Constant in Curved Space-Time. Preprints 2023, 2023052246.
4. 10.20944/preprints202305.2246.v3. [CrossRef]
5. Flores, H.G.; Gonçalves de Souza, M.I. RC Electrical Modelling of Black Hole. New Method to Calculate the Amount of Dark Matter and the Rotation Speed Curves in Galaxies. Preprints 2023, 2023092017. [CrossRef]
6. Arbab Ibrahim, (Abdus Salam Intentional Centre for Theoretical Physics (ICTP)- Trieste-Italy), in QUANTUM PHYSICS.
7. https://www.linkedin.com/groups/1892648/?highlightedUpdateUrn=urn%3Ali%3AgroupPost%3A1892648-7142083157524205568&q=highlightedFeedForGroups.
8. Kostya Trachenko, Vadim Brazhkin, Matteo Baggioli. Similarity between the kinematic viscosity of quark-gluon plasma and liquids at the viscosity minimum.
9. https://arxiv.org/pdf/2003.13506.pdf.
10. Cauê Muraro - Agência USP - 30/10/2007.
11. Cientistas brasileiros criam átomo artificial.
12. https://www.inovacaotecnologica.com.br/noticias/noticia.php?artigo=010160071030&id=010160071030.
13. Diego Marinho Rodrigues. A Correspondencia AdS/CFT: Um Estudo Introdutorio.
14. UNIVERSIDADE FEDERAL DO RIO DE JANEIRO, INSTITUTO DE FISICA.
15. https://pos.if.ufrj.br/wp-content/uploads/2021/06/Diego-Marinho_prelim.pdf.
16. Horatiu Nastase. Introduction to AdS-CFT.
17. Global Edge Institute, Tokyo Institute of Technology.
18. https://professores.ift.unesp.br/horatiu.nastase/AdS-CFTnotes.pdf.
19. Alberto Zaffaroni. Introduction to the AdS/CFT correspondence.
20. Universita di Milano-Bicocca and INFN, sezione di Milano-Bicocca, Piazza della Scienza, 3; I-20126 Milano, Italy.
21. https://laces.web.cern.ch/laces09/notes/dbranes/lezionilosanna.pdf.
22. Gaston Luciano Giordano. Aplicaciones de la Correspondencia AdS/CFT en el ambito de la Fısica de la Materia Condensada.
23. UNIVERSIDAD NACIONAL DE LA PLATA, TRABAJO DE TESIS DOCTORAL.
24. http://sedici.unlp.edu.ar/bitstream/handle/10915/68984/Documento_completo.pdf-PDFA.pdf?sequence=1&isAllowed=y.