Submitted:
09 January 2024
Posted:
10 January 2024
Read the latest preprint version here
Abstract
Keywords:
1. Introduction
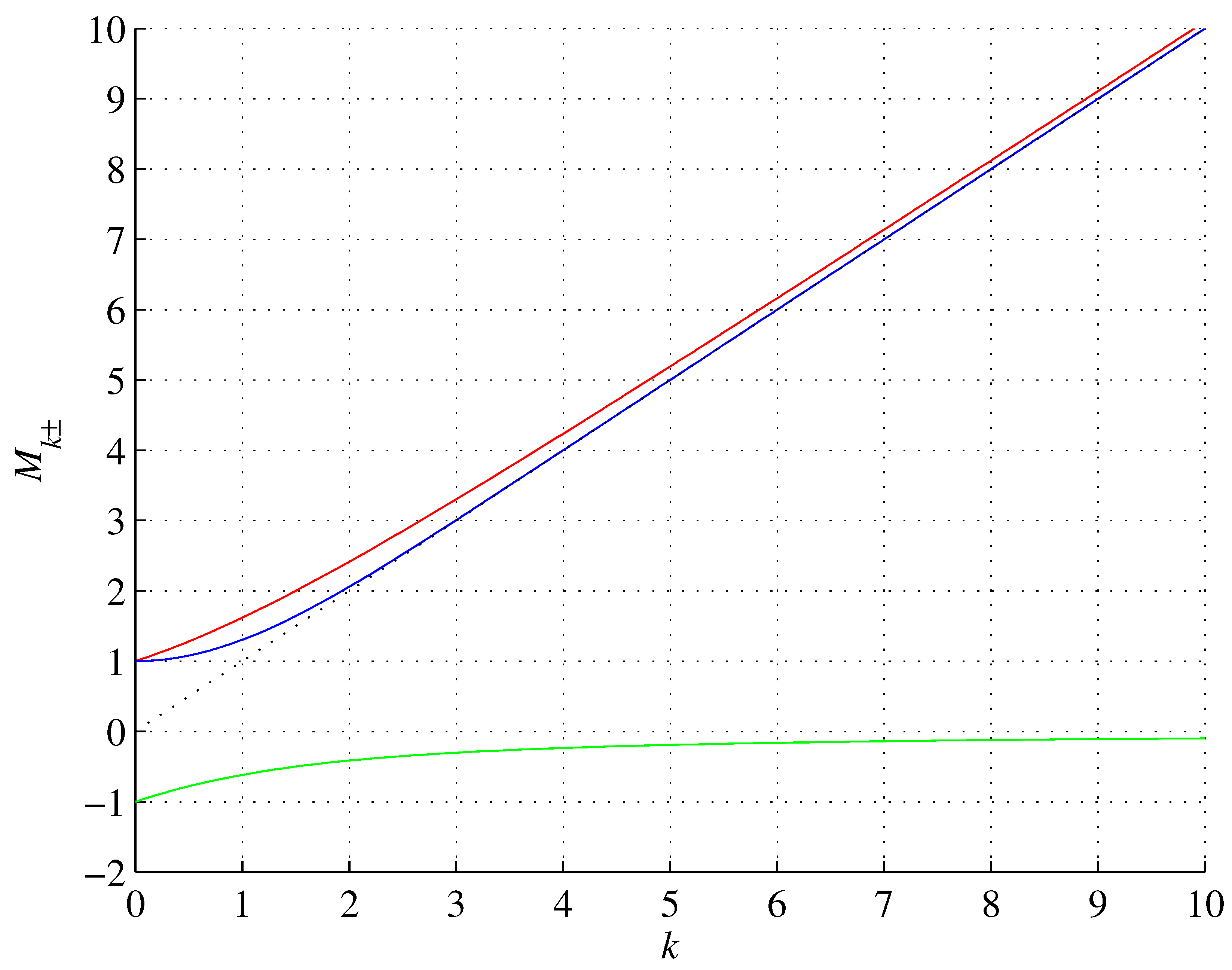
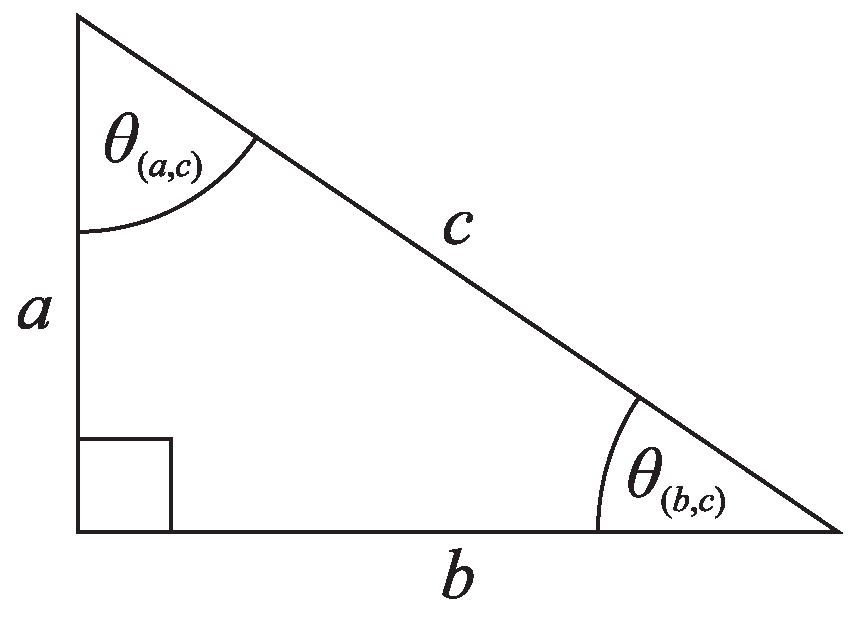
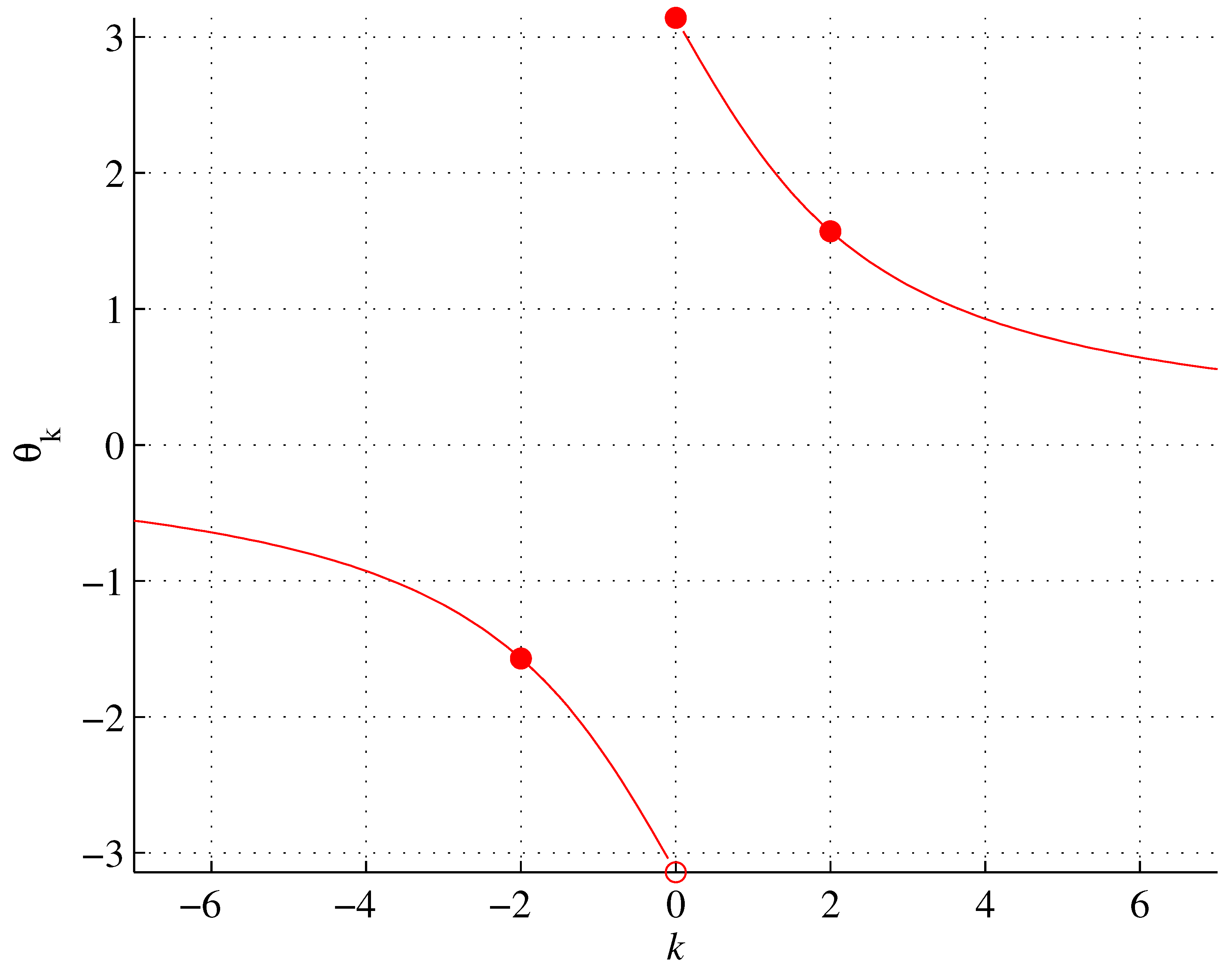
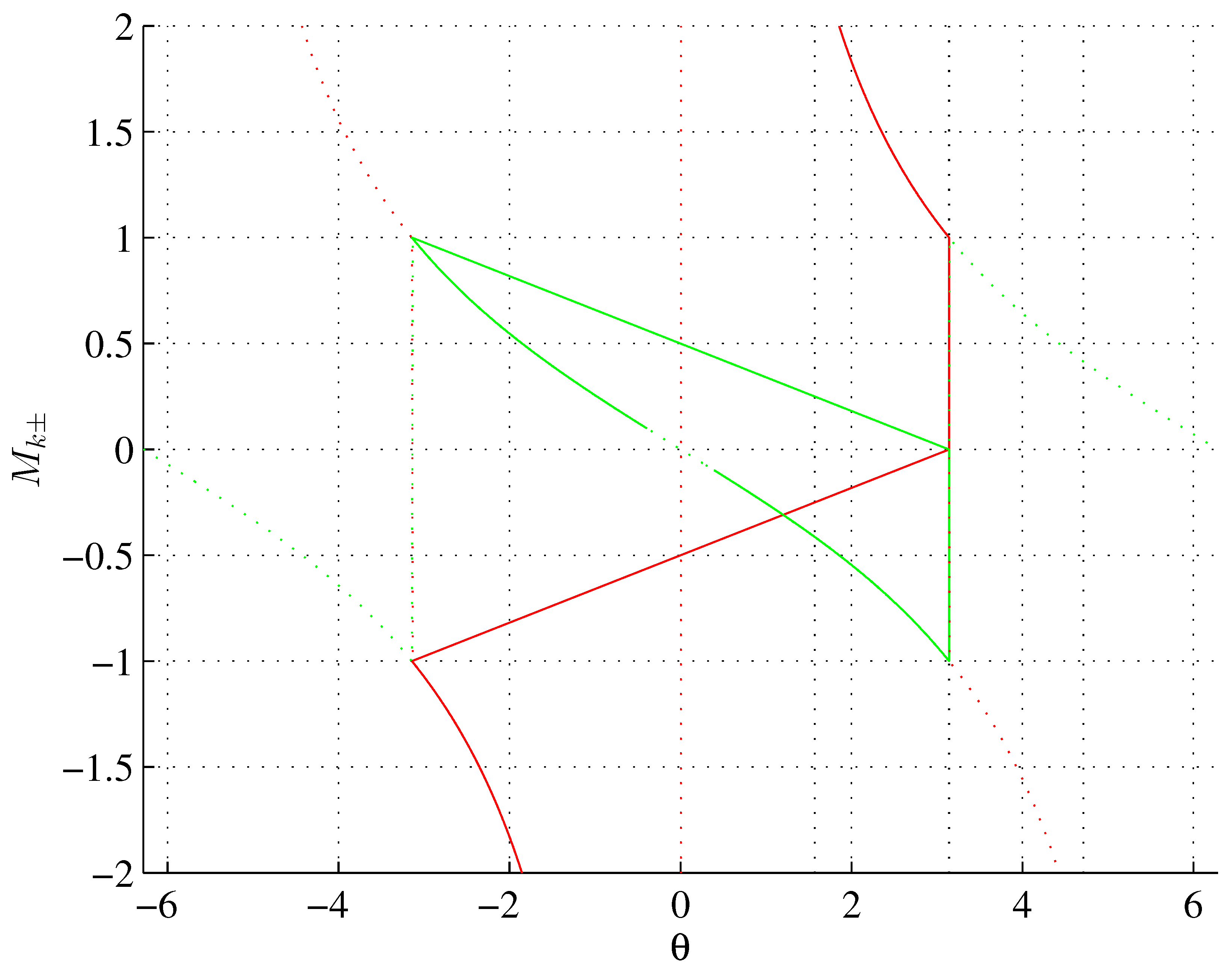
2. Results
Acknowledgments
References
- Łukaszyk, S. A new concept of probability metric and its applications in approximation of scattered data sets. Computational Mechanics 2004, 33, 299–304. [Google Scholar] [CrossRef]
- Łukaszyk, S.; Tomski, A. Omnidimensional Convex Polytopes. Symmetry 2023, 15, 755. [Google Scholar] [CrossRef]
- Rajput, C. Metallic Ratios in Primitive Pythagorean Triples : Metallic Means embedded in Pythagorean Triangles and other Right Triangles. JOURNAL OF ADVANCES IN MATHEMATICS 2021, 20, 312–344. [Google Scholar] [CrossRef]
| k | a | b | c | k | a | b | c | |
|---|---|---|---|---|---|---|---|---|
| 0.1 | -399 | 40 | 401 | 3.6 | 28 | 45 | 53 | |
| 0.2 | -99 | 20 | 101 | 3.7 | 969 | 1480 | 1769 | |
| 0.3 | -391 | 120 | 409 | 3.8 | 261 | 380 | 461 | |
| 0.4 | -12 | 5 | 13 | 3.9 | 1121 | 1560 | 1921 | |
| 0.5 | -15 | 8 | 17 | 4 | 3 | 4 | 5 | |
| 0.6 | -91 | 60 | 109 | 4.1 | 1281 | 1640 | 2081 | |
| 0.7 | -351 | 280 | 449 | 4.2 | 341 | 420 | 541 | |
| 0.8 | -21 | 20 | 29 | 4.3 | 1449 | 1720 | 2249 | |
| 0.9 | -319 | 360 | 481 | 4.4 | 48 | 55 | 73 | |
| 1 | -3 | 4 | 5 | 4.5 | 65 | 72 | 97 | |
| 1.1 | -279 | 440 | 521 | 4.6 | 429 | 460 | 629 | |
| 1.2 | -8 | 15 | 17 | 4.7 | 1809 | 1880 | 2609 | |
| 1.3 | -231 | 520 | 569 | 4.8 | 119 | 120 | 169 | |
| 1.4 | -51 | 140 | 149 | 4.9 | 2001 | 1960 | 2801 | |
| 1.5 | -7 | 24 | 25 | 5 | 21 | 20 | 29 | |
| 1.6 | -9 | 40 | 41 | 5.1 | 2201 | 2040 | 3001 | |
| 1.7 | -111 | 680 | 689 | 5.2 | 72 | 65 | 97 | |
| 1.8 | -19 | 180 | 181 | 5.3 | 2409 | 2120 | 3209 | |
| 1.9 | -39 | 760 | 761 | 5.4 | 629 | 540 | 829 | |
| 2 | 5.5 | 105 | 88 | 137 | ||||
| 2.1 | 41 | 840 | 841 | 5.6 | 171 | 140 | 221 | |
| 2.2 | 21 | 220 | 221 | 5.7 | 2849 | 2280 | 3649 | |
| 2.3 | 129 | 920 | 929 | 5.8 | 741 | 580 | 941 | |
| 2.4 | 11 | 60 | 61 | 5.9 | 3081 | 2360 | 3881 | |
| 2.5 | 9 | 40 | 41 | 6 | 4 | 3 | 5 | |
| 2.6 | 69 | 260 | 269 | 6.1 | 3321 | 2440 | 4121 | |
| 2.7 | 329 | 1080 | 1129 | 6.2 | 861 | 620 | 1061 | |
| 2.8 | 12 | 35 | 37 | 6.3 | 3569 | 2520 | 4369 | |
| 2.9 | 441 | 1160 | 1241 | 6.4 | 231 | 160 | 281 | |
| 3 | 5 | 12 | 13 | 6.5 | 153 | 104 | 185 | |
| 3.1 | 561 | 1240 | 1361 | 6.6 | 989 | 660 | 1189 | |
| 3.2 | 39 | 80 | 89 | 6.7 | 4089 | 2680 | 4889 | |
| 3.3 | 689 | 1320 | 1489 | 6.8 | 132 | 85 | 157 | |
| 3.4 | 189 | 340 | 389 | 6.9 | 4361 | 2760 | 5161 | |
| 3.5 | 33 | 56 | 65 | 7 | 45 | 28 | 53 | |
| For set | ||||||||
| E.g. for | ||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





