1. Introduction
Metallic ratios of
are defined as
being the roots of the quadratic equation
with the property
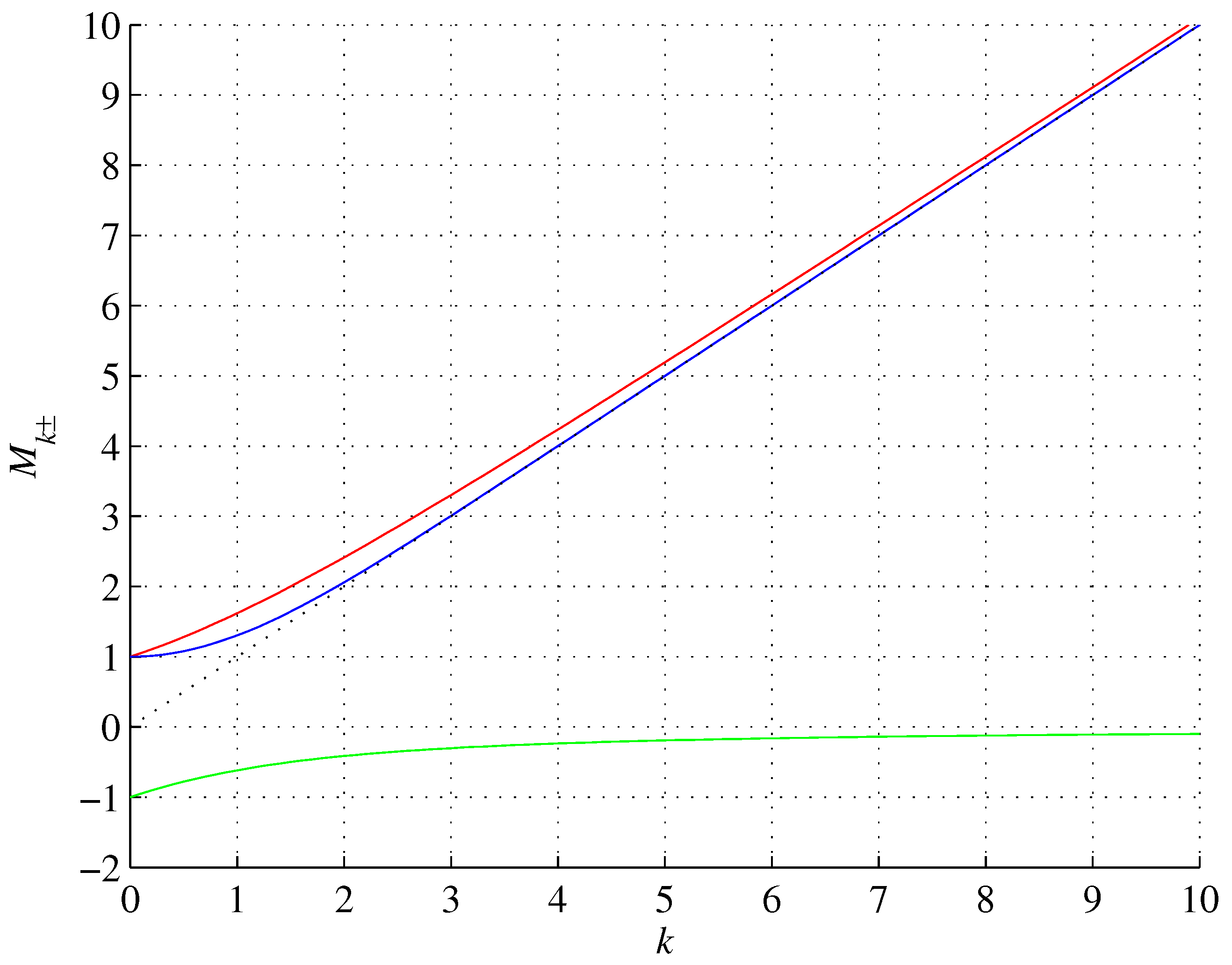
. They are shown in
Figure 1.
The positive metallic ratio
as a continuous function of
has the same property as the Łukaszyk-Karmowski (Ł-K) metric [
1] between two independent continuous random variables: It becomes asymptotic to
as
k goes to ifinity, as the
factor in the square root becomes negligible and
for large
k. Because the ratios (
1) are usually visualized as ratios of the edge lengths of a rectangle and these are assumed to be nonnegative, usually only the positive principal square root
of (
2) is considered, where for
the golden ratio is obtained, for
the silver ratio, for
the bronze ratio, etc. However, distance nonnegativity does not hold for the Ł–K metric [
1], for example; such axiomatization may be misleading [
2].
It was shown [
3] that for
the metallic ratios (
1) can be expressed by primitive Pythagorean triples, as
and for
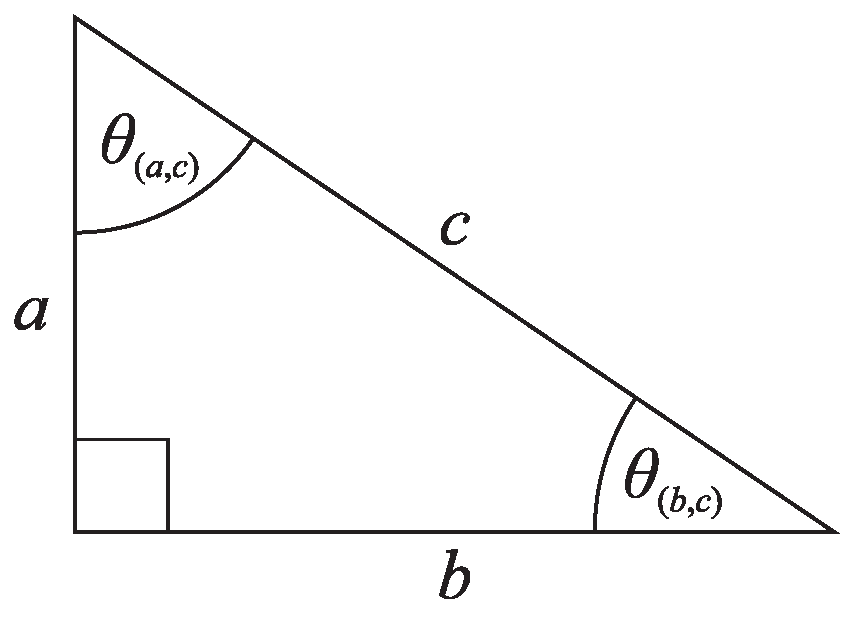
where
is the angle between a longer cathetus
b and hypotenuse
c of a right triangle defined by a Pythagorean triple, as shown in
Figure 2, whereas for
it is the angle between a hypotenuse and a shorter cathetus
a (
and
are defined by the same Pythagorean triples, respectively,
and
), and
For example the Pythagorean triple defines , the Pythagorean triple defines , the Pythagorean triple defines , and so on.
2. Results
Theorem 1. Metallic ratios are uniquely defined by an acute angle of a right triangle.
Proof. We express the RHS of the equation (
3) using half-angle formulae for sine and cosine, and substituting
since
, so
.
Multiplying the numerator and denominator of (
6) by
and performing some basic algebraic manipulations, we arrive at the quadratic equation for
having roots
corresponding to the metallic ratios (
1). □
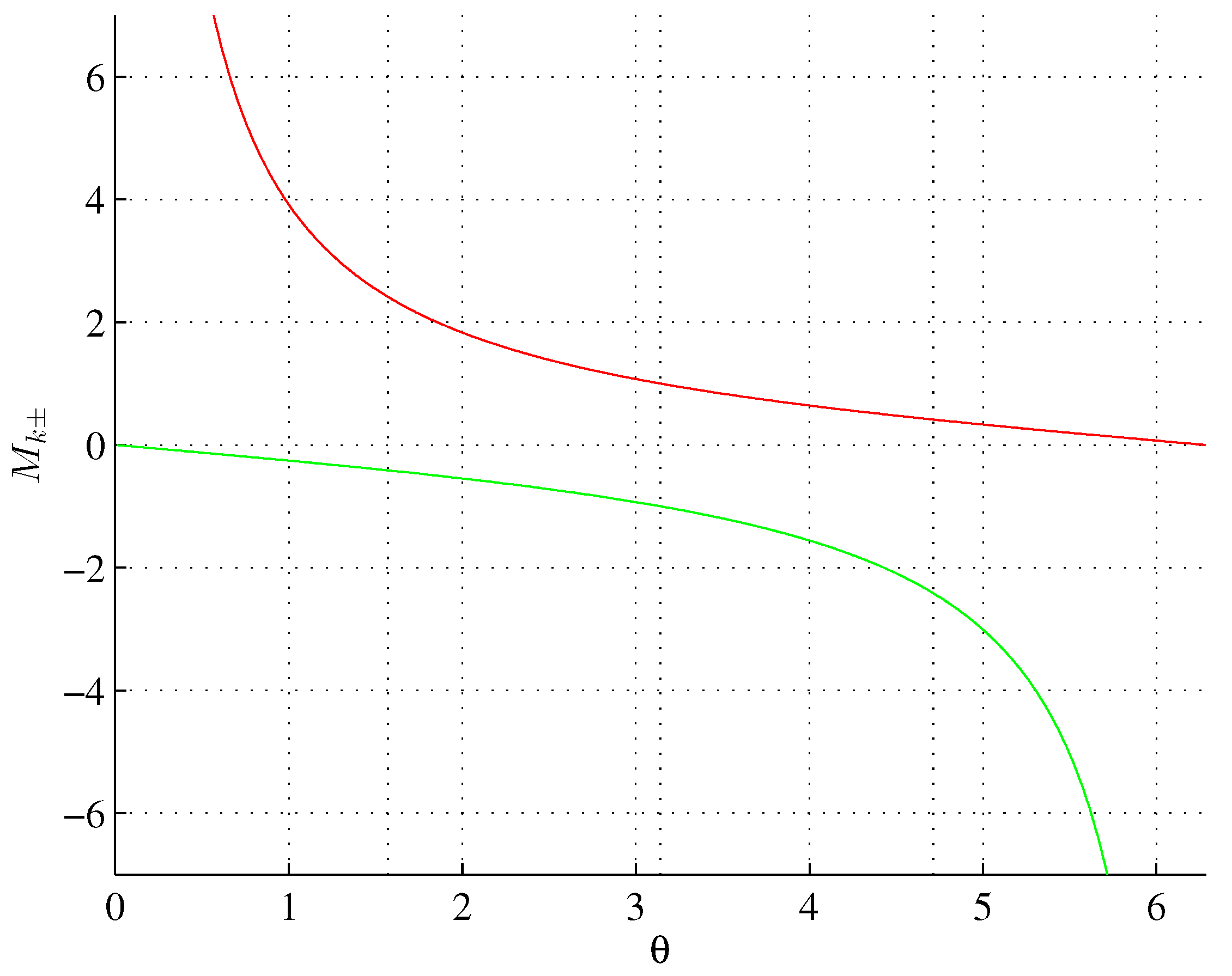
The metallic ratios
are shown in
Figure 3.
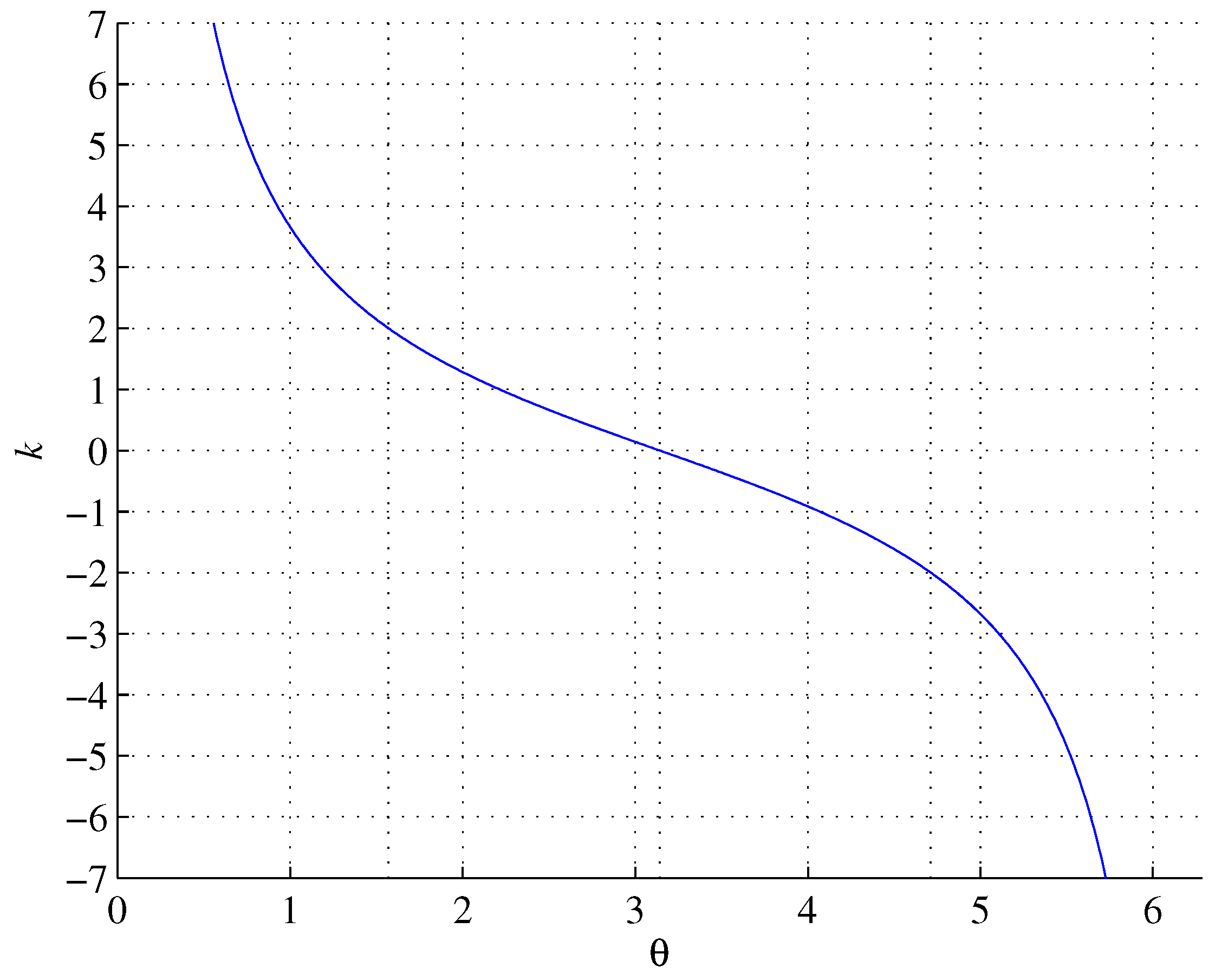
Equating relations (
1) and (
8) and solving for
k gives
as shown in
Figure 4.
Conjecture 1.
For the angle defining the metallic ratio is the argument of a normalized complex number , wherein for , is defined by a Pythagorean triple as
are catheti and c is hypotenuse of the right triangle shown in Figure 2, , and is undefined.
Conjecture (1) has been numerically validated. This form of
does not hold for irrational
k. For example
Acknowledgments
I thank my wife Magdalena Bartocha for her unwavering motivation and my friend, Renata Sobajda, for her prayers.
References
- Łukaszyk, S. A new concept of probability metric and its applications in approximation of scattered data sets. Computational Mechanics 2004, 33, 299–304. [Google Scholar] [CrossRef]
- Łukaszyk, S.; Tomski, A. Omnidimensional Convex Polytopes. Symmetry 2023, 15, 755. [Google Scholar] [CrossRef]
- Rajput, C. Metallic Ratios in Primitive Pythagorean Triples : Metallic Means embedded in Pythagorean Triangles and other Right Triangles. JOURNAL OF ADVANCES IN MATHEMATICS 2021, 20, 312–344. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).