Prerpints.org logo
Preprint
Review

Review: Fractal Geometry in Precipitation

Altmetrics

Downloads

145

Views

51

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

05 January 2024

Posted:

05 January 2024

You are already at the latest version

Alerts
Abstract
Rainfall, or more generally the precipitation process (flux), is a clear example of chaotic variables resulting from a highly nonlinear dynamical system, the atmosphere, represented by a set of physical equations such as the Navier-Stokes equations, energy balances and hydrological cycle among others. As a generalization of the Euclidean (ordinary) measurements, chaotic solutions of these equations are characterized by fractal dimensions, which are non-integer values that represent the complexity of variables like the precipitation. However, observed precipitation is measured as an aggregate variable over time, thus physical analysis of the observed fluxes is very limited. Therefore, this review aims to go through the different approaches used in the identification and analysis of the complexity of the observed precipitation, taking advantage of its geometry footprint. To address the review, it ranges from classical perspectives of fractal-based techniques to new perspectives at temporal and spatial scales as well as for classification of climatic features, including monofractal dimension, multifractal approaches, Hurst exponent, Shannon entropy and time scaling in intensity-duration-frequency curves.
Keywords: 
Subject: Environmental and Earth Sciences  -   Atmospheric Science and Meteorology

1. Introduction

1.1. Geometrical motivation

Observed precipitation is a chaotic variable that usually is represented by aggregated values in time series instead of physical fluxes as directly simulated by numerical weather prediction models (Monjo et al. 2023). Climate variability of precipitation is defined to range from the subseasonal and seasonal phases (Redolat et al. 2020, Albert et al. 2023, Al-Mutairi et al. 2023) to the multi-decadal and centennial fluctuations (Chen et al. 2022, Hasegawa et al. 2022; Liu et al. 2023; Rull et al. 2023, Silva-Muraja et al. 2023). A large number of its different variability modes presents self-similarity at most time scales, which is a key in the climatic characterization of its chaotic-related complexity (Morata et al. 2006; Omidvarnia et al. 2018; Redolat et al. 2023). Considering this idea, climate change detection and variability analysis can consider other measurements beyond the commonly used techniques such as average temporal statistics, spatial atmospheric patterns and compound extreme events (Hao et al. 2018, Monjo et al. 2020, Khan et al. 2023, Galiano et al. 2023). This review aims to identify both classical and emergent geometrical techniques used in the analysis of climate complexity of the precipitation. Therefore, a brief reminder of basic ideas of geometry is required to understand the subjacent motivation and most of the approaches reviewed here.
One of the most important concepts in geometry is the measurement or mathematical measure, which is a set of techniques that depends on the discipline considered (Velhinho et al. 2017, Gkelsinis and Karagrigoriou 2020). A measure is a function μ : s → R that assigns (scalar) values in R , to a subset s ⊂   S of elements of a system S , or to some of its states (also known as properties, observables or magnitudes). According to the theory of physical measurement, it is usual to distinguish between intensive (e.g. density, pressure, wind velocity, friction, temperature, viscosity) and extensive (e.g. mass, energy, duration, snow depth, precipitation amount, additive entropy) measurements (Inguaggiato et al. 2022, Biró and Deppma 2023). In measure theory of geometry, the ‘measure’ term is reserved only for the extensive properties of sets, assigning values only on positive real numbers. The most elementary measure of a set is that which relates to its ‘size’, that is length, area and volume, as the dimension d ∈ N is increasing from d = 1 in lengths to d = 3 in volumes, passing through d = 2 for surfaces; and the measure M is increasing as the power law M   ∝   L d of the representative length L .
In the case of the precipitation, one can enumerate a large set of different measurements: total amount or accumulation, precipitation event duration, wet/dry spell lengths and drop/hail size among others (Gobbo et al. 2022, Agbazo et al. 2023). Moreover, intensive measures of precipitation could be, for instance, rainfall intensity and drought severity indicators (Monjo 2016, Gaitán et al. 2020).
Paradoxically, some features of nature cannot be described using ‘natural dimensions’ (i.e. positive integer numbers) but require using new techniques such as the fractal theory (Meseguer-Ruiz et al. 2017, 2019, Monjo et al. 2020, 2023). The word “fractal” was presented by Mandelbrot (1974, 1975) to bring together a kind of objects that have played a historical role in mathematical development in the last third of the past century. The regular geometric shapes and structures of Euclid and their natural dimensions give way to new forms, complex, but underlying a scalar regularity with fractional dimensions.

1.2. Fractal measure background

The concept of fractal is used to designate objects that are too irregular to be described according to Euclidean geometry, but which are invariant by change of scale. Fractal geometry (Jahanmiri et al. 2022, Bhoria et al. 2023) is an extension of classical geometry and encompasses the description, classification and analysis of geometrically “complicated” subspaces. Generally, the structure and organization of a fractal set does not make it possible to specify where - in plain language - each point that composes it is located. Therefore, some relationship must be defined between the various structures observed in it for various levels of resolution. This relationship is formulated quantitatively by the concept of fractal dimension, which describes the scalar behavior of fractal structures (Meseguer-Ruiz et al. 2017, 2019).
As with fractal objects, scale-invariant systems and processes do not have a particular scale that is specific to them. Accordingly, a fractal process is one in which the same elementary action occurs at different scales, i.e., in which a part reproduces the whole. For the range of scales analyzed, the process statistics follow potential laws characterized by their exponents. The relationship between the statistics for the different scales will simply consist of scale ratios.
Unlike the Euclidean dimensions, which are always non-negative integers (0 for a point, 1 for a line, 2 for a plane, 3 for a three-dimensional space, etc.), fractal dimensions have a more general non-negative real value. To get a clearer picture of this, let us suppose a point moving on a plane describing a Brownian motion, i.e. a random motion tending to gradually complete or fill the plane (Anastassiou et al. 2023). At the beginning, its dimension will be 0, but at the same instant in which it begins to describe this movement, its fractal dimension will become 1, and immediately after, it will begin to increase the decimals, but without reaching two, since it will not complete this plane.
The postulates of fractal geometry have been used in the geographic discipline for more than three decades. It was introduced to measure the length of coastlines of the British Isles (Mandelbrot, 1967), and subsequently its use has spread prolifically to a multitude of studies in surveying. Some mathematical algorithms are now available to calculate the fractal dimension for linear and area entities. Indeed, not all geographic patterns are fractal at every scale. While the nature of some geographical multifractal phenomena has been well-explored, it remains to be determined why certain types of terrain align better with fractal geometry than others.
Since the idea of fractal objects was introduced to measure shoreline length at certain locations, this kind of analysis has been highly applied to several topographic studies. One of the possible applications has been focused on measuring and characterizing irregular linear features such as coastlines, to describe and characterize landforms, and to statistically regionalize spaces according to relief shape. However, not all these elements are fractal at all the studied scales. Fractal analysis can also be used to produce terrain simulations with a known dimension. Other applications focus on understanding the different geomorphological processes involved (Gao and Xia, 1996).
Thus, the problems of estimating area, length and point features are increasingly promoted largely by the growing interest in digital capture, processing and storage of geographically referenced data. Therefore, numerous drawbacks appear when carrying out composites of satellite images or aerial photographs that have been taken at different altitudes or with different resolution, and for which it becomes necessary to implement mathematical models around a Geographic Information System (GIS) in which fractals actively intervene (Tuček et al., 2011).
In hydrological basins, as an applied example, the most important principles of fractal objects, such as self-similarity and self-affinity, are reliably reproduced. Thus, numerous elements such as the length of the river network, the number of branches, the bifurcation coefficient, the density of branches per drainage unit, the perimeter and area of the basin itself, etc., can be treated as applications in fractal mathematical studies. The results obtained provide information on the knowledge of the hydrological characteristics of the area in question (Cheng et al., 2001). The works that deal with the precise measurement of the length of the coasts are the most abundant studies, yielding interesting results such as the length of a particular coast will vary depending on the fractal dimension of the same, considering the measurement of the same in terms of mapping at different scales (Martín-Vide, 1992; Zhu and Wang, 2002).
As can be deduced, the conceptual environment surrounding fractals is closely related to the spatial concept of scale, fundamental in Geography, since it is often a matter of both data and information integration in a multiscalar way. The high access to GIS has enabled an adequate environment that allows re-scaling data prior to the consequent integration of the data into the system. However, the challenges to understand patterns of spatial variation of the information itself is surpassed by the scarcity of suitable tools because the nature of the spatial variation of the information of interest is not always well analyzed and understood. These two patterns are modeled using geostatistical approaches that provide the possibility of re-scaling the spatial data (such as spatial interpolation multiple regression models). These types of regularizations provide information that can often describe the data better than the data itself (Atkinson and Tate, 2004), as is the case in many climate models and climate and weather reanalysis grids.
Climate studies have also applied the fractal analysis methodology, since some of its variables (pressure, precipitation, temperature…) show a fractal behavior (Rehman, 2009). From the data series of the three previously mentioned variables and their monthly and seasonal variability, it is possible to detect how regional climate models are not able to predict the local climate on a seasonal scale, since they only work with averaged quantities. Thus, interesting facts appear such as that, in regions like India, rainfall during the southwest monsoon is affected by the variability of temperature and pressure of the previous winter. Other fractal-based prediction indices are more reliable since they consider more climatic dynamics (Rangarajan and Sant, 1997; Rangarajan and Sant, 2004).
The analysis of rescaled ranges of annual mean temperatures at different meteorological stations in Hungary has shown that this variable follows a fractal behavior, both on time scales ranging from a few years to scales approaching the millennium (Bodri, 1994). These analyses could indicate that the existence of this fractal behavior is a characteristic of climate change during the study period. Variations of the fractal dimension values linked to the used time scale would show different behaviors at different scales.
In the same vein, that purely mathematical fractal theories play an important role in climate modeling has become evident not only on a regional scale, as explained above, but also on a global scale (van Hateren, 2013). The factors that most obviously affect planetary temperatures (response to solar cycles, large volcanic eruptions, increasing concentrations of greenhouse gasses and aerosols in the atmosphere) fit appropriately with those predicted by models created from introducing fractal theories.
However, other findings have appeared that propose new analysis processes to discriminate between climate temporal behavior data generated by climate models and observations from instrumental weather stations. These approaches combine monitoring of actual and model-generated data streams and fractal data analysis to identify differences in the correlation between observed and model-predicted series. Thus, from this comparison, it is concluded that the fractal approach allows to correctly discriminate the data, from which it follows that there is still the chance to improve climate change models supported by fractal theories (Nunes et al., 2011; Nunes et al., 2013).
In paleoclimatology, the study of soundings or “cores” extracted from glaciers have a key role in determining past climate conditions (Pelletier, 1997; Valdez-Cepeda et al., 2003). The analysis of the air bubbles confined in the ice reveals the chemical composition of the atmosphere at the time when the bubble was imprisoned, as well as the conditions under which the ice was formed, based on its level of compaction. The latter is determined by studying the conductivity of the ice at a known electrical impulse, and it has been found to be scale invariant over three different orders of magnitude in the depth of the ice core. This experiment carried out in Antarctica, from an ice core 3,190 m thick, makes it possible to establish climatic connections between the last 740,000 years, and, from fractal analysis, to provide information on the occurrence of glacial ages (King, 2005). Previous studies have linked Antarctic ice cores information with historical climate data obtained from sediments in the deep ocean (Raidl, 1996; Sahay and Sreenivasan, 1996). A Fractal approach provides evidence relates climate data from geographically distant locations, such as in Central-Europe (Bodri, 1994) and the Kamchatka Peninsula over the last 10,000 years (Gusev et al., 2003), or, on a shorter time scale, from sediment records in alluvial plains in the Mediterranean basin (Mazzarella and Rapetti, 2004).

1.3. Geometry in dynamical systems

The atmosphere is a highly nonlinear dynamical system, governed by physical equations such as the Navier-Stokes equations, energy balances and hydrological cycle among others. These well-known physical concepts are deeply studied in differential and computational geometry. A brief review of some basic definitions is presented here.
Dynamical system. As a starting point, most complex systems are easily addressable under the discrete geometry. Let a system S = ( X , f ) be defined as a set X of elements with characteristics or states and some law f that describes a (natural or not) behavior. Then, a dynamical system is that whose behavior depends on a variable assimilable to the time (Almatroud et al. 2020, Shen et al. 2022, Jiang et al. 2022). In the case of a discrete time (i.e. a natural number), the law is a continuous function f : N → R that determines the temporal evolution of the values of a state variable of the system (Almatroud et al. 2020, Jiang et al. 2022). For example, in the study on populations of biological species, the abundance of individuals x in the time n ∈ N can be simplified by the logistic map
x n = r · x n − 1 · 1 − x n − 1 ,
where r is a parameter that indicates relative reproduction rate compared to the competition rate (Moysis et al. 2020). Similarly, continuous variables like the wind components ( u ( t ) , v ( t ) ) of a frontal system (e.g. cold front) are also governed by an evolution law but with a real time t ∈ R . From the Newton’s second law, the (differential) equations of the simplest or geostrophic wind are (Zakinyan et al. 2016, Pimont et al. 2020):
d u ( t ) d t = F u t = − f x + f C · v t ,
d v ( t ) d t = F v ( t ) = − f x − f C · u ( t )
where f C is the Coriolis parameter and f x :=   f x , f y ≡ 1 ρ ∂ P ∂ x , ∂ P ∂ y   is the acceleration caused by the gradient of the pressure P at the position x , y ∈   R 2 for a fluid with density ρ . Under a computational perspective, differential equations can be expressed in terms of finite differences according to a discretization of the time t ≈ n δ   for some small-time lapse δ > 0 and n ∈ N (Suárez-Carreño et el. 2023). For example, u-component of the wind is now u ( t ) ≡ u ( n δ ) ≡ u n , then
d u ( n ) d t ≈ u n   −   u n − 1 δ   = F u ( n ) ⇒ u n = δ F u ( n ) + u n − 1
Therefore, differential geometry applied to atmospheric sciences can be computationally discretized and most of the properties are then inferred.
Non-linearity and chaos. A dynamical system is nonlinear if the governance law is not simply linear with respect to the temporal variable (Almatroud et al. 2020, Tusset et al. 2023). For example, in the case of the logistic map and the geostrophic wind have quadratic terms that provide a high complexity in their behavior. Solutions of the dynamical equations are known as orbits or paths, which are grouped in a phase space of positions ( u ( n ) ) and momenta ( d u ( n ) / d t ) according to the symplectic geometry (Prykarpatski et al. 2023). After a sufficient transitory time, stable solutions are attractors or attractive regions of the phase space, because the evolution of a given variable tends to approach these regions. In some cases, highly nonlinear systems present unpredictable solutions for a certain transitory time, due to a high transitivity and sensitivity to the initial conditions. Scientific community defines these cases as chaotic solutions or simply chaos (Zhao et al. 2023). A remarkable consequence of the chaotic systems is that phase space presents strange attractors, characterized by fractal measures (Takens 1981, Tusset et al. 2023). The Lorenz fractal is a very popular example derived from simplified Navier-Stokes equations (Frunzete 2022).
Self-similarity. Among others, fractals have a remarkable feature of being similar to themselves when two or more different scales are compared, like a homothety symmetry (e.g. similar triangles). This surprising character allows the use of stochastic cascading, spatial or temporal scaling methods and disaggregation of time series or spatial distributions (Lee 2022, Monjo et al. 2023).
Quasi-oscillations. In a chaotic dynamical system such as the atmosphere, most variables (precipitation, temperature, humidity and pressure among others) present a large number of different modes in both spatial and temporal variability. That is a set of diverse amplitudes of anomalies, with more regular or periodic (predictable) components and other unpredictable phases. These modes of variability are known as quasi-periodic oscillations or simply quasi-oscillations (Redolat et al. 2020, 2023). There exists a large number of techniques that aim to determine the periodicity level of quasi-oscillations, like the fast Fourier transformation and the wavelet analysis, which decompose temporal variability in a set of period oscillations (Guariglia 2023). Assuming some appropriate technique to model orbits without overfitting, residual unexplained variance would be a ‘pure chaotic’ component of the particular time series analyzed. In this case, other approaches (e.g, based on random probability distributions) are commonly used.

1.4. Structure of the review

After this introductory section, the review is structured in two main parts: Section 2 is focused on classical perspectives of fractal measures used in analysis of time series of precipitation, including monofractal and multifractal approaches, temporal concentration indices, and other measures such as Shannon entropy, Hurst exponent and IDF curves. On the other hand, Section 3 explores new perspectives of precipitation fractality at temporal and spatial scales as well as for classification of climatic features. Finally, Section 4 summarizes the main conclusions of the review.

2. Classical perspectives of precipitation fractality

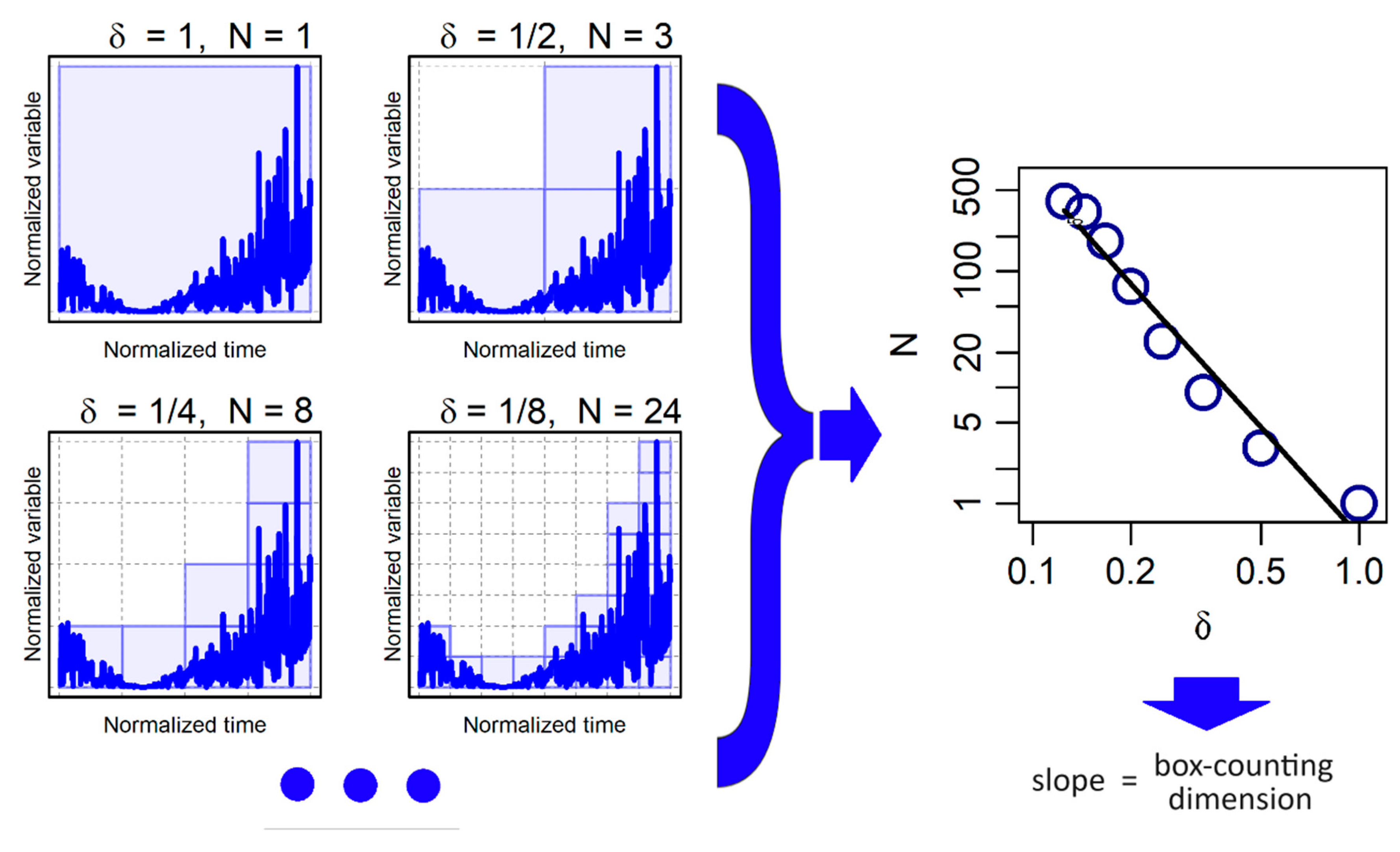
2.1. Monofractal dimension

As mentioned above, non-integer or fractional dimensions are naturally found for nonsmooth geometries with self similarly at different scales, which is usually assumed as a unique behavior so-called “monofractal”. For objects constructed by iterative processes (e.g. Cantor set, Sierpinski triangle and Koch curve), it is possible to define the Hausdorff-Besicovitch dimension DH by using the numbed N of self-similar fragments, that are rescaled copies (homothety) of the original object by applying a scaling factor of 1 / S . Thus, it is
D H = log ⁡   N log ⁡   S ,
This value always ranges between the topological dimension of the object (i.e. of a fragment) and the dimension of the support space, in which the object is contained. For the case of rainfall, self similarity is found when expected values of maximum average intensity I(t), are compared to the time scale t = 1/S, with relative units of intensity I(1) defined for t = 1 . Particularly, a related dimension n between 0 and 1 is the following (Monjo 2016, Monjo et al. 2023):
n H = l o g   N ( t ) l o g   S = l o g   I ( t ) / I ( 1 ) l o g   1 / t
Formally, Hausdorff dimension is defined by the Hausdorff measure H D which is the sum of all H δ D -volumes given by the infimum set U ={Ui} of countable delta-covers (i.e. covers with diameter delta) of the object when the delta approaches zero. If D is too high (i.e. D approaches the support-space dimension), H D is zero. On the other hand, if D is too small (close to the topological dimension), the value of H D is infinite.
Therefore, the Hausdorff dimension is uniquely defined by the lowest finite D that leads H D to be zero and the highest positive d that leads H D to infinity, so both values coincide. A simplified estimation of this monofractal dimension is the box-counting dimension, which uses a simple set of covers based on regular boxes. The box-counting approach is commonly used in the analysis of fractality in geometry, and has been then applied to rainfall (Foroutan-pour et al.1999).
The box counting method considers variable fields such as rainfall, which involves multiple scales and dimensions that characterize intense regions (Lovejoy et al., 1987). The box-counting method is based on the idea of separating data into boxes and counting the resulting number of boxes (Mandelbrot, 2004; Bai et al. 2021). When applied for the analysis of time series, the box-counting method aggregates neighboring data points by placing adjacent individuals into boxes. It explores how the results are influenced by the variation of the box size (i.e. resolution) (Figure 1).
The box-counting algorithm is straightforward and applicable to sets in any dimension. A fractal curve, characterized by infinite detail due to its self-similarity, exhibits an indefinite length that grows with the increasing resolution of the measuring instrument. The fractal dimension quantifies the augmentation in detail and, consequently, length with each change in resolution. For a fractal, the length (L) as a function of the measurement device’s resolution  is determined by:
L δ   = V 0 δ − D
Here, D represents the exponent known as the fractal dimension and V0 is a constant. In the case of regular curves, the length L() converges toward a constant value as  decreases.
Box-counting algorithms gauge L() for different  by tallying the number of non-overlapping boxes of size  needed to encompass the curve. These measurements are then fitted to the equation 3 to obtain an estimate of the fractal dimension, known as the box dimension (Breslin and Belward 1999). A set of time series data can be attributed with a fractal dimension by plotting it as a function of time and determining the box dimension. Eq. 3 remains valid within a finite range of box sizes, with the smallest boxes having a width of T (representing the resolution in time) and a height of a (representing the resolution of the data).
When monofractal techniques are not enough to adequately describe the behavior of a variable, a multifractal approach can be considered to represent the variability of the fractal dimensions as a function of the time scale considered (see Section 2.2.2).

2.2. Temporal concentration

2.2.1. Classical indices

Other (intensive) measures of the precipitation are its temporal concentration and irregularity. Since clouds are dynamical systems with spatial coordinates that change in the time, both concentration and irregularity are also reflected in the spatial distribution of the precipitation recorded.
Temporal concentration of precipitation can be measured at a climate scale or for individual precipitation events. Climatically, the whole time series provides all the statistics to estimate the well-known empirical Gini Index (GI) or its theoretical version adapted for precipitation, the Concentration Index (CI) of Martin-Vide (2004), usually calculated at a daily resolution (Monjo and Martin-Vide 2016). This indicator shows how concentrated is the daily rainfall in a typical year, comparing the total amount and the percentage of days needed to accumulate that amount, according to the Lorenz curve. For individual rainfall events, the most appropriate metric is the n-index (Monjo et al. 2009, 2023), which is linked to the box-counting and the monofractal dimension (Monjo 2016, Monjo et al. 2023) since it is a scaling exponent of averaged magnitudes (in this case, maximum averaged intensity). This index summarizes the behavior of a rainfall (or snowfall) event according the subdaily or supradaily time structure of the intensities (hyetographs), that is n → 0 for very regular precipitation (e.g. constant stratiform rainfall) and n → 1 for very irregular events (e.g. a punctual downburst from a thunderstorm). The most effective rainfall is logically found for n ≈   0.5 , since it combines both stratiform (advective flux) and deep convection in the same extreme event (Moncho et al 2011) (Figure 2).
Under a climatic perspective, subdaily time structure of the precipitation events can be averaged to build synthetic hyetographs. Most classical techniques are based on observed cumulative curves, such as the alternating block technique, the Huff’s quantiles (Huff 1967), the Pilgrim–Cordery curves (Cordery & Pilgrim 1984), and the Soil Conservation Service/Natural Resource Conservation Service (SCS/NRCS) Type I, II and III curves (Mishra et al. 2018). Alternatively, semi-empirical methods adjust smooth functions such as Gamma or Gaussian distribution, use simple triangles as in the Yen-Chow method, or piecewise functions such as the Sifalda storm and the Keifer-Chu curves, also known as Chicago method, among others (Huang 2011, Na and Yoo 2018).
Under a theoretical framework, temporal structure of the precipitation can also be simulated from stochastic processes of time scaling or disaggregation. For instance, the method of fragments is a daily-to-sub daily scaling that employs a nonpara-metric resampling technique and conditional probability distribution functions to relate daily precipitation sequences and the corresponding subdaily fragments from at-site records or other stations such as neighboring or more correlated ones (Li et al. 2018, Rafatnejad et al. 2022).
Random techniques used in weather generators (e.g. those based on multi-state Markov chains) produce concatenated wet/dry values of precipitation to build a synthetic time series (Rayneret al. 2016, Peleg et al.2017). Stochastic approaches can also simulate convective features of rainfall, considering power law spectrums in filtered autoregressive models such as the RainFARM method (D’Onofrio et al.2014) or using cumulative functions for extreme events like the Stochastorm method (Wilcox et al. 2021)

2.2.2. Multifractal approach

Beyond the classical techniques, multifractal approaches better represent the behavior of rainfall in time-scaling modeling and its disaggregating process. Stochastic cascade models, used in these cases, were originally developed in turbulence studies (Müller-Thomy 2020). Specifically, to understand temporal behavior of precipitation, universal multifractal parameters are commonly employed according to the range of variability given by the Levy index, which reports on the deviation from the monofractal case (Sun and Barros 2010). Other examples are the multiplicative cascade models, the micro-canonical cascade processes and log-ratio transformations based on standard normal spaces, which can be used to produce time-scaling of rainfall intensities (Gaume et al. 2007; Gao et al. 2018; Müller-Thomy 2020). Log-ratio relationships of the temporal variability can also be characterized by using the spectrum obtained from the multifractal analysis and the wavelet analysis (Guariglia 2023, Redolat et al. 2024).
Time-scaling processes of precipitation disaggregation can be modeled under the framework of probability distribution functions (Monjo et al. 2023). Particularly, averages of (statistical) q-moments are proportional to the power function given by the ratio or quotient of the scales involved (Garcia-Marin et al., 2013; Zhang et al., 2021). Therefore, for a synthetic rainfall event that is scaled from t0 to t duration, the expectation value or average〈·〉is estimated as follows:
〈 I q ( t ) 〉 ∼   〈 I q ( t 0 ) 〉 t 0 t ζ ( q )
where Iq(t0) and Iq(t0) are the q-moments of the variable (precipitation) for the timescales t  <  t0, and ζ(q) is the scaling moment function (multifractal spectrum), which is obtained from the Legendre transformation of the codimension function applied to the same variable (Masugi & Takuma, 2007; Sun & Barros, 2010). According to the Monjo et al. (2023), when monofractal hypothesis is assumed for intensity or velocity fields, an asymptotic power law is found with
ζ ( q ) ∼   ň   q
where the parameter ň summarizes the monofractal behavior, as a simple-scale cascading dimension that ranges between 0 and 1 (Monjo et al. 2023). For averaged rainfall intensities (i.e. q = 1), it is approximately equivalent to the Lipschitz–Hölder exponent and the monofractal Rényi dimension. Under a geometric perspective, it is the Minkowski–Bouligand box-counting dimension, which bounds the upper limit for the Hausdorff dimension (Bäcker et al., 2019; Schmitt & Huang, 2016).

2.3. Other measures

2.3.1. Entropy

Let a random variable τ of N possible states, with distribution P τ = p i i = 1 N   , the Shannon Entropy measure is defined as follows (Monjo 2016; Omidvarnia et al. 2018, Gkelsinis and Karagrigoriou 2020):
S X =   − K ∑ i = 1 n p i   ln ⁡ p i
The concept of Entropy was introduced by Shannon (1948) to refer to the degree of disorder implicit in a series, or to know the level of noise existing in this series, apart from the variability itself. In thermodynamics, entropy (H) quantifies the variety of specific arrangements possible within a thermodynamic system, often interpreted either as a measure of disorder or as an indicator of the system’s progression towards thermodynamic equilibrium. The entropy of an isolated system invariably increases, aligning with its tendency toward thermodynamic equilibrium, characterized by maximum entropy. However, systems that are not isolated may experience a decrease in entropy. As entropy is a function of a specific state, the alteration in entropy remains constant for any process transitioning from an initial state to a given final state. In communication theory, the information associated with an event i, such as the value of x(t), is defined as follows (Monjo 2016; Omidvarnia et al. 2018, Gkelsinis and Karagrigoriou 2020):
I i = − K ln ⁡ ( p i )
where pi is the probability of event i and K a constant that can be taken K = 1 for numerical computation.
After a sufficiently long-time t the total information of the i events in that time produced is:
I = t   E I i = − K   t ∑ i i p l n ( p i )
where E[Ii] is the expected value of Ii.
In turn, the entropy (Shanon, 1948) of a system from which, after a time t has elapsed, we have extracted information I, is defined as:
S X = I t   = − K ∑ i = 1 N p i ln ⁡ p i
Thus defined, the entropy becomes a characteristic parameter of the distribution of the variable. The entropy associated with a variable exhibiting a unimodal and Gaussian distribution will be lower than that of a bimodal distribution or a constant (random) distribution. Therefore, it serves as an indicator of the amplitude of the non-periodic components within the signal.

2.3.2. Hurst exponent

There are several methods for estimating the fractal dimension of a time series of data such as the box counting method and the correlation method (DeGrauwe et al. 1993, Peitgen and Saupe 1988). The utilization of these methods often poses challenges in terms of computational time and necessitates expertise for interpreting the computed fractal dimension. In this paper, we employed the Hurst exponent method, which offers a metric for assessing long-term memory and fractality in a time series. To calculate the Hurst exponent, one needs to gauge the dependence of the rescaled range on the observation time span δ. Several techniques exist for computing the Hurst exponent, with the R/S analysis being the oldest and most widely recognized method. Rescaled analysis or R/S analysis is favored for its straightforward implementation. It was proposed by Mandelbrot and Wallis (1969), based on the previous work of Hurst (1951).
The R/S analysis is used merely because it has been the conventional technique used for geophysical time records (Rangarajan and Sant, 1997). A time series with a total length of L is segmented into multiple shorter time series, each with lengths of δ = L, L/2, L/4, and so on.
The average rescaled range is then calculated for each value of δ.
For a time series of length δ, the rescaled range is calculated as follows (Selvaraj et al. 2011):
  • calculate the mean,
  • create a mean-adjusted series,
  • calculate the cumulative deviate series Z,
  • compute the range R,
  • compute the standard deviation S,
  • calculate the rescaled range R(δ) /S(δ) and average over all the partial time series of length δ.
Hurst found that (R/S) scales by power-law as time increases, which indicates
R δ S δ = C 0 δ H
Here C0 is a constant and H is called the Hurst exponent. To determine the Hurst exponent, we create a log-log plot of (R/S) against δ. The slope of the resulting regression line serves as an approximation of the Hurst exponent.
The values of the Hurst exponent range between 0 and 1. Based on the Hurst exponent value H, the following classifications of time series can be realized (Barbulescu et al. 2007):
  • ✓ A value of H = 0.5 suggests a series is random;
  • ✓ If 0 < H < 0.5, it suggests an anti-persistent series where up an upward value is more likely followed by a downward value, and vice versa;
  • ✓ If 0.5 < H < 1, it indicates a persistent series where the direction of the next value is more likely to be the same as the current value.
The Hurst exponent is connected to the fractal dimension D of the time series curve through the following equation:
D = 2 − H
The Hurst exponent, denoted as H and ranging from 0 to 1, reflects the nature of time series. When the fractal dimension D of a time series is 1.5, indicative of typical random motion, there is no correlation between amplitude changes in successive time intervals, making the process unpredictable. Conversely, as the fractal dimension decreases toward 1, the process shows more predictability, demonstrating persistent behavior. This suggests that future trends are increasingly likely to follow established patterns. In contrast, when the fractal dimension increases from 1.5 to 2, the process exhibits anti-persistence. That is, a decrease in the amplitude of the process is more likely to lead to an increase in the future (Rangarajan and Sant 2004). Notice that, for time series of precipitation P, an average intensity can be defined as follows:
I δ   ≔ P δ δ
With this, fractal dimension of the intensity (nI) is reduced by a unity:
n I   ≔   D − 1   =   1 − H
and, therefore, the value of nI is ranged between 0 and 1 like the Hurst exponent but with opposite behavior.

2.3.3. IDF curves

Precipitation intensity is a significant variable that defines physical-environmental processes such as water erosion, soil infiltration rates and the design of hydraulic works and water and soil conservation, among others. Regarding this last point, the design of works, the maximum annual intensity for a given duration and return period is used as the design rainfall and can be determined by the Intensity Duration Frequency (IDF) curves. IDF curves are developed from the analysis of the records of traditional rainfall stations, which record the rate of precipitation over time, on a band of millimeter paper (Sangüesa et al., 2021). From the analysis of these bands, precipitation intensities are analyzed in different periods, that may range from 15 minutes to 24 hours. But meteorological stations can be affected by instrumental changes or failures, resulting in a reduction in the temporal resolution of precipitation intensities and limiting the construction of IDF curves.
In this context, uncertainty arises about how the annual maximum intensity has varied for durations of less than 1 hour and whether this variability has an impact on the construction of IDF curves, which, if so, would affect the design of works, since the dimensions of these works are defined according to a family of IDF curves (Saad Al-Wagdany, 2020) or the mathematical model of these curves. Additionally, the period of change of seasons coincided with the decade of the megadrought in Chile, adding two factors that contribute to the uncertainty of the data collected. On one hand, with a lower temporal resolution of the infra-hourly data, and on the other hand, the presence of an observable drop in annual precipitation.
The construction of IDF curves requires: the maximum annual intensities, at sub-daily (ideally sub-hourly) resolution and a record length greater than 15 years. Based on the above, several authors (Pizarro et al., 2015; Kossieris et al., 2018; Nguyen et al., 2018; Diez-Sierra and del Jesus, 2019) have developed and implemented techniques for the temporal downscaling of rainfall intensities. Some of these methodologies are explained below:
i) Storm index or K-method
Pizarro et al. (2015) estimated the precipitation intensities of pluviometric stations with the storm index. This technique transforms the precipitation intensity in 24h, Iknown(24h, T), to a desired duration Isim(t, T), using a K factor for each return period T. This factor is estimated from nearby rainfall observatories with sub-daily data according to the following equation (Sangüesa et al. 2023):
K t ,   T   =   I o b s t ,   T I o b s 24 h ,   T       ⟹       I s i m t ,   T   = I k n o w n 24 h ,   T   K t , T  
where Iobs(t, T) s the intensity for a duration t and return period T, while I 24 h ,   T is the precipitation intensity of the pluviometric station for a return period T and duration of 24 hours.
On the other hand, it is not always possible to have rainfall stations in the area and therefore statistical methodologies have been designed to increase the temporal resolution of precipitation (Kossieris et al., 2018; Nguyen et al., 2018; Diez-Sierra and del Jesus, 2019), such as the following ones.
ii) Scale-invariance
This technique assumes the existence of a relationship in the behavior of intensities for different durations and that they possess the same distribution (Ghanmi et al., 2016; Nguyen et al., 2018; Monjo et al. 2023). Thus, the model is as follows:
I t ,   T   = I t 0 ,   T   t 0 t n  
where I is the precipitation intensity; t is the desired duration; t0 is the observed duration (e.g. 24h); T is the return period and n is the scaling exponent, which is assumed to be approximately constant (scale invariance), but it can depend on the return period and duration or resolution of the precipitation. Notice that it is an explicit example of K-factor such as:
K t ,   T   ≈   24 h t n t ,   T  
iii) Bartlett-Lewis rectangular pulse model
It is a Cluster-Poisson type model, whose main advantage is to simulate precipitation events, using rectangular pulses (Kossieris et al., 2018), allowing the estimation of precipitation intensities associated with durations shorter than those observed. The procedure for its adjustment is detailed in Teixeira-Gandra and Damé (2014) and Kossieris et al. (2018).
In addition to the aforementioned methods, it is possible to obtain intensities in areas without data by extrapolation or spatial interpolation of intensities (Hershfield, 1961; Kumari et al., 2016); however, this methodology requires having a wide network of stations with intensity data for its results to be reliable.

3. New perspectives of precipitation fractality

3.1. Temporal and spatial relationships

Due to the nature of a fractal object, it is intuitive to think that the application of Mandelbrot’s postulates has been based on the spatial behavior of the same patterns that would apply to fractal objects, even the query of whether it is indeed possible to make a fractal approximation to it has been directly posed (Sivakumar, 2001).
Thus, there are several studies that have been based on the fractal geometry of rainfall fields derived from the analysis of radar images, capable of showing, in great detail, the location and intensity of instantaneous precipitation, as well as elaborate simulations. These simulations show that these processes follow a scalar hierarchy that fits fractal models. The rich morphology of rainfall fields and their consequent statistical relationship exemplify the power of simple fractal models to generate complex fractal structures (Lovejoy and Mandelbrot, 1985).
Many physical systems in which structures that span large areas often consider scale-invariant intervals. In these cases, different size scales are related by an analysis involving the scale relation and in which the system has no particular size. Gravity causes differential stratification in the atmosphere, so the change of scale implies new dimensions. Processes that are very variable, such as rainfall, involve multiple scales and dimensions that characterize zones of varying intensities. Both functional box-counting and elliptic dimensional sampling have been used to analyze radar rainfall data to obtain the multiple dimensions of the rainfall distribution (Lovejoy et al., 1987, Kai et al., 1989, Tchiguirinskaia et al., 2012).
In the same vein, there are weather radar databases that provide rainfall intensity maps over areas with a sampling period ranging from 120 seconds to 15 minutes. Time series of two-dimensional rainfall rate maps have wide application in simulating rainfall dispersion and attenuation of radio signals if the sampling period is considerably shorter (10 seconds or less). But scanning large radar products at this rate is physically inoperable. A numerical procedure has been developed to interpolate the time series rain rate to shorter sampling periods. The proposed method is applicable to temporal radar interpolation derived from rainfall intensity maps and is based on scalar fractality properties measured experimentally from the rainfall intensity record in various time series, but when one wants to determine rainfall fields beyond 20 minutes, the model behaves erratically (Paulson, 2004).
Because of this enormous complexity, derived from the extreme variability of precipitation over large ranges of spatiotemporal scales, it is necessary to consider surrogates for rainfall in order to interpolate, such as radar reflectivities. Since precipitation and clouds are strongly coupled in a nonlinear fashion, scale invariance is not always satisfied (Lovejoy and Schertzer, 2006).
Along the same lines, the study of rainfall at a detailed scale, the so-called downscalling, is of paramount importance in modern hydrology, especially because of the need to develop practical tools for the possible generation of rainfall scenarios in urban hydrology. The development of radar technology together with the implementation of mesoscale models has constituted a great advance in this field, but with the problem that these models do not allow the knowledge of rainfall behavior at a scale of interest for rainfall-runoff studies at a more local level. The possibility of improving the models has been based on the isotropic and statistical homogeneity properties of self-similarity (Licznar and Deidda, 2014; Licznar et al., 2014). Certain episodes of intense precipitation, the summer convective rains, have been successfully modeled following these principles, which has led to great advances, reaching the point of calculating in this type of phenomena the advection velocity, for which it is necessary to use fractal models, which has made up for the intrinsic technical deficiencies of the tracking models (Deidda, 2000).
However, the reality is that the spatial behavior of precipitation better approaches to a multifractal function than to a fractal object itself. This means that one admits the passage from a fractal object, which has already been explained above, which remains invariant by change of scale, and which are characterized mainly by a number, to a type of objects that are characterized basically by a function, which is a limit probability distribution that has been plotted in an appropriate way, with double logarithmic scales (Mandelbrot, 1989).
These new advances have allowed progress in precipitation models (Chou, 2003), even simulating rainfall fields following multifractal properties, certifying this phenomenon scale invariance. Thus, it has been verified that the spatial distribution of precipitation and their accumulated amounts follow fractal properties. So, it is key to determine whether its temporal distribution follows these same principles.
As mentioned above, the ideas derived from fractal theoretical framework have a more intuitive application referred to spatial rather than in temporal distribution, where the visualization of the concept is complicated due to its abstract nature. When talking about spatial distribution and fractals, one can easily think that a rainfall field can have a fractal shape, and if one looks at the detail it is possible to verify that a part of the whole is represented, respecting self-similarity, or invariance by change of scale. Concerning the temporal aspect, the idea is harder to apply. First of all, it is necessary to start from the assumption that the change of scale happens at this point to detect whether precipitation has occurred in different time periods of a given duration, and then evaluate if this behavior is repeated in other intervals of longer and shorter lengths. Rainfall, being a non-linear hydrological process, exhibits wide variability over a wide range of temporal and spatial scales. The strong variability of rainfall makes it difficult to work with at the instrumental and statistical level.
The progress made through the application of the fractal properties of precipitation to prediction models, together with the already known hourly behavior of precipitation, has implemented new models that allow to determine quite accurately the amount of accumulated rainfall at the hourly level. A study was developed to analyze the multifractal properties on precipitation data in Tokyo, measured to an accuracy of 1 mm. Through a multifractal model based on the scaling properties of the temporal distribution of rainfall, the intensity distribution relationships in the available scale regime was analyzed. Different properties of precipitation time series that are relevant to the use of rainfall data in hydrologic studies were used to statistically determine the agreement level between the modeled and observed hourly series (Pathirana, 2001; Pathirana et al., 2003).
Following the same line of model implementation, a multitude of models have been developed in Hydrology from the fractal properties of the temporal and spatial distribution of precipitation (Zhou, 2004; Khan and Siddiqui, 2012). The utility of these models of watershed hydrologic processes is greatly increased when they can be extrapolated across spatial and temporal scales. Though current research in Hydrology and related disciplines is focused in describing and predicting processes at a different scale from that at which observations and measurements are made. The quantitative description of the fractal scale behavior of runoff and morphometry of the microstream network in agricultural watersheds has not yet been realized, while when the watersheds are already of notable entity, the same Horton’s laws, empirical, are already fractal in nature, and contribute to the better understanding of what is observed and relate the parts of a fluvial system to a growth process.
The analysis of the precipitation temporal fractality is often used to study the climatic dynamics that have affected the planet. Thus, some studies have found the fractal dimension of the curves representing sea level changes together with a modern fractal dimension from annual precipitation records, obtaining that sea level changes during the last 150,000 to 250,000 years present fractal dimensions comparable to those obtained for precipitation. However, for earlier periods, the values of the fractal dimension of precipitation calculated are quite different from those deduced from sea level changes, so it could be deduced that these changes would be less related to climatic variability and more to plate tectonics (Hsui et al., 1993).
Indeed, this type of dynamics has been identified in studies in peninsular Spain from long series (ninety years) of annual accumulated precipitation, and their analysis reveals that the distribution of this variable conforms to a fractal distribution (Oñate Rubalcaba, 1997). The results are similar to other paleoclimatic and meteorological records, showing the same magnitude order. Comparing the two timescales shows that these values are characteristic of a theoretical climate change over the entire spectral range of 10 to 1,000,000 years. These results contribute to the creation of a valid hypothesis for the interpolation of climate changes from one scale to another and also in applications such as the design of models for hydrological applications.
The calculation of the fractal dimension at the annual level can also be used to identify trends, which then have to be confirmed with some other type of procedure (such as the Mann Kendall test), in order to determine whether in the future, according to the different climate change scenarios, the accumulated quantities will be greater or less than the current ones. Such is the case that has been studied in the province of La Pampa (Argentina), where it has been confirmed that the projections made by the IPCC for this region according to the models are in line with the reality of the observed data (Pérez et al., 2009). A similar study has been carried out in Venezuela (Amaro et al., 2004) using data from ten meteorological stations with annual precipitation values, which fit a fractal distribution. With these results it is possible to explain climatic changes at different time scales in this study area.
The fractal behavior of precipitation is observed in climatically different regions, as demonstrated by Sivakumar (2000b). This study highlights the importance of high-resolution precipitation data for understanding the complexities of the dynamics of meteorological processes and describing them in an accurate way. The study analyzes the suitability of fractal postulates for understanding precipitation behavior and its transformation between time scales. The study, which employs a multifractal approach, follows research carried out earlier by the author (Sivakumar, 2000a) employing a mono fractal approach in which some preliminary indication was obtained about the possibility of the existence of multiple fractals. Rainfall data of three different resolutions, every six hours, every day, and weekly, observed over a period of 25 years in two different climatic regions: a subtropical climatic region (Leaf River Basin, Mississippi, USA); and an equatorial climate region (Singapore) have been analyzed. This study carried out a different methods investigation to determine the existence of multifractal behavior in the precipitation. The results showed the existence of multifractal behavior in different locations, with further support for the results obtained with the mono fractal approximation, and confirm the suitability of a multifractal framework for characterizing the observed precipitation behavior and suggest the general suitability of fractal theory for the transformation of precipitation from one-time scale to another.
In other world regions where the problem of water access and its increasingly scarce availability, knowledge of precipitation trends is presented as a critical matter for the future development. During the last four decades, monthly and annual precipitation data from six stations show, from fractal and nonlinear analysis, that precipitation in this area was decreasing, finding two precipitation regimes, with a change from 1980 onwards, coinciding with climate change projections in the area (Rehman and Siddiqi, 2009; Gao and Hou, 2012).
In this very same line, applications have also been made to studies in Europe, at the Cordoba observatory, with a data series of twenty-four years and with time scales ranging from 1 hour to six months, a study of the temporal structure was carried out, finding a good fit to a fractal function for an interval of low temporal values, demonstrating that the universal multifractal model is adequate to statistically describe the time series of rainfall recorded in Cordoba (Dunkerley, 2008a; García-Marín et al., 2008). However, it has been shown that extreme rainfall fits even more complex models than the multifractal ones, since it is affected by limiting periods, such as very short durations or very long return periods (Langousis et al., 2009; Veneziano and Furcolo, 2002; Veneziano et al., 2006).
In this type of studies, the temporal resolution with which one works plays a determining role, since working with hourly data, on the one hand, and daily data, on the other hand, already causes changes in the values of the fractal dimensions, also partly due to the influence of the most characteristic precipitation of each place (García Marín, 2007; López Lambraño, 2012). Moreover, this method allows the discrimination of better analysis methods for precipitation frequencies, agreeing with studies mentioned above (Gao and Hou, 2012), even being able to define the precipitation regime of a particular region (Dunkerley, 2010; Kutiel and Trigo, 2014; Reiser and Kutiel, 2010).
Likewise, the choice of a working time scale has meant, in all climatological studies in general, and in precipitation studies in particular, numerous problems that measurement instruments have not always allowed to solve, and therefore it has been necessary to resort to time intervals of records derived from each other (de Lima and Grasman, 1999; Dunkerley, 2008b; Kiely and Ivanova, 1999; Olsson and Niemczynowicz, 1996; Telesca et al., 2007).
In different studies about scaling properties in the precipitation mechanisms, the multifractal approach has been applied without considering the different rainfall generation mechanisms involved. In this context, rainfall processes are related to particular scales that depend on climatological characteristics, and also on regional and local meteorological mechanisms. It is derived that the chance that the multifractal behavior of rainfall may depend on its dominant generation mechanism. The application of fractal analysis methods has been carried out on rainfall data recorded again in Spain between 1994 and 2001, and on a selection of precipitation events recorded in the period ranging from 1927 to 1992. The multifractal parameters obtained have been significantly different in each case, which shows the influence of the rainfall generation mechanisms involved. This influence has also been highlighted in the analysis of the effects of seasonality on the multifractal behavior of rainfall (Rodríguez et al., 2013).
The choice of methodology to obtain the value of the fractal dimension of a precipitation time series also seems to be determinant (Breslin and Belward, 1999). A comparison is carried out between three methods to calculate the fractal dimension: box-counting and Hurst’s R/S analysis, these two methods being the most widely accepted, and a third method that uses “overlays” from precipitation variation intervals instead of the classical box-counting. The latter method shows better results than the others for the calculation of fractal dimensions of monthly precipitation time series in Queensland, Australia.
In other areas of the Mediterranean region, work has been carried out to determine the value of the fractal dimension (Ghanmi et al., 2013). In these studies, fractal dimension has been calculated for various time series at different resolutions (5-minute and daily) with different durations between them (2.5 years for the former, 137 years for the latter). Three self-similar structures were identified: micro-scale (from 5 minutes to 2 days) with a fractal dimension of 1.44, meso-scale (from 2 days to one week) and synoptic (from one week to eight months) with fractal dimension in both cases of 1.9. The interpretation of these results suggests that only the microscale and the transition to saturation, understood as the length of the interval that would encompass the total time series, are consistent, while the high fractal dimension relative to the synoptic scale could be affected by the tendency to saturation. In this study, a sensitivity analysis of the fractal dimension estimated from daily precipitation data was performed by varying the length of the series as well as with the intensity threshold for rainfall detection.
Kalauzi et al. (2009) propose a comparative study of the fractal dimension not only of precipitation, but also of other climatological variables, between a Mediterranean environment, Veneto (Italy), and a completely different environment, the province of Pastaza, in the Ecuadorian Amazon. In this case, the rates at which the self-similarity principle is reproduced in each series have been determined, being much lower in the province of Pastaza (4.4 years), modulated by ENSO, than in the Mediterranean environment of Veneto (10.3 years), where the influence of the solar activity cycle remains to be confirmed.
Another area where similar work has been carried out is the Tamil Nadu region, in the extreme southeast of the Indian subcontinent (Selvi and Selvaraj, 2011). In this study, the determination of the fractal dimension has been carried out from data between 1902-2008 (temporal resolution not specified) from the Hurst method, obtaining that the value of the dimension is 1.7895.
The fractal nature of the temporal distribution of precipitation cannot be doubted. However, there are few, if not practically nonexistent, studies that give a purely climatic meaning to this phenomenon on a human scale, a few years, and that give an explanation by means of the synoptic patterns that are at the origin of such behavior.

3.2. Classification of climatic features

Monofractal approaches can be used to classify precipitation systems according to their time structure and averaged concentration. Moncho et al. (2009) analyzed IDF curves in Spain and showed that the n-index for coastal areas is lower (n < 0.5) than for inner regions (n > 0.5), probably due to the difference between predominantly maritime advection of the coastal areas against the typical convective cycle of the farest zones. Later, Moncho el al. (2011) found that the most efficient rainfall in the world has an n-index very close to n = 0.5 at every time scales. The interpretation of the results is that purely stratiform rainfall is almost constant in intensity (n ~ 0), with a perfect wet advection, while the classical simple thunderstorms have an almost instantaneous microburst or even a downsburst (n ~ 1), very bounded by a short time period. Therefore, the perfectly organized combination (n ~ 0.5) is given by a constant wet feeding flow and a deep convection, distributed through multicellular systems with different maturity levels.
Considering the entire population of precipitation data, the n-index is statistically independent of the duration and intensity of the rainfall events (Monjo 2016). Only when the wettest events are considered (i.e., with a limited number of events that reduces the statistical noise), the n-index seems to be sensitive to the time resolution, duration and intensity. Specifically, Monjo (2016) found a relationship between time resolution (between 1 and 12 hours) given by:
n ( r ) = n ( r 0 ) + a   l n r r 0
where n ( r ) and n ( r 0 ) are the n-index for the time resolutions of r and r 0 respectively, while a = 0.028 ± 0.003   is an empirical parameter.
The sensitivity of the n-index with the type of rainfall (stratiform/convective) is also used to calibrate remote sensing of precipitation. For instance, Guardiola-Albert et al. (2017) fitted a different Marshall-Palmer ZR Relationship in a band-S weather radar, obtaining a clear distinction between predominantly convective and stratiform rainfall.
Fractality is also present in other features of the precipitation systems such as the wet/dry spells and the classification of meteorological droughts. Types of dry spells were defined by Monjo et al. (2020) according to the Cantor-based exponent, Ce. Compared to the Cantor set lacunarity, Ce = 1 indicates a perfect sequence of dry spells similar to the Cantor gaps, while Ce = 0 implies a sequence of very regular dry sequences, all of them with the same length. That is, the higher values of Ce, the closest to the Cantor lacunarity. Meteorological droughts can be classified by combining Ce and the expectation value of wet spell lengths (Table 1).

4. Concluding remarks

Geometric features of atmospheric patterns are reflected in the precipitation behavior at all the time scales, from the drop distribution to the longest sequences of dry spells. The measurements of these behaviors are represented by complexity, inequality or concentration indices such as the Hurst exponent, Gini index and the Shannon entropy, as well as more geometric measures related to fractal volumes. For example, fractional or fractal dimension (Hausdorff) is usually approximated by the box-counting dimension, which can be employed in time cascading or scaling (Figure 3). Disaggregation of daily rainfall at a subdaily scale is increasingly demanded in the most recent climate change studies to quantify the impacts of the rising atmospheric water content on the rainfall concentration.
This work reviewed how fractal measures support the analysis on climatic complexity of the precipitation, so allowing to identify possible changes in the natural variability of the regimes (e.g. wet-dry spells, meteorological droughts and other extreme values). Simplified indicators, such as the n-index, can be also used to represent chaotic behaviors and summarize the variability of the rainfall concentration over time or its role in scaling processes, which are required to build synthetic time series and IDF curves (Monjo et al. 2023).
The representation of such complexity by smoother-variability indicators is adequate to finally apply regression models or classical statistics (e.g. Gaussian metrics) to the aggregated values. For instance, Meseguer-Ruiz et al. (2017) estimated the fractal dimension of the temporal distribution of precipitation for the Iberian Peninsula and modeled it with a linear regression of two predictors: the concentration index and the Shannon entropy. Another example of smooth value’s analysis is commonly used in spatial interpolations: At a global scale, Monjo et al. (2020) and Galiano et al. (2024) represented the mean value of a Cantor-based exponent.
Definitely, fractal-based measures allow to expand the classical analysis to new perspectives for addressing emergent challenges under the context of climate change. Therefore, the analysis of evolution of the climatic averages should be complemented with this geometrical framework to identify possible changes in complexity of the natural variability such as the time structure in precipitation concentration.

References

  1. Agbazo, N.M.; Tall, M.; Sylla, M.B. Nonlinear Trend and Multiscale Variability of Dry Spells in Senegal (1951–2010). Atmosphere 2023, 14, 1359. [Google Scholar] [CrossRef]
  2. Albert, J.; Gulakaram, V.S.; Vissa, N.K.; Bhaskaran, P.K.; Dash, M.K. Recent Warming Trends in the Arabian Sea: Causative Factors and Physical Mechanisms. Climate 2023, 11, 35. [Google Scholar] [CrossRef]
  3. Al-Mutairi, M.; Labban, A.; Abdeldym, A.; Basset, H.A. Trend Analysis and Fluctuations of Winter Temperature over Saudi Arabia. Climate 2023, 11, 67. [Google Scholar] [CrossRef]
  4. Almatroud, A.O.; Khennaoui, A.-A.; Ouannas, A.; Grassi, G.; Al-Sawalha, M.M.; Gasri, A. Dynamical Analysis of a New Chaotic Fractional Discrete-Time System and Its Control. Entropy 2020, 22, 1344. [Google Scholar] [CrossRef]
  5. Amaro I. R., Demey J. R., Macchiavelli R. Aplicación del análisis R/S de Hurst para estudiar las propiedades fractales de la precipitación en Venezuela. Interciencia 2004, 29–11, 617–620.
  6. Anastassiou, G.A.; Kouloumpou, D. Approximation of Brownian Motion on Simple Graphs. Mathematics 2023, 11, 4329. [Google Scholar] [CrossRef]
  7. Atkinson, P.M.; Tate, N.J. Spatial Scale Problems and Geostatistical Solutions: A Review. Prof. Geogr. 2000, 52, 607–623. [Google Scholar] [CrossRef]
  8. Bäcker, A.; Haque, M.; Khaymovich, I.M. Multifractal dimensions for random matrices, chaotic quantum maps, and many-body systems. Phys. Rev. E 2019, 100, 032117. [Google Scholar] [CrossRef]
  9. Bai, Z.; Wu, Y.; Ma, D.; Xu, Y.-P. A new fractal-theory-based criterion for hydrological model calibration. Hydrol. Earth Syst. Sci. 2021, 25, 3675–3690. [Google Scholar] [CrossRef]
  10. Barbulescu A, Serban C, Maftei C. Evaluation of Hurst exponent for precipitation time series. Proceedings of the 14th WSEAS international conference on Computers: part of the 14th WSEAS CSCC multiconference. Volume II Latest Trends on Computers 2007, 2, 590–595.
  11. Biró, T.S.; Deppman, A. Non-Additive Entropy Formulas: Motivation and Derivations. Entropy 2023, 25, 1203. [Google Scholar] [CrossRef]
  12. Bhoria, A.; Panwar, A.; Sajid, M. Mandelbrot and Julia Sets of Transcendental Functions Using Picard–Thakur Iteration. Fractal Fract. 2023, 7, 768. [Google Scholar] [CrossRef]
  13. Bodri, L. Fractal analysis of climatic data: Mean annual temperature records in Hungary. Theor. Appl. Clim. 1994, 49, 53–57. [Google Scholar] [CrossRef]
  14. Breslin, M.; Belward, J. Fractal dimensions for rainfall time series. Math. Comput. Simul. 1999, 48, 437–446. [Google Scholar] [CrossRef]
  15. Chen, X.; Liu, Y.; Sun, Z.; Zhang, J.; Guan, T.; Jin, J.; Liu, C.; Wang, G.; Bao, Z. Centennial Precipitation Characteristics Change in Haihe River Basin, China. Atmosphere 2022, 13, 1025. [Google Scholar] [CrossRef]
  16. Cheng, Q.; Russell, H.; Sharpe, D.; Kenny, F.; Qin, P. GIS-based statistical and fractal/multifractal analysis of surface stream patterns in the Oak Ridges Moraine. Comput. Geosci. 2001, 27, 513–526. [Google Scholar] [CrossRef]
  17. Chou, Y. Short-term Rainfall Prediction using a Multifractal Model, Massachusetts Institute of Technology, Master’s Degree Thesis 2003, 53 pp.
  18. Cordery, I.; Pilgrim, D.H.; A Rowbottom, I. Time Patterns of Rainfall for Estimating Design Floods on a Frequency Basis. Water Sci. Technol. 1984, 16, 155–165. [Google Scholar] [CrossRef]
  19. D’onofrio, D.; Palazzi, E.; von Hardenberg, J.; Provenzale, A.; Calmanti, S. Stochastic Rainfall Downscaling of Climate Models. J. Hydrometeorol. 2014, 15, 830–843. [Google Scholar] [CrossRef]
  20. de Lima, M.; Grasman, J. Multifractal analysis of 15-min and daily rainfall from a semi-arid region in Portugal. J. Hydrol. 1999, 220, 1–11. [Google Scholar] [CrossRef]
  21. Deidda, R. Rainfall downscaling in a space-time multifractal framework. Water Resour. Res. 2000, 36, 1779–1794. [Google Scholar] [CrossRef]
  22. Peel, D.A.; DeGrauwe, P.; Dewachter, H.; Embrecht, M. Exchange Rate Theory: Chaotic Models of Foreign Exchange Markets. Economica 1994, 61, 402. [Google Scholar] [CrossRef]
  23. Diez-Sierra, J.; del Jesus, M. Subdaily Rainfall Estimation through Daily Rainfall Downscaling Using Random Forests in Spain. Water 2019, 11, 125. [Google Scholar] [CrossRef]
  24. Dunkerley, D. Rain event properties in nature and in rainfall simulation experiments: a comparative review with recommendations for increasingly systematic study and reporting. Hydrol. Process. 2008, 22, 4415–4435. [Google Scholar] [CrossRef]
  25. Dunkerley, D. Identifying individual rain events from pluviograph records: a review with analysis of data from an Australian dryland site. Hydrol. Process. 2008, 22, 5024–5036. [Google Scholar] [CrossRef]
  26. Dunkerley, D.L. How do the rain rates of sub-event intervals such as the maximum 5- and 15-min rates (I5 or I30) relate to the properties of the enclosing rainfall event? Hydrol. Process. 2010, 24, 2425–2439. [Google Scholar] [CrossRef]
  27. Foroutan-Pour, K.; Dutilleul, P.; Smith, D. Advances in the implementation of the box-counting method of fractal dimension estimation. Appl. Math. Comput. 1999, 105, 195–210. [Google Scholar] [CrossRef]
  28. Frunzete, M. Quality Evaluation for Reconstructing Chaotic Attractors. Mathematics 2022, 10, 4229. [Google Scholar] [CrossRef]
  29. Gaitán, E.; Monjo, R.; Pórtoles, J.; Pino-Otín, M.R. Impact of climate change on drought in Aragon (NE Spain). Sci. Total. Environ. 2020, 740, 140094. [Google Scholar] [CrossRef]
  30. Galiano, L.; Monjo, R.; Royé, D.; Martin-Vide, J. Will the world experience more fractal droughts? Atmos. Res. 2024 ATMOSRES-D-23-01485. (under review). [CrossRef]
  31. Gao, J.; Xia, Z.-G. Fractals in physical geography. Prog. Phys. Geogr. Earth Environ. 1996, 20, 178–191. [Google Scholar] [CrossRef]
  32. Gao M., Hou X. Trends and Multifractals Analyses of Precipitation Data from Shandong Peninsula, China, American. Journal of Environmental Sciences 2012, 8, 271–279.
  33. Gao, C.; Xu, Y.-P.; Zhu, Q.; Bai, Z.; Liu, L. Stochastic generation of daily rainfall events: A single-site rainfall model with Copula-based joint simulation of rainfall characteristics and classification and simulation of rainfall patterns. J. Hydrol. 2018, 564, 41–58. [Google Scholar] [CrossRef]
  34. García Marín, A.P. Análisis multifractal de series de datos pluviométricos en Andalucía, PhD Thesis, Departamento de Ingeniería Rural, Escuela Técnica Superior de Ingenieros Agrónomos y Montes, Universidad de Córdoba 2007, 162 pp.
  35. García-Marín, A.P. , Jiménez-Hornero F.J., Ayuso-Muñoz J.L. Universal multifractal description of an hourly rainfall time series from a location in southern Spain, Atmósfera 2008, 21(4): 347-355.
  36. García-Marín, A.P.; Ayuso-Muñoz, J.L.; Jiménez-Hornero, F.J.; Estévez, J. Selecting the best IDF model by using the multifractal approach. Hydrol. Process. 2013, 27, 433–443. [Google Scholar] [CrossRef]
  37. Gaume, E.; Mouhous, N.; Andrieu, H. Rainfall stochastic disaggregation models: Calibration and validation of a multiplicative cascade model. Adv. Water Resour. 2007, 30, 1301–1319. [Google Scholar] [CrossRef]
  38. Ghanmi, H.; Bargaoui, Z.; Mallet, C. Investigation of the fractal dimension of rainfall occurrence in a semi-arid Mediterranean climate. Hydrol. Sci. J. 2013, 58, 483–497. [Google Scholar] [CrossRef]
  39. Ghanmi, H.; Bargaoui, Z.; Mallet, C. Estimation of intensity-duration-frequency relationships according to the property of scale invariance and regionalization analysis in a Mediterranean coastal area. J. Hydrol. 2016, 541, 38–49. [Google Scholar] [CrossRef]
  40. Gkelsinis, T.; Karagrigoriou, A. Theoretical Aspects on Measures of Directed Information with Simulations. Mathematics 2020, 8, 587. [Google Scholar] [CrossRef]
  41. Gobbo, S.; Ghiraldini, A.; Dramis, A.; Ferro, N.D.; Morari, F. Estimation of Hail Damage Using Crop Models and Remote Sensing. Remote. Sens. 2021, 13, 2655. [Google Scholar] [CrossRef]
  42. Guariglia, E.; Guido, R.C.; Dalalana, G.J.P. From Wavelet Analysis to Fractional Calculus: A Review. Mathematics 2023, 11, 1606. [Google Scholar] [CrossRef]
  43. Guardiola-Albert, C.; Rivero-Honegger, C.; Monjo, R.; Díez-Herrero, A.; Yagüe, C.; Bodoque, J.M.; Tapiador, F.J. Automated convective and stratiform precipitation estimation in a small mountainous catchment using X-band radar data in Central Spain. J. Hydroinformatics 2017, 19, 315–330. [Google Scholar] [CrossRef]
  44. Gusev, A.A.; Ponomareva, V.V.; Braitseva, O.A.; Melekestsev, I.V.; Sulerzhitsky, L.D. Great explosive eruptions on Kamchatka during the last 10,000 years: Self-similar irregularity of the output of volcanic products. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
  45. Hao, Z.; Singh, V.P.; Hao, F. Compound Extremes in Hydroclimatology: A Review. Water 2018, 10, 718. [Google Scholar] [CrossRef]
  46. Hasegawa, H.; Katsuta, N.; Muraki, Y.; Heimhofer, U.; Ichinnorov, N.; Asahi, H.; Ando, H.; Yamamoto, K.; Murayama, M.; Ohta, T.; et al. Decadal–centennial-scale solar-linked climate variations and millennial-scale internal oscillations during the Early Cretaceous. Sci. Rep. 2022, 12, 21894. [Google Scholar] [CrossRef]
  47. Hershfield, D.M. Estimating the Probable Maximum Precipitation. J. Hydraul. Div. 1961, 87, 99–116. [Google Scholar] [CrossRef]
  48. Hsui, A.T.; Rust, K.A.; Klein, G.D. A fractal analysis of Quaternary, Cenozoic-Mesozoic, and Late Pennsylvanian sea level changes. J. Geophys. Res. 1993, 98, 21963–21967. [Google Scholar] [CrossRef]
  49. Huang, C.-C. Gaussian-distribution-based hyetographs and their relationships with debris flow initiation. J. Hydrol. 2011, 411, 251–265. [Google Scholar] [CrossRef]
  50. Huff, F.A. Time distribution of rainfall in heavy storms. Water Resour. Res. 1967, 3, 1007–1019. [Google Scholar] [CrossRef]
  51. Hurst, H.E. Long-Term Storage Capacity of Reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–808. [Google Scholar] [CrossRef]
  52. Inguaggiato, S.; Vita, F.; Diliberto, I.S.; Mazot, A.; Calderone, L.; Mastrolia, A.; Corrao, M. The Extensive Parameters as a Tool to Monitoring the Volcanic Activity: The Case Study of Vulcano Island (Italy). Remote. Sens. 2022, 14, 1283. [Google Scholar] [CrossRef]
  53. Jahanmiri, F.; Parker, D.C. An Overview of Fractal Geometry Applied to Urban Planning. Land 2022, 11, 475. [Google Scholar] [CrossRef]
  54. Jiang, Y.; Lu, T.; Pi, J.; Anwar, W. The Retentivity of Four Kinds of Shadowing Properties in Non-Autonomous Discrete Dynamical Systems. Entropy 2022, 24, 397. [Google Scholar] [CrossRef]
  55. Kai, S.; Yamada, T.; Ikuta, S.; Müller, S.C. Fractal Geometry of Precipitation Patterns. J. Phys. Soc. Jpn. 1989, 58, 3445–3448. [Google Scholar] [CrossRef]
  56. Kalauzi, A.; Cukic, M.; Millán, H.; Bonafoni, S.; Biondi, R. Comparison of fractal dimension oscillations and trends of rainfall data from Pastaza Province, Ecuador and Veneto, Italy. Atmospheric Res. 2009, 93, 673–679. [Google Scholar] [CrossRef]
  57. Khan, M.S.; Siddiqui T.A. Estimation of fractal dimension of a noisy time series. Int. J. Computer Appl. 2012, 45, 1–6. [CrossRef]
  58. Khan, M.; Bhattarai, R.; Chen, L. Elevated Risk of Compound Extreme Precipitation Preceded by Extreme Heat Events in the Upper Midwestern United States. Atmosphere 2023, 14, 1440. [Google Scholar] [CrossRef]
  59. King, M.R. Fractal analysis of eight glacial cycles from an Antarctic ice core. Chaos, Solitons Fractals 2005, 25, 5–10. [Google Scholar] [CrossRef]
  60. Kiely, G.; Ivanova, K. Multifractal analysis of hourly precipitation. Phys. Chem. Earth, Part B: Hydrol. Oceans Atmosphere 1999, 24, 781–786. [Google Scholar] [CrossRef]
  61. Kossieris, P.; Makropoulos, C.; Onof, C.; Koutsoyiannis, D. A rainfall disaggregation scheme for sub-hourly time scales: Coupling a Bartlett-Lewis based model with adjusting procedures. J. Hydrol. 2018, 556, 980–992. [Google Scholar] [CrossRef]
  62. Kumari, M., Basistha, A., Bakimchandra, O., Singh, C.K. Comparison of Spatial Interpolation Methods for Mapping Rainfall in Indian Himalayas of Uttarakhand Region. In: Raju, N. (eds) Geostatistical and Geospatial Approaches for the Characterization of Natural Resources in the Environment. Springer, Cham. 2016. [CrossRef]
  63. Kutiel, H.; Trigo, R.M. The rainfall regime in Lisbon in the last 150 years. Theor. Appl. Clim. 2014, 118, 387–403. [Google Scholar] [CrossRef]
  64. Langousis, A.; Veneziano, D.; Furcolo, P.; Lepore, C. Multifractal rainfall extremes: Theoretical analysis and practical estimation. Chaos, Solitons Fractals 2009, 39, 1182–1194. [Google Scholar] [CrossRef]
  65. Lee, B.H. Bootstrap Prediction Intervals of Temporal Disaggregation. Stats 2022, 5, 190–202. [Google Scholar] [CrossRef]
  66. Li, X.; Meshgi, A.; Wang, X.; Zhang, J.; Tay, S.H.X.; Pijcke, G.; Manocha, N.; Ong, M.; Nguyen, M.T.; Babovic, V. Three resampling approaches based on method of fragments for daily-to-subdaily precipitation disaggregation. Int. J. Clim. 2018, 38, e1119–e1138. [Google Scholar] [CrossRef]
  67. Licznar P., Deidda R. A space-time multifractal analysis on radar rainfall sequences from central Poland, EGU General Assembly. Geophysical Research Abstracts 2014, 16, 10485.
  68. Licznar P., De Michele C., Dzugaj D., Niesobska M. Variability of multifractal parameters in an urban precipitation monitoring network, EGU General Assembly 2014. Geophysical Research Abstracts 2014, 16, 4343.
  69. Liu, L.; Sun, W.; Liu, J.; Wan, L. Centennial Variation and Mechanism of the Extreme High Temperatures in Summer over China during the Holocene Forced by Total Solar Irradiance. Atmosphere 2023, 14, 1207. [Google Scholar] [CrossRef]
  70. López Lambraño, A.A. Análisis multifractal y modelación de la precipitación, PhD Thesis, Facultad de Ingeniería, Universidad Autónoma de Querétaro 2012.
  71. Lovejoy, S.; Mandelbrot, B.B. Fractal properties of rain, and a fractal model. Tellus A: Dyn. Meteorol. Oceanogr. 1985, 37A, 209–232. [Google Scholar] [CrossRef]
  72. Lovejoy, S.; Schertzer, D.; Tsonis, A.A. Functional Box-Counting and Multiple Elliptical Dimensions in Rain. Science 1987, 235, 1036–1038. [Google Scholar] [CrossRef]
  73. Lovejoy, S.; Schertzer, D. Multifractals, cloud radiances and rain. J. Hydrol. 2006, 322, 59–88. [Google Scholar] [CrossRef]
  74. Mandelbrot, B. How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef]
  75. Mandelbrot, B.B.; Wallis, J.R. Robustness of the rescaled range R/S in the measurement of noncyclic long run statistical dependence. Water Resour. Res. 1969, 5, 967–988. [Google Scholar] [CrossRef]
  76. Mandelbrot, B. Intermittent turbulence in self-similar cascades–divergence of high moments and dimension of car-rier. J. Fluid Mech. 1974, 62, 331–358. [Google Scholar] [CrossRef]
  77. Mandelbrot, B. Les Objects Fractals: Forme, Hasard et Dimension; Flammarion: Paris, France, 1975; Volume 17. [Google Scholar]
  78. Mandelbrot B.B. Multifractal Measures, especially for the Geophysicist. Pure and Applied Geophysics 1989, 131, 5–42. [CrossRef]
  79. Mandelbrot, B. B.: A fractal set is one for which the fractal (Hausdorff–Besicovitch) dimension strictly exceeds the topological dimension, Fractals and Chaos, 2004.
  80. Martín-Vide J. Dimensión fractal de las costas gallega y catalana. Notes de Geografia Física 1992, 20-21, 131–136.
  81. Martin-Vide, J. Spatial distribution of a daily precipitation concentration index in peninsular Spain. Int. J. Clim. 2004, 24, 959–971. [Google Scholar] [CrossRef]
  82. Masugi, M.; Takuma, T. Multi-fractal analysis of IP-network traffic for assessing time variations in scaling properties. Phys. D: Nonlinear Phenom. 2007, 225, 119–126. [Google Scholar] [CrossRef]
  83. Mazzarella, A.; Rapetti, F. Scale-invariance laws in the recurrence interval of extreme floods: an application to the upper Po river valley (northern Italy). J. Hydrol. 2004, 288, 264–271. [Google Scholar] [CrossRef]
  84. Meseguer-Ruiz, O.; Cantos, J.O.; Sarricolea, P.; Martín-Vide, J. The temporal fractality of precipitation in mainland Spain and the Balearic Islands and its relation to other precipitation variability indices. Int. J. Clim. 2016, 37, 849–860. [Google Scholar] [CrossRef]
  85. Meseguer-Ruiz, O.; Osborn, T.J.; Sarricolea, P.; Jones, P.D.; Cantos, J.O.; Serrano-Notivoli, R.; Martin-Vide, J. Definition of a temporal distribution index for high temporal resolution precipitation data over Peninsular Spain and the Balearic Islands: the fractal dimension; and its synoptic implications. Clim. Dyn. 2018, 52, 439–456. [Google Scholar] [CrossRef]
  86. Mishra, S.K.; Singh, V.P.; Singh, P.K. Revisiting the soilconservation service curve number method. In: Singh, V.,Yadav, S. & Yadava, R. (Eds.)Hydrologic modeling. Water Science and Technology Library 2019, 81, Singapore, Springer. [CrossRef]
  87. Moncho, R. Climatic study of the exponent “n” in IDF curves: application for the Iberian Peninsula. Tethys, J. Weather. Clim. West. Mediterr. 2009. [CrossRef]
  88. Moncho, R.; Belda, F.; Caselles, V. Distribución probabilística de los extremos globales de precipitación. Nimbus 2011, 27-28, 119–135. [Google Scholar]
  89. Monjo, R. Measure of rainfall time structure using the dimensionless n-index. Clim. Res. 2016, 67, 71–86. [Google Scholar] [CrossRef]
  90. Monjo, R.; Gaitán, E.; Pórtoles, J.; Ribalaygua, J.; Torres, L. Changes in extreme precipitation over Spain using statistical downscaling of CMIP5 projections. Int. J. Clim. 2015, 36, 757–769. [Google Scholar] [CrossRef]
  91. Monjo, R.; Martin-Vide, J. Daily precipitation concentration around the world according to several indices. Int. J. Clim. 2016, 36, 3828–3838. [Google Scholar] [CrossRef]
  92. Monjo, R.; Roye, D.; Martin-Vide, J. Meteorological drought lacunarity around the world and its classification. Earth Syst. Sci. Data 2020, 12, 741–752. [Google Scholar] [CrossRef]
  93. Monjo, R.; Locatelli, L.; Milligan, J.; Torres, L.; Velasco, M.; Gaitán, E.; Pórtoles, J.; Redolat, D.; Russo, B.; Ribalaygua, J. Estimation of future extreme rainfall in Barcelona (Spain) under monofractal hypothesis. Int. J. Clim. 2023, 43, 4047–4068. [Google Scholar] [CrossRef]
  94. Morata, A.; Martín, M.L.; Luna, M.Y.; Valero, F. Self-similarity patterns of precipitation in the Iberian Peninsula. Theor. Appl. Clim. 2005, 85, 41–59. [Google Scholar] [CrossRef]
  95. Moutahir, H.; Bellot, P.; Monjo, R.; Bellot, J.; Garcia, M.; Touhami, I. Likely effects of climate change on groundwater availability in a Mediterranean region of Southeastern Spain. Hydrol. Process. 2016, 31, 161–176. [Google Scholar] [CrossRef]
  96. Moysis, L.; Tutueva, A.; Volos, C.; Butusov, D.; Munoz-Pacheco, J.M.; Nistazakis, H. A Two-Parameter Modified Logistic Map and Its Application to Random Bit Generation. Symmetry 2020, 12, 829. [Google Scholar] [CrossRef]
  97. Mueller-Thomy, H. Temporal rainfall disaggregation using a micro-canonical cascade model: possibilities to improve the autocorrelation. Hydrol. Earth Syst. Sci. 2020, 24, 169–188. [Google Scholar] [CrossRef]
  98. Na, W.; Yoo, C. Evaluation of Rainfall Temporal Distribution Models with Annual Maximum Rainfall Events in Seoul, Korea. Water 2018, 10, 1468. [Google Scholar] [CrossRef]
  99. Nguyen, T.-H.; Nguyen, V.-T.; Nguyen, H.-L. A Spatio-Temporal Statistical Downscaling Approach to Deriving Extreme Rainfall IDF Relations at Ungauged Sites in the Context of Climate Change. EPiC Series in Engineering 2018, 3, 1539–1546. [Google Scholar]
  100. Nunes, S.A., Romani L.A.S., Avila A.M.H., Coltri P.P., Traina C., Cordeiro R.L.F., de Sousa E.P.M., Traina A.J.M. Fractal-based Analysis to Identify Trend Changes in Multiple Climate Time Series. J. Inform. Data Manag. 2011, 2, 51–57. [CrossRef]
  101. Nunes S.A., Romani L.A.S., Avila A.M.H., Coltri P.P., Traina C., Cordeiro R.L.F., de Sousa E.P.M., Traina A.J.M. Analysis of Large Scale Climate Data: How Well Climate Change Models and Data from Real Sensor Networks Agree?, pp. 517-526; in Schwabe D., Almeida V., Glaser H., Baeza-Yates R., Moon S. (Eds): Proceedings of the IW3C2 WWW 2013 Conference, IW3C2 2013, Rio de Janeiro, 1591 pp.
  102. Olsson, J.; Niemczynowicz, J. Multifractal analysis of daily spatial rainfall distributions. J. Hydrol. 1996, 187, 29–43. [Google Scholar] [CrossRef]
  103. Omidvarnia, A.; Mesbah, M.; Pedersen, M.; Jackson, G. Range Entropy: A Bridge between Signal Complexity and Self-Similarity. Entropy 2018, 20, 962. [Google Scholar] [CrossRef]
  104. Rubalcaba, J.J.O. Fractal analysis of climatic data: Annual precipitation records in Spain. Theor. Appl. Clim. 1997, 56, 83–87. [Google Scholar] [CrossRef]
  105. Pathirana A. Fractal modelling of rainfall: downscaling in time and space for hydrological applications, PhD Thesis, Civil Engineering Department, Tokyo University 2001, 145 pp.
  106. Pathirana, A.; Herath, S.; Yamada, T. Estimating rainfall distributions at high temporal resolutions using a multifractal model. Hydrol. Earth Syst. Sci. 2003, 7, 668–679. [Google Scholar] [CrossRef]
  107. Paulson, K.S. Fractal interpolation of rain rate time series. J. Geophys. Res. Atmos. 2004, 109. [Google Scholar] [CrossRef]
  108. Peitgen HO, Saupe D (1988) The Science of Fractal Images. Springer-Verlag, New York.
  109. Peleg, N.; Fatichi, S.; Paschalis, A.; Molnar, P.; Burlando, P. An advanced stochastic weather generator for simulating 2-D high-resolution climate variables. J. Adv. Model. Earth Syst. 2017, 9, 1595–1627. [Google Scholar] [CrossRef]
  110. Pelletier, J.D. Analysis and Modeling of the Natural Variability of Climate. J. Clim. 1997, 10, 1331–1342. [Google Scholar] [CrossRef]
  111. Pérez, S.P. Pérez S.P., Sierra E.M., Massobrio M.J., Momo F.R. Análisis fractal de la precipitación anual en el este de la Provincia de la Pampa, Argentina. Revista de Climatología 2009, 9, 25–31. [Google Scholar]
  112. Pimont, F.; Dupuy, J.-L.; Linn, R.R.; Sauer, J.A.; Muñoz-Esparza, D. Pressure-Gradient Forcing Methods for Large-Eddy Simulations of Flows in the Lower Atmospheric Boundary Layer. Atmosphere 2020, 11, 1343. [Google Scholar] [CrossRef]
  113. Pizarro, R.; Valdés, R.; Abarza, A.; Garcia-Chevesich, P. A simplified storm index method to extrapolate intensity-duration-frequency (IDF) curves for ungauged stations in central Chile. Hydrol. Process. 2014, 29, 641–652. [Google Scholar] [CrossRef]
  114. Prykarpatski, A.K.; Pukach, P.Y.; Vovk, M.I. Symplectic Geometry Aspects of the Parametrically-Dependent Kardar–Parisi–Zhang Equation of Spin Glasses Theory, Its Integrability and Related Thermodynamic Stability. Entropy 2023, 25, 308. [Google Scholar] [CrossRef]
  115. Rafatnejad, A.; Tavakolifar, H.; Nazif, S. Evaluation of the climate change impact on the extreme rainfall amounts using modified method of fragments for sub-daily rainfall disaggregation. Int. J. Clim. 2021, 42, 908–927. [Google Scholar] [CrossRef]
  116. Raidl, A. Estimating the fractal dimension,K 2 -entropy, and the predictability of the atmosphere. Czechoslov. J. Phys. 1996, 46, 293–328. [Google Scholar] [CrossRef]
  117. Rayner, D.; Achberger, C.; Chen, D. A multi-state weather generator for daily precipitation for the Torne River basin, northern Sweden/western Finland. Adv. Clim. Chang. Res. 2016, 7, 70–81. [Google Scholar] [CrossRef]
  118. Rangarajan, G.; Sant, D.A. A climate predictability index and its applications. Geophys. Res. Lett. 1997, 24, 1239–1242. [Google Scholar] [CrossRef]
  119. Rangarajan, G.; Sant, D.A. Fractal dimensional analysis of Indian climatic dynamics. Chaos, Solitons Fractals 2004, 19, 285–291. [Google Scholar] [CrossRef]
  120. Redolat, D.; Monjo, R.; Paradinas, C.; Pórtoles, J.; Gaitán, E.; Prado-Lopez, C.; Ribalaygua, J. Local decadal prediction according to statistical/dynamical approaches. Int. J. Clim. 2020, 40, 5671–5687. [Google Scholar] [CrossRef]
  121. Redolat, D.; Monjo, R. Statistical predictability of Euro-Mediterranean subseasonal anomalies: The TeWA approach. Weather. Forecast. 2024, -1. [Google Scholar] [CrossRef]
  122. Rehman, S. Study of Saudi Arabian climatic conditions using Hurst exponent and climatic predictability index. Chaos, Solitons Fractals 2009, 39, 499–509. [Google Scholar] [CrossRef]
  123. Rehman, S.; Siddiqi, A. Wavelet based hurst exponent and fractal dimensional analysis of Saudi climatic dynamics. Chaos, Solitons Fractals 2009, 40, 1081–1090. [Google Scholar] [CrossRef]
  124. Reiser, H.; Kutiel, H. Rainfall uncertainty in the Mediterranean: Intraseasonal rainfall distribution. Theor. Appl. Clim. 2009, 100, 105–121. [Google Scholar] [CrossRef]
  125. Rodríguez, R.; Casas, M.C.; Redaño, A. Multifractal analysis of the rainfall time distribution on the metropolitan area of Barcelona (Spain). Meteorol. Atmospheric Phys. 2013, 121, 181–187. [Google Scholar] [CrossRef]
  126. Rull, V.; Blasco, A.; Calero, M. .; Blaauw, M.; Vegas-Vilarrúbia, T. A Continuous Centennial Late Glacial-Early Holocene (15–10 cal kyr BP) Palynological Record from the Iberian Pyrenees and Regional Comparisons. Plants 2023, 12, 3644. [Google Scholar] [CrossRef]
  127. Al-Wagdany, A.S. Intensity-duration-frequency curve derivation from different rain gauge records. J. King Saud Univ. - Sci. 2020, 32, 3421–3431. [Google Scholar] [CrossRef]
  128. Sahay, J.D., Sreenivasan K.R. The search for a low-dimensional characterization of a local climate system. Philosophical Transactions of the Royal Society 1996, 354, 1715–1750. [CrossRef]
  129. Sangüesa, C.; Pizarro, R.; Ingram, B.; Ibáñez, A.; Rivera, D.; García-Chevesich, P.; Pino, J.; Pérez, F.; Balocchi, F.; Peña, F. Comparing Methods for the Regionalization of Intensity−Duration−Frequency (IDF) Curve Parameters in Sparsely-Gauged and Ungauged Areas of Central Chile. Hydrology 2023, 10, 179. [Google Scholar] [CrossRef]
  130. Sangüesa, C.; Rivera, D.; Pizarro, R.; García-Chevesich, P.; Ibáñez, A.; Pino, J. Spatial and temporal behavior of annual maximum sub-hourly rainfall intensities from 15-minute to 24-hour durations in central Chile. Aqua-LAC 2021, 13, 143–156. [Google Scholar] [CrossRef]
  131. Shen, B.-W.; Pielke, R.A.; Zeng, X. One Saddle Point and Two Types of Sensitivities within the Lorenz 1963 and 1969 Models. Atmosphere 2022, 13, 753. [Google Scholar] [CrossRef]
  132. Schmitt, F.G.; Huang, Y. Stochastic Analysis of Scaling Time Series: from Turbulence Theory to Applications; Cambridge University Press (CUP): Cambridge, United Kingdom, 2015. [Google Scholar]
  133. Selvi T., Selvaraj S. Fractal dimension analysis of Northeast monsoon of Tamil Nadu. Universal Journal of Environmental Research and Technology 2011, 1, 219–221.
  134. Muraja, D.O.S.; Klausner, V.; Prestes, A.; Aakala, T.; Macedo, H.G.; da Silva, I.R. Exploring the Centennial-Scale Climate History of Southern Brazil with Ocotea porosa (Nees & Mart.) Barroso Tree-Rings. Atmosphere 2023, 14, 1463. [Google Scholar] [CrossRef]
  135. Sivakumar, B. A preliminary investigation on the scaling behaviour of rainfall observed in two different climates. Hydrol. Sci. J. 2000, 45, 203–219. [Google Scholar] [CrossRef]
  136. Sivakumar, B. Fractal analysis of rainfall observed in two different climatic regions. Hydrol. Sci. J. 2000, 45, 727–738. [Google Scholar] [CrossRef]
  137. Sivakumar, B. Is a chaotic multi-fractal approach for rainfall possible? Hydrol. Process. 2001, 15, 943–955. [Google Scholar] [CrossRef]
  138. Suárez-Carreño, F.; Rosales-Romero, L.; Salazar, J.; Acosta-Vargas, P.; Mendoza-Cedeño, H.-F.; Verde-Luján, H.E.; Flor-Unda, O. Simulation of Wave Propagation Using Finite Differences in Oil Exploration. Appl. Sci. 2023, 13, 8852. [Google Scholar] [CrossRef]
  139. Sun, X.; Barros, A.P. An Evaluation of the Statistics of Rainfall Extremes in Rain Gauge Observations, and Satellite-Based and Reanalysis Products Using Universal Multifractals. J. Hydrometeorol. 2010, 11, 388–404. [Google Scholar] [CrossRef]
  140. Takens, F. Detecting Strange Attractors in Turbulence. In Dynamical Systems and Turbulence, Warwick 1980; Rand, D., Young, L.-S., Eds.; Springer: Berlin/Heidelberg, Germany, 1981; pp. 366–381. [Google Scholar]
  141. Tchiguirinskaia I., Schertzer D., Hoang, C.T., Lovejoy S. (2012): Multifractal study of three storms with different dynamics over the Paris region, Weather Radar and Hydrology Symp., Exeter, United Kingdom, IAHS, 421–426.
  142. Telesca, L.; Lapenna, V.; Scalcione, E.; Summa, D. Searching for time-scaling features in rainfall sequences. Chaos, Solitons Fractals 2007, 32, 35–41. [Google Scholar] [CrossRef]
  143. Teixeira-Gandra, C.F.A.; Damé, R.d.C.F. Bartlett-Lewis of rectangular pulse modified model: estimate of parameters for simulation of precipitation in sub-hourly duration. 2014, 34, 925–934. [CrossRef]
  144. Tuček P., Marek L. Paszto V., Janoška Z., Dančák M. (2011): Fractal perspectives of GIScience based on the leaf shape analysis, GeoComputation Conference Proceedings, University College London, pp. 169-176.
  145. Tusset, A.M.; Fuziki, M.E.K.; Balthazar, J.M.; Andrade, D.I.; Lenzi, G.G. Dynamic Analysis and Control of a Financial System with Chaotic Behavior Including Fractional Order. Fractal Fract. 2023, 7, 535. [Google Scholar] [CrossRef]
  146. Valdez-Cepeda, R.D.; Hernández-Ramírez, D.; Mendoza, B.; Valdés-Galicia, J.; Maravilla, D. Fractality of monthly extreme minimum temperature. Fractals 2003, 11, 137–144. [Google Scholar] [CrossRef]
  147. van Hateren, J.H. A fractal climate response function can simulate global average temperature trends of the modern era and the past millennium. Clim. Dyn. 2012, 40, 2651–2670. [Google Scholar] [CrossRef]
  148. Velhinho, J. Topics of Measure Theory on Infinite Dimensional Spaces. Mathematics 2017, 5, 44. [Google Scholar] [CrossRef]
  149. Veneziano, D.; Furcolo, P. Multifractality of rainfall and scaling of intensity-duration-frequency curves. Water Resour. Res. 2002, 38, 42–1. [Google Scholar] [CrossRef]
  150. Veneziano, D.; Langousis, A.; Furcolo, P. Multifractality and rainfall extremes: A review. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
  151. Wilcox, C.; Aly, C.; Vischel, T.; Panthou, G.; Blanchet, J.; Quantin, G.; Lebel, T. Stochastorm: A Stochastic Rainfall Simulator for Convective Storms. J. Hydrometeorol. 2021, 22, 387–404. [Google Scholar] [CrossRef]
  152. Zhang, L.; Li, H.; Liu, D.; Fu, Q.; Li, M.; Faiz, M.A.; Ali, S.; Khan, M.I.; Li, T. Application of an improved multifractal detrended fluctuation analysis approach for estimation of the complexity of daily precipitation. Int. J. Clim. 2021, 41, 4653–4671. [Google Scholar] [CrossRef]
  153. Zhao, Y.; Anwar, W.; Li, R.; Lu, T.; Mo, Z. Distributional Chaos and Sensitivity for a Class of Cyclic Permutation Maps. Mathematics 2023, 11, 3310. [Google Scholar] [CrossRef]
  154. Zakinyan, R.; Zakinyan, A.; Ryzhkov, R. Phases of the Isobaric Surface Shapes in the Geostrophic State of the Atmosphere and Connection to the Polar Vortices. Atmosphere 2016, 7, 126. [Google Scholar] [CrossRef]
  155. Zhou, X. (2004): Fractal and Multifractal Analysis of Runoff Time Series and Stream Networks in Agricultural Watersheds, PhD Thesis, Virginia Polytechnic Institute and State University, 135 pp.
  156. Zhu, X.-H.; Wang, J. On fractal mechanism of coastline. Chin. Geogr. Sci. 2002, 12, 142–145. [Google Scholar] [CrossRef]
Preprints 95545 g001
Figure 1. Flow chart for the use of the box-counting method to estimate the Hausdorff dimension of a time series: a) The number N of boxes occupied by the curve (blue line) depends on the box size δ; b) the relationship is an exponential law that decays.
Figure 1. Flow chart for the use of the box-counting method to estimate the Hausdorff dimension of a time series: a) The number N of boxes occupied by the curve (blue line) depends on the box size δ; b) the relationship is an exponential law that decays.
Preprints 95545 g001
Preprints 95545 g002
Figure 2. Monthly averages of sub-daily n-index (red lines) and rainfall normalised using the wettest month (bars) for 18 obser-vatories: (a) Hihifo (Wallis Island), (b) Princeton Aerodrome (Canada), (c) Colonia Juan Carras (Mexico), (d) Columbus Metro-politan Airport (Georgia, USA), (e) Salta airport (Argentina), (f) Belem airport (Brazil), (g) London/Heathrow airport (UK), (h) Ústí nad Orlicí (Czech Republic), (i) Milos (Greece), (j) Tamanrasset (Algeria), (k) Cape Columbine (South Africa), (l) Saint-Denis/Gillot (La Reunion), (m) Malye Karmakuly (Russia), (n) Vavuniya (Sri Lanka), (o) Chara Airport (Russia), (p) Toyooka(Japan), (q) Territory Grape Farm (Australia), (r) Auckland Aero Aws (New Zealand) (6) (PDF) Measure of rainfall time structure using the dimensionless n-index. Source: Monjo (2016).
Figure 2. Monthly averages of sub-daily n-index (red lines) and rainfall normalised using the wettest month (bars) for 18 obser-vatories: (a) Hihifo (Wallis Island), (b) Princeton Aerodrome (Canada), (c) Colonia Juan Carras (Mexico), (d) Columbus Metro-politan Airport (Georgia, USA), (e) Salta airport (Argentina), (f) Belem airport (Brazil), (g) London/Heathrow airport (UK), (h) Ústí nad Orlicí (Czech Republic), (i) Milos (Greece), (j) Tamanrasset (Algeria), (k) Cape Columbine (South Africa), (l) Saint-Denis/Gillot (La Reunion), (m) Malye Karmakuly (Russia), (n) Vavuniya (Sri Lanka), (o) Chara Airport (Russia), (p) Toyooka(Japan), (q) Territory Grape Farm (Australia), (r) Auckland Aero Aws (New Zealand) (6) (PDF) Measure of rainfall time structure using the dimensionless n-index. Source: Monjo (2016).
Preprints 95545 g002
Preprints 95545 g003
Figure 3. Scheme of fractal-related concepts applied to precipitation. Relationship between non-linearity, chaos and fractal measures. The most general approach is the multifractal analysis, which sometimes can be simplified with a monofractal dimension like the Hausdorff dimension, or its upper bound represented by the box-counting dimension. Ramifications to the n-index, Shannon entropy and Hurst exponent are also showed.
Figure 3. Scheme of fractal-related concepts applied to precipitation. Relationship between non-linearity, chaos and fractal measures. The most general approach is the multifractal analysis, which sometimes can be simplified with a monofractal dimension like the Hausdorff dimension, or its upper bound represented by the box-counting dimension. Ramifications to the n-index, Shannon entropy and Hurst exponent are also showed.
Preprints 95545 g003
Table 1. Climatic classification of meteorological droughts around the world according to the the dry-spell-spell (DSS) n-index and the averaged wet-spell length (WSL).
Table 1. Climatic classification of meteorological droughts around the world according to the the dry-spell-spell (DSS) n-index and the averaged wet-spell length (WSL).
Name Description DSS
n-index		 WSL (days) Examples of areas that experience this climate
Hs Long droughts with short wet spells​ > 0.4 < 3 Arid and semi-arid regions
Hl Long droughts with long wet spells ≥ 3 Tropical and monsoon regions
Ms Medium droughts with short wet spells [0.3, 0.4] < 3 Transition areas
Ml Medium droughts with long wet spells​ ≥ 3 Oceanic areas
Ls Short droughts with short wet spells​ < 0.3 < 3 Frequent extratropical-cyclonic areas
Ll Short droughts with long wet spells​ ≥ 3 Equatorial climate and regular polar jet streams (e.g. southern annular mode)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated