Lateral Convergence Deformation Prediction of Subway Shield Tunnel Based on Kalman Model

1. Introduction

In recent years, with the China's strong support for the development and utilization of underground space, more and more subway lines have been put into operation, and the safety and health problems of subway tunnels have gradually come to the fore. Shield tunneling is the most commonly used construction method of subway tunnels. The structural safety of subway tunnels using this method, which have a long life cycle, complex project, large investment and high risk, should be given great attention. The lateral convergence deformation of tunnel is a key index of the current status of tunnel structure, and also an important part in tunnel monitoring. On the one hand, the lateral convergence deformation of subway shield tunnel will gradually increase with the increase of service life. Excessive lateral deformation will cause concrete crushing, joint leakage, bolt yielding, insufficient limits, which can damage the structure of the tunnel and affect the operation safety of the tunnel [1]. On the other hand, with the increase of subway lines, it is inevitable to carry out loading and unloading construction activities around the built interval tunnels, such as the construction of high-rise buildings or excavation of adjacent tunnels. These behaviors may cause large lateral deformation of the tunnel, posing a threat to the safety of the tunnel structure. It is crucial to understand the lateral convergence deformation of the tunnel, but the window time of the subway shield tunnel is short during operation period, the detection work is restricted by various conditions, and consumes a lot of time and cost. Traditional detection methods can only achieve sampling detection. 3D laser scanning technology is a new technology that can quickly scan and accurately collect 3D coordinate information. The point cloud data obtained through this technology includes the horizontal diameter information of each segment of the shield tunnel, which helps to comprehensively grasp the lateral convergence deformation of the shield tunnel ring by ring and avoid the risk of false detection and missed detection. The accuracy of point cloud data can be precise to the millimeter level, with small point positioning errors. Multi period point cloud data is particularly suitable for prediction work in the time dimension. Using point cloud data to extract the horizontal diameter values of subway shield tunnel in multiple periods, predict the lateral convergence deformation of subway shield tunnels, judge the state of tunnel structures in advance, and avoid the occurrence of tunnel safety accidents. At present, the main methods for convergence prediction are numerical methods [2,3], empirical methods [4,5] and time series modeling. The prediction of numerical methods is achieved by simulating the actual tunnel construction and solving the mechanical equations, which has many problems such as large calculation, long time and the difficulty of determining the accurate finite element model parameters. The empirical method does not rely on the finite element model, but the empirical formula summarized by the empirical data has a smaller scope of application and lower prediction accuracy. The prediction of time series model includes ARIMA model [6,7,8], artificial neural network [9,10,11,12], grey prediction model [13,14,15,16,17], etc. It only needs to input the measured data of convergence deformation, and it has simple calculation and high efficiency. For example, Yi Ziwei [8] used ARIMA model to predict the convergent deformation value of subway tunnel during the operation period, and then judged the performance of subway tunnel structure; Jianbo Fei et al. [9] realized the prediction of tunnel arch settlement deformation value based on BPNN neural network and MARS machine learning regression algorithm; Xia Caichu et al. [17] studied the two grey models in detail and conducted a comparative analysis, and found that the GM(1,1) grey model has a better prediction effect on the tunnel horizontal diameter value. However, the existing time series prediction models have their own advantages and disadvantages: the ARIMA model has stable performance and wide applicability, but it requires no missing sequence and stationary data; the artificial neural network model has high prediction accuracy, but it is complicated and requires a large amount of training data; the grey prediction model can predict the data with small sample sizes, but the stability of the model is poor and the prediction accuracy is limited.

The lateral convergence deformation data of subway shield tunnel presents the characteristics of non-stationary, time-varying and random, and it is difficult to obtain a large amount of sample data. For the prediction of non-stationary small sample size data, the existing prediction models perform poorly. Kalman filtering is a prediction algorithm originally proposed by Kalman, an American engineer and mathematician, in the 1960s [18]. It is widely used in aerospace [19], military [20], communication and signal processing [21], finance [22], etc. Its principle is to weighted average the observed values of the system and the predicted values of the model, and finally get the optimal estimation of system state through continuous parameter iteration and updating. In this paper, a Kalman prediction model is constructed based on the Kalman filtering theory, which can predict the non-stationary data with small sample size under the condition of noise and interference in the system, and the model has small computation and high robustness, realizing the accurate prediction of the lateral convergence deformation of subway shield tunnels. In the first part of this paper, the principle of Kalman filtering, the parameter setting of the model and the evaluation criteria are introduced. The second part introduces the lateral convergence deformation prediction results of subway shield tunnel based on Kalman model combined with engineering examples. In the third part, we compare the Kalman model with GM(1,1) model and GM-Markov model, verify the accuracy of Kalman model, and discuss the lateral convergence deformation prediction performance of subway shield tunnel based on Kalman model on different scale data sets. Finally, the concluding remarks of this study are presented in the fourth part.

2. Lateral convergence deformation prediction of subway shield tunnel

2.1. Prediction model based on Kalman filtering theory

Kalman filtering is an algorithm that utilizes the state equation of a linear system to optimally estimate the system state, through the input and output observations of the system. The Kalman filtering model for discrete linear systems can be expressed by the following equation:

$$\begin{array}{c}{\mathrm{X}}_{\mathrm{K}+1}=\mathrm{A}\ast {\mathrm{X}}_{\mathrm{K}}+\mathrm{B}\ast {\mathrm{U}}_{\mathrm{K}}+{\mathrm{W}}_{\mathrm{K}}\end{array}$$

(1)

$$\begin{array}{c}{\mathrm{Z}}_{\mathrm{K}}=\mathrm{H}\ast {\mathrm{X}}_{\mathrm{K}}+{\mathrm{V}}_{\mathrm{K}}\end{array}$$

(2)

where ${\mathrm{X}}_{\mathrm{K}}$ is the state matrix of the system at moment K, A is the state transition matrix of the system, B is the control input matrix, ${\mathrm{U}}_{\mathrm{K}}$ is the control vector matrix at moment K, ${\mathrm{W}}_{\mathrm{K}}$ is the process noise matrix of the system at moment K, ${\mathrm{Z}}_{\mathrm{K}}$ is the measurement value of the system at moment K, H is the state observation matrix, and ${\mathrm{V}}_{\mathrm{K}}$ is the measurement noise matrix of the system at moment K. The noise ${\mathrm{W}}_{\mathrm{K}}$ and ${\mathrm{V}}_{\mathrm{K}}$ conforms to Gaussian distribution with covariances of Q and R, respectively. For a system without external forces, the $B{\ast \mathrm{U}}_{\mathrm{K}}$ term in equation (1) does not exist.

The advantage of Kalman filtering is to eliminate the influence of random disturbance error and obtain the data closest to the real situation [23]. It constantly adjusts the state according to the measured data during the operation process to improve the accuracy. The horizontal diameter data of subway shield tunnel has non-stationary, time-varying, and random characteristics. Iterating and adjusting the prediction model based on the horizontal diameter measured values can make the horizontal diameter predicted values more accurate. Therefore, the prediction model based on the Kalman filtering principle has outstanding performance in predicting the lateral convergence deformation of subway shield tunnel. The lateral convergence model of subway shield tunnel based on Kalman algorithm combines Bayes theorem and least squares estimation to estimate the system state in a recursive way. Bayes' theorem states that the posterior probability is calculated by observed data under the condition of known prior probability. In the model, the prior probability is the initial estimate of the system state, and the posterior probability is the optimal estimate of the system state. The least squares estimation determines the parameters by minimizing the square error between the observed values and the estimated values. The least squares estimation is applied in the model to determine the relationship between the estimated value and the measured value of the system state and to update the estimated values of the system state. The prediction model based on the Kalman filtering theory first predicts the state of the present moment according to the predicted value of the previous moment, that is, the prior state estimation, and then revises the prior state estimation by using the measured value of the present moment to obtain the optimal state estimation (posterior state estimation). The Kalman model is divided into two parts: prediction and update. In the prediction step, the prior state predicted value is passed to the next moment through the state transition matrix and the system covariance matrix is updated. In the update step, the optimal estimation is obtained through weighted prior state estimation and measurements. The specific steps are as follows:

Predicting the state of the system at moment K

$$\begin{array}{c}{\hat{\mathrm{x}}}_{\mathrm{K}}^{-}=\mathrm{A}{\hat{\mathrm{x}}}_{\mathrm{K}-1}\end{array}$$

(3)

Predicting the covariance matrix of the system at moment K

$$\begin{array}{c}{\mathrm{P}}_{\mathrm{K}}^{-}=\mathrm{A}{\mathrm{P}}_{\mathrm{K}-1}{\mathrm{A}}^{\mathrm{T}}+Q\end{array}$$

(4)

Equations (3) and (4) are the prediction part of the model, whose input values are the optimal estimation at moment K-1, the optimal covariance matrix of the system and the process noise covariance matrix, and the output values are the predicted value of the system at moment K and the predicted value of the system covariance matrix at moment K.

Calculating the Kalman gain

$$\begin{array}{c}{\mathrm{K}}_{\mathrm{K}}=\frac{{\mathrm{P}}_{\mathrm{K}}^{-}{\mathrm{H}}_{\mathrm{K}}^{\mathrm{T}}}{{\mathrm{H}}_{\mathrm{K}}{\mathrm{P}}_{\mathrm{K}}^{-}{\mathrm{H}}_{\mathrm{K}}^{\mathrm{T}}+\mathrm{R}}\end{array}$$

(5)

Updating the system state at moment K

$$\begin{array}{c}{\hat{\mathrm{x}}}_{\mathrm{K}}={\hat{\mathrm{x}}}_{\mathrm{K}}^{-}+{\mathrm{K}}_{\mathrm{K}}\left({\mathrm{Z}}_{\mathrm{K}}-{\mathrm{H}}_{\mathrm{K}}{\hat{\mathrm{x}}}_{\mathrm{K}}^{-}\right)\end{array}$$

(6)

Updating the covariance matrix of the system

$$\begin{array}{c}{\mathrm{P}}_{\mathrm{K}}=\left(1-{\mathrm{K}}_{\mathrm{K}}{\mathrm{H}}_{\mathrm{K}}\right){\mathrm{P}}_{\mathrm{K}}^{-}\end{array}$$

(7)

Equations (5-7) are the update part of the model, whose input values are the output values of the prediction part, the measurement value of the system, the measurement noise covariance and the state observation matrix, and the output values are the optimal estimation and the covariance matrix modified by the measurement value.

In the above Equations, ${\hat{\mathrm{x}}}_{\mathrm{K}}^{-}$ represents the predicted value of the prior state, ${\hat{\mathrm{x}}}_{\mathrm{K}}$ represents the optimal estimation of the state, ${\mathrm{K}}_{\mathrm{K}}$ represents the Kalman gain, ${\mathrm{P}}_{\mathrm{K}}$ represents the optimal covariance matrix of the system at moment K, and ${\mathrm{P}}_{\mathrm{k}}^{-}$ represents the predicted value of the covariance matrix of the system at moment K.

The Kalman prediction model not only has a small amount of computation and a fast running speed, but also can adjust the predicted value constantly according to the measured data, and can adapt well to different environment and noise conditions. In addition, the model estimates the system state by recursive way, which can reduce the impact of system noise and interference, ensuring the accuracy and robustness of the model. All in all, the Kalman prediction model has the advantages of high efficiency, self-adaptability and high robustness, which is suitable for the lateral convergence deformation prediction of subway shield tunnels.

There are also some variables in lateral convergence model of subway shield tunnel based on Kalman algorithm, which play an important role in the effectiveness of the model.

R is the covariance of the measurement noise with zero mean of the normal distribution, which represents the degree of trust in the measured value. The smaller the value of R, the higher the degree of trust in the measured value, and the faster the model convergence rate; the larger the value of R, the lower the trust in the measured value, and the slower the model convergence rate. It is inappropriate for R to be too large or too small. If the R value is too small, there will be oscillatory, and if it is too large, the model convergence speed will be slow.

Q is the covariance of the process noise with zero mean of the normal distribution, which represents the degree of trust in the model predicted value. The smaller the value of Q, the higher the degree of trust in the model predicted value; the larger the value of Q, the lower the degree of trust in the model predicted value, and the higher the degree of trust in the measured value. Too small a value of Q leads to system divergence.

The Kalman gain K refers to the degree of uncertainty changes after each update of the model, quantified by the covariance of the variables. With the iteration of the model, if the uncertainty decreases, the prediction results are more accurate and K plays a positive gain role, so Kalman gain is the core of the whole calculation process. In the process of model iteration, the prior estimation is modified by weighting the difference between the actual measured value and the prior estimation, and this weighting ratio is the Kalman gain. The convergence value of Kalman gain is Q/(Q+R), and the larger the value of K, the more reliable the measured value; the smaller the K value, the more reliable the prediction.

2.2. Parameter setting

For the one-dimensional lateral convergence model of subway shield tunnel based on Kalman algorithm, the process of setting initial parameters is as follows:

H=[1], H represents the state transition relationship between X and Z values. Since X and Z represent the horizontal diameter of the subway shield tunnel, which is a metric value of the same scale, the state observation matrix is set to [1].

A=[1], A represents the state transition relationship between multiple X values. The horizontal diameter of the subway shield tunnel does not show a unidirectional decline trend. The artificial adjustment of A value will cause the model deviation to become larger and larger over time, so A is set as a first-order unit matrix.

R=0.01, the instrument used for data collection is German Z+F 6012 series scanner, and the measurement accuracy of its section point is 10mm, and it needs to be consistent with the unit of the horizontal diameter measurement value of subway shield tunnel m, so the measurement noise is set to 0.01.

Q=$\frac{\sum （\mathrm{Z}-\overline{\mathrm{Z}}{）}^2}{n-1}$, Q takes the variance of the horizontal diameter measured value of subway shield tunnel and the variance is given by ${\sigma }^2=\frac{\sum （\mathrm{X}-\mathsf{\mu }{）}^2}{N}$, where ${\sigma }^2$ is the population variance, X is the variable, μ is the population mean and N is the number of population cases. In the actual calculation, the sample statistics are used to replace the population parameter. Sample variance is given by $S^2=\frac{\sum （\mathrm{X}-\overline{\mathrm{X}}{）}^2}{n-1}$, $S^2$ is the sample variance, X is the variable, $\overline{\mathrm{X}}$ is the sample mean, and n is the number of sample cases. The process noise Q of this lateral convergence model of subway shield tunnel based on Kalman algorithm is obtained by taking the variance of the subway shield tunnel horizontal diameter measurement Z.

P=[1], the initial value of P is the covariance of the system at the initial moment, which affects the convergence speed at the initial moment and has little impact on the overall convergence effect on the horizontal diameter of subway shield tunnel. It can be set to 1, and then P will be iterated continuously according to the change of Kalman gain and converge into the optimal estimated covariance matrix.

2.3. Evaluation criteria

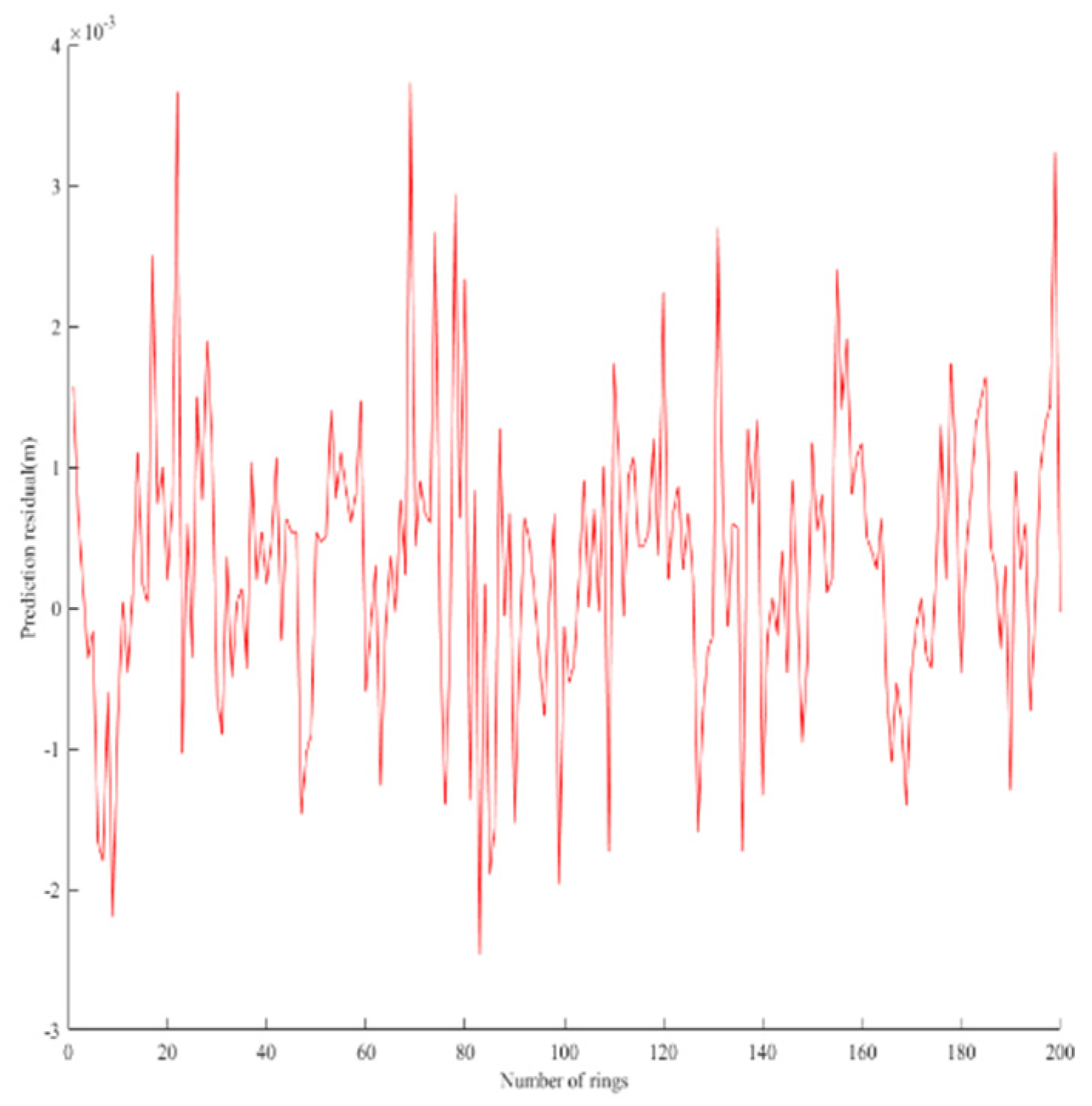
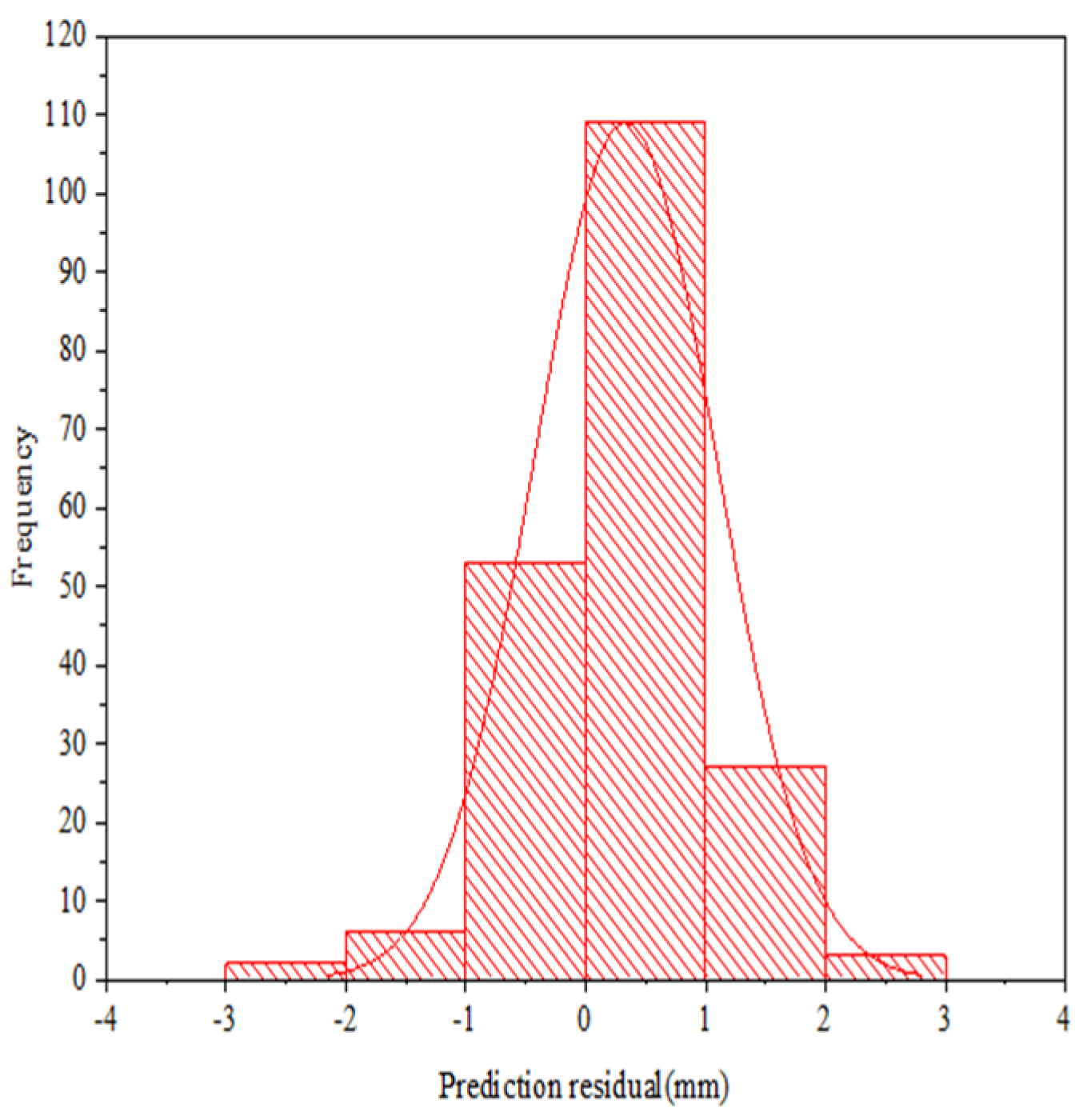
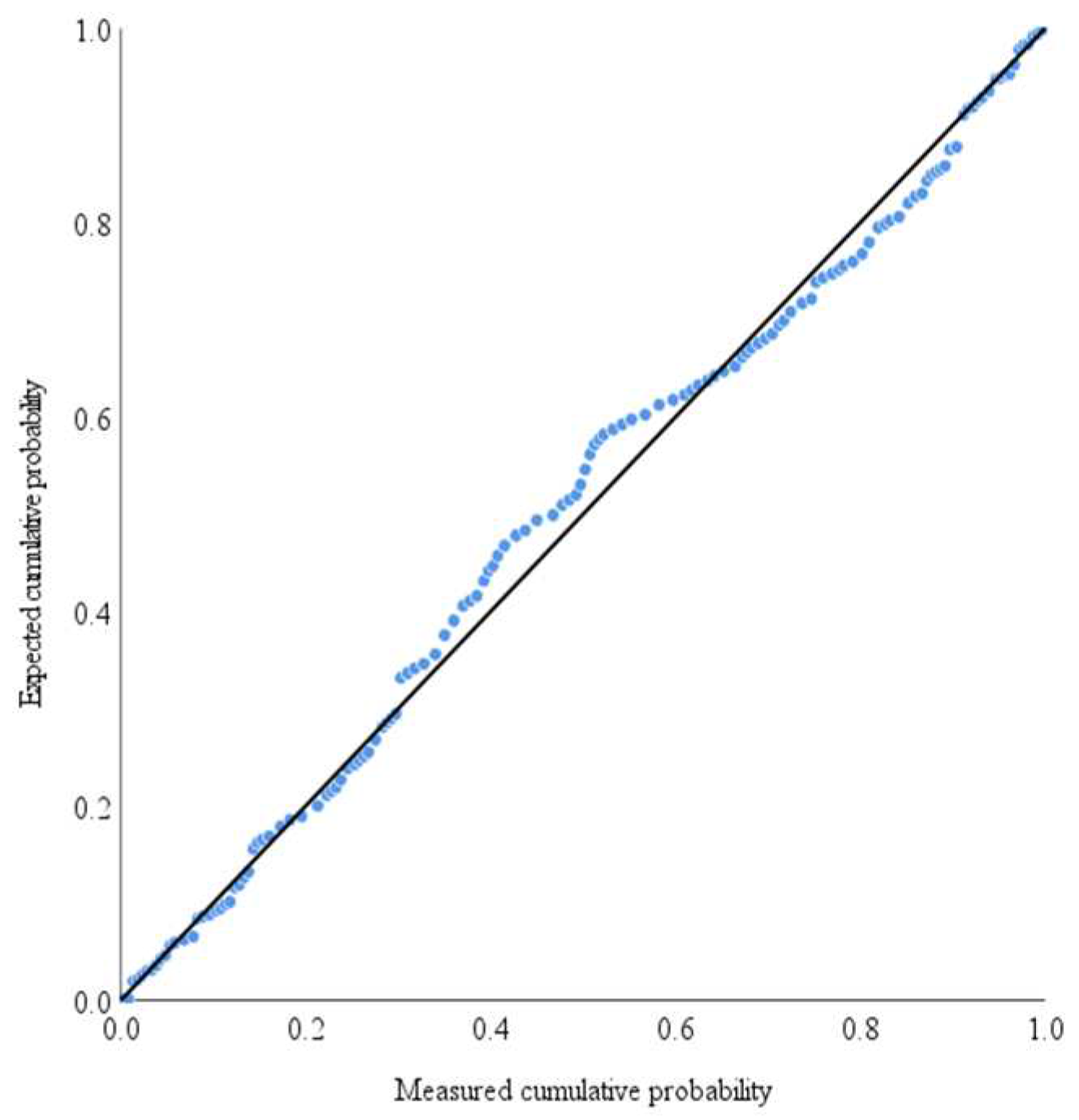
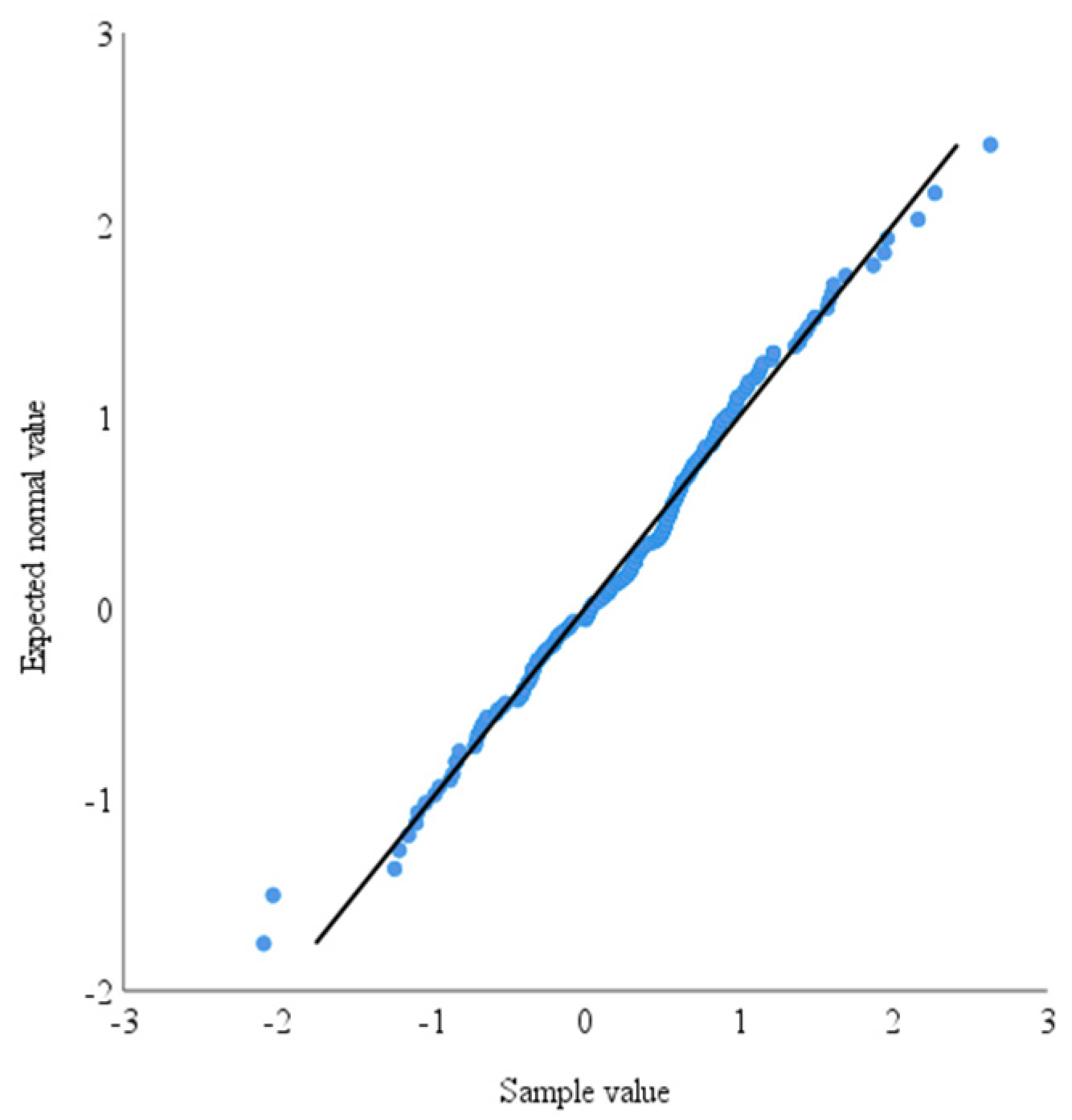
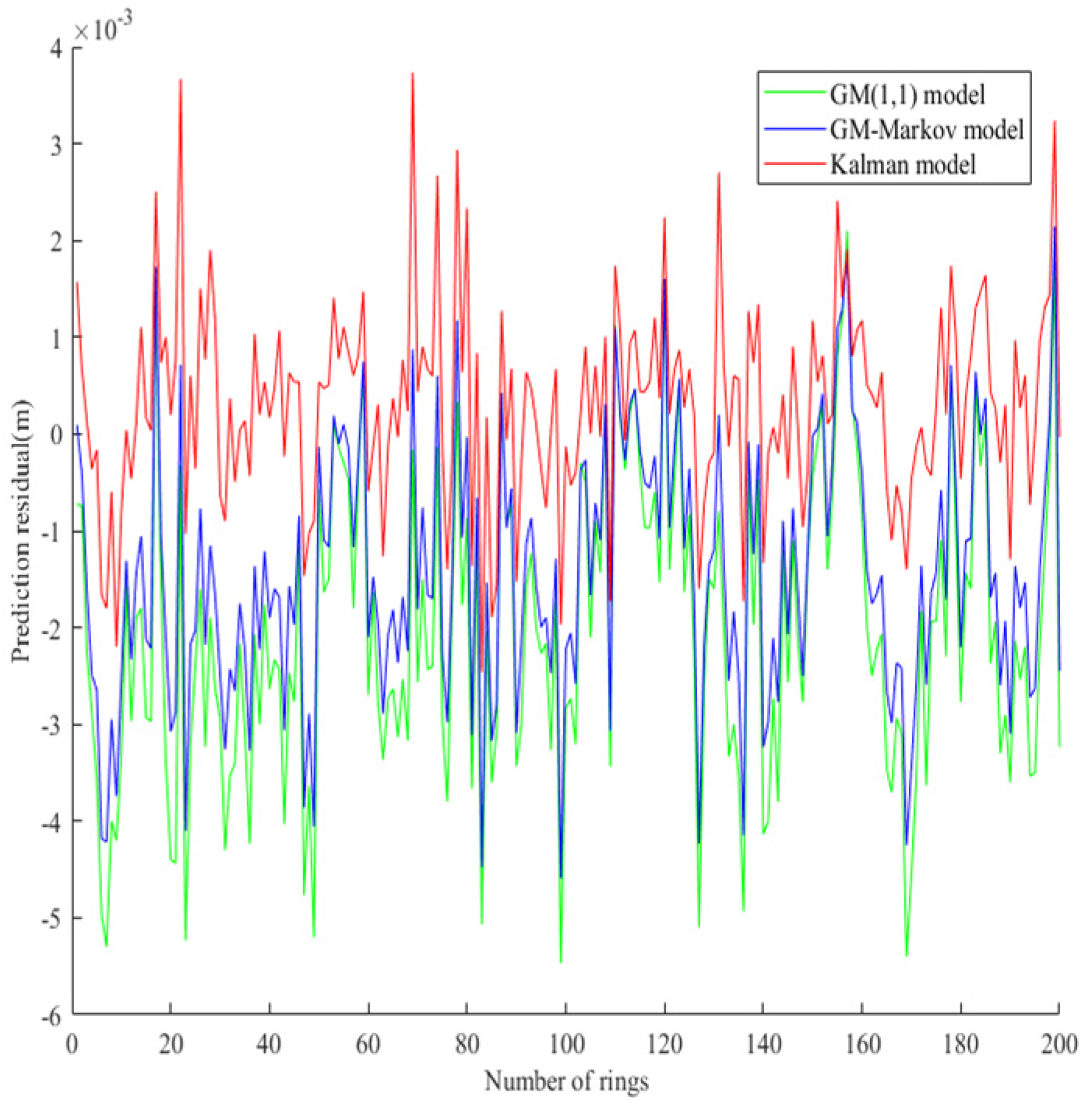
2.3.1. Prediction residual tests

The residual is the difference between the actual observed value and the fitted value, reflecting the portion of the dependent variable that is not explained by the independent variable. According to the central limit theorem, the mean values of a large number of mutually independent random variables tend to be normally distributed under certain conditions. The fact that the residuals conform to the normal distribution indicates that the residuals are random variables, and the model has a good fit to the random errors, which proves that the model has a high degree of fit and a strong prediction ability. Normality tests, skewness-kurtosis tests and graphical tests are commonly used to test whether the residual obeys a normal distribution.

The normality test methods are Shapiro-Wilk test and Kolmogorov-Smirnov test. The S-W test is suitable for sample size of less than 50 small sample test, and the K-S test is suitable for sample size of more than 50 large sample test. The original hypothesis of normality test is "If the population from which the sample comes has no significant difference from the normal distribution, it conforms to the normal distribution". If the significance of the P-value is less than 0.05, the original hypothesis is rejected, indicating that the data does not conform to the normal distribution; on the contrary, if the level is not significant, the original hypothesis is accepted and the data conforms to the normal distribution.

Skewness describes the skewness degree and direction of the data distribution. Skewness is greater than 0, the tail on the right side of the curve is longer, the data on the left side is denser, and the distribution is skewed to the right, when the mean > median > mode; skewness is less than 0, the tail on the left side of the curve is longer, the data on the right side is denser, and the distribution is skewed to the left, when the mode > median > mean. The larger the absolute value of skewness, the more skewed the data distribution. Kurtosis is a statistic that studies the degree of steepness and flatness of the data distribution curve. If the kurtosis is greater than 0, the data distribution is steeper than the peak state of the standard normal distribution; if the kurtosis is less than 0, the data distribution is flatter than the peak state of the standard normal distribution. The skewness and kurtosis of the standard normal distribution are both 0. For the actual sample data, we generally believe that if the absolute value of the kurtosis is less than 10 and the absolute value of the skewness is less than 3, then it can be basically accepted as a normal distribution [24].

The graphical tests includes histogram, P-P plot and Q-Q plot. If the histogram presents a "bell-shaped plot with a high center and low sides, and basic symmetry between the left and the right", the data follow a normal distribution. Probability-probability plot is a graph based on the relationship between the cumulative proportion of variables and the cumulative proportion of the specified distribution, which tests whether the data conforms to the specified distribution. When the data conform to the normal distribution, the points in the plot are approximately a straight line. Quantile-Quantile plot is a graphical comparison of the probability distribution of two probability distributions in different quantiles. When it is used to test whether the data conforms to the normal distribution law, the sample data is taken as the X-axis and the expected quantile of the normal value data is taken as the Y-axis to make the scatter plot. The higher the coincidence degree between the scatter point and the straight line, the more the sample data follows the normal distribution.

2.3.2. Comparison of prediction accuracy

At present, there are many methods to measure prediction accuracy, and the following types of measurement methods are mainly used for univariate time series data: scale-dependent measurements, percentage error-based measurements, and relative error-based measurements [25]. The scale-dependent measurements is usually based on absolute error or square error, and the commonly used indicators include mean square error (MSE), root mean square error (RMSE), mean absolute error (MAE), median absolute error (MedAE), and so on. The measurements based on percentage error are dependent of the data scale, and the commonly used indicators include mean absolute percentage error (MAPE), median absolute percentage error (MedAPE), root mean square percentage error (RMSPE), and so on. The relative error-based measurements need to be compared with the errors obtained by standard prediction methods, represented by indicators such as mean relative absolute error (MRAE) and median relative absolute error (MedRAE), and so on.

Considering the advantages and disadvantages of the above indicators, this paper decides to use RMSE and MAPE to measure the prediction accuracy of the model. RMSE is an indicator to measure the difference between the predicted value and the measured value of the model, which can better evaluate the degree of fitting of the model, and can be used to measure the accuracy of the same set of data by using different prediction models. MAPE shows the relative magnitude of deviation of the model prediction value in the form of percentage, which has the advantage of being independent of data scale, and therefore can be used to judge the prediction performance of different data sets.

$$\begin{array}{c}RMSE=\sqrt{\frac{1}{n}{\displaystyle {\displaystyle \sum }_{i=1}^n}{\left(y_i-{\widehat{y}}_i\right)}^2}\end{array}$$

(8)

$$\begin{array}{c}M\mathrm{A}PE=\frac{100\%}{n}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left|\frac{y_i-{\widehat{y}}_i}{y_i}\right|\end{array}$$

(9)

where $y_i$ is the measured value, ${\widehat{y}}_i$ is the predicted value, and n is the number of measured values

3. Case analysis

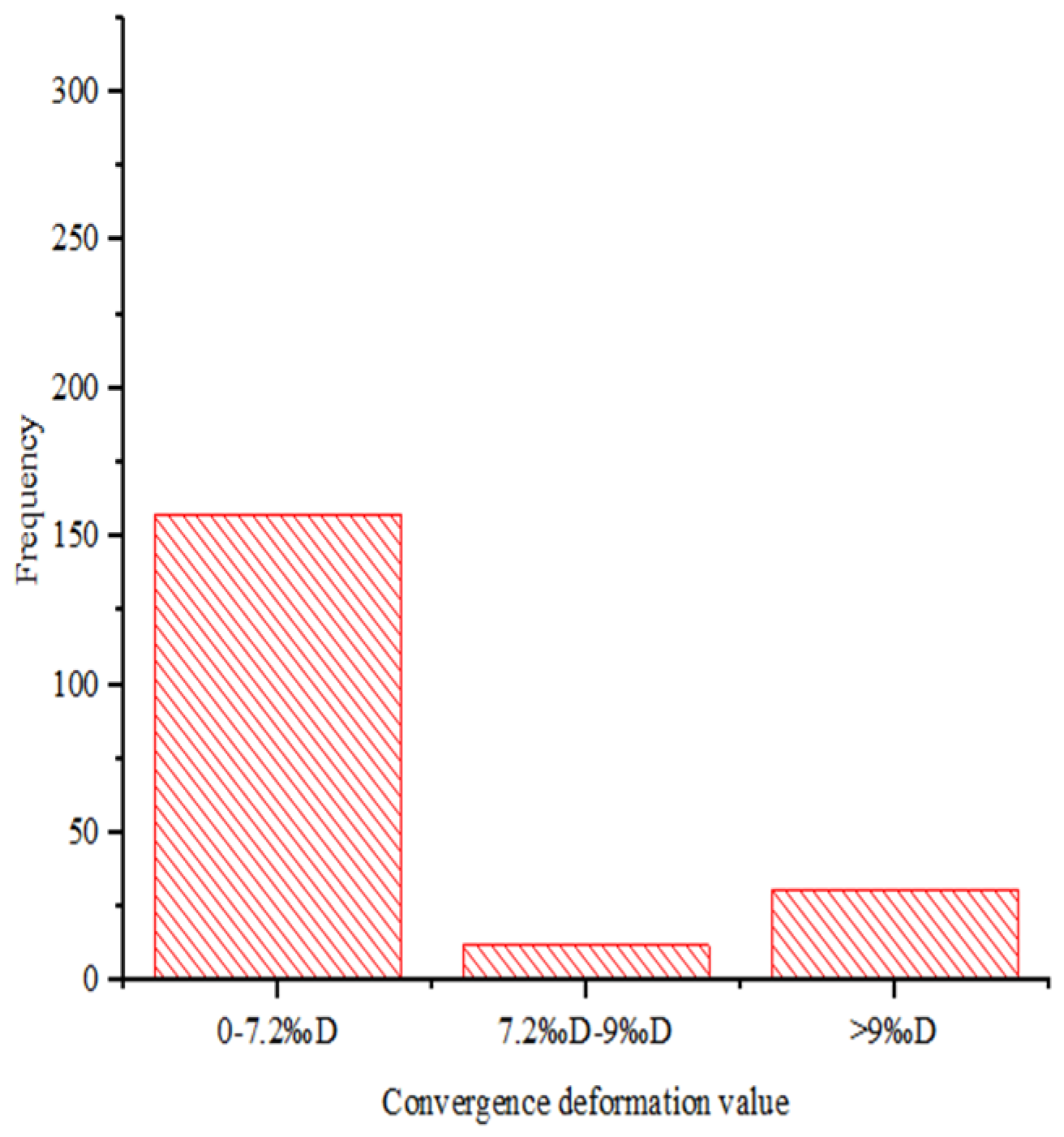
3.1. Project overview and testing data

The data in this paper are selected from the two-station section of a subway tunnel. The designed mileage of the section tunnel is DK12+043.600~DK12+618.236, among which the length of the left line tunnel is 526.356m, and the length of the right line tunnel is 538.301m. The project was completed and put into operation in 2013.The maximum buried depth of the interval tunnel is 19.04m, the minimum buried depth is 8.16m, and the tunnel passes through a large number of residential houses, mostly 1-8-storey buildings. The interval is constructed by shield method. The design inner diameter of the tunnel is 5.4m, the design outer diameter is 6m, and the width of the shield segment is 1.5m.

A mobile 3D laser scanner Amberg GRP5000 was used to collect 9 sets of point cloud data of subway shield tunnels in August 2018, February 2019, November 2019, June 2020, November 2020, May 2021, November 2021, March 2022 and September 2022. The point cloud data was projected onto a horizontal plane to obtain the tunnel boundary point cloud, which is the left and right endpoints of the tunnel horizontal diameter, thus obtaining the horizontal diameter of the subway shield tunnel ring by ring. A total of horizontal diameter values of the 200 ring segments of the tunnel were extracted. By utilizing the horizontal diameter data of multi ring subway shield tunnels, the lateral convergence deformation prediction accuracy of subway shield tunnel based on Kalman model can be fully verified. The lateral convergence deformation prediction performance of subway shield tunnel based on Kalman model in different scale data sets can also be analyzed by placing sample data of different periods.

For the shield tunnel with staggered splicing, the early warning value and safety value of convergence deformation are specified in the Technical Specification for Operation Monitoring of Urban Rail Transit Facilities (GB/T39559.3-2020). The early warning indicator is 7.2‰ of the tunnel outer diameter, and the safety indicator is 9‰ of the tunnel outer diameter. The over-limit of the convergence deformation value will affect the traffic safety of the tunnel. Taking the data of September 2022 as an example, there are 43 rings of 200 rings tubes in which the horizontal diameter reaches the warning limit, 31 rings in which the horizontal diameter exceeds the safety limit, and the rest of them meets the standard requirements, as shown in Figure 1.

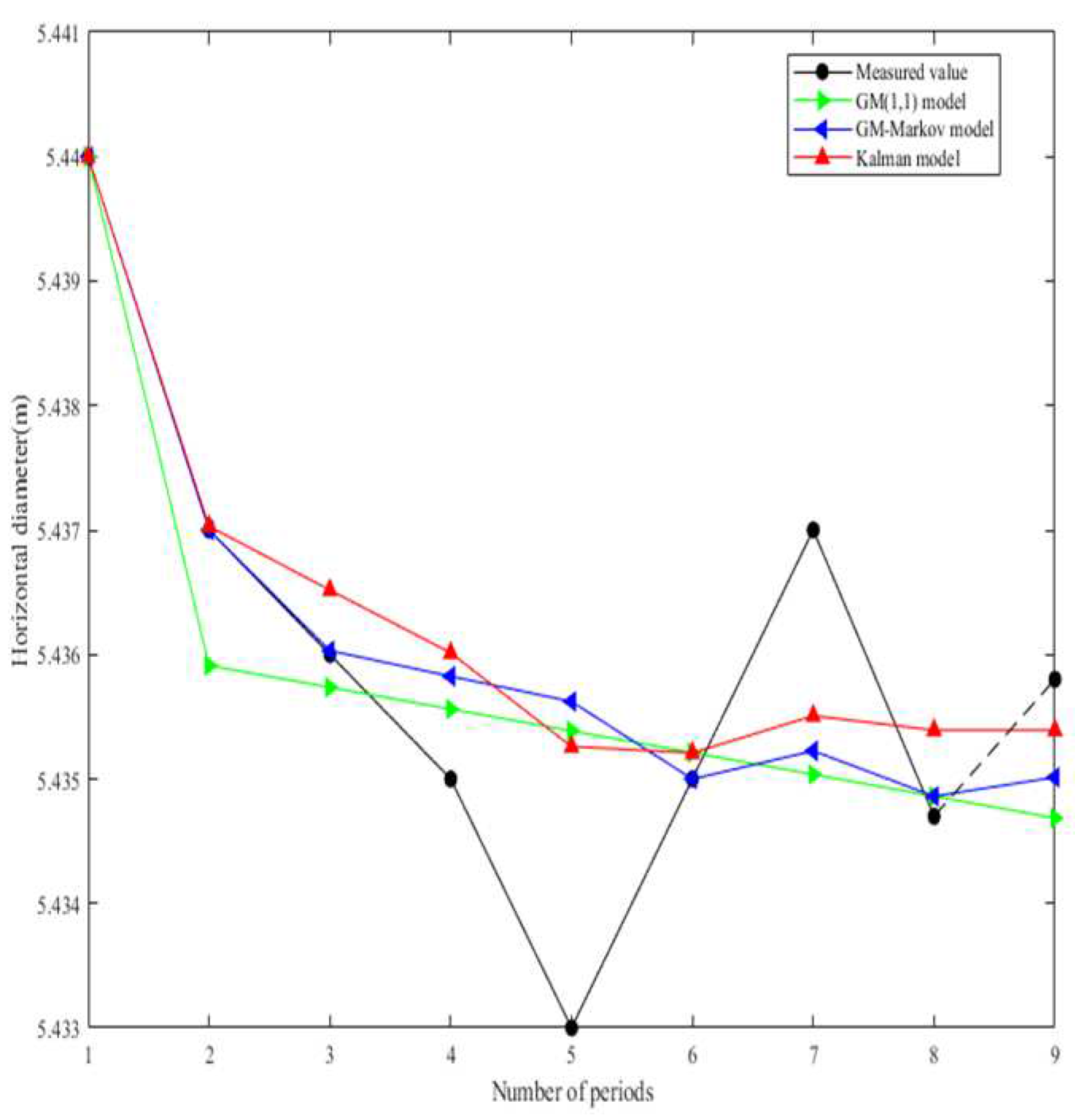
3.2. Lateral convergence model of subway shield tunnel based on Kalman algorithm

The data of the first eight periods of subway shield tunnel horizontal diameter are taken as the measured values, and Kalman equation is applied to predict the next period horizontal diameter, and compared with the measured values in the ninth periods to check the lateral convergence deformation prediction accuracy of subway shield tunnel based on Kalman model. Taking one of the ring segment as an example, Z=[5.44, 5.437, 5.436, 5.435, 5.433, 5.435, 5.437, 5.4347]. The lateral convergence model of subway shield tunnel based on Kalman algorithm was established on this sample, and run it through Matlab programming. The prediction results are shown in Figure 2, where the blue dashed line is the iterative process of the predicted value of the horizontal diameter. From the figure, it can be seen that the predicted value of the horizontal diameter in the ninth period is 5.4354m, while the measured value in the ninth period is 5.4358m, and the prediction residual is 0.0004m, that is, 0.4mm. In addition, by calculation, the root mean square error (RMSE) of the Kalman prediction model is obtained as 4.0828×10-4, and the mean absolute percentage error MAPE=0.0075, which can prove that the lateral convergence model of subway shield tunnel based on Kalman algorithm has small prediction residuals and high accuracy.

All the collected horizontal diameter values of 200 rings segment are predicted by the lateral convergence model of subway shield tunnel based on Kalman algorithm, and the overall root mean square error RMSE=8.2990×10-4 and the mean absolute percentage error MAPE=0.0124 were calculated. The optimal estimation values output by the prediction model was compared with the measured value. Figure 3 shows the comparison between the predicted value and the measured value of the Kalman model, and Figure 4 shows the prediction residual of the Kalman model. Combined with the image and the precision measurement indicator, it can be seen that the predicted value and measured value of the Kalman prediction model have a high degree of fit, and the residual value is small, and the prediction effect is great when applied to the multi-ring segments.

The lateral convergence deformation prediction residual of subway shield tunnel based on Kalman model is analyzed below to test whether it conforms to the normal distribution. According to the histogram of residual distribution predicted by Kalman model (Figure 5), there are 162 rings of its residuals are in the range of [-0.001,0.001]m, 33 rings are in the range of [-0.002,0.001]∪[0.002,0.001]m, 33 rings are in the range of [-0.002,0.001]m, only 5 rings are in the range of [-0.003,-0.002]∪[0.003,0.002]m, and the histogram presents a bell-shaped plot with high center and low sides. Through the K-S test of a large sample size, P=0.057>0.05 is obtained, which proved that the residual conformed to the normal distribution, so the Kalman prediction model has a high degree of fitting and strong prediction ability. The normality test results of the data are shown in Table 1. The normal distribution skewness of the residual is -0.128, which is less than 0, the tail on the left side of the curve is longer, and the data on the right side is denser, indicating that the normal distribution is skewed to the left; the kurtosis of the residual is 0.498, which is greater than 0, indicating that the peak state of the normal distribution is steeper. The mean value of the residual normal distribution is positive, indicating that the lateral convergence deformation prediction value of subway shield tunnel based on Kalman model is larger than the measured value.

In addition, the sample points in the normal P-P plot and Q-Q plot of the predicted residual (Figure 6 and Figure 7) are approximately a straight line, which also proves that they obey the normal distribution.

4. Discussion

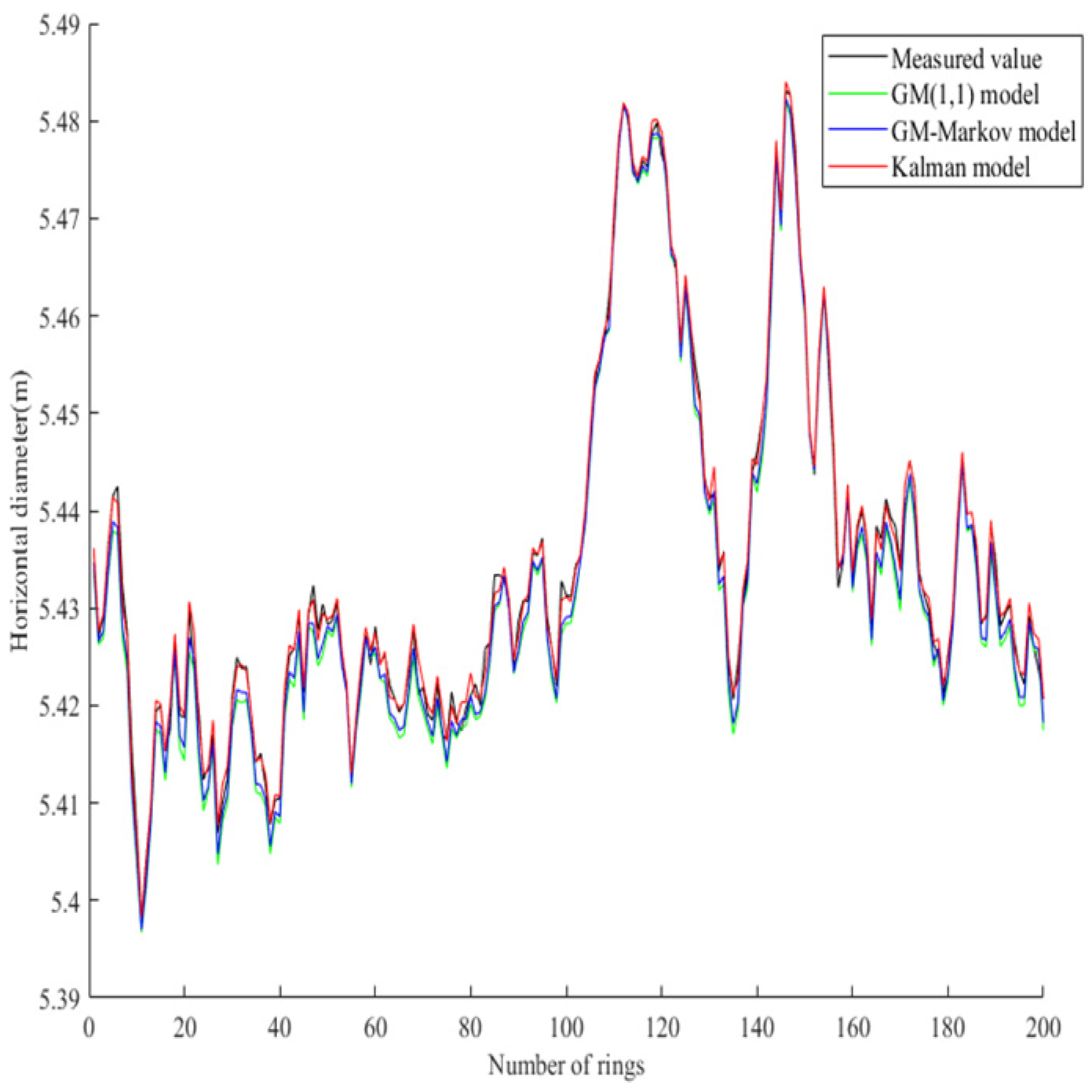
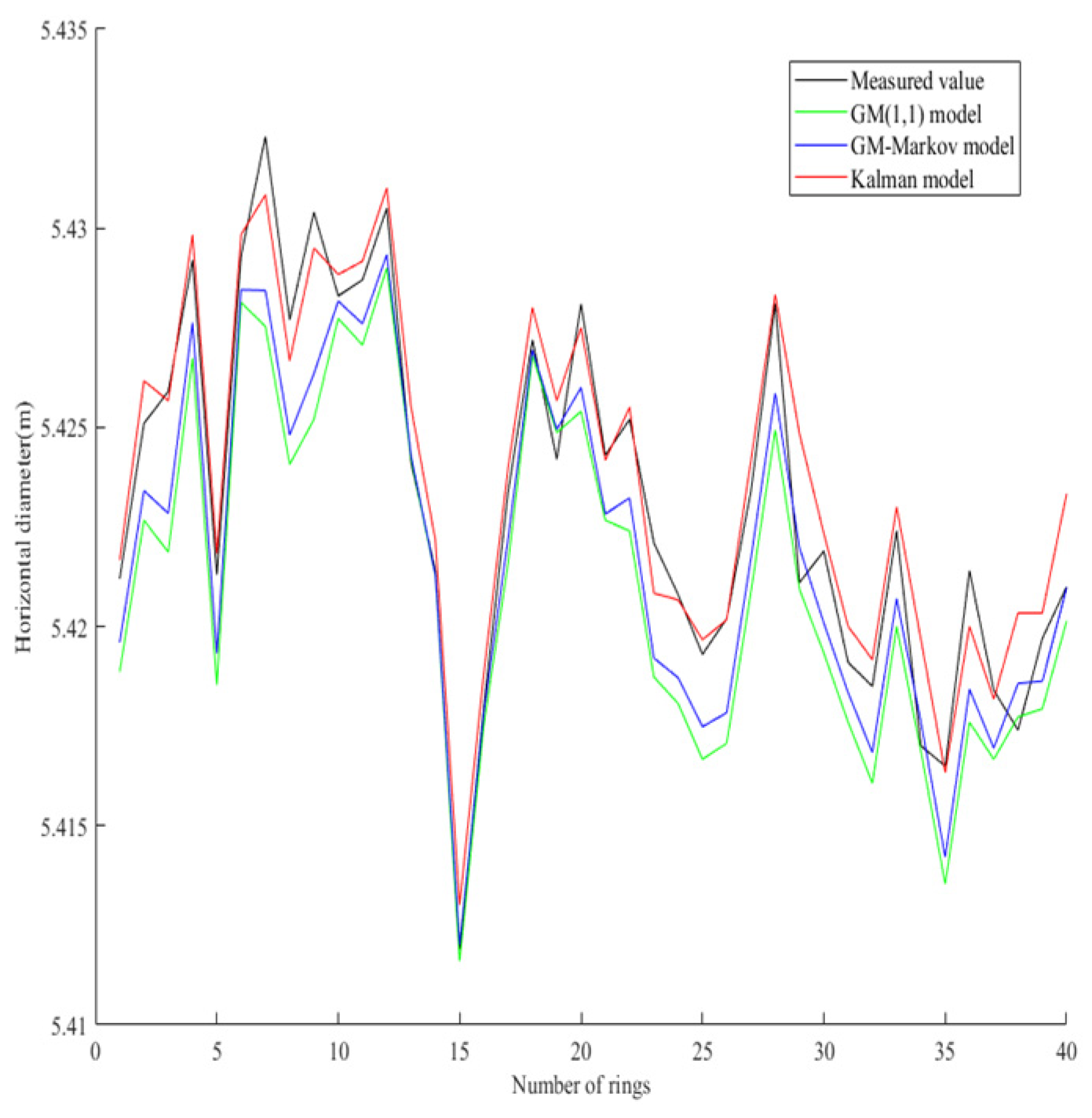
4.1. Comparison of prediction accuracy of multiple models

In order to further measure the lateral convergence deformation prediction accuracy of subway shield tunnel based on Kalman model, the GM(1,1) model and the GM-Markov model are chosen for comparison.

The GM(1,1) model refers to the grey model of single-variable first-order differential equation, which is the most widely used form of grey prediction. Its prediction principle is to change the original data without obvious regularity into a series with exponential growth pattern through accumulated generating, and construct a series of equal weights adjacent to the mean value of the accumulated generated sequence to eliminate the volatility and randomness of the original data. Since the form of solution of the first-order differential equation is exponential growth, the first-order differential equation model can be established for the sequence of equal weights of the adjacent mean. After that, the development coefficient and grey action are solved by the least square method, and substituted into the first-order differential equation, and the data are reversely calculated and the cumulative reduction is carried out so as to obtain the prediction value of the original sequence. The model adopts the method of accumulation and reduction, which does not need to find the statistical regular pattern of the original series, but directly converts it into a regular time series, weakens the unknown factors in the grey system, strengthens the influence degree of known factors, and is suitable for short-term prediction of small sample size data.

For the data showing volatility and trend, Markov chain is introduced to improve the fitting effect of grey model. The Markov chain is characterized by the fact that the future state of the system is only related to the present state, and has nothing to do with the past state, and the state transition has no after-effect. The GM-Markov model is to obtain the prediction value of the original data by using the GM(1,1) model, and then establish the GM(1,1) model with the residual difference between the original data and the prediction value to get the residual correction value. The positive and negative residuals are divided into two states, and the probability of each state transferring to each other is obtained based on the sample data, and the state transition matrix is constructed and the state probability of the final moment is obtained. The state with the greatest probability is selected as the final state, and the residual correction value in this state is used to correct the original data prediction value and accurately adjust the prediction result.

Figure 8 shows the prediction results comparison of the GM(1,1) model, the GM-Markov model and the Kalman model for single-ring segment. It can be seen from the figure that the prediction result of the GM(1,1) model is a straight line, and the fitting effect of volatility data is poor. However, the GM-Markov model is adjusted on the basis of the GM(1,1) model prediction curve, and the predicted result is closer to the actual measured value than that of the GM(1,1) model in later periods, and the prediction effect is better. Among the three models, the curve trend of Kalman model is the closest to the measured value, and the prediction effect is the best. Table 2 shows the calculation results of RMSE and MAPE of the three kinds of models for single ring segment. The RMSE and MAPE values of the Kalman model are smaller than those of the other two kinds of models, so it can be seen that the Kalman model has higher prediction accuracy.

The prediction results of the GM(1,1) model, the GM-Markov model and the Kalman model for 200 rings segments of shield tunnel are shown in Figure 9. For the convenience of observation and analysis, 40 consecutive rings segments are captured and plotted (Figure 10). The predicted value and residual value of each ring segment are shown in Table 3. It can be seen from Figure 10 that the red line representing the Kalman prediction model is closer to the black line representing the measured value than the green line and blue line representing the GM(1,1) prediction model and the GM-Markov prediction model respectively, indicating that the prediction effect of the Kalman model is better in the case of multi-ring segments, which proves the generality of the Kalman model.

Figure 11 shows the residuals of the prediction results of the three kinds of models for the 200 rings segments. The residuals of the Kalman model are mostly concentrated in the interval [-0.001,0.001]m, and the residuals are small, indicating that the Kalman model is stable and has good prediction effect. The residuals of the GM(1,1) model are distributed in the interval [-0.005,0.002]m, and the residuals of some prediction results are more significant, indicating that the prediction result of GM(1,1) model is unstable and the prediction effect is general. The residuals of the GM-Markov model are mainly concentrated in the interval of [-0.003,0.002]m, and a few prediction residuals can reach -0.005m. The prediction effect is better than the GM(1,1) model, but inferior to the Kalman model. In addition, the residuals of the GM(1,1) model and the GM-Markov model is mostly negative, which indicates that the prediction result of the GM(1,1) model and the GM-Markov model is smaller than the measured value.

The GM(1,1) model, GM-Markov model and Kalman model were used to predict the horizontal diameter of 200 rings segments, and the overall root mean square error (RMSE) and the mean absolute percentage error (MAPE) were shown in Table 4. The RMSE and MAPE values of the Kalman model are smaller than those of the other two kinds of models, indicating that Kalman model has higher prediction accuracy.

4.2. Prediction performance of Kalman model in different scale data sets

In order to measure the lateral convergence deformation prediction performance of subway shield tunnel based on Kalman model on data sets with different scales, the horizontal diameter convergence data of shield tunnel in the 1-4, 1-5, 1-6, 1-7 and 1-8 periods of 200 rings segments were selected as sample data to predict the convergence value of tunnel horizontal diameter for 5, 6, 7, 8, and 9 period, respectively. Figure 12 shows the RMSE and MAPE values of different scale data sets. When only 4 periods of data were used as sample data for prediction, the root mean square error RMSE=0.0037, which is increased by 131% compared with the 5 periods of data, and the mean absolute percentage error MAPE=0.0656, increased by 185% compared with the 5 periods of data, indicating that the prediction effect of 4 periods of data was not good. Using Kalman model to predict the convergence value of tunnel horizontal diameter should have at least 5 periods of data. With the number of periods of sample data increases, the RMSE and MAPE values of the Kalman model gradually decrease, indicating that the prediction accuracy of the model will be improved with the increase of sample data.

5. Conclusions

In this paper, the Kalman model is used to predict the lateral convergence deformation of subway shield tunnel, and the main conclusions are as follows:

• The lateral convergence model of subway shield tunnel based on Kalman algorithm performs well in the prediction of non-stationary data with small sample size. This model is efficient, adaptive and robust, and can accurately predict the lateral convergence deformation of subway shield tunnel;
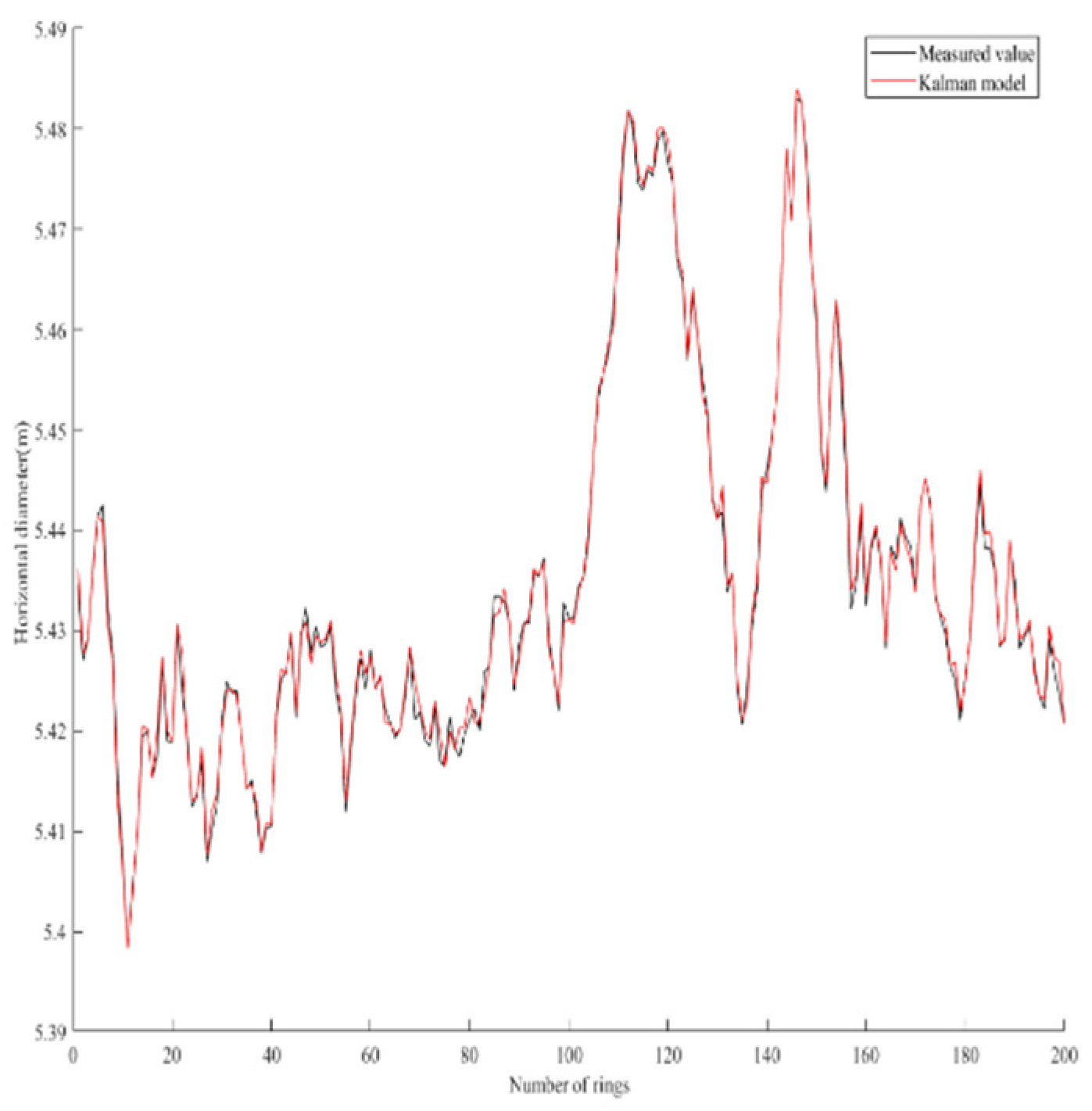
• For the prediction of horizontal diameter data of subway shield tunnel, comparing the Kalman model with the GM(1,1) model and the GM-Markov model, it is found that the lateral convergence model of subway shield tunnel based on Kalman algorithm has a high degree of fit with the horizontal diameter measured value, and the prediction residual is small, and the model effect is better. The RMSE and MAPE are introduced as evaluation indicators to verify the lateral convergence deformation prediction accuracy of subway shield tunnel based on Kalman model;
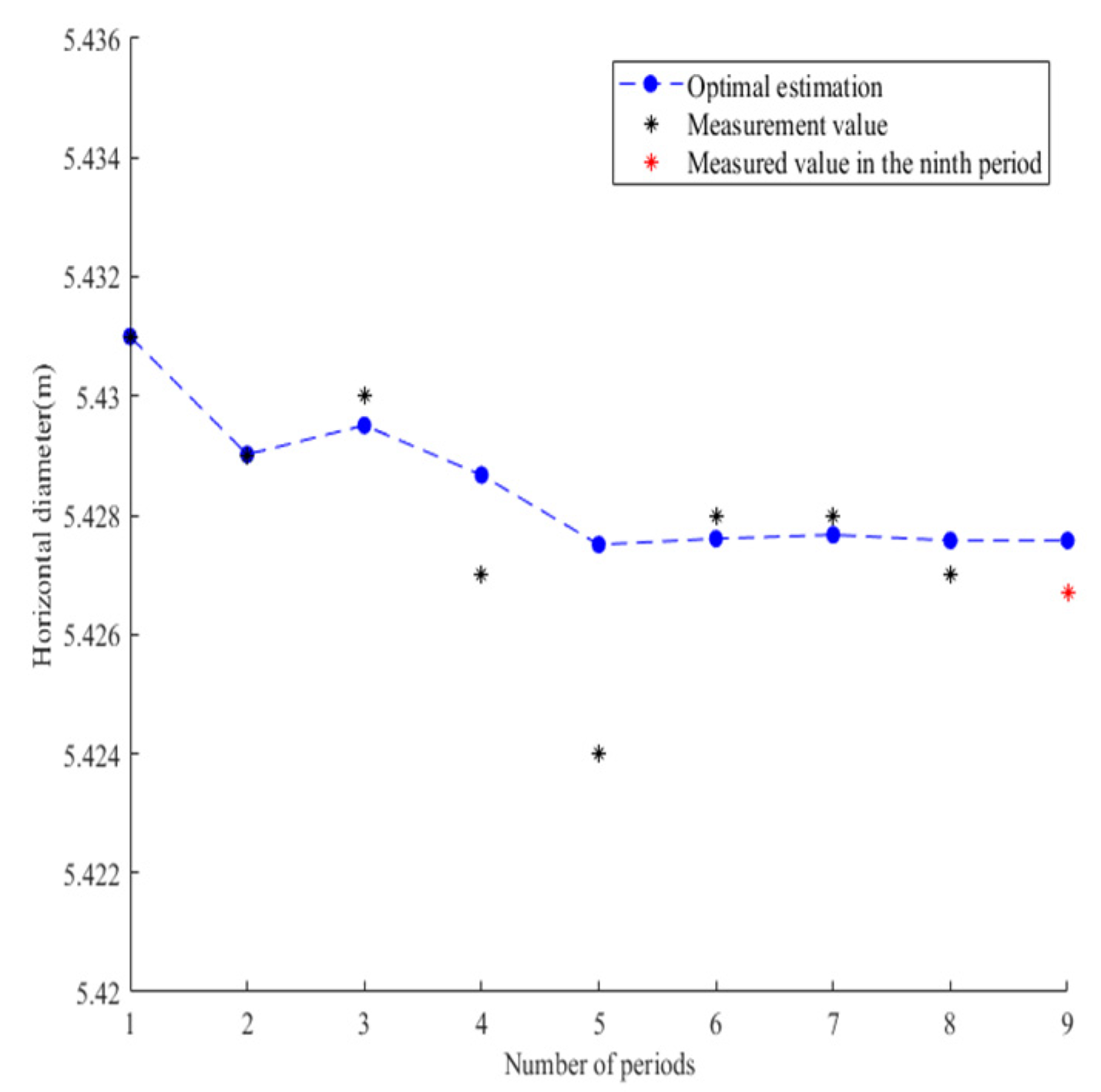
• By observing the lateral convergence deformation prediction performance of subway shield tunnel based on Kalman model on data sets of different scales, it is found that the at least 5 periods of horizontal diameter sample data of subway shield tunnels are required for predicting the lateral convergence deformation of subway shield tunnel, and the prediction accuracy of the model improves with the increase of the number of sample data periods. As the number of horizontal diameter sample data periods of subway shield tunnels increases, the lateral convergence deformation prediction accuracy of subway shield tunnel based on Kalman model is improved.