Submitted:
30 December 2023
Posted:
04 January 2024
You are already at the latest version
Abstract
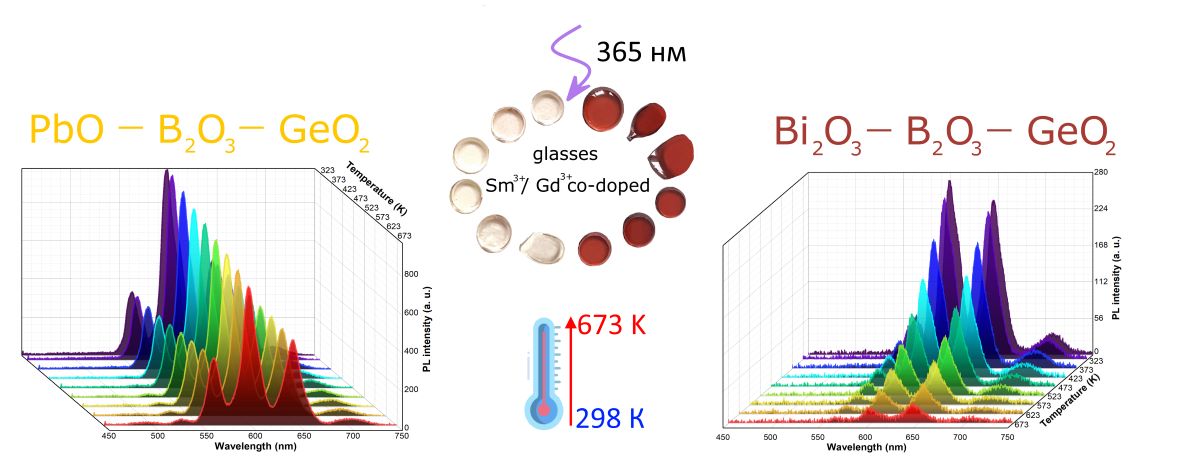
Keywords:
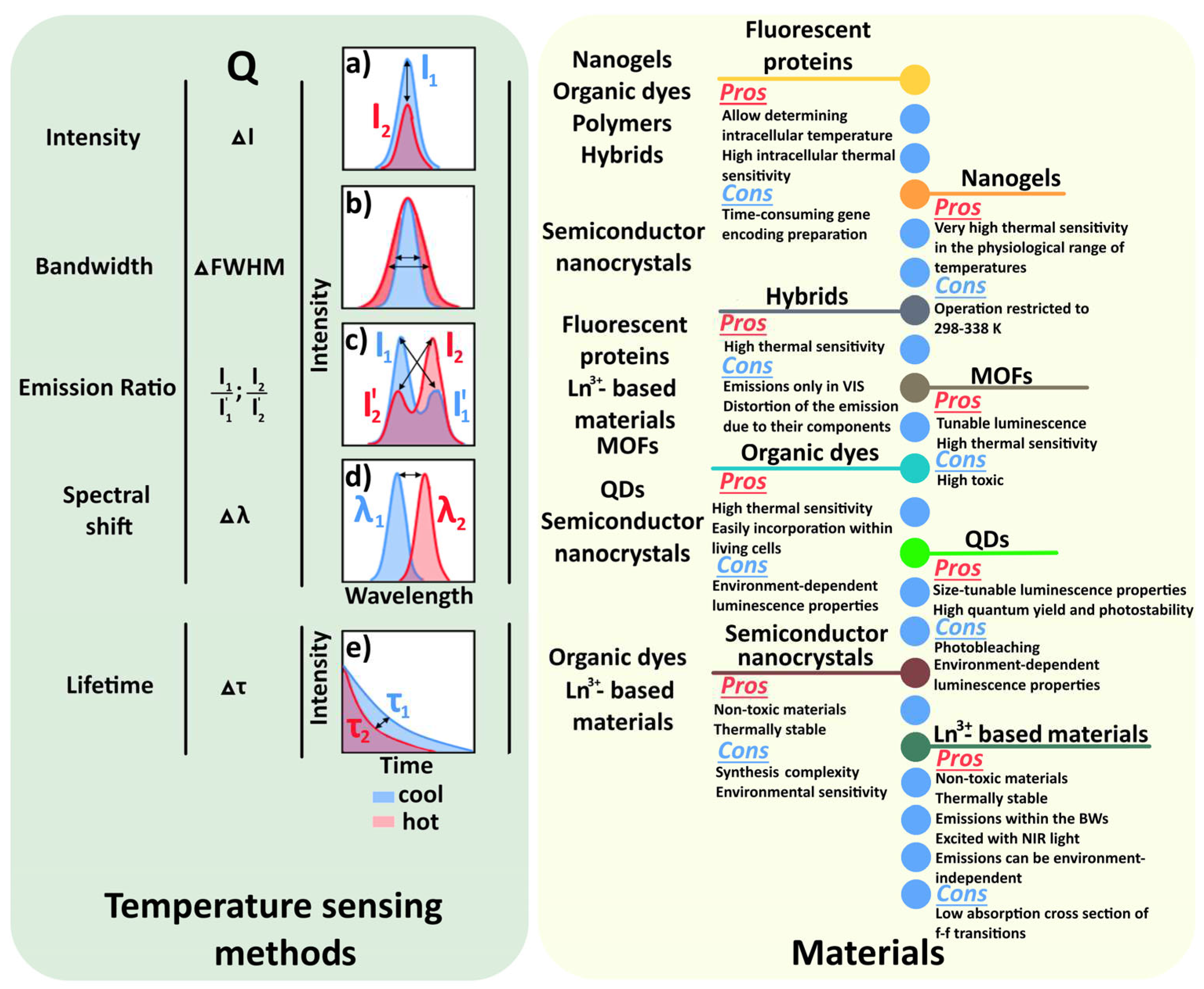
1. Introduction
2. Materials and Methods
2.1. Materials and synthesis
2.2. Characterization techniques
3. Experimental results
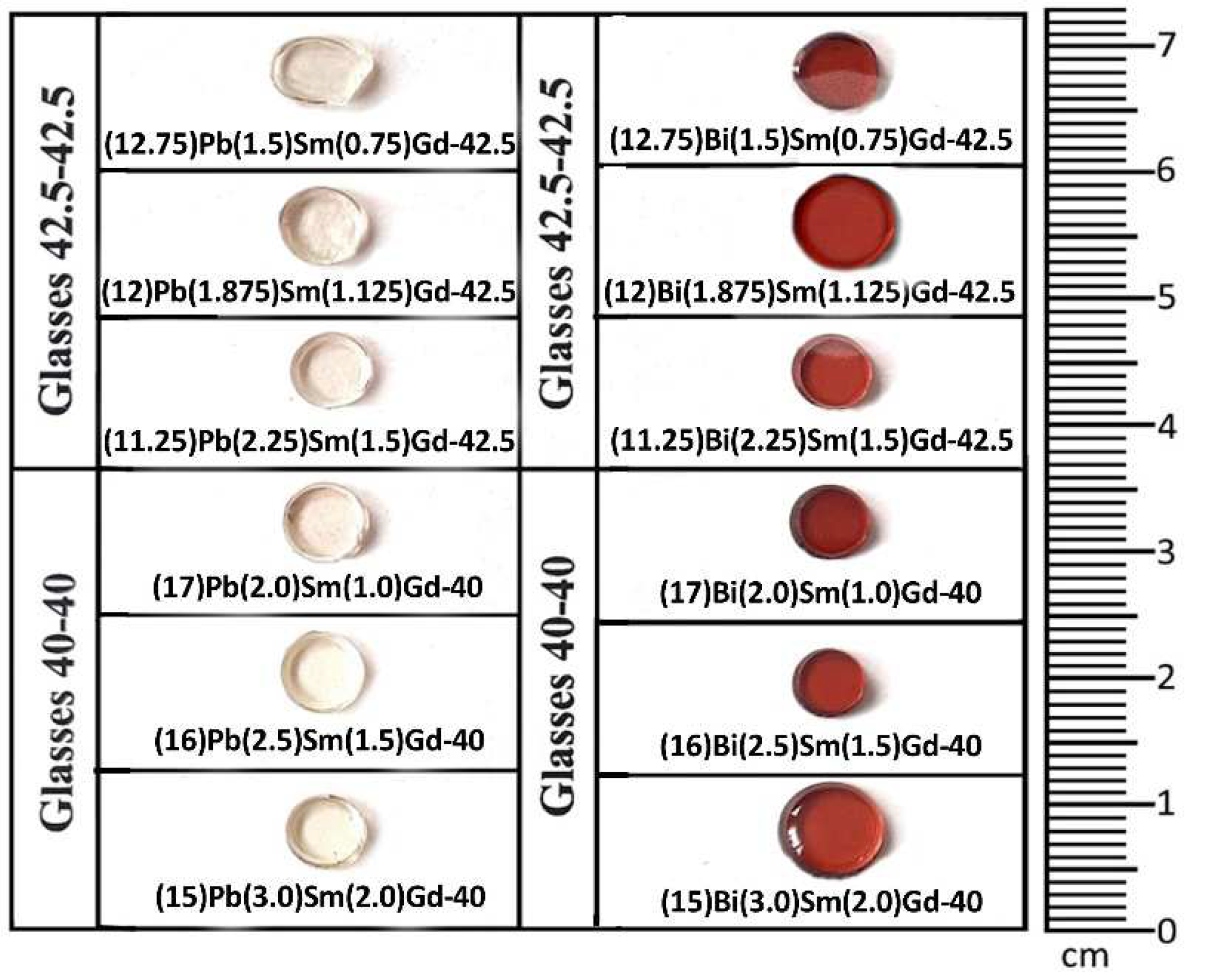
3.1. Glass samples
3.2. Glass structure characterisation
| Raman shift, cm–1 | Interpretation | Reference | |
|---|---|---|---|
| Pb-based | Bi-based | ||
| 390 | Bending modes of Ge–O–Ge bonds | [37] | |
| 465 | 460 | Symmetrical stretching of Ge−O−Ge bonds in 4- or 6-membered rings of Ge4+ in a tetrahedral arrangement |
[29,30,31] |
| 650 | Vibrations of 6-coordinated atom Ge (VI) | [30,38] | |
| 715 | Stretching vibration of the B-sublattice against the O-sublattice, a B–O–B out-of-plane ring vibration | [31] | |
| 800 | 800 | Vibration of the oxygen atoms in the boroxol ring |
[32,33] |
| 890 | Ge–O–Ge double degenerate vibration |
[39] | |
| 1315 | 1240 | B−O− stretching mode in metaborate structures | [33,34,35] |
| 1500 | Overlap of following modes: B–O– in BØ2O-, BØ2O- triangle linked to BØ4 unit, and stretching in BØ3 triangles | [36] | |
3.3. DSC characterisation and physical properties
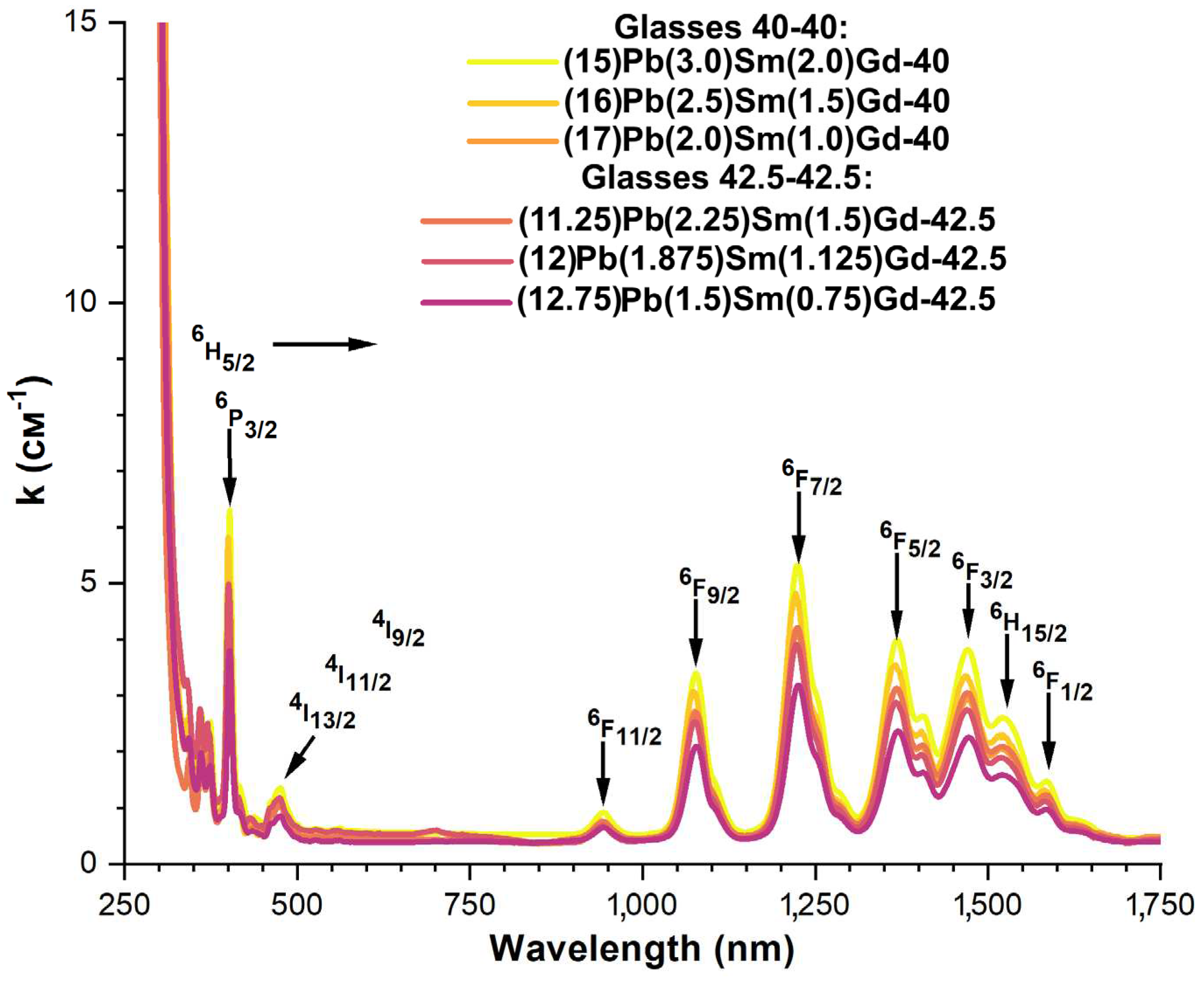
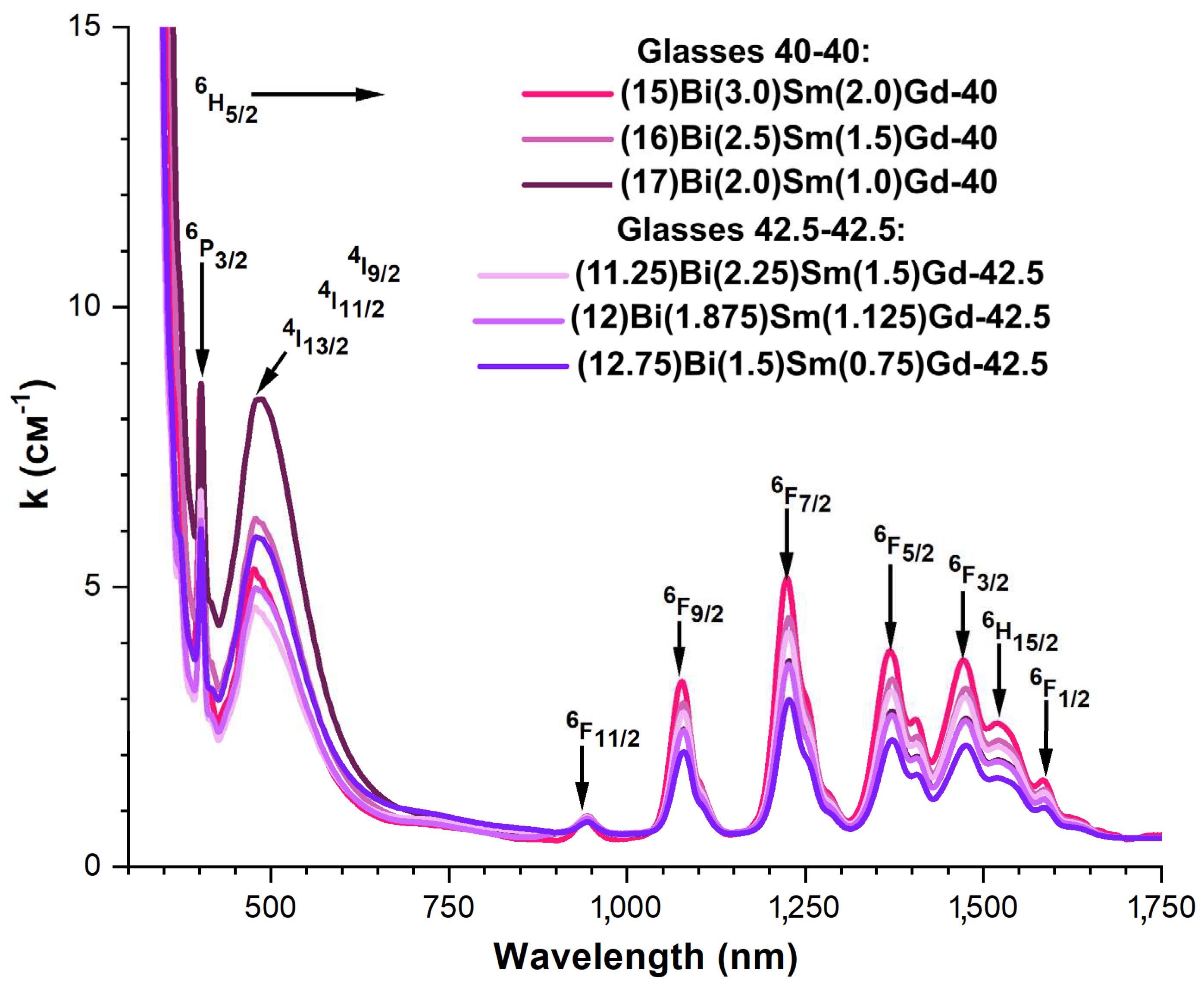
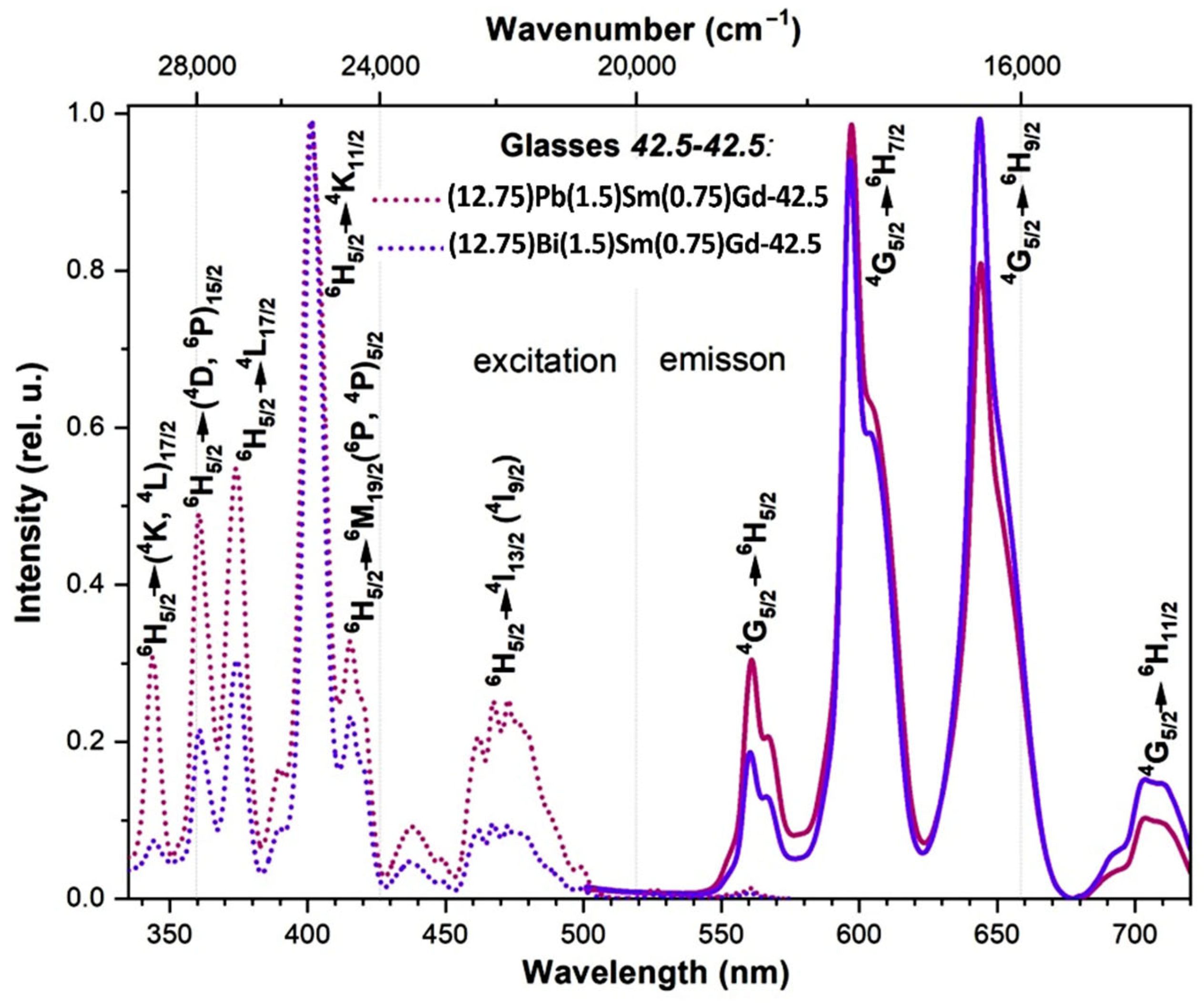
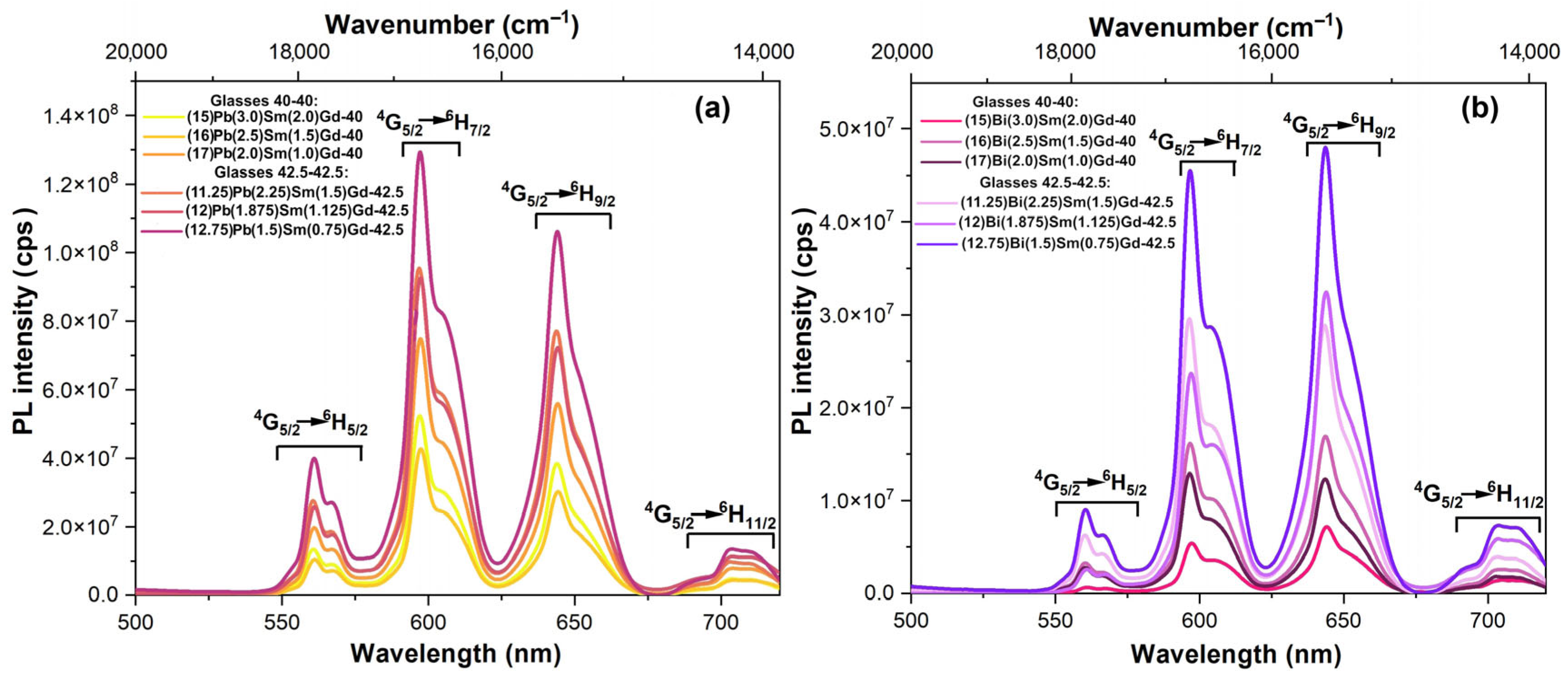
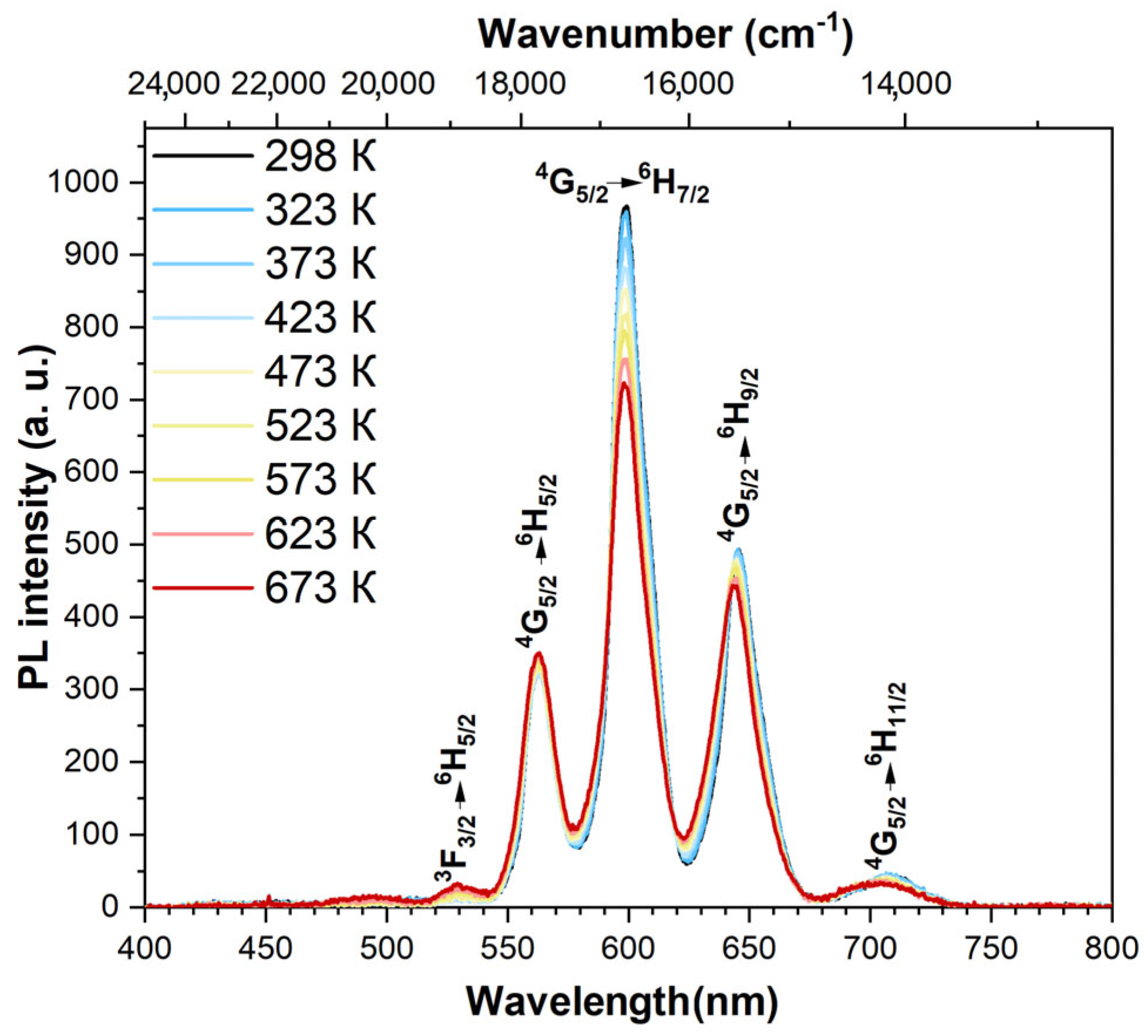
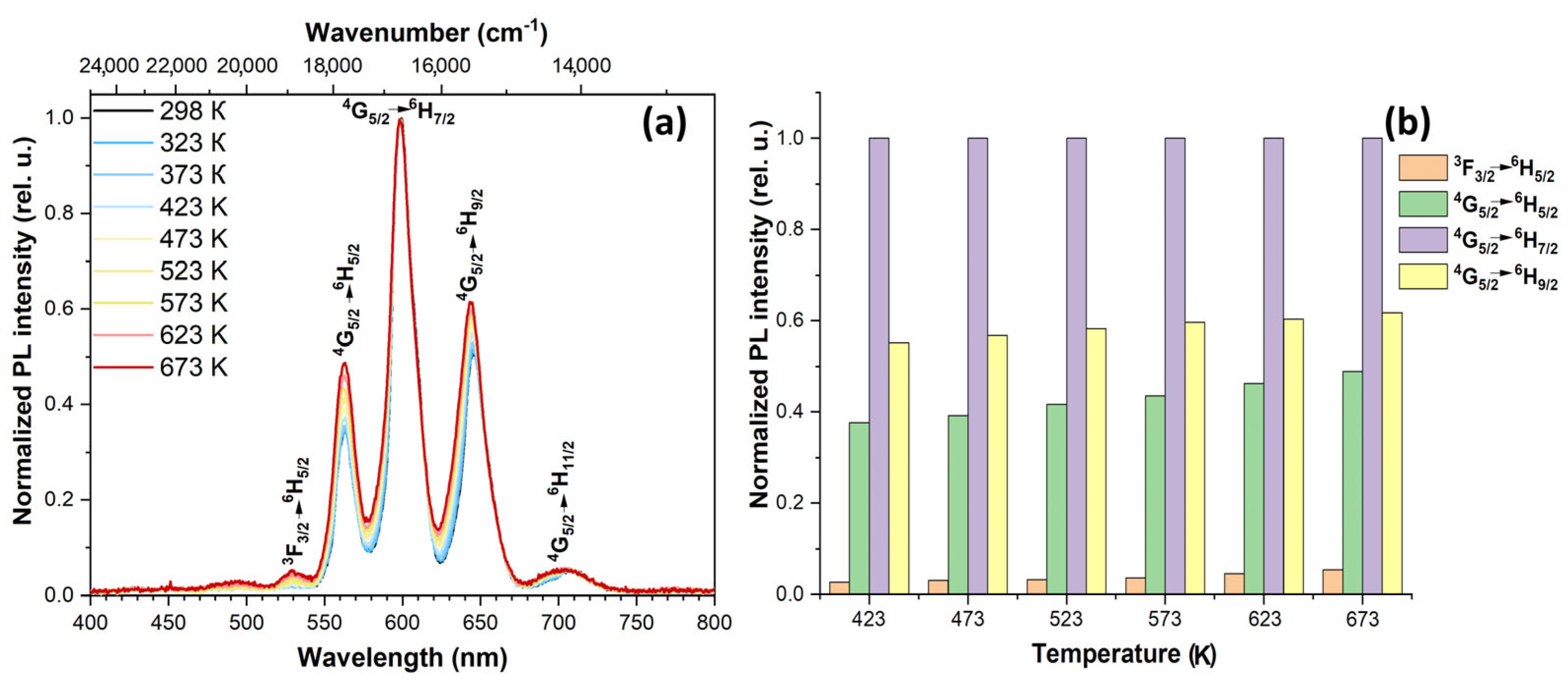
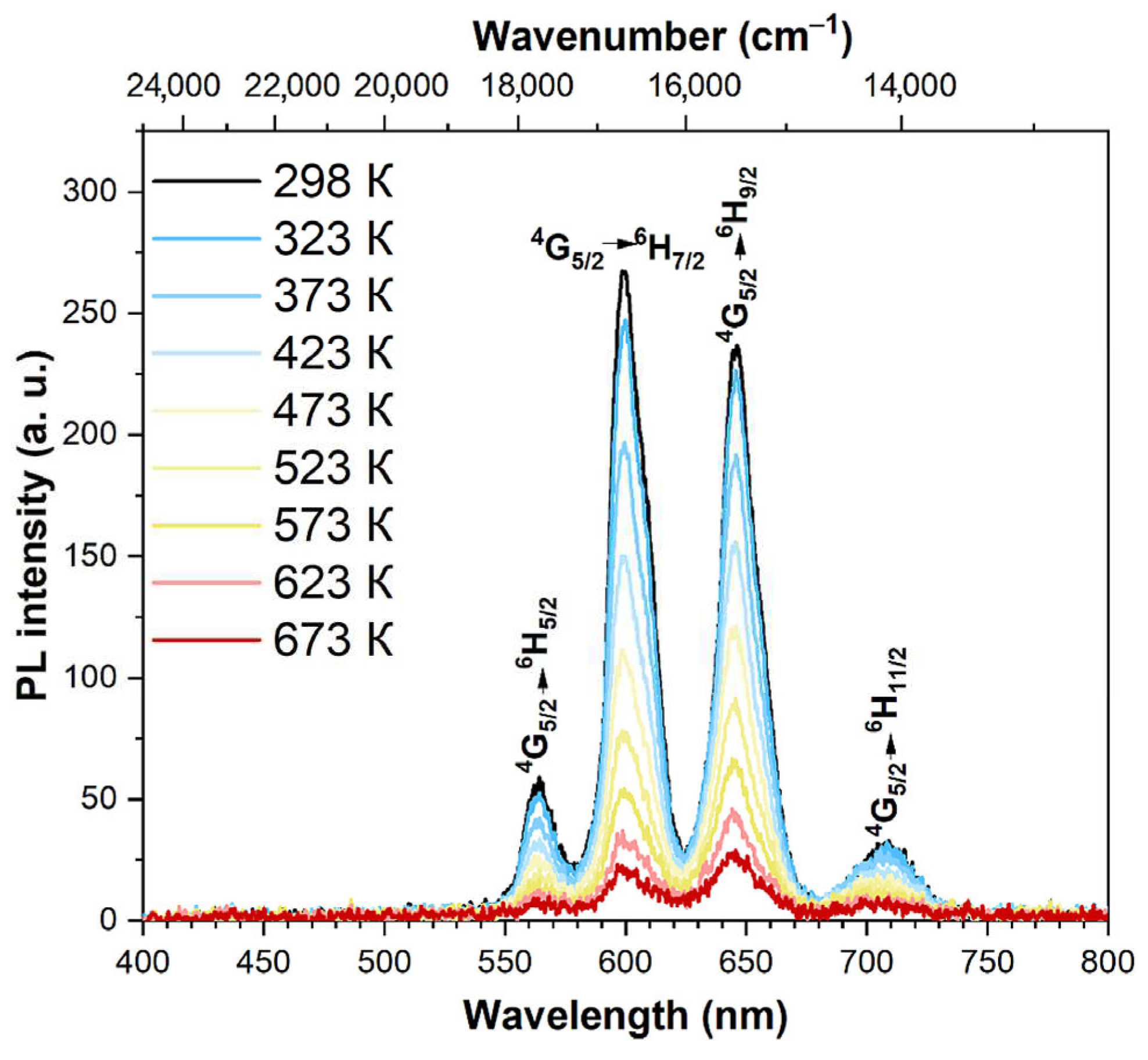
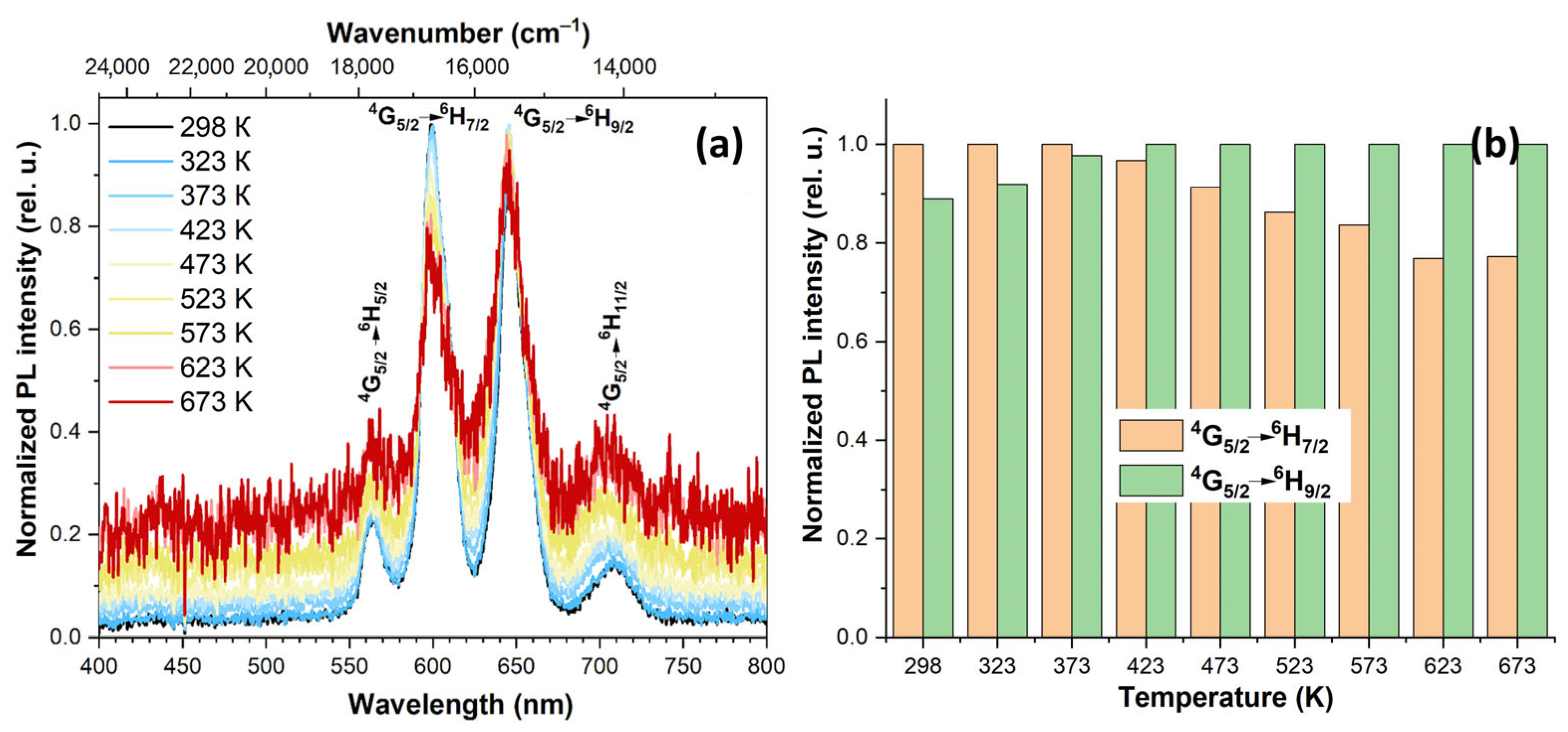
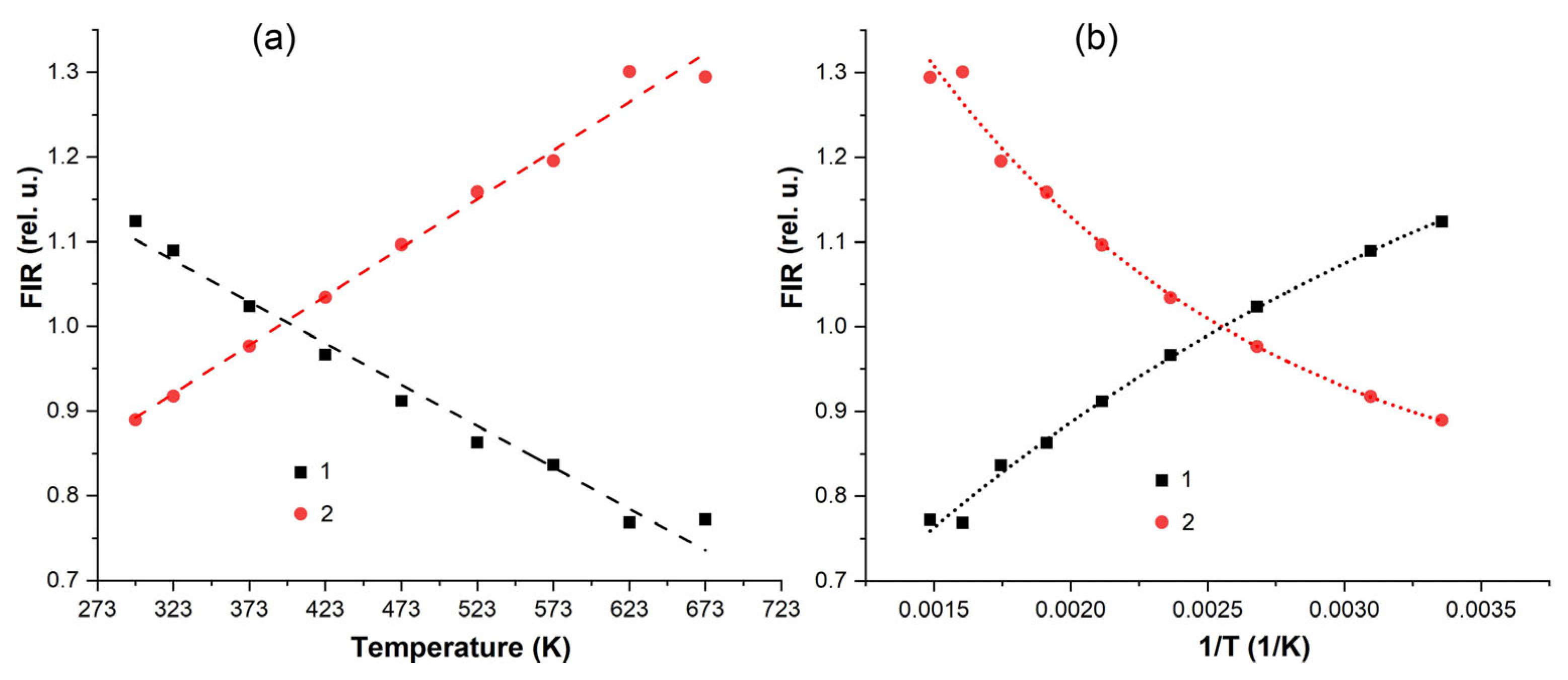
3.4. Spectral-luminescent properties
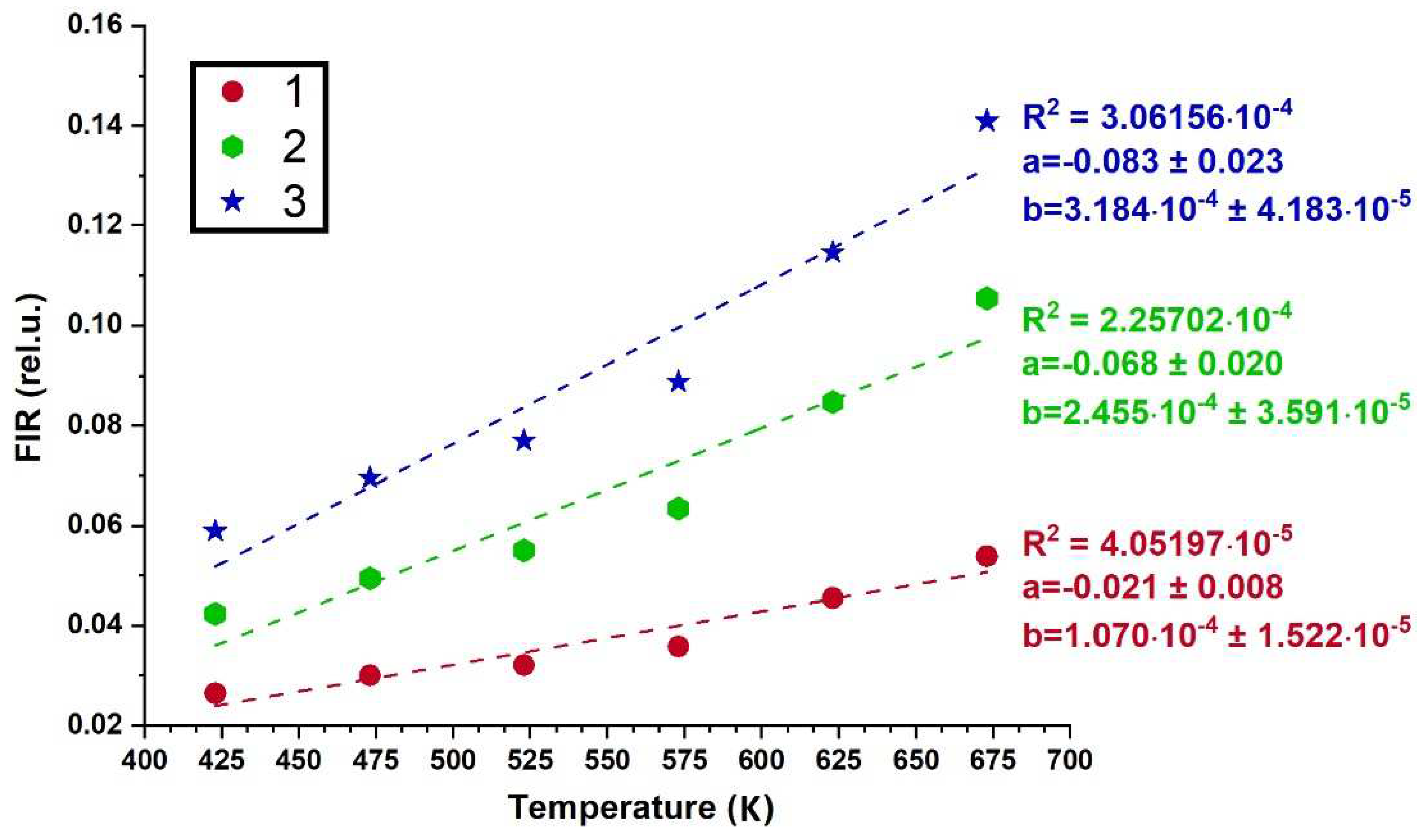
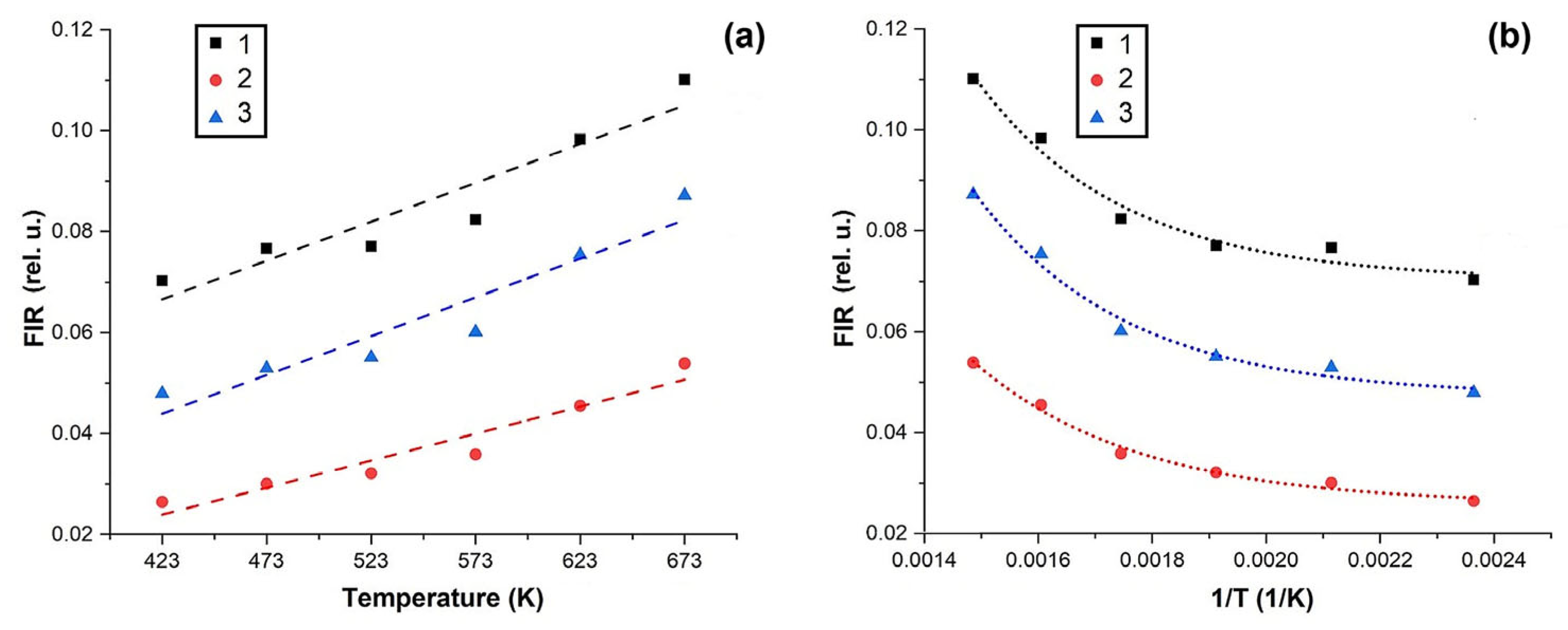
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Childs, P. R. N.; Greenwood, J. R.; Long, C. A. Review of temperature measurement. Rev. Sci. Instrum. 2000, 71, 2959–2978. [Google Scholar] [CrossRef]
- Michalski, L.; Eckersdorf, K.; Kucharski, J.; McGhee, J. Temperature measurement.; Publisher: Wiley, Chichester, UK, 2001. [Google Scholar]
- Beheim, G. Optical Temperature Sensors. Integrated Optics, Microstructures, and Sensors. 1995, 332, 285–313. [Google Scholar] [CrossRef]
- Wang, X.; Wolfbeis, O.S.; Meier, R. J. Luminescent probes and sensors for temperature. Chem. Soc. Rev. 2013, 42, 7834–7869. [Google Scholar] [CrossRef]
- Brites, C.D.; Lima, P.P.; Silva, N.J.; Millán, A.; Amaral, V.S.; Palacio, F.; Carlos, L.D. A luminescent molecular thermometer for long-term absolute temperature measurements at the nanoscale. Adv. Mater. 2010, 22, 4499–4504. [Google Scholar] [CrossRef] [PubMed]
- Dramićanin, M.D. Trends in luminescence thermometry. J. Appl. Phys. 2020, 128, 4. [Google Scholar] [CrossRef]
- Sutton, G.; Korniliou, S.; Andreu, A.; Wilson, D. Imaging luminescence thermometry to 750 °C for the heat treatment of common engineering alloys and com-parison with thermal imaging. Int. J. Thermophys. 2022, 43, 36. [Google Scholar] [CrossRef]
- van Swieten, T.P.; Yu, D.; Yu, T.; Vonk, S.J.; Suta, M.; Zhang, Q.A.; Meijerink, A.; Rabouw, F.T. Ho3+-based luminescent thermometer for sensitive sensing over a wide temperature range. Adv. Opt. Mater. 2021, 9, 2001518. [Google Scholar] [CrossRef]
- Bednarkiewicz, A.; Marciniak, L.; Carlos, L.D.; Jaque, D. Standardizing luminescence nanothermometry for biomedical applications. Nanoscale. 2020, 12, 14405–14421. [Google Scholar] [CrossRef] [PubMed]
- Lan, C. W.; Yu, W. C.; Hsu, W. C. Growth of Bulk Single Crystals. In Encyclopedia of Surface and Colloid Science, Third Edition; CRC Press, 2016; pp 2979–2990. [CrossRef]
- Avetissov, I.; Kostikov, V.; Meshkov, V.; Sukhanova, E.; Grishechkin, M.; Belov, S.; Sadovskiy, A. Modeling of Axial Vibrational Control Technique for CdTe VGF Crystal Growth under Controlled Cadmium Partial Pressure. J. Cryst. Growth 2014, 385, 88–94. [Google Scholar] [CrossRef]
- Jaque, D.; Vetrone, F. Luminescence nanothermometry. Nanoscale. 2012, 4, 4301–4326. [Google Scholar] [CrossRef]
- Abram, C.; Fond, B.; Beyrau, F. Temperature measurement techniques for gas and liquid flows using thermographic phosphor tracer particles. Prog. Energy Combust. Sci. 2018, 64, 93–156. [Google Scholar] [CrossRef]
- Suta, M.; Antić, Ž.; Ðorđević, V.; Kuzman, S.; Dramićanin, M.D.; Meijerink, A. Making Nd3+ a sensitive luminescent thermometer for physiological temperatures—An account of pitfalls in Boltzmann thermometry. Nanomaterials. 2020, 10, 543. [Google Scholar] [CrossRef] [PubMed]
- Suo, H.; Zhao, X.; Zhang, Z.; Wang, Y.; Sun, J.; Jin, M.; Guo, C. Rational design of ratiometric luminescence thermometry based on thermally coupled levels for bioapplications. Laser Photonics Rev. 2021, 15, 2000319. [Google Scholar] [CrossRef]
- Brities, C.D.S.; Millan, A. Handbook on the Physics and Chemistry of Rare Earths.; Publisher: Elsevier, North-Holland, 2016, pp. 339–427.
- Jaque, D.; Ramirez, M. O.; Bausá, L. E.; Solé, J. G.; Cavalli, E.; Speghini, A.; Bettinelli, M. Nd3+→Yb3+ energy transfer in YAl3(BO3)4 nonlinear laser crystal. Phys. Rev. B. 2003, 68, 35118. [Google Scholar] [CrossRef]
- Liu, X.; Akerboom, S.; de Jong, M.; Mutikainen, I.; Tanase, S.; Meijerink, A.; Bouwman, E. Mixed-Lanthanoid Metal–Organic Framework for Ratiometric Cryogenic Temperature Sensing. Inorg. Chem. 2015, 54, 11323–11329. [Google Scholar] [CrossRef]
- Brites, C. D. S.; Fiaczyk, K.; Ramalho, J. F. C. B.; Sójka, M.; Carlos, L. D.; Zych, E. Widening the Temperature Range of Luminescent Thermometers through the Intra- and Interconfigurational Transitions of Pr3+. Adv. Opt. Mater. 2018, 6, 1701318. [Google Scholar] [CrossRef]
- Runowski, M.; Woźny, P.; Stopikowska, N.; Martin, I. R.; Lavin, V.; Lis, S. Luminescent Nanothermometer Operating at Very High Temperature—Sensing up to 1000 K with Upconverting Nanoparticles (Yb3+/Tm3+). ACS Appl. Mater. Interfaces. 2020, 12, 43933–43941. [Google Scholar] [CrossRef]
- Allison, S. W.; Beshears, D. L.; Cates, M. R.; Scudiere, M. B.; Shaw, D. W.; Ellis, A. D. Luminescence of YAG:Dy and YAG:Dy, Er crystals to 1700 °C. Meas. Sci. Technol. 2019, 31, 044001. [Google Scholar] [CrossRef]
- Herrera, A.; Buchner, S.; Camerini, R. V.; Jacinto, C.; Balzaretti, N. M. Spectroscopic properties of B2O3–PbO–Bi2O3–GeO2 glass doped with Sm3+ and gold nanoparticles. Opt. Mater. 2016, 52, 230–236. [Google Scholar] [CrossRef]
- Gökçe, M.; Koçyiğit, D. Structural and optical properties of Gd+3 doped Bi2O3–GeO2 glasses and glass-ceramics. Mater. Res. Express. 2018, 2, 025203. [Google Scholar] [CrossRef]
- Gökçe, M.; Koçyiğit, D. Optical and luminescence characteristics of Sm3+ doped B2O3-GeO2-Gd2O3 glasses. Opt. Mater. 2018, 83, 233–240. [Google Scholar] [CrossRef]
- Lakshminarayana, G.; Meza-Rocha, A. N.; Soriano-Romero, O.; Huerta, E. F.; Caldino, U.; Lira, A.; Lee, D.-E.; Yoon, J.; Park, T. Analysis of fluorescence characteristics of Sm3+-doped B2O3-rich glasses for Orange-light-emitting diodes. J. Alloys Compd. 2021, 884, 161076. [Google Scholar] [CrossRef]
- Herrera, A.; Fernandes, R. G.; de Camargo, A. S. S.; Hernandes, A. C.; Buchnerd, S.; Jacinto, С.; Balzaretti, N. M. Visible-NIR emission and structural properties of Sm3+ doped heavy-metal oxide glass with composition B2O3-PbO-Bi2O3-GeO2. J. Lumin. 2015, 171, 106–111. [Google Scholar] [CrossRef]
- Rammah, Y.S.; Mahmoud, K.A.; Kavaz, E.; Kumar, A.; El-Agawany, F.I. The role of PbO/Bi2O3 insertion on the shielding characteristics of novel borate glasses. Ceram. Int. 2020, 15, 23357–23368. [Google Scholar] [CrossRef]
- Denker, B.; Galagan, B.; Osiko, V.; Sverchkov, S.; Dianov, E. Luminescent properties of Bi-doped boro-alumino-phosphate glasses. J. Appl. Phys. 2007, 87, 135–137. [Google Scholar] [CrossRef]
- Ren, J.; Eckert, H. Quantification of Short and Medium Range Order in Mixed Network Former Glasses of the System GeO2−NaPO3: A Combined NMR and X-Ray Photoelectron Spectroscopy Study. J. Phys. Chem. C, 2012; 116, 12747–12763. [Google Scholar] [CrossRef]
- Di Martino, D.; Santos, L.F.; Marques, A.C.; Almeida, R.M. Vibrational Spectra and Structure of Alkali Germanate Glasses. J. Non-Cryst. Solids, 2001; 293, 394–401. [Google Scholar] [CrossRef]
- Chakraborty, I.N.; Condrate, R.A. The Vibrational Spectra of B2O3-GeO2 Glasses. J. Non-Cryst. Solids, 1986; 81, 271–284. [Google Scholar] [CrossRef]
- Meera, B. N.; Sood, A. K.; Chandrabhas, N.; Ramakrishna, J. Raman study of lead borate glasses. J. Non-Cryst. Solids, 1990; 126, 224–230. [Google Scholar] [CrossRef]
- Yano, T.; Kunimine, N.; Shibata, S.; Yamane, M. Structural Investigation of Sodium Borate Glasses and Melts by Raman Spectroscopy. II. Conversion between BO4 and BO2O− Units at High Temperature. J. Non-Cryst. Solids, 2003; 321, 147–156. [Google Scholar] [CrossRef]
- Koroleva, O.N.; Shtenberg, M.V.; Zainullina, R.T.; Lebedeva, S.M.; Nevolina, L.A. Vibrational Spectroscopy and Density of K2O−B2O3−GeO2 Glasses with Variable B/Ge Ratio. Phys. Chem. Chem. Phys, 2019; 21, 12676–12684. [Google Scholar] [CrossRef]
- Yiannopoulos, Y.D.; Chryssikos, G.D.; Kamitsos, E.I. Structure and properties of alkaline earth borate glasses. Phys. Сhem. glasses, 2001; 42, 164–172. [Google Scholar]
- Knoblochova, K.; Ticha, H.; Schwarz, J.; Tichy, L. Raman spectra and optical properties of selected Bi2O3–PbO–B2O3–GeO2 glasses. Opt. Mater. 2009, 31, 895–898. [Google Scholar] [CrossRef]
- Henderson, G.S.; Wang, H.M. Germanium coordination and the germanate anomaly. Eur. J. of Mineral. 2002, 14, 733–744. [Google Scholar] [CrossRef]
- Kamitsos, E.I.; Yiannopoulos, Y.D.; Karakassides, M.A.; Chryssikos, G.D.; Jain, H. Raman and infrared structural investigation of xRb2O·(1-x)GeO2 glasses. J. Phys. Chem. 1996, 100, 11755–11765. [Google Scholar] [CrossRef]
- Fan, H.; Gao, G.; Wang, G.; Hu, L. Infrared, Raman and XPS spectroscopic studies of Bi2O3–B2O3–GeO2 glasses. Solid State Sci. 2010, 12, 541–545. [Google Scholar] [CrossRef]
- Błaszczak, K.; Adamczyk, A.; Wędzikowska, M.; Rokita, M. Infrared studies of devitrification Li2O·B2O3·2GeO2 glass. J. Mol. Struct, 2004; 704, 275–279. [Google Scholar] [CrossRef]
- Taqiullah, S. M.; Alshahrani, T.; Shariq, M.; Hakami, J.; Ahmad, N.; Alshehri, A. M.; Chaudhary, A.A.; Khan, S.M.; Shinde, S.M.; Slimani, Y.; Ansari, A.R.; Siddiqui, M.A.; Imran, M.; Khan, F. Utilization of infrared, Raman spectroscopy for structural analysis of alkali boro-germanate glasses. J. Taibah Univ. Sci. 2022, 16, 820–827. [Google Scholar] [CrossRef]
- Bolundut, L.; Pop, L.; Bosca, M.; Borodi, G.; Olar, L.; Suciu, R.C.; Pascuta, P.; Culea, E.; Stefan, R. Structural and spectroscopic properties of some neodymium-boro-germanate glasses and glass ceramics embedded with silver nanoparticles. Cer. Int. 2017, 43, 12232–12238. [Google Scholar] [CrossRef]
- Morassuti, C.Y.; Nunes, L.A.; Lima, S.M.; Andrade, L.H. Eu3+-doped alumino-phosphate glass for ratiometric thermometer based on the excited state absorption. J. Lumin. 2018, 193, 39–43. [Google Scholar] [CrossRef]
- Wantana, N.; Kaewjaeng, S.; Kothan, S.; Kim, H.J.; Kaewkhao, J. Energy transfer from Gd3+ to Sm3+ and luminescence characteristics of CaO–Gd2O3–SiO2–B2O3 scintillating glasses. J. Lumin. 2017, 181, 382–386. [Google Scholar] [CrossRef]
- Meng, X.G.; Qiu, J.R.; Peng, M.Y.; Chen, D.P.; Zhao, Q.Z.; Jiang, X.W.; Zhu, C.S. Near infrared broadband emission of bismuth-doped aluminophosphate glass. J. Opt. Express. 2005, 13, 1635–1642. [Google Scholar] [CrossRef] [PubMed]
- Jaiswal, V. V.; Bishnoi, S.; Swati, G.; Singh, P.; Lohia, N.; Bathula, S.; Haranath, D. Luminescence properties of yttrium gadolinium orthovanadate nanophosphors and efficient energy transfer from VO43− to Sm3+ via Gd3+ ions. Arabian Journal of Chemistry. 2020, 13, 474–480. [Google Scholar] [CrossRef]
- Kaczkan, M.; Boruc, Z.; Turczyński, S.; Malinowski, M. Effect of temperature on the luminescence of Sm3+ ions in YAM crystals. J. Alloys Compd. 2014, 612, 149–153. [Google Scholar] [CrossRef]
- Pritula, I.; Gayvoronsky, V.; Gromov, Y.; Kopylovsky, M.; Kolybaeva, M.; Puzikov, V.; Kosinova, A.; Savvin, Y.; Velikhov, Y.; Levchenko, A. Linear and nonlinear optical properties of dye-doped KDP crystals: Effect of thermal treatment. Opt. 2009; 15, 1141–1147. [Google Scholar] [CrossRef]
- Padlyak, B.; Ryba-Romanowski, W.; Lisiecki, R.; Adamiv, V.; Burak, Y.; Teslyuk, I.; Banaszak-Piechowska, A. Optical spectra and luminescence kinetics of the Sm3+ and Yb3+ centres in the lithium tetraborate glasses. Optica Applicata. 2010, 2, 427–438. [Google Scholar]
- Kirdsiri, K.; Raja Ramakrishna, R.; Damdee, B.; Kim, H. J.; Kaewjaeng, S.; Kothan, S.; Kaewkhao, J. Investigations of optical and luminescence features of Sm3+ doped Li2O-MO-B2O3 (M =Mg/Ca/Sr/Ba) glasses mixed with different modifier oxides as an orange light emitting phosphor for WLED’s. Journal of Alloys and Compounds. 2018, 749, 197–204. [Google Scholar] [CrossRef]
- Khan, I.; Rooh, G.; Rajaramakrishna, R.; Sirsittipokakun, N.; Kim, H. J.; Ruangtaweep, Y.; Kaewkhao, J. Spectroscopy Study of Sm3+ Doped Fluorosilicate Glasses for Orange Emission Solid-State Device Application. Glass Physics and Chemistry. 2019, 45, 447–458. [Google Scholar] [CrossRef]
- Ivanova, A.A.; Gontcharenko, V.E.; Lunev, A.M.; Sidoruk, A.V.; Arkhipov, I.A.; Taydakov, I.V.; Belousov, Y.A. New Carboxylate Anionic Sm-MOF: Synthesis, Structure and Effect of the Isomorphic Substitution of Sm3+ with Gd3+ and Tb3+ Ions on the Luminescent Properties. Inorganics, 2022, 10, 104. [Google Scholar] [CrossRef]
| Sample ID /Notation | Glass composition (mol.%) | Sample ID /Notation | Glass composition (mol.%) |
|---|---|---|---|
|
(12.75)Pb(1.5)Sm (0.75)Gd-42.5 |
42.5B2O3–42.5GeO2–12.75PbO–1.5Sm2O3–0.75Gd2O3 |
(12.75)Bi(1.5)Sm (0.75)Gd-42.5 |
42.5B2O3–42.5GeO2–12.75Bi2O3–1.5Sm2O3–0.75Gd2O3 |
|
(12)Pb (1.875)Sm (1.125)Gd-42.5 |
42.5B2O3–42.5GeO2–12PbO–1.875Sm2O3–1.125Gd2O3 |
(12)Bi(1.875)Sm (1.125)Gd-42.5 |
42.5B2O3–42.5GeO2–12Bi2O3–1.875Sm2O3–1.125Gd2O3 |
|
(11.25)Pb (2.25)Sm (1.5)Gd-42.5 |
42.5B2O3–42.5GeO2–11.25PbO–2.25Sm2O3–1.5Gd2O3 |
(11.25)Bi(2.25)Sm (1.5)Gd-42.5 |
42.5B2O3–42.5GeO2–11.25Bi2O3–2.25Sm2O3–1.5Gd2O3 |
|
(17)Pb(2.0)Sm (1.0)Gd-40 |
40B2O3–40GeO2–17PbO– 2Sm2O3–1Gd2O3 |
(17)Bi(2.0)Sm (1.0)Gd-40 |
40B2O3–40GeO2–17Bi2O3– 2Sm2O3–1Gd2O3 |
|
(16)Pb(2.5)Sm (1.5)Gd-40 |
40B2O3–40GeO2–16PbO– 2.5Sm2O3–1.5Gd2O3 |
(16)Bi(2.5)Sm (1.5)Gd-40 |
40B2O3–40GeO2–16Bi2O3– 2.5Sm2O3–1.5Gd2O3 |
|
(15)Pb(3.0)Sm (2.0)Gd-40 |
40B2O3–40GeO2–15PbO– 3Sm2O3–2Gd2O3 |
(15)Bi(3.0)Sm (2.0)Gd-40 |
40B2O3–40GeO2–15Bi2O3– 3Sm2O3–2Gd2O3 |
| Sample ID | Tg (K) | Sample ID | Tg (K) |
|---|---|---|---|
| (12.75)Pb(1.5)Sm(0.75)Gd-42.5 | 768 | (12.75)Bi(1.5)Sm(0.75)Gd-42.5 | 772 |
| (12)Pb(1.875)Sm(1.125)Gd-42.5 | 778 | (12)Bi(1.875)Sm(1.125)Gd-42.5 | 795 |
| (11.25)Pb(2.25)Sm(1.5)Gd-42.5 | 806 | (11.25)Bi(2.25)Sm(1.5)Gd-42.5 | 802 |
| (17)Pb(2.0)Sm(1.0)Gd-40 | 782 | (17)Bi(2.0)Sm(1.0)Gd-40 | 796 |
| (16)Pb(2.5)Sm(1.5)Gd-40 | 797 | (16)Bi(2.5)Sm(1.5)Gd-40 | 804 |
| (15)Pb(3.0)Sm(2.0)Gd-40 | 824 | (15)Bi(3.0)Sm(2.0)Gd-40 | 810 |
| Sample ID | Density (g/cm3) |
Refractive index at 589 nm |
Sample ID | Density (g/cm3) |
Refractive index at 589 nm |
|---|---|---|---|---|---|
| (12.75)Pb(1.5)Sm(0.75)Gd-42.5 | 4.060 | 1.68 | (12.75)Bi(1.5)Sm(0.75)Gd-42.5 | 4.655 | 1.78 |
| (12)Pb(1.875)Sm(1.125)Gd-42.5 | 4.030 | 1.68 | (12)Bi(1.875)Sm(1.125)Gd-42.5 | 4.630 | 1.77 |
| (11.25)Pb(2.25)Sm(1.5)Gd-42.5 | 4.015 | 1.68 | (11.25)Bi(2.25)Sm(1.5)Gd-42.5 | 4.600 | 1.76 |
| (17)Pb(2.0)Sm(1.0)Gd-40 | 4.390 | 1.72 | (17)Bi(2.0)Sm(1.0)Gd-40 | 5.060 | 1.82 |
| (16)Pb(2.5)Sm(1.5)Gd-40 | 4.370 | 1.72 | (16)Bi(2.5)Sm(1.5)Gd-40 | 5.010 | 1.80 |
| (15)Pb(3.0)Sm(2.0)Gd-40 | 4.270 | 1.72 | (15)Bi(3.0)Sm(2.0)Gd-40 | 4.990 | 1.78 |
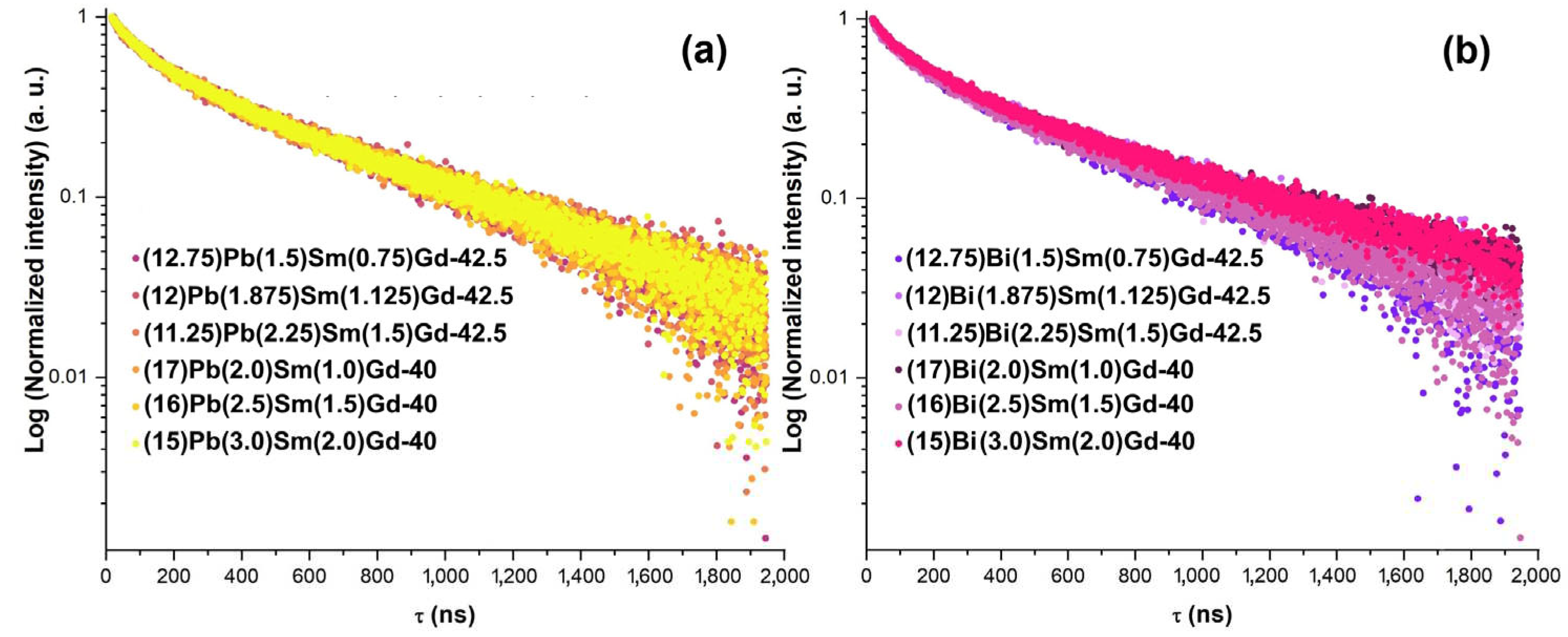
| Sample ID | τ1, (ns) | τ2, (ns) | Sample ID | τ1, (ns) | τ2, (ns) |
|---|---|---|---|---|---|
| (12.75)Pb(1.5)Sm(0.75)Gd-42.5 | 95.3 ± 1.9 | 608.8 ± 7.9 | (12.75)Bi(1.5)Sm(0.75)Gd-42.5 | 101.6 ± 2.2 | 609.0 ± 8.6 |
| (12)Pb(1.875)Sm(1.125)Gd-42.5 | 98.7 ± 2.0 | 618.7 ± 8.7 | (12)Bi(1.875)Sm(1.125)Gd-42.5 | 99.9 ± 2.1 | 619.7 ± 8.9 |
| (11.25)Pb(2.25)Sm(1.5)Gd-42.5 | 97.9 ± 2.2 | 604.6 ± 8.8 | (11.25)Bi(2.25)Sm(1.5)Gd-42.5 | 95.6 ± 1.9 | 586.0 ± 7.4 |
| (17)Pb(2.0)Sm(1.0)Gd-40 | 100.4 ± 2.0 | 616.4 ± 8.5 | (17)Bi(2.0)Sm(1.0)Gd-40 | 99.8 ± 2.1 | 617.7 ± 8.7 |
| (16)Pb(2.5)Sm(1.5)Gd-40 | 93.4 ± 2.3 | 600.6 ± 8.8 | (16)Bi(2.5)Sm(1.5)Gd-40 | 97.0 ± 2.2 | 623.4 ± 9.4 |
| (15)Pb(3.0)Sm(2.0)Gd-40 | 96.9 ± 2.3 | 604.5 ± 7.9 | (15)Bi(3.0)Sm(2.0)Gd-40 | 96.9 ± 2.1 | 602.7 ± 8.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





