A Sub-1-V Nanopower MOS-Only Voltage Reference

Preprint

Article

A Sub-1-V Nanopower MOS-Only Voltage Reference

Altmetrics

Downloads

108

Views

Comments

A peer-reviewed article of this preprint also exists.

Siqi Wang

Zhenghao Lu^*,Kunpeng Xu,Hongguang Dai,Zhanxia Wu,

Xiaopeng Yu

Siqi Wang

Zhenghao Lu^*,Kunpeng Xu,Hongguang Dai,Zhanxia Wu,

Xiaopeng Yu

This version is not peer-reviewed

Submitted:

30 December 2023

Posted:

30 December 2023

You are already at the latest version

Alerts

Abstract

A novel low-power MOS-only voltage reference is presented. The Enz-Krummenacher-Vittoz (EKV) model is adopted to provide a new perspective on the operating principle. The normalized charge density, introduced as a new variable, serves as an indicator when trimming the output temperature coefficient. The proposed voltage reference consists of a specific current generator and a 5-bit trimmable load. Thanks to the well-match between the current source stage and the output stage, the non-linear temperature dependence of carrier mobility is automatically canceled out. The circuit is designed in 55 nm COMS technology. The operating temperature ranges from -40 ∘C to 120 ∘C. The average temperature coefficient of the output voltage can be reduced to 21.7 ppm/∘C by trimming. The power consumption is only 23.2 nW with a supply voltage of 0.8 V. The line sensitivity and the power supply rejection ratio at 100 Hz are 0.011 %/V and -89 dB respectively.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

The low-power voltage reference is an essential circuit block in power-limited applications, such as the Internet of Things (IoT), portable devices, and biological interfaces. [1,2,3,4,5], As a constant reference quantity for the circuit system, the robustness and insensitivity of its output bring crucial impacts on the performance of the system. The voltage reference in such applications aims to keep a stable and constant output in any process, voltage, and temperature (PVT) with minimal power.

Currently, voltage reference sources can be roughly sorted into three categories: bipolar (BJT) references, CMOS references, and hybrid references. The traditional bipolar bandgap references (BGR) generate an output voltage of about 1.2 V (

V_{B G}

), which is relatively consistent among different process technologies. Despite that BGR has little process variation, it requires a supply voltage higher than 1 V [6,7,8]. This is not suitable for most low-power applications and is not available in some advanced technology nodes. Furthermore, the temperature coefficient (TC) of the conventional first-order BGR is relatively large. Meanwhile, high-order compensation technology inevitably makes the circuit topology more complex.

To realize a voltage reference operating with a sub-1-V supply, the latter two references have been developed [9,10,11,12,13]. The CMOS references are generally based on the temperature characteristics of the threshold voltage (

V_{T}

). The

V_{T}

based references (VTR) utilize the exponential relationship of MOS transistors biased in the subthreshold region to take the place of BJTs. The output voltage of VTRs usually is equal to the extrapolated value of the threshold voltage, thus allowing the lower supply voltage. Unfortunately, the process variation of its output voltage is larger compared to that of BGR. Some VTRs also need resistors to generate a controllable voltage proportional to the absolute temperature (PTAT). [14,15,16] Because the current is limited to very small, it can be seen that the resistor not only costs more mask layers in manufacturing but also occupies more chip area. In addition, some designs associate the different types of transistors [4,17,18], generating an output proportional to the difference of two threshold values (

V_{T 1} - V_{T 2}

). Although this technique can significantly reduce the supply voltage, it also requires the use of more masks and increases the process variations.

Recently, some works combined the principles of VTR and BGR, creating a hybrid voltage reference. [19,20,21] The hybrid reference generates a nominal value of

V_{B G} - V_{T}

with process dependence compensated by a dimension-induced side-effect. However, reducing the minimum supply voltage of the hybrid reference is challenging because of the fixed voltage drop between the base and emitter.

Based on the analyses above, we present a new VTR that only consists of one type of MOS transistor. A novel current source is proposed and discussed by a new approach. A simple trimming method is also adopted to further reduce the TC. The paper is organized as follows. Section 2 reviews the basic EKV model, and introduces it into the explanation of the principle of

V_{T}

based voltage reference. Section 3 presents the design of the proposed circuit and shows the detailed design considerations of each part. Section 4 gives the simulated results and the comparison with other works that have been reported in recent years. Section 5 concludes the paper.

2. Principle of MOS-only voltage reference

2.1. EKV Model

Before we look into the Enz-Krummenacher-Vittoz (EKV) model, it is admirable to revisit the conventional square-law model, which is widely adopted in textbooks. The drain current equation

I_{D}

of the square-law model is:

I_{D} = μ C_{ox} \frac{W}{L} [(V_{GS} - V_{TH}) V_{DS} - \frac{1}{2} V_{DS}^{2}],

(1)

where

μ

is the carrier mobility,

C_{o x}

is the gate oxide capacitance of unit area, W is the width of the MOS transistor, L is the length of the MOS transistor,

V_{G S}

and

V_{D S}

are respectively the gate and drain voltage referred to the source terminal. It is important to note that, to distinguish it from

V_{T}

V_{T H}

is the threshold voltage with respect to the source. It can be seen from Equation 1 that the thermal voltage

U_{T}

is not taken into account, which leads to the poor coherence between the equation and simulation in temperature-dependent performance. As a circuit module that is highly concerned with temperature characteristics, when designing and analyzing the voltage reference, the model should include a comprehensive representation of temperature characteristics. Thus we introduce the Enz-Krummenacher-Vittoz (EKV) model to explain and optimize the proposed voltage reference circuit.

The EKV model is a charge-based compact model proposed by Enz, Krummenacher, and Vittoz in Switzerland in 1995 [22]. The starting point of this model was to establish a single equation that could adapt to all inversion regions [23,24,25,26]. The drain current

I_{D}

of the EKV model is expressed through the normalized drain current i [27,28]:

i = \frac{I_{D}}{I_{S}},

(2)

where

I_{S}

is the specific current defined as:

I_{S} = 2 n {U_{T}}^{2} μ C_{o x} \frac{W}{L} = 2 n {U_{T}}^{2} μ C_{o x} K .

(3)

Here, n is the subthreshold slope factor of the MOS transistor, which varies between 1.3 and 2, depending on the process technology. K is called the aspect ratio.

The basic EKV model introduces a new variable

q_{x}

, called normalized mobile charge density, to value the amount of charge density at the location x along the channel. The normalized mobile charge density can be calculated from the non-equilibrium voltage

V_{x}

along the channel as:

V_{P} - V_{x} = U_{T} [2 (q_{x} - 1) + ln (q_{x})],

(4)

V_{P} = \frac{V_{G} - V_{T}}{n},

(5)

where

V_{T}

and

V_{G}

are the bulk-referenced threshold voltage and gate voltage respectively. and

V_{P}

is defined as the pinch-off voltage. The Equation 4 represents the relationship between the

V_{x}

and

q_{x}

at the location x. We can replace the subscript of x with S or D to obtain the charge density at the source or drain terminal. When we obtain the

q_{S}

and

q_{D}

based on the source and drain voltage, the normalized drain current of the transistor i can be derived as:

i = (q_{S}^{2} + q_{S}) - (q_{D}^{2} + q_{D}) .

(6)

On the right side of Equation 6, the square term

q^{2}

represents drift current, which is proportional to the surface potential strength. The linear term q represents diffusion current, which is proportional to the mobile charge density gradient. The part inside the first bracket is called forward current, and the part inside the second bracket is called reverse current. The Equation 6 is applicable to both saturated and non-saturated transistors. However, for saturated transistors, where the

V_{D}

is greater than the pinch-off voltage

V_{P}

, the current contributed by the second bracket can be neglected.

Above is the basic equation of the EKV model. It is admirable that the EKV model provides predictions of MOSFET behavior across all operating regions, including weak inversion, moderate inversion, and strong inversion. In addition, q not only represents the normalized charge density but also can serve as an index of channel inversion level. When q << 1, that is, q >

q^{2}

, the diffusion current is dominant. At this point, the channel is in weak inversion (WI). Similarly, q >> 1, the channel is in strong inversion (SI). When q = 1, the drift current is equal to the diffusion current, and the channel is in moderate inversion (MI).

2.2. MOS-only voltage reference operation principle

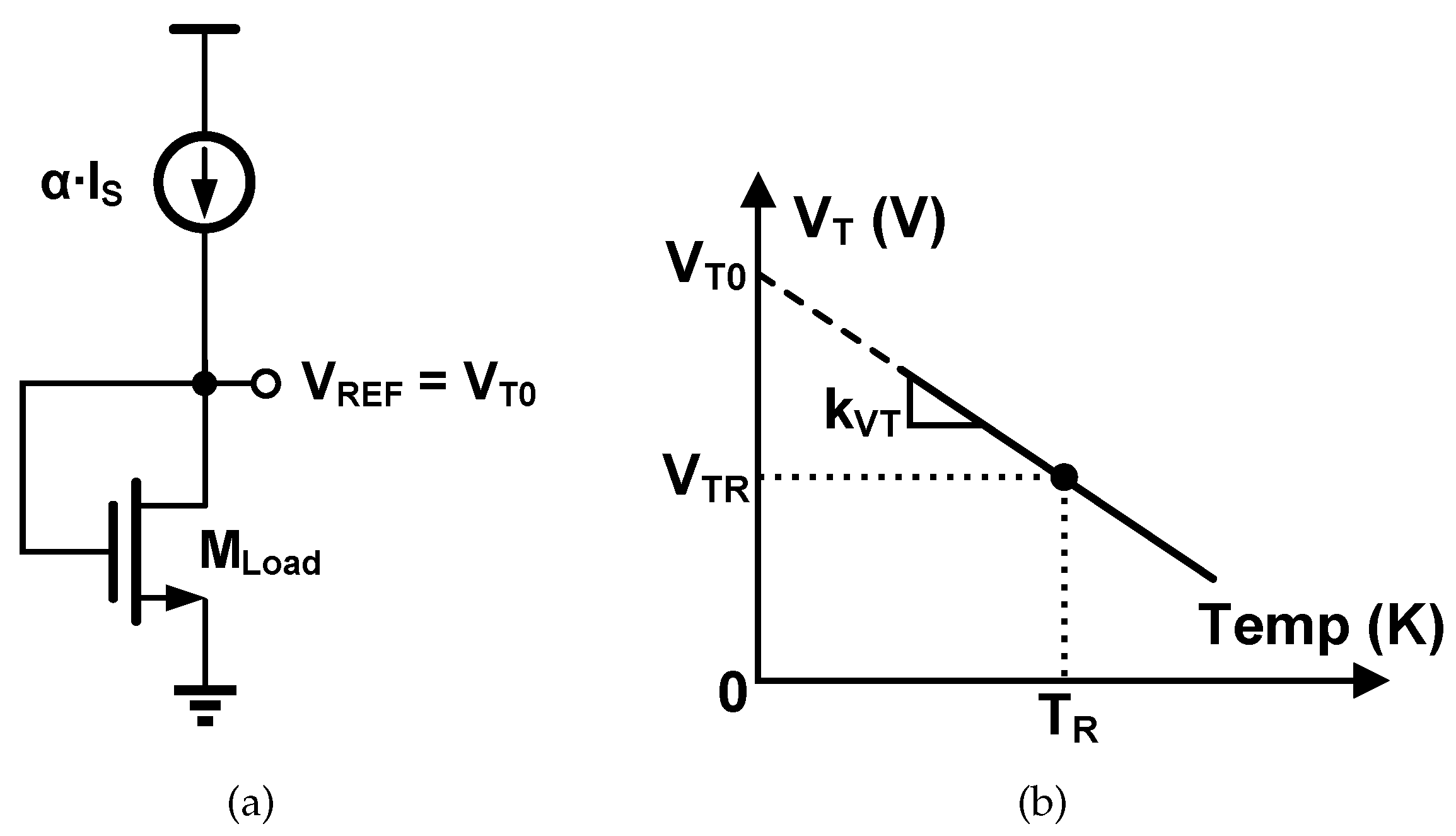
The basic principle of

V_{T}

based voltage reference is to bias a diode-connected MOSFET with a definite current that varies with temperature. The conceptual diagram is shown in Figure 1(a), and the following text details the analysis of how to determine the magnitude and the temperature dependence of this current.

As shown in Figure 1(b), the threshold voltage

V_{T}

is complementary to the absolute temperature (CTAT) with good linearity. Thus its temperature dependence can be represented by a linear function:

V_{T} = V_{T 0} - k_{V T} T,

(7)

where

k_{V T}

is the temperature coefficient (positive value), and

V_{T 0}

is the intersection when the line is extrapolated to absolute zero temperature.

According to the Equation 4 and 5, the gate voltage for a source grounded MOSFET can be expressed as:

V_{G} = n U_{T} [2 (q_{S} - 1) + ln (q_{S})] + V_{T}

(8)

The first term of Equation 8 is PTAT, and the second term is CTAT. In other words, to make the gate voltage a temperature-independent quantity

V_{R E F}

, the temperature coefficients of the two terms must complement each other.

\frac{n k_{b}}{e_{0}} [2 (q_{S} - 1) + ln (q_{S})] = k_{V T},

(9)

where

k_{b}

is the Boltzmann constant,

e_{0}

is the elementary charge. Unfortunately, Equation 9 does not have an analytical solution, but we can use the function

ω (x)

to represent the solution of the equation

y + ln (y) = x

ω (x)

can be found in the Symbolic Math Toolbox of MATLAB as a mathematical function

w r i g h t O m e g a

. Therefore,

q_{S}

can be expressed as:

q_{S} = \frac{1}{2} ω (\frac{k_{V T}}{k_{b} / e_{0}} + 2 + ln 2) .

(10)

Assuming the transistor is saturated, eliminate the reverse current, by combining Equations 2, 6 and 10, it can be determined that the required bias current is:

I_{D} = I_{S} \cdot \frac{1}{4} ω^{2} (\frac{k_{V T}}{k_{b} / e_{0}} + 2 + ln 2) = α I_{S},

(11)

where

α

is dimensionless constant. At this bias current, the gate voltage of the diode-connected transistor

M_{L o a d}

is equal to

V_{T 0}

. It should be noticed that the drain voltage of

M_{L o a d}

is also

V_{T 0}

, thus the assumption of saturation holds.

Through the analysis above, we can see that the key of

V_{T}

based voltage reference is to generate a current exactly proportional to the specific current

I_{S}

of the load transistor. It’s worth noting that when

q_{S}

deviates from our expected value, the right side of Equation8 introduces a temperature-dependent term. In other words, the target bias current biases the load transistor to a constant inversion level. Interestingly, the temperature characteristic of carrier mobility doesn’t appear in the analysis above. This is because as long as the bias current is proportional to the specific current, the non-linear temperature dependence of

μ

is automatically canceled out.

3. Circuit design

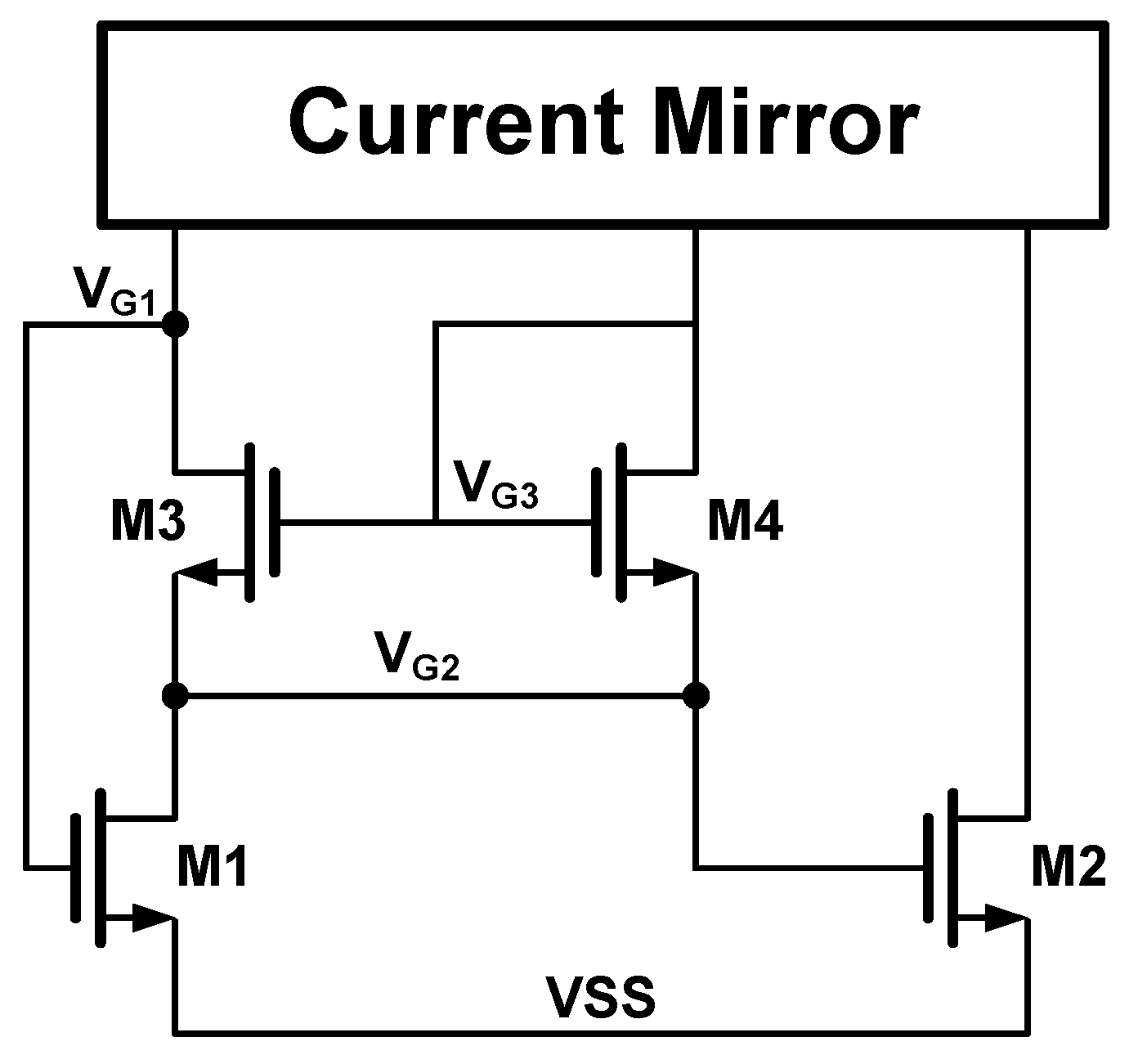
3.1. Proposed specific current source

Just as we concluded in Section 2.2, the key of the

V_{T}

based voltage reference is to design a specific current source. The core circuit of the proposed specific current source is shown in Figure 2. The devices in the circuit determining the current are

M_{1} - M_{4}

. To ensure the current generated matches the load transistor

M_{L o a d}

, the unit size of

M_{1} - M_{4}

is equal to the size of

M_{L o a d}

. In other words, to avoid

V_{T}

mismatch caused by inconsistent channel lengths, all NMOS transistors have identical unit sizes to eliminate the impact of second-order effects. In addition, the bulk terminals of all NMOS are connected to

V S S

The current mirror in the upper of Figure 2 could be replaced by either a simple PMOS current mirror or a cascoded one. For ease of explaining its operating principle, we assume that the current ratios of these three branches are equal. Thus the drain currents of

M_{1} - M_{4}

can be expressed as:

\frac{1}{2} i_{1} I_{S 1} = i_{2} I_{S 2} = i_{3} I_{S 3} = i_{4} I_{S 4} = I_{R} .

(12)

For each transistor, we can use Equation 4 and 6 to sequentially derive out the following relationships:

\begin{matrix} M_{1} : \{\begin{matrix} V_{P 1} = U_{T} [- 2 + ln (q_{S 1})] = \frac{V_{G 1} - V_{T}}{n} \\ i_{1} = q_{S 1} = \frac{2 I_{R}}{I_{S 1}} \end{matrix}; \end{matrix}

(13)

\begin{matrix} M_{2} : \{\begin{matrix} V_{P 2} = U_{T} [- 2 + ln (q_{S 2})] = \frac{V_{G 2} - V_{T}}{n} \\ i_{2} = q_{S 2} = \frac{I_{R}}{I_{S 2}} \end{matrix}; \end{matrix}

(14)

\begin{matrix} M_{3} : \{\begin{matrix} V_{P 3} - V_{G 2} = U_{T} [2 (q_{S 3} - 1)] \\ V_{P 3} - V_{G 1} = U_{T} [2 (q_{D 3} - 1)] \\ i_{3} = q_{S 3}^{2} - q_{D 3}^{2} = \frac{I_{R}}{I_{S 3}} \end{matrix}; \end{matrix}

(15)

\begin{matrix} M_{4} : \{\begin{matrix} V_{P 4} - V_{G 2} = U_{T} [2 (q_{S 4} - 1)] \\ i_{4} = q_{S 4}^{2} = \frac{I_{R}}{I_{S 4}} \end{matrix} . \end{matrix}

(16)

The equations listed above have been simplified based on the proper assumptions as follows: (i) The sizes of

M_{1}

and

M_{2}

are set large enough, thus, the

q_{1, 2} = I_{D 1, 2} / I_{S 1, 2} ≪ 1

. (ii) The sizes of

M_{3}

and

M_{4}

are set small enough, thus, the

q_{3, 4} = I_{D 3, 4} / I_{S 3, 4} ≫ 1

. Simply speaking,

M_{1, 2}

are in weak inversion level, and

M_{3, 4}

are in strong inversion level. By combining Equation 13 and Equation 14, we have:

V_{G 1} - V_{G 2} = n U_{T} ln (\frac{2 I_{S 2}}{I_{S 1}}) .

(17)

Since

V_{P 3}

is equal to

V_{P 4}

, we can easily determine that

q_{S 3}

and

q_{S 4}

are equal. When we take the difference of the first two rows of Equation 15, we can get another relationship of

V_{G 1}

and

V_{G 2}

V_{G 1} - V_{G 2} = 2 U_{T} (q_{S 3} - q_{D 3}) .

(18)

The third row of Equation 15 can also be written as:

{q_{S 3}}^{2} - {q_{D 3}}^{2} = \frac{I_{R}}{I_{S 3}} = \frac{q_{S 4}^{2} \cdot I_{S 4}}{I_{S 3}} = \frac{q_{S 3}^{2} \cdot I_{S 4}}{I_{S 3}} .

(19)

By substituting Equation 17 into Equation 18, we will have a quadratic equation of

q_{S 3}

q_{S 3}^{2} - {(q_{S 3} - c_{1})}^{2} = q_{S 3}^{2} \cdot c_{2},

(20)

where

c_{1} = \frac{1}{2} n ln (2 I_{S 2} / I_{S 1})

, and

c_{2} = I_{S 4} / I_{S 3}

. Finally, we can obtain the solution of Equation 20, and the produced current can be expressed as:

q_{S 3} = \frac{c_{1}}{c_{2}} (1 + \sqrt{1 - c_{2}}) = q_{S 4},

(21)

I_{R} = q_{S 4}^{2} \cdot I_{S 4} = \frac{c_{1}^{2}}{c_{2}^{2}} {(1 + \sqrt{1 - c_{2}})}^{2} \cdot I_{S 4} .

(22)

The other root of Equation 20 is discarded, as it does not comply with the assumption made before that

q_{S 3, D 3} ≫ 1

. If we substitute

c_{1}

and

c_{2}

with the aspect ratios of

M_{1} - M_{4}

, Equation 22 can be rewritten as:

I_{R} = \frac{1}{2} μ U_{T}^{2} C_{o x} n^{3} {ln}^{2} (\frac{2 K_{2}}{K_{1}}) \cdot \frac{K_{3}^{2}}{K_{4}} {(1 + \sqrt{1 - \frac{K_{4}}{K_{3}}})}^{2} .

(23)

Therefore, the current of each branch is proportional to the specific current. The temperature characteristic of

I_{R}

also follows the characteristic of the unit transistor.

3.2. Loop stability

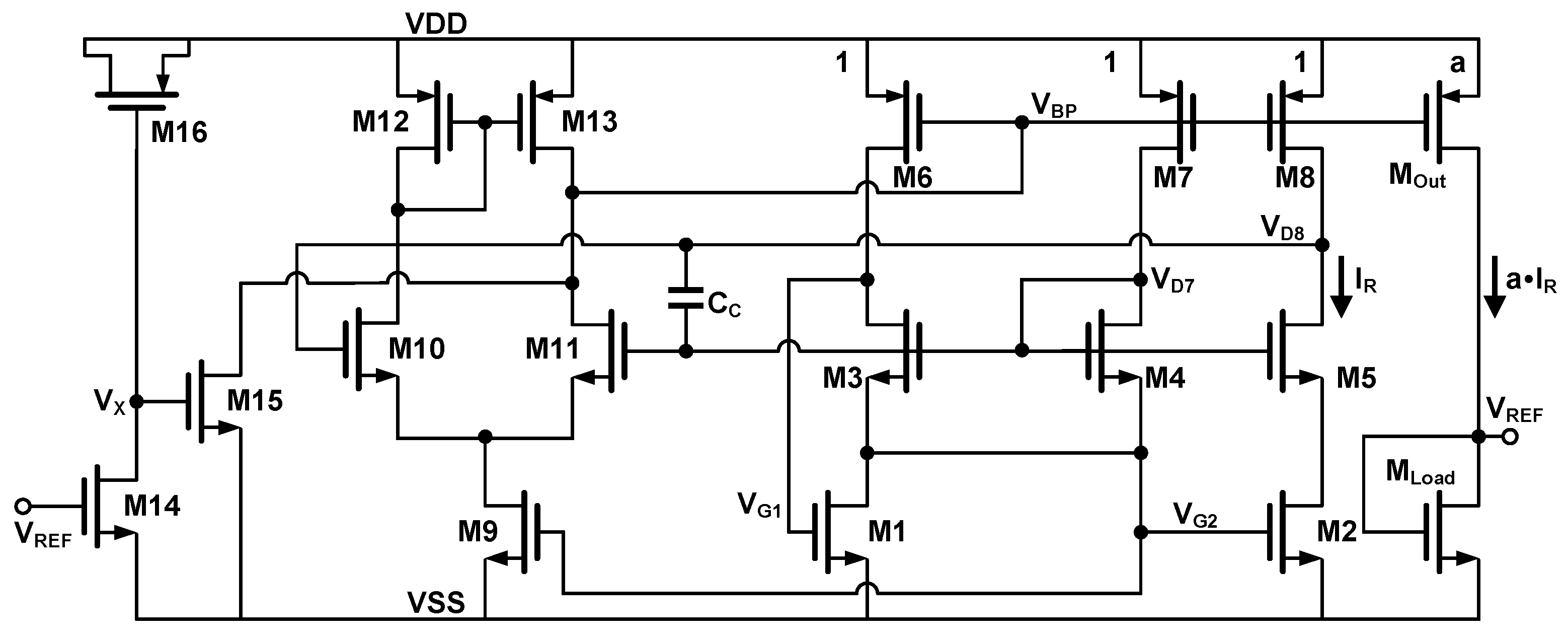
The complete schematic of the proposed voltage reference is given in Figure 3. A cascode transistor

M_{5}

is added to mitigate the difference of drain voltage between

M_{1}

and

M_{2}

. A differential amplifier is used to improve the accuracy of the current mirror and reduce the line sensitivity. While the amplifier enhances the loop gain, at the same time, the stability of the loop needs to be carefully analyzed. Thus, to prevent the parasitic oscillation of the circuit, a compensation capacitor

C_{C}

is added.

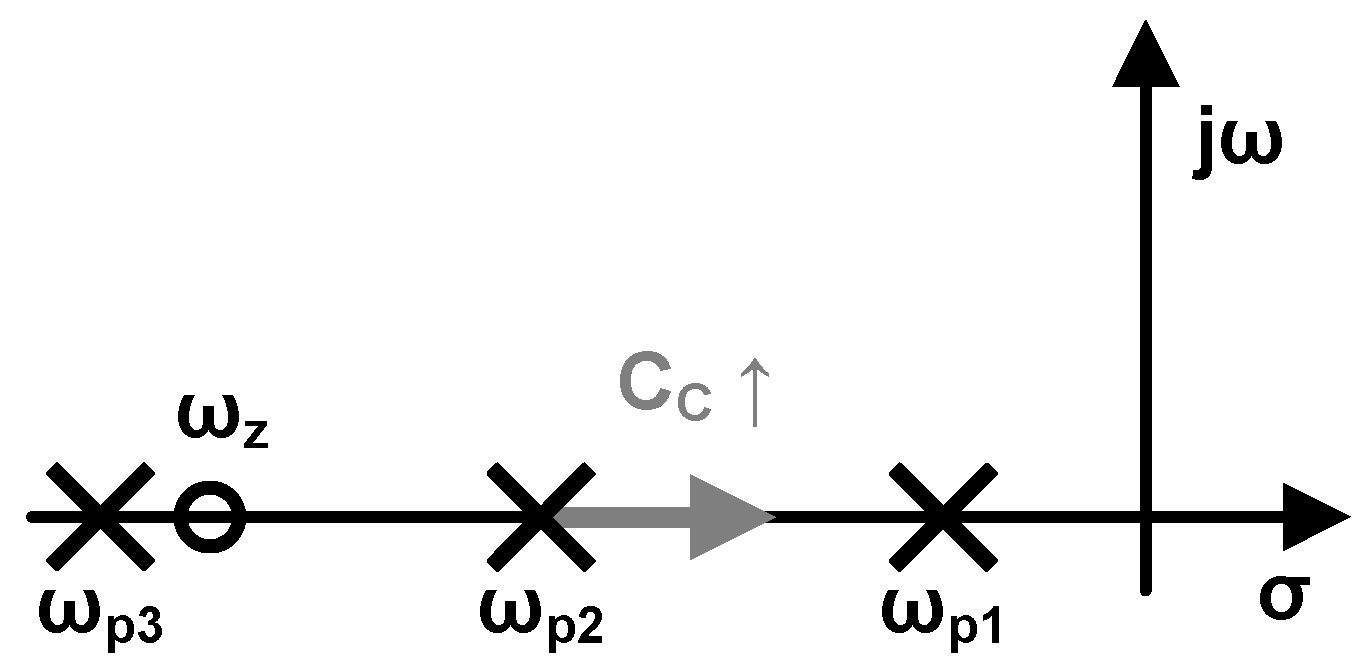
The proposed specific current source contains three branches, and both positive feedback and negative feedback exist in the loop. So the expression of the total loop gain is quite complex. Based on reasonable simplifications and comparison with simulation, the frequency response of the loop gain can be expressed as:

L G (s) = \frac{K (s - w_{z})}{(s - w_{p 1}) (s - w_{p 2}) (s - w_{p 3})},

(24)

where

\begin{matrix} w_{z} & = - \frac{g_{m 1}}{C_{g s 2}}; \\ w_{p 1} & = w_{o t a} = - \frac{g_{o t a}}{C_{o t a}}; \\ w_{p 2} & = - \frac{g_{d s p}}{C_{c} (1 + \frac{g_{m 2}}{g_{m 1}} + \frac{g_{m 2} g_{m 3}}{g_{m 4} g_{d s 3}})}; \\ w_{p 3} & = - \frac{g_{m 2}}{C_{g s 2}} \cdot (1 + \frac{g_{m 1}}{g_{m 2}} + \frac{g_{m 1}}{g_{d s 3}}); \\ L G (0) & = - \frac{g_{m p}}{g_{d s p}} \cdot \frac{g_{m 2}}{g_{d s 3}} \cdot (1 - \frac{g_{m_{3}}}{g_{m_{4}}}) \cdot \frac{g_{m o t a}}{g_{o t a}} . \end{matrix}

(25)

L G (0)

is the DC gain of the loop.

g_{o t a}

and

C_{o t a}

denote the conductance and capacitance at the output node of the amplifier. The loop gain contains one negative zero and three negative poles.

w_{p 1}

and

w_{p 2}

are much smaller than

w_{p 3}

, contributing a phase shift of

- 180^{\circ}

. Given that the current in

M_{1}

is twice that of

M_{2}

g_{m 1} / g_{m 2}

is approximately equal to 2. Hence,

w_{p 3}

is larger than the zero

w_{z}

, causing the phase to increase by

90^{\circ}

and then decrease by

90^{\circ}

. The distribution of the loop’s poles and zero is shown in Figure 4. As the compensating capacitance

C_{C}

increases,

w_{p 2}

moves towards the origin. By carefully locating two poles,

w_{p 1 - 2}

, it is possible to retain enough phase margin. The detailed stability results will be presented in the section on simulation results.

3.3. Output stage

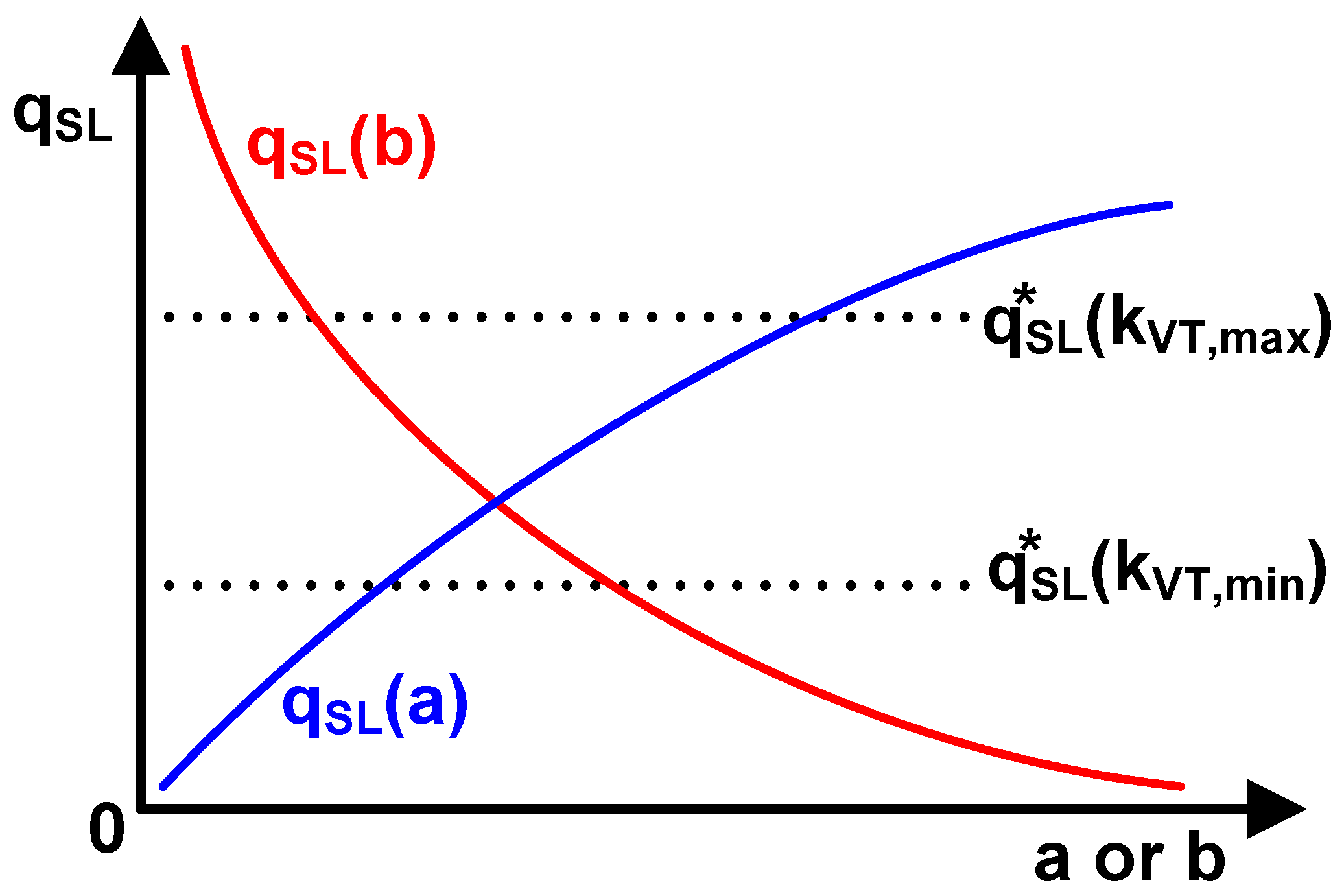
After generating the required current

I_{R}

, we can copy it into the load transistor with a certain proportion and obtain a reference voltage approximately equal to

V_{T 0}

. Due to the variation of

V_{T}

and its temperature coefficient during the actual manufacturing, it is necessary to perform trimming in the output branch. As follows, two methods of trimming will be presented. (i) Trimming the multiplier of

M_{L o a d}

; (ii) Trimming the copy ratio of the current mirror.

If we suppose the copy ratio of the PMOS current mirror is

1 : a

, and the aspect ratio of the load transistor is

K_{L}

q_{S L} = \sqrt{\frac{a K_{4}}{K_{L}}} \cdot q_{s 4} = \frac{c_{1}}{c_{2}} (1 + \sqrt{1 - c_{2}}) \cdot \sqrt{\frac{a}{b}},

(26)

where

b = K_{L} / K_{4}

. According to Equation 10, the trimming range determined by the variables a and b must cover the variations in

k_{V T}

caused by the process corner. The effects of a and b on the normalized charge density of

M_{L o a d}

are shown in Figure 5. The dashed line represents the target charge density, where the temperature coefficient should be zero.

q_{S L}^{*} (k_{V T, m a x})

corresponds to the case of a relatively large

k_{V T}

, and similarly the

q_{S L}^{*} (k_{V T, m i n})

does. Hence, the intersection points of two dashed lines and

q_{S L} (a)

, or

q_{S L} (b)

, indicate the minimum trimming range.

3.4. Start-up circuit

When the power supply voltage is applied, all branches in the voltage reference may remain zero. Thus, a start-up circuit formed by

M_{14} - M_{16}

is adopted to assist the circuit escape from the zero-current state [29].

In the initial start-up stage, due to

V_{R E F}

being zero,

M_{14}

is turned off. Therefore, the ramp-up of VDD is coupled to node

V_{S T}

through the MOS capacitor

M_{16}

. Once the voltage of

V_{S T}

exceeds the threshold voltage of

M_{15}

, the node

V_{B P}

will be pulled down, hence the branch current rising. Meanwhile,

V_{R E F}

will also rise until it reaches the final steady state. When

V_{R E F}

becomes the desired value, approximately

V_{T 0}

M_{14}

is turned on, discharging the node

V_{S T}

to ground. Finally,

M_{15}

is turned off, disconnecting the start-up circuit from the core circuit.

4. Simulation Results

4.1. Temperature Dependence before trimming

As explained in Section 3.3, we can trim the temperature coefficient by adjusting the size of the load transistor or the current mirror ratio. It is preferred to take the method of trimming load, thus the consumption of the circuit can be constant. The total current consumption of the proposed voltage reference is proportional to the specific current of the unit NMOS transistor. According to Equation 3, the power of the circuit is approximately a PTAT quantity. At room temperature, the generated specific current

I_{R}

is 3.6 nA. As we set the output current ratio a equal to 3, the total current is approximately 8 times that of

I_{R}

, i.e., 29.0nA. Across the entire temperature range, the total current increases from 19.3 nA at -40

° C

to 41.2 nA at 120

° C

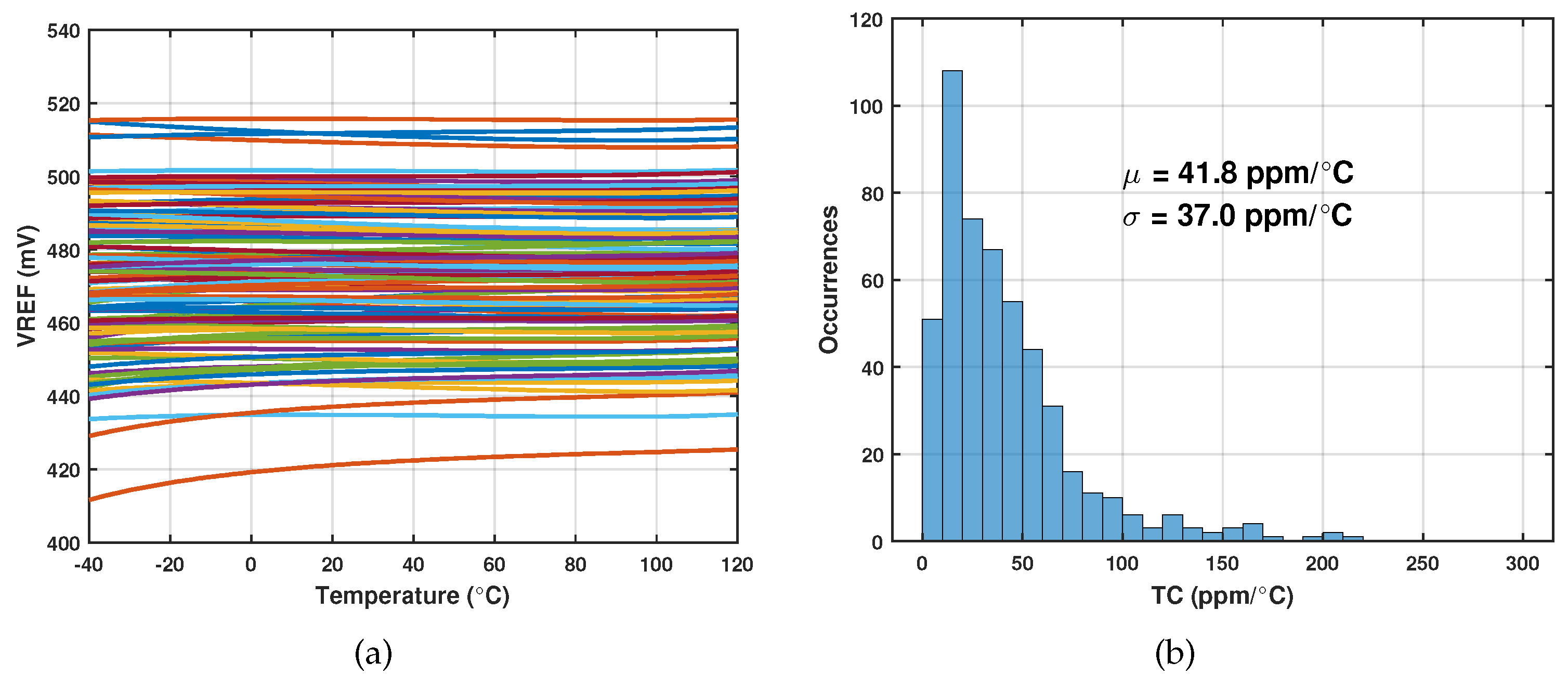
In order to determine the trimming range of the circuit, it is necessary to evaluate the temperature dependence before trimming. A Monte Carlo simulation of 500 samples is performed, sweeping the temperature from -40

° C

to 120

° C

. Both mismatch and corner variation are included in the model. To avoid making the figure too cluttered, only 100

V_{R E F}

curves are shown in Figure 6(a). Thanks to the fact that the specific current of

M_{L o a d}

is well-matched to the current generated, curves before trimming are relatively flat. The average value of

V_{R E F}

varies from 421 mV to 522 mV. Figure 6(b) shows the TC histogram of 500 samples. The mean of TC is about 41.8

p p m /^{\circ} C

, and the standard deviation is about 37.0

p p m /^{\circ} C

. The statistical distribution indicates that the temperature coefficient of the vast majority of samples is less than 100

p p m /^{\circ} C

, which can be easily reduced through trimming.

4.2. Temperature Dependence after trimming

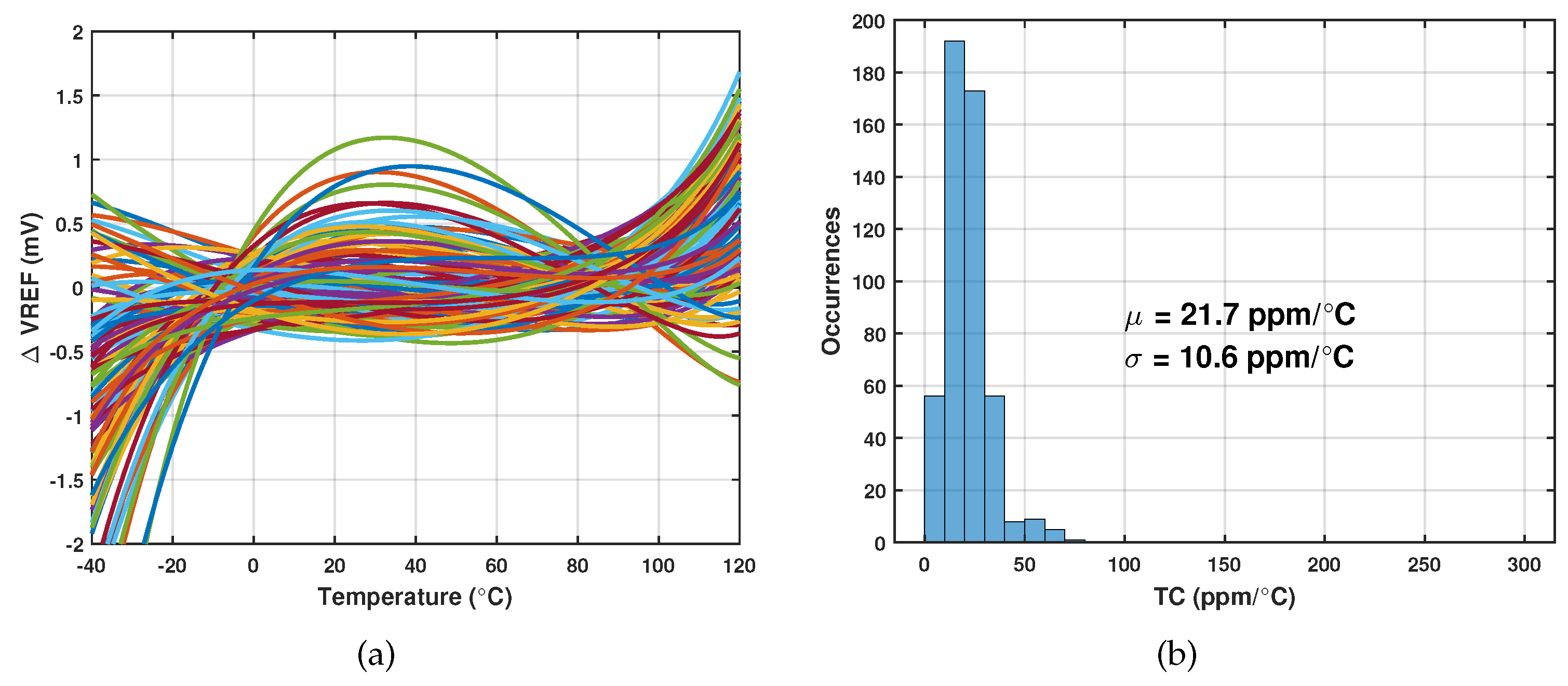
The process variation range of

V_{T 0}

is relatively wide, as Figure Figure 6(a) confirms. Therefore, we cannot use the one-point trimming methodology as BJT-based voltage reference does. The trimming method we adopted can be described as follows: (1) Sweep the trim bits at one ambient temperature, eg. 20

° C

, to obtain the voltage of

V_{R E F}

. (2) Sweep the trim bits at another ambient temperature, eg. 60

° C

, to obtain another set of output values. (3) Take the absolute difference between two sets of data. The trim bits corresponding to the minimum difference are the final bits we need.

A single NMOS switch is used to connect or disconnect the variable load transistors to the output. The size of the variable load follows a binary order, specifically 1, 1/2, 1/4, 1/16, and 1/32, with respect to the size of

M_{L o a d}

. Similarly, we performed a Monte Carlo simulation of 500 samples with the above trimming procedure. Figure 7(a) presents the trimmed output voltage after subtracting its mean value. The curves intersect at the two temperature points where we performed the trimming. The histogram in Figure 7(b) shows that the mean of TC is reduced to 21.7

p p m /^{\circ} C

and the standard deviation to 10.6

p p m /^{\circ} C

. 84.2 percent of the samples have a temperature coefficient below 30

p p m /^{\circ} C

, and 95.4 percent of the samples have a temperature coefficient below 40

p p m /^{\circ} C

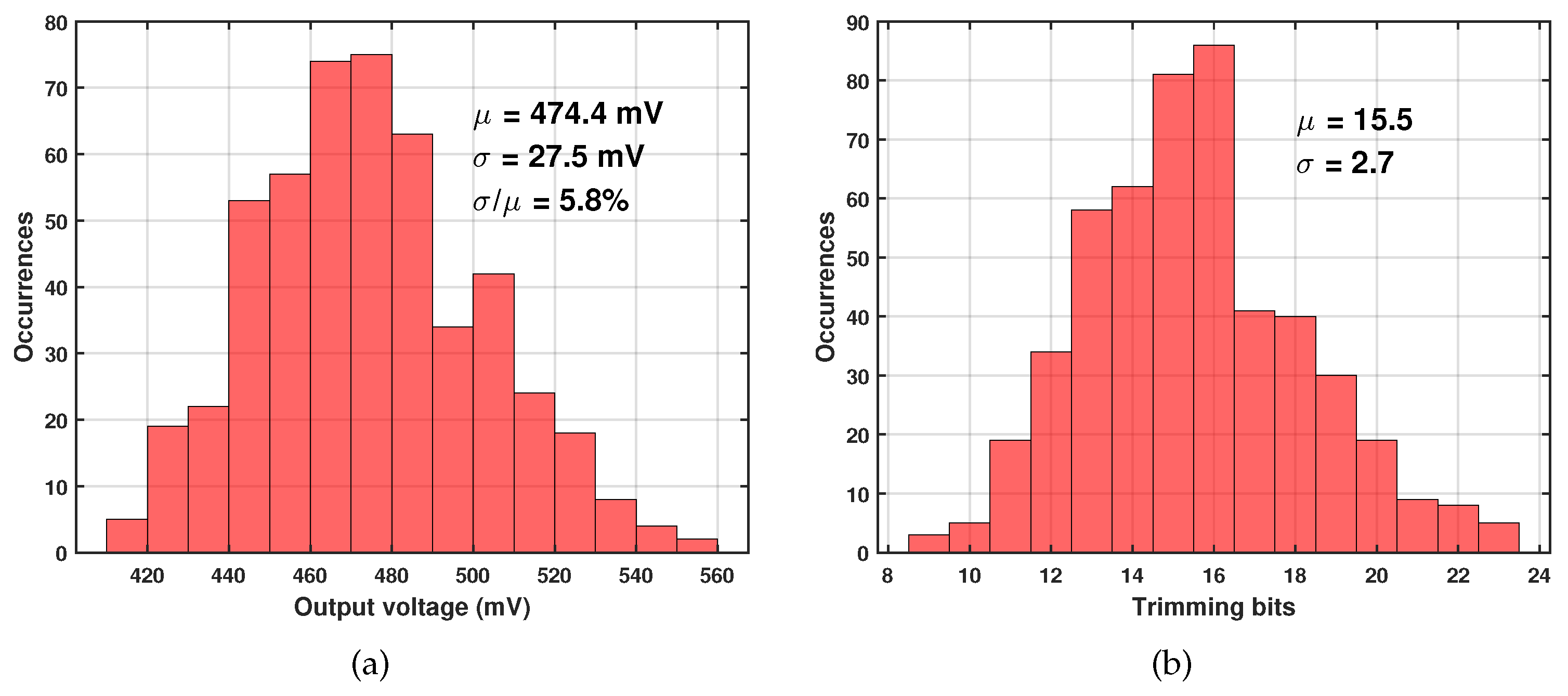
After calibration, the distribution of average output voltage and the final determined trimming bits are shown in Figure 8. The mean value of the

V_{R E F}

is 474.4 mV, roughly similar to the output under the typical process corner. As we adopted the global Monte Carlo model during simulation, the variation coefficient

σ / μ

is 5.8%, which is larger compared to the coefficient of BGR.

V_{R E F}

is relatively higher under the fast corner and lower under the slow corner, therefore the proposed voltage reference can also serve as an indicator of the NMOS corner. Figure 8(b) implies that the selection of a 5-bit trimming range can meet the needs of the vast majority of samples. The bits number varies from 9 to 23, and its mean value is around the half of

2^{5}

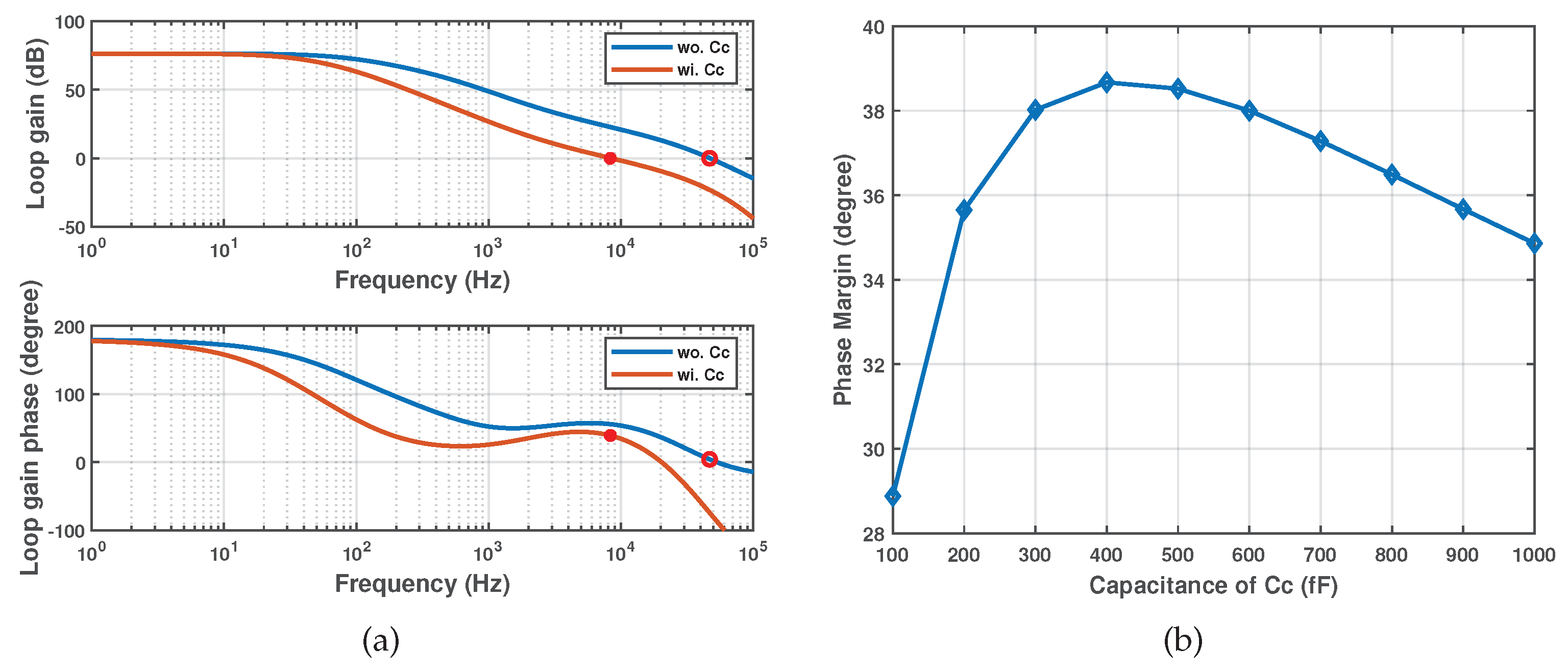
4.3. Frequency compensation

Figure 9(a) illustrates the frequency response of the loop gain with or without

C_{C}

. As explained in Section 3.2, the increasing of

C_{C}

compresses the unity gain bandwidth of the loop. When the unity gain bandwidth decreases, the frequency point corresponding to the phase margin first approaches

w_{p 3}

and then moves closer to

w_{z}

. In a figurative sense, the corresponding point will first climb a hill and then descend into a valley. The simulation result of phase margin versus

C_{C}

is shown in Figure 9(b). The capacitance value of the

C_{C}

is finally determined to be 400 fF, while the phase margin of the loop is 38.7

°

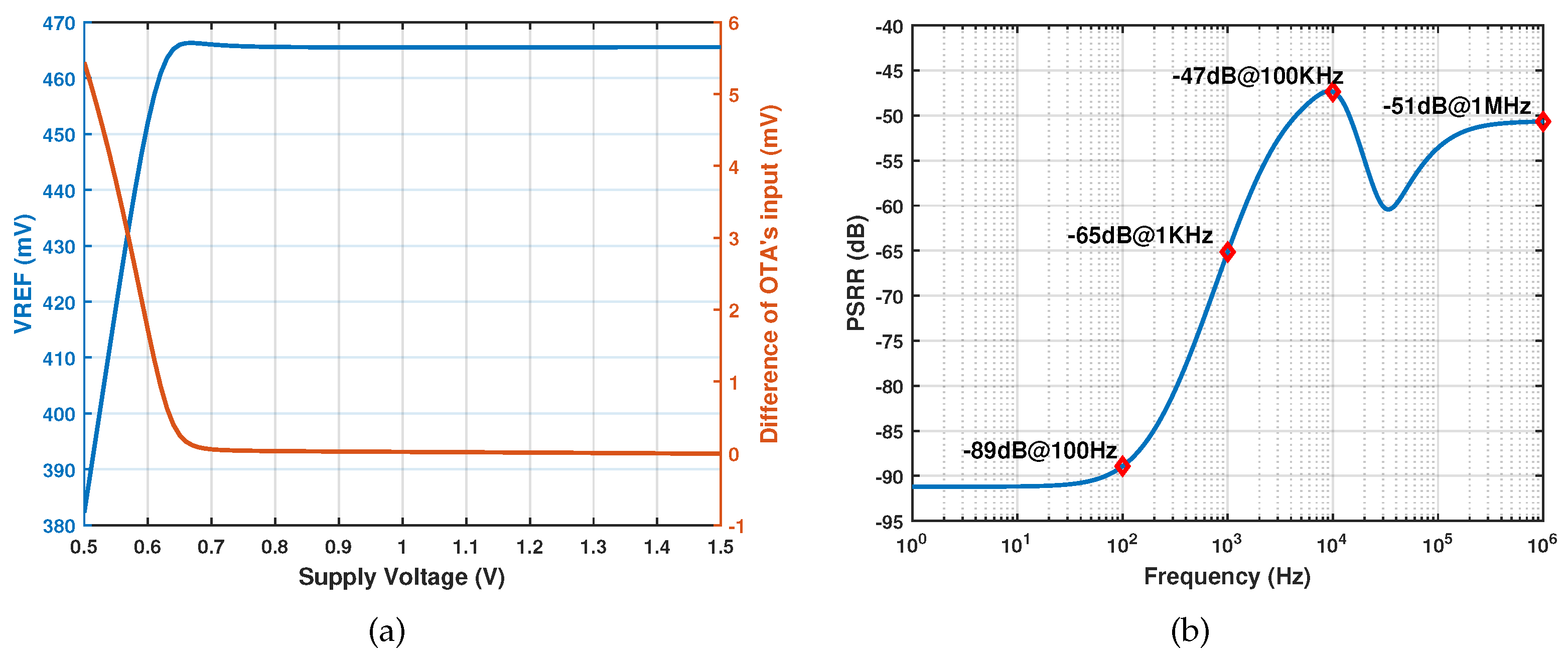
4.4. Supply dependence

The supply dependence of the proposed voltage reference was simulated at room temperature. Figure 10(a) shows the output voltage and the input difference of the amplifier as functions of VDD. The minimum supply voltage could be as low as 0.8 V, and the line sensitivity (LS) is 0.011 % ranging from 0.8 V to 1.5 V. The maximum supply voltage is mainly limited by the breakdown voltage of

V_{D S}

. The results also indicate that a lower supply voltage leads to inaccuracy in the specific current generator. The acceptable supply voltage depends not only on the voltage headroom of the PMOS current mirror but also on the allowable amplifier input residue. Because the larger the residue, the worse the temperature coefficient of

V_{R E F}

. Figure 10(b) shows the power supply rejection ratio (PSRR) with a load capacitance of 10 pF at room temperature. Thanks for the additional amplifier, the PSRR is -89 dB at 100 Hz.

Table 1 compares the performance of the proposed

V_{T}

based voltage reference with other reported works. It can be seen that the proposed reference is very competitive in many aspects. We balanced the circuit’s power and TC, adding an amplifier to improve LS with an acceptable current consumption. Thus our design shows an excellent supply independence among all works. Moreover, compared with [13], our design achieves a wider temperature range while keeping TC relatively equal. In addition, our design enables the majority of chips to achieve a small TC through a 5-bit trimming, which improves the yield in practical system applications.

5. Conclusions

This paper presents a 55 nm low-power

V_{T}

based voltage reference. The reference proposed only requires MOS transistors, and no BJTs or resistors are needed. A detailed explanation of the operating principle and design of the circuit was given with the EKV model. The reference consists of a novel specific current generator, a simple amplifier, a start-up circuit, and a trimmable output stage.

The simulation results showed a balanced trade-off between TC and power has been achieved. The proposed voltage reference has an average TC of 21.7

p p m /^{\circ} C

with a power consumption of 23.2 nW. The circuit also has excellent supply independence. Its line sensitivity is only 0.011 %/V, and PSRR is -89 dB at 100 Hz. The core area of the circuit is 0.009

m m^{2}

. Therefore, the proposed circuit is a suitable voltage reference module for low-power applications.

Author Contributions

Conceptualization, W.S.; methodology, W.S.; validation, W.S.; writing-original draft, W.S.; writing-review and editing, L.Z. and Y.X.; supervision, X.K.; project administration, D.H., and W.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Key Research and Development Program of China under Grant SQ2022YFB3200085.

Conflicts of Interest

The authors declare no conflict of interest.

References

Wang, J.; Sun, X.; Cheng, L. A Picowatt CMOS Voltage Reference Operating at 0.5-V Power Supply With Process and Temperature Compensation for Low-Power IoT Systems. IEEE Transactions on Circuits and Systems II: Express Briefs 2023, 70, 1336–1340. [Google Scholar] [CrossRef]
Parisi, A.; Finocchiaro, A.; Papotto, G.; Palmisano, G. Nano-Power CMOS Voltage Reference for RF-Powered Systems. IEEE Transactions on Circuits and Systems II: Express Briefs 2018, 65, 1425–1429. [Google Scholar] [CrossRef]
Zhu, Z.; Hu, J.; Wang, Y. A 0.45 V, Nano-Watt 0.033% Line Sensitivity MOSFET-Only Sub-Threshold Voltage Reference With No Amplifiers. IEEE Transactions on Circuits and Systems I: Regular Papers 2016, 63, 1370–1380. [Google Scholar] [CrossRef]
Yan, W.; Li, W.; Liu, R. Nanopower CMOS Sub-Bandgap Reference with 11 Ppm/°C Temperature Coefficient. Electronics Letters 2009, 45, 627. [Google Scholar] [CrossRef]
Zhang, H.; Liu, X.; Zhang, J.; Zhang, H.; Li, J.; Zhang, R.; Chen, S.; Carusone, A.C. A Nano-Watt MOS-Only Voltage Reference With High-Slope PTAT Voltage Generators. IEEE Transactions on Circuits and Systems II: Express Briefs 2018, 65, 1–5. [Google Scholar] [CrossRef]
Kim, M.; Cho, S. A Single BJT Bandgap Reference With Frequency Compensation Exploiting Mirror Pole. IEEE Journal of Solid-State Circuits 2021, 56, 2902–2912. [Google Scholar] [CrossRef]
Zhang, Z.; Zhan, C.; Wang, L.; Law, M.K. A - °C–125 °C 0.4-μA Low-Noise Bandgap Voltage Reference With 0.8-mA Load Driving Capability Using Shared Feedback Resistors. IEEE Transactions on Circuits and Systems II: Express Briefs 2022, 69, 4033–4037. [Google Scholar] [CrossRef]
Huang, W.; Liu, L.; Zhu, Z. A Sub-200nW All-in-One Bandgap Voltage and Current Reference Without Amplifiers. IEEE Transactions on Circuits and Systems II: Express Briefs 2021, 68, 121–125. [Google Scholar] [CrossRef]
Vita, G.D.; Iannaccone, G. A Sub-1 V, 10 Ppm/°C, Nanopower Voltage Reference Generator. 2006 Proceedings of the 32nd European Solid-State Circuits Conference, 2006, pp. 307–310.
Ueno, K.; Hirose, T.; Asai, T.; Amemiya, Y. A 300 nW, 15 Ppm/^\circ$C, 20 Ppm/V CMOS Voltage Reference Circuit Consisting of Subthreshold MOSFETs. IEEE Journal of Solid-State Circuits 2009, 44, 2047–2054. [Google Scholar] [CrossRef]
Qiao, H.; Zhan, C.; Chen, Y. A -40 °C to 140 °C Picowatt CMOS Voltage Reference With 0.25-V Power Supply. IEEE Transactions on Circuits and Systems II: Express Briefs 2021, 68, 3118–3122. [Google Scholar] [CrossRef]
Aminzadeh, H. All–MOS Self-Powered Subthreshold Voltage Reference with Enhanced Line Regulation. AEU - International Journal of Electronics and Communications 2020, 122, 153245. [Google Scholar] [CrossRef]
Luong, P.; Christoffersen, C.; Rossi-Aicardi, C.; Dualibe, C. Nanopower, Sub-1 V, CMOS Voltage References With Digitally-Trimmable Temperature Coefficients. IEEE Transactions on Circuits and Systems I: Regular Papers 2017, 64, 787–798. [Google Scholar] [CrossRef]
Navidi, M.M.; Graham, D.W. A Low-Power Voltage Reference Cell with a 1.5 V Output. Journal of Low Power Electronics and Applications 2018, 8, 19. [Google Scholar] [CrossRef]
Parisi, A.; Finocchiaro, A.; Palmisano, G. An accurate 1-V threshold voltage reference for ultra-low power applications. Microelectronics Journal 2017, 63, 155–159. [Google Scholar] [CrossRef]
Fan, H.; Fang, Z.; Li, Y.; Qian, Q.; Kang, X.; Chen, M.; Sun, W. A 3.38-Ppm/ ^∘ C Voltage Reference for Harsh Environment Applications Empowered by the In-Loop Resistance Trimming Technique. IEEE Transactions on Circuits and Systems II: Express Briefs 2023, pp. 1–1. [CrossRef]
Chen, Y.; Guo, J. A 42nA I _Q , 1.5–6V V _IN , Self-Regulated CMOS Voltage Reference With -93dB PSR at 10 Hz for Energy Harvesting Systems. IEEE Transactions on Circuits and Systems II: Express Briefs 2021, 68, 2357–2361. [Google Scholar] [CrossRef]
Seok, M.; Kim, G.; Blaauw, D.; Sylvester, D. A Portable 2-Transistor Picowatt Temperature-Compensated Voltage Reference Operating at 0.5 V. IEEE Journal of Solid-State Circuits 2012, 47, 2534–2545. [Google Scholar] [CrossRef]
Ji, Y.; Lee, J.; Kim, B.; Park, H.J.; Sim, J.Y. 18.8 A 192pW Hybrid Bandgap-Vth Reference with Process Dependence Compensated by a Dimension-Induced Side-Effect. 2019 IEEE International Solid-State Circuits Conference - (ISSCC), 2019, pp. 308–310. [CrossRef]
Liu, X.; Liang, S.; Liu, W.; Sun, P. A 2.5 Ppm/°C Voltage Reference Combining Traditional BGR and ZTC MOSFET High-Order Curvature Compensation. IEEE Transactions on Circuits and Systems II: Express Briefs 2021, 68, 1093–1097. [Google Scholar] [CrossRef]
Chowdary, G.; Kota, K.; Chatterjee, S. A 1-nW 95-ppm/°C 260-mV Startup-Less Bandgap-Based Voltage Reference. 2020 IEEE International Symposium on Circuits and Systems (ISCAS), 2020, pp. 1–4. [CrossRef]
Enz, C.C.; Krummenacher, F.; Vittoz, E.A. An analytical MOS transistor model valid in all regions of operation and dedicated to low-voltage and low-current applications. Analog integrated circuits and signal processing 1995, 8, 83–114. [Google Scholar] [CrossRef]
Enz, C.; Chicco, F.; Pezzotta, A. Nanoscale MOSFET Modeling: Part 1: The Simplified EKV Model for the Design of Low-Power Analog Circuits. IEEE Solid-State Circuits Magazine 2017, 9, 26–35. [Google Scholar] [CrossRef]
Enz, C.; Chicco, F.; Pezzotta, A. Nanoscale MOSFET Modeling: Part 2: Using the Inversion Coefficient as the Primary Design Parameter. IEEE Solid-State Circuits Magazine 2017, 9, 73–81. [Google Scholar] [CrossRef]
Enz, C.; Chalkiadaki, M.A.; Mangla, A. Low-power analog/RF circuit design based on the inversion coefficient. ESSCIRC Conference 2015-41st European Solid-State Circuits Conference (ESSCIRC). IEEE, 2015, pp. 202–208. [CrossRef]
Enz, C.; Pezzotta, A. Nanoscale MOSFET modeling for the design of low-power analog and RF circuits. 2016 MIXDES-23rd International Conference Mixed Design of Integrated Circuits and Systems. IEEE, 2016, pp. 21–26. [CrossRef]
Jespers, P. The gm/ID Methodology, a sizing tool for low-voltage analog CMOS Circuits: The semi-empirical and compact model approaches; Springer Science & Business Media, 2009.
Jespers, P.G.A.; Murmann, B. Systematic Design of Analog CMOS Circuits: Using Pre-Computed Lookup Tables; Cambridge University Press, 2017.
Alhasssan, N.; Zhou, Z.; Sánchez Sinencio, E. An All-MOSFET Sub-1-V Voltage Reference With a —51 –dB PSR up to 60 MHz. IEEE Transactions on Very Large Scale Integration (VLSI) Systems 2017, 25, 919–928. [Google Scholar] [CrossRef]
De Lima, V.F.; Klimach, H. A 37 nW MOSFET-Only Voltage Reference in 0.13 Mm CMOS. 2020 33rd Symposium on Integrated Circuits and Systems Design (SBCCI); IEEE: Campinas, Brazil, 2020; pp. 1–6. [CrossRef]

Figure 1. (a) The conceptual diagram of

V_{T}

based voltage reference; (b) the temperature characteristic of

V_{T}

Figure 1. (a) The conceptual diagram of

V_{T}

based voltage reference; (b) the temperature characteristic of

V_{T}

Figure 2. Core circuit of the proposed specific current source.

Figure 3. Schematic of the proposed

V_{T}

based voltage reference source.

Figure 3. Schematic of the proposed

V_{T}

based voltage reference source.

Figure 4. Pole-zero plot of loop gain.

Figure 5. The impact of trimming variables on the normalized charge density of

M_{L o a d}

Figure 5. The impact of trimming variables on the normalized charge density of

M_{L o a d}

Figure 6. Monte Carlo simulation results before trimming. (a) Temperature dependence of

V_{R E F}

; (b) histogram of temperature coefficient.

Figure 6. Monte Carlo simulation results before trimming. (a) Temperature dependence of

V_{R E F}

; (b) histogram of temperature coefficient.

Figure 7. Monte Carlo simulation results after trimming. (a) Temperature dependence of

V_{R E F}

; (b) histogram of temperature coefficient.

Figure 7. Monte Carlo simulation results after trimming. (a) Temperature dependence of

V_{R E F}

; (b) histogram of temperature coefficient.

Figure 8. Histogram after trimming. (a) Average output voltage; (b) determined trimming bits number.

Figure 9. Stability simulation results. (a) Frequency response of loop gain. (b) Phase margin as a function of

C_{C}

Figure 9. Stability simulation results. (a) Frequency response of loop gain. (b) Phase margin as a function of

C_{C}

Figure 10. Supply dependence simulation results. (a)

V_{R E F}

and difference of OTA’s input versus supply voltage. (b) PSRR with a

C_{L}

of 10 pF.

Figure 10. Supply dependence simulation results. (a)

V_{R E F}

and difference of OTA’s input versus supply voltage. (b) PSRR with a

C_{L}

of 10 pF.

Table 1. Comparison of the proposed voltage reference with previous works.

Parameter	This Work	[1]	[30]	[12]	[13]	[14]
Process (nm)	55	180	130	180	180	350
Temp. Range ( $° C$ )	-40 - 120	-10 - 100	-40 - 125	-40 - 125	-20 - 80	-70 - 85
TC ( $p p m /^{\circ} C$ )	21.7	90	28.8	17.05	21	42
$V_{R E F}$ (mV)	474.4	288	575.2	255	710	1520
$σ / μ$ (%)	5.8	0.574	4.32	0.2	12.3	2
Supply (V)	0.8 - 1.5	0.5 - 2	1 - 1.8	0.7 - 2	0.9 - 3	1.7 -3.3
LS (%/V)	0.011	0.23	0.071	0.615	0.26	10
Consumption (nW)	23.2	0.5	36.4	14	2.7	1110
PSRR (dB)	-89(@100Hz)	-45(@100Hz)	-54(@100Hz)	-91(@100Hz)	N/A	-35(@100Hz)
Area ( $m m^{2}$ )	0.009	0.0029	0.0033	N/A	0.068	0.06

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Sub-1-V Nanopower MOS-Only Voltage Reference

Abstract

1. Introduction

2. Principle of MOS-only voltage reference

2.1. EKV Model

2.2. MOS-only voltage reference operation principle

3. Circuit design

3.1. Proposed specific current source

3.2. Loop stability

3.3. Output stage

3.4. Start-up circuit

4. Simulation Results

4.1. Temperature Dependence before trimming

4.2. Temperature Dependence after trimming

4.3. Frequency compensation

4.4. Supply dependence

5. Conclusions

Author Contributions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe