Prerpints.org logo
Preprint
Review

Quantum Tomography: From Markovianity to Non-Markovianity

Altmetrics

Downloads

102

Views

52

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

28 December 2023

Posted:

29 December 2023

You are already at the latest version

Alerts
Abstract
Engineering of quantum computers requires reliable characterization of qubits, quantum operations, and even the entire hardware. Quantum tomography is an indispensable framework in quantum characterization, verification, and validation (QCVV), which has been widely accepted by researchers. According to the tomographic target, quantum tomography can be categorized into quantum state tomography (QST), quantum process tomography (QPT), gate set tomography (GST), process tensor tomography (PTT), and instrument set tomography (IST). Standard quantum tomography toolkits generally consist of basic linear inverse methods and statistical maximum likelihood estimation (MLE) based methods. Furthermore, the performance of standard methods, including effectiveness and efficiency, has been further developed by exploiting Bayesian estimation, neural networks, matrix completion techniques, etc. In this review, we introduce the fundamental quantum tomography techniques, including QST, QPT, GST, PTT, and IST. We first introduce the details of basic linear inverse methods. Then, the framework of MLE methods with constraints is summarized. Finally, we briefly introduce recent further research in developing the performance of tomography. This review provides a primary getting-start in developing quantum tomography, which promotes quantum computer development.
Keywords: 
Subject: Physical Sciences  -   Quantum Science and Technology

1. Introduction

Quantum tomography, as a significant framework in quantum characterization, verification, and validation (QCVV), is indispensable for manufacturing and developing quantum computers [1,2]. Results of tomography are generally considered as the foundation of quantum device calibration [3,4,5,6,7], quantum error mitigation (QEM) [8], and quantum error correction (QEC) [9,10,11], providing detailed information about qubits, quantum gates, as well as the quantum noise. In this framework, an experimenter prepares a set of experiments consisting of quantum states, circuits, and measurements. Then, a set of data is collected by executing the prepared experiments. Results of interest are derived by performing estimation algorithms.
Based on the common skeleton but different targets, main techniques are quantum state tomography (QST) [6,12,13,14], quantum process tomography (QPT) [15,16,17,18], and gate set tomography (GST) [5,19,20], process tensor tomography (PTT) [21,22], and instrument set tomography (IST) [23]. The effectiveness of these methods in characterizing the target components within specified assumptions has been proven. Furthermore, some methods have been used in developing real quantum hardware [4,24,25,26].
Tomography tools generally assume that components except for the target are knowable, which means the experimenter has full knowledge of non-target components or can learn their knowledge implicitly by learning algorithms. Relaxing knowable assumptions indicates the progress of comprehensiveness and practicality at a cost of complexity in terms of the number of experiments required and the post-processing.
The tomography first emerged by proposing QST [5,6,12] with the assumption that quantum gates and measurements are known to the experimenter. Therefore, one can construct a complete basis of the Hilbert-Schmidt space corresponding to the target quantum state. The black-box quantum state is mathematically reconstructed utilizing measurement probabilities and the knowledge of quantum gates and measurements. Analogously, The QPT [15,16,17,18] follows this approach, where the target is a black box quantum process, and the knowable assumptions are made to non-target quantum gates, quantum states, and measurements. Utilizing non-target quantum gates to compose state preparation and measurement (SPAM) circuits and combining them with known quantum states and measurements, complete bases are constructed before and after the black-box quantum process, respectively. Consequently, the QPT tries to recover a completely positive (CP) trace-preserving (TP) map between the input and output quantum states to represent the target process.
Developing from the QPT, GST was proposed based on the fact that all components are noisy. While applying tomography to quantum gates, QPT becomes inaccurate in the presence of SPAM errors. GST addressed this issue by independently modeling quantum gates, initial states, and measurements as tomography targets. Therefore, the GST explicitly separates the SPAM error into intrinsic and extrinsic errors. Intrinsic errors are inherent in the state preparation and measurement process, while extrinsic errors are introduced by performing quantum gates in SPAM circuits, facilitating QEC and QEM. Furthermore, GST exhibits gauge freedom up to a similarity transformation by a gauge matrix. This implies that an initialization error cannot be easily distinguished from a faulty measurement. As a result, GST provides a systematic method to simultaneously characterize quantum gates, initial states, and measurements. However, the scaling with system size is polynomially worse than QPT due to the requirement to characterize multiple gates at once.
The successes achieved by QST, QPT, and GST are based on the Markovian assumption, which means quantum processes the experimenter acts on the principle system preserves the state of the environment. However, sufficient evidence has indicated the presence of multi-time system-environment (SE) correlations [22]. Lack of consideration about SE correlations may lead to systematic error in the tomography. For instance, using QPT or GST to perform tomography on a black-box quantum process with SE correlations in the state preparation may cause theoretical violation of CP constraints [22]. This can disrupt tomography under the Markovian model and degrade the effectiveness of QEC codes.
PTT [21,22] initially aims to operationally characterize SE correlations. Based on the quantum stochastic process [27], a multi-time-step non-Markovian quantum system can be modeled by a principle system, an environment with the same dimensions as the system, SE unitaries act on both system and environment dimensions between adjacent time steps, and instruments that the experimenter applies to the system at time steps. In NISQ settings, those instruments, quantum gates, and measurements are the only components accessible to the experimenter. The PTT exploits the process tensor to represent all inaccessible parts consisting of the initial SE state and SE unitaries. By combining informationally complete instruments that span the space of CP and trace non-increasing (TNI) quantum operations, the process tensor is recovered. However, the PTT requires an exponential number of experiments with respect to the Markovian order, which limits large-scale implementations.
Growing out of PTT, the IST [23] was proposed to perform GST in non-Markovian situations. It tackles the inconsistency in characterizing SE correlations and instruments. For example, two inconsistent process tensors may be generated by two sets of imperfect instruments. Both SE correlations and instruments are targets. The IST successfully estimates the instrument and the SE correlations that are consistent with the measurement probabilities. However, it still suffers from the exponential number of experiments and the high complexity of post-processing.
In this review, we provide a fundamental introduction to quantum tomography techniques, including QST, QPT, GST, PTT, and IST. We briefly introduce the basic principles and direction of development of these techniques for readers to facilitate systematic comprehension.
This review is structured as follows. In Section 2, we briefly introduce mathematical representations for quantum tomography. Then, the basic frameworks for Markovian and non-Markovian quantum tomography are introduced in Section 3 and Section 4, respectively. In Section 5, we introduce the maximum likelihood estimation method as an indispensable statistical tool in the standard toolkit. Finally, further developments to enhance the performance of tomography are discussed in Section 6.
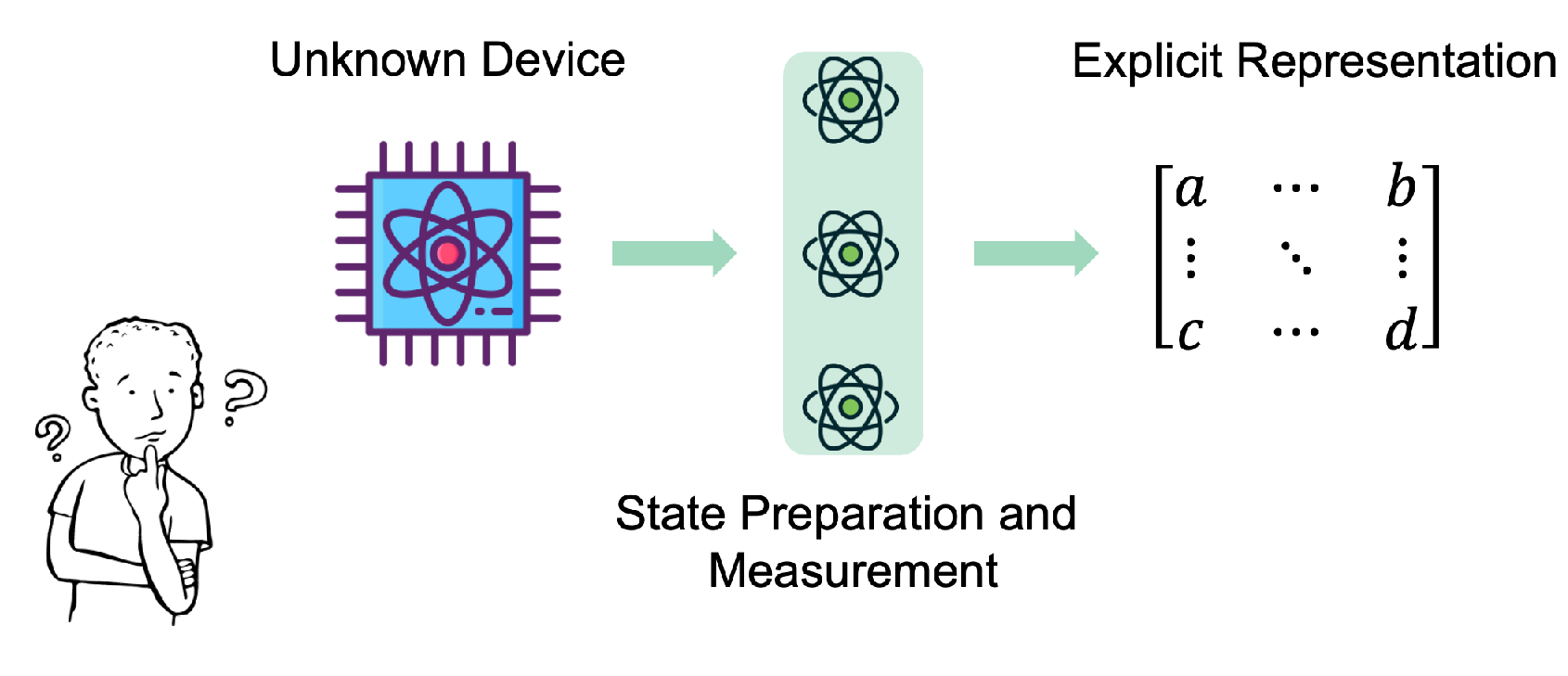
Preprints 94736 g001
Figure 1. Schematic view on quantum tomography. For an unknown quantum device, which can be a quantum state preparation circuit, quantum process, etc, one can obtain the explicit representation with some SPAM circuits.
Figure 1. Schematic view on quantum tomography. For an unknown quantum device, which can be a quantum state preparation circuit, quantum process, etc, one can obtain the explicit representation with some SPAM circuits.
Preprints 94736 g001

2. Preliminaries

Before introducing quantum tomography techniques, physical entities should be mathematically represented. In this section, the mathematical representations of quantum states, gates, and measurements are introduced. In the following, calligraphic notation is used to represent physical entities of quantum operations, such as quantum gates G and measurements M . The quantum state is written in the Roman alphabet, such as ρ . We primarily utilize the Pauli transfer matrix (PTM) formalism. Then, the Choi-Jamiolkowski isomorphism (CJI) representation is additionally introduced [22,28].
In the PTM representation, a quantum state ρ on a d-dimensional Hilbert space H d is represented by a superoperator | ρ 〉 〉 as a vector in d 2 -dimensional Hilbert-Schmidt space. We specify the basis of Hilbert-Schmidt space to be Pauli basis without loss of generality. Hence, elements of | ρ 〉 〉 represent coefficients of corresponding normalized Pauli matrix [5],
| ρ 〉 〉 = ∑ k Tr ( P k ρ ) | k 〉 〉 ,
where P k ∈ { I / 2 , X / 2 , Y / 2 , Z / 2 } ⊗ n is the k-th normalized Pauli matrix. Furthermore, a quantum measurement, which is described as an operator M, can be represented by a set of row vectors [5], i.e.,
M = ∑ k Tr ( P k M ) k ,
where k = | k 〉 〉 † . Let A B denote Tr A B , the probability of performing measurement M on ρ is represented as [5]
p = E ρ .
A quantum process A can be conveniently represented by a PTM defined as
( A ) i j = Tr P i A ( P j ) .
This definition describes the mapping between input and output quantum states. Notably, the output state ρ o u t is represented by the left product of input state ρ i n that
| ρ o u t 〉 〉 = A | ρ i n 〉 〉 .
Hence, the experimental probability result of the experiment, which involves a quantum state ρ , quantum process A , and measurement M , can be represented as
p = Tr M ∘ A ( ρ i ) = Tr M A ( ρ i ) = M A | ρ 〉 〉 .
The PTM constructs a mapping from the input state to the output state. It is easy to check and constrain the trace characteristics by examining the first row of PTM. For example, the trace-preserving (TP) constraints indicate the first row of PTM to be [ 1 , 0 , 0 , ⋯ , 0 ] [5]. However, it is difficult to intuitively represent the CP property.
Therefore, we also introduce the CJI representations. For a quantum process G , the CJI matrix is defined as [22,28]
ξ G = ∑ i j G | i 〉 〈 j | ⊗ | i 〉 〈 j | ,
where the output state can be determined by
ρ o u t = Tr i n [ ( I ⊗ ρ i n T ) ξ G ] .
Since the CJI matrix represents a quantum state without normalization, it is also referred to as the Choi state. The CP constraints for G are equivalent to the positive semi-definiteness of the ξ G .
Additionally, PTM representation A can be easily transformed into Choi-Jamiolkowski isomorphism (CJI) [22,28] representation ξ A , and vice versa, that
ξ A = 1 d 2 ∑ i j A i j P j ⊗ P i T ,
A i j = Tr P j ⊗ P i T ξ A .

3. Basic Markovian Tomography Framework

Considering a Markovian quantum experiment conducted by an experimenter with specified components consisting of quantum state ρ , circuit G , and measurement M , the probability of the experiment, whose samples are the only accessible outputs to the experimenter, is given by [5]
p = Tr [ M ∘ G ( ρ ) ] ,
where the PTM representation is
p = M G | ρ 〉 〉 .
Current quantum devices generally provide limited initial quantum states and quantum measurements. Therefore, the specified quantum state and measurement are referred to as the state preparation and measurement (SPAM) circuits that act on the initial states and native measurements. Then, the probability can be rewritten in the following form [5]
p     = Tr [ M ∘ E ∘ G ∘ F ( ρ ) ]
= M E G F | ρ 〉 〉 ,
where E and F represent the state preparation circuit and measurement circuit, respectively. In the following, the quantum state and measurement are referred to as the SPAM circuits acting on the initial state and native measurement, respectively. Moreover, the specified quantum states and measurements with index in experiments are implemented by specifying the SPAM circuits without loss of generality [5],
ρ i | ρ i 〉 〉 = F i | ρ 〉 〉 ,
M i M i = M E i .
The basic Markovian quantum tomography framework can be summarized in the following steps:
(1)
Experiment Preparation. Prepare a set of experiments, where each experiment consists of the quantum state, circuit, and measurement.
(2)
Data Collection. Execute the prepared experiments and record measurement samples.
(3)
Tomography Reconstruction. Reconstruct the tomographic target by performing a post-process algorithm based on the collected data.
In general, quantum tomography techniques assume that components except for tomographic targets are perfectly implemented as the knowledge to the experimenter, or implicitly learnable by learning algorithms. Experimenters usually prepare experiments that form a tomographically complete basis for the target to obtain sufficient information.
In this section, based on the linear inversion, we will introduce the basic methods of QST, QPT, and GST, i.e. LQST, LQPT, and LGST, respectively.

3.1. Basic QST

The task of QST is to find the explicit representation of an unknown quantum state σ ∈ H d [6,12,13,14]. The construction of a tomographically complete basis for the state is constructed by combining quantum circuits and measurements, which can be solely accomplished by measurements with identity circuits.
Let the set of measurement { M i } i = 0 d 2 be tomographically complete that { M i } i = 0 d 2 are linear independent. The probability of sampling a desired output value of M i is
p i = M i σ ,
which indicates the decomposition of the unknown quantum state σ . Since the measurement are known to the experimenter, the dual set of { M i } i = 0 d 2 − 1 can be determined as { | D j 〉 〉 } j = 0 d 2 − 1 by performing the linear inversion, where M i D j = δ i j .
Then the unknown quantum state can be reconstructed by
| σ ^ 〉 〉 = ∑ i = 0 d 2 − 1 p ^ i | D i 〉 〉 ,
where p ^ i = n i / n t is the estimated probability, n s is the number of the desired output value of M i in samples, and n t is the total sampling times.
The LQST requires at least d 2 experiments to collect complete information of the unknown quantum state, and the linear inverse process on a d 2 × d 2 matrix. The reconstructed state σ ^ is represented as a d 2 -dimensional real vector.

3.2. Basic QPT

The task of QPT is to find the explicit representation of an unknown quantum process G ∈ B ( H d ) , where B ( • ) represents the space of bounded linear operator on the operand space [15,16,17]. The process G can be treated as a map from the space of the input state to the space of the output state. Therefore, to construct a tomographically complete basis for the unknown quantum process, QPT requires a set of quantum states { ρ i } i = 0 d 2 − 1 and a set of quantum measurements { M j } i = 0 d 2 − 1 that simultaneously span H d , i.e. both { | ρ i 〉 〉 } i = 0 d 2 − 1 and { M j } j = 0 d 2 − 1 are linear independent.
Given ρ i and M j , The probability is
p i j = M j G | ρ i 〉 〉 ,
which indicates the coefficient of the map from ρ i to M j . Based on the known knowledge of quantum states and measurements, the dual sets of { | ρ i 〉 〉 } i = 0 d 2 − 1 and { M i } j = 0 d 2 − 1 can be determined as { β k } k = 0 d 2 − 1 and { | D l 〉 〉 } l = 0 d 2 − 1 , respectively, by performing the linear inversion. Then, the quantum process can be reconstructed by
G ^ = ∑ i , j = 0 d 2 − 1 p ^ i j | D j 〉 〉 β i ,
where p ^ i j is the estimated probability.
It can be observed that the construction of a tomographically complete basis requires d 4 experiments and processes linear inversion on d 2 × d 2 matrix twice. The reconstructed quantum process G ^ is saved as a d 2 × d 2 -dimensional PTM.

3.3. Basic GST

QST and QPT generally require non-target components to be perfectly implemented as the knowledge to the experimenter. However, nothing is absolutely perfect. While using QPT to characterize a set of quantum gates that are available to a quantum device, errors introduced by SPAM circuits impact the self-consistency of tomography, which motivate the development of GST [5,19,20]. Compared to QST and QPT, the goal of GST is to self-consistently and completely characterize a set of n k quantum gates { G k } , an initial quantum state ρ , and a native quantum measurement M . Based on the probability defined in (11), a quantum gate set is defined as [5]
G = { ρ , M , G 0 , ⋯ , G K } ,
where M is a 2-outcome measurement and G 0 is the null gate, which does nothing for no time. Based on the given gate set G , SPAM gates are defined as
F = { F 1 , F 2 , ⋯ , F d 2 } ,
where F i is composed of gates in the set { G k } , that is,
F i = G i L i ∘ ⋯ ∘ G i 2 ∘ G i 1 ,
where L i is the length of the i-th SPAM gate. Then, we can also obtain d 2 tomographically complete input quantum states { F j ( ρ ) } and d 2 measurement operators { M ∘ F i } . Therefore, we can obtain n k × d 4 probabilities,
p i k j = M F i G k F j | ρ 〉 〉
= ∑ r s M F i | r 〉 〉 r G k | s 〉 〉 s F j | ρ 〉 〉 .
Likewise, we can rewrite the above equality in the matrix form,
R k = A G k B ,
where
A = ∑ i | i 〉 〉 M F i , B = ∑ j F j | ρ 〉 〉 j ,
( R k ) i j = p i k j .
Experimentally measuring the values p i k j , we can obtain matrices { S k } , whose elements satisfy
E [ S k ] = R k , ∀ k .
Specially, we define
g = S 0 , E [ g ] = A B .
Furthermore, we define | ρ ˜ 〉 〉 and M ˜ , which can be estimated with experimental and satisfy
E [ | ρ ˜ 〉 〉 ] = ∑ i | i 〉 〉 M F i | ρ 〉 〉 ,
E [ M ˜ ] = ∑ j M F j | ρ 〉 〉 j ,
where M F i | ρ 〉 〉 is measurable.
Then, the unknown gate set can be recovered by performing convex optimization technology. Based on high-quality quantum devices, it is known a priori that the measured gates will differ from an ideal (target) set of gates by some very small error. Therefore, we have a target set G ′ = { | ρ ′ 〉 〉 , E ′ , G 0 ′ , ⋯ , G K ′ } and define
G ˜ k = g − 1 S k ≈ B − 1 R k B .
Then, we can find the estimation of matrix B via the following convex optimization problem,
B ^ = arg min B ˜ ∑ k = 1 K + 1 Tr G ˜ k − B ˜ − 1 G k ′ B ˜ 2 ,
where G K + 1 ′ = | ρ ′ 〉 〉 M ′ and G ˜ k = g − 1 | ρ ˜ 〉 〉 M ˜ . Lastly, we can recover the unknown gate set with
| ρ ^ 〉 〉 = B ^ | ρ ˜ 〉 ,
M ^ = M ˜ B ^ − 1 ,
G ^ k = B ^ G ˜ k B ^ − 1 .

4. Basic Non-Markovian Tomography Framework

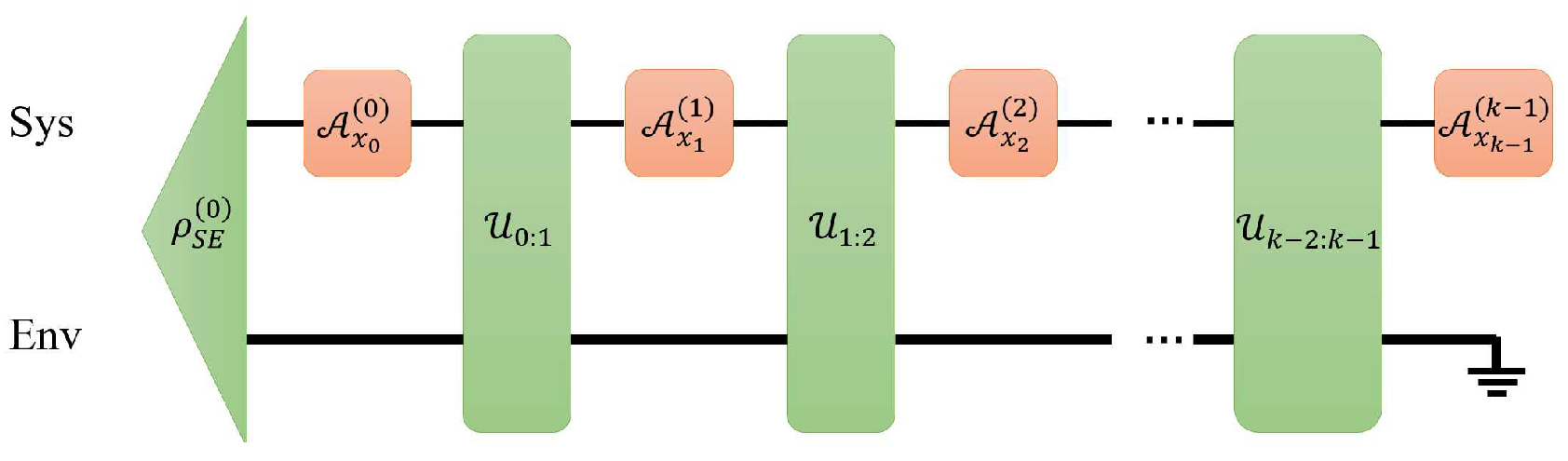
No system is isolated. Based on the quantum stochastic process theory [27,29], an open quantum system subjected to k-time-step interventions by quantum operations (instruments), such as quantum processes and measurements, can be modeled as shown in Figure 2. It utilizes a principle quantum system and an environment to represent the entire SE dimensions. At time step t, the experimenter applies an instrument A x t ( t ) from the t-available set J ( t ) = A x t ( t ) to the system. The instrument transforms the system state and outputs a value x t as the observation of the experimenter. Without loss of generality, the output x t is treated as the index of the instrument applied at time step t. Notably, there exists an SE unitary between adjacent time steps to represent the non-Markovian SE evolution. Therefore, the probability of obtaining a sequence of output value x = [ x 0 , x 1 , . . . , x k − 1 ] is represented by
p x = Tr A x k − 1 ( k − 1 ) U k − 2 k − 1 ⋯ A x 1 ( 1 ) U 0 : 1 A x 0 ( 0 ) ρ S E ( 0 )
= 〈 〈 0 S E | A x k − 1 ( k − 1 ) ∏ t = 0 k − 2 U t t + 1 A x t ( t ) | ρ S E ( 0 ) 〉 〉 ,
where we simplify the A x t ( t ) ⊗ I and A x t ( t ) ⊗ I into A x t ( t ) and A x t ( t ) , respectively, without confusing.
Non-negligible non-Markovian SE correlations of open quantum systems theoretically impact the tomography techniques designed under Markovian settings. A simple example to demonstrate the impact is the theoretical violation of CP constraints given in Example. 1 in [20,22] (c.f. Example A1 in Appendix A). The requirement of characterization of non-Markovian quantum correlations motivates non-Markovian quantum tomography techniques, such as process tensor tomography (PTT) and instrument set tomography (IST). Non-Markovian quantum tomography also exploits the 3-step skeleton as shown in Section 3, where each experiment in the first step of Experiment Preparation consists of instruments.
The target in the non-Markovian tomography should be further exclaimed. Based on the criterion of accessibility, the components are classified into accessible and inaccessible parts. Specifically, the only accessible components to the experimenter are the instruments acting on the principle system, while the initial SE state and SE unitaries remain inaccessible. Quantum stochastic process theory [27,29] utilizes the process tensor to represent all inaccessible parts as a map from the product of k spaces of CP and trace non-increasing (TNI) bounded operators on quantum states to the space of output quantum states. In this review, we principally adopt the definitions of process tensor T 0 k that
p x = T 0 k A x = T 0 k A x 0 ( 0 ) , ⋯ , A x k − 1 ( k − 1 ) ,
with physical properties:
(P1)
Linearity. T 0 k a A + b B = T 0 k a A + T 0 k b B , for any a . b ∈ R .
(P2)
Complete positivity. T 0 k ⊗ I a n c A S , a n c ≥ 0 , where I a n c is the identity process on the ancilla, for any instruments A S , a n c act on the system and the ancilla.
(P3)
Containment. T i j is contained in T l k , where l ≤ i ≤ j ≤ k .
Recently, the most acceptable mathematical representation of process tensor is the CJI matrix
Υ T 0 k = Tr E [ ξ U k − 2 k − 1 ★ ⋯ ★ ξ U 0 : 1 ★ ρ S E ( 0 ) ] ,
where ★ represents the link product defined in [22], ξ U is the Choi state of SE unitary U . This formulation indicates that the SE correlations of an open quantum system with k time step instrument interventions can be represented by a Choi state consisting of 2 k + 1 subsystems labeled by   k − 1 , k − 2 ⋯ , 1 , 0 , respectively. In this way, the output state can be determined by
p x = Tr Ξ x T Υ T 0 k ,
where Ξ x = ξ x k − 1 ( k − 1 ) ⊗ ⋯ ⊗ ξ x 0 ( 0 ) , and ξ x t ( t ) represent the Choi state of A x t ( t ) . It is easy to verify the linearity and complete positivity of Υ T 0 k . Furthermore, the process tensor of a sub-time span can be derived as
Υ T i j ( Ξ x l , ⋯ , x i − 1 ) = Tr l Ξ x k − 1 , ⋯ , x j ⊗ I l ⊗ Ξ x l , ⋯ , x i − 1 T Υ T l k ,
for any Ξ x k − 1 , ⋯ , x j because of the causality, where l =   j − 1 j − 2 ⋯ i + 1 i ¯ , and partial trace with label • ¯ means partial trace other dimensions except for •.
In this section, based on the linear inversion, we will introduce the basic methods of PTT and IST i.e. LPTT and LIST, respectively.

4.1. Basic PTT

Linear inverse process tensor tomography (LPTT) provides a principle and quick method for PTT [21,27]. The process tensor can be treated as a map from the space of k-time-step instruments to the probability. The tomography of process tensor requires the informationally complete (IC) available sets at all time steps, which means that the instruments in each available set span the space of bounded linear operator on the quantum state. Furthermore, we assume that instruments are perfectly implemented as the knowledge to the experimenter.
The experimenter prepares a set of experiments labeled by x that consists of all combinations of instruments. By performing the experiments, the experimenter collects estimated probabilities p ^ x .
Let D ( t ) = { χ x t ( t ) } be the dual set of t-available set J ( t ) = { ξ x t ( t ) } that Tr ( χ i ( t ) T ξ j ( t ) ) = δ i j . The process tensor can be reconstructed by
Υ ^ T 0 k = ∑ x p ^ x χ x k − 1 ( k − 1 ) ⊗ ⋯ ⊗ χ x 0 ( 0 ) .
Given a sequence of output y , it can be verified that
Tr Ξ y T Υ ^ T 0 k
= ∑ x p x ∏ t Tr [ χ x t ( t ) T ξ y t ( t ) ]
= ∑ x p x ∏ t δ x t y t
= p y .
Since IC available set at each time step consists of d 2 × d 2 instruments, LPTT requires d 4 k experiments to characterize the entire process tensor. However, the linear inverse procedures are applied independently on each time step to determine the dual set of the available set. This indicates k independent linear inverse procedures on d 4 × d 4 complex matrix. Nevertheless, it still requires the reconstruction of d 4 k matrix of the process tensor.

4.2. Basic IST

The emergence of instrument set tomography (IST) results from non-avoidable imperfect implementations of instruments while performing PTT [23]. The differences between the knowledge and the practical implementations of instruments may lead to systematic inconsistency of tomographic results. A simple example to show the inconsistency is that PTT generates two different process tensors utilizing two sets of imperfectly implemented IC instruments, respectively. Moreover, it is not always reasonable to require the quantum device to be characterized can formulate an IC available set at each time step. Recent superconductive quantum devices can hardly provide quantum gates that span the space of unitary when a time step is specified to be a time slot for applying a quantum gate [20,23]. Tomographic results should be responsible for all available quantum instruments that the quantum device can provide, which results in the requirement of self-consistency of the IST.
Equation (38) indicates that given the initial SE state, SE unitaries, and instruments, the probability can be determined. By exploiting the process tensor to represent all inaccessible components, the probability can be determined by specifying the instruments and the process tensor. Therefore, the full and reduced instrument set can be defined as
I full = J , U , ρ S E ( 0 ) ,
I reduced = J , T ,
respectively, where J = J ( t ) t = 0 k − 1 represents available sets, U = U t t + 1 t = 0 k − 2 is the set of SE unitaries, ρ S E ( 0 ) represents the initial SE state.
LIST consists of two sub-procedures. First, LIST fixes the linear relationship of available sets by measurement probabilities and knowledge of instruments. For time step t, the probability described in () can be reformed as
p x + x − ( x t ) = Tr B x + x − A x t ( t ) ,
where x + and x − represent the output values before and after time step t in a k-time-step experiment, respectively. This indicate the decomposition of A x t ( t ) on the inaccessible non-orthogonal basis
B ( t ) = B x + x − .
By adjusting x + and x − , the LIST tries to make the basis B ( t ) to be complete. Utilizing a unique integer α to denote x + x − as the index of the basis matrix, the LIST connects the measured probabilities and the basis as
p x t ( t ) = ( b 0 ( t ) ) † ( b 1 ( t ) ) † ⋮ ( b d 4 − 1 ( t ) ) † a x t ( t ) = B ( t ) a x t ( t ) ,
where a x t ( t ) and b α ( t ) represent the vectorization of the A x t ( t ) and B α ( t ) , respectively. If B ( t ) is invertible, we can obtain instruments
Ξ ( t ) = B ( t ) − 1 Γ ( t ) ,
where Ξ ( t ) = [ a 0 ( t ) , a 1 ( t ) , ⋯ , a m t − 1 ( t ) ] and Γ ( t ) = [ p 0 ( t ) , p 1 ( t ) , ⋯ , p m t − 1 ( t ) ] .
Assuming that the quantum instruments are well-implemented and approximately close to the ideal instruments, the inaccessible basis matrix can be optimized by
B ( t ) = arg min X ∑ t X Γ ( t ) − Ξ knowledge ( t ) F ,
where Ξ knowledge ( t ) represents the knowledge of instruments to the experimenter. Then, PTMs of instruments are recovered by devectorization of determined a x t ( t ) in Ξ ( t ) .
Then, the LIST performs the process tensor reconstruction to recover the process tensor. Utilized instruments are the maximum linear independent set of instruments in corresponding available sets. Details of process tensor reconstruction can be referred to in Section 4.1.
Note that the requirement of basis matrix optimization implies gauge freedom, which is also present in the GST. The optimal basis matrix is non-unique and results in the non-uniqueness of tomographic results. This implies that correlations introduced before the time step cannot be distinguished by correlations introduced after.

5. Maximum Likelihood Estimation based Methods

Maximum likelihood estimation (MLE) based methods [5,19,22,23,30,31] grew out of drawbacks of basic linear inverse methods. It should be highlighted that the precision of linear inverse methods highly relies on the accuracy of estimated probability generated by measurement sampling, which is of the order O ( 1 / n s ) , where n s is the number of samples. The probability estimation of finite measurement sampling introduces the sampling error, leading to a biased estimated probability. Subsequently, the result of the tomography target may not be physical, such as the CP violation of the estimated quantum state in QST. Experimenters may be interested in utilizing more experiment data to enhance the performance of the tomography. However, linear inverse methods lack the capability of extracting additional information from overcomplete data.
Addressing these issues, statistical methods are proposed based on the MLE, which enables the exploitation of overcomplete data to reduce the error of estimation. These methods compose the measurement data into a likelihood function L ( T ^ ) with respect to the estimated target T ^ requires to be maximized. The parameterization of the tomographic target also varies from method. Typically, quantum states, processes, and measurements can be directly parameterized by d 2 -dimensional real column vectors, d 2 × d 2 -dimensional real matrices, and d 2 -dimensional real row vectors, respectively, as their PTM representations.
The parameterization of SE correlations in non-Markovian situations is more complicated. While representing SE correlations by process tensor, it can be modeled by Cholesky decomposition of Choi state which naturally satisfies the CP constraints. The PTM representation of the process tensor is also available as described in Section 4. Furthermore, the SE correlations can also be represented by the initial SE state and SE unitaries, where the SE state can be represented by a d 4 -dimensional real column vector and each SE unitary can be modeled by a ( d 4 − 1 ) -dimensional real vector α whose i-th element represent the rotation angle on the ( i + 1 ) -th Pauli matrix, i.e. the estimated SE unitary is
V ^ ( α ) = PTM ( exp ( ι ∑ i α i P i + 1 ) ) ,
where ι 2 = − 1 .
Although several kinds of likelihood functions are proposed, we apply the most common likelihood as described in Appendix B, where maximizing L ( T ^ ) is equivalent to minimizing l ( T ^ ) with respect to the desired estimator p ^ as described in their basic framework. Remarkably, constraints are introduced in MLE methods to guarantee the result is physical. The details of constraints for tomography components are listed below:
State: A quantum state ρ ^ is constrained to be completely positive, meaning its density matrix must be positive semi-definite with unit trace,
ρ ^ ⪰ 0 ,
Tr ρ ^ = 1 .
This guarantees the probabilities of the system are positive with summation 1. Note that TP constraints can be efficiently represented by
| ρ ^ 〉 〉 = 1 .
Process: A quantum process is constrained to be CPTP. The CP constraints require the Choi state of G ^ to be completely positive,
ξ ^ G ⪰ 0 ,
which indicates that the process remains the CP property of the quantum state. Meanwhile, entries of the first row of its PTM are limited as
G ^ 0 j = δ 0 j
to guarantee the TP property, which indicates the summation of probabilities of the quantum state is 1.
Measurement: A quantum measurement M ^ and its complementary are constrained by completely positive that
M ^ = ∑ i M ^ i P i ⪰ 0 ,
I − M ^ ⪰ 0 ,
representing the positive outcome of probabilities.
Process Tensor: The process tensor T ^ should be constrained by CP and causality. The CP constraints require the Choi state of the process tensor to be positive semi-definite,
Υ ^ T ⪰ 0 .
Causality constraints result from that future events do not influence past statistics, as a generalization of trace preservation, which in the Choi state representation is
Tr   k − 1 Υ ^ T 0 k = I   k − 1 ⊗ Υ ^ T 0 k − 1 .
By superoperators of PTM representation, the causality constraints can be conveniently represented by
Υ ^ T 0 k P ban = 0 ,
P ban = I ⊗ 2 t + 1 ⊗ Q ˜ 2 t + 2 ⊗ Q 2 t + 3 ⊗ ⋯ ⊗ Q 2 k − 1 , ∀ t ,
Q ˜ ∈ P 1 , ⋯ , P d 2 − 1 ,
Q ∈ P 0 , P 1 , ⋯ , P d 2 − 1 .
Then, an optimization algorithm is performed to optimize the optimization problem
min T ^ l ( T ^ )
s . t . C o n s t r a i n t s o f T ^ .
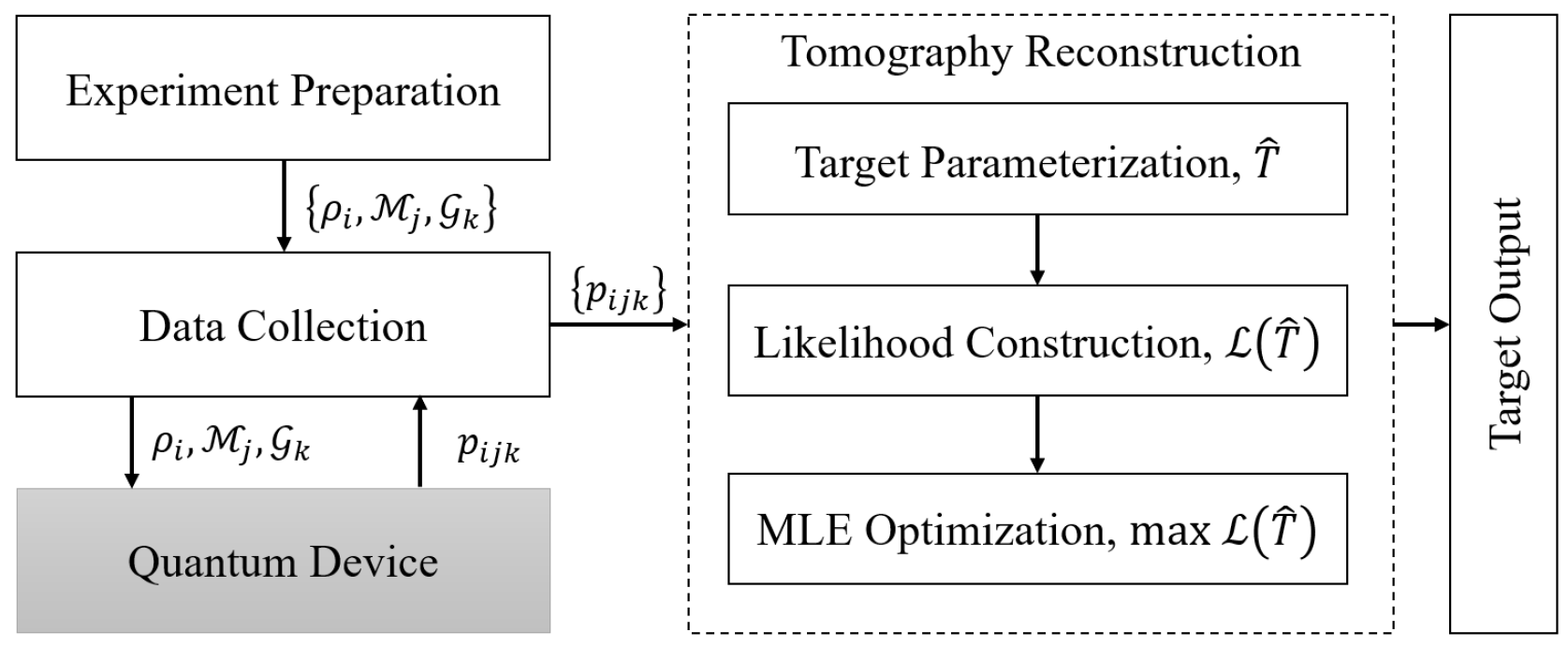
The workflow of MLE methods is demonstrated in Figure 3.
MLE methods fill the blank of constrained statistical methods within the standard quantum tomography toolkits, and have obtained wild acceptance from researchers. They provide physical implementable results by introducing constraints. The capability of utilizing overcomplete data promotes the accuracy of the tomography by extracting additional information compared with basic linear inverse methods. However, MLE methods are quite computationally resource-consuming. In the classic memory aspect, all MLE methods require saving exponentially large data with respect to the system dimension d to perform the optimization algorithm. In the time aspect, MLE methods require more experiments than the linear inverse methods which is exponentially large to d. Moreover, solving constrained optimization problems with an exponentially large number of parameters with respect to d is extremely time-consuming. Therefore, recent applications of MLE methods are limited to small-scale quantum systems.

6. Further Developments

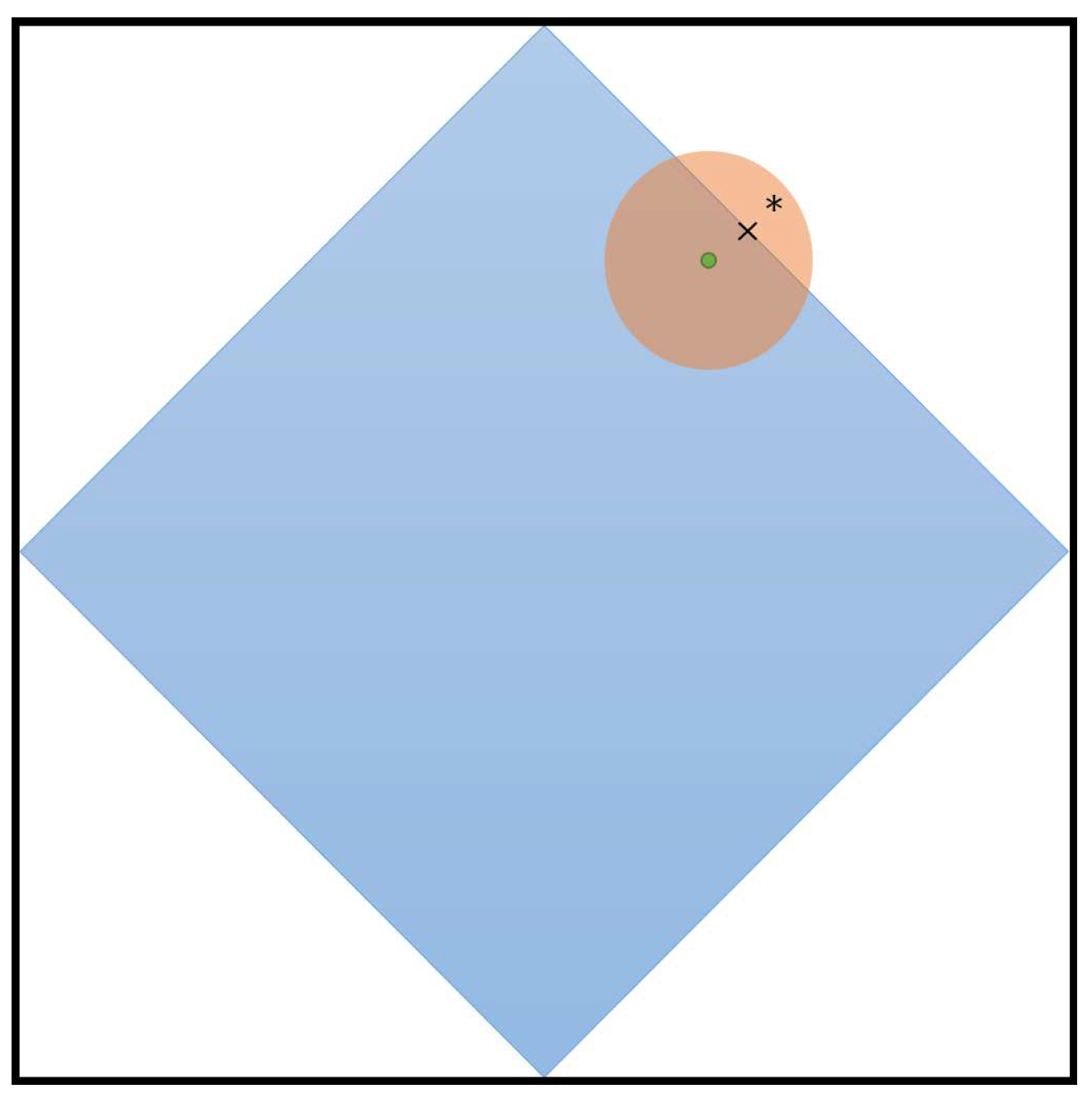
The performance of quantum tomography requires further development based on the standard quantum tomography methods consisting of linear inverse and MLE. First, the effectiveness of frequency-based standard methods requires further consideration. The estimated probabilities are biased with finite sampling, which results in the possibility of violation of physical implementability as it may occur in linear inverse methods. It seems that this problem has been solved by MLE methods. However, it can be verified that the MLE outputs the same result as linear inverse methods when using the same set of measurement data without constraints. The introduction of constraints forces the output to satisfy the physical requirement, which means the result lies on the boundary of feasible solutions, as shown in Figure 4. This indicates that no reasonable error bar can be applied in this estimation.
Bayesian tomographic methods are proposed for this systematic problem [13,18,32,33]. These methods propose meaningful formations for the estimation error of the target. The tomographic targets are assumed to obey a probability distribution. After optimization, the final target is set as the expectation of the distribution, which naturally has a reasonable error bar corresponding to the variance. Nevertheless, Bayesian methods are quite time-consuming due to the construction of distribution. Efficient Bayesian estimation for quantum tomography needs further research.
Then, the efficiency indicated by the accuracy gained from the unit number of experiments and the unit time of the post-process algorithm should be further improved. As previously introduced, the linear inverse provides relatively quick methods for tomography, but the accuracy is bounded by the reciprocal of the number of samples without the capability of utilizing additional data to improve the accuracy. Moreover, sampling errors may cause physical violations of results. The MLE methods have the capability of utilizing additional data with physical constraints. However, performing optimization algorithms to solve constrained optimization problems with an exponentially large number of parameters is time-consuming, which limits these methods to small-scale systems. Recently, researchers have proposed several methods to enhance the efficiency of quantum tomography.
Following the trend of the development of machine learning, a quantum tomography scheme utilizing the neural network has been proposed [34,35,36,37]. Typically, training and testing data sets consist of measurement results and prior tomographic results. Then, the neural network explicitly learns the map from measurement data to the tomographic target, and implicitly learns the knowledge of non-target components. To a certain extent, the absence of knowledge of non-target components mitigates the impact of imperfect implementations. Remarkably, when the training has been finished, neural-network-based methods have obtained higher accuracy with the same number of probability data inputs compared with the linear inverse method. It should be noted that neural-network-based methods may not generate physical implementable results due to the absence of constraints. However, physical constraints can be introduced into the cost function while performing neural network training, which results in time-consuming neural network training.
Another approach to enhance efficiency involves leveraging the prior structure of the tomographic target. In other words, incorporating certain assumptions about the tomographic target can prove beneficial. One well-known assumption is employed in Compressed Tomography [12,38,39], which posits that the tomographic target exhibits a low-rank characteristic. This methodology has evolved from matrix completion techniques, where the complete target matrix is reconstructed from incomplete elements using random sampling and a nuclear norm minimization algorithm. For instance, consider an unknown quantum state ρ with rank ( ρ ) ≤ r . By employing this approach, an estimate ρ ^ can be derived with only O ( r d log 2 d ) measurement settings. Additionally, other prior structural assumptions, such as matrix product states [40], permutationally invariant states [41], and similar concepts, also contribute significantly to enhancing efficiency.

Author Contributions

For research articles with several authors, a short paragraph specifying their individual contributions must be provided. The following statements should be used “Conceptualization, X.X. and Y.Y.; methodology, X.X.; software, X.X.; validation, X.X., Y.Y. and Z.Z.; formal analysis, X.X.; investigation, X.X.; resources, X.X.; data curation, X.X.; writing–original draft preparation, X.X.; writing–review and editing, X.X.; visualization, X.X.; supervision, X.X.; project administration, X.X.; funding acquisition, Y.Y. All authors have read and agreed to the published version of the manuscript.”, please turn to the CRediT taxonomy for the term explanation. Authorship must be limited to those who have contributed substantially to the work reported.

Funding

Please add: “This research received no external funding” or “This research was funded by NAME OF FUNDER grant number XXX.” and and “The APC was funded by XXX”. Check carefully that the details given are accurate and use the standard spelling of funding agency names at

Acknowledgments

We acknowledge funding from Suzhou Innovation and Entrepreneurship Pioneer Program (Grant No. ZXL2022424) and Jiangsu Province Industrial Foresight and Key Core Technology Research Plan (Grant No. BE202311).

Conflicts of Interest

Declare conflicts of interest or state “The authors declare no conflict of interest.” Authors must identify and declare any personal circumstances or interest that may be perceived as inappropriately influencing the representation or interpretation of reported research results. Any role of the funders in the design of the study; in the collection, analyses or interpretation of data; in the writing of the manuscript, or in the decision to publish the results must be declared in this section. If there is no role, please state “The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results”.

Appendix A Examples

Example A1 
(CP violation). Let the QPT target with SE correlations be
G S E = ∏ P = X , Y , Z cos ( w t ) I S ⊗ I E − sin ( w t ) P S ⊗ P E ,
which is a unitary. Let the initial SE state be
ρ S E ( 0 ) = 1 4 I S ⊗ I E + a → σ → S ⊗ I E + g Y S ⊗ Z E ,
where a → σ → S = [ a x , a y , a z ] [ X S , Y S , Z S ] † = a x X S + a y Y S + a z . Since the experimenter can only intervene in the system state, we prepare states by setting a → to be [ ± 1 , 0 , 0 ] T , [ 0 , 1 , 0 ] T , and [ 0 , 0 , 1 ] T . Hence, the Choi state of tomographic result G ^ is
ξ G ^ = 1 2 1 + c 2 0 − g c s 2 c 2 0 1 − c 2 0 − g c s − g c s 0 1 − c 2 0 2 c 2 − g c s 0 1 + c 2 ,
where c = cos ( 2 w t ) and s = sin ( 2 w t ) . There exist eigenvalues 1 2 [ 1 − c 2 ± 2 c s ] that may be negative and cause the theoretical CP violation.

Appendix B Likelihood Function

In this review, we utilize the likelihood function as described below. Let the probability be measured by repeating the experiment n s times and recording n i , which denotes how many times the desired output i occurs. Therefore, we use the general likelihood function
L ( T ^ ) = ∏ i ( p ^ i ) n i ( 1 − p ^ i ) n s − n i ,
where p ^ i is the probability estimator modeled by parameters of tomography target T ^ .
By exploiting the central limit theorem, each term of the likelihood can be rewritten as a normal distribution,
L ( T ^ ) = ∏ i exp − p ˜ i − p ^ i 2 σ i 2 ,
where p ˜ i = n i / n s represents the measured probability, σ i 2 = p ˜ i ( 1 − p ˜ i ) / n s is the sampling variance in the measurement m i . Exploiting the monotonic logarithm function, maximizing L is equivalent to minimizing the weighted mean square error
l ( T ^ ) = − log ( L ( T ^ ) ) = ∑ i p ˜ i − p ^ x 2 σ i 2 .

References

  1. M. Kliesch and I. Roth, Theory of quantum system certification, PRX Quantum 2, 010201 (2021).
  2. J. Eisert, D. Hangleiter, N. Walk, I. Roth, D. Markham, R. Parekh, U. Chabaud, and E. Kashefi, Quantum certification and benchmarking, Nature Reviews Physics 2, 382 (2020).
  3. G. M. D’Ariano, M. G. A. Paris, and M. F. Sacchi, Quantum tomography, Advances in Imaging and Electron Physics 128, 205 (2003).
  4. H. Häffner, W. Hänsel, C. F. Roos, J. Benhelm, D. Chek-al-kar, M. Chwalla, T. Körber, U. D. Rapol, M. Riebe, P. O. Schmidt, C. Becher, O. Gühne, W. Dür, and R. Blatt, Scalable multiparticle entanglement of trapped ions, Nature 438, 643 (2005).
  5. D. Greenbaum, Introduction to quantum gate set tomography, arXiv:1509.02921 [quant-ph] (2015), arxiv:1509.02921 [quant-ph].
  6. R. O’Donnell and J. Wright, Efficient quantum tomography, in Proceedings of the Forty-Eighth Annual ACM Symposium on Theory of Computing, STOC ’16 (Association for Computing Machinery, New York, NY, USA, 2016) pp. 899–912.
  7. C. Granade, C. Ferrie, and S. T. Flammia, Practical adaptive quantum tomography*, New Journal of Physics 19, 113017 (2017).
  8. Z. Cai, R. Babbush, S. C. Benjamin, S. Endo, W. J. Huggins, Y. Li, J. R. McClean, and T. E. O’Brien, Quantum error mitigation, Reviews of Modern Physics 95, 045005 (2023).
  9. D. A. Lidar and T. A. Brun, Quantum error correction (Cambridge university press, 2013).
  10. J. Roffe, Quantum error correction: An introductory guide, Contemporary Physics 60, 226 (2019).
  11. D. G. Cory, M. D. Price, W. Maas, E. Knill, R. Laflamme, W. H. Zurek, T. F. Havel, and S. S. Somaroo, Experimental quantum error correction, Physical Review Letters 81, 2152 (1998).
  12. D. Gross, Y.-K. Liu, S. T. Flammia, S. Becker, and J. Eisert, Quantum state tomography via compressed sensing, Physical Review Letters 105, 150401 (2010).
  13. R. Blume-Kohout, Optimal, reliable estimation of quantum states, New J. Phys. 12, 043034 (2010).
  14. M. Christandl and R. Renner, Reliable quantum state tomography, Physical Review Letters 109, 120403 (2012).
  15. M. Mohseni, A. T. Rezakhani, and D. A. Lidar, Quantum-process tomography: Resource analysis of different strategies, Physical Review A 77, 032322 (2008).
  16. S. T. Merkel, J. M. Gambetta, J. A. Smolin, S. Poletto, A. D. Córcoles, B. R. Johnson, C. A. Ryan, and M. Steffen, Self-consistent quantum process tomography, Physical Review A 87, 062119 (2013).
  17. M. Riebe, K. Kim, P. Schindler, T. Monz, P. O. Schmidt, T. K. Körber, W. Hänsel, H. Häffner, C. F. Roos, and R. Blatt, Process tomography of ion trap quantum gates, Physical Review Letters 97, 220407 (2006).
  18. K. Schultz, Exponential families for Bayesian quantum process tomography, Phys. Rev. A 100, 062316 (2019).
  19. E. Nielsen, J. K. Gamble, K. Rudinger, T. Scholten, K. Young, and R. Blume-Kohout, Gate set tomography, Quantum 5, 557 (2021).
  20. K. Rudinger, G. J. Ribeill, L. C. Govia, M. Ware, E. Nielsen, K. Young, T. A. Ohki, R. Blume-Kohout, and T. Proctor, Characterizing midcircuit measurements on a superconducting qubit using gate set tomography, Physical Review Applied 17, 014014 (2022).
  21. F. A. Pollock, C. Rodríguez-Rosario, T. Frauenheim, M. Paternostro, and K. Modi, Non-Markovian quantum processes: Complete framework and efficient characterization, Phys. Rev. A 97, 012127 (2018).
  22. G. White, F. Pollock, L. Hollenberg, K. Modi, and C. Hill, Non-markovian quantum process tomography, PRX Quantum 3, 020344 (2022).
  23. Z.-T. Li, C.-C. Zheng, F.-X. Meng, H. Zeng, T. Luan, Z.-C. Zhang, and X.-T. Yu, Non-markovian quantum gate set tomography (2023), arxiv:2307.14696 [quant-ph].
  24. J. Carolan, J. D. A. Meinecke, P. J. Shadbolt, N. J. Russell, N. Ismail, K. Wörhoff, T. Rudolph, M. G. Thompson, J. L. O’Brien, J. C. F. Matthews, and A. Laing, On the experimental verification of quantum complexity in linear optics, Nature Photonics 8, 621 (2014).
  25. A. I. Lvovsky and M. G. Raymer, Continuous-variable optical quantum-state tomography, Reviews of Modern Physics 81, 299 (2009).
  26. M. Bellini, A. S. Coelho, S. N. Filippov, V. I. Man’ko, and A. Zavatta, Towards higher precision and operational use of optical homodyne tomograms, Physical Review A 85, 052129 (2012).
  27. S. Milz and K. Modi, Quantum stochastic processes and quantum non-markovian phenomena, PRX Quantum 2, 030201 (2021).
  28. A. Jamiołkowski, Linear transformations which preserve trace and positive semidefiniteness of operators, Reports on Mathematical Physics 3, 275 (1972).
  29. E. B. Davies, Quantum stochastic processes, Communications in Mathematical Physics 15, 277 (1969).
  30. Z. Hradil, Quantum-state estimation, Physical Review A 55, R1561 (1997).
  31. J. Shang, Z. Zhang, and H. K. Ng, Superfast maximum-likelihood reconstruction for quantum tomography, Physical Review A 95, 062336 (2017).
  32. F. Huszár and N. M. T. Houlsby, Adaptive bayesian quantum tomography, Physical Review A 85, 052120 (2012).
  33. D. H. Mahler, L. A. Rozema, A. Darabi, C. Ferrie, R. Blume-Kohout, and A. M. Steinberg, Adaptive quantum state tomography improves accuracy quadratically, Physical Review Letters 111, 183601 (2013).
  34. M. Neugebauer, L. Fischer, A. Jäger, S. Czischek, S. Jochim, M. Weidemüller, and M. Gärttner, Neural-network quantum state tomography in a two-qubit experiment, Physical Review A 102, 042604 (2020).
  35. A. M. Palmieri, E. Kovlakov, F. Bianchi, D. Yudin, S. Straupe, J. D. Biamonte, and S. Kulik, Experimental neural network enhanced quantum tomography, npj Quantum Information 6, 1 (2020).
  36. G. Torlai, G. Mazzola, J. Carrasquilla, M. Troyer, R. Melko, and G. Carleo, Neural-network quantum state tomography, Nature Physics 14, 447 (2018).
  37. A. M. Palmieri, E. Kovlakov, F. Bianchi, D. Yudin, S. Straupe, J. D. Biamonte, and S. Kulik, Experimental neural network enhanced quantum tomography, npj Quantum Information 6, 1 (2020).
  38. M. Kliesch, R. Kueng, J. Eisert, and D. Gross, Guaranteed recovery of quantum processes from few measurements, Quantum 3, 171 (2019).
  39. I. Roth, R. Kueng, S. Kimmel, Y.-K. Liu, D. Gross, J. Eisert, and M. Kliesch, Recovering quantum gates from few average gate fidelities, PHYSICAL REVIEW LETTERS 10.1103/PhysRevLett.121.170502 (2018).
  40. M. Cramer, M. B. Plenio, S. T. Flammia, R. Somma, D. Gross, S. D. Bartlett, O. Landon-Cardinal, D. Poulin, and Y.-K. Liu, Efficient quantum state tomography, Nature Communications 1, 149 (2010).
  41. G. Tóth, W. Wieczorek, D. Gross, R. Krischek, C. Schwemmer, and H. Weinfurter, Permutationally invariant quantum tomography, Physical Review Letters 105, 250403 (2010).
Preprints 94736 g002
Figure 2. Model of operational open quantum process. Components marked by green blocks are inaccessible to the experimenter, while instruments marked by red blocks are the only accessible components.
Figure 2. Model of operational open quantum process. Components marked by green blocks are inaccessible to the experimenter, while instruments marked by red blocks are the only accessible components.
Preprints 94736 g002
Preprints 94736 g003
Figure 3. Workflow of MLE based quantum tomography. Components are specified in the Markovian settings for facilitating understanding, although the workflow is general for both Markovian and non-Markovian situations.
Figure 3. Workflow of MLE based quantum tomography. Components are specified in the Markovian settings for facilitating understanding, although the workflow is general for both Markovian and non-Markovian situations.
Preprints 94736 g003
Preprints 94736 g004
Figure 4. Utilizing the black box to represent the whole space of the tomographic target, the space of physical implementable results is represented by the blue region. The green dot is the ideal tomographic target to be characterized. Due to the probabilistic sampling, the sampled target may lie in the red region. Assuming the sampled target to be * out of physical implementable space, the MLE result lies on the boundary of the implementable region, which can be represented by ×.
Figure 4. Utilizing the black box to represent the whole space of the tomographic target, the space of physical implementable results is represented by the blue region. The green dot is the ideal tomographic target to be characterized. Due to the probabilistic sampling, the sampled target may lie in the red region. Assuming the sampled target to be * out of physical implementable space, the MLE result lies on the boundary of the implementable region, which can be represented by ×.
Preprints 94736 g004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated