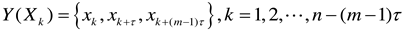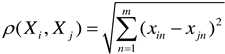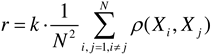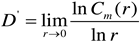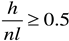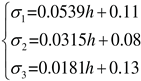1. Introduction
Mine water inrush represents a significant geological hazard in underground mining [
1,
2]. In the context of underwater and subsea mining operations, a protective isolation layer of specified thickness is conventionally employed as a safety barrier to segregate the mining zone from the surrounding aquatic environment [
3,
4]. Throughout the continuous extraction of ore deposits, the surrounding rock formations undergo intricate processes, including stress redistribution and seepage effects. These factors can contribute to the generation of secondary fractures within the rock mass, resulting in the degradation of the surrounding geological strata. This, in turn, can precipitate progressive deterioration of the expansive isolation layer, potentially culminating in catastrophic incidents such as roof collapses and water inrush events [
5,
6]. Consequently, the investigation of isolation layers within fractured geological mediums holds paramount significance in ensuring the safety and efficacy of underground mining practices [
7,
8].
Previous research has explored diverse approaches to address the challenges of undersea mining. Traditionally, the isolation layer has been treated as an ideal continuum body, with its thickness estimated using methods such as the thickness-span ratio [
9], the general arch approach [
10], and the load transfer intersection line technique [
11]. Additionally, numerical simulation tools like FLAC3D, PFC, and UDEC [
12] have gained widespread adoption due to their practicality and simplicity in analyzing the mechanical behavior of the isolation layer. However, it is well-established that underground rock strata are replete with adverse geological features, including joints and fractures [
13], whose intricate geometries make it nearly impossible to ascertain their true structure [
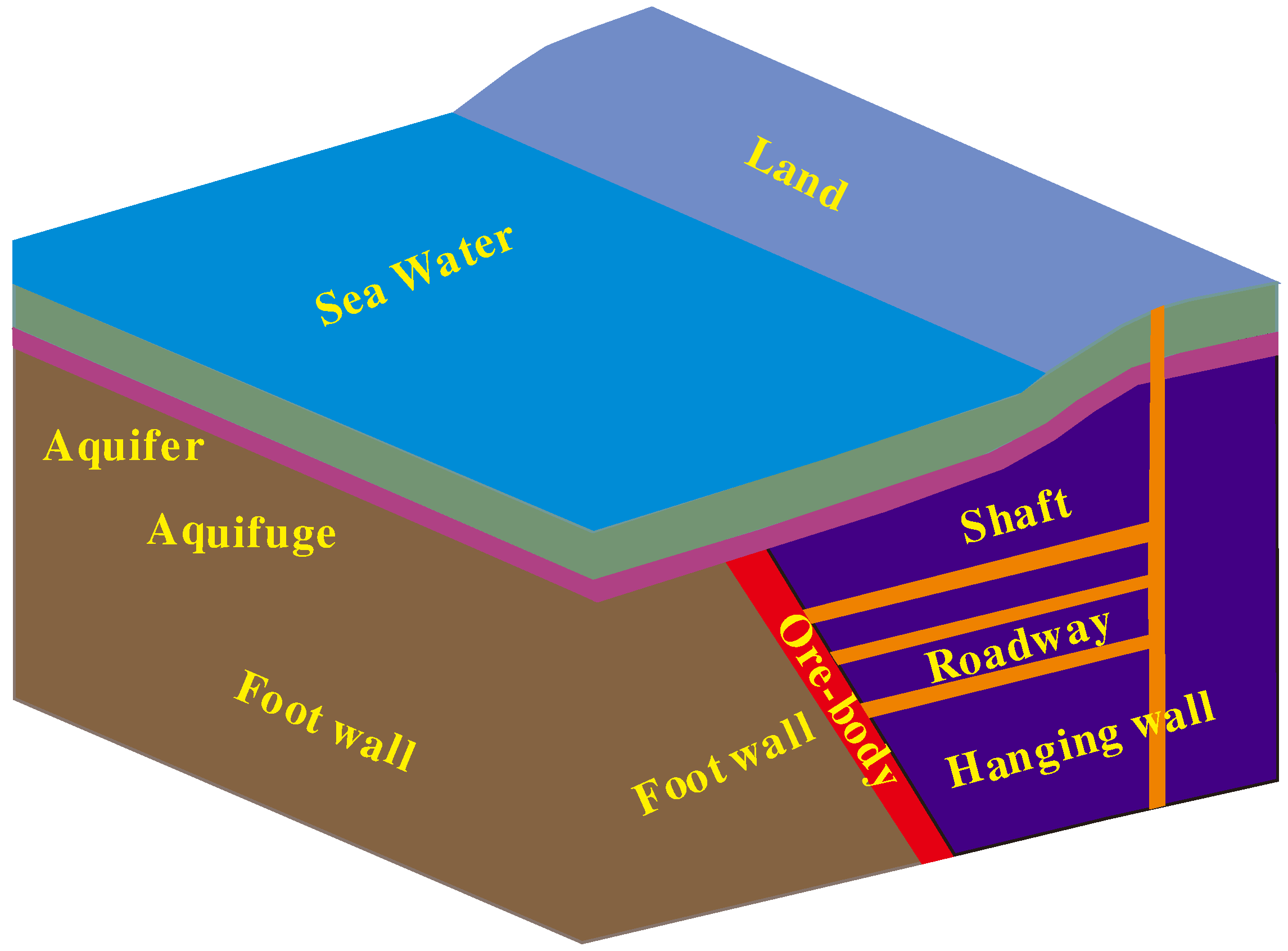
14]. Consequently, the utilization of continuum mechanics to investigate the isolation layer, without accounting for the influence of fractures, appears inherently flawed. In the context of undersea mining, exemplified by the Xinli mining area of the Sanshan Island gold mine, as depicted in
Figure 1, the extraction of high-grade ore deposits from the isolation layer while ensuring safety can optimize overall profitability. Recognizing that the evolutionary dynamics of fractured rock masses under seepage-mechanical coupling play a pivotal role in assessing the stability of underground mining, an exploration of the interplay between fracture evolution characteristics and the thickness of the isolation layer offers a novel avenue for enhancing the safety and efficiency of undersea mining.
Fortunately, the propagation and development of fractures within a rock mass can be effectively studied using the discrete element method. Within this methodological framework, two primary approaches are prominent: the Particle Flow Method [
15] and the Block Discrete Element Method [
16,
17]. The Particle Flow Method is particularly suited for delving into the micromechanics of rock masses [
18], while the Block Discrete Element Method finds its applicability in the intermediate realm, bridging the gap between continuous medium and particle discrete body analyses [
19,
20]. To enhance the simulation of fracture behavior within rock masses, a novel approach, the Bonded Block Model (BBM), has been introduced and integrated into 3DEC. This incorporation has yielded notably improved results [
21]. Research underscores that fractures exhibit self-similarity, a characteristic known as fractal behavior [
22]. Fractals, by their very nature, remain scale-independent, enabling their versatile application in characterizing fracture propagation [
23] and predicting the permeability of fractured rock formations [
24].
As demonstrated in prior research, both the discrete element method and fractal models have proven capable of elucidating the mechanical behaviors of fractured rock, taking into account both macro and micro-sized fracture characteristics. However, no previous studies have explored undersea mining through the synergistic application of fractal theory and the Bonded Block Model (BBM), an approach that holds promise and effectiveness. Hence, this study introduces a novel Fractal BBM model for simulating isolation layer mining, accompanied by the development of dedicated software to predict the optimal thickness within a three-dimensional (3D) numerical model. Subsequently, we conducted on-site monitoring and validation to assess the model's capacity to depict natural fractures and its efficacy in forecasting undersea isolation layer mining outcomes for the future.
2. Fractal Theory of Fractures
Self-similarity and fractal dimension represent fundamental attributes of fractal theory. In a more detailed context, fractal dimension provides a quantitative measure of the extent of self-similarity and irregularity within a fractal structure.
2.1. Fractal Dimension of Fractures in Rock
So far, the box dimension method [
25,
26] is one of the most common methods to calculate the fractal dimension of images. The basic calculation principle is shown as follows.
Assume
A(
x,
ԑ) to be a closed sphere with the center of
x and radius of
ԑ, of which
ԑ is a non-negative real number, and a non-empty compact set of
A in
X is created. For each positive
ԑ:
where
ԑ and
C are constant, and
N(
A,
ԑ) denote the minimum number of closed sphere covering A. Then the box dimension of
A is:
Let
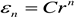
, where r is the side
length of box, then:
Let
Nn(
A) be the number of boxes intersect A, and the side length of box is 1/2
n, then:
In practical application, calculate the value of ln(2n) and lnNn(A) by counting the box number with different sizes, where n ranges from 1, 2, 3, …, N sequentially, curve can be draw with ln(2n) as abscissa and lnNn(A) as ordinate respectively.
2.2. Estimation of the Height of the Isolation Layer through Correlation Dimension
Within the realm of fractal theory, the correlation dimension stands out as one of the frequently employed fractal dimensions. To calculate the correlation dimension, the G-P algorithm, originally advanced by Grassberger and Procaccia [
27,
28], leverages the principles of embedding theory and phase space reconstruction.
Suppose a sequence with capacity n was obtained, namely
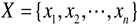
,
xi
could be extended into the phase distribution
Y(
Xk) of
m-dimensional phase space by a certain embedding dimension
m and
τ.
The expression of
Y(
Xk) is
where
k is the number of phase points in the reconstructed phase space. We can determine m and
τ by following steps below:
a. Calculate the distance between two adjacent phase
points of
xi and
xj (
i,
j, …,
N,
i≠
j)
b. Given any critical distance
r (
r>0), the probability that the distance between two phase points is less than r is calculated as
where
θ is the Heaviside function,
r is the given scale, in order to avoid discreteness, r can be given by Eq.(9):
where k is the corresponding coefficient, and k > 0.1
c. The correlation vector is the vector whose distance from the phase point is less than
r. Take the value of
r within a certain range, and the correlation dimension of the system can be defined as
To a certain extent, the correlation dimension can elucidate trends in variations, such as displacement and energy, shedding light on the rock's failure characteristics from a distinctive perspective. Consequently, the computed correlation dimension holds substantial importance as a foundational criterion for assessing both the stability of the rock mass and the requisite thickness of the isolation layer.
3. Experiments of Chamber Mining Undersea
In similar materials, there exists a multitude of micro-defects, which, under the influence of external forces, grow and merge, regardless of their varying sizes. This leads to localized damage within the material, resulting in acoustic emissions. Moreover, acoustic emission signals exhibit distinct characteristics during different stress stages. Experimental evidence demonstrates that the acoustic emission sequences of rock materials follow a fractal distribution not only in the time domain but also in the spatial domain. These acoustic emission signals form a series that evolves over time, and utilizing their fractal characteristics aids in studying the evolutionary patterns of rock damage and failure processes.
3.1. Similarity Simulation Test Platform for Undersea Mining
A comparable simulation test platform was established a to replicate undersea deposit mining conditions at Sanshandao Gold Mine. This simulation setup, illustrated in
Figure 2, comprises a horizontal side pressure loading apparatus, a vertical pressure loading mechanism, a testing framework, a hydraulic servo pump station, a control console, and measuring instruments. Notable technical specifications include a maximum vertical load capacity of 300 kN, hydraulic loading capabilities up to 1.0 MPa, horizontal displacement within the range of 0-100 mm, and a model dimensions measuring 1600 mm×800 mm×200 mm.
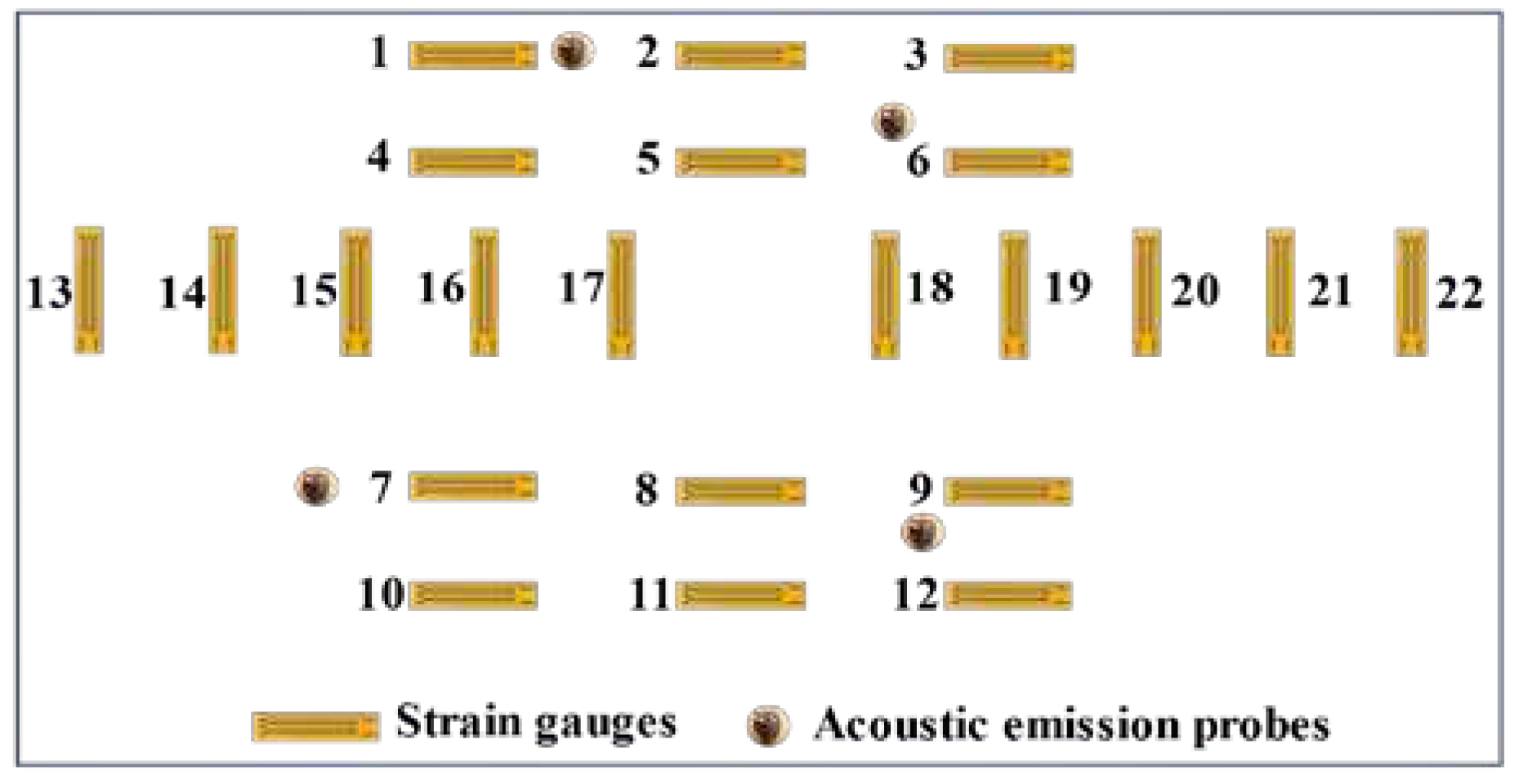
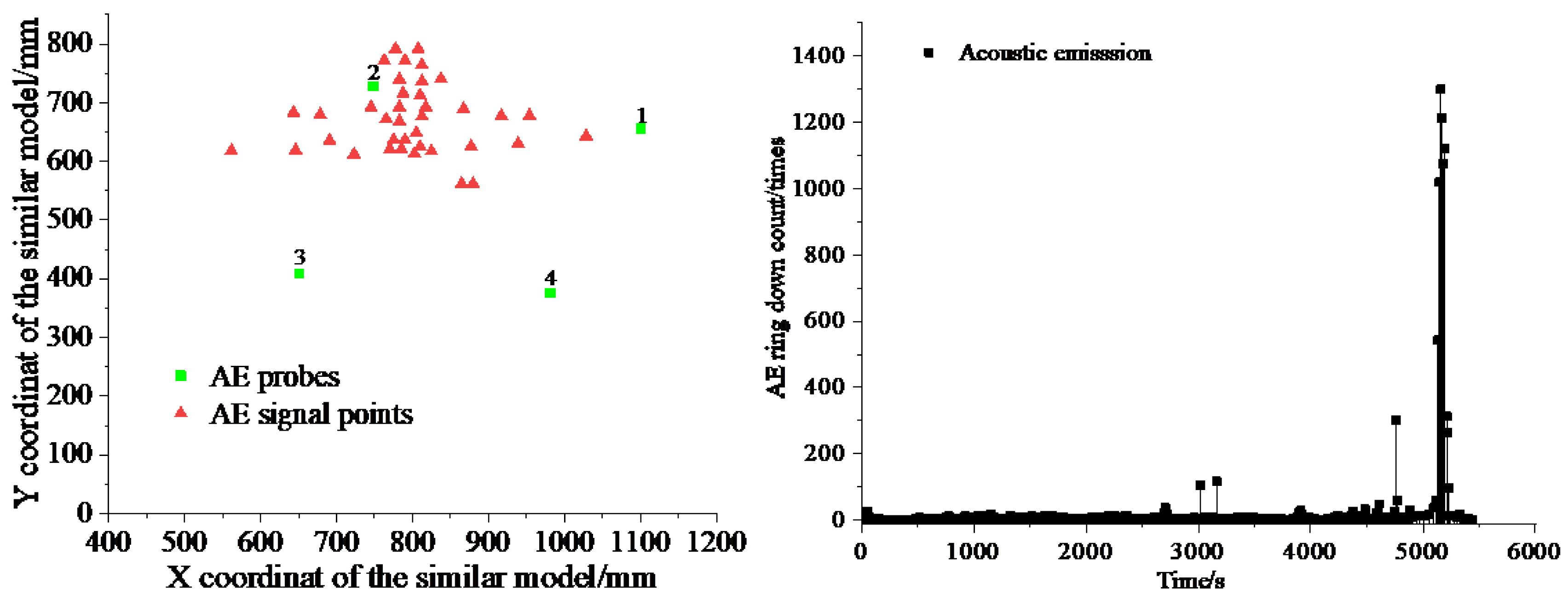
In the simulation experiment, solid paraffin and liquid paraffin were employed as cementing agents, while river sand and barite powder served as aggregates. To assess the deformation characteristics of the analogous test platforms, the experiment utilized the PCI-2 Acoustic Emission (AE) system for real-time monitoring of AE events. Additionally, a strain gauge was affixed and connected to the DH3816 static strain test system, as depicted in
Figure 3.
3.2. Estimation of the Isolation Layer Thickness of the Similar Model
The extraction of a specific thickness of waterproof rock pillars in underwater mining constitutes a pivotal element in ensuring safety during subaqueous mining operations. In accordance with the thickness-span ratio theory [
29], the critical criterion for preventing the rupture of these waterproof rock pillars is that the ratio of their height to the span of the stope must exceed 0.5, namely
where
h is the height of the waterproof rock pillar,
l is the span of the panel, and
n is the safety factor.
The experimental setup employed a similarity ratio of 1:200, and the excavation process was divided into ten sequential steps, gradually progressing from the center towards the sides, with each step involving an excavation depth of approximately 0.04 meters.
Figure 4 illustrates the stepwise excavation process within the simulated test, conducted under conditions mimicking a mining environment featuring 10 meters of seawater and 35 meters of sea mud. A safety roof thickness of 40 meters was maintained, and
Figure 4(a) to
Figure 4(f) depict photographs captured as the chamber's span reached 0.14 meters, 0.28 meters, and 0.4 meters, respectively. Based on the test outcomes, the similarity ratio and the safety thickness-span ratio formula were applied for analysis. It was determined that when the roof thickness exceeded 40 meters, there was no risk of water inrush within the rock formation. Conversely, when the roof thickness fell below 40 meters, characteristics indicative of water inrush in the rock formation emerged, as exemplified in
Figure 4(f).
3.3. Fractures Evolution of Isolation Layer under the Pressure and Seepage Coupling
In
Figure 4(f), following the completion of ten excavation steps, the AE system registered a robust signal at the central apex of the stope, coinciding with the onset of water inrush. Employing the localization capabilities of the acoustic emission system, it was determined that fractures were concentrated at the top center of the stope. As the span expanded, the acoustic emission signal at the stope's apex exhibited gradual amplification in tandem with ongoing excavation, as demonstrated in
Figure 5. Subsequently, throughout the course of the experiment, an increasing frequency of AE signals was observed, signifying the formation of a greater number of fractures.
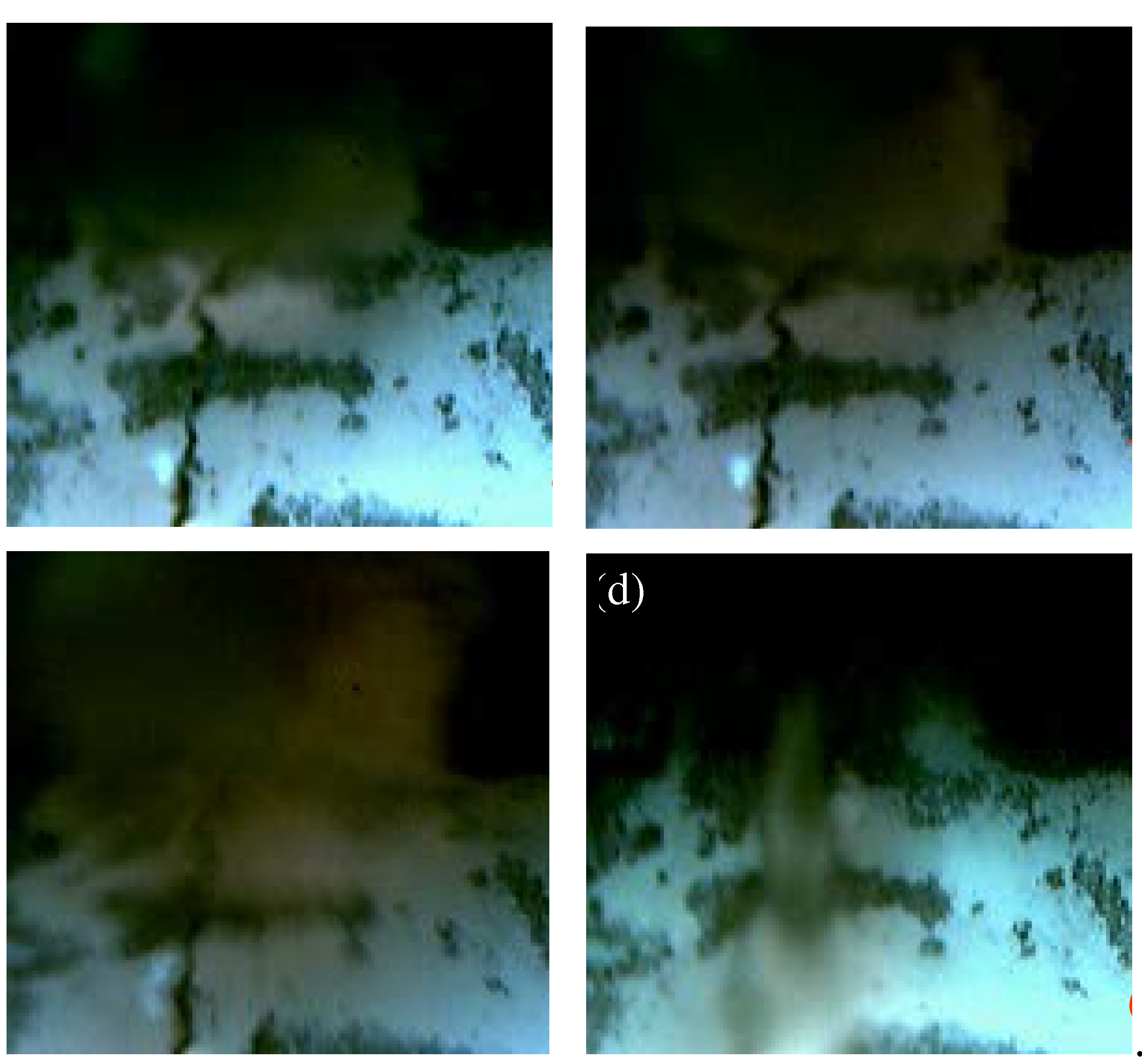
Upon a notable increase in AE signals, timely inspection was conducted using a stereo microscope, and microscopic measurement analysis software was employed to scrutinize the fissures. As illustrated in
Figure 6, the measurement graph depicts an average fissure width of 0.02 mm and a horizontal inclination angle of 20.58° for the upper fracture.
Figure 6 serves as a comparative illustration, showcasing conditions both before and after the emergence of fracture-induced water flow within the test module. The tests have conclusively demonstrated that once the distance between the stope roof and the fissures falls below 40 meters, pressurized water begins to erode the fissures continuously, eventually giving rise to a smoothly channelized conduit. This streamlined outflow of water from the fissures signifies a fundamental aspect of the model's water inrush failure mechanism.
.
4. Modelling the Mining of Isolation Layer Using Boned Block Model
The Bonded Block Model (BBM) approach simulates the initiation of cracks that can coalesce and/or propagate leading to extension and shear fracturing, as well as the rock (e.g., intact, jointed, or veined) strength dependency on confinement. Over the years, various representations of these components, such as elastic and inelastic zones as well as heterogeneous and homogeneous blocks and contacts (corresponding to distinct mineral grains and their associated mechanical properties), have been utilized to simulate diverse aspects of rock behavior.
4.1. Rock Mass Parameters Calibration of the Boned Block Model
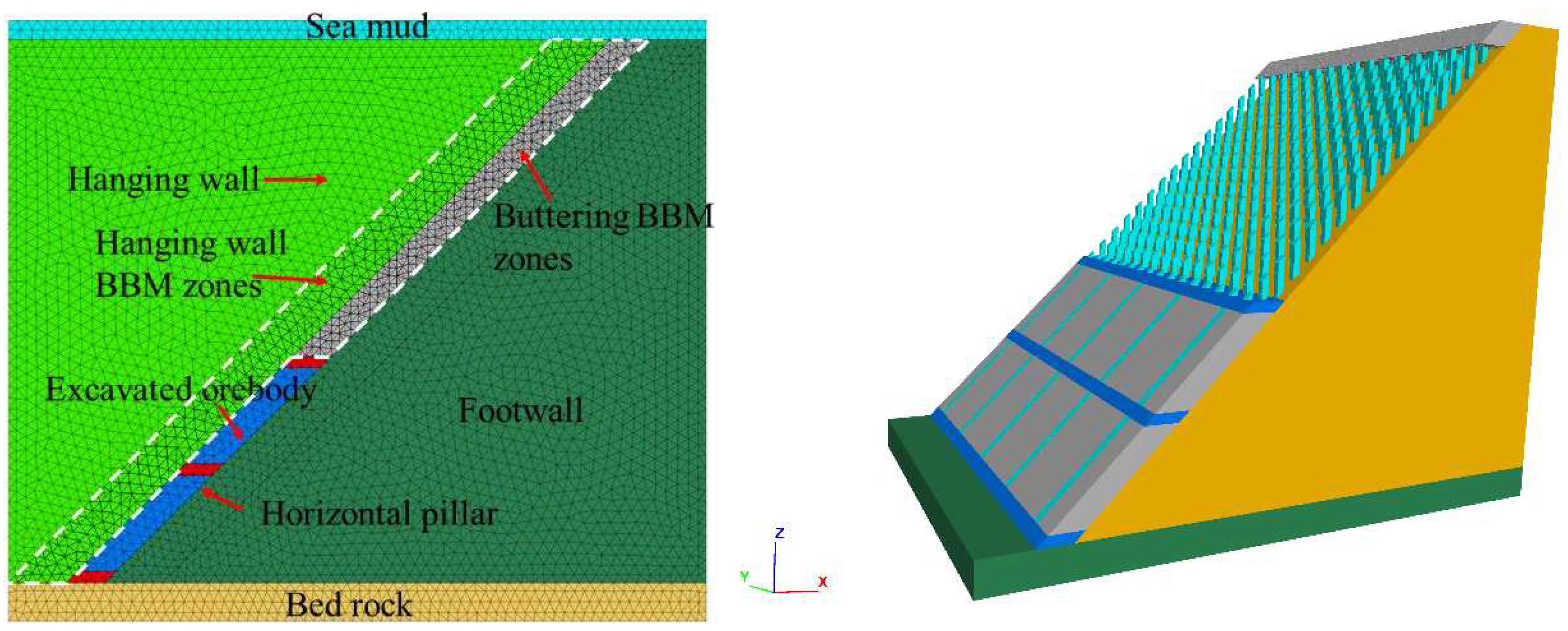
This study is conducted within the context of the Xinli mining area, focusing on a numerical model centered on the 55-line section of a substantial ore body. The primary objective is to investigate the dynamics of overlying strata movement and the evolution of mining-induced fissures within the isolation layer situated above -165 meters during the mining operation. For the sake of simplifying the modeling process, this simulation adopts a regular ore body with a uniform average thickness of 15 meters, disregarding the natural variation in ore body thickness. In the context of undersea mining activities, it is common for the expansion and alteration of rock formations to occur, resulting in seawater ingress predominantly from the upper strata, including the isolation layer.
The mechanical properties of the rock mass used in our analyses are derived from test results obtained from rock samples sourced from the Xinli mining area. These properties vary, as presented in
Table 1.
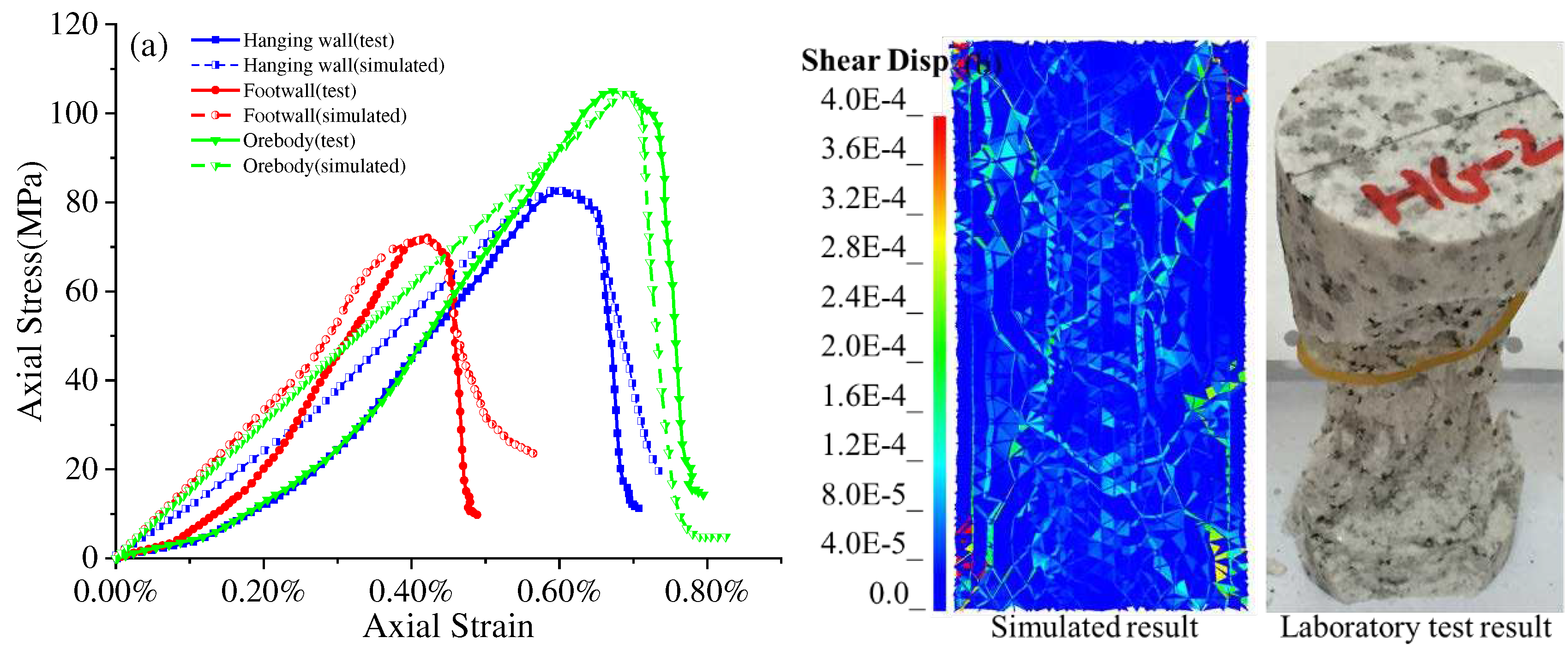
As
Figure 7 shows, for the uniaxial compression test simulation, a numerical model of block with a standard size of Ф50mm
100mm and an average side length of 3.0mm (the average particle size of the granite sample in the laboratory) is used.
Through the calibration of mesoscopic parameters, the corrected mesoscopic contact parameters of various types of ore rocks are shown in
Table 2.
4.2. Model Setup
The simulation of the isolation layer excavation was carried out using the 3DEC Bonded Block Model. In the Xinli mining area, ore bodies situated below the -165m level are mined using the high drift filling mining method, with a stage height of 50 meters and both roof and floor pillars having a thickness of 6 meters. For ore bodies above the -165m level, the point-pillar layered filling mining method is employed. In this mining area, the average horizontal thickness of the ore bodies ranges from 20 to 40 meters, with an average grade of approximately 3 g/t and an inclination angle typically between 33° and 67°. In our analysis, we maintain a constant orebody inclination angle of 62°, as depicted in
Figure 8.
4.3. Boundary Conditions and Initial Stress
Model loading was accomplished through the application of stress boundaries on the lateral and bottom surfaces, with a free boundary condition imposed on the top surface. Based on field investigations and regression analysis of geostress data, the initial stress undergoes depth-dependent changes, as represented in Eq. (1).
where σ
1, σ
3, and σ
2 correspond to the maximum horizontal principal stress, vertical principal stress, and minimum horizontal principal stress, respectively,
h is the depth. Notably, the maximum horizontal principal stress aligns with the NW direction, closely approximating the orientation of the maximum tectonic stress.
5. Numerical Simulation Results and Discussion
To ascertain the dynamic evolution of fracture fractal dimension and the alteration in fracture self-similarity, we conducted incremental mining on each layer of the established isolation layer mining model. The heterogeneous and inelastic Bonded Block Models (BBMs) have proven to be the most effective representation for modeling the comprehensive spectrum of rock fracture behaviors within the isolation layer, successfully aligning with all calibration targets.
5.1. Deformation of the Isolation Layer with Excavation
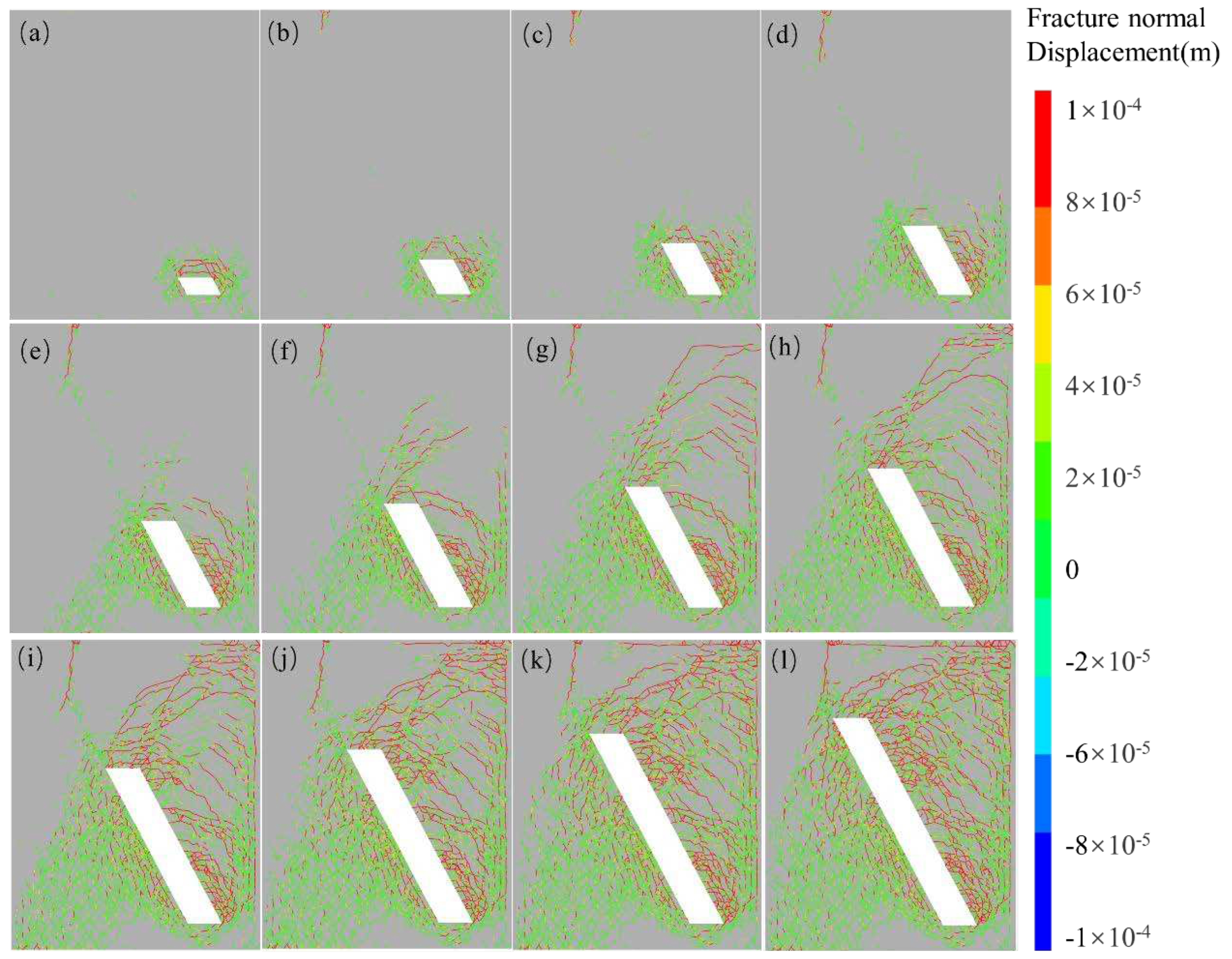
In this study, we first examined the dynamic evolution of fractures by investigating the deformation of the isolation layer. As depicted in
Figure 9, during the initial excavation of the isolation layer, the roof experienced a relatively substantial settlement, and as the isolation layer continued to be excavated, the settlement of the hanging wall's surrounding rock continued to increase, with an accelerating growth rate. A prominent master fracture, situated at the top of the isolation layer, emerged when excavation reached the -155-meter level. With further excavation, the rate of sedimentation in the hanging wall notably exceeded that of the footwall. Ultimately, the master fracture within the isolation layer penetrated the surrounding rock of the footwall. A significant transformation occurred after the complete penetration of the master fracture in the isolation layer: as the isolation layer continued to be excavated, conspicuous settlement in the surrounding rock of the footwall became evident.
In summary, it can deduce that the settlement of the surrounding rock was primarily governed by the behavior of the master fracture. Initially, the settlement of the footwall was impeded by the motion of the hanging wall. However, once the restriction was lifted, specifically when the master fracture was fully penetrated, pronounced deformation ensued in the footwall.
The maximum settlement, measuring 0.0153 meters, was observed in the hanging wall at the -165m level. In contrast, the deformation in the surrounding rock of the footwall diminishes progressively from top to bottom.
5.2. Fractal Evolution Characteristics of Rock Fractures
During the excavation of the orebody within the isolation layer, fracturing occurred at critically stressed contacts under stress-seepage coupling conditions. To further validate the mechanisms of isolation layer destruction, we examined the changes in the evolution of different types of fractures throughout the orebody excavation process.
Figure 10 illustrates the dynamic propagation of fractures around the isolation layer, revealing two distinct types: tensile and shear fractures. Several noteworthy patterns emerged from the evolution of fracturing.Upon analyzing the distribution of fractures, it became apparent that the surrounding rock of the hanging wall and the roof predominantly exhibited tensile fractures. A clear correlation emerged: the greater the number of tensile fractures, the more pronounced the settlement of the rock mass, a relationship consistently observed in the surrounding rock of the hanging wall. Conversely, the rock mass of the footwall primarily featured shear fractures. Closer to the excavation surface, the incidence of tensile fractures increased.
The observed phenomenon can be attributed to the excavation of the inclined isolation layer structure, which induced tensile extension of fractures within the hanging wall strata due to tectonic stress. Conversely, the footwall's surrounding rock experienced compression as a result of subsidence deformation in the surrounding rock of the hanging wall. This compression explains the prevalence of shear fractures in the footwall.
Evidently, as the thickness of the isolation layer decreases, there is a corresponding increase in the number of fractures. Fractal dimensions prove to be highly effective in quantitatively characterizing the propagation of these fractures. To achieve this quantification, we calculate the fractal dimension of these fractures. In practical applications, the computation involves determining the values of ln(2
n) and ln
Nn(
A) through a systematic enumeration of box sizes, with n incrementing sequentially from 1 to N. These values are then used to construct a curve, with ln(2
n) plotted on the abscissa and ln
Nn(
A) on the ordinate. In this paper, two-dimensional diagrams illustrating fracture propagation are employed to delineate their fractal attributes, as depicted in
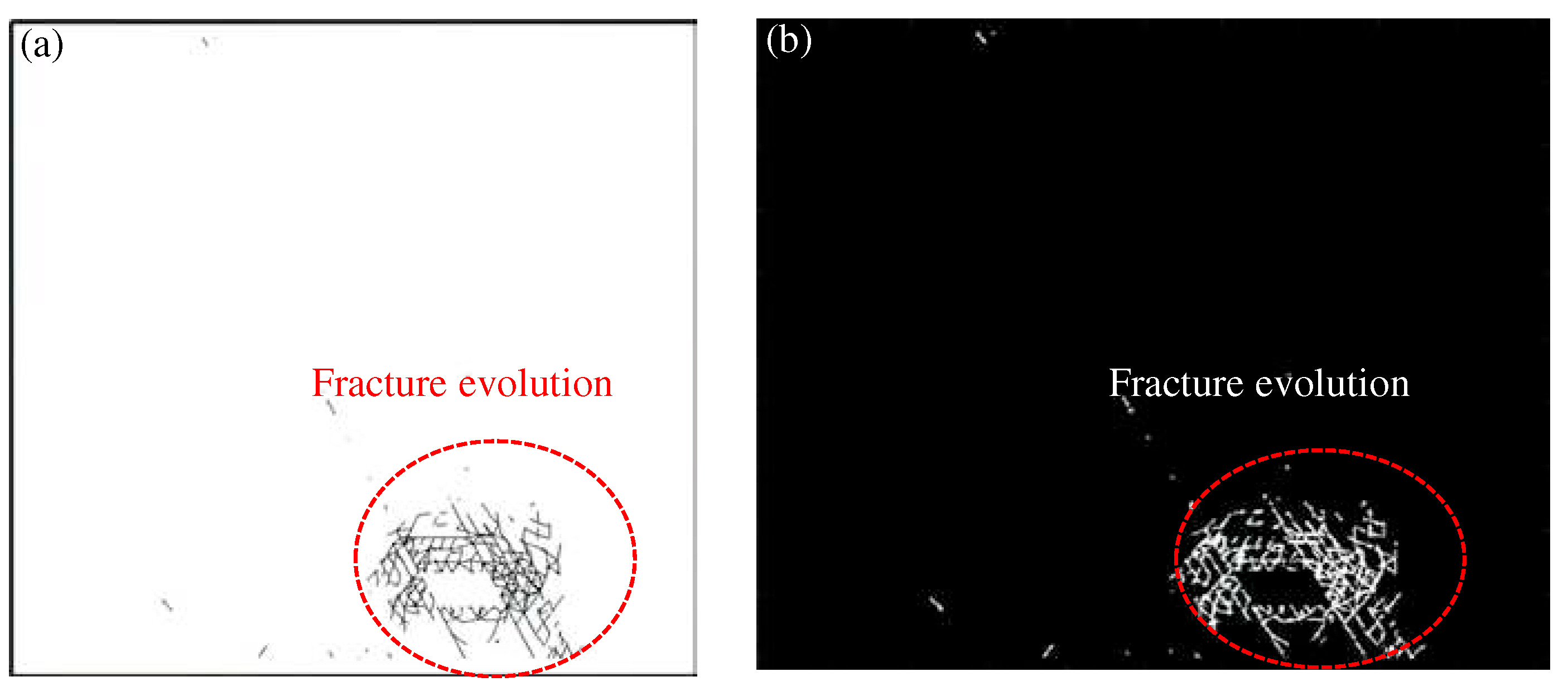
Figure 11.
Following image binarization processing, illustrated in
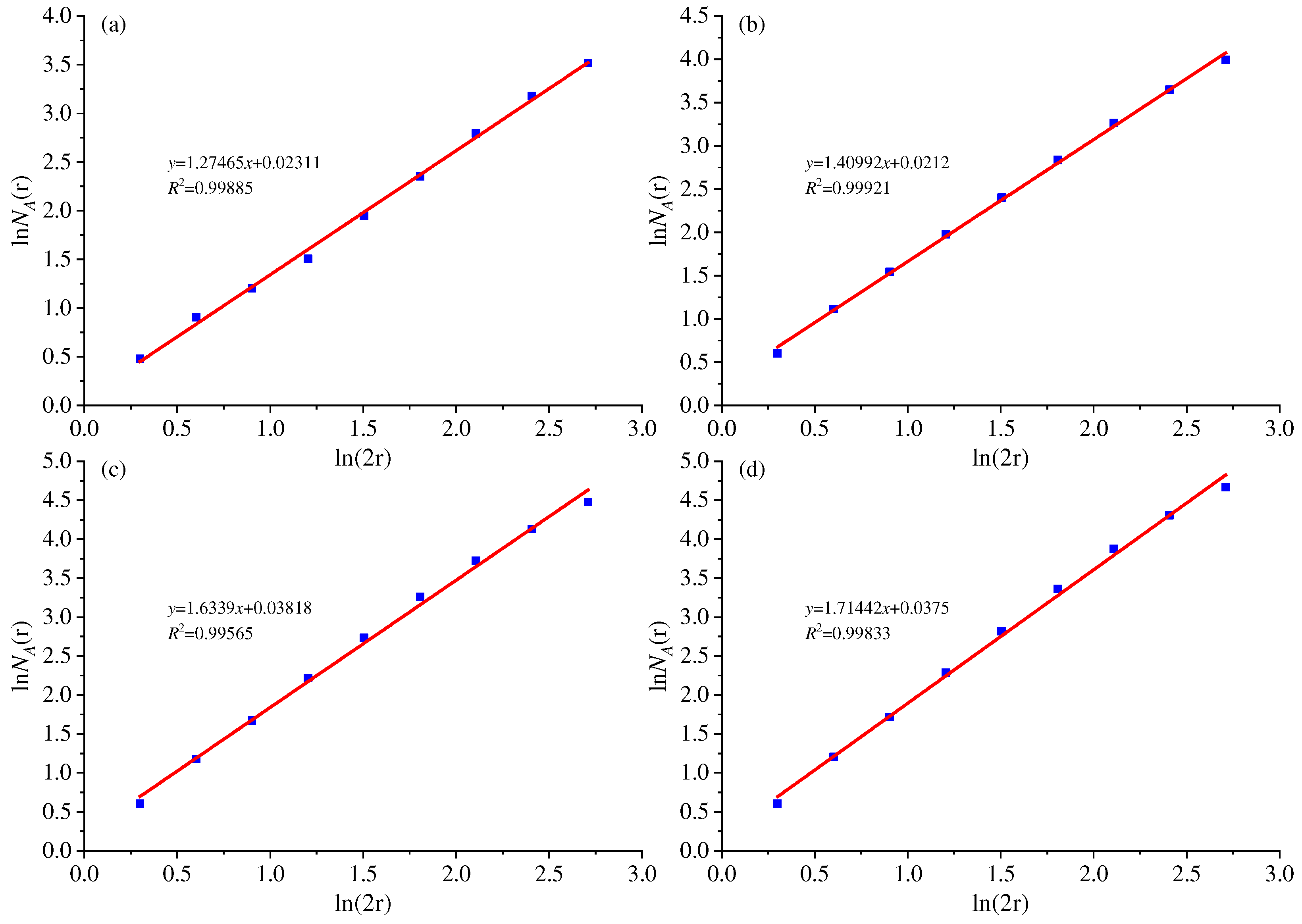
Figure 11, we successfully derived the fractal dimensions around the isolation layer. As indicated in
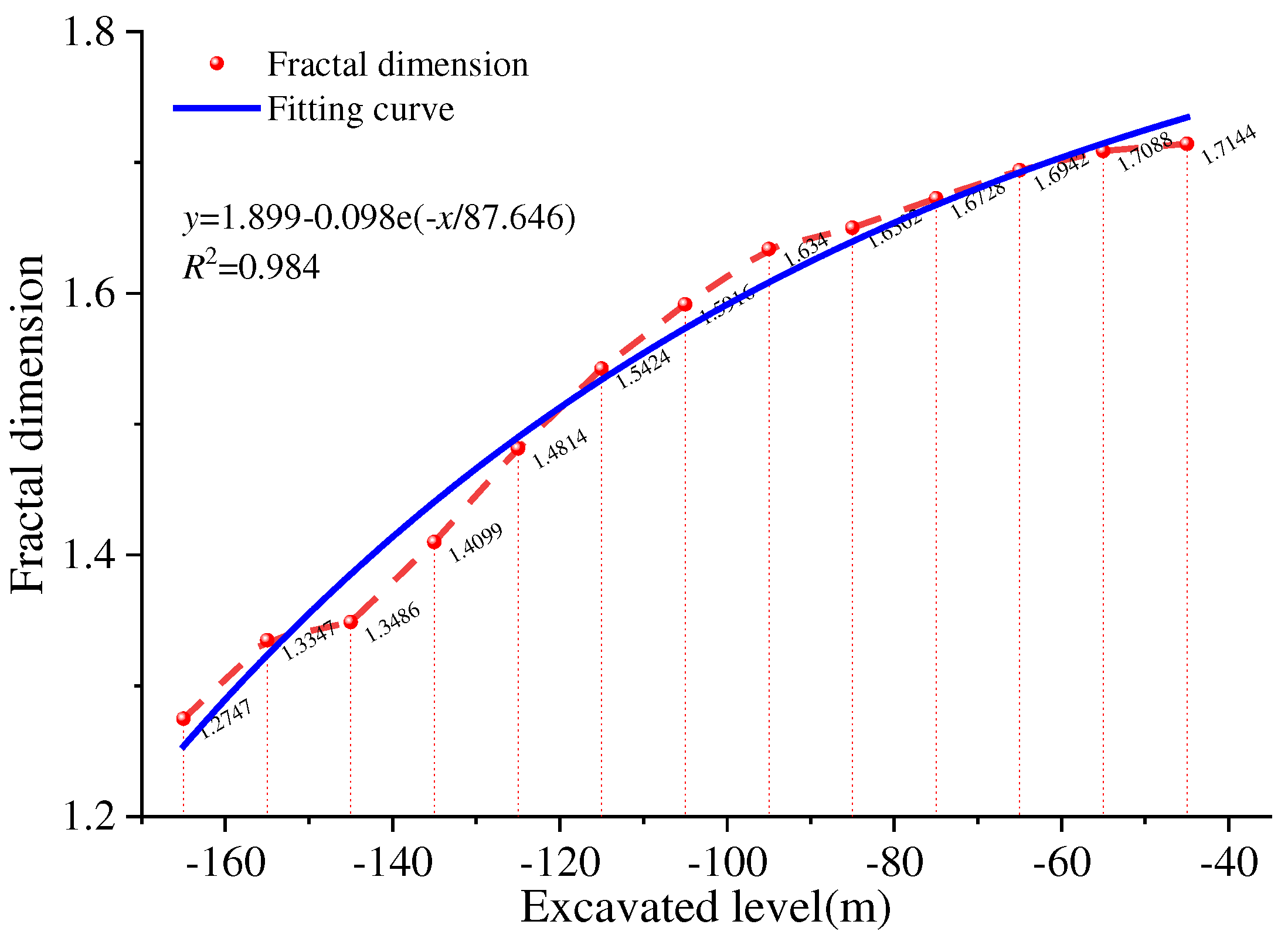
Figure 12, the trend in fracture numbers exhibited an approximately linear trajectory across various measurement scales, with the slope of this line representing the fractal dimension of the fractures. Specifically, after mining the orebody at levels -165m, -135m, -95m, and -45m, the calculated fractal dimensions were 1.275, 1.410, 1.633, and 1.714, respectively. In essence, this implies that the fractal dimension of the model demonstrated an increasing pattern, aligning with the expected behavior in fracture evolution.
Figure 13 illustrates the curve depicting the variations in fracture fractal dimensions. A discernible pattern emerges from this curve, revealing a progression from rapid increases to more gradual growth in the number of fractures. Notably, the slope of the fractal dimension curve in the initial half of the graph exceeds that in the latter half. In simpler terms, the fracture fractal dimension underwent rapid escalation until the isolation layer was mined down to the -115-meter level. Subsequently, the rate of growth in the fracture fractal dimension gradually diminished.
A noteworthy observation is that the connection between the master fracture and the footwall rock mass materializes when the isolation layer is excavated down to the -135-meter level, specifically during the fourth stage of excavation. At this juncture, the fracture fractal dimension attains a value of 1.4099, with the peak growth rate of the fractal dimension occurring at the -115-meter mining level. Subsequently, the growth rate of the fractal dimension exhibits a gradual decline. It is noteworthy that when the isolation layer thickness falls below 55 meters, the fractal dimension stabilizes at approximately 1.71, with minimal further variation.
5.3. Fracture Flow Characteristics of the Mining Area
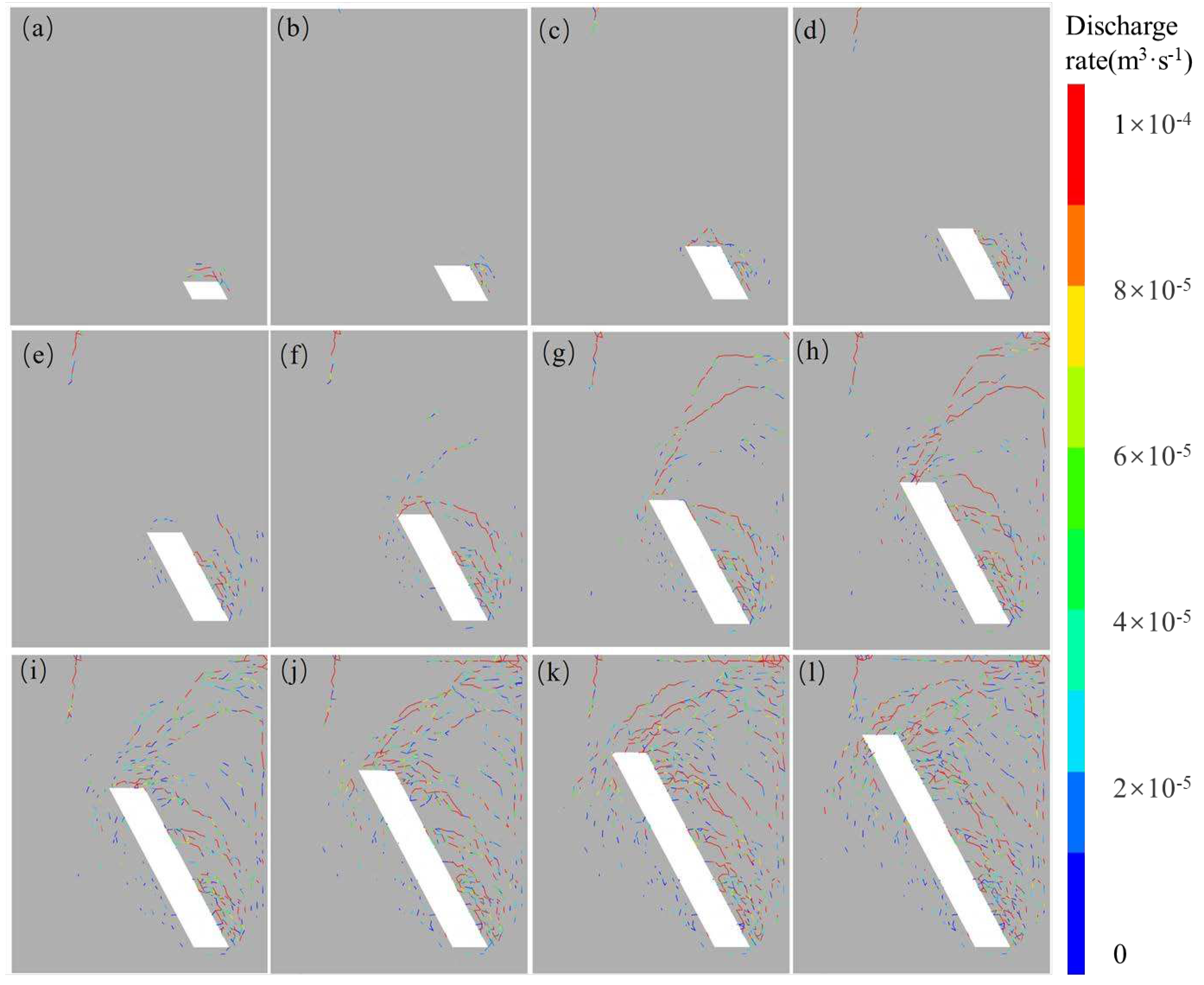
Based on the simulation results of flow patterns, the water flow discharge rate across the entire area is illustrated in
Figure 14. In the initial stages of isolation layer excavation, the water flow predominantly concentrated around the hanging wall rock mass and the goaf's roof. It's noteworthy that the water flow exceeded 100 ml/s upon the penetration and expansion of the master fracture within the isolation layer.
It is evident that there was a pronounced increase in water flow within the area experiencing tensile fracturing. This observation aligns with the findings of site investigations, as illustrated in
Figure 15. Specifically, when the thickness of the isolation layer was less than 105 meters, corresponding to a fracture fractal dimension greater than 1.542, both the roof and hanging wall of the goaf played a significant role as channels for substantial water inflow. This phenomenon directly corresponds to the point where the growth rate of the fractal dimension was maximized.
Furthermore, considering the model's width of 120 meters, a safety factor of 2 necessitates a safe thickness determined by the thickness-span ratio of 60 meters. In this context, the fractal dimension of fractures falls within the range of 1.694 to 1.708, with an average value of approximately 1.70. Consequently, it is reasonable to establish the limit fractal dimension of fractures as 1.70 while ensuring the safe mining of the isolation layer. However, when large amounts of seawater are absent, the critical objective is to prevent fracture connections between the hanging wall and the goaf within the isolation layer. Therefore, it is crucial to maintain the overall fractal dimension below 1.542 in this scenario.
6. Field Investigation and Verification
6.1. Observation Hole Experiment Method Verification
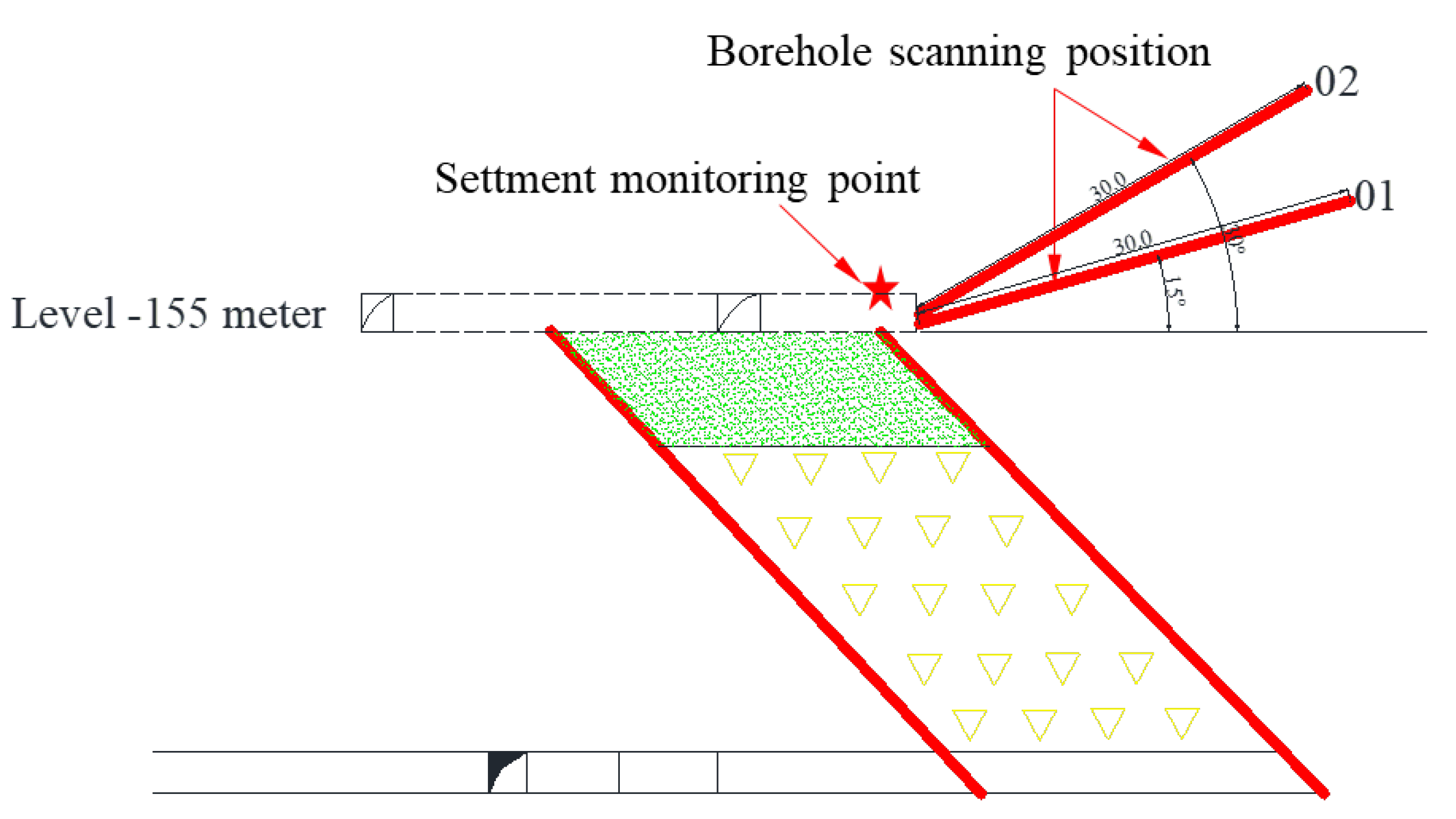
To validate the reliability of the simulation results, we utilized the isolation layer situated at -165 meters as the mining test stope. Concurrently, we performed core-drilling on the hanging wall at -155 meters, as depicted in
Figure 16. In light of this, we introduced an observation hole method to assess the extent of fracture propagation.
As depicted in
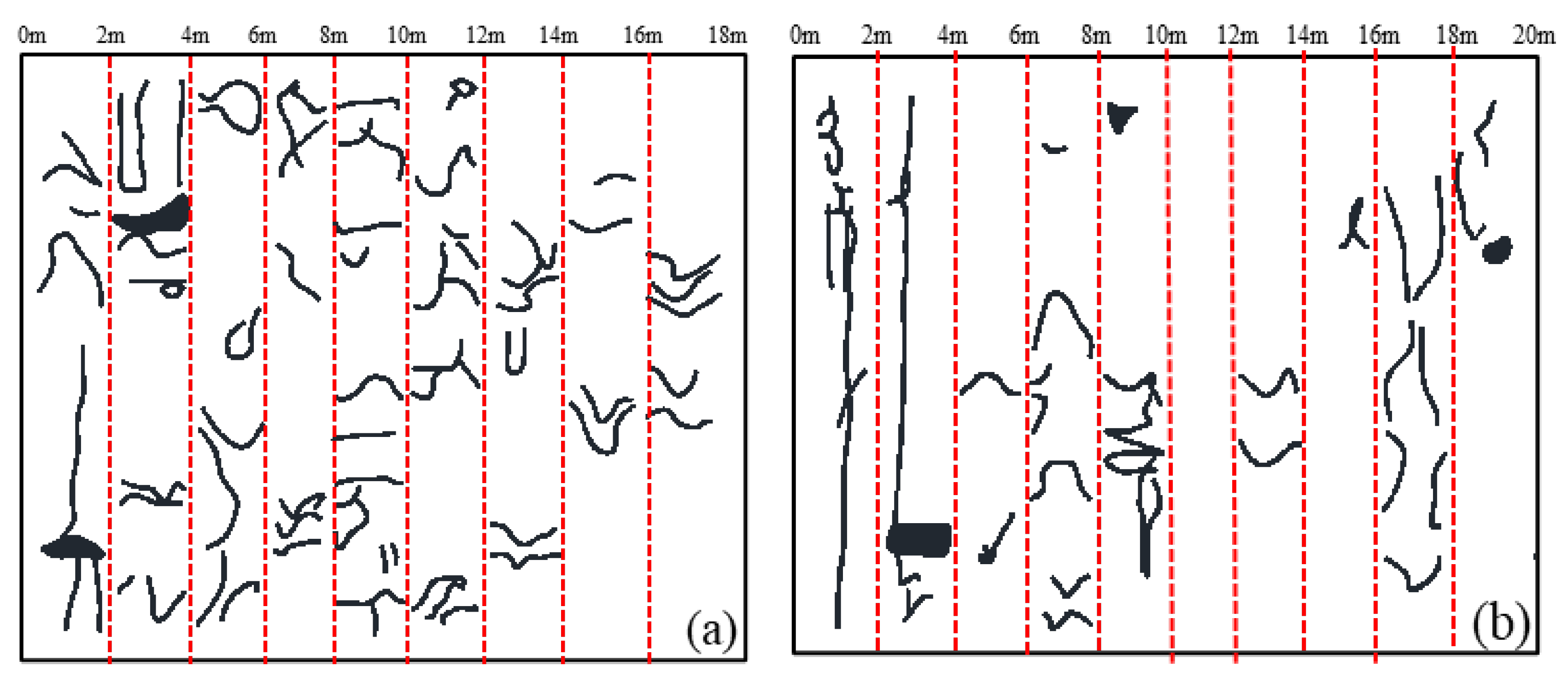
Figure 17, both No.01 and No.02 boreholes reached a depth of approximately 20 meters. For analytical purposes, the rock cores were segmented into 2-meter sections. The borehole image for No.01 covered a depth range from 0 to 19 meters, while the No.02 borehole image extended from 0 to 20 meters. The fractures identified through borehole scanning imaging were subjected to binarization, resulting in the fracture distributions illustrated in
Figure 18. Upon analyzing the spatial distribution of fractures within the borehole rock, it becomes evident that in the case of the No.01 borehole, fractures are more prominent in the length range of 0 meters to 12 meters, becoming relatively sparse between 12 meters and 18 meters. In contrast, for the No.02 borehole, fractures are relatively prevalent within the 0-meter to 12-meter range but less so in the 10-meter to 20-meter range, with no fractures observed between 10 meters and 12 meters. A comparison of these spatial distribution characteristics of fractures with
Figure 12 reveals that the simulated fracture development patterns closely align with the actual fracture development patterns.
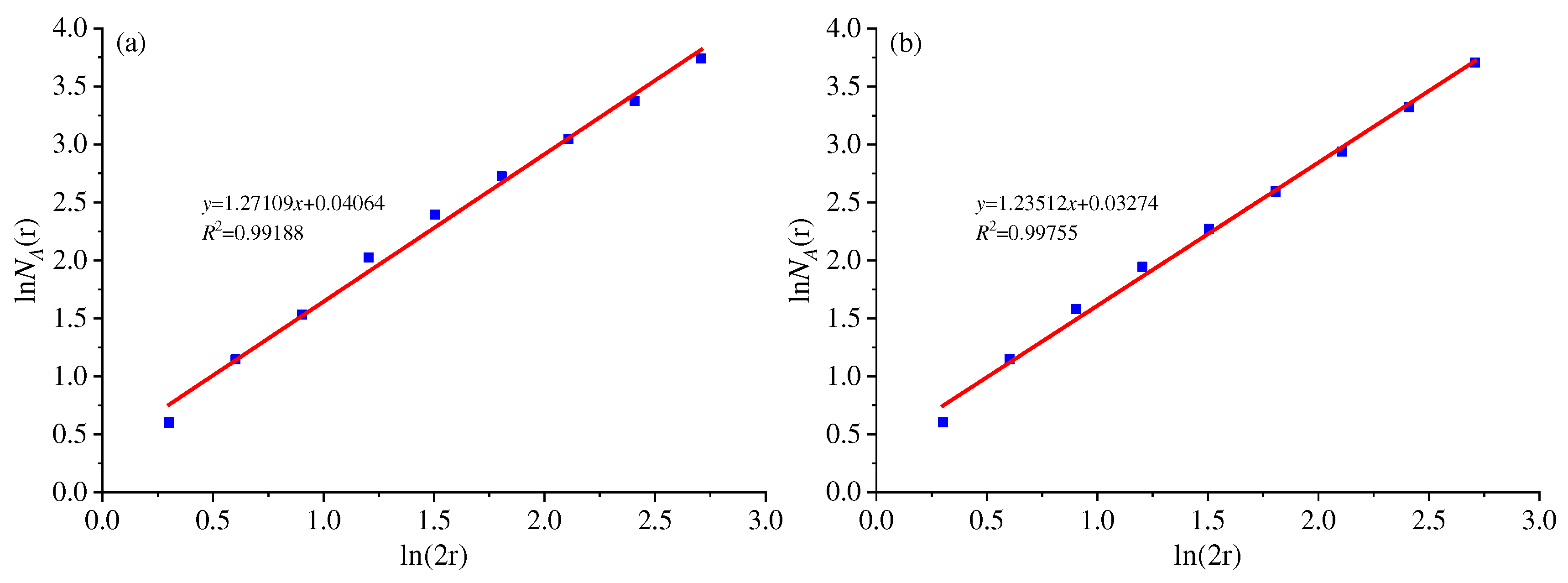
Upon obtaining the fracture distributions, we applied the box dimension calculation principle to process the original borehole images from
Figure 18. These borehole images were considered as having a size of 2.0 meters × 2.0 meters, covering grids with precision successively set at 0.2 meters, 0.1 meters, 0.05 meters, and 0.025 meters. Through regression analysis using Eq. (9), the regression equations for the rock fracture fractal dimensions of boreholes No.01 and No.02 were determined as follows:
y = 1.27109
x + 0.04064 and
y = 1.23512
x + 0.03274, respectively. The corresponding regression coefficients were R² = 0.99188 and R² = 0.99755, as shown in
Figure 18.
Since fractals exhibit self-similar characteristics, the local rock fracture fractal dimensions can be extrapolated to derive global fracture fractals. Therefore, we can infer that the fracture fractal dimension during the actual mining process at the -165m level falls within the range of 1.27109 to 1.23512, which closely aligns with the calculated result of 1.2747.
6.2. Settlement Monitoring Method Verification
The validation test was conducted using the settlement monitoring method, with the site settlement monitoring locations indicated in
Figure 17. Following mining at the -165m level, the settlement trends of the monitoring points are illustrated in
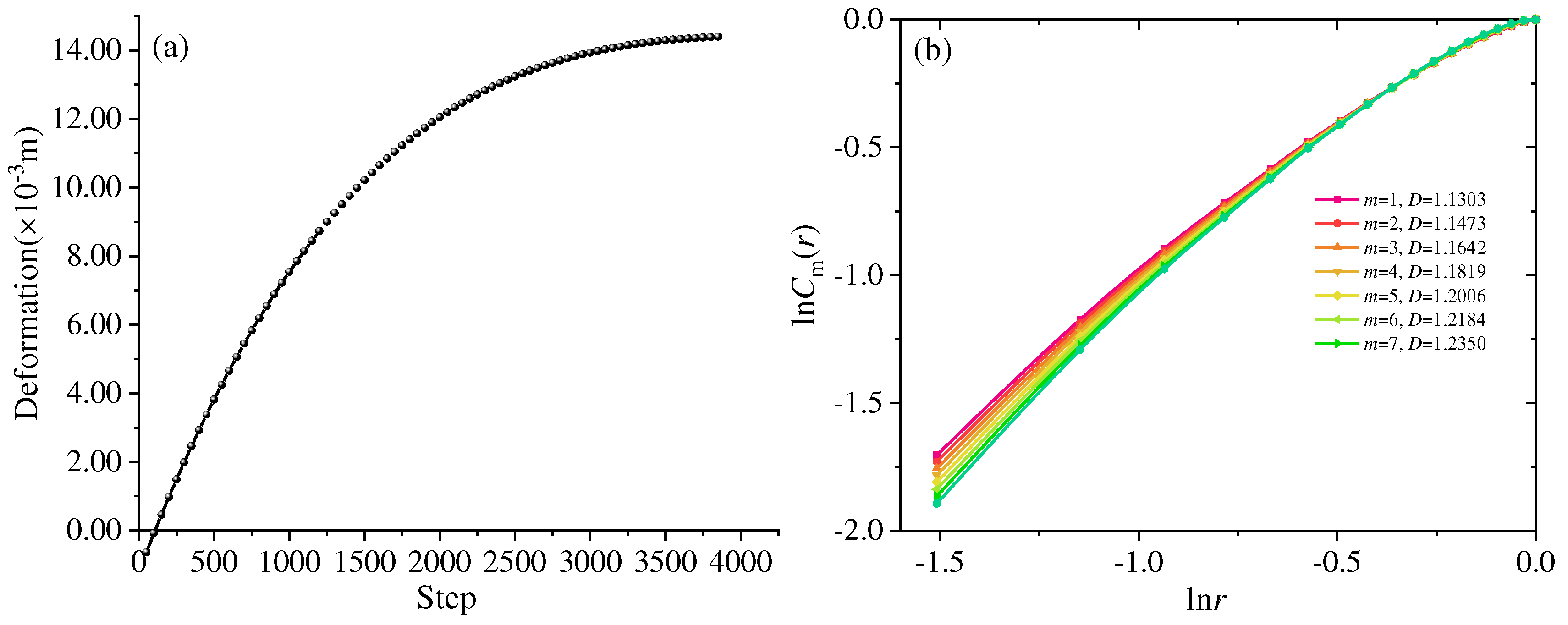
Figure 20(a), while the corresponding settlement simulation results are presented in
Figure 21(a). A comparison of these outcomes reveals a general alignment between the settlement trends of the monitoring points and the calculated settlements, with convergence observed at approximately 3500 days. In contrast, the settlement data obtained through actual monitoring stabilized at around 170 days. Ultimately, both settlement measurements reached approximately 0.15 meters.
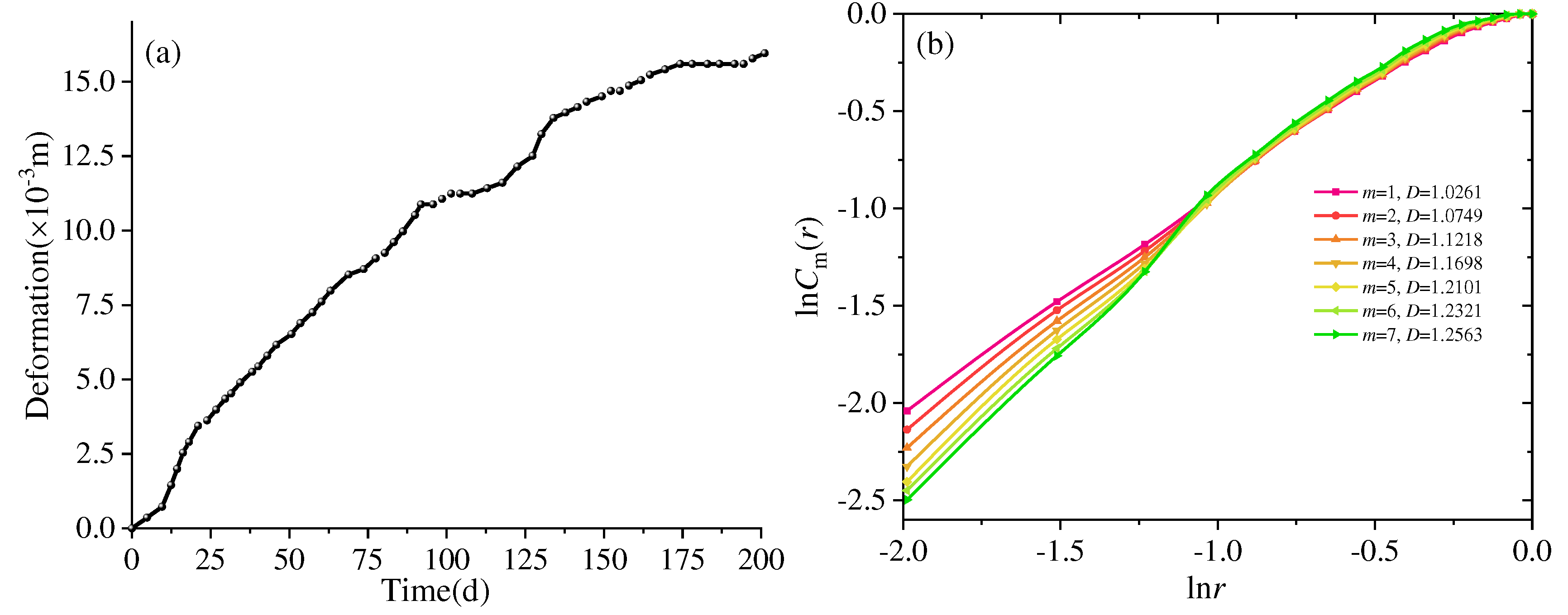
We utilized the phase space reconstruction method in conjunction with the G-P algorithm to compute the correlation dimension for the two types of settlements mentioned above. In
Figure 20(b) and
Figure 21(b), the correlation dimensions of the time series for monitoring settlement and calculated settlement are illustrated, respectively. The G-P algorithm was employed to calculate the corresponding correlation dimension as the embedding dimension of the time series ranged from 1 to 7. The slopes of the curves in
Figure 20(b) and
Figure 21(b) represent the correlation dimensions. The correlation dimension of the actual settlement ranged from 1.0261 to 1.2563, while that of the calculated settlement ranged from 1.1303 to 1.2350. Both the visual observation in the figures and the change pattern of the correlation dimension indicate that the correlation dimension of the actual settlement exhibits more pronounced variations with changes in the embedding dimension. This can be attributed to the fact that the monitored actual settlement experiences more significant fluctuations, while the calculated settlement curve displays smoother trends, resulting in a more pronounced alteration in the correlation dimension of the time series for the actual settlement.
Although some disparities exist between the measured and actual settlement patterns, the correlation dimension remained relatively stable when the embedding dimension was set to 5. Consequently, it can be reasonably deduced that the settlement's correlation dimension hovers around 1.23. In contrast, the correlation dimension of the settlement time series is marginally smaller than the fractal dimension of the fractures, albeit the numerical discrepancy is inconspicuous. As a result, the utilization of the BBM incorporated into 3DEC for safety prognostication in isolation layer mining has yielded significant success, signifying that the structurally controlled safety thickness should be 60 meters, while a safety thickness of 100 meters is required to prevent substantial seawater intrusion.
7. Conclusions
The evolution of fractures and damage in subsea isolation layers during underwater mining is a complex and critical process, with significant implications for the safety and sustainability of underwater mining projects. Risk assessments based on monitoring data are conducted to determine the safety of subsea mining operations. This involves considering the potential impact of fracture propagation on the stability of facilities and the environment. Taking into account various factors related to fracture damage evolution, adopting sustainable mining strategies is crucial to ensuring the long-term feasibility and environmental friendliness of underwater resource extraction. With these objectives in mind, this study investigates the dynamic damage evolution patterns of subsea isolation layer fractures. The main conclusions drawn from the research are as follows:
(1) The results obtained through the similar test align with the safe thickness determined by the thickness-span ratio. Acoustic emission findings indicate that damage in the model generally propagates from the central top to both sides.
(2) Discrete medium mechanics calculations reveal two critical fractal dimensions for surrounding rock during isolation layer excavation: one at 1.5 and the other at 1.70.
(3) Field investigations demonstrate that the fractal dimension of fractures in the midsection at -155m corresponds closely with the calculations from 3DEC. This suggests that determining the safe thickness of offshore isolation layers based on discrete medium mechanics is more accurate and rational. 3DEC can be effectively utilized for predicting the safety isolation layer's thickness in offshore mining.
(4) In scenarios where the fracture fractal dimension is unknown, the time series correlation dimension of displacement monitoring can serve as a crucial criterion for assessing the failure or stability of the isolation layer, proving invaluable in engineering applications.
Acknowledgments:
The present work was financially supported by Natural Science Foundation of Hunan Province (2023JJ40546), and Scientific Research Project of Education Department of Hunan Province (21A0264).
References
- Ma, D., Li, Q., Cai, Kc. et al. Understanding water inrush hazard of weak geological structure in deep mine engineering: A seepage-induced erosion model considering tortuosity. J. Cent. South Univ. 30, 517–529 (2023). [CrossRef]
- Ma, D., Duan, H., Zhang, J. et al. Numerical Simulation of Water–Silt Inrush Hazard of Fault Rock: A Three-Phase Flow Model. Rock Mech Rock Eng 55, 5163–5182 (2022). [CrossRef]
- Liu ZX, Dang WG, He XQ. Undersea safety mining of the large gold deposit in Xinli District of Sanshandao Gold Mine. Int J Min Met Mater 2012; 19(17): 574-583. [CrossRef]
- Wang L., Chen J, Qiao ZH, et al. Tribological behaviors of in situ TiB2 ceramic reinforced TiAl-based composites under sea water environment. Ceram Int 2017; 43(5): 4314-4323. [CrossRef]
- Ma, D., Duan, H., Zhang, J. et al. A state-of-the-art review on rock seepage mechanism of water inrush disaster in coal mines. Int J Coal Sci Technol 9, 50 (2022). [CrossRef]
- Peng K, Li XB, Wan CC, et al. Safe mining technology of undersea metal mine. T Nonferr Metal Soc 2012; 22(3), 740-746. [CrossRef]
- Zhao BC, Wang JB. Study on interval rupture mechanism and support optimization of layered roof. Eng Fail Anal 2022; 141: 106690. [CrossRef]
- Yang JX, Liu CY, Yu B, et al. The effect of a multi-gob, pier-type roof structure on coal pillar load-bearing capacity and stress distribution. Bull Eng Geol Environ 2015; 74: 1267–1273. [CrossRef]
- Zhang HB, Song WD, Fu JX. Analysis of large-span goaf roof instability critical parameters and stability. J Min Safety Eng 2014; 31(1): 66. (in Chinese).
- Liu ZX, Lu, T, Li Xiang, et al. Construction of reasonable pillar group for undersea mining in metal mine. T Nonferr Metal Soc 2018; 28(4): 757-765. [CrossRef]
- Li D, Zhang J, Sun Y, et al. Evaluation of Rockburst Hazard in Deep Coalmines with Large Protective Island Coal Pillars. Nat Resour Res 2021; 30: 1835–1847. [CrossRef]
- Wu WD, Bai JB, Wang XY, et al. Numerical Study of Failure Mechanisms and Control Techniques for a Gob-Side Yield Pillar in the Sijiazhuang Coal Mine, China. Rock Mech Rock Eng 2019; 52: 1231–1245. [CrossRef]
- Miao XX, Cui XM, Xu JL. The height of fractured water-conducting zone in undermined rock strata. Eng Geol 2011; 120(1-4): 32-39. [CrossRef]
- Davies RJ, Mathias SA, Moss J, et al. Hydraulic fractures: How far can they go?. Mar Petrol Geol 2012; 37(1): 1-6. [CrossRef]
- Baghbanan, A, Jing. Hydraulic properties of fractured rock masses with correlated fracture length and aperture. Int. J. Rock Mech. Min. Sci 2007; 44(5): 704–719. [CrossRef]
- Castro-Filgueira U, Alejano LR, Ivars, DM. Particle flow code simulation of intact and fissured granitic rock samples. J Rock Mech Geotech 2020; 12(5): 960-974. [CrossRef]
- Lak M, Fatehi M, Yarahmadi AR, et al. Discrete element modeling of explosion-induced fracture extension in jointed rock masses. J Min Environ 2019; 10(1): 125-138. [CrossRef]
- Ju Y, Wang Y, Su C, et al. Numerical analysis of the dynamic evolution of mining-induced stresses and fractures in multilayered rock strata using continuum-based discrete element methods. Int J Rock Mech Min 2019; 113: 191-210. [CrossRef]
- Tomac I, Gutierrez M. Micromechanics of hydraulic fracturing and damage in rock based on DEM modeling. Granular Matter 2020; 22: 1-17. [CrossRef]
- Di S, Xu W, Wang W, et al. Macro-mechanical properties of columnar jointed basaltic rock masses. J Cent South Univ T 2011; 18(6): 2143-2149. [CrossRef]
- Wang H, Song F, Chen, Y, et al. Stability analysis of fractured rock masses based on an extended key block theory considering the forces between blocks and block rotation. Tun Under Sp Tech 2023; 132: 104895. [CrossRef]
- Sinha S, Walton G. A study on Bonded Block Model (BBM) complexity for simulation of laboratory-scale stress-strain behavior in granitic rocks. Comput Geotech 2020; 118: 103363. [CrossRef]
- Ryvkin M, Shraga, R. Fracture toughness of hierarchical self-similar honeycombs. Int J Solids Struct 2018; 152, 151-160. [CrossRef]
- Archambault G, Rouleau A, Daigneault R, et al. Progressive failure of rock masses by a self similar anastomosing process of rupture at all scales and its scale effect on their shear strength. Scale Effects in Rock Masses 93. CRC Press 2020; 133-141.
- Sui L, Yu J, Cang D, et al. The fractal description model of rock fracture networks characterization. Chaos Solitons Fract 2019; 129: 71-76. [CrossRef]
- Miao T, Yu B, Duan Y, Fang Q. A fractal analysis of permeability for fracturedrocks. Int. J. Heat Mass Transf 2015; 81, 75–80. [CrossRef]
- Bisoi, AK, Mishra, J. On calculation of fractal dimension of images. Pattern Recog Lett 2001; 22(6-7), 631-637. [CrossRef]
- Klinkenberg B. A review of methods used to determine the fractal dimension of linear features. Math Geo 1994; 26: 23-46. [CrossRef]
- Foroutan-pour K, Dutilleul P, Smith, DL. Advances in the implementation of the box-counting method of fractal dimension estimation. Appl math comput 1999; 105(2-3): 195-210. [CrossRef]
- Grassberger, P. Grassberger-Procaccia algorithm. Scholarpedia 2007; 2(5): 3043. [CrossRef]
- Camastra F, Vinciarelli A. Intrinsic dimension estimation of data: An approach based on Grassberger–Procaccia's algorithm. Neural process lett 2001; 14: 27-34. [CrossRef]
- Wang FF, Dai HH, Giorgio I. A numerical comparison of the uniformly valid asymptotic plate equations with a 3D model: clamped rectangular incompressible elastic plates. Math Mech Solids 2022; 27(8): 1370-1396. [CrossRef]
Figure 1.
Geological structure diagram of Sanshandao gold deposit.
Figure 1.
Geological structure diagram of Sanshandao gold deposit.
Figure 2.
Similar simulation test system, (a) similar test model, (b) control system.
Figure 2.
Similar simulation test system, (a) similar test model, (b) control system.
Figure 3.
Arrangement of AE probe and strain gauge for similar simulation experiment.
Figure 3.
Arrangement of AE probe and strain gauge for similar simulation experiment.
Figure 4.
The gradual excavation process of the similar simulation test, (a) the second excavation step, (b) the second excavation step, (c) the sixth excavation step, (d) the nineth excavation step, (e) the tenth excavation step,. (f) water inrush after ten excavation steps.
Figure 4.
The gradual excavation process of the similar simulation test, (a) the second excavation step, (b) the second excavation step, (c) the sixth excavation step, (d) the nineth excavation step, (e) the tenth excavation step,. (f) water inrush after ten excavation steps.
Figure 5.
Acoustic emission distribution and signal (a) acoustic emission signal time-space distribution, (b) monitoring signals.
Figure 5.
Acoustic emission distribution and signal (a) acoustic emission signal time-space distribution, (b) monitoring signals.
Figure 6.
Fracture water flowing meso-process map (a) initial fracture propagation, (b) continuous fracture propagation, (c) fracture water channel formation, (d) fracture water channel completely connected.
Figure 6.
Fracture water flowing meso-process map (a) initial fracture propagation, (b) continuous fracture propagation, (c) fracture water channel formation, (d) fracture water channel completely connected.
Figure 7.
Uniaxial compression test simulation on Sanshandao Gold Mine, (a) stress strain relation of the experiment and simulation test; (b) failure mode with damage extent.
Figure 7.
Uniaxial compression test simulation on Sanshandao Gold Mine, (a) stress strain relation of the experiment and simulation test; (b) failure mode with damage extent.
Figure 8.
Lithologies and geological structures in the model.
Figure 8.
Lithologies and geological structures in the model.
Figure 9.
Vertical displacements(contours) and fracture extensions (white lines) after excavation at different levels, (a)~(l) corresponding to the excavation level of -165 meters to -55 meters.
Figure 9.
Vertical displacements(contours) and fracture extensions (white lines) after excavation at different levels, (a)~(l) corresponding to the excavation level of -165 meters to -55 meters.
Figure 10.
Simulated fracturing pattern as the isolation layer excavation, red line indicate tensile fractures and green line indicate shear fractures.
Figure 10.
Simulated fracturing pattern as the isolation layer excavation, red line indicate tensile fractures and green line indicate shear fractures.
Figure 11.
Image binarization processing of fracture extension evolution (Level -155 meters), (a) fracture propagation, (b) fracture binarization treatment.
Figure 11.
Image binarization processing of fracture extension evolution (Level -155 meters), (a) fracture propagation, (b) fracture binarization treatment.
Figure 12.
Fractal dimension around the isolation layer, (a) mining level -165m; (b) mining level -135m; (c) mining level -95m; (d) mining level -45m.
Figure 12.
Fractal dimension around the isolation layer, (a) mining level -165m; (b) mining level -135m; (c) mining level -95m; (d) mining level -45m.
Figure 13.
Rock mass fracture fractal dimension with mining steps.
Figure 13.
Rock mass fracture fractal dimension with mining steps.
Figure 14.
Fracture flow discharge rate after excavation at different mining levels,.(a)~(l) corresponding to the excavation level of -165 meters to -55 meters.
Figure 14.
Fracture flow discharge rate after excavation at different mining levels,.(a)~(l) corresponding to the excavation level of -165 meters to -55 meters.
Figure 15.
On-site investigation of crushing zone (a)and water inrush in hanging wall (b).
Figure 15.
On-site investigation of crushing zone (a)and water inrush in hanging wall (b).
Figure 16.
Borehole scanning and displacement monitoring point layout profile in level -155m.
Figure 16.
Borehole scanning and displacement monitoring point layout profile in level -155m.
Figure 17.
Borehole observation of rock fractures in undersea mining.
Figure 17.
Borehole observation of rock fractures in undersea mining.
Figure 18.
Distribution of rock fractures of borehole scanning, (a) No.01 and (b) No.02.
Figure 18.
Distribution of rock fractures of borehole scanning, (a) No.01 and (b) No.02.
Figure 19.
Fracture fractal dimension borehole (a) No.01 and (b) No.02.
Figure 19.
Fracture fractal dimension borehole (a) No.01 and (b) No.02.
Figure 20.
Actual settlement and its correlation dimension.
Figure 20.
Actual settlement and its correlation dimension.
Figure 21.
Simulated settlement and its correlation dimension.
Figure 21.
Simulated settlement and its correlation dimension.
Table 1.
Rock mechanical parameters of Sanshandao Gold Mine.
Table 1.
Rock mechanical parameters of Sanshandao Gold Mine.
| Lithology |
Density
(kg·m-3) |
Elastic Young's modulus, E (GPa) |
Poisson's ratio |
Tensile
Strength
(MPa) |
Cohesion
(MPa) |
Internal friction angle(°) |
Uniaxial comprehensive strength(MPa) |
| Hanging wall |
2706 |
13.44 |
0.20 |
3.18 |
5.72 |
30.60 |
82.03 |
| Orebody |
2709 |
15.02 |
0.19 |
3.72 |
6.43 |
32.60 |
102.95 |
| Footwall |
2635 |
17.10 |
0.24 |
4.31 |
5.72 |
36.94 |
72.07 |
Table 2.
Corrected microscopic parameters of bonded block model.
Table 2.
Corrected microscopic parameters of bonded block model.
| Contact |
Normal stiffness
(GPa·m-1) |
Shear stiffness, (GPa·m-1) |
Tensile
Strength
(MPa) |
Cohesion
(MPa) |
Internal friction angle(°) |
| Hanging wall |
324 |
105 |
4.35 |
12.19 |
29.72 |
| Orebody |
267 |
89 |
4.51 |
12.37 |
29.30 |
| Footwall |
163 |
61.9 |
4.28 |
11.82 |
29.63 |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
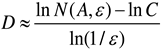
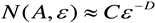
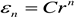 , where r is the side
length of box, then:
, where r is the side
length of box, then: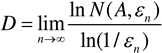
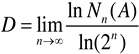
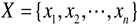 , xi
could be extended into the phase distribution Y(Xk) of
m-dimensional phase space by a certain embedding dimension m and τ.
The expression of Y(Xk) is
, xi
could be extended into the phase distribution Y(Xk) of
m-dimensional phase space by a certain embedding dimension m and τ.
The expression of Y(Xk) is