Submitted:
23 December 2023
Posted:
26 December 2023
Read the latest preprint version here
Abstract
Keywords:
1. Introduction
1. The theory
1.1. The Euler ensemble and its continuum limit
1.2. Small Euler ensemble at large N
2. The big Euler ensemble as a Markov process
2.1. Numerical Simulations
2.2. Scaling variables in continuum limit
3. Vorticity correlation
3.1. Exact relation with conditional probability density
3.2. Extracting conditional distribution from numerical data
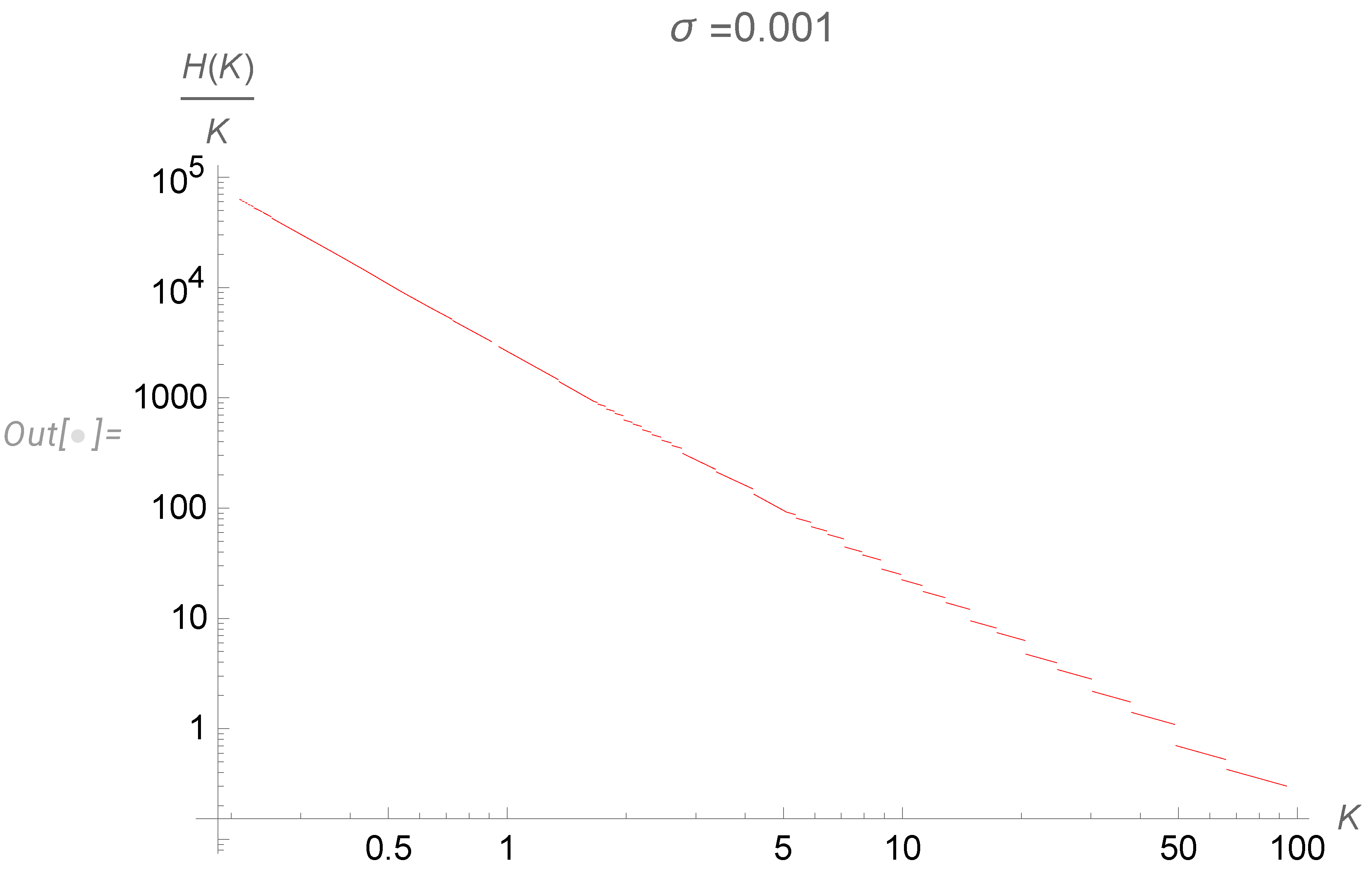
3.3. Final results for the energy spectrum
4. Comparison with real and numerical experiments
5. Conclusions
- We found continuum limit of distribution of scaling variables (33),(38) in the small Euler ensemble.
- The local slope of energy spectrum is , not counting jumps. The average slope is . The K41 spectrum lies in between.
- This universal energy spectrum depending on corresponds to the effective spatial scale , or in notations of [9].
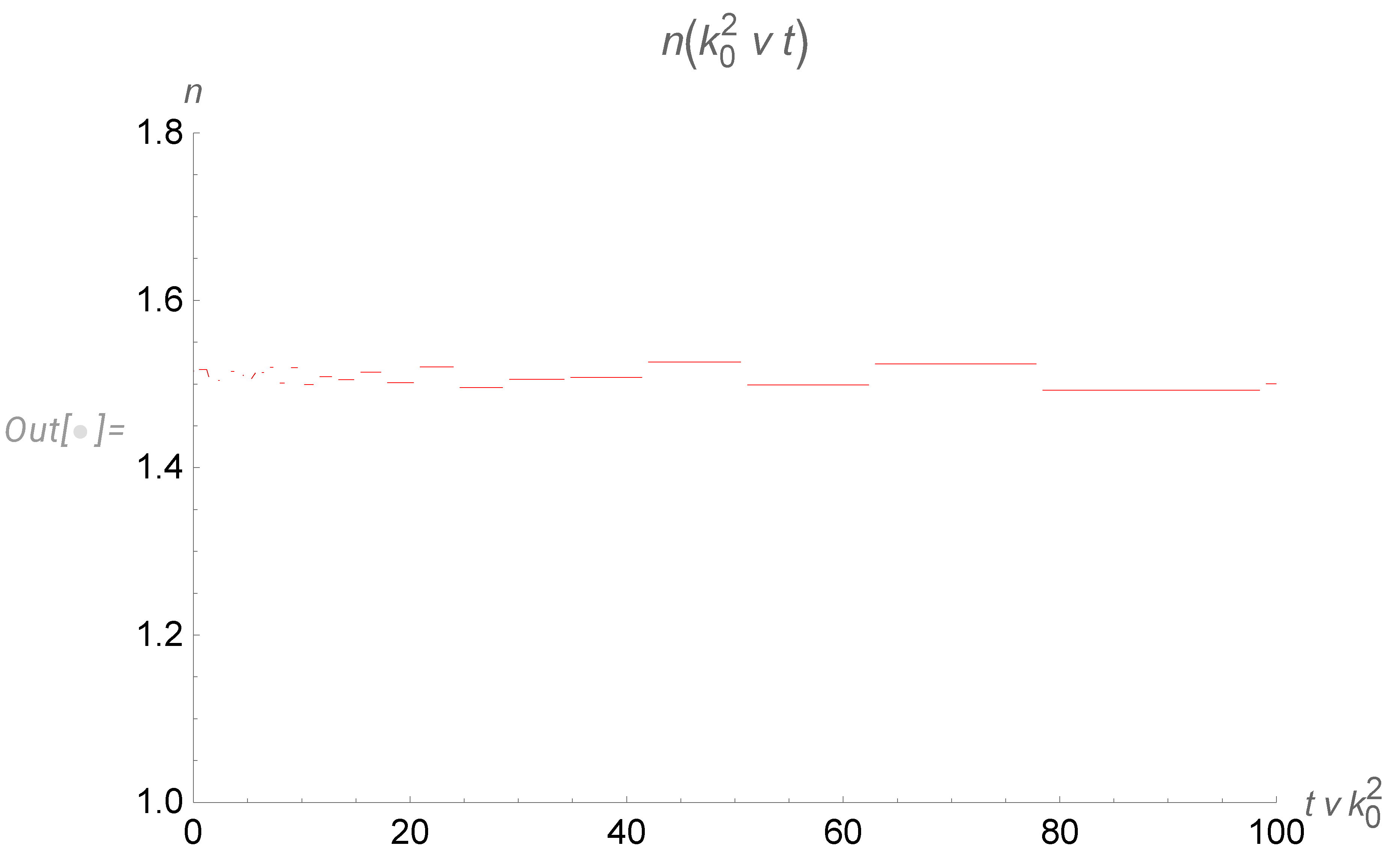
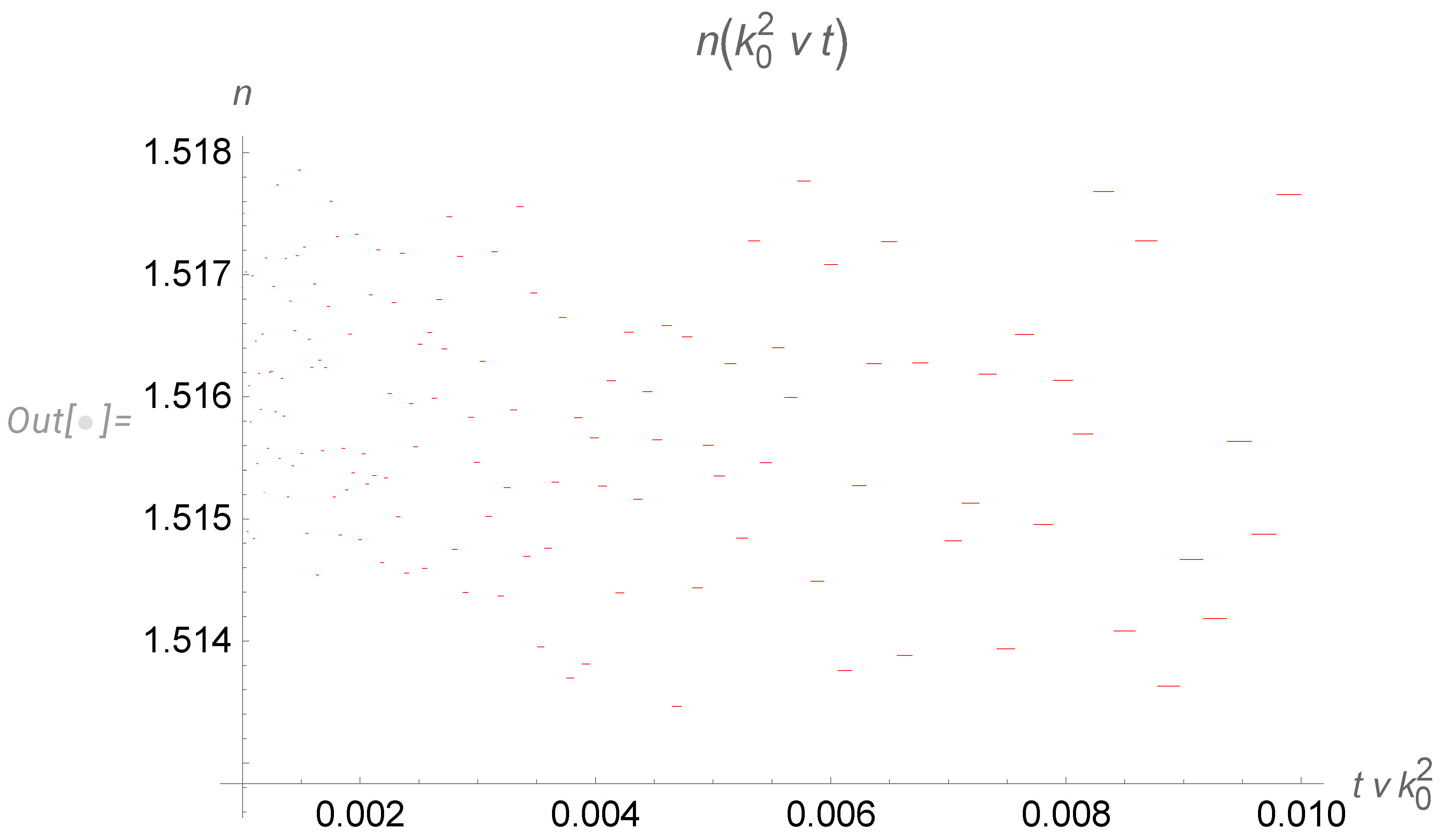
- The decay at a given time goes only at small enough wavelengths. At a fixed wavelength, the decay stops after some critical time, inversely proportional to the wavelength square.
- With the cutoff of our spectrum at the small wavelength corresponding to initial energy pumping (), we obtain discrete levels of the effective index . During decay, the index jumps down from one level to another, with level spacing increasing with time. These levels are universal numbers, given by the table (111).
Data Availability Statement
Acknowledgments
Appendix A Algorithms
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
References
- Migdal, A. Loop Equation and Area Law in Turbulence. In Quantum Field Theory and String Theory; Baulieu, L.; Dotsenko, V.; Kazakov, V.; Windey, P., Eds.; Springer US, 1995; pp. 193–231. [CrossRef]
- Makeenko, Y.; Migdal, A. Exact equation for the loop average in multicolor QCD. Physics Letters B 1979, 88, 135–137. [Google Scholar] [CrossRef]
- Migdal, A. Loop equations and 1N expansion. Physics Reports 1983, 201. [Google Scholar] [CrossRef]
- Migdal, A. To the Theory of Decaying Turbulence. Fractal and Fractional 2023, arXiv:physics.flu-dyn/2304.13719]7, 754. [Google Scholar] [CrossRef]
- Hardy, G.H.; Wright, E.M. An introduction to the theory of numbers, sixth ed.; Oxford University Press, Oxford, 2008; pp. xxii+621. Revised by D. R. Heath-Brown and J. H. Silverman, With a foreword by Andrew Wiles.
- Basak, D.; Zaharescu, A. Connections between Number Theory and the theory of Turbulence, 2024. To be published.
- Migdal, A. "NumericalAnalysisOfEulerEnsembleInDecayingTurbulence". "https://www.wolframcloud.com/obj/sasha.migdal/ Published/NumericalAnalysisOfEulerEnsembleInDecayingTurbulence.nb", 2023.
- Migdal, A. Statistical Equilibrium of Circulating Fluids. Physics Reports 2023, arXiv:physics.flu-dyn/2209.12312]1011C, 1–117. [Google Scholar] [CrossRef]
- Panickacheril John, J.; Donzis, D.A.; Sreenivasan, K.R. Laws of turbulence decay from direct numerical simulations. Philos. Trans. A Math. Phys. Eng. Sci. 2022, 380, 20210089. [Google Scholar] [CrossRef] [PubMed]
- Davidson, P.A.; Kaneda, Y.; Ishida, T. On the decay of isotropic turbulence. In Springer Proceedings in Physics; Springer Berlin Heidelberg: Berlin, Heidelberg, 2007; pp. 27–30. [Google Scholar]
- Migdal, A. LoopEquations. https://github.com/sashamigdal/LoopEquations.git, 2023.
- Migdal, A. Dual Theory of Decaying Turbulence: 1: Fermionic Representation., 2023.
- Lei, J.; Kadane, J.B. On the probability that two random integers are coprime. 2019; arXiv:math.PR/1806.00053]. [Google Scholar]

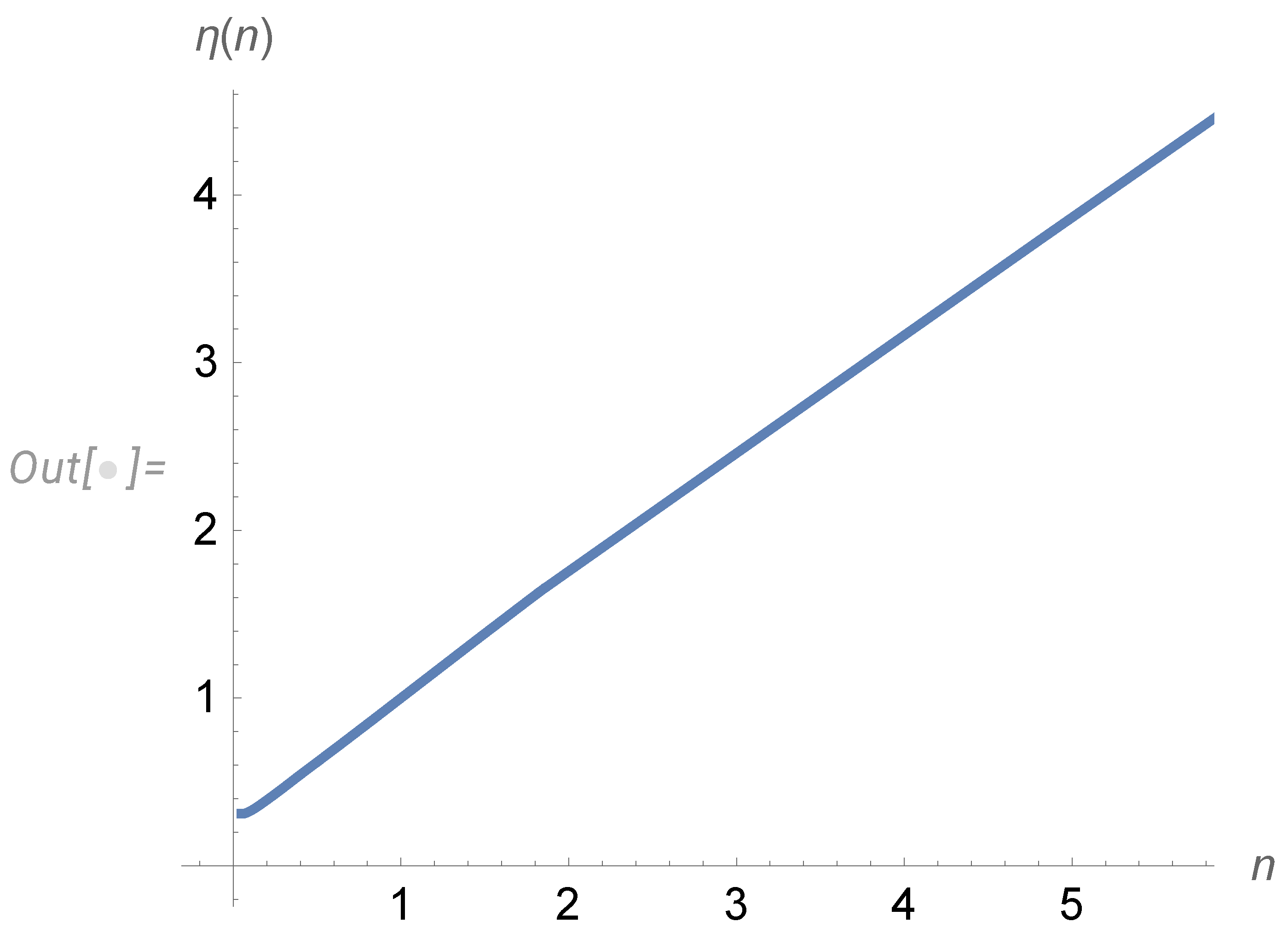
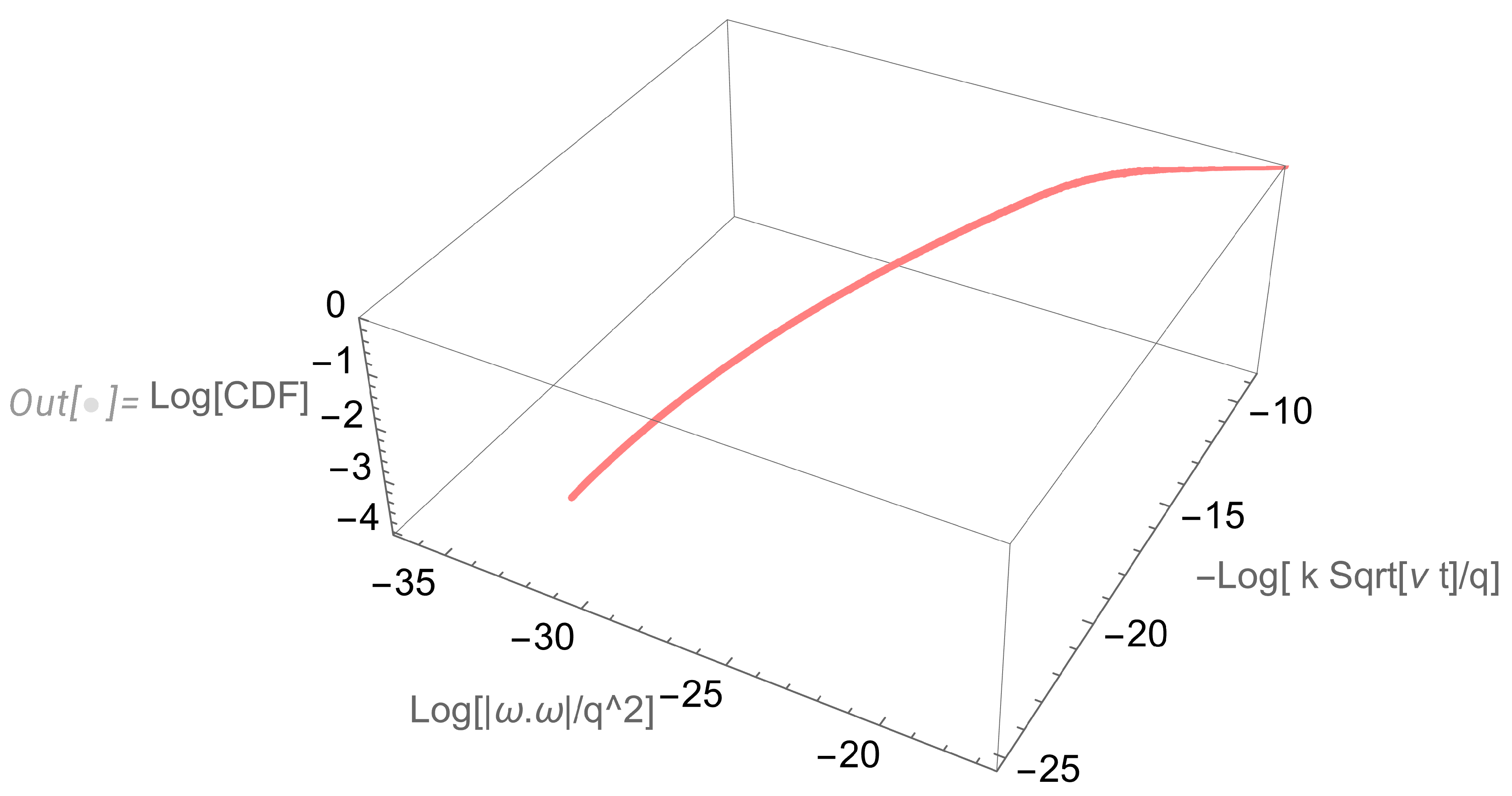
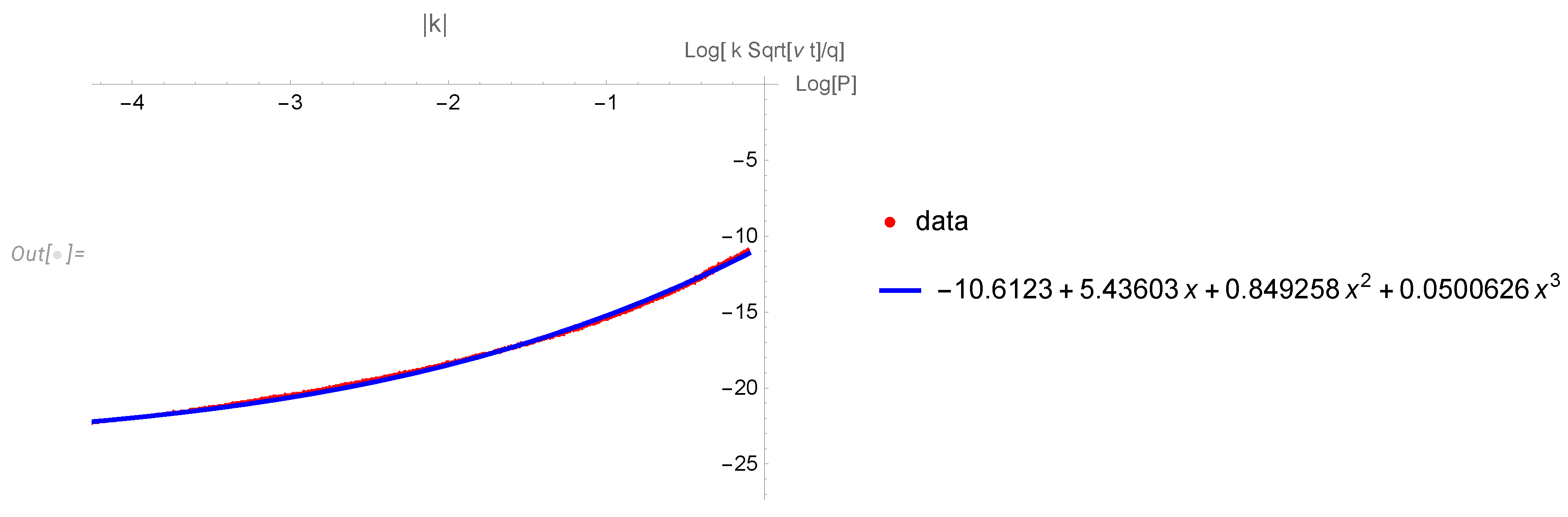
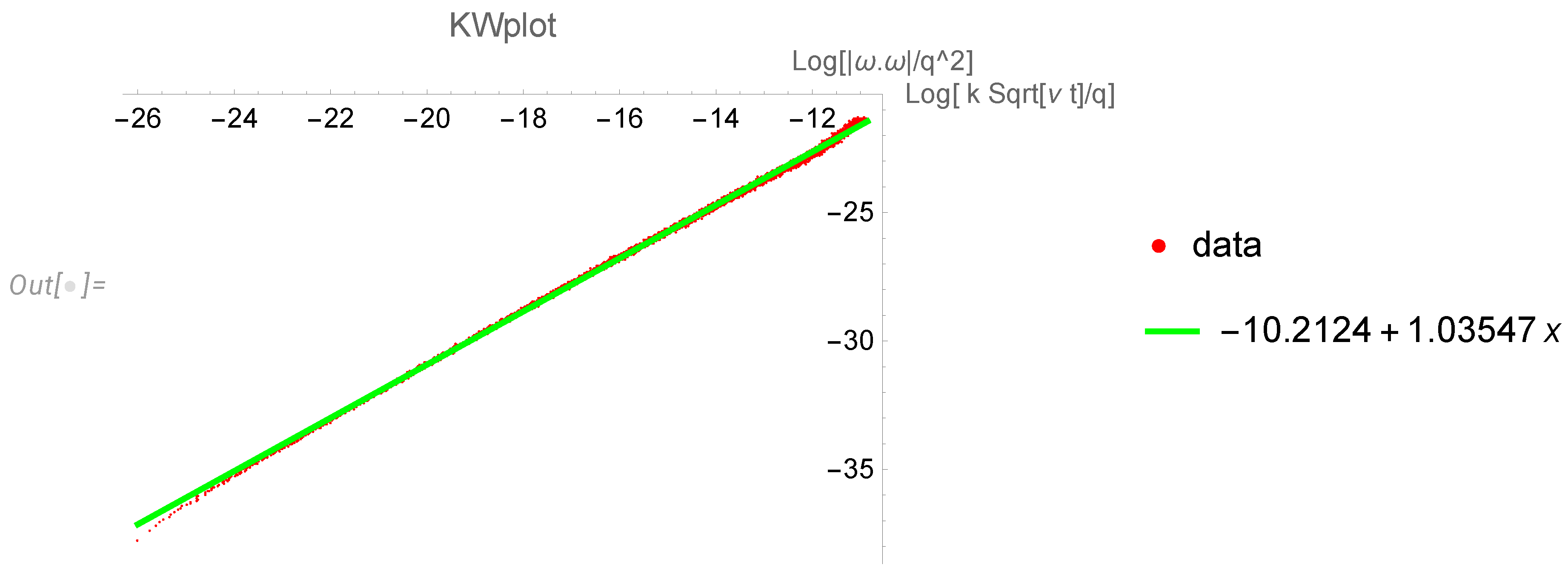
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




