3.1. The main features of the Overdamped Optical Phonon model
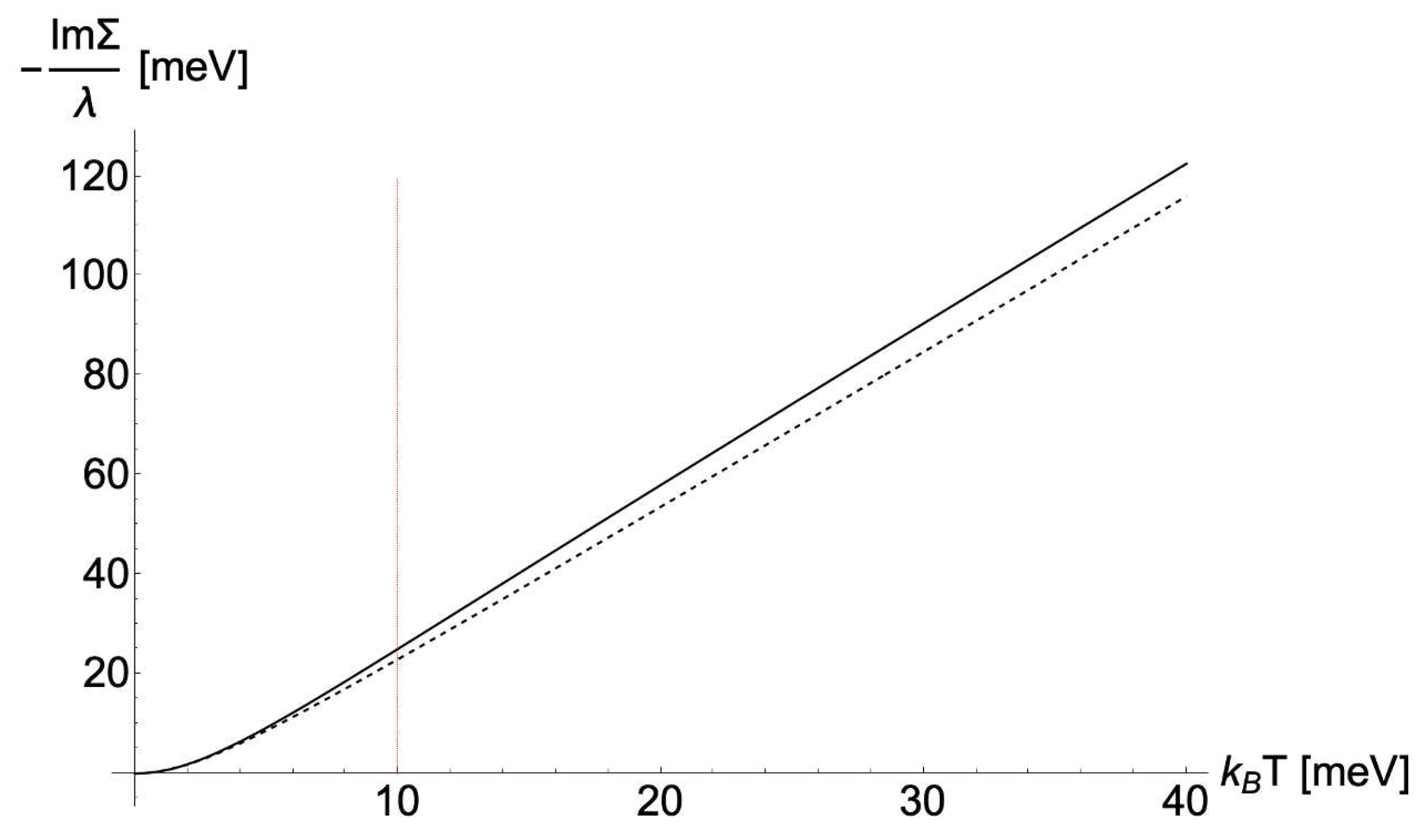
In light of what has been shown so far, we now discuss the most remarkable aspects and physical consequences of the model considered here. First of all, there is a characteristic energy scale that separates the asymptotic regimes both in frequency and in temperature. Below this scale the system is a standard Fermi liquid, which displays the usual and behavior of the imaginary part of the fermion self-energy. The quasiparticle mass renormalization at zero temperature only depends on the dimensionless parameter and there is no dependence.
On the other hand, for
, the system displays a linear-in-
T behavior in
. The same does not hold as far as the frequency dependence is concerned, since the seemingly linear-in-
behavior only arises in an extended range around an inflection point in
separating the
regime at low frequency and the
or constant regime at high frequency. It is quite important to stress that the different temperature and frequency behaviors stem from completely different physical mechanisms. In contrast to a MFL, where the underlying
-independent spectral density leads to a linear-in-
behavior of
down to
, the frequency dependence in the SFL scenario arises from the dynamical range of the collective mode. This range extends down to low frequency because of the damping and extends up to high frequencies when the overdamped character of the mode persists because of a large
, before the collective mode turns into a nearly propagating mode, at
. In passing, we notice the smoother shape of
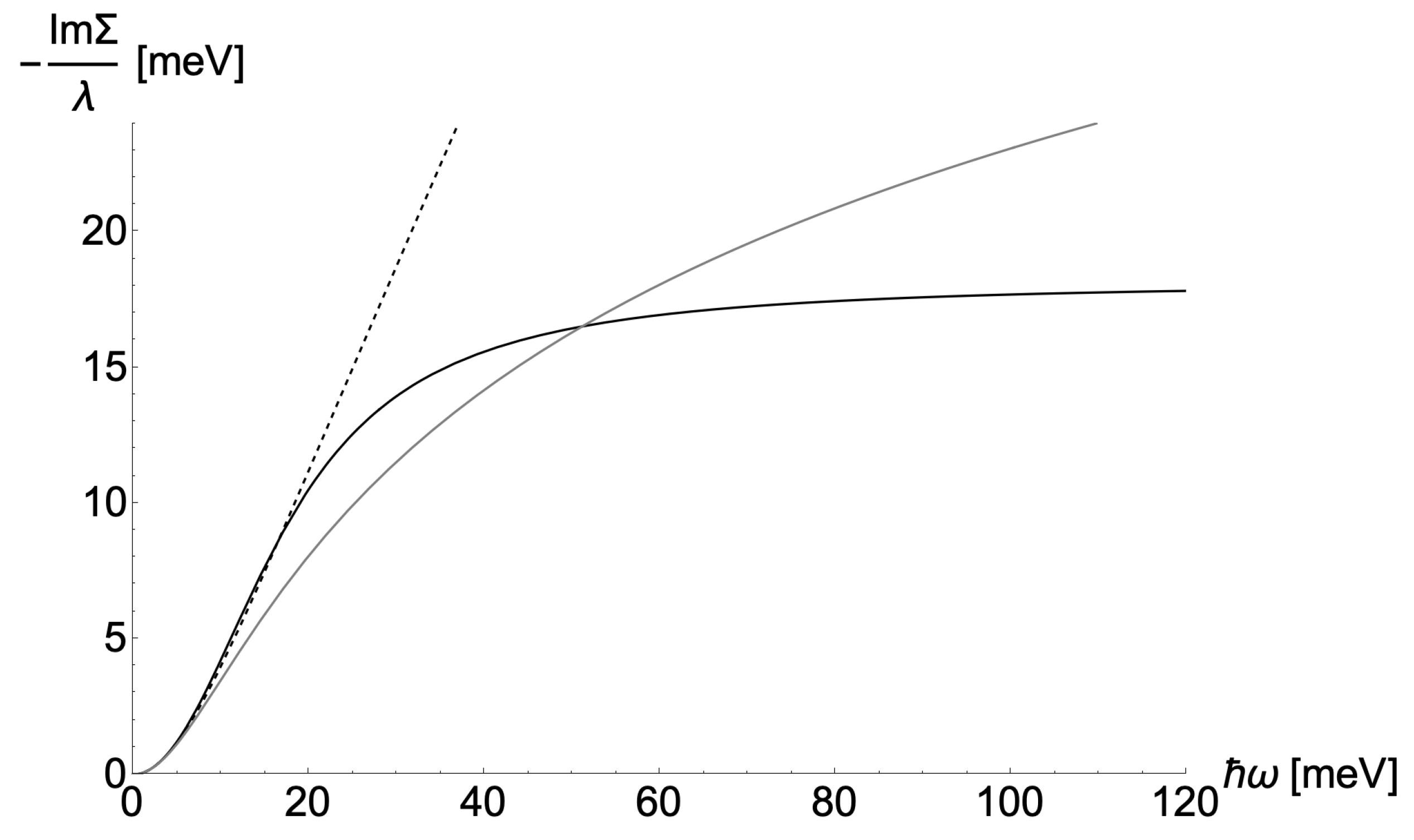
in
Figure 2 with respect to the usual step-like shape in undamped Einstein phonons [
21]. Instead, the truly linear-in-
T behavior of
arises from the classical statistical weight of the collective modes mediating the quasiparticle scattering. Owing to this different origin, there is no reason to expect any
scaling in the present model (notice that the other usual mechanism for scaling, namely the divergence of some correlation length near criticality is ineffective here, because the collective modes are massive and non-critical). Nevertheless, as a matter of fact, a seeming scaling
can be obtained because
can be fitted remarkably well over a sizable temperature and frequency range by an approximate form that is described in detail in
Appendix B, and can be further simplified, for the sake of exemplification, in the form
This expression captures the main features of
at all temperatures and at small/moderate frequencies, and allows to see how our model might display seeming scaling properties over a sizable range, where it not for the presence of a finite mass term
. It is interesting to note that it may be precisely a mass term
of order 10 meV that accounts for the small scaling violations at low frequencies in optical experiments in slightly overdoped cuprates [
6].
Moreover, this expression makes it clear that, for frequencies and temperatures much larger than , the imaginary part of the fermion self-energy bears strong similarities with the MFL model, where the fermion self-energy takes the form .
Eq. (
8) also makes it clear that in the linear regimes (both in temperature and in frequency) the slopes are independent of
and
M. This has an important consequence: for
, an approximate
scaling is obtained, as it is obvious because in this limit our approximate fitting form, Eq. (
8), reduces to the MFL form.
3.2. Connection with the Shrinking Fermi Liquid scenario
We now propose a straightforward connection of the presently studied model with the SFL model, as a possible explanation for the strange metallicity of many physical systems. In this regard, we first notice that, since the overdamped optical phonons mediating the inter-particle interaction have no momentum dependence, then the quasiparticle scattering rate coincides with the transport scattering rate. Moreover, owing to the momentum independence of the scattering mechanism, scattering processes obviously include also umklapp processes, responsible for momentum dissipation and non-zero conductivity at finite frequencies. Therefore, the linear regime of would coincide with a regime of linear-in-T resistivity, which is the most famous and prominent feature of strange metals.
According to our analysis, the linear-in-
T behavior stops below a Fermi liquid temperature scale
. In the strange metals, like, e.g., slightly overdoped superconducting cuprates, this linear resistivity is observed down to the superconducting critical temperature (of order of
K). This is of the same order of
, which in cuprates is estimated from RIXS experiments [
15,
22]. The comparison between the static and dynamical spectral densities of the CDF, allows one to estimate
M to be of order
and
to be of order one. Therefore, the linear-in-
T resistivity would be nicely accounted for by quasiparticles being scattered by CDF (as characterized by RIXS experiments [
16]) which, being weakly momentum dependent, are also reasonably well described by the present model. The same occurs as far as the linear-in-
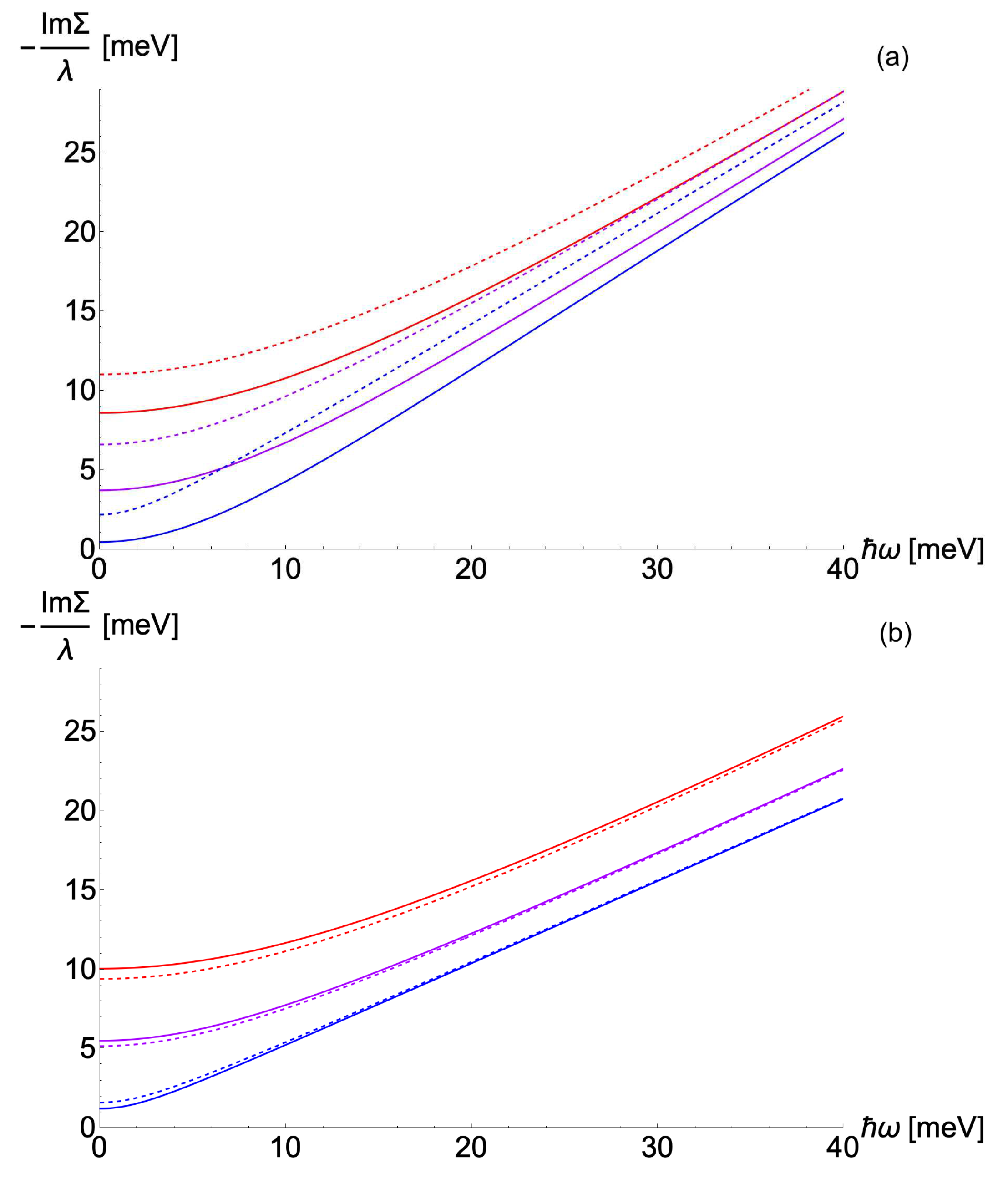
behavior is concerned, as schematized by the solid-line curves in
Figure 3a, where the (approximate) linear-in-
behavior of
at various fixed temperatures occurs above the
meV scale. On the other hand the solid lines at low temperature become substantially different from the dotted lines representing the MFL behavior, which we plot as a benchmark.
A similar failure arises when the linear-in-
T behavior in the d.c. resistivity is shown to persists down to
K, as found in transport experiments under strong magnetic field [
3,
8], obviously smaller than
,
if γ does not depend on temperature. To solve this difficulty, the possibility was considered in Refs. [
17,
18,
20] that
increases with lowering the temperature, when superconductivity is suppressed.
The value of
at low temperatures can be extracted from specific heat experiments. Indeed, it is quite natural that the boson collective modes contribute to the specific heat
, if their energy is low enough. It is then found [
17,
18] that the bosonic contribution to
is proportional to the damping coefficient
, and this could in turn be assumed to increase logarithmically in
T, to match the experimental growth of
[
7]. It is worth emphasizing that, in this scenario, the logarithmic divergence of
arises from the boson (collective-mode) contribution and not from the fermions, which behave as Fermi liquid quasiparticles, with a finite mass [see Eq. (
7)]. While a full microscopic model for this increase is still missing, a simplified model based on the interplay between CDF and diffusion modes of the electrons was also proposed in Ref. [
20] for two-dimensional systems, accounting for a logarithmic-in-
T increase of
, with decreasing
T. Then, assuming
, the whole Fermi liquid scale
shrinks, so that the region of Fermi liquid behavior is correspondingly reduced at lower temperatures. This behavior is reported in
Figure 3b. Here, it is evident that the Fermi liquid scale
shrinks with decreasing
T, in such a way as to keep the solid lines, reporting the numerical evaluation of
, close to the MFL dotted curves even at low temperatures. In order to have a better quantitative comparison between the two scenarios, we chose to use Eq. (
A2) [rather than the more schematic Eq.
8] as a fitting expression for
. As discussed in
Appendix B, this expression shares all the qualitative aspects of Eq. (
8) discussed so far, but in addition it also more precisely reproduces the slope of the linear part in
at
.
One could also wonder whether a T-dependent might alter the linear-in-T behavior of [hence, of the d.c. resistivity ]. The fact mentioned above, that the slope of does not depend on , comes at rescue, by allowing to keep the slope of unchanged while the Fermi liquid scale is progressively reduced at lower and lower temperatures.
Hence, our overdamped optical phonon model, once it is equipped with the additional feature of a increasing logarithmically with lowering T, gives rise to a SFL scenario. By (phenomenologically) assuming this temperature dependence of , to fit the experimentally measured , this scenario, although ultimately based on a Fermi liquid state at , mimics quite well (and it is, to any practical purpose, indistinguishable from) the MFL behavior, without invoking an unnecessary scaling in the boson spectrum.