1. Introduction
In the most energetically efficient Inertial Confinement Fusion (ICF) scheme with a “shock ignition” (SI), the processes of the capsule implosion with deuterium-tritium (DT) fuel and its subsequent “ignition” are separated in time [
1,
2]. After a uniform, close to adiabatic, compression of the capsule for several tens of nanoseconds, a thermonuclear fusion begins in the hottest and densest central region of the compressed target, which is additionally heated by a strong shock wave converging to the center. The latter is generated by even more powerful laser pulse with duration of several hundreds of picoseconds. During this time, the compressed fuel does not yet have time to expand. The escape of neutrons and their absorption in a fusion reactor blanket provide useful energy to the power cycle of the Inertial Fusion Energy (IFE) plant, whereas α-particles absorbed nearby in the dense DT fuel provide additional heating and thus support thermonuclear fusion in the rest of the fuel. The described scheme of the SI ICF can be implemented with laser pulses having a complex time shape with a short final spike, which power exceeds by one or two orders of magnitude the main driving pulse.
After a recent demonstration of the ignition in indirect compression experiments at NIF 3ω Nd glass facility [
3], the undoubted advantage of which is the homogeneity of target compression, the focus of the ICF research is shifting to the implementation of the advanced direct compression schemes, e.g., SI ICF with more efficient laser drivers. The laser driver for the IFE power station must meet a number of challenges; first of all, have the highest overall efficiency, short radiation wavelength
λ for efficient absorption in plasma and higher ablation pressure, and also temporal profiling of laser pulses for the SI ICF. Most of these requirements could be satisfied with e-beam-pumped KrF drivers [
4,
5].
Compared to solid-state lasers a KrF laser possesses:(i) a short lifetime of the excited B state of KrF molecule
τс≈ 2 ns (with taking into account a radiation decay time and quenching collisions); (ii) a low gain saturation parameters − saturation intensity
Is ≈ 2 MW/cm
2 for a quasi-stationary amplification of “long” nanosecond pulses with τ ≥
τc, for which an instant intensity manages the gain saturation, as well as saturation energy density
εs ≈ 2 mJ/cm
2 for “short” sub-nanosecond and picosecond pulses with
τ ≤
τc. Three orders of magnitude less
Is and
εs are well compensated by a larger gain volume of KrF lasers effectively pumped by e-beams. As a small
τс does not allow storing the population inversion in the gain medium during the pumping time
τp>>
τс (usually of a few hundred nanoseconds) an angular multiplexing scheme is conventionally used to extract effectively the pump energy from amplifiers in a train of time and angular separated pulses obtained by splitting the initial laser beam into multiple beamlets (see, e.g., [
5]). But a direct amplification of the entire SI ICF pulse shape meets difficulties as a steep high-intensity final spike strongly saturates the gain medium compared with a pulse foot. A precise precompensation of the saturation is required before pulse amplification which even more increases the spike to foot ratio of the initial pulse shape [
6]. An alternative approach is a simultaneous in time amplification of both long and short pulses in separate beamlets when the rest gain remaining in a course of a quasi-continuous amplification of long pulses allows in addition to amplify short pulses [
7,
8]. A combining of long and short pulses on a target after their demultiplexing makes it possible to produce a temporal shape required for the SI ICF.
The feasibility of a simultaneous amplification of high-energy long pulses (~50 J, 100 ns) on a par with a train of sub-ps pulses with a sub-TW peak power has been already demonstrated [
9]. Short pulses were generated by a Ti: Sapphire front-end which was frequency-tripled into the KrF amplification band [
8]. Unfortunately, a local growth of energy density in evolving filaments significantly reduced the amplifier gain while 3-photon absorption in CaF
2 windows (material of the choice) produced window degradation [
9]. Also, the filamentation of powerful UV pulses in atmospheric air strongly distorted the laser beam distribution [
10].
In the present study we deal with a nonlinear UV pulse compression, which differ favorably from other methods of generating short pulses using dye lasers or frequency tripling of a Ti: Sapphire laser by its simplicity, availability in terms of the cost and high contrast (the ratio of the peak power of the short pulse to the pre-pulse) determined by threshold nature of nonlinear processes. A nonlinear temporal compression of discharge-pumped KrF laser pulses was investigated through decades in high-pressure SF
6 and CH
4 gases which are the promising nonlinear matter [
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21]. It was shown that an effective pulse compression with an appropriate increase in a peak power can be obtained via a backward Stimulated Brillouin Scattering (SBS) [12−15,17,18,21], backward Stimulated Raman Scattering (SRS) [
11,
16], and their combination in a Four Wave Mixing (FWM) scheme [
19,
20]. An advantage of the SBS is a small frequency shift of the Stokes components (Δ
λB~ 10
-3 nm) compared to the width of the KrF laser gain bandwidth (Δ
λ~ 2 nm), which allows one further amplification of the compressed pulses in KrF amplifiers. However, a large dephasing time
T2 determined by a lifetime of hypersonic phonons in the medium namely 100−600 ps in compressed up to 10 atm gases and 30−150 ps in various SBS-active liquids, sets lower limits of the achievable pulse duration. SF
6 has the largest SBS gain among all gases (
gB ≈ 0.9×10
-2cm/MW). Among liquids transparent for a short KrF laser wavelength the best ones are fluorocarbons C
6F
14 and C
8F
18 (
gB ≈ 0.5×10
-2 cm/MW). The cell length
L for generation of the SBS is typically selected to be
gB×
I×L ≥ 25 for one pass just to exceed the SBS threshold.
The advantage of the SRS compression is a shorter phase dephasing time: in CH4 compressed up to 7.5 atm − T2 ~ 25ps, which makes it possible to obtain shorter picosecond pulses in a backward reflection. The disadvantage of the SRS is a significant shift in the wavelength of the Stokes components out of the KrF gain bandwidth ΔλR>>Δλ. To overcome this wavelength misalignment, the FWM of Stokes and anti-Stokes components was additionally used where the original frequency of the KrF laser wavelength was restored in temporally compressed pulses which could be further amplified in the chain of KrF amplifiers.
The present experiments were conceived to elucidate the competition between nonlinear SBS and SRS processes in compressed SF
6 and CH
4 gases in the case of backscattering and forward scattering, as well as for both a narrowband and broadband pump radiation with the goal to choose an effective temporary compression scheme of UV pulses generated by a standard discharge-pumped master oscillator. The obtained sub-ns pulses will be further implemented for combining the SI ICF pulse shape at a multistage e-beam-pumped GARPUN KrF laser facility [
8].
2. A Layout of Experiments
A discharge-pumped KrF laser EMG 150 TMSC 150 (Lambda Physik, GmbH) has been used in experiments on nonlinear scattering of λ = 248 nm radiation in high-pressure SF6 and CH4 gases. This is a two-chamber laser (oscillator and amplifier) with a common power supply operating in an injection-controlled scheme. When a narrow-band seed radiation from the oscillator was injected into an unstable resonator cavity of the amplifier, an output radiation had energy of up to 200 mJ in pulses of τ ≈ 20 ns FWHM, a beam divergence ~ 0.3 mrad and a narrow bandwidth of Δλ ≈ 1.2 ×10-3 nm (Δν ≈ 0.2 cm-1). Alternatively, with a blocked narrow-band oscillator the bandwidth of output radiation was Δλ ≈ 0.25 nm (Δν ≈ 40 cm-1), while other laser parameters changed slightly.
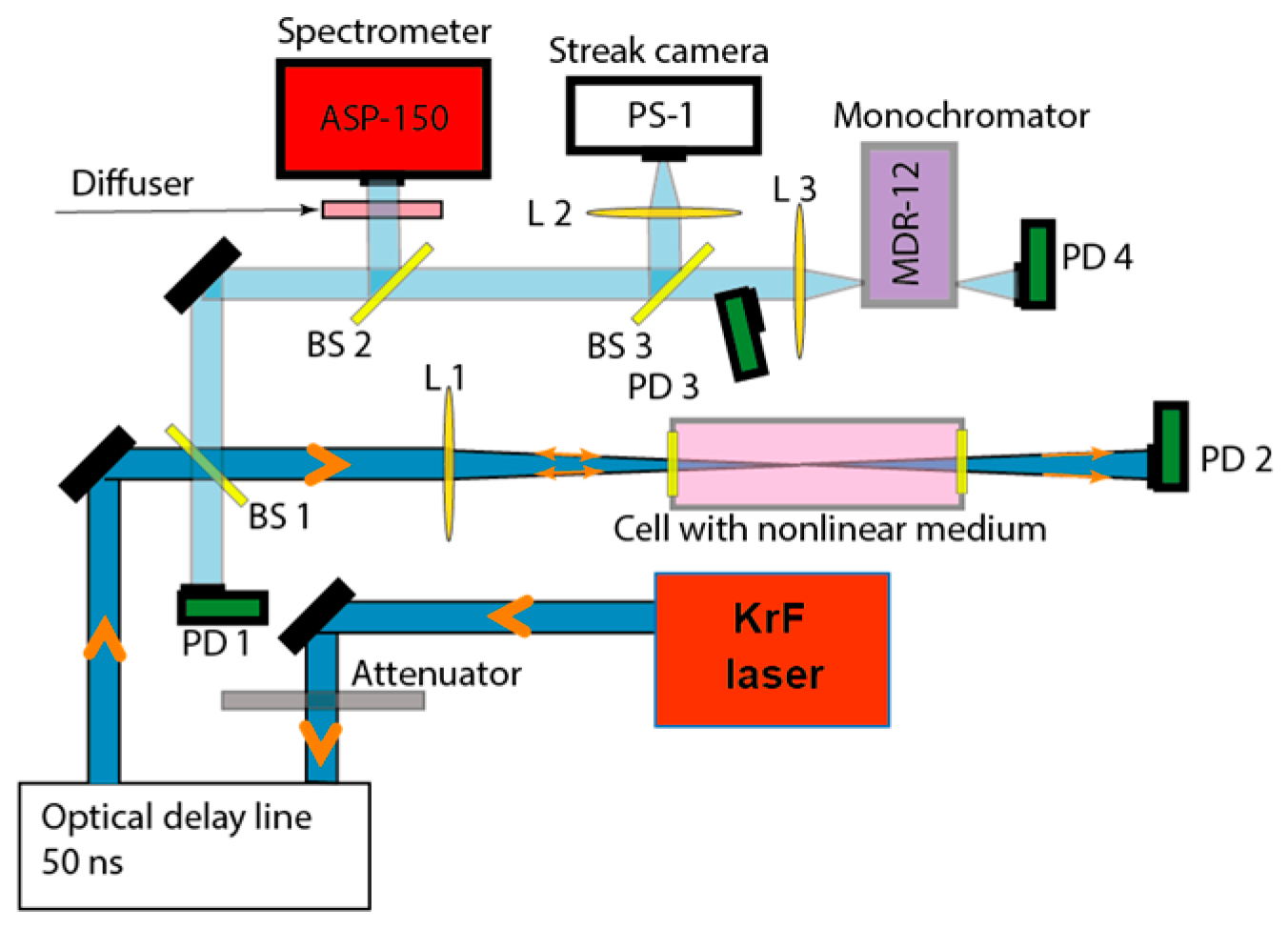
A backscattered radiation was monitored in a layout shown in
Figure 1. The laser energy before focusing in a gas cell was step-wise attenuated in the dynamic range 0.01−0.94 from the initial value
E using a nine-stage diffraction attenuator DVA-22-250 (Inst. of Automation and Electrometry SB RAS, Novosibirsk). The energy was measured by a PESO-SH-V2 calorimeter with a NOVA II display (Ophir Photonics, Israel). To monitor radiation time behavior high-speed photodiodes (Thorlabs DET10A) were used. The pulse shapes of the incident radiation, that passed through the cell with the nonlinear medium and that reflected back were recorded by photodiodes PD 1, PD 2 and PD 3, respectively with a TDS 3054C 500 MHz oscilloscope (Tektronix Inc., USA) with a time resolution ~ 1 ns. Even shorter UV pulses obtained by a nonlinear compression were measured by a streak camera PS-1/S1 (Institute of General Physics of the RAS, Moscow) with a picosecond time resolution. The images on the screen of the streak camera were registered with an Anima-PX reader (Optronics Gmbh). Time-integrated spectra of scattered radiation were recorded by an ASP-150 T (Avesta Project Ltd., Moscow) spectrometer with a spectral resolution ~ 0.3 nm. To illuminate an entrance slit of the spectrometer uniformly, a scattering diffuser was set in front of it. The temporal dynamics of scattered spectral components was studied using an MDR-12 grating monochromator (LOMO, St. Petersburg), which was tuned into a required wavelength range with a registration of the selected radiation by the PD 4 photodiode.
Due to a small spectral shift the radiation reflected by the SBS which has got into of the laser bandwidth, there was a potential danger to damage the output meniscus coupler of the laser and its output window by the radiation back reflected from the nonlinear medium when it was focused in an inverse converging wave of the unstable telescopic resonator. In this regard, a polarization decoupling of the incident radiation and that reflected back from the cell was foreseen with a help of quarter-wave phase plate and a polarizer. However, in the described below experiments an optical delay line of about 15 m long was used between the laser and the cell, thanks to which the reflected pulse returned back after 100 ns, i.e., to the moment when the gain in the laser decayed after a termination of a pumping discharge.
The cell with the SF6 had an inner diameter of 26 mm and a length of 250 cm, it was filled at a pressure of 10 atm. Plane-parallel windows made of fused silica glass KU-1 with a diameter of 40 mm and a thickness of 10 mm were used. The pump radiation was focused into the cell by lenses with focal lengths F= 0.8 or 2 m. Fresnel reflection from the windows was excluded from registration of backward radiation by a slight inclination of the cell axis relative to the axis of the incident radiation. The cell with CH4 at a pressure of 50 atm had an inner diameter of 20 mm and a length of 70 cm. It was closed from both sides with thick wedge-shaped windows of 30 mm in diameter, which excluded Fresnel reflection of the pump radiation being focused into the cell by a lens with F = 0.5 m.
The radiation distribution in a focal plane was measured by Spiricon SP620U profiler (Ophir Photonics), while K8 glass plate was used to convert UV laser light into green fluorescence [
10]. The focal distribution had a Gaussian-like symmetric central part and broad low-intensity wings, originated from a temporal evolution of laser light in the unstable resonator cavity of the laser [
22]. The distribution of pump radiation in a focal spot for all lenses used in the experiments remained similar and scaled proportionally to the focal length
F while a peak intensity in the spot
I varied as
. For a given pulse duration
τ ≈ 20 ns, the peak intensity in the center of a focal spot could be expressed via other variables
. Note that for the highest pump energy
Emax ≈ 120 mJ, and the shortest focal length
F= 0.5 m the maximal peak intensity 4.3×10
10 W/cm
2 was still less than the breakdown thresholds for gases under investigation.
3. Experimental results
The radiation reflected exactly backwards was recorded in the experiments with a narrow-band pumping of SF6 and CH4 gases , thus evidencing that an optical phase conjugation (OPC) was realized via SBS and SRS mechanisms. A quite different temporal behavior of the backscattered radiation, that is pulse compression in dependence on the pump energy Ep was observed in these two gases. Note, that for a broad-band pumping no backward reflection was detected at all in both gases. On the contrary, the SRS in a forward direction was more pronounced for a broad-band pumping in CH4.
3.1. Backscattering in SF6
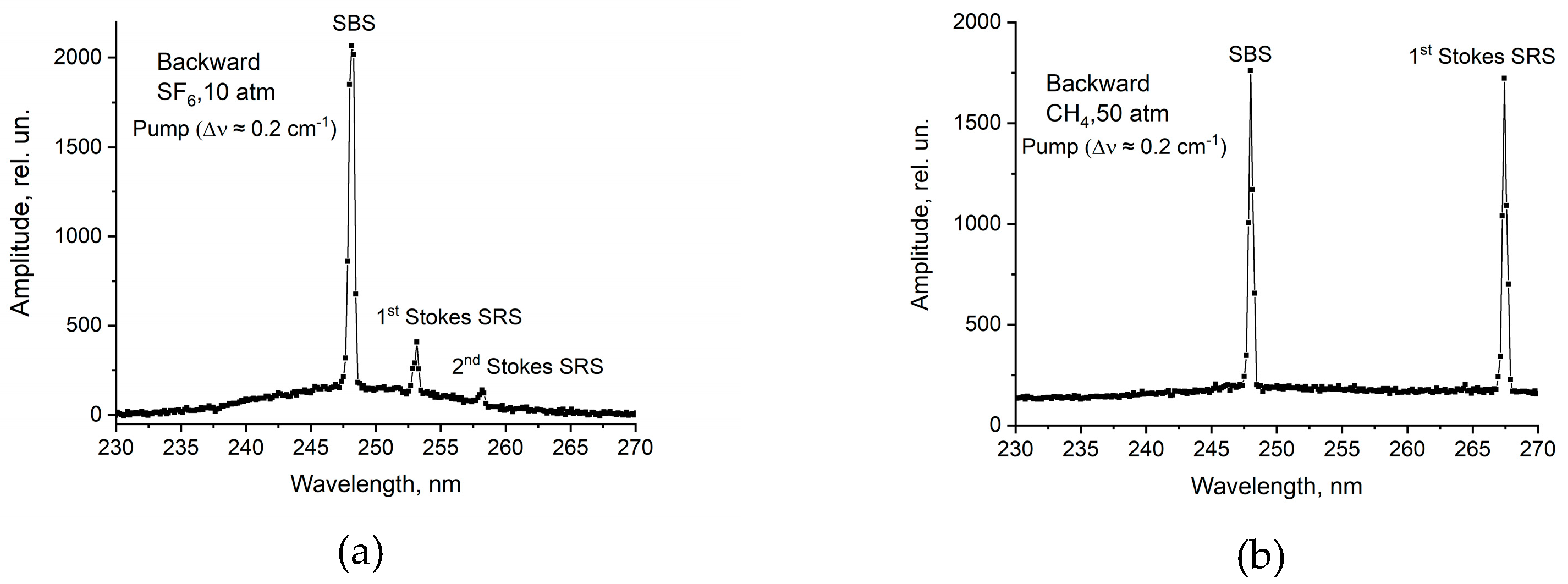
The time-integrated spectrum of the reflected radiation is shown in
Figure 2a. The spectral line widths were broadened by the ASP spectral resolution while broad pedestal arose due to scattered light inside the spectrometer. The most intensive peak at the wavelength λ= 248.4 nm corresponds to SBS which has a small shift relative to pump radiation bandwidth Δ
λB ≤ Δ
λ which is unresolved at the spectrometer. In addition to this practically “unshifted” SBS peak, the spectrum contains significantly weaker SRS peaks at λ=253.3 and 258.3 nm. The frequency shift for these 1-st and 2-nd order SRS components being a multiple of 775 cm
-1 quantum which corresponds to the strongest SRS line associated with completely symmetrical vibrations of the SF
6 molecule [
23]. A ratio of the 1-st SRS to the SBS peaks found from the time-integrated spectrum gives approximate ratio of the corresponding SRS and SBS energies which was
ESRS/
ESBS ≈ 1/6.5 for
Ep ≈ 120 mJ and fell down with decreasing the pump energy.
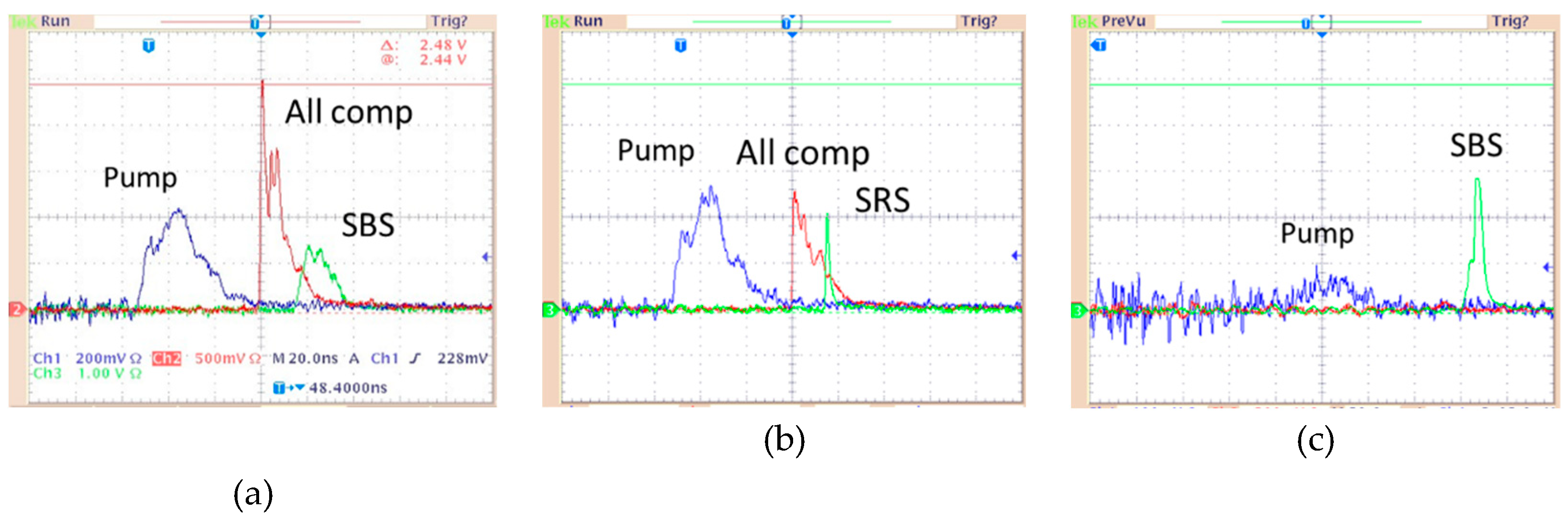
A study of the temporal dynamics of reflected radiation was carried out with
F = 2 m focusing lens. It shows a reduction of the leading edge of reflected pulses, the most significant for the SRS components (
Figure 3). Note that due to a difference in optical paths to the PDs and the lengths of their cables, the signals on the oscilloscope have different delays relative to the beginning of the time scan. For example, relative to the pump radiation (PD 1), the signal of reflected radiation in the entire spectral range including all scattered components (PD 3) is delayed by 33 ns, and reflected radiation of the selected spectral components SBS or SRS (PD 4) is delayed by 46 ns. The pulse length of the SBS component at the maximal pump energy of ~ 120 mJ was ~ 10 ns at the FWHM, i.e., twice less than the pump length of ~ 20 ns. The reflected SBS pulse length decreased down to 2−3 ns at the FWHM when pump energy approached the SBS threshold ~ 10 mJ (
Figure 3 c). The pulse length of the reflected SRS radiation, on the contrary, decreased with an increase of the pump energy above the threshold ~ 30 mJ; at
Ep ≈ 120 mJ it was 1−2 ns (
Figure 3 b) which was about the temporal resolution of the PD. Therefore, a fast streak camera was used to resolve components of the backscattered radiation. Possible explanation of SRS pulse shortening with pump intensity is discussed in
Section 4.
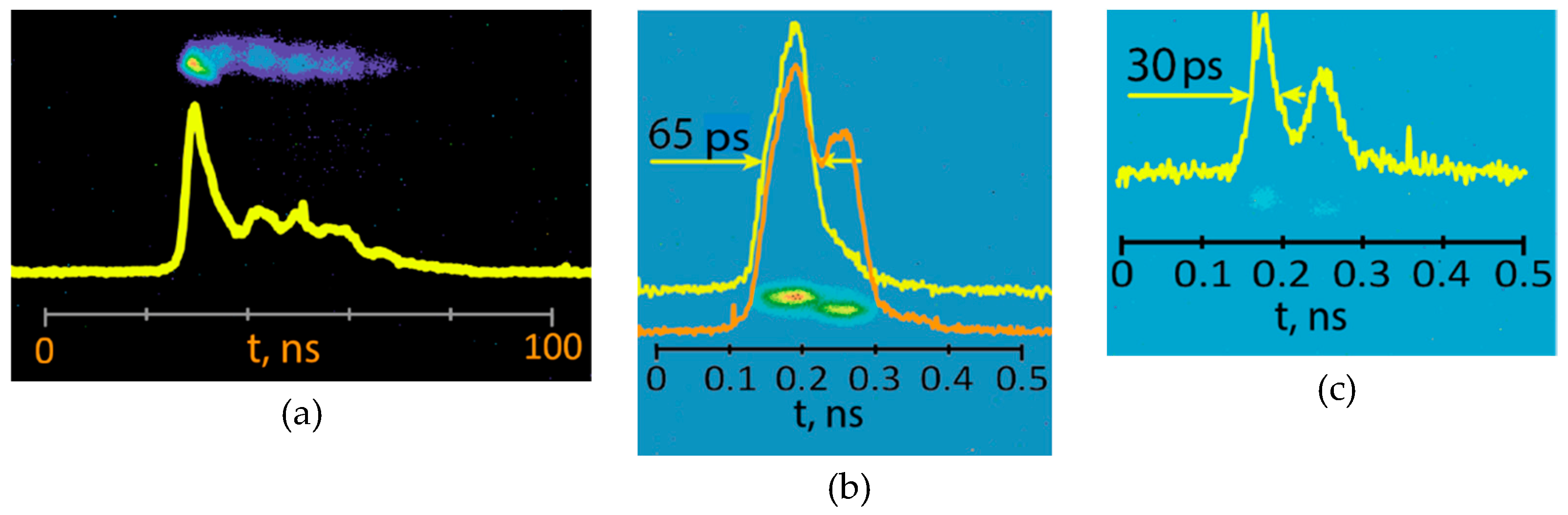
The streak camera images obtained with various scanning speeds are shown in
Figure 4a−c together with the temporal pulse profiles. The presence of two components with different time widths are evident in the image (a) with a 100 ns scanning time. A long-time component of ~ 50 ns corresponds to the SBS signal on the oscilloscope traces (
Figure 3a). The second, a short-time component, which is time-integrated and looks like a leading peak in the temporal profile of the image (a) is well resolved with shorter sweeping time 0.5 ns in images (b,c). Its length varying in the range 30−60 ps corresponds to the unresolved SRS signals in
Figure 3 b. The doubled structure of images separated across time (horizontal axis) and space (vertical axis) originates from a difference in the course of light reflected from two faces of the beam splitter plate that diverted radiation from the cell (BS 3 in
Figure 1). A single-humped and double-humped temporal profiles in the case (b) were obtained with different integration regions of the streak images in a perpendicular (space) direction which accounted for one or two spots.
3.2. Backscattering in CH4
In experiments with CH
4 cell, where a narrow-band pump radiation (focused with
F =0.5 m lens) was also reflected strictly backwards, the time-integral spectrum in addition to the main SBS peak at λ = 248.4 nm contained a peak at λ = 267.8 nm with a comparable amplitude (
Figure 2b). The frequency shift for the Stokes component 2917 cm
-1 corresponds to the strongest line in the SRS spectrum of CH
4 [
13]. The reflected signals for both the SBS and the SRS components gradually shortened with decreasing pump energy, however, the shortest pulses were ~ 4 ns (
Figure 5). The thresholds for the SBS ~ 6 mJ and for SRS − 30 mJ were close to the values in SF
6. Note that for a broad-band pump radiation no backward reflection was registered in experiments.
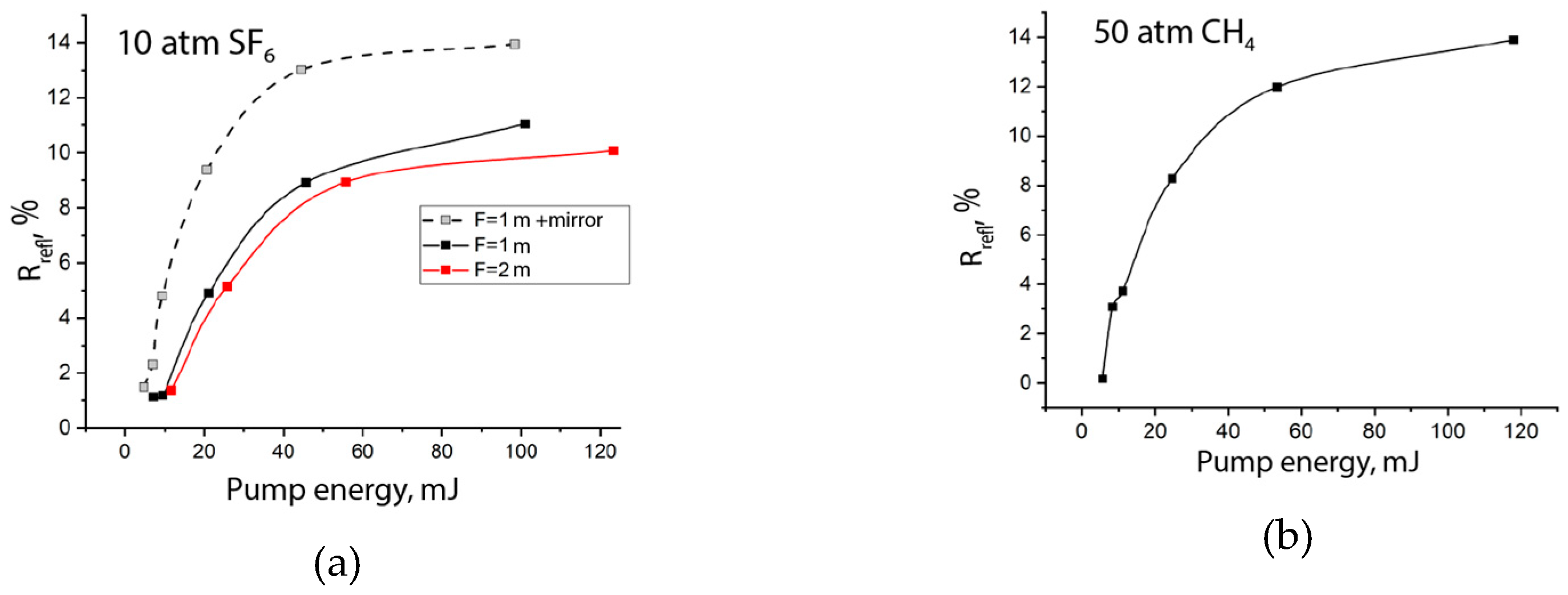
3.3. Backscattering efficiencies
Energies of the total (both SBS and SRS) backscattered radiation
Erefl and pump radiation
Ep were measured by calorimeters and the efficiency of a backward nonlinear reflection was calculated as
Rrefl =
Erefl/
Ep×100%. It is represented in
Figure 6 for SF
6 (a) and CH
4 (b). In both gases
Rrefl grew rapidly with increasing pump energy above the threshold of nonlinear reflection, gradually saturating at high
Ep. In SF
6 the maximum efficiency amounted (
Rrefl)
max ≈ 10% and was approximately equal for different focal lengths of the focusing lenses
F = 0.8 m and
F = 2 m. An additional mirror installed behind the cell increased
Rrefl especially at low pump energy (curve “F=1m +mirror”) which indicates that the radiation reflected by the mirror highly contributed to the nonlinear scattering process additively to a spontaneous scattering in the gas. At the highest pump energy, the maximum efficiency increased by 30% up to (
Rrefl)
max ≈ 14%. The maximum efficiency in CH
4 for the lens with
F = 0.5 m amounted (
Rrefl)
max ≈ 14% without any additional mirror. It should be noted once again that a ratio of the SRS to SBS radiation gradually decreased for lower pump energies.
3.4. Forward scattering in CH4
Forward radiation passed through a CH
4 cell was measured in the scheme similar to that shown in
Figure 1 with a
F = 50 cm lens being set behind the cell confocal with the focusing lens. This additional lens collimated both transmitted pump radiation and the forward-scattered one which were analyzed with the spectrometer and monochromator placed at ~ 7.5 m behind the cell. Similar to
Figure 1 a photodiode PD 3 measured the total radiation reflected by the lens L3 at the monochromator entrance while PD 4 − at its output at specific wavelengths of various spectral components.
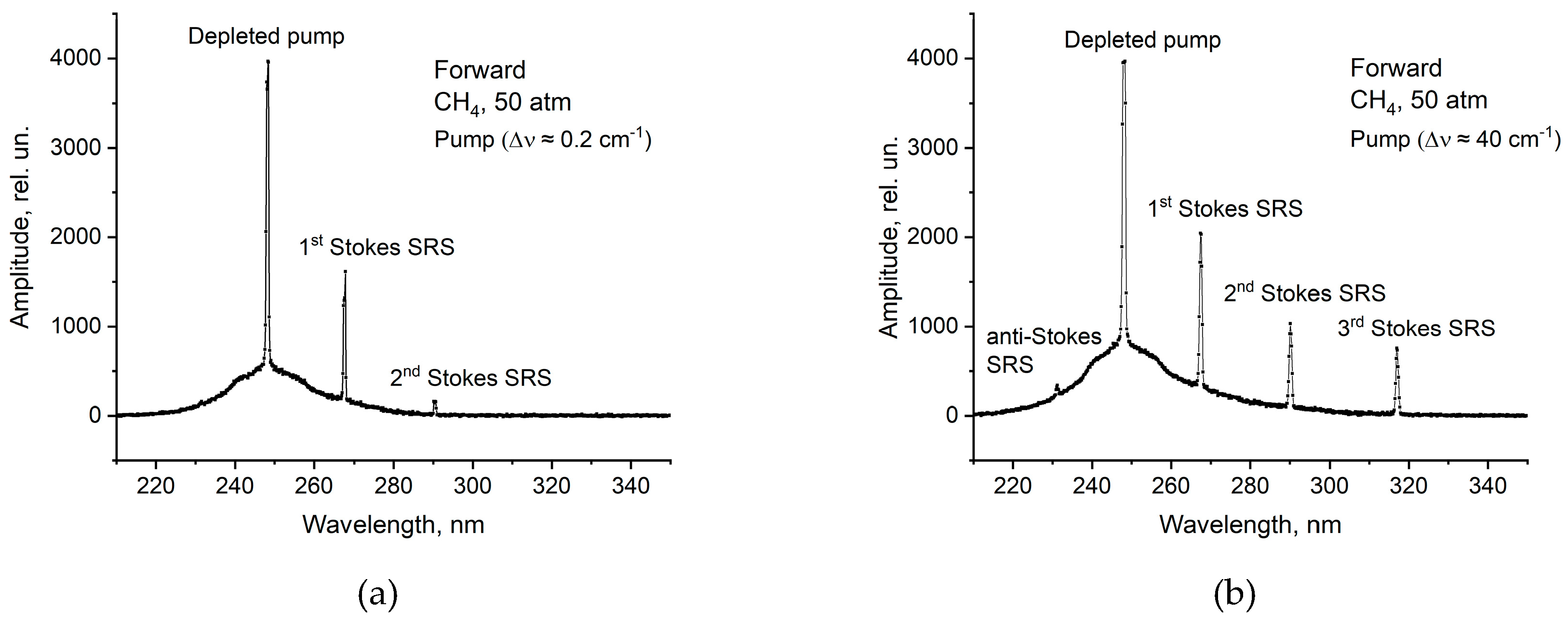
The spectra of a forward radiation through CH
4 cell are presented in
Figure 7 for both a narrow-band (a) and broad-band pump radiation (b). It is seen that for a narrow-band pumping besides the “wavelength-unshifted” main line at λ = 248.4 nm the spectrum contains the 1
st and 2
nd order Stokes SRS peaks at λ = 267.8 and 290.5 nm, respectively. For a broad-band pumping additional 3
rd order Stokes SRS peak at λ = 317.4 nm and a weak 1
st order anti-Stokes SRS peak at λ = 231.6 nm appeared in the spectrum which means that a cascade nonlinear process of high-order forward SRS component generation is more effective for a broadband pump radiation.
As no back-scattered light was registered for a broadband pumping, the oscilloscope signals for both forward radiation at λ ≈ 248.4 nm (passed through the monochromator) and total transmitted radiation including pumping and all scattered SRS components increased at the expense of suppressed back reflected radiation compared with a narrow-band pumping.
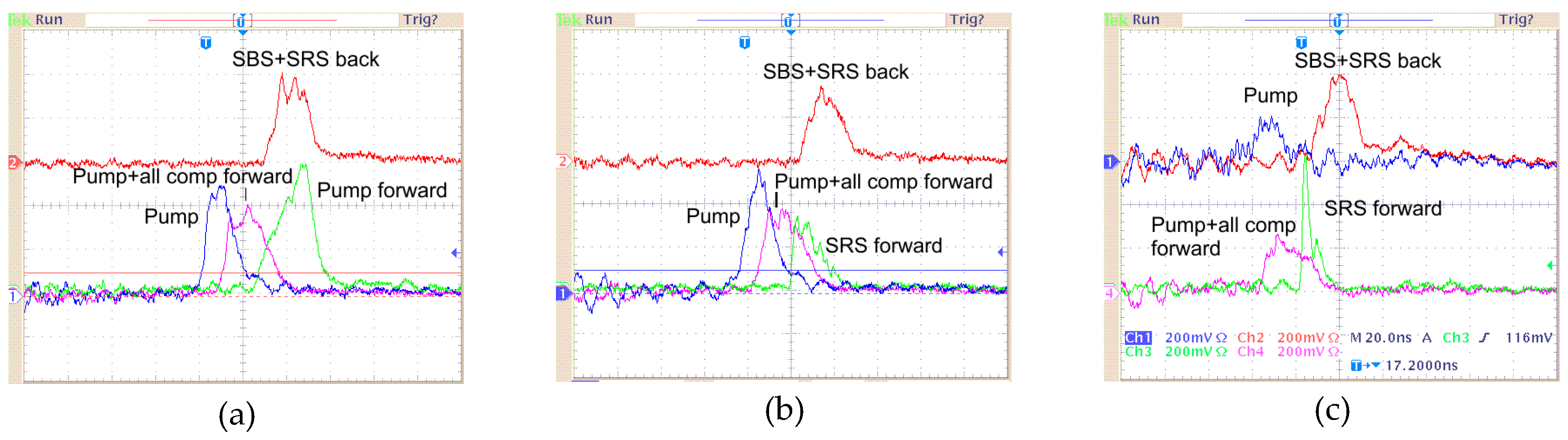
The pulse shapes for a narrow-band pump radiation measured in front of the cell, backscattered SBS and SRS components and transmitted radiation at specific wavelengths selected by the monochromator are shown in
Figure 8. At a high pump energy
Ep ≈ 120 mJ a pulse of transmitted radiation at λ = 248.4 nm has a slowly rising leading front and a steep trailing front compared with the pump pulse (a). It might be explained by a depletion of pump radiation being converted into backscattered SBS and SRS, as well as forward-scattered SRS. Oppositely, a pulse-form at λ = 267.8 nm for a forward 1
st SRS component has a steep leading front (b). However, the pulse widths for the pump, reflected back, total transmitted and forward-scattered SRS radiation were all comparable. The difference in transmitted pulse lengths became clear at a reduced pump energy
Ep ≈ 25 mJ (c). Forward SRS pulses shortened down to 3−4 ns while the transmitted radiation at λ = 248.4 nm did not change noticeably.
4. Discussion
The described above results demonstrate a strong competition between two nonlinear scattering processes SBS and SRS. Firstly, it was observed in compressed gases with a ruby laser [
24,
25], then was reported for shorter laser wavelengths (see e.g. [
12,
26]). Both the SBS and SRS, each having different dependences on gas pressure, could occur simultaneously even if one of them had higher gain coefficient in some region of parameters. Their interaction originates mainly of the change in a spatial distribution of optical fields altered (depleted) by an intense level of scattering. A backward SRS pulse compressors for KrF ICF were also discussed in [
16,
27,
28] where limitations from the other scattering processes were considered e.g., SBS and forward SRS. The latter was shown to be asymmetric relative to the backward SRS and was able going on with a broadband pumping, similar to present experiments.
Among other things, there is a discrepancy between our results on backscattering in SF
6 and experiments [
17] where in similar conditions no backscattered SRS radiation was measured at all. On the other hand, in accordance with present experiments, Tomov et al [
12] observed a short backward Raman scattering with a pulse duration in the range of 120−400 ps preceding the Brillouin backscattered signal. However, after the development of the SBS the SRS was suppressed because of the higher gain for the Brillouin mode.
Conventionally, the shortest scattered laser pulses are obtained near the threshold of corresponding stimulated scattering process. After exceeding the threshold, the rapidly growing Stokes signal results in depletion of the pump wave, so that pump intensity drops below the threshold and stimulated amplification is ended. With an increase in pump peak intensity, the threshold for stimulated scattering is exceeded for longer part of the pump pulse, that is why pulse width of the scattered signal should increase proportionally. In our experiments, this natural behavior holds for the backward SBS and forward SRS, while in the case of backward SRS in SF6 the Stokes pulse width has been found decreasing with an increase in pump pulse intensity. Below, we provide a simple theoretical consideration which allows to explain this anomalous dependence.
Conventional model of backward SRS is based on the following set of equations [
29,
30,
31]:
Here,
and
are the slow varying amplitudes of the forward pump and the backward Stokes waves,
and
, having the wavenumbers
, the frequencies
, and the group velocities
, respectively. The constants
and
describes linear attenuation at the pump and the Stokes waves, while
is the relaxation rate of the specific normal vibrational coordinate
where
is its slow varying amplitude and
is the resonant vibrational frequency,
. The light-matter coupling coefficients are
and
, where
are the refractive indices at the pump and the Stokes frequencies,
are respectively the number density of Raman-active molecules, their effective mass, and the derivative of the molecular polarizability with respect to the normal coordinate.
Introducing the new amplitude functions according to the following substitution
, one can rewrite (1) as
where
and
are the new attenuation coefficients. In view of the fact that the attenuation coefficient
is rather small so that
during the entire interaction process, one can solve Eqs. (2) within the perturbation theory. To the lowest order of the perturbation theory [
32], we put the exponents in the right-hand side of (2) being equal to unity and seek transient solutions of the following shape
where the transient coordinate
, and
characterizes the pulse width
. One can easily find that both the soliton-like solutions (3) satisfy the second and the third of Eqs. (2) when
The pump wave amplitude is then described as
Substituting (5) in the first of Eqs. (2), we find
Note that when we have the coefficient , the velocity of the transients exceeds the group velocity of the Stokes signal and all the amplitudes have the same phase. Vice versa, when we have , the amplitudes differ from by in phase and the transient velocity becomes less than the group velocity .
The above transient solutions describe backward SRS process in which the Stokes characteristic pulse width decreases with an increase in pump intensity. Really, the initial intensity of the pump laser pulse
corresponds to the limiting value of (5) at
, i.e.,
Here the characteristic threshold intensity
. According to (7), the pulse width of the Stokes pulse is large near the threshold intensity and gradually decreases with an increase in
, being of the order of
, i.e., of the order of the characteristic vibrational relaxation time of the Raman-active medium. This dependence qualitatively agrees with the experimental data in
Section 3.1.
5. Conclusions
Nonlinear pulse compression was obtained for a narrow-band KrF laser radiation in compressed gases. When KrF laser pulses with a 20 ns temporal width were focused into SF6 cell at 10 atm pressure both SBS and SRS optically phase conjugated backward reflection was registered with energy reflectivity 10−14%. While SBS pulse gradually shortened from 10 ns for high pump energy of 100 mJ to 2−3 ns when approaching the SBS threshold of ~ 10 mJ, the SRS pulse exhibited an abnormal behavior. It had the shortest width of 30−60 ps for the maximal pumping of 120 mJ and broadened near SRS threshold of ~30 mJ. The SRS pulse energy was about 2 mJ which corresponded to the peak power 5×107 W, and this was a tenfold higher than the pump power (120 mJ & 20 ns). The theoretical model predicted a soliton-like SRS pulse compression to a temporal width of the order of vibrational relaxation time.
In CH4 gas cell at 50-atm pressure both SBS and SRS optically phase conjugated backward reflection was observed for a narrow-band pumping with energy reflectivity 14%. There was no pulse compression of backward radiation, while in the forward direction SRS pulses shortened to 3−4 ns at reduced pumping. For a broad-band pumping (Δν ≈ 40 cm-1) a strong asymmetry was observed: a backward SRS and SBS reflection was absent at all while in a forward direction the spectra were enriched by high-order Stokes SRS components as well as by 1st anti-Stokes component.
Supplementary Materials
Any supporting information can be provided by V.D.Z. on the request.
Author Contributions
Conceptualization, V.D.Z. and I.V.S ; methodology, A.V.S., V.D.Z.; experimental investigation, A.V.S., G.E.M., P.V.V., N.N.U., and V.D.Z.; theoretical analysis, I.V.S.; writing—original draft preparation, V.D.Z.; writing—review and editing, N.N.U.; project administration, V.D.Z.; funding acquisition, V.D.Z. All authors have read and agreed to the published version of the manuscript.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We are grateful to Chetvertakov A.A., Karmazin L.I. and Khusainov S.N. from P. N. Lebedev Physical Institute—for their assistance in experiments.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Shcherbakov, V.A. Ignition of a laser-fusion target by a focusing shock wave. Sov. J. Plasma Phys. 1983, 9, 240–242. [Google Scholar]
- Betti, R.; Zhou, C.D.; Anderson, K.S.; Perkins, L.J.; Theobald, W.; Solodov, A.A. Shock ignition of thermonuclear fuel with high areal density. Phys. Rev. Lett. 2007, 98, 155001. [Google Scholar] [CrossRef] [PubMed]
- National Ignition Facility achieves fusion ignition. Available online: https://llnl.gov/news/national-fusion-facility-achievsignition (accessed on 14 December 2022); DOE National Laboratory Makes History by Achieving Fusion Ignition. Available online: https://energy.gov/articles/doe-national-laboratory-makes-history-achieving-fusion-ignition (accessed on 13 December 2022).
- Bodner, S.E.; Schmitt, A.J.; Sethian, J.D. Laser requirements for a laser fusion energy power plant. HPLSE 2013, 1, 2–10. [Google Scholar] [CrossRef]
- Obenschain, S.; Lehmberg, R.; Kehne, D.; Hegeler, F.; Wolford, M.; et al. High-energy krypton fluoride lasers for inertial fusion. Appl. Opt. 2015, 34, F103–F122. [Google Scholar] [CrossRef] [PubMed]
- Lehmberg, R.H.; Giuliani, J.L.; Schmitt, A.J. Pulse shaping and energy storage capabilities of angularly multiplexed KrF laser fusion drivers. J. Appl. Phys. 2009, 106, 023103. [Google Scholar] [CrossRef]
- Zvorykin, V.D.; Lebo, I.G.; Rozanov, V.B. On the feasibility of production of a source of thermonuclear neutrons on the basis of a KrF laser. Bull. of Lebedev Phys. Inst. 1997, No. 9-10. 20–29. [Google Scholar]
- Zvorykin, V.D.; Didenko, N.V.; Ionin, A.A.; Kholin, I.V.; Konyashenko, A.V.; et al. GARPUN-MTW: A hybrid Ti:Sapphire/KrF laser facility for simultaneous amplification of subpicosecond/nanosecond pulses relevant to fast-ignition ICF concept. Laser Part. Beams 2007, 25, 435–451. [Google Scholar] [CrossRef]
- Zvorykin, V.D.; Ionin, A.A.; Levchenko, A.O.; Mesyats, G.A.; Seleznev, L.V.; et al. Production of extended plasma channels in atmospheric air by amplitude-modulated UV radiation of GARPUN-MTW Ti : sapphire – KrF laser. Part 1. Regenerative amplification of subpicosecond pulses in a wide-aperture electron beam pumped KrF amplifier. Quantum Electron. 2013, 43, 332–338. [Google Scholar] [CrossRef]
- Zvorykin, V.D.; Shutov, A.V.; Ustinovskii, N.N. Review of nonlinear effects under TW-power PS pulses amplification in GARPUN-MTW Ti:sapphire-KrF laser facility. Matter Radiat. Extrem. 2020, 5, 045401. [Google Scholar] [CrossRef]
- Tomov, I.V.; Fedosejevs, R.; McKen, D.C.D.; Domier, C.; Offenberger, A.A. Phase conjugation and pulse compression of KrF-laser radiation by stimulated Raman scattering. Opt. Lett. 1983, 8, 9–11. [Google Scholar] [CrossRef] [PubMed]
- Tomov, I.V.; Fedosejevs, R.; McKen, D.C.D. High-efficiency stimulated Brillouin scattering of KrF laser radiation in SF6. Opt. Lett. 1984, 9, 405–407. [Google Scholar] [CrossRef] [PubMed]
- Fedosejevs, R.; Offenberger, A.A. Subnanosecond pulses from a KrF laser pumped SF6 Brillouin amplifier. IEEE J. Quantum Electron 1985, QE-21, 1558–1562. [Google Scholar] [CrossRef]
- Kurnit, N.A.; Thomas, S.J. Application of a phase-conjugate Brillouin mirror to generation of high-quality variable-duration KrF pulses. IEEE J. Quantum Electron 1989, QE-25, 421–429. [Google Scholar] [CrossRef]
- Offenberger, A.A.; Thompson, D.C.; Fedosejevs, R.; Harwood, B.; Santiago, J.; Manjunath, H.R. Experimental and modeling studies of a Brillouin amplifier. IEEE J. Quantum Electron. 1993, QE-29, 207–216. [Google Scholar] [CrossRef]
- Takahashi, E.; Matsumoto, Y.; Matsushima, I.; Okuda, I.; Owadano, Y.; Kuwahara, K. Compression of high power KrF laser pulse by backward Raman amplification. Fusion Eng. Des. 1999, 44, 133–136. [Google Scholar] [CrossRef]
- Kuwahara, K.; Takahashi, E.; Matsumoto, Y.; Kato, S.; Owadano, Y. Short-pulse generation by saturated KrF laser amplification of a steep Stokes pulse produced by two-step stimulated Brillouin scattering. J. Opt. Soc. Am. B 2000, 17, 1943–1947. [Google Scholar] [CrossRef]
- Takahashi, E.; Kuwahara, K.; Matsumoto, Y.; Okuda, I.; Matsushima, I. High-intensity short KrF laser-pulse generation by saturated amplification of truncated leading-edge pulse. Optics Commun. 2000, 185, 431–437. [Google Scholar] [CrossRef]
- Takahashi, E.; Losev, L.L.; Matsumoto, Y.; Okuda, I.; Matsushima, I.; et al. KrF laser picosecond pulse source by stimulated scattering processes. Optics Commun. 2003, 215, 163–167. [Google Scholar] [CrossRef]
- Takahashi, E.; Losev, L.L.; Matsumoto, Y.; Okuda, I.; Kato, S.; et al. 1 ps, 3 mJ KrF laser pulses generated using stimulated Raman scattering and fast Pockels cell. Optics Commun. 2005, 247, 149–152. [Google Scholar] [CrossRef]
- Lü, Z.; Wang, C.; Lin, D.; Wang, X. Investigation on stimulated Brillouin scattering pumped by broadband KrF laser. Proc SPIE 2005, 5627, 363–368. [Google Scholar] [CrossRef]
- Smetanin, I.V.; Shutov, A.V.; Ustinovskii, N.N.; Veliev, P.V.; Zvorykin, V.D. A new insight into high-aspect-ratio channel drilling in translucent dielectrics with a KrF laser for waveguide applications. Materials 2022, 15, 8347. [Google Scholar] [CrossRef] [PubMed]
- Wagner, N.L.; Wuest, A.; Christov, I.P.; Popmintchev, T.; Zhou, X.; et al. Monitoring molecular dynamics using coherent electrons from high harmonic generation. PNAS 2006, 103, 13279–13285. [Google Scholar] [CrossRef] [PubMed]
- Hagenlocker, E.E.; Rado, W.C. Stimulated Brillouin and Raman scattering in gases. Appl. Phys. Lett. 1965, 7, 236–238. [Google Scholar] [CrossRef]
- Minck, R.W.; Hagenlocker, E.E.; Rado, W.G. Simultaneous occurrence of and competition between stimulated optical-scattering processes in gases. J. Appl. Phys. 1967, 38, 2254–2260. [Google Scholar] [CrossRef]
- Sentrayan, K.; Kushawaha, V. Competition between steady state stimulated Raman and Brillouin scattering processes in CH4, and H2. J. Phys. D: Appl. Phys. 1993, 26, 15541560. [Google Scholar] [CrossRef]
- Murray, J.R.; Goldhar, J.; Eimerl, D.; Szoke, A. Raman pulse compression of excimer lasers for application to laser fusion. IEEE J. IEEE J. Quantum Electron. 1979, QE-15, 342–368. [Google Scholar] [CrossRef]
- Nishioka, H.; Kimura, K.; Ueda, K.; Takuma., H. High compression ratio backward Raman conversion for high brightness excimer laser systems. IEEE J. Quantum Electron. 1993, 29, 2251–2258. [Google Scholar] [CrossRef]
- Maier, M.; Kaiser, W.; Giordmaine, J.A. Backward Stimulated Raman Scattering. Phys. Rev. 1969, 117, 580–599. [Google Scholar] [CrossRef]
- Akhmanov, S.A.; Drabovich, K.N.; Sukhorukov, A.P.; Chirkin, A.S. Stimulated Raman Scattering in a field of ultrashort light pulses. Sov. Phys. JETP 1971, 32, 266–273. [Google Scholar]
- Boyd, R.W. Nonlinear Optics, 3rd ed.; Academic Press, 2008. [Google Scholar]
- Smetanin, I.V. Dissipative and non-dissipative solitons in the SRS-backscattering of laser radiation in underdense plasma. In: Laser-driven relativistic plasmas applied to science, energy, industry and medicine, Bulanov, S.V.; Yokoyama, A.; Malakhov, Yu. I.; Watanabe Y. Eds.; AIP Proceedings, 2012, Volume 1465, p. 107. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).