Prerpints.org logo
Preprint
Article

An Efficient and Robust ILU(k) Preconditioner for Steady-State Neutron Diffusion Problem Based on MOOSE

Altmetrics

Downloads

87

Views

40

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

27 November 2023

Posted:

28 November 2023

You are already at the latest version

Alerts
Abstract
Jacobian-free Newton Krylov (JFNK) is an attractive method to solve nonlinear equations in nuclear engineering systems, and has been successfully applied to steady-state neutron diffusion (k-eigenvalue) problems and multi-physics coupling problems. Preconditioning technique plays an important role in JFNK algorithm, significantly affecting computational efficiency. The key point is how to automatically construct a high-quality preconditioning matrix that can improve the convergence rate, and perform the preconditioning matrix factorization efficiently. An efficient reordering-based ILU(k) preconditioner is proposed to achieve the above objectives. In detail, the finite difference technique combined with the coloring algorithm is utilized to construct an efficient preconditioning matrix with low computational cost automatically. Furthermore, the reordering algorithm is employed for the ILU(k) to reduce the additional non-zero elements and pursue robust computational performance. A two-dimensional LRA neutron steady-state benchmark problem is used to evaluate the performance of the proposed preconditioning technique, and steady-state neutron diffusion problem with thermal-hydraulic feedback is also utilized as a supplement. The results show that coloring algorithms can efficiently and automatically construct the preconditioning matrix. The reordering-based ILU(k) preconditioner shows excellent robustness, avoiding the effect of fill-in levels k choice in incomplete LU factorization.
Keywords: 
Subject: Engineering  -   Energy and Fuel Technology

1. Introduction

Due to the inherently featured of multi-scale and multi-physical in the reactor systems, the nuclear reactor simulation is a multi-physics coupling calculation [1,2], where a nonlinear coupled partial differential equation system is used to describe the physical behavior at different scales and physics fields. The steady-state neutron diffusion k-eigenvalue problem is the fundamental component of the multi-physics system. After the discretization of these partial differential equations (PDEs), it usually leads to a nonlinear algebraic equation problem [3]. The iterative method is a preferred option for the large-scale problem, since its smaller storage and computational cost compared with the direct matrix inversion method. Compared with the widely-used traditional coupling methods, such as operator splitting method and Picard iteration method [4,5,6] Jacobian-free Newton-Krylov (JFNK) algorithm [7] is well-known due to its low storage and high-order convergence rate. JFNK algorithm has been widely used in the latest nuclear engineering simulation codes [8,9,10,11]. Based on the JFNK algorithm, a Multi-physics Object Oriented Simulation Environment (MOOSE) has been developed by Idaho National Laboratory (INL) targeted at the solution of coupled nonlinear PDEs [12]. MOOSE can facilitate the simulation of nuclear systems and many programs have been developed based on this framework, such as reactor multi-physics code MAMOTH [13], advanced thermal-hydraulic code Pronghorn [14], and two-phase thermal systems code RELAP-7 [15]. The related works of fuel performance analysis is carried out based on MOOSE due to the strong ability to simulate different mesh scales and multi-physics coupling calculation [16]. In addition, input uncertainty can be studied on MOOSE, which can provide high-fidelity modeling and a fundamental understanding of the various physical interactions [17]. MOOSE is a powerful simulation platform featured with finite element mesh system and extensible numerical solution system. However, the algorithms need to be further studied to pursue efficient and robust performance for MOOSE based applications.
This work focuses on preconditioning techniques to improve the performance of the JFNK method based on MOOSE. Based on the fully coupled concept, all the governing equations will be expressed in the form of residual functions. The Newton-Krylov iteration process in the JFNK algorithm is applied to solving nonlinear equations. The coefficient matrix of the Newton-Krylov system is called the Jacobian matrix. When the nonlinear coupling characteristics of the system are complex, the construction of the Jacobian matrix is complicated and even difficult to give analytical expressions due to the existence of the first-order partial derivative. Although the JFNK method does not need to construct a Jacobian matrix explicitly, its components can be used as preconditioner to accelerate the linear iterations. According to the principle of preconditioning, a faster convergence rate can be achieved when the preconditioning matrix is as consistent as possible with the Jacobian matrix. The widely-used preconditioning matrix is an approximation of the Jacobian matrix, such as retaining the matrix information of the main diagonal block region, which is called block Jacobi preconditioning. Two requirements need attention when preparing the preconditioning matrix. Firstly, the preconditioning matrix should be constructed cheaply and automatically. Secondly, the factorization process of the preconditioning matrix should be efficient enough. This work uses the Jacobian matrix as the coefficient matrix before factorization to pursue a rapid convergence rate. At the same time, the algorithms to improve the efficiency of the factorization process is also considered. These two requirements ensure the efficiency of the preconditioning process and overall solution.
The construction phase mainly focuses on the calculation of the preconditioning matrix elements. Most of the current preconditioners need to provide the analytical expression of elements, and MOOSE also supports the corresponding preconditioning strategy, which will be burdened and might introduce artificial errors. The finite difference technique can automatically generate the preconditioning matrix. Generally, this preconditioner does not consider the sparsity of the matrix, so it will bring a large computational cost. This preconditioner usually requires a number of residual function evaluations, leading to a relatively high computational cost. In this work, the coloring algorithms are used to reduce the number of residual function evaluations, as well as the computational cost.
After obtaining the preconditioning matrix, the factorization phase determines the quality and efficiency of the preconditioner. The incomplete LU factorization with fill-in level k algorithm (ILU(k)) is widely used in the preconditioning process because of its low computational complexity [18]. The computational efficiency highly depends on the choice of the fill-ins in factorization, which is a key issue for ILU-based preconditioner. Usually, the selection of the fill-in level is empirical in practice, but inappropriate fill-in level selection may decrease computational efficiency. In this work, the reordering-based ILU(k) algorithm [19] is developed to improve robustness of the fill-in level selection.
This work proposes an efficient and robust reordering-based ILU(k) preconditioner for solving the neutron diffusion problem based on MOOSE. The performance of proposed preconditioners is evaluated by the 2D-LRA neutron diffusion k-eigenvalue problem, as well as by a simplified neutron diffusion problem with thermal-hydraulic feedback as a supplement. This paper is organized as follows. Sec 2 briefly discusses the JFNK method and preconditioning technique. Sec 3 presents the coloring and reordering algorithms to improve the preconditioning efficiency and robustness. The newly developed preconditioner performance is provided in Sec 4. The paper is concluded in Sec 5.

2. Numerical Methods

2.1. Neutron k-Eigenvalue Problem and JFNK Method

The steady-state two-group neutron diffusion equations can be given by:
∇ ⋅ − D 1 ∇ ϕ 1 + Σ a , 1 ϕ 1 + Σ s , 1 → 2 ϕ 1 = 1 k ∑ g ' = 1,2 ν g ' Σ f , g ' ϕ g '
∇ ⋅ − D 2 ∇ ϕ 2 + Σ a , 2 ϕ 2 = Σ s , 1 → 2 ϕ 1
Where the numerical subscript and g ' represent the neutron energy group index. The first energy group is the fast group and the second one is the thermal group. The items ϕ , D , Σ a , Σ s , Σ f , ν , k represent the neutron flux, diffusion coefficient, absorption cross section, scattering cross section, fission cross section, average number of neutrons emitted per fission and multiplication factor, respectively. The steady-state neutron diffusion problem is also called the k-eigenvalue problem due to the existence of the multiplication factor k .
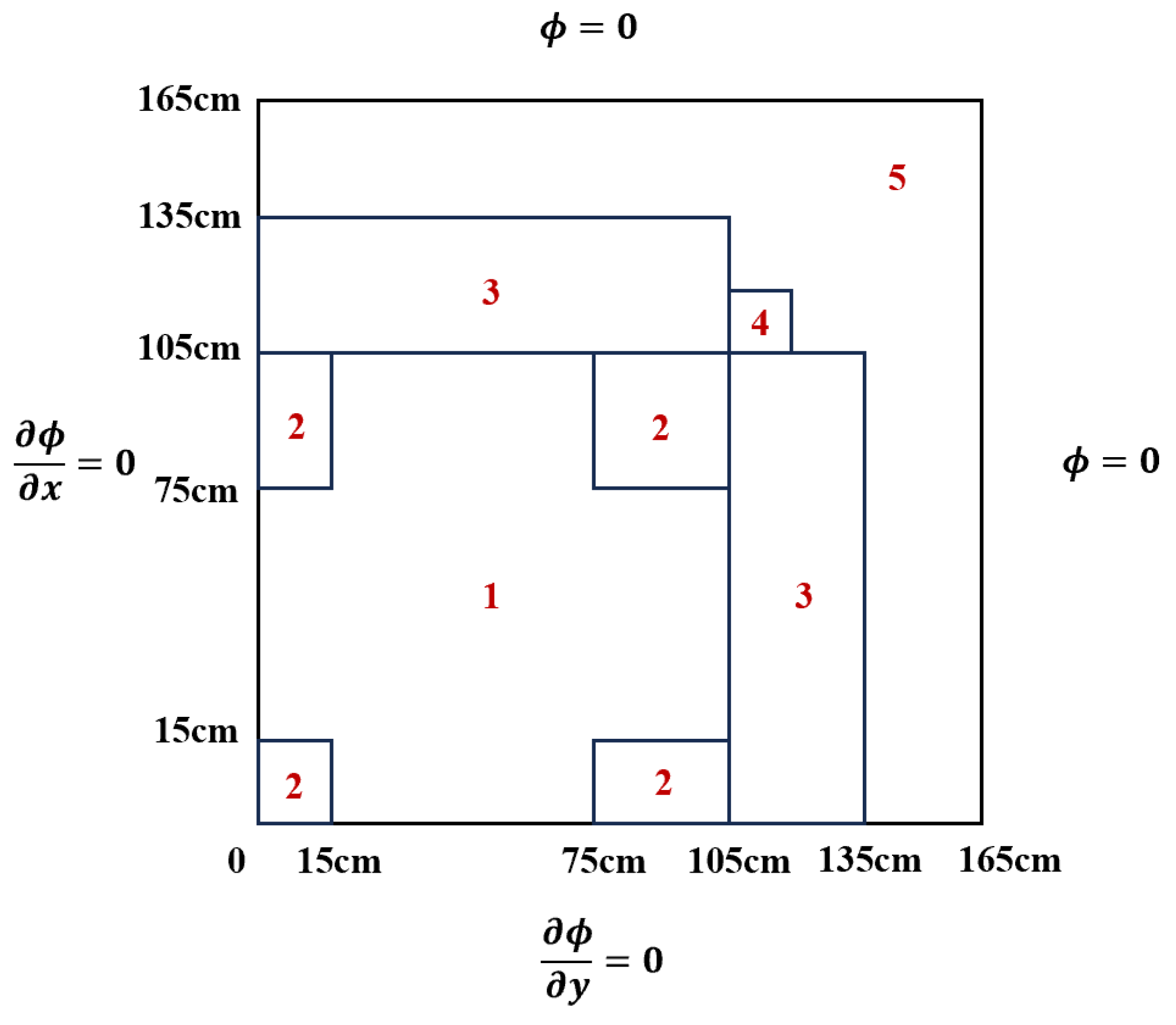
The two-dimensional LRA (Laboratorium für Reaktorregelung und Anlagensicherung) benchmark problem [20] is a well-known simplified neutron k-eigenvalue problem, which also contains the steady-state two-group neutron diffusion equation. The reference values of these coefficients in the LRA problem are given in Table 1. The reactor is square in the width of 330 c m , and a quarter has been modeled because of the symmetry as shown in Figure 1.
To simplify the following discussion, the k-eigenvalue problem (Eq.1 and Eq.2) is rewritten in matrix form:
M ϕ ⃑ = 1 k F ϕ ⃑
In Eq.3, ϕ ⃑ represents the two-group neutron flux after discretization of the equations. The term M is the discrete form of the sum of diffusion operator, absorption term and scattering term, while F represents the fission matrix and k is the eigenvalue of the system. This nonlinear system of equations is solved using JFNK method in this work. According to the Ref [21], the constraint equation of eigenvalue k can be defined as:
k = F ϕ ⃑  
This work uses a technique to treat k as an intermediate variable so that Eq.3 is eliminated in partial differential equations (PDEs). This treatment is inherited from the nonlinear elimination method, which is used to eliminate the nonlinear variables within PDEs to ensure the overall convergence of the system [22]. MOOSE has integrated this special treatment and developed the “NonlinearEigen” executioner to handle eigenvalue problems, and the detailed implementation can be found in Ref [21]. In MOOSE, the residual function required by the JFNK algorithm is defined as follows [21]:
f ϕ ⃑ = M ϕ ⃑ − 1 F ϕ ⃑ F ϕ ⃑  
JFNK method is a nonlinear solver featured with two iteration layers, including Newton iteration as the outer layer and Krylov subspace iteration as the inner layer. The basic concepts of JFNK method can be found in the literature [7]. Like most iterative methods, the convergence rate depends on the eigenvalue distribution of the system. Preconditioning can improve the convergence rate by clustering the eigenvalue distribution of the coefficient matrix. Preconditioning process is an equivalent transform of the original problem, by multiplying with the preconditioning matrix.
J P − 1 P δ ϕ ⃑ = − f ϕ ⃑  
Where δ ϕ ⃑ is the update step of the neutron flux vector in Newton iteration, and J is the Jacobian matrix and can be represented as a block matrix form:
J =   A 1 − ν 1 k Σ f , 1 − ν 1 k Σ f , 1 − Σ s , 1 → 2 A 2
It should be noted that Eq.7 is only a non-zero element structural representation of the Jacobian matrix. A 1 and A 2 are the discrete form of sum of diffusion operator and absorption term. The preconditioner P is an approximation of the Jacobian matrix J , and can be expressed as:
P =   J ~

2.2. Preconditioning Techniques in MOOSE

The original intention of the preconditioner is to improve the performance and reliability of Krylov subspace methods. Preconditioning attempts to improve the spectral properties of the coefficient matrix. It can cluster spectrum which results in rapid convergence, particularly when the preconditioned matrix is close to normal. Here are some basic preconditioning concepts.
If P is a nonsingular matrix that approximates A (in some sense).
P − 1 A ϕ ⃑ = P − 1 b ⃑  
Eq.9 is left preconditioning and has the same solution as original equations but easier to solve. The right preconditioning can be performed as:
A P − 1 y ⃑ = b ⃑ ,     ϕ ⃑ = P − 1 y ⃑
It is not necessary to compute P − 1 A or A P − 1 explicitly during Krylov subspace iterations. Instead, matrix-vector products and linear systems of the form P z ⃑ = r ⃑ are performed, which is utilized in JFNK method. As for residual minimizing methods, like GMRES [23], right preconditioning [24] is often used. In addition, the residuals for the right-preconditioned system are identical to the true residuals r ⃑ = b ⃑ − A ϕ ⃑ .
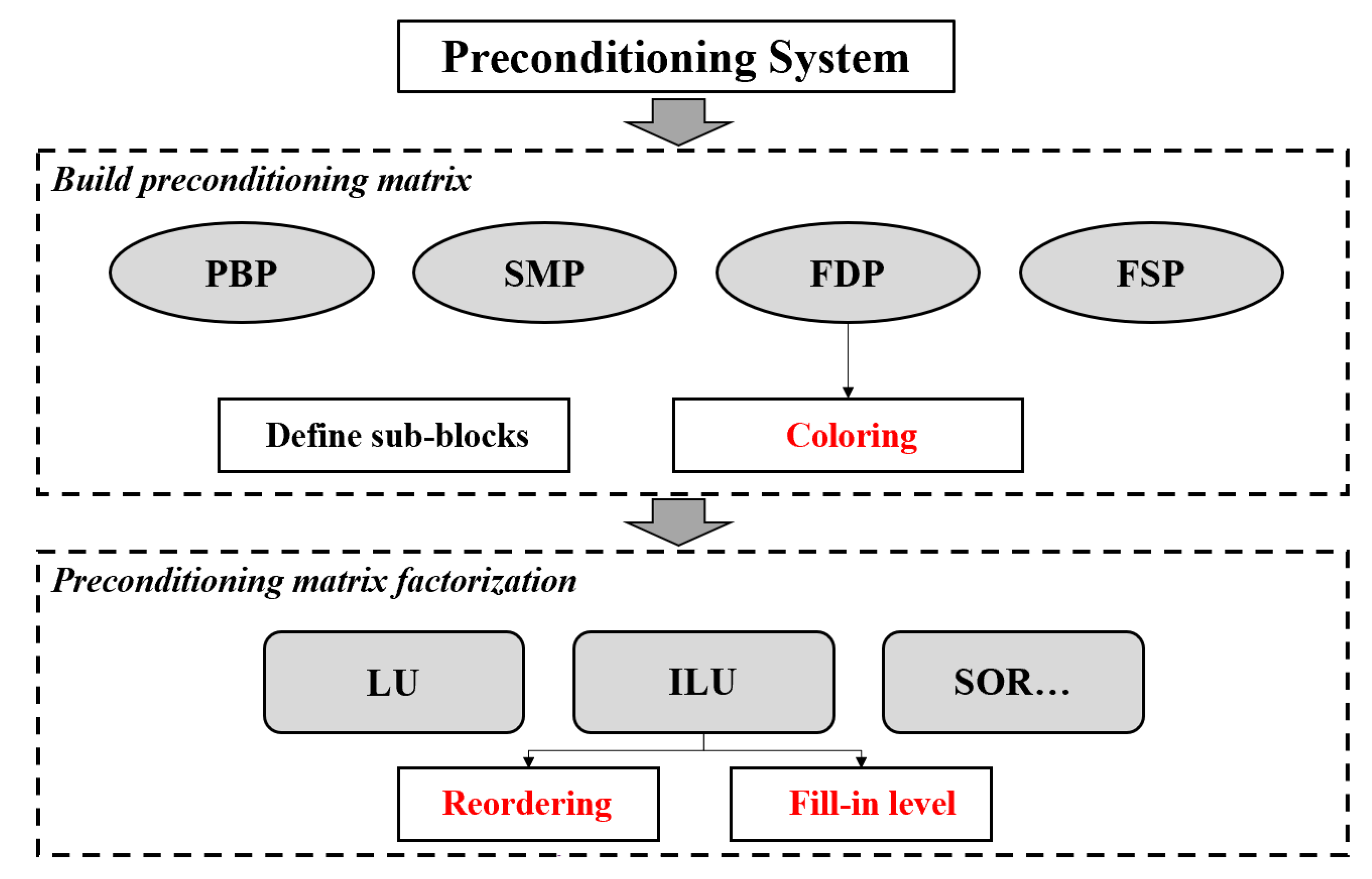
The preconditioning process can be divided into the matrix construction phase and matrix factorization phase, as depicted in Figure 2. The MOOSE platform provides a variety of preconditioning matrix construction methods, such as the physics-based preconditioner (PBP), single matrix preconditioner (SMP), and field split preconditioner (FSP). They can be used to describe the multi-physics coupling problems, and can also be used to depict the scattering and fission effects between neutron energy groups. These preconditioners need to provide analytical expressions to construct the coefficient matrix, that is, the coefficient matrix is constructed by grid material composition and cross section. Especially for multi-physics coupling problems with complex physical properties, giving the expressions of the coefficient matrix elements is difficult. The finite difference preconditioner (FDP) can construct preconditioning matrices automatically to find a more general preconditioner. However, it can be extremely slow since the external computational cost is required in the implementation of FDP. The coloring technique can significantly reduce the number of nonlinear function evaluations. This method can improve the computational efficiency of FDP based on the topological relationships of the coupling terms, and the details will be discussed in Sec 3.1.
As depicted in Figure 2, the matrix factorization method is required after building the preconditioning matrix. In MOOSE, the main factorization methods for the preconditioning matrix include the incomplete factorization method [25] and iterative method [3]. Each of these methods has its advantages and applicability. Incomplete LU factorization method (ILU) is often used in preconditioning because of its extremely low computational cost. Particular attention needs to be paid to the location of the fill-in elements during the factorization process, which is discussed in Sec3.2. Besides, the ILU factorization can be optimized according to the sparsity of the matrix, it can be referred to Sec 3.3 reordering method.

3. Numerical Techniques in Preconditioning

This section mainly discusses the numerical algorithms used in preconditioning. The coloring algorithm can significantly reduce the huge computational cost in FDP, which is discussed in Sec 3.1. Similarly, the computational cost of preconditioning factorization phase also deserves attention. ILU with reordering algorithm will enhance the computational behavior and its robustness, as provided in Sec 3.2 and Sec 3.3.

3.1. Coloring

The preconditioning matrix is a partial Jacobian matrix, which could be calculated automatically by finite difference of the nonlinear function. In this work, the coloring algorithms [26] is utilized for the preconditioning matrix to reduce the number of nonlinear function evaluations and enhance the computational performance. Here we briefly introduce the principle of coloring algorithms and different coloring types.
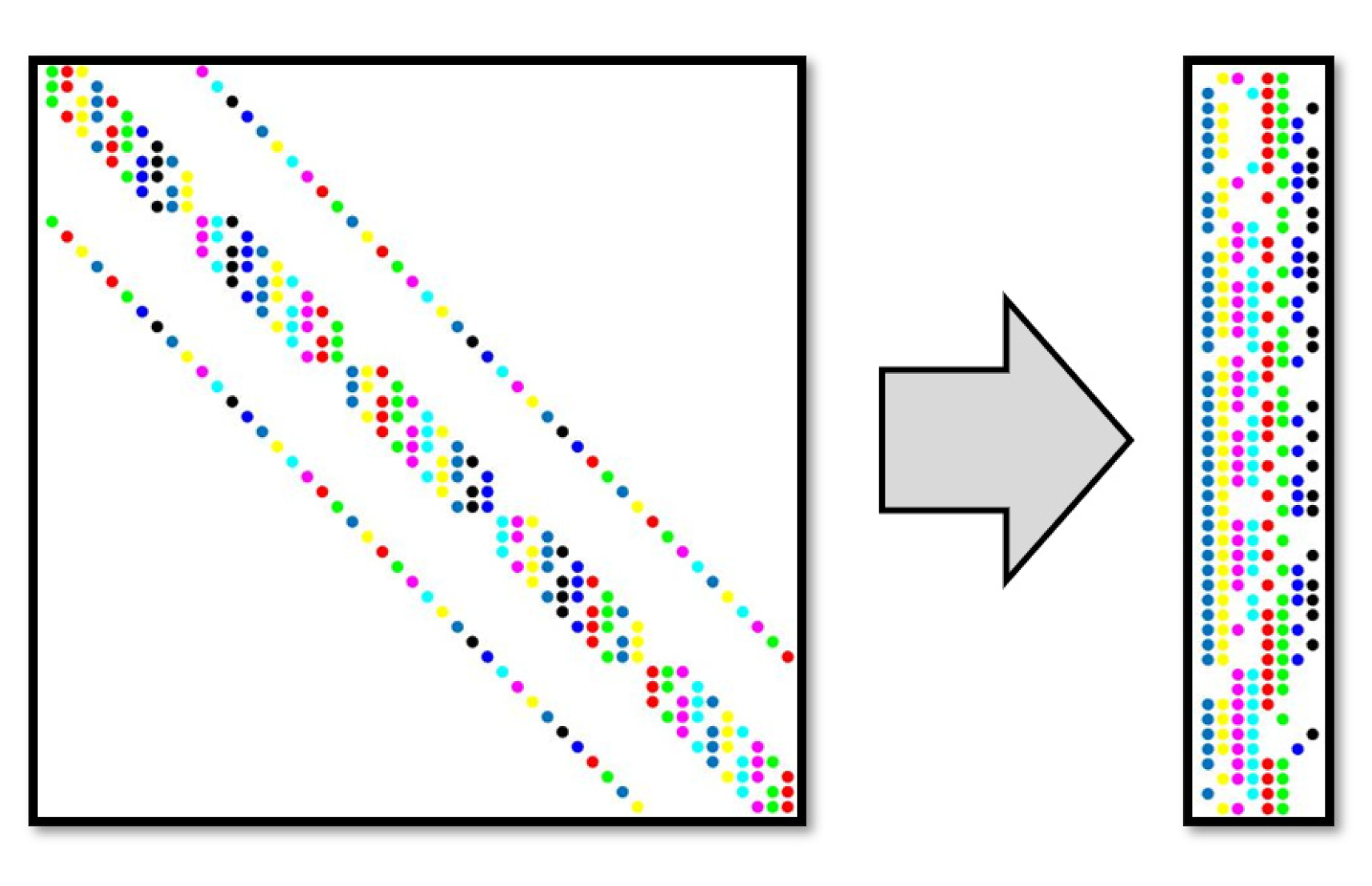
The nonlinear problem can be described by the residual function f : R n ⟶ R n , such as Eq.5 which describes the steady-state neutron diffusion problem. The number of elements in solution vectors is n = 50 for illustration, so the dimension of the preconditioning matrix is n × n as depicted in Figure 3. The color block in the figure represents the non-zero elements, and the blank denotes a zero entry in P . The colors in Figure 3 represent the number of colors, which means that non-zero elements will be divided into these groups. The coloring process will be described in detail below.
Define a unit vector e k   ∈ R n with 1 in the kth row and 0 in all other rows. Then the difference approximation can be rewritten in F x + ϵ e k − F x / ϵ ≈ P e k . The kth column of P can be estimated through an additional function evaluation F ( x + ϵ e k ) . Here ϵ is a small step size. Hence if sparsity is not utilized, the construction of a preconditioning matrix with n columns would require n additional function evaluations.
The columns of the preconditioning matrix could be divided into several groups, where any two columns in the same group are not both non-zeros in a common row. It means the columns in the same group are structurally orthogonal [27]. For example, the first column and the sixth column are structurally orthogonal in Figure 3. Now consider a column vector d with 1 in components corresponding to the indices of columns in structurally orthogonal group and 0 in other components, which in this case is d = [ 1,0 , 0,0 , 0,1 , 0 ,   … , 0 ] . The elements in structurally orthogonal columns can be easily acquired by differencing the function F ( x ) along the vector d . In this way, by partitioning the columns of the P into fewest groups, the required number of function evaluations is minimized. Figure 3 shows the preconditioning matrix of schematic neutron diffusion problem and its compressed representation. By reasonably dividing structurally orthogonal columns, the compressed matrix has only 8 columns. This means that only an additional 8 function evaluations F ( x + ϵ d ) are required to complete the construction of the preconditioning matrix.
Here are some basic graph theory definitions about the matrix and its coloring algorithms. A graph G is an ordered pair ( V , E ) containing vertex set V { V : v 1 , v 2 , v 3 , … … , v n } and edge set E . The degree of a vertex v i in a graph G is the number of edges having v i as an endpoint, and can be represented by d e g ( v i ) . The matrix could be expressed by a graph, where columns in the matrix are the vertices in the graph. If there is an edge links between two vertices, it means for these two corresponding columns in the matrix are non-orthogonal. The graph coloring issue is to find the coloring partition where any adjacent vertices have different colors. Therefore, the matrix coloring problem are equivalent to minimum graph coloring issue. The vertex will be gradually colored according to the order, and assign the smallest color not used by any of its neighbors. This method is also called greedy coloring algorithm [28], outlined in algorithm3.1.
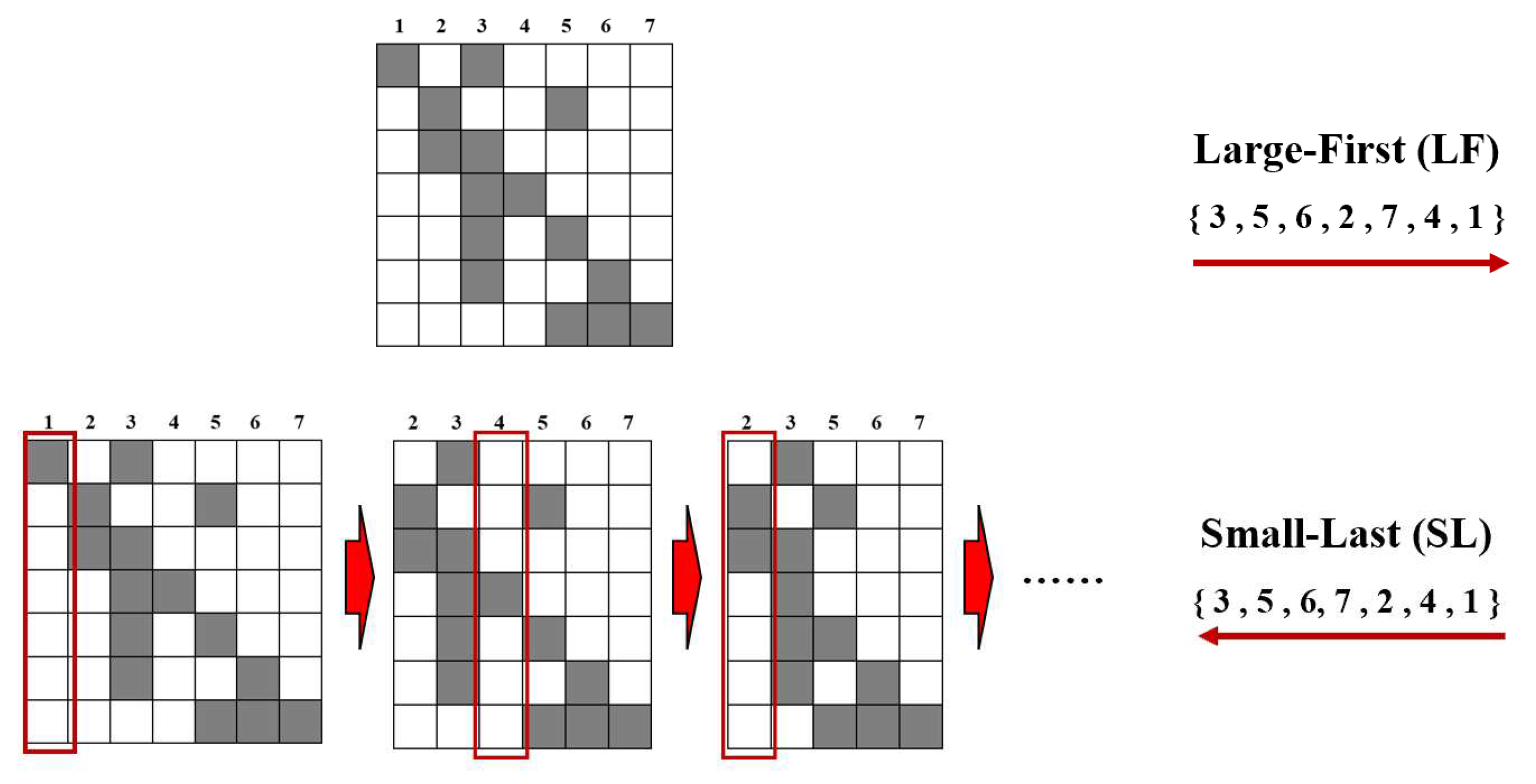
The coloring produced by the sequential algorithm is dependent on the ordering of columns [29]. Taking a matrix in Figure 4 as an example, { v 1 , v 2 , v 3 , v 4 , v 5 , v 6 , v 7 } denote columns in the preconditioning matrix and χ represents the number of colors. According to the truncated-max-degree bound theorem in graph theory [30], it is evident from the sequential coloring procedure that coloring the columns of large degree first will give upper bound of the coloring. The determination of a sequential coloring corresponding to such an ordering will be termed the largest-first algorithm (LF). 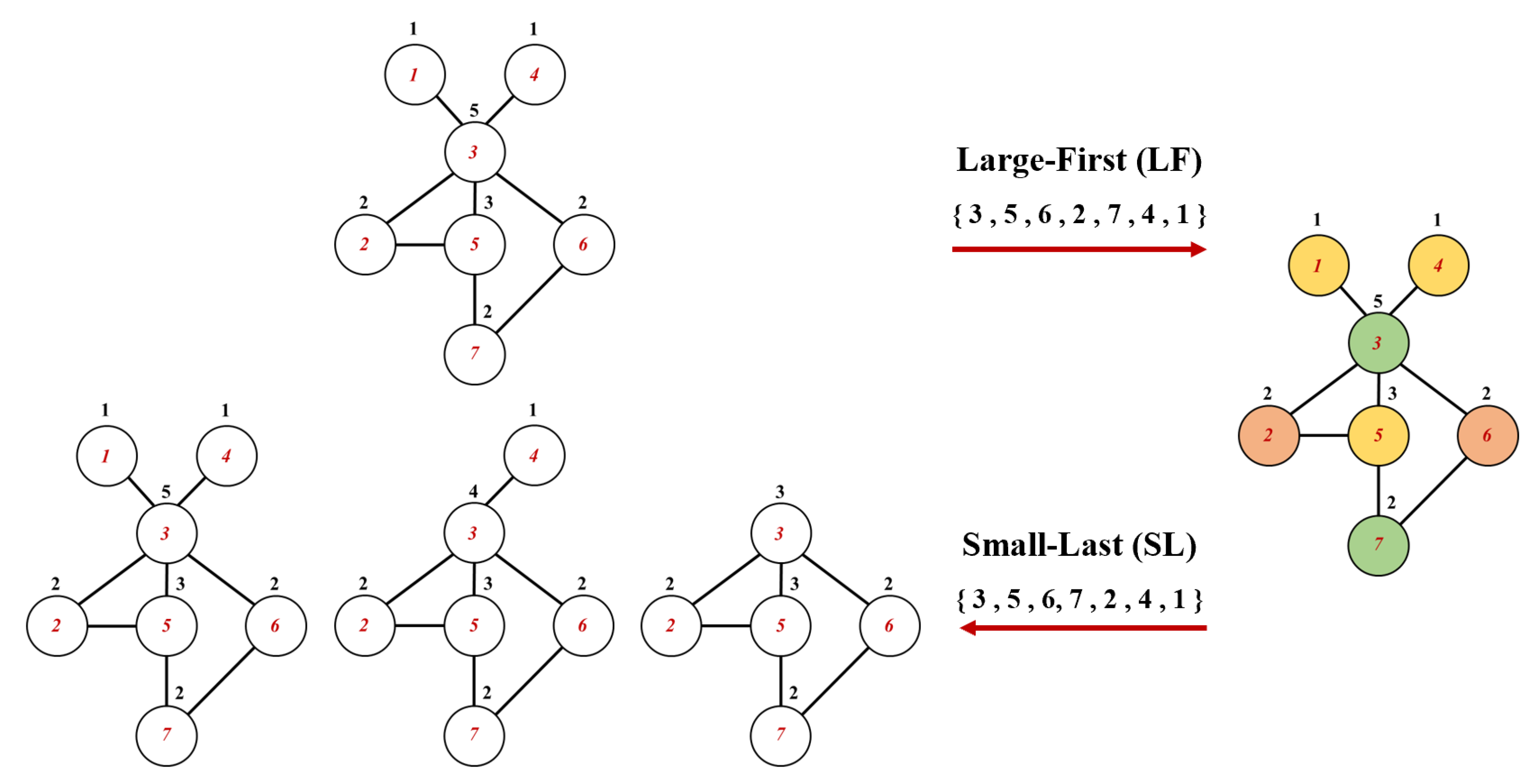The max-subgraph min-degree bound is always sharper than truncated-max degree bound in graph theory [31]. Inspired by this theorem, the small-last algorithm (SL) ranks the column of the smallest degree last and continues to search for such column in the remaining columns. The process of obtaining the ordering by LF and SL algorithms can refer to Figure 4. The gray squares in the figure represents the position of the non-zero elements. In Figure 4, column 3 is not orthogonal to column { v 1 , v 2 , v 4 , v 5 , v 6 } , which means that vertex 3 is linked to these vertices through edges in the graph. The index of vertex is represented in red numbers in Figure 5, and d e v ( v i ) is represented in black numbers. In addition, the two figures represent the matrix form and the graph form of the algorithms, respectively. The LF algorithm ranks the vertices with large degrees to the forefront of the ordering, while the SL algorithm ranks the vertices with small degrees to the end of the ordering. Note that the determination of a SL ordering has a feature of recursiveness not shared by the LF ordering procedure [32], which means that the ordered vertices need to be removed in the process to generate a new graph as present in Figure 5. Columns that have been ranked in the SL ordering will be removed from the matrix to form a degenerate matrix as shown in Figure 5. From the perspective of matrix form, the degrees of columns in SL ordering are over the degenerate matrix, whereas LF ordering utilizes only the degrees of columns in the whole matrix. After obtaining the ordering of the two algorithms, the vertices can be colored according to Algorithm 3.1. It should be noted that, in this case both coloring algorithms have the same orderings, as shown in Figure 5. In addition to these two methods, this work also evaluates the performance of the incidence degree (ID) coloring algorithm, and its specific principles can be referred to in the literature [33,34,35].
ALGORITHM 3.1 Sequential(greedy) coloring algorithm
 Procedure SEQ( G = ( V , E ) )
 Formulate a vertex ordering { v 1 , v 2 , v 3 , … … , v n }
 Assign v 1 as color 1
 For  i = 2 to n  do
  Assign v i the smallest color not used by any of its neighbors
  End for
End procedure

3.2. Incomplete LU Factorization Method

In the preconditioning, the computational cost highly depends on the process of matrix inversion, which is mainly realized by matrix factorization. Even though the matrix is sparse, extra fill-in non-zero elements usually take place after factorization. This means the triangular factor L and U are considerably less sparse than the original one. A new form of preconditioner P =   L ¯ U ¯ is obtained by discarding part (or all) of the fill-in non-zero elements during the factorization process [36]. This factorization can form a simple but effective preconditioner, also known as incomplete LU factorization.
To illustrate this method, we formally define a subset of matrix element locations S , in which the main diagonal and all i , j that a i j   ⊂   P   a i , j ≠ 0 } are usually included. Besides, S also contains other fill-ins, which are allowed to be non-zeros during the factorization process. Consequently, an incomplete factorization step can be described as:
a i j ← a i j − a i k a k k − 1 a k j ,         i f ( i , j ) ∈ S , a i j ,             o t h e r w i s e
Where k is recursive for k < i , j . If S is same as the non-zero positions in P , the no-fill ILU factorization, or ILU(0), is obtained. Subset S governs the dropping of fill-in in the incomplete factors, and becomes the criteria in different ILU variants [37]. However, no-fill ILU factorization can only provide a relatively low quality preconditioner. In order to obtain better preconditioning quality, more fill-ins need to be considered in incomplete factorization process.
A hierarchical ILU preconditioner based on the “level of fill-in” concept has been proposed [38]. The method defines a rule that govern the dropping of fill-in in the incomplete factors. The definition of “level of fill-in” is as follow, and the initial level of fill of a matrix entry a i , j is:
l e v i j = 0 ,         i f a i j ≠ 0 o r i = j ∞ ,         o t h e r w i s e
After an ILU process, the level of fill must be updated:
l e v i j = m i n l e v i j , l e v i k + l e v k j + 1
Let k be a nonnegative integer. In an ILU(k) preconditioner, all fill-ins whose level is greater than k are dropped. In many situations, ILU(1) has significant improvement over ILU(0), and the its computational cost is acceptable. With the increase of k , the computational cost and fill-ins will rise rapidly. For some complex problems, a higher fill-in level k is required in order to ensure a better preconditioning quality.

3.3. Reordering

Sparsity is the main feature of the preconditioning matrix, especially for the neutron eigenvalue problem. When ILU(k) factorization is used, it will introduce considerable computational cost in the pursuit of higher preconditioning quality and applying larger k. Exploring mathematical algorithms based on sparsity to increase factorization efficiency is essential. The reordering algorithms are chosen so that pivoting down the diagonal in order on the resulting permuted preconditioning matrix R P R T = L ¯ U ¯ produces much less fill-in. In addition, the order and permutation matrix R can save the cost when calculating the factors in L ¯ U ¯ [39]. The principle of the permutation is briefly described here.
Suppose an arbitrary n × n sparse matrix P = { a i , j } , determine a permutation matrix R such that R P R T has a small bandwidth and a small profile. The bandwidth of P is defined by the maximum of the set { i − j : a i , j ≠ 0 } . To acquire the profile of P , set f i = m i n ⁡ { j : a i , j ≠ 0 } with all a i , i ≠ 0 and let d i = i − f i . The profile is defined by ∑ 1 N d i . The permutation matrix can reduce storage and computational cost when solving linear equations. One of the main objectives is to cluster non-zeros as much as possible in the main diagonal. The generation of permutation matrices can be attributed to the reordering method, which focuses mainly on the bandwidth and profile of matrices. Moreover, the current mainstream reordering rule is based on graph theory.
According to the optimization objectives, reordering methods can be divided into two categories: reduced fill-in elements algorithm, and reduced bandwidths and profiles algorithm. The algorithms in the first category include the quotient minimum degree (QMD), the one-way dissection (1WD), and the nested dissection (ND) method [40]. 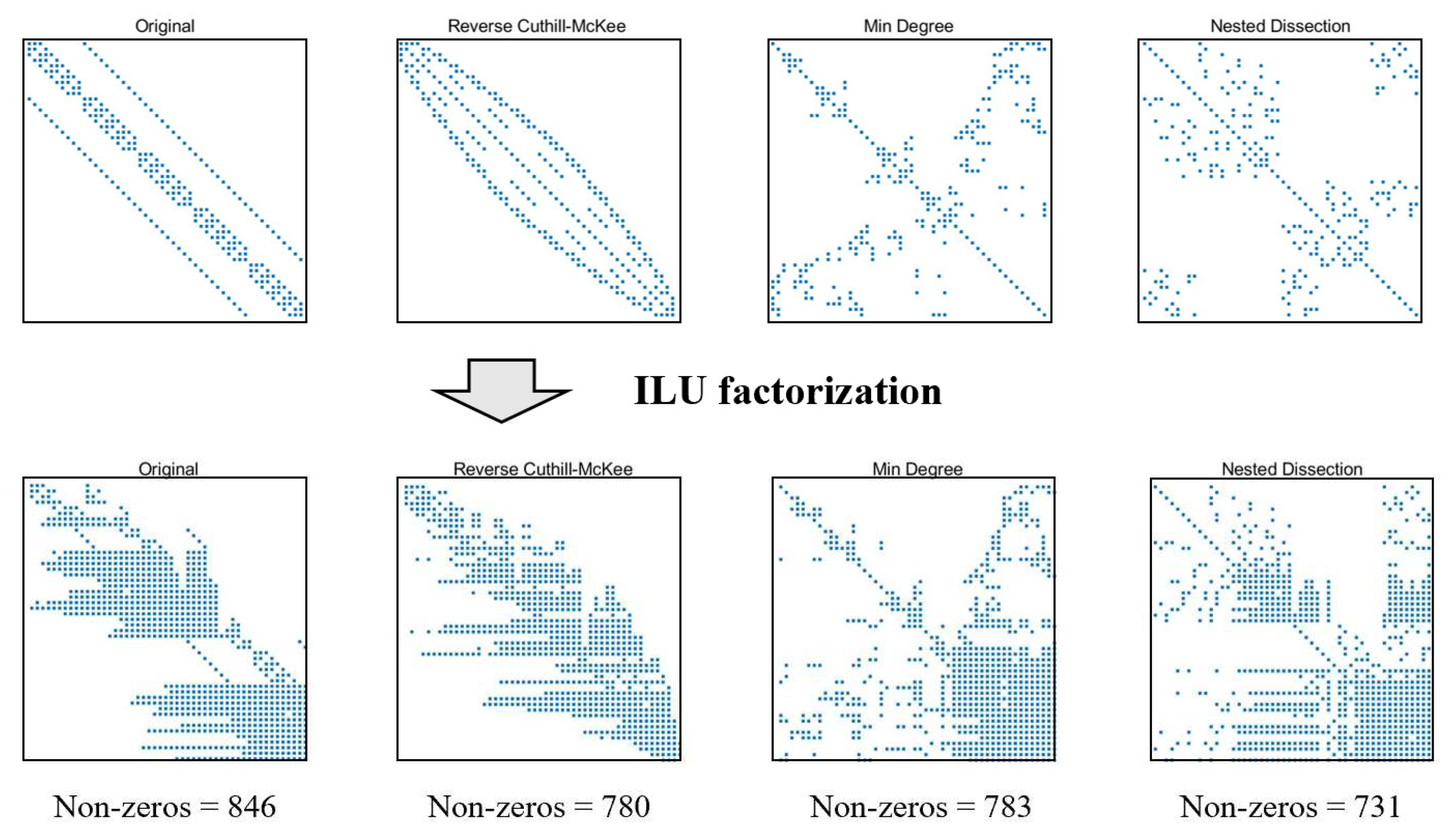While the algorithm belonging to the second category is mainly reverse Cuthill-McKee (RCM) method [41]. To illustrate the differences between several reordering methods, the steady state neutron diffusion model in Sec 3.1 is taken as an example to show the ILU factorization effect after different reordering algorithms. Because the matrix dimension is small, the ILU factorization with fill-in level 20 is used to show the different reordering algorithm performances. The structures of L ¯ U ¯ matrix after ILU(20) factorization by different reordering algorithms are shown in Figure 6. The general conclusion was that the reverse Cuthill-McKee (RCM) algorithms usually produced the smallest bandwidths. The QMD and ND method does not guarantee the optimal bandwidth, but reduces the filling elements and computational complexity during the matrix factorization. In addition, the ND algorithm usually guarantees the minimum number of filling elements. The effect of reordering depends on the specific sparse structure of the matrix, and there is no optimal algorithm at present.

4. Results and Discussions

The 2D-LRA benchmark is utilized to evaluate the performance of improved preconditioners. The mesh of the benchmark is generated by the mesh generation software, using a triangle adaptive mesh leading to 7696 meshes. The total degree of freedoms (DOFs) is 15392, including two groups of neutron flux variables. The MOOSE-v1.0 is used in this work and all programs are executed serially. This work does not involve the analysis of parallel performance. As mentioned before, we mainly focus on the construction and factorization processes to pursue an efficiency and robustness scheme. It is worth noting that the choice of optimal preconditioning is problem-related, and the article only reveals the effects of different numerical techniques.

4.1. Preconditioning Matrix Construction Techniques

In order to meet the requirement of automatically building the preconditioning matrix, FDP is used here. Besides, FDP can be used as a robust preconditioner, especially when the preconditioning matrix elements of the problem cannot be explicitly given. However, the direct use of FDP will bring a huge computational cost, which will seriously increase the whole solution time. The coloring method can utilize the sparse structure of the preconditioning matrix and partition the columns into the fewest groups of structurally orthogonal columns. Therefore, it can significantly reduce the evaluation times in FDP, and reduce the cost of constructing the preconditioning matrix. As shown in Table 2, the computational efficiency of the FDP with coloring could be about 60 times higher than that of the preconditioner without coloring algorithm.
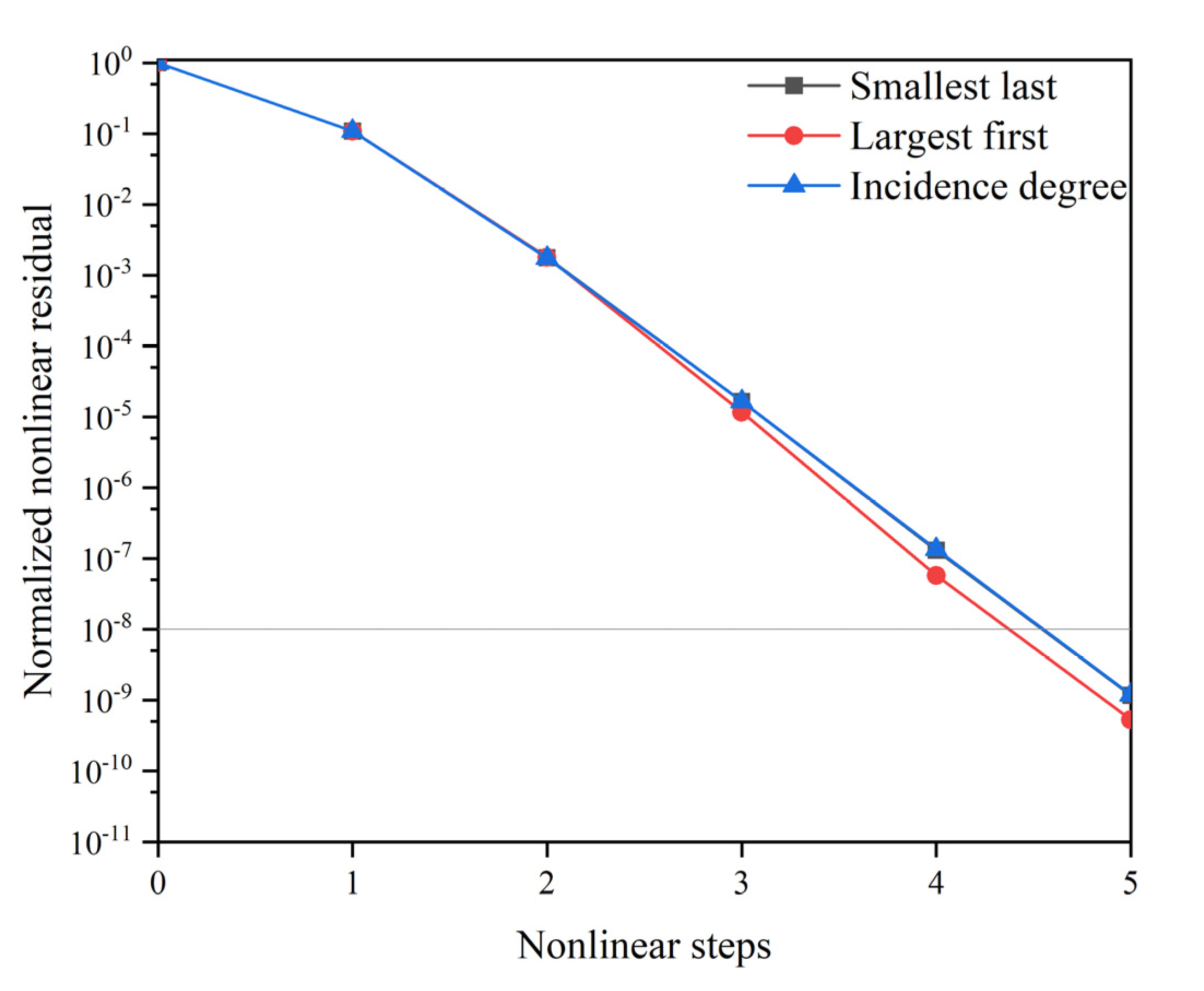
For each coloring algorithm we cite five statistics, including total computational time, numbers of residual evaluations, numbers of coloring, nonlinear steps, and total linear steps. The convergence criteria selected in this example are e r = 10 − 8 . Three coloring algorithms exhibit only a slight variation in these evaluation parameters. In addition, the number of colors needed by the SL algorithm tended to be slightly less than LF and ID algorithm. The results also show that the SL algorithm's min-degree bound is stricter than that of the LF algorithm, which can provide fewer colors. It is necessary to illustrate the enormous preconditioning construction cost when not using the coloring algorithm. This version of the MOOSE program does not optimize the calculation of the coefficient matrix. When the Jacobian matrix is used as a preconditioner’s coefficient matrix, the number of residual function calls is equal to degrees of freedom, which will bring a huge computational cost, especially for the problem with a large number of grids. By comparing the residual history in Figure 7, it can be inferred that the preconditioning matrices constructed by the three algorithms are identical. The “Normalized nonlinear residual” here represents the initial residual norm (L2 norm) as 1 , and the dotted line in Figure 7 also shows the convergence criterion of the algorithm. In fact, this is also consistent with the concepts of coloring that using sparsity to reduce the computational cost, but not change the matrix elements.

4.2. Preconditioning Matrix Factorization Techniques

After building the preconditioning matrix, it is also necessary to factorize it and ensure each iteration is affordable. The ILU(k) algorithm has been widely-used among existing preconditioners as a general-purpose technique. It should be noted that the numerical examples in this subsection are carried out using FDP with the SL coloring algorithm. All the comparisons here are to expose the performance of the factorization techniques.
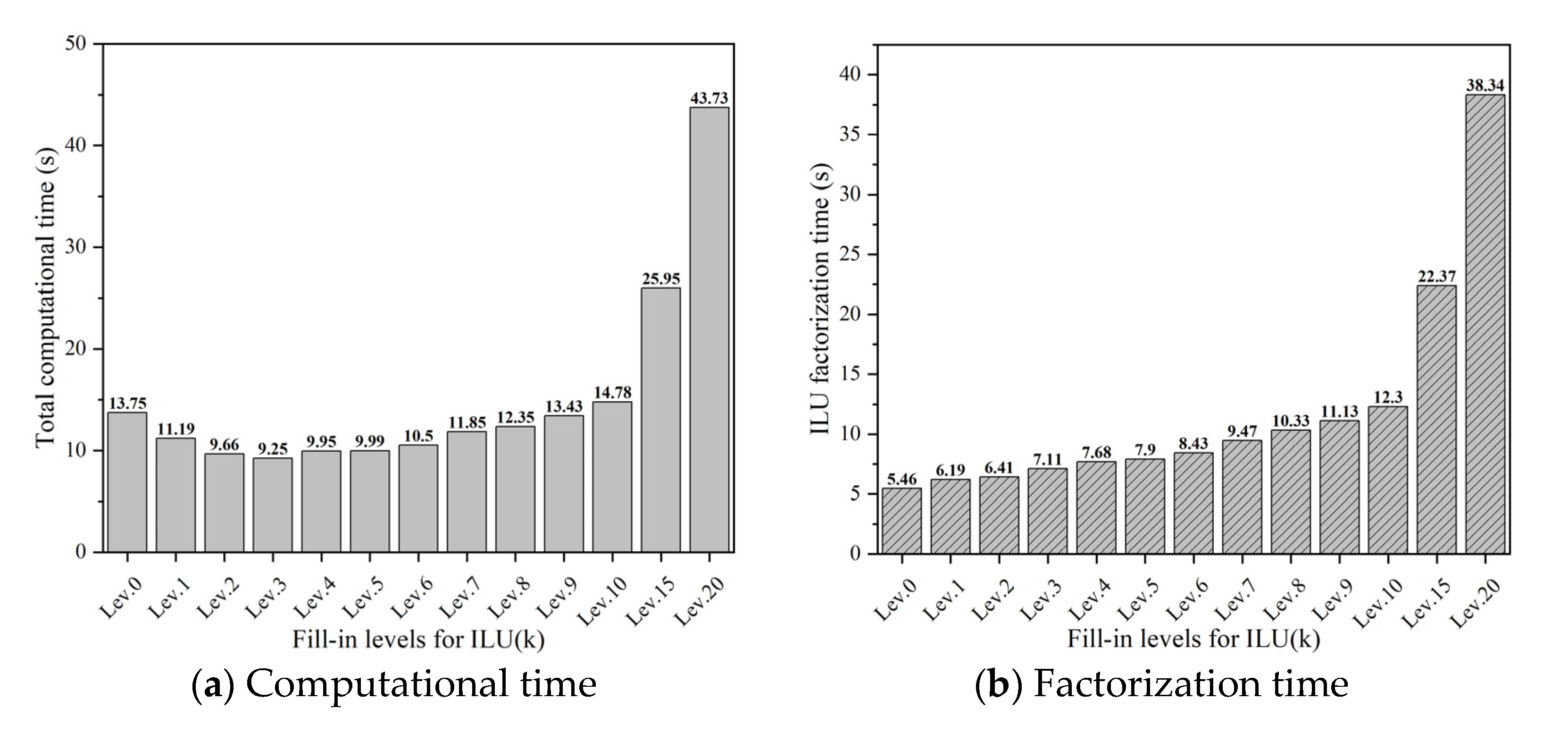
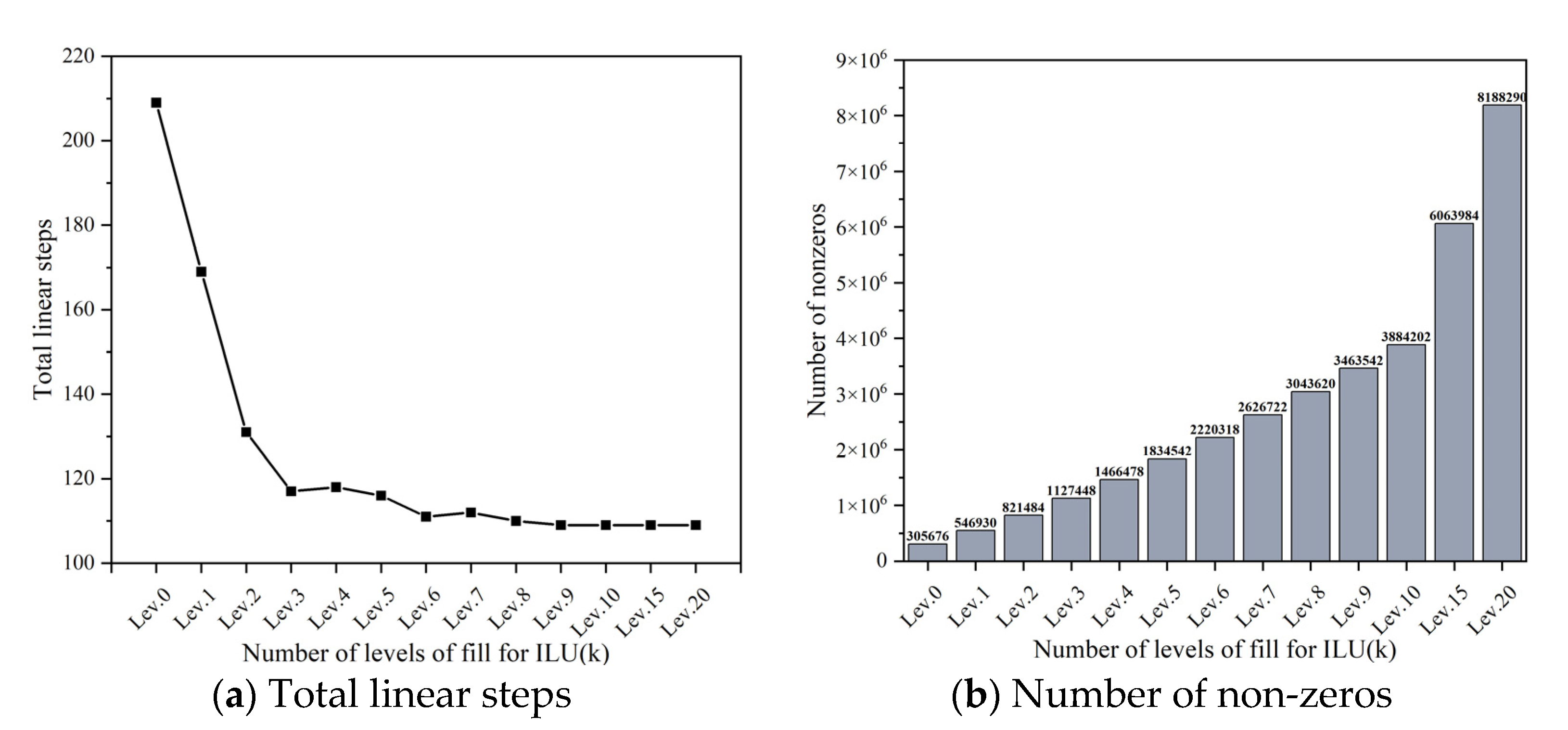
The total computational time and ILU factorization time for LRA problems under different fill-in levels the ILU(k) method are shown in Figure 8. Figure 9 shows total linear steps and non-zeros under different fill-in levels, where the coefficient matrix is automatically generated by FDP. Please note that although high fill-in levels, such as larger than 5, seem redundant for the simple LRA problem, they can provide some insights for the algorithm performance analysis. As illustrated in Figure 9, with increase in the fill-in level, the number of linear steps required for calculation will decrease due to the faster convergence rate. Thus, the number of linear iteration steps is reduced. At the same time, as the fill-in level increases, the number of non-zero elements in the factorized matrix also increases, which means more computational complexity. This ultimately leads to a rise in the factorization time of the ILU(k) method, as shown in Figure 8, where the factorization time of ILU(20) is 7 times that of ILU(0). The ILU factorization process dominates the entire computational cost at high fill-in levels. Therefore, the parameter fill-in level k is a key issue to make a balance between the factorization cost and the linear convergence rate. For this case, the total computational time is minimal at k = 3 . Please note that, in practice, the optimal fill-in level is not easy to determine, which is a problem-related topic.
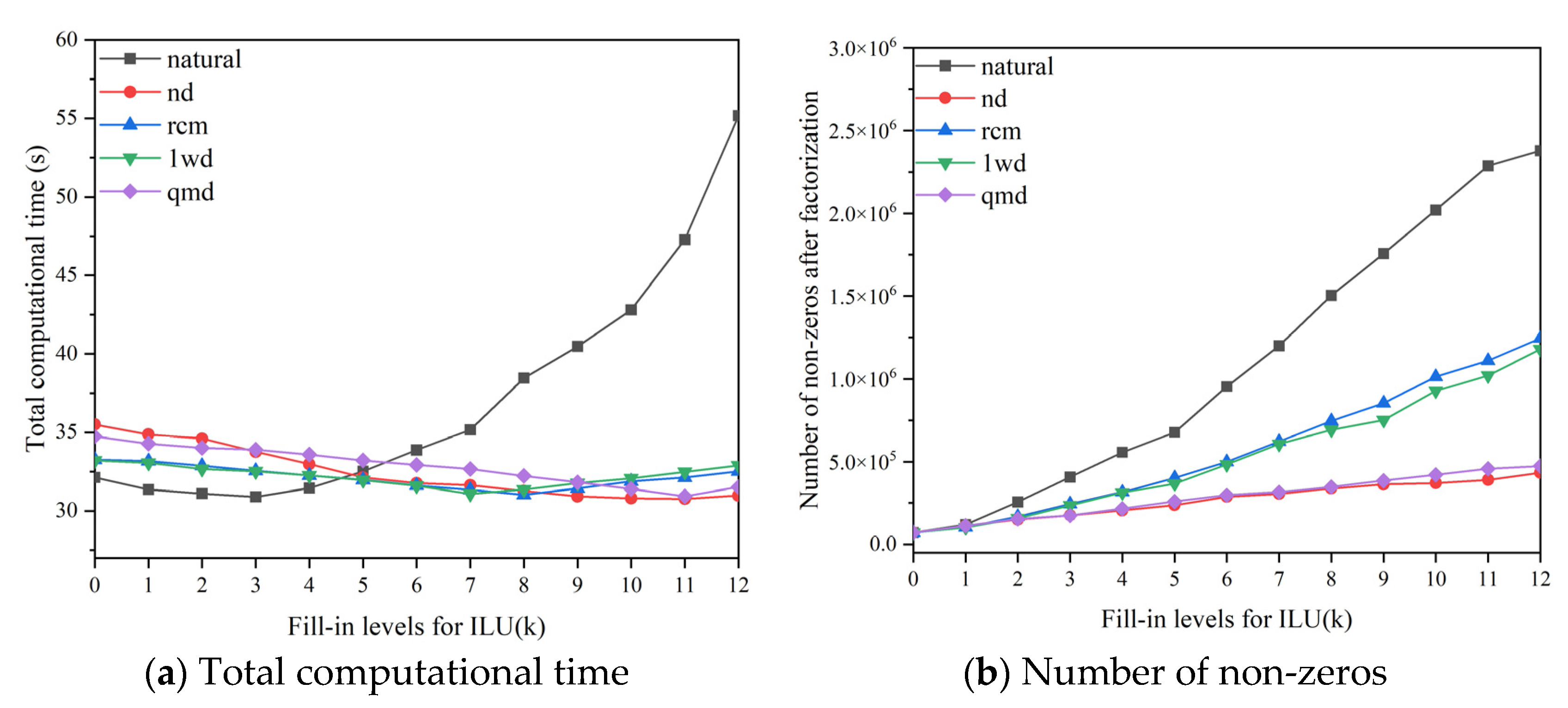
In order to find a robust preconditioner, the key point is to make the preconditioner not sensitive to the user-defined fill-in level k . Therefore, it should reduce the computational cost of ILU(k) at the high fill-in levels. Here, the reordering algorithms is used for the high fill-in level ILU factorization, and the fill-in levels of k = 10 are considered in this work.
The computational performance of the different reordering algorithms using ILU(10) is listed in Table 3. In this case, the number nonlinear/linear steps are the same. However, compared with the ILU(10) under the natural ordering, the number of non-zeros after factorizations under reordering algorithms is reduced, therefore, the total computational time of ILU(10) under reordering algorithms is less than that of natural ordering. In detail, for the one-way dissection (1WD) algorithm, it only reorders the preconditioning matrix from one direction (horizontal or vertical), so the number of non-zero elements after factorization is still relatively large, whose value is 2442293 in this case. The ND algorithm exhibits a better computational efficiency, reducing the computational time by 15% compared with natural ordering. The algorithm is based on the quotient graph for matrix factorization that can obtain minimum non-zeros. Please note that, the current LRA steady-state diffusion problem is a relatively simple case, in order to further analyze the performance of the reordering-based ILU(k) preconditioner, a steady-state neutron diffusion problem with thermal-hydraulic feedback is also utilized as a supplement.
It is a simplified 2-D PWR (Pressurized Water Reactor) reactor model, which includes the steady-state neutron diffusion equation as well as other three physical fields to consider the thermal-hydraulic feedback effect: coolant temperature, pressure and velocity. As with most reactor systems, the neutronics and thermal-hydraulics are tightly two-way coupled. The governing equations, coefficients, dimensions and boundary conditions can be found in the reference paper [42-43]. As a simplified model, a 40 × 40 cylindrical grid is used here. Here, the convergence criterion consistent with the previous example is used, and the SL coloring algorithm is used to generate the coefficient matrix automatically.
Figure 10 shows the results of the total computational time and the number of non-zero elements after factorization under different fill-in levels and reordering algorithms. The results of fill-in levels from 0 to 12 are provided, and the higher fill-in levels are redundant in practice for this multi-physics coupling problem. Compared with the ILU factorization under natural ordering, the total computational time of ILU with reordering algorithms is not sensitive to the fill-in levels. Additionally, the computational performances are close to the optimal computational cost for natural ordering, as shown in Figure 10.
In order to further discuss the features of reordering algorithms in detail, Table 4 summarizes the results of different reordering algorithms under the optimal fill-in levels. The factorization times of low fill-in levels are relatively small, but more nonlinear/linear steps are required to achieve convergence. The reordering algorithms can reduce the cost of factorization at high fill-in levels. Although it is still time-consuming, it can improve efficiency by reducing the number of iteration steps. As a result, The performance of ILU(11) with ND algorithm is slightly superior to ILU(3) with natural ordering. So, although natural ordering only could achieve good computational efficiency at low fill-in levels, such as k = 3 , the computational time will increase sharply as the fill-in level increases. The superiority of reordering algorithms emerges in this situation. The reordering-based ILU preconditioner can adapt to a wide range of fill-in levels without empirical selection.

5. Conclusions

Efficient and robust preconditioners is a key issue in solving nonlinear problems, especially in the JFNK method. A high linear convergence rate can be obtained by retaining the complete coefficient matrix and used for preconditioning. However, using the finite difference method to calculate the preconditioning matrix is time-consuming. An efficient preconditioning-based coloring algorithm is developed in this work, which significantly reduces the cost of finite difference computation by partitioning the columns of the coefficient matrix. In addition, the robust reordering-based ILU(k) preconditioner is developed which could achieve a high computational performance for a wide range of fill-in levels. As a preliminary work, the 2-D LRA neutron eigenvalue problem and a simplified PWR model are provided to demonstrate the performance of the preconditioner. The results show that the proposed preconditioner can automatically generate the preconditioning matrix and has strong robustness. The main conclusions are:
  • The proposed preconditioner can automatically generate matrices with high convergence rate. Combined with the coloring algorithms, the preconditioner can significantly improve the computational efficiency.
  • The reordering-based ILU(k) algorithm is an efficient preconditioning matrix factorization method. By using the incomplete factorization and the sparsity of the preconditioning matrix, the computational cost of matrix factorization under high fill-in level can be greatly reduced.
  • Reordering algorithms enhances the robustness of the preconditioner, and it can maintain high efficiency for wide range of fill-in levels using ILU factorization. The ND reordering algorithm shows better performance in this work, which can reduce 40% of the non-zero elements in the high fill-in levels after factorization.
The reordering-based ILU(k) factorization presented in this work exhibit good computational performance and robustness. Future work will focus on the performance of the proposed preconditioner for practical multi-physics coupling problems featured with complicated non-zero structure, especially when natural ordering cannot achieve the desired efficiency.

Acknowledgments

This study is supported by Beijing Natural Science Foundation No. 1212012, The National Natural Science Foundation of China No. 12275150, National Key R&D Program of China No. 2022YFB1903000, and Research Project of China National Nuclear Corporation.

References

  1. 1. Wu Y, Liu B, Zhang H, Guo J, Li F. A multi-level nonlinear elimination-based JFNK method for multi-scale multi-physics coupling problem in pebble-bed HTR. Annals of Nuclear Energy. 2022, 176.
  2. Novak A J, Peterson J W, Zou L, et al. Validation of Pronghorn friction-dominated porous media thermal- hydraulics model with the SANA experiments. Nuclear Engineering and Design 2019, 350, 182–194. [Google Scholar] [CrossRef]
  3. Benzi, M. Preconditioning Techniques for Large Linear Systems: A Survey. Journal of Computational Physics 2002, 182, 418–477. [Google Scholar] [CrossRef]
  4. Simon Y, David R. Development and Testing of TRACE/PARCS ECI Capability for Modelling CANDU Reactors with Reactor Regulating System Response. Science and Technology of Nuclear Installations 2022, 7500629. [Google Scholar]
  5. Shuaizheng L, Zhouyu L, and et al. Development of high-fidelity neutronics/thermal-hydraulics coupling system for the hexagonal reactor cores based on NECP-X/CTF. Annals of Nuclear Energy 2023, 188, 109822. [Google Scholar] [CrossRef]
  6. Surian P, Sukmanto D, Wahid L, et al. An Improved Steady-State and Transient Analysis of the RSG-GAS Reactor Core under RIA Conditions Using MTR-DYN and EUREKA-2/RR Codes. Science and Technology of Nuclear Installations 2022, 6030504. [Google Scholar]
  7. Knoll D, A. Jacobian-free Newton-Krylov methods: a survey of approaches and applications. J. Comput. Phys 2004, 193. [Google Scholar] [CrossRef]
  8. Wu Y, Liu B, Zhang H, Zhu K, et al. Accuracy and efficient solution of helical coiled once-through steam generator model using JFNK method. Annals of Nuclear Energy 2021, 159, 108290. [Google Scholar] [CrossRef]
  9. Fan J, Gou J, Huang J, Shan J. A fully-implicit numerical algorithm of two-fluid two-phase flow model using Jacobian-free Newton–Krylov method. International Journal for Numerical Methods in Fluids 2022, 95, 361–390.
  10. Hu G, Zou L, Daniel J. O'Grady. An integrated coupling model for solving multiscale fluid-fluid coupling problems in SAM code. Nuclear Engineering and Design 2023, 404, 112186. [Google Scholar] [CrossRef]
  11. Liu L, Wu Y, Liu B, Zhang H, et al. A modified JFNK method for solving the fundamental eigenmode in k-eigenvalue problem. Annals of Nuclear Energy 2022, 167, 108823. [Google Scholar] [CrossRef]
  12. Gaston D R, Permann C J, Peterson J W, et al. Physics-based multiscale coupling for full core nuclear reactor simulation. Annals of Nuclear Energy 2015, 84, 45–54. [Google Scholar] [CrossRef]
  13. DeHart M, Gleicher F, Laboure V; et al. MAMMOTH Theory Manual. Technical Report INL/EXT-19-54252. Idaho National Laboratory 2019. [Google Scholar]
  14. Lee J, Balestra P, Hassan Y, Muyshondt R, et al. Validation of Pronghorn Pressure Drop Correlations Against Pebble Bed Experiments. Nuclear Technology. 2022, 208, 1–37. [Google Scholar]
  15. Anders D, Berry R, Gaston D, et al. RELAP-7 Level 2 Milestone Report: Demonstration of a Steady State Single Phase PWR Simulation with RELAP-7. technical report, 2012.
  16. Liu Z, Xu X, Wu H, et al. Multidimensional multi-physics simulations of the supercritical water-cooled fuel rod behaviors based on a new fuel performance code developed on the MOOSE platform. Nuclear Engineering and Design 2023, 375. [Google Scholar]
  17. Hales J D, Novascone S R, Spencer B W, et al. Verification of the BISON fuel performance code. Annals of Nuclear Energy 2014, 71, 81–90. [Google Scholar] [CrossRef]
  18. Lin C J, More J J. Incomplete Cholesky factorizations with limited memory. SIAM J. Sci. Comput. 1999, 21, 24. [Google Scholar] [CrossRef]
  19. Cuthill E, Mckee J. Reducing the bandwidth of sparse symmetric matirces. Proceedings of 24th National Conference. Reducing the bandwidth of sparse symmetric matirces. Proceedings of 24th National Conference. ACM 1969, 157–172. [Google Scholar]
  20. Benchmark Problem Book, ANL-7416-Suppl. 2. Argonne National Laboratory, 1979.
  21. Executioner for eigenvalue problems. INL. https :mooseframework.inl.gov/source/execution-ers/NonlinearEigen.
  22. Zhang H, Guo J, Li F, et al. Efficient simultaneous solution of multi-physics multi-scale nonlinear coupled system in HTR reactor based on nonlinear elimination method. Annals of Nuclear Energy 2014, 114, 301–310. [Google Scholar]
  23. Anne, Greenbaum, Vlastimil, et al. Any Nonincreasing Convergence Curve is Possible for GMRES. SIAM Journal on Matrix Analysis and Applications 1996, 17, 465–469. [Google Scholar] [CrossRef]
  24. Saad, Y. Iterative Methods for Sparse Linear Systems; PWS Publishing: Boston, 1996. [Google Scholar]
  25. Bruun, A. Direct Methods for Sparse Matrices. Mathematics of Computation 1980, 9, 874. [Google Scholar]
  26. Hossain A, Steihaug T. Computing A Sparse Jacobian Matrix By Rows And Columns. Optimization Methods and Software 1998, 10, 33–48. [Google Scholar] [CrossRef]
  27. Hovland P D, Combinatorial problems in automatic differentiation, presented at the SIAM Workshop on Combinatorial Scientific Computing, 2004.
  28. Bondy J, A. Bounds for the chromatic number of a graph. Combinatorial Theory 1969, 7, 96–98. [Google Scholar] [CrossRef]
  29. Brooks R, L. On coloring the nodes of a network. Proc. Cambridge Philos. Soc. 1941, 37, 194–197. [Google Scholar] [CrossRef]
  30. Welsh D J, Powell M B. An upper bound for the chromatic number of a graph and its application to timetabling problems. An upper bound for the chromatic number of a graph and its application to timetabling problems. Computer Journal 1967, 1. [Google Scholar]
  31. Coleman T F, Moré J J. Estimation of sparse Jacobian matrices and graph coloring problems. SIAM Journal on Numerical Analysis 1984, 20, 187–209. [Google Scholar]
  32. Matula D W, Marble G, Isaacson J D. GRAPH COLORING ALGORITHMS. GRAPH COLORING ALGORITHMS. Graph Theory and Computing 1972, 109–122. [Google Scholar]
  33. Bozdag D, Çatalyürek, Gebremedhin A H, et al. A parallel distance-2 graph coloring algorithm for distributed memory computers[C].International Conference on High Performance Computing & Communications. Springer-Verlag, 2005.
  34. Coleman T F, Moré J J. Estimation of Sparse Jacobian Matrices and Graph Coloring Blems. Estimation of Sparse Jacobian Matrices and Graph Coloring Blems. SIAM Journal on Numerical Analysis 1983.
  35. Iii W, James W. A Conjugate Gradient-Truncated Direct Method for the Iterative Solution of the Reservoir Simulation Pressure Equation. Society of Petroleum Engineers Journal 1981, 21, 345–353. [Google Scholar] [CrossRef]
  36. Saad, Y. Finding Exact and Approximate Block Structures for ILU Preconditioning.SIAM Journal on Scientific Computing, 2003. [CrossRef]
  37. Gustafsson, I. A class of first order factorization methods. Bit Numerical Mathematics 1978, 18, 142–156. [Google Scholar] [CrossRef]
  38. Saad, Y. ILUT: A dual threshold incomplete LU factorization. Numerical Linear Algebra with Applications 2010, 1, 387–402. [Google Scholar] [CrossRef]
  39. Bolstad J H, Leaf G K, Lindeman A J, Kaper H G. An empirical investigation of reordering and data management for finite element systems of equations. Rep. ANL-8056, Argonne Nat. Lab, Argonne, Ill., 1973.
  40. Davis, T. A, Gilbert J.R, Larimore S.L. A column approximate minimum degree ordering algorithm. ACM Trans. Math. Soft. 2001, 30, 812–823. [Google Scholar]
  41. Cuthill E, McKee J. Reducing the bandwidth of sparse symmetric matirces. Reducing the bandwidth of sparse symmetric matirces. In Proc. Nat. ACM. 1969, 34. [Google Scholar]
  42. Liu L, Zhang H, Wu Y, et al. A modified JFNK with line search method for solving k-eigenvalue neutronics problems with thermal-hydraulics feedback. Nuclear Engineering and Technology. 2002, 55, 310–323. [Google Scholar]
  43. Zhang H, Guo J, Lu J, et al. The comparison between nonlinear and linear preconditioning JFNK method for transient neutronics/thermal-hydraulics coupling problem. Annals of Nuclear Energy. 2019, 132, 357–368. [Google Scholar] [CrossRef]
Preprints 91532 g001
Figure 1. Schematic of LRA benchmark (region numbers indicate material assignment).
Figure 1. Schematic of LRA benchmark (region numbers indicate material assignment).
Preprints 91532 g001
Preprints 91532 g002
Figure 2. Preconditioning system in MOOSE.
Figure 2. Preconditioning system in MOOSE.
Preprints 91532 g002
Preprints 91532 g003
Figure 3. Preconditioning matrix and its compressed representation in steady-state neutron diffusion problem.
Figure 3. Preconditioning matrix and its compressed representation in steady-state neutron diffusion problem.
Preprints 91532 g003
Preprints 91532 g004
Figure 4. Matrix form of generating large-first and small-last ordering.
Figure 4. Matrix form of generating large-first and small-last ordering.
Preprints 91532 g004
Preprints 91532 g005
Figure 5. Graph form of generating large-first/small-last ordering and the colored graph.
Figure 5. Graph form of generating large-first/small-last ordering and the colored graph.
Preprints 91532 g005
Preprints 91532 g006
Figure 6. Matrix structure of different reordering methods using ILU(20).
Figure 6. Matrix structure of different reordering methods using ILU(20).
Preprints 91532 g006
Preprints 91532 g007
Figure 7. Residual history in three coloring methods using FDP.
Figure 7. Residual history in three coloring methods using FDP.
Preprints 91532 g007
Preprints 91532 g008
Figure 8. The total computational time and factorization time in ILU(k) algorithm.
Figure 8. The total computational time and factorization time in ILU(k) algorithm.
Preprints 91532 g008
Preprints 91532 g009
Figure 9. The linear steps and non-zeros after ILU factorization.
Figure 9. The linear steps and non-zeros after ILU factorization.
Preprints 91532 g009
Preprints 91532 g010
Figure 10. The total computational time and non-zeros of ILU factorization for simplified PWR model.
Figure 10. The total computational time and non-zeros of ILU factorization for simplified PWR model.
Preprints 91532 g010
Table 1. Two group constants for the 2D-LRA benchmark [20].
Table 1. Two group constants for the 2D-LRA benchmark [20].
Region Group g D g ( c m ) ∑ a , g   c m − 1 ν ∑ f , g   c m − 1 ∑ s , 1 → 2   c m − 1
1 1 1.255 0.008252 0.004602 0.02533
2 0.211 0.1003 0.1091 -
2 1 1.268 0.007181 0.004609 0.02767
2 0.1902 0.07047 0.08675 -
3 1 1.259 0.008002 0.004663 0.02617
2 0.2091 0.08344 0.1021 -
4 1 1.259 0.008002 0.004663 0.02617
2 0.2091 0.073324 0.1021 -
5 1 1.257 0.0006034 0.0 0.04754
2 0.1592 0.01911 0.0 -
Table 2. Computing performance of different coloring methods.
Table 2. Computing performance of different coloring methods.
Smallest-last Large-first Incidence-degree No-coloring
Total computational time(s) 120.563 122.516 121.030 7276.910
Speed-up ratio 60.35 59.40 60.12 1
Preconditioner construction time(s) 1.872 1.882 1.858 7163.736
Numbers of residual evaluations 535 585 537 23658
Colors used 31 41 32 -
Nonlinear steps 5 5 5 5
Total linear steps 123 123 123 123
Table 3. Computing performance of different reordering algorithms in ILU(10).
Table 3. Computing performance of different reordering algorithms in ILU(10).
Natural 1WD ND QMD RCM
Total computational time 34.996 30.609 29.756 31.193 29.871
Non-zeros after factorizations 3884202 2442293 1879544 2337351 1919274
Number of residual evaluations 556 556 556 556 556
Nonlinear steps 11 11 11 11 11
Linear steps 225 225 225 225 225
Table 4. The optimal fill-in level and computational performance in different reordering algorithms.
Table 4. The optimal fill-in level and computational performance in different reordering algorithms.
Natural ND RCM 1WD QMD
Fill-in level k 3 11 8 7 11
Total computational time (s) 30.89 30.76 31.02 31.08 30.93
Factorization time (s) 23.26 26.35 24.33 24.26 26.52
Total nonlinear steps 6 3 4 4 3
Total linear steps 119 38 55 57 38
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated