Prerpints.org logo
Preprint
Article

Graph-based Neural Networks Framework using Microcontrollers for Energy-Efficient Traffic Forecasting

Altmetrics

Downloads

92

Views

29

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

27 November 2023

Posted:

27 November 2023

You are already at the latest version

Alerts
Abstract
The paper illustrates a general framework in which a neural network application can be easily integrated and proposes a traffic forecasting approach that uses neural networks based on graphs. The method minimizes the communication network (between vehicles and the database servers) load and represents a reasonable trade-off between communication network load and forecasting accuracy. Traffic prediction leads to the choice of less congested routes and therefore to the reduction of energy consumption. The traffic is forecasting using a LTSM neural network with a regression layer. The inputs of the neural network are sequences - obtained from graph that represent the road network - at specific moments of time that are read from traffic sensors or the outputs of neural network (forecasting sequences). The input sequences can be filtered to improve the forecasting accuracy. This general framework is based on Contiki IoT operating system that ensure support for wireless communication and efficient implementation of processes in a resource constrained system and it is particularized to implement a graph neural network. Two cases are studied: one case in which the traffic sensors are periodically read and the other case in which the traffic sensors are read when their values changes are detected. A comparison between the cases is made and the influence of filtering is evaluated. The obtained accuracy is very good, very close to the accuracy obtained in infinite precision simulation, and the computation time is low enough and the system can work in real time.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction and related work

Nowadays, neural networks can be implemented on embedded systems for speech recognition, object detection, human activity recognition, time series forecasting, etc.
Traffic prediction is an important problem nowadays due to the large number of vehicles that transit the road networks. Increased accuracy in predicting traffic will lead to the most efficient use of transport networks and help to make decisions to increase transport capacity on very congested routes. Also, traffic prediction shortens transport times between two points by choosing a less congested route.
One of the impactful applications of graph-based neural networks is improving the accuracy of the estimated arrival time by learning the structure and dynamics of the transport network through the neural network. Using such neural networks, future traffic prediction algorithms will be created (used for example by Google Maps) [18].
Using GNN is a challenge due to the spatial-temporal complexity, but there are advantages in relation to other classical neural networks (for example, convolutional neural networks that cannot represent the topological structure of a transport network).
For traffic prediction, a graph built according to the topology of the transport network is naturally used. The main problems that can be seen on this graph include the number and type of vehicles on the road, their speed, road events, etc. [21].
Another important problem studied in connection with the use of graphs in neural networks refers to the way of their representation. Basic ways of graph representation (adjacency matrix, neighbor matrix, distance matrix, Laplacian matrix) are shown in [21]. Graph transformation methods for better scalability such as GraphGPS described in [19] or TokenGT detailed in [20].
Code examples, in high level programming languages, that implement a neural network based on graphs, are illustrated in [21].
The use of microcontrollers for the implementation of neural networks (testing phase) must consider the memory requirement, processing accuracy and execution time. The continuous development of microcontroller architectures makes such implementations viable, but further research is still needed, especially for neural networks with a higher degree of complexity [22].
Data compression methods to reduce memory requirements are illustrated in article [23]. Some classical neural network architectures (recognition of human activity, image processing) have already been ported to microcontrollers [23].
However, implementation problems on devices with limited resources (not powerful computing systems) are not very much addressed in the literature. In the present work, the possibility of realizing an implementation on microcontrollers is studied and the performances are analyzed.
Terrestrial transport networks are modelled as graphs with destinations (cities) as nodes(vertices). Each node can have several edges representing the paths between cities. The nodes contain information about the number of vehicles transiting the coverage area of the sensor associated with that node. [1]
Transport networks can be dynamic and have complex dependencies. This means that spatial-temporal aspects must be considered. For a graph representation, each node will change its traffic values ​​over time. Traffic forecasting can be done using a neural network that considers both the spatial characteristic (the way the nodes are connected) and the temporal characteristic (modification of the traffic values ​​in the node over time). The inputs to the neural network are represented by graphs at different time points. The output of the neural network is a graph that has the predicted information (number of vehicles and their speed) in nodes and edges.
The following aspects are addressed in the paper:
  • what type of neural network should be chosen so that the implementation can be carried out on microcontrollers (with relatively limited resources)
  • what is the number of graphs at the input so that the prediction is as good as possible (the maximum number of time points)
  • how the graph can be represented to improve the neural network performance
  • evaluation of computing time and prediction accuracy.
The main issues encountered are low power consumption, numerical representation, memory requirements, and execution time.
On the other hand, the embedded system should be able to run all the necessary tasks required by the above-mentioned applications: acquire the data sensors, test the neural network, decide, and transmit it to a server for monitoring and to take further actions. It is no need that the neural network training to be run on the embedded node, since it can be run separately; the neural networks parameters are transmitted to embedded nodes.
This paper defines and analyses a framework for using neural networks to implement various embedded applications.
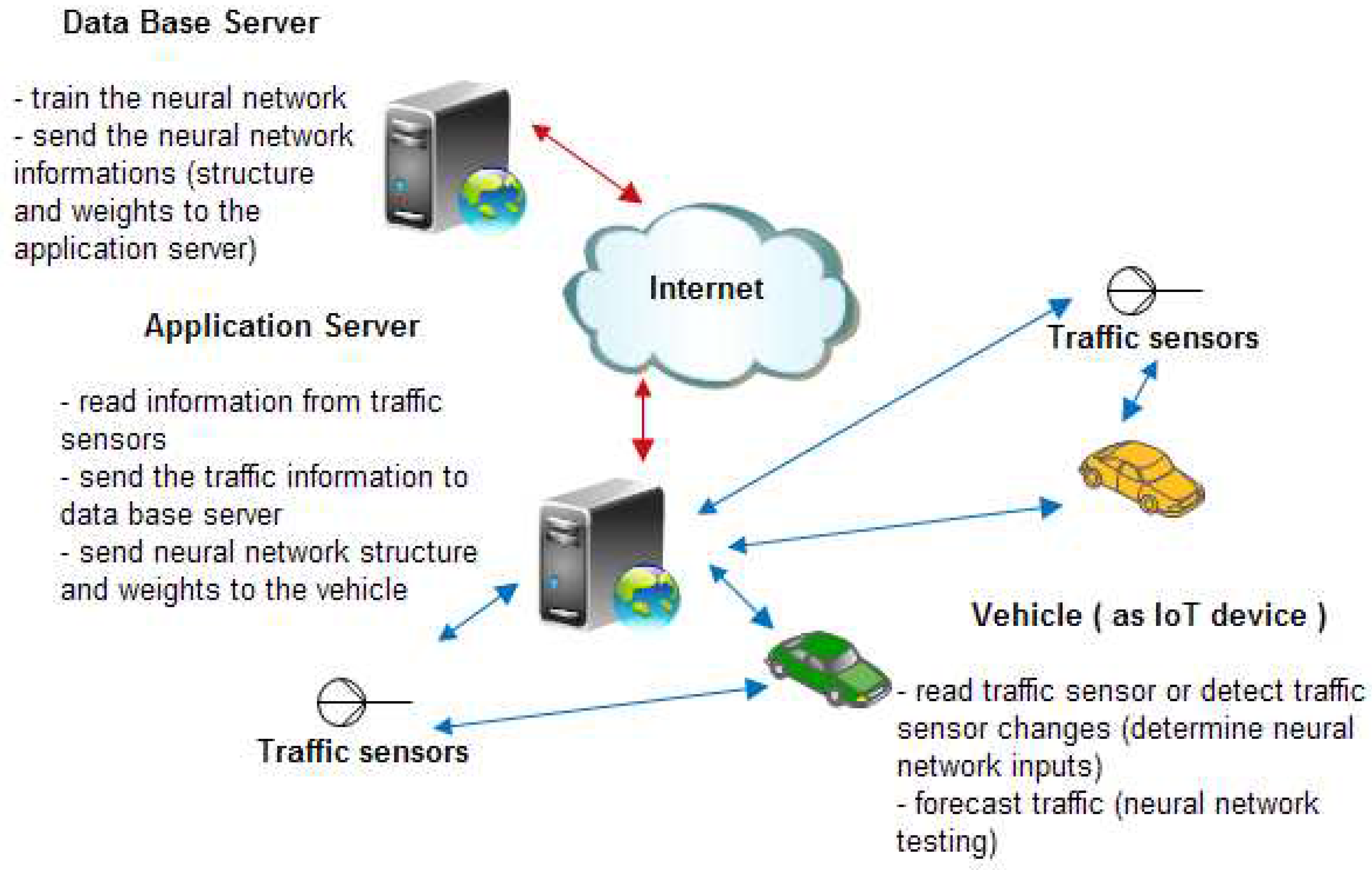
The system has two components: the developing phase and the operating phase. In the developing phase, the necessary sensor data (e.g., traffic information: number of vehicles that transit a specific node, their speeds) are collected by an application server that that transmit this data to a data base server that train a neural network and returns the neural network parameters to the vehicles via application server. In the operating phase, the neural network is tested, and a forecast will be made as it is shown in Figure 1.
In this work we will consider scenarios in which the vehicles transiting the roads request information about the traffic load and can predict the traffic to choose a route as short as possible to decrease road congestion, the travel time and amount of energy consumed [1,2]. The information is taken at specific moments of time from an application server which periodically updates its information from a database server.
The duration of the readings from the application server must be as short as possible to reduce the network load and to allow many vehicles to transit the same roads.
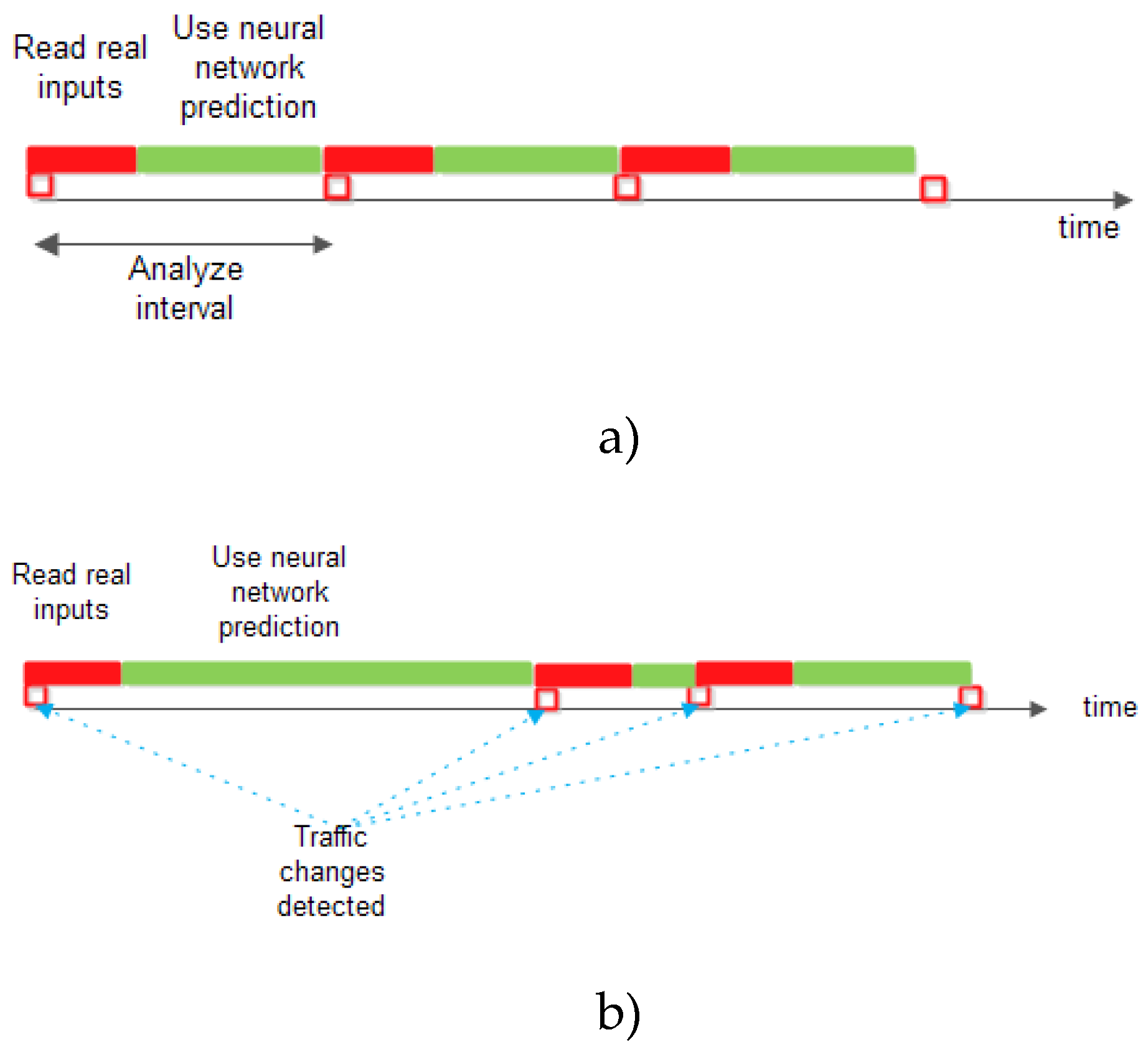
Two scenarios will be analysed: the first one, in which the traffic prediction will be done using a constant analysis duration in which the real information from the nodes will be read for a short period after which the traffic prediction will be done using the results provided by the neural network and the second in which the traffic changes in the nodes will be detected and the real information from the nodes will be read for a fixed duration and then the traffic prediction will be made from the neural network information until the next detection of a change in the real traffic.
For system implementation one can choose a solution consisting of a powerful system on the chip from Analog Devices (consisting of ADuCRF101 which integrates an ARM Cortex M3 MCU at 16 MHz clock, and a RF transceiver ADF7024) as hardware, and AD6LoWPAN (which is the 6LoWPAN - IPv6 over Low-Power Wireless Personal Area Networks, provided by Analog Devices) with IoT operating system Contiki, as software.
To make a prediction a Long Short-Term Memory (LSTM) neural network is involved. This type of recurrent neural network has been proved to have good results in sequence classification and their parameters were validated by simulating in MATLAB.
All the necessary functions that implement the neural network will be considered and evaluated to see if the entire system can perform in real time using a microcontroller.
Considering a wireless node network, in which a very important goal is energy conservation, specific implementation of threads (as starting / stopping radio communication) should be implemented. In such cases, the event-driven model - described by a finite state machine (FSM) is used. To simplify the system development, the threads can be replaced by protothreads, that can be written without having to design state machines [2].
The protothreads are a programming abstraction and they reduce the complexity of implementations of event-triggered systems by performing conditional blocking of event-triggered systems, without the overhead of full multi-threading systems. They are lightweight threads without their own stack. This is advantageous in memory constrained systems, where a stack for a thread uses a large part of the available memory.
Protothreads are based on a low-level mechanism named local continuations that can be set (the CPUs are captured) or resumed. A protothread is a C function with a single associated local continuation. The protothread’s local continuation is set before a conditional blocking. If the condition is true, the protothread executes a return statement to the caller program. At the next time, the protothread is running, the local continuation is resumed to the one that was previously set and cause the program to jump to the conditional blocking statement. The condition is revaluated and, if the condition is false, the protothread executes the function.
In this paper we consider the IoT application that is implemented with Contiki operating system support. The Contiki OS is intended for networked, memory-constrained and low-power wireless IoT devices. Contiki provides multitasking and has a built-in Internet Protocol Suite (TCP/IP stack) with low memory requirements.
The Contiki programming model is based on protothreads [3,4]. The operating system kernel invokes the protothread in response to an event (timers expired, messages posted from other processes, triggered sensors, incoming packets from a network neighbour node). In Contiki, the protothreads are cooperatively scheduled, therefore the process must always explicitly yield control back to the kernel at regular intervals by using a special protothread to block waiting for events while yielding control to the kernel between each event occurrences. Contiki supports inter-process communication using message passing through events.

2. The graph neural network

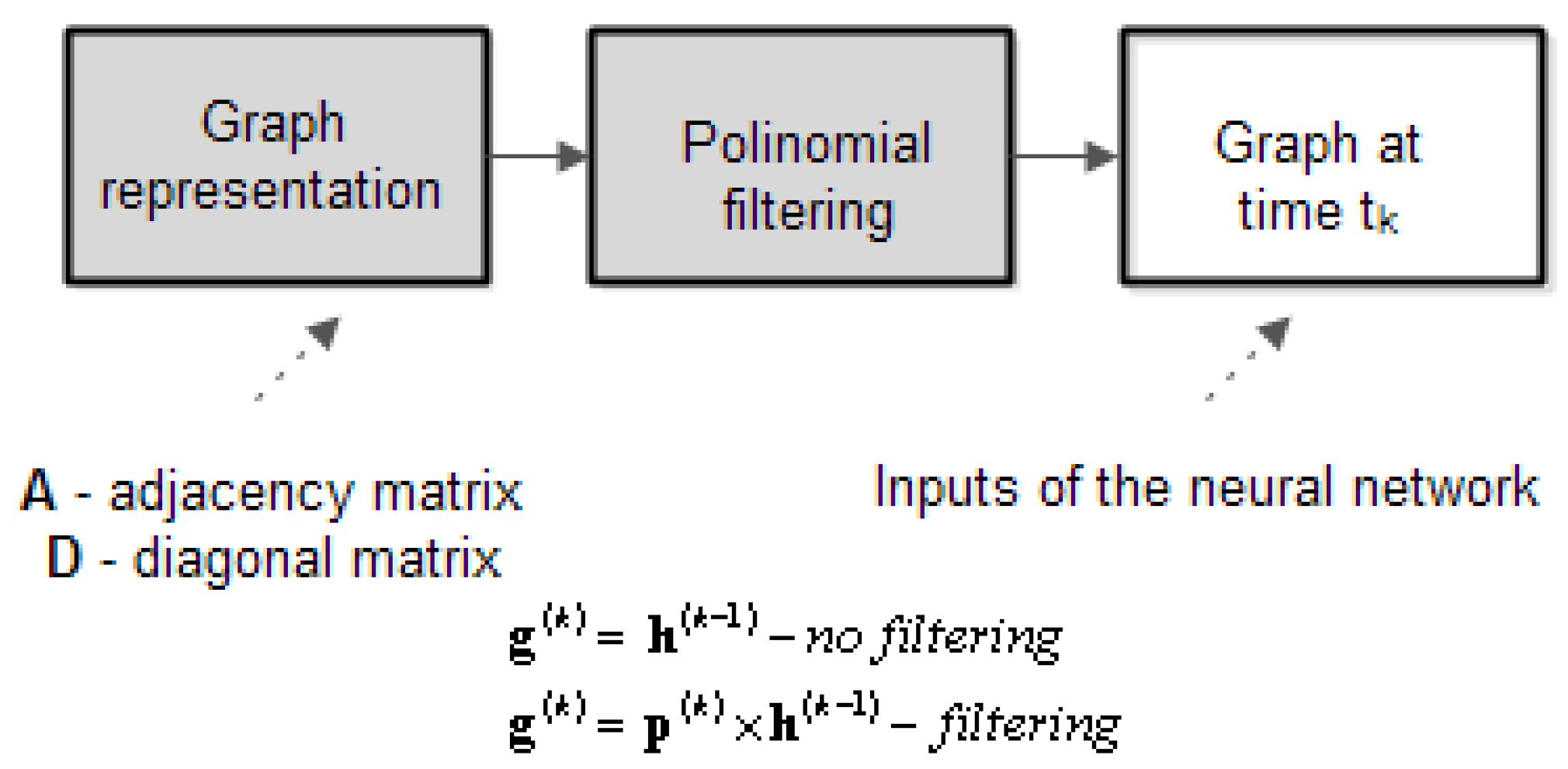
To use a graph as input in a neural network, the information associated with graph (e.g., node values, edges cost) should be converted in an appropriate form to be used as neural network input. Figure 2 illustrates how the graph can be represented with or without filtering. The greyed blocks transform the graph information, given as a vector (or matrix) that has on each line the data in a specific node. Each column represents a specific info for node. The way the graph is represented is presented below.
Given a graph G it is characterized by its adjacency matrix A = [ a i j ] ,   i ,   j = 1 ,   ...   , N where a i j indicates the existence of edge between nodes i ,   j (1 – presence, 0 – absence) and N is the number of nodes. Also, a node in graph G, is characterized by the degree of node which is the number of edges incident at node. A diagonal matrix is defined as: D = [ d i j ] ,   i ,   j = 1 ,   ...   , N   a n d   d i j = 0 ,   i f   i ≠ j ,   d i i = ∑ k = 1 N a i k
A difference matrix L   = D − A will be involved to build a polynomial as follows: p ( L )   =   w 0 I n   +   w 1 L   +   w 2 L 2   +   ...   + w d L d . The polynomial p ( L )   is a (n x n) matrix. We note the coefficients as vector w   =   [ w k ]   ,   k = 0 ,   1 ,   ... ,   d .
The polynomial p ( L ) will be used as a filter to calculate the neural network inputs (features). The generic algorithm for the testing phase of a graph neural network is illustrated bellow (the vector x represents the initial values in nodes of graph):
I n i t i a l i z a t i o n h ( 0 ) =   x w h i l e   ( e r r o r   >   minimum   error   )   d o g ( k )   =   p ( k )   ×   h ( k − 1 )   h ( k ) = σ ( g ( k ) ) o u t p u t =   P R E D I C T ( h ( k ) ) e r r o r =   | o u t p u t −   target | d o   e n d
The vector w represent the polynomial coefficients and x =   [   x 1   x 2   ...   x N   ] represents the initial values in the graph’s nodes. The terms x i can be vectors if nodes have more information (e.g., numbers of vehicle stored by type or speed). The function σ is the activation function (e.g., sigmoid). The superscript index k represents the discrete time index. In the above algorithm PREDICT indicates a regression layer that predicts the output from previous inputs and the target represents the expected output.
This algorithm is a generalization of some graph neural network algorithms. Therefore, the above presented algorithm represents a general framework that can be used to obtain specific implementations of known graph-based neural network [5]. For example, the equivalence with Graph Convolutional Networks (GCN) is proven below.
Consider a slight modification in definition of adjacency matrix, as follows: A = [ a i j ∑ j = 1 N a i j ] ,   i ,   j = 1 ,   ...   , N . Then, the non-zero terms in the diagonal matrix D   will be changed as d i i = 1 .
If w i = 0 ,   i =   2 ,   3 ,   ... ,   d then p ( L )   =   w 0 I n   +   w 1 L   =   w 0 I n   +   w 1 ( D − A ) and g ( k )   =   p ( k )   ×   h ( k − 1 ) = w 0 I n ×   h ( k − 1 )   +   w 1 I n ×   h ( k − 1 ) − w 1 A ×   h ( k − 1 ) = ( w 0 +   w 1 ) .   h ( k − 1 ) − w 1 A ×   h ( k − 1 ) which represents the formulas for GCN.

3. The System Implementation

To forecast traffic, the Long Short-Term Memory (LSTM) neural network is an appropriate choice because the inputs are time sequences (the traffic values in each node in the graph that represents the transport road network and considers the spatial-temporal characteristics of the inputs.
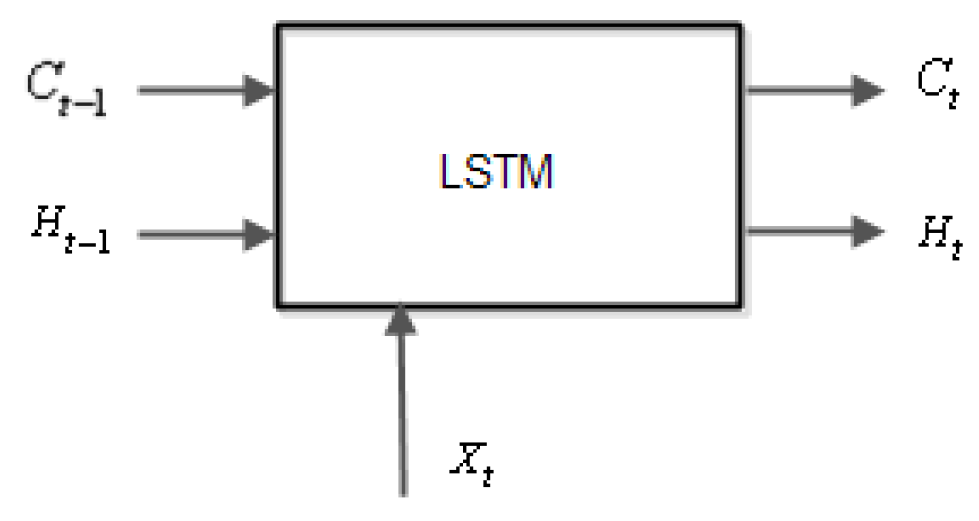
The LSTM network [6,7] is a recurrent neural network that processes input data by looping over time steps and updating its state, that contains information stored over all the previous time moments and consists of several cells as in the Figure 3.
At a given moment of time, t, the input cell is X t . The cell state at time t is C t , and the output is and H t . The initial value of C t − 1 and H t − 1 at t = 0 will be zero.
Assuming that X t , H t are ( M , 1 ) vectors, and B f ,   B i ,   B c , B o   are scalars, the weights w f ,   w i ,   w c ,   w o are ( 1 , M ) vectors, and the weights w   as scalar with M the number of features (inputs in neural network) and one output of neural network, then the LSTM computations are the following relations:
F t = sigmoid   ( ∑ i = 0 M − 1 [ w f ( i ) . H t − 1 ( i ) + w f ( i ) . X t ( i ) ] + B f ) I t = sigmoid   ( ∑ i = 0 M − 1 [ w i ( i ) . H t − 1 ( i ) + w i ( i ) . X t ( i ) ] + B i ) C t = F t .   C t − 1 +   I t   tanh   ( ∑ i = 0 M − 1 [ w c ( i ) . H t − 1 ( i ) + w c ( i ) . X t ( i ) ] + B c ) O t = sigmoid   ( ∑ i = 0 M − 1 [ w o ( i ) . H t − 1 ( i ) + w o ( i ) . X t ( i ) ] + B o ) H t = O t .   tanh   ( C t )
At each time step, the neural network learns to predict the value of the next time step (the inputs are shifted by one-time step) [8]. The sequence output is determined by a neural network regression layer. There are two methods of forecasting: open loop and closed loop forecasting. Open loop forecasting predicts the next time step in a sequence using only the input data (true input from traffic sensors). The output sequence is predicted using several past input sequences. Closed loop forecasting predicts using the previous predictions as input and does not require the true inputs values to make the prediction. To make the prediction for current time, this method uses the predicted value (past the neural network output) as input. The open loop forecasting method has the disadvantage of a greater network load because each vehicle on road should often read the traffic sensors, but the traffic forecasting is more accurate. On the other hand, the closed loop forecasting requires lesser readings of traffic sensors (and reduces the network load), but the forecasting is less accurate, depends on neural network accuracy and graph filtering.
Figure 4 shows the two proposed scenarios.
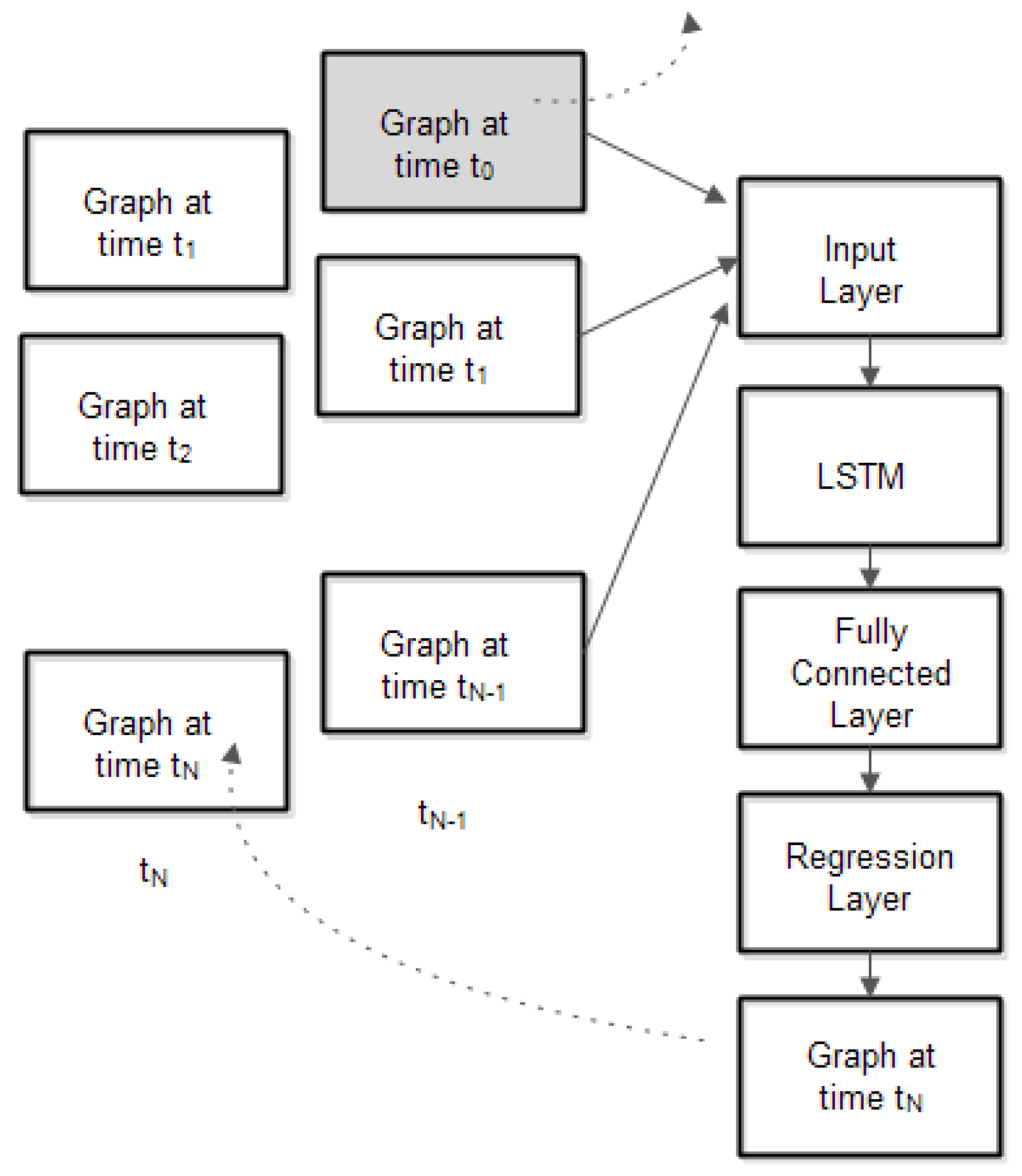
Figure 5 presents the neural network architecture with the following layers: input layer, LSTM layer, fully interconnected layer, and regression layer.
Fully connected layer computation is: O U T P U T = w ( i ) . H t
The neural network regression layer yields a predicted value by learning complex non-linear relationship.
The regression layer computes the half-mean-squared-error loss for regression tasks. For sequence-to-one regression networks, the loss function of the regression layer is the half-mean-squared-error of the predicted responses: l o s s = ∑ i = 0 C − 1 ( t i − y i ) 2 . The output of the regression layer is the predicted sequence (that is, the predicted values in all nodes).
The neural network training parameters are: 200 epochs with 7 observations each and 90% of observation used for training and learning rate 0.001.

4. Software Implementation

The framework for implementing neural network application using microcontrollers is based on an Analog Devices wireless sensor network (WSN) for Internet of Things (IoT) flexible and modular solution used as a development platform. The hardware includes a base station node and several sensor nodes that support different sensors (the sensors can be connected in any combination). To implement the proposed framework, we use a WSN module [9,10] (EV-ADRN-WSN1Z_BUNCH) in each vehicle and the base node (EVAL-ADuCRF101MK) as the application server.
The nodes run a firmware provided by Analog Devices (AD6LoWPAN01[11] - that is based on Contiki OS) as following: the base node is configured as border router to ensure communication between WSN nodes and data server in another IP network, responsible for IPv6 Prefix propagation within the LoWPAN, and the WSN nodes is configured as sensor node (read traffic data and communicate with router). The original code provided with the evaluation platform in AD6LoWPAN01 was modified to implement the proposed framework for neural network traffic forecasting applications.
The modified software has the flowcharts in Figure 6, Figure 7, and Figure 8.
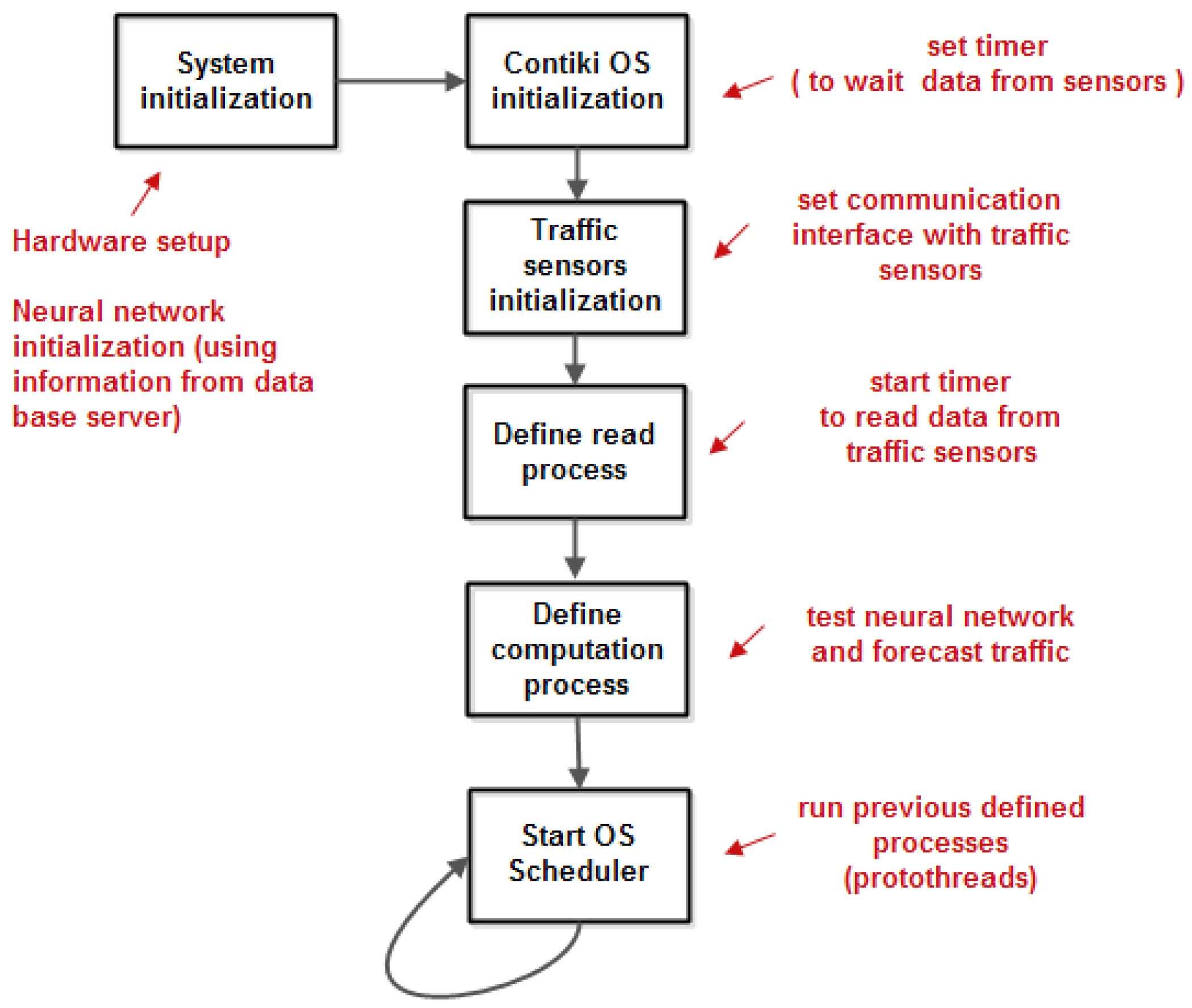
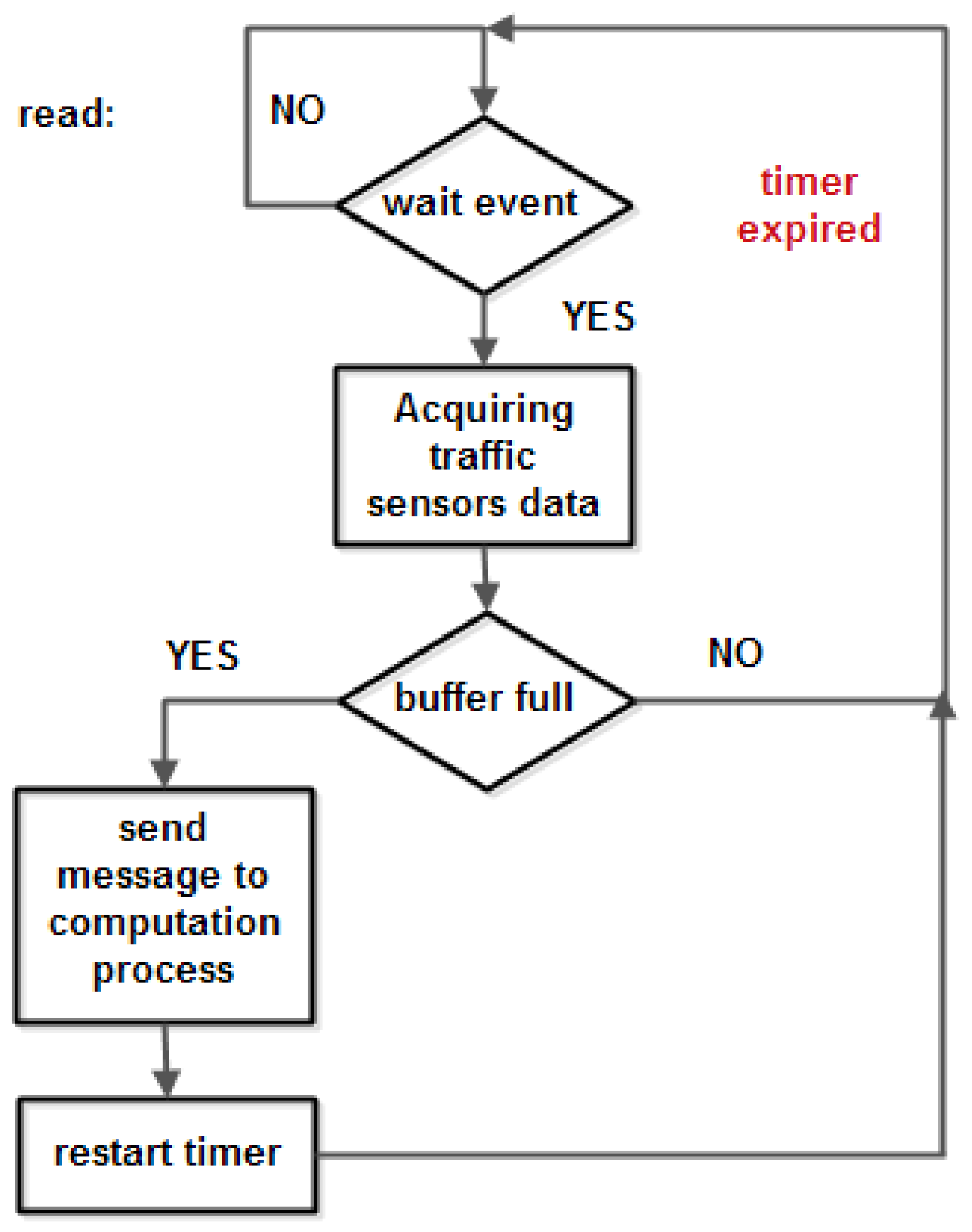
In Figure 6 one can observe the main software modules of the proposed flowchart: hardware and software initialization, sensors initialization, and the two new defined modules (implemented as protothreads): read process and computation process. The read process acquires traffic data sensors in a buffer at a configurable observation rate (in this paper the observation rate is between 1 Hz and 10 Hz) and when the data buffer is full it starts the computation process, as is illustrated in Figure 7.
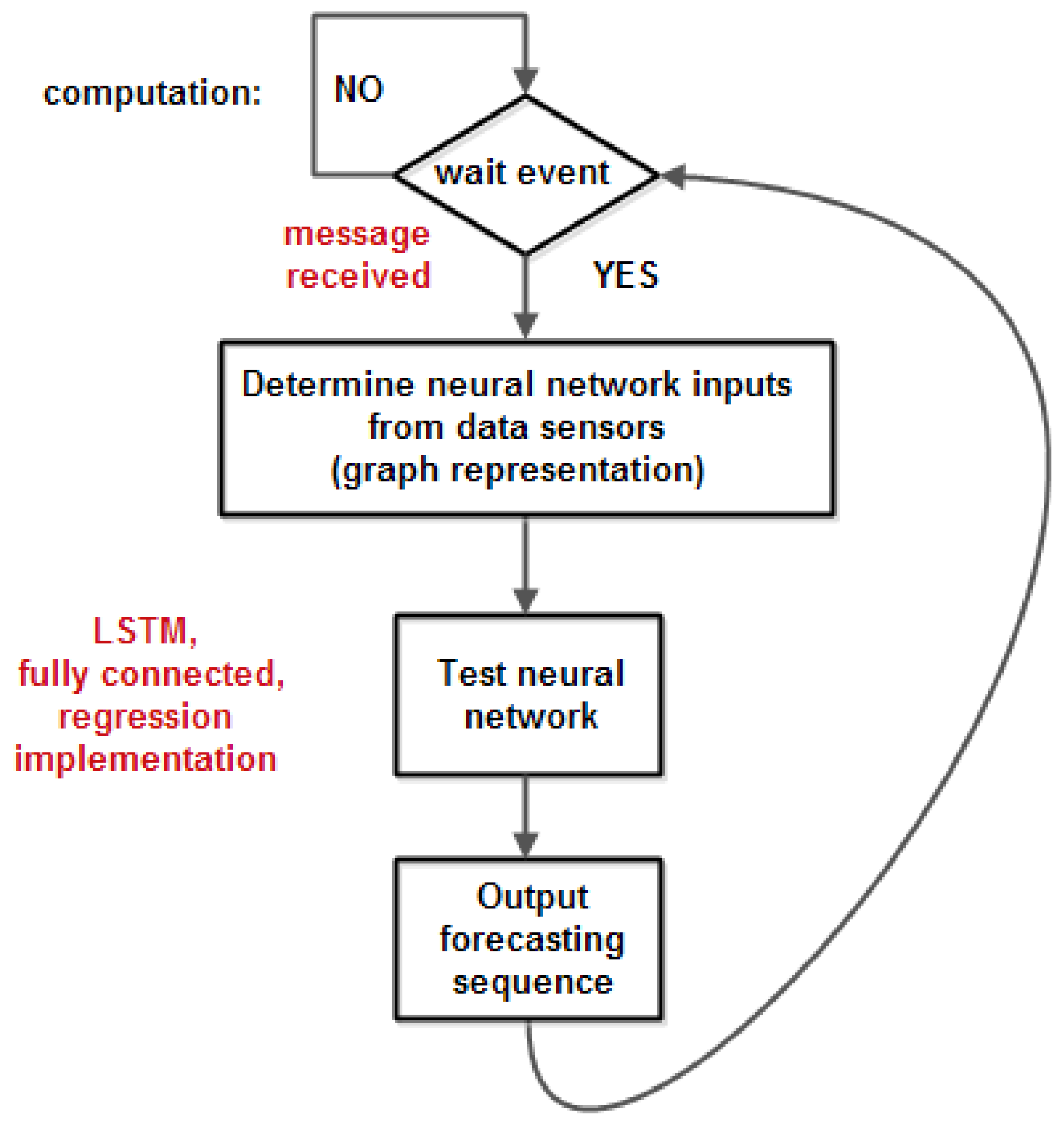
The computation process waits for a message from the read process and then tests the neural network – with the parameters and weights previously configured in the developing phase and makes a prediction. The flowchart of the computation process is shown in Figure 8.
The read process and computation process are run cyclical at a rate given by the filling of the data buffer.
The solution presented above involves the switching buffer technique [12]: two pairs of input and output buffers are switched to obtain a real time implementation (that is, without loss of input observations). Using an input buffer, it permits us to take a decision based on a large interval of time not after a single observation. In this way the accuracy of decision is improved (for example the decision may be taken considering the class that has majority in the given interval of time). The sampling period may vary between tens of milliseconds and several seconds, and the input buffer maximum length may be chosen up to 100. In our evaluation the sampling period of 1 second was chosen.
The necessary condition to have a real time implementation is:
I n p u t   b u f f e r   l e n g t h   ⋅ S a m p l i n g   p e r i o d ≥ B u f f e r   c o m p u t a t i o n   t i m e
We need to evaluate the computation time (that is, all the computation required by neural network test) to decide if the system runs in real time. One other issue is the numerical precision offered by the microcontroller to achieve the same prediction given by a floating-point implementation.

5. The Main Results

We consider a transport network consisting of 5-20 nodes (cities) with several routes. Each nod measures the inbound and outbound traffic. A vehicle on a road (an edge) should forecast the traffic to choose a route that is less busy to increase the transportation energy efficiency. The neural network was training using MATLAB) [13] and it was tested using a C language implementation on microcontrollers on each vehicle [8, 14]. The number of LSTM hidden layers is about 80 (our evaluation shows that the increasing of number of layers will not improve the neural network performance).
The number of processor cycles for function that implements LSTM relation are as following:
dot 857
sigmoid 164
tanh 59
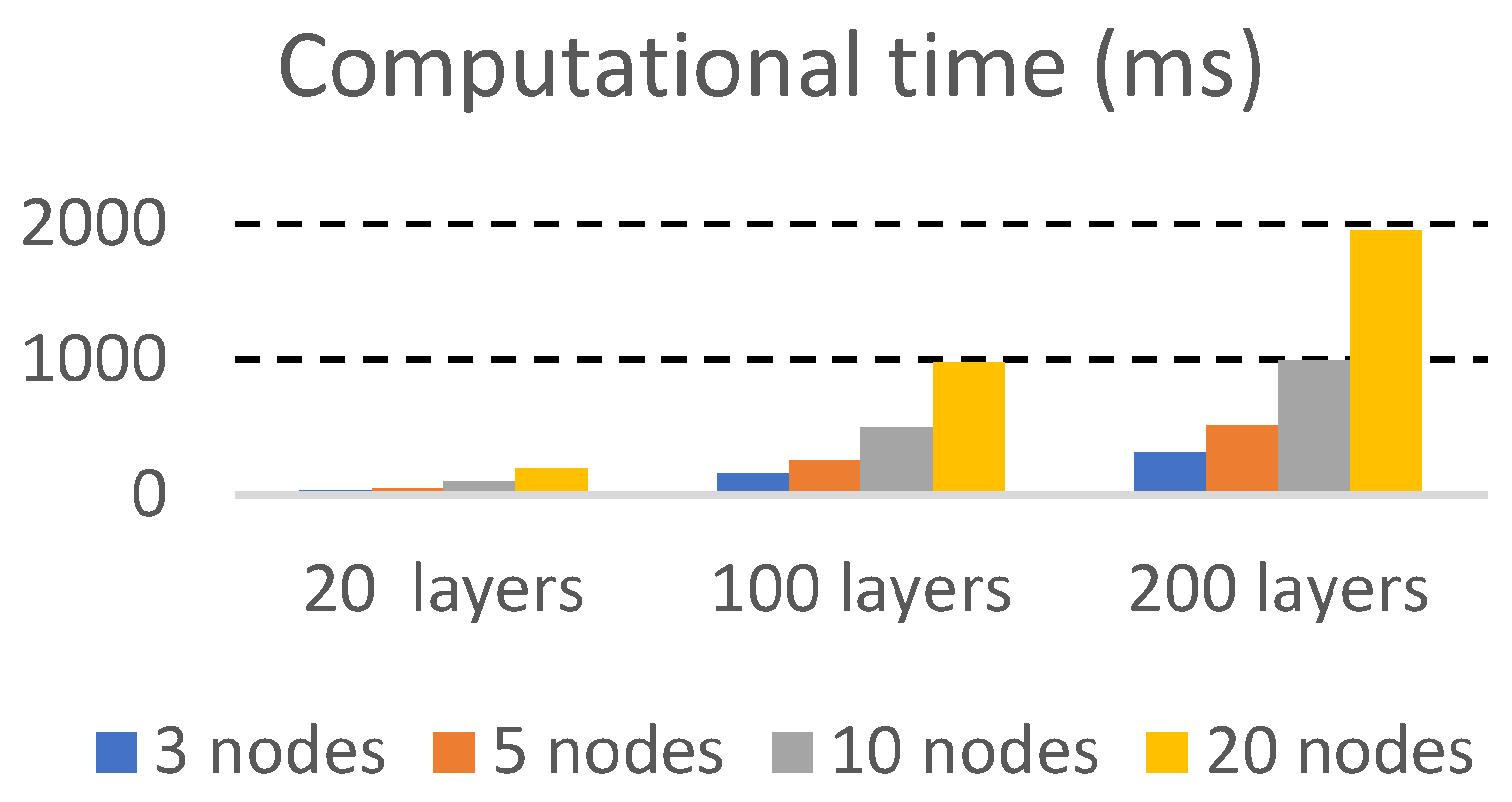
The execution time is quite reasonable, as is shown in Figure 9.
One can observe that the computational time is about 1 second for a neural network with about 100 layers. In Figure 9 the filtering is not considered, but in case of filtering the execution time will be increased less than 10%.
Considering a reasonable assumption that a decision can be made in maximum 60 seconds, this framework can be used for a traffic forecasting system with about 5 features (that is 5 adjacent nodes in each node), and an input buffer up to 600 observations.
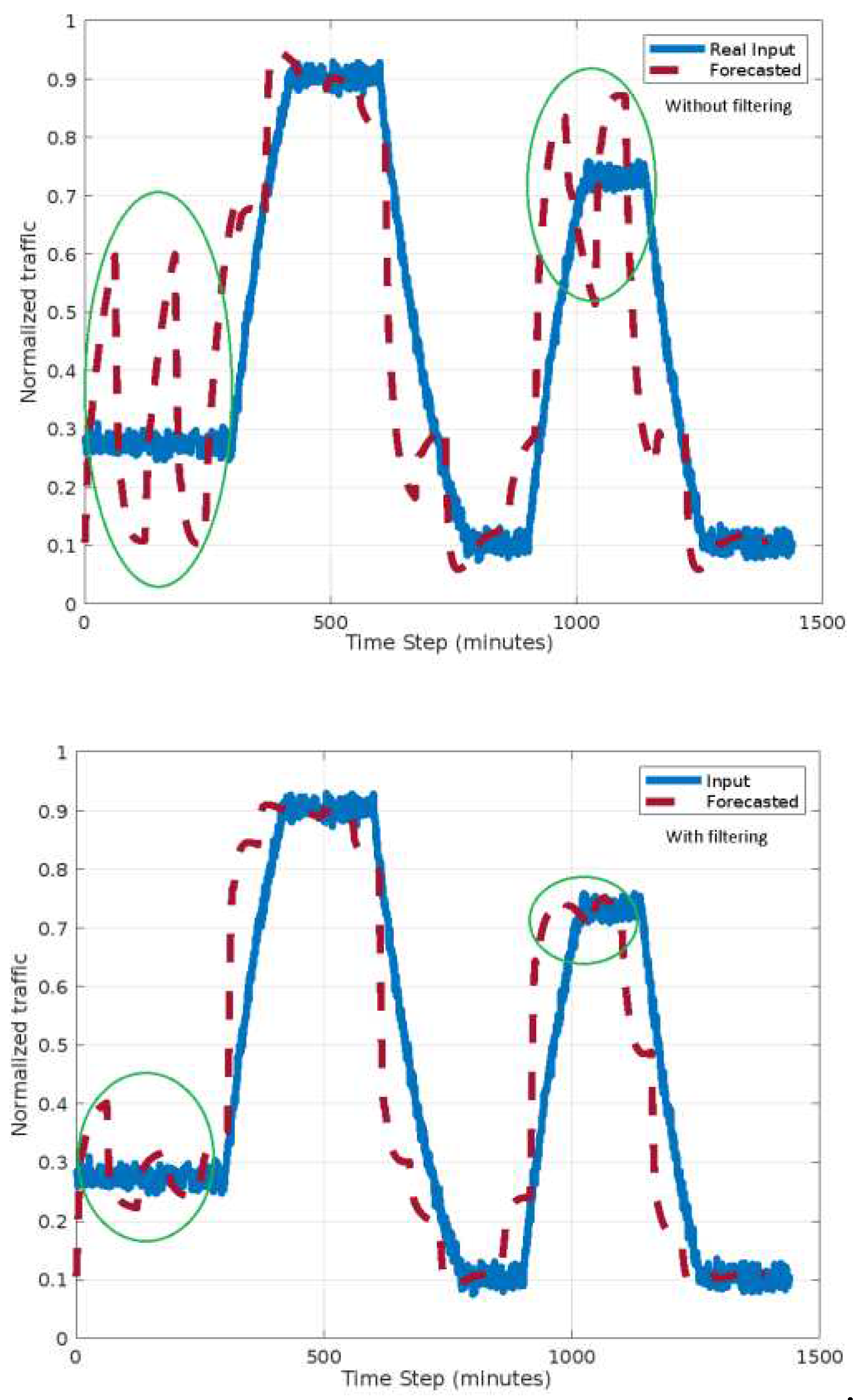
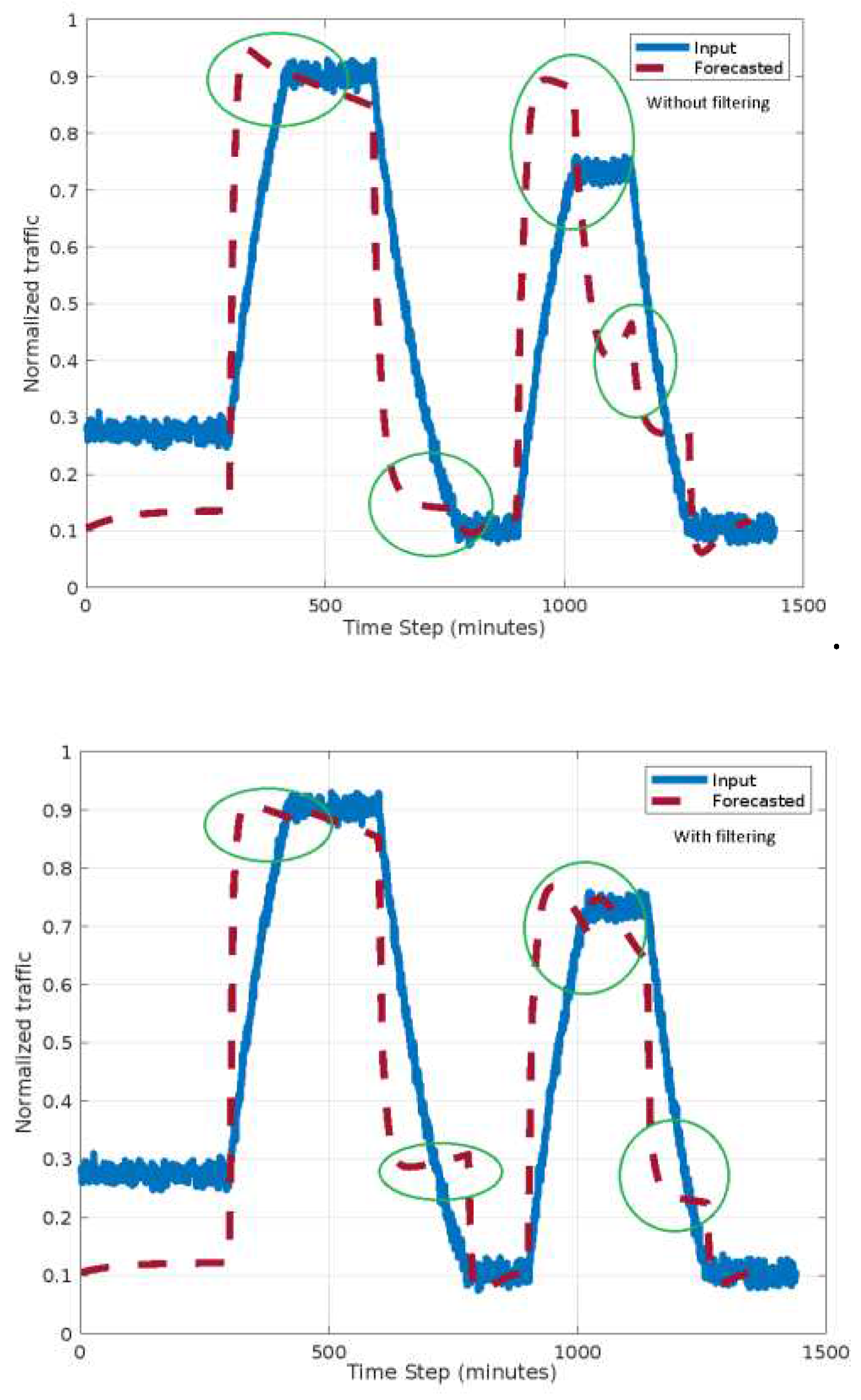
The above two scenarios were evaluated in terms of forecasting accuracy.
The first and second scenario results are shown in Figure 10 and Figure 11. The traffic is normalized to a maximum estimated traffic.
The circles in Figure 7 and Figure 8 indicate differences between the two scenarios both with and without filtering. One can observe that the forecast accuracy is better for the second scenario. The oscillations in forecasted traffic will be eliminated if the filtering is involved. This is due to a better choosing of analysis interval.
To obtain a quantitative performance evaluation of the forecasting system we compute the mean squared error as M S E = ∑ k = 1 N [ i n p u t ( k ) − f o r e c a s t e d ( k ) ] 2 and take the MSE mean value as metric to determine the forecast precision. It will also consider the load of the communication network as a ratio of the reading time of the sensors and the analysis time.
For the first scenario, the analysis interval is 60 minutes and for each analysis interval the real inputs are read in the first 10 minutes. In the second scenario, at each detected traffic sensors’ changes, the inputs are read for 10 seconds. In our experiments a real input change occurs, on average, at 140 seconds. The readings intervals are smaller in the second scenario (less than 5 minutes per hour); therefore, the communication network load is twice as small than in the first scenario. The detecting of changes will increase the computational time by about 5%. In both scenarios, one can observe better accuracy if filtering is involved.
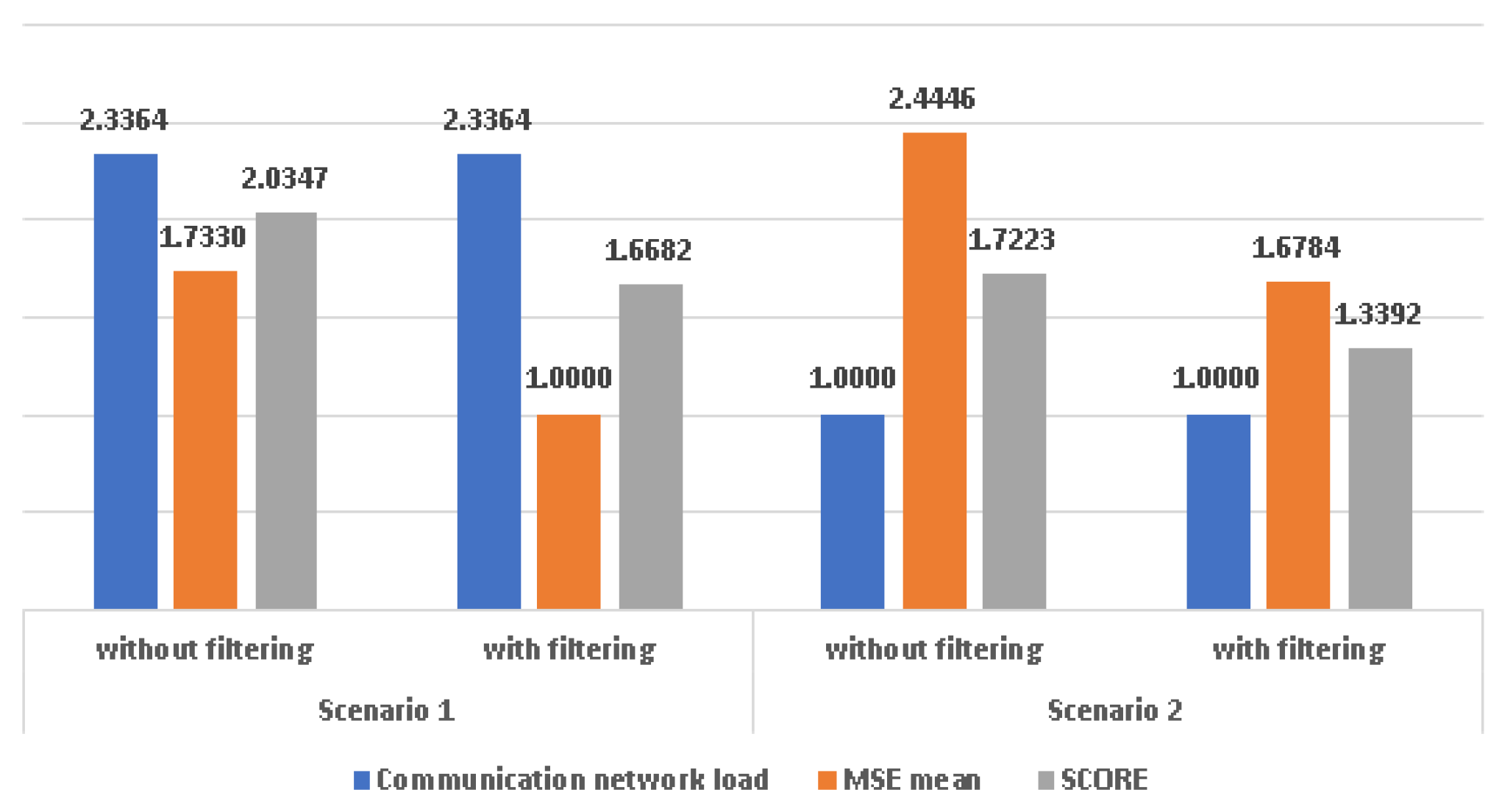
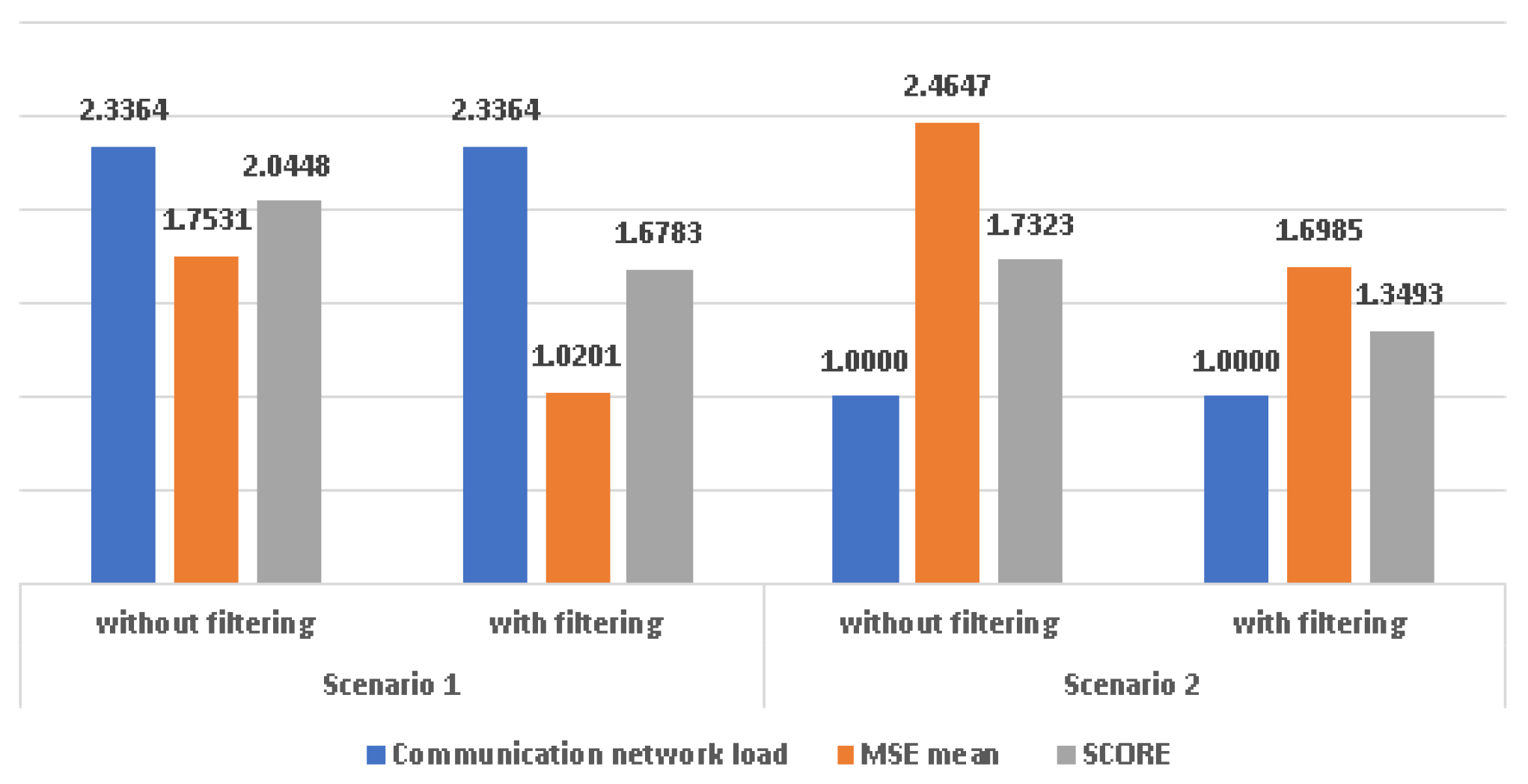
The global evaluation of the performance is given by a score calculated as an arithmetic mean between the MSE and the load of the communication network normalized to the load of the second scenario. Figure 12 indicates the overall performance of the forecasting system. In this figure the communication network load was normalized to the load in the second scenario.
The lower score is better. One can observe that scenario 2 has better performance and the filtering improves the performance in both scenarios.
Filtering improves accuracy in both scenarios.
The filtering leads to a greater improvement in the first scenario, that is simpler to implement. For the second scenario, that has a greater complexity, due the necessity to detect the significant change in the input, the filtering is useful, but the improvements are not so great as in the first scenario. Considering forecasting accuracy mean values, accuracy fluctuations and communication network load with equal weights, the second scenario with filtering has better overall performance than the rest of scenarios and the average overall improvement is about 27%. For both scenarios, the increasing of reading time intervals will lead to a better accuracy, but the communication network load will be increased. A trade-off between traffic forecasting accuracy and communication network load should consider determining the length of reading interval.

6. The numerical quantization Evaluation

The neural network described in section III was trained and tested in MATLAB to validate the traffic forecasting system and to compute the necessary parameters for a real time implementation using the previously described hardware and software platform. Using floating-point types on a microprocessor without a math coprocessor is inefficient, both in terms of code size and execution speed [15]. Therefore, you should consider replacing code that uses floating-point operations with code that uses integers, because these are more efficient. The Cortex M3 ARM architecture does not have a math co-processor and the operation required (especially activation function should be implemented in floating point). Our implementation uses the C compiler support for floating point representation. In the representation of a signed 32-bit floating-point number the exponent is 8 bits, and the mantissa is 23 bits. For a signed 64-bit floating-point number the exponent is 11 bits, and the mantissa is 52 bits.
The following functions: dot product, sigmoid, tanh was implemented in C language using 32-bit floating point variables representation to determine the forecasting system accuracy with finite precision. The statistics of quantization errors (mean and standard deviation) for dot product function are represented in Table 1. The quantization errors for this function are cumulative and therefore they depend on the number of features and number of classes. The statistics of quantization errors for the other mentioned functions are not dependent on the number of features. These statistics are depicted in Table 2.
The LSTM quantization errors (one layer) are illustrated in Table 3.
The above presented results show that the implementation of LSTM neural network as in section III, using a microcontroller with 32-bits precision, the quantization error has no major impact on the neural network comparing with using a personal computer (with infinite precision). The results in Figure 12 and Figure 13 consider the MSE mean normalized at MSE mean for scenario 1 with filtering.

7. Conclusion

This paper introduces a general framework to implement graph based neural network and proposes an approach to forecast traffic with good accuracy and reduced communication network load. Two scenarios are evaluated considering how often the vehicles read the traffic sensors: periodically or change triggered inputs reading. In both scenarios a LSTM neural network is involved. This neural network predicts the information in the graph node (traffic and./or speed on edges from node) using as features real or predicted traffic information. The input data filtering is also evaluated. The main results show that filtering improve the forecasting accuracy in both scenarios with a slight increase in computational effort. The second scenario can be performed better than the first scenario but is sensitive to relatively slow changes in the traffic.
Also, the paper analyzes and evaluates how a neural network can be implemented and tested using common microcontrollers. The impact of variables quantization in the prediction and the total system computation time were considered. The experiments show that the implementation of LSTM neural network has very good performance. The accuracy does not decrease significantly due to the finite precision of the microcontrollers’ registers, and the implementation time is in real-time for a reasonable number of features and classes in traffic forecasting system. The proposed neural network framework is flexible and requires a small memory amount for coding. It easily can be used to realize various neural network models.
More sophisticated models of graph based neural network testing using the proposed framework could be assessed.

Author Contributions

Conceptualization, S.Z. and M.V.; methodology, R.Z.; software, S.Z.; validation, D.G., R.Z. and M.V.; formal analysis, D.G.; investigation, M.V.; resources, M.V.; data curation, R.Z.; writing—original draft preparation, S.Z.; writing—review and editing, M.V., S.Z..; visualization, D.G.; funding acquisition, M.V. All authors have read and agreed to the published version of the manuscript.

Funding

The research leading to these results has received funding from the NO Grants 2014-2021, under Project contract no. 42/2021, RO-NO-2019-0499 -"A Massive MIMO Enabled IoT Platform with Networking Slicing for Beyond 5G IoV/V2X and Maritime Services" - SOLID-B5G

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Maryam Shaygan, Collin Meese, Wanxin Li, Xiaoliang (George) Zhao, Mark Nejad, Traffic prediction using artificial intelligence: Review of recent advances and emerging opportunities, Transportation Research Part C: Emerging Technologies, Volume 145, 2022, 103921, ISSN 0968-090X. [CrossRef]
  2. Mahmuda Akhtar, Sara Moridpour, "A Review of Traffic Congestion Prediction Using Artificial Intelligence", Journal of Advanced Transportation, vol. 2021, Article ID 8878011, 18 pages, 2021. [CrossRef]
  3. Bing Yu, Haoteng Yin, Zhanxing Zhu, "Spatio-Temporal Graph Convolutional Networks: A Deep Learning Framework for Traffic Forecasting", Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence, Pages 3634-3640. [CrossRef]
  4. Adam Dunkels, Oliver Schmidt, “Protothreads Lightweight, Stackless Threads in C”, SICS Technical Report T2005:05, ISSN 1100-3154, ISRN: SICS-T–2005/05-SE, March 2005.
  5. http://www.contiki-os.org/.
  6. Dunkels, Adam (2004), "Contiki – a lightweight and flexible operating system for tiny, networked sensors", Proceedings of the 29th Annual IEEE International Conference on Local Computer Networks., pp. 455–462.
  7. Sanchez-Lengeling, B. , Reif, E., Pearce, A. and Wiltschko, A., “A Gentle Introduction to Graph Neural Networks” 2021. Distill. [CrossRef]
  8. Graves, A. (2012) Long Short-Term Memory. In: Supervised Sequence Labelling with Recurrent Neural Networks. Studies in Computational Intelligence, vol 385. Springer, Berlin, Heidelberg. [CrossRef]
  9. https://colah.github.io/posts/2015-08-Understanding-LSTMs.
  10. Sorin Zoican, Roxana Zoican, and Dan Galatchi, "Terrestrial Traffic Forecasting using Graph-based Neural Networks", 2023 16th International Conference on Advanced Technologies, Systems and Services in Telecommunications (TELSIKS) – accepted to publication.
  11. S. Zoican, M. Vochin, R. Zoican and D. Galatchi, "Neural Network Testing Framework for Microcontrollers," 2022 14th International Conference on Communications (COMM), Bucharest, Romania, 2022, pp. 1-6. [CrossRef]
  12. https://www.analog.com/media/en/technical-documentation/user-guides/UG-480.pdf, accessed 15.02.2022.
  13. https://datatracker.ietf.org/wg/6lowpan/.
  14. Zoican, Sorin; Zoican, Roxana; Galatchi, Dan, “Methods for Real Time Implementation of Image Processing Algorithms”, University Politehnica of Bucharest Scientific Bulletin, Series C-Electrical Engineering and Computer Science, Vol. 77, Iss. 2, 2015, pp. 137-148, ISSN 2286-3540.
  15. https://www.mathworks.com/help/deeplearning/ug/time-series-forecasting-using-deep-learning.html.
  16. IAR C/C++ Compiler User Guide, https://wwwfiles.iar.com › AVR › webic › doc ›EWAVR_CompilerGuide.pdf.
  17. Novac, P.-E.; Boukli Hacene, G.; Pegatoquet, A.; Miramond, B.; Gripon, V. Quantization and Deployment of Deep Neural Networks on Microcontrollers. Sensors 2021, 21, 2984. [Google Scholar] [CrossRef] [PubMed]
  18. https://www.assemblyai.com/blog/ai-trends-graph-neural-networks.
  19. L Rampášek, M Galkin, VP Dwivedi, AT Luu, G Wolf, D Beaini, "Recipe for a general, powerful, scalable graph transformer", Advances in Neural Information Processing Systems, 2022.
  20. J Kim, D Nguyen, S Min, S Cho, M Lee, H Lee, S Hong, "Pure transformers are powerful graph learners", Advances in Neural Information Processing Systems, 2022.
  21. W Jiang, J Luo , "Graph neural network for traffic forecasting: A survey", Expert Systems with Applications, 2022 – Elsevier.
  22. E Liberis, ND Lane, Neural networks on microcontrollers: saving memory at inference via operator reordering, arXiv preprint arXiv:1910.05110.
  23. Saha, Swapnil Sayan & Sandha, Sandeep & Srivastava, Mani. (2022). Machine Learning for Microcontroller-Class Hardware: A Review. IEEE Sensors Journal. 22. 21362-21390. [CrossRef]
Preprints 91540 g001
Figure 1. Traffic forecasting system architecture.
Figure 1. Traffic forecasting system architecture.
Preprints 91540 g001
Preprints 91540 g002
Figure 2. Graph representation and filtering.
Figure 2. Graph representation and filtering.
Preprints 91540 g002
Preprints 91540 g003
Figure 3. LSTM neural network cell.
Figure 3. LSTM neural network cell.
Preprints 91540 g003
Preprints 91540 g004
Figure 4. Traffic forecasting scenarios: a) first scenario: constant analyse and reading intervals b) second scenario: input changes detecting, constant reading interval
Figure 4. Traffic forecasting scenarios: a) first scenario: constant analyse and reading intervals b) second scenario: input changes detecting, constant reading interval
Preprints 91540 g004
Preprints 91540 g005
Figure 5. Traffic forecasting using graph-based neural network.
Figure 5. Traffic forecasting using graph-based neural network.
Preprints 91540 g005
Preprints 91540 g006
Figure 6. The overall framework flowchart.
Figure 6. The overall framework flowchart.
Preprints 91540 g006
Preprints 91540 g007
Figure 7. The read process flowchart.
Figure 7. The read process flowchart.
Preprints 91540 g007
Preprints 91540 g008
Figure 8. The computation process flowchart.
Figure 8. The computation process flowchart.
Preprints 91540 g008
Preprints 91540 g009
Figure 9. Computational time vs number of layers and number of nodes in graph.
Figure 9. Computational time vs number of layers and number of nodes in graph.
Preprints 91540 g009
Preprints 91540 g010
Figure 10. Normalized forecasted traffic in first scenario.
Figure 10. Normalized forecasted traffic in first scenario.
Preprints 91540 g010
Preprints 91540 g011
Figure 11. Normalized forecasted traffic in second.
Figure 11. Normalized forecasted traffic in second.
Preprints 91540 g011
Preprints 91540 g012
Figure 12. Overall performance (infinite precision).
Figure 12. Overall performance (infinite precision).
Preprints 91540 g012
Preprints 91540 g013
Figure 13. Overall performance (32 bits precision precision).
Figure 13. Overall performance (32 bits precision precision).
Preprints 91540 g013
Table 1. The dot product quantization error mean and standard deviation.
Table 1. The dot product quantization error mean and standard deviation.
M 3 5 10 20
Error mean 0.011858 0.019425 0.038837 0.077625
Std. dev. 0.002957 0.004801 0.008251 0.015196
Table 2. The quantization error statistics.
Table 2. The quantization error statistics.
function sigmoid tanh
statistic
mean 0.00102 0.00369
std 0.00110 0.00153
Table 3. The LSTM quantization mean error and standard deviation.
Table 3. The LSTM quantization mean error and standard deviation.
M 3 5 10 20
Error mean 0.01627 0.01175 0.01185 0.01186
Std. dev. 0.01009 0.01087 0.01215 0.01226
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated