Prerpints.org logo
Preprint
Review

Recent Advances in the Numerical Solution of the Nonlinear Schrödinger Equation

Altmetrics

Downloads

116

Views

43

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

24 November 2023

Posted:

28 November 2023

You are already at the latest version

Alerts
Abstract
In this review we collect some recent achievements in the accurate and efficient solution of the Nonlinear Schrödinger Equation (NLSE), with the preservation of its Hamiltonian structure. This is achieved by using the energy-conserving Runge-Kutta methods named Hamiltonian Boundary Value Methods (HBVMs) after a proper space semi-discretization. The main facts about HBVMs, along with their application for solving the given problem, are here recalled and explained in detail. In particular, their use as spectral methods in time, which allows efficiently solving the problems with spectral space-time accuracy.
Keywords: 
Subject: Physical Sciences  -   Other

1. Introduction

In this paper we review the main facts about a recent approach for efficiently solving the following general form of (non-dimensional) Nonlinear Schrödinger Equation (NLSE),
i ψ t ( x , t ) + ψ x x ( x , t ) + f ′ ( | ψ ( x , t ) | 2 ) ψ ( x , t ) = 0 , ( x , t ) ∈ [ a , b ] × [ 0 , T ] ,
coupled with initial data and periodic boundary conditions, with i the imaginary unit, f : R → R a differentiable function, and f ′ its derivative.
Generally speaking, there are basically two ways in which NLSE enters physical and applied sciences. The first one is the appearance of the NLSE as the first-order approximation of a nonlinear dispersive system, such as the wave equation in a nonlinear medium. To this category belong the NLSE used in Fiber Optics [1], Plasma Physics [2,3,4], Geophysics [5,6] and Biology [7]. The other way NLSE appears in physics is as the single-particle, mean-field approximation of a many-particle linear system. This is typically the case of quantum mechanics, where the NLSE arises in several contexts, the most important being the description of the dynamics of a Bose-Einstein condensate. In this case the suitable NLSE is also known as Gross-Pitaevskii equation [8]. In most such applications, the NLSE is used in its more common form, i.e., with cubic nonlinearity, corresponding to f ( x ) = x 2 . However, higher-degree nonlinearities appear in important applications, among which it is worth mentioning the cubic-quintic NLSE, corresponding to f ( x ) = α x 2 − β x 3 , which is used to describe the propagation of ultrashort pulses in optical fibers [1,9,10,11] or high-density effects in Bose-Einstein condensates [12,13,14]. The NLSE is of course of great interest also from a purely mathematical viewpoint, especially in view of its profound connections with the theory of integrable PDEs, solitons and inverse scattering [15,16,17,18,19].
For all these reasons, the numerical solution of the NLSE has been the subject of investigation since a long time (see, e.g., [20,21,22,23,24] for early approaches). More recently, geometric numerical methods have been considered: as an example, we mention multi-symplectic methods (see, e.g., [25,26,27,28,29,30,31,32,33,34,35,36]), symplectic methods (see, e.g., [37,38,39,40,41,42,43,44]), and so forth (see, e.g., [45,46,47,48,49,50,51]). More recently, methods able to conserve the energy or other invariants (see, e.g., [52,53,54,55,56,57,58,59,60,61]) have been investigated: the methods we shall deal with, are exactly placed in this latter setting. The basic approach follows what suggested in [62, page 187], namely by suitably using the method of lines: if the PDEs are of Hamiltonian type, [...] the space discretization should be carried out in such a way that the resulting system of ODEs is Hamiltonian (for a suitable Poisson bracket). The latter system is then solved by using a geometric method for the time integration. Usually, symplectic methods [62,63,64,65,66] have been used for this purpose. Instead, in the present case, we shall consider energy-conserving methods, namely methods able to conserve the energy. Energy-conserving methods have been studied by many authors (see, e.g., [67,68,69,70]): we shall here consider the class of Hamiltonian Boundary Value Methods (HBVMs), which is a family of Runge-Kutta (RK) methods recently devised for the efficient numerical solution of Hamiltonian ODEs. We refer to [68,71] (and, in particular, to the monograph [67] 1) for the derivation and analysis of such methods, which have been devised within the framework of the so called line integral methods (see, e.g., the review paper [72]). We mention that generalizations and extensions of such approach have been also considered in [73,74,75,76,77,78,79,80,81,82,83,84,85]. HBVMs have been also considered for the efficient numerical solution of a number of Hamiltonian PDEs (see, e.g., [86,87,88,89,90]), among which the NLSE [91] and Manakov systems [92].
With this premise, the structure of the paper is as follows: in Section 2 we recall the basic facts about the NLSE along with its space semi-discretization; in Section 3 we review HBVMs and their properties; in Section 4 we give some details about the efficient implementation of such methods for numerically solving the NLSE (1); Section 5 contains a few numerical tests; at last some concluding remarks are given in Section 6.

2. Basic Facts about the NLSE and Its Space Semi-Discretization

We shall hereafter consider the real form of (1) by setting
Ψ ( x , t ) = u ( x , t ) + i v ( x , t ) .
Omitting, for the sake of brevity, the arguments ( x , t ) when unnecessary, one then obtains:
u t = − v x x − f ′ ( u 2 + v 2 ) v , v t = u x x + f ′ ( u 2 + v 2 ) u , ( x , t ) ∈ [ a , b ] × [ 0 , T ] ,
with the initial conditions
u ( x , 0 ) = u 0 ( x ) , v ( x , 0 ) = v 0 ( x ) , x ∈ [ a , b ] ,
and periodic boundary conditions (consequently, also u 0 ( x ) and v 0 ( x ) are assumed to be periodic). By defining the Hamiltonian functional
H [ u , v ] ( t ) = 1 2 ∫ a b u x ( x , t ) 2 + v x ( x , t ) 2 − f ( u ( x , t ) 2 + v ( x , t ) 2 ) d x ,
and considering that for any variations η , ν ∈ L 2 [ a , b ] , its functional derivatives are given by:
lim ε → 0 H [ u + ε η , v ] ( t ) − H [ u , v ] ( t ) ε = : ∫ a b δ δ u ( x ) H [ u , v ] ( t ) η ( x ) d x ≡ − ∫ a b u x x ( x , t ) + f ′ ( u ( x , t ) 2 + v ( x , t ) 2 ) u ( x , t ) η ( x ) d x , lim ε → 0 H [ u , v + ε ν ] ( t ) − H [ u , v ] ( t ) ε = : ∫ a b δ δ v ( x ) H [ u , v ] ( t ) ν ( x ) d x ≡ − ∫ a b v x x ( x , t ) + f ′ ( u ( x , t ) 2 + v ( x , t ) 2 ) v ( x , t ) ν ( x ) d x ,
one deduces that (3) has a Hamiltonian structure. In more detail, by defining
y = u v , J = 0 1 − 1 0 = − J ⊤ = − J − 1 , ∇ H [ y ] = δ H δ u δ H δ v ,
it is straightforward deriving that (3) can be rewritten as
y t = J ∇ H [ y ] ,
which is formally similar to a usual system of Hamiltonian ODEs.
Because of the periodic boundary conditions, it can be proved that H [ u , v ] ( t ) is a conserved quantity for all t ≥ 0 , as well as the mass
M 1 [ u , v ] ( t ) = ∫ a b u ( x , t ) 2 + v ( x , t ) 2 d x ,
and the momentum
M 2 [ u , v ] ( t ) = ∫ a b u ( x , t ) v x ( x , t ) − v ( x , t ) u x ( x , t ) d x .
Let us sketch the conservation of (8): the conservation of (5) and (9) can be similarly obtained (see, e.g., [91]):
d d t M 1 [ u , v ] ( t ) = 2 ∫ a b u ( x , t ) u t ( x , t ) + v ( x , t ) v t ( x , t ) d x = 2 ∫ a b u ( x , t ) − v x x ( x , t ) − f ′ ( u ( x , t ) 2 + v ( x , t ) 2 ) v ( x , t ) + v ( x , t ) u x x ( x , t ) + f ′ ( u ( x , t ) 2 + v ( x , t ) 2 ) u ( x , t ) d x = 2 ∫ a b d d x v ( x , t ) u x ( x , t ) − u ( x , t ) v x ( x , t ) d x = 0 ,
because of the periodic boundary conditions.

2.1. Space semi-discretization

Since u ( x , t ) and v ( x , t ) in (2) are assumed to be periodic functions of x ∈ [ a , b ] , we consider their expansion in space along the following orthonormal basis on [ a , b ] :2
ω 2 j ( x ) = 2 − δ j 0 b − a cos j x − a b − a 2 π , ω 2 j + 1 ( x ) = 2 b − a sin ( j + 1 ) x − a b − a 2 π , j = 0 , 1 , 2 , … ,
so that
∫ a b ω i ( x ) ω j ( x ) = δ i j , i , j = 0 , 1 , 2 , … ,
with δ i j denoting, as usual, the Kronecker delta. One then obtains that, for suitable time-dependent coefficients q j ( t ) , p j ( t ) , j ≥ 0 ,
u ( x , t ) = ∑ j ≥ 0 q j ( t ) ω j ( x ) , v ( x , t ) = ∑ j ≥ 0 p j ( t ) ω j ( x ) ,
which can be more compactly rewritten, by introducing the infinite vectors
ω ( x ) = ω 0 ( x ) ω 1 ( x ) ω 2 ( x ) ⋮ , q ( t ) = q 0 ( t ) q 1 ( t ) q 2 ( t ) ⋮ , p ( t ) = p 0 ( t ) p 1 ( t ) p 2 ( t ) ⋮ ,
as
u ( x , t ) = ω ( x ) ⊤ q ( t ) , v ( x , t ) = ω ( x ) ⊤ p ( t ) .
Further, by considering that
ω ′ ( x ) = D 1 ω ( x ) , ω ′ ′ ( x ) = D 1 2 ω ( x ) ≡ − D ω ( x ) ,
where, by setting hereafter I r the identity matrix of dimension r, and with reference to the matrix J defined in (6),
D 1 = 2 π b − a 0 1 · J 2 · J ⋱ , D = 4 π 2 ( b − a ) 2 0 1 2 · I 2 2 2 · I 2 ⋱ , D 1 = − D 1 ⊤ , D = D ⊤ ,
one deduces that it is possible to rewrite (3) as:
ω ( x ) ⊤ q ˙ ( t ) = ω ( x ) ⊤ D p ( t ) − f ′ ( ω ( x ) ⊤ q ( t ) ) 2 + ( ω ( x ) ⊤ p ( t ) ) 2 ω ( x ) ⊤ p ( t ) , ω ( x ) ⊤ p ˙ ( t ) = − ω ( x ) ⊤ D q ( t ) + f ′ ( ω ( x ) ⊤ q ( t ) ) 2 + ( ω ( x ) ⊤ p ( t ) ) 2 ω ( x ) ⊤ q ( t ) ,
with
ω ( x ) ⊤ q ( 0 ) = u 0 ( x ) , ω ( x ) ⊤ p ( 0 ) = v 0 ( x ) , x ∈ [ a , b ] .
Considering that
∫ a b ω ( x ) ω ( x ) ⊤ d x = I ,
the infinite dimensional identity matrix, left multiplication of the above equations by ω ( x ) then gives the following infinite system of ODEs (hereafter, we shall omit the argument t for q and p ):
q ˙ = D p − ∫ a b ω ( x ) f ′ ( ω ( x ) ⊤ q ) 2 + ( ω ( x ) ⊤ p ) 2 ω ( x ) ⊤ p d x , p ˙ = − D q + ∫ a b ω ( x ) f ′ ( ω ( x ) ⊤ q ) 2 + ( ω ( x ) ⊤ p ) 2 ω ( x ) ⊤ q d x , t ∈ [ 0 , T ] .
with the initial conditions:
q ( 0 ) = ∫ a b ω ( x ) u 0 ( x ) d x , p ( 0 ) = ∫ a b ω ( x ) v 0 ( x ) d x .
The following result holds true.
Theorem 1. 
The ODE system (16) is Hamiltonian w.r.t. the Hamiltonian
H ( q , p ) = 1 2 q ⊤ D q + p ⊤ D p − ∫ a b f ( ω ( x ) ⊤ q ) 2 + ( ω ( x ) ⊤ p ) 2 d x .
This latter, in turn, is equivalent to the Hamiltonian functional (5).
Proof. 
Since
q ˙ = ∂ ∂ p H ( q , p ) , p ˙ = − ∂ ∂ q H ( q , p ) ,
the first part of the statement clearly holds true. The second part follows from (12)–(15), considering that D = D 1 ⊤ D 1 , so that
q ⊤ D q = q ⊤ D 1 ⊤ D 1 q = ∫ a b q ⊤ D 1 ⊤ ω ( x ) ω ( x ) ⊤ D 1 q d x = ∫ a b ω ( x ) ⊤ D 1 q 2 d x = ∫ a b u x ( x , t ) 2 d x ,
and, similarly,
p ⊤ D p = ∫ a b v x ( x , t ) 2 d x .
  □
By using similar arguments, it is possible to prove the following result.
Theorem 2. 
The two functionals (8) and (9) can be rewritten, respectively, as:
M 1 ( q , p ) = ∫ a b ( ω ( x ) ⊤ q ) 2 + ( ω ( x ) ⊤ p ) 2 d x , M 2 ( q , p ) = − 2 q ⊤ D 1 p ,
with D 1 the infinite matrix defined in (14).

2.2. Truncating the infinite expansion

Clearly, we cannot actually solve the infinite system of ODEs (16): in order to obtain a computational procedure, we need to truncate the infinite expansions (10) to finite sums. I.e., for a conveniently large N,
u ( x , t ) = ∑ j = 0 2 N q j ( t ) ω j ( x ) , v ( x , t ) = ∑ j = 0 2 N p j ( t ) ω j ( x ) ,
where, for sake of brevity, hereafter we continue to use the same symbols u and v to denote the truncated approximations. Consequently, the infinite vectors in (11) are replaced with the following truncated ones,
ω ( x ) = ω 0 ( x ) ω 1 ( x ) ⋮ ω 2 N ( x ) , q ( t ) = q 0 ( t ) q 1 ( t ) ⋮ q 2 N ( t ) , p ( t ) = p 0 ( t ) p 1 ( t ) ⋮ p 2 N ( t ) .
In so doing (12) and (13) continue formally to hold, upon replacing the infinite matrices (14) with the following truncated ones of dimension ( 2 N + 1 ) × ( 2 N + 1 ) :
D 1 = 2 π b − a 0 1 · J ⋱ N · J , D = 4 π 2 ( b − a ) 2 0 1 2 · I 2 ⋱ N 2 · I 2 .
As is clear, the functions u ( x , t ) and v ( x , t ) in (20) belong, for each fixed t, to the finite-dimensional functional subspace   V N = span ω 0 ( x ) , ω 1 ( x ) , … , ω 2 N ( x ) ,  and will no longer, in general, satisfy the original continuous equations (3). However, by requiring the corresponding residual be orthogonal to V N , one formally retrieves again the equations (16)-(17) which, now, amount to a Hamiltonian system of ( 4 N + 2 ) ODEs with the Hamiltonian formally still given by (18) and mass and momentum given by (19), respectively.
We shall discuss the efficient numerical solution of the new finite-dimensional ODE-IVP (16)-(17) in the next sections. Preliminarily, we mention that:
  • the value of N is generally very large, in view of obtaining a spectrally accurate space semi-discretization;
  • having fixed N, the composite trapezoidal rule over the equally spaced points
    x i = a + i b − a m , i = 0 , 1 , … , m , m : = 2 N + 1 ,
    is conveniently used to retrieve the Fourier coefficients in (20). In fact, as an example,
    q j ( t ) = ∫ a b ω j ( x ) u ( x , t ) d x = ∑ k = 0 2 N q k ( t ) ∫ a b ω j ( x ) ω k ( x ) d x ,
    with the latter integrands being, by virtue of the prosthaphaeresis formulae, trigonometric polynomials of degree at most 2 N . Consequently, the composite trapezoidal rule over 2 N + 2 ≡ m + 1 equally spaced points is exact for computing them [93, page 155].3 Consequently, with reference to (23), and taking into account of the periodicity of the functions, one has:
    ∫ a b ω j ( x ) ω k ( x ) d x = 1 m ∑ i = 0 m − 1 ω j ( x i ) ω k ( x i ) = δ j k , ∀ j , k = 0 , … , 2 N ≡ m − 1 .
    Similar arguments apply, of course, for retrieving p j ( t ) .
For sake of completeness, let us give some more operative detail about the latter point. Because of the periodic boundary conditions, according to what exposed above, with reference to (20) one obtains (see (23)):
q j ( t ) = 1 m ∑ i = 0 m − 1 ω j ( x i ) u ( x i , t ) , p j ( t ) = 1 m ∑ i = 0 m − 1 ω j ( x i ) v ( x i , t ) , j = 0 , … , 2 N .
These quantities can be efficiently computed via the inverse DFT (e.g., the Matlab© function ifft) of the vectors
u = ( u ( x 0 , t ) , … , u ( x m − 1 , t ) ) and v = ( v ( x 0 , t ) , … , v ( x m − 1 , t ) ) ,
respectively. Specifically, considering that m − 1 = 2 N , if
( ϕ 0 , … , ϕ 2 N ) : = ifft ( u ) and ( ξ 0 , … , ξ 2 N ) : = ifft ( v ) ,
then, by using a Matlab© -like formalism, and avoiding for sake of brevity the argument t,
q 0 = ϕ 0 , q 2 j − 1 = 2 · imag ( ϕ j ) , q 2 j = 2 · real ( ϕ j ) , j = 1 , … , N ,
and, similarly,
p 0 = ξ 0 , p 2 j − 1 = 2 · imag ( ξ j ) , p 2 j = 2 · real ( ξ j ) , j = 1 , … , N .
Conversely, if (see (23))
μ = ( μ 0 , … , μ m − 1 ) : = real ( fft ( [ 0 , q 2 + i q 1 , … , q 2 N + i q 2 N − 1 ] , m ) )
and
χ = ( χ 0 , … , χ m − 1 ) : = real ( fft ( [ 0 , p 2 + i p 1 , … , p 2 N + i p 2 N − 1 ] , m ) ) ,
then (see (25)),
u = q 0 + 2 · μ , and v = p 0 + 2 · χ .
One then concludes that the evaluation of the Fourier coefficients, as well as the reconstruction of the approximated solution, can be done with a complexity of O ( m log m ) floating-point operations: this, in turn, allows using large values of N.

3. Hamiltonian Boundary Value Methods

In order to obtain a fully discrete method, we now consider the numerical solution of problem (16)-(17). In view of a more compact representation, let us introduce the block vector (see (21) and (23))
y = q p ∈ R 2 m ,
and denote by H ( y ) : = H ( q , p ) the Hamiltonian (18). Consequently, we can rewrite (16)-(17) as
y ˙ = J m ∇ H ( y ) , t ∈ [ 0 , T ] , y ( 0 ) = y 0 : = q ( 0 ) p ( 0 ) ,
having set (see (6))
J m : = J ⊗ I m ≡ I m − I m = − J m ⊤ .
Since
d d t H ( y ) = ∇ H ( y ) ⊤ y ˙ = ∇ H ( y ) ⊤ J m ∇ H ( y ) = 0 ,
due to the skew-symmetry of J m , we again retrieve the conservation of H and, hence, our aim is to derive energy-conserving methods, i.e., able to conserve the energy along the numerical trajectory. Such methods are derived within the so called framework of line integral methods (see, e.g., the monograph [67] or the review paper [72] ). In more details, if h is the considered timestep, we shall look for a suitable path σ such that:
σ ( 0 ) = y 0 , σ ( h ) = : y 1 ≈ y ( h ) , ∫ 0 1 ∇ H ( σ ( c h ) ) ⊤ σ ˙ ( c h ) d c = 0 .
These properties imply energy-conservation, since
H ( y 1 ) − H ( y 0 ) = H ( σ ( h ) ) − H ( σ ( 0 ) ) = h ∫ 0 1 ∇ H ( σ ( c h ) ) ⊤ σ ˙ ( c h ) d c = 0 .
Remark 1. 
We observe that for the continuous solution (28) the last property in (29) derives from the fact that the integrand identically vanishes. This is no more the case for the path σ characterizing the given method (29).
A straightforward way to derive paths satisfying (29) relies on the expansion of the vector field (27) along a suitable orthonormal basis, which we choose as the Legendre polynomial basis { P j } j ≥ 0 [68,71]:
P i ∈ Π i , ∫ 0 1 P i ( x ) P j ( x ) d x = δ i j , i , j = 0 , 1 , 2 , … ,
where, as usual, Π i denotes the vector space of polynomials of degree i. In so doing, one obtains:
y ˙ ( c h ) = ∑ j ≥ 0 P j ( c ) γ j ( y ) , c ∈ [ 0 , 1 ] , y ( 0 ) = y 0 ,
with the Fourier coefficients given by:
γ j ( y ) = J m ∫ 0 1 P j ( τ ) ∇ H ( y ( τ h ) ) d τ , j = 0 , 1 , 2 , … .
Integrating (31) side by side, and imposing the initial condition, one then obtains:
y ( c h ) = y 0 + h ∑ j ≥ 0 ∫ 0 c P j ( x ) d x γ j ( y ) , c ∈ [ 0 , 1 ] .
In particular, by taking into account (30) and (27),
y ( h ) = y 0 + h γ 0 ( y ) ≡ y 0 + h J m ∫ 0 1 ∇ H ( y ( τ h ) ) d τ ≡ y 0 + ∫ 0 h y ˙ ( t ) d t ,
i.e., one retrieves the usual Fundamental Theorem of Calculus. Concerning the Fourier coefficients (32), the following general result holds true.
Lemma 1. 
Let G : [ 0 , h ] → V , with V a vector space, admit a Taylor expansion at 0. Then,
∫ 0 1 P j ( τ ) G ( τ h ) d τ = O ( h j ) , j = 0 , 1 , 2 , … .
Proof. 
See [71, Lemma 1]. □
More in general, it can be proved the following, more general, result whose proof is omitted.
Lemma 2. 
Let G : [ 0 , h ] → V , with V a vector space, admit a Taylor expansion at 0 with remainder at the O ( h k ) term. Then,
∫ 0 1 P j ( τ ) G ( τ h ) d τ = O ( h min { j , k } ) , j = 0 , 1 , 2 , … .
In order to obtain a polynomial approximation σ ∈ Π s to y ( c h ) , it is enough truncating the infinite series in (31) and (33) to finite sums with s terms:
σ ˙ ( c h ) = ∑ j = 0 s − 1 P j ( c ) γ j ( σ ) , c ∈ [ 0 , 1 ] , σ ( 0 ) = y 0 ,
and
σ ( c h ) = y 0 + h ∑ j = 0 s − 1 ∫ 0 c P j ( x ) d x γ j ( σ ) , c ∈ [ 0 , 1 ] .
with γ j ( σ ) defined, similarly as in (32), as
γ j ( σ ) = J m ∫ 0 1 P j ( τ ) ∇ H ( σ ( τ h ) ) d τ , j = 0 , … , s − 1 .
In such a case, according to (29), the new approximation is given by
y 1 : = σ ( h ) = y 0 + h γ 0 ( σ ) .
As stated in the next theorem, the approximation procedure is energy-conserving.
Theorem 3. 
With reference to (18), (26)-(27), and (29), one has: H ( y 1 ) = H ( y 0 ) .
Proof. 
By virtue of (34), and taking into account (36), one obtains:
H ( y 1 ) − H ( y 0 ) = H ( σ ( h ) ) − H ( σ ( 0 ) ) = h ∫ 0 1 ∇ H ( σ ( c h ) ) ⊤ σ ˙ ( c h ) d c             = h ∫ 0 1 ∇ H ( σ ( c h ) ) ⊤ ∑ j = 0 s − 1 P j ( c ) γ j ( σ ) d c             = h ∑ j = 0 s − 1 ∫ 0 1 P j ( c ) ∇ H ( σ ( c h ) ) d c ⊤ J m ∫ 0 1 P j ( c ) ∇ H ( σ ( c h ) ) d c = 0 ,
due to the skew-symmetry of J m . □
Further, the following result can be proved, stating that we have derived an order 2 s approximation procedure.
Theorem 4. 
With reference to (26) and (29), one has: y 1 = y ( h ) + O ( h 2 s + 1 ) .
Proof. 
See [71, Theorem 1]. □
Interestingly enough, the problem of determining σ can be cast into the problem of finding the Fourier coefficients γ j ( σ ) . In fact, from (35) and (36), one deduces the following system of (generally nonlinear) equations:
γ j ( σ ) = J m ∫ 0 1 P j ( c ) ∇ H y 0 + h ∑ ℓ = 0 s − 1 ∫ 0 c P ℓ ( x ) d x γ ℓ ( σ ) d c , j = 0 , … , s − 1 .
Once this system is solved, the new approximation is formally given by (37), as above explained.

3.1. Discretization of the Fourier coefficients

Quoting Dahlquist and Bijörk [94, page 521], as is well known, even many relatively simple integrals cannot be expressed in finite terms of elementary functions, and thus must be evaluated by numerical methods. Within our framework, this quite obvious statement means that we cannot in general directly compute the Fourier coefficients (36): instead, we can approximate them by using a suitable quadrature rule, which we choose as the Gauss-Legendre formula of order 2 k , for a convenient k ≥ s , with abscissae { c i } given by the zeros of P k , i.e., such that P k ( c i ) = 0 , i = 1 , … , k , and weights
b i = ∫ 0 1 ∏ j ≠ i c − c j c i − c j d c , i = 1 , … , k .
In so doing, we obtain:
γ ^ j : = J m ∑ i = 1 k b i P j ( c i ) ∇ H ( σ ( c i h ) ) ≡ γ j ( σ ) + Δ j ( h ) , j = 0 , … , s − 1 ,
with Δ j ( h ) the quadrature error. For sake of brevity, we shall continue to use the same symbol σ for the new polynomial approximation obtained by formally substituting γ ^ j to γ j ( σ ) , j = 0 , … , s − 1 , in (34) and (35), with the new approximation now given by
y 1 : = σ ( h ) = y 0 + h γ ^ 0 ,
in place of (37), and the discrete problem
γ ^ j = J m ∑ i = 1 k b i P j ( c i ) ∇ H y 0 + h ∑ ℓ = 0 s − 1 ∫ 0 c i P ℓ ( x ) d x γ ^ ℓ , j = 0 , … , s − 1 ,
in place of (38).
Definition 1. 
The method defined by (39)–(41) is named Hamiltonian Boundary Value Method with parameters k and s: in short,HBVM ( k , s ) .
Concerning the quadrature error in (39), it is quite straightforward to prove that, assuming a suitably regular Hamiltonian function H, i.e., f ( x ) in (18), then:
  • in the relevant case where f ∈ Π ν , with ν ≥ 1 ,4 then the integrand in (36) is a polynomial of degree at most:
    ( ν − 1 ) 2 s + 2 s − 1 = 2 ν s − 1 .
    Consequently, the quadrature is exact, provided that
    ν ≤ k / s ;
  • conversely, since the quadrature error is proportional to the 2 k -th derivative of the integrand, then
    Δ j ( h ) = O ( h 2 k − j ) , j = 0 , … , s − 1 .
The above arguments, allows us to state the following conservation result.
Theorem 5. 
With reference to (18) and (26), if f ∈ Π ν with ν satisfying (42), then H ( y 1 ) = H ( y 0 ) . Conversely, H ( y 1 ) = H ( y 0 ) + O ( h 2 k + 1 )
Proof. 
The first part of the statement follows from Theorem 3, due to the fact that the quadrature is exact. The second part follows similarly, by considering that, by virtue of Lemma 1,
∫ 0 1 P j ( c ) ∇ H ( σ ( c h ) ) d c = O ( h j ) , j = 0 , … , s − 1 .
Consequently, from (39) and (43) one has:
H ( y 1 ) − H ( y 0 ) = H ( σ ( h ) ) − H ( σ ( 0 ) ) = h ∫ 0 1 ∇ H ( σ ( c h ) ) ⊤ σ ˙ ( c h ) d c             = h ∫ 0 1 ∇ H ( σ ( c h ) ) ⊤ ∑ j = 0 s − 1 P j ( c ) γ ^ j d c             = h ∫ 0 1 ∇ H ( σ ( c h ) ) ⊤ ∑ j = 0 s − 1 P j ( c ) γ j ( σ ) + Δ j ( h ) d c             = h ∑ j = 0 s − 1 ∫ 0 1 P j ( c ) ∇ H ( σ ( c h ) ) d c ⊤ J m ∫ 0 1 P j ( c ) ∇ H ( σ ( c h ) ) d c                       + h ∑ j = 0 s − 1 ∫ 0 1 P j ( c ) ∇ H ( σ ( c h ) ) d c ⊤ Δ j ( h ) = h ∑ j = 0 s − 1 O ( h j ) O ( h 2 k − j ) = O ( h 2 k + 1 ) ,
due to the skew-symmetry of J m . □
Remark 2. 
From the result of Theorem 5 it follows that:
● either an exact
● or apractical
energy conservation can always be gained, by choosing k large enough. In fact, in the latter case, it is enough that the energy error be within the roundoff error level.

3.2. Runge-Kutta form

The HBVM ( k , s ) method (39)–(41) can be seen to be a k-stage Runge-Kutta (RK) method. As matter of fact,
Y i : = σ ( c i h ) = y 0 + h ∑ ℓ = 0 s − 1 ∫ 0 c i P ℓ ( x ) d x γ ^ ℓ , i = 1 , … , k ,
can be regarded as its i-th stage. In fact, by plugging it at the r.h.s. that of (41), and considering (44), one obtains (by slightly adapting the indices) :
Y i = y 0 + h ∑ ℓ = 0 s − 1 ∫ 0 c i P ℓ ( x ) d x ∑ j = 1 k b j P ℓ ( c j ) J m ∇ H ( Y j ) = y 0 + h ∑ j = 1 k b j ∑ ℓ = 0 s − 1 ∫ 0 c i P ℓ ( x ) d x P ℓ ( c j ) ︸ = : a i j J m ∇ H ( Y j ) , i = 1 , … , k ,
with the new approximation given, considering that P 0 ( c ) ≡ 1 , by:
y 1 = y 0 + h ∑ i = 1 k b i J m ∇ H ( Y i ) .
Consequently, by setting b = ( b 1 , … , b k ) ⊤ and c = ( c 1 , … , c k ) ⊤ the vectors of the weights and the abscissae of the quadrature, and A = ( a i j ) ∈ R k × k (see (45)) the Butcher matrix, we have derived the k-stage RK method
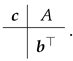
Preprints 91392 i001
Moreover, concerning the Butcher matrix, the following result holds true.
Theorem 6. 
Setting the matrices
P s = P 0 ( c 1 ) … P s − 1 ( c 1 ) ⋮ ⋮ P 0 ( c k ) … P s − 1 ( c k ) , Ω = b 1 ⋱ b k , I s = ∫ 0 c 1 P 0 ( x ) d x … ∫ 0 c 1 P s − 1 ( x ) d x ⋮ ⋮ ∫ 0 c k P 0 ( x ) d x … ∫ 0 c k P s − 1 ( x ) d x ,
one has that the Butcher matrix in (47) is given by:
A = I s P s ⊤ Ω .
Proof. 
The statement immediately follows by considering the ( i , j ) -th entry of the matrices at each member of (49). □
By defining the block vectors
Y = Y 1 ⋮ Y k , ∇ H ( Y ) = ∇ H ( Y 1 ) ⋮ ∇ H ( Y k ) ,
and e = ( 1 , … , 1 ) ⊤ ∈ R k , the stage equations (45) can be cast in vector form, by virtue of (49), as
Y = e ⊗ y 0 + h I s P s ⊤ Ω ⊗ J m ∇ H ( Y ) .
This latter equation can be, in turn, rewritten as
Y = e ⊗ y 0 + h I s ⊗ I 2 m γ ^ ,
having set (see (41) and (44))
γ ^ ≡ γ ^ 0 ⋮ γ ^ s − 1 = P s ⊤ Ω ⊗ J m ∇ H ( Y ) ,
the block vector with the (approximate) Fourier coefficients (41). By combining the last two equations, one then obtains
γ ^ = P s ⊤ Ω ⊗ J m ∇ H e ⊗ y 0 + h I s ⊗ I 2 m γ ^ .
Remark 3. 
In other words, even though a HBVM ( k , s ) method is a k-stage RK method and, therefore, its stage equation (50) has (block)-dimension k, the actual discrete problem to be solved at each time-step can be cast as (51), thus having (block)-dimension s,independentlyof k.
What exposed above, in turn, allows using relatively large values of k, in view of getting an (either exact of practical) conservation of the Hamiltonian, according to Theorem 5. The efficient solution of the discrete problem (51) will be discussed in Section 4.
We conclude this section by reporting the following additional result, concerning a HBVM ( k , s ) method. For the corresponding proofs we refer, .e.g., to the monograph [67].
Theorem 7. 
For all k ≥ s , a HBVM ( k , s ) method is symmetric and has order 2 s . When k = s it reduces to the s-stage Gauss-collocation method.

3.3. HBVMs as spectral methods in time

An interesting interpretation of HBVMs is that they can be regarded as spectral methods in time. In more detail, let us recall the expansion (31)-(32). Assuming that y ˙ ∈ L 2 [ 0 , h ] , it then follows that
∥ y ˙ ∥ L 2 2 = ∑ j ≥ 0 ∥ γ j ( y ) ∥ 2 < ∞ ⇒ ∥ γ j ( y ) ∥ → 0 , j → ∞ .
Consequently, if we are using a finite precision arithmetic with machine epsilon ε , and we choose the degree s of the polynomial approximation σ in (34)–(36) such that
∀ j ≥ s : ∥ γ j ( y ) ∥ < ε · max i = 0 , … , s − 1 ∥ γ i ( y ) ∥ ,
it then follows that
σ ( c h ) ≐ y ( c h ) , c ∈ [ 0 , 1 ] ,
where ≐ means equal within roundoff errors.
Definition 2. 
We shall refer to a HBVM ( k , s ) method such that k and s, with k > s , are large enough such that (see (36) and (39)) both
γ ^ j ≐ γ j ( σ ) , j = 0 , … , s − 1 ,
and (52) hold true, so that (53) follows, as a Spectral HBVMor, in short, SHBVM.5
The use of HBVMs as spectral methods in time has been studied in [95]. In particular, the choice of s has been investigated in [96], whereas, hereafter we shall consider the following choice for k [89]:
k = max { 20 , s + 2 } .

4. Efficient application of HBVMs to the NLSE

Solving the discrete problem (51) could be, in general, a severe computational issue, because of many reasons:
  • the high dimensionality, 2 m = 4 N + 2 (see (23), (24), and (26)), of the state space, if a spectrally accurate space semi-discretization is targeted;
  • the possible large (block)-size s of γ ^ , in view of the use of HBVMs as spectral methods in time;
  • the unpractical use of (51) to derive a straightforward fixed-point iteration, which would require the use of a very small stepsize h.
Consequently, we need an efficient Newton-type iteration for this purpose. To begin with, let us start considering the simplified Newton iteration for solving
G ( γ ^ ) : = γ ^ − P s ⊤ Ω ⊗ J m ∇ H e ⊗ y 0 + h I s ⊗ I 2 m γ ^ = 0 ,
which, in view of the fact that (see (48))
P s ⊤ Ω I s = ξ 0 − ξ 1 ξ 1 0 ⋱ ⋱ ⋱ − ξ s − 1 ξ s − 1 0 = : X s , ξ i = 1 2 | 4 i 2 − 1 | ,
reads
I 2 s m − h X s ⊗ J m ∇ 2 H ( y 0 ) Δ γ ^ r = − G ( γ ^ r ) , r = 0 , 1 , 2 , … ,
with γ ^ 0 = 0 a convenient initial guess. In this form, the iteration (57) would require the factorization of a 2 s m × 2 s m matrix at each time-step, which would be too expensive.
In this respect, a first improvement can be obtained by observing that the problem (16) has a leading linear part, according to (22), when N is large (as in the case when dealing with a spectrally accurate space semi-discretization). Consequently, we could consider the approximation
∇ 2 H ( y 0 ) ≈ J ⊗ D ,
with matrix J defined in (6). In so doing (57) simplifies to
I 2 s m − h X s ⊗ J ⊗ D Δ γ ^ r = − G ( γ ^ r ) , r = 0 , 1 , … ,
which has the advantage of having the same coefficient matrix for all time-steps. As is clear, however, this matrix has still dimension 2 s m × 2 s m , which can be again unpractical, when using HBVMs as SHBVMs, and considering that its factors are in general full.
The second, and more decisive, improvement can be obtained via a blended iteration for solving (58). The basic idea, which has been initially developed in a series of papers (see [97,98,99,100]) focused on block implicit methods for ODEs, and adapted in [101] (see also [102]) for HBVMs, relies on the combination of the equation (58) with an equivalent formulation, i.e.,
ρ s X s − 1 ⊗ I 2 m − h I s ⊗ J ⊗ D Δ γ ^ r = − ρ s X s − 1 ⊗ I 2 m G ( γ ^ r ) , r = 0 , 1 , … ,
with the scalar parameter ρ s defined as 6
ρ s = min λ ∈ σ ( X s ) | λ | ,
combined (i.e., blended) with weights
I s ⊗ Γ and I s ⊗ ( I 2 m − Γ ) ,
respectively, where
Γ = I 2 m − h ρ s J ⊗ D − 1 .
The good news is now twofold:
  • in so doing, the inverse of the coefficient matrix, required by the iterative procedure, can be seen to be given by I s ⊗ Γ , i.e., the same matrix defined above;
  • moreover, Γ is a very sparse matrix. As matter of fact, one directly verifies that:
    Γ = I 2 ⊗ ( I m + B 2 ) − 1 + J ⊗ B ( I m + B 2 ) − 1 , B = h ρ s D ,
    which can be stored in two vectors, containing the main diagonals of ( I m + B 2 ) − 1 and B ( I m + B 2 ) − 1 , respectively.
For sake of completeness, the resulting final algorithm is listed in Table 1, where we assume that Γ has been computed (once for all time-steps) through (60)-(61).
Remark 4. 
It must be stressed that, in order to obtain energy-conservation and spectral accuracy in time, the blendediteration in Table 1 has to be carried out until full machine accuracy is gained. This is, indeed, the implementation considered in the numerical tests.

5. Numerical examples

We now report a few numerical results, aimed at assessing the theoretical findings, and proving the effectiveness of HBVMs, especially when used as SHBVMs. All numerical tests have been carried out in Matlab© (Rel. 2023b) using a Silicon M2-based computer, with 16 GB of shared memory.

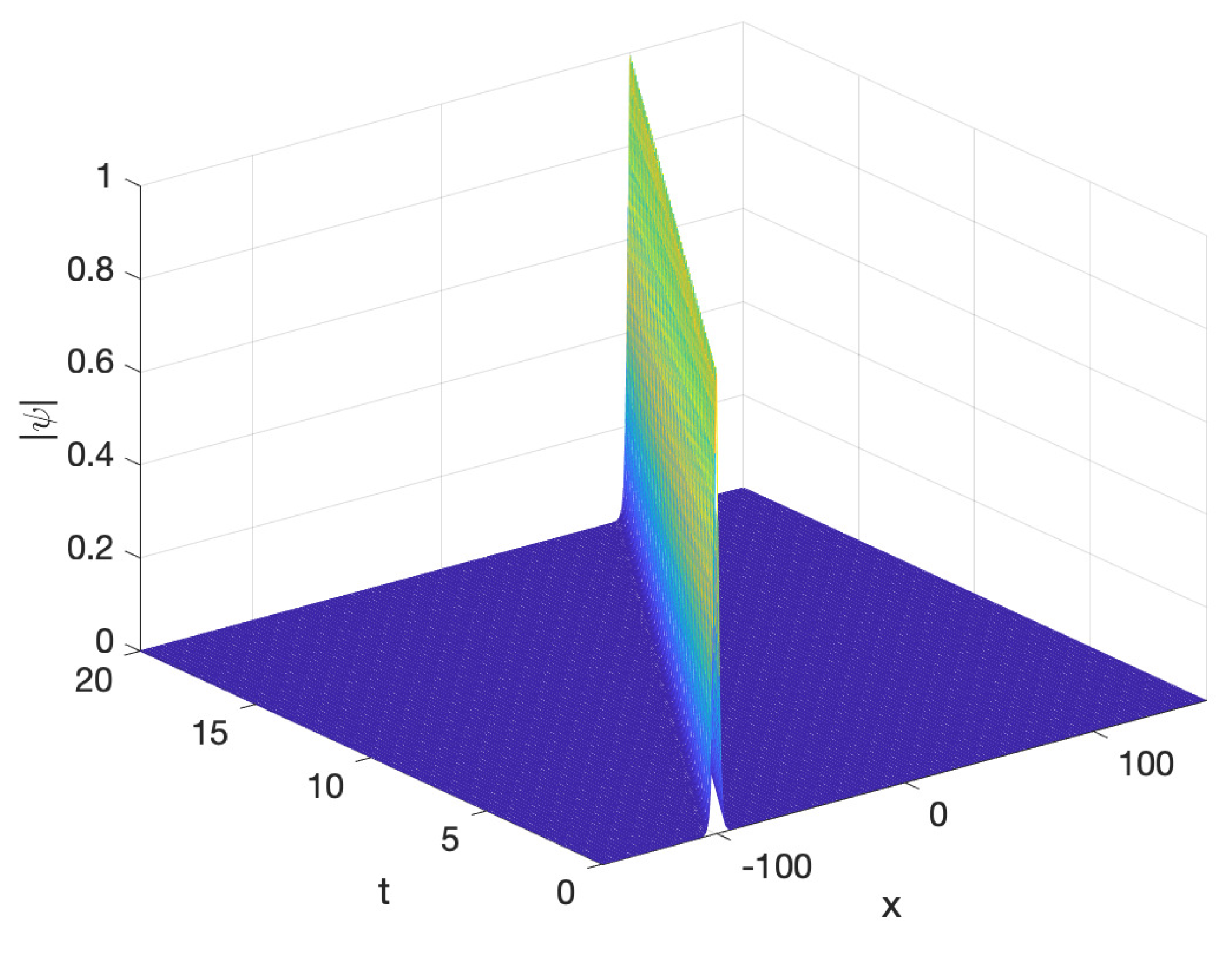
5.1. Example 1

The first test problem is given by the so called focusing case of the classical NLSE, for which f ( x ) = x 2 in (1). In such a case, the initial condition at t = 0 is taken from the (known) solution,
ψ ( x , t ) = sech ( x − x 0 − 2 κ t ) exp ( i ( ( 1 − κ 2 ) t + κ x ) ) , ( x , t ) ∈ [ − 160 , 160 ] × [ 0 , 20 ] ,
where we have used the parameters x 0 = − 100 and κ = 5 . Such solution, named bright soliton [18,103], is depicted in Figure 1.
We observe that, since f ( x ) is a polynomial of degree 2, then any HBVM ( 2 s , s ) is exactly energy-conserving and of order 2 s , according to Theorems 5 and 7. In particular, in such a case the HBVM(2,1) method coincides with the so called AVF method[70], used for solving the semi-discrete Hamiltonian problem (16)-(17). We shall solve the problem over the given time interval [ 0 , 20 ] by using the following methods (all implemented in the same code):
  • HBVM(2,1) (i.e., the AVF method), with stepsizes h = 2 − n 10 − 1 , n = 3 , 4 … , 12 ;
  • HBVM(4,2), with stepsizes h = 2 − n 10 − 1 , n = 1 , 2 … , 8 ;
  • HBVM(6,3), with step sizes h = 2 − n 10 − 1 , n = 0 , 1 … , 6 ;
  • HBVM(20,18), which is spectrally accurate in time, when using the stepsize h = 0.1 (i.e., it provides a SHBVM).
For all such methods we use a value of N = 1200 in (20)–(23). Consequently, we obtain a system of 4802 Hamiltonian ODEs (16). By using this value of N, the space semi-discretization error falls within the double precision IEEE roundoff error level. Further, the constant values of Hamiltonian, mass, and momentum in (18) and (19) are respectively given by:
H = 74 3 , M 1 = 2 , M 2 = − 1 32 .
We also compare the previous methods with the two explicit symplectic composition methods described in [37], coupling the standard second-order difference of the second space-derivative, with parameter Δ x , with a composition method of order 1 (S1) or 2 (S2) in time, so that, when using a stepsize Δ t , the error is either O ( Δ x 2 + Δ t ) or O ( Δ x 2 + Δ t 2 ) , respectively. However, because of stability constraints, Δ t is not independent of Δ x . In particular, we use Δ t = 1 2 Δ x 2 . Consequently, both methods are actually only first order accurate, since the error is O ( Δ x 2 ) = O ( Δ t ) for both of them. In light of this, we consider the methods S1 and S2 with discretization parameters:
Δ x = 0.32 n , Δ t = 1 2 0.32 n 2 , n = 5 , 10 , 20 , 40 , 80 ,
so that we have a space semi-discretization with 10 3 n + 1 points, for a total of [ 20 / Δ t ] timesteps, where [ · ] denotes the rounding of the argument. For all methods, we compare the errors in the last timestep.
The two plots in Figure 2 show the obtained results:
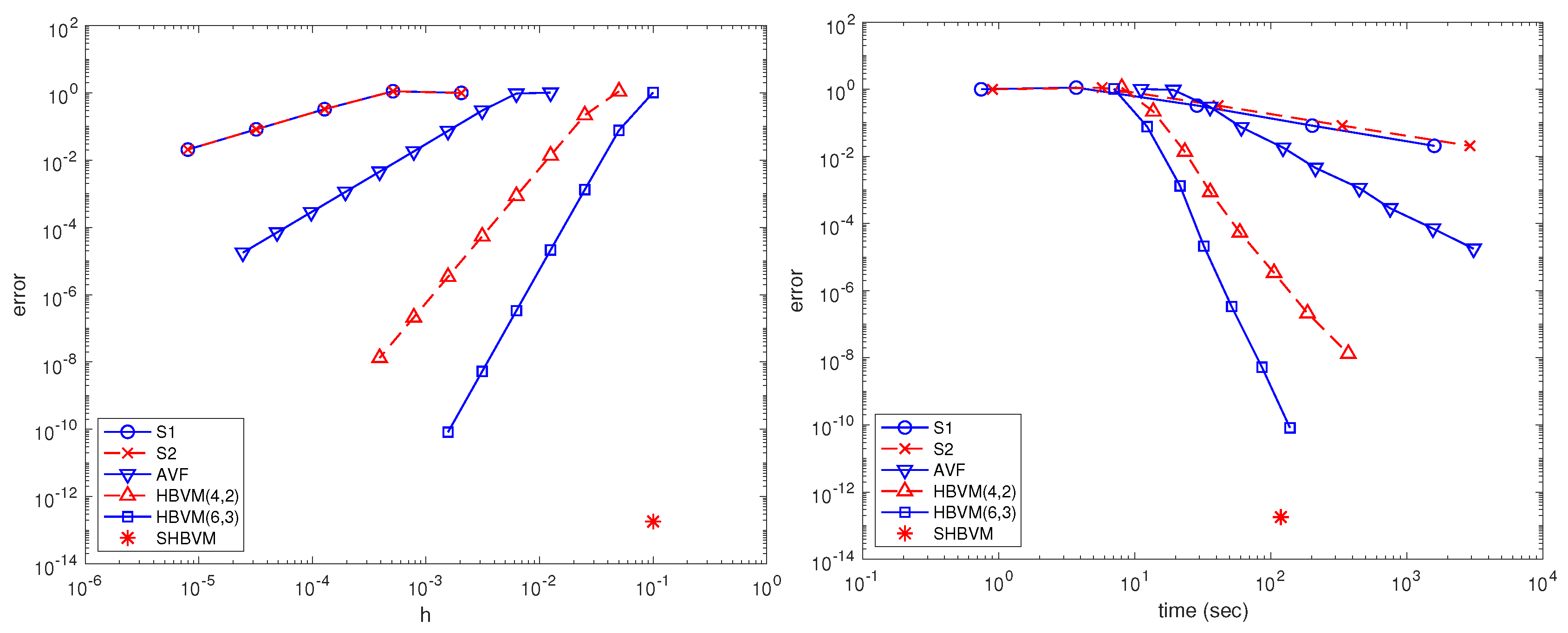
  • in the left-plot, we have the error versus the used stepsize, showing the predicted order:
    -
    1 for S1 and S2,
    -
    2 for HBVM(2,1) (i.e., the AVF method),
    -
    4 for HBVM(4,2),
    -
    6 for HBVM(6,3).
    Clearly, the SHBVM reaches full machine accuracy for the considered stepsize;
  • in the right-plot, we have the so called work-precision diagram, where the errors are plotted against the execution times (in sec). As one may see, the higher the order of the method, the better its performance, with the SHBVM reaching full accuracy in a moderate time.
From the obtained results, it clearly follows that the SHBVM is the method with the best performance. This conclusion is further confirmed by the plots in Figure 3, where there are:
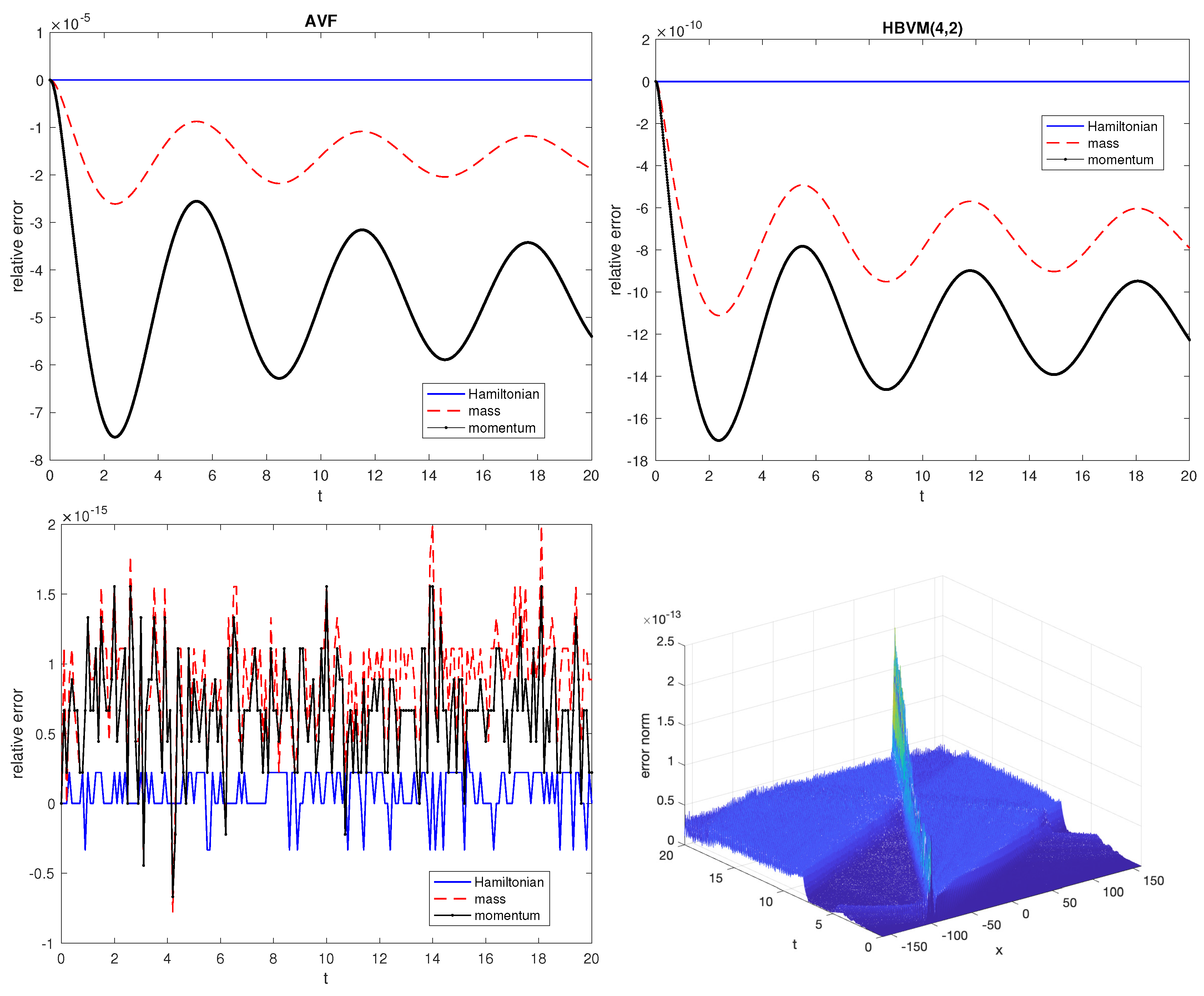
  • the relative errors in the Hamiltonian, mass, and momentum for the AVF and HBVM(4,2) methods used with stepsize h = 10 − 2 (upper plots);
  • the relative errors in the invariants for the SHBVM used with stepsize h = 0.1 (lower left-plot), and the modulus of the absolute error (lower right-plot).
From the pictures, one can see that all methods are energy-conserving, as expected. However, the AVF and HBVM(4,2) methods only approximately conserve the other invariants (though with no drift), unlike the SHBVM, for which they are conserved up to roundoff. For this latter method, also the solution error can be seen to be within the roundoff error level.
Preprints 91392 g003
Figure 3. Example 1: errors in the invariants for the AVF and HBVM(4,2) methods used with stepsize h = 10 − 2 (upper plots); errors in the invariants (lower left-plot) and in the solution (lower right-plot) for SHBVM used with the stepsize h = 0.1 .
Figure 3. Example 1: errors in the invariants for the AVF and HBVM(4,2) methods used with stepsize h = 10 − 2 (upper plots); errors in the invariants (lower left-plot) and in the solution (lower right-plot) for SHBVM used with the stepsize h = 0.1 .
Preprints 91392 g003

5.2. Example 2

We now consider the same equation used in the first example, but with a different initial condition. Namely (compare with (62)),
ψ ( x , 0 ) = sech ( x − x 0 ) exp ( i κ x ) + sech ( x + x 0 ) exp ( − i κ x ) , x ∈ [ − 160 , 160 ] ,
with the same parameters x 0 = − 100 and κ = 5 considered for (62). In this case, we have two bright solitons that collide at t = 10 and emerge after the crossing. In such a case, the values of the invariants are (compare with (63)):
H = 148 3 , M 1 = 4 , M 2 = 0 .
As in the previous example, we solve the problem by using a trigonometric polynomial of degree N = 1200 for the space semi-discretization, and covering the time interval [ 0 , 20 ] by using a stepsize:
  • h = 10 − 2 , for the AVF (i.e., HBVM(2,1)) and HBVM(4,2) methods;
  • h = 0.1 , for the HBVM(20,18) method, thus obtaining a spectrally accurate space-time method (SHBVM).
The obtained results are depicted in Figure 4, where one may find:7
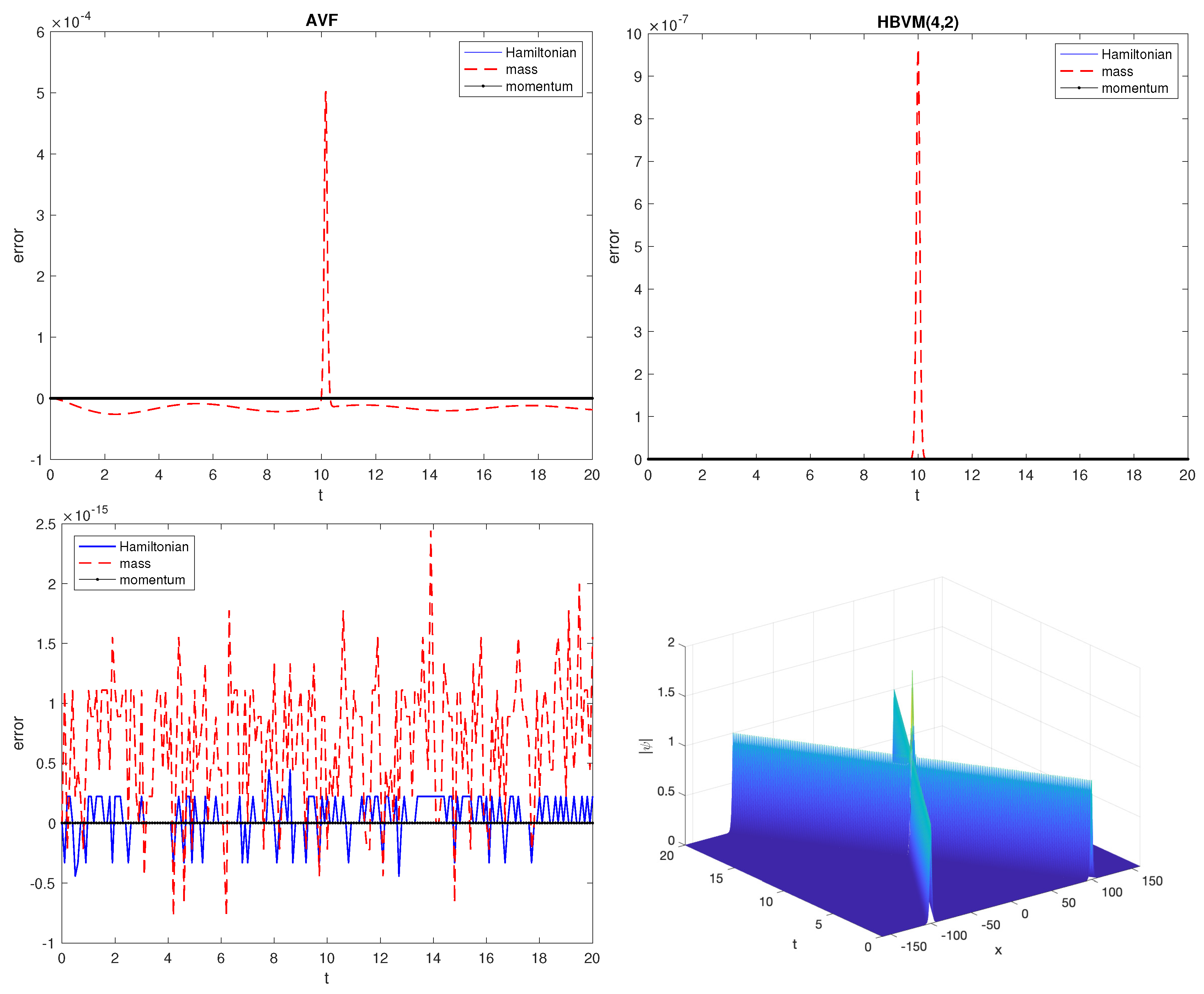
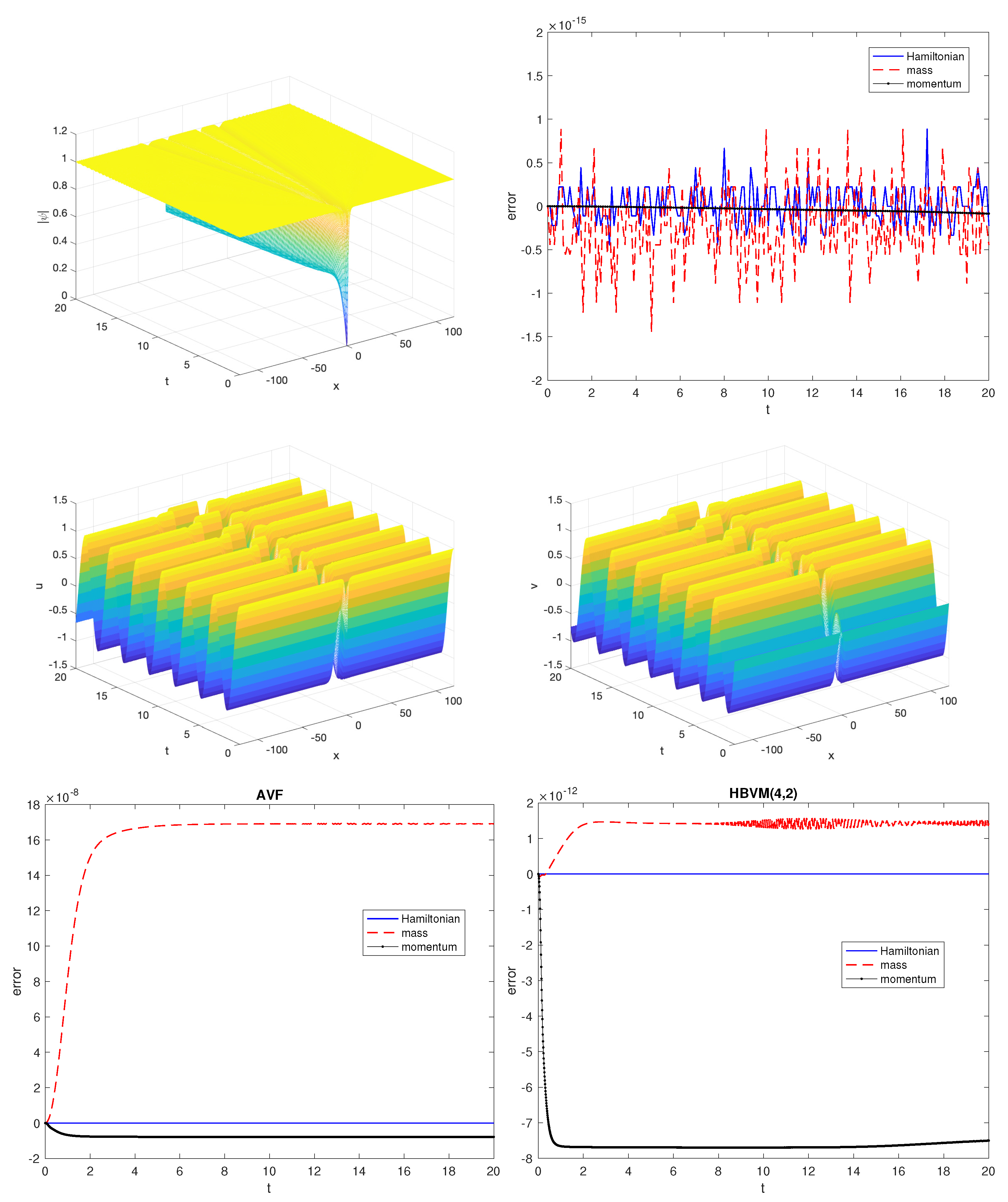
  • the errors in the invariants for the AVF and HBVM(4,2) methods (upper plots), which exactly conserve the energy H and the momentum M 2 , whereas there is a numerical “peak” in the mass M 1 , when the two solitons collide;
  • the errors in the invariants for the SHBVM method, along with the modulus of the computed solution, where one may see that the two solitons emerge after the collision at t = 10 (lower plots).
As one may see, the first two methods exhibit an artificial peak in the numerical mass, where the two solitons collide, whereas the SHBVM method has all the errors in the invariants within the roundoff error level and, remarkably enough, there are no peaks at t = 10 , where the two solitons cross.
Preprints 91392 g004
Figure 4. Example 2: errors in the invariants for the AVF and HBVM(4,2) methods used with stepsize h = 10 − 2 (upper plots, with the Hamiltonian and momentum errors, both within roundoff, overlapping); errors in the invariants and modulus of the computed solution for the SHBVM method used with stepsize h = 0.1 (lower plots).
Figure 4. Example 2: errors in the invariants for the AVF and HBVM(4,2) methods used with stepsize h = 10 − 2 (upper plots, with the Hamiltonian and momentum errors, both within roundoff, overlapping); errors in the invariants and modulus of the computed solution for the SHBVM method used with stepsize h = 0.1 (lower plots).
Preprints 91392 g004

5.3. Example 3

The next test problem is given by the so called defocusing case of the classical NLSE, for which f ( x ) = − x 2 in (1). It is known that this problem is much more challenging than the focusing case. The initial condition is taken as:
ψ ( x , 0 ) = ( 1 − sech ( x ) ) ( 1 − exp ( λ x 2 + i θ x ) ) , x ∈ [ − 120 , 120 ] .
We choose the parameters λ = − 2 and θ = 1 2 . The values of the invariants are given by:8
H ≈ 118 , M 1 ≈ 236 , M 2 ≈ 0 .
We solve this problem by using N = 1200 for the space semi-discretization and, for the time integration, a HBVM(22,20) with stepsize h = 0.1 for 200 timesteps (thus, covering the interval [ 0 , 20 ] ). The method turns out to be a SHBVM, for the considered stepsize. In Figure 5 we plot the obtained result: in the upper-left, the modulus of ψ ( x , t ) ; in the upper-right the errors in the invariants (relative, for the Hamiltonian and the mass, absolute for the momentum, according to (67)); in the middle plots are the real and imaginary parts of the solution, u and v, respectively; for comparison, we also plot the errors in the invariants for the AVF (i.e., HBVM(2,1)) and the HBVM(4,2) methods (lower plots), when using a stepsize h = 10 − 2 . As is clear, all methods conserve the energy, but the SHBVM exhibits a much better conservation of mass and momentum (always within the roundoff error level).

5.4. Example 4

As a last example, we consider the cubic-quintic nonlinear Schrödinger equation, introduced in the introduction (see also [104]), with f ( x ) = x 2 − 1 3 x 3 . We use the initial condition ψ ( x , 0 ) from (62), and the same space-time domain [ − 160 , 160 ] × [ 0 , 20 ] . In such a case, any HBVM ( 3 s , s ) method turns out to be energy conserving, according to Theorem 5. The values of the invariants are now given by:9
H ≈ 25 , M 1 = 2 , M 2 ≈ 0 .
In Figure 6 we plot the errors in the invariants for:10
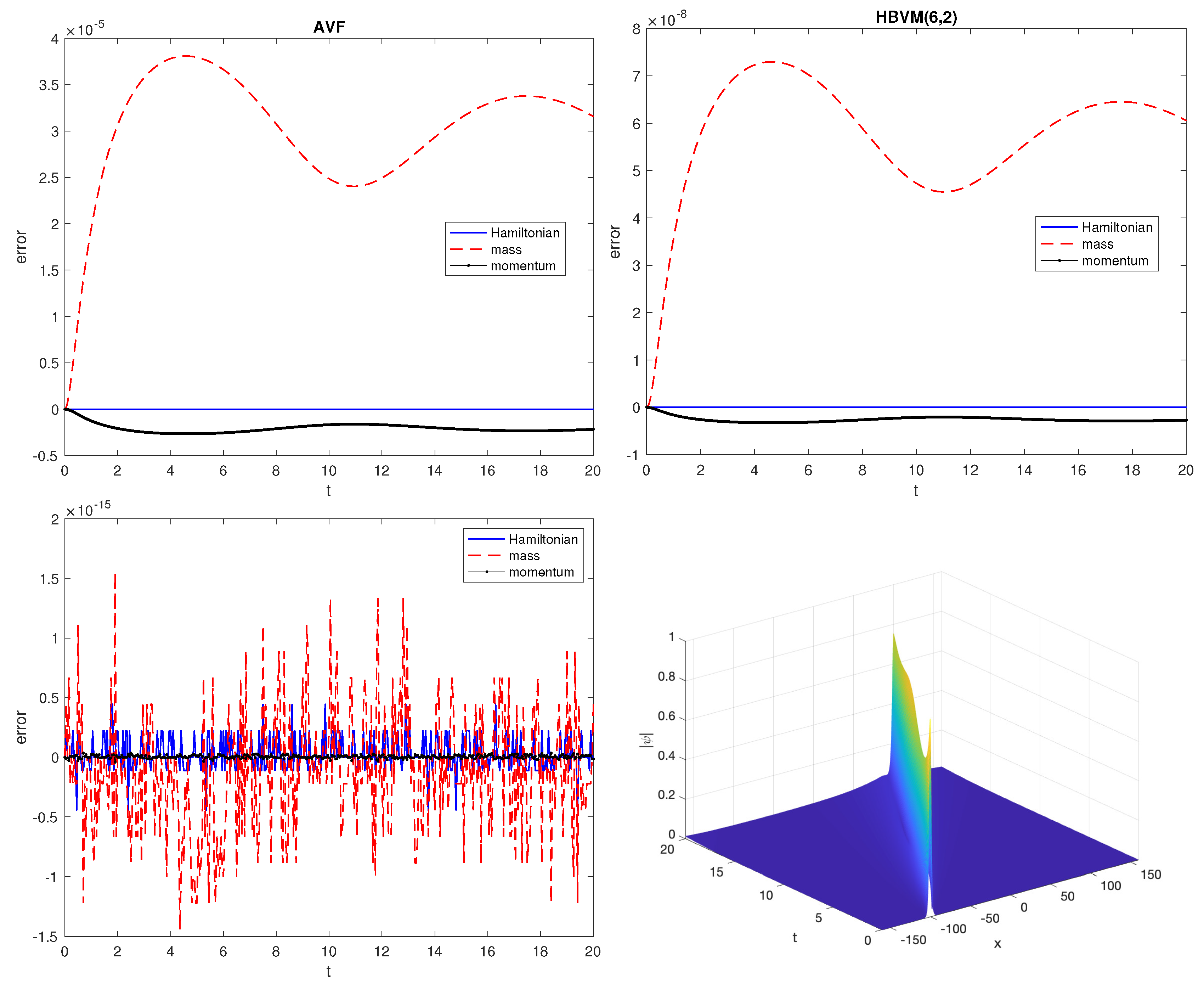
  • the AVF (i.e., HBVM(3,1)) and the HBVM(6,2) methods used with a stepsize h = 5 · 10 − 3 (upper plots);
  • the HBVM(20,18) method, which is spectrally accurate in time (i.e., it is a SHBVM), when using a stepsize h = 5 · 10 − 2 . We also plot the modulus of the computed solution (lower plots).
In all cases, we have used a trigonometric polynomial approximation of degree N = 1200 which, as in the case of the previous examples, turns out to provide a spectrally accurate space semi-discretization. From the obtained results, one infers that all methods are energy-conserving. However, only the SHBVM has all the errors in the invariants within the roundoff error level, whereas this is not the case for the other methods, though no numerical drift is observed.
Preprints 91392 g006
Figure 6. Example 4: errors in the invariants for the AVF and HBVM(6,2) methods used with stepsize h = 5 · 10 − 3 (upper plots); errors in the invariants (lower left-plot) and modulus of the computed solution (lower right-plot) for SHBVM used with the stepsize h = 5 · 10 − 2 .
Figure 6. Example 4: errors in the invariants for the AVF and HBVM(6,2) methods used with stepsize h = 5 · 10 − 3 (upper plots); errors in the invariants (lower left-plot) and modulus of the computed solution (lower right-plot) for SHBVM used with the stepsize h = 5 · 10 − 2 .
Preprints 91392 g006

6. Conclusions

In this paper, we have reviewed in major detail an effective approach for the numerical solution of the NLSE, when equipped with initial and periodic boundary conditions. After a space semi-discretization, obtained by using a classical Fourier expansion (because of the periodic boundary conditions), the time integration is carried out by using energy-conserving methods in the HBVMs class. The actual implementation of the methods, for the problem at hand, has been explained in full details. Also their use as spectral methods in time (SHBVM) has been recalled. In particular, the numerical tests here reported clearly show the advantage of SHBVMs over other existing methods. As a possible development of this approach, we mention the possibility of a parallel-in-time solution of the problem, following the approach in [105,106], as well as the extension to more space dimensions.

Funding

This research received no external funding.

Data Availability Statement

All used data are reported in the paper.

Conflicts of Interest

The authors declare no conflict of interest.

Notes

1
It is worth mentioning that the state-of-art Matlab© code hbvm.m is available at the web-site of the monograph [67],  http://web.math.unifi.it/users/brugnano/LIMbook/.
2
As is clear, this is nothing but the usual Fourier basis scaled and shifted in order to be orthonormal on the given interval [ a , b ] w.r.t. the usual L 2 inner product.
3
Actually, they reduce to m, with all unit weights, because of the periodic boundary conditions.
4
Actually, the case ν = 2 is referred to as the “classical” NLSE.
5
As is clear, both conditions are required, for (53) to hold true.
6
As is usual, σ ( X s ) denotes the spectrum of matrix X s .
7
According to (65) we consider the relative error for H and M 1 , and the absolute error for M 2 .
8
Rounded to the integer.
9
H and M 2 are rounded to the integer.
10
According to (68), we consider the relative error for H and M 1 , and the absolute error for M 2 .

References

  1. Agrawal, G.P. Nonlinear Fiber Optics; Academic Press, 2007. [Google Scholar]
  2. Chen, F.F. Plasma Physics and Controlled Fusion; Springer Verlag: Berlin, 2006. [Google Scholar]
  3. Pécseli, H.L. Waves and Oscillations in Plasmas; CRC Press: Boca Raton, 2013. [Google Scholar]
  4. Rutherford P., H. Nonlinear growth of the tearing mode. Physics of Fluids 1973, 16, 1903–1908. [Google Scholar] [CrossRef]
  5. Osborne, A. Nonlinear Ocean Waves and the Inverse Scattering Transform; Academic Press: Burlington, 2010. [Google Scholar]
  6. Petviashvili, V.; Pokhotelov, O. Solitary Waves in Plasmas and in the Atmosphere; Gordon and Breach: Philadelphia, 1992. [Google Scholar]
  7. Davydov, A.S. The theory of contraction of proteins under their excitation. Journal of Theoretical Biology 1973, 38, 559–569. [Google Scholar] [CrossRef] [PubMed]
  8. Pitaevskii, L.; Stringari, S. Bose-Einstein Condensation and Superfluidity; Oxford University Press, 2016. [Google Scholar]
  9. Akhmediev, N.; Ankiewicz, A. Dissipative Solitons; Springer: New York, 2005. [Google Scholar]
  10. Inslie, B. J.; Girdlestone, H.P.; Cotter, D. Semiconductor-doped fibre waveguides exhibiting picosecond optical nonlinearity. Electronics Letters 1987, 23, 405–406. [Google Scholar] [CrossRef]
  11. Peng, G.D.; Xiong, Z.; Chu, P.L. Photosensitivity and gratings in dye-doped polymer optical fibers. Optical Fiber Technology 1999, 5, 242–251. [Google Scholar] [CrossRef]
  12. Adhikari, S.K. Mean-field description of collapsing and exploding Bose-Einstein condensates. Phys. Rev. A 2002, 66, 13611–13619. [Google Scholar] [CrossRef]
  13. Kagan, Y.; Muryshev, A.E.; Shlyapnikov, G.V. Collapse and Bose-Einstein condensation in a trapped Bose gas with negative scattering length. Phys. Rev. Lett. 1998, 81, 933–937. [Google Scholar] [CrossRef]
  14. Saito, H.; Ueda, M. Intermittent implosion and pattern formation of trapped Bose-Einstein condensates with attractive interaction. Phys. Rev. Lett. 2001, 86, 1406–14011. [Google Scholar] [CrossRef]
  15. Ablowitz, M.J.; Clarkson, P.A. Solitons, Nonlinear Evolution Equations and Inverse Scattering; Cambridge University Press, 1991. [Google Scholar]
  16. Ablowitz, M.J.; Segur, H. Solitons and the Inverse Scattering Transform; SIAM: Philadelphia, 1981. [Google Scholar]
  17. Cazenave, T. An Introduction to Nonlinear Schrödinger Equations; UFRJ: Rio de Janeiro, 1996. [Google Scholar]
  18. Dodd, R.K.; Eibeck, J.C.; Gibbon, J.D.; Morris, H. Solitons and nonlinear wave equation; Academic Press, 1982. [Google Scholar]
  19. Drazin, P.G.; Johnson, R.S. Solitons: An Introduction; Cambridge University Press, 1989. [Google Scholar]
  20. Delfour, M.; Fortin, M.; Payr, G. Finite-difference solutions of a non-linear Schrödinger equation. J. Comp. Phys. 1981, 44(2), 277–288. [Google Scholar] [CrossRef]
  21. Sanz-Serna, J.M. Methods for the numerical solution of the nonlinear Schrödinger equation. Math. Comp. 1984, 43(167), 21–27. [Google Scholar] [CrossRef]
  22. Sanz-Serna, J.M.; Manoranjan, V.S. A method for the integration in time of certain partial differential equations. J. Comp. Phys. 1983, 52(2), 273–289. [Google Scholar] [CrossRef]
  23. Tourigny, Y.; Sanz-Serna, J.M. The Numerical Study of Blowup with Application to a Nonlinear Schrödinger Equation. J. Comp. Phys. 1992, 102, 407–416. [Google Scholar] [CrossRef]
  24. Weideman, J.A.C.; Herbst, B.M. Split-step methods for the solution of the nonlinear Schrödinger equation. SIAM J. Numer. Anal. 1986, 23, 485–507. [Google Scholar] [CrossRef]
  25. Bai, J. Multi-symplectic Runge-Kutta-Nyström methods for nonsmooth nonlinear Schrödinger equations. J. Math. Anal. Appl. 2016, 444, 721–736. [Google Scholar] [CrossRef]
  26. Bridges, T.J. Muti-symplectic structures and wave propagation. Math. Proc. Cambridge Philos. Soc. 1997, 121, 147–190. [Google Scholar] [CrossRef]
  27. Bridges, T.J.; Reich, S. Multi-symplectic integrators: Numerical schemes for Hamiltonian PDEs that conserve symplecticity. Physics Letters A 2001, 284, 184–193. [Google Scholar] [CrossRef]
  28. Bridges, T.J.; Reich, S. Numerical methods for Hamiltonian PDEs. J. Phys. A: Math. Gen. 2006, 39, 5287–5320. [Google Scholar] [CrossRef]
  29. Chen, J.B.; Qin, M.Z. Multi-symplectic Fourier pseudospectral method for the nonlinear Schrödinger equation. Electron. Trans. Numer. Anal. 2001, 12, 193–204. [Google Scholar]
  30. Chen, J.B.; Qin, M.Z. A multisymplectic variational integrator for the nonlinear Schrödinger equation. Numer. Meth. Part. Differ. Equ. 2002, 18, 523–536. [Google Scholar] [CrossRef]
  31. Chen, J.B.; Qin, M.Z.; Tang, Y.F. Symplectic and multi-symplectic methods for the nonlinear Schrödinger equation. Comput. Math. Appl. 2002, 43, 1095–1106. [Google Scholar] [CrossRef]
  32. Hong, J.; Liu, X.-Y.; Li, C. Multi-symplectic Runge–Kutta–Nyström methods for nonlinear Schrödinger equations with variable coefficients. J. Comput. Phys. 2007, 226, 1968–1984. [Google Scholar] [CrossRef]
  33. Islas, A.L.; Schober, C.M. On the preservation of phase space structure under multisymplectic discretization. J. Comput. Phys. 2004, 197, 585–609. [Google Scholar] [CrossRef]
  34. Islas, A.L.; Schober, C.M. Backward error analysis for multisymplectic discretizations of Hamiltonian PDEs. Math. Comp. Simul. 2005, 69, 290–303. [Google Scholar] [CrossRef]
  35. McLachlan, R.I.; Ryland, B.N.; Sun, Y. High order multisymplectic Runge-Kutta methods. SIAM J. Sci. Comput. 2014, 36, A2199–A2226. [Google Scholar] [CrossRef]
  36. Moore, B.; Reich, S. Multisymplectic integration methods for Hamiltonian PDEs. Future Gener. Comput. Syst. 2003, 19, 395–402. [Google Scholar] [CrossRef]
  37. Guan, H.; Jiao, Y.; Liu, J.; Tang, Y. Explicit Symplectic Methods for the Nonlinear Schrödinger Equation. Comm. Comp. Phys. 2009, 6(3), 639–654. [Google Scholar]
  38. Heitzinger, C.; Ringhofer, C. A note on the symplectic integration of the nonlinear Schrödinger equation. J. Comput. Electr. 2004, 3(1), 33–44. [Google Scholar] [CrossRef]
  39. Herbst, B.M.; Varadi, F.; Ablowitz, M.J. Symplectic methods for the nonlinear Schrödinger equation. Math. Comput. Simul. 1994, 37, 353–369. [Google Scholar] [CrossRef]
  40. Huang, Z.; Xu, J.; Sun, B.; Wu, B.; Wu, X. A new solution of Schrödinger equation based on symplectic algorithm. Comput. Math. Appl. 2015, 69, 1303–1312. [Google Scholar] [CrossRef]
  41. Kong, L.; Chen, M.; Yin, X. A novel kind of efficient symplectic scheme for Klein-Gordon-Schrödinger equation. Appl. Numer. Math. 2019, 135, 481–496. [Google Scholar] [CrossRef]
  42. Kong, L.; Zhang, J.; Cao, Y.; Duan, Y.; Huang, H. Semi-explicit symplectic partitioned Runge-Kutta Fourier pseudo-spectral scheme for Klein-Gordon-Schrödinger equations. Comput. Phys. Comm. 2010, 181, 1369–1377. [Google Scholar] [CrossRef]
  43. Tang, Y.F.; Vázquez, L.; Zhang, F.; Pérez-Garcí a, V.M. Symplectic methods for the nonlinear Schrödinger equation. Comp. & Math. with Appl. 1996, 32(5), 73–83. [Google Scholar]
  44. Zhu, B.; Tang, Y.; Zhang, R.; Zhang, Y. Symplectic simulation of dark solitons motion for nonlinear Schrödinger equation. Numer. Algorithms 2019, 81, 1485–1503. [Google Scholar] [CrossRef]
  45. Bambusi, D.; Faou, E.; Grébert, B. Existence and stability of solitons for fully discrete approximations of the nonlinear Schrödinger equation. Numer. Math. 2013, 123, 461–492. [Google Scholar] [CrossRef]
  46. Faou, E. Geometric Numerical Integration and Schrödinger Equations; European Mathematical Society, 2012. [Google Scholar]
  47. Faou, E.; Grébert, B.; Paturel, E. Birkhoff normal form for splitting methods applied to semilinear Hamiltonian PDEs. Part I. Finite-dimensional discretization. Numer. Math. 2010, 114, 459–490. [Google Scholar] [CrossRef]
  48. Gauckler, L.; Lubich, Ch. Splitting Integrators for Nonlinear Schrödinger Equations Over Long Times Found. Comput. Math. 2010, 10, 275–302. [Google Scholar]
  49. Hong, J.; Liu, Y. A novel numerical approach to simulating nonlinear Schrödinger equations with varying coefficients. Appl. Math. Lett. 2003, 16, 759–765. [Google Scholar] [CrossRef]
  50. Islas, A.L.; Karpeev, D.A.; Schober, C.M. Geometric integrators for the nonlinear Schrödinger equation. J. Comput. Phys. 2001, 173, 116–148. [Google Scholar] [CrossRef]
  51. Lubich, Ch. On splitting methods for Schrödinger-Poisson and cubic nonlinear Schrödinger equations. Math. Comp. 2008, 77, 2141–2153. [Google Scholar] [CrossRef]
  52. Li, J. Uniformly accurate nested Picard iterative schemes for nonlinear Schrödinger equation with highly oscillatory potential. Appl. Numer. Math. 2023, 192, 132–151. [Google Scholar] [CrossRef]
  53. Bai, J.; Ullah, H.; Li, C. Energy-preserving methods for non-smooth nonlinear Schrödinger equations. Appl. Numer. Math. 2023, 185, 188–202. [Google Scholar] [CrossRef]
  54. Cai, J.; Zhang, H. High-order conservative schemes for the nonlinear Schrödinger equation in the semiclassical limit. Appl. Math. Lett. 2023, 144. Paper No. 108703, 10 pp.. [Google Scholar] [CrossRef]
  55. Fei, Z.; Pérez-García, V.M.; Vázquez, L. Numerical simulation of nonlinear Schrödinger systems: a new conservative scheme. Appl. Math. Comput. 1995; 71, 165–177. [Google Scholar]
  56. Feng, X.; Li, B.; Ma, S. High-order mass and energy-conserving SAV Gauss collocation finite element methods for the nonlinear Schrödinger equation. SIAM J. Numer. Anal. 2021, 59, 1566–1591. [Google Scholar] [CrossRef]
  57. Gong, Y.; Wang, Q.; Wang, Y.; Cai, J. A conservative Fourier pseudo-spectral method for the nonlinear Schrödinger equation. J. Comput. Phys., 2017, 328, 354–370. [Google Scholar] [CrossRef]
  58. Guo, L.; Xu, Y. Energy Conserving Local Discontinuous Galerkin Methods for the Nonlinear Schrödinger Equation with Wave Operator. J. Sci. Comput. 2015, 65(2), 622–647. [Google Scholar] [CrossRef]
  59. Ma, S.; Wang, J.; Zhang, M.; Zhang, Z. Mass- and energy-conserving Gauss collocation methods for the nonlinear Schrödinger equation with a wave operator. Adv. Comput. Math. 2023; 49, no. 6, Paper No. 77. [Google Scholar]
  60. Yang, J.; Yi, N. A conservative SAV-RRK finite element method for the nonlinear Schrödinger equation. Adv. Appl. Math. Mech. 2023, 15, 583–601. [Google Scholar]
  61. Yin, F.; Fu, Y. Explicit high accuracy energy-preserving Lie-group sine pseudo-spectral methods for the coupled nonlinear Schrödinger equation. Appl. Numer. Math. 2024, 195, 1–16. [Google Scholar] [CrossRef]
  62. Sanz-Serna, J.M.; Calvo, M.P. Numerical Hamiltonian Problems; Chapman & Hall: London, UK, 1994. [Google Scholar]
  63. Benettin, G.; Giorgilli, A. On the Hamiltonian interpolation of near to the identity symplectic mappings with application to symplectic integration algorithms. J. Statist. Phys. 1994, 74, 1117–1143. [Google Scholar] [CrossRef]
  64. Blanes, S.; Casas, F. A concise introduction to geometric numerical integration; Chapman et Hall/CRC: Boca Raton, FL, USA, 2016. [Google Scholar]
  65. Hairer, E.; Lubich, C.; Wanner, G. Geometric Numerical Integration, 2nd ed.; Springer: Berlin, Germany, 2006. [Google Scholar]
  66. Leimkuhler, B.; Reich, S. Simulating Hamiltonian Dynamics; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
  67. Brugnano, L.; Iavernaro, F. Line Integral Methods for Conservative Problems; Chapman et Hall/CRC: Boca Raton, FL, USA, 2016. [Google Scholar]
  68. Brugnano, L.; Iavernaro, F.; Trigiante, D. Hamiltonian Boundary Value Methods (Energy Preserving Discrete Line Integral Methods). JNAIAM J. Numer. Anal. Ind. Appl. Math. 2010, 5, 17–37. [Google Scholar]
  69. Hairer, E. Energy-preserving variant of collocation methods. JNAIAM J. Numer. Anal. Ind. Appl. Math. 2010, 5, 73–84. [Google Scholar]
  70. Quispel, G.R.W.; McLaren, D.I. A new class of energy-preserving numerical integration methods. J. Phy. A 2008, 41, 045206. [Google Scholar] [CrossRef]
  71. Brugnano, L.; Iavernaro, F.; Trigiante, D. A simple framework for the derivation and analysis of effective one-step methods for ODEs. Appl. Math. Comput. 2012, 218, 8475–8485. [Google Scholar] [CrossRef]
  72. Brugnano, L.; Iavernaro, F. Line Integral Solution of Differential Problems. Axioms 2018, 7(2), 36. [Google Scholar] [CrossRef]
  73. Amodio, P.; Brugnano, L.; Iavernaro, F. Arbitrarily high-order energy-conserving methods for Poisson problems. Numer. Algorithms 2022, 91, 861–894. [Google Scholar] [CrossRef]
  74. Amodio, P.; Brugnano, L.; Frasca-Caccia, G.; Iavernaro, F. Arbitrarily high-order energy-conserving methods for Hamiltonian problems with holonomic constraints. J. Comp. Math. 2023. [Google Scholar] [CrossRef]
  75. Amodio, P.; Brugnano, L.; Iavernaro, F. Energy-conserving methods for Hamiltonian Boundary Value Problems and applications in astrodynamics. Adv. Comput. Math. 2015, 41, 881–905. [Google Scholar] [CrossRef]
  76. Amodio, P.; Brugnano, L.; Iavernaro, F. A note on the continuous-stage Runge-Kutta-(Nyström) formulation of Hamiltonian Boundary Value Methods (HBVMs). Appl. Math. Comput. 2019, 363, 124634. [Google Scholar] [CrossRef]
  77. Amodio, P.; Brugnano, L.; Iavernaro, F. Arbitrarily high-order methods for one-sided direct event location in discontinuous differential problems with nonlinear event function. Appl. Numer. Math. 2022, 179, 39–49. [Google Scholar] [CrossRef]
  78. Amodio, P.; Brugnano, L.; Iavernaro, F. Continuous-Stage Runge-Kutta approximation to Differential Problems. Axioms 2022, 11(5), 192. [Google Scholar] [CrossRef]
  79. Amodio, P.; Brugnano, L.; Iavernaro, F. (Spectral) Chebyshev collocation methods for solving differential equations. Numer. Algorithms 2023, 93, 1613–1638. [Google Scholar] [CrossRef]
  80. Brugnano, L.; Frasca-Caccia, G.; Iavernaro, F.; Vespri, V. A new framework for polynomial approximation to differential equations. Adv. Comput. Math. 2022, 48, 76. [Google Scholar] [CrossRef] [PubMed]
  81. Brugnano, L.; Gurioli, G.; Iavernaro, F. Analysis of Energy and QUadratic Invariant Preserving (EQUIP) methods. J. Comput. Appl. Math. 2018, 335, 51–73. [Google Scholar] [CrossRef]
  82. Brugnano, L.; Iavernaro, F.; Trigiante, D. A two-step, fourth-order method with energy preserving properties. Comput. Phys. Commun. 2012, 183, 1860–1868. [Google Scholar] [CrossRef]
  83. Brugnano, L.; Iavernaro, F.; Zhang, R. Arbitrarily high-order energy-preserving methods for simulating the gyrocenter dynamics of charged particles. J. Comput. Appl. Math. 2020, 380, 112994. [Google Scholar] [CrossRef]
  84. Brugnano, L.; Iavernaro, F. A general framework for solving differential equations. Annali dell’Università di Ferrara 2022, 68, 243–258. [Google Scholar] [CrossRef]
  85. Brugnano, L.; Montijano, I.J.; Rández, L. High-order energy-conserving Line Integral Methods for charged particle dynamics. Jour. Comput. Phys. 2019, 396, 209–227. [Google Scholar] [CrossRef]
  86. Brugnano, L.; Frasca-Caccia, G.; Iavernaro, F. Line Integral Solution of Hamiltonian PDEs. Mathematics 2019, 7(3), 275. [Google Scholar] [CrossRef]
  87. Brugnano, L.; Gurioli, G.; Sun, Y. Energy-conserving Hamiltonian Boundary Value Methods for the numerical solution of the Korteweg-de Vries equation. J. Comput. Appl. Math. 2019, 351, 117–135. [Google Scholar] [CrossRef]
  88. Brugnano, L.; Gurioli, G.; Zhang, C. Spectrally accurate energy-preserving methods for the numerical solution of the “Good” Boussinesq equation. Numer. Methods for Partial Differential Equations 2019, 35, 1343–1362. [Google Scholar] [CrossRef]
  89. Brugnano, L.; Iavernaro, F.; Montijano, I.J.; Rández, L. Spectrally accurate space-time solution of Hamiltonian PDEs. Numer. Algorithms 2019, 81, 1183–1202. [Google Scholar] [CrossRef]
  90. Brugnano, L.; Zhang, C.; Li, D. A class of energy-conserving Hamiltonian boundary value methods for nonlinear Schrödinger equation with wave operator. Commun. Nonlinear Sci. Numer. Simul. 2018, 60, 33–49. [Google Scholar] [CrossRef]
  91. Barletti, L.; Brugnano, L.; Frasca-Caccia, G.; Iavernaro, F. Energy-conserving methods for the nonlinear Schrödinger equation. Appl. Math. Comput. 2018, 318, 3–18. [Google Scholar] [CrossRef]
  92. Barletti, L.; Brugnano, L.; Tang, Y.; Zhu, B. Spectrally accurate space-time solution of Manakov systems. J. Comput. Appl. Math. 2020, 377, 112918. [Google Scholar] [CrossRef]
  93. Gautschi, W. Numerical Analysis. An Introduction; Birkhäuser: Boston, 1997. [Google Scholar]
  94. Dahlquist, G.; Björk, Å. Numerical Methods in Scientific Computing; SIAM: Philadelphia, PA, USA, 2008. [Google Scholar]
  95. Amodio, P.; Brugnano, L.; Iavernaro, F. Analysis of Spectral Hamiltonian Boundary Value Methods (SHBVMs) for the numerical solution of ODE problems. Numer. Algorithms 2020, 83, 1489–1508. [Google Scholar] [CrossRef]
  96. Brugnano, L.; Montijano, I.J.; Rández, L. On the effectiveness of spectral methods for the numerical solution of multi-frequency highly-oscillatory Hamiltonian problems. Numer. Algorithms 2019, 81, 345–376. [Google Scholar] [CrossRef]
  97. Brugnano, L.; Magherini, C. Blended Implementation of Block Implicit Methods for ODEs. Appl. Numer. Math. 2002, 42, 29–45. [Google Scholar] [CrossRef]
  98. Brugnano, L.; Magherini, C. Blended Implicit Methods for solving ODE and DAE problems, and their extension for second order problems. J. Comput. Appl. Math. 2007, 205, 777–790. [Google Scholar] [CrossRef]
  99. Brugnano, L.; Magherini, C. Recent advances in linear analysis of convergence for splittings for solving ODE problems. Appl. Numer. Math. 2009, 59, 542–557. [Google Scholar] [CrossRef]
  100. Brugnano, L.; Magherini, C.; Mugnai, F. Blended Implicit Methods for the Numerical Solution of DAE Problems. J. Comput. Appl. Math. 2006, 189, 34–50. [Google Scholar] [CrossRef]
  101. Brugnano, L.; Iavernaro, F.; Trigiante, D. A note on the efficient implementation of Hamiltonian BVMs. J. Comput. Appl. Math. 2011, 236, 375–383. [Google Scholar] [CrossRef]
  102. Brugnano, L.; Frasca-Caccia, G.; Iavernaro, F. Efficient implementation of Gauss collocation and Hamiltonian Boundary Value Methods. Numer. Algorithms 2014, 65, 633–650. [Google Scholar] [CrossRef]
  103. Konotop, V.V.; Vázquez, L. Nonlinear random waves; World Scientific: Singapore, 1994. [Google Scholar]
  104. Caplan, R.M.; Carretero-González, R.; Kevrekidis, P.G.; Malomed, B.A. Existence, stability, and scattering of bright vortices in the cubic-quintic nonlinear Schrödinger equation. Math. Comput. Simulation 2012, 82, 1150–1171. [Google Scholar] [CrossRef]
  105. Maday, Y.; Turinici, G. A parareal in time procedure for the control of partial differential equations. C. R. Acad. Sci. Paris, Ser. I, 2002, 335, 387–392. [Google Scholar] [CrossRef]
  106. Amodio, P.; Brugnano, L. Parallel implementation of block boundary value methods for ODEs. J. Comput. Appl. Math. 1997, 78, 197–211. [Google Scholar] [CrossRef]
Preprints 91392 g001
Figure 1. Example 1: plot of the modulus of ψ ( x , t ) in (62).
Figure 1. Example 1: plot of the modulus of ψ ( x , t ) in (62).
Preprints 91392 g001
Preprints 91392 g002
Figure 2. Example 1: error versus stepsize (left-plot) and error versus execution time (right-plot).
Figure 2. Example 1: error versus stepsize (left-plot) and error versus execution time (right-plot).
Preprints 91392 g002
Preprints 91392 g005
Figure 5. Example 3: modulus of the computed solution (upper left-plot), errors in the invariants (upper right-plot), and real and imaginary part of the solution (middle plots) for SHBVM used with stepsize h = 0.1 ; errors in the invariants for AVF and HBVM(4,2) used with stepsize h = 10 − 2 (lower plots).
Figure 5. Example 3: modulus of the computed solution (upper left-plot), errors in the invariants (upper right-plot), and real and imaginary part of the solution (middle plots) for SHBVM used with stepsize h = 0.1 ; errors in the invariants for AVF and HBVM(4,2) used with stepsize h = 10 − 2 (lower plots).
Preprints 91392 g005
Table 1. Blended iteration for solving (55).
Table 1. Blended iteration for solving (55).
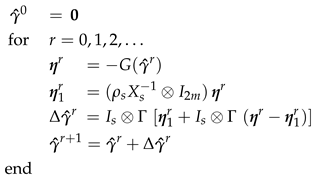Preprints 91392 i002
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated