A Blind Digital Image Watermarking Scheme Exploiting Elementary Cellular Automata Rule-30

1. Introduction

Multimedia security has gained prominence due to the internet’s tremendous development and widespread use. The easy access to the internet, increased use of social media, and influential developments in digital data modification and editing software have made unauthorized copying, editing, and manipulation of digital content so much easier, resulting in the necessity of digital content security and authentication. The watermarking of digital data is performed to accomplish objectives like the protection of copyright, the preservation of originality, the protection from illegal duplication, and the authentication of digital content [1]. Digital watermarking is a process that embeds digital data called watermark into the host document. The watermark is embedded in a manner that does not alter the host document and is invisible to the viewer. The embedded watermark is retrieved from the watermarked document using the extraction process. Digital watermarking ensures fortified security, copyright protection, temper resistance plus detection, verification of integrity, controlled copying, and monitored broadcasting of digital data [2].

There are many different ways, such as human perception, resistance, type of document, reversibility, and working domain, to categorize digital watermarking techniques into various groups [3]. According to human perception, watermarking techniques can be classified into two categories: visible and invisible [4]. The watermarks embedded using visible watermarking techniques can be perceived easily from the host image. Examples include company logos, QR codes, signatures, initials, etc., that are placed at the corners of the images or TV channels/videos. The watermarks embedded using invisible watermarking techniques are hidden in the host image to preserve imperceptibility and, therefore, are unnoticeable to the human eyes. Their applications include ownership confirmation, integrity management, and digital document authentication. Since invisible watermarks are made to be hard to spot and remove, they are often more robust than visible ones. However, their invisibility may make them less helpful at proving ownership or preventing unauthorized usage.

Based on the resistance level, invisible watermarking schemes can further be categorized into four groups: fragile, semi-fragile, robust, and hybrid approaches [3]. Fragile watermarking involves embedding a watermark in a host document in a way that any slight modification to the host would cause the watermark to be destroyed or altered. Fragile watermarking schemes are not resistant at all, and their goal is to detect tempering, verify the integrity, and authenticate the digital content. The watermarks embedded using semi-fragile watermarking approaches can resist some basic attacks/modifications like compression or resizing; nevertheless, they remain fragile to major attacks/modifications. Semi-fragile watermarks are frequently employed in cases where some content modifications are likely to happen, but any malicious or illegal modifications ought to be identified and prevented [5]. The robust watermarking approaches involve embedding a watermark in a host document in such a manner that it becomes challenging to alter or remove it even if the host undergoes standard operations like cropping, compression, filtering, scaling, or other types of modification. Robust watermarks are highly resistant and are intended to survive deliberate or accidental modifications to the watermarked content. The hybrid watermarking approach combines robust and fragile approaches to simultaneously offer verification of data integrity, data authentication, and copyright enforcement [3].

The digital watermarking procedure can be applied to different types of digital host documents like images, texts, audio, and videos to manage digital rights, protect the copyright, and identify the content. Digital image watermarking is a process that embeds information into the host image in a manner that the embedded information doesn’t alter the host image and is imperceptible to the viewer, which is then retrieved from the watermarked image during the extraction phase. Regarding digital watermarking, reversibility can be defined as the capability of the watermarking system to fully restore the original unwatermarked form of the host document after watermark embedment. Watermarking schemes are often categorized as irreversible watermarking and reversible watermarking based on reversibility. The irreversible watermarking schemes cannot completely restore the host document’s original form once the watermark has been embedded. In contrast, reversible watermarking schemes can fully restore the original form of the host document after watermark embedment and extraction.

Cellular automata (CA) are massively parallel computational architectures with the maximum level of granularity. It is a mathematical model that consists of the D-dimensional lattice of finite-state cells with local interaction. The system’s evolution is dependent on the evolution of each of its individual components. Simple rules and structures can result in a wide range of unpredictable patterns, making the cellular automata theory incredibly interesting. For instance, the behaviour of a Turing machine or any other CA can be simulated using the CA known as universal cellular automata. The CA is beneficial in a variety of applications due to its fundamental characteristics; the parallelism characteristic of CA makes it suitable for large-scale modelling and simulations. The complex structures, patterns, and behaviours produced by the global behaviour of the cells in the cellular space are impossible to predict based on the individual behaviour of cells. This characteristic of the CA is termed emergent behaviour. The CA is scalable and can be easily scaled down or up according to the dimensions of the system being simulated; as a result, the CA is suitable for a variety of applications. CA is a flexible and adaptable tool for simulation and modelling as it can simulate various systems by customizing the update rule and the initial values of the parameters to start up CA. The watermarking systems that are based on CA offer high privacy and security as it makes watermark detection and removal extremely challenging, thereby making it ideal for preserving delicate and valuable data.

This study aims to investigate ECA rule-30 for digital image watermarking. An extensive investigation that considered numerous pertinent sources and analytical techniques was conducted to accomplish this goal. The major contributions of this work are as follows:

• This paper presents a robust and secure digital image watermarking technique implemented in the spatial domain. It leverages the erratic and chaotic behaviour of the elementary cellular automata rule-30 to enhance the security and robustness of the watermarking system.
• The suggested blind watermarking technique perfectly balances imperceptibility, capacity, and robustness. By downsizing the grayscale watermark image to its two Most Significant Bits (MSBs) and encrypting the 2-MSBs watermark using ECA rule-30, the security attribute of the system is enhanced. Scrambling the host image with ECA rule-30 also distributes the watermark pixels, maximizing robustness against geometrical attacks.
• The proposed method outperforms several systems with similar competencies regarding imperceptibility, capacity, and robustness. The simulation’s findings demonstrate strong imperceptibility, as evaluated by the Peak Signal-to-Noise Ratio (PSNR), with an average value of 58.3735 dB. The experimental outcomes across a diverse range of standardized attack scenarios establish the ascendancy of the proposed algorithm over competing methodologies in the field of image watermarking.

The remaining portions of the article will be divided into multiple sections, each of which will focus on a different facet of the given problem. The following section of the literature review will discuss a detailed background of digital image watermarking techniques based on the working domain in which they are implemented. Section 3 introduces cellular automata, elementary cellular automata, and rule-30. Section 4 discusses the methodology of the proposed scheme. This will be followed by Section 5, where performance analysis and experimental discussion are presented. In Section 6, we will discuss the results of our technique, compare and analyze these results, and draw conclusions based on our findings. The summary of the main findings and suggestions for further study will be included in the part that concludes the article. With this framework, we want to present a vivid and insightful exploration of cellular automata-based digital image watermarking.

2. Related Work

The performance of the different digital image watermarking approaches depends on the domain in which they are being implemented. Based on the working domain, digital image watermarking algorithms can be classified into three groups: spatial domain watermarking, transform or frequency domain watermarking, and hybrid domain watermarking [6].

2.1. Spatial Domain Algorithms

In the spatial domain, the watermark information bits are embedded straight into the host image pixel values using various approaches like modification of Least Significant Bits (LSBs) [7,8,9,10,11] or Intermediate Significant Bits (ISBs) [12] of the host image, patchwork approach, Local Binary Pattern (LBP) approach [13], histogram modification approach [14,15], and approaches based on correlation [16,17,18] and spread spectrum [19,20,21]. The crucial characteristics of the watermarking system, imperceptibility, capacity, and robustness, have been perfectly balanced by spatial domain techniques. These techniques are more straightforward, more effective, and execute more quickly. In terms of capacity, these techniques allow the embedding of significant data. However, these methods only work effectively when the image has not been altered by humans or subjected to noise. A significant flaw with spatial domain watermarking is that the watermark can be removed through image cropping. Furthermore, a tiny watermark may be embedded repeatedly. Therefore, despite losing the majority of the image data due to numerous attacks, a single watermark remaining will be viewed as a success.

A digital image scrambling technique-based image watermarking approach using CA has been presented in [22] by Ye and Li. This work determines the fractal box dimensions of the CA and profoundly analyzes the chaotic properties of CA. In this approach, the fractal box dimensions are used to select the chaotic CA rule, then the host image is scrambled using that rule, and finally, the watermark is embedded in the scrambled image. The scrambled watermarked image is then descrambled to obtain the watermarked image. According to experimental findings, this technique is resistant to different attacks like compression, cropping, and noise; therefore, it is robust. A novel blind watermarking approach based on the game of life CA has been propounded by Adwan et al. in [7]. The Game-of-Life is the most well-known and robust rule of a CA. The proposed approach is implemented in the spatial domain, and it employs the LSB substitution technique for inserting the two most significant bits of the grayscale watermark into the host image. The suggested approach generates the k number of game-of-life generations and uses the locations of the live cells to insert data into the LSBs of the host image. According to the imperceptibility evaluation of the suggested scheme, the embedded watermark in the watermarked image is not perceptibly visible. The experimental findings demonstrate that the suggested approach is secure, simple, and robust enough against passive attacks.

A highly secure image watermarking approach based on the logistic map, the 2D Arnold’s cat map, and the 2D Game of Life cellular automata has been suggested by Moniruzzaman et al. [8]. In the proposed scheme, the security mechanism is ensured by scrambling both the grayscale host image and the binary watermark image. The host image is scrambled using the 2D Arnold’s cat map before the embedment of the watermark data into it. The initial configuration to start the Game of Life CA is set using the logistic map, and then the Game of Life CA is evolved to scramble the binary watermark image. At last, the scrambled watermark bits are inserted into the LSBs of the scrambled host image pixels. The suggested solution is used for image authentication and has the ability to avert unauthorized changes. Comparing the experimental findings of the proposed method to three other current chaos-based watermarking schemes depicts that the suggested approach significantly outperforms other approaches. The solitary constraint of this approach lies in its applicability exclusively to square images, as the Arnold transform’s functionality is confined to image dimensions of uniform size.

A reversible medical image watermarking method proposed by Tjokorda et al. [9] uses the LSB modification technique for tamper detection and recovery in the region of interest (ROI) of medical images. The experiments’ results indicate good performance and imply that the suggested watermarking approach more cleverly handles the attacks that target a particular area of the pictures, i.e., block tempering attacks. A secret image data hiding technique by Manjula and Danti [10] employs the (2-3-3) LSB approach to embed confidential data into the host image. The proposed method embeds secret image data having eight bits per pixel into the LSBs of the RGB host image. The (2-3-3) LSB approach embeds the first 2 bits in the red channel, the next 3 bits in the green channel, and the last 3 bits in the blue channel of the RGB host image. This approach offers promising results, considerably improving PSNR and MSE values compared to the prior technique.

An imperceptible digital image watermarking scheme for color images in the spatial domain has been propounded by Abraham and Paul [11]. The goal of this study is to develop a color image watermarking method that does not reduce the picture quality drastically or alter the perceptual color. Additionally, watermark data is inserted in every image block to provide the highest robustness against attacks and enable tamper detection and recovery features. This scheme uses M1 and M2 masks during the watermark embedding process. The watermark information is distributed to the nearby pixels in the chosen area using these masks. The embedding channel uses the M1 mask, and to account for the differences introduced in the embedding channel, the other color channels are adjusted using mask M2. After being tested on various images, the suggested algorithm assures excellent quality watermarked images that can withstand many attacks.

2.2. Transform Domain Algorithms

In the transform domain, the watermark data is not inserted directly into the host image but rather into the frequency coefficients of the host image. A number of transformational approaches have been devised for frequency coefficient generation, such as Discrete Wavelet Transform (DWT) [23], Discrete Cosine Transform (DCT) [4,24,25,26], Singular Value Decomposition (SVD) [4], Discrete Fourier Transform (DFT), Fast Fourier Transform (FFT), Cellular Automata Transform (CAT), Polar Harmonic Transform (PHT), and Hadamard. The transform domain watermarking techniques first transform the host image from the spatial domain to the frequency domain using any image transformation method in order to generate the coefficients and then alter these coefficients to embed the watermark data. Finally, the inverse transformation method is applied to obtain the watermarked image.

Laouamer and Tayan have proposed a robust semi-blind sensitive text image watermarking approach [25] that is DCT and linear interpolation-based. The main aim of this approach is to deal with the issues related to tamper detection, authenticity proof, integrity verification, and protection of digitally sensitive text images. This approach first transforms both the host image and the watermark image into YUV color space, and then both images are divided into 8 x 8 blocks. DCT is applied on each 8 x 8 block of both images, and finally, linear interpolation is applied on the quantized DCT coefficients to obtain the watermarked image. According to this study, a good trade-off between robustness and imperceptibility can be achieved if the watermark data is inserted into the medium-frequency (MF) components. The main contribution of this work is to extract the watermark perfectly from the attacked watermarked image. Roy and Pal [26] have employed DCT and repetition code to put forth a blind color watermarking technique for embedding multiple watermarks. The primary purpose of the proposed method is to enable copyright ownership protection and multiple owner authenticity validations. In this approach, the host image’s blue and green components are first fragmented into non-overlapping blocks, and then the DCT is applied to each block. This approach embeds two binary watermark logos scrambled using Arnold’s chaotic map before embedding. The watermark bits are embedded into the middle-frequency coefficients of blue and green components using repetition codes. The proposed approach shows high robustness, imperceptibility, and better PSNR value but exhibits high computational complexity.

Liu et al. [27] have propounded a DCT and fractal encoding-based digital image watermarking algorithm. The proposed algorithm combines the traditional DCT technique with the fractal encoding method. This approach encrypts the host image twice, first by encoding it with the fractal encoding and second by applying DCT on the encoded parameters. The experiments carried out show that the proposed approach has high robustness and a better PSNR value. Singh and Bhatnagar have presented a robust watermarking technique [28]. The techniques employed by this blind watermarking approach are integer DCT, dynamic stochastic resonance (DSR), and non-linear chaotic maps. In this approach, integer-DCT is applied to the host image to convert it into an integer linear transform, and the resulting coefficients are divided into non-overlapping blocks. Then, the Non-linear chaotic map is used to select the random blocks, which form the circulant matrix. The watermark bits are embedded into the circulant matrix by computing the singular values. This approach uses the dynamic stochastic resonance (DSR) phenomena for efficient watermark extraction. The verification step is included to deal with the false positive problem caused in SVD systems. The experiments carried out show that the proposed approach is robust and imperceptible against various attacks.

Ernawan et al. have propounded a DCT psycho-visual threshold-based digital image watermarking algorithm [29]. First, the host image is divided into non-overlapping blocks for watermark embedding, and their modified entropy is computed. Then, DCT is applied to the blocks having the lowest entropy values to obtain the middle-frequency coefficients. Some of these middle-frequency coefficient pairs are modified with a psycho-visual threshold to embed the watermark bits. The watermark is scrambled using Arnold Scrambling before embedding to strengthen the security levels. For evaluation of the proposed algorithm, the watermarked image had undergone various attacks like a median filter, low-pass filter, sharpening, JPEG and JPEG2000, image noise, and geometrical attacks such as image scaling and cropping. The results demonstrated that the proposed method is invisible and robust compared to the existing methods.

A novel color image watermarking scheme based on Discrete Cosine Transform (DCT) and Cellular Automata (CA) has been put forth by M Jana, and B Jana [30]. This study focuses on developing an image watermarking system with enhanced security and high embedding capacity without compromising the visual quality of the host image. The RGB host image is first separated into red, green, and blue channels. After that, each channel is partitioned into non-overlapping 8x8 blocks; subsequently, DCT is applied on each block, and Zigzag scanning is performed. To increase the security and the robustness of the proposed system, CA rule-15 is used to encrypt the watermark data prior to embedding and CA rule-85 is used for decryption purposes. The CA rule-340 and mapping table are used to modify the DCT coefficients and incorporate the encrypted watermark image. The propounded method is equated with the existing methods. Furthermore, the simulation findings demonstrate an average Peak Signal Noise Ratio (PSNR) value of 54 dB that signifies strong imperceptibility and concomitantly having a good embedding capacity of 1.48 bpp.

3. Methods and Materials

3.1. Cellular Automata

John von Neumann and Stanislaw Ulam are credited as inventors of cellular automata. In the late 1940s, Neumann proposed a theoretical model for artificial biological systems called the “Universal Constructor” that had the ability of self-reproduction and was comprised of a two-dimensional infinite grid of square cells; each cell had five neighbours, including itself, with 29 states per cell. While some people researched the subject during the 1950s and 1960s, its popularity only began to spread outside of academics in the 1970s with the development of Conway’s Game of Life. The Game of Life, developed by mathematician John Conway and hyped up by an article in Scientific American by Martin Gardner, is a simple two-dimensional totalistic cellular automaton with two states per cell using the Moore neighbourhood.

A Cellular automaton can be defined as a mathematical model having discrete space and time domains. This computational system is dynamic in nature, and simple rules govern its evolution. Formally, CA is defined by the quadruple A = (${\mathbb{Z}}^D$, S, N, f) where:

• ${\mathbf{Z}}^{\mathbf{D}}$ is a D-dimensional lattice, i.e., a regular arrangement of lattice-sites/points in Euclidean space which is discrete and is closed under subtraction and addition, called cellular space.
• S is a finite set of states.
• N is a neighborhood vector $(\overrightarrow{{\mathbf{n}}_{\mathbf{1}}},\overrightarrow{{\mathbf{n}}_{\mathbf{2}}},\overrightarrow{{\mathbf{n}}_{\mathbf{3}}}\dots \overrightarrow{{\mathbf{n}}_{\mathbf{m}}})$, comprising of m different cells of ${\mathbb{Z}}^D$ and is identified separately for every cell of the lattice ${\mathbb{Z}}^D$. For a given cell “x” a set of cells $\{x+\overrightarrow{n_i}|i=1,2,3,4\dots .m\}$ forms its neighborhood and from the property of lattice $(x+\overrightarrow{n_i})\in$${\mathbb{Z}}^D$.
• $\mathbf{f}:{\mathbf{S}}^{\mathbf{m}}⟶\mathbf{S}$ is the local transition function known as the local rule in CA that synchronously updates the state of every cell based on the current state of the cells in its neighbourhood.

All the cells in a cellular space are updated simultaneously using the same local update rule. A function/ mapping that assigns cells their states/values from the set of states (S) is called the configuration of the D-dimensional CA (${\mathbb{Z}}^D$) and all configurations are contained in the set ${\mathbf{S}}^{{\mathbf{Z}}^{\mathbf{D}}}$. Besides, the evolution of CA generations can be described as the hopping of the cellular space from one configuration to another according to its global transition function $\mathbf{G}:{\mathbf{S}}^{{\mathbf{Z}}^{\mathbf{D}}}⟶{\mathbf{S}}^{{\mathbf{Z}}^{\mathbf{D}}}$. One-dimensional cellular automata (1D CA) and two-dimensional cellular automata (2D CA) are the two most prevalent forms of CA. A finite or infinite set of identical cells/sites containing discrete variables arranged in the form of a linear array is referred to as 1D CA [31]. 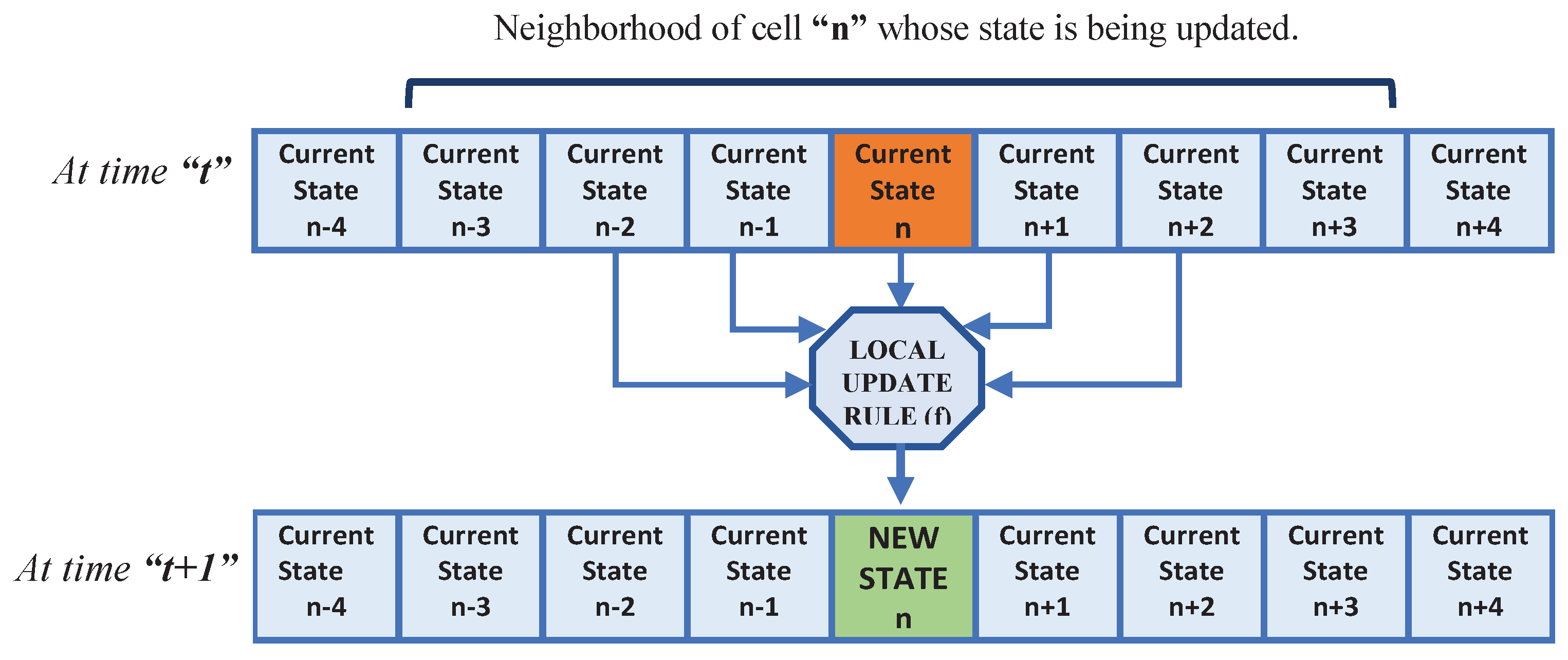Figure 1 depicts the 1D CA with a five-cell neighbourhood for updating the state of the cell “n” where the local rule depends on the current states of the two nearest left (n - 2, n - 1) and right (n + 1, n + 2) neighbours of the cell “n” and the current state of cell “n” itself. The transition function according to which this CA evolves is defined using Equation (1).

$$S_n(t+1)=f(S_{n-2}\left(t\right),S_{n-1}\left(t\right),S_n\left(t\right),S_{n+1}\left(t\right),S_{n+2}\left(t\right))$$

(1)

Where S_n-2(t), S_n-1(t), S_n+1(t), and S_n+2(t) are the current states of the neighbours at time t, S_n(t) is the current state of the cell “n” at time t, S_n(t+1) is the new state of the cell “n” at time t+1, and f is the local update rule.

Figure 1. 1D Cellular Automata with five-cell Neighborhood.

Figure 1. 1D Cellular Automata with five-cell Neighborhood.

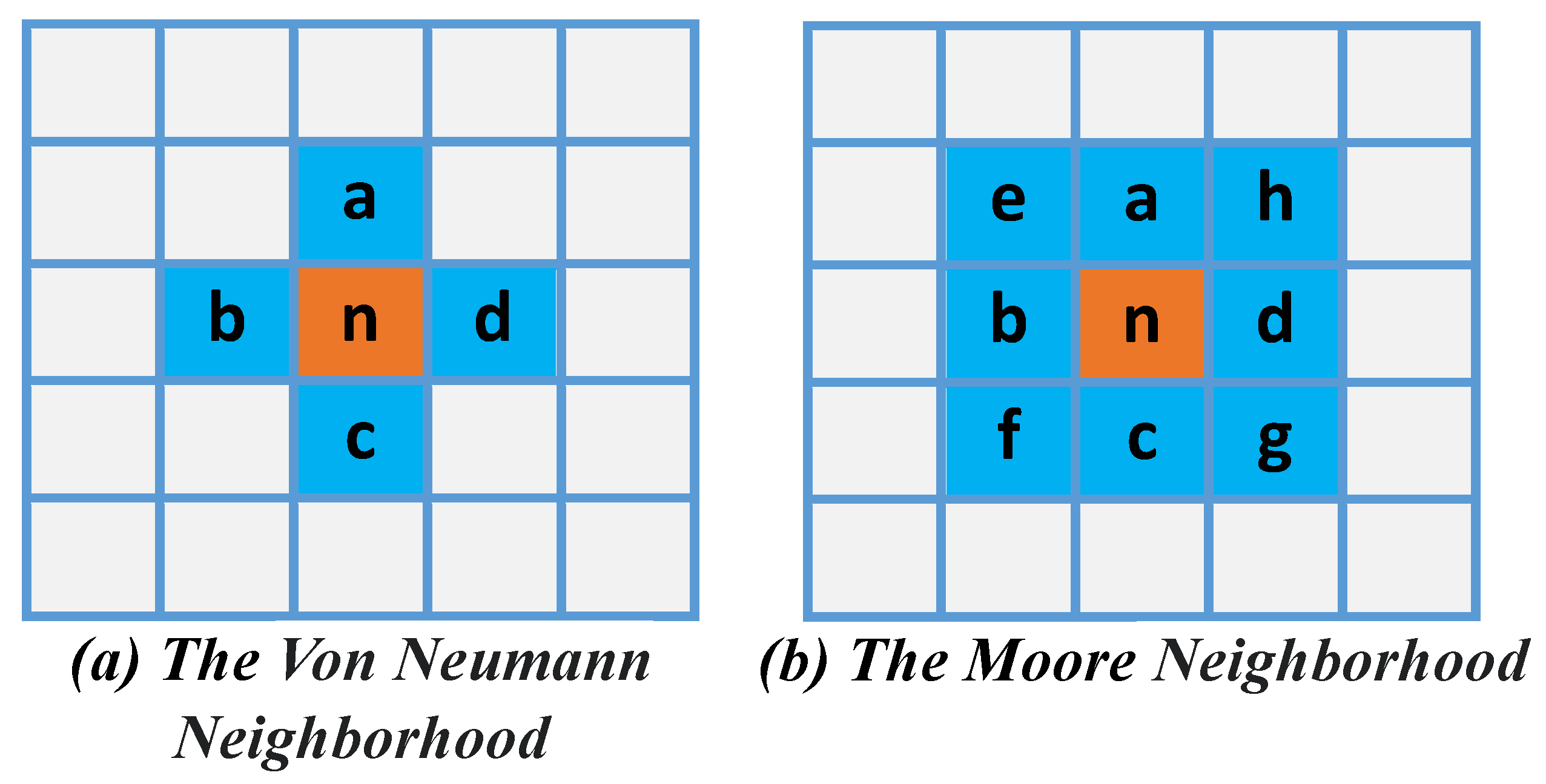
A 2D CA can be defined as a finite or infinite set of identical cells/sites containing discrete variables arranged in the form of a matrix/grid. For 2D CA, a number of neighbourhood structures are possible. Still, the von Neumann neighbourhood and the Moore neighbourhood are the two most prevalent neighbourhood structures illustrated in Figure 2a,b, respectively. The von Neumann/diamond-shaped/five-cell neighbourhood is defined as the set of cells that includes the central cell and its four adjoining perpendicular cells. Equation (2) illustrates the transition function of the five-cell neighbourhood.

$$S_n(t+1)=f(S_n\left(t\right),S_a\left(t\right),S_b\left(t\right),S_c\left(t\right),S_d\left(t\right))$$

(2)

The Moore/square-shaped/nine-cell neighbourhood is defined as the set of cells containing the central cell, its four adjoining perpendicular cells, and four adjoining diagonal cells. Equation (3) illustrates the transition function of the nine-cell neighbourhood.

$$S_n(t+1)=f(S_n\left(t\right),S_a\left(t\right),S_b\left(t\right),S_c\left(t\right),S_d\left(t\right),S_e\left(t\right),S_f\left(t\right),S_g\left(t\right),S_h\left(t\right))$$

(3)

Figure 2. 2D CA Neighborhood Structures.

Figure 2. 2D CA Neighborhood Structures.

3.1.1. Elementary Cellular Automata (ECA)

An elementary cellular automaton is the most basic form of 1D CA, extensively studied by Stephen Wolfram since the 1980s. Given the defining characteristics of a CA, the potential scenario in its most basic form is the linear array of cells with two states (0 or 1) per cell and the neighbourhood set S = (the cell, its immediate right neighbour, its immediate left neighbour). This basic scenario is termed elementary cellular automata, illustrated using the transition function in Equation (4).

$$S_n(t+1)=f(S_{n-1}\left(t\right),S_n\left(t\right),S_{n+1}\left(t\right))$$

(4)

Since there are two states and three neighbours for each cell, this leads to 2³ = 8 possible ways to configure the neighbourhood, and therefore there are only 2²³= 256 total ECA rulesets possible. The Wolfram code, developed by Stephen Wolfram, presented a method for assigning numbers between 0 and 255 to each rule, and this method has now become a norm. Interestingly, Wolfram has categorized these 256 rulesets into four possible classifications based on the increasing complexities of their behaviours [32].

• Class (I) Uniformity: The evolution of almost all the initial configurations rapidly leads to stable, uniform structures, thus completely losing randomness, if any.
• Class (II) Oscillation: The evolution of almost every initial configuration results in patterns that are either stable after a large number of generations or tend to repeat themselves. The initial configuration may lose some of its randomness, but some remains.
• Class (III) Random: The evolution of most of the initial configuration results in chaotic or completely pseudo-random sequences.
• Class (IV) Complexity: Almost all the initial configurations evolve into complex structures with intriguing ways of interaction.

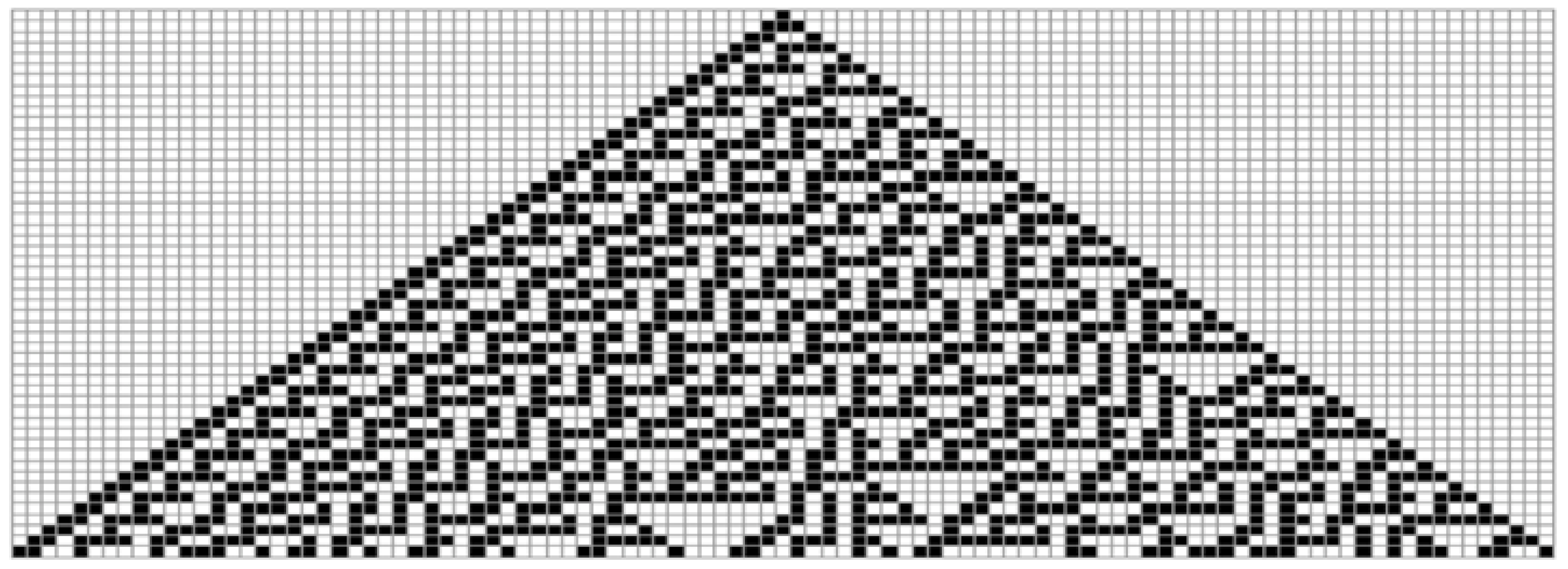
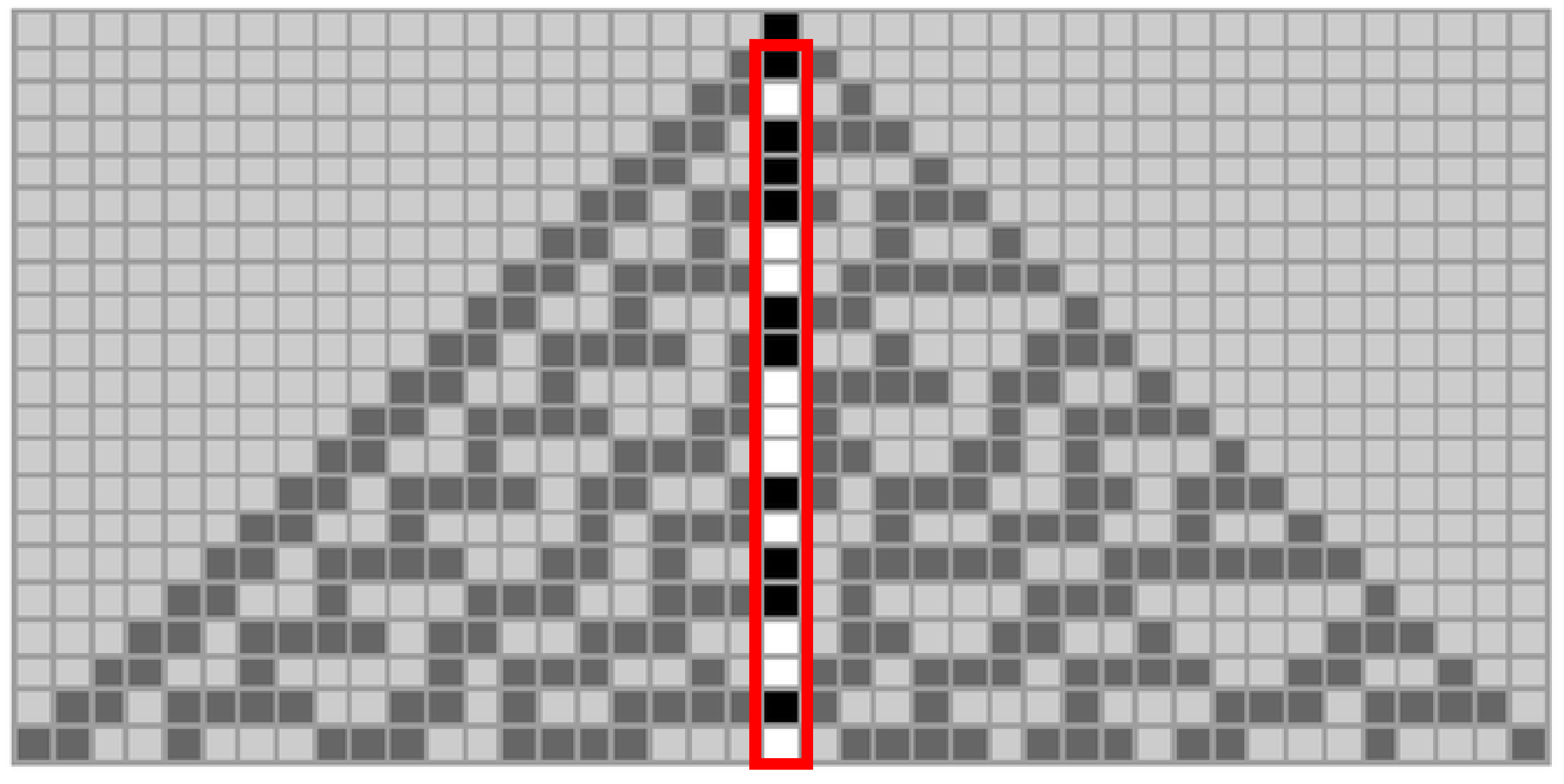
Rule-30: is an elementary cellular automata rule that belongs to a class (III) of Wolfram’s classification because of its chaotic and erratic behaviour. The ruleset for ECA Rule-30 is depicted in Figure 3, and Figure 4 illustrates the first fifty evolutions of the ECA, which is updated using rule-30 with the initial configuration being a single middle black cell. Rule-30 generates random configurations from simple initial states, which makes it remarkable, and that is why Mathematica has also employed it as a random number generator [33]. It is left permutative, thus highly sensitive to the initial states, as a tiny difference in one state had a significant impact on subsequent results [34]. The whole set of NIST statistical tests was applied to the output of rule-30 to analyze and evaluate its randomness, and it was found that except for one, all the tests were passed [35]. It was also shown that for better performance, it is important to have an effective window size, and a size of 200 bits is believed to be sufficient for better randomness [36].

3.2. Proposed Image Watermarking Scheme

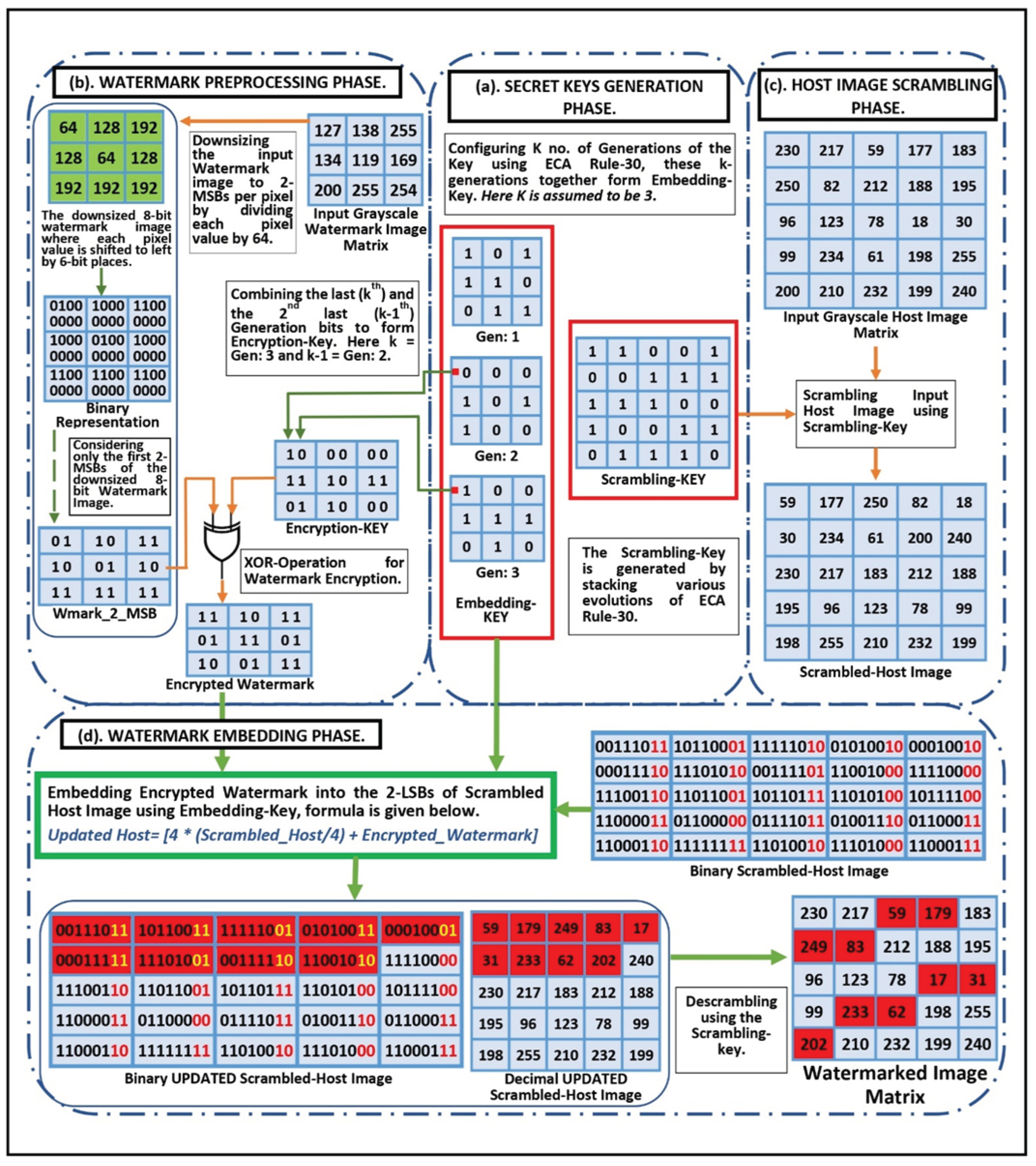
The proposed digital image watermarking method is a spatial domain approach in which watermark bits are embedded into the LSBs of the host image. The crucial characteristics of the watermarking system, imperceptibility, capacity, and robustness, have been perfectly balanced by spatial domain techniques. These techniques are simpler, more effective, and execute more quickly. In this approach, a grayscale host image of size (Hm X Hn), a grayscale watermark image of size (Wm X Wn), and the secret keys (embedding-key and scrambling-key) generated using CA have been considered as the inputs. The proposed scheme is based on powerful ECA rule-30, which is an ideal source of randomness. Confusion can result from the fact that we are viewing a 2D representation of the 1D CA. It should be noted that the proposed scheme constructs the two-dimensional representation out of a large number of evolutions of one-dimensional output data. Nevertheless, the CA system is purely one-dimensional. This scheme is divided into five phases: the Secret Keys Generation Phase, the Watermark Preprocessing Phase, the Host Image Scrambling Phase, the Watermark Embedding Phase, and the Watermark Extraction Phase.

3.2.1. The Secret Keys Generation Phase

This is a prime part of the proposed watermarking scheme, as the two distinct shared secret keys are generated in this phase using ECA. One is the embedding key, which is of the size of the watermark image, i.e., (Wm X Wn), and the second is the scrambling key, which is of the size of the host image, i.e., (Hm X Hn) as shown in Figure 5a.

For the embedding-key generation, this scheme employs the ECA as the linear array of window size of 201 bits/cells contained within the periodic boundaries. Our CA starts off with all the white cells (i.e., all bits equal to zero) except the middle cell of the window, which is the bit at index 101 (array index starts at 1), which is black (i.e., one). The ECA with the above-mentioned parameters is evolved using local update ‘Rule-30 ’ for the “n” number of evolutions, where “n” depends on the size of the watermark image and the number of generations. From each of these n-evolutions, we collect the middle bits as shown in Figure 6, and this bit sequence is taken as the output, which forms the embedding-key matrix after layout modification from 1D to 2D. This scheme configures k number of such matrixes termed as generations of the embedding key to increase the chaoticity of the scheme while embedding.

To generate the scrambling key, the initial values of the parameters to start up ECA remain the same as the initial parameter values set for embedding-key generation, except the window size of the linear array, which is changed to be equal to the number of columns in the host image. This ECA arrangement has also evolved using Rule-30. Once the formation of the triangular structure is complete, we start stacking the output of every evolution in the downward direction for the number of iterations to construct the scrambling key, where the ‘number of iterations’/ ‘height of the stack’ is equal to the number of rows in the host image.

It’s critical to keep in note that the aforementioned CA arrangement is not a 2D CA at all, but rather the output of 1D CA organized in the form of a matrix.

3.2.2. The Watermark Preprocessing Phase

Before inserting watermark information into the host image, watermark data should be preprocessed first. The motive of watermark data preprocessing is to downsize the grayscale watermark image to its two Most Significant Bits (MSBs) and level up the suggested system’s security attribute by encrypting the watermark information before it is embedded. The watermark preprocessing phase is further divided into Downsizing the Watermark and Encrypting the Watermark as depicted in Figure 5b.

3.2.3. Downsizing The Watermark

To address the imperceptibility requirements of the digital image watermarking system, the suggested method does not embed the entire grayscale watermark image but rather embeds the two most significant bits of each pixel of the grayscale watermark image. To make that happen, a grayscale watermark image having (Wm * Wn) number of pixels with 8 bits per pixel is downsized to 2-MSBs per pixel by simply dividing each pixel value by 64, as shown in Equation (5).

$$Wmark\_2\_MSB(i,j)=\frac{Wmark(i,j)}{64}$$

(5)

Where Wmark (i, j) is the watermark 8-bit-pixel value at index (i, j) and Wmark_2_MSB (i, j) is the watermark pixel value reduced to 2-MSBs as division by 64 repeatedly shifts the pixel bits to the right by 6-bit places, where the six rightmost bits get discarded. Six places on the left are set to zero.

3.2.4. Encrypting Watermark

After downsizing the watermark image to 2-MSBs, it undergoes an encryption process to add another level of security to the proposed algorithm. To accomplish the encryption task, the Bitwise XOR operation is applied to the watermark data in order to hide it. The perfectly balanced nature, straightforward implementation, and low computation costs are the significant properties of the XOR operator that make it a better option to be utilized for encryption purposes. This approach forms an entirely random two-bit encryption key by simply combining every last (k^th) and the second last (k-1^th) generation bits at similar indexes of the embedding key. The construction of the encryption key is numerically depicted in Figure 5b. Furthermore, the bitwise XOR operation of the 2-bits of the watermark data at index (i,j) is performed with the 2-bits of the encryption key at index (i,j) as shown in Equation (6), and this operation is performed on every element of the matrix.

$$Encrypted\_Watermark(i,j)=Wmark\_2\_MSB(i,j)\oplus Encryption\_Key(i,j)$$

(6)

3.2.5. The Host Image Scrambling Phase

In the proposed approach, the encrypted watermark is not embedded directly into the host image pixels. Instead, the host image first gets scrambled using the scrambling key, as shown in Figure 5c. The motto behind scrambling the host image is to distribute the watermark pixels throughout the host image and thus achieve high robustness against geometrical attacks like cropping. In the proposed approach, the process of embedding the encrypted watermark data is performed on the LSBs of the scrambled host image, after which it is descrambled, which results in the distribution of the encrypted watermark pixels in every part of the host image that is the case of eliminating the correlation between the pixels embedded with watermark data and therefore, enhancing resistance against potential geometrical attacks. The host image scrambling process is numerically depicted in Figure 5c and works according to the principle given below.

STEP 1:

for i=1 to RowSize do

for j=1 to colSize do

if scrambling_key(i,j) == 0 then

scrambled_host(row, col) = Host_Image (i,j);

end if

end for

end for

STEP 2:

for i=1 to RowSize do

for j=1 to colSize do

if scrambling_key(i,j) == 1 then

scrambled_host(row, col) = Host_Image (i,j);

end if

end for

end for

3.2.6. The Watermark Embedding Phase

The insertion of the preprocessed watermark data into the scrambled host image using the above-generated Rule-30-based embedding key is explained in this section. The numerical illustration of the watermark embedding phase is shown in Figure 5d. The encrypted watermark pixel values to be embedded are selected randomly based on the locations of the live cells (1s) in all the generations of the embedding-key starting from the first to the K^th generation and after covering all the live cells if there still are watermark pixel values left to be embedded then these values are also selected randomly based on the locations of the dead cells (0s) in the embedding-key starting again from the first to K^th generation. In the proposed scheme, the selected two-bit watermark data is inserted into the two-LSBs of the host image pixel values using the addition operation; therefore, it becomes obligatory to clear the previous values of the two-LSBs of the selected host image pixels and set them to zero which is achieved by first dividing and then multiplying each of them by four. The scrambled host image pixel values into which watermark data is to be embedded are selected in a sequential manner starting from the first pixel to the ‘n^th’ pixel where n = (Wm * Wn), i.e., the length of the watermark image. The pixels forming the selected sequence are not correlated at all as the host image is already scrambled and thus robust against the potential geometrical attacks. Subsequent to the insertion of all the 2-bit watermark pixel values, the updated scrambled host image is descrambled using the scrambling key that finally produces the watermarked image. The complete embedding process is described using pseudocode notation in the next section.

3.2.7. The Pseudocode Description of the Watermark Embedding Process.

The Algorithm 1 presents the pseudocode of the watermark embedding process of the proposed CA-based digital image watermarking scheme.

Algorithm 1 Watermark Embedding Algorithm

Input: Host (Hm*Hn), Scrambling_key (Hm*Hn), Embedding_key (Wm*Wn), and Watermark(Wm*Wn). Output: Watermarked_Image.    1: procedureEmbedding($HostImage,Scrambling\_key,Embedding\_key,Watermark$)       2:     $Wmark\_2\_MSB\leftarrow Downsizing\left(Watermark\right);$       3:     $Encrypted\_Watermark\leftarrow bitxor(Wmark\_2\_MSB,Encryption\_key);$       4:     $Scrambled\_Host\leftarrow Scrambling(Host,Scrambling\_key);$    ▹ The (Wm*Wn) Embedding_key consists of K (Wm*Wn) generations (Gen1, Gen2, Gen3 ..... GenK).       5:     $row\leftarrow 1;col\leftarrow 1;$    ▹ Covering the locations of the live cells (1s) in Gen1.       6:     for $i\leftarrow 1$ to $Wm$ do       7:         for $j\leftarrow 1$ to $Wn$ do       8:            if (Gen1[i][j] = 1) then       9:                $temp:=\left(floor\right(Scrambled\_Host\left[row\right]\left[col\right]/4)*4);$    ▹ The two MSBs of the encrypted watermark at index (i, j) are added to the two LSBs of the scrambled host image pixel at index (row, col).       10:                $Updated\_Scrambled\_Host\left[row\right]\left[col\right]:=temp+Encrypted\_Watermark\left[i\right]\left[j\right];$       11:                $col:=col+1;$       12:            end if      13:         end for      14:     end for   ▹ Covering the locations of the live cells in GenT, where T = 2, 3, 4...K and S = 1, 2, 3…T-1.       15:     for $i\leftarrow 1$ to $Wm$ do       16:         for $j\leftarrow 1$ to $Wn$ do       17:            if $\left(GenT\right[i\left]\right[j]=1)\mathbf{and}\left(GenS\right[i\left]\right[j]\ne 1)$ then       18:                $temp:=\left(floor\right(Scrambled\_Host\left[row\right]\left[col\right]/4)*4);$       19:                $Updated\_Scrambled\_Host\left[row\right]\left[col\right]:=temp+Encrypted\_Watermark\left[i\right]\left[j\right];$       20:                $col:=col+1;$       21:            end if      22:         end for      23:     end for   ▹ After covering all live cells, the pixel values at dead cells (0s) are selected       24:     for $i\leftarrow 1$ to $Wm$ do       25:         for $j\leftarrow 1$ to $Wn$ do       26:            if $\left(GenT\right[i\left]\right[j]=0)\mathbf{and}\left(GenS\right[i\left]\right[j]\ne 1)$ then    ▹$WhereT=1,2,3...K;S=1,2,3\dots KandS\ne T.$       27:                $temp:=\left(floor\right(Scrambled\_Host\left[row\right]\left[col\right]/4)*4);$       28:                $Updated\_Scrambled\_Host\left[row\right]\left[col\right]:=temp+Encrypted\_Watermark\left[i\right]\left[j\right];$       29:                $col:=col+1;$       30:            end if      31:         end for      32:     end for   ▹ Till all the watermark image bits are embedded.       33:     Watermarked_Image := Descrambling (Updated_Scrambled_Host, Scrambling_key)       34:     return $Watermarked\_Image;$       35: end procedure

3.2.8. The Watermark Extraction Phase

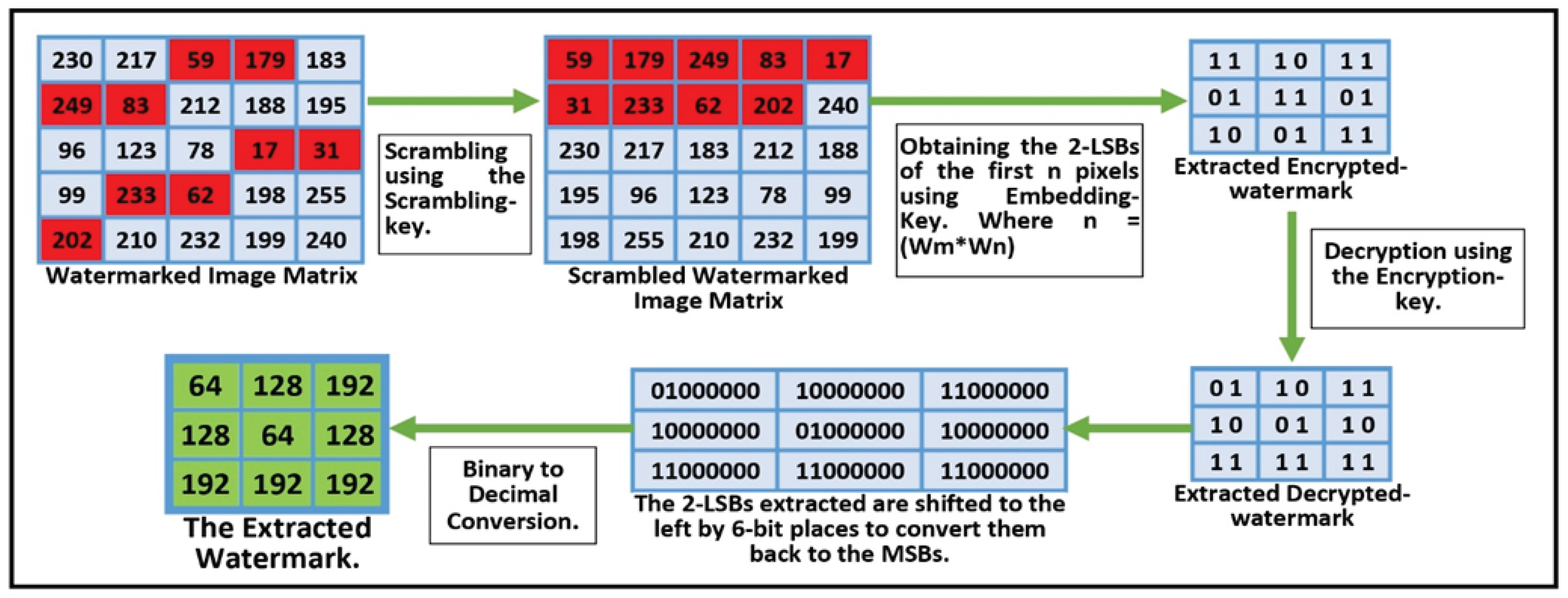
To retrieve the watermark image that was embedded using a specific technique, the inverse procedure of that technique is carried out, called watermark extraction. In the proposed scheme to extract the watermark, the watermarked image is first scrambled using the same scrambling key that was used during embedding. Then, from the scrambled watermarked image, the sets of 2-LSBs of the first n pixels are extracted where n = (Wm*Wn). These extracted n-sets of 2-LSBs are arranged in a (Wm X Wn) matrix based on the locations of all the live cells (1s) first and then the locations of the dead cells (0s) in all the generations of the embedding key. However, the retrieved watermark data is still encrypted and, therefore, undergoes a decryption process in which the Bitwise XOR operation of extracted watermark data with the encryption key is performed. Following decryption, each 2-bit pixel is shifted to the left by 6-bit places in order to get converted to the 8-bit pixel, as a result, extracted LSBs become the MSBs of the extracted watermark image after six left bit-shifts. The numerical illustration of the complete watermark extraction phase is shown in Figure 7.

4. Performance Analysis and Experimental Discussion

In this section, the effectiveness of the proposed algorithm is analyzed. The performance of the suggested scheme is evaluated by computing the various robustness and imperceptibility quality metrics and comparing the results with several existing algorithms [7,8,22].

4.1. Experimental Setup

The proposed watermarking scheme is implemented on the computer system with the following configuration: Intel Core i5-2410M CPU @ 2.30 GHz, 4.00 GB RAM, and Windows 7 Ultimate 64-bit SP1 operating system. It is designed, programmed, and analyzed using the MATLAB R2020a [39] platform. The grayscale logo image of size 128x64 is considered the watermark image while testing the proposed approach. The performance testing of the suggested scheme is performed on the dataset of 42 test host images shown in Figure 8. These test images are collected from various standard image databases, which are USC-SIPI [40], The Cell Image Library [41,42], The Cancer Imaging Archive (TCIA) [43], STARE [44], National Archives Catalog [45], NASA [46], and MATLAB Toolbox [39]. Some of the images in the dataset were originally color images and, therefore, required conversion to grayscale with a bit depth of eight, and that was achieved using MATLAB built-in image type conversion functions. The proposed algorithm was tested on the test host images of different dimensions and formats like png, tif, tiff, jpg, etc. The original size of the test images was not altered at all except for those from the NASA library, in which the size of huge images was reduced. To determine the efficiency of the suggested watermark system, its test results were compared with several existing systems.

4.2. Performance Evaluation Metrics

The most significant attributes, imperceptibility, robustness, and payload of the digital image watermarking system are computed by various image quality metrics that are given below. In contrast, when calculating the evaluation metrics, the original host image is used as a reference image to determine the quality of the watermarked images.

4.2.1. Imperceptibility

Imperceptibility refers to the notion that after embedding watermark data into the host image, its perceptual quality should be identical to the original host image. The five below-mentioned performance evaluation metrics are calculated to evaluate the imperceptibility attribute of the proposed watermarking system.

• Mean-Squared Error (MSE): The averaged intensity between the original host and the watermarked image is calculated using Mean Square Error. It gauges the degree to which a pixel varies from its original state. The smaller MSE value signifies that the watermarked image resembles the original host image. Equation (7) is used to determine MSE.

  $$MSE=\frac{1}{MN}\sum _{m=1}^M\sum _{n=1}^N{(H{I}_{(m,n)}-W{I}_{(m,n)})}^2$$

  (7)
  Where HI_(m,n) and WI_(m,n) denote the pixel values at index (m,n) in the original host image and the watermarked image, respectively, and MxN is the size of the images.
• Root Mean-Squared Error (RMSE): It is a quality assessment metric that is used for the error magnitude evaluation. It is derived by simply square rooting the MSE as illustrated in Equation (8).

  $$RMSE=\sqrt{MSE}$$

  (8)
• Peak Signal-to-Noise Ratio (PSNR): The well-known image quality metric widely used to evaluate the perceptual quality of the watermarked images with reference to the original host images is PSNR. It is derived from the MSE and is expressed as the ratio of the maximum pixel intensity to the power of the distortion. The PSNR value should be at least greater than 35 dB; the higher PSNR value denotes better imperceptibility. Equation (9) is used to determine PSNR.

  $$PSNR=10{log}_{10}\frac{{255}^2}{MSE}$$

  (9)
• Structural Similarity (SSIM) Index: The perceptual quality assessment metric that is used to measure the similarity between the original host image and the watermarked image is SSIM. The watermarked image has great perceptual quality if the SSIM value is close to 1. The SSIM of the watermarked image with reference to the original host image is determined using Equation (10).

  $$SSIM(HI,WI)=\frac{(2{\mu }_{HI}{\mu }_{WI}+C1)(2{\sigma }_{HIWI}+C2)}{({\mu }_{HI}^2+{\mu }_{WI}^2+C1)({\sigma }_{HI}^2+{\sigma }_{WI}^2+C2)}$$

  (10)
  Where µ_HI and µ_WI are the averages, ${\sigma }_{HI}^2$ and ${\sigma }_{WI}^2$ are the variances, and ${\sigma }_{HIWI}$ is the covariance of the original host image and watermarked image, respectively. C1 = (k1L)² and C2 = (k2L)²; L = (2^Bits/Pixel - 1), k1 = 0.01 and k2 = 0.03.
• Universal Quality Index (Q-Index): The distortion within an image is determined by the Q-Index. The range of the Q-Index is [-1 to 1], and its best possible value can be 1, indicating that the images are identical. The three parameters required to calculate the Q-Index are correlation, luminance, and contrast, which are calculated using Equation (11).

  $$Q=\frac{{\sigma }_{HIWI}}{{\sigma }_{HI}.{\sigma }_{WI}}.\frac{2\overline{HI}.\overline{WI}}{{\left(\overline{HI}\right)}^2+{\left(\overline{WI}\right)}^2}.\frac{(2{\sigma }_{HI}.{\sigma }_{WI}}{({\sigma }_{HI}^2.{\sigma }_{WI}^2)}$$

  (11)

4.2.2. Robustness

The robustness of the image watermarking system is a measure of the ability of the embedded watermark to resist and remain unaffected by various intentional and unintentional attacks, thus implying the system’s reliability. To evaluate the robustness attribute of the proposed watermarking system, the original watermark is compared to the extracted watermark using the below-mentioned performance evaluation metrics.

• Correlation Coefficient (CC): When evaluating a watermarking scheme’s robustness to various attacks and transformations, the correlation coefficient is an essential statistical measure to consider. It gives information about how well the system will maintain the watermark’s integrity and tolerate changes while retaining the ability to allow accurate watermark extraction. The correlation coefficient quantifies the intensity and direction of the linear relationship between the original watermark and the extracted watermark. Equation (12) can be used to determine the correlation coefficient value, which ranges from 0 to 1.

  $$CC(OW,EW)=\frac{{\sum }_{(m=1)}^M{\sum }_{(n=1)}^N(O{W}_{(m,n)}-\overline{OW})(E{W}_{(m,n)}-\overline{EW}))}{\sqrt{\left({\sum }_{(m=1)}^M{\sum }_{(n=1)}^N{(O{W}_{(m,n)}-\overline{OW})}^2\right)\left({\sum }_{(m=1)}^M{\sum }_{(n=1)}^N{(E{W}_{(m,n)}-\overline{EW})}^2\right)}}$$

  (12)
  Where OW_(m,n) and EW_(m,n) denote the pixel values at index (m,n) in the original watermark image and the extracted watermark image, respectively. The $\overline{OW}$ is the mean of the original watermark image, and the $\overline{EW}$ is the mean of the extracted watermark image.
• Bit Error Ratio (BER): The ratio of the total number of errored/corrupted bits to the total number of bits in the image is referred to as the bit error ratio and is calculated using Equation (13).

  $$BER=\frac{\left(TotalErroredBits\right)}{\left(TotalBits\right)}$$

  (13)

5. Comparative Analysis

The performance of the suggested method in terms of robustness and imperceptibility is discussed in this section.

5.1. Imperceptibility Analysis

The imperceptibility results of the proposed watermarking scheme are compared to the current state-of-the-art cellular automata-based methods to analyze the relative performance of the proposed scheme. Table 2 includes the multiple image quality metrics to determine the effectiveness of different image watermarking methods in terms of their imperceptibility. The values of these metrics are compared across multiple techniques, namely Ye and Li [22], Adwan et al. [7], Moniruzzaman et al. [8], and the Proposed Scheme. The lower MSE and RMSE values and the higher PSNR, SSIM, and Q-Index values are indicators of the superior perceptual quality of an image. It has been determined that among the evaluated techniques, the proposed scheme consistently outperforms the other assessed schemes in all metrics. It repeatedly results in the lowest MSE values for all the test images, reflecting higher accuracy in watermarked images. The proposed scheme also emphasizes its potential to reduce the average difference between the original and watermarked images by having the lowest RMSE values. Regarding PSNR, the proposed scheme consistently performs better than the other techniques. It can be observed that greater PSNR values are constantly obtained for all the test images in the dataset by the proposed Scheme, which implies greater retention of image details and less quality loss than the other techniques under evaluation. The higher SSIM results further demonstrate the positive aspects of the proposed scheme in retaining the image’s structural information and its capacity to preserve the visual composition and attributes of the original images. Finally, the higher values of the perceptual quality metric Q-Index indicate that the proposed scheme generates watermarked images with better overall quality.

After accounting for all the given parameters, we can certainly infer that the proposed scheme demonstrates strong performance in the grayscale image watermarking process. It consistently performs better than the other techniques (Ye and Li [22], Adwan et al. [7], and Moniruzzaman et al. [8]) in terms of lower MSE and RMSE values, and higher PSNR, SSIM, and Q-Index values thus assuring the superior perceptual quality of the watermarked image. The proposed scheme can be seen as a reliable and high perceptual quality approach for performing digital grayscale image watermarking tasks.

5.2. Robustness Analysis

This section provides a comprehensive assessment of the robustness of the proposed scheme when subjected to an extensive spectrum of deliberate attacks. The proposed watermarking algorithm has undergone a meticulous evaluation on an extensive dataset comprising 42 diverse test images, aimed at assessing its robustness against a wide spectrum of potential attacks, with the evaluation criterion being the Correlation Coefficient (CC), the Number of Erroneous Bits (NEB), and the Bit Error Ratio (BER). The consequential findings, stemming from the execution of multifarious attack scenarios upon the watermarked images, are comprehensively documented in Table 3 and Table 4 for detailed examination and analysis.

5.2.1. Robustness against Cropping Attacks

An intentional removal or trimming of portions of a digital image with the goal to change its content or context—possibly leading to misinterpretation or removal of copyright information and watermarks are known as image cropping attacks. It is a kind of modification that compromises the integrity of an image, and can vary in scale and intent. This analysis aims to evaluate the robustness of a proposed watermarking technique under various cropping scenarios. The watermarked images are manipulated by applying different cropping percentages such as 6%, 10%, 20% and 35% at different segments like top-left, top-right, bottom-left, bottom-right, center and, all the sides of the watermarked images. The impact of these cropping scenarios on the extracted watermark quality is assessed, specifically considering correlation coefficients and bit error ratios. The analysis according to the Table 3 underscores that the proposed watermarking technique is highly robust as it maintains a high correlation coefficient even with substantial cropping. It also demonstrates that the proposed scheme is effective at preserving watermark integrity across different cropping scenarios.

5.2.2. Robustness against Noise Attacks

A noise attack denotes the unwanted introduction of stochastic perturbations, or “noise,” into watermarked images, leading to a degradation in image fidelity and perceptual acuity. Noise manifests diversely, manifesting as erratic pixel fluctuations within images, the emergence of granular patterns, sporadic conspicuous anomalies in luminosity, or the distortion of chromatic properties. The incursion of noise can be attributed to various sources, encompassing electromagnetic interference, the propagation of signals with imperfections or distortions, or the inherent limitations of data acquisition apparatuses. The watermarked images were subjected to the addition of Speckle and Salt & Pepper noises in order to assess the proposed watermarking scheme’s robustness against noise attacks. The salt & pepper noises with varying noise densities and multiple variances of the speckle noise were introduced into the watermarked images to evaluate the proposed approach. Table 4 shows the results for the salt & pepper noise with noise density = 0.01 and speckle noise with variance = 0.01 and the outcomes imply that the proposed scheme is very robust to these kind of attacks.

5.2.3. Robustness against Sharpening Attacks

The image processing procedure designed to heighten image acuity and refine its visual details is sharpening. When it comes to digital image alteration, a “sharpening attack” is an intentional attempt to utilize image sharpening techniques to make a watermark on an image less visible or effective. Such an attack usually aims to hide, modify, or remove a watermark (such as a logo or copyright notice) that has been superimposed on an image in order to preserve its ownership or copyright. Enhancing the contrast and sharpness of the image might make the watermark less visible or perhaps unreadable. To determine how robust the proposed strategy is, the impact of sharpening attacks on the extracted watermark quality is evaluated. The sharpening attacks of varying strengths i.e, multiple values for amount variable at multiple radiuses are applied to the watermark images. The study based on Table 4 highlights how robust the suggested watermarking method is since it keeps a high correlation coefficient even when there is significant sharpening. It also shows that the suggested scheme works well to maintain watermark integrity under various sharpening conditions.

6. Conclusions and Future Work

Cellular automata (CA) are a notable and sophisticated model that has shown considerable potential in improving the security and reliability of digital assets when it comes to digital image watermarking. CA-based watermarking techniques have demonstrated several impressive qualities, such as robustness to frequent attacks, the embedded watermarks’ imperceptibility, and effective data embedding in images. Through this research, we have explored a CA-based watermarking strategy governed by rule-30, which demonstrated its efficacy in protecting digital images against unauthorized use, unauthorized modification, and infringement on intellectual property.

Even if there have been a lot of noteworthy advances in the field of CA-based digital image watermarking, there are still a lot of uncharted territories that want more research and development. Fortifying CA-based watermarking approaches against a larger range of threats should be the primary focus of future research endeavors. To make these techniques more resistant to a wider range of attacks, such as geometric transformations, compression-induced distortions, and complex signal processing techniques, this may involve discovering more complex rule sets and carefully integrating machine learning paradigms. The security component must be given prominent attention. The vulnerability of CA-based watermarking techniques to complex and advanced attacks should be thoroughly examined in future investigations. One of the key goals is to maximize the watermarking capacity while preserving the image’s visual quality. Subsequent research endeavors may explore and develop algorithms that augment data-hiding efficacy, guaranteeing that watermarks remain undetectable while concurrently optimizing the amount of information that may be incorporated. A promising direction for future research is to modify CA-based watermarking techniques for real-time use. This could apply to the watermarking of videos or the protection of streaming media, where quick data processing is critical.

To sum up, the integration of cellular automata with digital image watermarking has shown considerable potential and cracked the gate to further study and development. Dedicated efforts in this area have the potential to offer safe and effective ways to protect digital assets in an increasingly digital environment as the digital world grows and develops over time.