Prerpints.org logo
Preprint
Article

Li on a Ch Divacancy Self-Healed Graphane: A First -Principles Study

Altmetrics

Downloads

105

Views

173

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

22 November 2023

Posted:

22 November 2023

You are already at the latest version

Alerts
Abstract
The possibility of using graphane monolayer crystals as the electrode material is becoming popular. Graphane is stable at room temperature and has large surface area, but its chemical inertness hinders its direct interactions with Li ions. In this study, we performed density functional theory calculations to study the energetic stability, structural and electronic properties of Li on graphane with various CH divacancy configurations (v12, v13 and v14 ). The results show that adsorption of Li atom reduces the formation energy of the CH divacancy configurations. The Li-v12 is most stable with the highest binding energy of 3.25 eV/Li and relaxes to in-plane with other C atoms. Altering the Li charge state to have Li−1-v12 or Li+1 -v12 affects the energetic stability and electronic characters of Li-v12 . The Li−1-v12 (Li +1-v 12 ) enhances (reduces) the binding force between Li and v 12 configuration, and furthermore it improves (deteriorates) the conductivity of the structure. Further investigation of graphane with vacancies is encouraged due to these intriguing observations, as it holds promise for potential utilization as an electrode material.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

1. Introduction

Lithium-ion batteries (LIBs) have been widely used as power sources for most of electronic devices[1]. The LIBs are known to be non-toxic, have long discharging rate, have high energy density etc[1,2,3]. The most used electrode in LIBs is graphite [1]. Nevertheless, many properties, such as the specific capacity, are unlikely to meet the increasing future demand for high energy. The search for alternative electrode materials with distinct properties from graphite is rapidly intensifying [4,5,6]. The two-dimensional (2D) materials are emerging as promising candidates to address future energy demands due to their high electrical conductivity, reduced dimensionality, high thermodynamic stability, large surface area etc., distinguishing them from their bulk counterpart [7,8,9]. These properties make 2D materials well suited to accommodate a greater number of Li atoms, among other advantages.
Graphane [10] monolayer material falls under materials belonging to the graphene derivatives were each carbon is bonded to hydrogen atom in an alternating pattern. The realization of graphane was first reported by Sluiter et al. [11], based on the density functional theory (DFT). Graphane was later synthesized [12,13] by applying hydrogen plasma to graphene monolayer samples. The graphane samples were found to be stable at room temperatures [12]. Each carbon atom’s bonding network takes on the form of sp3 hybridization due to the presence of hydrogen atoms [13].
Experimental studies report that graphane has insulating characters [12]. This was supported by the theoretical studies which predicted the energy band gap of 3.50 eV (standard DFT) [10], 5.40 eV (GW)[14], 4.21 eV (HSE06)[15]. Graphane has a large surface area, high volumetric capacity, non-toxic samples [13,16,17]. These indicators suggest that a graphane monolayer could find utility in a range of technological application. The focus of this work is on the mechanisms of enchoring the Li ions on the graphane monolayer for electrode exploitation. Theoretically, an inertness [13,16,17] (under ambient conditions) of C atoms conjugating graphane monolayer due to the sp3 bonding network could physisorb instead of chermisorbing Li ions, which will be a setback for encoring Li atoms. Watcharinyanon et al. [18] studied intercalation of Li ions on graphane using experimental techniques. They reported that instead of bonding with the substrate Li atoms form islands among themselves. The DFT studies by Yang et al. [19] revealed that Li ions are screened by H atoms, as such no chemisorption takes place.
The modification of graphane monolayer for possibility of enhancing Li interaction is necessary. Several methods are known for introducing reactive sites on graphane, potentially enhancing its interaction with Li ions. These methods include structural modification like creating vacancies, doping, strain application, among others [13,16,17,20]. Creation of vacancies in graphane can primarily be in different forms: hydrogen (H) vacancy, carbon (C) vacancy, carbon-hydrogen (CH) vacancy.The creation of multiple vacancies is also possible in graphane monolayer. H divacancy, trivacancy and CH divacancy, trivacancy have been created in graphane monolayer. These vacancies can be created by applying high or low ions bombardment, and they can also occur during synthetic processes [13,16,17,20]. Numerous properties of these mentioned vacancies have been examined, ranging from their energetic stabilities to their magnetic properties [13,16,17,20,21,22,23,24]. With the exception of the divacancy structure, all other types of vacancies introduce mid-gap states within the band gap and exhibit magnetic properties.
The structural and electronic behavior of CH divacancies in graphane have been studied using DFT [24]. The structural reconstruction of the two adjacent vacancies has been reported, which break the hexagonal symmetry and translates into the new 5-8-5 defect structure that is thermodynamically stable. Graphane with 5-8-5 defect structure is characterized as a wide band gap material [24]. Considering the potential of utilizing graphane with this defect structure as an electrode holds merit. Notably, the adsorption of Li ions onto the graphane with 5-8-5 defect structure remains unexplored. A comprehensive understanding of how Li anchors at different charge states on graphane is imperative. This helps to understand the energetic and electronic behavior of Li during charging and discharging. This study intends to understand the energetic stabilities (formation energy and binding energy), structural properties (bondlength) and electronic properties (density of states) of Li on the graphane with 5-8-5 defect structure at different Li charge states (+1 or -1). This study relies on a spin-polarized density functional theory approach, and the outcomes will serve as a reference for the experimentalists to corroborate their findings during practical synthesis and characterization processes.
This manuscript is arranged as follows: the computational details and equations for calculating formation and binding energies are presented in section 2. The results of Li on graphane monolayer with vacancies are summarized in section 3. Section 4 concludes the results.

2. Computational Details

All the spin polarized calculations in this study have been performed using hybrid density functional theory (DFT) approach implemented within the Vienna ab initio simulation package (VASP) code [25]. The chosen hybrid exchange correlation functional is the Heyd, Scuseria, and Ernzerhof (HSE06) [26], which the PBE functional is mixed with the non-local Fock. The Fock mixing parameter used is 0.25 which it is known to give the correct band gap of 2D materials. In this study it was selected with the intention of enhancing the magnitude of the band gap and providing a more accurate description of the positions of electronic states induced by defects within the band gap. For the description of pseudopotentials, the projector augmented wave (PAW) methods [27] with C atoms represented as 2s22p2, H atoms represented by 1 s 1 and Li adatom represented as 2s1 valence electrons.
The kinetic energy cut-off of 500 eV was used for the expansion of the plane wavefunctions. For sampling the Brillouin zone of graphane monolayer, the 6×6×1 k-mesh grid was used, employing the Monkhorst-Pack scheme [28] method. This k-mesh grid is doubled during the density of states calculations. The atomic positions were allowed to relaxe until their residual forces are less than 0.01 eVÅ−1 utilizing the Hellman-Feynman theorem. The total energies of the structures were allowed to converge to within 10−7 eV during the self-consistent field calculations of each relaxation. The 9×9 supercell of graphane was used for all our calculations. This supercell size was chosen to ensure that the divacancy interaction between the cell images along the x and y direction is minimal. The separation spacing between the layers was set to the converged 20 Å , to avoid unwanted interactions due to periodic images.
To study the energetic stability of Li on a graphane with various CH divacancy configurations (v12, v13 and v14), their formation energies were calculated employing the Zhang-Northrup expression [29] below:
E f ( C H ) = E t o t ( C H ) − E t o t ( G ) − ∑ i n i μ i ,
where E t o t ( C H ) is the total energy of Li on a CH divacancy configuration in a 6×6 graphane supercell and E t o t ( G ) is the total energy of 6×6 pristine graphane. The μ i in equation 1 represents the chemical potential of H, C and Li atoms calculated as the total energies per atom of isolated hydrogen molecules in a large box, graphene and Li in bulk body centered cube (BCC), respectively. n i represents the number of atomic species (H, C and Li atoms) removed or adsorbed on the graphane monolayer system.
To assess the interactions between the Li adatoms and various configurations of CH divacancies in graphane monolayer, we calculated the binding energies as follows:
E b = E t o t ( C H L i ) − E t o t ( C H ) − n L i E t o t ( L i ) n L i ,
where E ( C H L i ) is the total energy of Li adatom on a CH divacancy in a 6×6 graphane supercell, E ( C H ) is the total energy of 6×6 graphane with divacancy and E ( L i ) is the total energy per adatom of Li in a bulk body centered cube (BCC).

3. Results and Discussion

3.1. Proposed Structures Studied

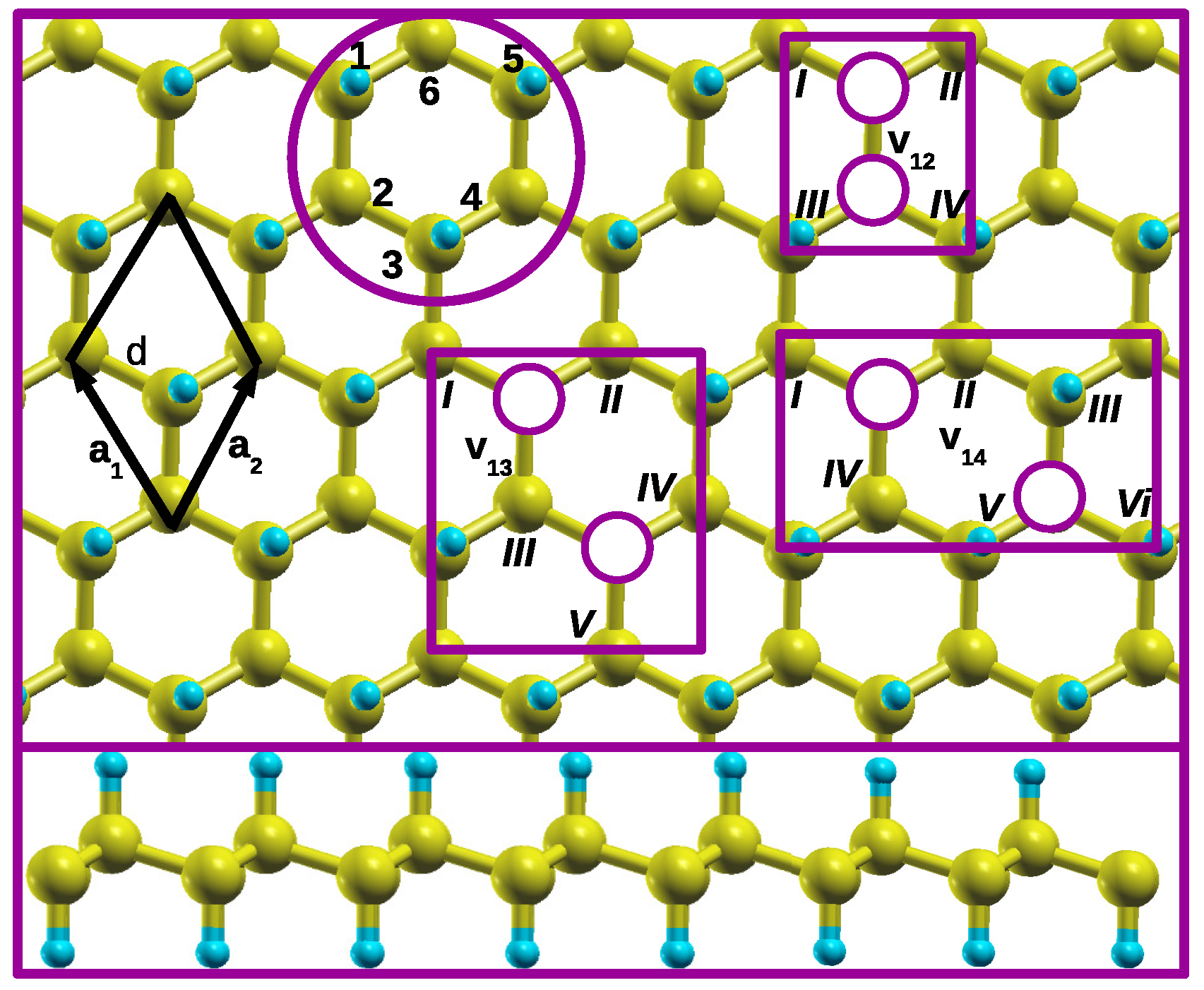
Firstly, we demonstrate how different CH pair divacancy configurations are identified on an isolated single hexagon in a graphane monolayer. A single hexagon in a graphane monolayer is shown in Figure 1 circled with purple. The numbers 1-6, position around an isolated single hexagon, serve as labels for the CH pairs that should be removed during the vacancies creation in this study. These numbers 1-6 are also used to name different vacancy configurations. In this paper, we report a systematic study of different CH pair divacancy configurations presented in Figure 1.
Three distinct configurations are identified as follows: (1) v12 configuration, this configuration consist of a CH divacancy where two CH pairs are adjacent to each other. It is denoted as v 12 configuration, meaning that two adjacent CH pairs are removed from positions 1 and 2 of the single hexagon, as illustrated in Figure 1. (2) v13 divacancy configuration, in this configuration there are two CH pairs vacancies at positions 1 and 3, with which CH pair at position 2 separate them. (3) v 14 configuration, this configuration represents the two CH pair vacancies at positions 1 and 4, facing each other, and separated by the two CH adjacent pairs. These configurations describe different arrangements of CH pair vacancies within the hexagonal structure.

3.2. Thermodynamic Stability and Structural Properties of Different CH Vacancy Configurations

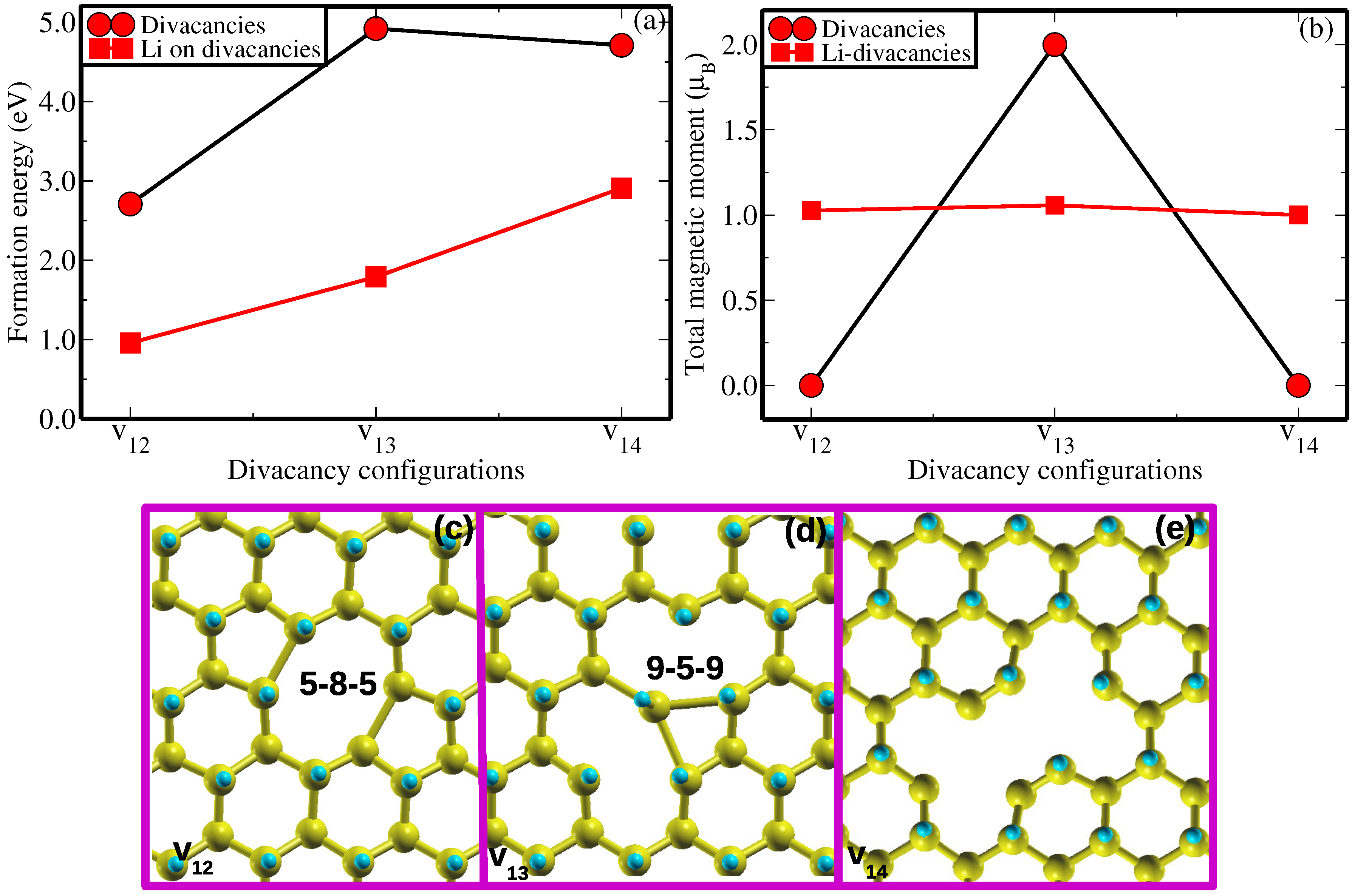
As a common practice in first-principles work, the relative stabilities of various vacancy defects configurations in the host materials are evaluated through the formation energy analysis. In this study, we conduct a comparative analysis of energetic stability of previously mentioned distinct divacancy configurations, namely v12, v 13 and v14. This comparison is based on their calculated formation energies ( E F o r m (v)), as illustrated in Figure 2 and indicated by the red circles. All calculations are computed at the same level of accuracy. As shown in Figure 2a, divacancy configuration v12 has the lowest formation energy of 2.71 eV/ v C H . This value is 2.21 eV/ v C H and 2.00 eV/ v C H lower than those of v 13 and v 14 , respectively. Perhaps this could be the reason the previous study [24] only report properties of v 12 divacancy configuration. As is often observed in many material studies, we have observed that the thermodynamic stability of the v 12 , v 13 and v 14 configurations is significantly influenced by the structural reconstruction and the behavior of dangling bonds around the vacancy within a graphane layered structure, after relaxation.
In v 12 configuration (seen in Figure 2c), the pair dangling C atoms I and I I as well as the C atoms I I I and I V attract each other ’to a certain extent’ forming a weak bondlength of d I , I I = d I I I , I V = 1.99 Å after geometry optimization. This structural reconstruction or self-healing forms a ’peculiar’ vacancy defect type of 5-8-5 divacancy structure as shown in Figure 2c, is in good agreement with the results of Ref [24]. Such type of defect has experimentally been realized in graphene, the mother of graphane, using the high-energy ion beams creating a stable carbon chain [30]. Figure 2b shows that v 12 lacks a magnetic moment, indicating that structural reconstruction of the dangling C atoms suppresses any potential magnetic moment in agreement with Ref [24].
In a v 13 divacancy configuration, a C atom I I I having possibly two unpaid electrons (based on electronic counting) relaxes towards another two C atoms I I and I V . The equivalent bond distances d I I I , I I and d I I I , I V of 2.42 Å are formed between C atoms I I I and I I as well as between C atoms I I I and I V , respectively. This reconstruction of v 13 divacancy configuration yields an unusual defect structure of 9-4-9 type (see Figure 2d). It is possible that the construction of 9-4-9 defect structure does not saturates all the dangling bonds surrounding the vacancy, hence the magnetic moment of 1 μ B has been achieved (Figure 2b). This could be attributed to the C atoms I and I I I each still having an unpaired electron after structural relaxation. Figure 2e presents the relaxed geometry of a v 14 divacancy configuration. The C atoms I, II, III, IV, V and VI are unable to rearrange to form any typical vacancy defect. Based on electron counting, v 14 remains with six unpaired electrons (one electron on each C atom I, II, III, IV, V and VI) after structural relaxation. The absent of total magnetic moment in this system (Figure 2b) could be the result of the cancellation of opposite electronic spins.

3.3. Effect of Li on the Energetic Stability and Structural Properties of Different CH Vacancy Configurations

We now examine the effects of Li atom on the energetic stabilities, structural and electronic properties of v 12 , v 13 and v 14 configurations. Initially, we adsorbed Li atom on the biggest hollow site of each vacancy configuration, i.e v 12 (octagon site), v 13 (nanogon site) and v 14 (largest site). Figure 2a shows the effect of Li atom on the energetic stability of v 12 , v 13 and v 14 configurations. It is noted that the Li atom energetically stabilizes the v 12 , v 13 and v 14 configurations through reduction of their formation energies. The formation energy of Li- v 12 configuration, which is 0.96 eV, suggests that although it is endothermic (requiring an input of energy), it can be relatively easily synthesized compared to the Li- v 13 and Li- v 14 configurations.
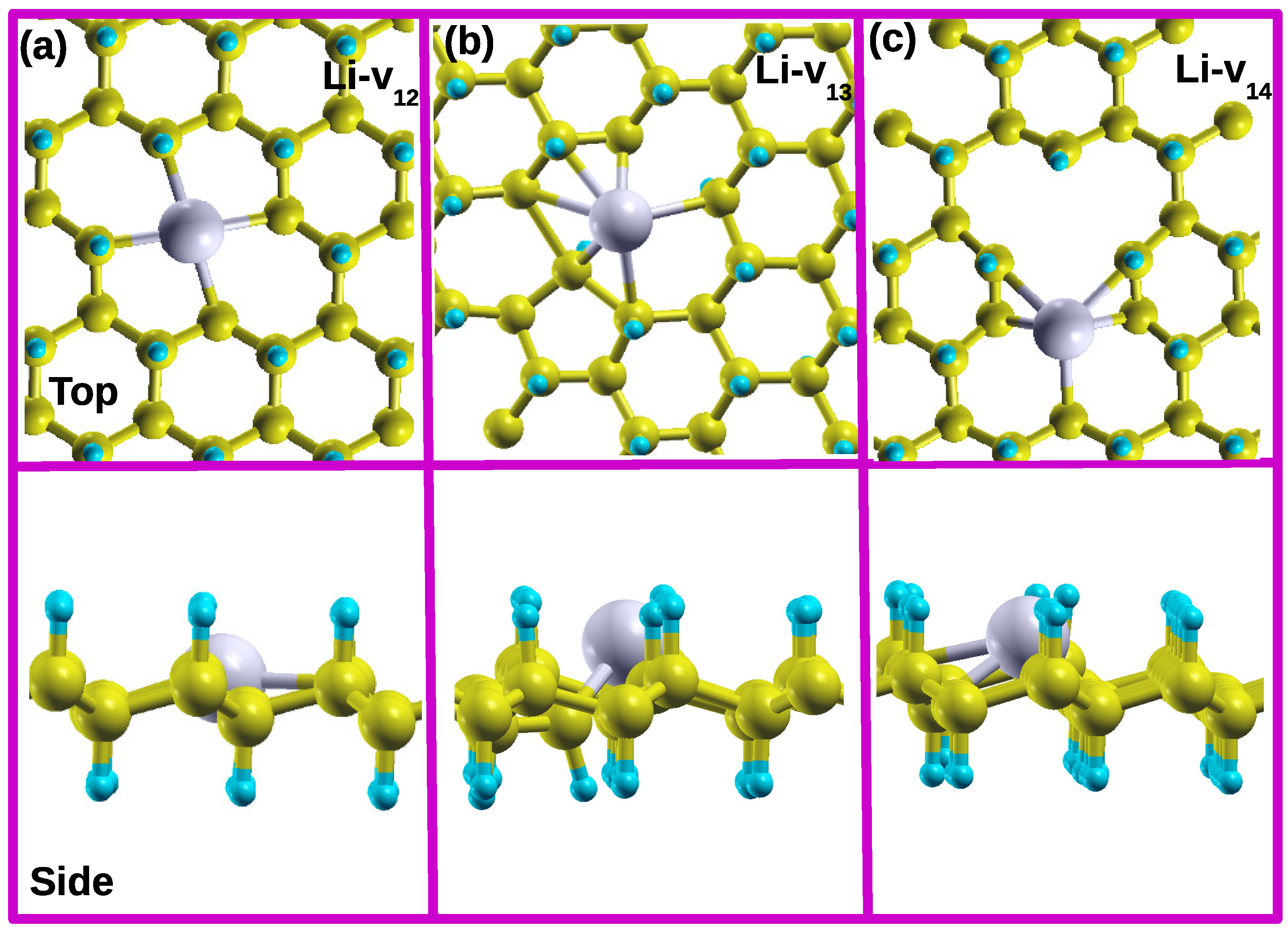
Figure 3a–c present the relaxed structures of Li atom on the different CH divacancy configurations Li- v 12 , Li- v 13 and Li- v 14 , respectively. In these configurations, the Li atom relaxes closer to the hollow site, which has an impact on the local vacancy structures. Figure 3(a) shows that in the case of Li- v 12 , Li atom remains within the octagon hollow site leading to a height of 0.00 Å (insertion to remain in-plane with other C atoms). Consequently, this results in an increase in the bond distances d I I I , I I and d I I I , I V to 2.63 Å equivalently. This has led to the high amount of the binding force (greater enchoring) between Li and the substrate with a binding energy of 3.25 eV. The Li- v 12 interactions induced a magnetic moment of 1.00 μ B as shown in Figure 2b. Figure 3b shows that Li- v 13 buckled up after relaxation, hence this leads to a height of 0.62 Å with a binding energy of 2.07 eV. Figure 2b shows that Li adsorption on a v 13 reduces the magnetic moment from 2.00 μ B to 1.00 μ B . In this configuration, the vacancy defect structure of 9-4-9 reconstructs to create a penta ring and v C H (closest to each other) separated by a newly formed bondlength d I I I , I I of 1.72 Å. The latter value is less than that of its counterpart in 5-8-5 defect without a Li atom. In the Li- v 14 configuration, the Li atom relaxes to a height of 1.54 Å with a binding energy of 1.99 eV. Notably, there is no significant reconstruction observed in this configuration, as depicted in Figure 3c.
The binding energies for Li- v 12 , Li- v 13 and Li- v 14 configurations, respectively, are relatively larger than that of Li on pristine graphene (1.04) eV [31] and on a single vacancy ( v C H ) in graphane [15], calculated on the same level of accuracy. The binding energies between Li and v 12 , v 13 and v 14 configurations are more than the Li bulk cohesive energy (1.63 eV), suggesting no chances of Li clusters formation but possible short time Li charging.

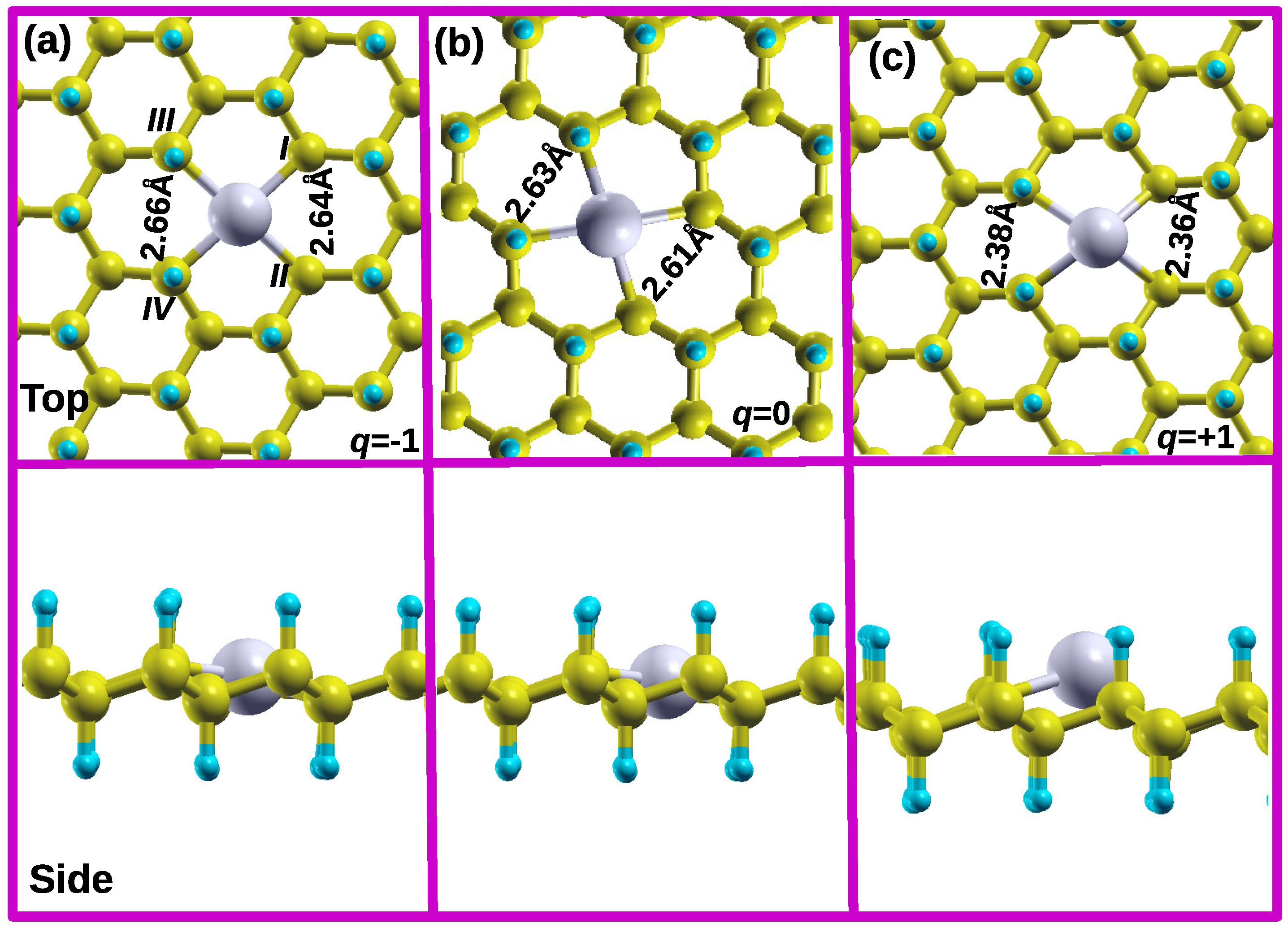
3.4. Influence of Different Charge States (-1, and +1) on the Energetic Stability, Structural and Electronic Properties of Li- v 12

In this section, we examined the effects of Li charge state alteration on the energetics, local structure around the v 12 vacancy and electronic properties (DOS) and make camprison with those of the uncharged structure. The charge states considered on Li- v 12 are q = -1 and +1 of which their respective structures are denoted as L i − 1 - v 12 and L i + 1 - v 12 . The binding energies for L i − 1 - v 12 and L i + 1 - v 12 structures are 3.21 eV and 2.24 eV respectively. In comparison with the uncharged binding energy shown in Table 1, the charge doping reduces the binding force between the Li atom and v 12 substrate, significantly in configuration L i + 1 - v 12 .
In the case of an addition of electron (L i − 1 - v 12 ), a Li atom remains within the octagon hollow site, maintaining the same in-plane level with other C atoms leading to a height of 0.00 Å as shown in Figure 4a. Figure 4a shows that the bond distances d I I I , I I and d I I I , I V increases slightly by 0.03 Å as compared to uncharged Li- v 12 (Figure 4b), which is an indication that an addition of electron in to the system (L i − 1 - v 12 ) increases the repulsion force between the C atoms surrounding the Li atom. For the removal of electron (L i + 1 - v 12 ), Li atoms moves slightly upward to a height of 0.51 Å. Figure 4b shows that the bond distances d I I I , I I and d I I I , I V decreases significantly by 0.25 Å as compared to uncharged Li- v 12 (see Figure 4b). This is an indication that the removal of electron from the system (L i + 1 - v 12 ) enhances the attraction force between the C atoms surrounding the Li atom.
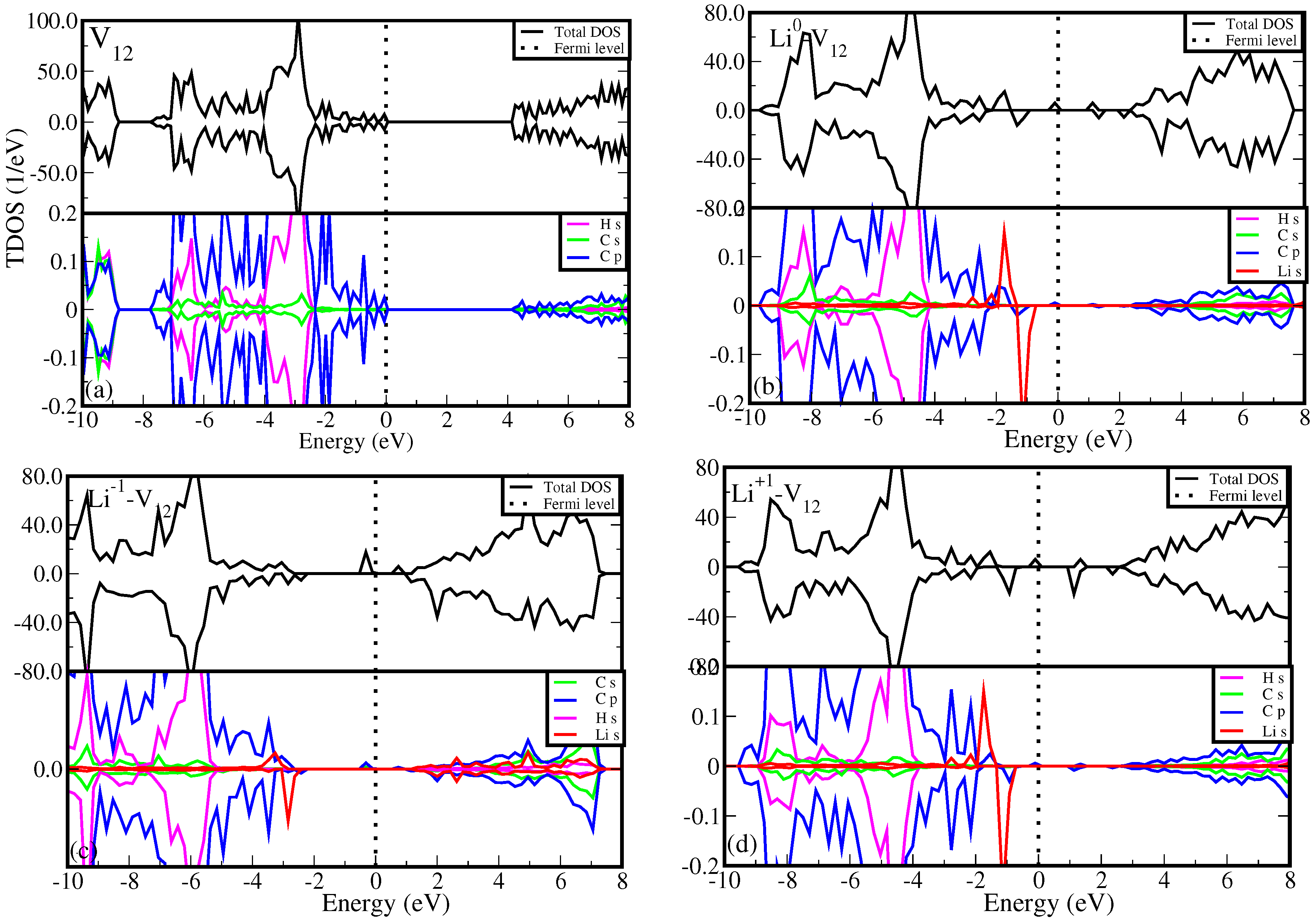
Figure 5 presents the density of states (DOS) for the most stable Li- v 12 configuration, comparing with that of without Li counterpart ( v 12 ). Figure 5a (top panel) shows that v 12 has the insulating features with a wide band gap of 4.18 eV (HSE06) between the valence band maximum (VBM) and conduction band minimum (CBM). The VBM and CBM are mainly contributed by the carbon p orbital states as shown on Figure 5a (bottom panel). This is in agreement with Pujari et al. [24] reporting that the carbon atoms surrounding the divacancy rearrange to form two new σ bonds leading to the formation of 5-8-5 ringed structure with a band gap of 3.00 eV (GGA). Figure 5b (top panel) shows the effects of Li atoms on the DOS of v 12 . It is noted that Li atom shifts the Fermi level from the VBM towards the middle of the band gap (suggesting an excess of electrons in the system). It also introduces the occupied and unoccupied states at distinct positions with some crossing the Fermi level in a spin up channel, suggesting metallic character. The observed states are due to hybridization of carbon p orbital and Li s orbital states (Figure 5b (bottom panel)). An addition of electron into the system (L i − 1 - v 12 ) shifts the Fermi level further towards the CBM Figure 5c. It is interesting to realize that the partially filled mid gap states as shown in Figure 5b becomes fully occupied in Figure 5c. The removal of electron from the system (L i + 1 - v 12 ) shifts the Fermi level back towards the VBM (Figure 5d). Retaining the metallic character of the system with the partially filled states crossing the Fermi level. Alteration of charge states of Li atom changes the electronic behavior of Li- v 12 structure. We propose that graphane with Li- v 12 may serve as a suitable electrode material for LIBs. This suitability arises from the potential enhancement of electronic transmission performance mechanisms facilitated by the newly identified Li states.

4. Conclusions

The adsorption mechanisms of Li on graphane with various CH divacancy ( v 12 , v 13 and v 14 ) configurations have been studied using DFT approach. Firstly, we compared the energetic stability (formation energies) and structural aspects (bond lengths) for v 12 , v 13 and v 14 configurations. Employing structural optimization calculations, it was established that there is a vacancy reconstruction leading to a new defect configuration surrounded by the hexagonal rings in graphane. The v 12 translated to 5-8-5 defect configuration and is the most stable CH divacancy configuration. Furthermore, we adsorbed Li on v 12 , v 13 and v 14 configurations. The formation energy annalys revealed that Li tends to stabilizes these CH vacancies, with Li- v 12 being most stable and Li atom relaxes to the same in-plane level with C atoms on the octagon ring. Li interacts strongly with v 12 at a highest binding energy of 3.25 eV/Li, more than the Li bulk cohesive energy of 1.63 eV/Li. The charge doping L i − 1 - v 12 or L i + 1 - v 12 alters the energetic stability, structural properties and electronic characters of Li- v 12 . The L i − 1 - v 12 configuration has more binding energy that L i + 1 - v 12 configuration. The electronic density of states plot for L i − 1 - v 12 reveals an abundance of electrons and increase in conductivity. These interesting observation encourages further studies on designing graphane with vacancies and its characterization for LIBs.

Acknowledgments

The authors acknowledge the University of Pretoria for financial support and availability of computational resources. We express gratitude to the National Institute for Theoretical and Computational Sciences (NITheCS) for funding. Center for high performance computing (CHPC) in cape town is acknowledged for state-of-the-art resources.

References

  1. J.M. Tarascon, M. Armand. Nature 2001, 414, 359. [Google Scholar]
  2. N. Oyama, T. Tatsuma, T. Sato, T. Sotomura. Nature 1995, 374, 196. [CrossRef]
  3. D.P. Dubal, O. Ayyad, V. Ruiz, P. Gómezromero. Chem. Soc. Rev. 2015, 44, 1777. [CrossRef] [PubMed]
  4. H. Wang, L.F. Cui, Y. Yang, C.H. Sanchez, J.T. Robinson. J. Am. Chem. Soc. 2010, 132, 13978. [CrossRef] [PubMed]
  5. F. Zou, X. Hu, Z. Li, Q. Long, C. Hu. Adv. Mater. 2014, 26, 6622. [CrossRef] [PubMed]
  6. X. Sun,W. Si, X. Liu, J. Deng, L. Xi. Nano Energy 2014, 9, 168. [CrossRef]
  7. K-S. Chen, I. Balla, N. S. Luu, and M. C. Hersam. Emerging opportunities for two- dimensional materials in lithium-ion batteries. ACS Energy Letters 2017, 9, 2026–2034. [CrossRef]
  8. L. Peng, Y. Zhu, D. Chen, R. S. Ruoff, and G. Yu. Two-dimensional materials for beyond- lithium-ion batteries. Adv. Energ Mater. 2016, 11, 1600025. [CrossRef]
  9. H. Li, Y. Shi, M-H. Chiu, and L-J. Li. Emerging energy applications of two-dimensional layered transition metal dichalcogenides. Nano Energy 2015, 18, 293–305, ISSN 2211-2855. doi: https: URL https://www.sciencedirect.com/science/article/pii/S2211285515004024.. [CrossRef]
  10. J. O. Sofo, A. S. Chaudhari, and G. D. Barber, Phys. Rev. B. 2007, 75, 153401.
  11. M.H.F. Sluiter, Y. Kawazoe, Cluster expansion method for adsorption: application to hydrogen chemisorption on graphene.[?]hys Rev B. 2003, 68, 085410.
  12. D. C. Elias, R. R. Nair, T. M. G. Mohiuddin, S. V. Morozov, P. Blake, M. P. Halsall. A. C. Ferrari, D. W Boukhvalov, M. I. Katsnelson, A. K. Geim, and K. S. Novoselov, Science. 2009, 323, 610.
  13. C. Zhou, S. Chen, J. Lou, J. Wang, Q. Yang, C. Liu, D. Huang and T. Zhu, Nanoscale Research Letters. 2014, 9, 26.
  14. S. Lebègue, M. Klintenberg, O. Eriksson, M. I. Katsnelson., Phys Rev B. 2009, 79, 245117.
  15. R.E. Mapasha, M.P. Molepo, N. Chetty, RSC Adv. 2017, 7, 39748–39757.
  16. H. Sahin, O. Leenaerts, S. K. Singh, and F. M. Peeters, Wires Comput. Mol. Sci. 2015, 5, 255.
  17. E. Keith, Jr. Whitener, J. Vac. Sci. Technol A. 2018, 36, 05G401. [CrossRef]
  18. S. Watcharinyanon, C. Virojanadara, J. Osiecki, A. Zakharov, R. Yakimova, R. Uhrberg, and L. Johansson. Hydrogen interca-lation of graphene grown on 6h-sic(0001), Surf. Scie., 2011, 605, 1662–1668. [CrossRef]
  19. Y.E. Yang, Y. Xiao, and X.H. Yan. Charge distribution of lithium-doped graphane/graphene hybrid system: Role of nearly-free electronic states. Sol. Stat. Commun. 2016, 229, 43–48. [CrossRef]
  20. Sahin H, Ataca C, Ciraci S. Electronic and magnetic properties of graphane nanoribbons. Phys Rev B 2010, 81, 205417. [CrossRef]
  21. H. Sahin, C. Ataca, and S. Ciraci, Magnetization of graphane by dehydrogenation. Appl. Phys. Lett. 2009, 95, 222510. [CrossRef]
  22. J. Berashevich, and T. Chakraborty, Sustained ferromagnetism induced by H-vacancies in graphane. Nanotechnology 2010, 21, 355201. [CrossRef] [PubMed]
  23. R E Mapasha, M P Molepo and N Chetty, Phys. E. 79, 52-58 (2016). 2016, 79, 52–58.
  24. B. S. Pujari and D.G. Kanhere, J. Phys. Chem. C. 2009, 113, 21063.
  25. G. Kresse and J. Hafner, Phys. Rev. B. 1993, 47, 558.
  26. J. Heyd, G. E. Scuseria, and M. Ernzerhof, J. Chem. Phys. 118, 8207 (2003); 124, 219906 (2006)..
  27. P. E. Blochl, Phys. Rev. B. 1994, 50, 17953.
  28. H. J. Monkhorst and J. D. Pack 1976. Phys. Rev. B 1976, 13, 5188.
  29. S. B. Zhang and J. E. Northrup, Phys. Rev. Lett. 1991, 67, 2339.
  30. Jin C, Lan H, Peng L, Suenaga K, Iijima S. Phys Rev Lett, 2009, 102, 205501.
  31. K.T. Chan, J.B. Neaton, M.L. Cohen. Phys. Rev. 2008, 77, 235430. [CrossRef]
  32. A. M. Garay-Tapia, A. H. Romero, V. Barone, J. Chem. Theory Comput. 2012, 8, 1064–1071.
Preprints 91160 g001
Figure 1. Top panel present top view of the ball-and-stick model of graphane structure, while bottom panel present side views of graphane structure. Different CH pair divacancy configurations v 12 , v 13 and v 14 positions are shown. The white and purple circles hide the numerically labeled CH pair vacancies that are created. The rectangular shapes that enclose vacancy configurations primarily connect the carbon atoms through their potential dangling bonds before undergoing structural relaxation. These carbon atoms are labeled with the roman numbers. The black rhombus shape represents the primitive unit cell of graphane structure, consisting of two C and two H atoms. The vectors a 1 and a 2 correspond to its Bravais lattice vectors. The C and H atoms are represented by the yellow and light blue spheres respectively.
Figure 1. Top panel present top view of the ball-and-stick model of graphane structure, while bottom panel present side views of graphane structure. Different CH pair divacancy configurations v 12 , v 13 and v 14 positions are shown. The white and purple circles hide the numerically labeled CH pair vacancies that are created. The rectangular shapes that enclose vacancy configurations primarily connect the carbon atoms through their potential dangling bonds before undergoing structural relaxation. These carbon atoms are labeled with the roman numbers. The black rhombus shape represents the primitive unit cell of graphane structure, consisting of two C and two H atoms. The vectors a 1 and a 2 correspond to its Bravais lattice vectors. The C and H atoms are represented by the yellow and light blue spheres respectively.
Preprints 91160 g001
Preprints 91160 g002
Figure 2. (a) The formation energies of different CH divacancy configurations ( v 12 , v 13 and v 14 ) are indicated by the circle spheres while those of a Li atom on the different CH divacancy configurations (Li- v 12 , Li- v 13 and Li- v 14 ) are represented by the square shapes.(b) The total magnetic moments arising from the v 12 , v 13 and v 14 configurations are indicated by the circle spheres while those influenced by a Li atom adsorption on the different CH divacancy configurations (Li- v 12 , Li- v 13 and Li- v 14 ) are represented by the square shapes. (c-e) The relaxed structures of different CH divacancy configurations ( v 12 , v 13 and v 14 ) created in a 9×9 supercell. Each divacancy configuration reconstructs to form a peculiar type of a topology defect.
Figure 2. (a) The formation energies of different CH divacancy configurations ( v 12 , v 13 and v 14 ) are indicated by the circle spheres while those of a Li atom on the different CH divacancy configurations (Li- v 12 , Li- v 13 and Li- v 14 ) are represented by the square shapes.(b) The total magnetic moments arising from the v 12 , v 13 and v 14 configurations are indicated by the circle spheres while those influenced by a Li atom adsorption on the different CH divacancy configurations (Li- v 12 , Li- v 13 and Li- v 14 ) are represented by the square shapes. (c-e) The relaxed structures of different CH divacancy configurations ( v 12 , v 13 and v 14 ) created in a 9×9 supercell. Each divacancy configuration reconstructs to form a peculiar type of a topology defect.
Preprints 91160 g002
Preprints 91160 g003
Figure 3. The relaxed structures of Li atom on the different CH divacancy configurations (a) Li- v 12 , (b) Li- v 13 and (c) Li- v 14 created in a 9×9 supercell. In some configurations, Li atom enforces divacancy configuration reconstruction.
Figure 3. The relaxed structures of Li atom on the different CH divacancy configurations (a) Li- v 12 , (b) Li- v 13 and (c) Li- v 14 created in a 9×9 supercell. In some configurations, Li atom enforces divacancy configuration reconstruction.
Preprints 91160 g003
Preprints 91160 g004
Figure 4. The relaxed structures of Li- v 12 at different charge states; (a) L i − 1 - v 12 , (b) L i 0 - v 12 and L i + 1 - v 12 .
Figure 4. The relaxed structures of Li- v 12 at different charge states; (a) L i − 1 - v 12 , (b) L i 0 - v 12 and L i + 1 - v 12 .
Preprints 91160 g004
Preprints 91160 g005
Figure 5. The calculated density of states for (a) v 12 , (b) Li- v 12 , (c) L i − 1 - v 12 and (d) L i + 1 - v 12 . For each sub figure, the top panel represents total density of states, while the bottom panel represents the partial density of states. The Fermi level is set to 0.00 eV and marked by the vertical dashed line.
Figure 5. The calculated density of states for (a) v 12 , (b) Li- v 12 , (c) L i − 1 - v 12 and (d) L i + 1 - v 12 . For each sub figure, the top panel represents total density of states, while the bottom panel represents the partial density of states. The Fermi level is set to 0.00 eV and marked by the vertical dashed line.
Preprints 91160 g005
Table 1. Comparing the binding energies E b (in eV) and distances between Li atom and graphane d L i (in Å) for Li- v 12 , Li- v 13 and Li- v 14 configurations with that of Li on graphene (Li- g r a p h e n e ).
Table 1. Comparing the binding energies E b (in eV) and distances between Li atom and graphane d L i (in Å) for Li- v 12 , Li- v 13 and Li- v 14 configurations with that of Li on graphene (Li- g r a p h e n e ).
Configurations E B d L i Vacancy reconstruction
Li- v 12 3.25 0.00 5-8-5 changes to divacancy symmetry
Li- v 13 2.07 0.62 9-4-9 translates to penta ring and v C H
Li- v 14 1.99 1.14 None
Li- v C H 1.72a 1.54a None
Li- g r a p h e n e 1.10b, 1.29c 1.71b 1.69c None
aRef[15],bRef[31] and cRef[32].
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated