Variable Selection for Sparse Logistic Regression with Grouped Variables

1. Introduction

Logistic regression models are a powerful and popular technique for modeling the relationship between the predictors and a categorical response variable. Let $(x_1,y_1),\cdots ,(x_n,y_n)$ be independent pairs of observed data which are realizations of random vector $(X,Y)$, with $p-$dimensional predictors $X\in {\mathbb{R}}^p$ and univariate binary response variable $Y\in \{0,1\}$. $(X,Y)$ is assumed to satisfy

$$\mathbb{P}(Y=1|X=x)=G\left(x^T{\beta }^0\right)=\frac{exp\left(x^T{\beta }^0\right)}{1+exp\left(x^T{\beta }^0\right)},$$

(1)

where ${\beta }^0\in {\mathbb{R}}^p$ is a regression vector to be estimated. We are especially concerned with a sparse logistic regression problem when the dimension p is high and the sample size n might be small, the so-called "small n, large p" framework, which is a variable selection problem for high-dimensional data.

When dealing with high-dimensional data, there are usually two important considerations: model sparsity and prediction accuracy. The Lasso [1] was proposed to address these two objectives since Lasso can determine submodels with a moderate number of parameters that still fit the data adequately. There are also other similar methods include SCAD [2], elastic net [3], Dantzig selector [4], MCP [5] and so on. In high-dimensional logistic regression models, the topics for Lasso study range from the asymptotic results, including the consistency and asymptotic distribution of the estimator, e.g., Huang et al. [6], Bianco et al. [7], to the non-asymptotic results, including the non-asymptotic oracle inequalities on the estimation and prediction errors, e.g., Abramovich et al. [8], Huang et al. [9] and Yin [10].

In many applications, predictors can often be thought of as grouped. For example, in genome-wide association studies (GWAS), genes usually do not act individually, but are reflected in the covariation of several genes with each other. Or in histologically normal epithelium (NlEpi) studies, we need to consider the non-linear effects of genes for microarray data. Similar to the Lasso, considering this grouped information in the modeling process should improve the interpretability and the accuracy of the model. Yuan and Lin [11] proposed an extension of the Lasso, called the Group Lasso, which imposes an $L_2$ penalty to individual groups of variables and then an $L_1$ penalty to the resulting block norms, rather than only an $L_1$ penalty to individual variables. Suppsose $x_i$ and ${\beta }^0$ in model (1) are divided into g known groups, where we consider a partition $\{G_1,\cdots ,G_g\}$ of $\{1,\cdots ,p\}$ into groups and denote the cardinality of a group $G_l$ by $|G_l|$, $x_i={(x_{i\left(1\right)}^T,x_{i\left(2\right)}^T,\cdots ,x_{i\left(g\right)}^T)}^T$, ${\beta }^0={({\left({\beta }_{\left(1\right)}^0\right)}^T,{\left({\beta }_{\left(2\right)}^0\right)}^T,\cdots ,{\left({\beta }_{\left(g\right)}^0\right)}^T)}^T$, $x_{i\left(l\right)}\in {\mathbb{R}}^{|G_l|}$, ${\beta }_{\left(l\right)}^0\in {\mathbb{R}}^{|G_l|}$. We wish to achieves sparsity at the level of groups, i.e., to ${\beta }^0$ such that ${\beta }_{\left(l\right)}^0=0$ for some of the groups $l\in \{1,\cdots ,g\}$. When using high-dimensional logistic regression models, the Group Lasso provides an estimator for ${\beta }^0$:

$${\widehat{\beta }}^{GL}:=\underset{\beta \in {\mathbb{R}}^p}{argmin}\frac{1}{n}\sum _{i=1}^n\left\{log\left(1+exp\left(x_i^T\beta \right)\right)-\left(x_i^T\beta \right)y_i\right\}+\lambda \sum _{l=1}^g{\omega }_l{\parallel {\beta }_{\left(l\right)}\parallel }_2,$$

(2)

where $\lambda \ge 0$ is a tuning parameter which controls the amount of penalization, ${\omega }_l=\sqrt{|G_l|}$ is used to normalize across groups of different sizes, and ${\parallel ·\parallel }_2$ denotes the $L_2$ norm of a vector. Meier et al. [12] established the asymptotic consistency theory of the Group Lasso for logistic regression, Wang et al. [13] analyzed the rates of convergence, Blazere et al. [14] stated oracle inequalities and Kwemou [15] studied non-asymptotic oracle inequalities. Other important references are the works of Nowakowski et al. [16] and Zhang et al. [17]. In terms of computational algorithms, Meier et al. [12] applied the block coordinate descent algorithm of Tseng [18] to Group Lasso for logistic regression, Breheny and Huang [19] proposed the Group descent algorithm. These approaches are sufficiently fast for computing the exact coefficients at those selected values of $\lambda$.

However, it is well known that the Lasso (or the Group Lasso) in linear regression models, the respective optimal values of tuning parameter $\lambda$ depend on the unknown parameter ${\sigma }^2$, the homogeneous noise variance, and its the accurate estimation is generally more difficult when $p\gg n$. To solve this problem, Belloni et al. [20] proposed square-root Lasso, which removed this unknown parameter by using a weighted score function (i.e. the square root of empirical loss function). Bunea et al. [21] extended the ideas behind the square-root Lasso for group selection and developed the Group square-root Lasso. Inspired by Group square-root Lasso, we propose a new penalized weighted score function method, which alternatively replaces the original score function (i.e. the gradient of negative loglikelihood function) with a weighted score function (Huang and Wang [22]), to study sparse logistic regression with Group Lasso penalty. We get convergence rates for the estimation error and provide a direct choice for the tuning parameter. Moreover, we propose a modified block coordinate descent algorithm based on the weighted score function, which greatly optimizes the computational complexity.

The framework of this paper is as follows. In Section 2, we apply this idea behind the Group square-root Lasso to sparse logisitic models and develop our method, the penalized weighted score function method. In Section 3, we propose asymptotic bounds for our new estimator and a direct selection for the tuning parameter. In Section 4, we provide weighted block coordinate descent algorithm. In Section 5, numerical simulations show the advantages of our algorithm in terms of selection effects and computational time. In Section 6, we present real data for genes and musk to support the simulation and theoretical results. The Section 7 concludes our work. All proofs are given in Appendix.

$\mathbf{Notation}:$ Throughout the paper, denote by $I=\{l:\parallel {\beta }_{\left(l\right)}^0{\parallel }_2\ne 0\}$ the non-zero coordinate of ${\beta }^0$ and let $s=\mathrm{card}\left\{I\right\}$ be the number of non-zero elements of ${\beta }^0$. For all $\delta \in {\mathbb{R}}^p$ and subset I, we denote by ${\delta }_I$ that has the same coordinates as $\delta$ on I and zero coordinates on the complement $I^C$ of I. For a function $f\left(\beta \right)\in \mathbb{R}$, we denote by $\nabla f\left(\beta \right)\in {\mathbb{R}}^p$ its gradient and $\mathcal{H}\left(\beta \right)\in {\mathbb{R}}^{p\times p}$ its Hessian matrix at $\beta \in {\mathbb{R}}^p$. Define the $L_q$ norm of any vector v as ${\parallel v\parallel }_q=({\sum }_i|v_i{{|}^q)}^{1/q}$ and for any vector $\beta \in {\mathbb{R}}^p$ with group structures, denote the block norm of $\beta$ for any $0\le q\le \infty$ as ${\parallel \beta \parallel }_{2,q}=({\sum }_{l=1}^g\parallel {\beta }_{\left(l\right)}{{\parallel }_2^q)}^{1/q}$. In particular, ${\parallel \beta \parallel }_{2,0}={\sum }_{l=1}^g{1}_{{\beta }_{\left(l\right)}\ne 0}$ indicates the number of non-zero groups, ${\parallel \beta \parallel }_{2,1}={\sum }_{l=1}^g{\parallel {\beta }_{\left(l\right)}\parallel }_2$ represents the form of Group Lasso, ${\parallel \beta \parallel }_{2,2}={\parallel \beta \parallel }_2$ denotes $L_2$ norm, and ${\parallel \beta \parallel }_{2,\infty }={max}_l{\parallel {\beta }_{\left(l\right)}\parallel }_2$ means the largest $L_2$ norm of all groups. Moreover $\Phi \left(x\right)$ denotes the cumulative distribution function of the standard normal distribution.

2. Penalized weighted score function method

Recall model (1), the loss function (i.e. the negative loglikelihood) is given by

$$\ell \left(\beta \right)=\frac{1}{n}\sum _{i=1}^n\left\{log\left(1+exp\left(x_i^T\beta \right)\right)-\left(x_i^T\beta \right)y_i\right\},$$

leading to the score function

$$\nabla \ell \left(\beta \right)=\frac{1}{n}\sum _{i=1}^n(G\left(x_i^T\beta \right)-y_i)x_i.$$

Note that the solution ${\widehat{\beta }}^{GL}$ of model (2) satisfies KKT conditions defined as follows

$$\left\{\begin{array}{cc}\frac{1}{n}\sum _{i=1}^n(G\left(x_i^T{\widehat{\beta }}^{GL}\right)-y_i)x_{i\left(l\right)}=-\lambda {\omega }_l{\widehat{\beta }}_{\left(l\right)}^{GL}/{\parallel {\widehat{\beta }}_{\left(l\right)}^{GL}\parallel }_2,\hfill & \mathrm{if}{\widehat{\beta }}_{\left(l\right)}^{GL}\ne 0,\hfill \\ |\frac{1}{n}\sum _{i=1}^n(G\left(x_i^T{\widehat{\beta }}^{GL}\right)-y_i)x_{i\left(l\right)}|\le \lambda {\omega }_l,\hfill & \mathrm{if}{\widehat{\beta }}_{\left(l\right)}^{GL}=0,\hfill \end{array}\right.$$

(3)

for all $l=1,\cdots ,g$. The left side of equation (3) is the score function for logistic regression with group structure, which shows that ${\widehat{\beta }}^{GL}$ is actually a penalized score function estimator. To obtain a good estimator, usually we require that the inequality $\lambda {\omega }_l\ge c{\parallel \nabla \ell \left({\beta }^0\right)\parallel }_{2,\infty }$ for all $l=1,\cdots ,g$ and some constant $c\ge 1$ holds with high probability (Meier et al. [12] and Kwemou [15]). However, the random part $G\left(x_i^T{\beta }^0\right)-y_i$ for $\nabla \ell \left({\beta }^0\right)$, the score function valued at $\beta ={\beta }^0$, has variance $G\left(x_i^T{\beta }^0\right)(1-G\left(x_i^T{\beta }^0\right))$, which is also the variance of the binary random variable $Y_i|X_i=x_i$. Obviously, binary noises are not homogeneous like noises of the linear regression models, a unique tuning parameter for all of the different coefficient is not a good choice.

We apply the idea from Group square-root Lasso to solve the above problem on choosing tuning parameter, and develop our method as follows. Huang and Wang [22] formed a class of root-consistent estimating functions by weighted score function for logistic regression

$$\nabla {\ell }_{\psi }\left(\beta \right)=\frac{1}{n}\sum _{i=1}^n\psi \left(x_i^T\beta \right)(G\left(x_i^T\beta \right)-y_i)x_i,$$

(4)

where $\psi (·)$ is the weighted function of $x_i^T\beta$. This requires choosing a suitable weighed function to ensure that $\nabla {\ell }_{\psi }\left(\beta \right)$ is almost integrable for $\beta$. Then, replacing the score function in equation (3) with the weighted score function, we develop a penalized weighted score function estimate $\widehat{\beta }$, which is a solution of the following equation:

$$\left\{\begin{array}{cc}\frac{1}{n}\sum _{i=1}^n\psi \left(x_i^T\widehat{\beta }\right)(G\left(x_i^T\widehat{\beta }\right)-y_i)x_{i\left(l\right)}=-\lambda {\omega }_l{\widehat{\beta }}_{\left(l\right)}/{\parallel {\widehat{\beta }}_{\left(l\right)}\parallel }_2,\hfill & \mathrm{if}{\widehat{\beta }}_{\left(l\right)}\ne 0,\hfill \\ |\frac{1}{n}\sum _{i=1}^n\psi \left(x_i^T\widehat{\beta }\right)(G\left(x_i^T\widehat{\beta }\right)-y_i)x_{i\left(l\right)}|\le \lambda {\omega }_l,\hfill & \mathrm{if}{\widehat{\beta }}_{\left(l\right)}=0.\hfill \end{array}\right.$$

(5)

Let ${\ell }_{\psi }\left(\beta \right)$ be the loss function corresponding to the weighted score function (4), the solution to Equation (5) is equivalent to solve the following optimization problem:

$$\widehat{\beta }:=\underset{\beta \in {\mathbb{R}}^p}{argmin}\left\{{\ell }_{\psi }\left(\beta \right)+\lambda \sum _{l=1}^g{\omega }_l{\parallel {\beta }_{\left(l\right)}\parallel }_2\right\}.$$

(6)

Our method is motivated by Bunea et al. [21] minimization of the Group square-root Lasso for linear model:

$${\widehat{\beta }}^{GSL}:=\underset{\beta \in {\mathbb{R}}^p}{argmin}\left\{\frac{{\parallel \mathbb{Y}-\mathbb{X}\beta \parallel }_2}{\sqrt{n}}+\frac{\lambda }{n}\sum _{l=1}^g{\omega }_l{\parallel {\beta }_{\left(l\right)}\parallel }_2\right\},$$

where $\mathbb{Y}\in {\mathbb{R}}^{n\times 1}$ and $\mathbb{X}\in {\mathbb{R}}^{n\times p}$. When $\parallel \mathbb{Y}-\mathbb{X}{\widehat{\beta }}^{GSL}{\parallel }_2$ is non-zero, the Group square-root Lasso estimator ${\widehat{\beta }}^{GSL}$ satisfies the KKT condition

$$\left\{\begin{array}{cc}\sqrt{n}\sum _{i=1}^n(\parallel \mathbb{Y}-\mathbb{X}{\widehat{\beta }}^{GSL}{\parallel }_2{)}^{-1}(y_i-x_i^T{\widehat{\beta }}^{GSL})x_{i\left(l\right)}=\lambda {\omega }_l{\widehat{\beta }}_{\left(l\right)}^{GSL}/{\parallel {\widehat{\beta }}_{\left(l\right)}^{GSL}\parallel }_2,\hfill & \mathrm{if}{\widehat{\beta }}_{\left(l\right)}^{GSL}\ne 0,\hfill \\ |\sqrt{n}\sum _{i=1}^n(\parallel \mathbb{Y}-\mathbb{X}{\widehat{\beta }}^{GSL}{\parallel }_2{)}^{-1}(y_i-x_i^T{\widehat{\beta }}^{GSL})x_{i\left(l\right)}|\le \lambda {\omega }_l,\hfill & \mathrm{if}{\widehat{\beta }}_{\left(l\right)}^{GSL}=0.\hfill \end{array}\right.$$

(7)

Compared with the KKT conditions for Group square-root Lasso and Group Lasso, the Group square-root Lasso adds the weighted function $(\sqrt{n}\parallel \mathbb{Y}-\mathbb{X}{\widehat{\beta }}^{GSL}{{\parallel }_2)}^{-1}$ to estimate the homogeneous noise variance, which allows the tuning parameter $\lambda$ independent of the homogeneous noise variance. Thus, the Group square-root Lasso is able to estimate for the grouped variables and direct choice for the tuning parameter simultaneously.

A drawback of Group square-root Lasso is that it can only directly select the tuning parameter in a linear regression models. However, in logistic regression models, there is no direct way to select the tuning parameter. The penalized weighted score function method implements this scheme. We will discuss this in more detail in the next section.

3. Statistical properties

In this section, we will establish non-asymptotic oracle inequalities for the penalized weighted score function estimate and give a direct choice for tuning parameter.

Throughout this paper, we consider a fixed design setting (i.e., $x_1,\cdots ,x_n$ are consider deterministic), and we make the following assumptions:

(A1)

There exists a positive constant $\mathcal{M}<\infty$ such that ${max}_{1\le i\le n}{max}_{1\le l\le g}\sqrt{{\sum }_{j\in G_l}{x}_{ij}^2}\le \mathcal{M}$.

(A2)

The $n,p$ satisfy that $n\le p=o\left(e^{n^{1/3}}\right)$, and $p/ϵ>2$ for $ϵ\in (0,1)$.

(A3)

There exists $\mathcal{N}\left({\beta }^0\right)>0$ such that

$${\mathcal{N}}^2\left({\beta }^0\right)=\underset{1\le j\le p}{max}\left\{\frac{1}{n}\sum _{1\le i\le n}{\psi }^2\left(x_i^T{\beta }^0\right)G\left(x_i^T{\beta }^0\right)(1-G\left(x_i^T{\beta }^0\right))x_{ij}^2\right\}.$$

(A4)

Let ${\ell }_{\psi }(·):{\mathbb{R}}^p\mapsto \mathbb{R}$ be a convex three times differentiable function such that for all $u,v\in {\mathbb{R}}^P$, the function $g\left(t\right)={\ell }_{\psi }(u+tv)$ satisfies for all $t\in \mathbb{R}$, $|g^{{\text{}}^{\prime \prime \prime }}\left(t\right)|\le {\tau }_0{max}_{1\le i\le n}\left|x_i^{T}v\right|g^{{\text{}}^{\prime \prime }}\left(t\right)$, where ${\tau }_0>0$ is a constant.

The assumption (A1) strictly controls the bounds of predictors, since the real data we collected was often bounded. The assumption (A2) controls the sparsity of the data and the lower bound on the probability that the non-asymptotic property holds. The assumption (A3) makes sure the variance of each component of $\nabla {\ell }_{\psi }\left({\beta }^0\right)$ is bounded with choosing a suitable weighted function $\psi (·)$. The assumption (A4) is similar to the proposition 1 proposed by Bach [23]. Under the assumption (A4), we can obtain lower and upper Taylor expansions of the loss function ${\ell }_{\psi }(·)$, using which we can derive non-asymptotic results.

Moreover, restricted eigenvalue condition plays a key role in deriving oracle inequalities. For the Group Lasso problem of high-dimensional linear regression models, the oracle property under the group restricted eigenvalue condition was discussed by Hu et al. [24] and extended to logistic regression models by Zhang et al. [17]. To establish the desired group restricted eigenvalue condition, we introduce the following group restricted set

$${\Theta }_{\alpha }=:\left\{\vartheta \in {\mathbb{R}}^p:\parallel W_{I^C}{\vartheta }_{\left(I^C\right)}{\parallel }_{2,1}\le \alpha {\parallel W_I{\vartheta }_{\left(I\right)}\parallel }_{2,1},\alpha >0\right\},$$

(8)

which is a grouped version of the restricted set ${\theta }_{\alpha }=:\left\{\vartheta \in {\mathbb{R}}^p:\parallel {\vartheta }_{I^C}{\parallel }_1\le \alpha {\parallel {\vartheta }_I\parallel }_1\right\}$ mentioned in Bickel et al. [25], where $W_I$ is a diagonal matrix with the jth diagonal element ${\omega }_j$ if $j\in I$, and 0 otherwise. Based on the group restricted set (8), we propose the following group restricted eigenvalue condition:

(A5)

For some integer s such that $1<s<g$ and a positive number $\alpha$, the follow condition holds

$$\mu (s,\alpha )\stackrel{▵}{=}\underset{\genfrac{}{}{0pt}{}{I\subseteq \{1,\cdots ,g\}}{\left|I\right|\le s}}{min}\underset{\genfrac{}{}{0pt}{}{\delta \ne 0}{\delta \in {\Theta }_{\alpha }}}{min}\frac{{\left({\delta }^T{\mathcal{H}}_{\psi }\left({\beta }^0\right)\delta \right)}^{1/2}}{\parallel W_I{\delta }_{\left(I\right)}{\parallel }_{2,2}}>0,$$

(9)

where ${\mathcal{H}}_{\psi }\left({\beta }^0\right)$ is the Hessian matrix for ${\ell }_{\psi }\left({\beta }^0\right)$. Different from the restricted eigenvalue condition mentioned in Bickel et al. [25] for linear regression models, the group restricted eigenvalue condition for logistic regression is converted from the $L_2$ norm to the block norm for the denominator part and from the Gram matrix to the Hessian matrix ${\mathcal{H}}_{\psi }\left({\beta }^0\right)$ for the numerator part of (9).

Remark 1.

The Hessian matrix of ${\ell }_{\psi }\left(\beta \right)$ is given by

$$\begin{array}{cc}\hfill {\mathcal{H}}_{\psi }\left(\beta \right)& =\frac{1}{n}\sum _{i=1}^n\left\{\nabla \psi \left(x_i^T\beta \right)\left[\frac{exp\left(x_i^T\beta \right)}{1+exp\left(x_i^T\beta \right)}-y_i\right]+\psi \left(x_i^T\beta \right)\frac{exp\left(x_i^T\beta \right)}{{(1+exp\left(x_i^T\beta \right))}^2}\right\}{x}_i{x}_i^T\hfill \\ \hfill & =\frac{1}{n}\sum _{i=1}^n\left\{\nabla \psi \left(x_i^T\beta \right)\left[G\left(x_i^T\beta \right)-y_i\right]+\psi \left(x_i^T\beta \right)G\left(x_i^T\beta \right)(1-G\left(x_i^T\beta \right))\right\}{x}_i{x}_i^T.\hfill \end{array}$$

Bach [23] has already shown the Hessian matrix of $\ell \left(\beta \right)$ is positive definite on some restricted sets. If the chosen weighted function $\psi \left(x_i^T\beta \right)$ makes the loss function ${\ell }_{\psi }\left(\beta \right)$ satisfy the assumption (A3), ${\mathcal{H}}_{\psi }\left(\beta \right)$ is also positive definite on the group restricted set (8). Such weighed functions in fact exist and will be described later. In addition, the group restricted eigenvalue condition can effectively control the estimation error, enabling the estimation with good statistical properties and reliable results.

Theorem 1.

Assume that (A1), (A2), (A3), (A4) are satisfied. Let $\lambda <\frac{k(1-z)\mu (s,\alpha )}{4{\tau }_0\mathcal{M}s},z\in (0,1)$ and $k<{min}_{1\le l\le g}{\omega }_l$. Let λ be a tuning parameter chosen such that

$$\lambda {\omega }_l=\frac{\mathcal{N}\left({\beta }^0\right)}{z}\sqrt{\frac{|G_l|}{n}}{\Phi }^{-1}(1-\frac{ϵ}{2p}).$$

(10)

Then, with probability of at least $1-ϵ(1+o(1\left)\right)$, we have the following:

1. A group restricted set $\widehat{\beta }-{\beta }^0\in {\Theta }_{\alpha }$ with $\alpha =\frac{1+z}{1-z}$.

2. Under the group restricted eigenvalue condition (A5), the block norm estimation error are

$$\parallel \widehat{\beta }-{\beta }^0{\parallel }_{2,1}\le \frac{2k\lambda s}{(\underset{1\le l\le g}{min}{\omega }_l-k)(1-z)\mu (s,\alpha )},$$

(11)

$$\parallel \widehat{\beta }-{\beta }^0{\parallel }_{2,q}^q\le {\left(\frac{2k\lambda s}{(\underset{1\le l\le g}{min}{\omega }_l-k)(1-z)\mu (s,\alpha )}\right)}^q,\mathit{forall}1<q<2,$$

(12)

respectively, and the error of the loss function ${\ell }_{\psi }$ is

$$|{\ell }_{\psi }\left(\widehat{\beta }\right)-{\ell }_{\psi }\left({\beta }^0\right)|\le \frac{2\underset{1\le l\le g}{min}{\omega }_l{\lambda }^{2}s}{(\underset{1\le l\le g}{min}{\omega }_l-k)(1-z)\mu (s,\alpha )}.$$

(13)

The non-asymptotic oracle inequalities for the true coefficient ${\beta }^0$ are provided in (11) and (12). Unfortunately, the parameter $\mathcal{N}\left({\beta }^0\right)$ is influenced by the true coefficient ${\beta }^0$, so that the choice of $\lambda$ also depends on ${\beta }^0$. Therefore, we will choose the suitable $\psi \left(x_i^T{\beta }^0\right)$ to solve this problem in the next theorem.

Theorem 2.

Choose the weight function in the following form

$$\psi \left(x_i^T{\beta }^0\right)=\frac{1}{2}\left(exp\left(\frac{x_i^T{\beta }^0}{2}\right)+exp(-\frac{x_i^T{\beta }^0}{2})\right).$$

(14)

Under assumptions (A2) and (A3) we choose the tuning parameter as

$$\lambda {\omega }_l=\frac{\sqrt{|G_l|\underset{1\le j\le p}{max}\left(\sum _{i=1}^n{x}_{ij}^2\right)}}{2nz}{\Phi }^{-1}(1-\frac{ϵ}{2p}).$$

(15)

Then, under the assumptions of Theorem 1 with probability at least $1-ϵ(1+o(1\left)\right)$ we have inequalities (11), (12) and (13).

In Theorem 2, Yin [10] gives a discussion for the order of ${\Phi }^{-1}(1-\frac{ϵ}{2p})$ in (15), and proving that ${\Phi }^{-1}(1-\frac{ϵ}{2p})\sim \mathcal{O}\left(\sqrt{log(2p/ϵ)}\right)$. When $|G_l|=1$ for $l=1,2,\cdots ,g$, our estimate $\widehat{\beta }$ is a Lasso estimate and its theoretical properties have been well studied in Yin [10].

Remark 2.

If $\psi \left(x_i^T{\beta }^0\right)$ is given as in Theorem 2, the loss function, weighted score function and the Hessian matrix, respectively, are given by

$$\left\{\begin{array}{c}{\ell }_{\psi }\left({\beta }^0\right)=\frac{1}{n}\sum _{i=1}^n\left\{(1-y_i)exp\left(\frac{x_i^T{\beta }^0}{2}\right)+y_{i}exp(-\frac{x_i^T{\beta }^0}{2})\right\},\hfill \\ \nabla {\ell }_{\psi }\left({\beta }^0\right)=\frac{1}{2n}\sum _{i=1}^n\left\{(1-y_i)exp\left(\frac{x_i^T{\beta }^0}{2}\right)-y_{i}exp(-\frac{x_i^T{\beta }^0}{2})\right\}{x}_i,\hfill \\ {\mathcal{H}}_{\psi }\left({\beta }^0\right)=\frac{1}{4n}\sum _{i=1}^n\left\{(1-y_i)exp\left(\frac{x_i^T{\beta }^0}{2}\right)+y_{i}exp(-\frac{x_i^T{\beta }^0}{2})\right\}{x}_i{x}_i^T.\hfill \end{array}\right.$$

Clearly, the Hessian matrix given as a weighting function of the form of Theorem 2 is positive definite.

4. Weighted block coordinate descent algorithm

We apply the techniques of the block coordinate descent algorithm to the penalized weighted score function. Choose the weighted function as the form of (14) and set $\beta =\widehat{\beta }+\zeta$, then a second-order Taylor expansion of the loss function ${\ell }_{\psi }\left(\beta \right)$ in equation (6) has

$$\mathcal{D}(\widehat{\beta }+\zeta )=\left\{\left({\ell }_{\psi }\left(\widehat{\beta }\right)+{\zeta }^T\nabla {\ell }_{\psi }\left(\widehat{\beta }\right)+\frac{1}{2}{\zeta }^T{\mathcal{H}}_{\psi }\left(\widehat{\beta }\right)\zeta \right)+\lambda {\parallel W(\widehat{\beta }+\zeta )\parallel }_{2,1}\right\},$$

(16)

Now we consider minimization $\mathcal{D}(\widehat{\beta }+\zeta )$ with respect to the lth group of penalized parameters , it mean that

$$\nabla {\ell }_{\psi }{\left(\widehat{\beta }\right)}_{\left(l\right)}+{\mathcal{H}}_{\psi }{\left(\widehat{\beta }\right)}_{\left(l\right)}{\zeta }_{\left(l\right)}+\lambda {\omega }_l\frac{{\widehat{\beta }}_{\left(l\right)}+{\zeta }_{\left(l\right)}}{\parallel {\widehat{\beta }}_{\left(l\right)}+{\zeta }_{\left(l\right)}{\parallel }_2}=0.$$

(17)

Inspired by Meier et al. [12] assumptions, setting the sub-matrix ${\mathcal{H}}_{\psi }{\left(\widehat{\beta }\right)}_{\left(l\right)}$ is of the form ${\mathcal{H}}_{\psi }{\left(\widehat{\beta }\right)}_{\left(l\right)}=h_{\psi }{\left(\widehat{\beta }\right)}_{\left(l\right)}{I}_{\left(l\right)}$, which choose $h_{\psi }{\left(\widehat{\beta }\right)}_{\left(l\right)}=-max\{\mathrm{diag}(-{\mathcal{H}}_{\psi }{\left(\widehat{\beta }\right)}_{\left(l\right)}),r_0\}$, where $r_0$ is a lower bound to ensure convergence. Then, simplifying equation (17) gives

$$\left(\frac{\lambda {\omega }_l}{\parallel {\widehat{\beta }}_{\left(l\right)}+{\zeta }_{\left(l\right)}\parallel }+h_{\psi }{\left(\widehat{\beta }\right)}_{\left(l\right)}\right)({\widehat{\beta }}_{\left(l\right)}+{\zeta }_{\left(l\right)})={\mathcal{H}}_{\psi }{\left(\widehat{\beta }\right)}_{\left(l\right)}{\widehat{\beta }}_{\left(l\right)}-\nabla {\ell }_{\psi }{\left(\widehat{\beta }\right)}_{\left(l\right)}.$$

This leads to the following equivalence equation

$$\frac{{\widehat{\beta }}_{\left(l\right)}+{\zeta }_{\left(l\right)}}{\parallel {\widehat{\beta }}_{\left(l\right)}+{\zeta }_{\left(l\right)}{\parallel }_2}=\frac{{\mathcal{H}}_{\psi }{\left(\widehat{\beta }\right)}_{\left(l\right)}{\widehat{\beta }}_{\left(l\right)}-\nabla {\ell }_{\psi }{\left(\widehat{\beta }\right)}_{\left(l\right)}}{\parallel {\mathcal{H}}_{\psi }{\left(\widehat{\beta }\right)}_{\left(l\right)}{\widehat{\beta }}_{\left(l\right)}-\nabla {\ell }_{\psi }{\left(\widehat{\beta }\right)}_{\left(l\right)}{\parallel }_2}.$$

(18)

According to equation (15) and Remark 2, it is obtained that:

If $\parallel {\mathcal{H}}_{\psi }{\left(\widehat{\beta }\right)}_{\left(l\right)}{\widehat{\beta }}_{\left(l\right)}-\nabla {\ell }_{\psi }{\left(\widehat{\beta }\right)}_{\left(l\right)}{\parallel }_2\le \lambda {\omega }_l$, the value of $\zeta$ at the k-th iteration is given by

$${\zeta }_{\left(l\right)}^{\left(k\right)}=-{\widehat{\beta }}_{\left(l\right)}^{\left(k\right)},$$

otherwise

$${\zeta }_{\left(l\right)}^{\left(k\right)}=-\frac{1}{h_{\psi }{\left({\widehat{\beta }}^{\left(k\right)}\right)}_{\left(l\right)}}\left(\nabla {\ell }_{\psi }{\left({\widehat{\beta }}^{\left(k\right)}\right)}_{\left(l\right)}+\frac{x_{\left(l\right)}}{\parallel x_{\left(l\right)}{\parallel }_2}\frac{\sqrt{|G_l|\underset{1\le j\le p}{max}\left(\sum _{i=1}^n{x}_{ij}^2\right)}}{2nz}{\Phi }^{-1}(1-\frac{ϵ}{2p})\right).$$

If ${\zeta }_{\left(l\right)}^{\left(k\right)}\ne 0$, we use the Armijo rule of Tseng and Yun [26] to select the step factor ${\sigma }^{\left(k\right)}$ as follows:

Armijo rule

Finally, the update direction is calculated for the gradient of the parameters and the parameters are updated according to a certain step size

$${\widehat{\beta }}_{\left(l\right)}^{(k+1)}={\widehat{\beta }}_{\left(l\right)}^{\left(k\right)}+{\sigma }^{\left(k\right)}{\zeta }_{\left(l\right)}^{\left(k\right)}.$$

The weighted block coordinate gradient descent algorithm is given by Table 1. In general, selecting the tuning parameter $\lambda$ using cross-validation method is complicated. As we know from Table 1, the algorithm eliminates the selection process for the tuning parameter $\lambda {\omega }_l$. Given an initial value ${\widehat{\beta }}^{\left(0\right)}$, we can then iterate directly over the ${\widehat{\beta }}^{\left(0\right)}$ until it converges to the range which we expect.

It is worth noting that we have given a direct choice (15) for $\lambda$ under a specific weight function $\psi \left(x_i^T{\beta }^0\right)$ given by (14), so the weighted block coordinate gradient descent algorithm will be computationally faster than working iteratively on a fixed grid of tuning parameters $\lambda$ (see Meier et al. [12]). If choosing other weight functions, the weighted block coordinate gradient descent algorithm can still be used to solve (6). But then the tuning parameter $\lambda$ depends on ${\beta }^0$ (unknown), some cross-validation can be used for choosing the parameter $\lambda$.

5. Simulations

In this section, we use simulated datasets to evaluate the performance of the penalized weighted score function estimator. Meier [12] describes block coordinate gradient descent algorithm using the R package grplasso. We modify grplasso, named wgrplasso, and use it to describe the weighted block coordinate gradient descent algorithm. We compare the performance of the wgrplasso algorithm, R package grpreg developed by Breheny [19] and the R package gglasso developed by Yang and Zou [27]. Three main aspects of model performance are considered: correctness of variable selection and accuracy of coefficient estimation, and running time of the algorithm. The evaluation indicators for the model include the following:

• TP: the number of predicted non-zero values in the non-zero coefficient set when determining the model
• TN: the number of predicted zero values in the zero coefficient set when determining the model
• FP: the number of predicted non-zero values in the zero coefficient set when determining the model
• FN: the number of predicted zero values in the non-zero coefficient set when determining the model
• TPR: the ratio of predicted non-zero values in the non-zero coefficient set when determining the model, which is calculated by the following formulation:

  $$TPR=\frac{TP}{TP+FN}.$$
• Accur: the ratio of accurate predictions when determining the model, which is calculated by the following formulation:

  $$Accur=\frac{TP+TN}{TP+TN+FP+FN}.$$
• Time: the running time of the algorithm.
• BNE: the block norm of the estimation error, which is calculated by the following formulation:

  $$BNE=\parallel \widehat{\beta }{-\beta \parallel }_{2,1}.$$

The sample size was 200. We set values of $p=300$, 600, and 900, and generated 100 random datasets to repeat the simulation. We set $ϵ$ to 0.01 and 0.05 and uniformly specify the true non-zero coefficient parameters of the logistic regression models as

$$\beta =(1,\underset{\begin{array}{c}30\end{array}}{\underbrace{{\underbrace{1,\cdots ,1}}_{\begin{array}{c}3\end{array}},\cdots ,{\underbrace{1,\cdots ,1}}_{\begin{array}{c}3\end{array}}}},\underset{\begin{array}{c}p-30\end{array}}{\underbrace{0,\cdots ,0}}).$$

For the log odd $\eta$ setting, we consider the following four different models.

(a) In Model I, the observed data X assume sampling from a multivariate normal distribution and the log odd $\eta$ is considered to be the linear case, where the data between groups are independent but the data within groups are correlated. We set the size of each group to 3 and assume that the data within the groups obey $X_i\sim N(0,{\Sigma }_{i,jk})$, where ${\Sigma }_i=0.5^{|j-k|}$. Thus, the observed data can then be defined as $X\sim N(0,\Sigma )$, where $\Sigma =diag({\Sigma }_1,\cdots ,{\Sigma }_{\frac{p}{3}})$.

(b) In Model II, the observed data X is assumed to be the sum of two uniform distributions and the log odd $\eta$ is considered to be the linear case. Assume that the p-dimensional vectors $Z_1,\cdots ,Z_p$ and W are generated independently and through a uniform distribution of $[-1,1]$. Thus, the observed data can be defined as $X_i=Z_i+W$.

The log odds $\eta$ for Model I and Model II are then defined as follows

$$\eta ={\beta }_0+X_1{\beta }_1+\cdots +X_p{\beta }_p.$$

(c) In Model III, the observed data X is assumed to follow a standard multivariate normal distribution and the log ogg $\eta$ is considered to be additive case. Assuming that X obeys the $\frac{p}{3}$-dimensional standard normal distribution, the observed data can therefore be defined as $X\sim N(0,I_{\frac{p}{3}})$.

(d) In Model IV, the observed data X is assumed to be the sum of two uniform distributions and the log odd $\eta$ is considered to be the additive case. This means assume that the $\frac{p}{3}$-dimensional vectors $Z_1,\cdots ,Z_{\frac{p}{3}}$ and W are generated independently by a uniform distribution of $[-1,1]$. Thus, the observed data can be defined as $X_i=Z_i+W$.

The log odds $\eta$ for Model III and Model IV are then defined as follows

$$\eta ={\beta }_0+X_1{\beta }_1+X_1^2{\beta }_2+X_1^3{\beta }_3+\cdots +X_{\frac{p}{3}}{\beta }_{p-2}+X_{\frac{p}{3}}^2{\beta }_{p-1}+X_{\frac{p}{3}}^3{\beta }_p.$$

Then, the dataset for the response variable Y was generated by the logistic regression models

$$\mathbb{P}(Y=1|\eta )=\frac{1}{1+exp\left({\eta }^{-1}\right)}.$$

Table 2 shows the average simulation results of the three algorithms for the linear case, and Figure plots the point-line plots of Model I and Model II for TPR, Accur, Time and MSE.

First, from the TPR perspective, all three algorithms show excellent selection results when the normal distribution assumption is adopted. However, when the uniform distribution assumption is used, the wgrplasso algorithm shows higher correct selection in the nonzero set than the other algorithms, and the wgrplasso algorithm is also more stable in terms of variance.

Second, from the Accur perspective, compared to the gepreg algorithm, the wgrplasso and gglasso algorithms maintain a high selection effect under the assumption of normal distribution. However, Accur is also affected by FP, and the gepreg algorithm and gglasso algorithm are not stable enough to control FP from the perspective of variance. In addition, under the assumption of uniform distribution, both in terms of the effect of selection and the stability of variance, the wgrplasso algorithm has lower control on the FP aspect, which makes the wgrplasso algorithm perform better than the other algorithms in terms of Accur.

Third, from the Time perspective, using the wgrplasso algorithm saves a lot of time, both for the normal distribution assumption and the uniform distribution assumption.

And last, from the BNE perspective, under the assumption of normal distribution, the BNE obtained by wgrplasso and gglasso algorithms are similar and smaller than that obtained by grpreg algorithm. However, under the assumption of uniform distribution, compared with gglasso algorithm and grpreg algorithm, The BNE obtained by wgrplasso algorithm is smaller, which means that wgrplasso algorithm performs better.

Figure 1. Average TPR, Accur, Time and BNE plots for 100 repetitions of the three algorithms in Model I and Model II.

Figure 1. Average TPR, Accur, Time and BNE plots for 100 repetitions of the three algorithms in Model I and Model II.

Table 3 gives the simulation results of the three algorithms for the additive case, and Figure plots the point line plots of Models III and IV for TPR, Accur, Time and BNE.

The simulation results show that the grpreg algorithm and the gglasso algorithm in the additive case are reduce both in terms of TPR and Accur, and also show through the variance that the grpreg algorithm and the gglasso algorithm also do not have a stable selection, as well as increasing computational time overhead and BNE. However, wgrplasso obtains similar results in the additive case as in the linear case, and still maintains a better selection. Regardless of TPR, Accur and BNE, the wgrplasso algorithm performs better than the other algorithms, and the advantage in Time is even more obvious.

Figure 2. Average TPR, Accur, Time and BNE plots for 100 repetitions of the three algorithms in Model III and Model IV.

Figure 2. Average TPR, Accur, Time and BNE plots for 100 repetitions of the three algorithms in Model III and Model IV.

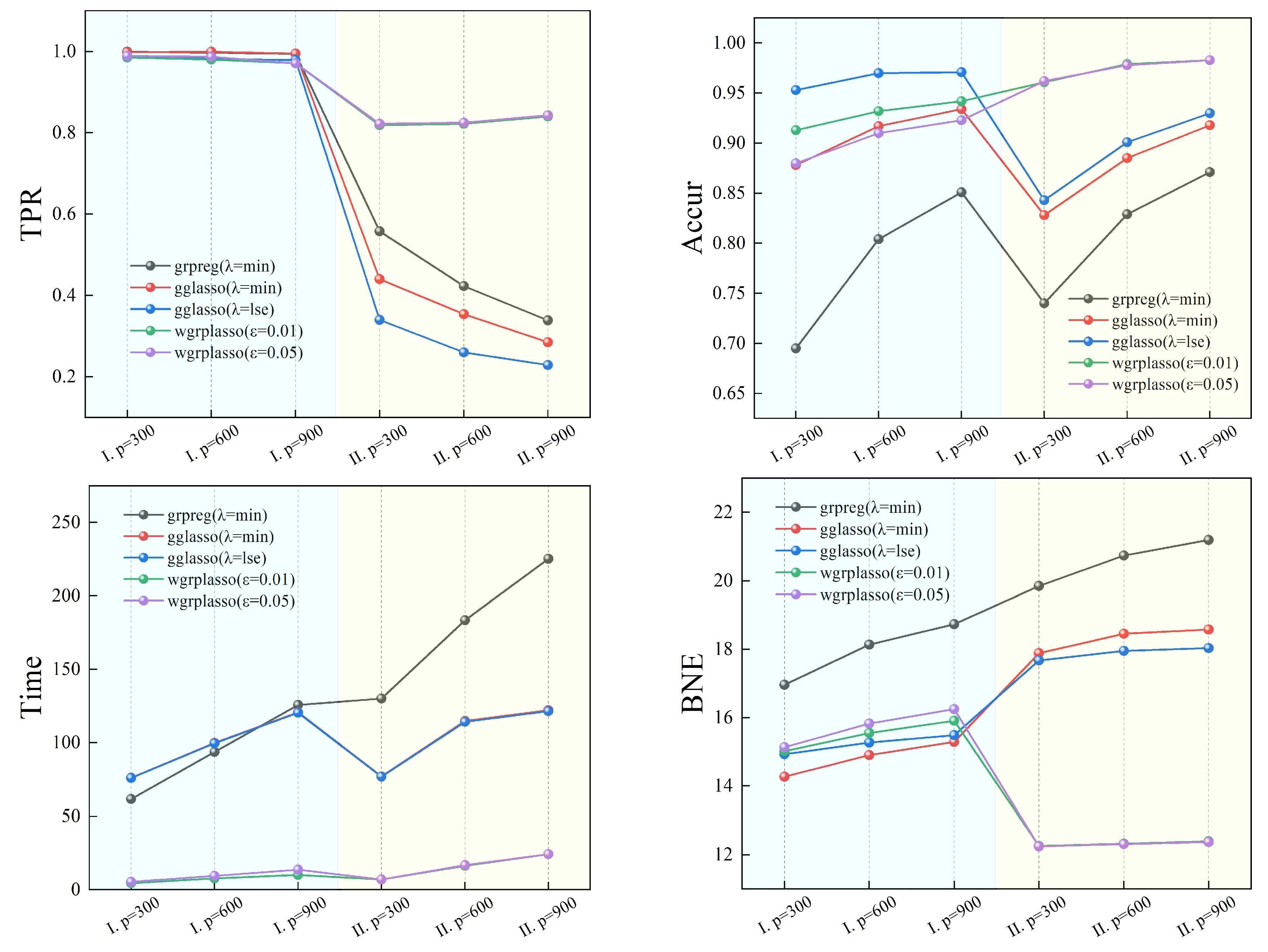
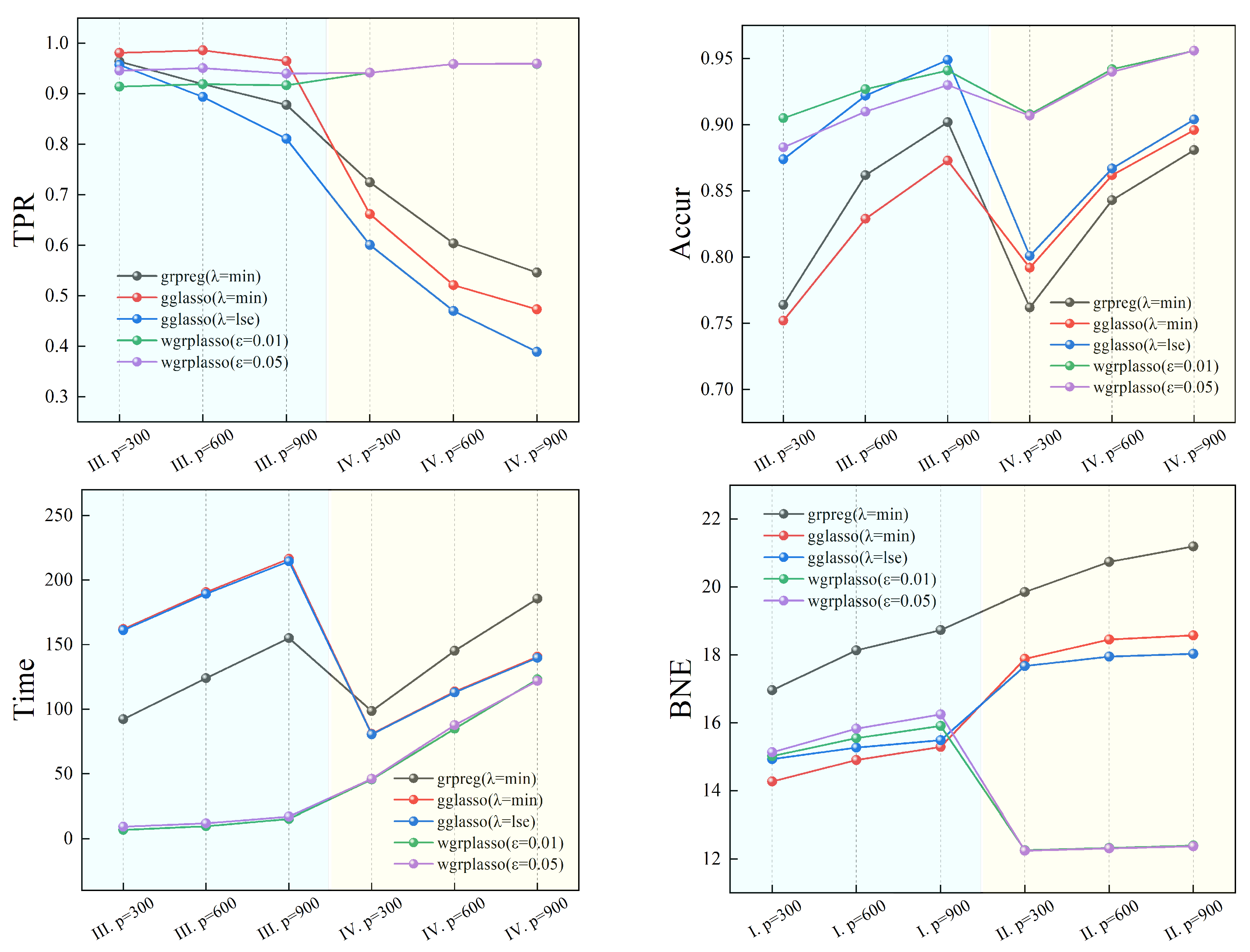
6. Real data

In this section, we apply our proposed estimates to analyze two real data. The first data comes from the molecular shape and conformation of musk. The second data comes from histologically normal epithelial cells from breast cancer patients and cancer-free prophylactic mastectomy patients. As in the previous section, we set $ϵ$ to 0.01 and 0.05, respectively. In Section 6.1 we compare the number of variables selected and the computation time of the three algorithms in the above simulation, and in Section 6.2 we compare the prediction accuracy and the computation time.

6.1. Studies on the molecular structure of Muscadine

The R package of kernlab contains the molecular shape and conformation of musk in the native dataset musk. The data contains a data frame of 476 observations for the following 167 variables. The first 162 of these variables are the distance characteristics of the rays, measured relative to the origin along which each ray is placed. Any experiment with the data should treat these features as being on any continuous scale. Variable 163 is the distance of the oxygen atom to a specified point in 3-space. Variable 164 is the x-displacement from the specified point. Variable 165 is the Y-displacement from the specified point. Variable 166 is the Z displacement from the specified point. The variable 167 tells us that 0 means no musk and 1 means musk.

We used 3/4 of the data for training and performed a third-order B-spline basis function expansion on the training data, and then use the wgrplasso, grpreg, gglasso, and glmnet algorithms for estimation on the expanded training data, respectively. The remaining 1/4 of the data was used as a test, and the estimated coefficients were used to predict the test data, comparing the prediction accuracy, model size, and time for each of the four algorithms. Table 4 gives the experimental results of 100 repetitions.

The experimental results show that wgrplasso has the highest prediction accuracy among the four algorithms, indicating that the algorithm is able to identify the target class more accurately in the task of categorizing musk data, and wgrplasso also exhibits shorter computation time without sacrificing accuracy. This makes the wgrplasso algorithm the preferred algorithm for dealing with the problem of categorizing musk datasets.

6.2. Gene expression studies in epithelial cells of breast cancer patients

We obtained microarray data from the NCBI Gene Expression Omnibus for patient histological epithelial cells. (https://www.ncbi.nlm.nih.gov/geo/) under accession GSE20437. The dataset consists of 42 samples with 22,283 variables. It consists of microarray gene expression data collected from the histologically normal epithelium (NlEpi) from 18 breast cancer patients (HN), 18 undergoing breast reduction (RM) and 6 cancer-free prophylactic mastectomies (PM) in high-risk women. Graham et al. [28] have shown that genes are differentially expressed between HM and RM samples. This is more fully discussed in Yang and Zou [27]. Here, we consider the effect of genes on HM and RM. Similar to Yang and Zou [27] approach to the data, fitting the sparse additive logistic regression model using the Group Lasso penalty while selecting the significant additive components.

As with the setup in Section 6.1, we continue to train with 3/4 of the data and expand the training data using a third-order B-spline basis function and treated them as a group to reflect the role in the additive models, leading to a grouped regression problem with n = 36 and p = 66849. All data were then standardized so that the mean of each original variable was zero and the sample variance was in units. This experiment was repeated 100 times to get the prediction error. We built a complete observational model for the one of experiments, and report the selected genes in wgrplasso, grpreg and gglasso algorithms. These results are listed in Table 5. We observe that the wgrplasso and gglasso algorithms selects more variables than the grpreg algorithm, and wgrplasso has less prediction errors. Summarizing the above results, our proposed penalized weighted score function method can pick much more meaningful variables for explanation and prediction.

7. Conclusion

In our work, we propose the penalized weighted score function method for Group Lasso under logistic regression models. We determine an upper bound on the error of parameter estimation at high probability, and a direct choice of the tuning parameter under a specific weighted function. Under the direct choice of the tuning parameter, we improve the block coordinate descent algorithm to reduce computational time and complexity. Simulation results show that our method not only exhibits better statistical accuracy, but also calculaters faster than competing methods. Indeed, our approach can be extended to other generalized linear models with sparse group structure, which will be a future research.