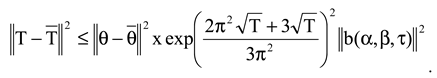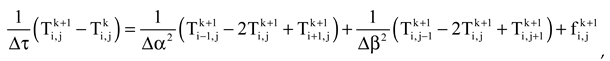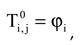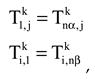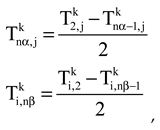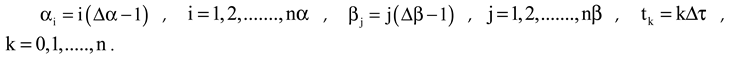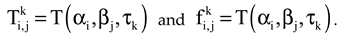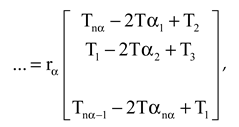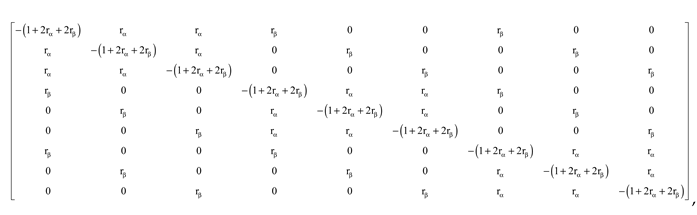1. Introduction
The investigation of mathematical model for a great number of important applications such as chemical diffusions [
1,
2] application in the heat conduction problems, application of heat conduction problems [
3,
4,
5], population dynamics [
6], thermoelasticity [
7], medical science, electrochemistry [
8], engineering, and control theory require the analysis of the analyses of two-dimensional parabolic partial differential equations with nonlocal boundary conditions [
9,
10,
11].
Heat diffusion equation is one of the two-dimensional quasilinear parabolic problem. Heat diffusion equation is used for determining temperature distribution in every region of the domain at desired time for conduction heat transfer problems. Heat transfer by conduction consists of a temperature differences in a solid or stationary fluid. Information of temperature distribution for a solid can be used to determine structural integrity through the determination of thermal stresses, expansions, deflections and cracks. Evaluation and propagation of granite thermal stress and thermal crack with time are shown in
Figure 1 under different temperatures conditions [
12]. The temperature distribution could also be used for optimizing the thickness of an insulating material or for determining the compatibility of the material and the special coatings or adhesives used [
13].
Initial and boundary conditions are required for solving the two-dimensional quasilinear parabolic problem such as the heat diffusion equation. Some of boundary conditions for heat diffusion equation, Dirichlet (or first kind) determines the fixed temperature at surfaces. For example, the surface is very close to this when it comes into contact with a melting solid and/or boiling liquid. In both cases, heat transfer occurs at the surface, while the surfaces remain at the temperature of phase changing process [
13]. Neumann (or the second type) corresponds to the presence of constant heat flux on the surface. This heat flux is related to the temperature at the surface according to Fourier’s law. It can be accomplished by bonding a thin electric heater to the surface. A special case of this situation corresponds to a perfectly insulated or adiabatic surface. Periodic boundary condition is combined with Dirichlet and Neumann boundary conditions [
14], and it is set to isolate repeating temperature distribution in solution domain [
15].
A special case of the nonlocal boundary [
16] condition, the periodic boundary condition, is used in present investigation. Generally, periodic boundary condition is often used in numerical simulations and mathematical models. Also, the periodic boundary condition results from many important applications in heat transfer, fluid dynamics, life sciences and used lunar theory [
14,
17,
18].
In order to solve two-dimensional quasilinear parabolic problem, there are several numerical methods, such as finite difference methods [
19,
20], finite element methods [
21,
22], finite volume methods [
23], lattice Boltzmann Method [
15,
24,
25]. Denghan solve the one-dimensional heat diffusion equation numerically with finite difference method [
26]. In this study, three different schemes were used, namely, backward time centered space (BTCS) implicit scheme, the implicit Crandll’s method, forward time centered space (FTCS) explicit scheme and the Dufort-Frankel three-level techniques. Crank-Nicolson implicit scheme is used to solve numerically for one-dimensional heat diffusion equation with inverse coefficient by Baglan et al [
27]. Kanca and Baglan solve the two-dimensional heat diffusion equation with periodic boundary conditions analytically and numerically [
28]. Fourier method and implicit finite difference scheme are used for analytical and numerical solutions. Hamila et al. [
29] searched the effect of change in thermal conductivity on several transient heat transfer problems with using lattice Boltzmann method (LBM). Benchmark problems containing conduction and/or radiation with constant thermal conductivity were calculated and simulated. Heat diffusion equation were solved numerically using exclusively the lattice Boltzmann method. Numerical results are so close with available result in the literature.
The finite difference method is one of the existing numerical methods which is considered in present investigation can be applied to solve partial differential equations. Finite difference method is based on the discretization of differential equations by finite difference equations. Finite difference approximations have algebraic forms and relate the value of dependent variable at one point in the solution region, to the values at some neighboring points. Using Taylor series is the most usual way to construct these approximations. The numerical method recommended here is the implicit finite difference method. This method supports second order accurate in the spatial grid sizes and first order time grid size. The explicit finite scheme has restriction of determining time step size due to stability requirements for the numerical solution of the two-dimensional heat diffusion equation.
In the present paper, we prove the existence, uniqueness, and continuous dependence of the solution on the data and obtain the numerical solution by Fourier Method and Picard’s successive approximation of the two-dimensional heat diffusion problem with periodic boundary conditions [
14,
27,
28]. For numerical solution, implicit finite difference approximation is used. Numerical solution has a good agreement with analytical solution.
2. The Problem with Periodic Boundary Conditions
Let’s examine the problem given below;
where Fourier Coefficients:
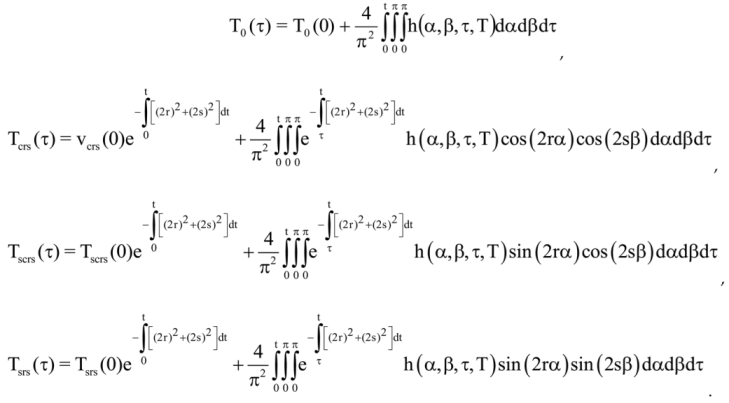
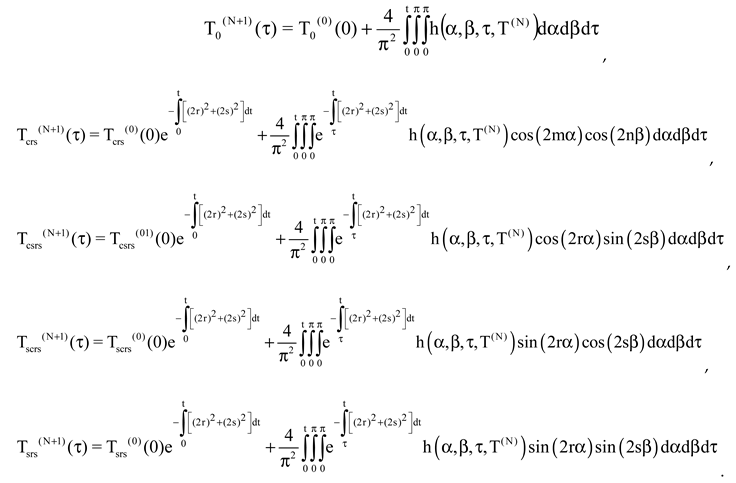
Then we obtain the solution:
3. Analytical solution of the Problem
Let's assume the following rules for the functions used in the problem:

where
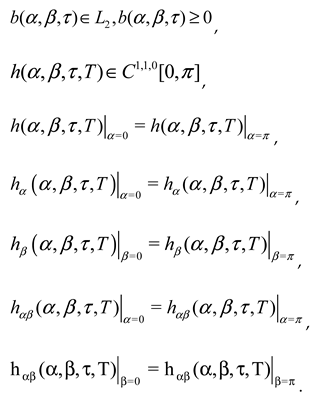
Definition 1.
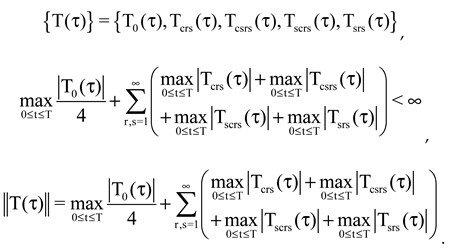 is called Banach (B) norm.
is called Banach (B) norm.
Theorem 1. Let the assumptions (A)-(B) be satisfied. Then the problem has a unique solution.
Proof. As iteration for the problem
Applying Cauchy, Bessel, Hölder inequalities, Lipschitz condition, we have
From the theorem .
We get since
Let us show that,
is converged for
.

Applying Cauchy, Bessel, Hölder inequalities, Lipschitz condition, we have
where let
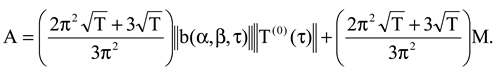
.
Applying for the step N,
We obtain
.
Let us show that, is converged for .
Applying Cauchy, Bessel, Hölder inequalities, Lipschitz condition, we have
From the Gronwall’s inequality,
From Eq. 12, we get
To show the uniqueness, we get two solutions the problem .
Applying Cauchy, Bessel, Hölder inequalities, Lipschitz condition, we have
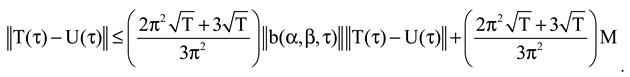
From the Gronwall’s inequality,
We get
4. Stability of Solution
Theorem 2. Let the assumptions (A)-(B) be satisfied. Then the problem is constantly dependent on the data.
Proof.
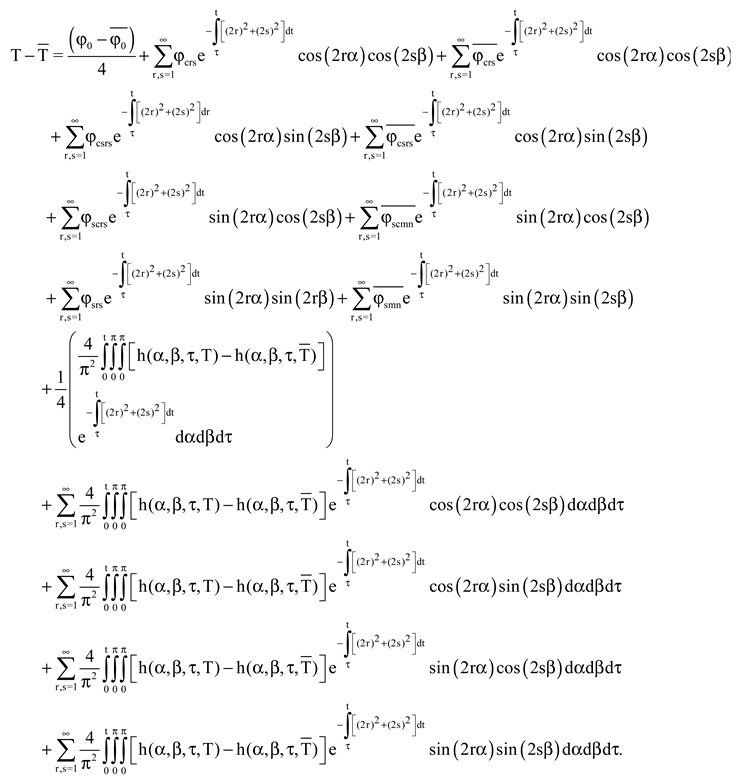
Applying Cauchy, Bessel, Hölder inequalities and Lipschitz condition, we have
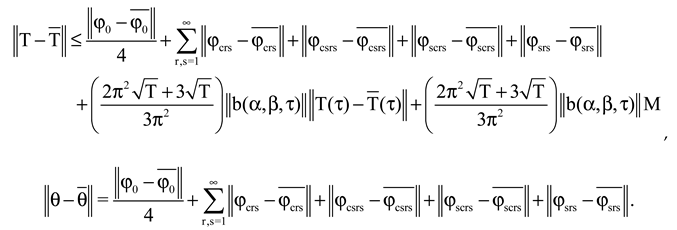
From the Gronwall’s inequality,
From Eq. 14, for
. Then
.
5. Numerical Method for Problem
In this section, we use implicit finite-difference approximation of the discretized problem (1)-(4);
where the computational domain
is discretized as follows:
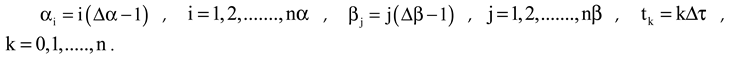
Where
,
and
are the space α direction, space β direction and time steps, respectively. nx, ny and n is are three positive integers.
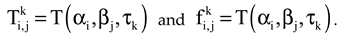
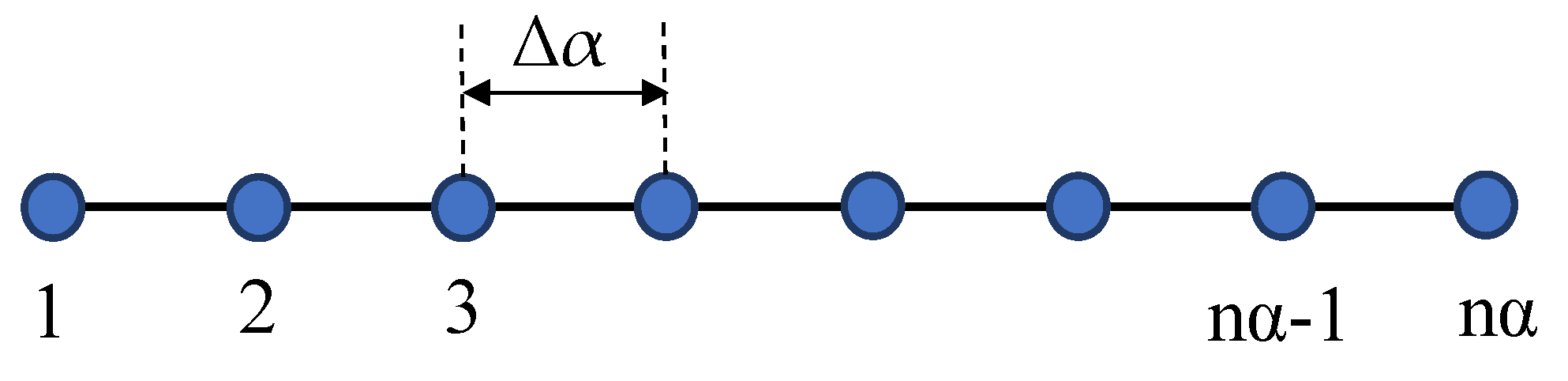
In order to define periodic boundary condition (Eq. 17 and 18) for implicit finite difference scheme, one-dimensional schematic figure with numerical meshes is represented in
Figure 2. Point-1 and point-nα are boundary points of one-dimensional solution domain. When we determine spatial dicretization with finite difference scheme, the used finite difference formulations are defined as;
where
, and the coefficient matrix can be rewrittwen for one-dimensional solution domain.
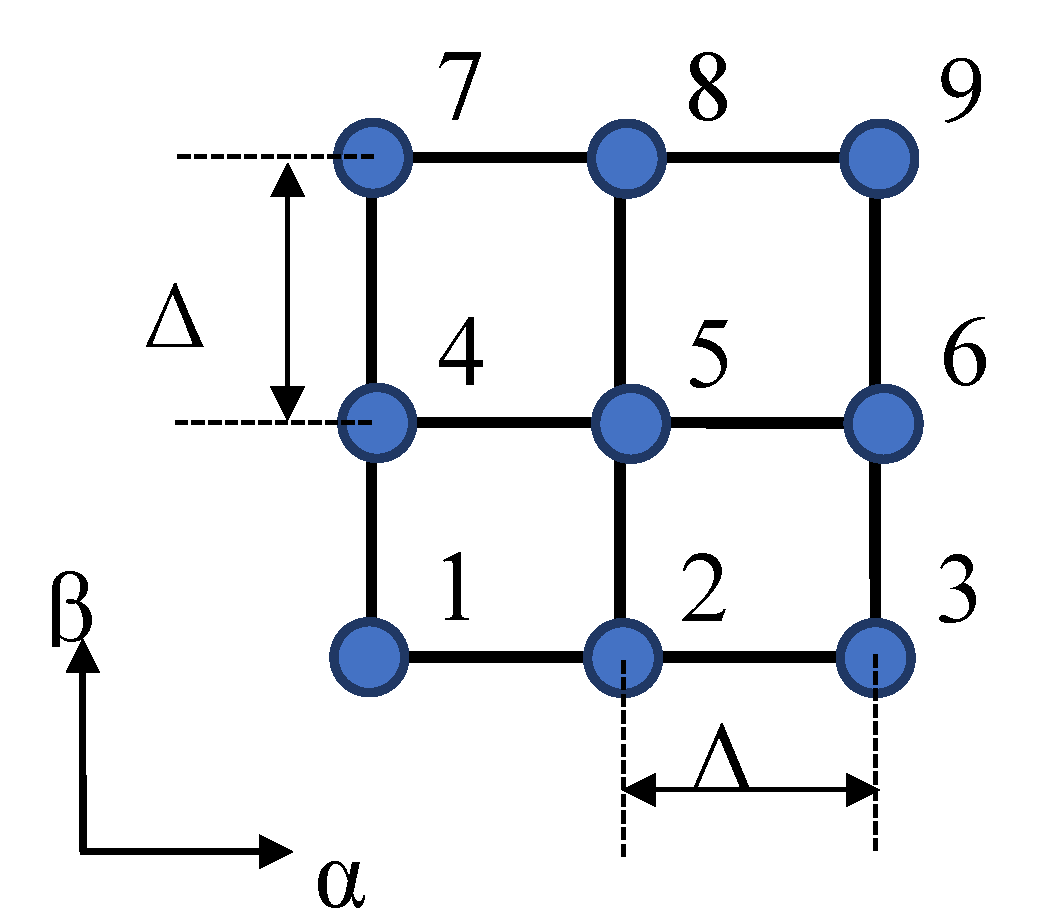
This one-dimensional formulation and coefficient matrix can be extended in two-dimensional solution domain. Two-dimensional schematic figure with numerical meshes (9 finite difference meshes) is represented in
Figure 3. Of course, matrix is constructed for 9 finite difference meshes, therefore the matrix size is 9×9. Point-1, 2 and 3 are periodic with 7, 8 and 9, respectively, at β-direction. Point-1, 4 and 7 are periodic with 3, 6 and 9, respectively, at α direction. Coefficient matrix can be written as;
where
. If large number of meshes are used, the matrix can be extended in a same way. For example, if we have 20 meshes both α and β directions, our matrix size will be 400×400, total element of matrix is 160 000, and our matrix can be constructed in a same manner to define points of periodic boundary condition and inner (no periodic boundary condition points).
Example 1.
Consider the heat diffision problem with heat source (1)-(4):
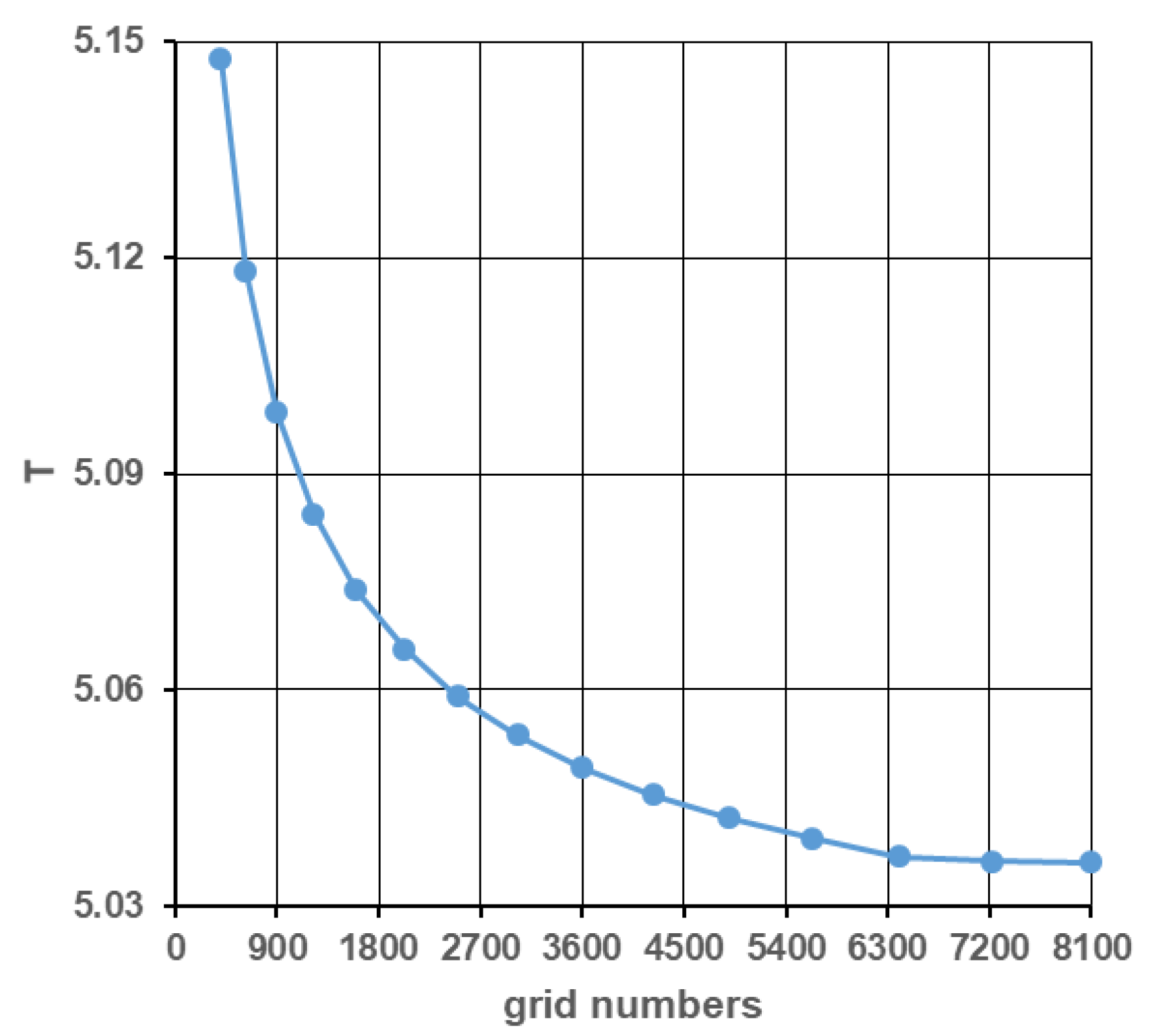
We determine the time step size is . Discretization of spaces or mesh sizes of α and β directions are considered equal (). In order to determine, mesh size of α and β directions, grid independency study is done. For grid-independence study, fifteen different grid resolutions are used.
In α and β directions, the same numbers of grid are used because of equal grid size (
) are considered. For every grid resolutions, we observed area-weighted averaged value of temperature for whole solution domain.
Figure 4 shows the grid independent study of area-weighted averaged value of temperature. According to
Figure 4, mesh number of 6400 is taken as grid independent mesh number. In this case, eighty grids are used for α and β directions, therefore our mesh size of α and β directions are get as 0.03926875.
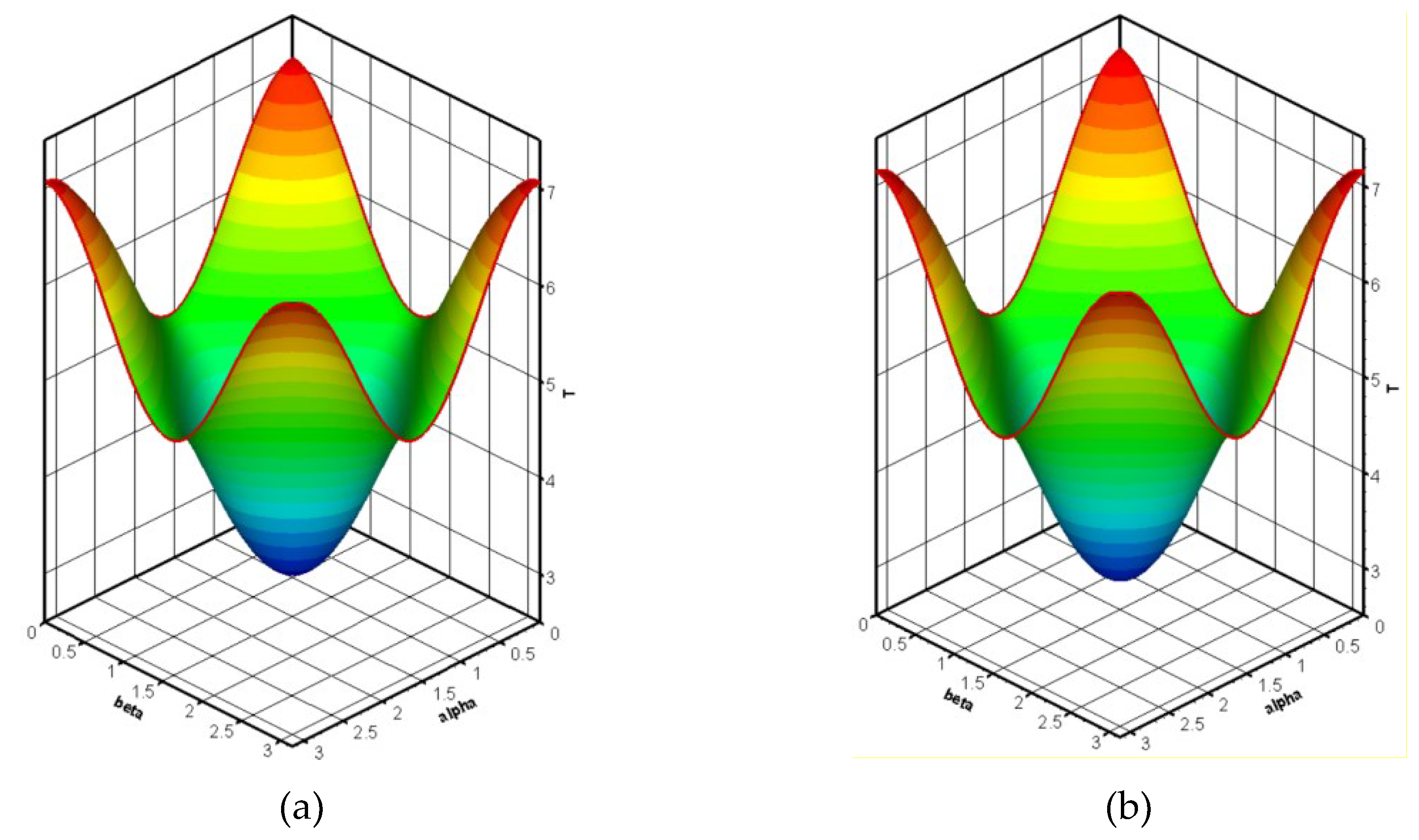
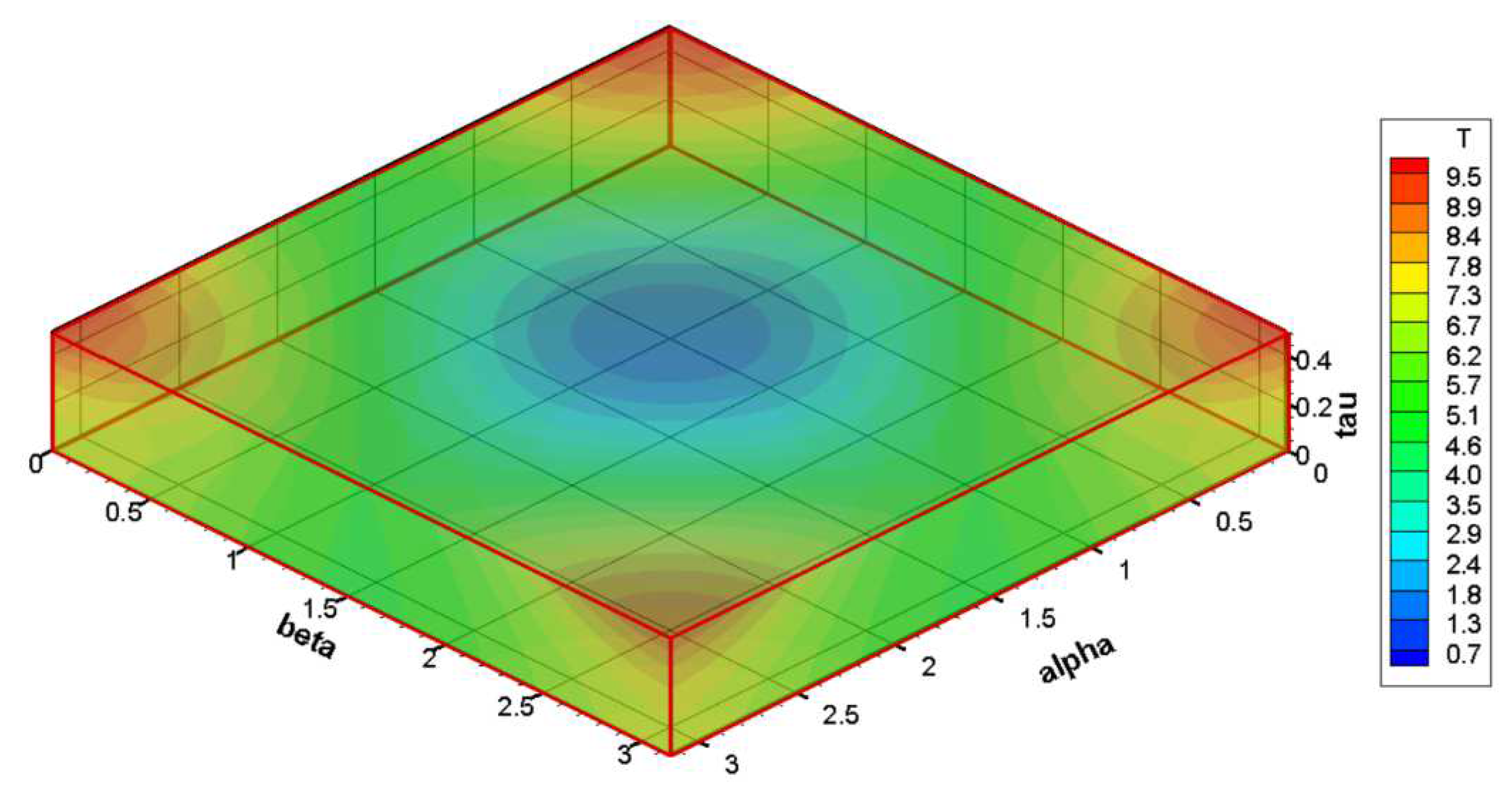
Figure 5 shows (a) exact and (b) numerical solutions for temperature with time at 0.1s. The exact and numerical solutions are paraboloid. Maximum and minimum temperature values are observed at corners and at the middle of the solution domain, respectively. Because of periodic boundary conditions at side of solution domain, temperatures are same at side of the solution domain. Also, exact and numerical solutions are so quite similar.
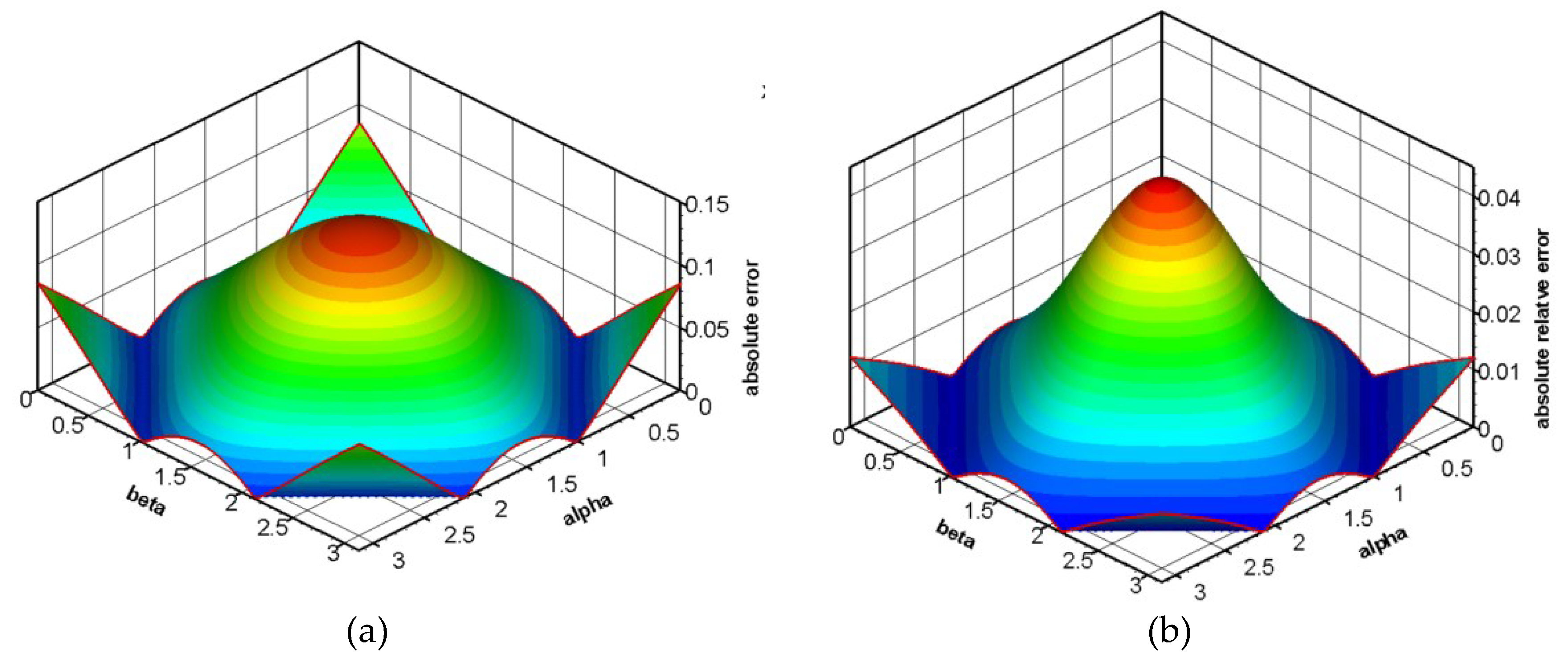
Figure 6 shows (a) absolute error and (b) relative absolute error for temperature with time at 0.1s. Absolute error is the absolute value of the difference between exact solution value and numerical solution. According to
Figure 6a, maximum absolute error is shown at center of the solution domain, also at corners of the solution domain, absolute error is higher. At center of solution domain, approximately absolute error of 0.1 is observed. Relative absolute error is the ratio of the absolute error to the exact solution. The magnitude of the absolute error in terms of the exact solution is determined with using relative absolute error. Like in absolute error, maximum relative error which is 0.03 is observed at the center of the solution domain. At corners of the solution domain, relative absolute error is order of 0.01. As the time increases, absolute error and relative absolute error remain in the same order, and these error are in reasonable.
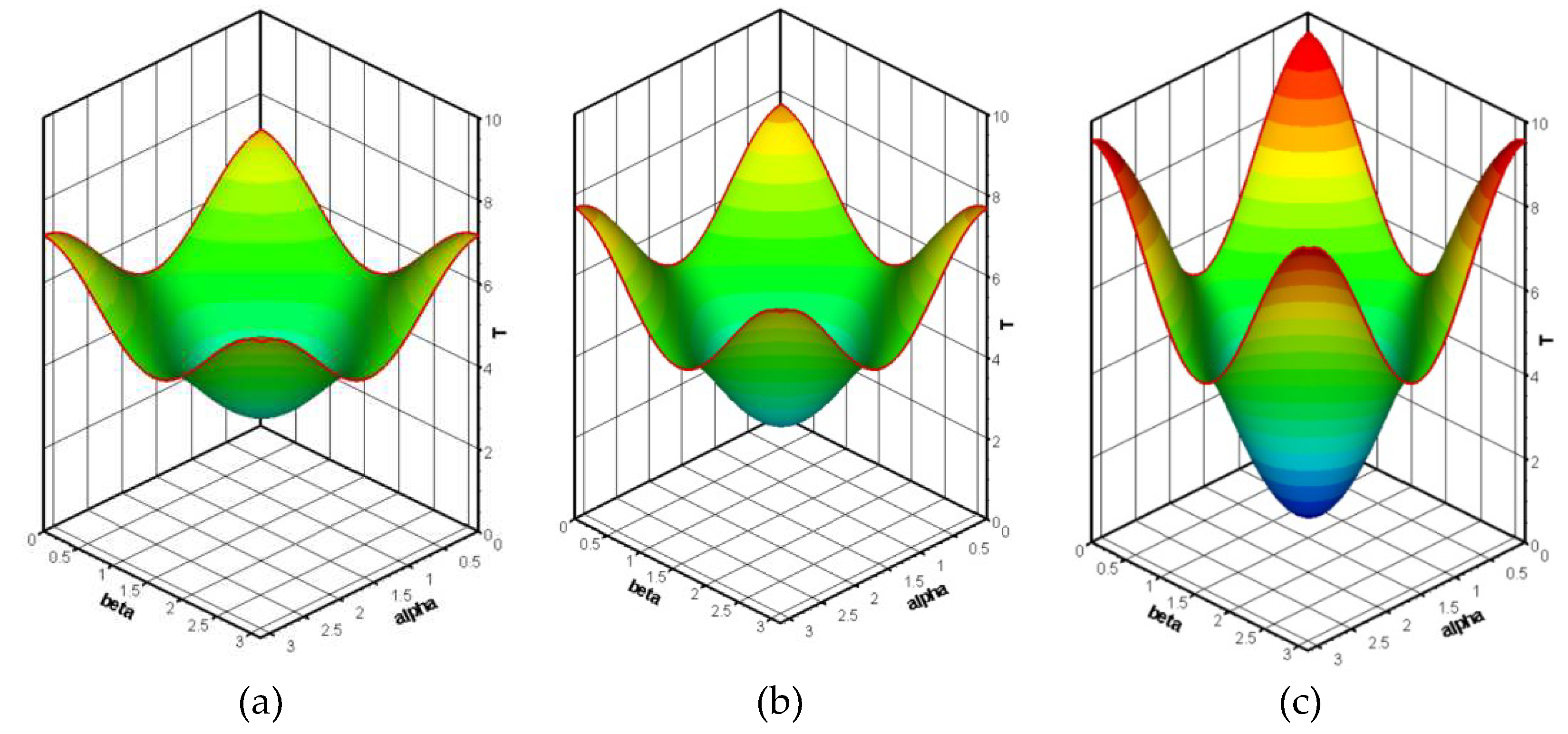
Figure 7 presents the numerical predictions of temperature distributions at time (a) 0.1s, (b) 0.25s and (c) 0.5s. As one can see, temperature distributions at the specific times are paraboloid. The concavity of the parabolite increases with time. The minimum and the maximum values of temperature are appeared at center and corners of the solution domain, respectively, at all times.
In order to see all times in one figure,
Figure 8 presents the distribution of temperature with time range from 0s to 0.5s. Paraboloid are not shown here. Maximum and minimum temperature values are observed at the corners and center of the solution domain, respectively, at all times. Also with increasing time, temperature values of corners increase and temperature values of centers decreases.
7. Conclusions
Analytical and numerical investigation of two-dimensional heat diffusion problem with heat source is done. This problem is quasi-linear parabolic problem, and we use initial condition and periodic boundary condition to determine temperature in the solution domain. Because of the problem is nonlinear, Picard’s successive approximation theorem is used. Under certain conditions of natural regularity and consistency imposed upon the input data, we constituie the existence, uniqueness and constant dependence of the solution on the data using the generalized Fourier method. Implicit finite difference scheme is used for the numerical solution. The number of numerical meshes where results do not change is determined according to grid independence study. In the light of analytical and numerical solution, distribution of temperature is paraboloid at the certain time. With increasing time, concavity of parabolic increases. At the time of 0.1s, maximum absolute error and relative error are occurred at the middle of the solution domain, they are, 0.1, 0.03, respectively. Therefore, we can say that analytical solution and numerical solutions are close each other. Also, with increasing time, degrees of absolute and relative absolute errors are same.
References
- Permikin, D.V.; Zverev, V.S. Mathematical model on surface reaction diffusion in the presence of chemical reaction. International Journal of Heat and Mass Transfer 2013, 57, 215-221. [CrossRef]
- Tredenick, E.C.; Farewell, T.W.; Forster, W.A. Modeling of diffusion of a hydrophilic ionic fertilizer in plant cuticles: surfactant and hygroscopic effects. Front Plant Sci. 2018, 9, 1888. [CrossRef]
- Canon, J.R. The solution of the heat equation subject to the specification of energy. Quarterly of Appl. Mathematics 1963, 21(2), 155-160. [CrossRef]
- Canon, J.R. Determination of an unknown heat source from overspecified boundary data. SIAM Journal on Numerical Analysis 1968, 5(2), 275-286. [CrossRef]
- Zhu, Q.; Tran, H.; Yang, H. Heat conduction: Mathematical modeling and experimental data. J Emerging Investigators 2021, 4, 1-4. [CrossRef]
- Venkatesha, P.; Eunice, G.B.; Akshaya, B.; Arya Kumari, S. Mathematical modeling of population growth. Int. J. Sci. Eng Management 2017, 2(11), 117-121.
- Avey, M.; Fantuzzi, N.; Sofiyev, A. Mathematical modeling and analytical solution of thermoelectric stability problem of functionally graded nanocomposite cylinders within different theories. Mathematics 2022, 10, 1081.
- Turnbull, A.; Ferriss, D.H. Mathematical modelling of the electrochemistry in corrosion fatigue cracks in structural steel cathodically protected in sea water. Corrosion Science 1986, 26(8), 601-628. [CrossRef]
- Dehghan, M. Implicit locally one-dimensional methods for two-dimensional diffusion with a non-local boundary condition. Math. Computers Simulation 1999, 49, 331-349. [CrossRef]
- Siddique, M. Solving two-dimensional diffusion equations with nonlocal boundary conditions by a special class of Padé approximants. Systemics, Cybernetics and Informatics 2010, 8(4), 23-29.
- Mohebbi, A. A numerical algorithm for determination of a control parameter in two-dimensional parabolic inverse problems. ACTA Mathematics Appicatae Sinica, English Series 2015, 31(1), 213-224. [CrossRef]
- Li, Q.; Yin, T.; Li, X.; Shu, R. Experimental and numerical investigation on thermal damage of granite subjected to heating and cooling. Mathematics 2021, 9, 3027. [CrossRef]
- Bergmann, T.L.; Lavine, A.S.; Incropera, F.P.; Dewitt, D.P. Fundamentals of Heat and Mass Transfer, 7th ed.; John Wiley&Sons: Danver, USA, 2011.
- Baglan, I.; Kanca, F. Two-dimensional inverse quasilinear parabolic problems with periodic boundary conditions. Applicable Analysis 2019, 98(8), 1549-1565. https://doi.org/10.1080/00036811.2018.1434149. [CrossRef]
- Mohamad, A.A. Lattice Boltzmann Method Fundamentals and Engineering Applications with Computer Codes, 2nd ed.; Springer-Verlag London Ltd.: London, England, 2019.
- Afshar, S.; Soltanalizadeh, B. Solution of the two-dimensional second-order diffusion equation with nonlocal boundary conditions. Int. J. Pure Appl. Math. 2014, 94(2), 119-131. https://doi.org/10.12732/ijpam.v94i2.1. [CrossRef]
- Rao, Y.; Zhang, Y.; Xu, Y.; Ke, H. Experimental study and numerical analysis of heat transfer enhancement and turbulent flow over shallowly dimples channel surfaces. Int. J. Heat Mass Transf. 2020, 160, 120195. [CrossRef]
- Hill, G.W. On the part of the motion of the lunar perigee which is a function of the mean motions of the sun and moon. Acta Math 1886, 8, 1-36. [CrossRef]
- Morton, K.W.; Mayers, D.F. Numerical Solution of Partial Differential Equation, 2nd ed.; Cambridge University Press: Cambridge, England, 2005.
- Dmitriev, V.G.; Danilin, A.N.; Popova, A.R.; Pshenichnova, N.V. Numerical analysis of deformation characteristics of elastic inhomogeneous rotational shells at arbitrary displacements and rotating angles. Computation 2022, 10, 184. [CrossRef]
- Benim, A.C.; Zinser, W. Investigation into finite element analysis of confined turbulent flows using a k-ε model of turbulence. Compt. Methods Appl. Mech. Engineering 1985, 51(1-3), 507-523. [CrossRef]
- Benim, A.C.; Finite element analysis of confined turbulent swirling flows. Int. J. Num. Meth. Fluids 1990, 11(6), 697-717.
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics, 2nd ed.; Pearson, Prentice Hall: London, England, 2007.
- Chen, S.; Doolen, G.D. Lattice Boltzmann method for fluid flows. Annual Review Fluid Mech. 1998, 30, 329-364. [CrossRef]
- Succi, S. The Lattice Boltzmann Equation for fluid Dynamics and Beyond; Oxford University Press: Oxford, England, 200.
- Denghan, M. Efficient techniques for the second-order parabolic equation subject to nonlocal specifications . Appl. Num. Math. 2005, 12(1), 39-62.
- Baglan, I.; Kanca, F.; Mishra, V.N. Determination of an unknown heat source from integral overdetermination condition. Iran J. Sci. Technol. Trans. Sci. 2018, 42, 1373-1382. [CrossRef]
- Kanca, F.; Baglan, I. Solution of the boundary-value problem of heat conduction with parabolic conditions. Ukrainian Math. J. 2020, 72(2), 232-245.
- Hamila, R.; Chaabane, R.; Askri, F.; Jemni, A.; Nasrallah, S. B. Lattice Boltzmann method for heat transfer problems with variable thermal conductivity. Int. J. Heat Tech. 2017, 35(2), 313-324. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
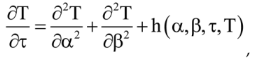
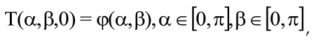
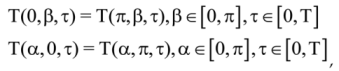
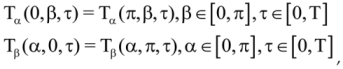
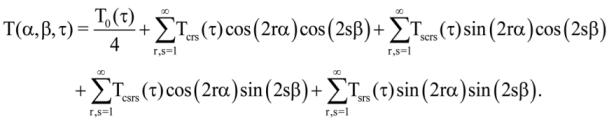
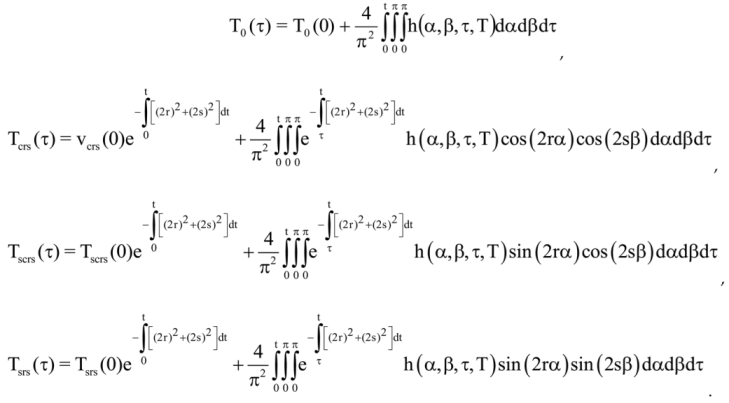 Then we obtain the solution:
Then we obtain the solution:
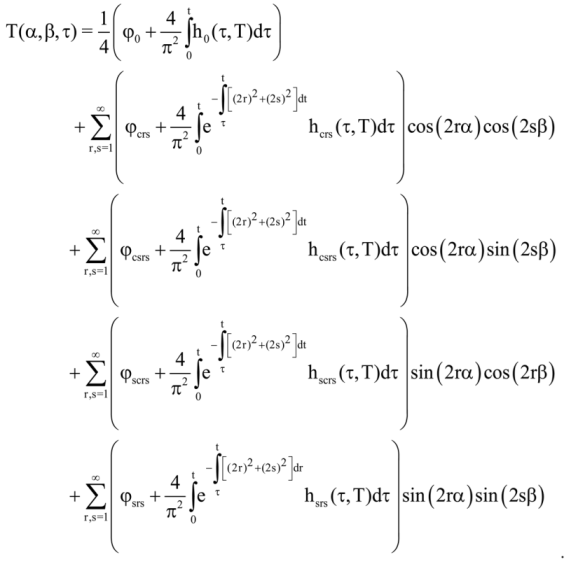
 where
where
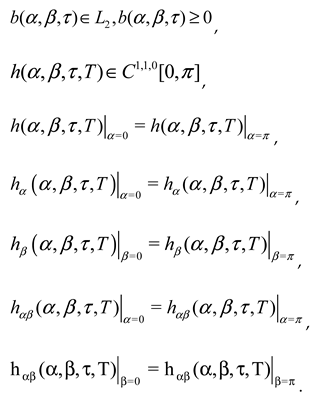
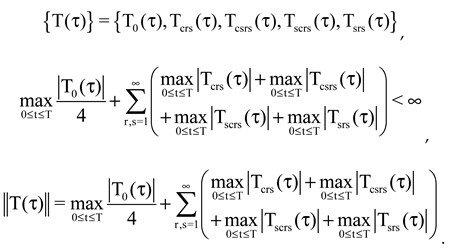 is called Banach (B) norm.
is called Banach (B) norm.

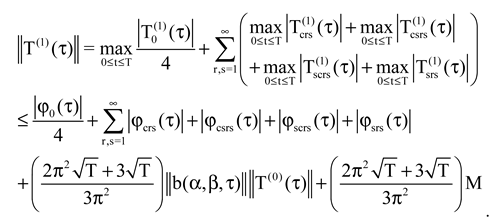
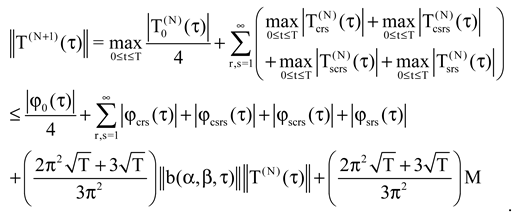
 Applying Cauchy, Bessel, Hölder inequalities, Lipschitz condition, we have
Applying Cauchy, Bessel, Hölder inequalities, Lipschitz condition, we have
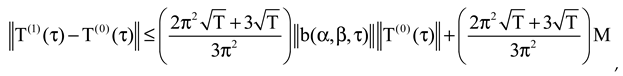
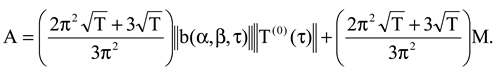 .
.
 From the Gronwall’s inequality,
From the Gronwall’s inequality,
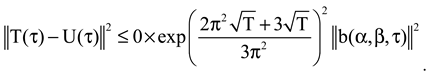
 Applying Cauchy, Bessel, Hölder inequalities and Lipschitz condition, we have
Applying Cauchy, Bessel, Hölder inequalities and Lipschitz condition, we have
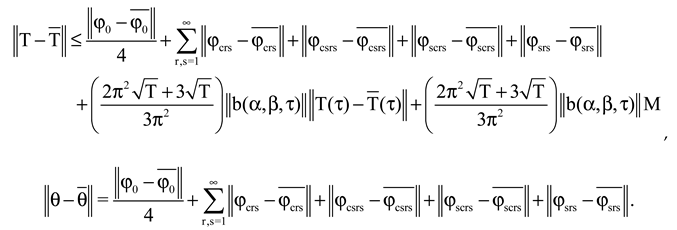 From the Gronwall’s inequality,
From the Gronwall’s inequality,