Prerpints.org logo
Preprint
Communication

Mid-Infrared Complex Refractive Index Spectra of Polycrystalline Copper-Nitride Films by IR-VASE Ellipsometry and Their FIB-SEM Porosity

Altmetrics

Downloads

133

Views

55

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

07 November 2023

Posted:

08 November 2023

You are already at the latest version

Alerts
Abstract
Copper-nitride (Cu3N) semiconductor material is attracting much attention as a potential, next-generation thin-film solar-light absorber in solar cells. In this communication, polycrystalline Cu3N thin films were prepared using reactive-RF-magnetron-sputtering deposition, at room temperature, onto glass and silicon substrates. The very-broadband optical properties of the Cu3N thin film layers were studied by UV-MIR (0.2-40 μm) ellipsometry and optical transmission, to be able to achieve the goal of a low-cost absorber material to replace the conventional silicon. The reactive-RF-sputtered Cu3N films were also investigated by focused ion beam scanning electron microscopy, and both FTIR and Raman spectroscopies.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

1. Introduction

There is a need to innovate in eco-friendly, advanced materials to provide the answer to the social demand for sustainable energy [1,2,3]. Determination and understanding of the optical properties of polycrystalline copper-nitride ( Cu 3 N) thin films, such as refractive index and extinction coefficient and bandgap energy, are important to carry out a photovoltaic-cell design, in which the Cu 3 N material acts as solar-light absorber [4,5,6]. It would open the door to the next, flexible third-generation of photovoltaic technologies that could benefit from this material. The practical application of copper-nitride layers mainly depends upon the size of its optical bandgap. This nitride is an non-toxic choice to consider as a possible alternative for tellurium-based materials.
Paradoxically, despite the great expectations that the metastable indirect-gap Cu 3 N semiconductor is awakening because of its optical and energy-storage properties, it is not yet employed in a specific solar cell. The development of a low-cost Cu 3 N semiconductor, free of critical materials, and prepared with easy growth techniques for industrial scaling, such as reactive-RF-magnetron-sputtering deposition, is nowadays considered a hot topic in emerging-technology photovoltaics. In other words, more research is still needed because there is yet relatively scarce information about the potential use of Cu 3 N as an element of a solar cell.
The present communication reports the feasible and successful preparation of the Cu 3 N binary compound, with an anti-ReO3 cubic crystal structure, importantly, at room temperature, onto glass and silicon substrates, and using two different gaseous environments: (i) an Ar-free environment, based only upon nitrogen ( N 2 ), and (ii) a mix of N 2 and Ar [7,8,9]. Focused ion beam scanning electron microscopy (FIB-SEM) was employed to determine the surface morphology of the Cu 3 N thin-layer samples under study. There is a clear interest in the analysis of porosity in the present Cu 3 N films by this FIB-SEM technique. It has been considered for production of Cu 3 N layers, to take advantage from the existing porosity of the copper-nitride layers grown at oblique angle.
We then calculated the complex refractive index, n ˜ = n + i k (n is the real refractive index and k is the extinction coefficient), of the copper-nitride layers employing UV-MIR spectroscopic ellipsometry [10,11,12], for the first time, to the best of our knowledge. It should be emphasized that in this study was additionally performed, as the main novelty, spectro-ellipsometric measurements in the infrared spectral range, up to 40 μ m, in which molecular vibrations, and both free-charge-carrier and phonon (lattice) absorption are probed, thus providing very valuable and diverse information about the material. It has also to be stressed that the UV-visible spectral range is just sensitive to the electronic states and excitons. Besides information about the layer thickness, modeling of the IR ellipsometric spectra therefore provides useful information on the chemical, structural and infrared properties of the Cu 3 N thin films.

2. Experimental Procedure

We grew Cu 3 N thin films by reactive-radio-frequency-magnetron sputtering, at room temperature, 50-W RF-power, and working gas pressure of 5.0 Pa, onto glass and silicon substrates; we used partial nitrogen pressures of 0.8 and 1.0. Details regarding the deposition conditions are listed in Table 1.
Focused ion beam scanning electron microscopy was employed to study the topography of Cu 3 N layers. The focused-ion-beam technique was used to obtain transversal trenches and remove material from the surface, for measuring pore sizes, using the software ImageJ. Further details are found elsewhere [5].
UV-Visible-NIR spectroscopic ellipsometry (SE) measurements were used to acquire the ellipsometric angles Ψ and Δ , on a Woollam vertical variable-angle-of-incidence rotating-analyzer ellipsometer. Data were obtained at three angles of 50 ∘ , 60 ∘ , and 70 ∘ , respectively. Novel infrared spectroscopic ellipsometry (IRSE) measurements were also carried out on a Woollam IR-VASE Mark II ellipsometer, integrating a Fourier-transform infrared interferometer source. The experimental SE and IRSE data were modeled using the WVASE software package, version 3.942. FTIR measurements were performed using a Perkin-Elmer 100 FTIR spectrometer. Raman measurements were carried out employing a dispersive spectrometer Horiba-Jobin-Yvon LabRam HR 800. Normal-incidence optical transmission was also measured using a double-beam spectrophotometer (Lambda 1050 ultraviolet-visible-near infrared spectrometer, Perkin Elmer).

3. Results and discussion

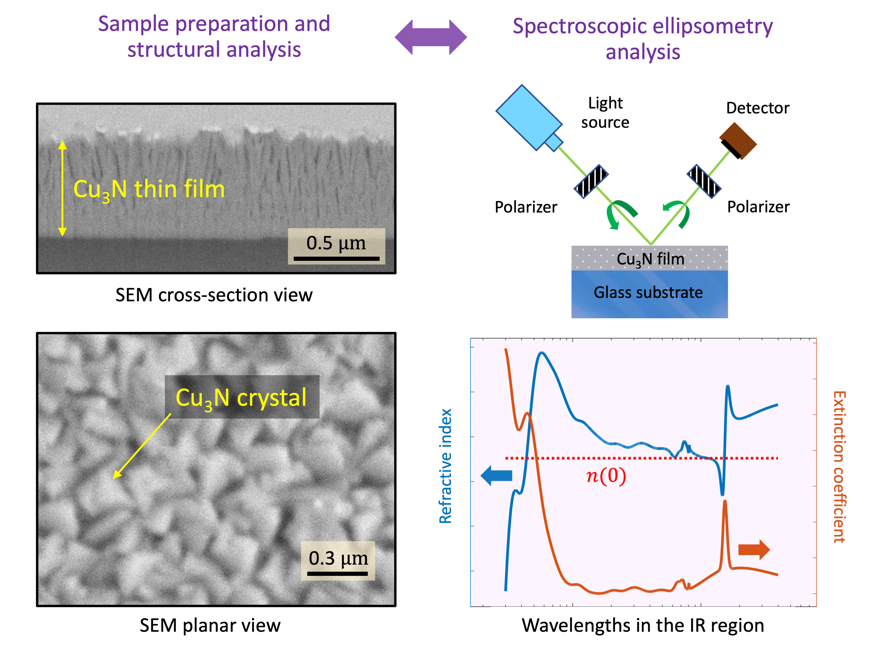
3.1. FIB-SEM Microscopy Study

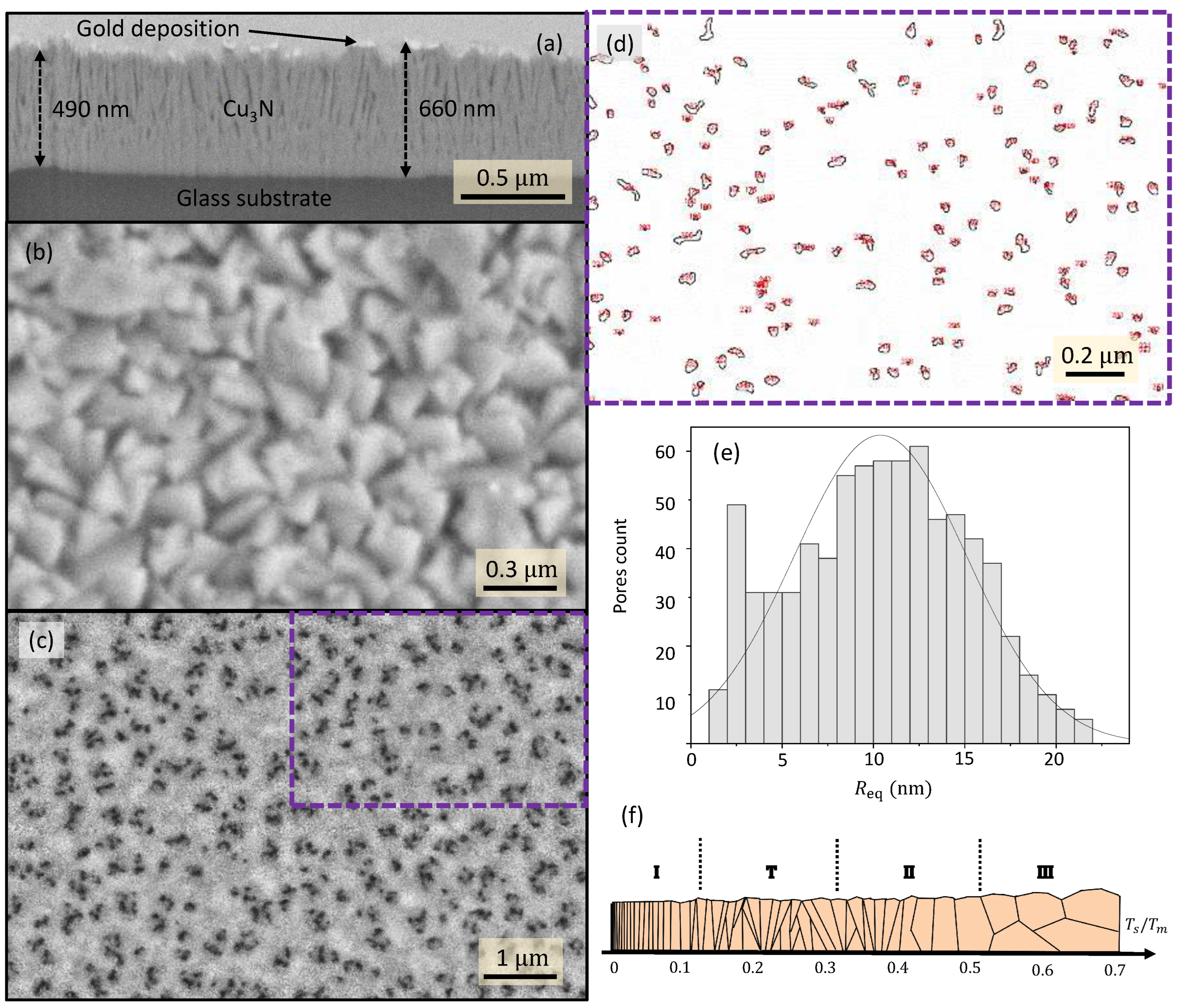
The Cu 3 N thin films exhibited a columnar formation, as shown in Figure 1a (the maximum and the minimum values of the film thickness are indicated in the micrograph). It is observed that the copper-nitride microstructure through about the first 100 nm (samples #1460 and #1490), or around the first 200 nm (sample #1360), from the glass surface, is undoubtedly compacted, while voided spaces between the Cu 3 N-layer columns are clear in the rest of the layer thickness. This is the columnar-structure ‘zone’ 2 of the Thornton structural zone model [13]; it consists of columnar and compact grains, with high density and smooth surfaces.
It is verified that the T s / T m ratio must obey the condition, 0.3 < T s / T m < 0.5 , in this particular zone 2, where T s is the substrate temperature during deposition, and T m is the coating-material melting point, which is well-known to be above 740 K, the decomposition temperature of Cu 3 N. Hence, it is clear that the columnar structure of Cu 3 N results from being grown at room temperature and low working-gas pressure. The value of the T s / T m ratio in our RF-sputtering depositions is found to be 0.41, certainly a value corresponding to the zone-2 category. Figure 1b displays an SEM micrograph of the surface of sample #1460. Cu 3 N pillars met at its surface, giving place to a conglomerated structure with many sealed ‘closed’ pores.
The FIB-SEM porosity of sample #1360 (see Figure 2a) was quantified using images such as the one in Figure 1c. The pore map in Figure 1d, on the other hand, was obtained using the software ImageJ from the region indicated by a dashed frame in Figure 1c. This software is commonly utilized to measure particle sizes from images. It has similarly and successfully been used in this work to obtain the equivalent pore radii. Figure 1d shows the pore perimeter (black lines), and the numbering (in red) that ImageJ uses to identify each particular pore. Pore areas, A pore ’s, were automatically measured from the map, and the corresponding values of the equivalent pore radius, R eq , were obtained using the expression: R eq = A pore / π . Figure 1d displays the corresponding histogram for the values calculated from the SEM image in Figure 1c; the mean equivalent radius in this particular sample was found to be 10.4 ± 4.7 nm.

3.2. UV-MIR Ellipsometric Analysis

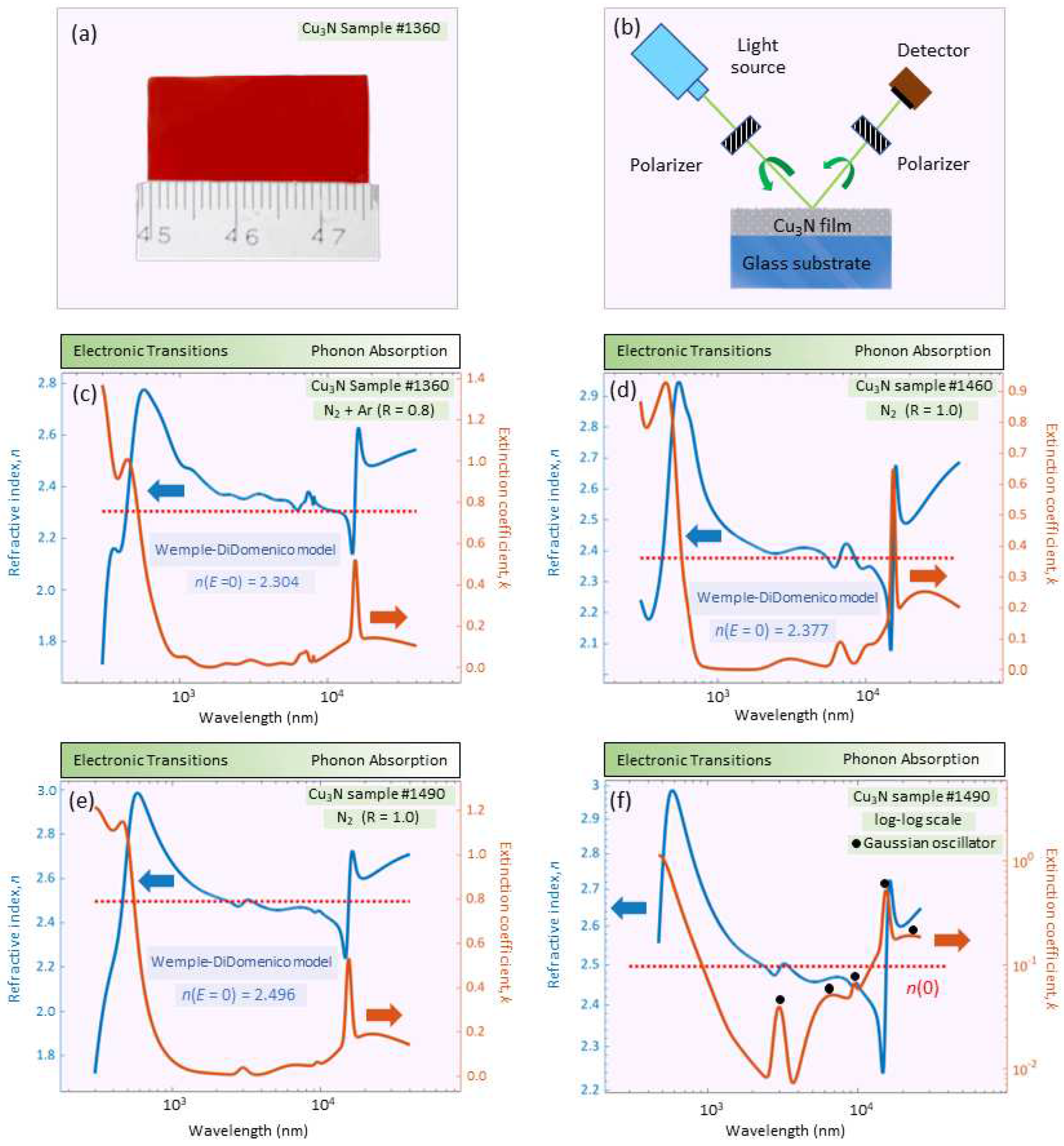
Optical and infrared ellipsometric data (see Figure 2b) were fit over the ample range of 200 − 40 , 000 nm ( 0.031 − 6.2 eV), simultaneously with normal-incidence optical transmission data (200-2500 nm, or 0.5-6.2 eV). The best-fit ellipsometric model required, in the case of sample #1490, the introduction of a 46-nm-thick surface-roughness layer (Table 1).
Figure 2 shows the best-fit very-broadband optical constants, n and k, for the Cu 3 N samples. Table 1 gives information about the necessary number of oscillators in order to predict the dielectric functions contained in the so-called GenOsc layer, for all Cu 3 N samples. The excellent comparison between the surface roughness determined by both spectro-ellipsometry and atomic-force-microscopy is also shown in Table 1. In addition, two major spectral features are seen in the optical constants of Cu 3 N: A UV-Visible absorption edge with a peak at approximately 2.47 eV, and a second sharp resonant absorption in the infrared near a wavelength of 15,480 nm, both peaks for the particular case of #1490 layer. The specific UV-Visible absorption edge, with a clear peak, was modeled by combining a Gaussian and a Tauc-Lorentz oscillator [14,15,16]. Gaussian oscillators were also added to fit the two ellipsometric angles, Ψ and Δ , in the rest of the spectral range under study, for the #1490 sample. The extremely-sharp resonant absorption peak at 646 cm − 1 (Figure 3a), on the other hand, determined by ellipsometry, and reported for the first time, suggests that this sample is of polycrystalline nature. This peak was modeled using a Gaussian oscillator, though it could also have been used instead a Lorentz oscillator.
Dielectrics and semiconductors are generally transparent at near-IR (NIR) wavelengths. These materials absorb light in the UV and visible ranges due to valence-electron transitions. Above the bandgap, we find interband transitions from the valence to the condition bands, with the corresponding absorption of photons, at energies higher than that of such a bandgap. Many will also show the IR absorption due to the presence of intraband transitions within the valence band, molecular vibrations, phonons, or free charge carriers. In our Cu 3 N samples, the free-carrier Drude model clearly failed to accurately predict the IR response. Therefore, the associated free-charge-carrier density must be necessarily smaller than approximately 10 17 cm−3, the corresponding detection limit for the IR-VASE ellipsometric technique. Lastly, Figure 2c-f shows the very-broadband complex refractive index, n ˜ , for Cu 3 N from the UV to the MIR, reported for the first time, and dearly illustrates the aforementioned UV-Visible absorption due to the valence-electron transitions; moreover, copper-nitride is quasi-transparent across the remaining visible and NIR regions, until the presence of phonon does occur in the middle-infrared range of the spectra of the extinction coefficient, k, displayed in Figure 2c-f.
The crystal structure of Cu3N belongs to the space group, Pm 3 ¯ m, where in the unit cell contains one formula unit. According to the space group theory there are 12 phonon modes (lattice vibrations) at the center of the first Brillouin zone ( Γ critical point), among which nine are optic modes with irreducible representation: Γ = 2 T 1 u + 1 T 2 u . The T 1 u are infrared active, and the T 2 u modes are optically inactive (silent modes). Yu et al. [17] calculated the frequencies of Cu 3 N. Γ -point optical modes, and found that a peak at around 651 cm − 1 corresponds to the Cu-N high-frequency stretching mode, T 1 u , while another band at about 154 cm − 1 corresponds to the Cu-N-Cu bending mode, T 2 u .
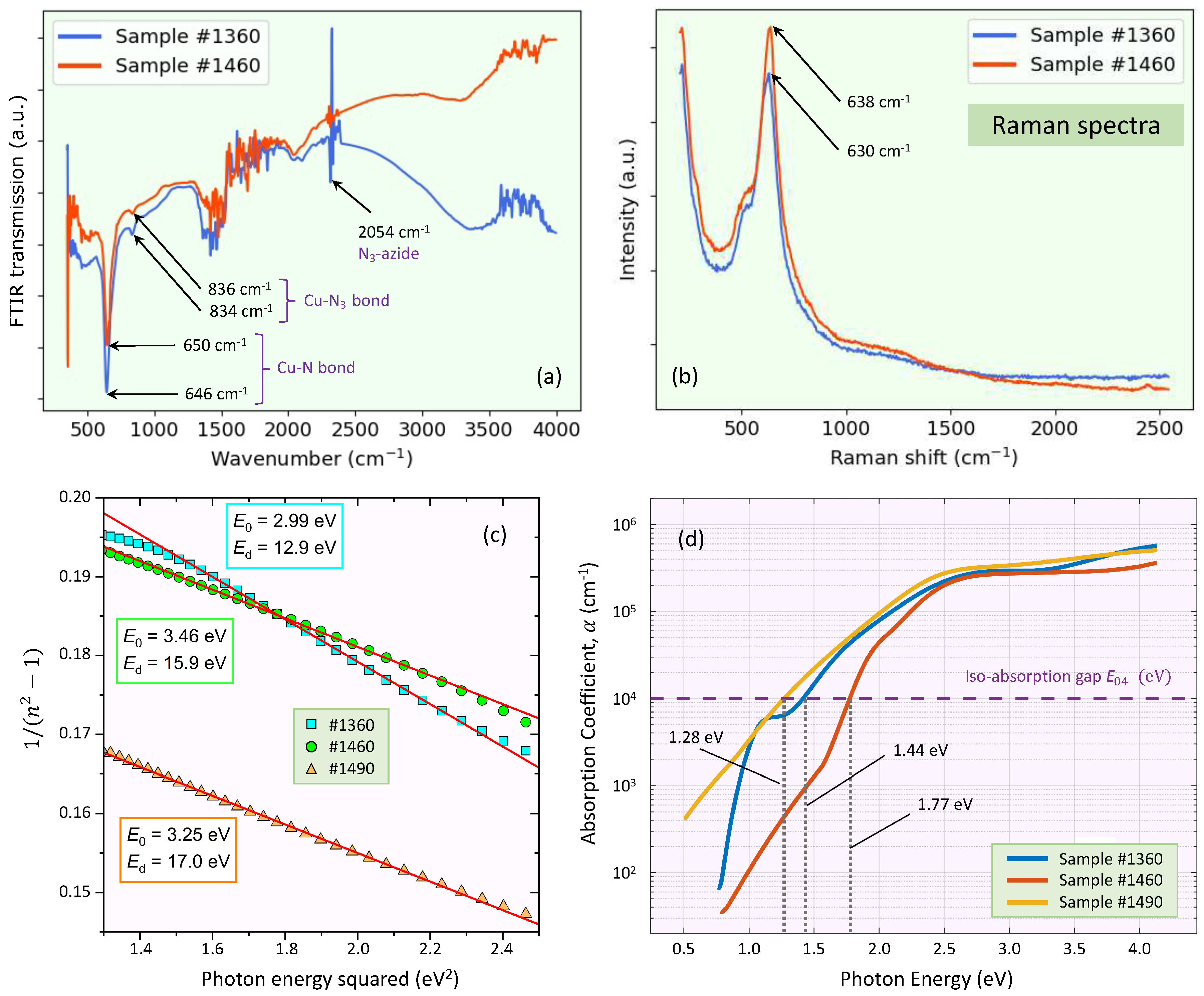
Concerning the previously mentioned UV-Visible absorption edge, Figure 3d displays the graph of the absorption coefficient spectrum, α ( E ) , versus photon energy, for the three Cu 3 N samples, calculated from both ellipsometric and intensity transmission measurements. These plots allow us to determine the iso-absorption gap E 04 , the energy value at which α = 10 4 cm − 1 . The obtained values of structural-defect-related Urbach energy parameter E u [18] are also listed in Table 1. According to the literature, Cu 3 N shows E u values ranging from 105 to 238 meV [6], therefore, our obtained values of E u are closely within this reported range. The iso-absorption gap, E 04 , for being empirical, is less sensitive to interpretational difficulties associated to the optical bandgap, and, therefore, is in use as a common alternative practical definition of the optical bandgap in poly-crystalline and non-crystalline semiconductors.
It should be emphasized that the values of the index of refraction reported in our present ellipsometric study are clearly much higher than those measured for Cu 3 N with the prism coupling technique [19]. We considered that the values of the refractive index found with the latter technique, surprisingly around 1.5 at four wavelengths in the NIR region, are notably underestimated, taking into account that the values determined in our study are very consistent with those previously reported in the literature [20], calculated making use of the popular Swanepoel transmission-envelope-method.

3.3. FTIR and Raman analysis

For an illustrative comparison, the Cu 3 N thin-film samples were also analyzed by FTIR transmission spectroscopy. The representative FTIR transmission spectra are shown in Figure 3a. The positions of the corresponding Cu 3 N-phonon mode are all of them at around 645 cm − 1 , in excellent agreement indeed with those independently calculated by infrared ellipsometry (i.e., this single band confirmed the creation of the Cu-N chemical bond). This would indicate that the amount of nitrogen contained within the sputtering gas atmosphere was adequate to form the Cu 3 N phase. A weak peak around 835 cm − 1 , assigned to the Cu- N 3 chemical bond, was also observed in the two cases. In addition, a peak at 2049 cm − 1 also appeared in the FTIR transmission spectra, corresponding to the stretching vibration of the N 3 -azide.
Figure 3b displays the representative Raman spectra of two of the Cu 3 N thin layers. Notably, we have observed Raman shifts at 638 cm − 1 and 630 cm − 1 , respectively, which are characteristic values of the Raman shift associated with Cu 3 N. It has to be pointed out that, although the first-order Raman signal for a perfect crystalline Cu 3 N is not allowed, Raman modes can be activated in the presence of structural disorder (e.g., a small crystalline size and/or the presence of structural defects). The increase in Urbach energy, E u , is primarily related to the increase of those structural defects (see Table 1).

3.4. Using the sub-gap Wemple-didomenico single-oscillator dispersion model

We focus next on fitting the obtained Cu 3 N refractive-index dispersion below the bandgap to the Wemple-DiDomenico single-effective-oscillator expression [21]:
n 2 ( E ) − 1 = E 0 E d E 0 2 − E 2 ,
where E 0 is the energy of the effective dispersion oscillator, and E d is the dispersion energy or oscillator strength. By plotting ( n 2 − 1 ) − 1 versus E 2 (Figure 3c), the two parameters E 0 and E d were determined. The obtained values of these Wemple-DiDomenico dispersion parameters, E 0 and E d , are all indicated in Figure 3c. The oscillator energy E 0 is considered an ‘average’ energy gap. For the dispersion energy, E d , on the other hand, a relationship was proposed [21]:
E d ( eV ) = β N c Z a N e ,
where β is a two-valued constant, 0.37 ± 0.04 eV for covalent materials, and 0.26 ± 0.03 eV for more ionic materials. N c is the coordination number of the cation nearest neighbor to the anion (copper in our case, with N c = 2 ), Z a is the formal valency of the anion (nitrogen in our binary compound, with Z a = 3 ), and N e is the effective number of valence electrons per nitrogen anion. In the Cu 3 N binary compound,
N e = ( 3 valence-electron / 1 Cu-cation ) + ( 5 valence-electrons / 1 N-anion ) ( 1 N-anion )
We are not including the Cu d-electrons in our ‘electron count’ [21]. For this Cu 3 N material, we do not expect the d 10 -core electron contribution, as observed in Cu halides: It would imply that we have to necessarily add 10 more electrons to the present ‘electron count’, N e . This would give rise to a clear disagreement between the experimental and calculated values of the dispersion-energy parameter, E d , as will be shown next.
The particular value of E d in copper nitride calculated by the use of Eq. 3, is found to be 17.8 eV. The small differences with the experimental values of E d presented in Figure 3c, and especially in the most-discrepant case of sample #1360, can reasonably be explained by the reported lack of stoichiometry of the studied sputtered Cu 3 N films (the Cu/N-ratio was found to be smaller than the expected ratio of 3) [4]. Moreover, the long-wavelength value of the refractive index, n ( E = 0 ) , displayed in Figure 2c-f, is given by the following expression:
n ( 0 ) = 1 + E d E 0 .
Significantly, the values of these static refractive indices are consistent with the data independently obtained by the IR-VASE ellipsometry (see the values of n ( E ) in Figure 2c-f). In addition, it also seems reasonable to propose that the determined values of n ( 0 ) increase with the mass density of the Cu 3 N samples. The less dense Cu 3 N film is the specimen #1360, according to its value of n ( 0 ) , 2.304, and the denser layer is the sample #1490, whose value of the static refractive index has been found to be 2.496. The ‘in-between’ case is the one of the film #1460, with n ( 0 ) = 2.377 .
Furthermore, the existing correspondence between the Wemple-DiDomenico oscillator-energy parameter, E 0 , and the so-called ‘Wemple-DiDomenico gap’, E g WD , is generally expressed as E 0 ≈ 2 × E g WD [22]. For the Cu 3 N compound, the value of E g WD obtained from the dispersion parameter E 0 goes from 1.50 eV, for sample #1360, to 1.73 eV for sample #1460, very close to the indicated values of the iso-absorption gap, E 04 .

4. Concluding remarks

This investigation has unambiguously demonstrated the usefulness of the very-wide-spectral coverage (0.2 – 40 μ m), of state-of-art spectroscopic ellipsometry, allowing the highly-accurate determination of the complex refractive index, n ˜ = n + i k , in the UV-MIR spectral range, for the first time, using only just one technique. The addition of the normal-incidence optical transmission has increased sensitivity to small UV-Visible absorption features in our reactive-RF-magnetron-sputtered Cu 3 N thin layers, deposited onto room-temperature glass and silicon substrates. The Cu 3 N samples investigated exhibit valence-electron transitions to energies above and below the bandgap that all of them can be successfully represented by Gaussian oscillators. Based on FIB-SEM microscopy, the Cu 3 N micro-structural features were described in detail, following the well-known Thornton structural zone model. Also, the alternate practical iso-absorption gap, E 04 (thus avoiding the use of the sometimes ill-defined optical-bandgap parameter), exhibited a strong dependence upon growth conditions. It must be pointed out that the obtained values of E 04 , interestingly, are found to be very close, indeed, to those of the reported indirect bandgap [5], thus indicating that they are mutually corroborated. Hence, we can conclude that a semiconductor material with values of E 04 between 1.3 and 1.8 eV could be considered suitable as a solar-light absorber. Last but not least, it is worth mentioning than an optical gap of approximately 1.5 eV is considered an ideal and optimum value for the solar spectrum in a PV cell.

Author Contributions

E. Márquez: conceptulization, methodology, writing (original draft). E. Blanco: methodology, formal analysis, software. J.M. Mánuel: methodology, formal analysis, software. M. Ballester: software, visualization, writing (review and editing). M. García-Gurrea: software, visualization, writing (review and editing). S.M. Fernández: investigation, data curation, resources, funding acquisition. M.I. Rodríguez-Tapiador: investigation, data curation, funding acquisition. F. Willomitzer: supervision, validation, writting (review and editing). A.K. Katsaggelos: supervision, validation, writing, (review and editing).

Funding

This study received financial support from MCIN/AEI/10.13039/501100011033, under grant PID2019-109215RB-C42. This funding is part of the economic recovery investment and reform measures under the Next Generation EU.

Data Availability Statement

The data employed in this study can be obtained from the corresponding author upon request.

Acknowledgments

The authors thank Dr. L. González-Souto for their invaluable assistance. J.M. Mánuel wishes to express gratitude to the “Central Service for Research in Science and Technology” (SC-ICYT) at the University of Cádiz.

Conflicts of Interest

The authors confirm that there are no conflicts of interest associated with this publication.

References

  1. Aihua, J.; Meng, Q.; Jianrong, X. Preparation, structure, properties, and application of copper nitride (Cu3N) thin films: A review. J. Mater. Sci. Technol. 2018, 34, 1467–1473. [Google Scholar]
  2. Zakutayev, A. Design of nitride semiconductors for solar energy conversion. J. Mater. Chem. A 2016, 4, 6742–6754. [Google Scholar] [CrossRef]
  3. Borsa, D.; Boerma, D. Growth, structural and optical properties of Cu3N films. Surf. Sci. 2004, 548, 95–105. [Google Scholar] [CrossRef]
  4. Rodríguez-Tapiador, M.I.; Merino, J.; Jawhari, T.; Muñoz-Rosas, A.L.; Bertomeu, J.; Fernández, S. Impact of the RF Power on the Copper Nitride Films Deposited in a Pure Nitrogen Environment for Applications as Eco-Friendly Solar Absorber. Materials 2023, 16, 1508. [Google Scholar] [CrossRef] [PubMed]
  5. Márquez, E.; Blanco, E.; García-Gurrea, M.; Cintado Puerta, M.; Domínguez de la Vega, M.; Ballester, M.; Mánuel, J.; Rodríguez-Tapiador, M.; Fernández, S. Optical Properties of Reactive RF Magnetron Sputtered Polycrystalline Cu3N Thin Films Determined by UV/Visible/NIR Spectroscopic Ellipsometry: An Eco-Friendly Solar Light Absorber. Coatings 2023, 13, 1148. [Google Scholar] [CrossRef]
  6. Rodríguez-Tapiador, M.; Asensi, J.; Roldán, M.; Merino, J.; Bertomeu, J.; Fernández, S. Copper Nitride: A Versatile Semiconductor with Great Potential for Next-Generation Photovoltaics. Coatings 2023, 13, 1094. [Google Scholar] [CrossRef]
  7. Wang, J.; Chen, J.; Yuan, X.; Wu, Z.; Miao, B.; Yan, P. Copper nitride (Cu3N) thin films deposited by RF magnetron sputtering. Journal of Crystal Growth 2006, 286, 407–412. [Google Scholar] [CrossRef]
  8. Yuan, X.; Yan, P.; Liu, J. Preparation and characterization of copper nitride films at various nitrogen contents by reactive radio-frequency magnetron sputtering. Materials letters 2006, 60, 1809–1812. [Google Scholar] [CrossRef]
  9. Hadian, F.; Rahmati, A.; Movla, H.; Khaksar, M. Reactive DC magnetron sputter deposited copper nitride nano-crystalline thin films: Growth and characterization. Vacuum 2012, 86, 1067–1072. [Google Scholar] [CrossRef]
  10. Tompkins, H.G.; Hilfiker, J.N. Spectroscopic ellipsometry: practical application to thin film characterization; Momentum Press, 2015.
  11. Blanco, E.; Domínguez, M.; González-Leal, J.; Márquez, E.; Outón, J.; Ramírez-del Solar, M. Insights into the annealing process of sol-gel TiO2 films leading to anatase development: The interrelationship between microstructure and optical properties. Appl. Surf. Sci. 2018, 439, 736–748. [Google Scholar] [CrossRef]
  12. Márquez, E.; Blanco, E.; García-Vázquez, C.; Díaz, J.; Saugar, E. Spectroscopic ellipsometry study of non-hydrogenated fully amorphous silicon films deposited by room-temperature radio-frequency magnetron sputtering on glass: Influence of the argon pressure. J. Non Cryst. Solids 2020, 547, 120305. [Google Scholar] [CrossRef]
  13. Thornton, J.A. High Rate Thick Film Growth. Annu. Rev. Mater. Res. 1977, 7, 239–260. [Google Scholar] [CrossRef]
  14. Jellison Jr, G.E.; Modine, F.A. Parameterization of the optical functions of amorphous materials in the interband region. Appl. Phys. Lett. 1996, 69, 371. [Google Scholar] [CrossRef]
  15. Ballester, M.; García, M.; Márquez, A.P.; Blanco, E.; Minkov, D.; Fernández-Ruano, S.; Willomitzer, F.; Cossairt, O.; Márquez, E. Application of the Holomorphic Tauc-Lorentz-Urbach Function to Extract the Optical Constants of Amorphous Semiconductor Thin Films. Coatings 2022, 12, 1549. [Google Scholar] [CrossRef]
  16. Marquez, E.; Ballester, M.; Garcia, M.; Cintado, M.; Marquez, A.; Ruiz, J.; Fernández, S.; Blanco, E.; Willomitzer, F.; Katsaggelos, A. Complex dielectric function of H-free a-Si films: Photovoltaic light absorber. Mater. Lett. 2023, 345, 134485. [Google Scholar] [CrossRef]
  17. Yu, W.; Zhao, J.; Jin, C. Simultaneous softening of Cu 3 N phonon modes along the T 2 line under pressure: A first-principles calculation. Physical Review B 2005, 72, 214116. [Google Scholar] [CrossRef]
  18. Urbach, F. The Long-Wavelength Edge of Photographic Sensitivity and of the Electronic Absorption of Solids. Phys. Rev. 1953, 92, 1324. [Google Scholar] [CrossRef]
  19. Figueira, C.; Del Rosario, G.; Pulgliese, D.; Rodriguez-Tapiador, M.; Fernández, S. Effect of Argon on the Properties of Copper Nirtide Fabricated by Magnetron Sputtering for the Next Generation of Solar Absorbers. Materials 2022, 15, 8973. [Google Scholar] [CrossRef] [PubMed]
  20. Reddy, K.V.S.; Uthanna, S. Effect of sputtering power on the physical properties of Cu3N films formed by DC magnetron sputtering. Synthesis and Reactivity in Inorganic, Metal-Organic, and Nano-Metal Chemistry 2007, 37, 393–395. [Google Scholar] [CrossRef]
  21. Wemple, S.; DiDomenico Jr, M. Behavior of the electronic dielectric constant in covalent and ionic materials. Phys. Rev. B 1971, 3, 1338. [Google Scholar] [CrossRef]
  22. Tanaka, K. Optical properties and photoinduced changes in amorphous AsS films. Thin Solid Films 1980, 66, 271–279. [Google Scholar] [CrossRef]
Preprints 89899 g001
Figure 1. SEM micrographs of (a) cross-section and (b) planar views, both of sample #1490. (c) SEM image revealing the internal porosity of sample #1360, and (d) a pore size map obtained using ImageJ software, with (e) its associated histogram for the pore equivalent radii. (f) The well-known Thornton structural zone model is presented for comparison [13].
Figure 1. SEM micrographs of (a) cross-section and (b) planar views, both of sample #1490. (c) SEM image revealing the internal porosity of sample #1360, and (d) a pore size map obtained using ImageJ software, with (e) its associated histogram for the pore equivalent radii. (f) The well-known Thornton structural zone model is presented for comparison [13].
Preprints 89899 g001
Preprints 89899 g002
Figure 2. (a) A representative sample photo, and (b) a schematic ellipsometry set-up. Optical functions n and k of samples (c) #1360, (d) #1460, (e) #1490. (f) The log-log scale of sample #1490.
Figure 2. (a) A representative sample photo, and (b) a schematic ellipsometry set-up. Optical functions n and k of samples (c) #1360, (d) #1460, (e) #1490. (f) The log-log scale of sample #1490.
Preprints 89899 g002
Preprints 89899 g003
Figure 3. (a) FTIR transmission spectra of Cu 3 N. (b) Raman spectra of Cu 3 N. (c) Wemple-DiDomenico plots. (d) Optical-absorption edges.
Figure 3. (a) FTIR transmission spectra of Cu 3 N. (b) Raman spectra of Cu 3 N. (c) Wemple-DiDomenico plots. (d) Optical-absorption edges.
Preprints 89899 g003
Table 1. Deposition conditions for Cu 3 N thin films and their very-broadband optical properties.
Table 1. Deposition conditions for Cu 3 N thin films and their very-broadband optical properties.
Preprints 89899 i001
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated