Modelling Method for Aeroelastic Low Engine Order Excitation Originating from Upstream Vanes’ Geometrical Variability

1. Introduction

The increasing depth of detail required in the modelling of turbomachinery performance has caused the introduction of probabilistic approaches in different fields. The geometrical variability in particular has been addressed as a source of uncertainty. Although geometrical deviation from the nominal design may have different causes, the manufacturing process on its own contributes to the geometrical variability of turbomachinery components.

The impact of manufacturing geometrical variability on turbomachinery aerodynamic performance in particular was already presented in literature. Garzon and Darmofal [1] considered the impact of aerofoils manufacturing geometrical variability on an axial compressor's aerothermal performance. Surface scans were used to characterize the geometry from a set of measurement data. Lange et al. [2] proposed a parametrization method to characterize aerofoils optical surface measurements to represent the variability. The method was used to characterize deviations from the nominal design and could be used to investigate the impact on the steady state aerodynamic performance [3,4]. Lange et al. [4] showed in particular the importance of a multi-passage representation of the investigated compressor stage. This is required to evaluate the impact on the performance accurately, representing the geometrical differences between neighbouring passages. On the other side, for each passage included in the computations, the computational cost for the CFD solutions and the variability domain are also expanded.

Historically the study of blade vibrations has been crucial in the development of turbomachinery, being described in the past as the dominant factor having an influence on the machines quality and reliability [5]. Deviations from the nominal cyclic symmetry are of particular interest in the context of aeroelasticity. Within this field, we refer to these deviations in general as mistuning. The mistuning of turbomachinery components was largely studied with respect to the structural dynamics, as it potentially leads to local amplification of the vibration amplitudes [6,7,8]. To take into consideration the impact of mistuning, Whitehead [9] first proposed a conservative design limit for bladed disks. A less conservative limit was defined by Martel and Corral [10], considering the number of active modes, thus taking into account the modal coupling within blade mode families. In recent years was shown the possibility to identify the structural mistuning, and therefore the passage-to-passage scatter of natural frequencies, from surface measurements of real components [11,12]. Through the identification of the mistuning it is possible to predict the structure behaviour in aeromechanic reduced order model. An example is the Subset of Nominal Modes (SNM) model proposed by Yang and Griffin [13,14], which represents the vibration of the mistuned system with a subset of the nominal geometry modes. Nonetheless, the geometrical mistuning of a stage affects also the flow traversing it, resulting in a mistuning of the flow interacting with the downstream stages.

From an aeroelastic point of view, a large effort was done in representing the unsteady flow in a reduced domain. Mata et al. [15] proposed a method to represent of rotor-stator interactions in a single passage setup. A method to represent a non-axisymmetric flow on a reduced number of passages was presented by Stapelfeldt et al. [16,17]. The methodology was shown to be capable of representing a flow with a known spatial/temporal periodicity in a sparse single passage assembly, significantly reducing the computational cost. The geometrical mistuning of a blade-row causes a mistuning of the flow field for the downstream row. This can be seen as the cause of non-axisymmetric flow downstream. For instance, the geometrical variability of the single aerofoils of a stage stator would cause a flow mistuning for the following stage rotor blades. The flow mistuning impacts the aeroelastic forced response, affecting the excitation harmonics amplitudes. The harmonics present in the flow field are though in general unknown. These are usually identified as multiples of the shaft speed, namely Engine Orders (EO). Of particular interest are the Low Engine Orders (LEO) of excitation introduced in the system.

In a previously published study [18] the authors investigated the impact of a stator geometrical variability on the excitation forces for the downstream rotor. A stochastic model for stator vanes geometrical variability was created, using a set of optical surface scans. The aeroelastic forces on the downstream rotor were investigated using a single passage unsteady CFD solver. A reconstruction algorithm was proposed to predict the resulting forces over a full revolution of the shaft. In particular, the reconstruction was found to overestimate the LEOs amplitudes, but correctly identify the LEOs pattern. The limitations are considered to be due to the oversimplification of the geometry representation in the single passage solutions. Considering the probabilistic analysis of aeroelastic forces, Figaschewsky et al. [19] investigated the impact of the upstream nozzle guide vane (NGV) pitch angle’s variability. For the computation of the forces a full annulus unsteady CFD setup was used, representing a unit response for a single disturbed NGV. The resulting forcing considering a fully mistuned NGV (in terms of pitch angle) could be predicted through a superposition of the individual unit responses.

When introducing a stochastic source of uncertainty as the manufacturing geometrical variability, the investigation of the mistuned unsteady aerodynamics is not easily solved. The difficulties are associated to the large domain of the variability as well as the computational cost required to represent the axial asymmetry. This paper wants to propose a method to evaluate the impact of a stochastic source of geometrical variability on the aeroelastic excitation forces. The manufacturing geometrical variability of an axial compressor Variable Stator Vane (VSV) is considered. The objective is to evaluate how different stator geometries arbitrarily ordered around the annulus may affect the traversing unsteady flow field. The impact on the aeroelastic excitation forces on the downstream rotor blade integrated disk (blisk) is finally investigated.

2. Materials and Methods

In the following, the method used for the representation of the mistuned aeroelastic forces is presented. A first section describes the representation of the manufacturing geometrical variability for VSVs measured as optical surface scans. Next, the geometry of the test rig used as study case will be described. Finally, the CFD setup will be presented, introducing the reduced domain for the computation aeroelastic forces.

2.1. Aerofoils Geometrical Variability

The description of the geometrical variability is based on the information relative to optical surface scans. A set of VSV optical scans was available to the authors to investigate the impact of the manufacturing process on the aerofoils geometry. The characterisation of the measurements was done using the parametrization method proposed by Lange et al. in [2]. The aerofoils are represented as a set of radial sections, each described in a two-dimensional space with as set of numerical parameters. Figure 1 shows the radial sections were distributed over a single blade geometry.

A total of 93 radial sections are used for the parametrization, ranging from 4% to 96% of the aerofoils height. Fillets and gaps’ sizes are omitted from the geometrical representation. The three dimensional surface is defined with an interpolation/extrapolation process over the modelled sections. This is described in more detail in the following section.

The parametrization technique is applied to the 36 optical surface scans as well as to the respective nominal CAD geometry. This allows to represent the available measures as geometrical offsets from the design intent. In particular, the geometrical deviations ${\mathsf{\Delta }}_b$ for the surface scan of every blade $b$ were calculated as the difference between the parametric characterisation ${\widehat{S}}_b$ of that blade and the nominal aerofoil geometric parameters ${\widehat{S}}_N$:

$${\mathsf{\Delta }}_b={\widehat{S}}_b-{\widehat{S}}_N.$$

(1)

The resulting 36 geometrical deviations ${\mathsf{\Delta }}_b$ are considered to be deterministic in this study. No further modelling was done to represent the geometrical variability of the VSV geometries. This could be representative of a dataset for a set of existing manufactured vanes which have to be assembled in a machine. The vanes are designed with the same geometry and manufactured individually, therefore the assembly order may be arbitrary. However, the method can be expanded to consider a stochastic geometry, defining an appropriate geometrical model as proposed in [20].

2.2. Study Case

The geometry of the test rig Rig250 from the German Aerospace Centre (DLR) is used as a study case. The rig is a 4.5 stage axial compressor. The geometrical deviations are applied to the first stage variable stator vane (VSV1). The resulting aeroelastic excitation forces are studied for the second stage rotor blisk (R2).

The quantity of interest for the study are the aeroelastic excitation forces, with particular focus on the LEO harmonics. Considering the equation of motion for a bladed disk in the rotating frame of reference, the structure displacement vector $\mathit{x}$ can be represented through the modes matrix $\mathsf{\Phi }$ and the modal displacement vector $\mathit{q}$:

$$\mathit{M}\ddot{\mathit{x}}+\left(\mathit{G}+\mathit{D}\right)\dot{\mathit{x}}+\mathit{K}\mathit{x}=\mathit{f},$$

(2)

$$\mathit{x}=\mathsf{\Phi }\mathit{q},$$

(3)

were $\mathit{M}$, $\mathit{G}$, $\mathit{D}$ and $\mathit{K}$ are respectively the mass, gyroscopic, structural damping and stiffness matrices. The forces $\mathit{f}$ acting on the system are in the right hand side of the equation of motion.

Following the formulation of Crawley [6], the modal forces ${\mathsf{\Phi }}^T\mathit{f}$ are divided in external aerodynamic excitation forces ${\mathit{F}}^e$ and motion induced forces ${\mathit{F}}^d$. Both terms are functions of time $t$, while only the latter depends on the displacement:

$${\mathsf{\Phi }}^T\mathit{f}={\mathit{F}}^e(t)+{\mathit{F}}^d(t,\mathit{q}).$$

(4)

The external aerodynamic excitation forces ${\mathit{F}}^e$ are investigated. These depend on the interaction with the unsteady flow field. As for the formulation in Equation (4), no blade motion is considered for their computation.

The compressor is represented at 90% of its nominal mechanical speed. This configuration is considered to be representative of resonance conditions for two R2 vibration modes. The mode shapes of interest are represented in Figure 2 as total displacement amplitudes. The modes are the first flap mode (Mode 1F) and a higher mode (Mode H). The vibration modes were computed using the commercial finite element software Abaqus, considering rotational speed and material temperature. The steady aerodynamic gas loading is neglected in this case. The mode shapes of interest were interpolated to the CFD mesh. The displacement shown in Figure 2 is representative of the resulting total displacement amplitudes on the CFD nodes.

For the fluid-dynamics computations, the Rolls-Royce CFD software AU3D, developed at Imperial College London, is used. The solver uses unsteady, compressible, Favre-averaged Navier-Stokes equations to represent the three-dimensional flow. A finite volume formulation on semi-structured grids and a second order time integration are implemented. Sayma et al. [21] describe in detail the flow model and provide two validation cases for turbomachinery.

The computations use the one equation Spalart-Allmaras turbulence model. The near walls flow field is computed utilizing wall functions, with $y^{+}~30$ values. Fillets and varying gap sizes are included in the CFD model. The VSV1 fillets were excluded from the CFD model when investigating the geometrical deviations, as these are not included in the geometries characterisation. The single passage mesh counts approximately $2\times {10}^6$ cells for each blade row, with approximately 120 radial levels.

A steady state CFD solution at the considered working point is solved considering a single passage of all the 4.5 stages. The boundary conditions are extracted from available measurement data. In Figure 3, a comparison is shown between measurement data and CFD results of the radial total pressure profiles at the inlet of the VSV1 and VSV2. The flow field in this condition results subsonic.

The steady state results are used as initial solution for the unsteady computations. Boundary conditions for the latter are extracted from the steady state mixing planes.

2.3. Reduced CFD Domain

A sector representation of the different rows is proposed as reduced model to represent the flow field. Single sectors including one or more aerofoils are represented in the CFD for each blade-row. The number of blades is limited to integer fractions of the total number of aerofoils for the blade-row. Cyclic symmetric boundary conditions are used to represent the full geometry. The full annulus flow field is reconstructed over the sliding planes connecting the different blade-rows for the unsteady computations as presented by Stapelfeldt et al. [16]. A Fourier decomposition in the frequency domain allows this, using the information relative to the individual blade-rows. A sector representation is chosen in this case over a sparse single passage assembly to capture the local deviations. The sector model will be named Multi-Passage Multi-blade Row (MPMR).

A sector model is presented in Figure 4a, where the VSV1, R2 and VSV2 are included. This Stator-Rotor-Stator (SRS) configuration is used only as validation of the method in this work. This configuration was chosen as the EO 12 would be present due to the interaction between the VSV1 wakes and the VSV2 potential field (respective blade-counts: 36 and 48). The number of blades per sector was therefore chosen to be at least $1/12$ of the circumference. In Figure 4b the modal forcing result for the tuned nominal geometry using the MPMR are validated with a FA CFD solution. The method could therefore be used to explore also large computational domains.

In general, for the mistuned case the excitation forces would depend on the geometry of the full annulus of the mistuned blade-row. This would imply that all the aerofoils in the blade-row would need to be represented in the CFD solution. Considering a probabilistic study of this phenomenon, knowing that any permutation of the same vane set would also affect the result, the representation of the full geometries would make the solution unfeasible. Considering moreover the vane geometries as uncertain, the FA CFD would be even more prohibitive. Therefore, it is of interest to define a method to represent the disturbances in a reduced CFD model. This ideally would contain the lowest possible number of passages for each blade-row to reduce the computational cost. Moreover, it is of interest to represent the fewest possible mistuned geometries in each CFD computation (a single one if possible). This would reduce the variability space to explore when considering a probabilistic study. Finally, it is necessary to define a reconstruction algorithm to predict the forcing disturbances for the downstream blade-row over a full rotation of the shaft, starting from the reduced CFD data.

2.4. Mistuned Stator Configuration

The application of the geometrical deviations is based on the parametrization method introduced in a previous section. The geometry parametric offsets ${\mathsf{\Delta }}_b$ obtained from the optical surface scans are applied to the hot nominal geometry parametrization $S_N$ of the Rig250 VSV1. The parametric description of the mistuned blades $S_b$ can be defined as follows:

$${\widehat{S}}_b={\widehat{S}}_N+{\mathsf{\Delta }}_b.$$

(5)

The representation of the manufactured geometries as an offset from the nominal design allowed to apply the measured deviations, described in a cold setup (static, ambient pressure and temperature), to the hot aerofoil geometries in the machine. Moreover, this allowed transferring the measured deviations on the Rig250 VSV1. The measurements were conducted on a different component due to a lack of data for the rig. The assumption is accepted for the similarity of the two geometries and preferred over a random representation of the variability.

As the parameters characterized the aerofoils on a set of radial sections, the three-dimensional geometry of these could be recreated from the $S_b$ values. Further points of the aerofoil were calculated through a quadratic interpolation over the three closest sections. For the extrapolation at the hub and shroud, an interpolation was done over the two closest mistuned sections and the nominal geometry hub/shroud section.

The geometrical deviation of a different optical surface scan were used for each of the 36 VSV1 stator vanes in the assembly. An arbitrary ordering of the vanes was assumed to represent a single mistuned configuration of the stators vane. A comparison between the tuned nominal geometry and the mistuned geometry is shown in Figure 5a for the Full Annulus (FA).

Two unsteady CFD simulations representing the FA of the VSV1 and R2 geometries were computed. For the time resolution of all the unsteady computations, 240 time steps were used to resolve the passage of a rotor aerofoil between two VSV1 vanes. This was found to be sufficient to capture the unsteadiness. At first, the tuned system is represented. The second simulation included the mistuned VSV1 geometry generated and the nominal R2 geometry. In both configurations, the modal excitation forces for the two mode shapes of interest result identical for all the rotor blades (with an appropriate phase shift).

In Figure 5b the computed forcing results are reported. The forcing is represented as normalized amplitudes of its harmonics (EO) for the tuned and mistuned FA geometries. The normalization is done with respect to the maximum amplitude observed in a stator-rotor-stator configuration (maximum ”FA Tuned SRS” in Figure 4b). In the tuned case, only the harmonics relative to the VSV1 vane count (EO 36 and multiples) are present. In the mistuned case the introduction of asymmetry causes the excitation to range over a larger spectrum of harmonics. Compared to the nominal forcing, in the mistuned case an amplification of the EO 30 and 72 amplitudes is observed. Moreover, a variety of LEO is introduced as the system.

3. Results

The study investigates if it is possible to represent the impact of the upstream row mistuning on the aeroelastic excitation forces in this reduced domain. Of primary interest are the following topics:

• the number of aerofoils per stage required to represent the physics;
• the number of mistuned aerofoil geometries required in each CFD computation to represent the deviations;
• methods to reconstruct the forcing spectra starting from multiple MPMR solutions.

In this section two different methods will be proposed. The first one is the extension of the work presented in [18], which used only single passages of the geometries in the CFD. The method is extended to use MPMR solutions as input, predicting the FA forcing as a mixture of these (”MPMR Forcing Mixture”). The results correctly predict the overall forcing function, but it was not possible to capture the LEO amplitudes. The second method presented is adapted to represent unit responses in the MPMR solution, predicting the FA forcing as a superposition of these (”MPMR Forcing Superposition”). The reconstruction captures the physics of the problem from a set of MPMR solutions, representing in each a single mistuned VSV.

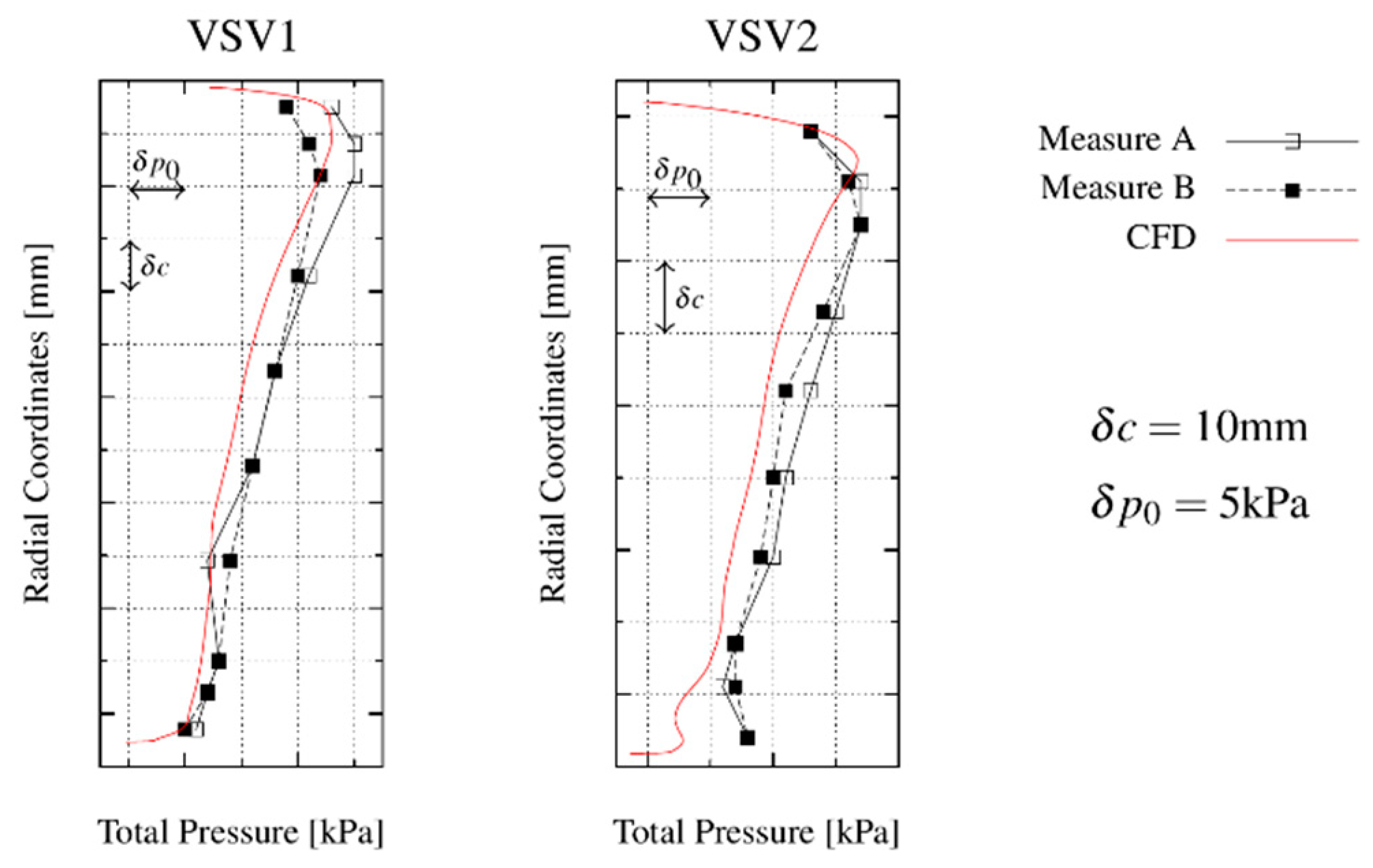
For simplicity, the domain is reduced to the VSV1 and R2 rows. The VSV1 geometries are limited to the 36 deviations obtained from the optical surface scans.

3.1. MPMR Forcing Mixture

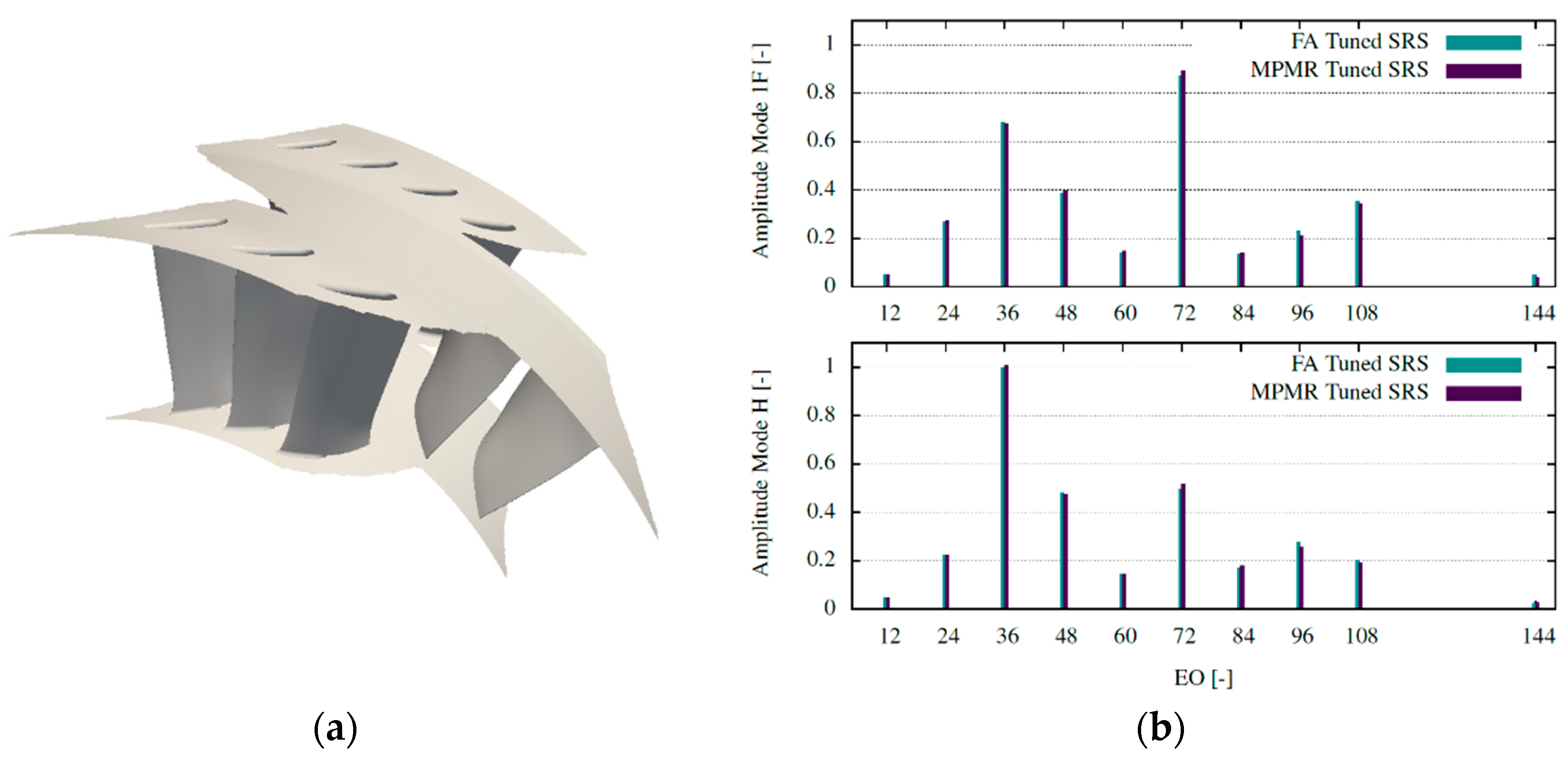
This method aims to verify if the local flow deviations downstream of the single mistuned VSV are sufficient to represent the overall mistuned flow. The reduced CFD setup includes three passages of the stator in a single sector. A single passage of the rotor is added, as for this row, the nominal geometry is used. In Figure 6a the represented CFD domain is shown.

All three VSV1 aerofoils in each computation include the geometrical deviations modelled. Moreover, the vanes order considered for the investigated FA setup is kept. One simulation is run for each of the 36 assembly vanes. For each run, the geometry of the vane of interest is placed in the centre of the computational domain. The directly adjacent geometries on the suction and pressure side are the respective ones in the FA assembly.

The presence of multiple mistuned vanes in each MPMR solution would be a limitation when looking at a stochastic representation of the geometries. This would imply that the geometrical variability space generated on the single blade deviations would be tripled. The inclusion of 3 mistuned blades per solution is chosen to assess the methods capabilities in an example, using a small sector of the annulus, but with a high fidelity in terms of geometry.

As a result of each simulation, a forcing function $f_{b,m}^{(M)}(t)$ on the R2 blade is calculated. The subscripts indicate the VSV1 blade $b\in [1; 36]$ at the centre of the sector and the R2 vibration mode $m$ considered. The superscript $(M)$ indicates that these solutions were computed using the CFD setup for the mixture method here presented. We indicate with N the number of total assembly vanes (N = 36 for VSV1).

The FA forcing prediction ${\widehat{f}}_m^{\left(M,FA\right)}(t)$ for the mode $m$ is computed as a mixture of MPMR solutions, using the definitions in Equations (6), (7) and (8). Indicating with $t_R$ the time required for a revolution, $t_{BP}=t_R/N$ represents a vane passing time interval. A phase shift is added to the MPMR solutions, such as $t=0$ coincides with the wake of the central assembly vane. This is identified with the position of a minimum for the EO 36 in the nominal forcing function.

To ensure the continuity of the predicted FA forcing, each $f_{b,m}^{\left(M\right)}(t)$ is mixed with the results centred on the neighbouring blades. This is done in the form of a weighted average over a selected time frame $t_{wa}={\mathrm{t}}_{\mathrm{B}\mathrm{P}}/20$.

The first blade $b=1$ and the last blade $b=N$ in the assembly are adjacent. To represent this in a short notation, we define: $f_{b=0,m}^{\left(M\right)}=f_{b=N,m}^{\left(M\right)}$ and $f_{b=N+1,m}^{\left(M\right)}=f_{b=1,m}^{\left(M\right)}$.

$${\widehat{f}}_{b,m}^{\left(M\right)}(t)=\left\{\begin{array}{c}{f}_{b,m}^{\left(M\right)}\left(t\right)+k_m\left(f_{b-1,m}^{\left(M\right)}\left(t+t_{BP}\right)-f_{b,m}^{\left(M\right)}\left(t\right)\right) \forall t\in [t_0, t_1[\\ f_{b,m}^{\left(M\right)}\left(t\right) \forall t\in [t_1, t_2[\\ f_{b,m}^{\left(M\right)}\left(t\right)+k_p\left(f_{b+1,m}^{\left(M\right)}\left(t-t_{BP}\right)-f_{b,m}^{\left(M\right)}\left(t\right)\right) \forall t\in [t_2, t_3[\end{array}\right.,$$

(6)

$$k_m=\frac{1}{2}\left(\frac{t-t_1}{t_0-t_1}\right), k_p=\frac{1}{2}\left(\frac{t-t_2}{t_3-t_2}\right),$$

(7)

$$t_0=-\frac{t_{BP}}{2}, t_1=t_{wa}-\frac{t_{BP}}{2}, t_2=\frac{t_{BP}}{2}-t_{wa}, t_3=\frac{t_{BP}}{2}.$$

(8)

The reconstruction of the modal forcing ${\widehat{f}}_m^{\left(M,FA\right)}(t)$ over one revolution is obtained as a concatenation of the weighted averages ${\widehat{f}}_{b,m}^{\left(M\right)}(t)$ for the single sectors. The periodic function over the full annulus is defined for a single period of length $t_R$, coinciding with the EO 1.

$${\widehat{f}}_m^{\left(M,FA\right)}\left(t\right)=\left\{\begin{array}{c}{\widehat{f}}_{b=1,m}^{\left(M\right)}\left(t\right) \forall t\in \left[-\frac{t_{BP}}{2},\frac{t_{BP}}{2}\right[ \\ {\widehat{f}}_{b=2,m}^{\left(M\right)}\left(t-t_{BP}\right) \forall t\in \left[\frac{t_{BP}}{2},\frac{3}{2}{t}_{BP}\right[ \\ ⋮\\ {\widehat{f}}_{b=N,m}^{\left(M\right)}\left(t-(N-1)t_{BP}\right) \forall t\in \left[t_R-\frac{3}{2}{t}_{BP}, t_R-\frac{t_{BP}}{2}\right[\end{array}\right.,$$

(9)

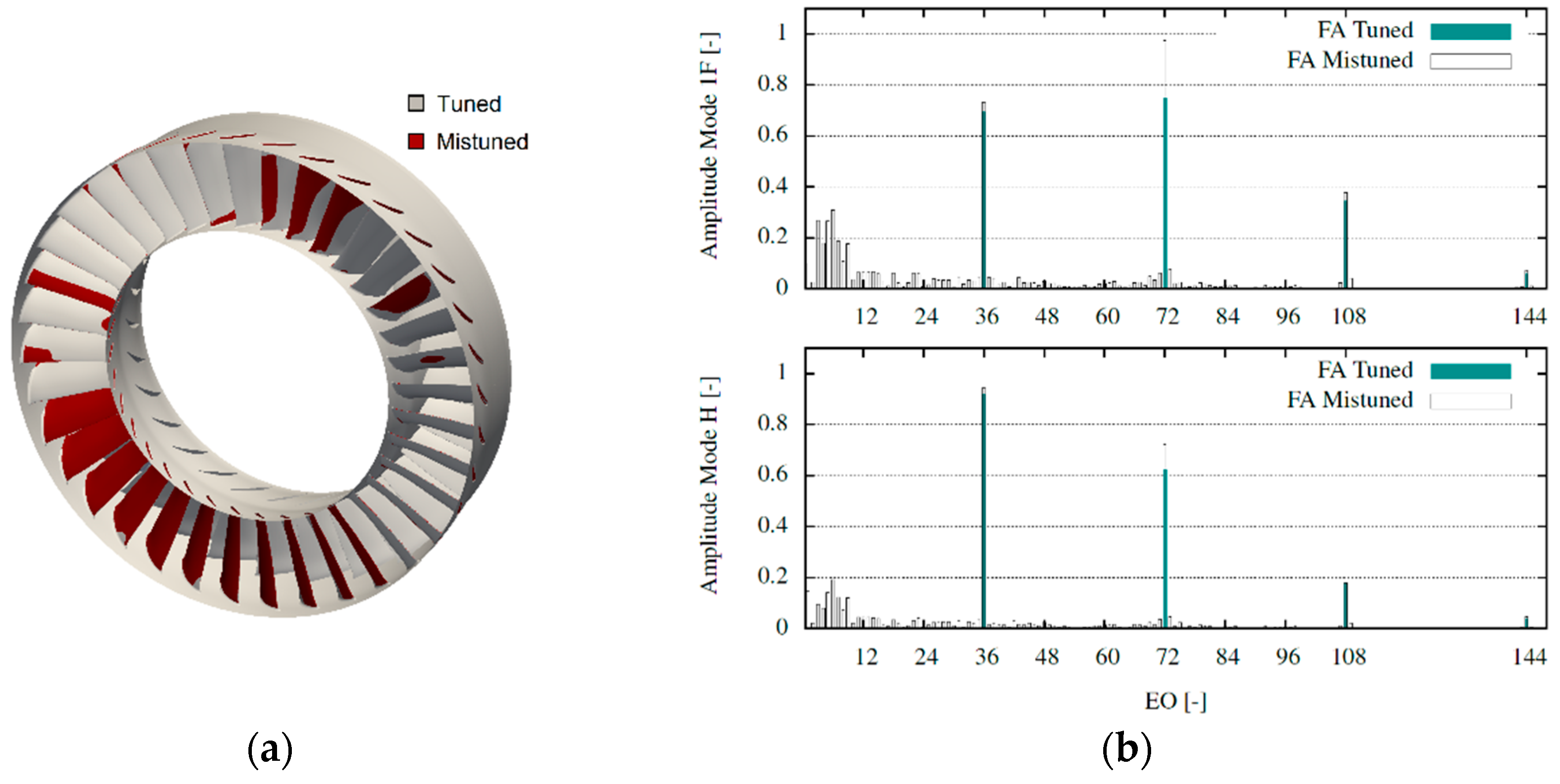
The FA modal forcing predicted from the mixture of MPMR solutions could therefore be analysed in terms of its spectrum. The resulting forcing prediction is computed for the mistuned configuration presented in Figure 5a. The computed FA CFD solution can therefore be compared with the prediction using the MPMR mixtures. The normalized spectra for the two solution methods are presented in Figure 6b for the two investigated vibration modes.

The results show an overall good prediction of the excitation harmonics, but the LEO are not captured. The harmonic relative to the vane count of the upstream stator (EO 36) and its upper harmonics are correctly predicted. These are also amplified by the mistuning (see Figure 5b) and the mixture can represent correctly the amplification. On the other side, the introduced lower harmonics are not represented by the method. It can therefore be concluded that the mixture correctly represents the local deviations, but these are insufficient to represent the lower excitation harmonics.

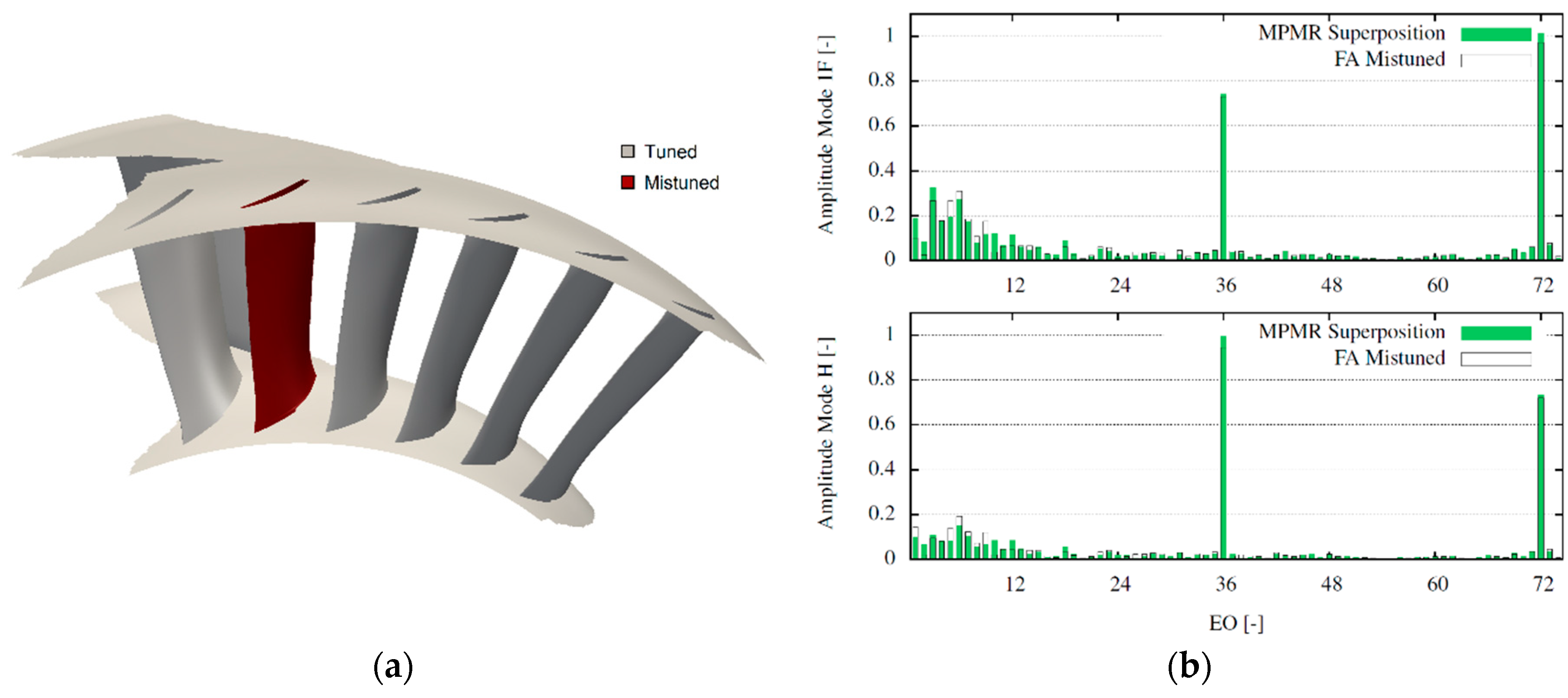
3.2. MPMR Forcing Superposition

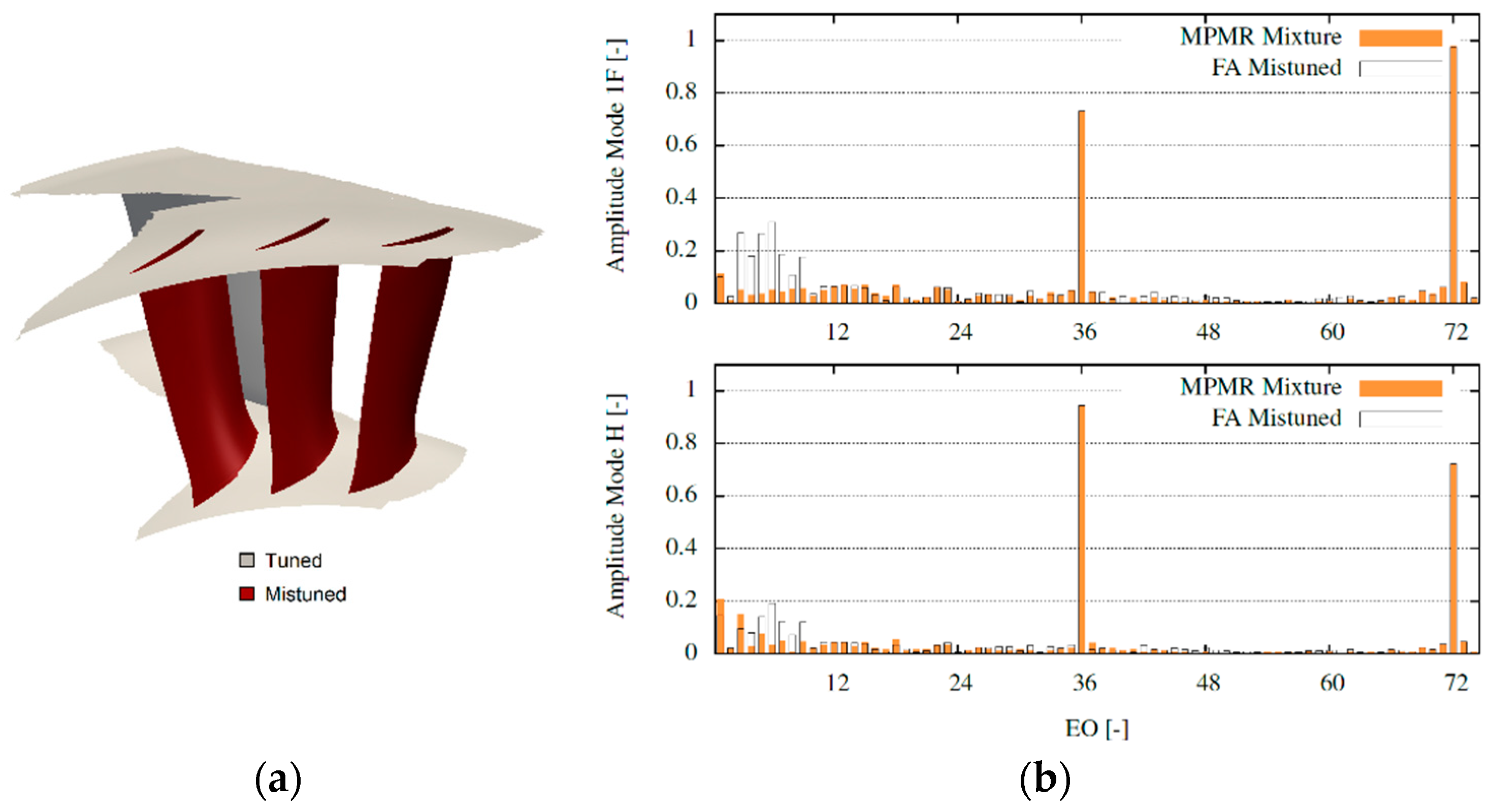
The proposed second and final method aims to represent a larger domain in the CFD to capture also the LEO introduced by the mistuning. The reduced CFD setup in this case included six passages of the stator in a single sector. A single passage of the rotor is still added, as for this row the nominal geometry is used. In Figure 7a the represented CFD domain is shown.

In this case, a single stator vane in the sector included the geometrical deviations. Further aerofoils are described with the nominal geometry of the vane. This allows to represent individually the disturbances due to the single mistuned geometry, namely the unit responses. Moreover, the geometrical deviations of a single aerofoil per simulation would need to be considered in a probabilistic study. As presented by Figaschewsky et al. [19] for differences in pitch angle, unit responses computed in a FA setup could be superimposed to represent the total mistuned system. It is of interest here to consider complex three-dimensional deviations of the geometry. Moreover, in order to reduce the computational time, the method is redefined to be adapted to the sector CFD setup.

As a result of each simulation, a forcing function $f_{b,m}^{\left(S\right)}(t)$ on the R2 blade is calculated. The subscripts indicate the VSV1 single blade $b\in \left[\mathrm{1,36}\right]$ with applied geometrical variability in the sector and the R2 vibration mode $m$ considered. The superscript $(S)$ indicates that these solutions are computed using the CFD setup for the superposition method here presented.

The FA forcing prediction ${\widehat{f}}_m^{\left(S,FA\right)}(t)$ is computed as a superposition of the MPMR unit responses, using the definitions in Equations (10) to (13). We indicate with N the number of total assembly vanes (N = 36 for VSV1). Being as previously $t_R$ the time required for a revolution, $t_{BP}=t_R/N$ represents a vane passing time interval. Also for the MPMR solutions, the wake of the assembly mistuned vane is identified with a minimum of the EO 36 in the nominal forcing function. This is used to define the time step $t=0$.

In the MPMR stator vanes sector $M$ airfoils are included (here $M=6$). This imposes an artificial periodicity to the sector geometry. In particular the solution is representative of $N/M$ blades over the full annulus with applied the same ${\mathsf{\Delta }}_p$ geometrical disturbances, evenly spaced over the circumference. Therefore a period $t_S=M t_R/N$ is imposed to the MPMR solutions.

A mean force ${\overline{f}}_m^{\left(S\right)}(t)$ is defined from the MPMR solutions. As the $f_{b,m}^{\left(S\right)}(t)$ are discrete and periodic, a discrete Fourier transform (DFT) can be applied. The mean force is computed averaging over all the $N$ MPMR solutions only the harmonics which are multiples of $M$, as these represent the vane passing frequency. The ${\overline{f}}_m^{\left(S\right)}(t)$ is computed with the inverse transform to the time domain. This allows to define a forcing disturbance function $n_{b,m}^{\left(S\right)}(t)$ for all the MPMR solutions. A filter $\mathcal{F}$ is applied to the disturbances, considering a fixed filter window $t_{fw}=t_{BP}$:

$$n_{b,m}^{\left(S\right)}\left(t\right)=\left(f_{b,m}^{\left(S\right)}\left(t\right)-{\overline{f}}_m^{\left(S\right)}(t)\right)\times \mathcal{F},$$

(10)

$$\mathcal{F}=\left\{\begin{array}{c}1 \forall t\in [0,\frac{t_S}{2}-t_{fw}[ \\ \frac{t_S-2t}{2t_{wf}} \forall t\in [\frac{t_S}{2}-t_{fw},\frac{t_S}{2}[ \\ \frac{2t-t_S}{2t_{wf}} \forall t\in [\frac{t_S}{2},\frac{t_S}{2}+t_{wf}[ \\ 1 \forall t\in [\frac{t_s}{2}+t_{fw},t_S[ \end{array}\right..$$

(11)

The mean force ${\overline{f}}_m^{\left(S\right)}(t)$ can be considered periodic. The disturbance $n_{b,m}^{\left(S\right)}\left(t\right)$ for the individual vanes has to be limited in the respective sector. The periodicity of the disturbances, having period length equal $t_S$, is artificially introduced by the cyclic symmetric boundary. Therefore, only one period per vane has to be used for the superposition. In doing this, the filter $\mathcal{F}$ ensures continuity to the individual noise terms. The local disturbances $n_{b,m}^{\left(S\right)}\left(t\right)$ have to be expanded to a respective FA disturbance, taking in consideration the respective blade $b$ position.

We define the FA disturbance ${\widehat{n}}_{b,m}^{\left(S\right)}(t)$ for each blade $b$ over one shaft revolution as follows. The $n_{b,m}^{\left(S\right)}(t)$ values are considered over one period $t_S$. The disturbance introduced by each vane is considered null outside the period $t_S$ for the rest of the revolution. An appropriate phase shift is added to account for the blade $b$ position in the assembly. The FA disturbances are periodic and described over one $t_R$ period:

$${\widehat{n}}_{b,m}^{\left(S\right)}\left(t\right)=\left\{\begin{array}{c}0 \forall t\in [\frac{t_S}{2}+\delta t_b,t_R-\frac{t_S}{2}+\delta t_b[\\ n_{b,m}^{\left(S\right)}\left(t-\delta t_b\right) \forall t\in [-\frac{t_S}{2}+\delta t_b,\frac{t_S}{2}+\delta t_b[ \end{array}\right.,$$

(12)

$$\delta t_b=\left(b-1\right)t_{BP}.$$

(13)

The FA forcing prediction ${\widehat{f}}_m^{\left(S,FA\right)}(t)$ is formulated as follows, superimposing the MPMR unit responses. It is defined as a superposition of the average extracted forcing ${\overline{f}}_m^{\left(S\right)}(t)$ and the individual ${\widehat{n}}_{b,m}^{\left(S\right)}(t)$ disturbances for all the vanes:

$${\widehat{f}}_m^{\left(S,FA\right)}\left(t\right)={\overline{f}}_m^{\left(S\right)}\left(t\right)+{\sum }_{b=1}^N{\widehat{n}}_{b,m}^{\left(S\right)}(t).$$

(14)

The FA modal forcing predicted from the MPMR superposition can be analysed in terms of its spectrum. The resulting forcing prediction is computed for the mistuned configuration presented in Figure 5a, using an according vanes order and phase shift. The computed FA CFD solution is compared with the prediction. The normalized spectra for the two solutions are presented in Figure 7b for the two investigated vibration modes.

The results show that the method can capture the full spectra of the excitation forces for the two vibration modes. The amplification of the vane passing frequency (EO 36) and its higher harmonics are captured as well as the introduced LEO. It is possible though to see a certain prediction inaccuracy with regard to some of these harmonics amplitude. 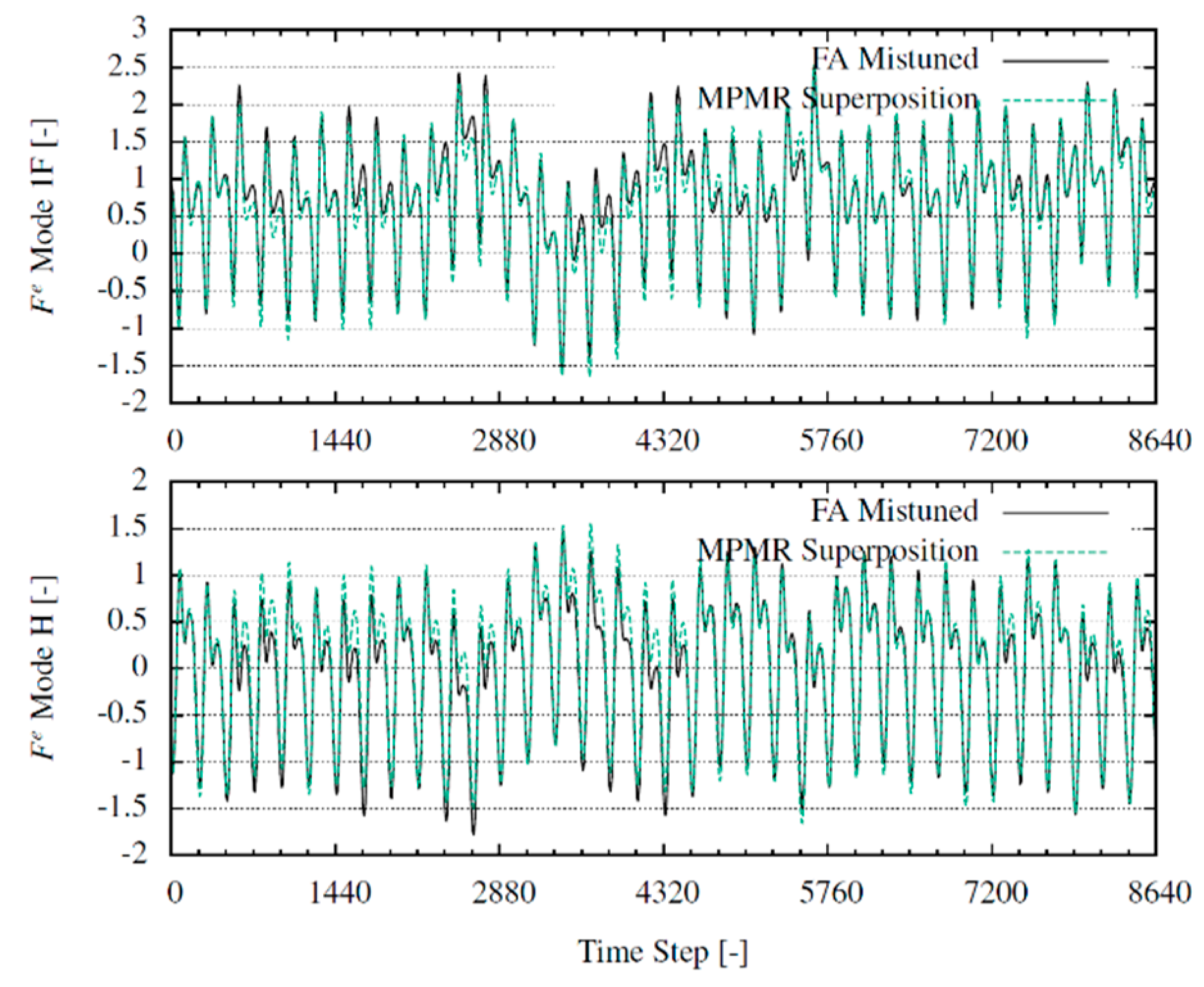To verify that the model is representative of the aerodynamic mistuning, in Figure 8 the excitation forces $F^e$ are plotted in the time domain. The forces are normalized such as the nominal excitation would oscillate between 1 and -1. It is possible here to compare the results computed with the FA CFD and the MPMR superposition. A period of length $t_R$ is represented, coinciding with one full shaft revolution. The prediction is shown here to be capable of capturing the physics of the problem correctly.

The loss in accuracy is judged to be caused by an insufficient number of vanes included in the VSV1 sector. The sector in the example represents $1/6$ of the full annulus. Hence, the cyclic symmetry imposed to reduced the CFD domain may be the cause of the inaccuracy. The only set parameter of the method is the filter window $t_{fw}$, which does not influence significantly the final result. In addition, small changes in the identification of the geometrically mistuned vane wake seem not to affect relevantly the result.

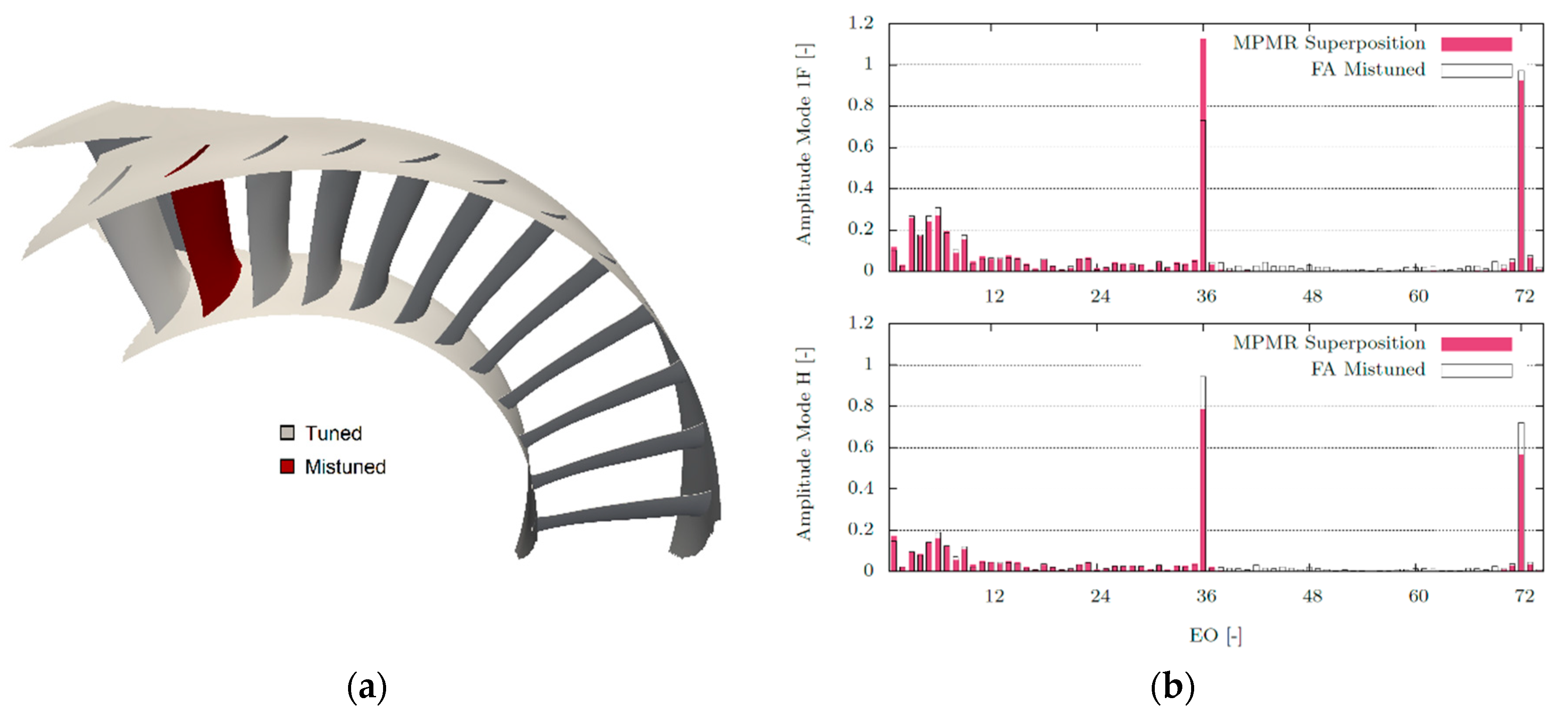
To investigate the influence of the stator sector size on the superposition result, the study was repeated with a larger number $M$ of stator blades. A total of $M=12$ blades are included in the new setup, equivalent to $1/3$ of the FA for this specific geometry. The resulting MPMR domain for the calculation of the unit responses is shown in Figure 9a. In Figure 9b the resulting rotor forcing superposition for the investigated mistuning pattern is compared with the FA CFD. The results show an increased accuracy in the prediction of the LEO, compared to the $M=6$ case in Figure 7b. However, a larger error is observed in the prediction of the EO 36 and 72. This is attributed to the inclusion in the MPMR of several stator blades with the nominal geometry. These EOs showed to be affected by the mistuning (see Figure 5b). To address this issue in future studies, a mean geometry of the measured aerofoils can be defined to replace the nominal aerofoils in the MPMR unit responses computation. This can give a better representation of the mean flow and therefore a higher accuracy of the reconstruction. This is supported by the high accuracy in the prediction of those harmonics in the “MPMR Forcing Mixture” method.

The results indicate that the problem can be considered linear, even when considering a set of real mistuned stator geometries assembled in an arbitrary order. The disturbances introduced by the individual real stator aerofoils on the flow with respect to the nominal tuned system can be linearly superimposed to represent the assembly. This reduces the problem of modelling this type of flow mistuning to the modelling of the disturbances caused by individual stators. The variability space can therefore be limited to the characterisation of the single aerofoil. Moreover, the CFD domain can be reduced to a sector representation of the stages.

To investigate a different ordering of the stator vanes with this method, it would be sufficient to change the different vanes relative phase. Therefore, having available a set of $N$ MPMR solutions, any permutation of those vanes in a FA setup can be solved algebraically.

4. Discussion

A method to calculate aeroelastic excitation forces on an axial compressor rotor in presence of an upstream geometrically mistuned stator is presented. The problem requires in general the description of the flow over the full annulus of the machine. The individual stator geometries and their relative position cause the non-axisymmetric flow affecting the rotor aeroelastics. This alters the amplitudes of the excitation harmonics, introducing in particular a set of low engine orders, which are not present for a tuned geometry.

This paper proposes two modelling methods to describe the phenomenon. The forces are computed in a reduced CFD model, limited to a sector domain. In both cases, the dataset of optical surface scans to represent the manufacturing geometrical variability of axial compressor stator vanes. Real engine geometries, acquired from measurement data, can therefore be included in the study.

A first proposed approach (”Forcing Mixture”) shows how local flow information is insufficient to represent the full spectrum of the forces, although the amplifications of the harmonics connected with the stator vane count (here EO 36 and multiples) are accurately captured.

The second proposed modelling method (”Forcing Superposition”) considers a single sector of the stator and a single passage of the downstream rotor. The stator sector includes a single aerofoil with applied geometrical deviations. The rotor forcing over a shaft revolution for a fully mistuned stator can be predicted superimposing the disturbances originating from the single real stator geometries, namely the unit responses. This indicates that the problem can be considered linear in the combination of disturbances from single passages. The method opens up the possibility for a probabilistic study:

• the geometrical variability space can be limited to the characterisation of the single aerofoil;
• the CFD domain can be limited to a sector of the geometry of interest, including a single mistuned aerofoil per solution;
• rotor modal excitation force disturbances can be linearly superimposed to represent the system;
• the full forcing spectrum is reconstructed from the single unit responses, for any arbitrary ordering of the mistuned vanes.

For the considered compressor stage, $1/3$ of the full annulus allowed to compute the unit responses and accurately predict the introduced LEO. For future investigations, it is recommended the definition of a mean mistuned geometry from the measured data. This can be used to represent the sectors with fixed geometry in the calculation of the unit responses, helping in the description of the mean flow.

The disturbances computed for this study show patterns unique to each vane. No common trend could be observed. Nevertheless, we cannot exclude on a larger dataset the possibility of interpolation between different geometries. Moreover, the creation of a stochastic model for the geometrical variability [20] would allow describing probabilistically the problem.