1. Introduction
Numerous applications of the classical generalized Langevin equation (CGLE) have been used to describe simple and complex systems. Most of the descriptions are based on Zwanzig’s model where the interaction of the external field affects only the particle dynamics. Thus, the fluctuation-dissipation theorem (FDT) is linear with the static friction coefficient of the bath fluid [
1]. Nieuwenhuizen and Allahverdyan [
2] worked out the CGLE in the configuration space including an extra term due to the interactions among the bath particles, and Jiménez and Velazco [
3] replacing the colored noise by an Ornstein-Uhlenbeck process; the external force is time dependent. Paredes, Medina, and Colmenares [
4] applied the CGLE in the whole phase space. However, afterward, Daldrop, Kowalik, and Netz [
5] applied molecular dynamic simulations to a particle in a thermal bath interacting with a parabolic potential, finding the memory kernel and friction depending on the field frequency. In a previous author’s work [
6] the description was modeled by deriving a new generalized version (NGLE) to include a specific field interaction with the bath. The FDT is Kubo’s type with the above frequency dependency. Acceptable results were obtained for the kernel and the friction function.
The present work aims to extend the description of the NGLE to the realm of thermodynamics. In this respect, the objective is to determine the entropy and its rate and compare them with the results obtained from the CGLE.
We begin with a resumé of the general equations already derived followed by an analysis of the results. The article ends with a general conclusion.
2. Basic equations
The system is a particle of mass
M immersed in a bath of
N harmonic oscillators held at temperature
T where both subsystems interact with a parabolic potential
. The NGLE was derived in [
6] and given by:
where the dot over a variable denotes its time derivative. Its solution reads,
where
is the susceptibility of the system, parameter
is the Drude’s spectral density cutoff frequency of the bath harmonic oscillators,
is the mass ratio of the tag particle to a single bath particle,
is the static friction coefficient, and
are the initial position and the effective frequency felt by the particle, respectively. Function
where the memory kernel
is a composite function involving cosine and sine integral functions of the complex field frequency
H. It reads,
The noise
is Gaussian and colored with zero mean and a correlation obeying an FDT of Kubo’s type
. The friction function
is the integral of
over the frequency
. It is a function too large to display containing Si, Ci, Ei, and the natural log functions of different complex terms of the field frequency. From now on, the Boltzmann constant and
M are set to 1.
We use the associated reduced position Fokker-Planck equation (FPE) for the probability density function associated with Eq. (
2) instead of the bi-variate general one involving velocity and position. It was already obtained in [
7] in a different context, reading,
with a solution given by the Gaussian
The steady-state
is obtained from Eq. (8). It renders the Gaussian
where
.
According to [
8,
9,
10], the mean heat
evolves with time as
where
. After making the substitutions, we find
The irreversible Gibbs entropy of the Brownian particle, equivalent to Shannon’s, and the entropy rate
are
In a system at equilibrium, the response function is the correlation of the fluctuations subjected to disturbances of the external field. The detailed balance relation is broken if it is out of equilibrium for stationary systems. Therefore, there is a continuous degradation of energy to the thermal reservoir. This behavior occurs along the trajectory, where the correlation of the fluctuations reduces to the conventional FDT if the velocity fluctuations are written in terms of the local mean velocity [
11].
In the detailed balance restoration, Van den Broeck and Esposito [
12] integrate by part
giving two contributions compiling a non-adiabatic part
due to the presence of driving, the external field, and an adiabatic one because of a non-equilibrium constrain, the temperature in our case. They, however, introduce the so-called excess
representing the dissipation due to the presence of the reservoir. The latter is the systematic entropy generated by the bath degrees of freedom [
13]. They propose then an equivalent entropy balance equation for the total entropy production as,
Similar equations hold for the Zwanzig’s CGLE [
14,
15,
16] replacing
by
and the memory kernel substituted by the well-known exponential decay
obeying the original Kubo’s FDT
[
1].
We will compare the results obtained by the two versions of the generalized Langevin equations NGLE and CGLE.
3. Discussion of numerical results
Because the external potential is time-independent, no work is produced. The interchange of heat between the particles and the bath is needed for the whole system to be kept isothermal and steady.
All calculations [
17] were made for the parameter set of Ref. [
6], namely,
. We choose
representing the approximated midpoint between the branches of
displayed in Fig. 3 of [
6]. Black curves identify the set
while the red ones are for
and an arbitrary
. Blue curves designate the NGLE at a frequency as low as
and
. The procedure to compare NGLE with the CGLE must suit the memory kernel, Eq. (
6), to the new initial conditions of the system. Noticing from Fig 3 of [
6] that at very low
the frequency-dependent friction is equal to its static value
, we evaluate
at such a frequency which can be fitted as
. It gives
which together with the substitution
and
defines fully the CGLE. They are displayed as dashed blue plots.
The numerical calculations then require first the determination of the memory kernel given by Eq. (
6). Before the calculation, it is smoothed to suppress the spurious data at log times [
6] to find next the susceptibility
through the inversion of Eq. (3). Using a method designed by Fox for the CGLE [
18], the noise correlation
becomes analytical which for our problem renders
Once these quantities are calculated then the standard deviation
and
follow and all functions are fully specified.
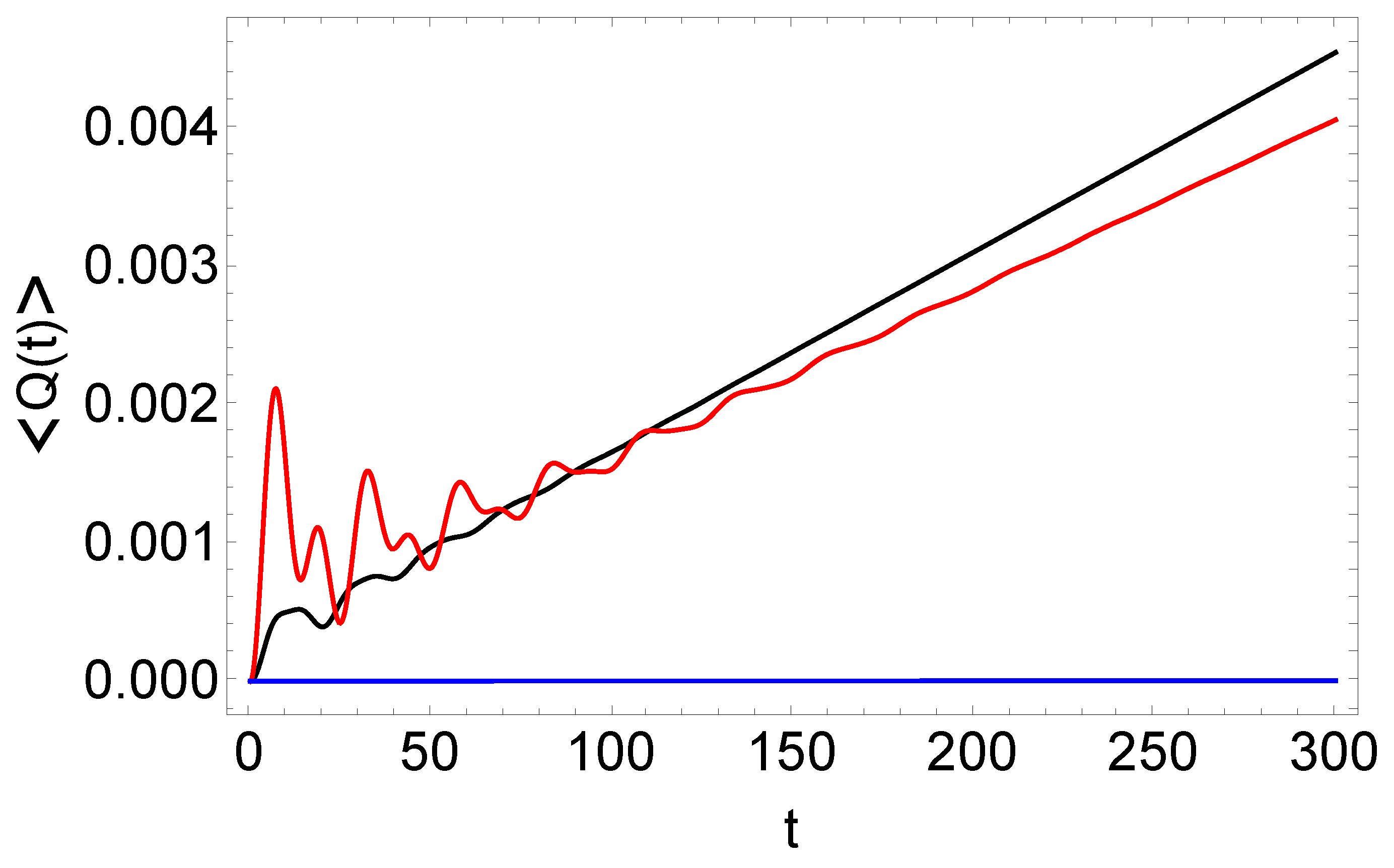
The effect of the external field is to heat the tagged and reservoir particles in different proportions, so on average, some heat is absorbed by the tagged particles to keep a steady temperature.
Figure 1 displays this effect as the mean heat. The dissipation of the average heat in the system increases to keep it isothermal; it is smaller for
(black curve). Curves for NGLE at low
(
, blue) and the CGLE (dashed blue) have significantly low magnitude and are almost identical, which is not a surprise because both descriptions are for the same static friction coefficient. Oscillations increase with the temperature.
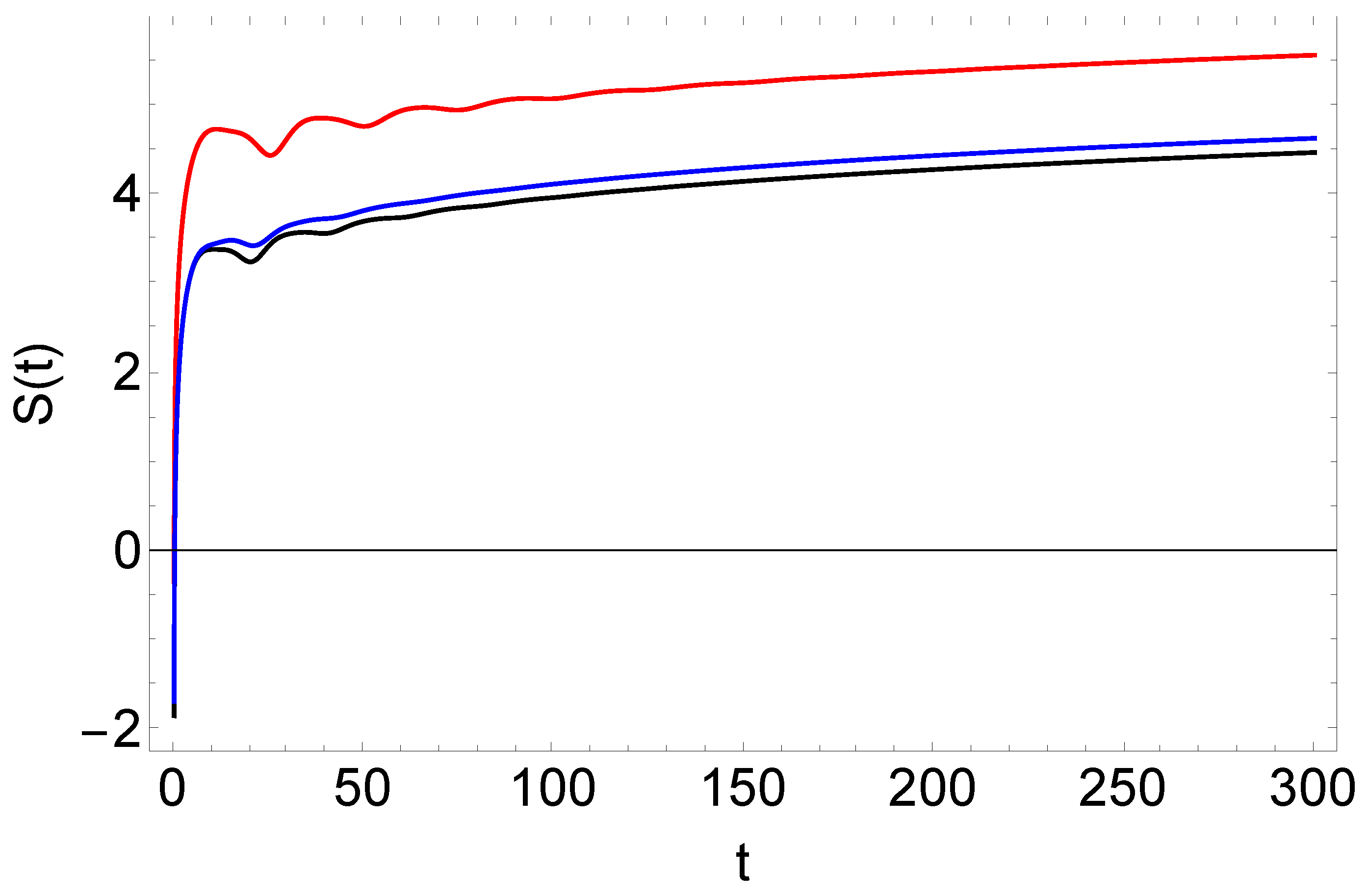
Figure 2 shows the entropy of the whole system, where a smoothed behavior for
appears, which is also an indication of reaching a steady state. It is positive because the system is isolated. The omission of the physical field-bath interaction (blue) overestimates the total entropy by a little compared to NGLE (black). The difference is irrelevant but will become significant in discussing the entropy production. All curves display a small oscillation at the beginning. Previous works have found that when the interaction field-bath is off, and a classical underdamped Markovian Langevin describes the dynamics,
monotonically increases and saturates to a constant value instead [
19]. The same behavior occurs with a single oscillation at the beginning when the bath particle interactions are included [
2]
The processes responsible for the appearance of the initial oscillations might be due to the heat bath. One approximate way to explain it is by calculating the entropy production as we will show next.
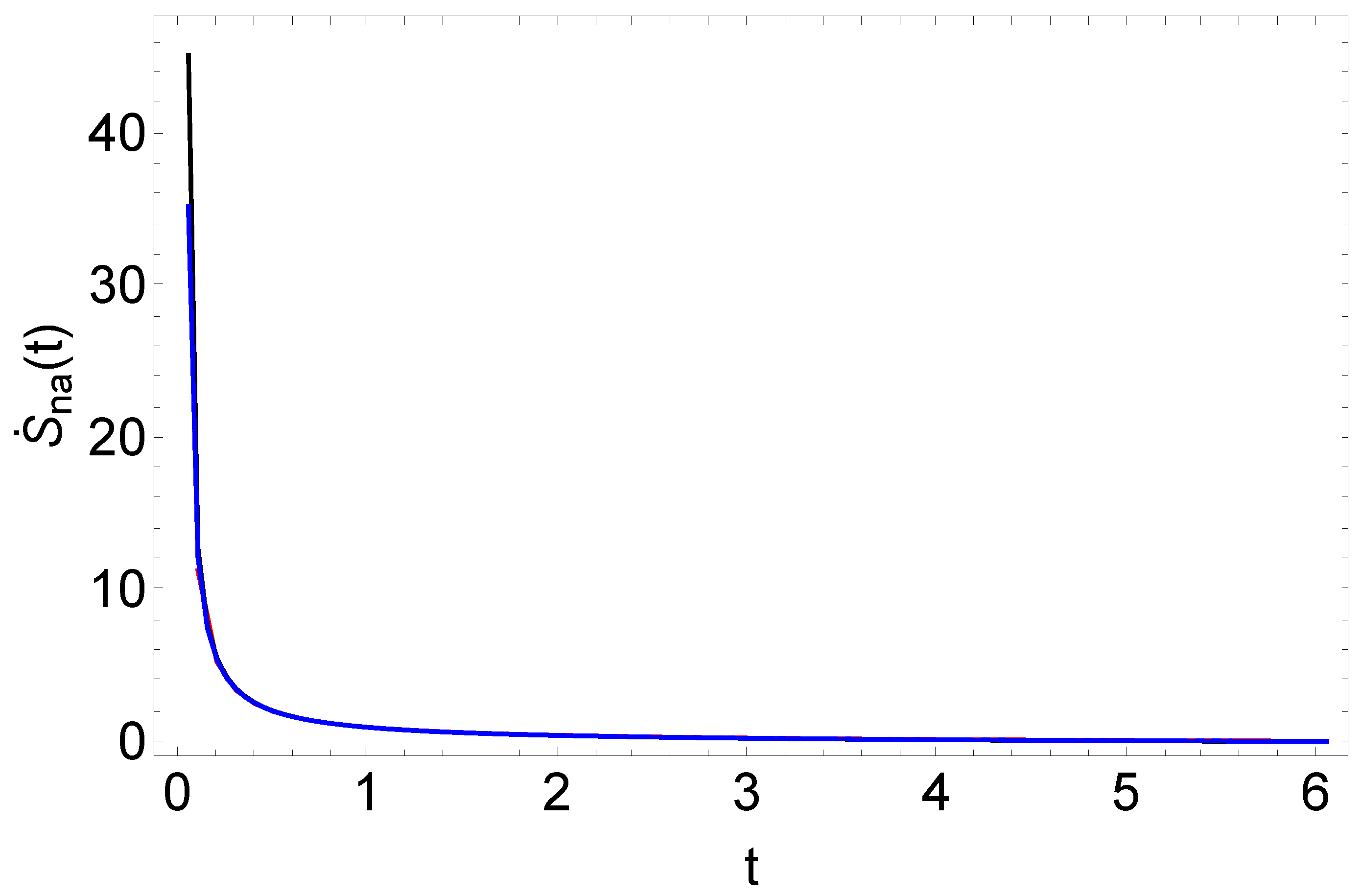
The entropy production rate
due to the field is depicted in
Figure 3. It is positive as should be [
12]. All curves collapse to a single plot to indicate that no matter the parameters defining the system, the field effects seem to generate almost the same rate of entropy production. Any minor difference disappears because of the scale. It goes to zero as the PDF relaxes to the uniform equilibrium distribution. This production rate doesn’t provide information about the oscillations appearing in
.
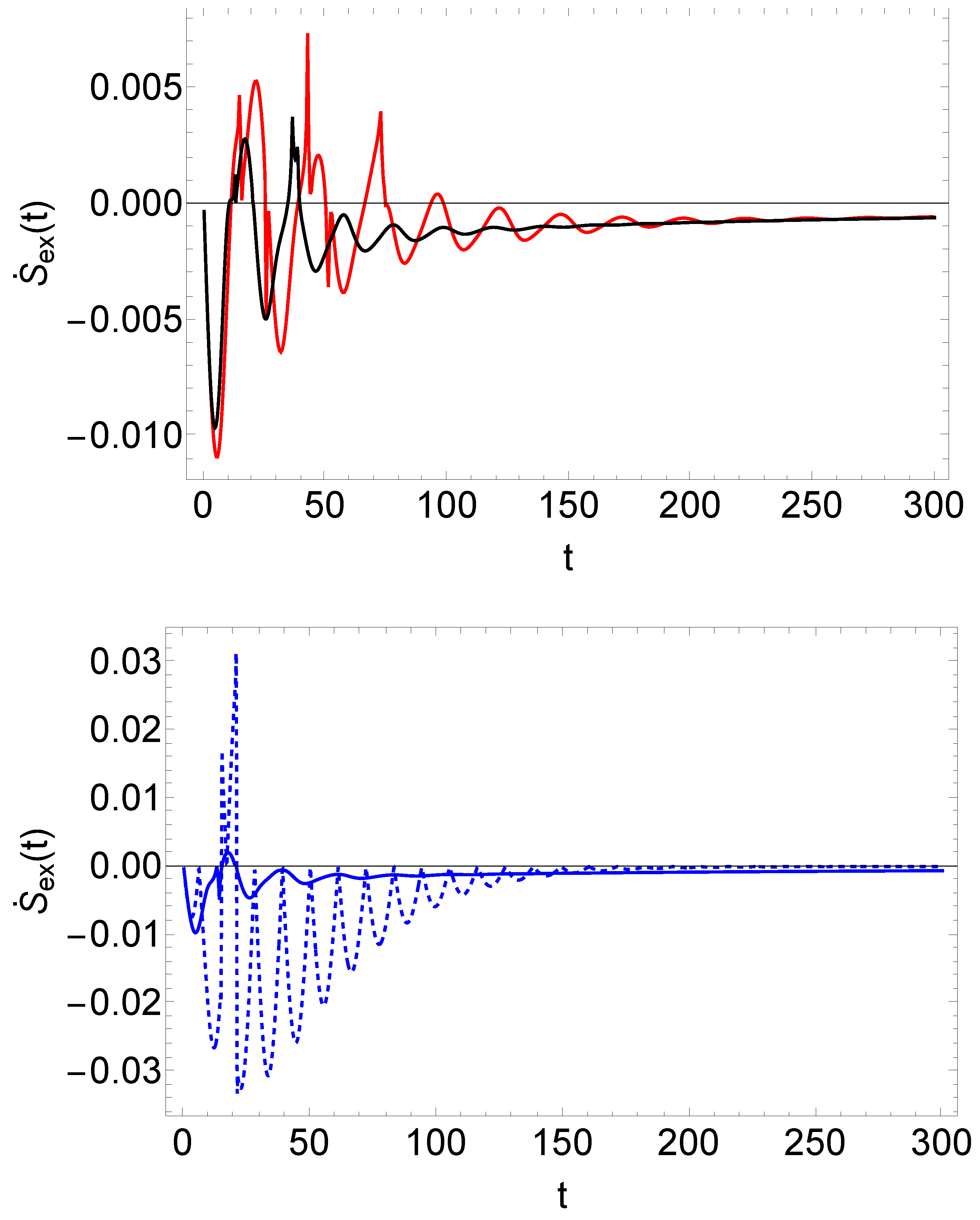
However, the monotonic behavior of
changes dramatically by examining
, that is, the net effect of the heat transfer by/from the bath.
Figure 4 displays this property where the oscillations appear. They are due to the irreversible heat transfer process, which tends to vanish as time evolves. An increasing steady heat flux from the reservoir, different from zero, is kept in the system to ensure the system’s steady state.
Because of the low magnitude of , the major contribution to comes from . The entropy production obtained from Eq. (18) (not shown) is just complying with the second law.
Unlike the simple system of a Brownian motion on a circle worked in [
12] where the adiabatic and non-adiabatic contributions are positively satisfying Jensen inequality [
20],
is not a convex function as required by Jensen [
21] but an oscillating one. There is no contradiction with the second law because the definition (
21) involves two separate interacting subsystems where the bath is not isolated, delivering heat to the particles to be returned afterward [
22]. What is important is that
agrees with the second law and mathematically is a convex function obeying Jensen’s inequality.
4. Conclusion
Since the results obtained from the NGLE, Eq. (
1), acceptably describe the MD calculations of Daldrop, Kowalitz, and Netz [
5] for the same system, should be taken into consideration to observe the effect of the field-bath interaction in the already calculation of other properties as free energies and work with time-dependent external protocols. These should include, to cite a few, the previous works on the classical Langevin equation in the versions with an exponential memory kernel [
3,
4] and both Markovians, overdamped [
23,
24] and inertial [
25].
The effect of the field-bath interaction when the kernel is an exponential decay is just NGLE determined at minimal frequencies. It allows a direct comparison with the CGLE [
3,
4].
The published works in the Markovian regime use a time-dependent parabolic field of the kind
where
is an external protocol of free choice. However, the objective is the determination of the optimal driving, which optimizes the mechanical work done by/on the particle for the initial conditions set. To derive it, the Euler-Lagrange formalism [
26] is applied to the function defining the mechanical work. The corresponding equation when the interaction field-bath is on requires making the substitution
in Eq. (
1) to get a similar equation, which after rearrangement is,
Therefore, the corresponding Markovian system described by Eq. (24) can be compared with the cited works [
23,
24,
25].
Unlike the previous versions where the interaction field bath is off, the protocol, work, entropy, and the FPE now depend on the characteristics of the bath through the effective frequency , which in turn is itself a function of the field frequency .