A New Mixed Fractional Derivative with Application to Computational Biology

1. Introduction

In recent years, fractional mathematical modeling involving nonlocal fractional derivatives plays a robust tool and constitutes a new resource to capture the dynamics of complex systems having memory effects or hereditary characteristics. Such systems arising from various fields including physics, fluid mechanics, material science, signal processing, engineering, chemistry, biology, medicine, finance, social sciences, economics and ecology.

In the literature, there are two main types of nonlocal fractional derivatives. The first named the fractional derivatives with singular kernels like Riemann-Liouville fractional derivative [1,2] and Caputo fractional derivative which was introduced by Caputo in 1967 [3] to find the analytic expression for a linear dissipative mechanism whose quality factor (Q) is almost frequency independent over large frequency ranges. The second ones have non-singular kernels such as the Caputo-Fabrizio (CF) derivative [4] introduced by Caputo and Fabrizio in 2015 to avoid the singularity existing in [3]. In 2016, Atangana and Baleanu [5] proposed a fractional derivative to model the flow of heat transfer through a material with different scale or heterogeneous. In 2020, Al-Refai [6] presented a weighted fractional derivative based on Atangana-Baleanu (AB) fractional derivative [5]. By means of the Laplace transform, he solved an associated linear fractional differential equation.

Recently, a new generalized Hattaf fractional (GHF) derivative with non-singular kernel has been introduced in [7] to cover the CF [4], the AB [5] and the weighted AB [6] fractional derivatives. A new class of fractal-fractional derivatives was derived from the GHF derivative and the new generalized fractal derivative [8] that covers the Hausdorff fractal derivative [9] used to model the anomalous diffusion process. Furthermore, the new GHF derivative was used by many researchers to describe the dynamics of various phenomena arising from several areas of science and engineering [10,11,12,13,14].

The first aim of the present paper is to introduce a new definition of nonlocal fractional derivative that includes and generalizes numerous fractional derivatives with singular and non-singular kernels such as Riemann-Liouville [1,2], Caputo [3], CF [4], AB [5] and the weighted AB [6] fractional derivatives. The new introduced definition also includes the GHF derivative [7], the power fractional derivative [15], as well as the new fractional derivative with Mittag-Leffler kernel of two parameters intoduced in [16] and applied to thermal science.

On the other hand, most fractional differential equations (FDEs) involving nonlocal fractional derivatives are complex and cannot solved analytically. For this reason, various numerical methods have been proposed to approximate the solutions of such FDEs. For instance, a numerical method that recovers the classical Euler’s scheme for ordinary differential equations (ODEs) was introduced in [17] to approximate the solutions of FDEs with GHF derivative. Another numerical method for GHF derivative was developed in [18] to solve numerically nonlinear biological systems of FDEs arising from virology.

The second aim of this paper is to develop a numerical method to approximate the solutions of FDEs with the new mixed fractional derivative mentioned in the first objective. The developed numerical method includes the three recent numerical schemes presented in [18,19,20] and it is based on Lagrange polynomial interpolation.

The remainder of the present paper is organized as follows. Section 2 defines the new mixed fractional derivative in both Caputo and Riemann-Liouville senses and presents the particular cases of such mixed fractional derivative available in the previous studies. Section 3 deals with Laplace transform of the new mixed fractional derivative. Section 4 gives the fractional integral associated to the new mixed fractional derivative and its special cases. Section 5 establishes new important formulas and properties for the new differential and integral operators. Furthermore, Section 6 is devoted to the new developed numerical method. Finally, Section 8 ends the paper with an application to computational biology.

2. The new mixed fractional derivative

This section defines the new mixed fractional derivative in the sense of Caputo and Riemann-Liouville.

Definition 2.1.

Let $(p,q)\in {[0,1]}^2$, $r,m>0$ and $u\in H^1(a,b)$. The mixed fractional derivative of the function $u\left(t\right)$ of order p in Caputo sense with respect to the weight function $w\left(t\right)$ is given as follows:

$${}^C{D}_{a,t,w,\delta }^{p,q,r,m}u\left(t\right)=\frac{H(p+q-1)}{2-p-q}\frac{1}{w\left(t\right)}{\int }_a^t{(t-\tau )}^{q-1}{E}_{r,q}[-\delta {\mu }_{p,q}{(t-\tau )}^m]\frac{d}{d\tau }\left(wu\right)\left(\tau \right)d\tau ,$$

(1)

where $\delta \in {\mathbb{R}}^{\ast }$, $w\in C^1(a,b)$, $w,w^{\prime }>0$ on [a,b], $H(.)$ is a normalization function such that $H\left(0\right)=H\left(1\right)=1$, ${\mu }_{p,q}={\displaystyle \frac{p+q-1}{2-p-q}}$ and ${\displaystyle E_{r,q}\left(t\right)=\sum _{k=0}^{+\infty }\frac{t^k}{\Gamma (rk+q)}}$ is the Wiman function [21] called also Mittag-Leffler function with two parameters r and q.

Definition 2.1 includes several existing fractional derivatives with singular and non-singular kernels. For instance,

• When $q=1-p$ and $w\left(t\right)=1$, we get the Caputo fractional derivative [3] with singular kernel given by

  $${}^C{D}_{a,t,1,\delta }^{p,1-p,r,m}u\left(t\right)=\frac{1}{\Gamma (1-p)}{\int }_a^t{(t-\tau )}^{-p}{u}^{\prime }\left(\tau \right)d\tau .$$
• When $q=r=m=\delta =1$ and $w\left(t\right)=1$, we obtain the CF fractional derivative [4] with non-singular given by

  $${}^C{D}_{a,t,1,1}^{p,1,1,1}u\left(t\right)=\frac{H\left(p\right)}{1-p}{\int }_a^{t}exp[-{\mu }_{p,1}{(t-\tau )}^m]u^{\prime }\left(\tau \right)d\tau ,$$

  where ${\mu }_{p,1}=\frac{p}{1-p}$.
• When $q=\delta =1$, $r=m=p$ and $w\left(t\right)=1$, we get the AB fractional derivative [5] given by

  $${}^C{D}_{a,t,1,1}^{p,1,p,p}u\left(t\right)=\frac{H\left(p\right)}{1-p}{\int }_a^t{E}_p[-{\mu }_{p,1}{(t-\tau )}^p]u^{\prime }\left(\tau \right)d\tau .$$
• When $q=\delta =1$ and $r=m=p$, we find the weighted AB fractional derivative [6] given by

  $${}^C{D}_{a,t,w,1}^{p,1,p,p}u\left(t\right)=\frac{H\left(p\right)}{1-p}\frac{1}{w\left(t\right)}{\int }_a^t{E}_p[-{\mu }_{p,1}{(t-\tau )}^p]\frac{d}{d\tau }\left(wu\right)\left(\tau \right)d\tau .$$
• When $q=\delta =1$, we obtain the GHF derivative [7] given by

  $${}^C{D}_{a,t,w,1}^{p,1,r,m}u\left(t\right)=\frac{H\left(p\right)}{1-p}\frac{1}{w\left(t\right)}{\int }_a^t{E}_r[-{\mu }_{p,1}{(t-\tau )}^m]\frac{d}{d\tau }\left(wu\right)\left(\tau \right)d\tau .$$
• When $q=1$, $m=r$ and $\delta =ln\left(\overline{p}\right)$ (with $\overline{p}>0$), we get the power fractional derivative [15] given by

  $${}^C{D}_{a,t,w,ln\left(\overline{p}\right)}^{p,1,r,r}u\left(t\right)=\frac{H\left(p\right)}{1-p}\frac{1}{w\left(t\right)}{\int }_a^t{E}_r[-ln\left(\overline{p}\right){\mu }_{p,1}{(t-\tau )}^r]\frac{d}{d\tau }\left(wu\right)\left(\tau \right)d\tau .$$
• When $\delta =1$, $m=r=p$ and $w\left(t\right)=1$, we obtain the fractional derivative introduced in [16] given by

  $${}^C{D}_{a,t,1,1}^{p,q,p,p}u\left(t\right)=\frac{H(p+q-1)}{2-p-q}{\int }_a^t{(t-\tau )}^{q-1}{E}_{p,q}[-{\mu }_{p,q}{(t-\tau )}^p]u^{\prime }\left(\tau \right)d\tau .$$

Now, we define the new mixed fractional derivative in Riemann-Liouville sense.

Definition 2.2.

Let $(p,q)\in {[0,1]}^2$, $r,m>0$ and $u\in H^1(a,b)$. The mixed fractional derivative of the function $u\left(t\right)$ of order p in Riemann-Liouville sense with respect to the weight function $w\left(t\right)$ is given as follows:

$${}^R{D}_{a,t,w,\delta }^{p,q,r,m}u\left(t\right)=\frac{H(p+q-1)}{2-p-q}\frac{1}{w\left(t\right)}\frac{d}{dt}{\int }_a^t{(t-\tau )}^{q-1}{E}_{r,q}[-\delta {\mu }_{p,q}{(t-\tau )}^m]w\left(\tau \right)u\left(\tau \right)d\tau .$$

(2)

Obviously, when $q=1-p$ and $w\left(t\right)=1$, we obtain the Riemann-Liouville fractional derivative [1,2] with singular kernel. In addition, we have the following result.

Theorem 2.3.

Let $wu$ be an analytic function. Then

$${\displaystyle {}^R{D}_{a,t,w,\delta }^{p,q,r,m}u\left(t\right)={}^C{D}_{a,t,w,\delta }^{p,q,r,m}u\left(t\right)+\frac{H(p+q-1){(t-a)}^{q-1}}{(2-p-q)w\left(t\right)}{E}_{r,q}[-\delta {\mu }_{p,q}{(t-a)}^m]\left(wu\right)\left(a\right).}$$

(3)

Proof. 

We have $wu$ is an analytic function. Then ${\displaystyle \left(wu\right)\left(\tau \right)=\sum _{n=0}^{+\infty }\frac{{\left(wf\right)}^{\left(n\right)}\left(t\right)}{n!}{(\tau -t)}^n}$ and

$$\begin{array}{ccc}\hfill {\displaystyle {}^R{D}_{a,t,w,\delta }^{p,q,r,m}u\left(t\right)}& =& \frac{H(p+q-1)}{(2-p-q)w\left(t\right)}\frac{d}{dt}\sum _{n=0}^{+\infty }\sum _{k=0}^{+\infty }\frac{{(-1)}^n{(-\delta {\mu }_{p,q})}^k{\left(wu\right)}^{\left(n\right)}\left(t\right)}{n!\Gamma (rk+q)}{\int }_a^t{(t-\tau )}^{mk+n+q-1}d\tau \hfill \\ & =& \frac{H(p+q-1)}{(2-p-q)w\left(t\right)}\frac{d}{dt}\sum _{n=0}^{+\infty }\sum _{k=0}^{+\infty }\frac{{(-1)}^n{(-\delta {\mu }_{p,q})}^k{\left(wu\right)}^{\left(n\right)}\left(t\right){(t-a)}^{mk+n+q}}{n!\Gamma (rk+q)(mk+n+q)}\hfill \\ & =& \frac{H(p+q-1)}{(2-p-q)w\left(t\right)}[\sum _{n=0}^{+\infty }\sum _{k=0}^{+\infty }\frac{{(-1)}^n{(-\delta {\mu }_{p,q})}^k{\left(wu\right)}^{(n+1)}\left(t\right){(t-a)}^{mk+n+q}}{n!\Gamma (rk+q)(mk+n+q)}\hfill \\ & & +\sum _{n=0}^{+\infty }\sum _{k=0}^{+\infty }\frac{{(-1)}^n{(-\delta {\mu }_{p,q})}^k}{n!\Gamma (rk+q)}{\left(wu\right)}^{\left(n\right)}\left(t\right){(t-a)}^{mk+n+q-1}]\hfill \\ & =& \frac{H(p+q-1)}{(2-p-q)w\left(t\right)}[\sum _{n=0}^{+\infty }\sum _{k=0}^{+\infty }\frac{{(-1)}^n{(-\delta {\mu }_{p,q})}^k{\left(wu\right)}^{(n+1)}\left(t\right)}{n!\Gamma (rk+q)}{\int }_a^t{(t-\tau )}^{mk+n+q-1}d\tau \hfill \\ & & +\sum _{n=0}^{+\infty }\frac{{(-1)}^n}{n!}{\left(wu\right)}^{\left(n\right)}\left(t\right){(t-a)}^{n+q-1}\sum _{k=0}^{+\infty }\frac{{(-\delta {\mu }_{p,q})}^k}{\Gamma (rk+q)}{(t-a)}^{mk}]\hfill \\ & =& {\displaystyle {}^C{D}_{a,t,w,\delta }^{p,q,r,m}u\left(t\right)+\frac{H(p+q-1)}{(2-p-q)w\left(t\right)}{(t-a)}^{q-1}{E}_{r,q}[-\delta {\mu }_{p,q}{(t-a)}^m]\left(wu\right)\left(a\right).}\hfill \end{array}$$

This ends the proof. □

Theorem 2.3 extends the results in Theorem 1 of [7] for $q=\delta =1$ and in Theorem 4.2 of [16] for $\delta =1$, $m=r=p$ and $w\left(t\right)=1$.

3. Laplace transform of the new mixed fractional derivative

In this section, we first need the following result.

Lemma 3.1.

The Laplace transform of $t^{q-1}{E}_{r,q}(-\delta {\mu }_{p,q}{t}^m)$ is given by

$$\mathcal{L}\left\{t^{q-1}{E}_{r,q}(-\delta {\mu }_{p,q}{t}^m)\right\}\left(s\right)=\frac{1}{s^q}\sum _{k=0}^{+\infty }{\left(\frac{-\delta {\mu }_{p,q}}{s^m}\right)}^k\frac{\Gamma (mk+q)}{\Gamma (rk+q)}.$$

(4)

If $m=r$, then

$$\mathcal{L}\left\{t^{q-1}{E}_{r,q}(-\delta {\mu }_{p,q}{t}^r)\right\}\left(s\right)=\frac{s^{r-q}}{s^r+\delta {\mu }_{p,q}},\left|{\displaystyle \frac{\delta {\mu }_{p,q}}{s^m}}\right|<1.$$

(5)

Proof. 

According to the definition of the Wiman function, we get

$$\begin{array}{ccc}\hfill \mathcal{L}\left\{t^{q-1}{E}_{r,q}(-\delta {\mu }_{p,q}{t}^m)\right\}\left(s\right)& =& \mathcal{L}\left\{\sum _{k=0}^{+\infty }\frac{{(-\delta {\mu }_{p,q})}^k}{\Gamma (rk+q)}{t}^{mk+q-1}\right\}\left(s\right)\hfill \\ & =& \sum _{k=0}^{+\infty }\frac{{(-\delta {\mu }_{p,q})}^k}{\Gamma (rk+q)}\mathcal{L}\left\{t^{mk+q-1}\right\}\left(s\right)\hfill \\ & =& \frac{1}{s^q}\sum _{k=0}^{+\infty }{\left(\frac{-\delta {\mu }_{p,q}}{s^m}\right)}^k\frac{\Gamma (mk+q)}{\Gamma (rk+q)}.\hfill \end{array}$$

In particular, if $m=r$, then

$$\mathcal{L}\left\{t^{q-1}{E}_{r,q}(-\delta {\mu }_{p,q}{t}^r)\right\}\left(s\right)=\frac{s^{r-q}}{s^r+\delta {\mu }_{p,q}},\left|{\displaystyle \frac{\delta {\mu }_{p,q}}{s^m}}\right|<1.$$

This completes the proof. □

By a simple application of Lemma 3.1, we obtain the following theorem.

Theorem 3.2.

(i) 

The Laplace transform of ${\displaystyle w\left(t\right){}^C{D}_{0,t,w,\delta }^{p,q,r,m}u\left(t\right)}$ is given by

$${\displaystyle \mathcal{L}\left\{w\left(t\right){}^C{D}_{0,t,w,\delta }^{p,q,r,m}u\left(t\right)\right\}=\frac{H(p+q-1)\left[s\mathcal{L}\right\{w\left(t\right)u\left(t\right)\}-(wu\left)\right(0\left)\right]}{(2-p-q)s^q}\sum _{k=0}^{+\infty }{\left(\frac{-\delta {\mu }_{p,q}}{s^m}\right)}^k\frac{\Gamma (mk+q)}{\Gamma (rk+q)}.}$$

(6)

In particular, we have

$${\displaystyle \mathcal{L}\left\{w\left(t\right){}^C{D}_{0,t,w,\delta }^{p,q,r,r}u\left(t\right)\right\}=\frac{H(p+q-1)}{2-p-q}\frac{s^{r-q+1}\mathcal{L}\left\{w\left(t\right)u\left(t\right)\right\}-s^{r-q}w\left(0\right)u\left(0\right)}{s^r+\delta {\mu }_{p,q}}.}$$

(7)

(ii) 

The Laplace transform of ${\displaystyle w\left(t\right){}^R{D}_{0,t,w,\delta }^{p,q,r,m}u\left(t\right)}$ is given by

$${\displaystyle \mathcal{L}\left\{w\left(t\right){}^R{D}_{0,t,w,\delta }^{p,q,r,m}u\left(t\right)\right\}=\frac{H(p+q-1))}{(2-p-q)s^{q-1}}\mathcal{L}\left\{w\left(t\right)u\left(t\right)\right\}\sum _{k=0}^{+\infty }{\left(\frac{-\delta {\mu }_{p,q}}{s^m}\right)}^k\frac{\Gamma (mk+q)}{\Gamma (rk+q)}.}$$

(8)

In particular, we have

$${\displaystyle \mathcal{L}\left\{w\left(t\right){}^R{D}_{0,t,w,\delta }^{p,q,r,r}u\left(t\right)\right\}=\frac{H(p+q-1)}{2-p-q}\frac{s^{r-q+1}\mathcal{L}\left\{w\left(t\right)u\left(t\right)\right\}}{s^r+\delta {\mu }_{p,q}}.}$$

(9)

Remark 3.3.

Lemma 3.1 and Theorem 3.2 extend the results presented in [7] for the new GHF derivative, it suffices to take $q=\delta =1$.

4. The associate fractional integral

In this section, we define the fractional integral associated to the new mixed fractional derivative. First, we consider the following fractional differential equation:

$${\displaystyle {}^R{D}_{0,t,w,\delta }^{p,q,r,r}v\left(t\right)=u\left(t\right).}$$

(10)

Lemma 4.1.

Eq. (10) has a unique solution given by

$$v\left(t\right)=\left\{\begin{array}{cc}{\displaystyle \frac{2-p-q}{H(p+q-1)}\left[{}^{RL}{\mathcal{I}}_{a,w}^{1-q}u\left(t\right)+\delta {\mu }_{p,q}{}^{RL}{\mathcal{I}}_{a,w}^{1+r-q}u\left(t\right)\right],}\hfill & \mathit{if}q\ne 1;\hfill \\ {\displaystyle \frac{1-p}{H\left(p\right)}u\left(t\right)+\frac{\delta p}{H\left(p\right)}{}^{RL}{\mathcal{I}}_{a,w}^{r}u\left(t\right),}\hfill & \mathit{if}q=1,\hfill \end{array}\right.$$

(11)

where ${\displaystyle {}^{RL}{\mathcal{I}}_{a,w}^{\alpha }}$ is the standard weighted Riemann-Liouville fractional integral of order α given by

$${\displaystyle {}^{RL}{\mathcal{I}}_{a,w}^{\alpha }u\left(t\right)=\frac{1}{\Gamma \left(\alpha \right)}\frac{1}{w\left(t\right)}{\int }_a^t{(t-\tau )}^{\alpha -1}w\left(\tau \right)u\left(\tau \right)d\tau .}$$

(12)

Proof. 

From (10), we have

$${\displaystyle w\left(t\right){}^R{D}_{0,t,w,\delta }^{p,q,r,r}v\left(t\right)=w\left(t\right)u\left(t\right).}$$

By applying Theorem 3.2, we get

$$\begin{array}{ccc}\hfill \mathcal{L}\left\{w\right(t\left)v\right(t\left)\right\}\left(s\right)& =& \frac{2-p-q}{H(p+q-1)}\frac{1}{s^{1-q}}\mathcal{L}\left\{w\left(t\right)u\left(t\right)\right\}\left(s\right)+\frac{2-p-q}{H(p+q-1)}\frac{\delta {\mu }_{p,q}}{s^{r-q+1}}\mathcal{L}\left\{w\left(t\right)u\left(t\right)\right\}\left(s\right).\hfill \end{array}$$

• When $q=1$, we have

  $$\begin{array}{ccc}\hfill \mathcal{L}\left\{w\right(t\left)v\right(t\left)\right\}\left(s\right)& =& \frac{1-p}{H\left(p\right)}\mathcal{L}\left\{w\left(t\right)u\left(t\right)\right\}\left(s\right)+\frac{1-p}{H\left(p\right)}\frac{\delta {\mu }_{p,1}}{s^r}\mathcal{L}\left\{w\left(t\right)u\left(t\right)\right\}\left(s\right)\hfill \\ & =& \frac{1-p}{H\left(p\right)}\mathcal{L}\left\{w\left(t\right)u\left(t\right)\right\}\left(s\right)+\frac{1-p}{H\left(p\right)}\frac{\delta {\mu }_{p,1}}{\Gamma \left(r\right)}\mathcal{L}\{t^{r-1}\ast \left(wu\right)\left(t\right)\}\left(s\right).\hfill \end{array}$$
  By taking the inverse Laplace, we get

  $$w\left(t\right)v\left(t\right)=\frac{1-p}{H\left(p\right)}w\left(t\right)u\left(t\right)+\frac{1-p}{H\left(p\right)}\frac{\delta {\mu }_{p,1}}{\Gamma \left(r\right)}\left(t^{r-1}\ast \left(wu\right)\left(t\right)\right).$$
  Hence,

  $$v\left(t\right)=\frac{1-p}{H\left(p\right)}u\left(t\right)+\frac{\delta p}{H\left(p\right)\Gamma \left(r\right)}\frac{1}{w\left(t\right)}{\int }_a^t{(t-\tau )}^{r-1}w\left(\tau \right)u\left(\tau \right)d\tau .$$

  (13)
• When $q\ne 1$, we have

  $$\begin{array}{ccc}\hfill \mathcal{L}\left\{w\right(t\left)v\right(t\left)\right\}\left(s\right)& =& \frac{2-p-q}{H(p+q-1)\Gamma (1-q)}\mathcal{L}\{t^{-q}\ast w\left(t\right)u\left(t\right)\}\left(s\right)\hfill \\ & & +\frac{2-p-q}{H(p+q-1)\Gamma (r-q+1)}\mathcal{L}\{t^{r-q}\ast \left(wu\right)\left(t\right)\}\left(s\right).\hfill \end{array}$$
  By passage to the inverse Laplace, we obtain

  $$\begin{array}{ccc}\hfill w\left(t\right)v\left(t\right)& =& \frac{2-p-q}{H(p+q-1)\Gamma (1-q)}\left(t^{-q}\ast w\left(t\right)u\left(t\right)\right)\hfill \\ & & +\frac{2-p-q}{H(p+q-1)\Gamma (r-q+1)}\left(t^{r-q}\ast \left(wu\right)\left(t\right)\right),\hfill \end{array}$$

  which leads to

  $${\displaystyle v\left(t\right)=\frac{2-p-q}{H(p+q-1)}\left[{}^{RL}{\mathcal{I}}_{a,w}^{1-q}u\left(t\right)+\delta {\mu }_{p,q}{}^{RL}{\mathcal{I}}_{a,w}^{1+r-q}u\left(t\right)\right].}$$

  (14)

This completes the proof. □

Definition 4.2.

If $m=r$, then the fractional integral associated to the new mixed fractional derivative is defined as follows

$$I_{a,t,w,\delta }^{p,q,r}u\left(t\right)=\left\{\begin{array}{cc}{\displaystyle \frac{2-p-q}{H(p+q-1)}\left[{}^{RL}{\mathcal{I}}_{a,w}^{1-q}u\left(t\right)+\delta {\mu }_{p,q}{}^{RL}{\mathcal{I}}_{a,w}^{1+r-q}u\left(t\right)\right],}\hfill & \mathit{if}q\ne 1;\hfill \\ {\displaystyle \frac{1-p}{H\left(p\right)}u\left(t\right)+\frac{\delta p}{H\left(p\right)}{}^{RL}{\mathcal{I}}_{a,w}^{r}u\left(t\right),}\hfill & \mathit{if}q=1.\hfill \end{array}\right.$$

(15)

Remark 4.3.

The associate integral defined above includes a variety of fractional integral operators. For instance,

(i) 

If $\delta =1$, $r=p$ and $w\left(t\right)=1$, then (15) reduced to the new fractional integral presented in [16].

(ii) 

If $q=\delta =1$, then (15) reduced to the new GHF integral introduced in [7] that includes the Atangana-Baleanu fractional integral [5] and the weighted Atangana-Baleanu fractional integral [6].

(iii) 

If $p=q=1$, then (15) reduced to the standard weighted Riemann-Liouville fractional integral of order r and to ordinary integral when $r=1$ and $w\left(t\right)=1$.

5. Fondamental properties of the new differential and integral operators

In this section, we establish new important formulas and properties for the new differential and integral operators.

For simplicity, we denote ${\displaystyle {}^C{D}_{a,t,w,\delta }^{p,q,r,r}}$ by ${\mathcal{D}}_{a,w,\delta }^{p,q,r}$ and $I_{a,t,w,\delta }^{p,q,r}$ by ${\mathcal{I}}_{a,w,\delta }^{p,q,r}$.

Lemma 5.1.

The mixed fractional derivative ${\mathcal{D}}_{a,w,\delta }^{p,q,r}$ can be expressed as follows:

$${\mathcal{D}}_{a,w,\delta }^{p,q,r}u\left(t\right)=\frac{H(p+q-1)}{2-p-q}\sum _{k=0}^{+\infty }{(-\delta {\mu }_{p,q})}^k{}^{RL}{\mathcal{I}}_{a,w}^{kr+q}\left(\frac{{\left(wu\right)}^{\prime }}{w}\right)\left(t\right).$$

(16)

Proof. 

Since the Mittag-Leffler function $E_{p,q}\left(t\right)$ is an entire function of t, then ${\mathcal{D}}_{a,w,\delta }^{p,q,r}$ can be expressed as follows:

$$\begin{array}{ccc}\hfill {\mathcal{D}}_{a,w,\delta }^{p,q,r}u\left(t\right)& =& \frac{H(p+q-1)}{2-p-q}\frac{1}{w\left(t\right)}\sum _{k=0}^{+\infty }\frac{{(-\delta {\mu }_{p,q})}^k}{\Gamma (rk+q)}{\int }_a^t{(t-\tau )}^{rk+q-1}{\left(wu\right)}^{\prime }\left(\tau \right)d\tau \hfill \\ & =& \frac{H(p+q-1)}{2-p-q}\sum _{k=0}^{+\infty }{(-\delta {\mu }_{p,q})}^k\frac{1}{\Gamma (rk+q)}\frac{1}{w\left(t\right)}{\int }_a^t{(t-\tau )}^{rk+q-1}{\left(wu\right)}^{\prime }\left(\tau \right)d\tau \hfill \\ & =& \frac{H(p+q-1)}{2-p-q}\sum _{k=0}^{+\infty }{(-\delta {\mu }_{p,q})}^k{}^{RL}{\mathcal{I}}_{a,w}^{kr+q}\left(\frac{{\left(wu\right)}^{\prime }}{w}\right)\left(t\right).\hfill \end{array}$$

This ends the proof. □

Remark 5.2.

Lemma 5.1 extends the recent result established by Zitane and Torres in Lemma 3 of [20].

Theorem 5.3.

Let $(p,q)\in {[0,1]}^2$, $r>0$, $\delta \in {\mathbb{R}}^{\ast }$ and $u\in H^1(a,b)$. Then, we have the following property:

$${\mathcal{I}}_{a,w,\delta }^{p,q,r}\left({\mathcal{D}}_{a,w,\delta }^{p,q,r}u\right)\left(t\right)=u\left(t\right)-\frac{w\left(a\right)u\left(a\right)}{w\left(t\right)}.$$

(17)

Proof. 

When $q\ne 1$, we have

$${\displaystyle {\mathcal{I}}_{a,w,\delta }^{p,q,r}\left({\mathcal{D}}_{a,w,\delta }^{p,q,r}u\right)\left(t\right)=\frac{2-p-q}{H(p+q-1)}\left[{}^{RL}{\mathcal{I}}_{a,w}^{1-q}\left({\mathcal{D}}_{a,w,\delta }^{p,q,r}u\right)\left(t\right)+\delta {\mu }_{p,q}{}^{RL}{\mathcal{I}}_{a,w}^{1+r-q}\left({\mathcal{D}}_{a,w,\delta }^{p,q,r}u\right)\left(t\right)\right].}$$

By applying Lemma 5.1, we get

$$\begin{array}{ccc}\hfill {\mathcal{I}}_{a,w,\delta }^{p,q,r}\left({\mathcal{D}}_{a,w,\delta }^{p,q,r}u\right)\left(t\right)& =& {\displaystyle {}^{RL}{\mathcal{I}}_{a,w}^{1-q}\left[\sum _{k=0}^{+\infty }{(-\delta {\mu }_{p,q})}^k{}^{RL}{\mathcal{I}}_{a,w}^{kr+q}\left(\frac{{\left(wu\right)}^{\prime }}{w}\right)\left(t\right)\right]}\hfill \\ & & {\displaystyle +\delta {\mu }_{p,q}{}^{RL}{\mathcal{I}}_{a,w}^{1+r-q}\left[\sum _{k=0}^{+\infty }{(-\delta {\mu }_{p,q})}^k{}^{RL}{\mathcal{I}}_{a,w}^{kr+q}\left(\frac{{\left(wu\right)}^{\prime }}{w}\right)\left(t\right)\right]}\hfill \\ & =& \sum _{k=0}^{+\infty }{(-\delta {\mu }_{p,q})}^k{}^{RL}{\mathcal{I}}_{a,w}^{kr+1}\left(\frac{{\left(wu\right)}^{\prime }}{w}\right)\left(t\right)-\sum _{k=1}^{+\infty }{(-\delta {\mu }_{p,q})}^k{}^{RL}{\mathcal{I}}_{a,w}^{kr+1}\left(\frac{{\left(wu\right)}^{\prime }}{w}\right)\left(t\right)\hfill \\ & =& {}^{RL}{\mathcal{I}}_{a,w}^1\left(\frac{{\left(wu\right)}^{\prime }}{w}\right)\left(t\right)\hfill \\ & =& \frac{1}{w\left(t\right)}{\int }_a^t{\left(wu\right)}^{\prime }\left(\tau \right)d\tau =u\left(t\right)-\frac{w\left(a\right)u\left(a\right)}{w\left(t\right)}.\hfill \end{array}$$

For $q=1$, we have

$$\begin{array}{ccc}\hfill {\mathcal{I}}_{a,w,\delta }^{p,1,r}\left({\mathcal{D}}_{a,w,\delta }^{p,1,r}u\right)\left(t\right)& =& {\displaystyle \frac{1-p}{H\left(p\right)}({\mathcal{D}}_{a,w,\delta }^{p,q,r}u)\left(t\right)+\frac{\delta p}{H\left(p\right)}{}^{RL}{\mathcal{I}}_{a,w}^r\left({\mathcal{D}}_{a,w,\delta }^{p,q,r}u\right)\left(t\right)}\hfill \\ & =& \sum _{k=0}^{+\infty }{(-\delta {\mu }_{p,1})}^k{}^{RL}{\mathcal{I}}_{a,w}^{kr+1}\left(\frac{{\left(wu\right)}^{\prime }}{w}\right)\left(t\right)\hfill \\ & & {\displaystyle +\delta {\mu }_{p,1}{}^{RL}{\mathcal{I}}_{a,w}^r\left[\sum _{k=0}^{+\infty }{(-\delta {\mu }_{p,1})}^k{}^{RL}{\mathcal{I}}_{a,w}^{kr+1}\left(\frac{{\left(wu\right)}^{\prime }}{w}\right)\left(t\right)\right]}\hfill \\ & =& \sum _{k=0}^{+\infty }{(-\delta {\mu }_{p,1})}^k{}^{RL}{\mathcal{I}}_{a,w}^{kr+1}\left(\frac{{\left(wu\right)}^{\prime }}{w}\right)\left(t\right)-\sum _{k=1}^{+\infty }{(-\delta {\mu }_{p,1})}^k{}^{RL}{\mathcal{I}}_{a,w}^{kr+1}\left(\frac{{\left(wu\right)}^{\prime }}{w}\right)\left(t\right)\hfill \\ & =& {}^{RL}{\mathcal{I}}_{a,w}^1\left(\frac{{\left(wu\right)}^{\prime }}{w}\right)\left(t\right)\hfill \\ & =& u\left(t\right)-\frac{w\left(a\right)u\left(a\right)}{w\left(t\right)}.\hfill \end{array}$$

Hence, the proof is completed. □

It is obvious that when $w\left(t\right)=1$, we obtain the following first corollary of Theorem 5.3 that extends the Newton-Leibniz formula given in [22].

Corollary 5.4.

The new mixed fractional derivative and integral satisfy the Newton-Leibniz formula. In other words, we have

$${\mathcal{I}}_{a,1,\delta }^{p,q,r}\left({\mathcal{D}}_{a,1,\delta }^{p,q,r}u\right)\left(t\right)=u\left(t\right)-u\left(a\right).$$

(18)

Clearly, ${\mathcal{D}}_{a,1,\delta }^{p,q,r}\left(c\right)=0$ for all constant function $u\left(t\right)=c$. Moreover, we have the following result.

Corollary 5.5.

Let u be a solution of the following fractional differential equation

$${\mathcal{D}}_{a,1,\delta }^{p,q,r}u\left(t\right)=0.$$

(19)

Then the function u is a constant function.

Proof. 

It follows from (18) that $u\left(t\right)=u\left(a\right)$. This proves that u is a constant function. □

6. Numerical scheme

In this section, we first develop a numerical method to approximate the solution of the following FDE with the new mixed fractional derivative given by

$${\mathcal{D}}_{a,w,\delta }^{p,q,r}y\left(t\right)=f\left(t,y\left(t\right)\right),$$

(20)

subject to the given initial condition

$$y\left(a\right)=y_0.$$

From Theorem 5.3, Eq. (20) can be converted into the following fractional integral equation:

$$\begin{array}{c}\hfill y\left(t\right)-{\displaystyle \frac{y\left(a\right)w\left(a\right)}{w\left(t\right)}}={\mathcal{I}}_{a,w,\delta }^{p,q,r}f\left(t,y\left(t\right)\right).\end{array}$$

(21)

So, we discuss to cases. When $q=1$, we have

$${\displaystyle y\left(t\right)-{\displaystyle \frac{y\left(a\right)w\left(a\right)}{w\left(t\right)}}=\frac{1-p}{H\left(p\right)}f\left(t,y\left(t\right)\right)+\frac{\delta p}{H\left(p\right)}{}^{RL}{\mathcal{I}}_{a,w}^{r}f\left(t,y\left(t\right)\right),}$$

which implies that

$$\begin{array}{c}\hfill y\left(t\right)={\displaystyle \frac{y\left(a\right)w\left(a\right)}{w\left(t\right)}}+{\displaystyle \frac{1-p}{H\left(p\right)}}f\left(t,y\left(t\right)\right)+{\displaystyle \frac{\delta p}{H\left(p\right)\Gamma \left(r\right)}}{\displaystyle \frac{1}{w\left(t\right)}}{\int }_a^t{(t-\tau )}^{r-1}w\left(\tau \right)f\left(\tau ,y\left(\tau \right)\right)d\tau .\end{array}$$

(22)

Let $\Delta t$ be the discretization step and $t_n=a+n\Delta t$, with $n\in \mathrm{I}\mathrm{N}$. We have

$$\begin{array}{ccc}\hfill y\left(t_{n+1}\right)& =& {\displaystyle \frac{y_{0}w\left(a\right)}{w\left(t_n\right)}}+{\displaystyle \frac{1-p}{H\left(p\right)}}f\left(t_n,y\left(t_n\right)\right)\hfill \\ & & +{\displaystyle \frac{\delta p}{H\left(p\right)\Gamma \left(r\right)w\left(t_n\right)}}{\int }_a^{t_{n+1}}{(t_{n+1}-\tau )}^{r-1}w\left(\tau \right)f\left(\tau ,y\left(\tau \right)\right)d\tau .\hfill \end{array}$$

Then

$$\begin{array}{ccc}\hfill y\left(t_{n+1}\right)& =& {\displaystyle \frac{y_{0}w\left(a\right)}{w\left(t_n\right)}}+{\displaystyle \frac{1-p}{H\left(p\right)}}f\left(t_n,y\left(t_n\right)\right)\hfill \\ & & +{\displaystyle \frac{\delta p}{H\left(p\right)\Gamma \left(r\right)w\left(t_n\right)}}\sum _{k=0}^n{\int }_{t_k}^{t_{k+1}}{(t_{n+1}-\tau )}^{r-1}g\left(\tau ,y\left(\tau \right)\right)d\tau ,\hfill \end{array}$$

(23)

where $g\left(\tau ,y\left(\tau \right)\right)=w\left(\tau \right)f\left(\tau ,y\left(\tau \right)\right)$. The function g can be approximated over $[t_k,t_{k+1}]$ by means of the Lagrange polynomial interpolation as follows:

$$\begin{array}{ccc}\hfill P_k\left(\tau \right)& =& {\displaystyle \frac{\tau -t_k}{t_{k-1}-t_k}}g\left(t_{k-1},y\left(t_{k-1}\right)\right)+{\displaystyle \frac{\tau -t_{k-1}}{t_k-t_{k-1}}}g\left(t_k,y\left(t_k\right)\right),\hfill \\ & \simeq & {\displaystyle \frac{g(t_{k-1},y_{k-1})}{\Delta t}}(t_k-\tau )+{\displaystyle \frac{g(t_k,y_k)}{\Delta t}}(\tau -t_{k-1}).\hfill \end{array}$$

(24)

Hence,

$$\begin{array}{ccc}\hfill y\left(t_{n+1}\right)& =& {\displaystyle \frac{y_{0}w\left(0\right)}{w\left(t_n\right)}}+{\displaystyle \frac{1-p}{H\left(p\right)}}f\left(t_n,y_n\right)\hfill \\ & & +{\displaystyle \frac{\delta p}{H\left(p\right)\Gamma \left(r\right)w\left(t_n\right)}}\sum _{k=0}^n[{\displaystyle \frac{g\left(t_k,y_k\right)}{\Delta t}}{\int }_{t_k}^{t_{k+1}}\left(\tau -t_{k-1}\right){\left(t_{n+1}-\tau \right)}^{r-1}d\tau \hfill \\ & & +{\displaystyle \frac{g\left(t_{k-1},x_{k-1}\right)}{\Delta t}}{\int }_{t_k}^{t_{k+1}}\left(t_k-\tau \right){\left(t_{n+1}-\tau \right)}^{r-1}d\tau ].\hfill \end{array}$$

Since

$$\begin{array}{ccc}\hfill {\int }_{t_k}^{t_{k+1}}{(t_{n+1}-\tau )}^{r-1}(\tau -t_{k-1})d\tau & =& {\displaystyle \frac{{(\Delta t)}^{r+1}}{r(r+1)}}[{(n-k+1)}^r(n-k+2+r)\hfill \\ & & -{(n-k)}^r(n-k+2+2r)],\hfill \end{array}$$

(25)

and

$$\begin{array}{ccc}\hfill {\int }_{t_k}^{t_{k+1}}{(t_{n+1}-\tau )}^{r-1}(t_k-\tau )d\tau & =& {\displaystyle \frac{{(\Delta t)}^{r+1}}{r(r+1)}}[{(n-k)}^r(n-k+1+r)\hfill \\ & & -{(n-k+1)}^{r+1}],\hfill \end{array}$$

(26)

we have the following numerical scheme for the case $q=1$:

$$\begin{array}{ccc}\hfill y_{n+1}& =& {\displaystyle \frac{y_{0}w\left(0\right)}{w\left(t_n\right)}}+{\displaystyle \frac{1-p}{H\left(p\right)}}f\left(t_n,y_n\right)\hfill \\ \hfill & & +{\displaystyle \frac{\delta p{(\Delta t)}^r}{H\left(p\right)\Gamma (r+2)w\left(t_n\right)}}\sum _{k=0}^n(w\left(t_k\right)f\left(t_k,y_k\right){\mathcal{A}}_{n,k}^r\hfill \\ & & +w\left(t_{k-1}\right)f\left(t_{k-1},y_{k-1}\right){\mathcal{B}}_{n,k}^r),\hfill \end{array}$$

(27)

where

$$\begin{array}{ccc}\hfill {\mathcal{A}}_{n,k}^r& =& {(n-k+1)}^r(n-k+2+r)-{(n-k)}^r(n-k+2+2r),\hfill \\ \hfill {\mathcal{B}}_{n,k}^r& =& {(n-k)}^r(n-k+1+r)-{(n-k+1)}^{r+1}.\hfill \end{array}$$

Remark 6.1.

The numerical scheme given in (27) covers the numerical method of Hattaf et al. [18] when $q=\delta =1$, Toufik and Atangana [19] when $w\left(t\right)=1$, $q=\delta =1$ and $r=p$, as well as the recent numerical scheme presented in [20] when $q=1$ and $\delta =ln\left(\overline{p}\right)$ with $\overline{p}>0$.

For $q\ne 1$, Eq. (21) becomes

$$\begin{array}{ccc}\hfill y\left(t\right)& =& {\displaystyle \frac{y\left(a\right)w\left(a\right)}{w\left(t\right)}}+{\displaystyle \frac{2-p-q}{H(p+q-1)w\left(t\right)}}[{\displaystyle \frac{1}{\Gamma (1-q)}}{\int }_a^t{(t-\tau )}^{-q}w\left(\tau \right)f\left(\tau ,y\left(\tau \right)\right)d\tau \hfill \\ & & +{\displaystyle \frac{\delta {\mu }_{p,q}}{\Gamma (r-q+1)}}{\int }_a^t{(t-\tau )}^{r-q}w\left(\tau \right)f\left(\tau ,y\left(\tau \right)\right)d\tau ].\hfill \end{array}$$

Thus,

$$\begin{array}{ccc}\hfill y\left(t_{n+1}\right)& =& {\displaystyle \frac{y\left(a\right)w\left(a\right)}{w\left(t_n\right)}}+{\displaystyle \frac{2-p-q}{H(p+q-1)w\left(t_n\right)}}[{\displaystyle \frac{1}{\Gamma (1-q)}}\sum _{k=0}^n{\int }_{t_k}^{t_{k+1}}{(t_{n+1}-\tau )}^{-q}g\left(\tau ,y\left(\tau \right)\right)d\tau \hfill \\ & & +{\displaystyle \frac{\delta {\mu }_{p,q}}{\Gamma (r-q+1)}}\sum _{k=0}^n{\int }_{t_k}^{t_{k+1}}{(t_{n+1}-\tau )}^{r-q}g\left(\tau ,y\left(\tau \right)\right)d\tau ].\hfill \end{array}$$

Similarly, we obtain the following scheme for the case $q\ne 1$:

$$\begin{array}{ccc}\hfill y_{n+1}& =& {\displaystyle \frac{y_{0}w\left(a\right)}{w\left(t_n\right)}}+{\displaystyle \frac{(2-p-q){(\Delta t)}^{1-q}}{H(p+q-1)w\left(t_n\right)}}\left[{\displaystyle \frac{1}{\Gamma (3-q)}}\sum _{k=0}^n\right(w\left(t_k\right)f\left(t_k,y_k\right){\mathcal{A}}_{n,k}^r\hfill \\ \hfill & & +w\left(t_{k-1}\right)f\left(t_{k-1},y_{k-1}\right){\mathcal{B}}_{n,k}^r)+{\displaystyle \frac{\delta {\mu }_{p,q}{(\Delta t)}^r}{\Gamma (r-q+3)}}\sum _{k=0}^n(w\left(t_k\right)f\left(t_k,y_k\right){\mathcal{A}}_{n,k}^{r-q+1}\hfill \\ & & +w\left(t_{k-1}\right)f\left(t_{k-1},y_{k-1}\right){\mathcal{B}}_{n,k}^{r-q+1}\left)\right].\hfill \end{array}$$

(28)

To illustrate our numerical scheme, we consider the following FDE with the mixed fractional derivative:

$$\left\{\begin{array}{c}{\mathcal{D}}_{a,w,\delta }^{p,1,r}y\left(t\right)=t^2{e}^{-t},\hfill \\ y\left(0\right)=0.\hfill \end{array}\right.$$

(29)

Let $w\left(t\right)=e^{-t}$. By applying the fractional integral to both sides of (29) and using Theorem 5.3, we obtain the exact solution of (29), which is given by

$$y\left(t\right)=\left({\displaystyle \frac{1-p}{H\left(p\right)}}+{\displaystyle \frac{2p\delta t^r}{H\left(p\right)\Gamma (r+3)}}\right)t^2{e}^{-t}.$$

(30)

Now, we apply the developed numerical scheme for the case $q=1$ presented in (27) to approximate the solution of (29). For all numerical simulations, we choose the normalisation function as follows

$$H\left(p\right)=1-p+{\displaystyle \frac{p}{\Gamma \left(p\right)}}.$$

(31)

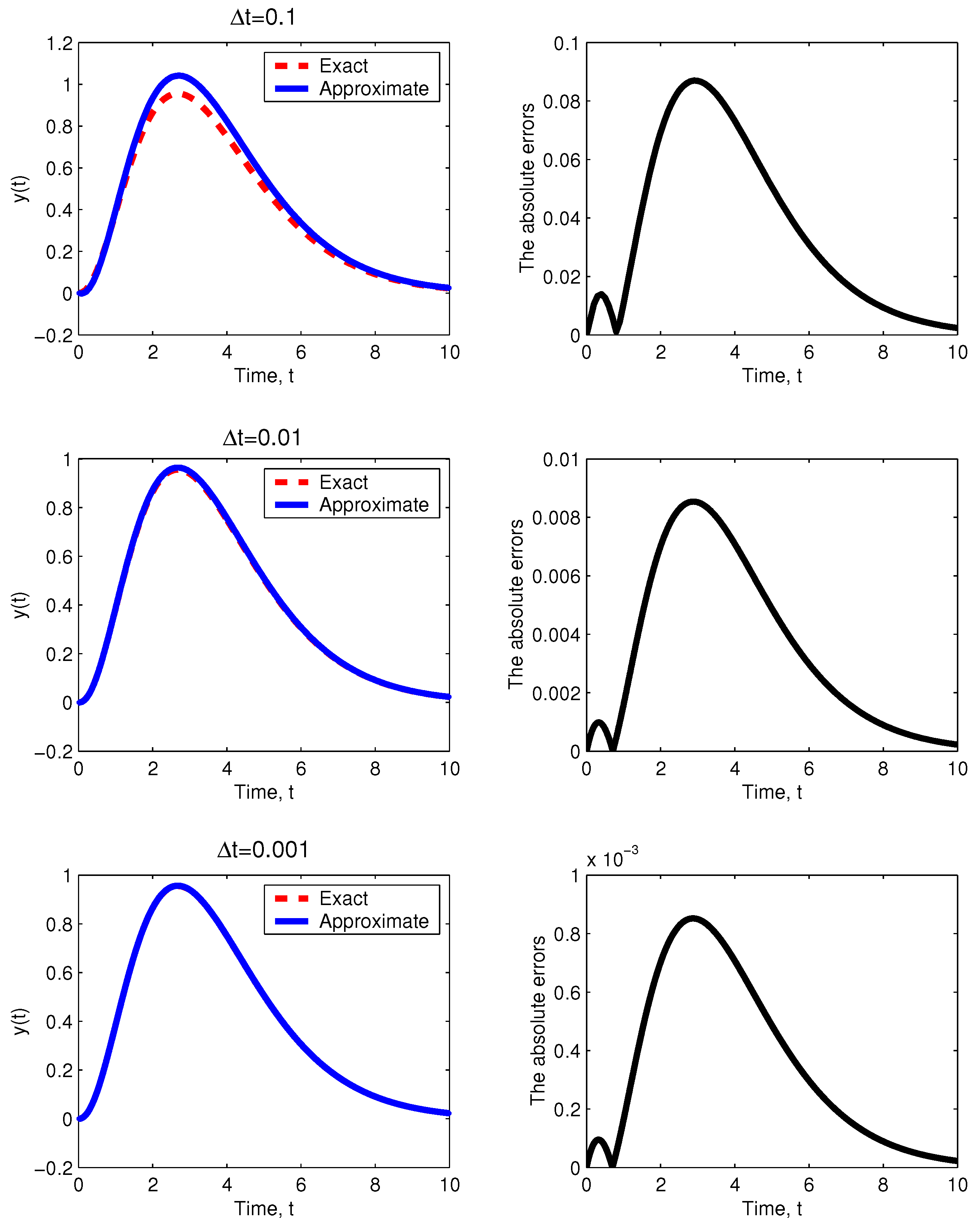
The comparaison between the exact and approximate solutions of (29) with the corresponding absolute errors is visualized in Figure 1 for different values of $\Delta t$, $p=0.7$, $r=0.8$ and $\delta =2.5$. Furthermore, Table 1 presents the maximum error for numerous values of $\Delta t$.

From Figure 1, we notice that the developed numerical scheme gives a very good agreement between the exact and approximate solutions for different values of the discretization step $\Delta t$. Also, Table 1 shows that the convergence of the numerical approximation depends on the discretization step $\Delta t$. By comparing the exact and approximate solutions, we deduce that the new developed numerical scheme is very effective and rapidly converges to the exact solution.

7. Application to computational biology

Computational biology is a branch of biology used mathematical modeling and computational simulations in order to understand biological systems and relationships. Now, consider the following FDE system describing the evolution of cell population in human body:

$${\mathcal{D}}_{0,w,\delta }^{p,1,r}N\left(t\right)=\lambda -dN\left(t\right),$$

(32)

where $N\left(t\right)$ is the total cell population produced at rate $\lambda$ and die naturally at rate d. Applying Laplace transform to (32), we get

$$\mathcal{L}\left\{w\left(t\right){\mathcal{D}}_{0,w,\delta }^{p,1,r}N\left(t\right)\right\}=\lambda \mathcal{L}\left\{w\left(t\right)\right\}-d\mathcal{L}\left\{w\left(t\right)N\left(t\right)\right\}.$$

According Theorem 3.2, we have

$$\mathcal{L}\left\{w\left(t\right)N\left(t\right)\right\}\left(s\right)=\frac{H\left(p\right)w\left(0\right)N\left(0\right)s^{r-1}}{[H\left(p\right)+d(1-p)]s^r+dp\delta }+\frac{\lambda (1-p)s^{\beta }+p\lambda \delta }{[N\left(p\right)+d(1-p)]s^r+dp\delta }\mathcal{L}\left\{w\left(t\right)\right\}\left(s\right).$$

Then

$$\mathcal{L}\left\{w\left(t\right)N\left(t\right)\right\}\left(s\right)=\frac{H\left(p\right)w\left(0\right)N\left(0\right)s^{r-1}}{a_p{s}^r+dp\delta }+\frac{\lambda (1-p)s^{\beta }+p\lambda \delta }{a_p{s}^r+dp\delta }\mathcal{L}\left\{w\left(t\right)\right\}\left(s\right),$$

where $a_p=H\left(p\right)+d(1-p)$. Hence,

$$\begin{array}{ccc}\hfill \mathcal{L}\left\{w\right(t\left)N\right(t\left)\right\}\left(s\right)& =& \frac{H\left(p\right)w\left(0\right)N\left(0\right)}{a_p}\frac{s^{r-1}}{s^r+\frac{dp\delta }{a_p}}+\frac{\lambda (1-p)}{a_p}\frac{s^{r-1}}{s^r+\frac{dp\delta }{a_{\alpha }}}s\mathcal{L}\left\{w\left(t\right)\right\}\left(s\right)\hfill \\ & & +\frac{p\lambda \delta }{a_p}\frac{1}{s^r+\frac{dp\delta }{a_p}}\mathcal{L}\left\{w\left(t\right)\right\}\left(s\right)\hfill \\ & =& \frac{H\left(p\right)w\left(0\right)N\left(0\right)}{a_p}\mathcal{L}\left\{E_r\left(-\frac{dp\delta }{a_p}{t}^r\right)\right\}\hfill \\ & & +\frac{\lambda (1-p)}{a_p}\mathcal{L}\left\{E_r\left(-\frac{dp\delta }{a_p}{t}^r\right)\right\}\left(\mathcal{L}\left\{w^{\prime }\left(t\right)\right\}+w\left(0\right)\right)\hfill \\ & & -\frac{\lambda }{d}\mathcal{L}\left\{\frac{d}{dt}{E}_r\left(-\frac{dp\delta }{a_p}{t}^r\right)\right\}\mathcal{L}\left\{w\left(t\right)\right\}.\hfill \end{array}$$

Thus,

$$\begin{array}{ccc}\hfill w\left(t\right)N\left(t\right)& =& \frac{H\left(p\right)w\left(0\right)N\left(0\right)}{a_p}{E}_r\left(-\frac{dp\delta }{a_p}{t}^r\right)+\frac{\lambda (1-p)}{a_p}{E}_r\left(-\frac{dp\delta }{a_p}{t}^r\right)\ast w^{\prime }\left(t\right)\hfill \\ & & +\frac{\lambda (1-p)w\left(0\right)}{a_p}{E}_r\left(-\frac{dp\delta }{a_p}{t}^r\right)-\frac{\lambda }{d}\frac{d}{dt}{E}_r\left(-\frac{dp\delta }{a_p}{t}^r\right)\ast w\left(t\right).\hfill \end{array}$$

On the other hand, we have

$$\frac{d}{dt}{E}_r\left(-\frac{dp\delta }{a_p}{t}^r\right)\ast w\left(t\right)=E_r\left(-\frac{dp\delta }{a_p}{t}^r\right)w\left(0\right)-w\left(t\right)+E_r\left(-\frac{dp\delta }{a_p}{t}^r\right)\ast w^{\prime }\left(t\right).$$

This leads to

$$N\left(t\right)=\frac{\lambda }{d}+\frac{H\left(p\right)w\left(0\right)}{a_{p}w\left(t\right)}\left(N\left(0\right)-\frac{\lambda }{d}\right)E_r\left(-\frac{dp\delta }{a_p}{t}^r\right)-\frac{\lambda H\left(p\right)}{d{a}_{p}w\left(t\right)}{E}_r\left(-\frac{dp\delta }{a_p}{t}^r\right)\ast w^{\prime }\left(t\right).$$

(33)

When the weight function is constant, Eq. (33) becomes

$$N\left(t\right)=\frac{\lambda }{d}+\frac{H\left(p\right)w\left(0\right)}{a_{p}w\left(t\right)}\left(N\left(0\right)-\frac{\lambda }{d}\right)E_r\left(-\frac{dp\delta }{a_p}{t}^r\right).$$

(34)

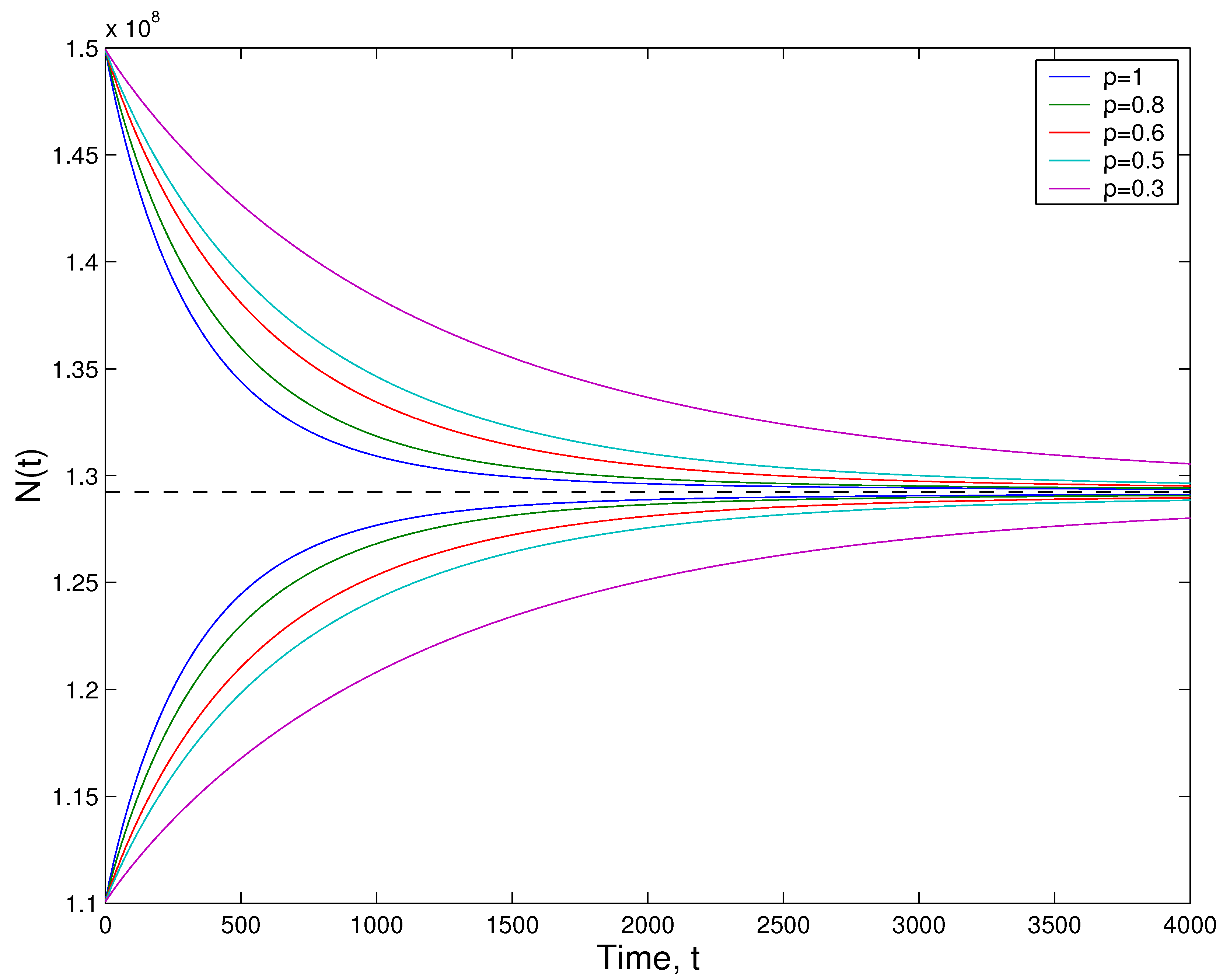
For liver cells also called hepatocytes, $\lambda =5.04\pm 0.71\times {10}^5$ cell/ml/day [23] and $d=0.0039$ day${}^{-1}$ [24]. Figure 1 shows the impact of order p on dynamical behavior of the solutions of (32) with two initial conditions $N\left(0\right)=1.1\times {10}^8$ and $N\left(0\right)=1.5\times {10}^8$ cells/ml, for $\delta =1$ and $r=0.95$.

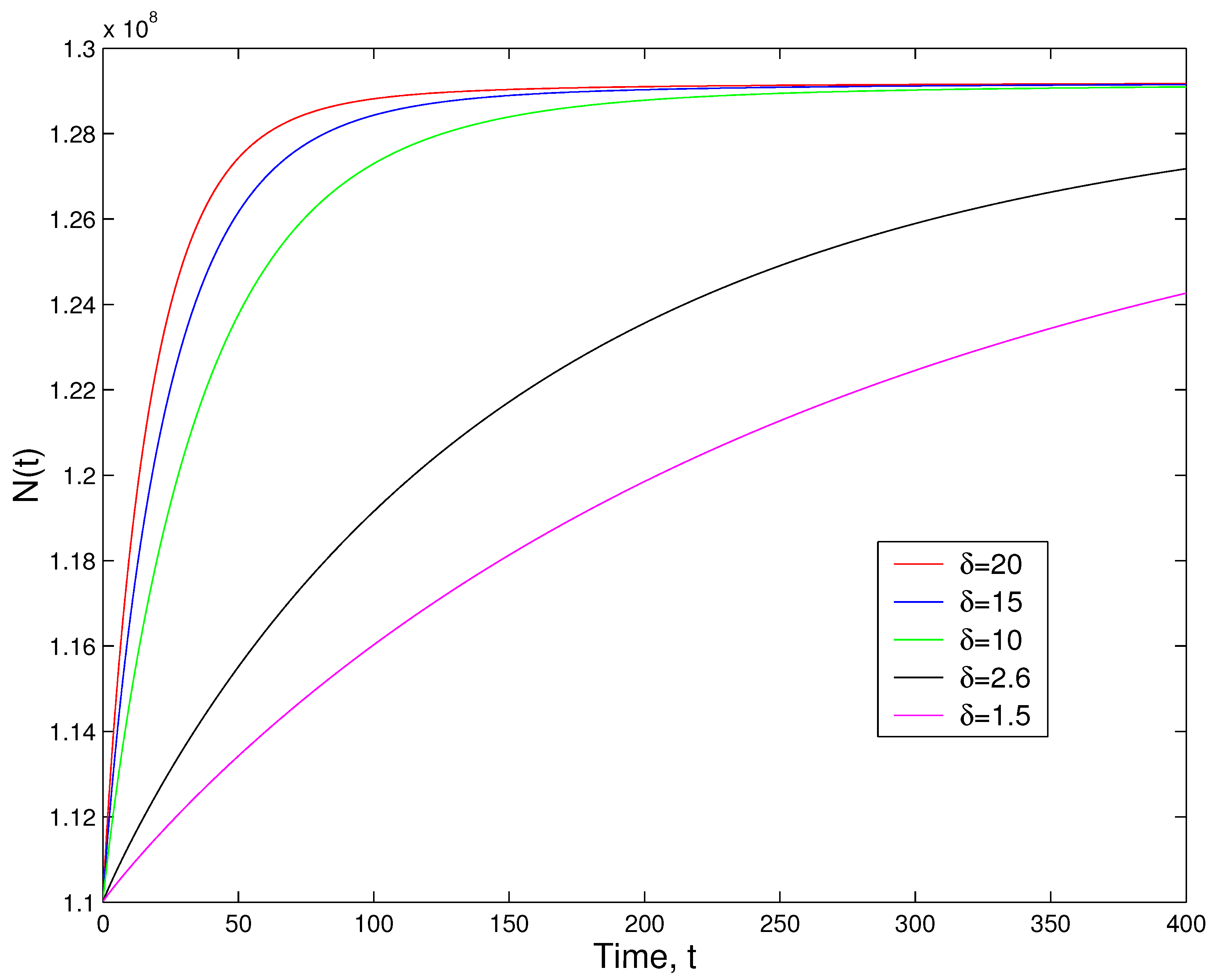
Now, we investigate the impact of the parameter p on the dynamics of (32) with $p=0.8$ and $r=0.95$. Figure 2 demonstrates this impact.