How Long Can the Spiral Arms of Disc Galaxies Be Optically Observed?

1. Introduction

Spiral galaxies are the most fascinating celestial objects in the universe, attracting observers with their rich and ever-changing spiral patterns that radiate a profound sense of beauty. These mesmerizing phenomena can solely be witnessed through optical instruments, with advanced tools like the Hubble Space Telescope and the James Webb Space Telescope enhancing our ability to explore them. Such observations depend entirely on the intensity of light emitted by the stars within these galaxies. Nonetheless, as is the case with all-natural phenomena, spiral arms too follow a unique evolutionary trajectory, with a beginning and an end. This leads us to the intriguing inquiry: how long can we continue to optically observe the spiral arms of galaxies?

This question is closely entwined with the lifespan of the spiral patterns exhibited by disc galaxies, a subject that has been the focus of extensive research in the past. However, the results of these studies have been marked by inconsistency and lack of a definitive conclusion. Sellwood contends that recurrent, short-lived transient spiral patterns are favored [1], while Hao et al. reported that spiral patterns may persist for extended periods [2]. A key challenge lies in the absence of a clear delineation between "long" and "short" in this context. To answer this question with precision, we must gain a deeper understanding of the mechanisms governing the formation and evolution of spiral arms in galaxies, a field that, regrettably, has yet to achieve clarity. Over the years, several hypotheses have been put forth to elucidate the formation of spiral arms, encompassing the Density Wave Theory (DWT) [3,4], the Swing Amplification theory [5], the Manifold theory [6,7,8,9,10], and the author's own proposal, the Rotating Two Arm Sprinkler Emission (ROTASE) theory [11]. Saha and Elmegreen, drawing from N-body simulations, proposed that spiral wave modes might experience slow growth during the initial 1 to 2 billion years and subsequently evolve rapidly, reaching a relatively large amplitude within the next billion years. Following this phase, they maintain a constant pattern speed for an additional 5 billion years [12]. Can the spiral arms be optically observed for a span of 5 billion years after they are fully developed?

Nevertheless, certain fundamental facts about spiral arms can guide us in addressing some facets of this intriguing question:

• Spiral galaxies take on a flat, disc-like shape and rotate about their centers.
• The spiral arms boast significantly higher rates of new star formation when compared to other non-arm regions. These new stars consume hydrogen, increasing the local luminosity and giving rise to the optical visibility of the spiral arms.
• The rotation of the spiral arms occurs independently of the galactic material (such as gases, interstellar dust, and all stars), with the spiral arms rotating as a "rigid body" at a constant angular speed. In contrast, the galactic material orbits the galactic center with a flat differential rotation [14,15].

Given these fundamental insights, we can delve further into the intriguing question at hand.

2. Evolution of Optically Observed Spiral Arms in a Simplified Spiral Galaxy

The galaxy J101652.52, as depicted in Figure 1, serves as an excellent candidate for a model galaxy to explore the question at hand. The left side of Figure 1 presents the original image of the galaxy, showcasing a grand design pattern characterized by luminous, widely open, unblemished, and well-structured spiral arms that exhibit perfect central symmetry.

On the right side of Figure 1, the spiral arm fitting has been executed using the galactic spiral equation derived from the ROTASE model [11]. In this representation, the red and yellow lines correspond to the fittings for the northern and southern arms, respectively, while the orange line designates the galactic bar. Here, R signifies the maximum radius, marking the outermost boundary of the observed spiral arm at the moment, and Rb denotes the radius of the galactic bar, representing half its length. The ratio R/Rb equals 5.2. Notably, the dashed yellow and red lines indicate the potential past positions of the spiral arms about 75° in rotation angle relative to their current orientation.

Evidently, this galaxy undergoes clockwise rotation around its galactic center. A close examination of the original image reveals distinct characteristics: the front side of the spiral arms appears crisp, featuring a well-defined edge, and luminosity diminishes rapidly. Conversely, the rear side displays a pronounced trailing effect, marked by a gradual reduction in luminosity. The trailing effect of this galaxy has been extensively explored in a prior study [11], offering valuable insights into the dynamics and evolution of the system. Remarkably, this model galaxy exclusively exhibits the trailing effect on its rear side. This observation strongly implies that the entire spiral arms rotate at a faster rate than the galactic matter does. New stars exit the spiral arms at the rear side, leading to a luminosity gradient resulting from the aging of these stars and the gradual depletion of available hydrogen within them after their formation. The blue arc labeled as ABCD represents the orbital rotation of the galactic matter around the galactic center.

Within this particular galaxy, it is evident that the spiral arms are firmly tethered to the galactic bar, a pattern that aligns with the majority of observed galaxies. While there are a few exceptions in which the spiral arms appear to disengage from the galactic bars, it's worth noting that, in some of these exceptional cases, further investigation has revealed that the connection between the spiral arms and their respective galactic bars remains intact. Notable examples include galaxies like MCG+00-04-051 and NGC 4548 [11].

This body of evidence allows us to make a reasonably confident assumption: that, as a general rule, spiral arms are bound to their galactic bars, forming a cohesive unit that rotates in unison.

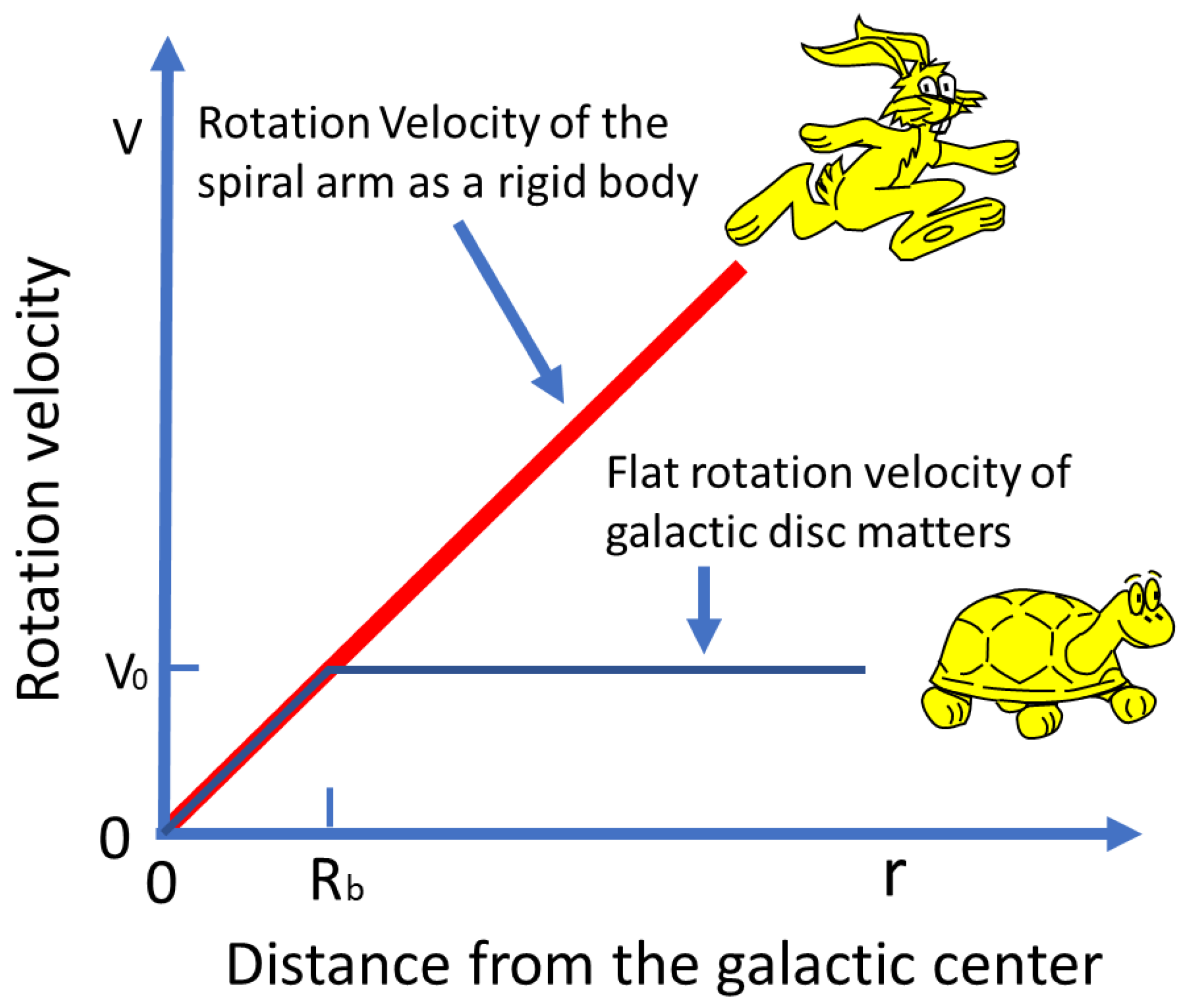
Generally, the rotational velocity of galactic matter exhibits a linear increase with radius when that radius falls within the bounds of the galactic bar. Beyond the galactic bar, the rotation speed remains approximately constant [14,15]. To visualize this, we can examine the orbital rotation velocities of both the spiral arm and the galactic matter, as depicted in Figure 2. The orbital rotation velocity of the spiral arm steadily escalates with radius, ultimately rotating at a considerably higher speed than the galactic matter. To simplify this concept, one can liken these significantly different rotations to the famous fable of the rabbit and the turtle, with the spiral arm rotation akin to the swift rabbit and the galactic matter rotation akin to the steady but slower-moving turtle. Of course, in this new race, the rabbit has learned the lessons from the previous race and will run as hard as he can without stop and nap, and never make any mistakes again.

Despite various proposed models aimed at elucidating the mechanisms behind the formation of spiral arms in galaxies, none of these models have garnered conclusive confirmation. As a result, there is presently no reliable method for describing the evolution of spiral patterns in galaxies. Nevertheless, it is widely acknowledged that spiral arms are regions with markedly higher rates of new star formation than other parts of the galaxy. The formation of new stars hinges on the availability of sufficient hydrogen as raw material. Therefore, we can approach the question posed in the title by considering the availability of hydrogen within galaxies.

In the context of this paper, the illustrations and analysis are rooted in a set of assumptions for an idealized and simplified galaxy model:

• The galaxy is well-isolated from other galaxies. The spiral arms and galactic bar are conjoined and rotate as a unified, rigid body, maintaining a constant angular speed. The orbital rotation velocity increases proportionally with radius.
• Beyond the galactic bar, the galactic matter, which includes stars, interstellar dust, gases, and more, undergoes differential rotation, following a flat rotation velocity. This differential rotation results in these components moving along perfect circular paths without radial movement.
• There is no influx of additional hydrogen from external sources into the galaxy following its initial formation.
• The rate of new star formation in the spiral arms significantly surpasses that in other regions of the galaxy.
• The mechanism responsible for the formation of the spiral arms remains consistent and active throughout the period under consideration.

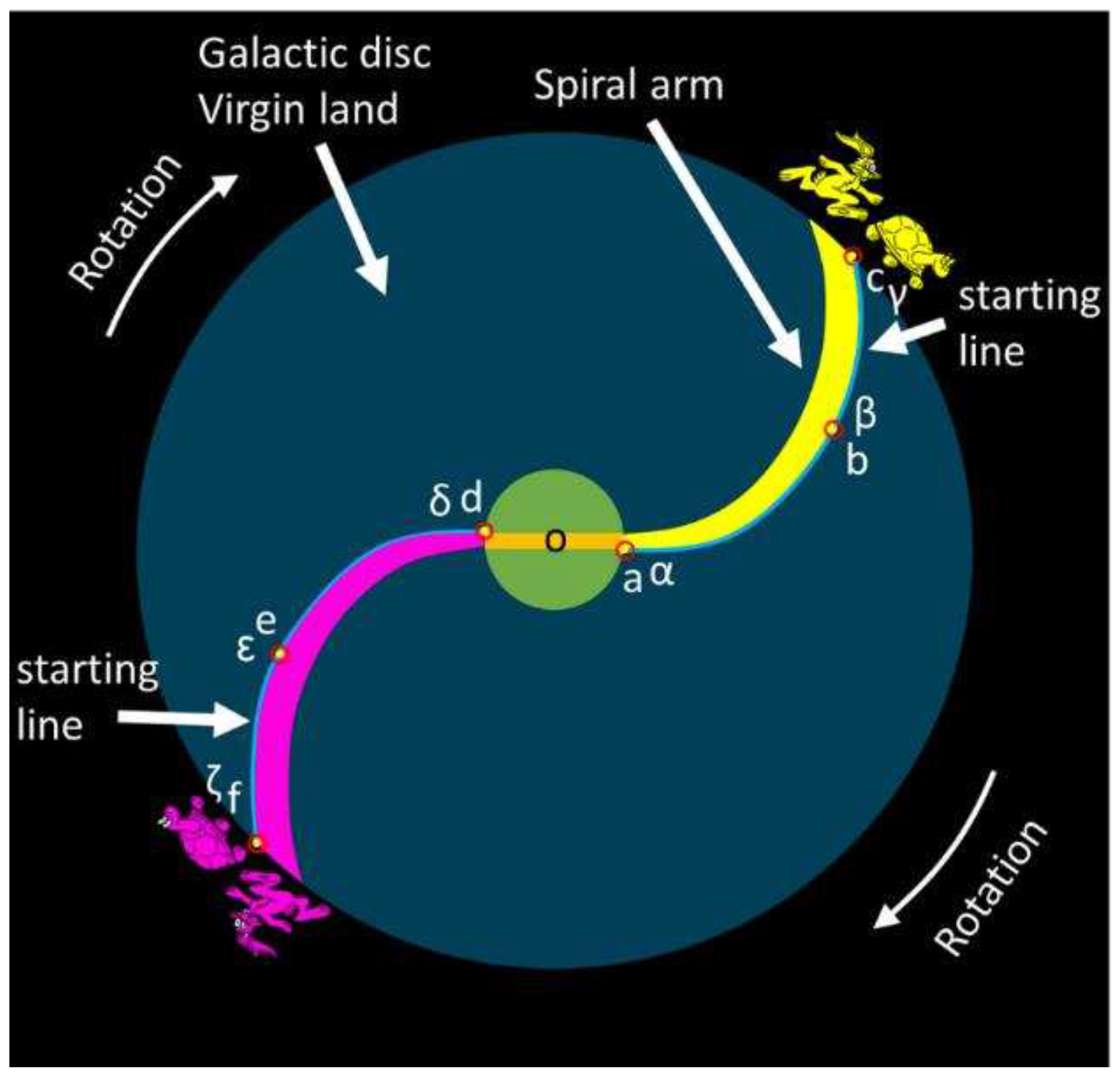
Using the galaxy J101652.52 as the model, Figure 3 depicts an idealized and simplified barred spiral galaxy based on the assumption that the spiral arms are instantaneously formed (neglecting the process of spiral arm formation for the time being). In this depiction, the entire galactic disk is presumed to be replete with hydrogen and other materials necessary for star formation. This region is referred to as the "virgin land."

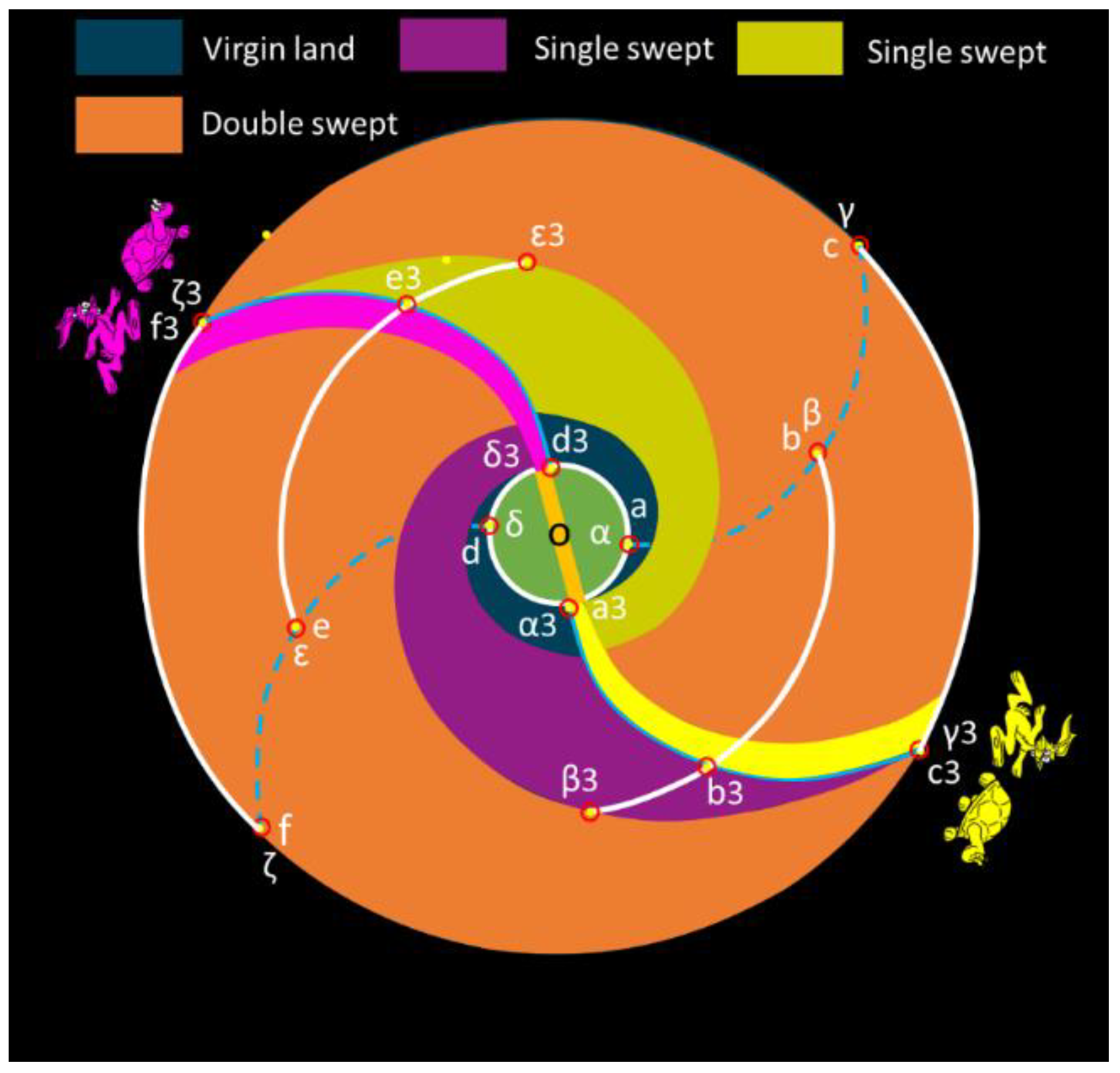
The galactic bar is initially positioned horizontally. The ratio of the outer edge of the galactic disk (R) to the radius of the galactic bar (Rb) stands at 6 (R/Rb = 6). Two spiral arms are represented by yellow and purple colors, respectively. The galaxy rotates in a clockwise direction, and two blue lines at the front side of spiral arms denote the rotational tracking positions of the spiral arms. The letters a, b, c, d, e, and f correspond to tracking points for the spiral arms during their rotation, while the Greek letters α, β, γ, δ, ε, and ζ designate tracking points for the galactic materials throughout the rotation.

At the outset of the rotation, the tracking points of the spiral arms align with the tracking points of the galactic materials, as visually depicted in Figure 3. A yellow rabbit located at point c symbolizes the outer edge of the yellow spiral arm, and a yellow turtle situated at point γ represents the outer boundary of the galactic materials in the disk. This arrangement also applies to the purple spiral arm, represented by a purple rabbit and purple turtle.

Following a 90° rotation of the galactic bar and the spiral arms, the galactic bar assumes a vertical position, as visually depicted in Figure 4. At this juncture, the tracking points for the spiral arms, denoted by a, b, c, d, e, and f, have advanced to positions a1, b1, c, d1, e1, and f1, respectively. Simultaneously, the galactic materials continue their rotation with a flat differential velocity, with tracking points α, β, γ, δ, ε, and ζ moving along white lines to reach positions α1, β1, γ1, δ1, ε1, and ζ1.

Here, it's important to note that the spiral arms rotate at a faster pace than the galactic materials, leading to the arms sweeping through the galactic matter. New stars form as galactic matter enters the spiral arms on their front side and exit the arms on their rear side. This process results in the creation of new stars and contributes to the depletion of available hydrogen and other star-building materials in the areas swept by the spiral arms. These areas are represented by the yellow shadow area, which is swept by the yellow spiral arm and is termed the "single swept area." The same concept applies to the purple shadow area. These shadow regions experience a significant reduction in available hydrogen and other star-building materials.

Due to the substantial difference in rotational velocities, the yellow rabbit is notably distant from the yellow turtle, emphasizing the varying rates of rotation between the spiral arms and the galactic materials. In this scenario, approximately 34% of the total area within the galactic disc constitutes the single swept area, while the remaining 66% of the disc area remains in a state of "virgin land," featuring an abundance of hydrogen and other essential star-building materials.

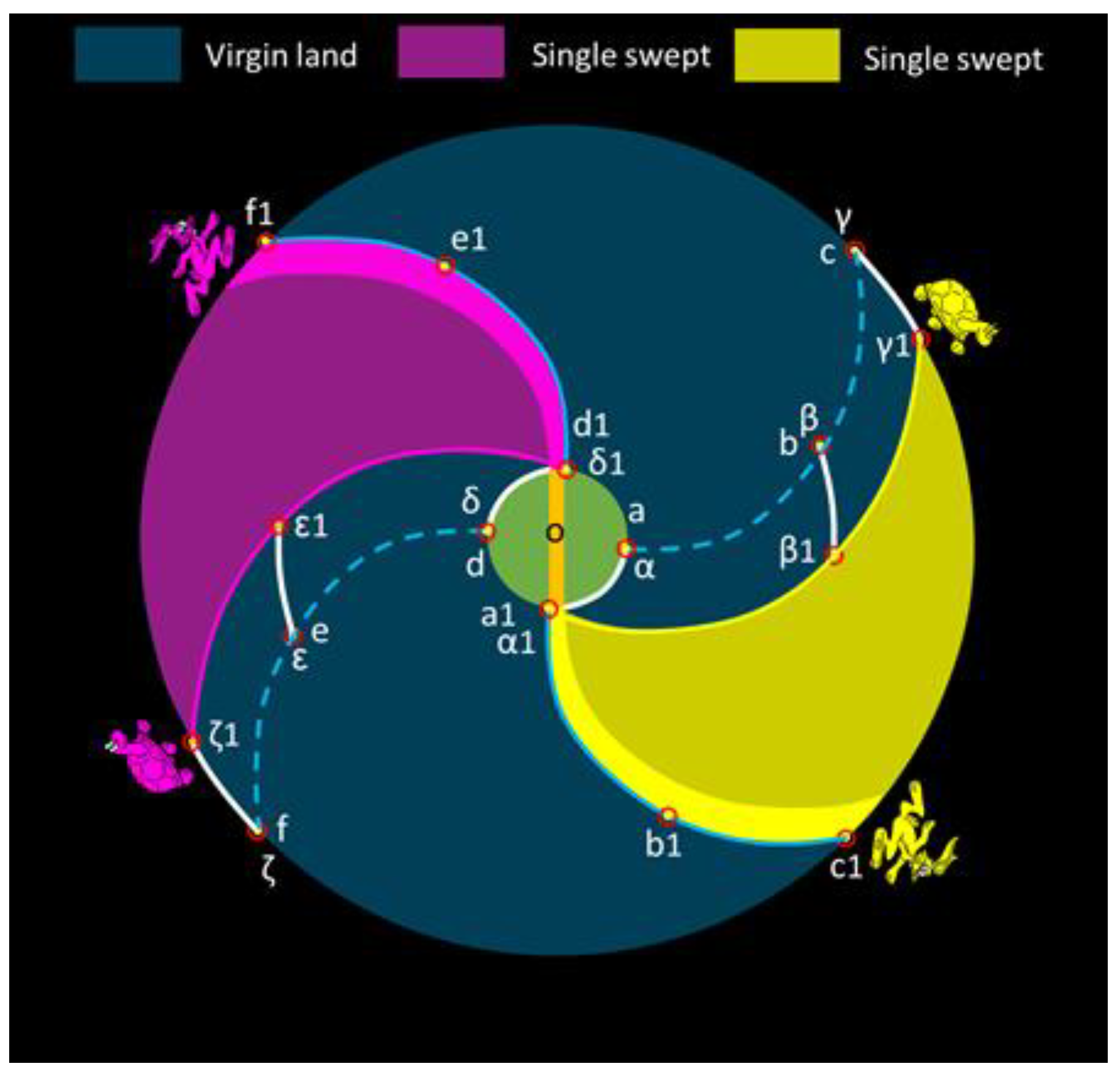
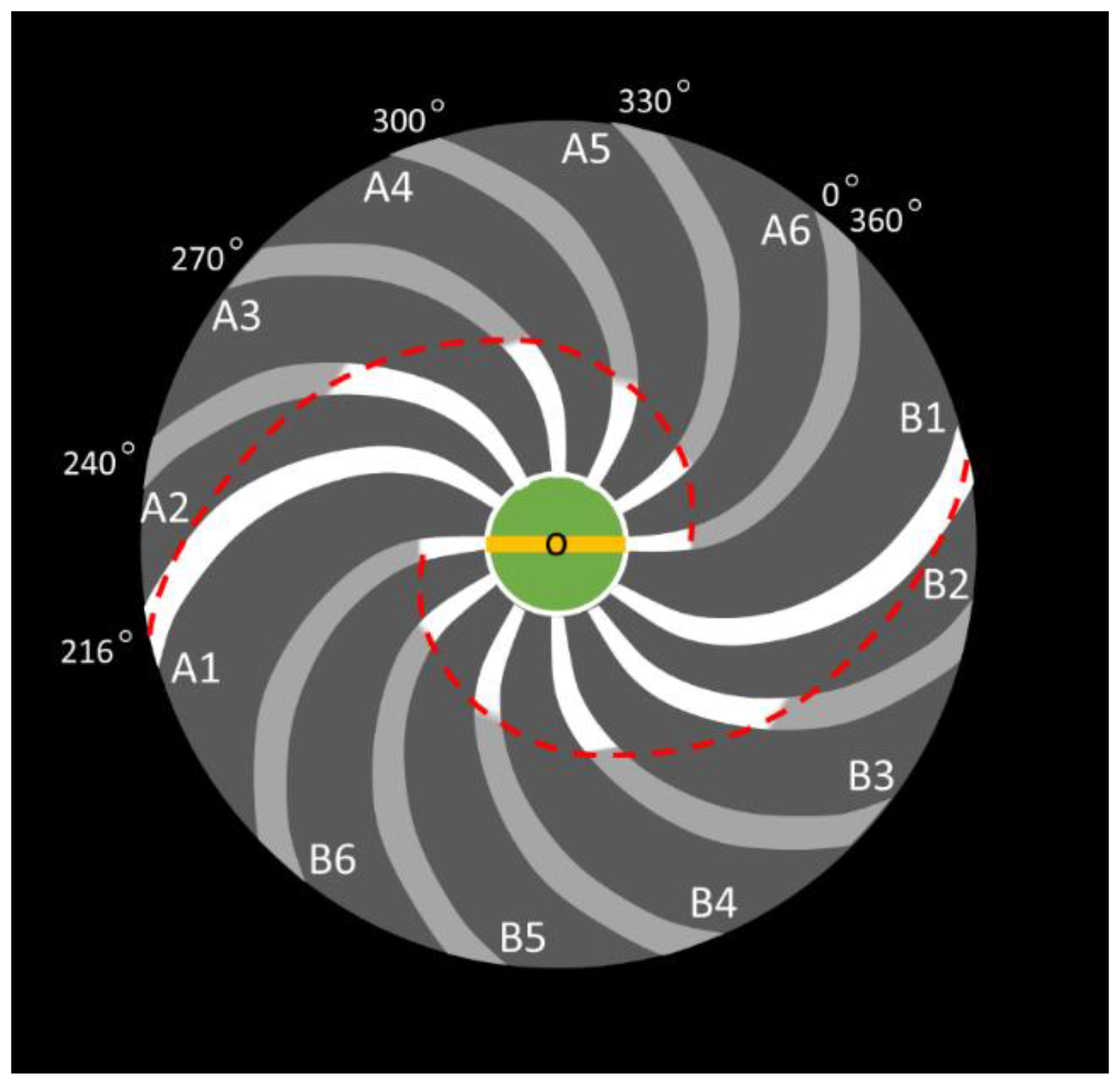
Following an approximately 216° rotation of the galactic bar, a significant development occurs, illustrated in Figure 5. At this point, the yellow rabbit has caught up to the purple turtle, and the purple rabbit has similarly caught up to the yellow turtle. The tracking points for the spiral arms are now positioned at a2, b2, c2, d2, e2, and f2, while the tracking points for the galactic matter have advanced to positions α2, β2, γ2, δ2, ε2, and ζ2.

This particular configuration marks a significant change in the galaxy's dynamics. Around 86% of the total area within the galactic disc has now been subject to a single sweep by the spiral arms, leaving only approximately 14% of the total area in a state of "virgin land." This phase is referred to as a "half loop," denoting the moment when the yellow rabbit catches up with the purple turtle.

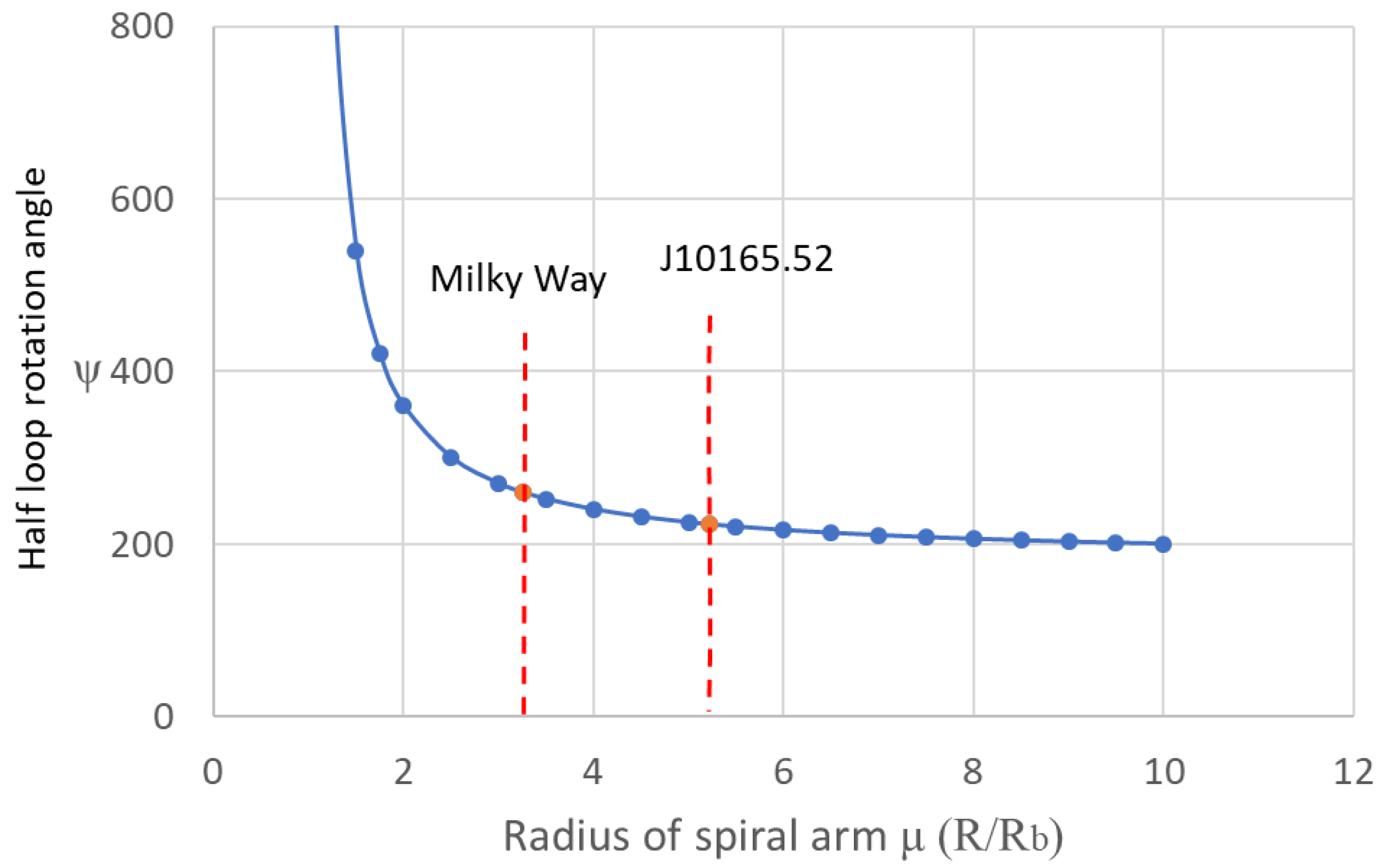
The rotation angle of the 'half loop' is determined by the ratio of the radius of the point of interest on the spiral arm to the radius of the galactic bar. For instance, it requires a greater rotation for point b2 to synchronize with point ε2. The relationship between the rotation angle ψ (in degrees) of the half loop and the radius ratio μ (=R/Rb), defined as the radius (R) of the point of interest relative to the radius (Rb) of the galactic bar, can be described as follows:

$$\psi =180\ast \frac{\mu }{\mu -1}$$

(1)

The variable μ can be regarded as the radius of the point on the spiral arm, measured in units of the galactic bar. Figure 6 illustrates the variation in the half loop rotation angle ψ in relation to μ. Notably, the half loop rotation angles for the Milky Way (μ = 3.6, as determined from the current visual representation of the Milky Way) and the galaxy J10165.52 (μ = 5.2) are also indicated.

Following the "half loop" rotation, the yellow spiral arm proceeds to rotate forward and encounters the previously single-swept purple area. This marks the initiation of the second sweeping or "double sweeping." In the context of the Density Wave Theory (DWT), this phase is associated with the galactic matter entering the spiral wave and undergoing a second compression.

During this double sweeping, the rate of new star formation significantly decreases due to the substantial depletion of available hydrogen and other star-building materials in the previously single-swept area. This decrease occurs under the assumption that no additional hydrogen or star-forming matter enters the galaxy from external sources following the galaxy's initial formation. Consequently, the luminosity of the spiral arm gradually diminishes along the length of the spiral arm toward the bar's end during its continued rotation.

For the sake of clarity and simplification, two levels of brightness are defined in the illustration:

"Full brightness" refers to the brightness of the spiral arm sweeping the virgin land.

"Reduced brightness" represents the brightness of the spiral arm sweeping the single-swept area.

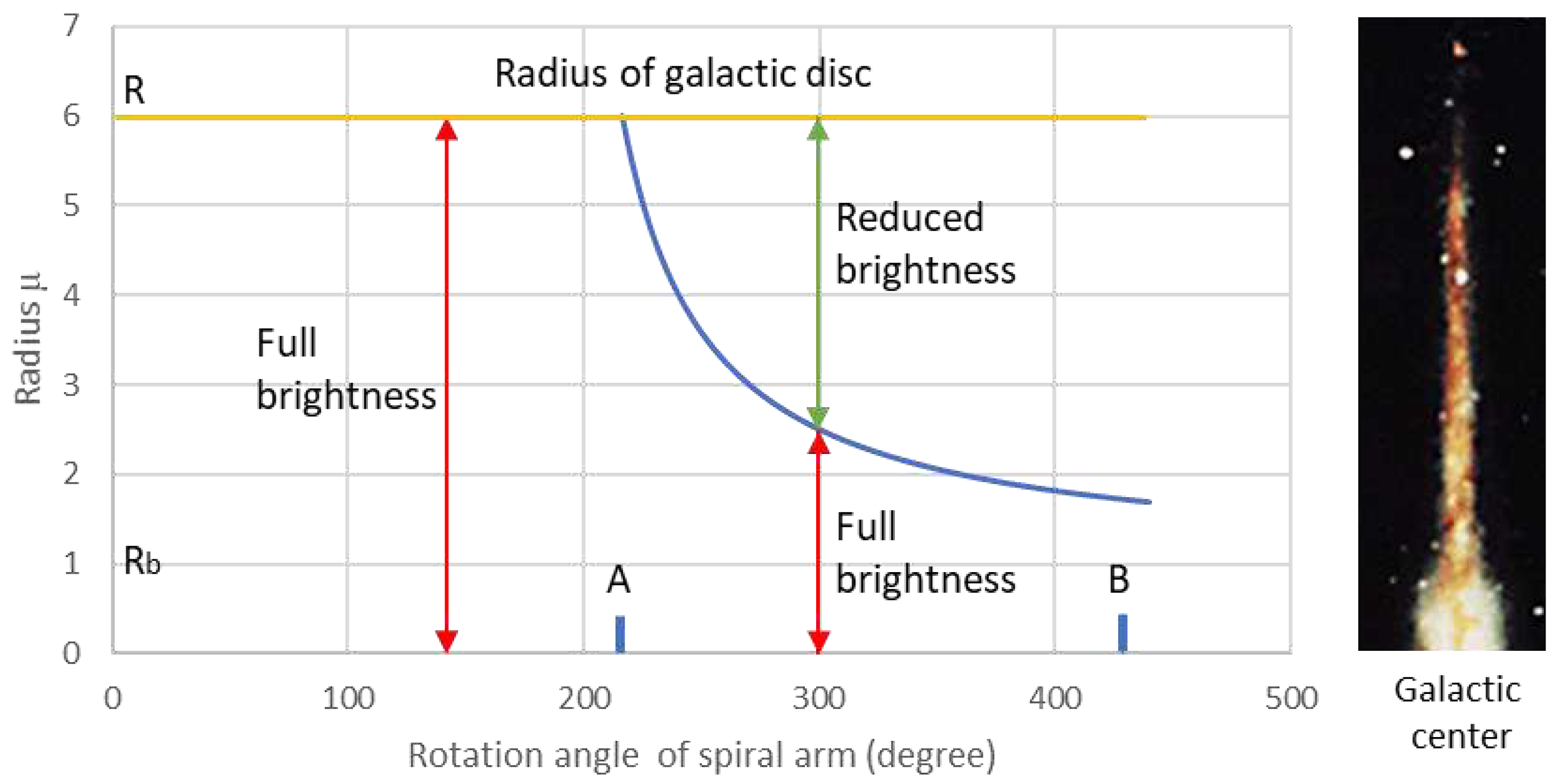
As the spiral arm continues to rotate, the length of the reduced brightness section of the spiral arm progressively increases, while the full brightness section gradually decreases. This transformation is visually depicted in Figure 7. The horizontal orange line in the figure represents the radius of the galactic disc in this model (μ = 6), while the red double-arrow line symbolizes the spiral arm section with full brightness, and the green double-arrow line signifies the spiral arm section with reduced brightness.

On the right side of the image, there is a representation of half of the side view of the Milky Way, illustrating how the thickness and density of the galactic disc gradually decrease with increasing radius. This further adds context to the changes in brightness and star formation within the spiral arms as they sweep through the galactic matter.

In Figure 8, the graphic illustration details the change in the luminosity of the spiral arms as a function of the rotation angle. Let's analyze this in conjunction with the information from Figure 3, Figure 5 and Figure 7 to better understand the depicted sequence.

As per Figure 3, the spiral arms, which were assumed to be "instantly established," commence their clockwise rotation from the 0° position with full brightness which is not shown due to overlap by the later spiral arms of 360°rotation. During this initial phase, the entire length of the spiral arms sweeps through the "virgin area," characterized by an abundance of hydrogen and other star-forming materials. Consequently, the spiral arms radiate at full brightness during this period. This period extends from the starting position at 0° to 216° of rotation, corresponding to the section from 0 to A in Figure 7.

However, after reaching point A (at 216°) in Figure 7, marked as A1 and B1 in Figure 8 for both spiral arms, a pivotal transition occurs. The spiral arms begin to sweep the "single-swept area," where the quantity of available hydrogen and other star-forming materials is significantly diminished.

Consequently, the rate of new star formation in this region undergoes a substantial reduction, resulting in a decrease in the luminosity of the spiral arms due to this "double sweeping." In the meantime, the partial sections of the spiral arms continue to sweep the remaining "virgin land" area, generating spiral arms with full brightness.

As the spiral arms rotate further, the length of the spiral arms with full brightness gradually decreases, following the trajectory indicated by the blue curve in Figure 7. Simultaneously, the length of the spiral arms with reduced brightness steadily increases. To provide some context, if the initial radius of the spiral arms with full brightness at the starting position is set to 6 (as represented by the orange line in Figure 7), then the radius of the spiral arms with full brightness diminishes to 4 at a rotation angle of 240° and decreases to 2.5 at 300°, and so forth. Figure 8 illustrates this phenomenon by displaying how the radius of the full brightness spiral arms decreases with the rotation angle, as indicated by the red dashed curves.

A pertinent question arises: Can we optically observe spiral arms with reduced brightness under normal conditions? To address this, we must consider at least two factors. First, the reduction in the thickness and density of the galactic disc as demonstrated by the Milky Way in Figure 7. Second, in a real galaxy like J101652.52 depicted in Figure 1, the formation of spiral arms is a protracted process during which a substantial amount of hydrogen and other star-forming materials are already depleted. Consequently, it is likely that the spiral arms with reduced brightness are exceedingly faint and may not be observable under standard conditions. They might only become detectable with advanced instruments that operate at longer wavelengths, such as the James Webb Space Telescope.

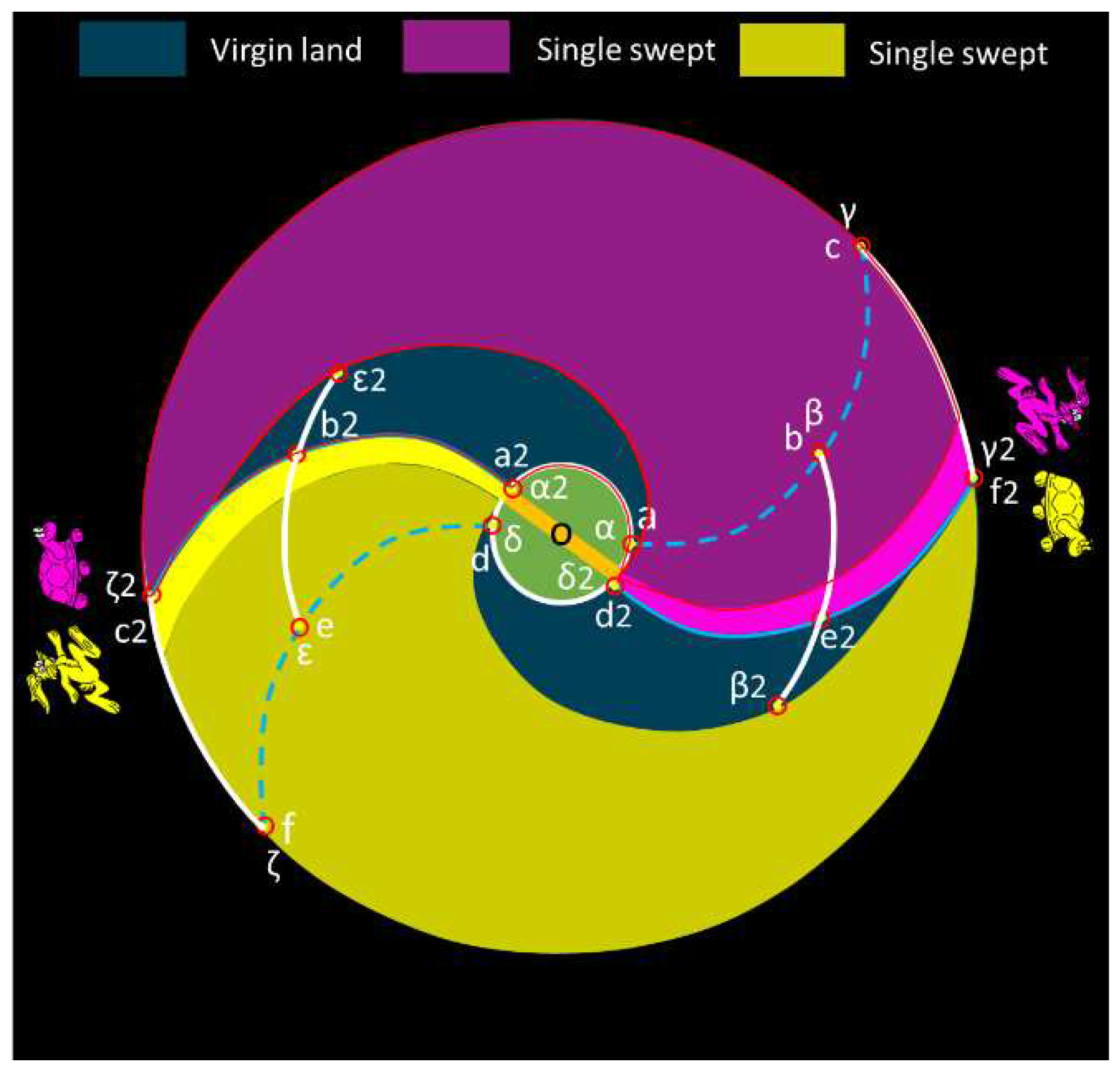
After another half-loop rotation (equivalent to a total of 432°), the yellow rabbit catches up with the yellow turtle, and the purple rabbit catches up with the purple turtle, as illustrated in Figure 9. This occurrence is referred to as a full-loop rotation. Following a full-loop rotation, approximately 78% of the disk area experiences double sweeping—meaning it is swept by both the yellow arm and the purple arm—while about 18% of the disk area undergoes a single sweep. Only about 4% of the disk area remains as the virgin land.

If the spiral arms continue rotating beyond the 432° point, it would initiate a third sweeping or third compression by the Density Wave Theory. Realistically, there may not be sufficient hydrogen available for a significant number of new star formations, rendering the spiral arm not optically observable at normal conditions, even if the mechanism for star formation remains operational. At this stage, the galaxy has used up most of its interstellar star building matter and therefore has very little ongoing star formation. As a result, it consists mainly of aging stars like a lenticular galaxy. N-body simulations conducted by Saha and Elmergreen [12] suggest that two-arm spiral wave modes may endure for approximately 5 billion years, possibly up to 20 rotations in the case of the Milky Way. If spiral arm formation adheres to the DWT, galactic matter remains compressed within the density waves, potentially giving rise to new rocky stars without the requisite hydrogen from the remaining galactic matter. As a result, the galaxy might be deemed "inactive" in terms of new star formation. In other words, the extended persistence of spiral wave modes does not guarantee their optical observability over such prolonged time spans.

The actual conditions of galaxies may differ or deviate significantly from the ideal model presented in Figure 3. For instance, spiral arms, like those observed in the galaxy J101652.52, require a substantial amount of time to grow to their current observed size, as indicated by N-body simulations [12]. This growth process may span approximately 1 billion years, during which a significant portion of hydrogen and other star-forming materials would have been consumed.

For galaxies that align with the simplified galaxy outlined earlier, it can be inferred that the upper limit for observing well-defined spiral patterns may persist for only a period of one to two rotations after the complete development of the spiral arms regardless of any specific mechanism of spiral arm formation. However, a significant shift occurs if additional hydrogen resources are introduced into galaxies during their evolution, either through accretion from the surrounding environment or via galactic mergers. In such scenarios, the situation is drastically altered.

3. Description of a Possible Evolution of the Optically Observed Spiral Arms of the Galaxy J101652.52

Based on the previous illustration, we can derive a plausible scenario for the evolution of optically observable spiral arms in the galaxy J101652.52. To do so, we make the following assumptions:

• The galaxy remains stable with all its physical properties unchanged throughout the period under consideration. This includes no alterations in the size, distribution of matter, orbital rotation, or the mechanism responsible for spiral arm formation. The spiral arms continue to form according to the current mechanism.
• The ratio of the radius R of the outer edge of the galactic disc to the radius Rb of the galactic bar remains constant at 5.2 for this galaxy in the future.

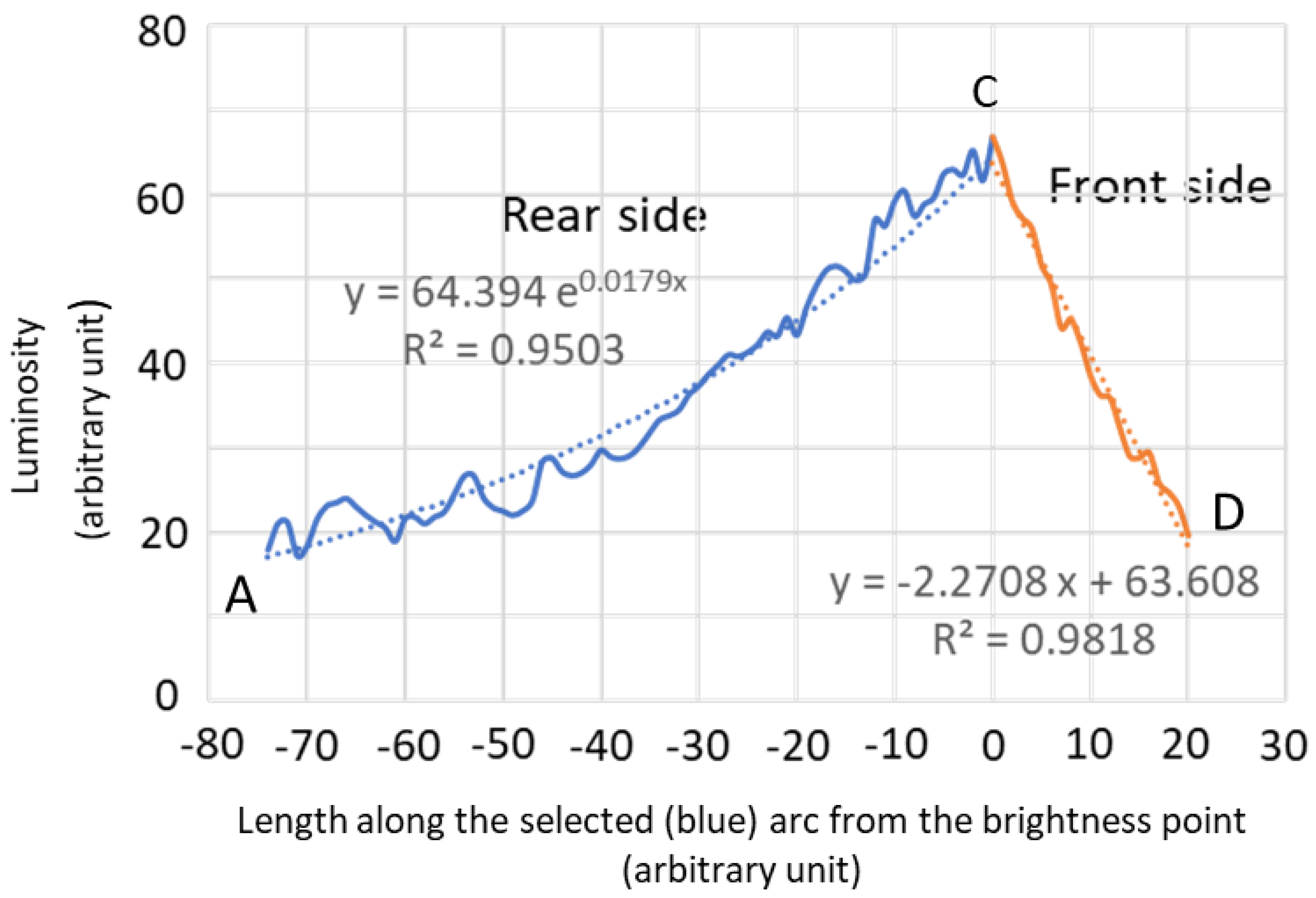
According to the equation (1), the half-loop rotation angle is estimated to be 223° for the galaxy J101652.52. It's worth noting that this galaxy exhibits a strong rear-side trailing effect, as indicated previously [11], suggesting that the entire spiral arms rotate at a faster rate than the galactic matter. Therefore, the series of illustrations presented from Figure 3 to Figure 9 can be applied to describe the evolutionary process for this galaxy. However, in this real galaxy, the spiral arms are not formed instantly and the spiral arms may have already rotated for significant amount of time. The luminosity profile along the blue circular path in Figure 1 right has been previously extracted and visualized in Figure 10.

The blue line extending from point C to point A in Figure 10 visually represents the gradual change in luminosity, from the maximum brightness to the background level, along the blue arc corresponding to the C to A segment in Figure 1 (on the right). To provide some context, in Figure 1, the yellow dashed lines as the point A located at denote the hypothetical positions of the spiral arms about 75° in the past. This suggests that the spiral arms of the galaxy were already in existence at least 75° rotation time ago.

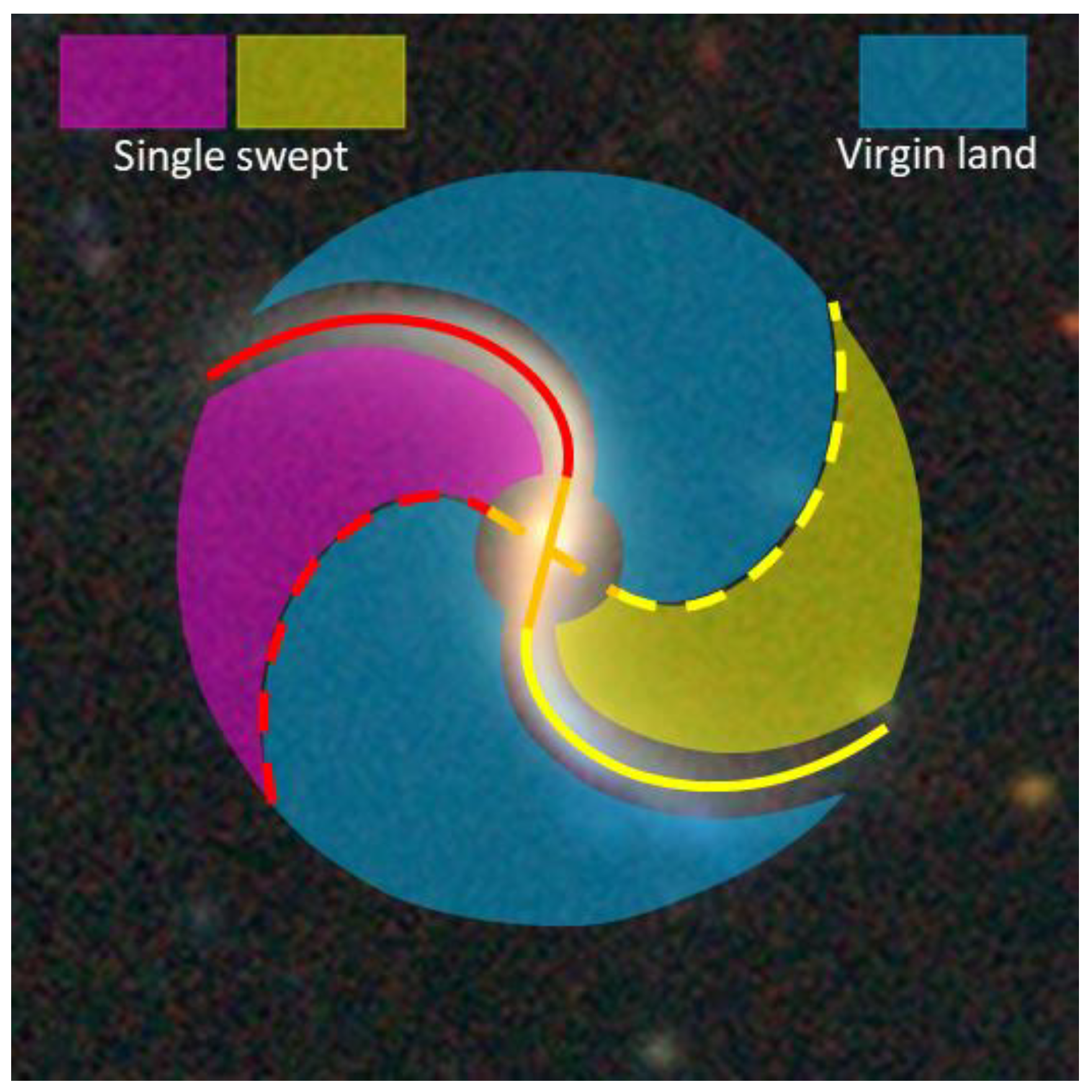
As a result, the shaded regions in purple and yellow, which account for approximately 38% of the total disc area in Figure 11, have undergone at least one sweeping by the spiral arms. The significant reduction in available hydrogens and other star-building materials in these shaded areas is a natural consequence of this sweeping. On the other hand, the unshaded blue regions, constituting around 62% of the total disc area, are assumed to represent virgin land. In other words, they have presumably never been swept by the spiral arms and are presumed to be rich in hydrogens and other materials suitable for star formation.

As the spiral arms continue their rotation and reach approximately 148° into the future (adding this to the 75° from the past for a total of 223°), a significant transition occurs. At this point, the spiral arms commence the process of sweeping through areas that have previously been single-swept, initiating the double sweeping. This phase leads to the division of the spiral arms into two distinct sections:

Outer sections: These parts of the spiral arms will be located in the double-swept regions, where the availability of materials necessary for new star formation, such as hydrogens, is considerably reduced. Consequently, the rate of new star formation in these sections will be significantly lower, leading to a considerable reduction in the luminosity of these areas. In some cases, these outer sections may even become invisible when observed under normal conditions. As the rotation progresses, the length of these sections will gradually increase following the double-arrow green line as shown in Figure 7.

Inner sections: In contrast, the inner sections of the spiral arms continue to sweep through the virgin land, areas rich in hydrogens and other star-building materials. Here, the luminosity remains high, but it gradually decreases as the rotation advances, following the double-arrow red line from Figure 7.

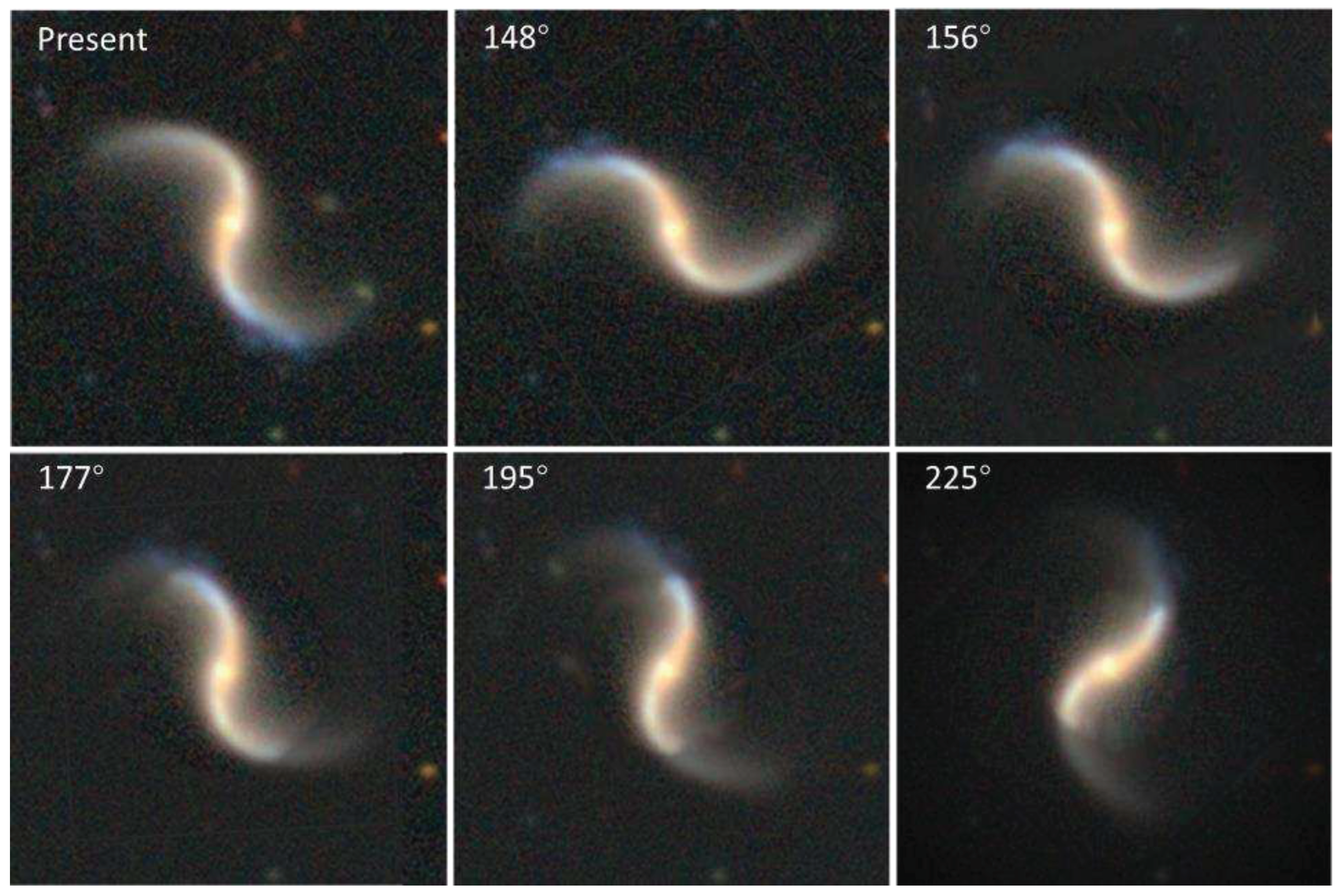
Figure 12 illustrates a potential scenario for the evolution of optically observable spiral arms as the galaxy's rotation continues under the assumptions that the galaxy's properties remain stable, including the unchanged mechanism of spiral arm formation. From approximately 148° to 225° into the future, the portions of the spiral arms that remain optically observable will have been reduced to just 48% of their original radius. This marks a significant transformation in the appearance and characteristics of the spiral arms.

The future possible evolution of the galaxy J101652.52, as depicted in Figure 12, is contingent on the adherence to specific assumptions. The actual evolution of this galaxy in the near future may or may not align with the scenario presented in Figure 12. However, this illustration serves as a valuable reference for predicting its future development under the specified assumptions.

It's important to note that there is no available data regarding the rotation pattern speed of the spiral arms in this galaxy. In the absence of direct measurements, we can use data from our Milky Way as a reference point. In the Milky Way, the spiral pattern rotation period is estimated to be about 245 million years [13]. Assuming that the spiral pattern rotation period of J101652.52 is similar to that of the Milky Way, we can extrapolate that approximately 148 million years later, the radius of the observable spiral pattern in J101652.52 would have decreased to roughly half its current size.

However, a consideration arises regarding the timeline for the development and evolution of the current spiral arms in this galaxy. These spiral arms likely took a substantial amount of time to form from scratch and would have consumed a significant portion of available hydrogens and other star-forming materials during their development. Consequently, the initially assumed "virgin land" as shown in Figure 11 should be significantly smaller. This implies that the optically observed spiral arms would start to shrink much earlier than the 148° rotation mark in the future or may already be shrinking.

The analysis results presented here favor the notion of short-lived spiral patterns due to the gradual decrease of the availability of hydrogens after the formation of well-isolated galaxies. The optically observed spiral arms will start to shrink at the half-loop point. For Milky Way with spiral pattern rotation period of 245 Myr [13] and the half-loop rotation angle 250 ° as a reference, a full-loop rotation only takes about 340 Myr. This is very short time compared to the lifespan of Milky Way which could be formed at about 13.6 billion years ago. Therefore, for the most of the well-isolated spiral galaxies, the beauty of the spirals might be just a blip like the one-time firework show.

4. Possible Winding Problem of the Spiral Arms of Milky Way?

Shen and Zheng's report regarding the Milky Way indicates that the rotation period of the galactic bar falls within the range of 160 to 180 million years [18]. In contrast, the rotation period of the spiral arm pattern is reported to be approximately 220 to 360 million years [16]. This data is adapted by Wikipedia website as of today. Dias et. al. report that the rotation velocity of the spiral arm pattern of Milky Way is roughly 28.2 km/s/kpc or an estimated 245 million years for the spiral arm pattern's rotation period [13]. This data reveals a significant disparity in the rotation periods of the galactic bar and the spiral arm pattern, suggesting a potential winding problem for the spiral arms. Compounding this issue is the fact that over 95% of observed barred galaxies exhibit a clear attachment of the spiral arms to the bar ends.

Despite these findings, when the author reached out to numerous renowned astronomers for insights into this potential winding problem based on the reported data, no satisfactory explanations were provided.

If the spiral arms are indeed bound to the galactic bars and rotate as a rigid body, then one would expect the bar and the spiral arms to have the same rotation periods. Conversely, if the spiral arms are not tightly bound to the galactic bars and instead rotate independently with different rotation pattern speeds, the angle of separation between the spiral arm ends and the bars could vary randomly between 0° and 90° within the galactic disc among all available images of spiral galaxies. For instance, using the Milky Way as an example, where the average rotation period of the galactic bar is reported as 170 million years [18] and the average spiral arm pattern rotation speed stands at 28.2 km/s per kiloparsec, equivalent to a spiral pattern rotation period of 245 million years [13], after the galactic bar has rotated approximately 90 degrees, the spiral arms would have rotated by only about 62°.

Figure 13 showcases the galaxy MCG+00-04-051, also known as SDSS J011430.80+001928.3, which clearly displays a broken connection between the spiral arms and the galactic bar ends. This pattern suggests that the spiral arms and the galactic bars may be rotating independently with different rotation speeds. If this interpretation holds true, it raises questions about the prevalence of such broken connections in barred spiral galaxies, potentially challenging the conventional understanding.

However, it's worth noting that at present, this specific case of broken connection between the spiral arms and bar ends can be explained by the ROTASE model. Future models or research may provide further insights into this phenomenon.

If the spiral arms possess a soft or malleable structure and remain bound to the galactic bar ends during rotation, the winding problem is likely to be a significant concern. The observed disparity in the rotation periods of galactic bars and spiral arm patterns, coupled with the attachment of spiral arms to the bar ends in over 95% of observed barred galaxies, suggests that there may be a complex issue involving the observation accuracy and the reliability of the proposed mechanism for the spiral arm formation.

The potential winding problem presents a fascinating challenge in our understanding of galactic dynamics and the formation of spiral structures within barred galaxies. Researchers continue to investigate and explore the intricate mechanisms that govern these structures to gain a more comprehensive understanding of the processes involved. This exploration may also provide insights into whether there are alternative models or explanations for the observed spiral patterns in barred galaxies.

5. Discussion

The previous illustration offers an upper limit for the duration during which well-developed spiral arms can be optically observed under normal observational conditions in an idealized model of a simplified spiral galaxy, as constrained by five key assumptions. To comprehensively understand the entire spectrum of spiral arm evolution, it is crucial to identify a plausible and reasonable mechanism underlying their formation.

Many images of spiral galaxies showcase spiral structures that not only possess a striking visual beauty but also exhibit a remarkable mathematical simplicity. These spiral patterns can be elegantly described using a single mathematical differential equation (2) with one adjustable parameter, ρ(θ). Here, θ represents the angle of galactic bar rotation, signifying the passage of time from the current position of the galactic bars as time zero. It is important to note that all spiral arms in this framework have formed in the past, and ρ(θ) can exhibit various forms of time dependence.

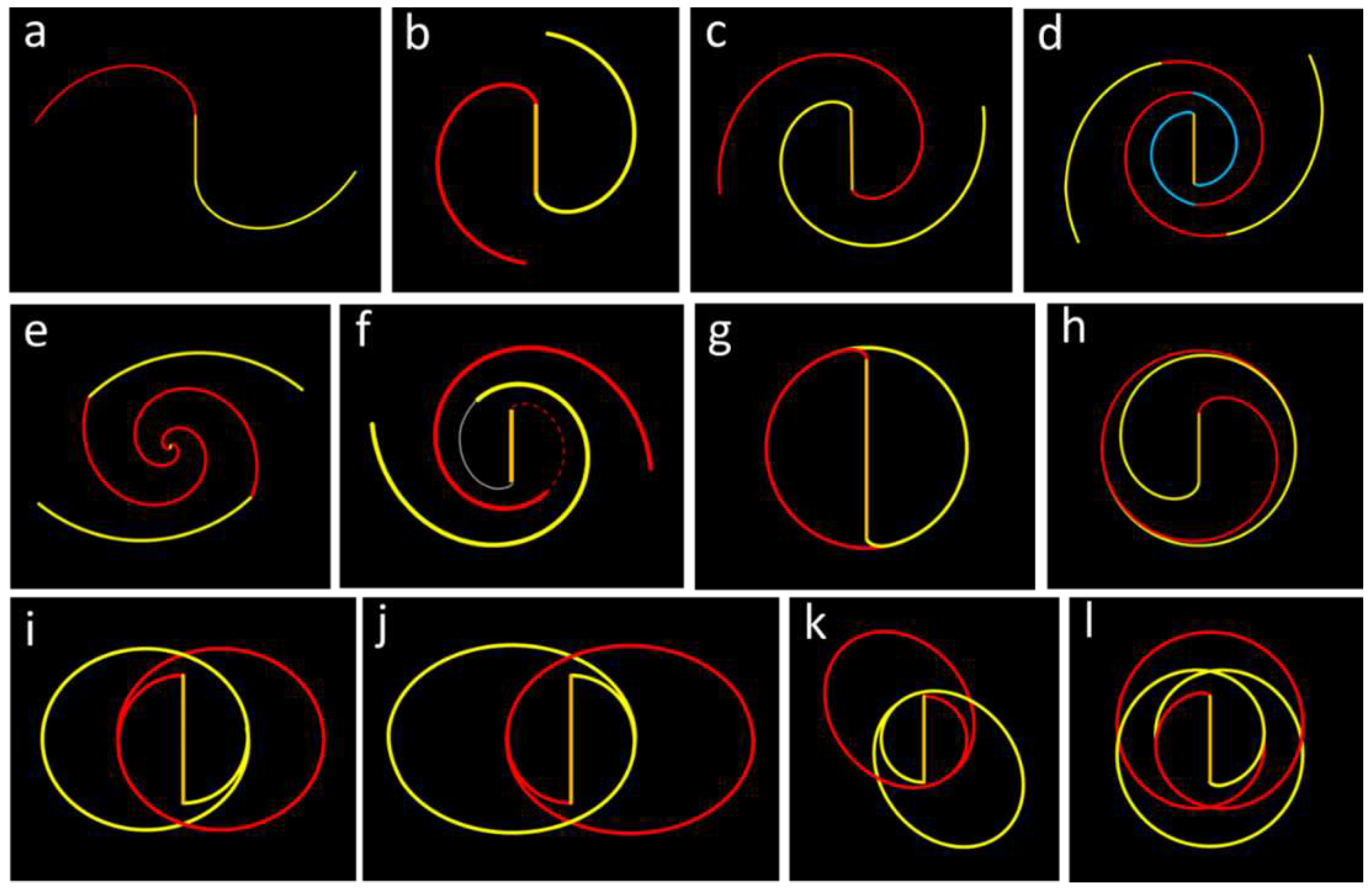
Figure 14 presents 12 face-on spiral patterns fitted to selected spiral galaxies. These patterns are generated using the galactic spiral equation (2) derived from the ROTASE model, omitting the Euler rotation. Each spiral is characterized by a specific parameter, ρ(θ), and listed in previous work [11], various forms of ρ(θ) are detailed, including constants, linear changes with time θ, Gaussian equations, and more. These 12 spirals collectively illustrate a broad spectrum of spiral morphologies observed in actual galaxies, highlighting the diversity of spiral patterns that can be described using this mathematical framework.

$$\left\{\begin{array}{c}dx=R_b\ast \frac{y}{\sqrt{x^2+y^2}} d\theta \\ \\ dy=R_b\ast \left(\rho \left(\theta \right)-\frac{x}{\sqrt{x^2+y^2}} \right) d\theta \end{array}\right.$$

(2)

The general formulas for the ρ(θ) change with time “θ” can be written as:

$$\rho \left(\theta \right)=f\left(\theta \right)\ast exp\left(-k{\left(\theta -{\theta }_0\right)}^2\right)$$

(3)

Figure 14a–f provide a visual overview mathematical spiral curves of galaxies featuring open spiral patterns, showcasing a progression from simple to intricate patterns with k = 0. In Figure 14a, we observe the galaxy J101652.52 with two simple and widely spaced spirals. Figure 14d represents the galaxy UGC 6093, characterized by spirals fitted using three sections, while Figure 14e showcases the renowned galaxy NGC 5194, also known as M51, featuring two-section spirals. Finally, Figure 14f presents the galaxy SDSSJ011430.80+001928.3, which exhibits spiral arms that one arm is still weakly connected to the galactic bar end through the dashed red spiral and the other spiral arm does not connect to the galactic bar end. Despite this, the galaxy displays beautiful, smooth spirals with perfect central symmetry.

Figure 14g–l depict mathematical spiral curves of galaxies with ring structures, ranging from simple to complex, where the parameter ρ(θ) follows a Gaussian equation with different values of k and θ_0, and f(θ) remains constant. Figure 14i showcases the galaxy CGCG-119-82, distinguished by a perfect ring and a robust bar without visible spirals, or its spirals may be too short to be seen. Figure 14i, 14j, and 14k feature 8-shaped double ring patterns with two arm crossings, following the Chain-link crossing style as described in author’s previous work [11]. Lastly, Figure 14l introduces the galaxy NGC 1079 with a double-8-shaped double ring pattern. Remarkably, this complex ring pattern can still be accurately described using the galactic spiral equation (2) as detailed in author’s previous work [11]. Notably, galaxies NGC 3081 and ESO 507-16 share the same double-8-shaped double ring pattern [19,20].

The visual and artistic beauty of these spiral galaxies, coupled with their mathematical elegance, is clearly illustrated. The amazing and intricate patterns observed on a cosmic scale demonstrate the remarkable precision and artistry of the natural world, guided by specific mathematical principles that reflect a superlative engineering design, reminiscent of a divine craftsman. The ROTASE model, while not without its imperfections and potential flaws, demonstrates the feasibility of mathematically describing the majority of spiral galaxies using a single equation with a single parameter. This serves as a reminder that nature often adheres to principles of simplicity, as evidenced by the universality of fundamental equations governing different realms of science and the cosmos. Just as the motion of common objects can be described by Newton's second law of motion with the simplest mathematical equation F = ma in the physics, no matter how complex the motion is; the structures and motions of objects at molecular-level and smaller regions follow Schrödinger's equation; and the properties and motions in the space-time and gravity follow the Einstein’s field equation. Therefore, the universe operates under overarching laws, with mathematics serving as the tool for executing these laws guided by the principle of simplicity.

Currently, the Density Wave Theory (DWT) stands as the leading explanation for spiral arm formation in galaxies. However, an increasing body of evidence has emerged to suggest that DWT may only satisfactorily explain the spiral structure in a fraction of spiral galaxies [21,22]. This observation has led many to contemplate the possibility that diverse spiral structures might originate from distinct mechanisms. However, this notion of "multi-mechanistic" explanations appears to run counter to the inherent principle of simplicity in nature.

Furthermore, DWT lacks the capability to precisely specify how density waves are initiated at the very inception of the spiral arm formation process. Given these limitations and considering the wealth of variations observed in spiral structures, the author posits that all spiral patterns observed in galaxies should be attributed to a single underlying mechanism. This mechanism should possess the flexibility to account for the variations in spiral structures by adjusting specific parameters. The age gradient (or color gradient) of stars, often used as tracers, and other physical phenomena associated with spiral arms are then viewed as side effects or the natural consequences of the spiral arm formation and evolution.

This assertion garners support from the fact that over 95% of spiral galaxies exhibit common characteristics. These shared traits encompass: (1) the well-defined and mathematically predictable nature of spiral arms, which tend to conform to specific mathematical functions when analyzed; (2) the attachment of spiral arms to the ends of galactic bars; (3) the prominent central symmetry displayed by spiral arms; and (4) the gradual decline in quality along the lines of spiral arms, not determined by their distance from the galactic centers. This gradual quality degradation serves as a temporal indicator of spiral arm development, with exemplary cases found in galaxies like UGC 12646 and NGC 4618 [11]. These commonalities strongly suggest that a single, versatile mechanism, operating under varying parameters, underlies the generation of these diverse spiral patterns.

Hence, we should possess a high degree of confidence in the idea that a singular, comprehensive physical mechanism exists which can effectively elucidate the formation and evolution of spiral arms across all spiral galaxies. This mechanism would also offer a straightforward mathematical framework, permitting the uniform description of spiral patterns in all spiral galaxies by adjusting one or a few key parameters. This realization would be akin to a dazzling crown jewel, capable of unlocking many of the universe's enigmatic secrets and profoundly advancing our understanding of galaxies and the cosmos as a whole.

The quest for such a unified physical mechanism would undoubtedly be a thrilling, exhilarating endeavor, comparable in excitement and challenge to the concept of interstellar travel. However, it would also come laden with difficulties and uncertainties. It's important to acknowledge that at this moment, such a physical mechanism remains a conjecture and, realistically, more of a dream. In closing, the wisdom of Isaac Newton's words resonates, "Nature is pleased with simplicity. And nature is no dummy."

6. Summary

The idealized and simplified model of the spiral galaxy presented in this paper, paints a picture of spiral galaxies where the visible spiral arms gradually diminish in length after reaching their maximum extent. This decline initiates at the half-loop rotation point due to a substantial decrease in available hydrogen, and the spiral arms eventually become realistically invisible after a full-loop rotation, the galaxy mainly consists aging stars with very little ongoing star formation, even though the formation mechanism may still remain active for an extended period. In essence, these spiral arms appear to be short-lived relative to the galaxies' lifetimes, suggesting that the process of forming spiral arms may be a unique, one-time event without replenishment of hydrogens.

However, it's important to note that real spiral galaxies may not match all aspects of the simplified ideal galaxy. In actuality, developing spiral arms should consume a significant amount of time, and substantial quantities of hydrogen are expended during this formative period. This could result in the actual duration of observable spiral arms being considerably shorter than what is depicted in the ideal model. Nonetheless, the outcomes of this analysis offer valuable insights into the likely evolution of spiral arms.

It is reasonable to assert that a concise and universal mechanism for spiral arm formation in disk galaxies should exist, capable of describing the process while adjusting one or a few key parameters. This mechanism can provide a comprehensive mathematical framework to consistently depict the various spiral patterns encountered, with some exceptions being explainable within this mechanism. The observational data relating to the spiral pattern speed and the rotational speed of the galactic bar in the Milky Way should be subjected to thorough verification, taking into consideration the potential issue of winding and possible other related issues.