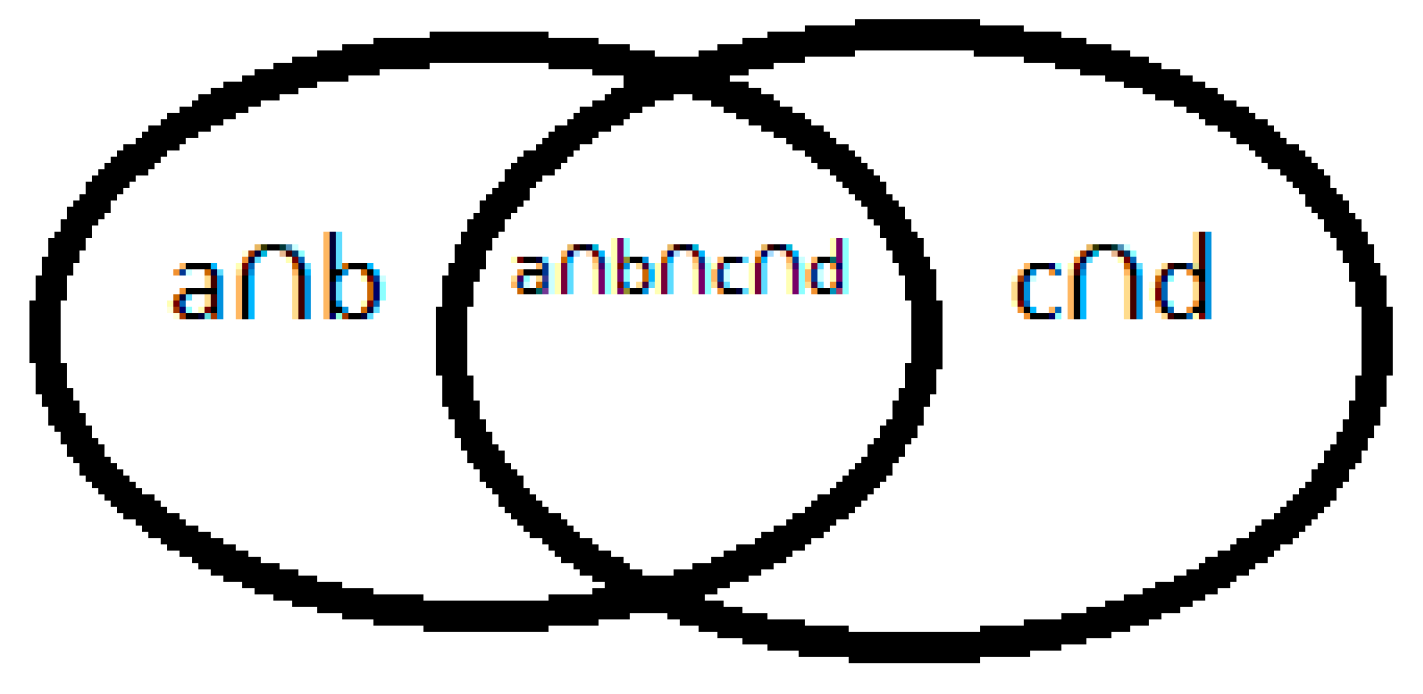Bounded Number Theory: A Study on the Negation of Infinite Numbers in Parts or Completely

1. Introduction

The objective of the theory is the denial that the number is infinite, because to affirm that the numbers are infinite configures an irrational practice, because it disrespects the meaning of the mathematics that involves the characteristics of the physical spaces. Thus, the theory contributes to a better understanding of the progression of numbers, helping in coherent mathematical teaching.

The theory of limited numbers: says that the practice of stating that the number is infinite is wrong, because mathematics has the function of representing elements or facts, that is, it describes the world with rigor and precision. Also, number belongs to physical space, as a physical space is different from other physical spaces due to the difference in properties between them, so there is no infinite element or infinite fact, that is, there is no infinite number. What exists are elements or facts that fill the physical spaces.

To defend that the number is limited, you need to understand two things:

• the meaning of math
• The different physical spaces

Therefore, it is necessary to make an association between the meaning of mathematics and physical spaces. Thus, it is possible to understand that in fact the number belongs to the physical space and therefore the number is limited due to the difference of physical spaces that does not allow any infinite element or infinite fact, only if all physical spaces are equal the number would be infinite.

2. Sense of mathematics

The knowledge of mathematics today is not the same as it was at the beginning of the history of mathematics, because in the trajectory of thousands of years ago there was evolution in the knowledge of mathematics, as well as in the future of thousands of years mathematics will continue to evolve its knowledge, with the objective describing the world with rigor and precision.

The first signs of knowledge of mathematics occurred due to the need to represent elements, giving rise to mathematicsthat emerged in Ancient Egypt and the Babylonian Empire, around 3500 BC.However, in prehistory, human beings already used the concepts of counting and measuring. An example of the first elements to represent were the stones and the sheep, where each stone represented a sheep. An example if there were 15 stones and because there were also 15 sheep, in this case two stones are missing during the count and because there are also two sheep missing. This need to represent the elements in the case of sheep arose with the aim of avoiding losses of sheep, that is, to avoid losses.

The emergence of the representation of elements aims to describe the world with rigor and precision. So many people benefit from math because mathematics makes life easier for everyone, as is the case with the sheep counter who, because of mathematics, did not suffer any harm.

Therefore, based on the meaning of mathematics, it is possible to state that mathematics is related to physical spaces.

3. The use of mathematics in everything

Also, mathematics is used in many things such as probability, which looks at the possibility of an event occurring. The percentage is used to compare quantities, profits, discounts, and losses. Geometry is present in road signs, houses and buildings. The quadratic or 2-degree function is used to calculate projectile launches and motions. In trigonometry it is possible to determine the height of a certain building and measure the distance between the earth and the moon. The proportion has application in decreasing or increasing amounts, an example would be the amount of food. Set theory helps determine the number of respondents and their groups. The exponential function explains radioactive decay, ecological and sociological growth. [3,4,5,6,7]

4. Detailed examples of using math

Example 01: A group of friends made up of 8 people goes to eat at a pizzeria, where they buy 2 pizzas with 8 slices each, that is, 16 slices in total. When the two pizzas arrive, one of the friends tries to arrange for everyone to eat the same amount of slices, so the division calculation was made: if the total is 16 slices and there are 8 people to eat, each person can eat 2 slices equally each .

In this case, the division is calculated so that none of the 8 friends eats more or less than any member of the group, the division arises to maintain equality.

Example 02:in a research has intensely the presence of mathematics in his work. A survey, for example, aims to know the profile of criminality in Brazil, that is, characteristics of criminality. The numbers indicate the reality of crime in Brazil: the poorest regions have more violence, the richest regions have less violence.

In this case, it is up to public policies to act in the poorest regions, through the application of opportunities for people to escape poverty. All this because the numbers present information, and from that it is possible to deduce solutions.

Example 03:Mathematics is strongly linked to health, as numbers indicate information that may be contained in food products or medical tests. The information, through numbers, can tell the ideal amount of consumption or not of this food. In addition, medical tests can diagnose an illness. In that case, numbers can help humanity stay healthy.

Example 04:Numbers can help with person safety by showing limits for people in elevator, boat, plane and car. The limits are known through a study with numbers. In addition, the numbers indicate the speed limit of a means of transport.

Example 05:The existence of commerce depends on mathematics, as the product that commerce sells has a value, but the value can be changed as you seek the ideal profit from the product.

In this case, knowledge of the number is fundamental to know the value of a product, in order to obtain the desired profit.

In general, mathematics is present in everything, that is, in any physical space, because it arose from the need to describe the world with rigor and precision. [6]

5. The various physical spaces

The physical spaces that exist in the world are different from each other, as each physical space has its characteristics that are different from other physical spaces. Example: The volcanic space is different from the characteristics of ice in Antarctica, that is, the temperature of the volcano is between 800 and 1200, while in Antarctica it is -89, in addition to other characteristics that differentiate these spaces. Therefore, the various physical spaces constitute facts or specific elements detached from all physical spaces due to their characteristics. In this sense, there is no infinite fact or element. [4,5]

6. Examples of physical spaces that reinforce the theory

Volcano: it has a high temperature that is between 800 and 1200, so it does not allow elements such as: animals and objects.

Universe: the universe is expanding, and one day it contracts, in this context, the universe is not infinite, because in the future there are new measures due to expansion or contraction, already in contraction there may be the end of the universe.

Sun: in the sun there is no oxygen due to its characteristics, and the sun is not permanent, since the estimated life is about 10 billion years.

Antarctica: has a temperature of -89.9, in this sense, they do not allow many animals adapted to the hot climate.

Water: it interacts with many polar chemicals, but polar ones do not interact with water, such as the relationship between water and oil.

Production of energy: it is not infinite. Since the water, sun and wind that help in energy production are not infinite

Shopping: it is not infinite, because financial crises occur.

To reinforce the understanding of the limited number, let's use coherent imagination (respecting scientific concepts) to represent the real world through an example:

Table 1. imagination of varied physical spaces.

1

2

3

4

5

.....

Source: prepared by the author.

Table 1. imagination of varied physical spaces.

1

2

3

4

5

.....

Source: prepared by the author.

The universe is made up of countless spaces, let's imagine that squares 1, 2, 3, 4, 5... It represents some of the physical spaces that make up the universe, space 1 is the city of Rio de Janeiro, space 2 is the volcano, space 3 is the Amazon, space 4 is Antarctica and space 5 is the city of Belém.

→

stating that the balls in high production can be infinite, this is an error, as it can fill spaces 1, 3, 4 and 5. However, minus space 2 which is the volcano, as the volcano has properties that do not allow such elements.

→

stating that Antarctic animals in high production of new species can have activities in all spaces, this is a mistake, as these animals cannot live, mainly, in spaces 2 and 3.

Set of different elements or facts related to each other, which is a possibility in mathematics, such as: A+B+C+D...... an infinite relationship is not possible, as it does not describe an event in parts capable of facilitating some understanding. A relationship between different elements or facts is only possible when it is possible to represent an event in parts capable of facilitating some understanding. So mathematics tends to the limit.

Observation: according to science, two bodies cannot occupy the same space at the same time.

7. Representation and its relations

CF X → EF X ≠ CF Y → EF Y ∴ ∃ lim

CF X = physical concept x

EF X = element or fact x

CF Y = physical concept y

EF Y = element or fact y

8. The violation of the real world

Science has the function of explaining and describing the natural world, thus stating that the number is infinite for the reason that on paper and pen it is possible to count infinitely in mathematics, it is an inconsistent practice, because on paper and pen it does not take into account the concepts of physical spaces. Also, it should be understood that mathematics and physics are related to each other, so concluding that the number is infinite in pen and paper is a violation of the real world.

EX: The XY element would only be infinite if there were conditions in all the physical spaces to receive the XY element, in addition, the XY element to be infinite must occupy all the physical spaces, in addition, the physical spaces must be infinite. Therefore, the coherent count depends on the element and the physical space.

9. The theory linked to open calculus

The theory of bounded numbers is linked to some open calculations, considering that there are calculations linked to the idea of infinity and, in addition, the presented theory shows that mathematics is related to physical spaces that involve more open calculations. Therefore, bounded number theory helps to solve the open calculus. [1,2]

From the information presented, it is possible to apply the deductive method of science to build a reasoning of the millennium calculations and other open calculations. These are the following deductions:

9.1. Riemann Hypothesis

Riemann's hypothesis was the firstproposedbyBernard Riemann in 1859.

The theory states that the distribution of prime numbers is not random (as it is classified), but may follow a pattern described by an equation called the "Riemann zeta function"Solution:If people generalize by stating that numbers are infinite, then people are mistaken in saying that numbers are infinite because there is no infinite representation of an element or fact in the form of a number example: two apples being divided into two people 2 ÷ 2 an apple each will receive, it is a representation of an element or fact in the form of a number, if there is no way to know if there is a representation of an element or infinite fact in the form of a number there is no way to know it says that the numbers are infinite, given that there are several varied physical spaces. However, attempts may arise to claim that there are infinite elements or facts (all misconceptions), citing an example in the representation of elements:

Example: gases in the atmosphere can be considered infinite

This is a mistake, because the space of the universe has no atmosphere, so it would be correct to say that on planet Earth it is filling this space. It must be taken into account that space can be a limitation of an element or representation in fact, when observing its characteristics that may differ from other spaces.

Another example to reinforce the reasoning:

Example: Infinite Marbles can be filled in all spaces.

Wrong, because marbles don't fill all spaces once, for example: you can't fill a volcano. Given that in volcanic space the characteristics do not allow such objects.

9.2. Birch and swinnerton-dyer conjecture

The Birch and Swinerton-Dyer conjecturewas stated in 1965 and states a condition for a flat algebraic curve, f(x, y) = 0, defined over rationals - thatItis,with arguments x,y∈Q—having infinitely many rational points—thatThat's it, (x,y) solution of f(x,y) =0, with x,y∈Q—as the circumference.

Solution: Both for representing facts and for elements, infinity does not exist, because what exists is a filling of physical spaces, where physical spaces are limited, due to their characteristics that do not allow infinite facts or elements. Therefore, there are no infinite rational points on elliptic curves and no multiple solutions for each congruence.

9.3. Problem n versus Np

OP vs. NP refers to the speed at which a computer can perform a task such as factoring a number. In this task, important in cryptography, the

The objective is to find the set of prime numbers that, when multiplied, produce the same number.

Solution: Subject for explanation: traveler's box

On a long trip, several physical spaces (several taking into account that the properties in another space are different) if travelers have in mind several spaces that vary round trip, so on the round trip the times also vary, due to space-time . Time would be equal to a round trip being in space it does not change due to the interference of factors belonging to space, that is, it is difficult not to vary.

Therefore, P is a subset of NP, but not part of the whole set; so on a round trip there is little variance (because it's a subset) compared to being the traveler who takes the most trips.

The longer the subset travels, the greater the time variance.

9.4. Hodge's Conjecture

Hodge's Conjecture, in algebraic geometry, the claim that for certain "nice" spaces (projective algebraic manifolds), their complicated shapes can be covered (approximated) by a collection of simpler geometric pieces called algebraic cycles.

Solution: By the notion of physical space, it is understood that co-homologated classes that occupy a physical space cannot form geometric objects, as they are already occupied, as they have the same properties.

Non-homologous sets can be subsets of another class if they have some property in common and a different one forming another class.

Set of totally homologous cannot form another class because they have totally equal properties.

Note: Only two millennium calculations were not solved (Yang-mills theory and mass gap hypothesis and Navier-Stokes equations) due to difficulties encountered.

9.5. Beal's Conjecture

If ax+by=cz, where a, b and c arepositive integer andx,y,z≥3, then a,b,c have a common prime factor - meaning that a, b and c are divisible by the same prime number. Solution:

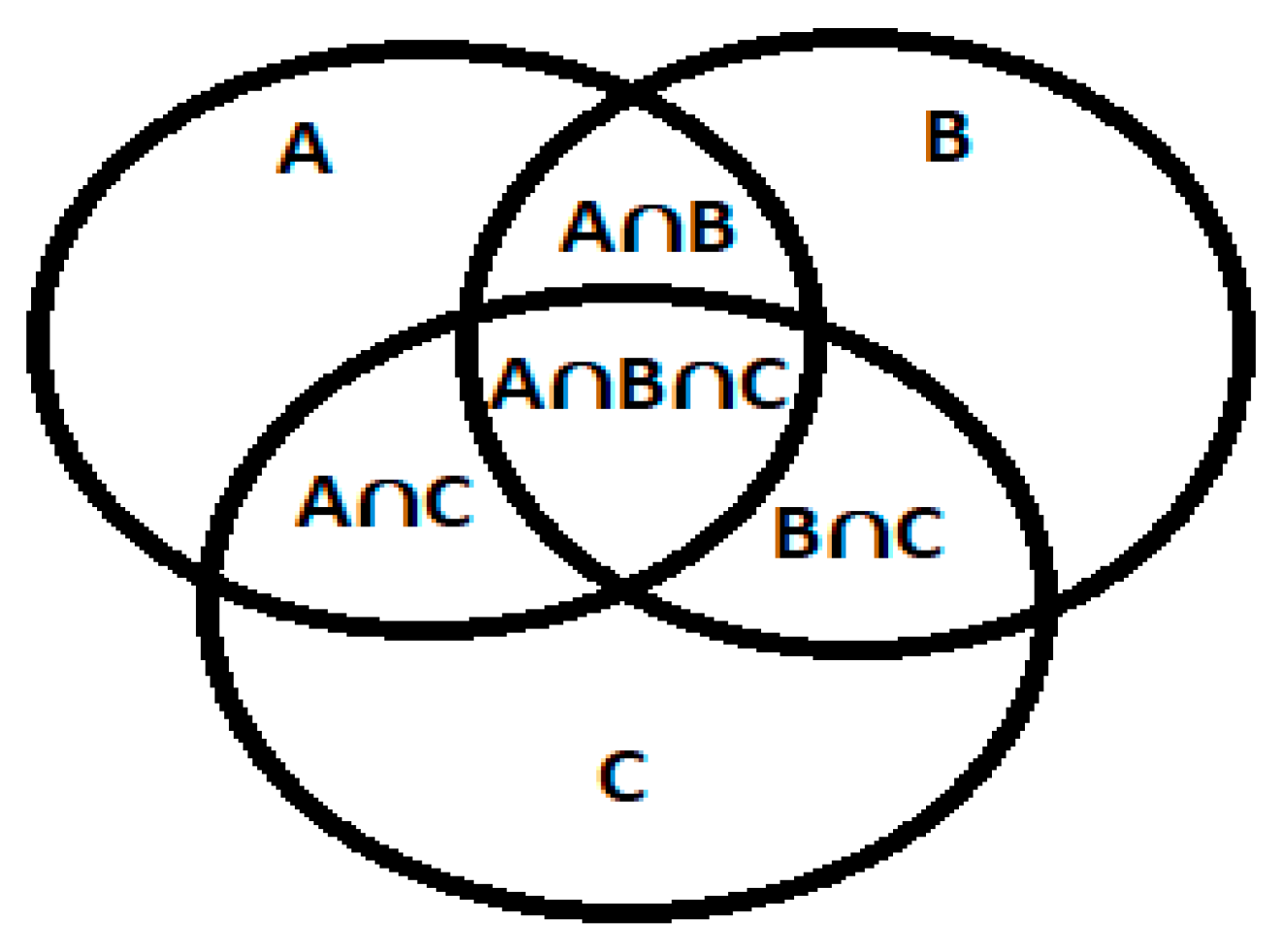
A number x,y,z ≥ 3 is an exponent of ax + by= cz , so A,B and C is a factor of the prime number, due to 3 physical spaces joined together, being able to form 4 new physical spaces: 1 new physical space that has ABC, and other 3 physical spaces that are: AB, AC and BC that were formed by a, b and c. moreover, the space abc in another analysis cannot be formed by origins of 2 sets of divisible parts (even) or 2 odd sets Therefore, from 3 spaces x,y,z ≥ 3 it is possible that the number has prime properties , that is, fractions, but they do not have infinite possibilities due to the theory of bounded numbers (in this case the spaces are different from each other in certain cases).

Figure 1. imagination of the relationship of physical spaces A, B and C. Source: prepared by the author.

Figure 1. imagination of the relationship of physical spaces A, B and C. Source: prepared by the author.

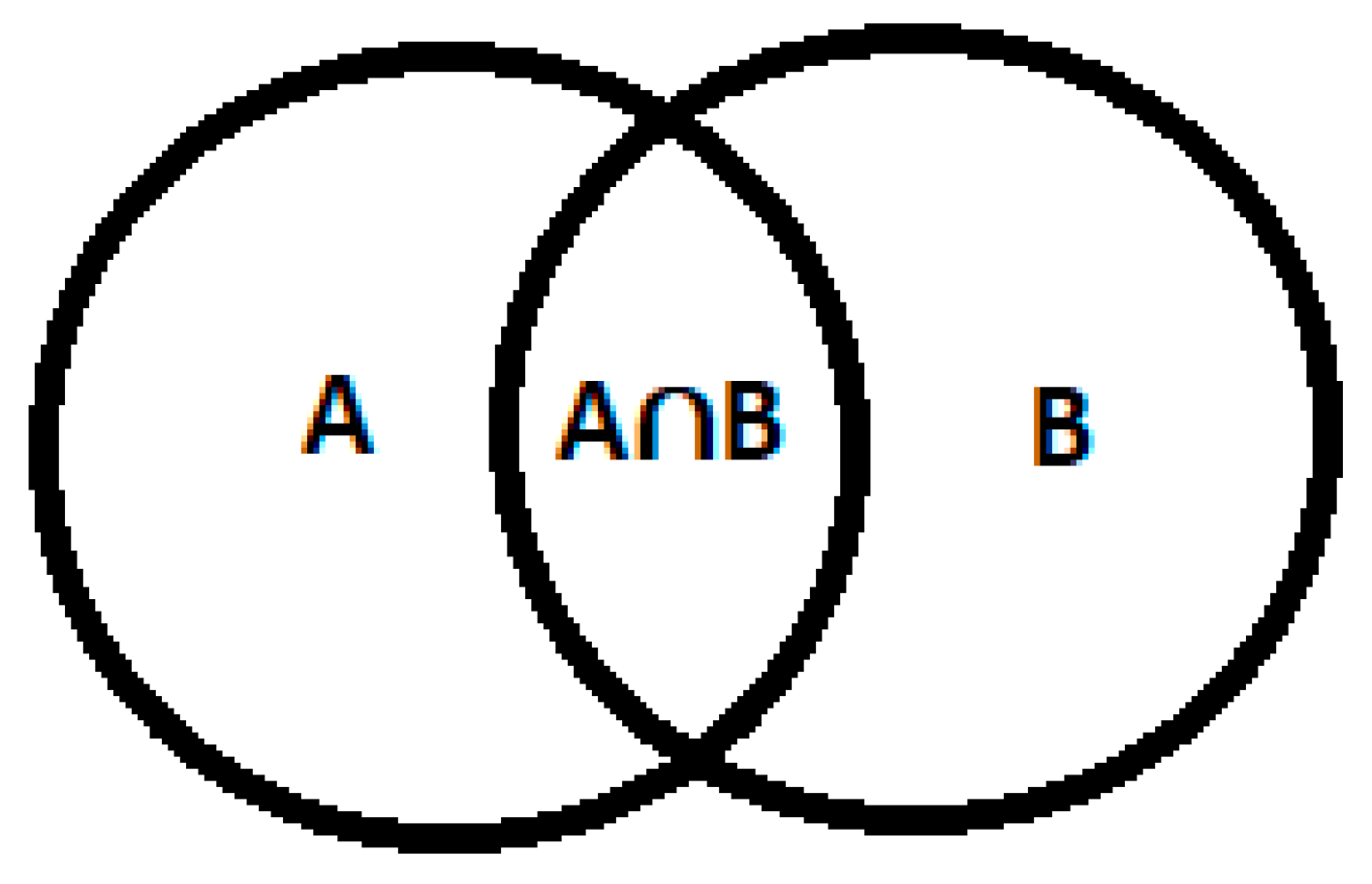
N=2 forms a new physical space AB having A and b in common, forming a single new physical space AB, so A and B are fractionated from a single physical space formed, being possible N=2:

Figure 2. imagination of the relationship between physical spaces A and B. Source: prepared by the author.

Figure 2. imagination of the relationship between physical spaces A and B. Source: prepared by the author.

But it is possible to observe that in an exponent 3 the sums occur in sequence, therefore, there are differences between sums in sequence and simple sums. Thus, depending on the relationship, primary origins or different pairs of simple sums can have origins, because in the sequence sum, more areas can be distributed.

Therefore, the idea of the union relation of the parts provides the best understanding of the explanation of the solution of Beal's conjecture.

9.6. Goldbach's Conjecture

Every even number greater than 2 can be written as the sum of two primes.

Solution:

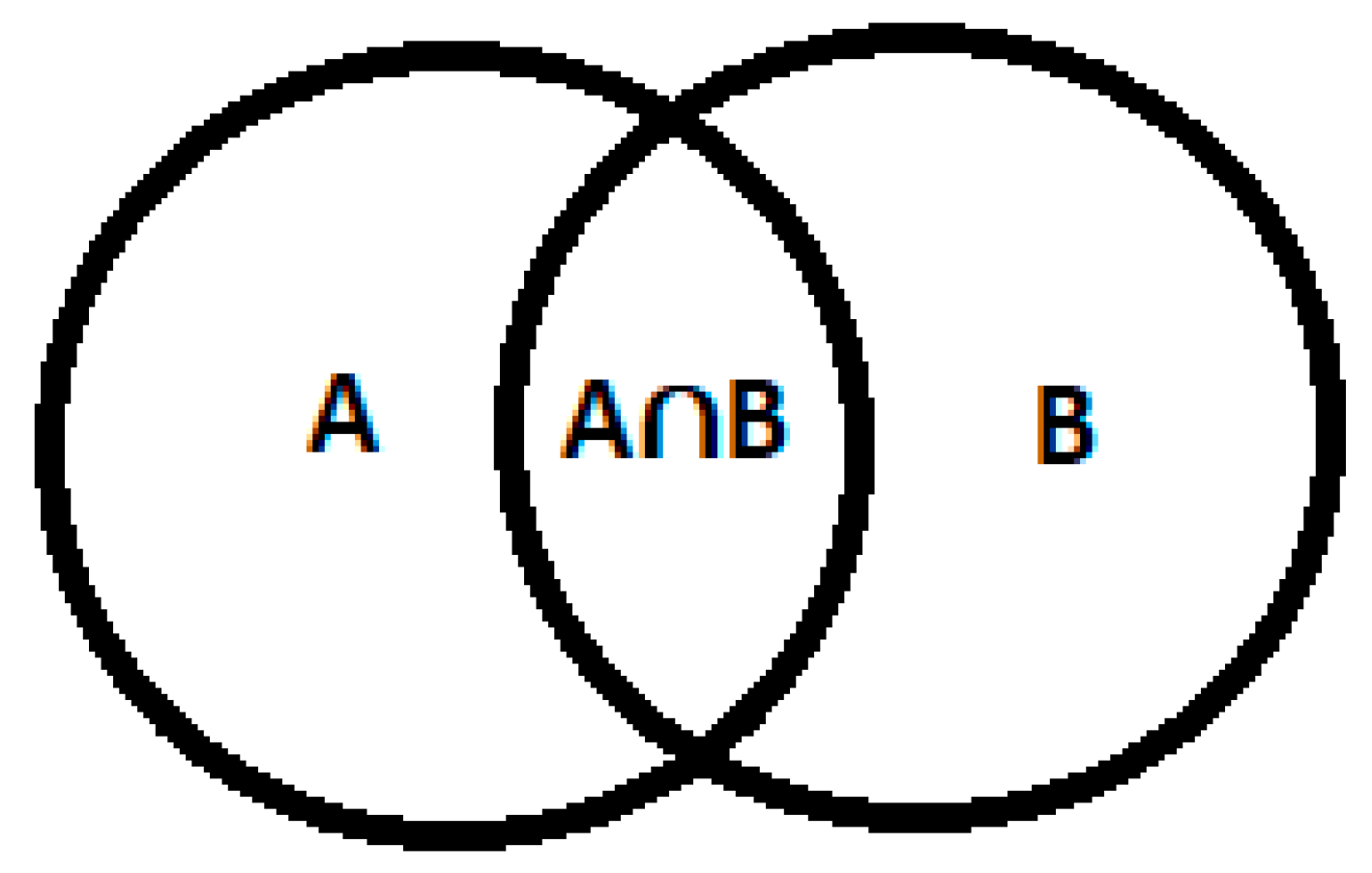
Two fractional numbers iscapable of forming an integer, that is, an even space,because the union of the prime number A with the prime number B occurs, forming an integer, that is, even, butnoinfinite due to the theory of bounded numbers.

Figure 3. imagination of the relationship between physical spaces A and B. Source: prepared by the author.

Figure 3. imagination of the relationship between physical spaces A and B. Source: prepared by the author.

Two even numbers ab and cd are capable of forming a pair greater than abcd and can be divided into parts ab and cd.

Figure 4. imagination of the relationship between the physical spaces ab and cd. Source: prepared by the author.

Figure 4. imagination of the relationship between the physical spaces ab and cd. Source: prepared by the author.

A pair ab and an impac c is capable of forming an impa abc, since abc cannot be divided into parts of two areas, leaving ab on one side and c on the other side.

Figure 5. imagination of the relationship between the physical spaces ab and c. Source: prepared by the author.

Figure 5. imagination of the relationship between the physical spaces ab and c. Source: prepared by the author.

9.7. Fermat-Catalan conjecture

The Fermat-Catalan conjectuream+bn=ck only a finite number of solutions when a,b,carepositive coprime integersem,n,k are positive integers that

¹+1+1<1.

𝑚𝑛𝑘

Solution:

According to the theory of limited numbers, the number is limited due to the difference in physical space between them, the number would only be infinite if all spaces were equal.

Note: the number belongs to physical space as it is in accordance with the meaning of mathematics.

9.8. Conjecture of twin primes

The conjecture of twin primes says that there are infinitely many twin primes, but so far this claim has not been proven or disproved.

Solution:

According to the theory of limited numbers, the number is limited due to differences in physical spaces between them, the number would only be infinite if all spaces were equal.

Note: the number belongs to space as it is in line with the meaning of mathematics.

9.9. Erdos Conjecture

Erdősconjecture about arithmetic progressions was postulated byPaulErdősand is treated in the area of ​​additive combinatorics. It states that if A is a set of positive integers in which the sum of their reciprocals differs, then this set has an arithmetic progression of any size.

Solution:

According to the theory of limited numbers, the number is limited due to differences in physical spaces between them, the number would only be infinite if all spaces were equal.

10. Conclusion

It is worth mentioning, therefore, that mathematics and spaces are related to each other, and from the information presented it is possible to deduce that the numbers are limited.

Since number belongs to space in the form of element or fact, since mathematics aims to describe the world with rigor and precision. Also, the world is made up of multiple physical spaces, so the number is limited as there is no infinite element or fact. The number would only be infinite if there were some element that belongs to all physical spaces or some fact forever.

There are numerous theories that claim that the universe is not eternal, and if the universe is not eternal, therefore, no fact is infinite. On the other hand, there is no existence of infinite elements due to differences in physical spaces, with this, mathematics not having infinite elements or facts, it is possible to confirm the theory of limited number. But if the universe is eternal, certain facts can be infinite, then the theory of bounded numbers is partially correct, as the elements are not infinite due to differences in physical spaces.

It would be unscientific to say that the number is infinite, just because on paper and pen it is possible to count numbers infinitely. In paper and pen it doesn't take into account the physical concepts of spaces, so in fact in paper and pen it can have infinite mathematics, because in paper and pen it is possible to violate the real world.

Through the theory of bounded numbers it is possible to seek a plausible solution for some open calculations.