Prerpints.org logo

You are currently viewing a beta version of our website. If you spot anything unusual, kindly let us know.

Leave Feedback
Preprint
Article

Global Optimization Theories and Techniques for COVID-19

Altmetrics

Downloads

156

Views

50

Comments

0

This version is not peer-reviewed

Preprints on COVID-19 and SARS-CoV-2

Submitted:

26 October 2023

Posted:

27 October 2023

You are already at the latest version

Alerts
Abstract
As the COVID-19 pandemic has caused enormous damage to society, economy and public health security, it is crucial to combat the epidemic and allocate social and health resources effectively. Global optimization algorithms are extensively used in many domains to find optimal solutions to complex problems. Thus, a survey of three typical global optimizations applied on the COVID-19 pandemic is timely. This article is structured into three typical global optimization algorithms - Genetic Algorithm, Particle Swarm Optimization, and Cat Swarm Optimization - and summarizes the framework models and practical applications, as well as other optimization methods that may be applied to COVID-19. Finally, current unresolved challenges and future research opportunities to be explored are summarized.
Keywords: 
Subject: Medicine and Pharmacology  -   Epidemiology and Infectious Diseases

Introduction of COVID-19

COVID-19, short for "Coronavirus Disease 2019," is a highly contagious viral illness caused by the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) [1]. It was first identified in December 2019 in the city of Wuhan, Hubei province, China, and has since evolved into a global pandemic [2]. COVID-19 primarily spreads through respiratory droplets when an infected person coughs, sneezes, or talks, making it easily transmissible from person to person. The symptoms of COVID-19 can vary widely but commonly include fever, cough, shortness of breath, fatigue, and loss of taste or smell. However, there are some individuals which carry the virus remain asymptomatic [3]. However, others can develop severe respiratory problems, leading to pneumonia and potentially life-threatening complications, particularly in older adults and individuals with underlying health conditions [4].
To combat the spread of COVID-19, public health measures such as mask-wearing, social distancing, and frequent handwashing have been recommended. Widespread lockdowns and travel restrictions were also implemented in many countries to reduce transmission rates [5]. Vaccines have played a crucial role in the fight against the virus, with multiple vaccines developed and distributed globally to protect against severe illness and reduce transmission [6]. The COVID-19 pandemic has had profound societal, economic, and public health impacts. It has overwhelmed healthcare systems, caused significant loss of life, and disrupted daily life worldwide [7]. Efforts to control the pandemic have also highlighted the importance of global collaboration and the need for preparedness in the face of future infectious disease threats [8]. As the situation continues to evolve, ongoing research, vaccination campaigns, and public health interventions remain critical in managing and ultimately ending the pandemic.
The remaining paper is organized as follow: Section 2 presents an overview of the methodology of Global Optimization. Sections 3, 4, and 5 detail the application of Genetic Algorithms, Particle Swarm Optimization and Cat Swarm Optimization to the COVID-19 epidemic. In Section 6, we also show others global optimization algorithms. Finally, we summarised the current challenges encountered by global optimization in addressing the COVID-19 pandemic in Section 7. Section 8 concludes and looks to the future of global optimization applied in the COVID-19.

Introduction of Global Optimization

Global optimization is a mathematical and computational approach aimed at finding the best possible solution or outcome in a given problem across the entire feasible solution space. The global optimization method is particularly useful when dealing with complex problems with multiple variables and constraints, where the goal is to identify the global optimum, which represents the absolute best solution, rather than merely a local or suboptimal solution [9].
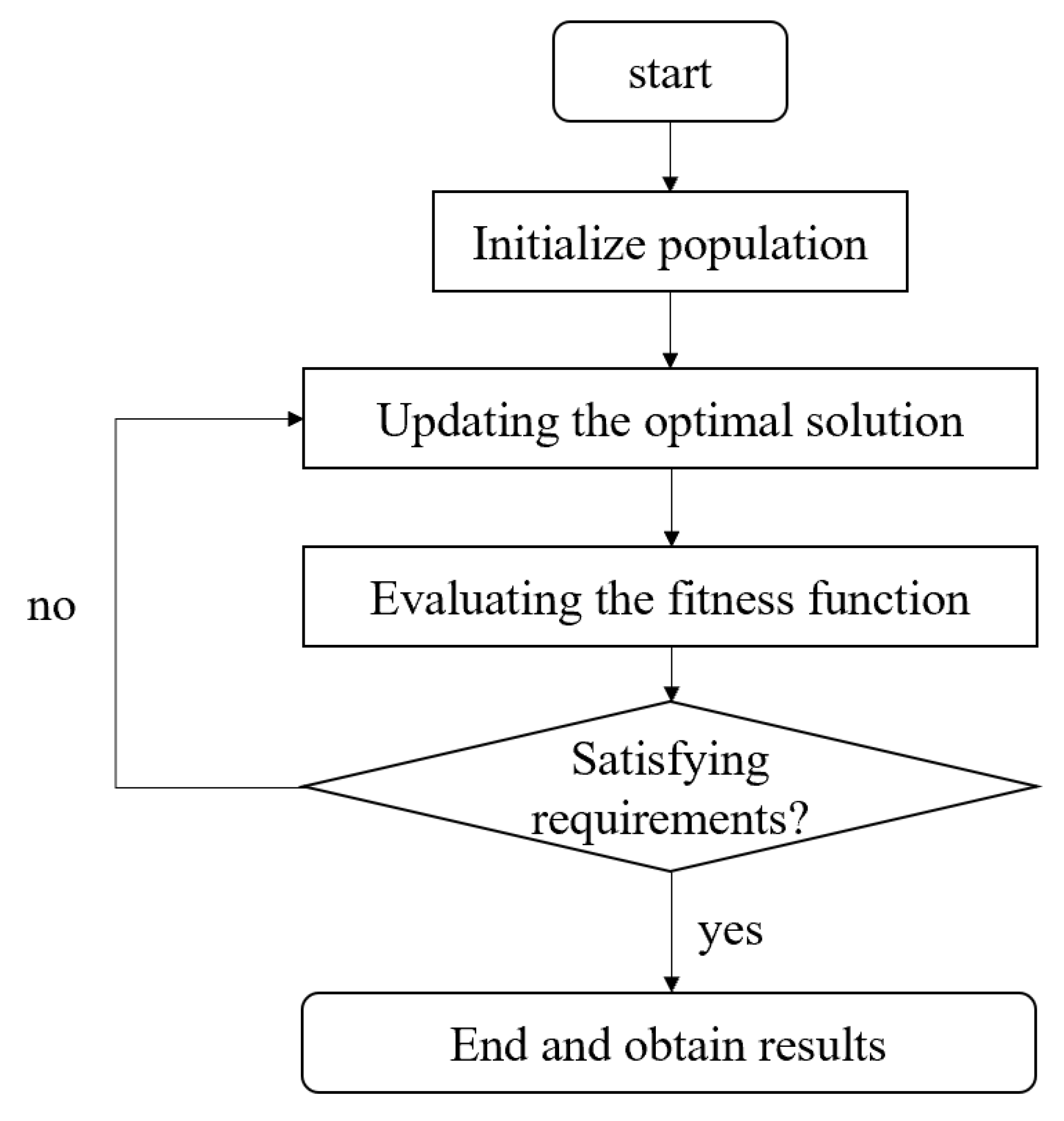
In global optimization, the objective is to minimize or maximize an objective function while satisfying all specified constraints [10]. Figure 1 illustrates how global optimization seeks an optimal solution by iteratively updating the target population on the entire feasible solution space. Global optimization can apply to a wide range of fields and industries, including engineering, finance, machine learning, and scientific research, where finding the best solution can have significant real-world implications [11]. Examples of global optimization problems include finding the most efficient design of a complex structure, optimizing investment portfolios, or discovering the best set of parameters for a machine learning model [12].
One of the main challenges in global optimization is that the objective function may be non-convex, meaning it contains multiple local minima and maxima [13]. Traditional optimization methods, like gradient descent, can get stuck in these local optima and fail to reach the global optimum [14]. To address the issue, global optimization algorithms are designed to explore the entire solution space systematically, often using probabilistic or heuristic techniques to escape local optima and converge towards the global solution [15].
Several global optimization techniques exist, such as genetic algorithms, simulated annealing, particle swarm optimization, and Bayesian optimization [16]. These methods employ various strategies to balance exploration (searching different regions of the solution space) and exploitation (refining the current best solution) to efficiently find the global optimum. Global optimization is a crucial tool in various fields where finding the absolute best solution is essential for improving processes, making informed decisions, and solving complex problems efficiently [17].

Genetic Algorithm for COVID-19

Genetic algorithms (GAs) have been used in various ways to aid in the fight against COVID-19 [18]. While GAs are not a direct treatment or cure for the virus, they are a powerful computational tool that can assist in several aspects of pandemic management and research.
We define the operation of crossover, mutation, and selection on all individuals in a population as SGA. The following equation is a formal representation of the genetic algorithm:
S G A = C , E , P 0 , M , ∅ , Γ , ψ , T
where
C : individual’s coding mode
E : individual’s fitness function
P 0 : initial population
M : the size of the population
ϕ : selection operator
Γ : crossover operator
ψ : mutation operator
T : genetic algorithm termination conditions
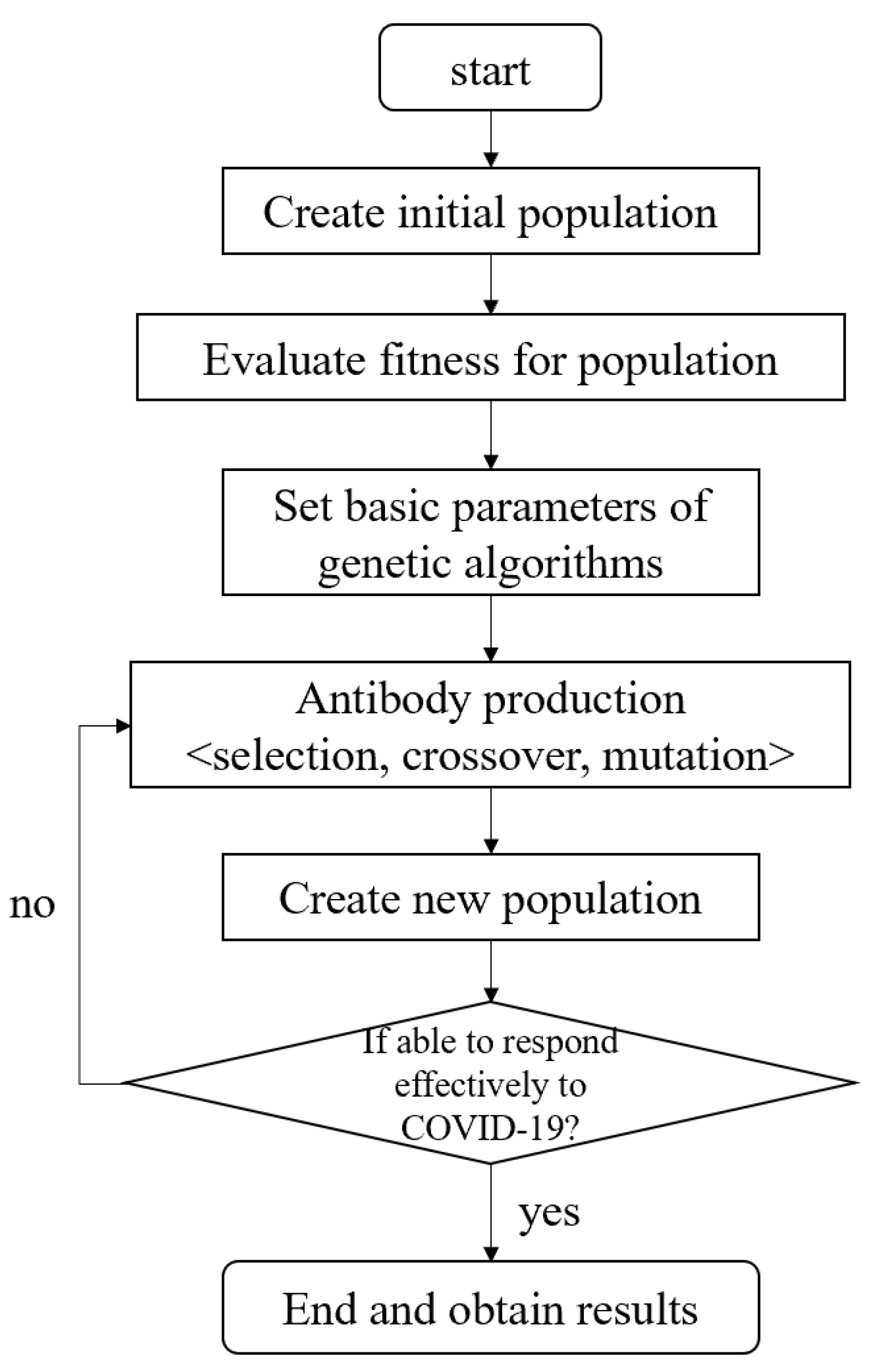
Genetic algorithms can be applied to vaccine development by optimizing the selection of antigens or epitopes for vaccine candidates [19,20]. Figure 2 depicts the application of the genetic algorithms to screening epitopes for COVID-19 vaccine. GAs can explore a vast space of possible combinations to identify the most immunogenic and effective components for a COVID-19 vaccine. GAs accelerates the vaccine development process by narrowing down potential candidates and optimizing their effectiveness.
GAs can assist in drug discovery by optimizing the molecular structures of potential antiviral compounds [21]. Researchers use GAs to explore and evolve chemical structures that have a higher probability of inhibiting the virus's replication or reducing its virulence. The approach can lead to the discovery of novel therapeutic agents to treat COVID-19.
Genetic algorithms can be employed in epidemiological models to optimize parameters and predict disease spread more accurately [22]. By fine-tuning model parameters through GA-based optimization, researchers can develop more reliable models to guide public health interventions, such as social distancing measures or vaccination strategies.
During the pandemic, optimizing the allocation of healthcare resources, such as ventilators, hospital beds, and medical personnel, has been crucial. Genetic algorithms can help in optimizing resource allocation by considering factors such as demand, capacity constraints, and geographical distribution, ensuring that resources are allocated efficiently and effectively [23].
GAs can assist in optimizing contact tracing efforts by identifying high-risk individuals or locations in disease transmission networks [24]. By analysing contact data and evolving network structures through genetic algorithms, public health authorities can prioritize contact tracing efforts where they are most likely to be effective in controlling the virus's spread.

Particle Swarm Optimization for COVID-19

Particle Swarm Optimization (PSO) is a computational optimization technique inspired by the social behavior of birds and fish [25]. While PSO itself is not a direct solution for addressing COVID-19, it can be applied in several ways to assist in managing the pandemic more effectively [26]:
At each iteration t , the i th particle is represented by a vector x i t in multidimensional space to characterize its position. The vector v i t is used to characterize its velocity. Suppose that each particle has two attributes, we define the velocity attribute as V i t = ( v i , 1 t , v i , 2 t , … , v i , D t ) ,the position attribute as X i t = ( x i , 1 t , x i , 2 t , … , x i , D t ) .The following equation represents the update of particle velocity in the particle swarm algorithm:
V i , d t + 1 = W v i , d t + r 1 C 1 P i , d t − X i , d t + r 2 C 2 G i , d t − X i , d t ,
where
C 1 : the cognitive parameter
C 2 : the social parameter
W : inertia factor
D: spatial dimensions of problem
r 1 , r 2 : uniformly distributed random numbers in [0, 1]
There is a threshold for every velocity vector, and we define the maximum of velocity as MaxV. The following equation represents the update of particle position in the particle swarm algorithm:
X i , d t + 1 = x i , d t + v i , d t + 1 .
PSO can be used to optimize the molecular structures of potential antiviral compounds [27]. By simulating particles representing chemical structures and evolving them through iterations, PSO helps identify promising drug candidates for COVID-19 treatment. The approach accelerates the drug discovery process by systematically exploring the chemical space to find compounds with higher efficacy and lower toxicity.
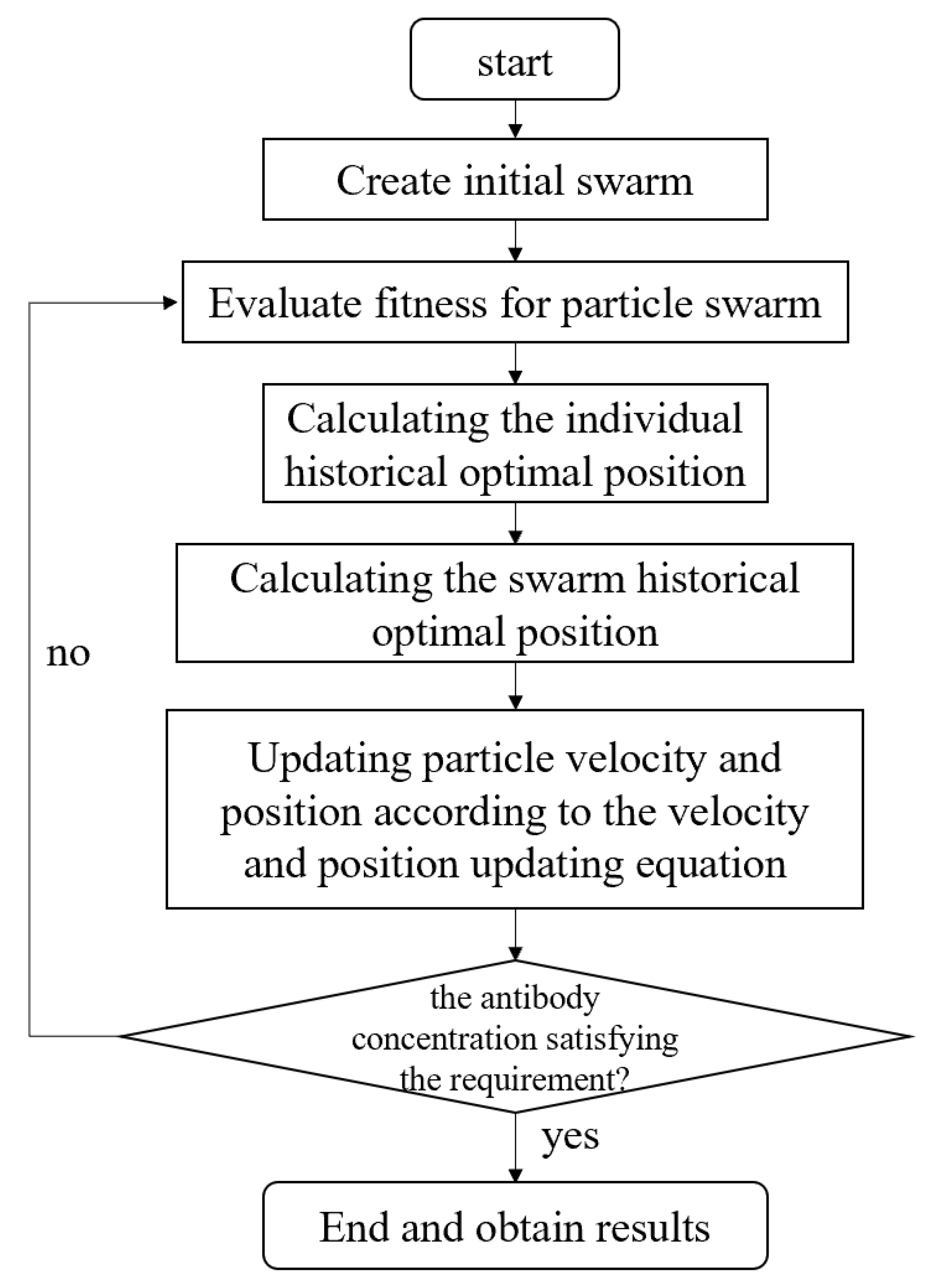
Similar to drug discovery, PSO can assist in the selection of antigen sequences for COVID-19 vaccines [28]. Figure 3 depicts the application of particle swarm optimization to selecting antigens or epitopes for the COVID-19 vaccine. It can optimize the choice of epitopes or antigens to create a vaccine with a strong immune response. PSO-based algorithms can search through the vast space of possible antigen combinations to design vaccines that are more effective in inducing immunity against the virus.
PSO can enhance epidemiological models used to predict disease spread and inform public health interventions [29]. By fine-tuning model parameters, such as transmission rates or population mobility patterns, through PSO optimization, researchers can create more accurate and reliable models. PSO helps authorities make informed decisions about interventions like social distancing, mask mandates, and vaccination campaigns.
PSO can assist in optimizing the allocation of healthcare resources during the pandemic [30]. It can be used to determine the most efficient distribution of resources, such as ventilators, hospital beds, and medical staff, to areas with the highest demand. PSO ensures that limited resources are utilized optimally, especially in regions facing surges in COVID-19 cases.
PSO can aid in optimizing contact tracing efforts and predicting the spread of the virus [31]. By evolving contact network structures through PSO, public health agencies can identify key individuals or locations that contribute significantly to transmission. This information helps prioritize contact tracing and control measures in areas where they can have the greatest impact.

Cat Swarm Optimization for COVID-19

Cat Swarm Optimization (CSO) is a nature-inspired optimization algorithm based on the social behaviors of cats [32], which can be applied to assist in addressing various aspects of the COVID-19 pandemic[33].
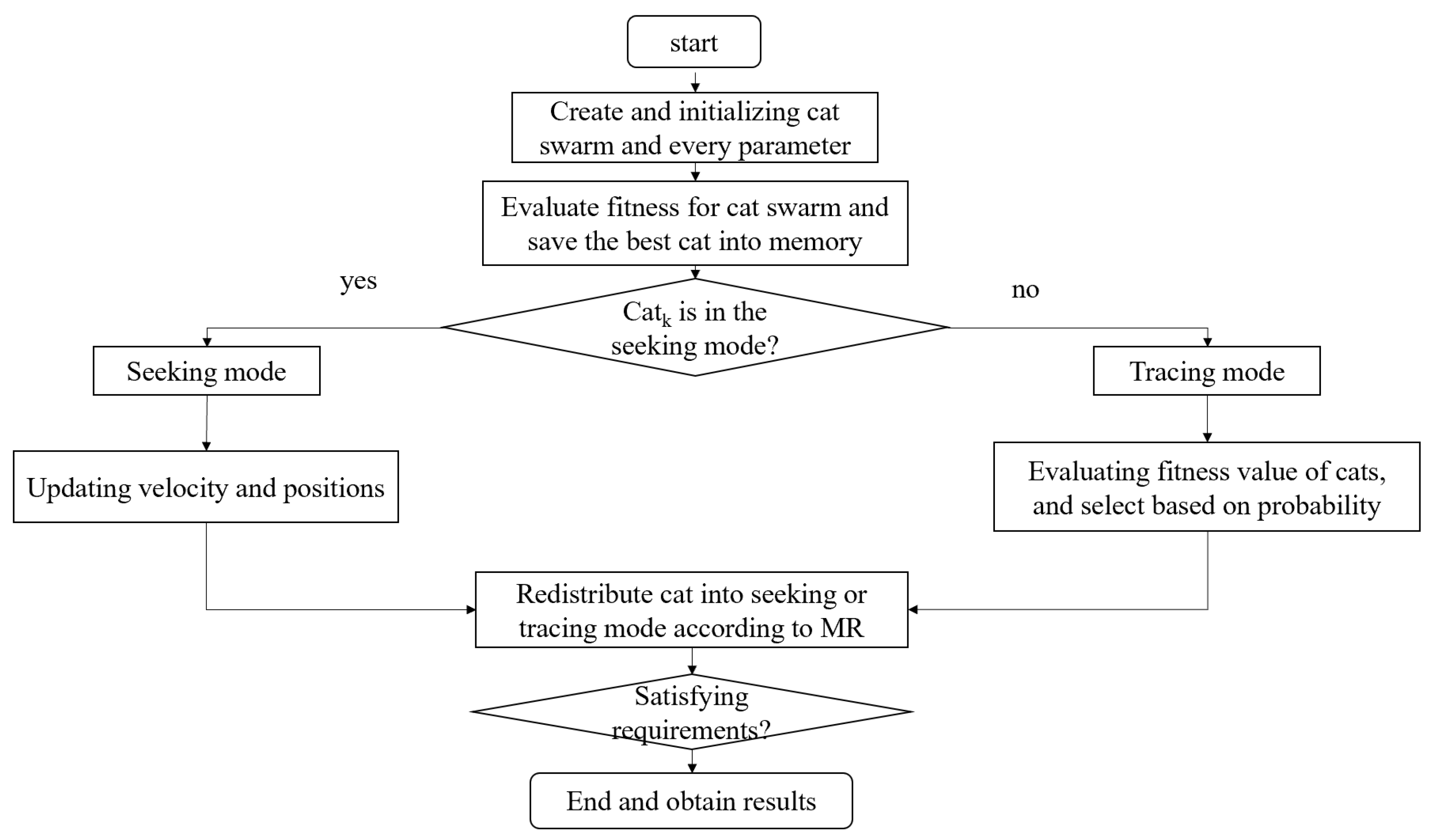
The CSO algorithm consists of two modes, the tracking mode and the finding mode. Each "cat" represents a solution set with its own location, fitness value, and flag. Seeking mode contains four fundamental parameters: seeking memory pool (SMP), seeking range of the selected dimension (SRD), counts of dimension to change (CDC), and self-position considering (SPC). The SMP specifies the size of the cat's search memory, equal to the number of candidate locations. The cat will choose to go to one of locations. CDC defines the number of dimensions ranged in [0, 1]. SRD defines the amount of mutation and modifications for those dimensions that were selected by the CDC. SPC is a boolean value that specifies whether to use the current position of the cat as a candidate position for the next iteration. Tracing Mode replicates the tracking behavior of the cat. In the first iteration, all dimensions of the cat's position are random velocity values. However, in later steps, the velocity values need to be updated. Figure 4 describes the process of cat swarm optimization in detail.
CSO can play a role in optimizing the molecular structures of potential antiviral drugs [34]. By simulating a swarm of "cat" agents exploring the chemical space, CSO can identify promising compounds for COVID-19 treatment. It helps researchers find drug candidates that are more likely to inhibit the virus's replication or reduce its virulence, thus expediting the drug discovery process.
Similar to drug discovery, CSO can aid in the selection of antigen sequences for COVID-19 vaccines. It optimizes the choice of epitopes or antigens to create a vaccine that triggers a robust immune response [35]. CSO-based algorithms systematically search through antigen combinations to design vaccines that are more effective at inducing immunity against the virus. CSO can enhance epidemiological models used to predict disease spread and inform public health interventions [36]. By optimizing model parameters (e.g., transmission rates, contact patterns) through CSO, researchers can create more accurate and reliable models. Meanwhile, CSO can help authorities make data-driven decisions about interventions like social distancing, mask mandates, and vaccination strategies.
CSO can assist in optimizing the allocation of healthcare resources during the pandemic [37]. It can determine the most efficient distribution of resources, such as ventilators, hospital beds, and medical personnel, to areas with the highest need. CSO ensures that limited resources are utilized optimally, especially in regions facing surges in COVID-19 cases.
CSO can aid in optimizing contact tracing efforts and predicting the spread of the virus [38]. By evolving contact network structures through CSO, public health agencies can identify key individuals or locations that significantly contribute to transmission. The information helps prioritize contact tracing and control measures in areas where they can have the greatest impact.

Other Optimizations Tools

From Table 1, we list and describe briefly some optimization tools that can be applied in the COVID-19 epidemic.
Differential Evolution (DE): Differential Evolution is a population-based optimization algorithm that employs a strategy of evolving potential solutions through mutation, recombination, and selection. It is particularly effective in solving continuous optimization problems [39].
Tabu Search (TS): Tabu Search is a metaheuristic optimization method that utilizes a memory structure to keep track of previously visited solutions [40]. It prevents revisiting the same solutions and employs diverse search strategies to explore the solution space efficiently.
Harmony Search (HS): Harmony Search is inspired by the process of musicians improvising to find pleasing melodies. It generates candidate solutions through a process of improvisation, harmony memory, and pitch adjustment, making it suitable for various optimization problems [41].
Ant Colony Optimization (ACO): ACO is inspired by the foraging behavior of ants. It uses a population of artificial ants to explore solution spaces, with pheromone trails guiding their search. ACO is commonly used for combinatorial optimization problems [42].
Genetic Programming (GP): Genetic Programming is an extension of Genetic Algorithms that evolves computer programs or mathematical expressions to optimize a specific objective function [43]. It is useful for symbolic regression, automated code generation, and evolving control strategies.
Firefly Algorithm (FA): The Firefly Algorithm is based on the flashing behavior of fireflies. Fireflies adjust their flashing patterns to find mates, which is mimicked in the optimization algorithm to find optimal solutions in multi-objective optimization problems [44].
Memory-based Genetic Algorithms (MGA): MGA is an optimization technique that makes use of a memory to improve the intensification capability of GA. MGA tries to improve the search capability of GA by enhancing the reinforcement and expanding the local and global search [45].

Challenges

Global optimization for addressing the COVID-19 pandemic presents several challenges due to the complexity and urgency of the situation [46]. Figure 5 includes some of the key challenges:
High-Dimensional Solution Spaces: Many COVID-19-related optimization problems involve a high number of variables and parameters, such as in drug discovery or vaccine design [47]. The sheer dimensionality of these solution spaces can make optimization computationally demanding and time-consuming.
Non-Convexity: The objective functions in COVID-19 optimization problems are often non-convex, meaning they have multiple local optima [48]. Traditional optimization methods can struggle to find the global optimum in such cases, leading to the risk of settling for suboptimal solutions.
Limited Data and Uncertainty: In the early stages of the pandemic, data on the virus and its effects were limited and continuously evolving. The uncertainty introduced by the limited data can make it challenging to build accurate models and formulate optimization problems with precise parameters [49].
Rapidly Changing Conditions: The COVID-19 situation has been highly dynamic, with changing infection rates, new variants, and evolving public health guidelines. Optimization solutions need to be adaptable to these changing conditions.
Ethical Considerations: In vaccine distribution and resource allocation, ethical considerations play a significant role [50]. Decisions must balance optimization objectives with principles like fairness, equity, and social justice.

Discussion and Conclusion

Global optimization techniques have played a crucial role in addressing various aspects of the COVID-19 pandemic, ranging from drug discovery and vaccine design to epidemiological modeling and resource allocation. As researchers continue to explore the application of optimization in the context of COVID-19, several conclusions and avenues for future studies have emerged:
Effective Tools for Complex Problems: Global optimization algorithms like Genetic Algorithms, Particle Swarm Optimization, and others have demonstrated their effectiveness in tackling complex, high-dimensional problems related to COVID-19. These methods can expedite the development of treatments and vaccines, optimize resource allocation, and enhance epidemiological modelling [51].
Interdisciplinary Collaboration: The success of global optimization in pandemic management underscores the importance of interdisciplinary collaboration. Future studies should encourage collaboration between optimization experts, epidemiologists, biologists, medical professionals, and policymakers to ensure that optimization techniques are effectively integrated into real-world decision-making processes [52].
Data-Driven Approaches: The availability of data is crucial for effective global optimization. Future research should focus on improving data collection, sharing, and analysis to support optimization efforts [53]. The process of Data-Driven Approaches includes the development of real-time data sources, data privacy solutions, and data-driven models.
Adaptability and Resilience: COVID-19 has demonstrated the need for optimization solutions that are adaptable and resilient to rapidly changing conditions. Future studies should explore how optimization algorithms can be designed to accommodate evolving parameters, emerging variants, and dynamic public health guidelines.
Ethical Considerations: As optimization techniques are applied to critical decision-making processes, future research should address the ethical considerations surrounding resource allocation, vaccine distribution, and public health interventions [54]. Studies should explore approaches that balance optimization objectives with fairness, equity, and social justice.
In conclusion, global optimization techniques have proven to be valuable tools in the fight against COVID-19. Future studies should continue to advance these methods, address challenges, and explore innovative ways to integrate optimization into pandemic response strategies. By doing so, researchers can contribute to more effective decision-making processes and improved public health outcomes during pandemics.

Data availability statement

Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.

Acknowledgments

The paper is supported by Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD).

Conflict of interest

All authors declare that they have no conflict of interest.

References

  1. Y. Zhang, X. Y. Zhang, X. Zhang, and W. Zhu, “ANC: Attention Network for COVID-19 Explainable Diagnosis Based on Convolutional Block Attention Module,” Computer Modeling in Engineering & Sciences 127(3) (2021): 1037–1058. [CrossRef]
  2. F. He, Y. F. He, Y. Deng, and W. Li, “Coronavirus disease 2019: What we know?,” Journal of Medical Virology 92(7) (2020): 719–725. [CrossRef]
  3. D. Zhao et al., “A Comparative Study on the Clinical Features of Coronavirus 2019 (COVID-19) Pneumonia With Other Pneumonias,” Clinical Infectious Diseases: An Official Publication of the Infectious Diseases Society of America 71(15) (2020): 756–761. [CrossRef]
  4. P. Ann et al., “Age Differences in Risk and Resilience Factors in COVID-19-Related Stress,” The Journals of Gerontology: Series B (2) (2020): 2. [CrossRef]
  5. C. Tisdell, “Economic, social and political issues raised by the COVID-19 pandemic,” Economic Analysis and Policy 68(C) (2020): 17–28. [CrossRef]
  6. Y.-D. Zhang et al., “Pseudo Zernike Moment and Deep Stacked Sparse Autoencoder for COVID-19 Diagnosis,” Computers, Materials & Continua 69(3) (2021): 3145–3162. [CrossRef]
  7. Shah and O., C. Coiado, “COVID-19 vaccine and booster hesitation around the world: A literature review,” Frontiers in Medicine 9 (2022): 1054557. [CrossRef]
  8. Alakija, “Leveraging lessons from the COVID-19 pandemic to strengthen low-income and middle-income country preparedness for future global health threats,” The Lancet Infectious Diseases 23(8) (2023): e310–e317. [CrossRef]
  9. T. Weise et al., “Global Optimization Algorithms and their Application to Distributed Systems,”.
  10. M. Schonlau, “Computer Experiments and Global Optimization,”.
  11. M. J. Sasena, P. Papalambros, and P. Goovaerts, “Exploration of Metamodeling Sampling Criteria for Constrained Global Optimization,” Engineering Optimization 34(3) (2002): 263–278. [CrossRef]
  12. H. M. Torun and M. Swaminathan, “High-Dimensional Global Optimization Method for High-Frequency Electronic Design,” IEEE Transactions on Microwave Theory and Techniques 67(6) (2019): 2128–2142. [CrossRef]
  13. “A collection of test problems for constrained global optimization algorithms.”. [CrossRef]
  14. Sebastian Ruder, “An overview of gradient descent optimization algorithms.” arXiv, 2017. [CrossRef]
  15. J. S. Arora et al., “Global optimization methods for engineering applications: A review,” Structural Optimization 9(3–4) (1995): 137–159. [CrossRef]
  16. Younis and, Z. Dong, “Trends, features, and tests of common and recently introduced global optimization methods,” Engineering Optimization 42(8) (2010): 691–718. [CrossRef]
  17. S. Arora and S. Singh, “Butterfly optimization algorithm: a novel approach for global optimization,” Soft Computing 23(3) (2019): 715–734. [CrossRef]
  18. D. Li et al., “Plasmonic Biosensor Augmented by a Genetic Algorithm for Ultra-Rapid, Label-Free, and Multi-Functional Detection of COVID-19,” Analytical Chemistry 93(27) (2021): 9437–9444. [CrossRef]
  19. M. Pennisi, G. M. Pennisi, G. Russo, and F. Pappalardo, “Combining Parallel Genetic Algorithms and Machine Learning to Improve the Research of Optimal Vaccination Protocols,” 2018 26th Euromicro International Conference on Parallel, Distributed and Network-based Processing (PDP) (2018): 399–405. [CrossRef]
  20. R. L. Forestal and S. Pi, “A hybrid approach based on ELECTRE III -genetic algorithm and TOPSIS method for selection of optimal COVID -19 vaccines,” Journal of Multi-Criteria Decision Analysis 29(1–2) (2022): 80–91. [CrossRef]
  21. G. K.-M. Goh and J. A. Foster, “Evolving Molecules for Drug Design Using Genetic Algorithms via Molecular Trees,”.
  22. Z. Qiu et al., “Application of genetic algorithm combined with improved SEIR model in predicting the epidemic trend of COVID-19, China,” Scientific Reports 12(1) (2022): 8910. [CrossRef]
  23. A. Apornak et al., “Human resources optimization in hospital emergency using the genetic algorithm approach,” International Journal of Healthcare Management 14(4) (2021): 1441–1448. [CrossRef]
  24. E. Agbehadji et al., “Review of Big Data Analytics, Artificial Intelligence and Nature-Inspired Computing Models towards Accurate Detection of COVID-19 Pandemic Cases and Contact Tracing,” International Journal of Environmental Research and Public Health 17(15) (2020): 5330. [CrossRef]
  25. Ke-Lin Du and M. N., S. Swamy, “Particle Swarm Optimization,” in Search and Optimization by Metaheuristics, (Cham: Springer International Publishing, 2016), 153–173. [CrossRef]
  26. P. Piotrowski and A. E. Piotrowska, “Differential evolution and particle swarm optimization against COVID-19,” Artificial Intelligence Review 55(3) (2022): 2149–2219. [CrossRef]
  27. E. H. Houssein et al., “A novel hybrid Harris hawks optimization and support vector machines for drug design and discovery,” Computers & Chemical Engineering 133 (2020): 106656. [CrossRef]
  28. H. Li et al., “IPSMT: Multi-objective optimization of multipath transmission strategy based on improved immune particle swarm algorithm in wireless sensor networks,” Applied Soft Computing 121 (2022): 108705. [CrossRef]
  29. C. Zhan et al., “Optimizing Broad Learning System Hyper-parameters through Particle Swarm Optimization for Predicting COVID-19 in 184 Countries,” 2020 IEEE International Conference on E-health Networking, Application & Services (HEALTHCOM) (2021): 1–6. [CrossRef]
  30. T. Yang et al., “Comparison of health-oriented cross-regional allocation strategies for the COVID-19 vaccine: a mathematical modelling study,” Annals of Medicine 54(1) (2022): 941–952. [CrossRef]
  31. D. A et al., “Prediction on transmission trajectory of COVID-19 based on particle swarm algorithm - ScienceDirect,” (2021). [CrossRef]
  32. Shu-Chuan Chu, Pei-wei Tsai, and Jeng-Shyang Pan, “Cat Swarm Optimization,” in PRICAI 2006: Trends in Artificial Intelligence, 4099, eds Qiang Yang and Geoff Webb (Berlin, Heidelberg: Springer Berlin Heidelberg, 2006), 854–858. [CrossRef]
  33. P. Renukadevi and A. Rajiv Kannan, “Covid-19 Forecasting with Deep Learning-based Half-binomial Distribution Cat Swarm Optimization,” Computer Systems Science and Engineering 44(1) (2023): 629–645. [CrossRef]
  34. R. Zhou, Y. R. Zhou, Y. Zhang, and K. He, “A novel hybrid binary whale optimization algorithm with chameleon hunting mechanism for wrapper feature selection in QSAR classification model:A drug-induced liver injury case study,” Expert Systems with Applications 234 (2023): 121015. [CrossRef]
  35. P. Angaitkar, R. R. P. Angaitkar, R. R. Janghel, and T. P. Sahu, “gHPCSO: Gaussian Distribution Based Hybrid Particle Cat Swarm Optimization for Linear B-cell Epitope Prediction,” International Journal of Information Technology 15(5) (2023): 2805–2818. [CrossRef]
  36. Nuari, A. Damayanti, and A. B. Pratiwi, “Cat swarm optimization and Levenberg-Marquardt for model identification and prediction identification and prediction tuberculosis disease spreading,” Journal of Physics: Conference Series 1494(1) (2020): 012005. [CrossRef]
  37. T. Saravanan and S. Saravanakumar, “Enhancing investigations in data migration and security using sequence cover cat and cover particle swarm optimization in the fog paradigm,” International Journal of Intelligent Networks 3 (2022): 204–212. [CrossRef]
  38. L. Guo et al., “A modified cat swarm optimization based maximum power point tracking method for photovoltaic system under partially shaded condition,” Energy 144 (2018): 501–514. [CrossRef]
  39. F. Neri and V. Tirronen, “Recent advances in differential evolution: a survey and experimental analysis,” Artificial Intelligence Review 33(1–2) (2010): 61–106. [CrossRef]
  40. Fred Glover and Manuel Laguna, “Tabu Search,” in Handbook of Combinatorial Optimization: Volume1–3, eds Ding-Zhu Du and Panos M. Pardalos (Boston, MA: Springer US, 1998), 2093–2229. [CrossRef]
  41. S. Lee and Z. W. Geem, “A new meta-heuristic algorithm for continuous engineering optimization: harmony search theory and practice,” Computer Methods in Applied Mechanics and Engineering 194(36) (2005): 3902–3933. [CrossRef]
  42. M. Dorigo, M. M. Dorigo, M. Birattari, and T. Stutzle, “Ant colony optimization,” IEEE Computational Intelligence Magazine 1(4) (2006): 28–39. [CrossRef]
  43. L. Ribeiro Filho, P. C. L. Ribeiro Filho, P. C. Treleaven, and C. Alippi, “Genetic-algorithm programming environments,” Computer 27(6) (1994): 28–43. [CrossRef]
  44. I. Fister et al., “A comprehensive review of firefly algorithms,” Swarm and Evolutionary Computation 13 (2013): 34–46. [CrossRef]
  45. A. Askarzadeh, “A Memory-Based Genetic Algorithm for Optimization of Power Generation in a Microgrid,” IEEE Transactions on Sustainable Energy 9(3) (2018): 1081–1089. [CrossRef]
  46. K. El‐Boghdadly et al., “SARS-CoV-2 infection, COVID-19 and timing of elective surgery: A multidisciplinary consensus statement on behalf of the Association of Anaesthetists, the Centre for Peri-operative Care, the Federation of Surgical Specialty Associations, the Royal College of Anaesthetists and the Royal College of Surgeons of England,” Anaesthesia 76(7) (2021): 940–946. [CrossRef]
  47. M. Zhong et al., “A hierarchical multi-leadership sine cosine algorithm to dissolving global optimization and data classification: The COVID-19 case study,” Computers in Biology and Medicine 164 (2023): 107212. [CrossRef]
  48. S. Hao et al., “Performance optimization of hunger games search for multi-threshold COVID-19 image segmentation,” Multimedia Tools and Applications (2023). [CrossRef]
  49. J. Sheng et al., “COVID-19 Pandemic in the New Era of Big Data Analytics: Methodological Innovations and Future Research Directions,” British Journal of Management 32(4) (2021): 1164–1183. [CrossRef]
  50. E. Nakazawa, H. Ino, and A. Akabayashi, “Chronology of COVID-19 Cases on the Diamond Princess Cruise Ship and Ethical Considerations: A Report From Japan,” Disaster Medicine and Public Health Preparedness 14(4) (2020): 506–513. [CrossRef]
  51. Y. Ma et al., “COVID-19 Spreading Prediction with Enhanced SEIR Model,” 2020 International Conference on Artificial Intelligence and Computer Engineering (ICAICE) (2020): 383–386. [CrossRef]
  52. M. Abu Haleeqa et al., “Optimizing Supportive Care in COVID-19 Patients: A Multidisciplinary Approach,” Journal of Multidisciplinary Healthcare Volume 13 (2020): 877–880. [CrossRef]
  53. S. Ghamizi et al., “Data-driven Simulation and Optimization for Covid-19 Exit Strategies,” Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (2020): 3434–3442. [CrossRef]
  54. et al. L. Matrajt et al., “Vaccine optimization for COVID-19: Who to vaccinate first?,” SCIENCE ADVANCES 7 (2021): eabf1374. [CrossRef]
Preprints 88802 g001
Figure 1. Flowchart of Genetic Algorithm.
Figure 1. Flowchart of Genetic Algorithm.
Preprints 88802 g001
Preprints 88802 g002
Figure 2. Flowchart of genetic algorithm applied to develop COVID-19 vaccine.
Figure 2. Flowchart of genetic algorithm applied to develop COVID-19 vaccine.
Preprints 88802 g002
Preprints 88802 g003
Figure 3. Flowchart of particle swarm algorithm applied to develop COVID-19 vaccine.
Figure 3. Flowchart of particle swarm algorithm applied to develop COVID-19 vaccine.
Preprints 88802 g003
Preprints 88802 g004
Figure 4. Flowchart of cat swarm algorithm.
Figure 4. Flowchart of cat swarm algorithm.
Preprints 88802 g004
Preprints 88802 g005
Figure 5. The challenge of global optimization for addressing the COVID-19 pandemic.
Figure 5. The challenge of global optimization for addressing the COVID-19 pandemic.
Preprints 88802 g005
Table 1. Summary of other optimization tools.
Table 1. Summary of other optimization tools.
Optimizations Tool Abbreviation Time Description
Genetic algorithms GAs 1975 A search algorithm based on natural selection and genetics conjectures.
Particle Swarm Optimization PSO 1995 An algorithm based on the social behavior of birds.
Cat Swarm Optimization CSO 2006 A nature-inspired optimization algorithm based on the social behaviors of cats.
Differential Evolution DE 1995 It uses the difference between randomly sampled pairs of object vectors to guide the mutation process.
Tabu Search TS 1986 An optimization algorithm that simulates human intelligence
Harmony Search HS 2001 Music-based meta-heuristic optimization algorithms
Ant Colony Optimization ACO 1991 Swarm intelligence algorithms inspired by the behavior of ants foraging in nature
Genetic Programming GP 1992 A type of evolutionary algorithm inheriting the idea of genetic algorithms
Firefly Algorithm FA 2009 An algorithm primarily simulates the behavior of fireflies that are attracted to each other based on the brightness of individuals
Memory-based Genetic Algorithms MGA 2017 An optimization algorithm optimally shares the power generation task among a number of DERs.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Differential Evolution: A Survey and Analysis

Tarik Eltaeib

et al.

Applied Sciences,

2018

IDEINFO: An Improved Vector-Weighted Optimization Algorithm

Lixin Zhao

et al.

Applied Sciences,

2023

Pareto Optimization or Cascaded Weighted Sum: A Comparison of Concepts

Wilfried Jakob

et al.

Algorithms,

2014

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated