Prerpints.org logo
Preprint
Review

Application of Intracranial Compliance in Clinical Approaches for Brain Disorders

This version is not peer-reviewed.

Submitted:

26 October 2023

Posted:

27 October 2023

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
Intracranial compliance (ICC) plays a pivotal role in understanding the underlying mechanisms of various brain disorders and is of great clinical importance. Therefore, addressing the challenges in practical application of ICC is crucial for neurosurgeons. This study explored the significance of ICC assessment considering the time-dependency of specific brain disorders through two distinct approaches: short and large time elapsed (TE) in measuring volume or intracranial pressure (ICP) changes in the ICC equation (∆Volume/∆ICP). Variations in ICC values were observed across various ICC assessment methods and different TE values. Notably, the compensatory response of the brain exhibited non-monotonic and variable changes in a large TE for certain brain disorders, diverging from patterns observed in short TE assessments. Furthermore, the recovery behavior of the brain changed under different brain disorders when exposed to short and long TE conditions. These findings emphasized the dynamic nature of ICC and provided valuable insights into the correct practical assessment of ICC by selecting the appropriate TE, as well as considering the differences in strain rates and loading durations on the brain in different brain disorders. These insights also shed light on the reasons why, despite its clinical significance, ICC monitoring has not yet become a standard component of clinical care, unlike ICP monitoring.
Keywords: 
Intracranial compliance
;  
Viscous component
;  
Time-dependent disorders
;  
Brain disorder
;  
Strain rate
;  
Cerebrospinal fluid
;  
Brain biomechanics
;  
Clinical application.
Subject: 
Medicine and Pharmacology  -   Neuroscience and Neurology

1. Introduction

Brain disorders affect 6.75% of the American adult population [1] and constitute a significant cause of morbidity worldwide, with their incidence steadily increasing [2]. Prediction of treatment outcomes for brain disorders can be difficult, even in patients with similar clinical conditions. Clinical overlaps and similarities in medical imaging can also lead to misdiagnosis between various brain disorders such as normal pressure hydrocephalus (NPH) and Parkinson’s or Alzheimer’s disease [3,4,5]. The complexities in treatment outcomes may be related to the lack of clear and comprehensive knowledge concerning the mechanisms behind brain disorders. Brain tissue is a complex biomaterial with a highly heterogeneous and anisotropic microstructure, variable biomechanical properties, and dynamic behavior that can change in response to different loadings due to various brain disorders [6]. The brain’s ability to adapt to volume change is important to clarify the complexities of some brain disorders. Intracranial compliance (ICC) refers to the volume-buffering capacity and the ability of the intracranial system to adjust its volume in order to maintain stable intracranial pressure (ICP). Maintaining stable ICP is crucial for cerebral blood flow system, preventing tissue damage, and ensuring optimal neural activity [7]. ICC is a critical parameter to understanding the mechanisms underlying some brain disorders and the brain’s responses to various pathological processes [8]. It can also be useful in predicting clinical outcomes in some brain disorders such as hydrocephalus, cerebral atrophy, intracranial hypertension, traumatic brain injury, and intracranial hematoma. Therefore, gaining a conceptual understanding of how to change ICC in various types of brain disorders and how it can be used in different brain pathologies for its clinical applications is of great significance in the diagnosis and management of brain disorders.
The basis for ICC measurement was first suggested 70 years ago in an animal study [9]. Subsequent research has consistently emphasized the clinical significance, efficacy, and sensitivity of ICC in diagnosing and evaluating treatment outcomes across a spectrum of brain disorders. However, the practical implementation of ICC as an evaluative tool for neurosurgeons presents intricate challenges. In contrast, ICP stands as a well-established practical metric for studying a wide array of brain disorders. The threshold levels of ICP for both healthy individuals and patients have also been thoroughly defined [10]. Nevertheless, ICP cannot function as a substitute for ICC due to its inability to account for volume changes and its lower sensitivity in evaluating specific disorders, such as NPH. The present review is dedicated to addressing these concerns and discussing the challenges and difficulties associated with the practical application of ICC for neurosurgeons in evaluating brain disorders.

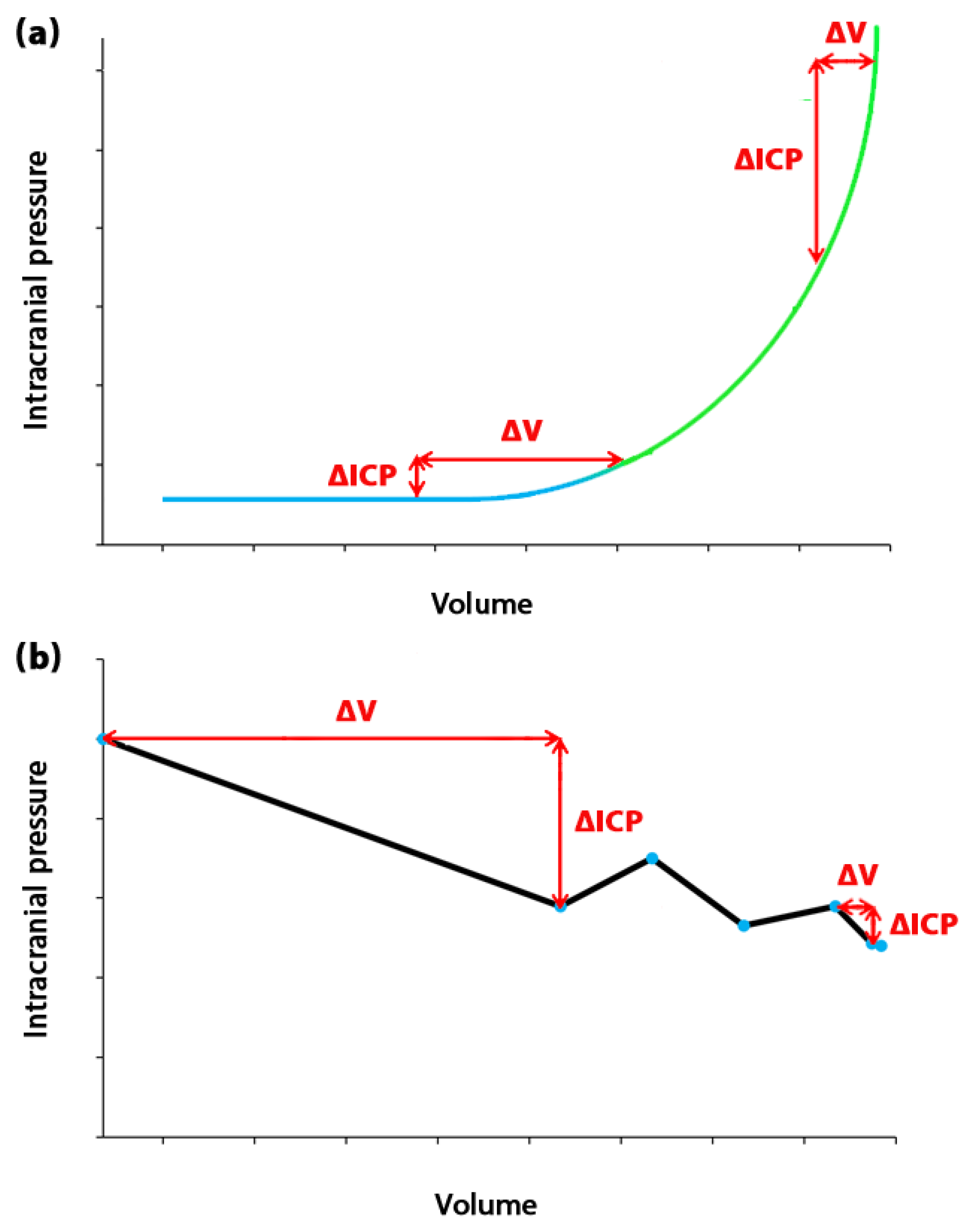
2. Measurement, calculation, and estimation of ICC

The primary techniques for direct measurement of ICC involve monitoring changes in cerebrospinal fluid (CSF) volume within the craniospinal space. These techniques are generally based on the Marmarou method, and they are invasive, carrying a higher risk of complications. Furthermore, in specific clinical scenarios, even a minor alteration in CSF volume can result in a detrimental change in ICP, leading to unpredictable clinical consequences. Okon et al also revealed that these techniques, which generally involve the injection of excessive fluid, might not be suitable in cases of elevated ICP [11]. Similarly, Smielewski et al demonstrated that these techniques, including constant infusion, constant pressure infusion, bolus manipulation, and lumbar ventricular perfusion, could lead to potential errors in pressure readings due to possible vasomotor responses [12]. Hence, there was a need to explore alternatives for assessing ICC without adding or removing fluid from the craniospinal space which might involve manipulating the natural CSF circulation system and non-invasive methods emerged as superior options. Pioneering efforts by Alperin et al marked the first attempt to calculate ICC non-invasively through computer simulations [13,14]. We also developed and optimized the non-invasive ICC calculation employing computer simulations and mathematical analyses [15,16,17,18,19]. Additionally, we designed and fabricated an in vitro model for experimental ICC measurements [20]. Several other studies have endeavored to gauge ICC non-invasively, although they were unable to directly measure or calculate ICC values. Instead, they attempted to estimate ICC effects indirectly based on measurable parameters such as optic nerve sheath diameter [21], transcranial Doppler ultrasound [22], ICP waveform morphology [23], and bioelectrical models [24]. These methods for ICC measurement, calculation, and estimation have been introduced and utilized in some studies to assess ICC. For practical applications of these methods, the choice of method for assessing ICC can depend on the individual case and the preferences of the physician. For instance, estimation methods, although they cannot assess exact ICC values and can only estimate the general trend of ICC changes, can be suggested more viable in neurological emergency situations compared to relatively slower computer simulations or invasive ICC measurements.

3. Viscous component of the brain

The brain is composed of different substructures, including white and gray matter, blood vessels, neurons, and fluids such as extracellular fluid. Previous studies modeled the brain as a poroelastic structure based on brain consolidation theory [25]. The brain poroelastic model assumed the brain to be a porous medium consisting of solid and fluid phases. This model described the time-dependent behavior of both solid and fluid phases of the brain and the interaction between them. On the other hand, brain substructures have different viscous time-dependent properties that contribute to the brain’s overall damping characteristics. Previous studies also confirmed that a viscous time-dependent component must be considered in the definition of the brain model [26]. Hence, in addition to the importance of the scale of strain (short or large) in the brain model, the viscous time-dependent component is also necessary to achieve agreement between mathematical biphasic characteristics and experimental material properties of the brain [27]. Hrapko et al used a large strain viscoelastic framework to define one of the most prominent time-dependent stress-strain models for the brain [28]. Various studies have also tried to consider a viscous time-dependent component in the brain model under a viscoelastic, hyper-viscoelastic, or poro-hyperviscoelastic model (Table 1). Gholampour et al and Cheng et al used a poro-viscoelastic model to define the most appropriate constitutive model for the brain [15,18,29]. On the other hand, Elkin et al showed that the best conformity with experimental data is obtained when the viscoelastic component of the brain is fitted to the shear modulus ( G r t ) using the Prony series [30]. Hence, we applied this method to consider the parameter of time (t) in our poro-viscoelastic brain model using equation 1 [15,18].
G r t = G 0 ( 1 − ∑ k = 1 N g k p ( 1 − e − t τ k ) )
where G 0 , g k p , and τ k in equation 1 are input shear modulus, relaxation modulus, and relaxation time, respectively. It can be deduced that, regarding the proven impact of the viscous component in the mathematical and computational models of the brain, the role of time and the time-dependency of the brain are irrefutable in studying the brain and, consequently, brain disorders.

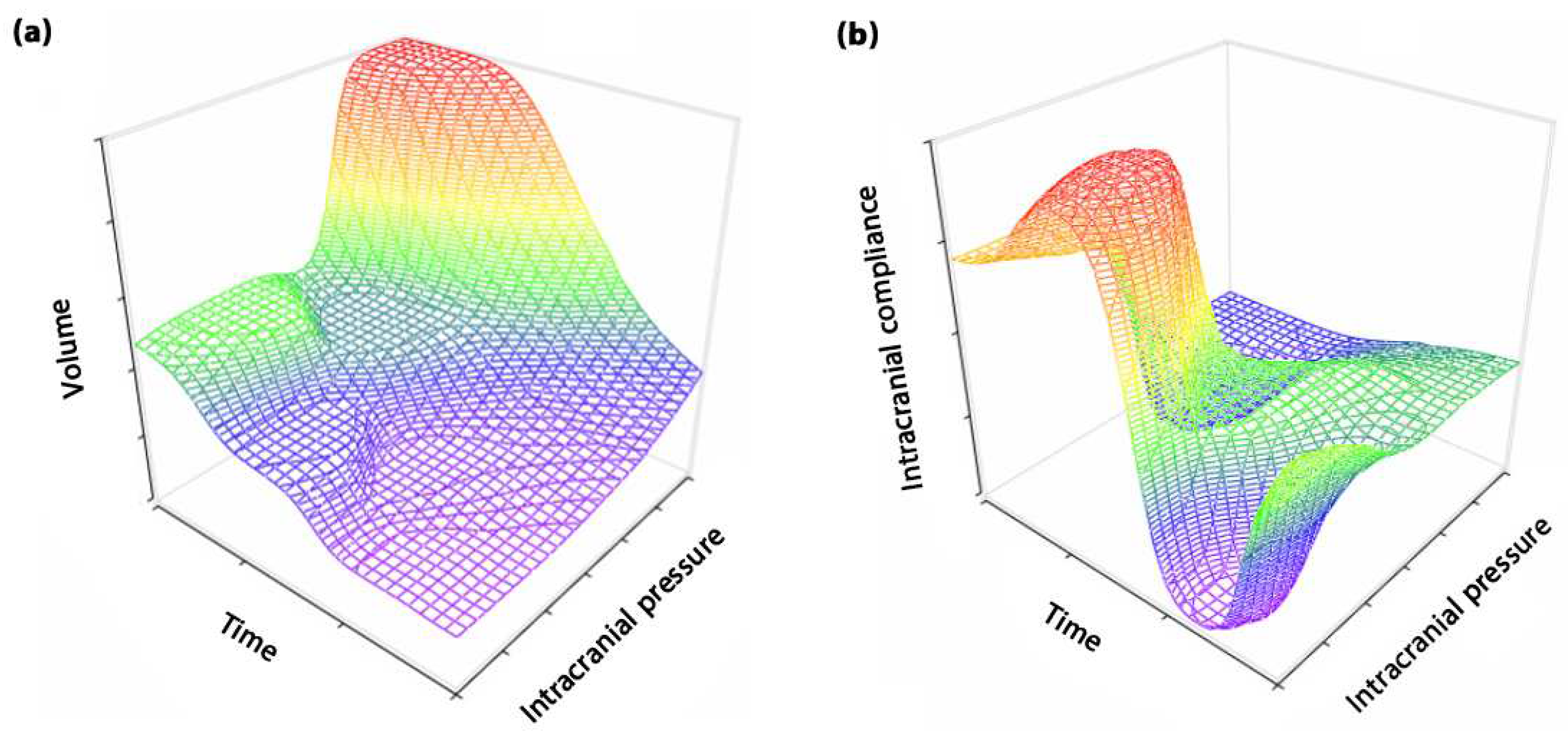
4. The role of time in ICC definition

The measurement and calculation of ICC in all previous methods were based on the classic equation of ICC, conventionally defined using the change in volume divided by the change in ICP (Eq. 2). The industrial materials, except for specific types of composites, are non-viscous and their behavior is independent of time. Hence, the parameters used in the ICC equation (changes in volume and pressure) have adequate potential to define compliance in these materials. Nevertheless, the brain models mentioned above demonstrated that the physiological and biomechanical functions of the brain are time-dependent (as discussed in the preceding section). Our previous study also showed the importance of the creep behavior (time-dependent deformation) of brain tissue in the treatment process of some brain disorders such as hydrocephalus [16]. Furthermore, the onset and progression of certain brain disorders occur over time. For instance, NPH, intracranial hypertension and hydrocephalus often manifest gradually, with many patients experiencing elevated ICP over extended periods [15,31]. Previous studies have also proved time-dependency and long-term alterations in CSF dynamics and brain morphometric parameters in patients with CSF disorders [15,19,32,33]. Therefore, in addition to the defined parameters in the ICC equation, time may also play a significant role in the formulation and, consequently, in the measurement/calculation of ICC. Certain previous studies formulated compliance based on pressures and volumes of cerebral blood and CSF [34,35,36]. Some studies defined ICC based on the elastic modulus of brain tissue, ICP, and intracranial volume [37,38,39]. Additionally, others formulated ICC based on the dynamics of injected CSF, ICP, and resistance to CSF outflow in invasive ICC measurement methods [40]. However, these studies have not directly considered the parameter of time in their ICC equations. We considered that the ICC equation can remain in its general form (Eq. 2) and consider the effect of time in the concept of “change”. “Change” of volume or ICP in the ICC equation (Eq. 2) means V2-V1 or ICP2-ICP1 [31]. It can be deduced that we can consider the time elapsed (TE) between the measurements of V2 and V1, or ICP2 and ICP1 as representative of the parameter of time in the ICC equation.
I C C = V o l u m e   c h a n g e   ( ∆ V ) I n t r a c r a n i a l   p r e s s u r e   c h a n g e    ( ∆   I C P ) = V 2 − V 1 I C P 2 − I C P 1
Table 1. Different time-dependent brain models.
Table 1. Different time-dependent brain models.
Brain model Authors, year Type of brain disorder Solving method Brain regions Source
Poroelastic Yuan
Et al, 2022		 Healthy subjects under drug infusion Mathematical analysis based on arbitrary Lagrange-Eulerian equations White matter [41]
Lambride
Et al, 2020		 Brain injury Finite element method Single region [42]
Guo
Et al, 2018		 Alzheimer’s disease Finite element method White matter [43]
Gholampour et al, 2014 and 2015 Non-communicating hydrocephalus Fluid-structure interaction Single region [44,45]
Viscoelastic Li et al,
2021		 Healthy subject Finite element method Grey and white matter [46]
Siegkas
et al, 2019		 Brain injury Finite element method Single region [47]
Gholampour et al, 2017 Hydrocephalus Fluid-structure interaction Single region [19,33]
Harpko
et al, 2006		 Healthy subject Mathematical analysis White matter [28]
Hyper-viscoelastic Menghani
et al, 2023		 Head impact Finite element method Basal ganglia, cerebral hemispheres, and corpus callosum [48]
Wang
et al, 2018		 Brain injury Finite element method Grey matter, white matter, and pia mater [49]
Wilkie
et al, 2012		 Hydrocephalus Mathematical analysis using fractional Zener model Single region [50]
Dutta-Roy, 2011 Normal pressure hydrocephalus Finite element method Single region [51]
Poro-viscoelastic Gholampour
et al, 2022 and 2023		 Communicating hydrocephalus Fluid-structure interaction Single region [16,17,31]
Pavan
Et al, 2022		 Brain injury Finite element method One region [52]
Gholampour, 2018 Non-communicating hydrocephalus Fluid-structure interaction Single region [15]
Cheng
et al, 2010		 Non-communicating hydrocephalus Finite element method White matter [29]
Poro-hyperviscoelastic Hosseini-Farid et al, 2020 Healthy subject Finite element method Grey and white matter [53]
Forte
et al, 2017		 Healthy subject Finite element method Grey and white matter [54]

5. Approaches to TE in ICC assessment

Differences in ICC values across different assessment methods, as well as different TE values, are evident in Table 2. These significant differences, characterized by inconsistency ICC results, may provide insight into why, despite the clinical importance of ICC, its monitoring, unlike ICP monitoring, has not yet become a standard component of clinical care [55]. Table 2 also indicated that the values of TE in previous non-invasive ICC measurement methods (in vitro, lumped model, and computer simulation) were less than one minute [15,20]. The corresponding values for TE in previous invasive ICC measurement methods (bolus injection and lumbar or ventricular infusion) had different values (Table 2). These differences may be attributed to variations in the clinical conditions of the patients and the different time taken to reach plateau ICP during the test. Hence, a question will be raised whether these TEs used in previous non-invasive and invasive ICC measurements are sufficiently long to demonstrate the complete effect of the brain’s viscous time-dependent component. This component, reflecting the brain’s load-history-dependent behavior, pertains to its ability to dissipate external loading and resist deformation. Consequently, considering the influence of this component is essential for accurate assessment of ICC. Hence, addressing this question is essential to ensuring the effective application of ICC in practical scenarios. Recently, we demonstrated that before two months, the complete effect of the viscous component of the brain had not yet appeared in the hydrocephalic brain [16,31]. This means that the appropriate TE for measuring ICC in hydrocephalus patients should not be short and should be at least two months. Evaluating the brains of healthy rats subjected to loading due to electrode implantation also revealed that the effects of loading did not completely dissipate within two months and brain material properties, such as shear and elastic modules, did not stabilize during this period, somehow mirroring ICC behavior [56]. Similarly, Boulet et al obtained comparable results, confirming significant changes in brain stiffness in rat brains over a month-long period [57]. Therefore, building on previous studies, we can categorize the evaluation of ICC into two approaches: ICC in a short TE and ICC in a large TE [31]. Comparing ICC behavior using these two different approaches can be helpful in clarifying certain complexities related to application of ICC for some brain disorders. For example, Eide and Brean showed when the ICC decreases in NPH patients in a short TE, the brain material behaves similarly to a linear elastic [58]. While, another study showed that the changes in elastance, stiffness, and creep of the brain in a large TE were non-linear and non-monotonic in patients with communicating hydrocephalus [16]. Therefore, the correct choice of TE (short or large) directly affects the degree to which the impacts of the viscous component of the brain are realized and also affects the arrival of brain material properties to a stable condition, allowing for the correct assessment of ICC.

6. Discussion

The complex and dynamic behavior of the brain can change in response to various loadings associated with different brain disorders, and ICC plays a crucial role in understanding the mechanisms and complexities underlying these changes. As a result, the challenges pertaining to the practical application of ICC are of significant importance in the context of brain disorders, and this review is specifically designed to address these concerns. We emphasized the significance of TE as a representation of the time parameter in the ICC equation, drawing from previous research findings. Additionally, our research highlights that in certain brain disorders, the changes in brain material properties do not stabilize within a short TE, emphasizing the dynamic nature of these conditions across various time scales, including a large TE. Furthermore, our exploration reveals that the selection of TE, be it short or large, directly influences the manifestation of the brain’s viscous component. Consequently, this review highlights that the selection of TE (short or large) directly impacts the accuracy of ICC assessment.
In addition to assessing ICC behavior under two TE approaches, it is crucial to analyze the impact of these approaches (short or large TE) on the changes in the volume-ICP curve (VI curve). Because ICC represents the slope of this curve (Eq. 2), and the curve itself plays a prominent role in understanding the compensatory response of the brain in different brain disorders. Previous studies strongly believed the trend of the VI curve to be monotonic over short TE in patients with different types of brain disorders (Figure 1a) [13,67,68]. However, Okon et al expressed doubts about the monotonic trend of VI curves in the short TE [69]. They showed that the trend of this curve in patients with idiopathic intracranial hypertension was not necessarily monotonic. Our evaluations showed that the trend of this curve is non-monotonic in hydrocephalus patients in a large TE (fifteen months after treatment) (Figure 1b and Figure 2a) [16,31]. We also showed that in a large TE, ICC does not necessarily increase with decreasing ICP level (Figure 2b), and the ICC oscillatory increases during the treatment process (Figure 2b) [16,31]. It can also be understood from a study by Tisell et al that there is a non-monotonic trend in the VI curve over a large TE (three months after treatment) in hydrocephalus patients [70]. Hence, the compensatory response of the brain can have non-monotonic and variable changes in a large TE in certain brain disorders (Figure 2). Therefore, it can be deduced that the trend of the compensatory response of the brain, which plays a prominent role in ICC assessments, may be different over short or large TE in certain brain disorders.
The correct choice of TE (short or large) depends on the strain rate and loading time in that particular brain disorder under assessment for ICC. Strain rate is a measure of how quickly the brain is being deformed under loading caused by a brain disorder. The loading time refers to the duration of the loading that is applied to the brain in a specific brain disorder and it is a measure of how long the brain is being subjected to loading. The strain rate and loading time vary across different types of brain disorders. For instance, these parameters significantly differ in traumatic brain injury and some time-dependent brain disorders such as hydrocephalus. Therefore, it can be inferred that the practical utilization of ICC depends on the strain rate and loading duration specific to each individual brain disorder, taking into account the two approaches used in ICC assessment.
Previous studies showed descents in the VI curve at certain times in a large TE for some disorders like hydrocephalus (Figure 1b) because of the non-monotonic trend of this curve [16,31]. Similar descents were also demonstrable in a study by Tisell et al [70]. This means in the context of ICC assessment using a large TE approach, ICC values and consequently the compensatory response of brain tissue, may partially recover at specific times. This is worth mentioning when the brain is in an uncompensated status in a short TE, it is traditionally defined as a high-risk condition [55]. However, the temporary uncompensatory responses of the brain caused by the non-monotonic trend of the VI curve in a large TE can not necessarily be deduced as a high-risk condition. In addition, two separate compensatory reserve zones were shown in the VI curve in a short TE (Figure 1a: blue and green colors). The ICC values and pulse amplitude of ICP change in these two zones. However, the VI curve in a large TE was not divisible into specific meaningful compensatory reserve zones in hydrocephalus patients (Figure 1b). Overall, the general trend (mono-exponential) and compensatory reserve zones (two zones) of the VI curve in a short TE were approximately the same in different types of brain disorders such as hydrocephalus [13,71], brain edema [67], and brain injury [68], and they were different from a large TE approach.
In order to measure or calculate ICC, two statuses, labeled 1 and 2, are required to calculate the ‘change’ in volume and ICP (Eq. 2). In emergency conditions of certain brain disorders, such as hydrocephalus, which involve a large strain rate and loading duration, the ICC in a large TE approach may not be applicable due to the time needed to establish these two statuses for the ICC equation. In such scenarios, ICC estimation methods may prove more useful. However, in cases like NPH, ICC can be exclusively used for diagnosis and evaluating treatment outcomes. This is because the conditions of these patients are not always emergencies; NPH is generally a time-dependent disease, and other available indicators such as ICP, gait analysis, or cognitive examinations may not always be effective to evaluate these diseases [72,73]. It’s worth noting that there is no established numerical threshold for ICC values for the practical use of ICC as a clinical indicator for these conditions, even for diseases like NPH or in non-emergency situations. Expanding optimized computer simulation methods [18] for non-invasive ICC calculations in future studies could be beneficial in addressing this concern by defining a threshold level between ICC values in healthy subjects and those in patients.
The recovery behavior of the brain during the treatment process (unloading condition) is of great importance in the management of brain disorders [16]. The previous studies have demonstrated that the biomechanical response of the brain in loading (i.e., afflicted with a brain disorder) and unloading (i.e., during some treatment processes) conditions is different [74]. Elastic hysteresis behavior of the brain is one of the primary reasons for this difference specifically in disorders caused by cyclic loading, i.e. in hydrocephalus and intracranial hypertension that are caused by pulsatile elevated ICP. The theory of elastic hysteresis of the brain states that the brain stores energy during loading, however, not all of this energy is released during unloading, as some of it is dissipated due to internal friction. This leads to a residual (permanent) deformation in brain tissue after the treatment process. The differences in residual deformation of the hydrocephalic brain were reported in short and large TEs [16,27]. This theory which is provided by Lesniak et al confirmed the direct impact of elastic hysteresis behavior of the brain on ICC changes [75]. Comparing ICC values in loading and unloading conditions over a large TE in future studies can be useful for developing the theory of elastic hysteresis. This comparison can further clarify how ICC changes in loading and unloading conditions in a large TE, potentially enhancing the practical utility of ICC in time-dependent brain disorders. In addition, previous studies showed a decrease in glymphatic drainage and ICC value in a short TE for patients with NPH, traumatic brain injury, and Alzheimer’s diseases [76,77,78]. Evaluation of the changes in ICC and glymphatic drainage in a large TE in future studies may be useful to support the hypothesis of glymphatic dysfunction as the underlying pathophysiology of time-dependent brain disorders such as NPH and Alzheimer’s diseases

7. Conclusions

The review has underscored the critical role of selecting the appropriate TE in ICC assessment for clinical applications. We clarified that ICC values, brain biomechanical response, and the compensatory response of the brain can exhibit non-monotonic and variable changes in specific brain disorders over a large TE, in contrast to short TE assessments. These observations emphasize the dynamic nature of ICC and shed light on the reasons behind the lack of standardization in ICC monitoring for practical applicants, despite its clinical significance. Future studies comparing ICC values in the presence of a brain disorder and during treatment under different TEs may provide valuable insights into the complexities associated with the practical use of ICC in evaluating time-dependent brain disorders.

Author Contributions

SG contributed to the Conceptualization, Design of study, Investigation, Methodology, Project administration, Resources, and Writing the manuscript.

Funding

The Margaret Hackett Family Program (MHFP).

Institutional Review Board Statement

The process of study design and performing procedures were approved by the institutional human IRB committee and performed in accordance with the ethics committee guidelines of the University of Chicago based on the 1964 Helsinki Declaration and its later amendments.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Borlongan, C.V.; Burns, J.; Tajiri, N.; Stahl, C.E.; Weinbren, N.L.; Shojo, H.; Sanberg, P.R.; Emerich, D.F.; Kaneko, Y.; van Loveren, H.R. Epidemiological survey-based formulae to approximate incidence and prevalence of neurological disorders in the United States: a meta-analysis. PLoS One 2013, 8, e78490. [Google Scholar] [CrossRef] [PubMed]
  2. Lima Giacobbo, B.; Doorduin, J.; Klein, H.C.; Dierckx, R.A.; Bromberg, E.; de Vries, E.F. Brain-derived neurotrophic factor in brain disorders: focus on neuroinflammation. Molecular neurobiology 2019, 56, 3295–3312. [Google Scholar] [CrossRef] [PubMed]
  3. Pomeraniec, I.J.; Bond, A.E.; Lopes, M.B.; Jane, J.A. Concurrent Alzheimer’s pathology in patients with clinical normal pressure hydrocephalus: correlation of high-volume lumbar puncture results, cortical brain biopsies, and outcomes. Journal of neurosurgery 2016, 124, 382–388. [Google Scholar] [CrossRef] [PubMed]
  4. Reeves, B.C.; Karimy, J.K.; Kundishora, A.J.; Mestre, H.; Cerci, H.M.; Matouk, C.; Alper, S.L.; Lundgaard, I.; Nedergaard, M.; Kahle, K.T. Glymphatic system impairment in Alzheimer’s disease and idiopathic normal pressure hydrocephalus. Trends in molecular medicine 2020, 26, 285–295. [Google Scholar] [CrossRef] [PubMed]
  5. Kockum, K.; Virhammar, J.; Riklund, K.; Söderström, L.; Larsson, E.-M.; Laurell, K. Diagnostic accuracy of the iNPH Radscale in idiopathic normal pressure hydrocephalus. PloS One 2020, 15, e0232275. [Google Scholar] [CrossRef] [PubMed]
  6. Budday, S.; Ovaert, T.C.; Holzapfel, G.A.; Steinmann, P.; Kuhl, E. Fifty shades of brain: a review on the mechanical testing and modeling of brain tissue. Archives of Computational Methods in Engineering 2020, 27, 1187–1230. [Google Scholar] [CrossRef]
  7. Ursino, M.; Lodi, C.A. A simple mathematical model of the interaction between intracranial pressure and cerebral hemodynamics. Journal of applied physiology 1997, 82, 1256–1269. [Google Scholar] [CrossRef]
  8. Kiening, K.; Schoening, W.; Stover, J.; Unterberg, A. Continuous monitoring of intracranial compliance after severe head injury: relation to data quality, intracranial pressure and brain tissue PO2. British journal of neurosurgery 2003, 17, 311–318. [Google Scholar] [CrossRef]
  9. Ryder, H.W.; Espey, F.F.; Kimbell, F.D.; Penka, E.J.; Rosenauer, A.; Podolsky, B.; Evans, J.P. The mechanism of the change in cerebrospinal fluid pressure following an induced change in the volume of the fluid space. The Journal of laboratory and clinical medicine 1953, 41, 428–435. [Google Scholar]
  10. Czosnyka, M.; Pickard, J.D. Monitoring and interpretation of intracranial pressure. Journal of Neurology, Neurosurgery & Psychiatry 2004, 75, 813–821. [Google Scholar]
  11. Okon, M.D.; Roberts, C.J.; Mahmoud, A.M.; Springer, A.N.; Small, R.H.; McGregor, J.M.; Katz, S.E. Characteristics of the cerebrospinal fluid pressure waveform and craniospinal compliance in idiopathic intracranial hypertension subjects. Fluids Barriers CNS 2018, 15, 21. [Google Scholar] [CrossRef] [PubMed]
  12. Smielewski, P.; Czosnyka, M.; Roszkowski, M.; Walencik, A. Identification of the cerebrospinal compensatory mechanisms via computer-controlled drainage of the cerebrospinal fluid. Child's Nervous System 1995, 11, 297–300. [Google Scholar] [CrossRef]
  13. Alperin, N.J.; Lee, S.H.; Loth, F.; Raksin, P.B.; Lichtor, T. MR-Intracranial pressure (ICP): a method to measure intracranial elastance and pressure noninvasively by means of MR imaging: baboon and human study. Radiology 2000, 217, 877–885. [Google Scholar] [CrossRef]
  14. Tain, R.-W.; Alperin, N. Noninvasive intracranial compliance from MRI-based measurements of transcranial blood and CSF flows: indirect versus direct approach. IEEE transactions on biomedical engineering 2008, 56, 544–551. [Google Scholar] [CrossRef]
  15. Gholampour, S. FSI simulation of CSF hydrodynamic changes in a large population of non-communicating hydrocephalus patients during treatment process with regard to their clinical symptoms. PLoS One 2018, 13, e0196216. [Google Scholar] [CrossRef] [PubMed]
  16. Gholampour, S.; Frim, D.; Yamini, B. Long-term recovery behavior of brain tissue in hydrocephalus patients after shunting. Communications Biology 2022, 5, 1–13. [Google Scholar] [CrossRef]
  17. Gholampour, S.; Balasundaram, H.; Thiyagarajan, P.; Droessler, J. A mathematical framework for the dynamic interaction of pulsatile blood, brain, and cerebrospinal fluid. Computer Methods and Programs in Biomedicine 2023, 231, 107209. [Google Scholar] [CrossRef]
  18. Gholampour, S.; Fatouraee, N. Boundary conditions investigation to improve computer simulation of cerebrospinal fluid dynamics in hydrocephalus patients. Communications biology 2021, 4, 1–15. [Google Scholar] [CrossRef]
  19. Gholampour, S.; Fatouraee, N.; Seddighi, A.; Seddighi, A. Numerical simulation of cerebrospinal fluid hydrodynamics in the healing process of hydrocephalus patients. Journal of Applied Mechanics and Technical Physics 2017, 58, 386–391. [Google Scholar] [CrossRef]
  20. Gholampour, S.; Bahmani, M. Hydrodynamic comparison of shunt and endoscopic third ventriculostomy in adult hydrocephalus using in vitro models and fluid-structure interaction simulation. Comput Methods Programs Biomed 2021, 204, 106049. [Google Scholar] [CrossRef]
  21. Sahu, S.; Panda, N.; Swain, A.; Mathew, P.; Singla, N.; Gupta, S.; Jangra, K.; Bhardwaj, A.; Bhagat, H. Optic Nerve Sheath Diameter: Correlation With Intra-Ventricular Intracranial Measurements in Predicting Dysfunctional Intracranial Compliance. Cureus 2021, 13. [Google Scholar] [CrossRef]
  22. Wu, K.-C.; Sunwoo, J.; Sheriff, F.; Farzam, P.; Farzam, P.Y.; Orihuela-Espina, F.; LaRose, S.L.; Monk, A.D.; Aziz-Sultan, M.A.; Patel, N. Validation of diffuse correlation spectroscopy measures of critical closing pressure against transcranial Doppler ultrasound in stroke patients. Journal of biomedical optics 2021, 26, 036008–036008. [Google Scholar] [CrossRef]
  23. Brasil, S.; Solla, D.J.F.; Nogueira, R.d.C.; Teixeira, M.J.; Malbouisson, L.M.S.; Paiva, W.d.S. A Novel Noninvasive Technique for Intracranial Pressure Waveform Monitoring in Critical Care. Journal of Personalized Medicine 2021, 11, 1302. [Google Scholar] [CrossRef]
  24. Baghbani, R. An Electrical Model of Hydrocephalus Shunt Incorporating the CSF Dynamics. Sci Rep 2019, 9, 9751. [Google Scholar] [CrossRef]
  25. Misra, J.; Chakravarty, S. A poroelastic spheroidal shell model for studying the problem of head injury. Journal of mathematical analysis and applications 1984, 103, 332–343. [Google Scholar] [CrossRef]
  26. Chatelin, S.; Constantinesco, A.; Willinger, R. Fifty years of brain tissue mechanical testing: from in vitro to in vivo investigations. Biorheology 2010, 47, 255–276. [Google Scholar] [CrossRef]
  27. Franceschini, G.; Bigoni, D.; Regitnig, P.; Holzapfel, G.A. Brain tissue deforms similarly to filled elastomers and follows consolidation theory. Journal of the Mechanics and Physics of Solids 2006, 54, 2592–2620. [Google Scholar] [CrossRef]
  28. Hrapko, M.; Van Dommelen, J.; Peters, G.; Wismans, J. The mechanical behaviour of brain tissue: large strain response and constitutive modelling. Biorheology 2006, 43, 623–636. [Google Scholar]
  29. Cheng, S.; Bilston, L.E. Computational model of the cerebral ventricles in hydrocephalus. Journal of biomechanical engineering 2010, 132. [Google Scholar] [CrossRef]
  30. Elkin, B.S.; Ilankovan, A.I.; Morrison III, B. A detailed viscoelastic characterization of the P17 and adult rat brain. Journal of neurotrauma 2011, 28, 2235–2244. [Google Scholar] [CrossRef] [PubMed]
  31. Gholampour, S.; Yamini, B.; Droessler, J.; Frim, D. A New Definition for Intracranial Compliance to Evaluate Adult Hydrocephalus After Shunting. Front. Bioeng. Biotechnol. 10, 900644.
  32. Tuli, S.; O'Hayon, B.; Drake, J.; Clarke, M.; Kestle, J. Change in ventricular size and effect of ventricular catheter placement in pediatric patients with shunted hydrocephalus. Neurosurgery 1999, 45, 1329–1333, discussion 1333–1325. [Google Scholar] [CrossRef]
  33. Gholampour, S.; Fatouraee, N.; Seddighi, A.S.; Seddighi, A. Evaluating the effect of hydrocephalus cause on the manner of changes in the effective parameters and clinical symptoms of the disease. Journal of Clinical Neuroscience 2017, 35, 50–55. [Google Scholar] [CrossRef]
  34. Czosnyka, M.; Citerio, G. Brain compliance: the old story with a new ‘et cetera’. Springer: 2012; Vol. 38, pp 925-927.
  35. Portella, G.; Cormio, M.; Citerio, G.; Contant, C.; Kiening, K.; Enblad, P.; Piper, I. Continuous cerebral compliance monitoring in severe head injury: its relationship with intracranial pressure and cerebral perfusion pressure. Acta neurochirurgica 2005, 147, 707–713. [Google Scholar] [CrossRef] [PubMed]
  36. Gaohua, L.; Kimura, H. A mathematical model of intracranial pressure dynamics for brain hypothermia treatment. Journal of theoretical biology 2006, 238, 882–900. [Google Scholar] [CrossRef] [PubMed]
  37. Eklund, A.; Smielewski, P.; Chambers, I.; Alperin, N.; Malm, J.; Czosnyka, M.; Marmarou, A. Assessment of cerebrospinal fluid outflow resistance. Medical & biological engineering & computing 2007, 45, 719–735. [Google Scholar]
  38. Kazimierska, A.; Kasprowicz, M.; Czosnyka, M.; Placek, M.M.; Baledent, O.; Smielewski, P.; Czosnyka, Z. Compliance of the cerebrospinal space: Comparison of three methods. Acta Neurochirurgica 2021, 163, 1979–1989. [Google Scholar] [CrossRef] [PubMed]
  39. Czosnyka, M.; Czosnyka, Z.; Agarwal-Harding, K.J.; Pickard, J.D. Modeling of CSF dynamics: legacy of Professor Anthony Marmarou. In Hydrocephalus; Springer, 2012; pp. 9–14. [Google Scholar]
  40. Xu, H.; Fame, R.M.; Sadegh, C.; Sutin, J.; Naranjo, C.; Syau, D.; Cui, J.; Shipley, F.B.; Vernon, A.; Gao, F. Choroid plexus NKCC1 mediates cerebrospinal fluid clearance during mouse early postnatal development. Nature communications 2021, 12, 1–16. [Google Scholar] [CrossRef] [PubMed]
  41. Yuan, T.; Zhan, W.; Jamal, A.; Dini, D. On the microstructurally driven heterogeneous response of brain white matter to drug infusion pressure. Biomechanics and Modeling in Mechanobiology 2022, 21, 1299–1316. [Google Scholar] [CrossRef]
  42. Lambride, C.; Christodoulou, N.; Michail, A.; Vavourakis, V.; Stylianopoulos, T. Decompressive craniectomy of post-traumatic brain injury: an in silico modelling approach for intracranial hypertension management. Scientific reports 2020, 10, 18673. [Google Scholar] [CrossRef]
  43. Guo, L.; Vardakis, J.C.; Lassila, T.; Mitolo, M.; Ravikumar, N.; Chou, D.; Lange, M.; Sarrami-Foroushani, A.; Tully, B.J.; Taylor, Z.A. Subject-specific multi-poroelastic model for exploring the risk factors associated with the early stages of Alzheimer's disease. Interface focus 2018, 8, 20170019. [Google Scholar] [CrossRef] [PubMed]
  44. Gholampour, S.; Fatouraee, N.; Seddighi, A.S.; Yazdani, S.O. A Hydrodynamical Study to propose a numerical Index for evaluating the CSF conditions in cerebralventricular system. International Clinical Neuroscience Journal 2014, 1, 1–9. [Google Scholar]
  45. Gholampour, S.; Seddighi, A.; Fatouraee, N. Relationship between Spinal fluid and Cerebrospinal fluid as an index for assessment of non-communicating hydrocephalus. Modares Mechanical Engineering 2015, 14. [Google Scholar]
  46. Li, W.; Shepherd, D.E.; Espino, D.M. Investigation of the compressive viscoelastic properties of brain tissue under time and frequency dependent loading conditions. Annals of Biomedical Engineering 2021, 49, 3737–3747. [Google Scholar] [CrossRef]
  47. Siegkas, P.; Sharp, D.J.; Ghajari, M. The traumatic brain injury mitigation effects of a new viscoelastic add-on liner. Scientific reports 2019, 9, 3471. [Google Scholar] [CrossRef]
  48. Menghani, R.R.; Das, A.; Kraft, R.H. A sensor-enabled cloud-based computing platform for computational brain biomechanics. Computer Methods and Programs in Biomedicine 2023, 107470. [Google Scholar] [CrossRef]
  49. Wang, F.; Han, Y.; Wang, B.; Peng, Q.; Huang, X.; Miller, K.; Wittek, A. Prediction of brain deformations and risk of traumatic brain injury due to closed-head impact: quantitative analysis of the effects of boundary conditions and brain tissue constitutive model. Biomechanics and Modeling in Mechanobiology 2018, 17, 1165–1185. [Google Scholar] [CrossRef]
  50. Wilkie, K.P.; Drapaca, C.S.; Sivaloganathan, S. A mathematical investigation of the role of intracranial pressure pulsations and small gradients in the pathogenesis of hydrocephalus. International journal of numerical analysis & modeling. Series B 2012, 3, 36. [Google Scholar]
  51. Dutta-Roy, T. Does Normal Pressure Hydrocephalus Have Mechanistic Causes? University of Western Australia; 2011.
  52. Pavan, P.G.; Nasim, M.; Brasco, V.; Spadoni, S.; Paoloni, F.; d'Avella, D.; Khosroshahi, S.F.; de Cesare, N.; Gupta, K.; Galvanetto, U. Development of detailed finite element models for in silico analyses of brain impact dynamics. Computer Methods and Programs in Biomedicine 2022, 227, 107225. [Google Scholar] [CrossRef] [PubMed]
  53. Hosseini-Farid, M.; Ramzanpour, M.; McLean, J.; Ziejewski, M.; Karami, G. A poro-hyper-viscoelastic rate-dependent constitutive modeling for the analysis of brain tissues. Journal of the Mechanical Behavior of Biomedical Materials 2020, 102, 103475. [Google Scholar] [CrossRef] [PubMed]
  54. Forte, A.E.; Gentleman, S.M.; Dini, D. On the characterization of the heterogeneous mechanical response of human brain tissue. Biomechanics and modeling in mechanobiology 2017, 16, 907–920. [Google Scholar] [CrossRef] [PubMed]
  55. Heldt, T.; Zoerle, T.; Teichmann, D.; Stocchetti, N. Intracranial pressure and intracranial elastance monitoring in neurocritical care. Annual review of biomedical engineering 2019, 21, 523–549. [Google Scholar] [CrossRef] [PubMed]
  56. Sridharan, A.; Rajan, S.D.; Muthuswamy, J. Long-term changes in the material properties of brain tissue at the implant–tissue interface. Journal of neural engineering 2013, 10, 066001. [Google Scholar] [CrossRef] [PubMed]
  57. Boulet, T.; Kelso, M.L.; Othman, S.F. Microscopic magnetic resonance elastography of traumatic brain injury model. Journal of neuroscience methods 2011, 201, 296–306. [Google Scholar] [CrossRef] [PubMed]
  58. Eide, P.K.; Brean, A. Cerebrospinal fluid pulse pressure amplitude during lumbar infusion in idiopathic normal pressure hydrocephalus can predict response to shunting. Cerebrospinal fluid research 2010, 7, 1–11. [Google Scholar] [CrossRef] [PubMed]
  59. Eide, P.K. The pathophysiology of chronic noncommunicating hydrocephalus: lessons from continuous intracranial pressure monitoring and ventricular infusion testing. Journal of neurosurgery 2017, 129, 220–233. [Google Scholar] [CrossRef] [PubMed]
  60. Mase, M.; Miyati, T.; Yamada, K.; Kasai, H.; Hara, M.; Shibamoto, Y. Non-invasive measurement of intracranial compliance using cine MRI in normal pressure hydrocephalus. In Intracranial Pressure and Brain Monitoring XII; Springer, 2005; pp. 303–306. [Google Scholar]
  61. Meier, U.; Bartels, P. The importance of the intrathecal infusion test in the diagnostic of normal-pressure hydrocephalus. European neurology 2001, 46, 178–186. [Google Scholar] [CrossRef] [PubMed]
  62. Sahuquillo, J.; Rubio, E.; Codina, A.; Molins, A.; Guitart, J.; Poca, M.; Chasampi, A. Reappraisal of the intracranial pressure and cerebrospinal fluid dynamics in patients with the so-called “normal pressure hydrocephalus” syndrome. Acta neurochirurgica 1991, 112, 50–61. [Google Scholar] [CrossRef]
  63. Lokossou, A.; Balédent, O.; Garnotel, S.; Page, G.; Balardy, L.; Czosnyka, Z.; Payoux, P.; Schmidt, E. ICP monitoring and phase-contrast MRI to investigate intracranial compliance. In Intracranial Pressure & Neuromonitoring XVI; Springer, 2018; pp. 247–253. [Google Scholar]
  64. Eide, P.K. The correlation between pulsatile intracranial pressure and indices of intracranial pressure-volume reserve capacity: results from ventricular infusion testing. Journal of neurosurgery 2016, 125, 1493–1503. [Google Scholar] [CrossRef]
  65. Czosnyka, M.; Batorski, L.; Roszkowski, M.; Tomaszewski, J.; Wocjan, J.; Walencik, A.; Zabolotny, W. Cerebrospinal compensation in hydrocephalic children. Child's Nervous System 1993, 9, 17–22. [Google Scholar] [CrossRef]
  66. Shapiro, K.; Fried, A. Pressure-volume relationships in shunt-dependent childhood hydrocephalus: The zone of pressure instability in children with acute deterioration. Journal of neurosurgery 1986, 64, 390–396. [Google Scholar] [CrossRef] [PubMed]
  67. Jeong, J.-H. The Pathophysiology of Brain Edema and Intracranial Hypertension. Journal of Neurocritical Care 2016, 9, 59–62. [Google Scholar] [CrossRef]
  68. Piper, I. Intracranial pressure and elastance. Head injury 1997, 101–120. [Google Scholar]
  69. Okon, M.D.; Roberts, C.J.; Mahmoud, A.M.; Springer, A.N.; Small, R.H.; McGregor, J.M.; Katz, S.E. Characteristics of the cerebrospinal fluid pressure waveform and craniospinal compliance in idiopathic intracranial hypertension subjects. Fluids and Barriers of the CNS 2018, 15, 1–7. [Google Scholar] [CrossRef] [PubMed]
  70. Tisell, M.; Edsbagge, M.; Stephensen, H.; Czosnyka, M.; Wikkelsø, C. Elastance correlates with outcome after endoscopic third ventriculostomy in adults with hydrocephalus caused by primary aqueductal stenosis. Neurosurgery 2002, 50, 70–77. [Google Scholar] [PubMed]
  71. Eide, P.; Park, E.H.; Madsen, J. Arterial blood pressure vs intracranial pressure in normal pressure hydrocephalus. Acta neurologica scandinavica 2010, 122, 262–269. [Google Scholar] [CrossRef] [PubMed]
  72. Thavarajasingam, S.G.; El-Khatib, M.; Rea, M.; Russo, S.; Lemcke, J.; Al-Nusair, L.; Vajkoczy, P. Clinical predictors of shunt response in the diagnosis and treatment of idiopathic normal pressure hydrocephalus: a systematic review and meta-analysis. Acta Neurochirurgica 2021, 163, 2641–2672. [Google Scholar] [CrossRef] [PubMed]
  73. Gholampour, S.; Nguyen, A.; Chaudry, S. Intracranial compliance, resistance to CSF-outflow, and pressure-volume index in hydrocephalus patients: A systematic review and meta-analysis. IRBM 2023, 100785. [Google Scholar] [CrossRef]
  74. Budday, S.; Sommer, G.; Holzapfel, G.; Steinmann, P.; Kuhl, E. Viscoelastic parameter identification of human brain tissue. Journal of the mechanical behavior of biomedical materials 2017, 74, 463–476. [Google Scholar] [CrossRef]
  75. Lesniak, M.; Clatterbuck, R.; Rigamonti, D.; Williams, M. Low pressure hydrocephalus and ventriculomegaly: hysteresis, non-linear dynamics, and the benefits of CSF diversion. British journal of neurosurgery 2002, 16, 555–561. [Google Scholar] [CrossRef]
  76. Ringstad, G.; Vatnehol, S.A.S.; Eide, P.K. Glymphatic MRI in idiopathic normal pressure hydrocephalus. Brain 2017, 140, 2691–2705. [Google Scholar] [CrossRef] [PubMed]
  77. Taoka, T.; Masutani, Y.; Kawai, H.; Nakane, T.; Matsuoka, K.; Yasuno, F.; Kishimoto, T.; Naganawa, S. Evaluation of glymphatic system activity with the diffusion MR technique: diffusion tensor image analysis along the perivascular space (DTI-ALPS) in Alzheimer’s disease cases. Japanese journal of radiology 2017, 35, 172–178. [Google Scholar] [CrossRef] [PubMed]
  78. Iliff, J.J.; Chen, M.J.; Plog, B.A.; Zeppenfeld, D.M.; Soltero, M.; Yang, L.; Singh, I.; Deane, R.; Nedergaard, M. Impairment of glymphatic pathway function promotes tau pathology after traumatic brain injury. Journal of Neuroscience 2014, 34, 16180–16193. [Google Scholar] [CrossRef] [PubMed]
Preprints 88815 g001
Figure 1. Volume-ICP relationships in short and large TEs. (a) shows the monotonic trend of volume-ICP curve in a short TE. Two compensatory reserve zones are shown. The first zone is the upper reserve zone (blue line). In this zone, the ICP remains relatively stable despite changes in volume. This is due to the brain’s ability to compensate by reducing the volume of CSF and increasing blood flow out of the brain. Another zone is the lower reserve zone (green line). In this zone, the brain’s compensatory mechanisms are exhausted, and further increases in volume lead to a rapid increase in ICP to reach a plateau ICP. (b) shows the non-monotonic trend of the volume-ICP curve in a large TE after treatment for a hydrocephalus patient. The compensatory response of the brain could somewhat recover at certain times in a large TE. This curve is not divisible into some specific compensatory reserve zones. ICP: Intracranial pressure, ICC: Intracranial compliance, TE: Time elapsed, CSF: Cerebrospinal fluid.
Figure 1. Volume-ICP relationships in short and large TEs. (a) shows the monotonic trend of volume-ICP curve in a short TE. Two compensatory reserve zones are shown. The first zone is the upper reserve zone (blue line). In this zone, the ICP remains relatively stable despite changes in volume. This is due to the brain’s ability to compensate by reducing the volume of CSF and increasing blood flow out of the brain. Another zone is the lower reserve zone (green line). In this zone, the brain’s compensatory mechanisms are exhausted, and further increases in volume lead to a rapid increase in ICP to reach a plateau ICP. (b) shows the non-monotonic trend of the volume-ICP curve in a large TE after treatment for a hydrocephalus patient. The compensatory response of the brain could somewhat recover at certain times in a large TE. This curve is not divisible into some specific compensatory reserve zones. ICP: Intracranial pressure, ICC: Intracranial compliance, TE: Time elapsed, CSF: Cerebrospinal fluid.
Preprints 88815 g001
Preprints 88815 g002
Figure 2. Changes in compensatory response of the brain in a large TE. (a) shows the changes in volume and ICP at different time points in a large TE. This shows that the parameter of time, in addition to volume and ICP, can affect the compensatory response of the brain in a large TE – contrasting with short TE. (b) shows changes in ICC with ICP at different time points. This shows that the ICC trend and the compensatory response of the brain can have non-monotonic and variable changes in a large TE. ICP: Intracranial pressure, ICC: Intracranial compliance, TE: Time elapsed.
Figure 2. Changes in compensatory response of the brain in a large TE. (a) shows the changes in volume and ICP at different time points in a large TE. This shows that the parameter of time, in addition to volume and ICP, can affect the compensatory response of the brain in a large TE – contrasting with short TE. (b) shows changes in ICC with ICP at different time points. This shows that the ICC trend and the compensatory response of the brain can have non-monotonic and variable changes in a large TE. ICP: Intracranial pressure, ICC: Intracranial compliance, TE: Time elapsed.
Preprints 88815 g002
Table 2. Comparison of differences in values and measurement methods of intracranial compliance, as well as the time elapsed (TE), in hydrocephalus patients.
Table 2. Comparison of differences in values and measurement methods of intracranial compliance, as well as the time elapsed (TE), in hydrocephalus patients.
Age Type of hydrocephalus Authors, year Intracranial compliance measurement method Procedure type Intracranial compliance (ml/mmHg) Time elapsed
(minute)		 Source
Adult Noncommunicating hydrocephalus Gholampour et al, 2021 Computer simulation Non-invasive 0.78 0.17 [20]
Eide,
2017 		Ventricular constant-flow infusion Invasive 0.60 15.5 [59]
Normal pressure hydrocephalus Kazmierska et al, 2021 Computer-assisted constant-flow infusion Invasive 0.27 13.2 [38]
Mase
et al. 2005		 Computer simulation Non-invasive 0.003 --- [60]
Meier and Bartels, 2001 Computer-assisted constant-flow intrathecal infusion Invasive 0.36 10.5 [61]
Sahuquillo et al, 1991 Bolus injection,
Lumbar and ventricular constant-flow infusion		 Invasive 0.33 15.0 [62]
Communicating hydrocephalus Eide,
2017 		Ventricular constant-flow infusion Invasive 0.66 15.5 [59]
Hydrocephalus Lokossou
et al, 2018		 Lumbar constant-flow infusion Invasive 0.23 --- [63]
Eide,
2016		 Ventricular constant-flow infusion Invasive 0.6 15.5 [64]
Pediatric Noncommunicating hydrocephalus Czosnyka
et al, 1993 		Computer-assisted lumbar infusion Invasive 1.27 6.3 [65]
Acute hydrocephalus Czosnyka
et al, 1993		 Computer-assisted lumbar infusion Invasive 0.97 6.3 [65]
Hydrocephalus Shapiro and Fried, 1986 Bolus withdrawal and injection Invasive 0.32 --- [66]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

112

Views

63

Comments

0

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

Email

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated