Submitted:
24 October 2023
Posted:
25 October 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
1.1. The medical malpractice in Italy: liability rule and definition of claims reserve
1.2. Structure and main ideas
2. Theoretical background
2.1. Run-Off triangles and Chain-Ladder approach
2.2. Generalized Linear Model
- the function p is not linear;
- the explicative variables don’t take values from the interval ;
- the variance is not constant;
- it is not possible to assume the response variable Y following the normal distribution.
2.3. Quasi-likelihood function
2.4. Gauss-Newton algorithm
2.4.1. The Hessian modification
2.4.2. Limits of the GN algorithm
2.5. The genetic algorithm
2.6. Expectation values and error estimation
3. Comparison with SoA Models
3.1. Comparison with [22]
3.2. Comparison with [23]
4. The health care study: the case of claims in the Tuscany Region
4.1. Preliminary analysis
- Time evolution of the paid claims;
- Single payment for years of the specific claim;
- Total paid amounts.
4.2. Chain Ladder Results
4.3. Stochastic Approach Results
5. Conclusion
Acknowledgments
Conflicts of Interest
References
- Institute of Medicine (U.S.) Committee on Quality of Health Care in America. To Err is Human - Building a safer health system.
- Delivering quality health services: a global imperative for universal health coverage. OECD, World Health Organization & World Bank Group. OECD Publishing.
- 2021. State of Health in the EU: Italy. OECD, European Commission & European Observatory on Health Systems and Policies. OECD Publishing.
- Conn, Andrew, Nicholas Gould, and Philippe Toint. 1991, 04. A globally convergent augmented lagrangian algorithm for optimization with general constraints and simple bounds. SIAM Journal on Numerical Analysis 28. [CrossRef]
- Conn, Andrew, Nicholas Gould, and Philippe Toint. 1997. A globally convergent augmented lagrangian barrier algorithm for optimization with general inequality constraints and simple bounds. Mathematics of Computation 66, 261–268. [CrossRef]
- D. Mushinski; S. Zahran; A. Frazier. 2022. Physician behaviour, malpractice risk and defensive medicine: an investigation of cesarean deliveries. Health Economics, Policy and Law. [CrossRef]
- England, Peter and Richard Verrall. 1999. Analytic and bootstrap estimates of prediction errors in claims reserving. Insurance: Mathematics and Economics 25(3), 281–293. [CrossRef]
- England, P D and R J Verrall. 2002. Stochastic claims reserving in general insurance. British Actuarial Journal 8, 443–544.
- Fletcher, R. 2000. Practical Methods of Optimization, 2nd Edition. Wiley. [CrossRef]
- Goldberg, David E. 1989. Genetic Algorithms in Search, Optimization and Machine Learning. Addison-Wesley Longman Publishing Co., Inc.
- Hess, Klaus Th. and Klaus D Schmidt. 2002. A comparison of models for the chain–ladder method. Insurance: Mathematics and Economics 31, 351–364. [CrossRef]
- Hindley, David. 2017, 10. Claims Reserving in General Insurance. Cambridge University Press. [CrossRef]
- Jorge Nocedal and Stephen J. Wright. 2006. Numerical Optimization (2e ed.). New York, NY, USA: Springer.
- Kendall, Maurice George and Alan Stuart. 1967. The Advanced Theory of Statistics (2 ed.). Hafner.
- Larsen, Christian Roholte. 2007. An individual claims reserving model. ASTIN Bulletin 37(1), 113–132. [CrossRef]
- Mascarenhas, Walter. 2013, 09. The divergence of the bfgs and gauss-newton methods. Mathematical Programming 147. [CrossRef]
- Nelder, John Ashworth and Robert William Maclagan Wedderburn. 1972. Generalized Linear Model. Journal of the Royal Statistical Society: Series A 135, 370. [CrossRef]
- Nuno, Grembi Veronica; Garoupa. 2013. Delays in medical malpractice litigation in civil law jurisdictions: Some evidence from the italian court of cassation. Health Economics, Policy and Law. 8(4), 423–452. [CrossRef]
- Renshaw, A E and R J Verrall. 1998, 10. A stochastic model underlying the chain-ladder technique. British Actuarial Journal 4, 903–923. [CrossRef]
- Schmidt, Klaus D. 2006. Methods and models of loss reserving based on run-off triangles: A unifying survey. Casualty Actuarial Society Forum 2006, 269–317.
- Schmidt, Klaus D. 2012. Loss prediction based on run-off triangles. AStA Advances in Statistical Analysis 96, 265 – 310. [CrossRef]
- Strascia, Stefano Cavastracci and Agostino Tripodi. 2018. Overdispersed-poisson model in claims reserving: Closed tool for one-year volatility in glm framework. Risks 6. [CrossRef]
- Verdonck, Tim, Martine Van Wouwe, and Jan Dhaene. 2009. A robustification of the chain-ladder method. North American Actuarial Journal 13, 280 – 298. [CrossRef]
- Veronica, Bertoli Paola; Grembi. 2018. Courts, scheduled damages, and medical malpractice insurance. Empirical Economics 55, 831–854. [CrossRef]
- Verrall, R.J. 2000. An investigation into stochastic claims reserving models and the chain-ladder technique. Insurance: Mathematics and Economics 26(1), 91–99. [CrossRef]
- Verrall, R J. 1991. Chain ladder and maximum likelihood. Journal of the Institute of Actuaries (1886-1994) 118, 489–499.
- Wedderburn, R W M. 1974. Quasi-likelihood functions, generalized linear models, and the gauss-newton method. Biometrika 61, 439 – 447. [CrossRef]
- Wedderburn, R W M. 1976. On the existence and uniqueness of the maximum likelihood estimates for certain generalized linear models. Biometrika 63, 27 – 32. [CrossRef]
| 1 | Data in the present paper are smoothed for policy and legal motivations. |
| 2 | A nuisance parameter is any unspecified parameter necessary to ensure that the model describes the system adequately. In our case, it represents the dispersion of the measured data. |
| 0 | 1 | … | j | … | J | ||
|---|---|---|---|---|---|---|---|
| 1 | … | … | |||||
| 2 | … | … | |||||
| ... | ... | ... | ... | ||||
| i | … | ||||||
| ... | ... | ... | |||||
| I |
| 0 | 1 | … | j | … | J | ||
|---|---|---|---|---|---|---|---|
| 1 | … | … | |||||
| 2 | … | … | |||||
| ... | ... | ... | ... | ... | ... | ||
| i | … | … | |||||
| ... | ... | ... | ... | ... | ... | ||
| … | … | ||||||
| I | … | … |
| Budget year (t) |
Paid (103 €) Literature |
(103 €) Literature |
(103 €) Residue (Eq. 46) |
(103 €) Residue (Eq. 47) |
|---|---|---|---|---|
| 0 | 22.60 | - | 22.60 ± 1.43 | 22.60 ± 1.43 |
| 1 | 62.32 | - | 62.32 ± 5.70 | 62.32 ± 5.65 |
| 2 | 101.93 | - | 101.93 ± 9.25 | 101.93 ± 9.03 |
| 3 | 124.59 | - | 124.59 ± 12.12 | 124.59 ± 11.57 |
| 4 | 152.04 | - | 152.04 ± 14.82 | 152.04 ± 13.85 |
| 5 | 188.65 | - | 188.65 ± 17.33 | 188.65 ± 16.03 |
| 6 | 185.31 | - | 185.31 ± 19.72 | 185.31 ± 18.45 |
| 7 | 203.38 | - | 203.38 ± 21.77 | 203.38 ± 20.40 |
| 8 | 213.67 | - | 213.67 ± 23.03 | 213.67 ± 21.37 |
| 9 | 207.65 | - | 207.65 ± 23.39 | 207.65 ± 21.63 |
| 10 | 197.67 | - | 197.67 ± 23.64 | 197.67 ± 21.84 |
| 11 | 184.68 | - | 184.68 ± 24.99 | 184.68 ± 23.10 |
| 12 | 194.08 | - | 194.08 ± 29.10 | 194.08 ± 27.00 |
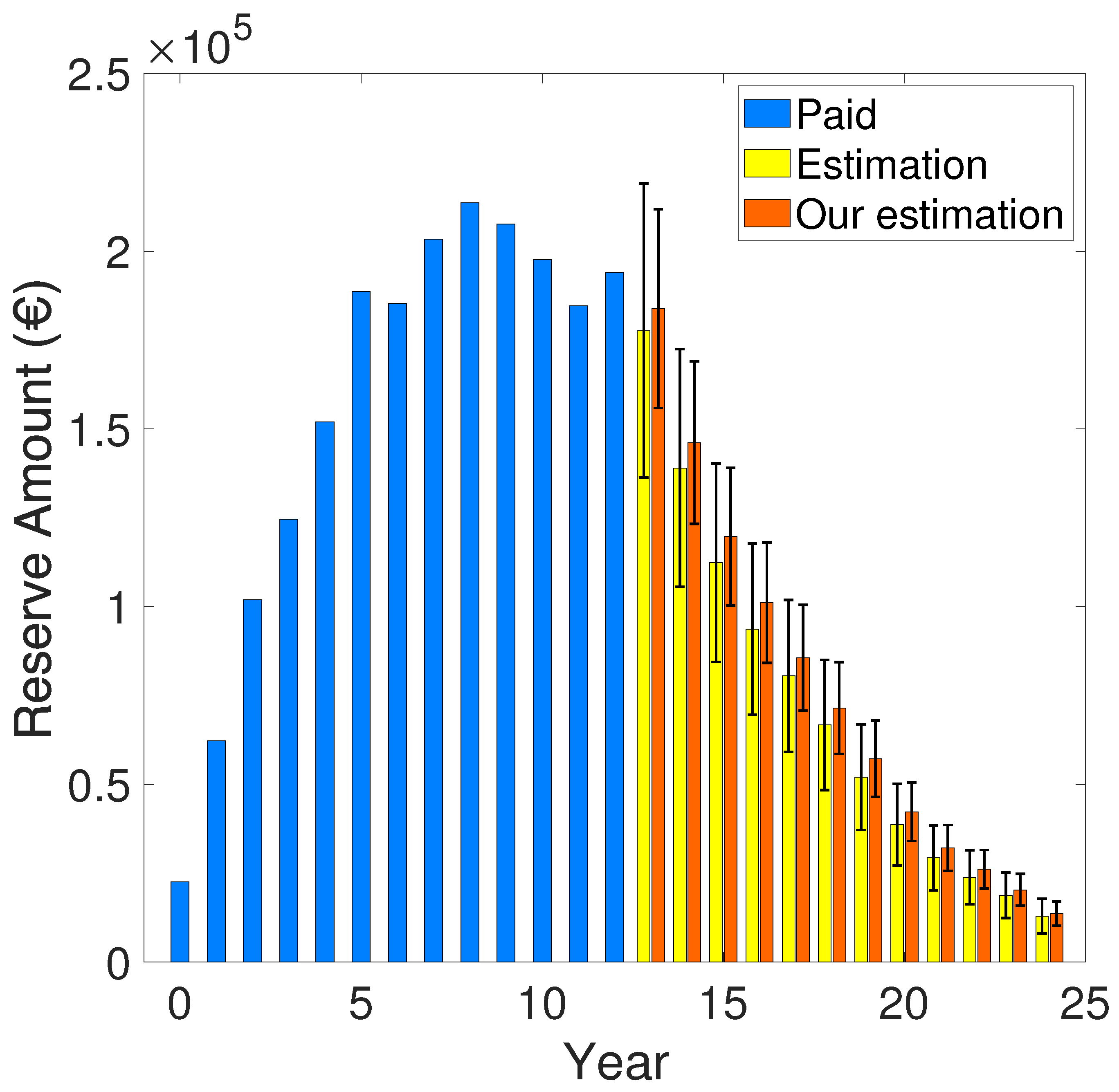
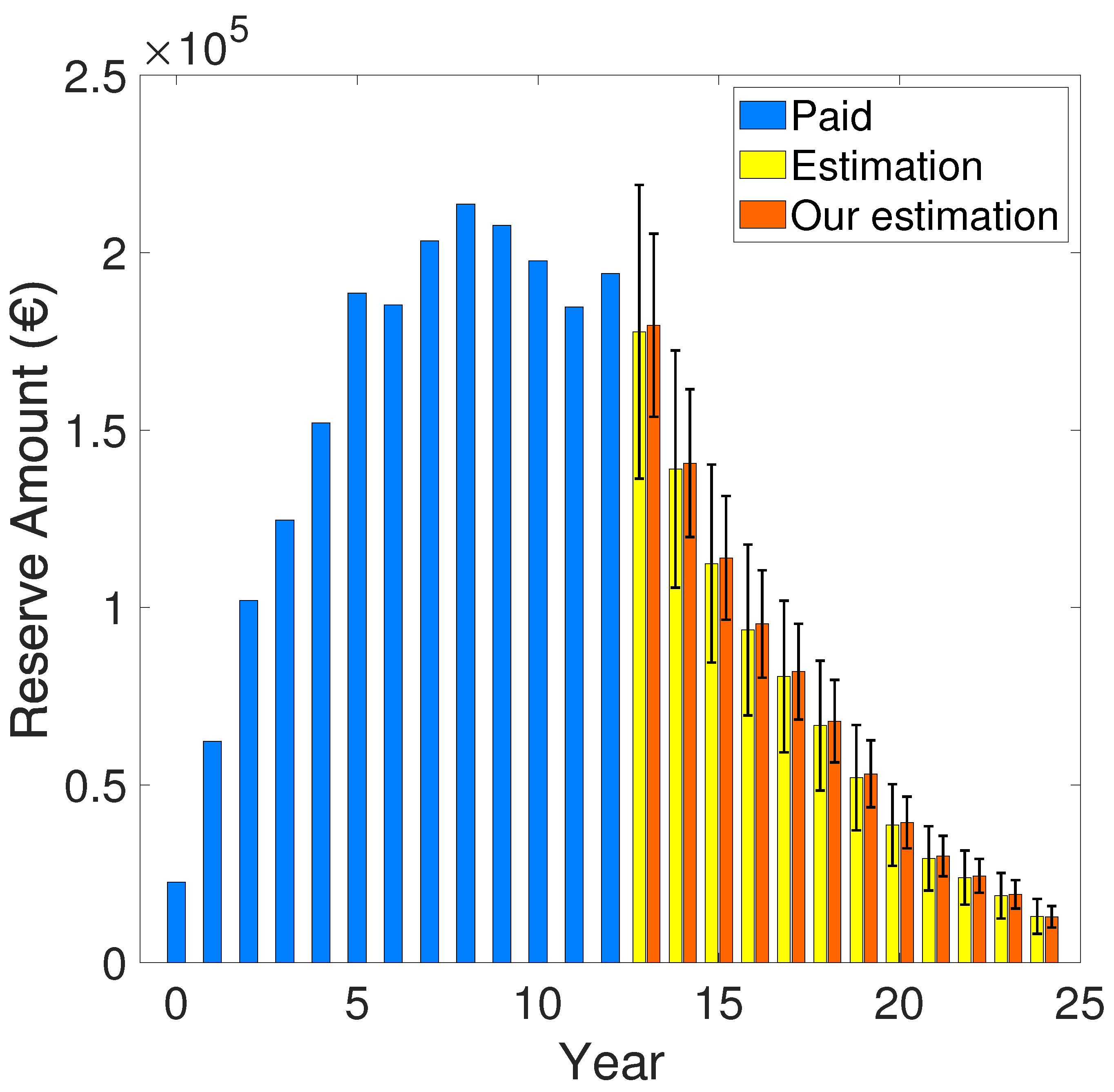
| 13 | - | 177.71 ± 41.39 | 183.87 ± 27.96 | 179.53 ± 25.78 |
| 14 | - | 139.04 ± 33.41 | 146.17 ± 22.90 | 140.69 ± 20.80 |
| 15 | - | 112.39 ± 27.91 | 119.75 ± 19.38 | 113.99 ± 17.43 |
| 16 | - | 93.69 ± 24.06 | 101.15 ± 16.98 | 95.37 ± 15.13 |
| 17 | - | 80.55 ± 21.36 | 85.66 ± 14.89 | 81.93 ± 13.48 |
| 18 | - | 66.73 ± 18.32 | 71.52 ± 12.90 | 67.97 ± 11.61 |
| 19 | - | 52.05 ± 14.84 | 57.26 ± 10.72 | 53.14 ± 9.43 |
| 20 | - | 38.71 ± 11.50 | 42.30 ± 8.21 | 39.44 ± 7.26 |
| 21 | - | 29.33 ± 9.05 | 32.14 ± 6.44 | 29.97 ± 5.71 |
| 22 | - | 23.89 ± 7.62 | 26.14 ± 5.41 | 24.38 ± 4.78 |
| 23 | - | 18.78 ± 6.39 | 20.36 ± 4.50 | 19.19 ± 4.00 |
| 24 | - | 12.95 ± 4.93 | 13.69 ± 3.40 | 12.85 ± 3.01 |
| Residue (Eq. 46) |
Reference | ( €) | ||
|---|---|---|---|---|
| [22] | 8.46 ± 2.20 | |||
| Our work | 9.00 ± 1.54 | |||
| Residue (Eq. 47) |
Reference | ( €) | ||
| [22] | 8.46 ± 2.20 | |||
| Our work | 8.58 ± 1.38 |
| Budget year (t) |
Paid (106 €) Literature |
(106 €) Literature |
(106 €) Residue (Eq. 46) |
(106 €) Residue (Eq. 47) |
|---|---|---|---|---|
| 0 | 135.34 | - | 135.34 ± 3.05 | 135.34 ± 2.92 |
| 1 | 216.03 | - | 216.03 ± 7.56 | 216.03 ± 7.38 |
| 2 | 294.31 | - | 294.31 ± 11.12 | 294.31 ± 10.84 |
| 3 | 353.38 | - | 353.38 ± 14.22 | 353.38 ± 13.84 |
| 4 | 431.01 | - | 431.01 ± 17.14 | 431.01 ± 16.69 |
| 5 | 463.80 | - | 463.80 ± 19.19 | 463.80 ± 18.65 |
| 6 | 478.03 | - | 478.03 ± 20.99 | 478.03 ± 20.33 |
| 7 | 493.10 | - | 493.10 ± 22.89 | 493.10 ± 22.20 |
| 8 | 507.59 | - | 507.59 ± 25.35 | 507.59 ± 24.53 |
| 9 | 535.26 | - | 535.26 ± 28.75 | 535.26 ± 27.84 |
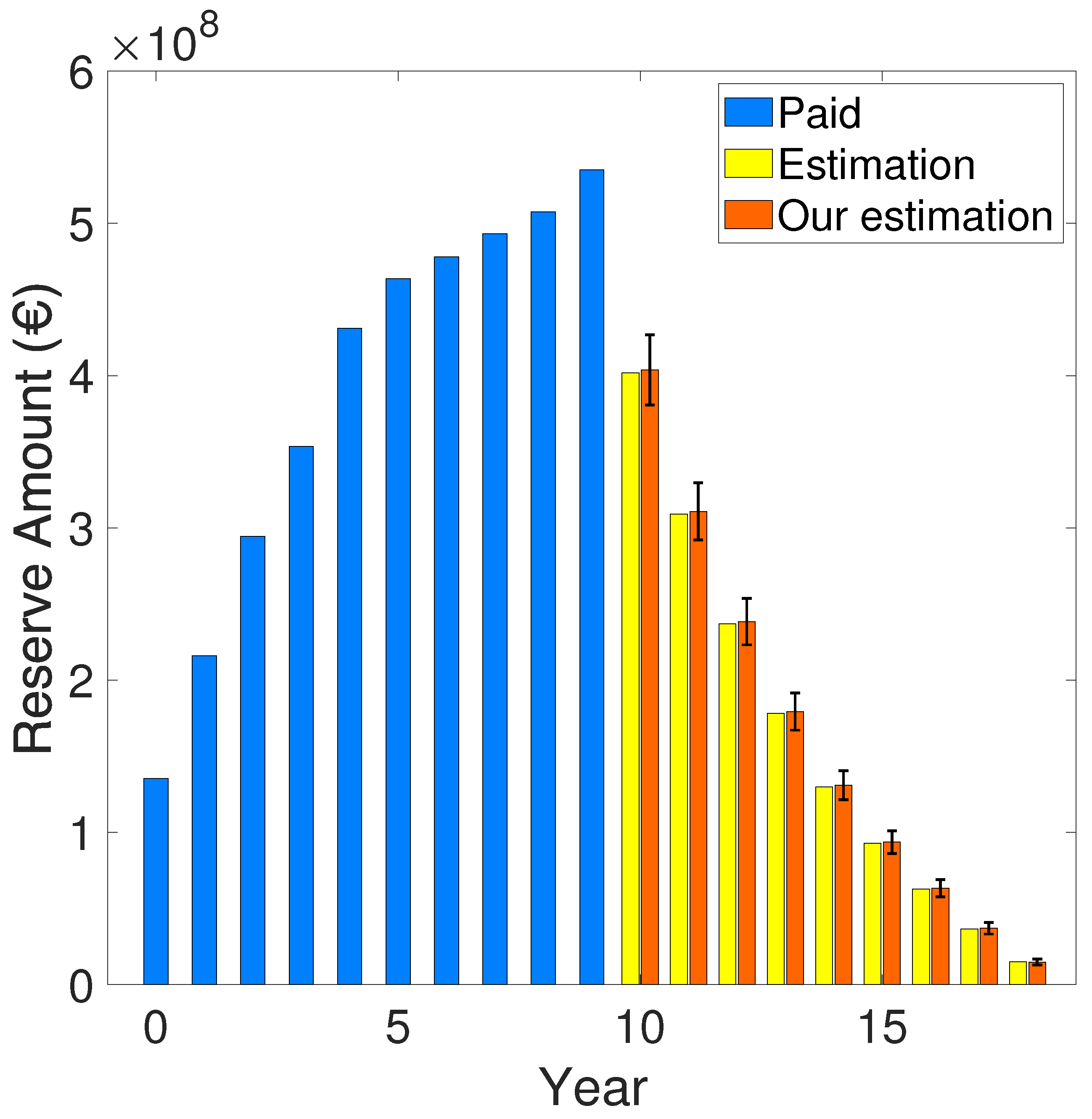
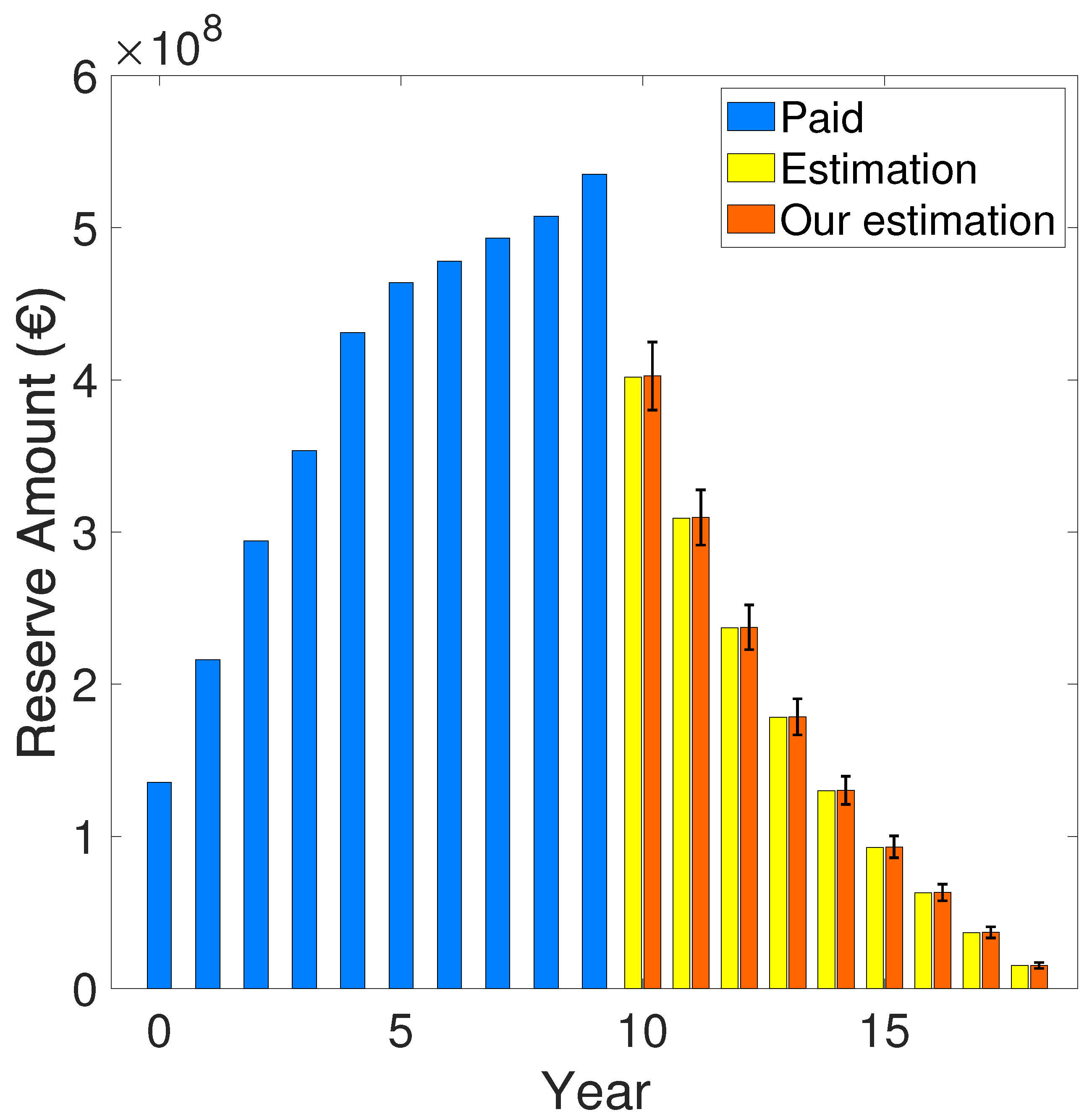
| 10 | - | 401.96 | 403.74 ± 23.07 | 402.54 ± 22.35 |
| 11 | - | 309.07 | 310.82 ± 18.74 | 309.57 ± 18.13 |
| 12 | - | 236.98 | 238.43 ± 15.25 | 237.42 ± 14.75 |
| 13 | - | 178.16 | 179.39 ± 12.26 | 178.56 ± 11.86 |
| 14 | - | 129.86 | 131.02 ± 9.57 | 130.23 ± 9.24 |
| 15 | - | 92.78 | 93.62 ± 7.45 | 93.08 ± 7.19 |
| 16 | - | 62.85 | 63.36 ± 5.61 | 63.08 ± 5.43 |
| 17 | - | 36.63 | 37.03 ± 3.82 | 36.83 ± 3.69 |
| 18 | - | 15.12 | 14.87 ± 1.93 | 15.11 ± 1.90 |
| Residue (Eq. 46) |
Reference | ( €) | ||
|---|---|---|---|---|
| [23] | - | - | 1.46 | |
| Our work | 1.47 ± 0.09 | |||
| Residue (Eq. 47) |
Reference | ( €) | ||
| [23] | - | - | 1.46 | |
| Our work | 1.47 ± 0.09 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2010 | 2.80 | 5.94 | 10.1 | 5.00 | 4.06 | 4.28 | 2.74 | 1.98 | 2.64 | 1.06 | 1.20 | 1.27 |
| 2011 | 2.13 | 11.3 | 6.15 | 1.79 | 2.82 | 4.29 | 5.26 | 7.76 | 4.91 | 3.35 | 1.43 | |
| 2012 | 0.95 | 7.61 | 7.19 | 3.25 | 4.77 | 3.08 | 5.03 | 5.65 | 3.64 | 1.74 | ||
| 2013 | 0.72 | 8.66 | 5.68 | 1.63 | 3.44 | 4.06 | 4.89 | 3.95 | 2.50 | |||
| 2014 | 0.97 | 9.76 | 7.67 | 6.49 | 4.07 | 5.66 | 4.41 | 3.90 | ||||
| 2015 | 1.50 | 11.4 | 7.17 | 3.95 | 6.52 | 5.76 | 7.87 | |||||
| 2016 | 1.15 | 5.14 | 9.14 | 9.74 | 3.33 | 2.95 | ||||||
| 2017 | 0.19 | 6.96 | 8.92 | 5.77 | 3.63 | |||||||
| 2018 | 0.10 | 5.90 | 9.36 | 3.68 | ||||||||
| 2019 | 2.35 | 5.55 | 10.9 | |||||||||
| 2020 | 0.27 | 6.57 | ||||||||||
| 2021 | 0.81 |
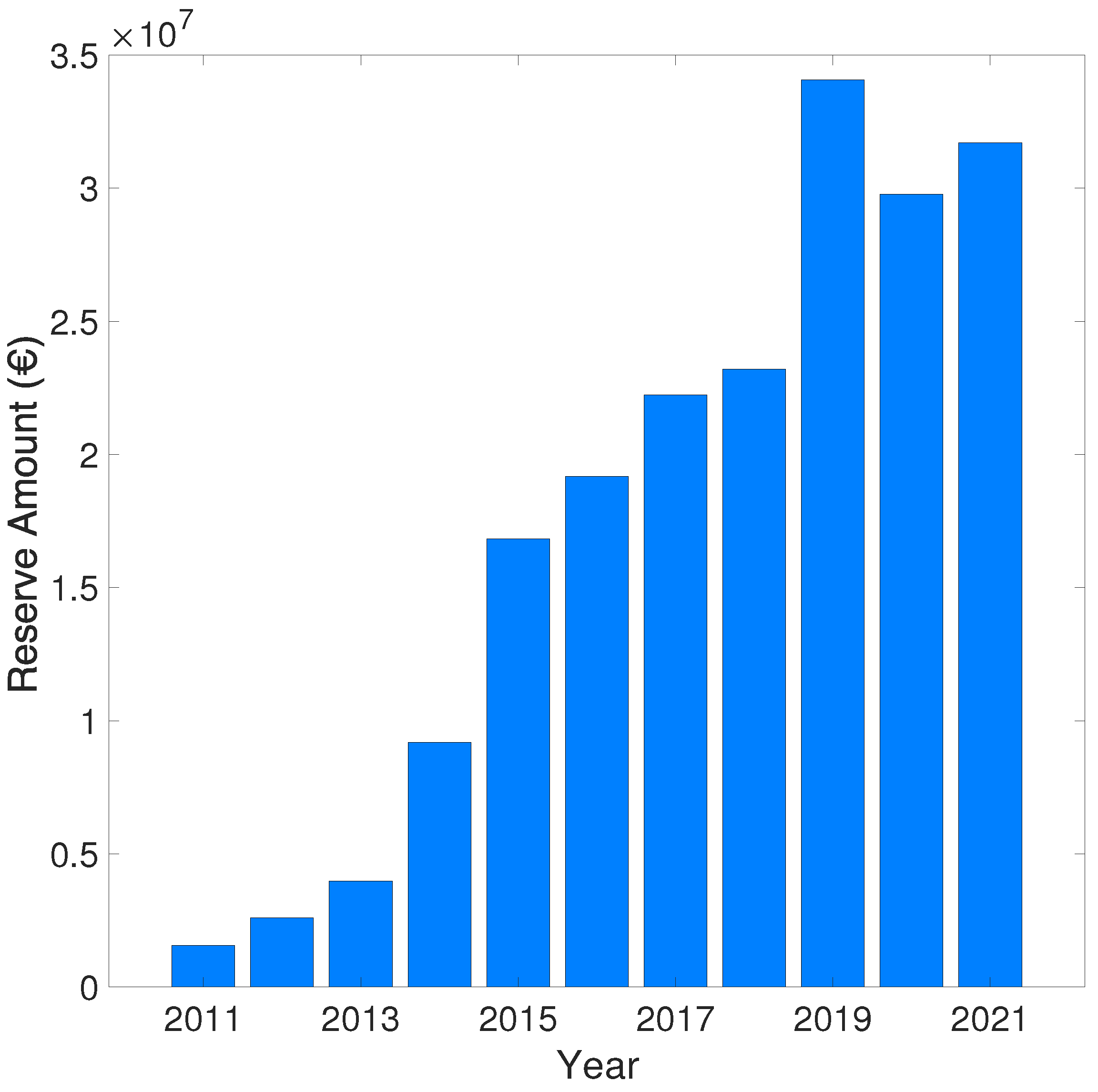
| t | (€) |
|---|---|
| 2011 | |
| 2012 | |
| 2013 | |
| 2014 | |
| 2015 | |
| 2016 | |
| 2017 | |
| 2018 | |
| 2019 | |
| 2020 | |
| 2021 |
| Residue (Eq. 46) | Residue (Eq. 47) | ||||
|---|---|---|---|---|---|
| Variable | Value | Error | Variable | Value | Error |
| c | 14.183 | 0.221 | c | 14.109 | 0.226 |
| 0.175 | 0.155 | 0.197 | 0.156 | ||
| -0.022 | 0.164 | 0.002 | 0.165 | ||
| -0.103 | 0.170 | -0.114 | 0.172 | ||
| 0.126 | 0.165 | 0.140 | 0.166 | ||
| 0.286 | 0.165 | 0.313 | 0.166 | ||
| 0.191 | 0.177 | 0.178 | 0.179 | ||
| 0.048 | 0.193 | 0.055 | 0.195 | ||
| -0.011 | 0.209 | -0.047 | 0.213 | ||
| 0.164 | 0.217 | 0.190 | 0.216 | ||
| -0.158 | 0.313 | -0.191 | 0.320 | ||
| -0.572 | 0.889 | -0.498 | 0.883 | ||
| 1.655 | 0.205 | 1.701 | 0.210 | ||
| 1.682 | 0.207 | 1.740 | 0.212 | ||
| 1.244 | 0.220 | 1.247 | 0.226 | ||
| 0.994 | 0.233 | 1.034 | 0.237 | ||
| 1.026 | 0.237 | 1.075 | 0.241 | ||
| 1.216 | 0.238 | 1.248 | 0.242 | ||
| 1.239 | 0.248 | 1.252 | 0.253 | ||
| 0.894 | 0.285 | 0.925 | 0.289 | ||
| 0.430 | 0.355 | 0.418 | 0.364 | ||
| -0.186 | 0.522 | -0.124 | 0.519 | ||
| -0.125 | 0.724 | -0.051 | 0.719 | ||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2010 | 1.44 | 7.55 | 7.76 | 5.01 | 3.90 | 4.03 | 4.87 | 4.98 | 3.53 | 2.22 | 1.20 | 1.27 |
| 2011 | 1.72 | 9.00 | 9.24 | 5.97 | 4.65 | 4.80 | 5.80 | 5.94 | 4.20 | 2.64 | 1.43 | 1.52 |
| 2012 | 1.41 | 7.39 | 7.59 | 4.90 | 3.82 | 3.94 | 4.77 | 4.87 | 3.45 | 2.17 | 1.17 | 1.25 |
| 2013 | 1.30 | 6.81 | 7.00 | 4.52 | 3.52 | 3.63 | 4.39 | 4.49 | 3.18 | 2.00 | 1.08 | 1.15 |
| 2014 | 1.64 | 8.57 | 8.80 | 5.68 | 4.42 | 4.57 | 5.52 | 5.65 | 4.00 | 2.52 | 1.36 | 1.44 |
| 2015 | 1.92 | 10.1 | 10.3 | 6.67 | 5.19 | 5.36 | 6.48 | 6.63 | 4.70 | 2.95 | 1.60 | 1.70 |
| 2016 | 1.75 | 9.14 | 9.39 | 6.06 | 4.72 | 4.88 | 5.89 | 6.03 | 4.27 | 2.69 | 1.45 | 1.54 |
| 2017 | 1.52 | 7.93 | 8.14 | 5.26 | 4.09 | 4.23 | 5.11 | 5.23 | 3.70 | 2.33 | 1.26 | 1.34 |
| 2018 | 1.43 | 7.47 | 7.68 | 4.96 | 3.86 | 3.99 | 4.82 | 4.93 | 3.49 | 2.20 | 1.19 | 1.26 |
| 2019 | 1.70 | 8.90 | 9.14 | 5.90 | 4.60 | 4.75 | 5.74 | 5.87 | 4.16 | 2.62 | 1.41 | 1.50 |
| 2020 | 1.23 | 6.45 | 6.63 | 4.28 | 3.33 | 3.44 | 4.16 | 4.25 | 3.01 | 1.90 | 1.02 | 1.09 |
| 2021 | 0.81 | 4.26 | 4.38 | 2.83 | 2.20 | 2.27 | 2.75 | 2.81 | 1.99 | 1.25 | 0.68 | 0.72 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2010 | 1.34 | 7.35 | 7.64 | 4.67 | 3.77 | 3.93 | 4.67 | 4.69 | 3.38 | 2.04 | 1.18 | 1.27 |
| 2011 | 1.63 | 8.95 | 9.30 | 5.68 | 4.59 | 4.79 | 5.69 | 5.71 | 4.12 | 2.48 | 1.44 | 1.55 |
| 2012 | 1.34 | 7.36 | 7.66 | 4.68 | 3.78 | 3.94 | 4.68 | 4.70 | 3.39 | 2.04 | 1.19 | 1.28 |
| 2013 | 1.20 | 6.56 | 6.82 | 4.17 | 3.37 | 3.51 | 4.17 | 4.19 | 3.02 | 1.82 | 1.06 | 1.14 |
| 2014 | 1.54 | 8.45 | 8.79 | 5.37 | 4.34 | 4.52 | 5.37 | 5.40 | 3.89 | 2.34 | 1.36 | 1.47 |
| 2015 | 1.83 | 10.0 | 10.4 | 6.38 | 5.16 | 5.37 | 6.38 | 6.41 | 4.62 | 2.79 | 1.62 | 1.74 |
| 2016 | 1.60 | 8.78 | 9.13 | 5.58 | 4.51 | 4.70 | 5.58 | 5.61 | 4.04 | 2.43 | 1.42 | 1.52 |
| 2017 | 1.42 | 7.77 | 8.07 | 4.93 | 3.99 | 4.15 | 4.93 | 4.96 | 3.58 | 2.15 | 1.25 | 1.35 |
| 2018 | 1.28 | 7.01 | 7.29 | 4.45 | 3.60 | 3.75 | 4.46 | 4.48 | 3.23 | 1.94 | 1.13 | 1.22 |
| 2019 | 1.62 | 8.88 | 9.24 | 5.64 | 4.56 | 4.75 | 5.64 | 5.67 | 4.09 | 2.46 | 1.43 | 1.54 |
| 2020 | 1.11 | 6.07 | 6.31 | 3.86 | 3.12 | 3.25 | 3.86 | 3.88 | 2.79 | 1.68 | 0.98 | 1.05 |
| 2021 | 0.81 | 4.47 | 4.64 | 2.84 | 2.29 | 2.39 | 2.84 | 2.85 | 2.06 | 1.24 | 0.72 | 0.77 |
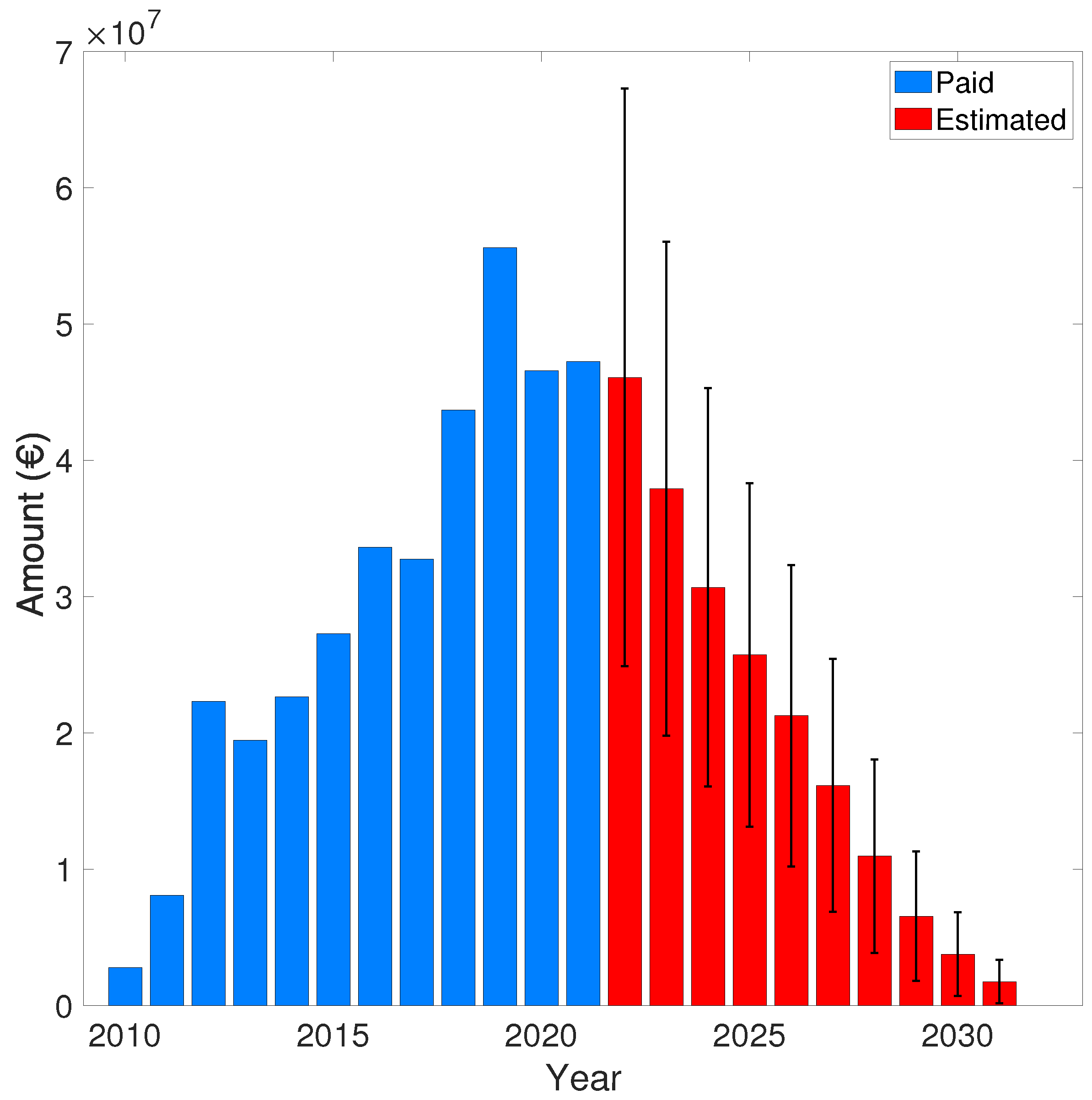
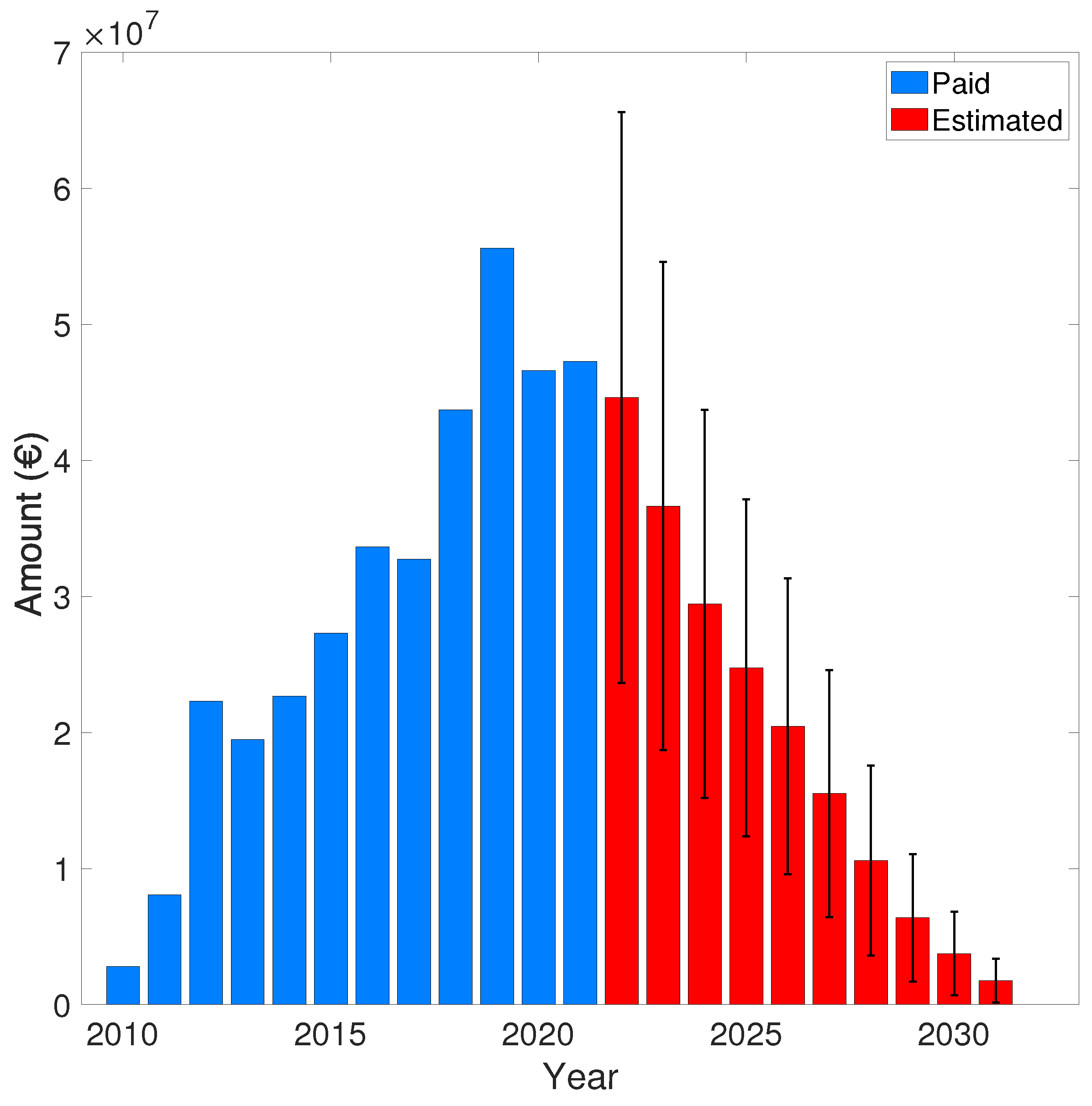
| Budget year (t) |
(106 €) Paid Amount |
(106 €) Residue (Eq. 46) |
(106 €) Residue (Eq. 47) |
|---|---|---|---|
| 2010 | 2.80 | 1.44 ± 0.32 | 1.34 ± 0.30 |
| 2011 | 8.08 | 9.27 ± 2.74 | 8.98 ± 2.71 |
| 2012 | 22.3 | 18.2 ± 5.79 | 17.9 ± 5.83 |
| 2013 | 19.5 | 22.9 ± 7.61 | 22.5 ± 7.63 |
| 2014 | 22.7 | 25.9 ± 8.76 | 25.2 ± 8.69 |
| 2015 | 27.3 | 31.1 ± 10.6 | 30.3 ± 10.5 |
| 2016 | 33.6 | 38.6 ± 13.3 | 37.8 ± 13.3 |
| 2017 | 32.8 | 44.9 ± 15.7 | 43.7 ± 15.5 |
| 2018 | 43.7 | 47.7 ± 17.0 | 46.2 ± 16.8 |
| 2019 | 55.6 | 48.8 ± 17.9 | 47.0 ± 17.5 |
| 2020 | 46.6 | 50.5 ± 19.1 | 48.7 ± 18.8 |
| 2021 | 47.3 | 50.5 ± 20.7 | 48.8 ± 20.3 |
| 2022 | - | 46.1 ± 21.2 | 44.6 ± 21.0 |
| 2023 | - | 37.9 ± 18.1 | 36.7 ± 17.9 |
| 2024 | - | 30.7 ± 14.6 | 29.4 ± 14.3 |
| 2025 | - | 25.7 ± 12.6 | 24.8 ± 12.4 |
| 2026 | - | 21.3 ± 11.1 | 20.5 ± 10.9 |
| 2027 | - | 16.2 ± 9.27 | 15.5 ± 9.08 |
| 2028 | - | 11.0 ± 7.10 | 10.6 ± 6.97 |
| 2029 | - | 6.56 ± 4.75 | 6.39 ± 4.69 |
| 2030 | - | 3.78 ± 3.08 | 3.76 ± 3.06 |
| 2031 | - | 1.76 ± 1.60 | 1.77 ± 1.62 |
| (106 €) | (106 €) | |||
| Measured | - | - | 47.3 | - |
| CL (Table 8) | - | - | 31.7 | - |
| Residue (Eq. 46) | 6.78 × 103 | 6.05 × 105 | 50.5 ± 20.7 | 201 ± 103 |
| Residue (Eq. 47) | 3.27 × 107 | 5.94 × 105 | 48.8 ± 20.3 | 194 ± 102 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





