Submitted:
24 October 2023
Posted:
25 October 2023
You are already at the latest version
Abstract
Keywords:
MSC: 65K10; 90C52; 90C26
1. Introduction
1.1. A Quantum Spectral PRP CG Algorithm
2. Convergence Analysis
- A1.
- The level set is bounded, where the starting point is .
- A2.
- There exists a constant such that θ is continuously quantum differentiable in the neighborhood N of Ω and its quantum gradient is Lipschitz continuous such that
- A3.
- The following inequality holds for λ large enough:
3. Numerical Illustration
3.1. Test on UO Problems
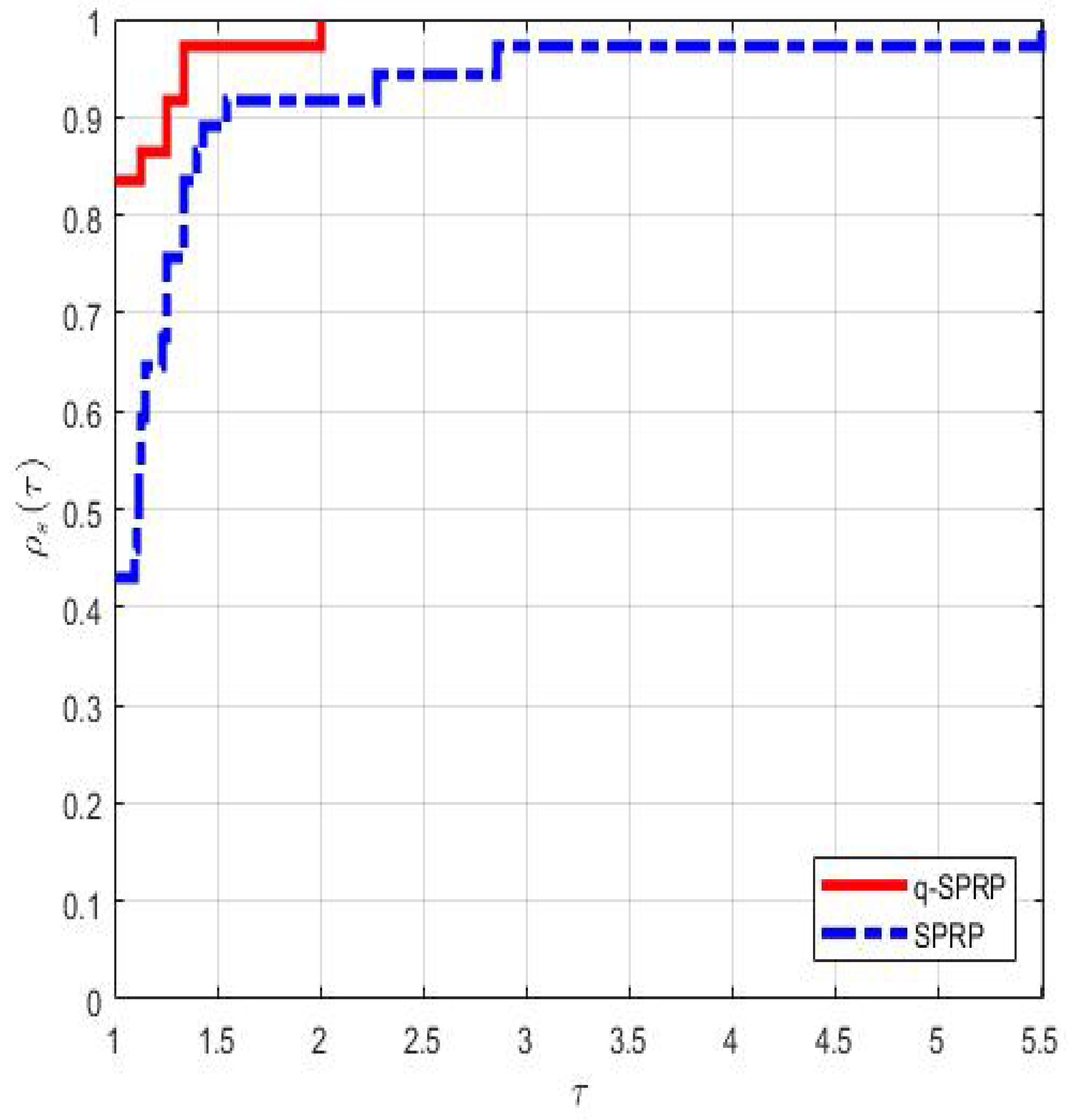
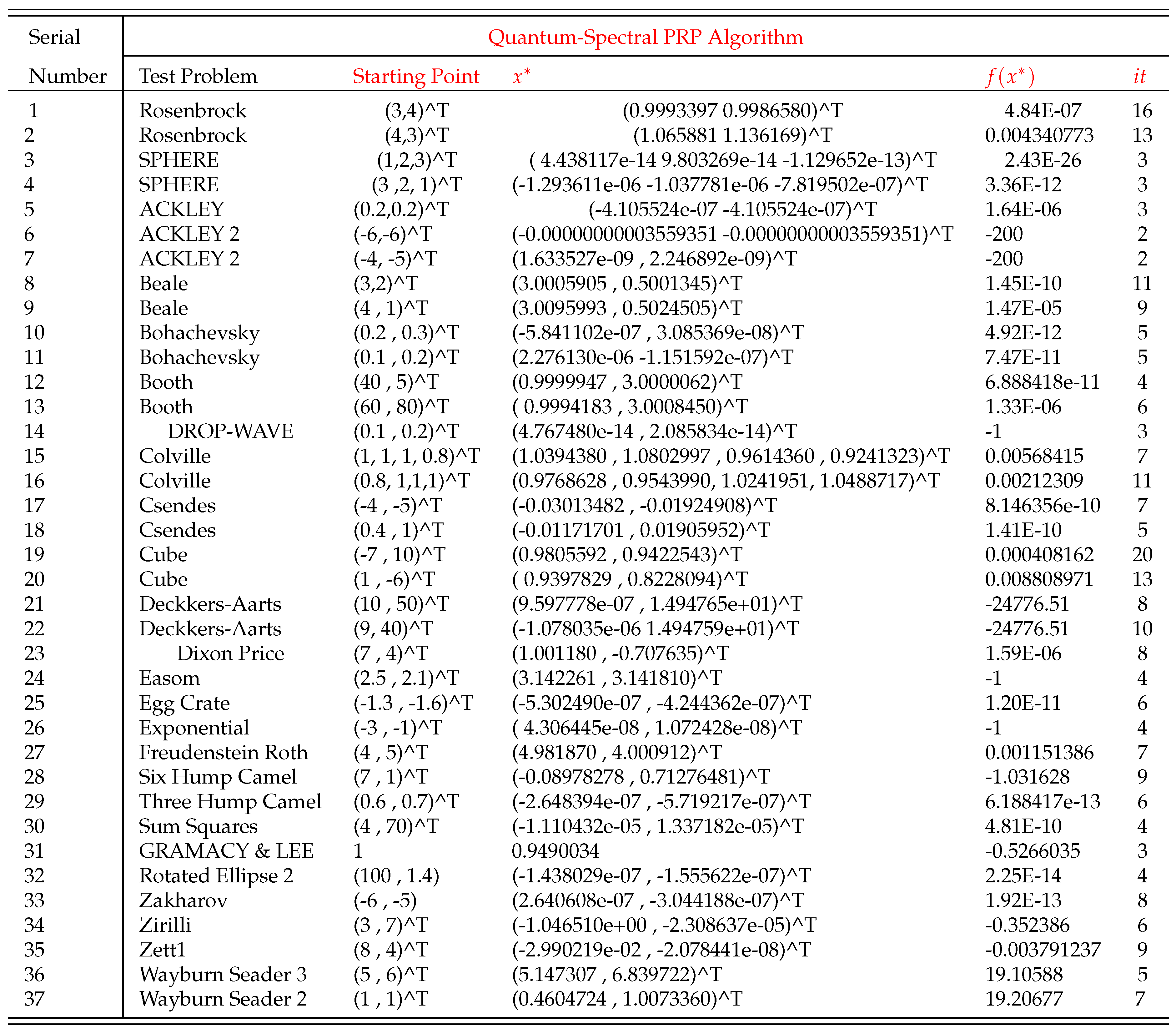
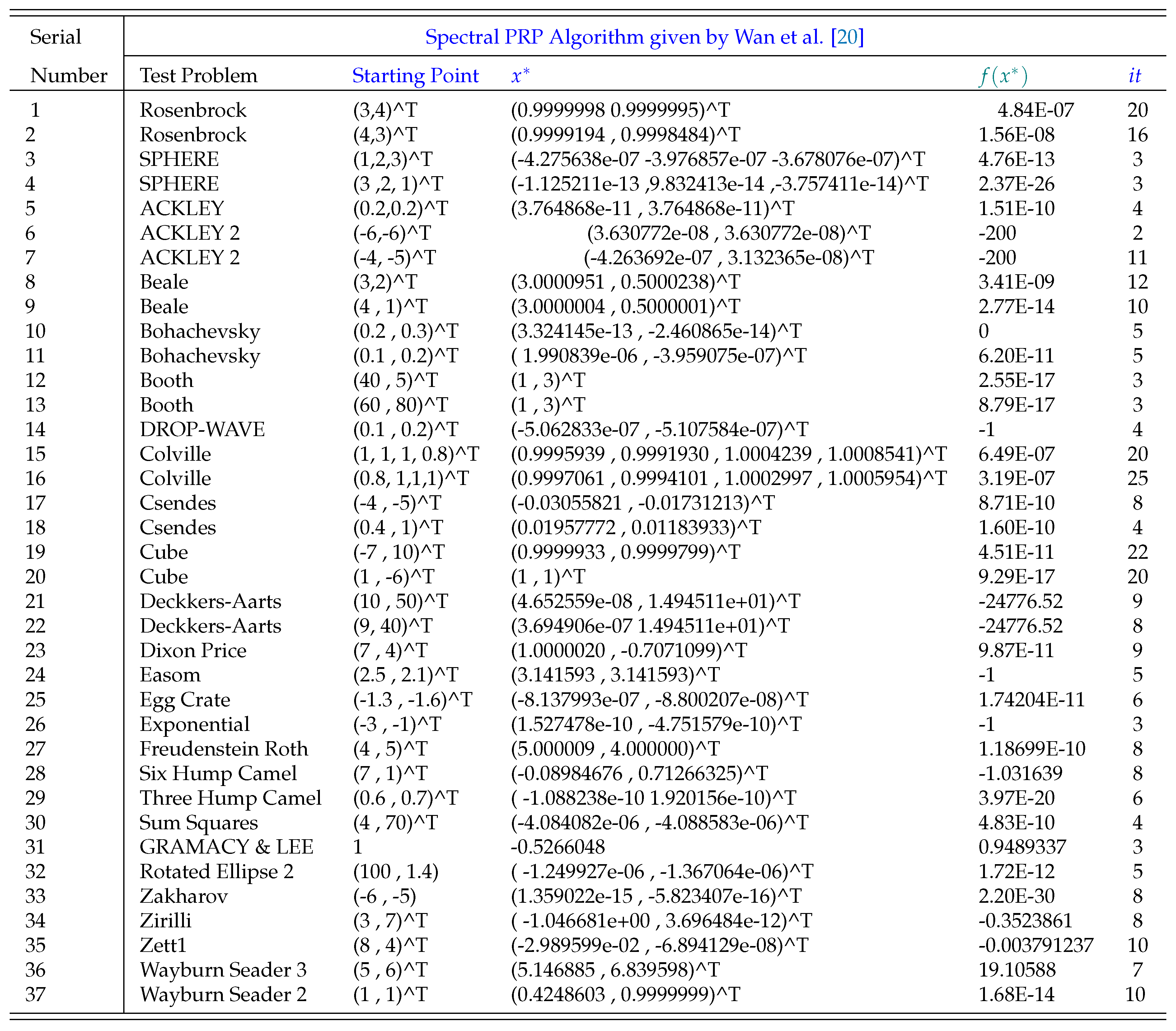
4. Conclusion
Acknowledgments
References
- Mishra, S.K.; Ram, B. Conjugate gradient methods. In Introduction to Unconstrained Optimization with R; Springer, 2019; pp. 211–244. [Google Scholar]
- Babaie-Kafaki, S. A survey on the Dai–Liao family of nonlinear conjugate gradient methods. RAIRO-Operations Research 2023, 57, 43–58. [Google Scholar] [CrossRef]
- Wu, X.; Shao, H.; Liu, P.; Zhang, Y.; Zhuo, Y. An efficient conjugate gradient-based algorithm for unconstrained optimization and its projection extension to large-scale constrained nonlinear equations with applications in signal recovery and image denoising problems. Journal of Computational and Applied Mathematics 2023, 422, 114879. [Google Scholar] [CrossRef]
- Liu, J.; Du, S.; Chen, Y. A sufficient descent nonlinear conjugate gradient method for solving M-tensor equations. Journal of Computational and Applied Mathematics 2020, 371, 112709. [Google Scholar] [CrossRef]
- Andrei, N. On three-term conjugate gradient algorithms for unconstrained optimization. Applied Mathematics and Computation 2013, 219, 6316–6327. [Google Scholar] [CrossRef]
- Dai, Y.h.; Yuan, Y. An efficient hybrid conjugate gradient method for unconstrained optimization. Annals of Operations Research 2001, 103, 33–47. [Google Scholar] [CrossRef]
- Shanno, D.F. Conjugate gradient methods with inexact searches. Mathematics of operations research 1978, 3, 244–256. [Google Scholar] [CrossRef]
- Johnson, O.G.; Micchelli, C.A.; Paul, G. Polynomial preconditioners for conjugate gradient calculations. SIAM Journal on Numerical Analysis 1983, 20, 362–376. [Google Scholar] [CrossRef]
- Wei, Z.; Li, G.; Qi, L. New nonlinear conjugate gradient formulas for large-scale unconstrained optimization problems. Applied Mathematics and computation 2006, 179, 407–430. [Google Scholar] [CrossRef]
- Mishra, S.K.; Ram, B. Steepest descent method. In Introduction to Unconstrained Optimization with R; Springer, 2019; pp. 131–173. [Google Scholar]
- Mishra, S.K.; Chakraborty, S.K.; Samei, M.E.; Ram, B. A q-Polak–Ribière–Polyak conjugate gradient algorithm for unconstrained optimization problems. Journal of Inequalities and Applications 2021, 2021, 1–29. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, W.; Li, D.H. A descent modified Polak–Ribière–Polyak conjugate gradient method and its global convergence. IMA Journal of Numerical Analysis 2006, 26, 629–640. [Google Scholar] [CrossRef]
- Soterroni, A.C.; Galski, R.L.; Ramos, F.M. The q-gradient vector for unconstrained continuous optimization problems. In Operations Research Proceedings 2010; Springer, 2011; pp. 365–370. [Google Scholar]
- Gouvêa, É.J.; Regis, R.G.; Soterroni, A.C.; Scarabello, M.C.; Ramos, F.M. Global optimization using q-gradients. European Journal of Operational Research 2016, 251, 727–738. [Google Scholar] [CrossRef]
- Chakraborty, S.K.; Panda, G. Newton like line search method using q-calculus. In Proceedings of the International Conference on Mathematics and Computing; Springer, 2017; pp. 196–208. [Google Scholar]
- Mishra, S.K.; Panda, G.; Ansary, M.A.T.; Ram, B. On q-Newton’s method for unconstrained multiobjective optimization problems. Journal of Applied Mathematics and Computing 2020, 63, 391–410. [Google Scholar] [CrossRef]
- Lai, K.K.; Mishra, S.K.; Panda, G.; Ansary, M.A.T.; Ram, B. On q-steepest descent method for unconstrained multiobjective optimization problems. AIMS Mathematics 2020, 5, 5521–5540. [Google Scholar]
- Mishra, S.K.; Panda, G.; Chakraborty, S.K.; Samei, M.E.; Ram, B. On q-BFGS algorithm for unconstrained optimization problems. Advances in Difference Equations 2020, 2020, 1–24. [Google Scholar] [CrossRef]
- Lai, K.K.; Mishra, S.K.; Panda, G.; Chakraborty, S.K.; Samei, M.E.; Ram, B. A limited memory q-BFGS algorithm for unconstrained optimization problems. Journal of Applied Mathematics and Computing 2021, 66, 183–202. [Google Scholar] [CrossRef]
- Wan, Z.; Yang, Z.; Wang, Y. New spectral PRP conjugate gradient method for unconstrained optimization. Applied Mathematics Letters 2011, 24, 16–22. [Google Scholar] [CrossRef]
- Hu, Q.; Zhang, H.; Zhou, Z.; Chen, Y. A class of improved conjugate gradient methods for nonconvex unconstrained optimization. Numerical Linear Algebra with Applications 2023, 30, e2482. [Google Scholar] [CrossRef]
- Gilbert, J.C.; Nocedal, J. Global convergence properties of conjugate gradient methods for optimization. SIAM Journal on optimization 1992, 2, 21–42. [Google Scholar] [CrossRef]
- Polyak, B.T. The conjugate gradient method in extremal problems. USSR Computational Mathematics and Mathematical Physics 1969, 9, 94–112. [Google Scholar] [CrossRef]
- Powell, M.J.D. Restart procedures for the conjugate gradient method. Mathematical programming 1977, 12, 241–254. [Google Scholar] [CrossRef]
- Powell, M.J. Nonconvex minimization calculations and the conjugate gradient method. In Numerical analysis; Springer, 1984; pp. 122–141. [Google Scholar]
- Wang, C.y.; Chen, Y.y.; Du, S.q. Further insight into the Shamanskii modification of Newton method. Applied mathematics and computation 2006, 180, 46–52. [Google Scholar] [CrossRef]
- Jamil, M.; Yang, X.S. A literature survey of benchmark functions for global optimisation problems. International Journal of Mathematical Modelling and Numerical Optimisation 2013, 4, 150–194. [Google Scholar] [CrossRef]
- Dolan, E.D.; Moré, J.J. Benchmarking optimization software with performance profiles. Mathematical Programming 2002, 91, 201–213. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





