Application of Quantum Computers and Their Unique Properties for Constrained Optimization in Engineering Problems: Welded Beam Design

1. Introduction

Optimisation problems constitute a fundamental category of mathematical challenges aimed at identifying the best possible solution within defined constraints. In practical terms, this involves maximising or minimising an objective function, which represents efficiency, cost, or another property of the analysed system. The resolution of optimisation problems is particularly significant in the field of engineering, where the design and optimisation of structures, processes, and technological systems play a pivotal role[1,2].

In engineering, optimisation problems frequently encompass complex design decisions, such as minimising material costs, maximising structural strength, or improving system efficiency. These problems are inherently challenging due to numerous constraints, including stresses, loads, deformations, and geometric limitations. The optimisation of real-world engineering problems, such as the design of mechanical components or load-bearing structures, is critical for reducing production costs, enhancing safety and performance, and improving the environmental efficiency of engineering processes.

A well-documented example of an optimisation problem in engineering is the welded beam design problem. This task involves determining the optimal dimensions of structural components to minimise production costs while adhering to constraints related to stresses, buckling, and deflection. This problem serves as a prominent benchmark in the literature for evaluating the performance of advanced optimisation algorithms [3].

In recent years, quantum computers, such as systems developed by D-Wave, have emerged as a promising tool for tackling challenging optimisation problems. Quantum computers leverage phenomena of quantum mechanics, including superposition, entanglement, and quantum tunnelling, enabling the simultaneous exploration of numerous solutions in the search space. D-Wave’s specific approach, known as quantum annealing, is particularly effective in solving combinatorial optimisation problems. This method exploits the natural tendency of physical systems to move towards a state of minimum energy, facilitating the identification of low-energy states that correspond to optimal or near-optimal solutions [4,5].

Thus, optimisation using advanced tools like D-Wave systems opens new horizons in addressing complex engineering challenges while improving the precision and efficiency of the design process [6,7].

This integration of cutting-edge computational methodologies into engineering optimisation marks a transformative step towards solving intricate problems with enhanced speed and accuracy.

2. Problem spawanej belki jako problem optymalizacujny

The optimization of a welded beam design involves finding the optimal dimensions of structural elements to minimize production costs while simultaneously meeting specified strength and geometric constraints, as illustrated in the diagram (Figure 1) where the key variable names are highlighted [8,9,10].

Figure 1. This is a figure. Schemes follow the same formatting.

Figure 1. This is a figure. Schemes follow the same formatting.

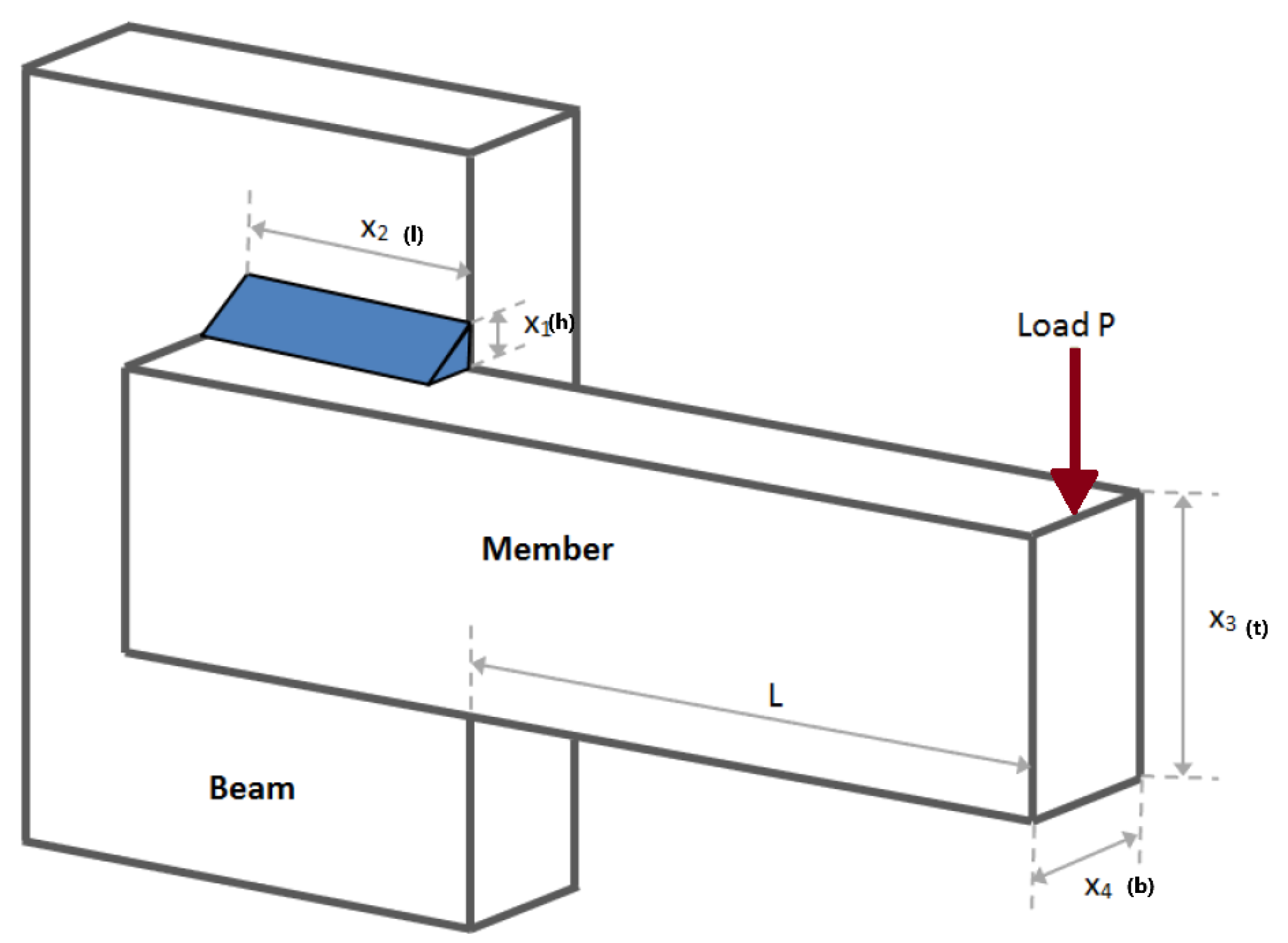
Design Variables

(1)

$x_1=h$: Height of the weld.

(2)

$x_2=l$: Length of the weld.

(3)

$x_3=t$: Thickness of the beam.

(4)

$x_4=b$: Width of the beam.

Objective Function

The fabrication cost $f\left(X\right)$ to be minimized is:

$$f\left(X\right)=1.10471x_1^2+0.04811x_3{x}_4(14.0+x_2)$$

(1)

Constraints

The design is subject to the following constraints:

(1)

Shear Stress ($g_1$):

$$\tau \left(X\right)-{\tau }_{\max }\le 0$$

(2)

(2)

Bending Stress ($g_2$):

$$\sigma \left(X\right)-{\sigma }_{\max }\le 0$$

(3)

(3)

Deflection ($g_3$):

$$\delta \left(X\right)-{\delta }_{\max }\le 0$$

(4)

(4)

Geometry ($g_4$):

$$x_1-x_4\le 0$$

(5)

(5)

Buckling Load ($g_5$):

$$P-P_c\left(X\right)\le 0$$

(6)

(6)

Minimum Thickness ($g_6$):

$$0.125-x_1\le 0$$

(7)

(7)

Cost Limit ($g_7$):

$$f\left(X\right)-5.0\le 0$$

(8)

Design Variables’ Ranges

$$0.1\le x_1\le 2,0.1\le x_2\le 10,0.1\le x_3\le 10,0.1\le x_4\le 2$$

(9)

Material Properties and Parameters

• Applied force: $P=600\mathrm{lb}$,
• Beam length: $L=14\mathrm{in}$,
• Maximum deflection: ${\delta }_{\max }=0.25\mathrm{in}$,
• Young’s modulus: $E=30\times {10}^6\mathrm{psi}$,
• Shear modulus: $G=12\times {10}^6\mathrm{psi}$,
• Maximum shear stress: ${\tau }_{\max }=13,600\mathrm{psi}$,
• Maximum bending stress: ${\sigma }_{\max }=30,000\mathrm{psi}$.

Stress and Deflection Formulas

(1)

Shear Stress ($\tau$):

$$\tau =\sqrt{{\tau }^{\prime 2}+{\displaystyle \frac{{\tau }^{\prime }{\tau }^{\prime \prime }}{x_2^{2}R}}+{\tau }^{\prime \prime 2}}$$

(10)

where:

$${\tau }^{\prime }={\displaystyle \frac{P}{\sqrt{2}{x}_1{x}_2}},{\tau }^{\prime \prime }={\displaystyle \frac{M}{R}},M=P\left(L+{\displaystyle \frac{x_2}{2}}\right),R=\sqrt{{\displaystyle \frac{x_2^2}{4}}+{\left({\displaystyle \frac{x_1+x_3}{2}}\right)}^2}.$$

(11)

(2)

Bending Stress ($\sigma$):

$$\sigma ={\displaystyle \frac{6PL}{x_4{x}_3^2}}$$

(12)

(3)

Deflection ($\delta$):

$$\delta ={\displaystyle \frac{6P{L}^3}{E{x}_3^2{x}_4}}$$

(13)

(4)

Buckling Load ($P_c$):

$$P_c={\displaystyle \frac{4.013E\sqrt{\frac{x_3^2{x}_4^6}{36L^2}}\left(1-\frac{x_3}{2L}\sqrt{\frac{E}{4G}}\right)}{L^2}}$$

(14)

3. Quadratic Unconstrained Binary Optimization (QUBO)

Quadratic Unconstrained Binary Optimization (QUBO) is an optimization problem in which we seek a vector of binary variables $\mathbf{x}\in {\{0,1\}}^n$ that minimizes (or maximizes) a quadratic objective function:

$$f\left(\mathbf{x}\right)={\mathbf{x}}^T\mathbf{Q}\mathbf{x},$$

(28)

where $\mathbf{Q}$ is an $n\times n$ square matrix (often symmetric). Written in detail:

$$f\left(\mathbf{x}\right)=\sum _{i=1}^n\sum _{j=1}^{n}Q[i,j]x_i{x}_j.$$

(29)

The term Unconstrained indicates that, in its baseline form, QUBO does not include additional explicit constraints other than the binary nature of the variables. In practical scenarios that require specific constraints (e.g., limiting sums of certain variables), these are introduced as penalty terms in the objective, preserving the quadratic form.

3.1. Basic Elements of QUBO

(1)

Binary variables

Each component $x_i$ of the vector $\mathbf{x}$ can only be 0 or 1.

(2)

The matrix $\mathbf{Q}$

• Diagonal elements $\mathbf{Q}[i,i]$ capture the contribution of each variable $x_i$ (the “linear” part in the binary sense, since $x_i^2=x_i$ for $x_i\in \{0,1\}$).
• Off-diagonal elements $\mathbf{Q}[i,j]$ (for $i\ne j$) describe the interaction between variables $x_i$ and $x_j$.

(3)

Objective function

It is given by ${\mathbf{x}}^T\mathbf{Q}\mathbf{x}$. Typically, one aims to minimize this function, though maximizing is also possible by inverting the sign of the relevant terms in $\mathbf{Q}$.

(4)

Constraint penalties

In real-world applications, constraints (e.g., ${\sum }_i{x}_i\le k$) are introduced by adding penalty terms to the objective, for instance:

$$\lambda {\left(\sum _{i=1}^n{x}_i-k\right)}^2,$$

(17)

where $\lambda$ is sufficiently large so that violating the constraint becomes too costly.

3.2. Applications of QUBO

• Combinatorial optimization problems. For example:
  • Max-Cut: partitioning a graph’s vertices into two sets to maximize the sum of edges “cut” by that partition.
  • SAT (Satisfiability): logical formulas can be mapped to QUBO by introducing penalties for unsatisfied clauses.
  • Traveling Salesman Problem (TSP): minimizing the total route distance while visiting each city exactly once.
• Business optimization.
  • Knapsack Problem: choosing a subset of items under capacity constraints.
  • Production planning and scheduling: allocating tasks to resources.
  • Resource allocation: selecting investment projects with limited budgets.
• Machine learning.
  • Clustering: minimizing a chosen error function to group data points.
  • Feature selection: choosing an optimal subset of features for classification tasks.

3.3. Solving QUBO

Classical methods

• Simulated Annealing, Genetic Algorithms, Tabu Search: metaheuristics that search the space of solutions.
• Hybrid methods combining exact search (e.g., integer programming) with heuristic approaches.

Quantum methods

• Quantum Annealing: realized on machines like D-Wave, where QUBO is expressed as an equivalent Ising problem.
• Gate-based algorithms: e.g., QAOA (Quantum Approximate Optimization Algorithm), requiring additional implementation steps and an active area of research.

QUBO is a universal model for binary optimization, allowing representation of numerous complex real-world and theoretical problems. It has a single unified form ${\mathbf{x}}^T\mathbf{Q}\mathbf{x}$ that is naturally compatible both with classical heuristic approaches and quantum annealers. Its broad range of applications spans from purely theoretical problems (such as SAT or Max-Cut) to practical tasks in business (scheduling, resource allocation) and machine learning (feature selection, clustering). By adding penalty terms, it is straightforward to incorporate various constraints while preserving the core quadratic structure.

4. Formulating Welded Beam Design as QUBO

4.1. Objective Function

The cost function to be minimized is given by:

$$f\left(X\right)=1.10471x_1^2+0.04811x_3{x}_4(14.0+x_2).$$

(18)

To express this in QUBO:

• Each design variable ($x_1,x_2,x_3,x_4$) is discretized into a finite range of values, represented as binary vectors.
• Each variable $x_i$ is described as:

  $$x_i=\sum _{j=1}^n{2}^{j-1}{q}_{ij},$$

  (32)

where $q_{ij}\in \{0,1\}$ are binary variables, and n is the number of bits.

The objective function in binary form:

$$f\left(Q\right)=1.10471{\left(\sum _{j=1}^n{2}^{j-1}{q}_{1j}\right)}^2+0.04811\left(\sum _{j=1}^n{2}^{j-1}{q}_{3j}\right)\left(\sum _{j=1}^n{2}^{j-1}{q}_{4j}\right)(14.0+\sum _{j=1}^n{2}^{j-1}{q}_{2j})$$

(33)

4.2. Constraints

Each constraint is transformed into a quadratic expression with a penalty $C_g$ for violations. The penalty terms are added to the objective function as follows:

$$F\left(Q\right)=f\left(Q\right)+\lambda \sum _g{C}_g,$$

(34)

where $\lambda$ is the weighting coefficient.

4.3. Constraints

1. Shear Stress ($g_1$):

$$\tau \left(Q\right)-{\tau }_{\max }\le 0,$$

(35)

where $\tau \left(Q\right)$ is computed in binary form as described above.

Penalty:

$$C_1=max{(0,\tau \left(Q\right)-{\tau }_{\max })}^2.$$

(36)

2. Bending Stress ($g_2$):

$$\sigma \left(Q\right)-{\sigma }_{\max }\le 0.$$

(37)

Penalty:

$$C_2=max{(0,\sigma \left(Q\right)-{\sigma }_{\max })}^2.$$

(38)

3. Deflection ($g_3$):

$$\delta \left(Q\right)-{\delta }_{\max }\le 0.$$

(39)

Penalty:

$$C_3=max{(0,\delta \left(Q\right)-{\delta }_{\max })}^2.$$

(40)

4. Geometry ($g_4$):

$$x_1-x_4\le 0.$$

(41)

Penalty:

$$C_4=max{(0,x_1-x_4)}^2.$$

(42)

5. Buckling Load ($g_5$):

$$P-P_c\left(Q\right)\le 0.$$

(43)

Penalty:

$$C_5=max{(0,P-P_c\left(Q\right))}^2.$$

(44)

6. Minimum Thickness ($g_6$):

$$0.125-x_1\le 0.$$

(45)

Penalty:

$$C_6=max{(0,0.125-x_1)}^2.$$

(46)

7. Cost Limit ($g_7$):

$$f\left(Q\right)-5.0\le 0.$$

(47)

Penalty:

$$C_7=max{(0,f\left(Q\right)-5.0)}^2.$$

(48)

4.4. QUBO Matrix

The objective function and penalties can be written as a quadratic binary form:

$$F\left(Q\right)=\sum _i{a}_i{q}_i+\sum _{i,j}{b}_{ij}{q}_i{q}_j.$$

(49)

Where:

• $a_i$ are the linear weights for the binary variables,
• $b_{ij}$ are the quadratic interaction coefficients between the variables.

For each constraint $C_g$, the appropriate $a_i$ and $b_{ij}$ elements in the QUBO matrix Q are calculated and added to the objective function.

5. Results

Below are the results of research on structural optimization using the quantum properties of the D-Wave system. The results of other algorithms, such as the Whale Optimization Algorithm (WOA), Gravitational Search Algorithm (GSA), Goose Algorithm (GOOSE), and Particle Swarm Optimization (PSO), are sourced from the literature. The names in the Table 1, Quantum Start 1 and Quantum Start 2, represent the results of optimization using the D-Wave system.

Meanwhile, the Table 2 and Table 3 presents the parameters for the lowest cost values obtained for the solutions Quantum Start 1 and Quantum Start 2.

Table 1. Comparison of algorithm performance.

Algorithm Name	Best Result	Result Source
WOA	1.732	(Mirjalili & Lewis, 2016)
PSO	1.742	(Mirjalili & Lewis, 2016)
GOOSE	3.188	arxiv2024
GSA	3.576	(Mirjalili & Lewis, 2016)
Quantum Start 1	1.234	–
Quantum Start 2	1.016	–

Table 1. Comparison of algorithm performance.

Algorithm Name	Best Result	Result Source
WOA	1.732	(Mirjalili & Lewis, 2016)
PSO	1.742	(Mirjalili & Lewis, 2016)
GOOSE	3.188	arxiv2024
GSA	3.576	(Mirjalili & Lewis, 2016)
Quantum Start 1	1.234	–
Quantum Start 2	1.016	–

Table 2. Parameters for Quantum Start 1.

Parameter	Value
x1 (Height of weld)	0.3533
x2 (Length of weld)	6.0400
x3 (Height of beam)	2.0800
x4 (Width of beam)	2.0000

Table 2. Parameters for Quantum Start 1.

Parameter	Value
x1 (Height of weld)	0.3533
x2 (Length of weld)	6.0400
x3 (Height of beam)	2.0800
x4 (Width of beam)	2.0000

Table 3. Parameters for Quantum Start 2.

Parameter	Value
x1 (Height of weld)	0.3533
x2 (Length of weld)	4.7200
x3 (Height of beam)	4.7200
x4 (Width of beam)	0.8600

Table 3. Parameters for Quantum Start 2.

Parameter	Value
x1 (Height of weld)	0.3533
x2 (Length of weld)	4.7200
x3 (Height of beam)	4.7200
x4 (Width of beam)	0.8600

In both cases of quantum optimization, the energy obtained was 5,954,303.3448 and 2,452,399.0500, respectively. In one case, the energy was 1,640.2799 for the best solution of 0.5646, which is an exception and should be subjected to detailed investigation. As can be seen, optimization using D-Wave yields good results. Moreover, the properties of this system suggest that the optimization of highly complex structures can be performed very quickly and with excellent results.

6. Discussion

The presented research findings indicate a significant impact of optimization on solving engineering problems, particularly those related to structural design. This type of optimization plays a crucial role in cost reduction, which consequently leads to decreased financial and environmental burdens. Minimizing material consumption and designing more efficient structures can contribute to the sustainable development of structural engineering and other technical fields.

The obtained results have been compared with data from the literature, where classical heuristic methods such as the Whale Optimization Algorithm (WOA), Gravitational Search Algorithm (GSA), Goose Algorithm (GOOSE), and Particle Swarm Optimization (PSO) were applied. It has been demonstrated that leveraging the properties of quantum computers in the structural optimization process can yield results that are at least comparable, and in some cases superior, to traditional methods. This is a significant discovery, suggesting the potential applicability of quantum algorithms to a broad range of engineering problems.

The article presents the potential applications of quantum optimization; however, at this stage, the research remains exploratory due to the limited availability of quantum computers. Despite this limitation, the obtained results provide a solid foundation for further investigations into the implementation of these technologies in engineering practice. The author intends to expand the scope of analyzed cases and increase the complexity of the optimized structures in future studies to assess the scalability and effectiveness of the method in more complex problems.

In conclusion, it has been demonstrated that quantum optimization can serve as a viable alternative to classical heuristic methods. The presented findings indicate that it is capable of delivering solutions of comparable or superior quality, making it a promising research direction for the optimization of engineering problems.

7. Conclusions

The conducted research has demonstrated that quantum optimization can serve as an effective alternative to classical heuristic methods in solving engineering problems, particularly in structural design. The obtained results suggest that utilizing quantum computers enables the achievement of comparable or superior solutions while also offering the potential for significant acceleration of computational processes.

Despite the limited access to advanced quantum systems, the results of the conducted experiments provide a solid foundation for further research.

In conclusion, quantum optimization exhibits substantial potential in engineering, and its continued development may lead to significant cost savings and environmental benefits.