Towards Dynamic Fuzzy Rule Interpolation via Density-Based Rule Promotion from Interpolated Outcomes

Fuzzy Rule Interpolation (FRI) offers an innovative methodology for inferring outcomes from data points that match no established rules in a sparse fuzzy rule base. Generally, a traditional fuzzy rule-based system suffers from the inability to perform inference while facing an unmatched observation, given a sparse fuzzy rule base that is derived from insufficient data or inadequate human experience and that fails to cover parts of a specific problem domain. Fortunately, starting with a sparse rule base, Fuzzy Rule Interpolation (FRI) can help to formulate interpolated rules specifically in instances where observations fail to activate any existing rule. An interpolated rule gives a result called consequent, which is related to the unmatched observation so that the inference system will not fail to generate an outcome corresponding to the observation as the output. Conventionally, these interpolated rules will be discarded after obtaining outcomes. However, valuable information may be potentially embedded within those discarded rules addressing the limitation regarding the coverage of the original sparse knowledge space. Moreover, without exploiting the potential value of the interpolated rules, the fuzzy inference system based on a sparse rule base will never improve its efficiency and robustness in the long run. Therefore, this underscores the necessity for Dynamic Fuzzy Rule Interpolation (D-FRI), which aims to collate interpolated rules that cover particular knowledge spaces absent in the sparse rule base. Intuitively, those frequently appeared interpolated rules are considered valuable because future observations are more likely to hit the respective problem areas. Promoting selected interpolated rules to the sparse rule base can enhance the overall coverage of the knowledge space and increase the inference efficiency over time. This paper introduces a framework for Dynamic Fuzzy Rule Interpolation that integrates the widely used Transformation-based Fuzzy Rule Interpolation (T-FRI) with an effective form of clustering of interpolated results. Experimental findings validate the effectiveness of this approach.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

In a traditional fuzzy inference system with a sparse rule base, the absence of a corresponding rule for an observation results in the failure to generate any inferred outcome. Here, a sparse rule base means that the inference system lacks certain knowledge coverage of a problem domain. Furthermore, when applied to real-world problems, a static rule base may also lose its relevance and effectiveness due to the nature of the dynamics of the underlying changing world. Fuzzy rule interpolation (FRI) approaches introduce a novel way to enhance the reasoning potential [1,2,3,4,5], when the rule base is incomplete and especially when it can dynamically update itself.

In general, there exist two categories of Fuzzy Rule Interpolation (FRI) methodologies. The first approach is centred on the utilisation of

α

-cuts, whereby the

α

-cut of an interpolated consequent is calculated from the

α

-cuts of its antecedents, as outlined by the Resolution Principle [6,7,8]. The second methodology employs the concept of similarity of fuzzy value and analogical reasoning [9,10,11,12,13,14,15,16]. Specifically, within this latter category, an FRI algorithm generates intermediate fuzzy rules based on the principle of similarity. Among such methods, Transformation-Based Fuzzy Rule Interpolation (T-FRI) is the most popular [11,12]. T-FRI can manage multiple fuzzy rules in both rule interpolation and extrapolation while guaranteeing the uniqueness, convexity, and normality of the interpolated fuzzy sets. Furthermore, it accommodates multiple antecedent variables and varying shapes of membership functions. Consequently, this paper takes classical T-FRI techniques to generate interpolated rules, forming the foundation for a novel dynamic FRI methodology.

In the seminal T-FRI method, intermediate rules artificially generated through Fuzzy Rule Interpolation (FRI) are discarded once an interpolated outcome is derived. Nonetheless, these interpolated rules may embed information that holds the potential to extend the coverage of a sparse rule base. Therefore, developing a methodology for collecting the interpolated rules generated during the FRI procedure is imperative for formulating a dynamic fuzzy rule interpolation mechanism.

In dynamic fuzzy reasoning, adaptive rule-based methodologies have gained popularity for traditional fuzzy systems that employ a dense rule base. These systems often apply various optimisation techniques to improve inference accuracy by cultivating a dynamic and dense rule base [17,18,19,20,21]. However, these adaptive strategies, built upon a dense rule base, can hardly apply to sparse rule-based fuzzy systems where the rules are inadequate for comprehensive coverage of the problem domain. Approaches designed for sparse rule-based dynamic fuzzy rule interpolation are unfortunately rather limited. One such approach is fundamentally framed within a predefined quantity space of domain variables, called hyper-cubes [22]. This technique employs K-means clustering and genetic algorithms (GA) to sort through hyper-cubes of interpolated rules. Subsequently, it generates a new rule from the selected hyper-cube via a weighting process. Whilst simple in conception, it forms the foundation of Dynamic Fuzzy Rule Interpolation (D-FRI) strategies and is fundamental for future methodologies that seek to manipulate pools of interpolated rules.

Learning from interpolated rules involving multiple antecedent variables can be interpreted as a complex task of optimisation or clustering. Techniques like Genetic Algorithms (GA) and Particle Swarm Optimisation (PSO) are prominent in the domain of systems learning and optimisation. Meanwhile, clustering methodologies such as K-Means, Mean-Shift, Density-Based Spatial Clustering of Applications with Noise (DBSCAN) [23] and Ordering Points To Identify the Clustering Structure (OPTICS) [24] exist. Based on recent findings from applying Harmony Search as an optimisation method and DBSCAN as a clustering method [25,26], the density-based rule promotion approach is proven effective. Notably, OPTICS is an improved version of DBSCAN as a density-based clustering algorithm. Unlike K-Means, where every data point is ultimately categorised into a cluster, OPTICS has the capability to filter out noise data, effectively excluding noise from the constructed clusters. When employed to select rules from a pool of interpolated rules, OPTICS can help to mitigate the influence of outliers and assemble clusters largely populated by commonly encountered observations. Consequently, the interpolated results within these clusters are more generalised and more reliable for referencing in a dynamic system. Inspired by this observation, the present work applies OPTICS to implement a novel approach to D-FRI.

This paper is structured as follows. Section 2 introduces the core computational mechanism of T-FRI and that of OPTICS. Section 3 illustrates the proposed OPTICS-assisted density-based dynamic fuzzy rule interpolation framework. Section 4 provides experimental results over different data sets. Section 4.3 presents a discussion regarding the experimental results. Finally, Section 5 concludes the paper and outlines the potential improvements that would be interesting to be made in future.

2. Foundational Work

This section provides an overview of the fundamental principles and procedural steps of T-FRI and OPTICS. Within the context of this paper, as with many recent techniques developed in the literature, triangular membership functions are employed to represent fuzzy sets, both for popularity and for simplicity.

2.1. Transformation-Based Fuzzy Rule Interpolation (T-FRI)

Without losing generality, the structure of a sparse rule base can be denoted as

R

, which includes

R_{i} \in R

fuzzy rules [11,12]. The specific rule format is delineated as follows:

R_{i} : IF x_{1} is A_{i, 1} AND . . . AND x_{N} is A_{i, N} THEN y is B_{i},

where i spans the set

{1, \dots, | R |}

, with the term

| R |

signifying the total count of rules present in the rule base. In the given domain, each

x_{j}

with

j \in {1, \dots, N}

represents an antecedent variable, with N indicating the overall number of these variables. The notation

A_{i, j}

indicates the linguistic value attributed to the variable

x_{j}

within the rule

R_{i}

, and it can be represented as the triangular fuzzy set

(a_{0, j}, a_{1, j}, a_{2, j})

. Here,

a_{0, j}

and

a_{2, j}

define the left and right boundaries of the support (where the membership values become zero), and

a_{1, j}

denotes the peak of the triangular fuzzy set (with a membership value of one).

Considering an instance O, it is typically denoted by the sequence

A_{O, 1}, \dots, A_{O, j}

with

j \in {1, \dots, N}

. In this sequence,

A_{O, j} = (a_{0}, a_{1}, a_{2})

represents a specific triangular fuzzy value of the variable

x_{j}

. For any triangular fuzzy set A, defined as

(a_{0}, a_{1}, a_{2})

, its representative value, termed as

r e p (A)

, can be described as the average of its three defining points, which is given by:

r e p (A) = (a_{0} + a_{1} + a_{2}) / 3

(1)

Building upon the foundational concepts outlined above, T-FRI employs the following key procedures when an observation fails to match any rules within the sparse rule base.

Closest Rules Determination. Euclidean distance metric is applied while measuring distances between a rule and an observation (or between two rules). The algorithm selects the rules closest to the unmatched observation to initiate the interpolation procedure. The distance between a rule

R_{i}

and the observation O is computed by aggregating the component distances between them, as shown below:

d (R_{i}, O) = \sqrt{\sum_{j = 1}^{N} d_{j}^{2}}, d_{j} = \frac{d (A_{i, j}, A_{O, j})}{r a n g e_{x_{j}}}

(2)

where

d (A_{i, j}, A_{O, j}) = | r e p (A_{i, j}) - r e p (A_{O, j}) |

defines the distance between the representative values in the domain of the

j^{t h}

antecedent variable. Additionally, the term

r a n g e_{x_{j}}

is calculated as the difference between the maximum and minimum values of the variable

x_{j}

within its domain.

Intermediate Rule Construction. The normalised displacement factor, symbolised as

ω_{i, j}

, represents the significance or weight of the

j^{t h}

antecedent in the

i^{t h}

rule:

ω_{i, j} = \frac{ω_{i, j}^{†}}{\sum_{i = 1}^{M} ω_{i, j}^{†}}

(3)

where M (with

M \geq 2

) indicates the count of rules selected based on their minimum distance values related to observation O. The weight

ω_{i, j}^{†}

is given by:

ω_{i, j}^{†} = \frac{1}{1 + d (A_{O, j}, A_{i, j})}

(4)

Intermediate fuzzy terms, denoted as

A_{j}^{† †}

, are calculated utilising the antecedents from the nearest M rules:

A_{j}^{† †} = \sum_{i = 1}^{M} ω_{i, j} A_{i, j}

(5)

These intermediate fuzzy terms are subsequently adjusted to

A_{j}^{†}

in order to ensure their representative values aligning with those of

A_{O, j}

A_{j}^{†} = A_{j}^{† †} + δ_{j} r a n g e_{x_{j}}

(6)

where

δ_{j}

quantifies the offset between

A_{O, j}

and

A_{j}^{†}

in the domain of the

j^{t h}

variable:

δ_{j} = \frac{r e p (A_{O, j}) - r e p (A_{j}^{†})}{r a n g e_{x_{j}}}

(7)

From this, the intermediate consequent, symbolised as

B^{†}

, is derived similarly to Equation (6). The aggregated weights

ω_{B_{i}}

and shift

δ_{B}

are calculated from the respective values of

A_{j}^{†}

, such that

ω_{B_{i}} = \frac{1}{N} \sum_{j = 1}^{N} ω_{i, j}, δ_{B} = \frac{1}{N} \sum_{j = 1}^{N} δ_{j}

(8)

Scale Transformation. Let

A_{S j}

be represented by the fuzzy set

(a_{0}^{† †}, a_{1}^{† †}, a_{2}^{† †})

, resulting from a scale transformation applied to the

j^{t h}

intermediate antecedent value

A_{j}^{†} = (a_{0}^{†}, a_{1}^{†}, a_{2}^{†})

. Given a scaling ratio

s_{j}

, the components of

A_{S j}

are defined as:

a_{0}^{† †} = \frac{a_{0}^{†} (1 + 2 s_{j}) + a_{1}^{†} (1 - s_{j}) + a_{2}^{†} (1 - s_{j})}{3}

(9)

a_{1}^{† †} = \frac{a_{0}^{†} (1 - s_{j}) + a_{1}^{†} (1 + 2 s_{j}) + a_{2}^{†} (1 - s_{j})}{3}

(10)

a_{2}^{† †} = \frac{a_{0}^{†} (1 - s_{j}) + a_{1}^{†} (1 - s_{j}) + a_{2}^{†} (1 + 2 s_{j})}{3}

(11)

This means that the scale rate

s_{j}

is determined by

s_{j} = \frac{a_{2}^{† †} - a_{0}^{† †}}{a_{2}^{†} - a_{0}^{†}}

(12)

For the corresponding consequent, the scaling factor

s_{B}

is then computed using:

s_{B} = \frac{\sum_{j = 1}^{N} s_{j}}{N}

(13)

Move Transformation.

A_{S j}

, after performing a scale transformation, is then shifted based on a move rate

m_{j}

. This adjustment ensures that the final scaled and shifted fuzzy set retains the geometric properties of the observed value

A_{O, j}

. In implementation, mathematically, this implies that the move rate

m_{j}

is determined such that

m_{j} = \frac{3 (a_{0} - a_{0}^{† †})}{a_{1}^{† †} - a_{0}^{† †}}

(14)

where

a_{0}

is the lower limit of the support of

A_{O, j} = (a_{0}, a_{1}, a_{2})

. From this, the move factor

m_{B}

for the consequent can then be derived as below:

m_{B} = \frac{\sum_{j = 1}^{N} m_{j}}{N}

(15)

Interpolated Consequent Calculation. In adherence to the analogical reasoning principle, the determined parameters

s_{B}

(from the scaling transformation) and

m_{B}

(from the move transformation) are collectively utilised to calculate the consequent of the intermediary rule

B^{†}

. As a result, the interpolated outcome

B_{O}

is generated in reaction to the unmatched observation in question. This methodology ensures that the computed output by the FRI algorithm, while derived from intermediate rules, closely reflects the characteristics of the given observation, thus maintaining the intuition behind the entire inference process.

2.2. OPTICS Clustering

OPTICS, a data density-based clustering algorithm [24], builds upon the foundation of DBSCAN [23], aiming to identify clusters of varying densities. Notable advantages of OPTICS over K-means and DBSCAN include its adeptness at detecting clusters of various densities, its independence from pre-specifying the number of clusters (a requirement in K-means), its ability to identify clusters of non-spherical shapes (unlike the sphere-bound K-means), and its proficiency in distinguishing between noise and clustered data. This last trait is shared with DBSCAN but contrasts with K-means, which assumes every data point belongs to one and only one cluster.

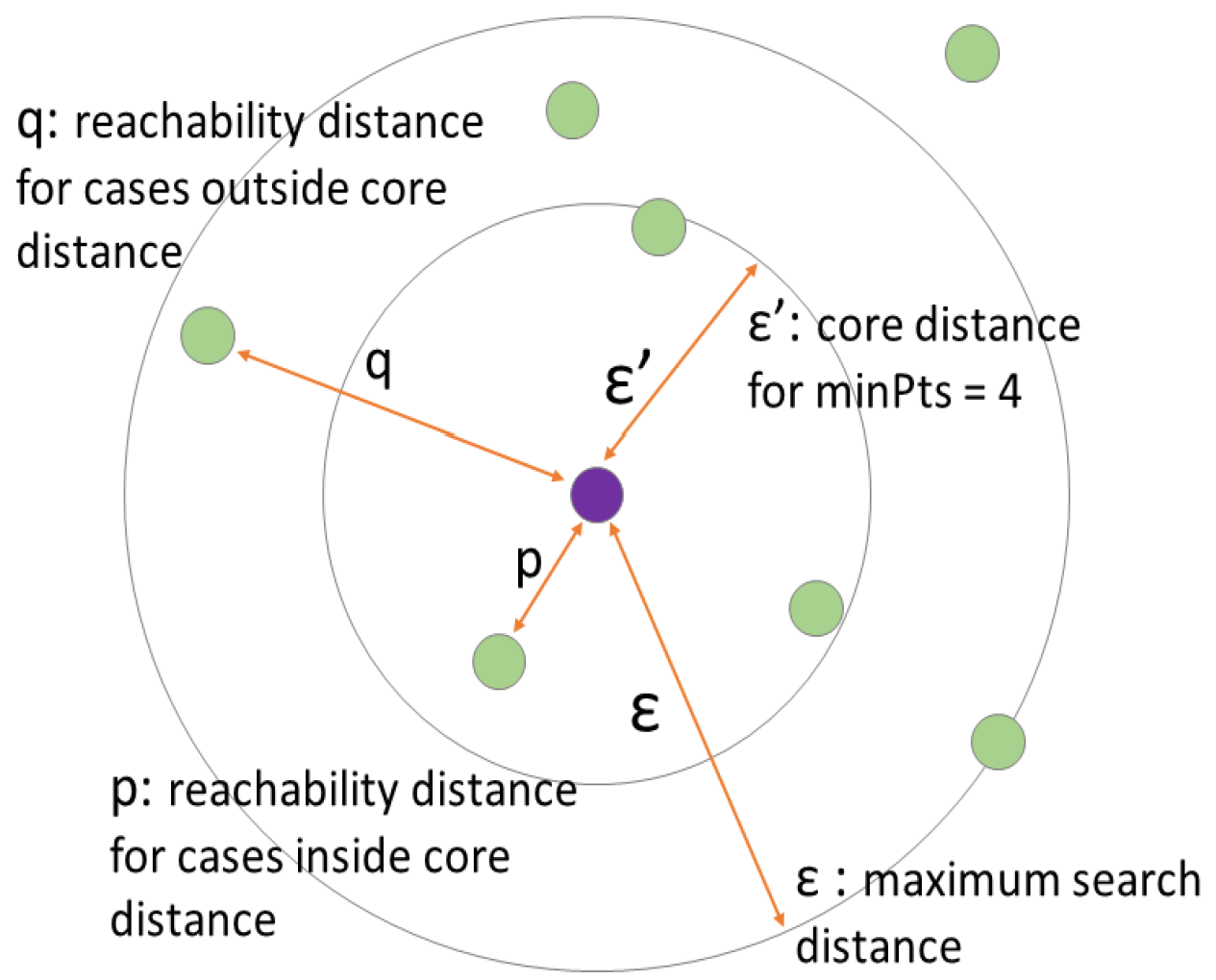
In addition, OPTICS provides a hierarchical cluster structure, allowing for nested clusters, a feature missing in both K-means and DBSCAN, which is measured by the parameter

ξ

, the minimum steepness on the reachability plot that forms a cluster boundary. However, OPTICS can be sensitive to its parameter settings, particularly the minimum number of points needed to define a cluster. Its computational complexity may also be more demanding because, unlike DBSCAN, where the maximum radius of the neighbourhood

ε

is fixed; in OPTICS,

ε

is devised to identify clusters across all scales, especially with large datasets. Nonetheless, in practice, for most datasets and specifically with an appropriate indexing mechanism, OPTICS runs efficiently: often close to

O (n log n)

. Yet, it should be noted that degenerate cases can push the complexity closer to

O (n^{2})

. For completion, Table 1 presents the basic concepts and parameters concerning OPTICS and Figure 1 provides a simple illustration of its working.

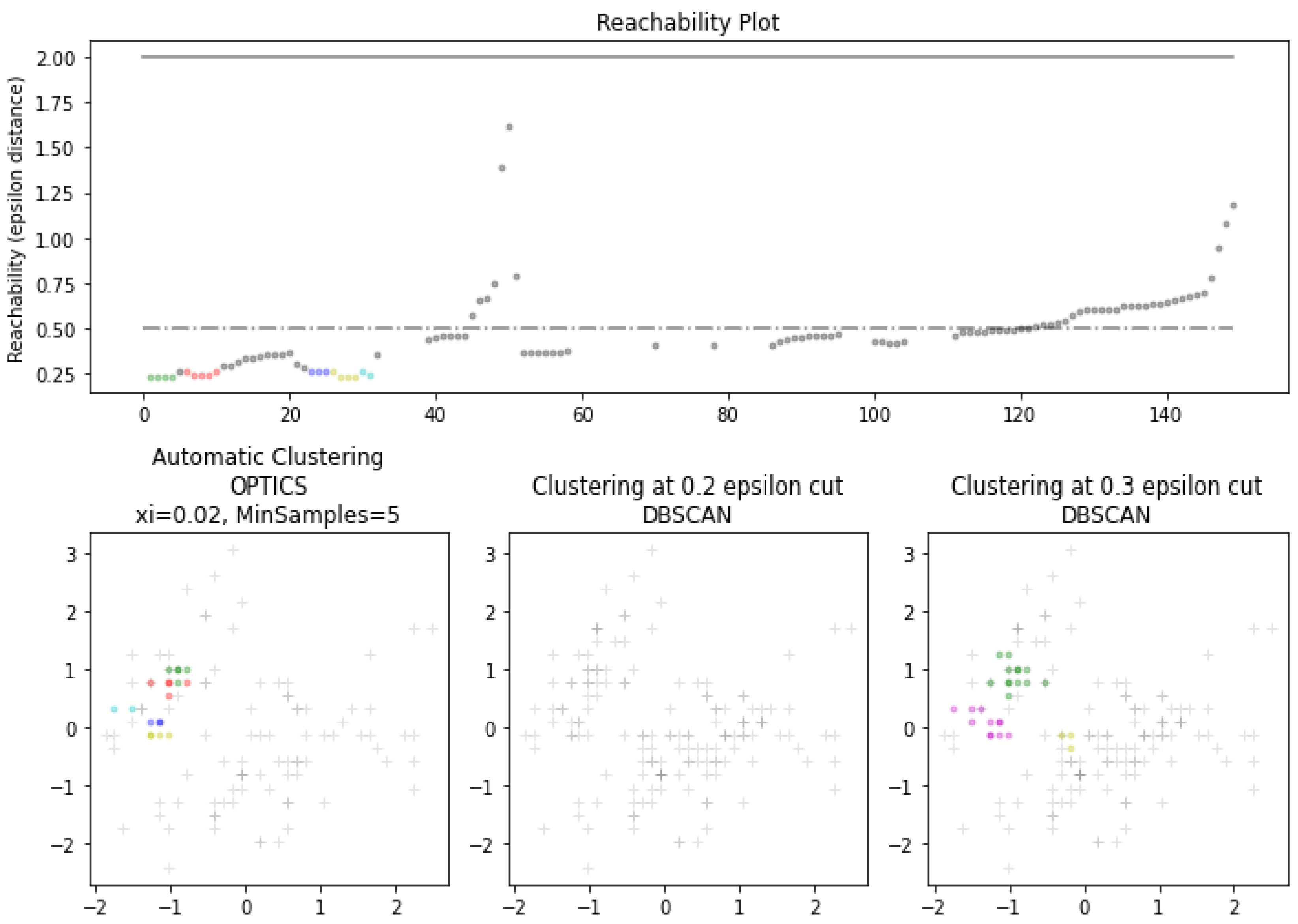
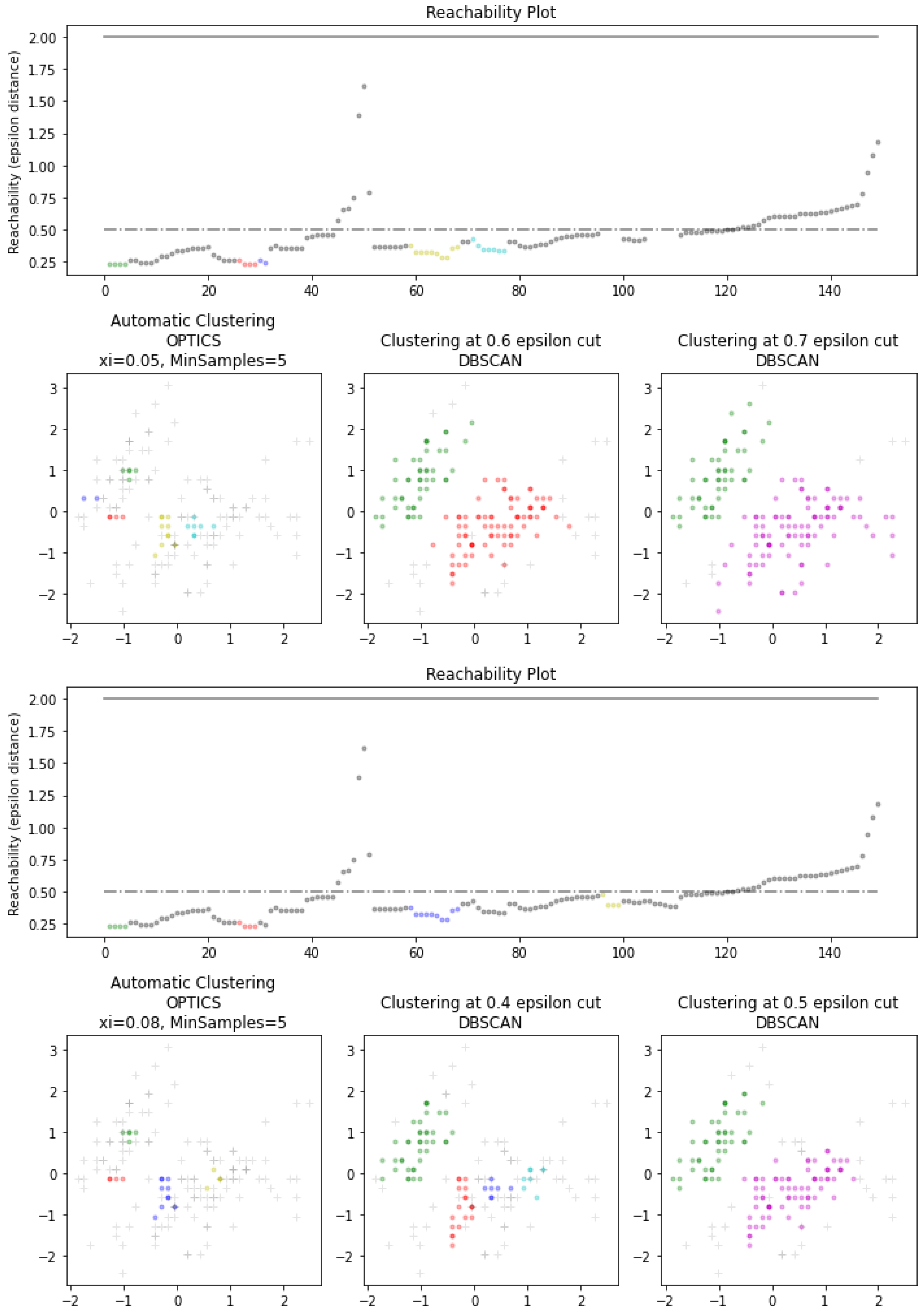
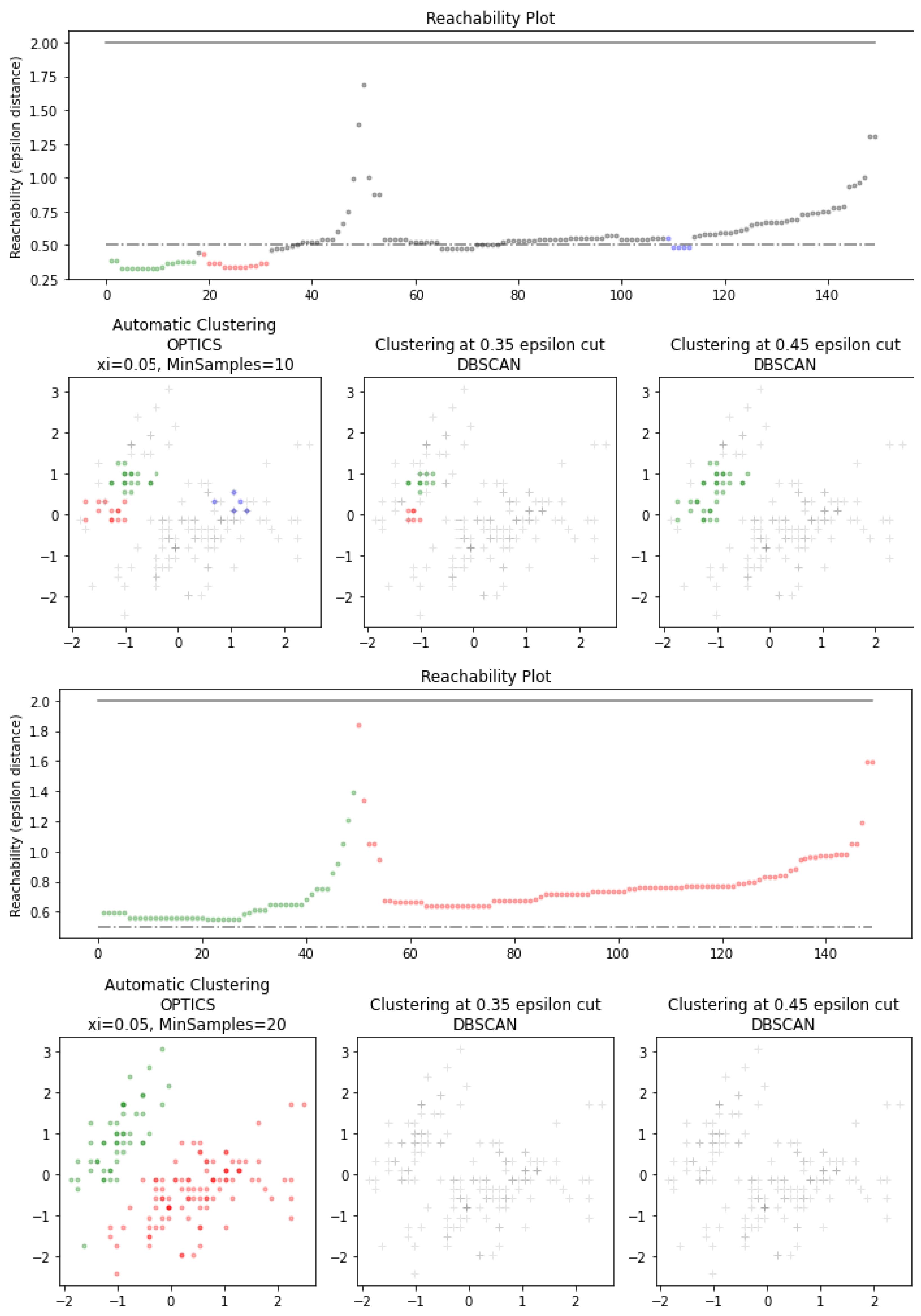
More formally, Algorithm 1 outlines the process of OPTICS. In addition, Figure 2 shows the impact of different parameters set upon the results of OPTICS clustering (as compared to the employment of DBSCAN) with respect to the classical Iris dataset [27]. NOte that both algorithms share the same

M i n S a m p l e

in defining the minimum size of a cluster, while DBSCAN purely depends on fixed epsilon value and OPTICS uses

ξ

to define reachability without a fixed epsilon value. It can be seen from the illustrations given in this figure that under different settings, results from the OPTICS clustering algorithm (regarding variation of

ξ

) exhibit more effective clusters (in smaller groups and located in more dense areas). This forms sharp contrast with the outcomes of applying DBSCAN where clusters give relatively larger clusters across varying densities, and it may even generate no clusters when encountering a greater

M i n S a m p l e

value. The above empirical findings indicate that OPTICS offers better robustness while determining groups within a dense area of data points. In particular, this differs from the existing GA-based approach [22] that utilises pre-defined hypercubes to depict the knowledge space. Applying a clustering algorithm avoids strict boundaries like the hypercubes. Furthermore, the reachability feature in OPTICS introduces a new level of robustness on top of DBSCAN, which can determine tighter clusters, facilitating the approach proposed herein to investigate the generalisation of the interpolated rules with more informative content.

Algorithm 1 OPTICS Clustering Algorithm

Start:
Procedure OPTICS $(Dataset D, MinPts, ξ, maxSamples)$ :
Step 1. Initialise all points in D as unprocessed; set $O r d e r e d L i s t = \emptyset$
and $S e e d L i s t$ as an empty priority queue.
Step 2. For each $p o i n t$ in D, if $p o i n t$ is unprocessed:
Obtain neighbours with RegionQuery and process $p o i n t$ .
If $p o i n t$ is a core point:
Add its unprocessed neighbours to $S e e d L i s t$ with their respective
reachability distances.
Step 3. While $S e e d L i s t$ is not empty:
Pop point p with smallest reachability distance from $S e e d L i s t$ .
Mark p as processed and add to $O r d e r e d L i s t$ .
If p is a core point:
For each unprocessed neighbour n of p:
Update reachability distance of n and add/update its position in $S e e d L i s t$ .
Step 4. Return $O r d e r e d L i s t$ .
End.
Function RegionQuery $(p o i n t, ξ, maxSamples)$ :
Return all points within reachability distance considering $ξ$ and restricted
by maxSamples.
End.

3. Density Based Dynamic Fuzzy Rule Interpolation

This section describes the proposed method employing OPTICS to construct a dynamic fuzzy rule interpolation, hereafter abbreviated to OPTICS-D-FRI.

3.1. Structure of Proposed Approach

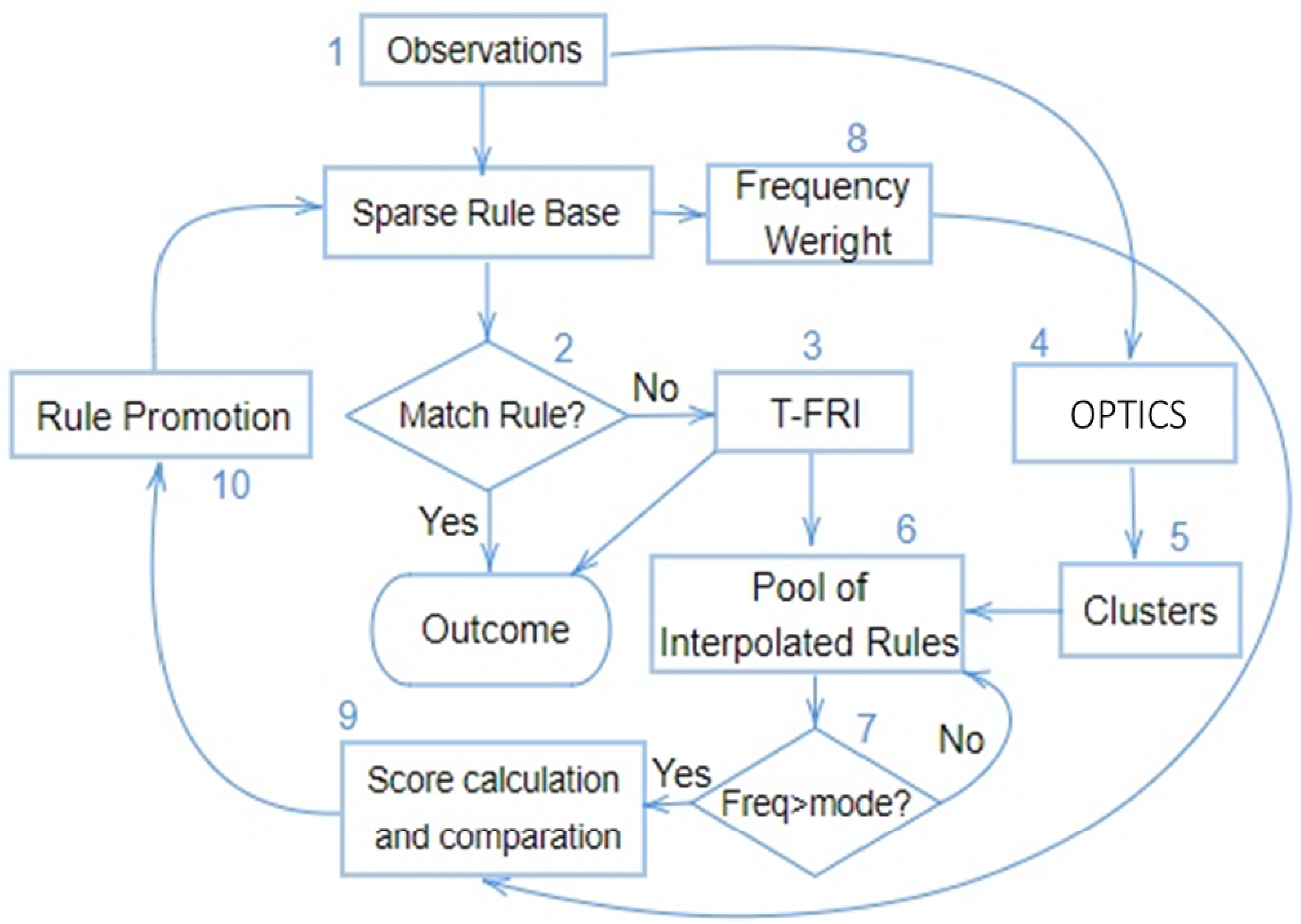
To provide an overview, Figure 3 illustrates the structure of OPTICS-D-FRI. Throughout the subsequent procedure, steps are enumerated with a notation ’(k)’, representing the sequence of operations as depicted in Figure 3.

Initiated with a sparse rule base, denoted as

R

, and one of unseen observations (which has not been utilised to derive any outcome), the first step of the inference process tests whether any rule exists within

R

that can match the observation; if so, the respective rule is triggered to produce the outcome. In scenarios where the observation does not match any rule (2), the T-FRI (3) is employed to begin the rule interpolation process. The outcome,

R_{i}^{T}

, is accumulated into a pool of interpolated rules. After accumulating a complete batch of observations in the interpolated pool (6), the OPTICS algorithm clusters these observation points (4). Then, the interpolated rules are categorised in alignment with the clustering outcomes of the observations (5-6). After that, the recurrence frequency of interpolated rules within each cluster is calculated. Those rules

R_{i}^{S} : A_{m, 1}, A_{m, 2}, \dots, A_{m, N}, B_{z}

(with m denoting the number of attributes in the rule antecedent space and z representing the fuzzy consequent) of a frequency

F r e q_{R_{i}^{S}}

surpassing the mode frequency

m o d e (F r e q_{C_{i}})

within the cluster

C_{i}

, are selected to progress onto the subsequent phase (7).

Regarding every potential outcome

B_{z}

(8), the next stage computes a linguistic attribute frequency weight, as outlined in [26], represented by (

W_{s p a r s e}^{B_{z}} = [W_{A 0}^{0}, W_{A 1}^{1}, \dots, W_{A N}^{N}]

), where (

W_{A N}^{N} = [a_{N 0}, a_{N 1}, \dots, a_{N m}]

) and

a_{N m}

signifies the frequency weight of an attribute within the antecedent

A_{N}

corresponding to

B_{z}

. The procedure following this calculates a score,

S c o r e_{B} = [S_{B 1}, S_{B 2}, \dots, S_{B z}]

, for each consequent

B_{z}

regarding the antecedent linguistic attributes of the rules

R_{i}^{S} : A_{m, 1}, A_{m, 2}, \dots, A_{m, N}

(9). If the resultant score,

S_{B z}

, for

B_{z}

from the rule

R_{i}^{S} : A_{m, 1}, A_{m, 2}, \dots, A_{m, N}, B_{z}

is the highest, the rule is selected (10) and promoted into the original sparse rule base, leading to an enriched or promoted rule base

P = R \cup {R_{i}^{S}}

(10). Conversely, if score

S_{B z}

does not stand out within

S c o r e_{B}

, the consequent

B_{z}

will be substituted by

B_{z} = B_{M A X (S c o r e_{B})}

, and then the entire process iterates.

Note that the computational complexity of OPTICS and that of T-FRI [12] are

O_{O P T I C S} (n^{2})

and

O_{T - F R I} (n^{2})

respectively. Therefore, the overall computational complexity of the proposed approach is

O_{O P T I C S - D - F R I} = O_{O P T I C S} (n^{2}) + O_{T - F R I} (n^{2})

. This means that

O_{O P T I C S - D - F R I} = O (n^{2})

3.2. Membership Frequency Weight Calculation and Interpolated Rule Promotion

Apart from the generic structure proposed for OPTICS-D-FRI, a key contribution of this work is providing a means for computing the membership frequency weights that are exploited to decide on whether an interpolated rule should be promoted to becoming a generalised rule to enrich the existing sparse rule base. Algorithm 2 summarises the underlying procedure for such computation.

Algorithm 2 Frequency Weight Application

Start:
Input: Sparse Rule Base $R^{S}$ ,

$R_{i} : IF x_{1} is A_{i, 1} AND . . . AND x_{N} is A_{i, N} THEN y is B_{i},$

where i spans the set ${1, \dots, | R^{S} |}$ with $| R^{S} |$ denoting the total count of rules present in the sparse rule base, N indicates the overall number of these variables, and the notation $A_{i, j}$ indicates the linguistic value attributed to the variable $x_{j}$ within the rule $R_{i}$ (herein represented as a triangular fuzzy set $(a_{0, j}, a_{1, j}, a_{2, j})$ ).
Output: Frequency Weights Table and Frequency Score
Step 1. For each rule $R_{i}$ in $R^{S}$ :
Extract representative values $R e p (A_{i, j}) = (a_{0, j}, a_{1, j}, a_{2, j}) / 3$ from each antecedent and $R e p (B) \in {0, 1, \dots, C}$ from consequent (where C is the total number of decision categories, e.g., number of possible classes for classification problems).
Step 2. Identify all q different rules per decision category $R e p (B) \in {0, 1, \dots, C}$ and calculate the frequency by $1 / n$ from each antecedent domain, where n stands for number of unique $R e p (A_{i, j})$ within q different rules of each class, with $i \in {1, \dots, q}$ in each domain $j \in {1, \dots, N}$ .
Step 3. Update frequency weights table of each antecedent domain regarding each possible class $R e p (B) \in {0, 1, \dots, C}$ .
Step 4. Compute $R e p (A_{f j})$ on each interpolated rule and match against frequency weights $W_{f} = (w_{1}, w_{2}, \dots, w_{j})$ within frequency weights table for each $R e p (B) \in {0, 1, \dots, C}$ .
Step 5. Sum frequency weights $S_{R e p (B)} = w_{1} + w_{2} + \dots + w_{j}$ for each $R e p (B) \in {0, 1, \dots, C}$ , resulting in $S c o r e_{B} = [S_{R e p (B) = 0}, S_{R e p (B) = 1}, \dots, S_{R e p (B) = C}]$
Step 6. Take $M a x (S c o r e_{B}) = M a x [S_{R e p (B) = 0}, S_{R e p (B) = 1}, \dots, S_{R e p (B) = C}]$ , and replace interpolated consequent with outcome of $M a x (S c o r e_{B})$ .
End.

To aid in understanding, a demonstration of how to compute frequency weights is provided here, based on a sparse rule base as indicated in Table 2. For simplicity, suppose that all fuzzy terms are represented by their respective representative values. This table shows that one of three membership functions (say,

M_{0}, M_{1}

and

M_{2}

) may be taken by each of the three antecedent variables at a time, and that there are three potential consequent values too. For classification tasks, the consequent values may be crisp, denoting three different classes (say, classes 0, 1 and 2). Thus, the first row of this table represents a fuzzy rule, stating that "If

x_{1}

A_{1}

and

x_{2}

A_{2}

and

x_{3}

A_{3}

then y is 0" where fuzzy sets

A_{1}

A_{2}

A_{3}

and

B_{2}

are defined with certain membership functions

M_{1}

M_{0}

and

M_{1}

(whose representative values are 1, 0 and 1), respectively. The use of representative values herein helps simplify the explanation of the relevant calculations.

For example, consider the two rules that each conclude with class 0 (i.e., the first and last one, where

R e p (B = 0)

). Both rules are associated with the second membership function (

R e p (A_{1}) = 1

). However, regarding the first antecedent variable there is just one unique fuzzy set for it to take, so

1 / 1 = 1

for this variable. Regarding the second antecedent variable, it involves two different fuzzy sets (

M_{0}

and

M_{1}

) as depicted by

R e p (A_{1})

and

R e p (A_{2})

, which gives

1 / 2 = 0.5

for each unique variable. Generalising the intuition underlying this example, the frequency weights can be determined following the procedure in Algorithm 2.

The results are displayed in Table 3, again denoted using their representative values for fuzzy terms.

From the above, again for illustration, suppose that after step (7), the interpolated rule taken from the pool for checking is

R_{i}^{S}

: [

R e p (A_{1}) = 1

R e p (A_{2}) = 2

R e p (A_{3}) = 1

R e p (B) = 0

] (whose interpretation in terms of a conventional product rule for classification is obvious). Matching it against the frequency weights computed from the existing sparse rule base leads to the following: The

S c o r e_{B} = [S_{R e p (B) = 0} : 1 + 0 + 1 = 2, S_{R e p (B) = 1} : 0 + 1 + 0 = 1, S_{R e p (B) = 2} : 0 + 0 + 1 = 1]

. In this case,

R e p (B) = 0

is associated with the highest score, while the selected rule is concerned with the same outcome. Therefore, this selected interpolated rule is promoted, becoming a new rule in the sparse rule base.

4. Experimental Investigations

This section explains the experimental setup and discusses the results of applying the proposed OPTICS-D-FRI.

4.1. Datasets and Experimental Setup

As an initial attempt towards the development of a comprehensive dynamic fuzzy rule interpolative reasoning tool, five classical datasets, namely Iris, Yeast, Banana, Glass and Tae, are herein employed to validate the performance of the methodology presented. Note that given the restriction on the size of the Iris dataset, which contains just 150 observations, it is necessary to incorporate data simulation techniques to ensure a more robust assessment of the proposed approach. For this purpose, the Iris dataset has been artificially expanded using the ’faux’ package [28] in the R environment. Detailed description of all five datasets is presented in Table 4.

For each application problem (i.e., dataset) the dataset is partitioned into three distinct categories. This partition is randomly carried out other than the sizes of the partitioned sub-datasets being pre-specified: One of which comprises 50% of the total data is used to form a dense rule base for each problem, denoted as

D

. The resulting rule base covers the majority of the problem domain and is intended to be the gold-standard for subsequent comparative studies when a sparse rule base is used. Adopting a conventional data-fitting algorithm as delineated in [29] facilitates the rule generation process. More advanced rule induction techniques (e.g., the method of [30]) may be utilised as the alternative if preferred, for enhanced outcomes. After the formation of a dense rule base

D

, a strategic rule reduction by randomly dropping 30% of the rules from the dense rule base is done to create a sparse rule base, with the remaining 70% being regarded as the sparse rule base

R

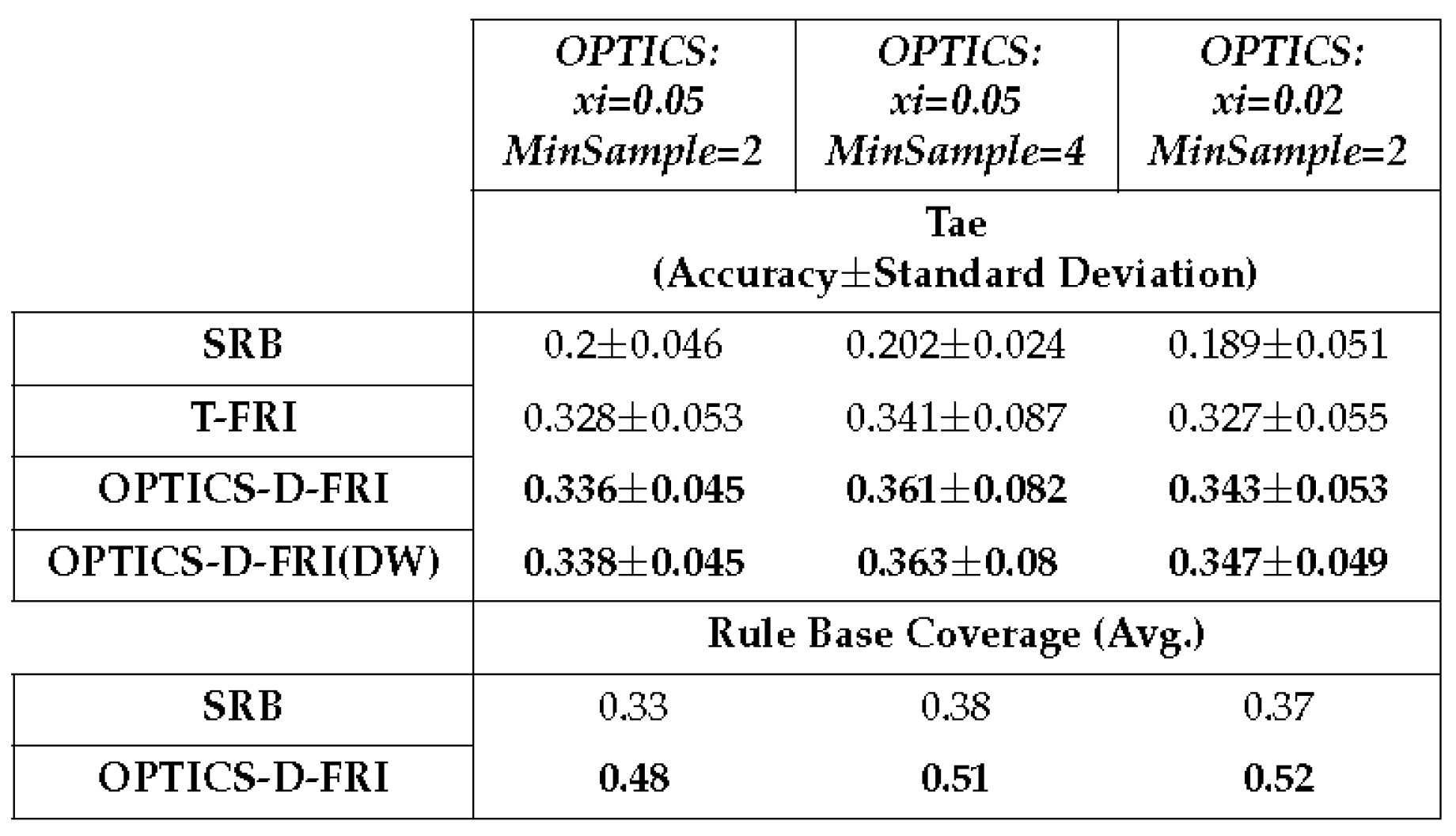
The other two sub-datasets, each containing 25% of the original data, are used separately for dynamic fuzzy rule interpolation (when no rules match a novel observation) and final testing. In particular, the sub-dataset for final testing is adopted to evaluate the performance of the interpolated and subsequently promoted rule base,

P

. Additionally, by calculating the membership frequency weight of the promoted rule base

P

(which adds the promoted rule into the original sparse rule base and recalculates the frequency weights of the entire promoted rule base). As a result, the dynamically promoted rule base with weights

P_{D}

, denoted by OPTICS-D-FRI(DW), is also evaluated using this third sub-dataset.

A 10x10 cross-validation is implemented on the test datasets to evaluate the proposed OPTICS-D-FRI algorithm. For easy comparison, metrics such as average accuracy and associated standard deviation regarding the employment of conventional rule-firing with just the sparse rule base (SRB), T-FRI, OPTICS-D-FRI, and the dynamically weighted OPTICS-D-FRI are presented. Within these tables, the better performances are shown in bold font.

4.2. Experimental Results

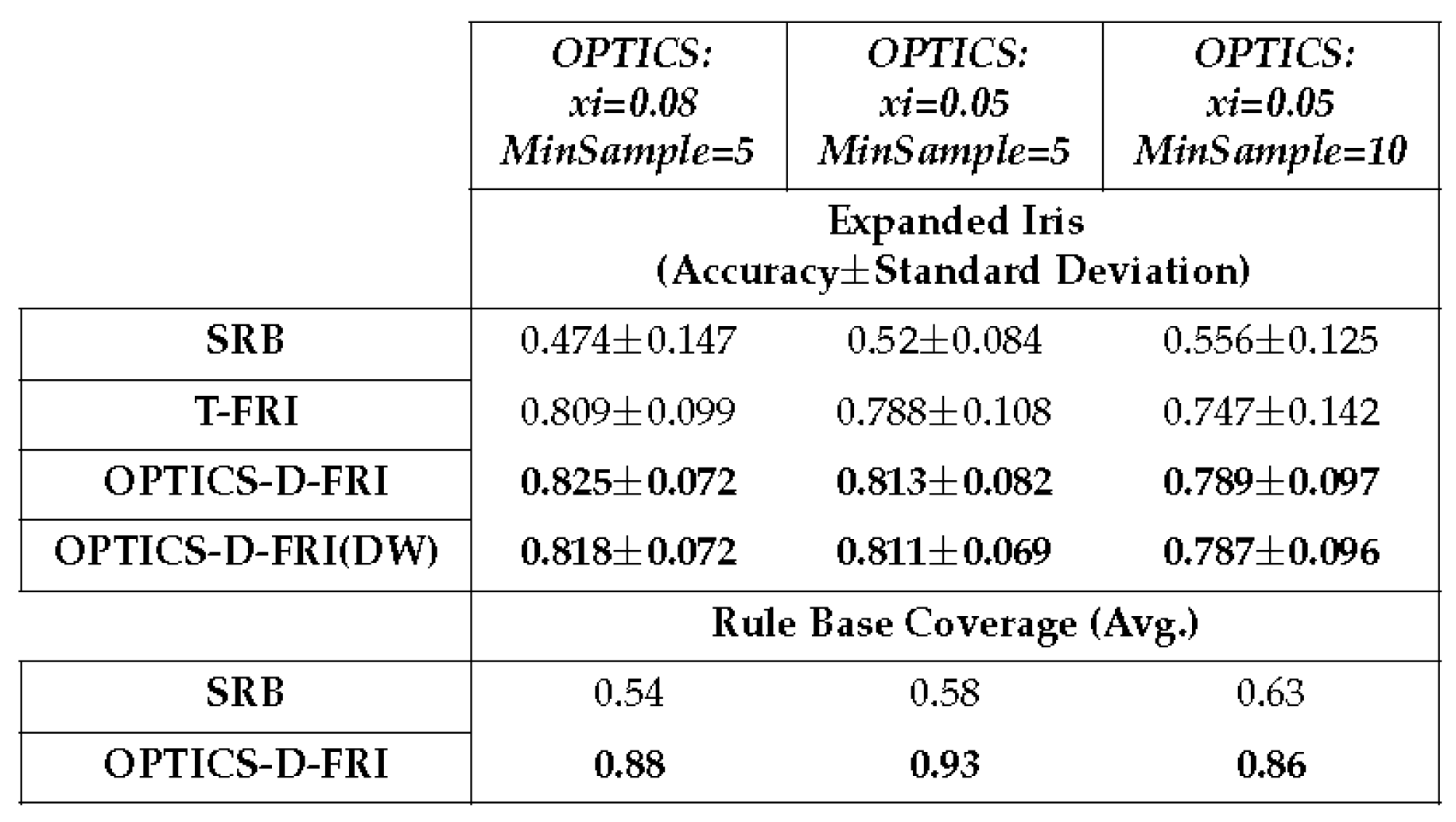
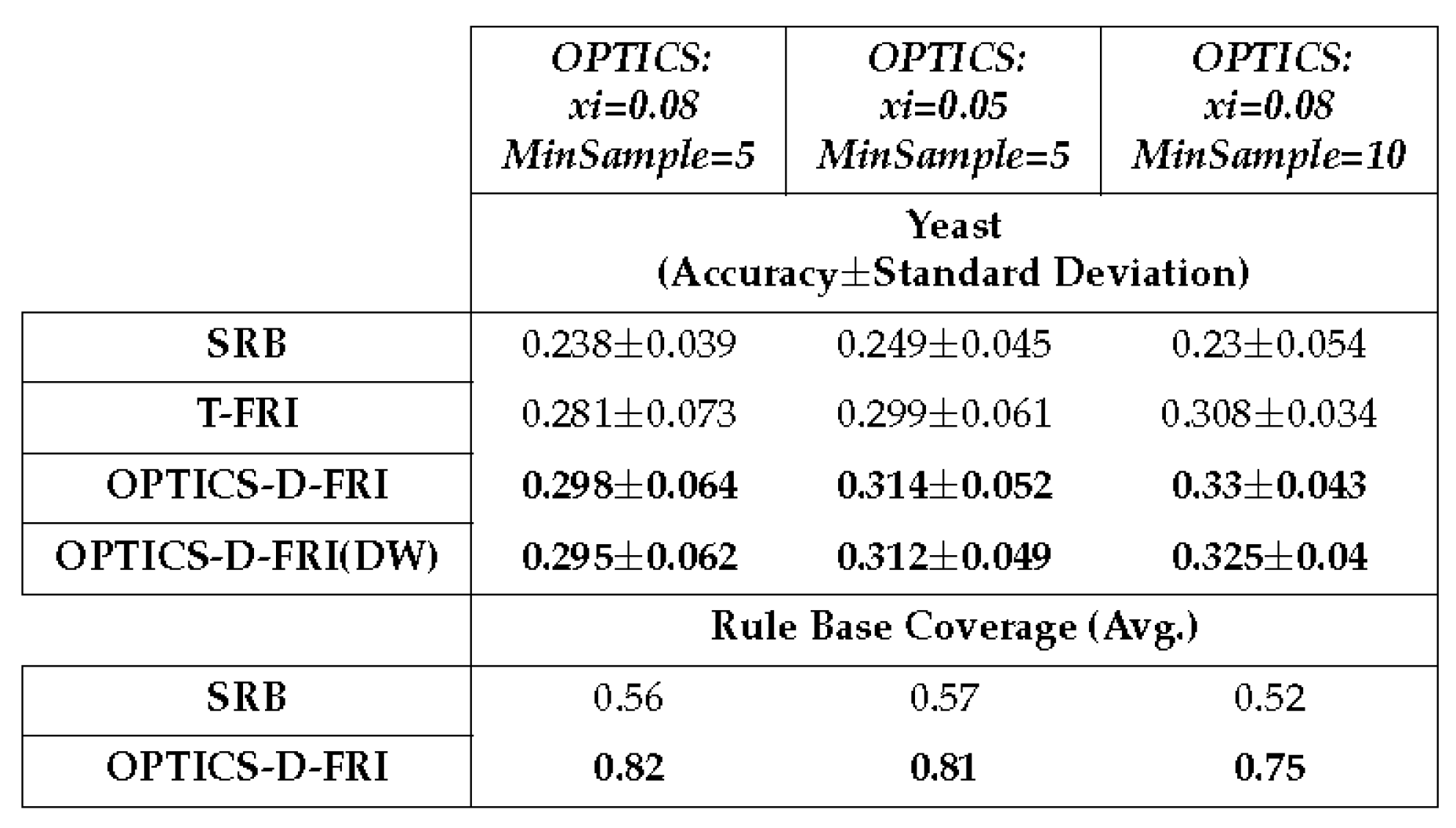
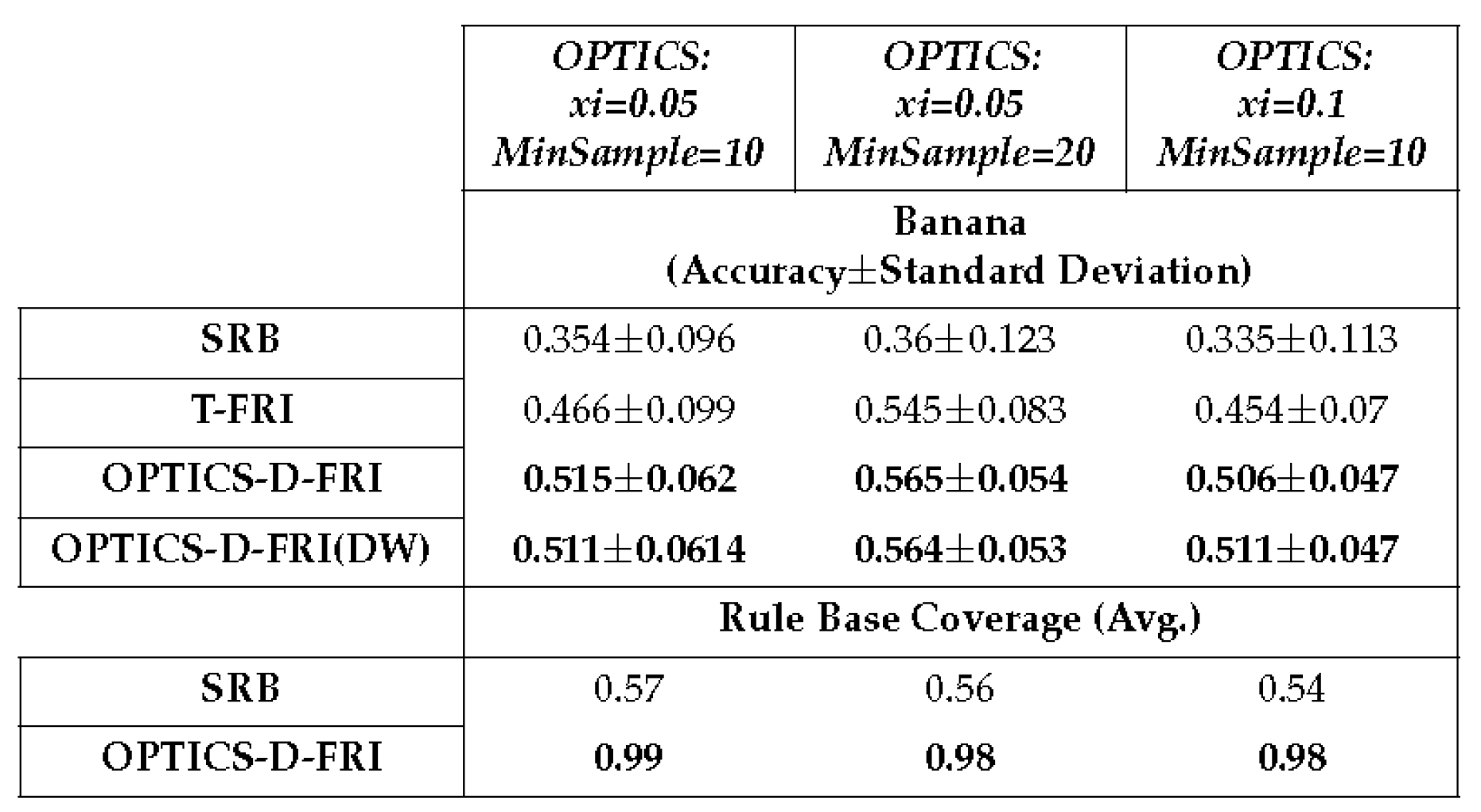
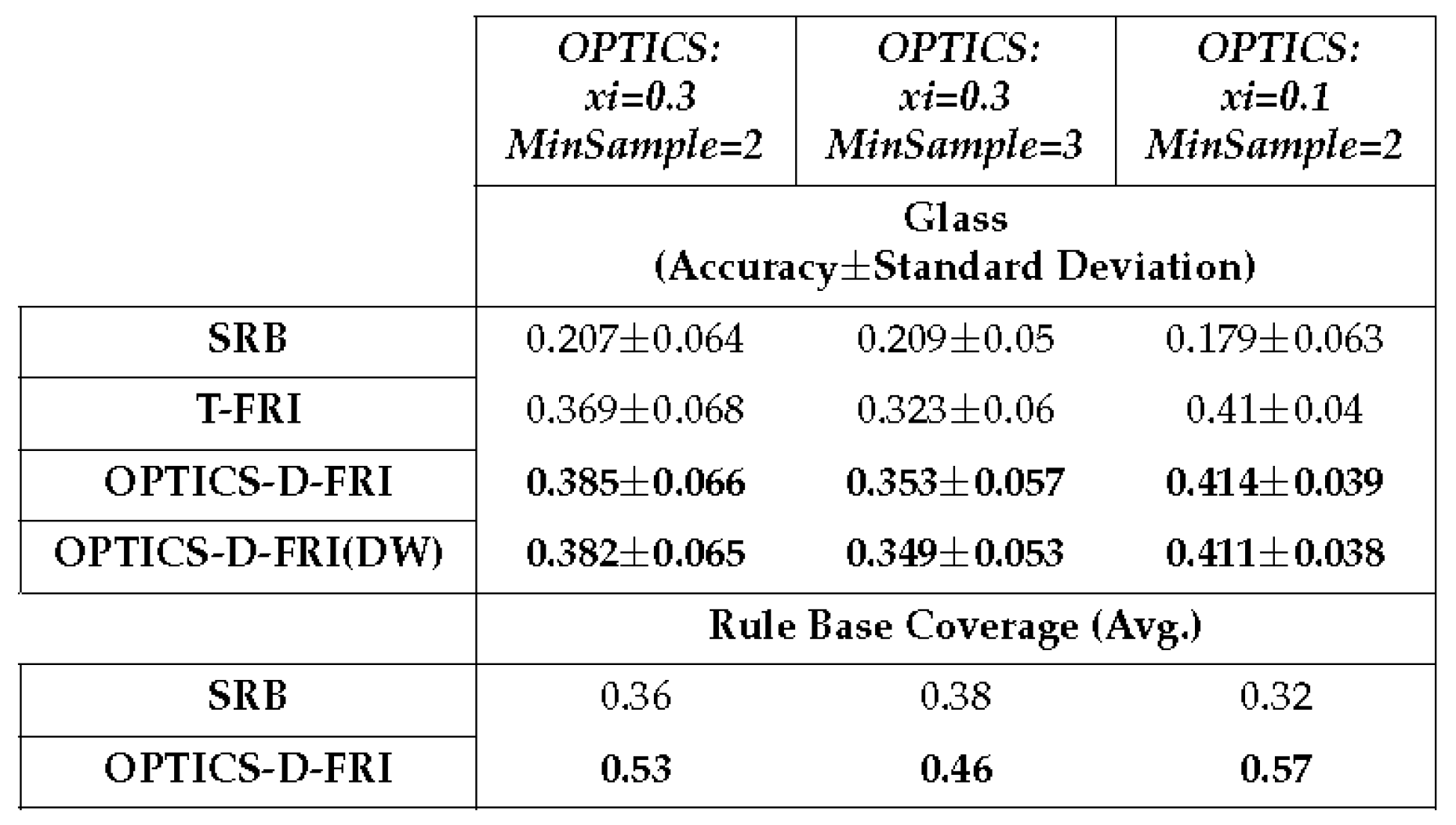
The results of performance evaluation are presented in the following five tables, with each corresponding to a given dataset. According to these results, the proposed OPTICS-D-FRI methodology proficiently clusters rules for unmatched observations. The introduction of the frequency weight method enables a dynamic equilibrium between T-FRI interpolated rules and those from the original sparse rule base, demonstrating a capability to simulate human reasoning. The inference outcomes from using the present approach improve significantly over those attainable by running conventional FRI methods given just a sparse rule base. The performance is strengthened by utilising the frequency weights derived from the sparse rule base. The promoted rules exhibit an accuracy that is at least equal to, and often higher than, the interpolated rules.

Table 5. 10 ×10 cross-validation on Expanded Iris dataset, with four membership functions defined for each antecedent variable.

Table 6. 10×10 cross-validation on Yeast dataset, with four membership functions defined for each antecedent variable.

Table 7. 10×10 cross-validation on Banana dataset, with four membership functions defined for each antecedent variable.

Table 8. 10×10 cross-validation on Glass dataset, with four membership functions defined for each antecedent variable.

Table 9. 10×10 cross-validation on Tae dataset, with four membership functions defined for each antecedent variable.

4.3. Discussion

In implementing both OPTICS and T-FRI, the Euclidean distance metric is uniformly employed for distance measurement. Within the OPTICS algorithm, the parameter denoted as

M i n S a m p l e

dictates the general size of the resulting clusters, essentially controlling the number of samples assigned to a specific cluster. Prior to parameter configuration, conducting an exploratory analysis of the problem domain (or dataset) is required. As an illustration, the Iris dataset has four features with distinctive clustering boundaries spanning four distinct classes. Conversely, the Yeast dataset is distributed across nine features, pairing with ten classes. Exploring the dataset and investigating the clustering performance is therefore necessary instead of randomly setting up OPTICS parameters; domain-specific insights can facilitate optimal cluster formation.

In empirical studies, it is observed that the

M i n S a m p l e

parameter controls the size of the clusters. Consequently, in the present preliminary experimental investigations, the other parameter,

M i n P t s

(the minimum number of samples to form a cluster), is fixed at two. Furthermore, the number of membership functions is equally assigned onto the span of antecedent space without any designated design, which may lead to the overall low accuracy on these datasets. This does not adversely affect this study since it is the relative performance that is considered amongst different approaches. An optimised domain partition can be expected to produce better outcomes. From the results obtained, the promoted rules not only enlarge the coverage of the original sparse rule base but also enable the inference system to attain better accuracy in comparison to the use of traditional T-FRI.

Upon closer examination of the experimental results, it can be observed that certain promoted rules align with some of those rules (intentionally removed for testing purposes) from the original dense rule base. This observation underscores the effectiveness of the proposed approach. This suggests that promoted rules can help improve the efficiency of the over inference system, particularly when observations close to previously unmatched data are introduced. It allows the execution of reasoning under such conditions with simple pattern-matching, subsequently reducing the need of FRI processes and hence, saving computational efforts while strengthening reasoning accuracy. Furthermore, merging a dynamic attribute weighting mechanism with the traditional T-FRI method, which accounts for the newly promoted rules in frequency weight calculation, offers considerable promise in enhancing the performance of a fuzzy rule-based system.

5. Conclusion

This paper has proposed an initial approach for creating a dynamic FRI framework by integrating the OPTICS clustering algorithm with the conventional T-FRI. It works by extracting information embedded within interpolated rules in relation to new and unmatched observations. It also introduces a novel way of determining populated regions, by clustering the new observations and annotating the group of interpolated rules, thereby eliminating the need for predefined hyper-cubes. Notably, the proposed OPTICS-D-FRI demonstrates enhanced performance over traditional FRI in inference accuracy.

Being an initial attempt to combine OPTICS and T-FRI for a dynamic FRI framework, this study also identifies several critical aspects for further refinement. For example, the current method requires specific predefined parameters, including

M i n S a m p l e

and

ξ

for OPTICS. Investigating a mechanism to automatically evaluate observations and determine such parameters remains as further research. Also, the foundational framework combining OPTICS is not strictly bound to the T-FRI method used in this study. Thus, a possible future direction is to examine the integration of alternative FRI methods and to evaluate their performance.

Recent advancements in the FRI literature highlight the efficacy of approximate reasoning that utilise attribute-weighted rules or rule base stricture [31], with an emphasis on employing attribute ranking mechanisms, as proposed in [32,33]. A density-based approach for fuzzy rule interpolation has also been proposed recently [34]. Frequency weighting benefits both attribute ranking and FRI, especially when integrating higher-order FRI [35] with rule induction and feature selection strategies [36], to address more complex application scenarios. Another exciting exploration involves assessing dynamically weighted attribute frequency calculations, particularly with the inclusion of newly promoted rules. Lastly, while the present validation is based on five classical datasets, broader empirical investigations involving more complex datasets, such as mammographic risk analysis [37,38], are necessary to reveal the potential and limitations of the proposed framework fully.

Author Contributions

Conceptualisation, J.L. and Q.S.; methodology, J.L. and C.S.; software, J.L.; validation, C.S., J.L. and Q.S.; formal analysis, J.L.; investigation, J.L. and C.S.; resources, J.L.; writing—original draft preparation, J.L..; writing—review and editing, C.S. and Q.S.; visualization, J.L.; supervision, C.S. and Q.S.; project administration, J.L. and C.S.; funding acquisition, C.S. and Q.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The data presented in this study are public datasets

Acknowledgments

The authors are grateful to the anonymous reviewers for their helpful comments on the earlier conference paper, which was recommended for consideration of producing an expanded version for inclusion in this special issue. The first author is supported in part by Aberystwyth University PhD scholarships.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:

MDPI	Multidisciplinary Digital Publishing Institute
DOAJ	Directory of Open Access Journals
FRI	Fuzzy Rule Interpolation
D-FRI	Dynamic Fuzzy Rule Interpolation
T-FRI	Transformation-Based Fuzzy Rule Interpolation
OPTICS	Ordering Points To Identify the Clustering Structure
GA	Genetic Algorithm
PSO	Particle Swarm Optimisation
DBSCAN	Density-Based Spatial Clustering of Applications with Noise
OPTICS-D-FRI	OPTICS assisted Dynamic Fuzzy Rule Interpolation

References

Dubois, D.; Prade, H. On fuzzy interpolation. International Journal Of General System 1999, 28, 103–114. [Google Scholar] [CrossRef]
Kóczy, L.; Hirota, K. Approximate reasoning by linear rule interpolation and general approximation. International Journal of Approximate Reasoning 1993, 9, 197–225. [Google Scholar] [CrossRef]
Kóczy, L.; Hirota, K. Interpolative reasoning with insufficient evidence in sparse fuzzy rule bases. Information Sciences 1993, 71, 169–201. [Google Scholar] [CrossRef]
Saga, S.; Makino, H.; Sasaki, J.I. A method for modeling freehand curves—The fuzzy spline interpolation. Systems and Computers in Japan 1995, 26, 77–87. [Google Scholar] [CrossRef]
Li, F.; Shang, C.; Li, Y.; Yang, J.; Shen, Q. Approximate reasoning with fuzzy rule interpolation: background and recent advances. Artificial Intelligence Review 2021, 54, 4543–4590. [Google Scholar] [CrossRef]
Gedeon, T.; Kóczy, L. Conservation of fuzziness in rule interpolation. Proc. of the Symp. on New Trends in Control of Large Scale Systems, 1996, Vol. 1, pp. 13–19.
Hsiao, W.H.; Chen, S.M.; Lee, C.H. A new interpolative reasoning method in sparse rule-based systems. Fuzzy Sets and Systems 1998, 93, 17–22. [Google Scholar] [CrossRef]
Kóczy, L.T.; Hirota, K.; Gedeon, T.D. Fuzzy Rule Interpolation by the Conservation of Relative Fuzziness. J. Adv. Comput. Intell. Intell. Informatics 2000, 4, 95–101. [Google Scholar] [CrossRef]
Baranyi, P.; Gedeon, T.D.; Koczy, L. Rule interpolation by spatial geometric representation. Proc. IPMU, 1996, Vol. 96, pp. 483–488.
Bouchon-Meunier, B.; Marsala, C.; Rifqi, M. Interpolative reasoning based on graduality. Ninth IEEE International Conference on Fuzzy Systems. FUZZ-IEEE 2000 (Cat. No. 00CH37063). IEEE, 2000, Vol. 1, pp. 483–487.
Huang, Z.; Shen, Q. Fuzzy interpolative reasoning via scale and move transformations. IEEE Transactions on Fuzzy Systems 2006, 14, 340–359. [Google Scholar] [CrossRef]
Huang, Z.; Shen, Q. Fuzzy interpolation and extrapolation: A practical approach. IEEE Transactions on Fuzzy Systems 2008, 16, 13–28. [Google Scholar] [CrossRef]
Jenei, S.; Klement, E.P.; Konzel, R. Interpolation and extrapolation of fuzzy quantities–The multiple-dimensional case. Soft Computing 2002, 6, 258–270. [Google Scholar] [CrossRef]
Johanyák, Z.C.; Kovács, S. Fuzzy rule interpolation by the least squares method. 7th International Symposium of Hungarian Researchers on Computational Intelligence (HUCI 2006), 2006, Vol. 2425, pp. 495–506.
Wu, Z.Q.; Masaharu, M.; Shi, Y. An improvement to Kóczy and Hirota’s interpolative reasoning in sparse fuzzy rule bases. International Journal of Approximate Reasoning 1996, 15, 185–201. [Google Scholar] [CrossRef]
Lee, L.W.; Chen, S.M. Fuzzy interpolative reasoning for sparse fuzzy rule-based systems based on the ranking values of fuzzy sets. Expert systems with applications 2008, 35, 850–864. [Google Scholar] [CrossRef]
Åström, K.J.; Wittenmark, B. Adaptive control; Courier Corporation, 2013.
Liu, B.D.; Chen, C.Y.; Tsao, J.Y. Design of adaptive fuzzy logic controller based on linguistic-hedge concepts and genetic algorithms. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics) 2001, 31, 32–53. [Google Scholar]
Mohan, S.; Bhanot, S. Comparative study of some adaptive fuzzy algorithms for manipulator control. International Journal of Computational Intelligence 2006, 3, 303–311. [Google Scholar]
Wang, Y.; Deng, H.; Chen, Z. Adaptive fuzzy logic controller with rule-based changeable universe of discourse for a nonlinear MIMO system. 5th International Conference on Intelligent Systems Design and Applications (ISDA’05). IEEE, 2005, pp. 8–13.
Labiod, S.; Boucherit, M.S.; Guerra, T.M. Adaptive fuzzy control of a class of MIMO nonlinear systems. Fuzzy sets and systems 2005, 151, 59–77. [Google Scholar] [CrossRef]
Naik, N.; Diao, R.; Shen, Q. Dynamic fuzzy rule interpolation and its application to intrusion detection. IEEE Transactions on Fuzzy Systems 2017, 26, 1878–1892. [Google Scholar] [CrossRef]
Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. ; others. A density-based algorithm for discovering clusters in large spatial databases with noise. kdd, 1996, Vol. 96, pp. 226–231.
Ankerst, M.; Breunig, M.M.; Kriegel, H.P.; Sander, J. OPTICS: Ordering points to identify the clustering structure. ACM Sigmod record 1999, 28, 49–60. [Google Scholar] [CrossRef]
Lin, J.; Shang, C.; Shen, Q. Towards Dynamic Fuzzy Rule Interpolation with Harmony Search. Proceedings of the 21st Annual Workshop on Computational Intelligence., 2022.
Lin, J.; Xu, R.; Shang, C.; Shen, Q. Towards Dynamic Fuzzy Rule Interpolation via Density-Based Spatial Clustering of Interpolated Outcomes. Proceedings of the 2023 IEEE International Conference on Fuzzy Systems. IEEE Press, 2023.
Fisher, R.A. The use of multiple measurements in taxonomic problems. Annals of eugenics 1936, 7, 179–188. [Google Scholar] [CrossRef]
DeBruine, L. faux: Simulation for Factorial Designs, 2021. R package version 1.1.0. [CrossRef]
Wang, L.X.; Mendel, J. Generating fuzzy rules by learning from examples. IEEE Transactions on Systems, Man, and Cybernetics 1992, 22, 1414–1427. [Google Scholar] [CrossRef]
Chen, T.; Shang, C.; Su, P.; Shen, Q. Induction of accurate and interpretable fuzzy rules from preliminary crisp representation. Knowledge-Based Systems 2018, 146, 152–166. [Google Scholar] [CrossRef]
Jiang, C.; Jin, S.; Shang, C.; Shen, Q. Towards utilization of rule base structure to support fuzzy rule interpolation. Expert Systems 2023, 40, e13097. [Google Scholar] [CrossRef]
Li, F.; Li, Y.; Shang, C.; Shen, Q. Fuzzy knowledge-based prediction through weighted rule interpolation. IEEE Transactions on Cybernetics 2020, 50, 4508–4517. [Google Scholar] [CrossRef] [PubMed]
Li, F.; Shang, C.; Li, Y.; Yang, J.; Shen, Q. Interpolation with just two nearest neighbouring weighted fuzzy rules. IEEE Transactions on Fuzzy Systems 2020, 28, 2255–2262. [Google Scholar] [CrossRef]
Gao, F. Density-based approach for fuzzy rule interpolation. Applied Soft Computing 2023, 143, 110402. [Google Scholar] [CrossRef]
Chen, C.; MacParthaláin, N.; Li, Y.; Price, C.; Quek, C.; Shen, Q. Rough-fuzzy rule interpolation. Information Sciences 2016, 351, 1–17. [Google Scholar] [CrossRef]
Jensen, R.; Cornelis, C.; Shen, Q. Hybrid fuzzy-rough rule induction and feature selection. 2009 IEEE International Conference on Fuzzy Systems, 2009, pp. 1151–1156.
Li, F.; Shan, C.; Li, Y.; Shen, Q. Interpretable mammographic mass classification with fuzzy interpolative reasoning. Knowledge-Based Systems 2020, 191, 105279. [Google Scholar] [CrossRef]
Dounis, A.; Avramopoulos, A.N.; Kallergi, M. Advanced Fuzzy Sets and Genetic Algorithm Optimizer for Mammographic Image Enhancement. Electronics 2023, 12, 3269. [Google Scholar] [CrossRef]

Figure 1. Illustration for OPTICS.

Figure 2. Different OPTICS clustering settings on Iris dataset.

Figure 3. Proposed OPTICS-D-FRI framework.

Table 1. Concepts and parameters of OPTICS clustering algorithm.

Concept	Definition
$ξ$	Parameter used to specify the steepness that defines a cluster in reachability plot, with clusters determined as
	regions in reachability plot that exhibit a steep decrease, followed by a gentler increase in reachability distance.
MinPts	Minimum number of points needed to form a dense region, signifying that at least MinPts points are contained
	within its $ε$ -neighbourhood for it to be considered a core point.
Reachability Distance	Smallest distance to reach a point while considering density (number of points) in the neighbourhood.
Core Distance	Smallest radius required for a point to cover MinPts points in its neighbourhood.
Ordering	Sequence in which points are processed, resulting in cluster ordering rather than explicit cluster assignments.

Table 2. Example Sparse Rule Base Represented with Representative Values.

$R e p (A_{1})$	$R e p (A_{2})$	$R e p (A_{3})$	$R e p (B)$
1	0	1	0
2	1	1	2
0	2	0	1
2	0	1	2
1	1	1	0

Table 3. Frequency Weights of Sparse Rule Base.

	$R e p (A_{1})$			$R e p (A_{2})$			$R e p (A_{3})$
$R e p (B)$	$M_{0}$	$M_{1}$	$M_{2}$	$M_{0}$	$M_{1}$	$M_{2}$	$M_{0}$	$M_{1}$	$M_{2}$
0	0	1	0	0.5	0.5	0	0	1	0
1	1	0	0	0	0	1	1	0	0
2	0	0	1	0.5	0.5	0	0	1	0

Table 4. Description of Datasets.

	Iris (Expanded)	Yeast	Banana	Glass	Tae
Features	4	9	2	9	6
Classes	3	10	2	7	3
Sample Size	1500	1484	5300	214	151

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Towards Dynamic Fuzzy Rule Interpolation via Density-Based Rule Promotion from Interpolated Outcomes

Abstract

1. Introduction

2. Foundational Work

2.1. Transformation-Based Fuzzy Rule Interpolation (T-FRI)

2.2. OPTICS Clustering

3. Density Based Dynamic Fuzzy Rule Interpolation

3.1. Structure of Proposed Approach

3.2. Membership Frequency Weight Calculation and Interpolated Rule Promotion

4. Experimental Investigations

4.1. Datasets and Experimental Setup

4.2. Experimental Results

4.3. Discussion

5. Conclusion

Author Contributions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

Abbreviations

References

MDPI Initiatives

Important Links

Subscribe