1. Introduction
Recarbonization is drinking water treatment to increase water quality parameters as calcium and magnesium content in drinking water with low level of minerals content. A large body of scientific evidence attributed health problems to these biogenic elements. In addition to this, very low concentrations of calcium and magnesium in water have been recognized as the cause of the problems with corrosive and aggressive impacts. Water with a very low level of minerals is unstable and unbuffered. Various treatment methods can be applied increase the mineral content of drinking water, each offering several advantages and disadvantages. Fluidized bed reactor offers the potential to increase the interfacial reaction surface and overall reaction rate and appears a new approach in water treatment.
The recarbonization process is a water treatment technology that is used to improve the quality of drinking water with a low concentration of calcium and magnesium. The aim of the process is to increase the content of calcium and magnesium in for human consumption. Therefore, the variability in the chemical composition of water that people use for drinking and cooking from the same source has combination of chemical elements for a relatively long period during their lifetime until they move to another location [
1,
2].
A large body of studies in different countries have shown a direct relationship between the content of minerals in supplied drinking water and their effect on human health. With a low content of Ca2+ and Mg2+ in drinking water, the quality of life deteriorates.
Studies indicate that there is an increased incidence/mortality Studies indicate that there is increased healthy problems mainly from cardiovascular diseases, but also from oncological diseases, diabetes mellitus, diseases of the digestive system and respiratory tract. A strong chronic impact on human health has been investigated especially in magnesium deficiency and it is believed that magnesium it is necessary to add to drinking water if its content is below the endorsed norm [
3,
4,
5,
6,
7].
Most authors of studies state that in drinking water that is beneficial to health, the content of calcium should be in the scale of 20-80 mg/L and magnesium 10-50 mg/L [
2,
8,
9,
10,
11,
12,
13]. Biogenic elements such as calcium and magnesium are not only essential from a health point of view. They are also of technological importance, because soft water, which contains low concentrations of calcium and magnesium, has a corrosive and aggressive effect on distribution pipes [
14].
Despite the demonstrable significance of calcium and magnesium in drinking water, there are no precisely defined limits in the world that would legally define their optimal range of concentration in drinking water required. In the Slovak legislation, the limit of calcium and magnesium is stated only as a recommended content [
2,
10].
To improve the quality of life, the recarbonization process should be applied to places where drinking water is poorly mineralized. There are many ways to recarbonization. It is carried out with the help of alkaline and acidic reagents in an appropriate ratio, so that substances necessary for health are present in the water, and it is desirable that in the event of an overdose of some reagents, there is no damage from a technological and health point of view [
15].
One of the simplest and most effective methods of recarbonization is the direct dosing of chemical solutions of biogenic elements, which can be prepared ex situ or in situ from solid material. Calcium chloride is most added in combination with sodium bicarbonate. Although it is a very simple process, the biggest disadvantage of this process is the cost of chemicals. For this reason, this approach has very limited application [
15,
16].
Another and especially more affordable method is the use of carbonates with carbon dioxide. This technique is very popular in water treatment technology. Soft water flows through a layer of material that is composed of limestone and magnesium carbonates, or through a layer of limestone and magnesite. However, the water flowing through the layer of material must contain excess carbon dioxide or it can be dosed directly into the treated water inflow [
17,
18]. However, for the process, it is advantageous to use a mass that contains both biogenic elements. Suitable candidates for the recarbonization treatment are dolomite and HCD, which can provide both biogenic elements in a one-step recarbonization treatment with the dosage of only one type of material.
A new approach in water treatment is the improvement of the efficiency of water remineralization using half-calcined dolomite and carbon dioxide in a fluid reactor. The significance of the claims is moderate, as this method is known and used, but specific conditions, including the type of reactor, may affect the output efficiency. According to our knowledge and literature search, a FBRR has not been used for drinking water remineralization so far. On the other hand, the dissertation of Van Schagen [
19] and conference paper Kramer et al. [
20] focused on modelling the management of drinking water treatment plants was published. They presented the results of investigation on a pellet reactor with a fluidized bed to perform the reverse process, i.e., the decarbonization of water with a high content of total hardness.
The authors [
21] registered the invention, which the patent office also assessed regarding a detailed search in the literature. The results confirmed the originality of this solution and in 2023 the patent was accepted.
This research was carried out with our participation as a co-investigator of the project [
22]. The project was aimed at enriching tap water with biogenic elements in real conditions.
Our previous research carried out in a laboratory FBRR showed effectivity of the mineralization process of drinking water [
21]. The research was focused on comparing different recarbonization materials and comparing the performance of the recarbonization process in fixed and fluidized bed and investigation the hydrodynamic characteristics of the FBRR. Measurements were made with different fractions of the recarbonization material. The effect of water and carbon dioxide flow on the performance of the process was studied. Changes in the particle size of the material during the process were monitored. The results show that half-calcined dolomite is the most suitable material. The results of preliminary experiments showed a positive influence of fluid bed hydrodynamics and increased speed of the recarbonization process due to the presence of CO2. The concentration of calcium and magnesium ions obtained in a recirculating fluidized bed reactor at a liquid flow rate equal to the minimum fluidization speed of the particles used was almost twice as high as their concentration obtained in a fixed bed reactor. Continuous feeding of CO2. to the FBRR resulted in an increase in the rate of recarbonization by about one order of magnitude in comparison to the process without CO2. feeding. A first-order kinetic model describes the data from the recarbonization process with good accuracy. The kinetics of the recarbonized process is described with good accuracy by a first-order model. A very good description of the hydrodynamic characteristics of the fluidized bed was achieved using the Richardson and Zaki expansion model [
20,
23].
However, most of the previous experiments were performed in a recirculating fluidized bed reactor. The main idea was the preparation of a concentrate of calcium and magnesium ions. Preliminary tests have shown that a fixed HCD bed and a single passage of water through the bed cannot provide the desired enhancement of drinking water with the biogenic elements in question. Considering the intensity of contact between liquid and solid substances, we decided to use a fluidized bed system with an internal circulation loop for the preparation of the concentrate [
21,
24].
It is well known that a batch reaction system is not advantageous for a large volume of treated water. Due to the prospectively large volumes of processed water, we considered carrying out further research of this process in a newly designed continuous system with a solid or fluidized bed (
Figure 1).
Another change in the new proposed reaction system is related to apply the particle fractions of HCD. It is generally known that to smaller solid particles corresponds the faster the process. However, conditions for fluidized bed applications include particles of reasonable size in terms of HCD bed pressure drop (and associated fluid pumping costs), solid material handling (high proportion of dust), and material losses when the water flows through the bed of grain material. From these points of view, we decided to use a larger fraction (2-4 mm) of HCD particles for further research and anticipated practical applications [
24].
The aim of the work is to test the system designed in this way and based on experimental data, to quantify the main parameters of the process (threshold fluidization speed, porosity of the fluid layer, expansion of the fluid layer, saturation process, influence of operating parameters (flows of water and CO2, recarbonization materials), balance of material flows. Next the goal is to develop regression models to describe the dependencies between individual quantities and to determine the optimal process conditions using these models. The results will be used in the operation and further expansion of the FBRR and the recarbonization reaction system.
2. Materials and Methods
2.1. Fluidized Bed Reactor
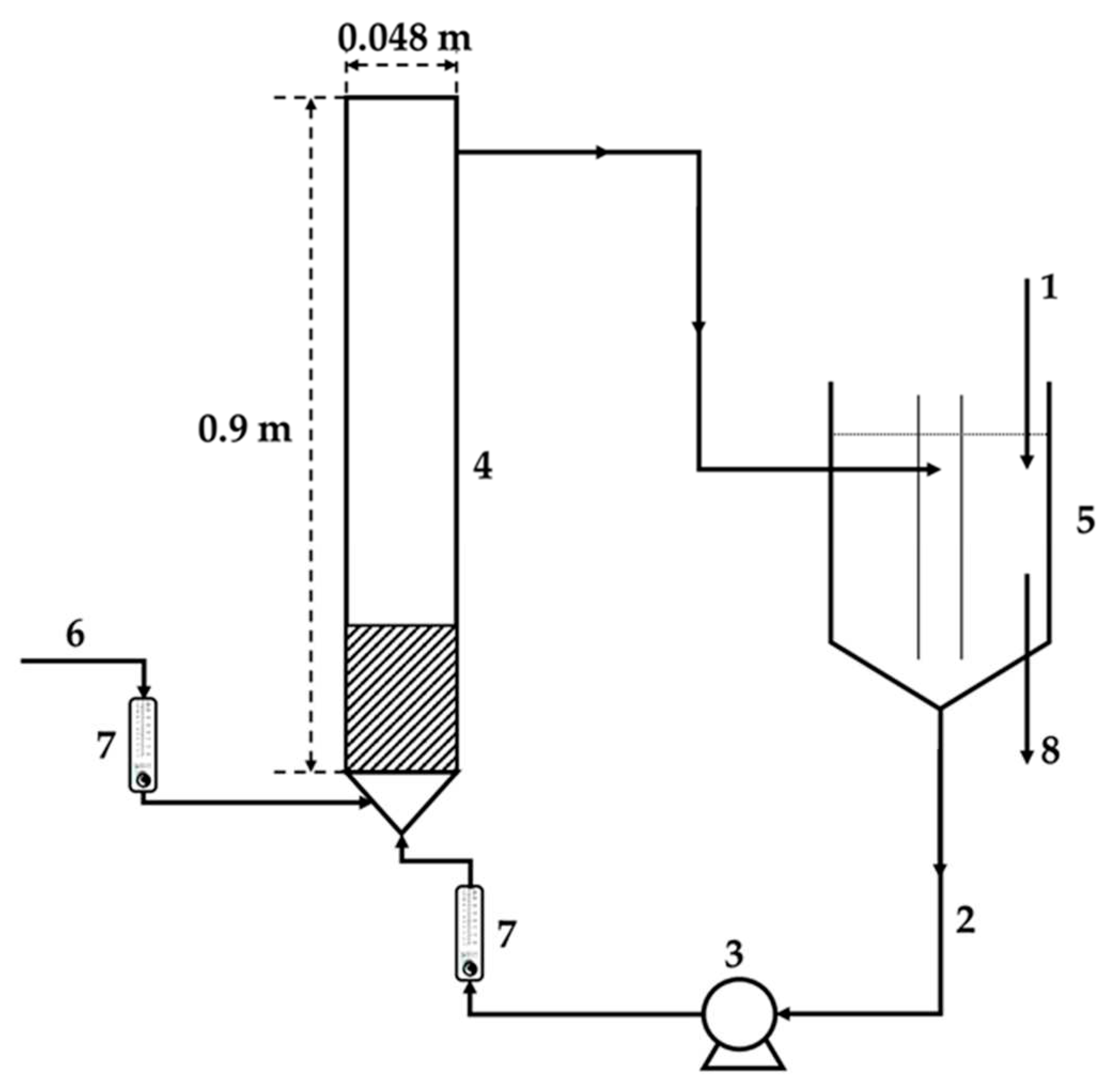
The drinking water recarbonization system is shown in
Figure 1. 1Treated water (1) will be pumped from the water reservoir/tank (5) through the FBRR (4) and back). To maintain intensive contact of liquid and HCD particles, FBRR with an internal circulation loop (2) was designed. Carbon dioxide (6) is, like recirculated water fed under the distribution grate. The water tank serves to accumulate concentrate with an optimal concentration of calcium and magnesium salts for the recarbonization process. At the same time, the outlet of recarbonized water (8) from the water tank is mixed with drinking water in the distribution system in the required ratio. In this tank, possibly washed-out fine particles from the FBRR can be removed.
2.1.1. Hydraulics of fluidised bed reactor
Important parameter of fluidized bed is minimum fluidization velocity. This velocity is strongly affected by particles geometry, density, and their shape. The physical properties of fluids are also important parameter affecting fluidization characteristics (expansion, etc). The Richardson and Zaki [
20,
23] correlation is widely used to describe the expansion of fluidized bed:
where ε is fluidized bed porosity, dimensionless. U superficial velocity, L/T. U
t particle terminal velocity, L/T and n bed expansion parameter, dimensionless.
where ρ
s is particles density, M/L
3.
l liquid density, M/L
3. g gravitational acceleration, L
2/T. C
d drag coefficient, dimensionless and d
p particles diameter, L.
The overall bed voidage is given by:
where V
p is the total volume of fluidised bed, L
3. A is the bed cross-sectional area, L
2 and h the overall fluidised bed height, L.
Since the particles can change physical properties (particle’s diameter) and hydrodynamic behaviour of fluidised bed, correlation for the bed expansion parameter and drag coefficient were developed experimentally for fluidised bed reactor in the forms as follows [
26]:
where Re
t is Reynolds number for particles terminal velocity, dimensionless.
s solid density, M/L
3. μ - dynamic viscosity of liquid, Pa s and
a,
b,
c,
d parameters of empirical correlation equations, dimensionless.
Diameter d
p of half-calcined dolomite (HCD) particles was expressed by the geometric mean, L:
where d
1 and d
2 are diameters of two mesh of sieve fraction, L,
2.2. Materials Used
Recarbonization experiments were performed using the recarbonization materials Half-calcined dolomite (HCD) Magno Dol (Akdolit) and Semidol. HCD is prepared from dolomite containing 50% CaCO3 and 50% MgCO3 at temperatures of 650-800°C. This treatment causes the decomposition of MgCO3 into MgO. The content CaCO3 does not change.
During the recarbonization process, the following equations take place:
HCD is mostly used as a granular material in recarbonization filters where the water flows downwards. In the HCD layer, the reaction between carbon dioxide and HCD takes place according to the above equations. During these reactions, HCD is gradually consumed and needs to be replenished. The recarbonization reactor needs to be washed regularly to prevent sintering of the filter filling due to the excretion of CaCO3. During washing, dust particles are also washed out, which are created by the breakdown of HCD grains [
27]. When using FBRR, the mentioned problems related to the need to wash the layer are eliminated.
2.3. Water saturation with calcium and magnesium
The kinetics of the recarbonization process during previous experiments was proven by the first-order equation:
where Ct is the total concentration of calcium and magnesium (mmol/l) for the reaction time t, C
eq is the equilibrium concentration of calcium and/or magnesium (mmol/l), d
c is the rate constant of dissolution of Ca
2+ and/or Mg
2+ ions [1/min] and t is the reaction time (min).
Integration of Eq. (10) yields between the boundary values of C = C
0 and t = 0 and t = t and for the case that C
0 = 0: The equation Eq. (10) can be modified by integration for the boundary values C = C0 and t = 0 and t = t and C0 = 0 into the resulting form:
2.4. Applied Analytical Methods
The process of recarbonization was monitored with a focus on monitoring the conductivity, pH and determining the content of calcium and magnesium ions. A WTW Multi 3420 conductometer was used to measure conductivity. A JENWAY 3510 pH meter was used for continuous monitoring. The content of Ca
2+ and Mg
2+ ions was determined by complexometric method using the indicator Eriochrome Black T. The concentration of Ca2+ was carried out by chelatometric method with EDTA using murexide as an indicator. The concentration of magnesium was calculated from the total content of Ca
2+ + Mg
2+ and the determination of the content of Ca
2+ [
25].
2.5. Multiple regression analysis
The experimental values of (Ca
2+ +Mg
2+) concentrations, the maximum concentrations of these ions C
max in the treated water (the dependent variables Y) at different flow rates of water, carbon dioxide and the reaction time (independent variables X
i, X
j, ...) were processed by multiple regression using general regression equation for two independent variables in the form:
where a
0, a
j, a
jj and a
ij are regression coefficients.
Depending on the number of measurements was applied linear equation (the three independent variables, 4 parameters), or quadratic equation (6 parameters of the three independent variables), and for the greater number of measurements of the quadratic equation with mutual links (10 parameters for three independent variables).
2.6. Processing of experimental data
The values of used nonlinear hydraulic model (Eqs. 1, 2, 4, 5) and recarbonization equation (Eq. 11) were determined by a grid search optimization [
28]. To determine the values of the parameters of applied form of general regression equation (22), which corresponds to the minimum value of the objective function was used Nelder-Mead simplex optimization method [
23,
29]. The optimum values of independent variables X
i, X
j,.. for the calculated parameter values corresponding to the minimum objective function for the dependent variable Y were also determined by the grid search optimization method [
28].
The residual sum of squares () between the experimental and predicted values of dependent variables (Eq. 13), i.e., fluidized bed expansion, fluidized bed height or Ca2+ + Mg2+ concentration given by the models, divided by its number of degrees of freedom ν was used as the objective function.
On a qualitative description was used objective function as the sum of squares between experimental and predicted values of heights of expanded fluidized bed. Among them is then calculated residual dispersion):
where
n is number of measurements and
m is parameters number.
Correlation coefficient (Eq. 14) was applied for a qualitative description of the relationship between two variables:
where
is dispersion (Eq. 15):
3. Results
3.1. Lab-scale FBRR
3.1.1. Hydraulic characteristics
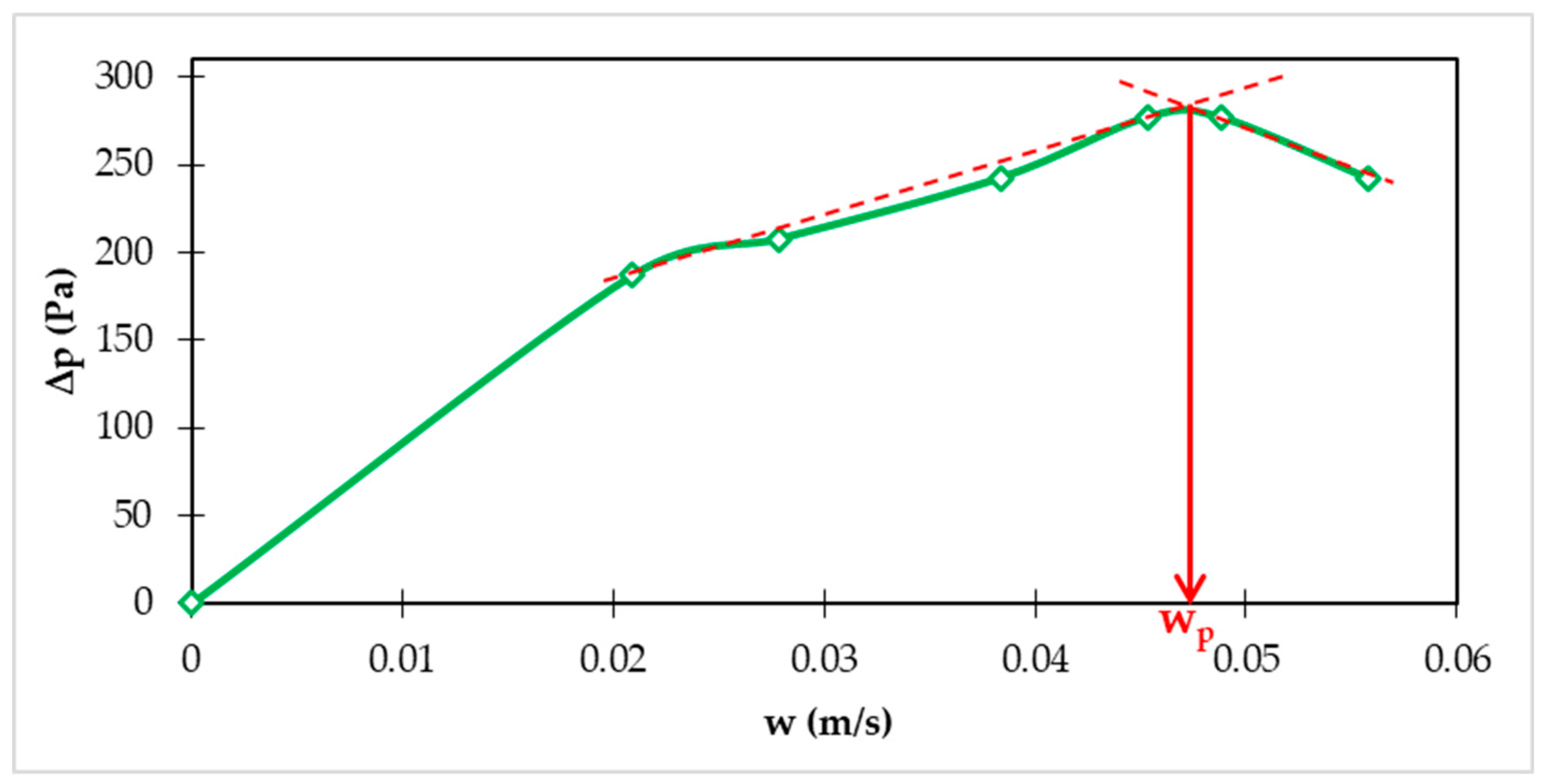
Hydraulic conditions in the FBRR are affected by particle size and density. These basic design parameters of the FBRR also affect the superficial liquid velocity, which is required for the required expansion of the fluidized bed in the FBRR. This expansion requires adequate internal circulation of particles and internal recirculation of water, which at the same time is related to a significant part of the operating costs. The minimum fluidization speed corresponds to the fluid flow rate at which the particles begin to move. At higher flow rates, expansion occurs and the height and volume of the particle layer increase due to the dissipated mechanical energy. The value of the minimum fluidization speed (wp) can be determined based on the measured values of the dependence of the pressure loss (ΔP) on the superficial liquid velocity (w).
Figure 2 shows dependence of pressure drop (ΔP) in the FBRR on superficial fluid velocity (w) [
23].
360 g of HCD were used in these experiments. The value of the minimum fluidization velocity wp = 0.0475 m/s was determined by the graphic method.
The measurements were carried out under the following conditions:
Particle mass in the bed: mc = 0.36 kg
Voidage of fixed bed: ε = 0.4217
Volume of fixed bed of solids: Vs = 0.266∙10-3 m3
Cross-sectional area of the column: Ap = 1.8∙10-3 m2.
We used the experimental values of the dependence of the height of the expanded layer on the water flow and the above data to calculate the parameter values of the expansion equations (Equations 4 to 6) using the grid search optimization method. The values of the parameters and the correlation coefficient are shown in
Table 1.
3.1.2. Saturation of the reactor
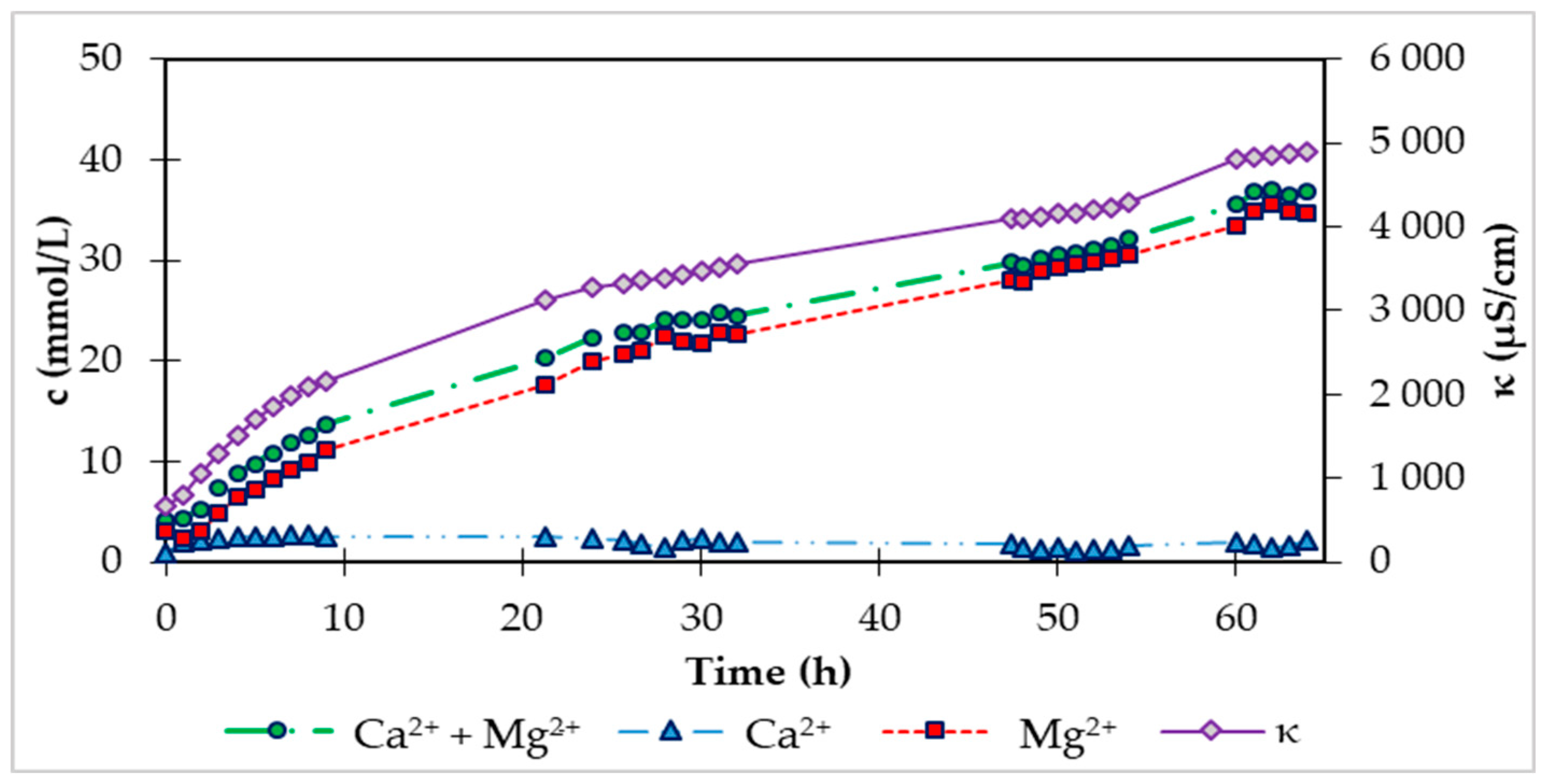
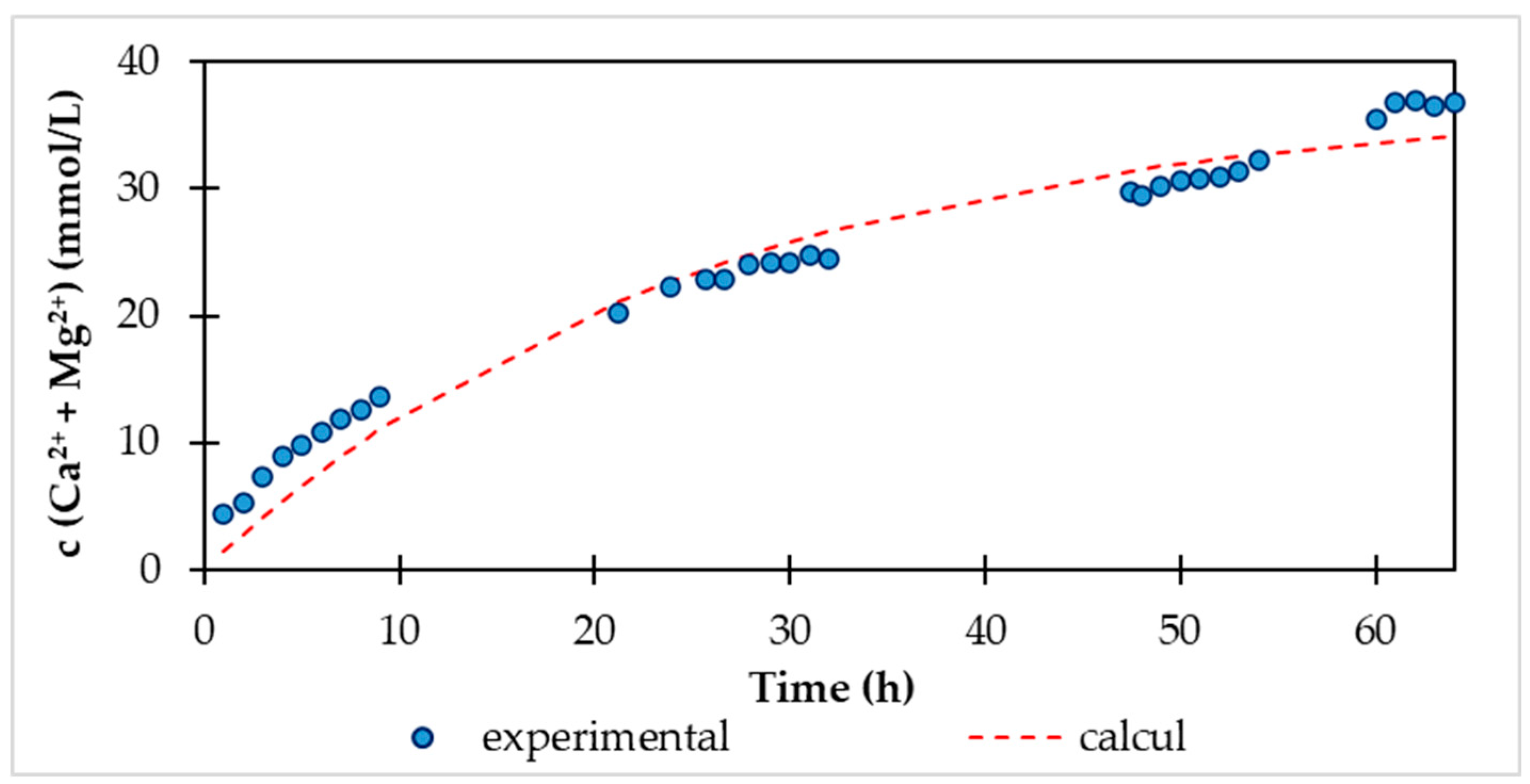
At the beginning of the experiment, we added 360 g of fraction 2-4 mm HCD Magno Dol (Akdolit) to the fluidization reactor. The immobile layer of solid particles in the reactor reached a height of 14.0 cm. After starting the carbon dioxide supply with a flow rate of 0.5 L/min and internal recirculation of water between the storage tank and the fluidized bed reactor with a flow rate of 6.8 L/min, we observed a height of the fluidized bed of solid particles of 15.1 cm. The saturation phase lasted 64 hours, during which we continuously recorded parameters such as pH and conductivity with a digital multimeter and analytically determined the concentrations of calcium and magnesium in the storage tank. Using conductivity (κ), we can also express the increase in the sum of the concentration of Ca
2+ and Mg
2+ ions, because the conductivity grows directly proportional to the concentration of ions in the solution. In
Figure 3 shows this increase in conductivity and at the same time analytically determined concentrations of Ca
2+ and Mg
2+ ions in the storage tank during the saturation phase.
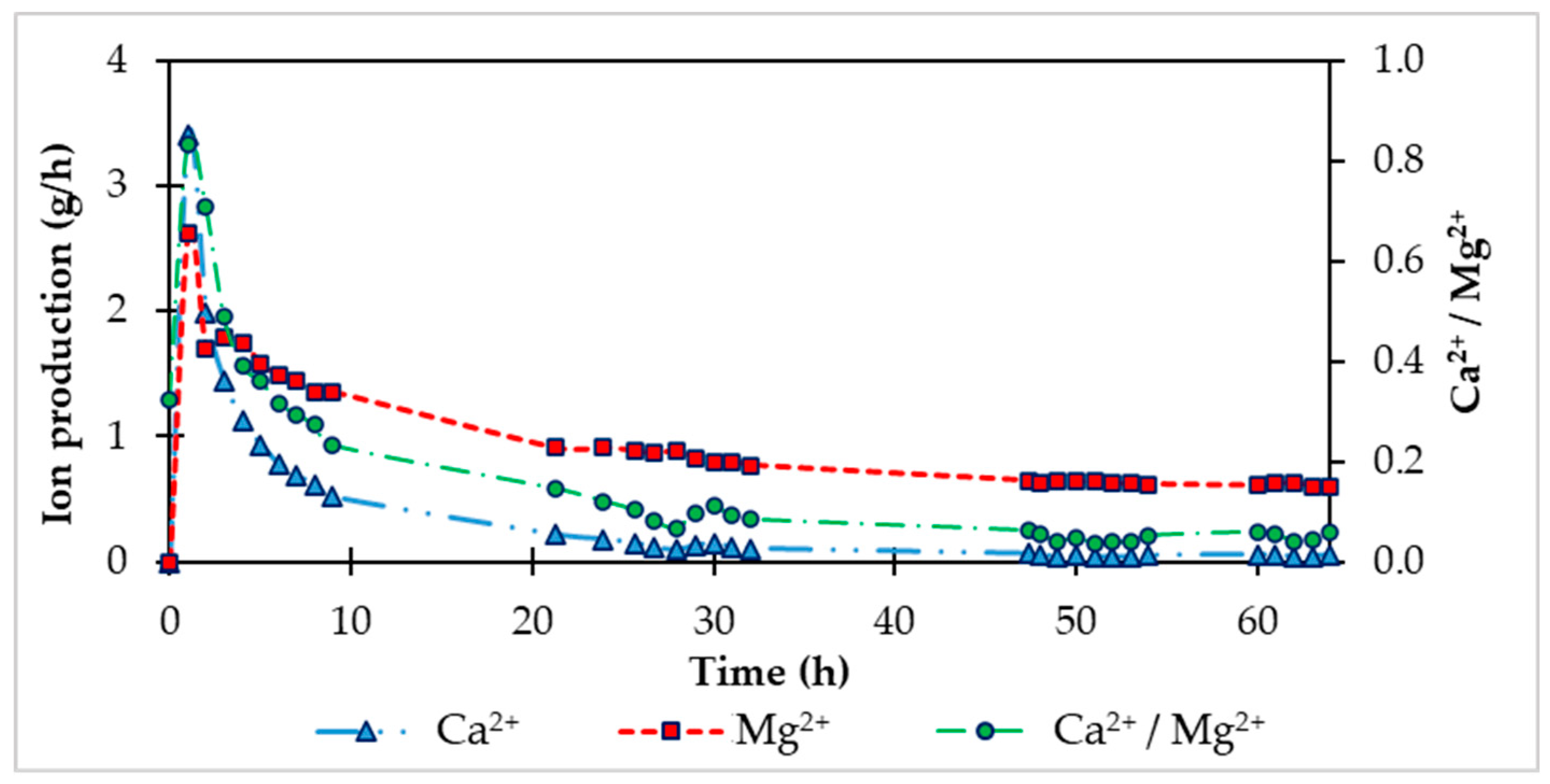
The production (product of concentration and water flow) of calcium and magnesium ions Mg
2+ and Ca
2+ was calculated- During the first 9 hours of the saturated phase (
Figure 4), Mg
2+ production was in the range of 1.3-2.6 g/h. In the next hours of the saturation phase it fell below 1.0 g/h. Ca
2+ production was initially 1.3 g/h on average during the first 9 hours of saturation and decreased with time to 0.06 g/h specifically in the 64th hour of saturation. This decrease in produced ions in water is due to consumption, or dissolution of individual HCD components. To prevent completely zero production of ions, during the recarbonization process, we added HCD doses to the fluidization reactor, which are listed in
Table 2.
To compare the monitored variables at the beginning and end of saturation, the given measured data are given in
Table 3.
According to the measured values of c (Ca
2++Mg
2+) depending on the reaction time, we calculated the values of the kinetic parameters of the recarbonization equation (11), where the purpose function of the calculation was the sum of squared deviations between the experimental and calculated values. The values of kinetic parameters and statistical characteristics are given in
Table 4. The content of Ca
2++Mg
2+ experimentally determined and calculated using the kinetic equation is shown in
Figure 5.
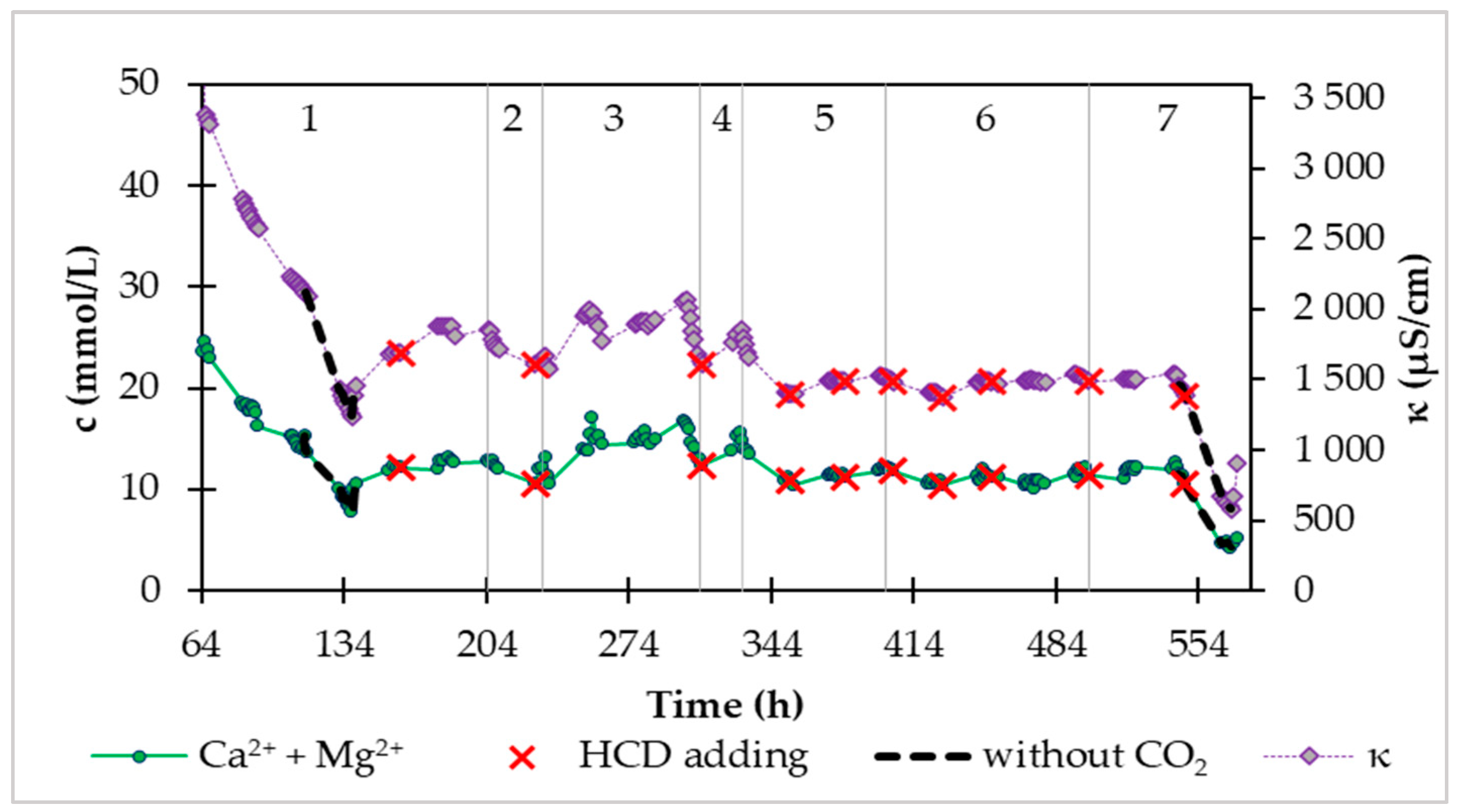
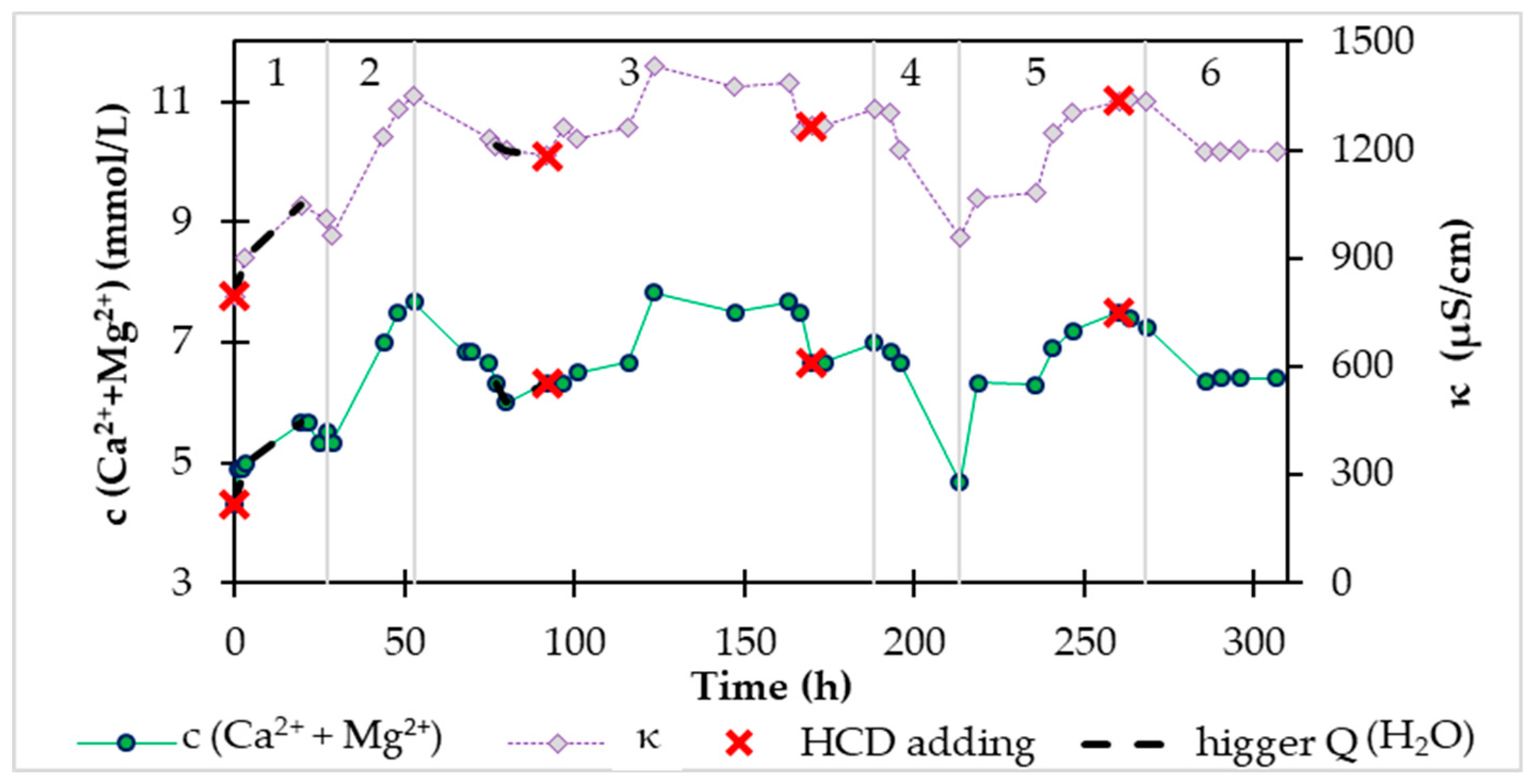
After 64 hours of the saturation phase, we started the continuous supply of water from the water supply network to the device and the outflow of treated water, followed by the so-called continuous phase. Water from the supply network contained 40.08 mg/L Ca2+, 75.33 mg/L Mg2+, and the sum of calcium and magnesium is equal to 4.10 mmol/L. The goal was to enrich the water from the distribution network with calcium and magnesium ions. The recarbonization process in continuous mode lasted 508.8 hours, and together with the initial saturation, the total recarbonization time was 572.8 hours.
During the saturation phase, we also monitored the conductivity, pH, and content of calcium and magnesium in the continuous phase. In
Figure 6 shows the time dependence of the conductivity and molar concentration of Ca
2++Mg
2+ during the continuous phase. The mentioned dependence in
Figure 6 we divided it into 7 areas according to the inflow of water from the distribution network and carbon dioxide.
In area 1 (
Figure 6), which followed immediately after saturation, we set the continuous water flow to 20 mL/min and the carbon dioxide supply was at the level of 0.5 L/min. After the introduction of a continuous inflow of water, the concentration of calcium and magnesium in the storage tank began to decrease from 26.3 mmol/L to 12.8 mmol/L, which represents a decrease of up to half. At the same time, the determined values in the storage tank are the same as the outflow values of the system. In this area 1 (
Figure 6) there is also a section during which CO
2 was not supplied to the system. In the mentioned section, we observe a faster decrease in the concentration of Ca
2++Mg
2+, while the concentration of Ca
2++Mg
2+ started to rise during the subsequent supply of CO2. The same section is also in area 7, where even after the addition of HCD, but without CO
2 access, the concentration of Ca
2++Mg
2+ dropped significantly, and when the CO
2 supply was re-introduced, the concentration of Ca
2++Mg
2+ increased. In the mentioned two sections without CO
2 access, we were convinced of the seriousness of the presence of carbon dioxide, which needs to be supplied to the system to increase the solubility of HCD in water.
In area 2 in
Figure 6 at Q(CO
2) = 0.5 L/min, the inflow of water from the distribution network was increased from 20 mL/min to 53 mL/min and we observe a decrease in concentration by only 2 mmol/L. At the end of this area, we dosed the new HCD Magno Dol (Akdolit) into the system to increase the concentration of ions.
We continued to increase the inflow in area 3 (
Figure 6), where the inflow of treated water was 63 – 68 mL/min. By 277 hours, the CO
2 flow was at the level of 0.5 L/min, and after this time, the CO
2 flow increased to 0.52 – 0.54 L/min with constant water supply from the distribution network. The effect of the change in this flow rate can be observed in area 3 (
Figure 6) as an initial increase in the concentration of Ca
2++Mg
2+, which then started to decrease, apparently due to the consumption of HCD. That is why we added recarbonization material to the system and reduced the flow of water from the water network to 58 mL/min. The behavior of the system after the addition of HCD Magno Dol (Akdolit) with reduced water flow and maintained CO
2 flow from area 3 (
Figure 6) can be seen in area 4 (
Figure 6), where the concentration of Ca
2++Mg
2+ started to rise again. After increasing the concentration of Ca
2++Mg
2+ to a value of 15.6 mmol/L, we suddenly increased the water flow from the distribution network up to 70-76 mL/min, which we reduced to 60 mL/min after twenty hours, because we noticed a sharper decrease in Ca
2++Mg
2+ concentration. After this drop in concentration to 10.8 mmol/L, we dosed another amount of HCD Magno Dol (Akdolit) into the system and gradually reduced the flow of water to 56 mL/min and carbon dioxide to 0.33 L/min, while the concentration of calcium and magnesium in drinking water was relatively stable.
In area 6 (
Figure 6), we monitored the behavior of the system with small gradual changes in water flow in the range of 60-66 mL/min with gradual changes in CO
2 flow from 0.23 L/min to 0.35 L/min with more frequent replenishment of the mass. In this region 6 (
Figure 6), we observed Ca
2++Mg
2+ concentration values with a maximum difference of 2 mmol/L, which occurred when the experimental conditions were changed.
We carried out a gradual reduction of the CO
2 flow at water inflows of 50 – 57 mL/min in area 7 (
Figure 6), where we exposed the system to the already mentioned zero CO
2 flow.
3.1.3. Regression analysis of experimental results
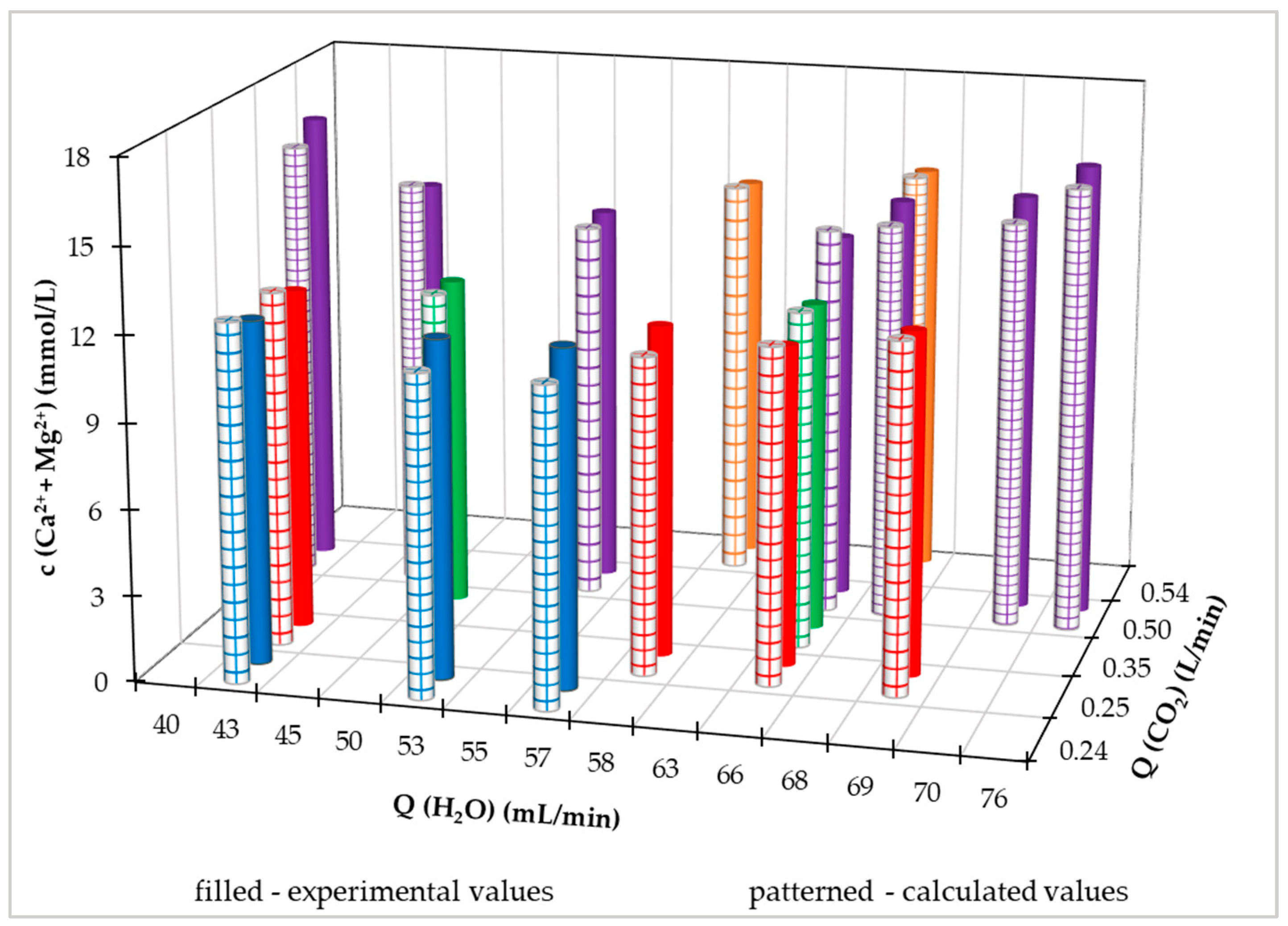
We used the regression equation (12) and optimized its parameters to describe the behavior of the continuous recarbonization system at different flows of supplied treated drinking water and flows of carbon dioxide.
Using the mentioned regression model with the Nelder-Mead method for parameter optimization, we determined with 95% probability the values of the parameters of the regression equation, which are listed in
Table 5. The correlation coefficient of the model with the specified parameter values is 0.9570, that is, the determined quadratic equation with mutual links of independent variables is suitable for describing the process.
According to the determined values of the parameters, the regression equation took the form:
where c(Ca
2++Mg
2+) is the concentration of calcium and magnesium (mmol/L) and Q(H
2O), Q(CO
2) are the flow of water and carbon dioxide. Using this equation, we calculated the concentration of Ca
2++Mg
2+ and in
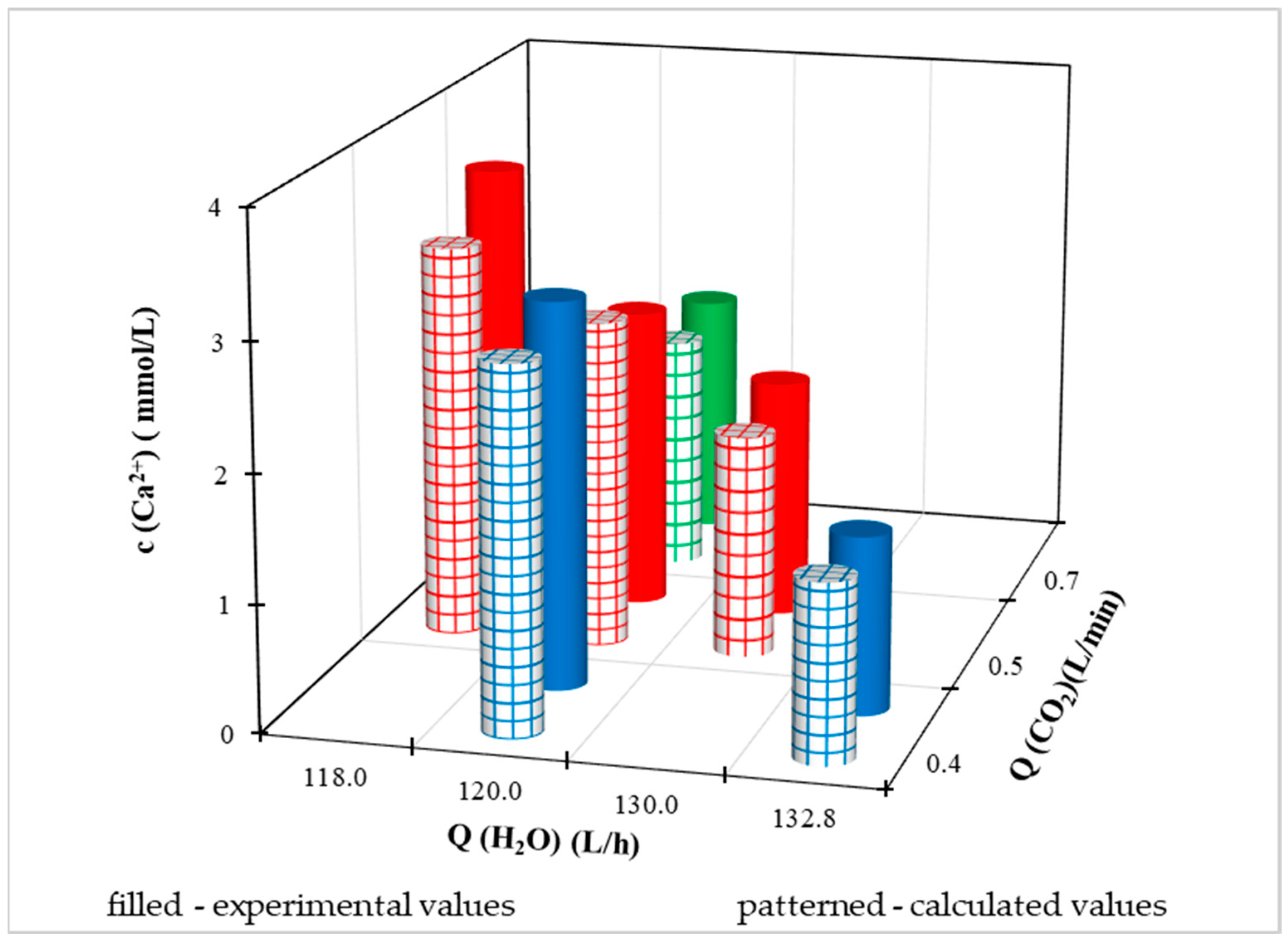
Figure 7 we illustrated in a three-dimensional graph the comparison of calculated values with measured values. It is clear from the above graph that the highest achieved measured and calculated value of the Ca
2++Mg
2+ concentration is at a CO
2 flow rate of 0.5 L/min and a value of the supplied treated drinking water flow rate of 76 mL/min. However, we can assume that with the mentioned water flow rate of 76 mL/min, the experimental concentration of Ca
2++Mg
2+ would be even higher with a higher CO
2 flow rate, which is also confirmed by the calculation using equation (16) optimization, we determined with 95% probability the values of the parameters of the regression equation (16).
For a more illustrative comparison of the measured values with the calculated values using equation (16), we constructed a two-dimensional graph in
Figure S1 (Supplementary materials), in which the Ca
2++Mg
2+ concentration values from different inflows of treated water from the distribution network are shown. From
Figure S1, we can also see that the process (without the first saturation phase) is described by the above-mentioned quadratic equation with mutual interconnections of parameters (Eq. 16), which has a convex shape.
In the statistical treatment of dependence
we also calculated the value of the coefficient of determination, which is 0.919. This value of coefficient of determination (R
2) indicates that 91.9% variability of the total variability in sum concentration of calcium and magnesium cations was attributed to investigated experimental independent variables. The remaining 8% is the influence of non-included independent variables. Thus, it can be concluded that developed model (Eq. 16) adequately describes relationship between studied variables.
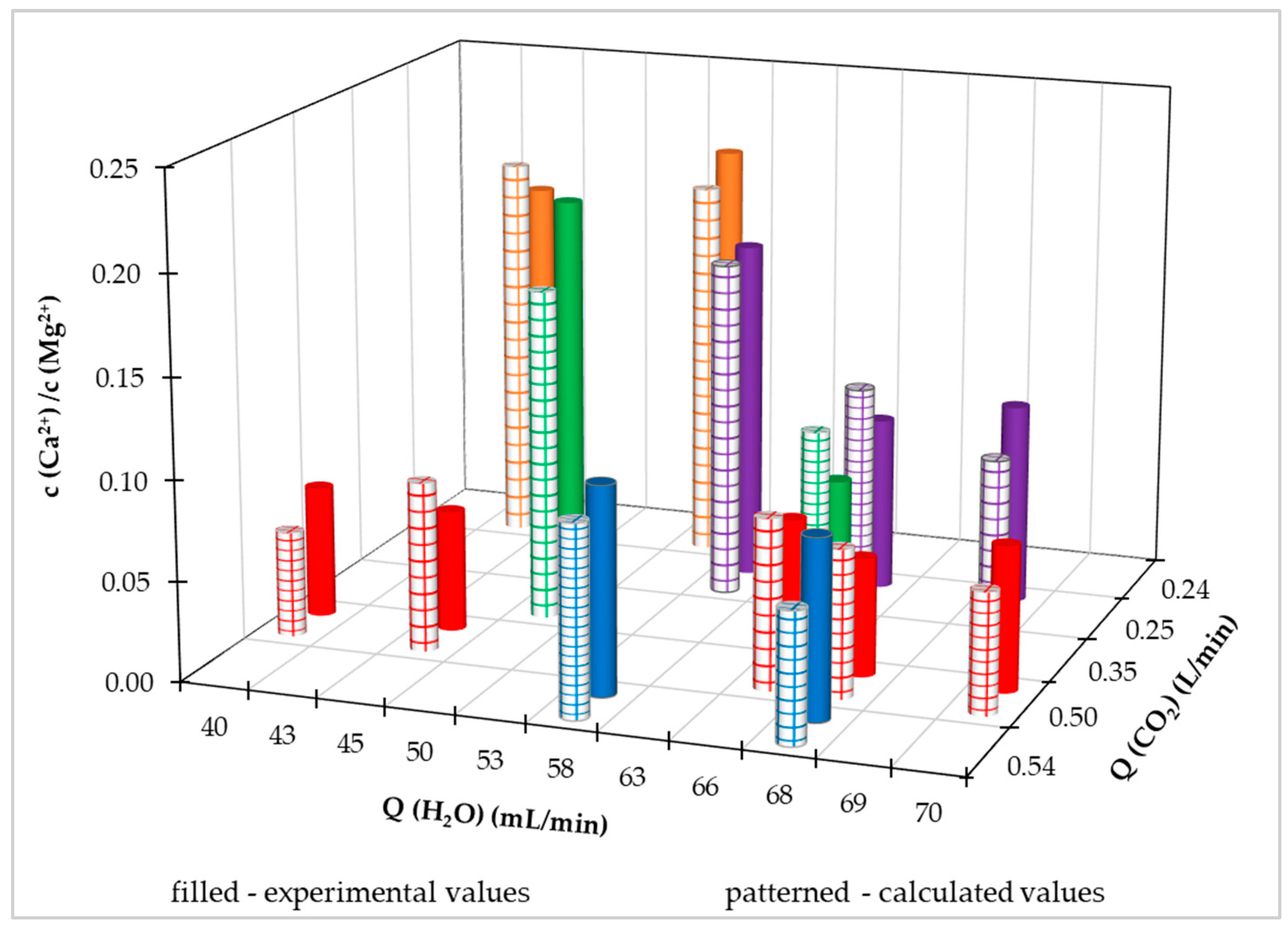
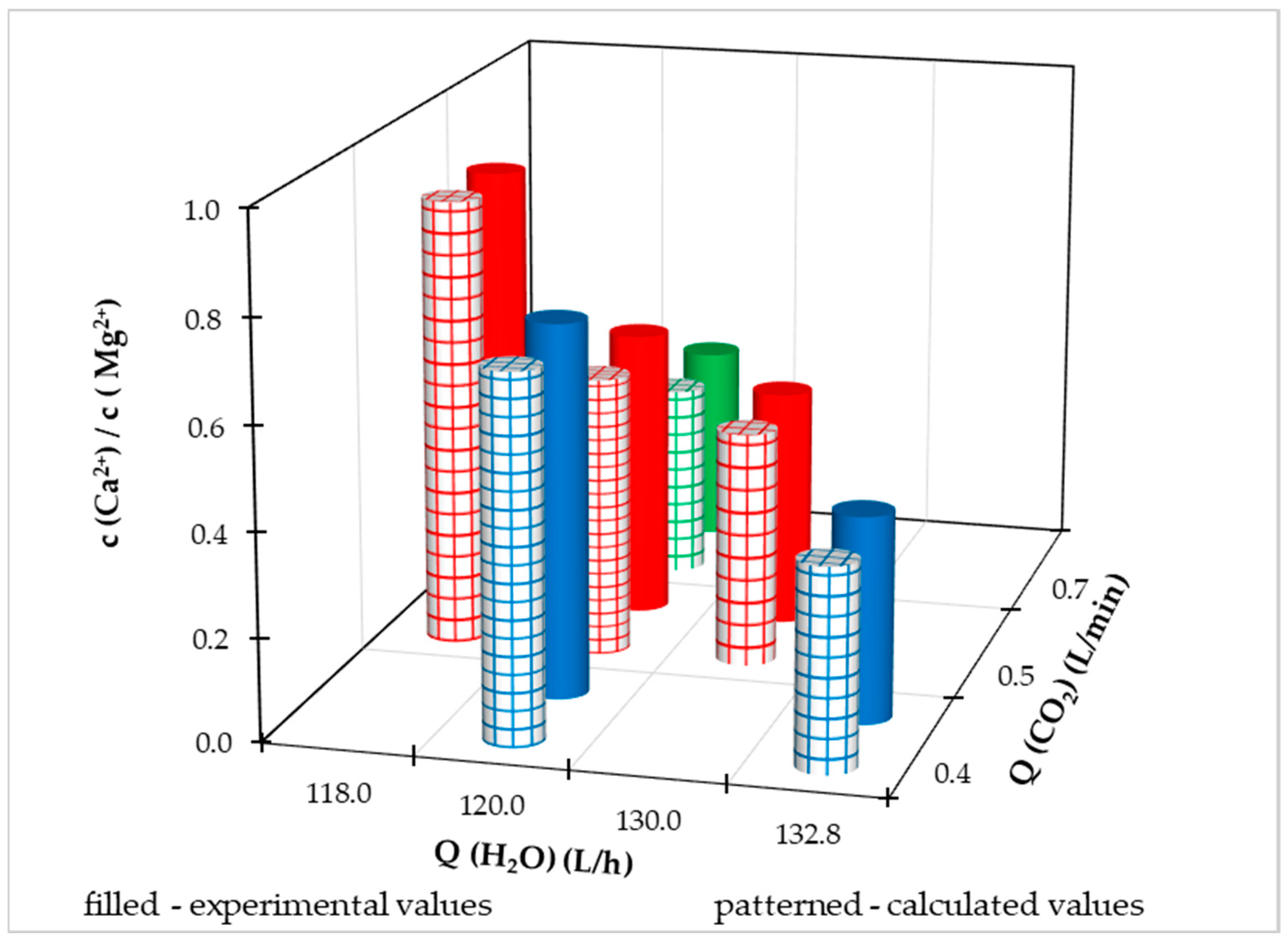
We also applied the regression model of the quadratic equation with mutual links of independent variables for the dependence of the ratio of calcium and magnesium on the flow of carbon dioxide and supplied water from the distribution network. The model of the regression equation took the form (18) and the determined values of the parameters are listed in
Table 6.
where P
1 to P
12 are parameters of the regression equation, c(Ca
2+) / c(Mg
2+) is the molar concentration ratio of calcium and magnesium, and Q(H
2O), Q(CO
2) are the flow of water and carbon dioxide. Using this equation, we calculated the concentration of Ca
2++Mg
2+.
We compared the measured values of the ratio of the molar content of calcium and magnesium with the calculated values using the regression equation (18) in
Figure 8. The correlation coefficient between measured and calculated values is 0.922 and the coefficient of determination is 0.850.
3.1.4. Optimizing the conditions of the recarbonization process in laboratory FBRR
We used the determined values of the parameters of the regression equations (16) and (18) to determine the optimal conditions of the process, i.e., independent variables, or CO2 and H2O flows. Using the grid search of the optimization method, we determined the values of these flows for the maximum and minimum value of the dependent variable in question. The optimal process conditions were determined for the range of values of the independent variables at which the experiments were performed.
For the optimal conditions of the dependent variable c(Ca
2++Mg
2+), we also calculated the optimal values of the ratio c(Ca
2+) / c(Mg
2+). Also, for optimal conditions of maximum and minimum values of the c(Ca
2+) / c(Mg
2+) ratio, we calculated optimal values of the sum of c(Ca
2++Mg
2+) concentrations. The results are presented in
Table 7 and
Table 8.
From the results of process optimization in laboratory FBRR within the investigated range of values of independent variables, i.e., the flow of carbon dioxide 0.24 - 0.54 L/min and water from the distribution network 40 - 76 mL/min means that it is not possible to achieve the recommended molar ratio of calcium and magnesium in drinking water of 0.6 - 1.0 [
30].
3.2. Pilot reactor
We operated the pilot FBRR in flow mode with continuous inflow and outflow of treated drinking water without an initial saturation phase. The initial concentration of the sum of calcium and magnesium ions in the treated water was 4.3 mmol/L. At the beginning of the experiment, we dosed 20.6 kg of HCD Magno Dol (Akdolit) into the fluidized bed reactor. The time dependence of conductivity and concentration of calcium and magnesium ions in drinking water is shown in
Figure 9.
The course of the development of monitored quantities in
Figure 9 we divided into seven areas according to the flow of carbon dioxide. The CO
2 flow rate for individual areas is shown in
Table 9.
For the first 27 hours, area 1 (
Figure 9), we operated the reactor at Q(CO
2) = 0.4 L/min and the flow of treated drinking water from the distribution network was initially 132.8 L/h, while later we stabilized it at a value of 120 L/h. The concentration of Ca
2++Mg
2+ during 27 hours of operation was increased by approximately 1 mmol/L.
In area 2 (
Figure 9), after 27 hours, to achieve a higher concentration of calcium and magnesium ions with a constant inflow of treated water, we increased the flow of carbon dioxide to the level of 0.7 L/min. With an increased flow of carbon dioxide, the content of calcium and magnesium in the drinking water was significantly increased up to 7.7 mmol/L. At this concentration, which we considered sufficiently high, we reduced the carbon dioxide flow to a value of 0.5 L/min order to stabilize the outflow concentration and prevent its further increase.
The course of the process at a constant CO
2 flow rate of 0.5 L/min is shown in area 3 in
Figure 9. The concentration of calcium and magnesium in the drinking water after 15 hours decreased more than expected, by approximately 1.5 mmol/L. This decrease could also have occurred because of a slight increase in the inflow of treated water from 120 L/h to 132.8 L/h and wear of the HCD in the reactor. We dosed HCD Magno Dol (Akdolit) weighing 3.4 kg into the reactor. and adjusted the water inflow from the distribution network to 120 L/h. The concentration of Ca
2++Mg
2+ started to rise again and stabilized at approximately 7.5 mmol/L. At the next observed decrease in concentration, we again dosed another amount of HCD.
We can assume that for a steady effluent concentration of calcium and magnesium in drinking water at a carbon dioxide flow rate of 0.5 L/min and a water inflow from the water network of 120 L/h, it is necessary to dose into the pilot FBRR every 75 hours approximately 3 .5 kg of new HCD Magno Dol (Akdolit).
During 188 hours of operation, the equipment reduced the CO
2 flow to 0.3 L/min for 24 hours. The concentration of calcium and magnesium ions in the water dropped significantly from 7.0 mmol/L to 4.7 mmol/L. When the CO
2 flow rate is again increased to 0.5 L/min at a constant Q(H
2O) = 120 L/h in area 5 (
Figure 9), we observe a further increase in the content of Ca
2++Mg
2+ ions by 1.5 mmol/L. Based on this observation, we can state that if there is a brief loss of carbon dioxide supply to the system during operation in practice, after re-introduction of CO
2, the system can be returned to steady state in approximately less than 4 days, according to the flow of reintroduced carbon dioxide.
Before the end of area 5 (
Figure 9) we added the new recarbonization material HCD Magno Dol (Akdolit) and during the first 8 hours after dosing we recorded a steady concentration of calcium and magnesium in the drinking water of approximately c(Ca
2++Mg
2+) = 7.3 mmol/L. After this stabilization, we again reduced the CO
2 flow in the system to the level of 0.4 L/min area 6 in
Figure 9, where we observe a significant effect of lower CO
2 flow, where even with sufficient recarbonization mass, there was a decrease in c(Ca
2++Mg
2+), which was stabilized at a value of 6.4 mmol/L within five hours.
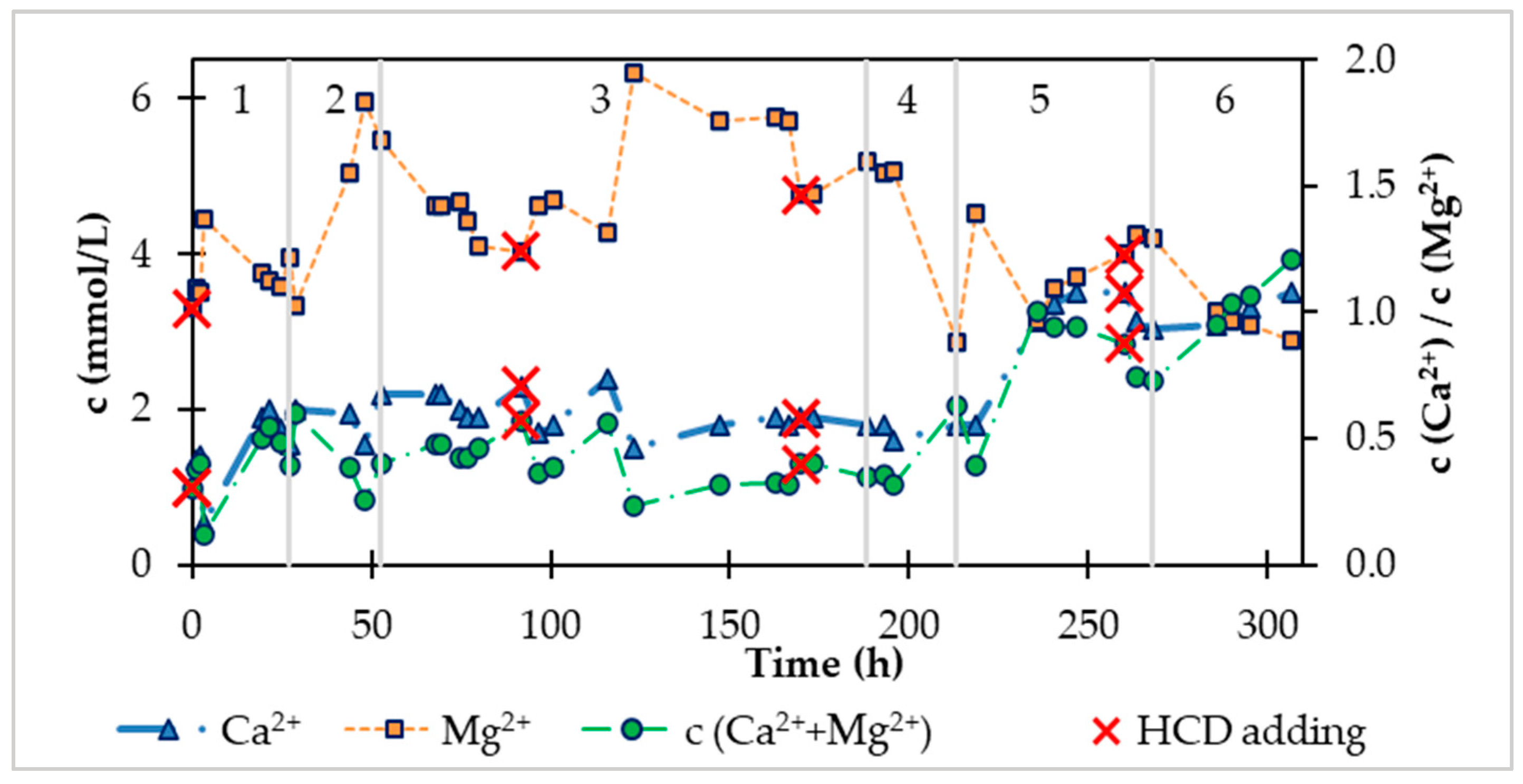
In addition to the total content of calcium and magnesium in water, their ratio, i.e., the content of individual ions, is also important. The calculated value of the ratio of calcium and magnesium according to the recommended content of individual elements in drinking water [
30] should be in the range of 0.6 to 1.0. The temporal evolution of the concentrations of individual ions is illustrated in
Figure 10. We can see that after increasing the carbon dioxide flows (region 2 and 5 in
Figure 10), magnesium ions are released into the water in a much higher amount than calcium ions. When dissolving HCD in water, a high flow of carbon dioxide stimulates the dissolution of the magnesium component of HCD.
After each dosing of a new amount of HCD, the value of the ratio of calcium to magnesium content is lower. This is probably due to the higher solubility of the magnesium component of the HCD, while the surface and porosity of the recarbonization material also changes during dissolution, and the ions inside the pores become more accessible. It is known that the used HCD Magno Dol (Akdolit) has a higher content of calcium component, therefore, after exhausting the magnesium component from the mass, we expected a gradual increase in the concentration ratio of calcium and magnesium ions.
During 213 hours of operation of the pilot FBRR, the Ca
2+/Mg
2+ ratio in Figure10 changes periodically in the range of 0.2 – 0.6. With a reduced flow of carbon dioxide (area 4,
Figure 10) with its increase again (area 5,
Figure 10), we observe an increase in c(Ca
2+)/c(Mg
2+) up to a value equal to 1.0. We can assume that if the experiment were to continue in area 6 (
Figure 10) after further dosing of the recarbonization mass, we would keep the ratio of calcium and magnesium at a value close to 1.0 with a constant inflow of treated drinking water. 120 L/h and CO
2 flow 0.4 L/min.
3.2.1. Statistical processing of experimental results
For the mathematical description of the process of enriching drinking water with calcium and magnesium, we used a quadratic equation model with interrelationships between independent variables, i.e., the flow of carbon dioxide Q(CO2) and the flow of treated drinking water from the distribution network Q(H2O).
We applied the regression equation (12) for 4 different dependent variables:
c(Ca2+ + Mg2+),
c(Ca2+) / c (Mg2+),
c(Mg2+),
c(Ca2+).
Through statistical processing, we obtained 4 regression models of the quadratic equation with mutual links Q(CO
2), Q(H
2O) and determined the parameter values of these models with 95% probability, which are listed in
Table 10.
We assessed the quality of the description of the recarbonization process using equation (12) with determined parameter values by the RXY correlation coefficient, which acquires relatively high values for the individual dependencies of the variable depending on Q(CO2), Q(H2O). Based on the values of the correlation coefficients, we can conclude a good agreement between the measured and calculated values of the dependent variables.
To assess the influence of independent variables on the process, we used the coefficient of determination
. In
Table 10 the values of the individual coefficients of determination are listed, which range from 0.8755 to 0.9858. We can say that the recarbonization process in a pilot FBRR is 88% to 99% influenced by the flow of carbon dioxide and water from the water network.
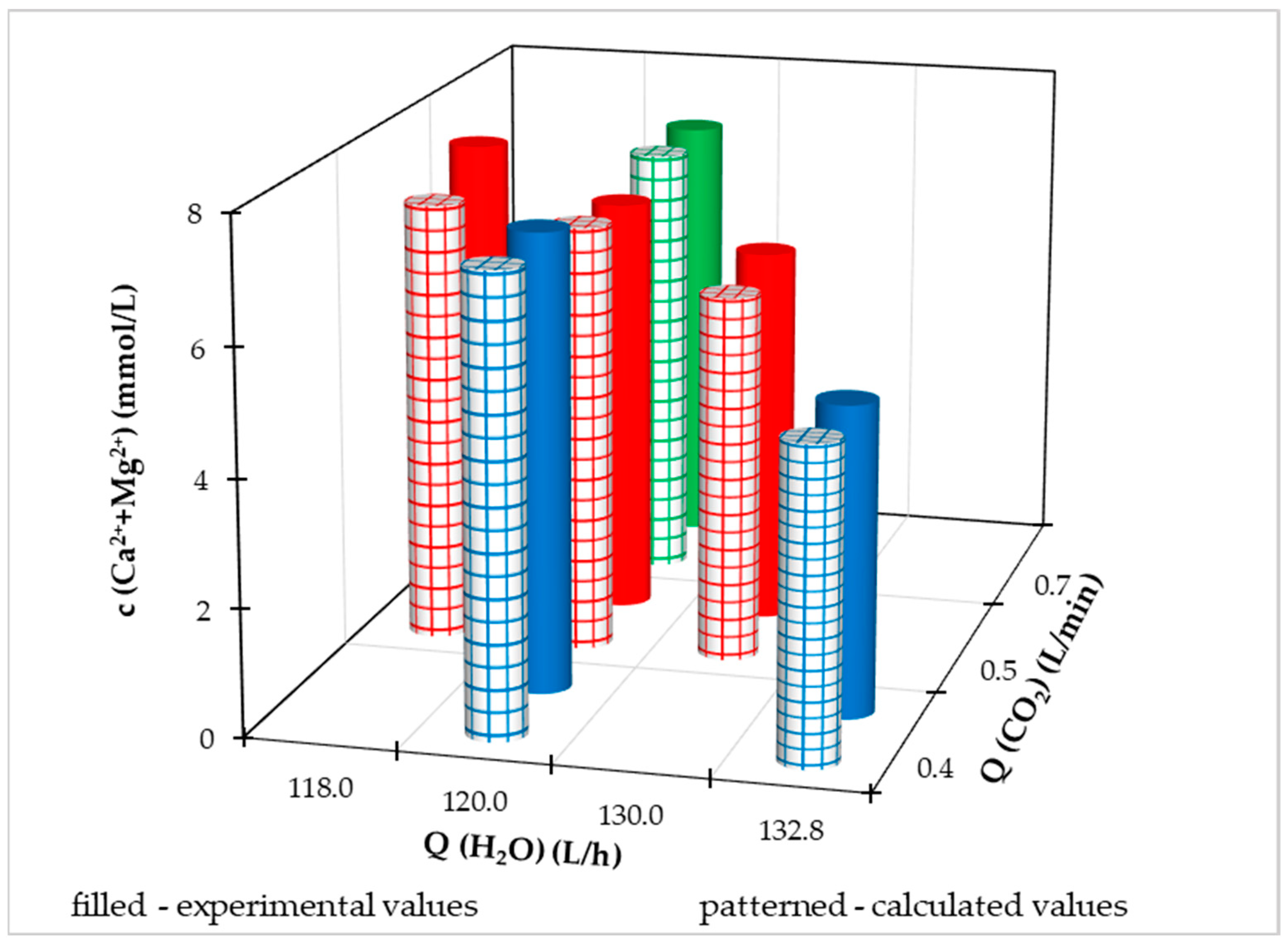
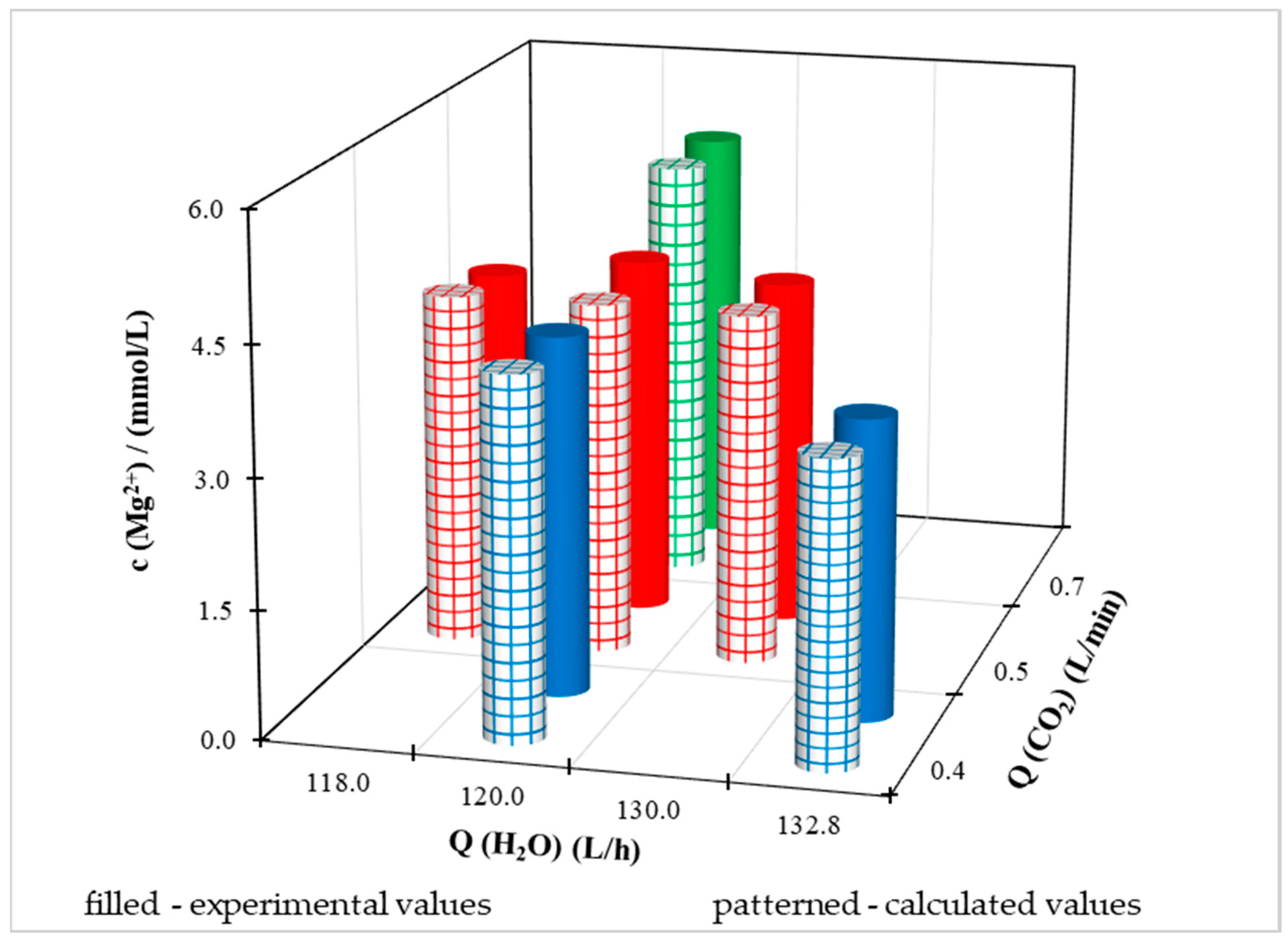
Experimental data and calculated values using a multiple regression equation at different Q(CO
2) and Q(H
2O) for individual dependent variables are illustrated in
Figure 11,
Figure 12,
Figure 13 and
Figure 14. Because the pilot FBRR is a larger reaction system and stabilization of the process when conditions change takes longer than in the laboratory, we approached the change of independent variables during the experiment with caution and changed them gradually, slightly.
For a clearer comparison of the values of the dependent variable, we have shown in
Figures S2 to S5 illustrated the achieved measured and calculated values at different flow rates of treated drinking water from the distribution network at a constant flow rate Q(CO
2) = 0.5 L/min. Based on the illustrated graphs, we can claim that with a constant flow of carbon dioxide, as the flow of water from the water supply network increases (up to a maximum of 132.8 L/h):
reduces the sum of the molar concentration of calcium and magnesium ions in drinking water,
reduces the molar concentration of calcium ions in drinking water,
reduces the ratio of the molar content of calcium and magnesium in drinking water.
Regarding the magnesium content, we cannot say such a conclusion unequivocally, because in
Figure S3., where the molar concentration of Mg
2+ is shown, the dependence of the concave shape for experimental values. At the minimum and maximum water flow from the distribution network, the experimental concentration of magnesium ions is lower than at the mean value of Q(H
2O). With the calculated values of c (Mg
2+), the difference in magnesium ion concentration is in the order of hundredths, based on which we can conclude that the value is quasi-steady.
A comparison of the measured and calculated values of the dependent variable at a constant water flow from the water supply network of 120 L/h and different CO
2 flows is shown in
Figures S6 and S7.
If we evaluate the process with a constant flow of water from the distribution network and different flows of CO2 supplied to the system, we can deduce:
as the CO2 flow increases, the ratio of the molar content of Ca2+ and Mg2+ decreases,
with increasing CO2 flow, the molar concentration of Mg2+ in drinking water also increases,
at the same time as the CO2 flow increases, the molar concentration of Ca2+ in drinking water decreases.
As the Mg2+ content increases and the Ca2+ content decreases with increasing CO2 flow, the sum of concentrations does not have a clear decreasing/increasing trend with increasing CO2 flow.
3.2.3. Optimization of the process in the pilot FBRR
Using the Solver program in MS Excel using the non-linear algorithm solution method, we calculated the optimal values of the independent variables (Q(CO
2), Q(H
2O)) in the pilot FBRR for the maximum and minimum value depending on the regression equations with determined parameter values (
Table 12) variables. We performed optimization calculations within the range of experimental conditions:
Using the determined values of the parameters of the regression equations, for the maximum values of the dependent variables, see
Table 12 we can notice the same conditions for all four dependent variables.
The maximum concentration of the sum of calcium and magnesium in drinking water, which can be achieved under the conditions Q(CO2) = 0.4 L/min and Q(H2O) = 118.0 L/h is 7.59 mmol/L. At the same time, under these process conditions, a content of calcium ions of 3.53 mmol/L is reached, i.e., 141.5 mg/L and magnesium ions 4.3 mmol/L, which represents 104.5 mg/L. The value of the molar ratio of calcium and magnesium in drinking water can be reached to a maximum of 1.14 under the above-mentioned process conditions.
Under the stated conditions of the process in
Table 12 drinking water is prepared, which is very hard [
31] and is satisfactory from a health point of view.
In
Table 13 the determined process conditions for the minimum values of the dependent variable are listed. We can see that during the recarbonization process in a pilot FBRR, it is possible to achieve minimum concentrations of Ca
2+ and (Ca
2++Mg
2+) ions that correspond to the recommended range according to Annex no. 1 to the Decree of the Ministry of Health of the Slovak Republic no. 247/2017 Coll [
30], even the specified minimum magnesium content in drinking water is higher than the recommended range. At the same time, under process conditions that correspond to the minimum value of the dependent variable, it is not possible to achieve the required ratio of molar content of calcium and magnesium in drinking water of 0.6 − 1.0.
3.2.2. Comparison of the used two recarbonization materials
We also operated the pilot FBRR with the 2.5-4.5 mm HCD Semidol recarbonizing material. During operation with this material, we maintained a constant flow of carbon dioxide Q(CO2) = 0.4 L/min and the inflow of treated drinking water from the distribution network Q(H2O) ≈ 120 L/h.
Both HCDs Semidol and Magno Dol (Akdolit) have approximately the same chemical composition, volume density and carbon dioxide consumption per unit weight of the material prescribed by the supplier. HCD Semidol is a more fragile material compared to HCD Magno Dol (Akdolit) and when dosing HCD Semidol into the device, we noticed a lot of HCD dust particles.
When operating a pilot FBRR using HCD Semidol, we can achieve higher average concentrations and outflow values of magnesium ions (
Table 13). However, the conditions of the recarbonization process with Magno Dol (Akdolit) were not constant during the entire operation as in the operation with HCD Semidol, therefore the comparison of the average effluent concentrations during the process is not relevant.
For a more accurate comparison of the used materials, we used the balance values, which we related to the HCD weight unit. These values are shown in
Table 15.
In the process with HCD Magno Dol (Akdolit), a smaller amount of the added HCD reacted (51.0%) than in the operation with HCD Semidol (79.9%). Even though a smaller amount of HCD Magno Dol (Akdolit) reacted during the process, the production of magnesium and calcium ions per kilogram of reacted amount of HCD is higher than with HCD Semidol. The same applies to the kilogram of added mass.
Since it is necessary to supply carbon dioxide to the system, when comparing the balance values of carbon dioxide, its consumption of 1.14 kg per 1 kg of added HCD Magno Dol (Akdolit) is close to the value stated by the manufacturer (1.2 - 1.3 kg). For HCD Semidol, the consumption is approximately 30% lower, i.e., 0.79 kg CO2 / kg HCD. The stated consumption of carbon dioxide per kilogram of added Semidol material is also lower than stated by the manufacturer (1.2 - 1.3 kg). The reason for the lower consumption may be the fragility of the material and the occurrence of particles smaller than 2.5 - 4.5 mm.
To compare the used recarbonization materials in practice, we performed balance calculations for the conditions of a real water treatment plant, where the introduction of a tested pilot FBRR into operation is being considered. The goal is to treat water with an annual water flow of 11 000 m3 with the required increase in magnesium ion content by 10 mg/L. It means that the annual increase of magnesium ions is 110 kg.
Annual consumption of carbon dioxide and compared materials under the same process conditions are shown in
Table 16.
Based on the above-mentioned balance calculations for the the potential water treatment plant when HCD Magno Dol (Akdolit) is used, the annual consumption of HCD is 874.7 kg, which includes 989.6 kg of CO2 per year. When using HCD Semidol, the annual consumption of material is only 43.3 kg higher, but the consumption of carbon dioxide is more than 200 kg lower, i.e., 721.2 kg of CO2 per year when using HCD Semidol.
In addition to enriching the water with magnesium ions, calcium ions are also released from the recarbonization mass. The amounts of Ca
2+ released during the production of 110 kg of Mg
2+ per year are shown in
Table 17.
The production of calcium during the long-term operation of the FBRR can be considered significant in view of the current requirements placed on the quality of drinking water [
30]. Annually, 38% more calcium ions are released from the Magno Dol material (Akdolit) compared to the Semidol material. When drinking water is enriched with magnesium by 10 mg/L using HCD Magno Dol (Akdolit), this represents an increase in calcium content by 8.2 mg/L. While when using HCD Semidol, the content of calcium ions increases by 5.1 mg/L. The operator’s decision on the choice of material can also be influenced by the current selling price of materials.
4. Discussion
Recarbonization of drinking water is aimed at increasing the quality of water with a very low content of magnesium and calcium minerals. These biogenic elements are important not only for human health, but also for reducing the problems related to the corrosive and aggressive effects of soft water on the materials of the drinking water distribution system. Water with very low total hardness is unstable and unbuffered.
Considering the demonstrable positive relationship between the content of Ca2+, Mg2+ and human health, the application of the recarbonization process appears to be a beneficial perspective for improving the quality of life in areas where the source of drinking water is poor in these biogenic elements. The use of a fluidized bed recarbonization reactor (FBRR) offers the possibility of treating large volumes of drinking water in a relatively short time and in smaller facilities.
The process of enhancement drinking water with biogenic and water stabilizing calcium and magnesium ions has been investigated. Chemistry of the process is based on half-calcined dolomite in combination with carbon dioxide. High interface reaction surface, homogenization of reaction conditions and intensifying potential of fluidized bed reactor represent novel approach to investigated recarbonization process and reactor techniques also in drinking water industry.
This process is characterized using renewable sources of raw materials with a minimal amount of produced waste, which is environmentally acceptable. The proposed drinking water recarbonization technology using a fluidized bed recarbonization reactor for the preparation of concentrate in a side-stream arrangement with respect to the drinking water distribution in main-stream minimizes the energy requirements, which are only related to water recirculation near the threshold velocity. In addition, the supply of carbon dioxide under the liquid distributor in the reactor also contributes to the reduction of the required supplied energy.
It is known from published experimental results that it is advantageous to use half-calcined dolomite (HCD) in combination with CO2 when enriching drinking water with calcium and magnesium. Half-calcinated dolomite is commercially available from several companies, and for this reason we also focused on testing two HCDs, Magno Dol (Akdolit) and Semidol with similar fractions. The results showed that even though they are chemically the same materials, they are of different quality. In general, with the same amount of magnesium ions released, a different amount of calcium ions is released, and the consumption of recarbonization materials is different. From a practical point of view, it is advisable to conduct experiments that would deal with the influence of operating parameters on the recarbonization process when using Semidol and compare the results with the operation of MagnoDol (Akdolit).
Experimental and mathematical modelling of the recarbonization process aimed at increasing the content of these biogenic elements in water was carried out in the continuous laboratory and pilot scale fluidized bed reactors. Water remineralization using half-calcined dolomite (HCD) and carbon dioxide in a fluidized bed reactor is a novelty in water treatment. Although the chemistry of the process is known and to be used, the specific conditions in this type of reactor can significantly affect the efficiency of the process. In the presented work, we deal with the possibility of the recarbonization process in a fluidized bed reactor.
The influence of operating conditions (Q(CO2), freshwater inflow and dose of HCD on some quality indicators of treated drinking water (c (Ca2+), c(Mg2+), amount of Ca2++Mg2+, Ca/Mg) was investigated. Subsequently, the operating conditions were optimized for the minimum and maximum value of the mentioned qualitative indicators. The results show that the Mg2+ concentration is more significantly affected by the amount of HCD in the system and the CO2. flow. The influence of the freshwater inflow on the Mg2+ content is to a lesser extent. At a constant CO2 flow thus, as the inflow of tap water increases, the Ca2+ content decreases and the Mg2+content increases, resulting in a decrease in the Ca/Mg molar ratio.
However, the Ca/Mg ratio can be effectively controlled by adding an appropriate amount of HCD at certain time intervals. The overproduction of ions can be easily controlled by the flow of CO2. When using HCD Semidol, the annual consumption of recarbonization material is higher by approx. 5% and at the same time the annual consumption of carbon dioxide is lower by approx. 27% compared to the operation of the device with HCD Magno Dol (Akdolit). With an increase of Mg2+ by 10mg/L, the increase in the concentration of calcium ions is higher by 38% when using the recarbonization mass Magno Dol (Akdolit) compared to HCD Semidol.
The results of experimental measurements were processed by regression analysis and optimization methods. Statistical models were developed to describe the dependence between the above water quality indicators and operating parameters. Using the grid search optimization method, the optimal values of operating parameters were determined for the maximum and minimum values of monitored drinking water quality indicators. Each source of drinking water has a different quality, so it is important to investigate the effect of basic operating conditions on the recarbonization process. Knowing the influence of operating conditions facilitates the design of such a device in practice, and the recarbonization process can be optimized so that the treated drinking water meets the required quality.
The laboratory and pilot FBRRs were designed, built and verified for soft water treatment. The results of measured hydraulic characteristics of the fluidized bed and the values of the optimal conditions of the recarbonization process make it possible to make the operation of the recarbonization system more efficient and its further expansion to full operation.
5. Conclusion
The use of the recarbonization process in a fluidized bed reactor using carbon dioxide and recarbonization materials based on half-calcined dolomite is novel technology for enriching drinking water with calcium and magnesium. Among the main advantages of using a fluidized bed is a relatively large contact area between the solid particles and the liquid, which minimizes the residence time of the liquid phase in the reactor. With this advantage, it is possible to adjust large volumes of drinking water in a short time. The aim of this work was experimental and mathematical modelling of the operation of a laboratory and pilot FBRR using CO2 and selected recarbonization materials.
The laboratory FBRR using HCD Magno Dol (Akdolit) with a grain size of 2-4 mm was operated in two ways. The first method was operation of a batch reactor with internal water recirculation (saturation phase). The second method was continuous operation after initial saturation, during which enriched drinking water was supplied from the water network to the storage tank (preparation of calcium and magnesium ion concentrate). The same flow of concentrate was diverted from this tank to the water distribution network, where it was mixed with enriched drinking water. The initial saturation phase lasted 64 hours at a constant CO2 flow rate of 0.5Ll/min.
To describe the saturation process, we used the recarbonization equation (Eq. 11), for which the parameter values cmax = 37.1 mmol/L and dC = 3.95∙10−2 L/min were determined.
The continuous phase lasted another 505.8 hours and was operated at different values of water flow from the distribution network drinking water and carbon dioxide inflow in the ranges as follow:
Using multiple regression analysis and using the Nelder-Mead simplex optimization method, we determined the values of the parameters of the regression model of the quadratic equation with mutual links. We used these parameter values in the optimization of the process conditions for the maximum and minimum values of the dependent variables c(Ca2++Mg2+), c(Ca2+) and c(Ca2+) / c(Mg2+) using grid search optimization method.
During the operation of the laboratory FBRR, the minimum value of the sum of calcium and magnesium ions was 10.9 mmol/L, and the maximum value of the sum of these ions was 16.2 mmol/L. Both values comply with the recommended values according to Annex no. 1 to the decree of the Ministry of Health of the Slovak Republic no. 247/2017 Coll.
From the optimization calculations for the maximum and minimum values of the molar ratio of calcium and magnesium in drinking water, it follows that the values of the ratios do not correspond to the requirements according to the above-mentioned decree of the Ministry of Health no. Slovak republic. The maximum calculated value of the molar ratio of calcium and magnesium for experimental conditions is 0.20, while the minimum recommended value according to the recommended content of individual ions in drinking water is 0.6.
We operated the Pilot FBRR with a fraction of 2 − 4 mm HCD Magno Dol (Akdolit) without an initial saturation phase. Considering that the pilot FBRR is a larger device and the stabilization of the process when the conditions change takes longer than in the laboratory FBRR, we varied the conditions of the recarbonization process (Q(CO2), Q(H2O)) in smaller ranges:
In these ranges of process conditions, with an increasing flow of carbon dioxide at a constant flow of tap water, the sum of the molar concentration of calcium and magnesium decreases, the molar content of calcium ions and the molar ratio of calcium decrease. magnesium in drinking water also decreases, while the magnesium concentration is basically stable according to the calculated values. On the contrary, with a constant flow of carbon dioxide, as the flow of water from the distribution network increases, the molar concentration of magnesium ions increases, the molar concentration of calcium decreases, and thus the ratio of molar concentrations of calcium and magnesium also decreases.
For both the laboratory and pilot FBRR, we determined the values of the parameters of the regression equation and subsequently optimized the conditions for achieving the minimum and maximum values of the dependent variables.
For the pilot FBRR, we focused on four dependent variables - c(Ca2++Mg2+), c(Mg2+), c(Ca2+) and c(Ca2+) / c(Mg2+)
The specified conditions for the maximum values of the dependent variables are the same. With a water flow from the drinking water distribution network of 118.0 L/h and a carbon dioxide flow of 0.4 L/min, the following maximum values were reached:
The maximum calculated values of the dependent variables are above the range of recommended values, and drinking water meets the requirements for its quality from a health point of view.
Using optimization calculations, the following minimum values of the dependent variables were obtained:
The above-mentioned minimum values of the dependent variables correspond to the process conditions of the independent variables of carbon dioxide at the level of 0.4 and the flow of treated water in the range of 127.3 - 132.8 l/h.
Under these conditions, the concentrations of calcium ions meet the recommended content, while the magnesium content even exceeds the recommended range and the ratio of calcium and magnesium content does not meet the recommended values according to Annex no. 1 to decree no. 247/2017 Coll., which establishes details on drinking water quality, drinking water quality control, monitoring program and risk management in drinking water supply.
The pilot FBRR was also operated with half-calcined Semidol dolomite with a grain size of 2.5 - 4.5 mm. The aim was to compare the operation using these different recarbonization materials in the treatment of drinking water with an annual volume flow of 11,000 m3 with an increase of magnesium ions by 10 mg/L. When using HCD Semidol, the annual consumption of material is higher by approx. 5% and at the same time the annual consumption of carbon dioxide is lower by approx. 27% compared to the operation of the equipment with HCD Magno Dol (Akdolit). In addition to magnesium, calcium is also released from the mass. The increase in the concentration of calcium ions is higher by 38% when using the recarbonization material Magno Dol (Akdolit) compared to HCD Semidol.
The resulting choice of recarbonization material is up to the operator, who can decide based on the price ratios of the materials used or from the point of view of the added value of the production of calcium ions in drinking water.
The stated minimum values of the dependent variables correspond to the process conditions of the independent variables of carbon dioxide at the level of 0.4 and the flow rate of treated water in the range of 127.3 – 132.8 L/h.
Supplementary Materials
The following supporting information can be downloaded at the website of this paper posted on Preprints.org.
Author Contributions
Conceptualization, J.D. (Ján Derco) and J.D. (Jozef Dudáš); methodology, J.D. (Ján Derco); software, T.K. (Tomáš Kurák); validation, NŠ (Nikola Šoltýsová) and J.D. (Ján Derco); formal analysis, N.Š.; investigation, T.K., N.Š and A.V. (Anna Vajíčeková); resources, all authors.; data curation, J.D. (Ján Derco); writing—original draft preparation, J.D. (Ján Derco); writing—review and editing, J.D. (Ján Derco); visualization, N.Š.; supervision, A.V.; project administration, N.Š. and A.V.; All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by “Improvement of health status of population of the Slovak Republic through drinking water re-carbonization” LIFE - Water and Health LIFE17 ENV/SK/000036.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rubenowitz, E.; Axelsson, G.; Rylander, R. Magnesium in Drinking Water and Death from Acute Myocardial Infarction. American Journal of Epidemiology 1996, 143, 456–462. [Google Scholar] [CrossRef] [PubMed]
- Rosborg, I. Drinking Water Minerals and Mineral Balance; Springer, 2014.
- Rylander, R.; Bonevik, H.; Rubenowitz, E. Magnesium and Calcium in Drinking Water and Cardiovascular Mortality. Scandinavian Journal of Work, Environment & Health 1991, 17, 91–94. [Google Scholar]
- Yang, C.-Y. Calcium and Magnesium in Drinking Water and Risk of Death from Cerebrovascular Disease. Stroke 1998, 29, 411–414. [Google Scholar] [CrossRef] [PubMed]
- Rosanoff, A. The High Heart Health Value of Drinking-Water Magnesium. Medical Hypotheses 2013, 81, 1063–1065. [Google Scholar] [CrossRef] [PubMed]
- Rylander, R. Magnesium in Drinking Water – a Case for Prevention? Journal of Water and Health 2013, 12, 34–40. [Google Scholar] [CrossRef] [PubMed]
- Szymoniak, L.; Claveau-Mallet, D.; Haddad, M.; Barbeau, B. Application of Magnesium Oxide Media for Remineralization and Removal of Divalent Metals in Drinking Water Treatment: A Review. Water 2022, 14. [Google Scholar] [CrossRef]
- Kaluza, J.; Orsini, N.; Levitan, E.B.; Brzozowska, A.; Roszkowski, W.; Wolk, A. Dietary Calcium and Magnesium Intake and Mortality: A Prospective Study of Men. American Journal of Epidemiology 2010, 171, 801–807. [Google Scholar] [CrossRef] [PubMed]
- Cotruvo, J. Drinking Water Quality and Contaminants Guidebook; Chapman and Hall/CRC: Milton, 2018; ISBN 9781351110464. [Google Scholar]
- WHO Guidelines for Drinking-Water Quality; 4th ed.; World Health Organization: Geneva, Switzerland, 2011; p. 531.
- Jiang, L.; He, P.; Chen, J.; Liu, Y.; Liu, D.; Qin, G.; Tan, N. Magnesium Levels in Drinking Water and Coronary Heart Disease Mortality Risk: A Meta-Analysis. Nutrients 2016, 8, 5. [Google Scholar] [CrossRef] [PubMed]
- Barloková, D.; Ilavský, J.; Kapusta, O.; Šimko, V. Importance of Calcium and Magnesium in Water - Water Hardening. IOP Conference Series: Earth and Environmental Science 2017, 92, 012002. [Google Scholar] [CrossRef]
- Rapant, S.; Letkovičová, A.; Jurkovičová, D.; Kosmovský, V.; Kožíšek, F.; Jurkovič, Ľ. Differences in Health Status of Slovak Municipalities Supplied with Drinking Water of Different Hardness Values. Environmental Geochemistry & Health 2021, 43, 2665–2677. [Google Scholar]
- Whelton, A.J.; Dietrich, A.M.; Burlingame, G.A.; Schechs, M.; Duncan, S.E. Minerals in Drinking Water: Impacts on Taste and Importance to Consumer Health. Water Science and Technology 2007, 55, 283–291. [Google Scholar] [CrossRef]
- Nelson, N.; De Luca, A. Remineralization and Stabilization of Desalinated Water. Pathways and Challenges for Efficient Desalination 2022.
- Birnhack, L.; Shlesinger, N.; Lahav, O. A Cost-Effective Method for Improving the Quality of Inland Desalinated Brackish Water Destined for Agricultural Irrigation. Desalination 2010, 262, 152–160. [Google Scholar] [CrossRef]
- Bang, D.P. Upflow Limestone Contactor for Soft and Desalinated Water. Master Thesis, Delft University of Technology, Delft, The Netherlands, 2012. [Google Scholar]
- Lehmann, O.; Birnhack, L.; Lahav, O. Design Aspects of Calcite-Dissolution Reactors Applied for Post Treatment of Desalinated Water. Desalination 2013, 314, 1–9. [Google Scholar] [CrossRef]
- Van Schagen, K.M. Model-Based Control of Drinking-Water Treatment Plants. Doctoral Thesis, Technical University of Delft, The Netherlands, 2009. [Google Scholar]
- Kramer, O.; Jobse, M.A.; Baars, E.T.; van der Helm, A.W.C.; Colin, M.G.; Kors, L.J.; van Vugt, W.H. Model-Based Prediction of Fluid Bed State in Full-Scale Drinking Water Pellet Softening Reactors. In Proceedings of the Proceedings of the 2nd IWA New Developments in IT & Water conference; pp. 20158–10.
- Derco, J.; Dudáš, J.; Luptáková, A.; Vrabeľ, M. Method of Increasing the Content of Mineral Substances in Water and Equipment for Performing This Method. (Industrial Property Office of the Slovak Republic—WebRegisters PP 50035-2018). Available online: https://wbr.indprop.gov.sk/WebRegistre/Patent/Detail/50035-2018.
- Life—Water and Health, Life17 ENV/SK/000036. Available online: http://fns.uniba.sk/lifewaterhealth/.
- Richardson, J.F.; Zaki, W.N. Sedimentation and Fluidisation: Part I. Trans. Instn. Chem. Eng. 1954, 32, 35–53. [Google Scholar] [CrossRef]
- Dudáš, J.; Derco, J.; Kurák, T.; Šoltýsová, N.; Jelemenský, Ľ.; Vrabeľ, M. Design, Scale-Up, and Construction of Drinking Water Recarbonization Fluidized Bed Reactor System. Processes 2022, 10, 2068. [Google Scholar] [CrossRef]
- Rice, E.W.; Baird, R.B.; Eaton, A.D.; Clesceri, L.S. American Public Health Association; American Water Works Association; Water Environment Federation Standard Methods for Examination of Water and Wastewater 2012; Washington, Dc: American Public Health Assn, 2012.
- Mulcahy, L.T.; Shieh, W.K.; Lamotta, E.J. Simplified Mathematical Models for a Fludized Bed Biofilm Reactors. The American Institute of Chemical Engineers 1981, 209, 273–285. [Google Scholar]
- Olejko, Š. Study of Drinking Water Treatability and Environmental Aspects of Water Flows. Sub-task 02: Treatment of Drinking Water Mineralization; Final report of the task 1999; VÚVH: Bratislava, Slovakia.
- Dang, J.S.; Harvey, D.M.; Jobbagy, A.; Grady, C.P.L. Evaluation of Biodegradation Kinetics with Respirometric Data. Research Journal of the Water Pollution Control Federation 1989, 61, 1711–1721. [Google Scholar]
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. The Computer Journal 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Ministry of Health of the Slovak Republic Decree No. 247/2017 Coll. Slovak Standard Values for Drinking Water. 2017; Available online: https://www.slov-lex.sk/pravne-predpisy/SK/ZZ/2017/247/20171015.
- Pitter, P. Hydrochemistry; 5th ed.; University of chemistry and technology: Prague, Czech Republic, 2015; p. 792.
Figure 1.
Scheme of the laboratory water recarbonization system - FBRR and water storage tank, 1 – tap water supply, 2 – internal water recirculation, 3 – pump, 4 – fluidized reactor, 5 – water tank, 6 – inlet of CO2, 7 – flow meter, 8 – outlet of concentrated water.
Figure 1.
Scheme of the laboratory water recarbonization system - FBRR and water storage tank, 1 – tap water supply, 2 – internal water recirculation, 3 – pump, 4 – fluidized reactor, 5 – water tank, 6 – inlet of CO2, 7 – flow meter, 8 – outlet of concentrated water.
Figure 2.
Experimental dependence of pressure loss (ΔP) on superficial velocity (w) for fraction of 2.0-4.0 mm of HC dolomite Magno Dol (Akdolit).
Figure 2.
Experimental dependence of pressure loss (ΔP) on superficial velocity (w) for fraction of 2.0-4.0 mm of HC dolomite Magno Dol (Akdolit).
Figure 3.
Time dependence of conductivity and Ca2+ and Mg2+ concentrations during saturation of laboratory FBRR.
Figure 3.
Time dependence of conductivity and Ca2+ and Mg2+ concentrations during saturation of laboratory FBRR.
Figure 4.
Time dependence of the production of Mg2+ and Ca2+ and the ratio of molar concentrations of ions during the carbonation phase of the laboratory FBRR.
Figure 4.
Time dependence of the production of Mg2+ and Ca2+ and the ratio of molar concentrations of ions during the carbonation phase of the laboratory FBRR.
Figure 5.
Time dependence of Ca2++Mg2+ content during the saturation phase of laboratory FBRR.
Figure 5.
Time dependence of Ca2++Mg2+ content during the saturation phase of laboratory FBRR.
Figure 6.
Time dependence of conductivity and molar concentration of Ca2++Mg2+ during the continuous phase in the laboratory FBRR.
Figure 6.
Time dependence of conductivity and molar concentration of Ca2++Mg2+ during the continuous phase in the laboratory FBRR.
Figure 7.
Calculated and measured values of Ca2++Mg2+ concentration during continuous operation of laboratory FBRR.
Figure 7.
Calculated and measured values of Ca2++Mg2+ concentration during continuous operation of laboratory FBRR.
Figure 8.
Calculated and measured values of c(Ca2+) / c(Mg2+) during continuous operation of the laboratory FBRR.
Figure 8.
Calculated and measured values of c(Ca2+) / c(Mg2+) during continuous operation of the laboratory FBRR.
Figure 9.
Time dependence of conductivity and molar concentration of Ca2++Mg2+ during operation of pilot FBRR.
Figure 9.
Time dependence of conductivity and molar concentration of Ca2++Mg2+ during operation of pilot FBRR.
Figure 10.
Time dependence of the molar concentrations of Ca2+ and Mg2+ and the ratio of the molar concentrations of Ca2+ and Mg2+ during the operation of pilot FBRR.
Figure 10.
Time dependence of the molar concentrations of Ca2+ and Mg2+ and the ratio of the molar concentrations of Ca2+ and Mg2+ during the operation of pilot FBRR.
Figure 11.
Experimental and calculated values of molar concentration of Ca2++Mg2+.
Figure 11.
Experimental and calculated values of molar concentration of Ca2++Mg2+.
Figure 12.
Experimental and calculated values of molar concentration of Mg2+.
Figure 12.
Experimental and calculated values of molar concentration of Mg2+.
Figure 13.
Experimental and calculated values of molar concentration of Ca2+.
Figure 13.
Experimental and calculated values of molar concentration of Ca2+.
Figure 14.
Experimental and calculated values of molar concentration of Ca2+ a Mg2+.
Figure 14.
Experimental and calculated values of molar concentration of Ca2+ a Mg2+.
Table 1.
Values of parameters of hydraulic equations.
Table 1.
Values of parameters of hydraulic equations.
| A |
B |
c |
d |
cd
|
n |
RXY
|
| 34.2 |
0.712 |
4.97 |
6.39 |
0.23 |
3.18 |
0.700 |
Table 2.
Doses of HCD Magno Dol (Akdolit) to the laboratory FBRR during saturation.
Table 2.
Doses of HCD Magno Dol (Akdolit) to the laboratory FBRR during saturation.
HCD refill time
[h] |
HCD dose
[g] |
Hight of fluidized bed
[cm] |
| 0 |
360 |
- |
| 9 |
29.1 |
15.9 |
| 53 |
36.8 |
14.9 |
Table 3.
Measured data at the beginning and end of saturation of the laboratory FBRR.
Table 3.
Measured data at the beginning and end of saturation of the laboratory FBRR.
(h) |
pH
(-) |
κ
(µS/cm) |
c (Ca2++Mg2+)
(mmol/L) |
cm (Ca2+)
(mg/L) |
cm (Mg2+)
(mg/L) |
| 0 |
7.000 |
672 |
4.10 |
40.08 |
75.33 |
| 64 |
7.512 |
4 900 |
36.75 |
84.17 |
842.0 |
Table 4.
Values of the kinetic parameters of the recarbonization equation (11) and statistical characteristics.
Table 4.
Values of the kinetic parameters of the recarbonization equation (11) and statistical characteristics.
cmax
(mmol/L) |
dC
(1/min) |
|
|
RXY
|
| 37.10 |
3.95∙10−2
|
118.6 |
4.77 |
0.9611 |
Table 5.
Parameter values of the laboratory FBRR regression equation model for the dependence c (Ca2++Mg2+) = f (Q(CO2), Q(H2O)).
Table 5.
Parameter values of the laboratory FBRR regression equation model for the dependence c (Ca2++Mg2+) = f (Q(CO2), Q(H2O)).
| Parameter |
Value |
| P0
|
33.994 |
| P1
|
2.790 |
| P2
|
− 0.847 |
| P11
|
10.000 |
| P22
|
0.007 |
| P12
|
− 0.021 |
Table 6.
Parameter values of the laboratory FBRR regression equation model for the dependence c(Ca2+) / c(Mg2+) = f (Q(CO2), Q(H2O)).
Table 6.
Parameter values of the laboratory FBRR regression equation model for the dependence c(Ca2+) / c(Mg2+) = f (Q(CO2), Q(H2O)).
| Parameter |
Value |
| P0
|
-0.1249 |
| P1
|
-0.8076 |
| P2
|
0.0194 |
| P11
|
-0.4775 |
| P22
|
-0.0002 |
| P12
|
0.0160 |
Table 7.
Results of the optimization of the process conditions of recarbonization for the dependent variable of c(Ca2++ Mg2+).
Table 7.
Results of the optimization of the process conditions of recarbonization for the dependent variable of c(Ca2++ Mg2+).
| Value |
c(Ca2++Mg2+)
(mmol/L) |
Q(CO2)
(L/min) |
Q(H2O)
(mL/min) |
c(Ca2+) / c(Mg2+) |
| Maximum |
16.2 |
0.54 |
76.0 |
0.005 |
| Minimum |
10.9 |
0.24 |
57.2 |
0.175 |
Table 8.
Results of the optimization of the process conditions of recarbonization for the dependent variable of the ratio c(Ca2+) / c(Mg2+).
Table 8.
Results of the optimization of the process conditions of recarbonization for the dependent variable of the ratio c(Ca2+) / c(Mg2+).
| Value |
c(Ca2+) / c(Mg2+) |
Q(CO2)
(L/min) |
Q(H2O)
mL/min) |
c(Ca2+ + Mg2+) |
| Maximum |
0,200 |
0,24 |
47,1 |
11,6 |
| Minimum |
0,053 |
0,54 |
70,0 |
14,8 |
Table 9.
Flows of carbon dioxide for individual areas shown in
Figure 9 and
Figure 10.
Table 9.
Flows of carbon dioxide for individual areas shown in
Figure 9 and
Figure 10.
| Area |
Q(CO2) (L/min) |
| 1 |
0.4 |
| 2 |
0.7 |
| 3 |
0.5 |
| 4 |
0.3 |
| 5 |
0.5 |
| 6 |
0.4 |
Table 10.
Parameter values of equation (12) and statistical characteristics for individual dependent variables Y.
Table 10.
Parameter values of equation (12) and statistical characteristics for individual dependent variables Y.
| |
Dependent variables Y |
| Parameter |
c(Ca2++Mg2+) |
c(Ca2+)/c(Mg2+) |
c(Mg2+) |
c(Ca2+) |
| P0
|
90.785 |
238.760 |
29.965 |
288.433 |
| P1
|
− 118.575 |
− 67.015 |
−75.558 |
− 86.230 |
| P2
|
− 0.788 |
− 3.546 |
− 0.123 |
− 4.160 |
| P11
|
16.279 |
2.524 |
16.645 |
− 3.577 |
| P22
|
1.09·10−3
|
1.31·10−2
|
− 5.17·10−4
|
1.49·10−2
|
| P12
|
0.834 |
0.526 |
0.500 |
0.724 |
| RXY
|
0.9635 |
0.9929 |
0.9796 |
0.9357 |
| RXY2
|
0.9597 |
0.8755 |
0.9858 |
0.9283 |
Table 12.
Optimization of the conditions of the process in the pilot FBRR for the maximum values of the dependent variables.
Table 12.
Optimization of the conditions of the process in the pilot FBRR for the maximum values of the dependent variables.
| Dependent variables |
Value |
Q(CO2)
(L/min) |
Q(H2O)
(L/h) |
| c(Ca2++Mg2+) |
7.59 mmol/L |
0.40 |
118.00 |
| c(Mg2+) |
4.30 mmol/L |
0.40 |
118.00 |
| c(Ca2+) |
3.53 mmol/L |
0.40 |
118.00 |
| c(Ca2+) /c(Mg2+) |
1.14 |
0.40 |
118.00 |
Table 13.
Optimization of the conditions of the process in the pilot FBRR for the minimum values of the dependent variables.
Table 13.
Optimization of the conditions of the process in the pilot FBRR for the minimum values of the dependent variables.
| Dependent variables |
Value |
Q(CO2)
(L/min) |
Q(H2O)
(L/h) |
| c(Ca2++Mg2+) |
4.93 mmol/L |
0.40 |
132.80 |
| c(Mg2+) |
3.52 mmol/L |
0.40 |
132.80 |
| c(Ca2+) |
1.30 mmol/L |
0.40 |
130.24 |
| c(Ca2+) /c(Mg2+) |
6.93·10−4
|
0.40 |
127.35 |
Table 14.
Average concentration values achieved when using different HCDs.
Table 14.
Average concentration values achieved when using different HCDs.
| |
Magno Dol (Akdolit) |
Semidol |
| Average inflow of freshwater (L/h) |
121.8 |
119.7 |
| Average c(Mg2+) (mg/L) |
105.3 |
146.2 |
| Average c(Ca2+) (mg/L) |
86.5 |
70.5 |
| Average outflow Mg2+ (g/h) |
12.8 |
16.6 |
| Average outflow Ca2+ (g/h) |
10.5 |
8.5 |
Table 15.
Balance values after using two different materials.
Table 15.
Balance values after using two different materials.
| |
Magno Dol (Akdolit) |
Semidol |
| Reaction time (h) |
306.6 |
167.0 |
| Total added HCD (kg) |
31.2 |
23.1 |
| Reacted amount of HCD (kg) |
15.9 |
18.4 |
| Reacted HCD to added HCD (%) |
51.0 |
79.9 |
| Total consumption of CO2 (kg) |
35.3 |
18.2 |
| Total production of Mg2+ (kg) |
3.92 |
2.77 |
| Total production of Ca2+ (kg) |
3.22 |
1.41 |
Average production of Mg2+
per added HCD (g/kg) |
125.8 |
119.8 |
Average production of Ca2+
per added HCD (g/kg) |
103.2 |
61.2 |
Average production of Mg2+
per reacted HCD (g/kg) |
246.8 |
149.9 |
Average production of Ca2+
per reacted HCD (g/kg) |
202.5 |
76.5 |
CO2 consumption
per added HCD (kg/kg) |
1.13 |
0.79 |
CO2 consumption
per reacted HCD (kg/kg) |
2.22 |
0.98 |
Table 16.
Consumption of CO2 and material in a pilot FBRR with an increase of 110 kg Mg2+ per year.
Table 16.
Consumption of CO2 and material in a pilot FBRR with an increase of 110 kg Mg2+ per year.
| |
Magno Dol (Akdolit) |
Semidol |
| HCD consumption (kg/year) |
874.7 |
917.9 |
| CO2 consumption (kg/year) |
989.6 |
721.2 |
Table 17.
Ca2+ released and increases Ca2+ in by different material in pilot FBRR with an increase of 110 kg Mg2+ per year.
Table 17.
Ca2+ released and increases Ca2+ in by different material in pilot FBRR with an increase of 110 kg Mg2+ per year.
| |
Magno Dol (Akdolit) |
Semidol |
| Released Ca2+ (kg/year))
|
90.3 |
56.2 |
| Increases c (Ca2+) (mg/L) |
8.2 |
5.1 |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).