Prerpints.org logo
Preprint
Review

Alloy Quasicrystals: Perspectives and Some Open Questions at Forty Years

Altmetrics

Downloads

109

Views

67

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

16 October 2023

Posted:

16 October 2023

You are already at the latest version

Alerts
Abstract
Four decades have elapsed since the first quasiperiodic crystal was discovered in the Al-Mn alloy system, and many progresses have been made during this time interval in the science of quasicrystals (QCs). Notwithstanding this, a significant number of open questions still remain regarding both fundamental and technological aspects. For instance: What are QCs good for? How can we improve the current provisional QC definition? What is the role of the underlying quasiperiodic order and the characteristic inflation symmetry of these compounds in the emergence of their unusual physicochemical properties? or, What is the nature of chemical bonding in QCs formed in such different sorts of materials as alloys, oxides, or organic polymers? In this essay I will discuss these, and other closely related, issues from an interdisciplinary perspective and will comment on appealing prospectives in the field for the years to come.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

1. An unexpected discovery

In 1984 the existence of a novel ordering principle in condensed matter was announced to the scientific community [1]. This new matter phase was able to diffract electrons like a typical single crystal does, but it exhibited icosahedral point group symmetry, which is inconsistent with periodic lattice translations in three dimensions. Notwithstanding this, the remarkable sharpness of the obtained electron diffraction patterns clearly indicated a high coherency of the electrons spatial interference, comparable to the one usually encountered in classical periodic crystals [2]. The nature of the underlying long-range order was explained by invoking the mathematical notion of quasiperiodic (QP) functions [3], thereby widening the concept of ordered arrangement of matter from that based in periodic distribution of atoms through the space to that corresponding to QP ones [4]. Accordingly, these new materials were dubbed quasiperiodic crystals, or quasicrystals (QCs) for short. Therefore, QCs can be envisioned as long-range ordered materials with a symmetry incompatible with translation invariance. Daniel Shechtman was awarded the Nobel Prize in Chemistry 2011 "for the discovery of quasicrystals", almost thirty years after he made such a discovery in 1982, when he was studying the atomic structure of a binary alloy belonging to the Al-Mn system, with atomic composition Al86Mn14.
About forty-three years before, in 1939, A. J. Bradley and H. J. Goldschmidt had performed a systematic study of the Al-Cu-Fe alloy system phase diagram at 873 K, and they were able to identify all the observed intermetallic structures by X-ray powder diffraction except one phase with a composition Al6Cu2Fe, which was referred to as Ψ phase [5,6]. Quite remarkably, they reported that no known indexation scheme could be properly asigned to this phase, whose atomic structure remained unknown until 1987, when A. P. Tsai and co-workers realized that it corresponds to a thermodynamically stable icosahedral QC (iQC) with a dodecahedral growth habit morphology [7].
In a similar vein, in 1955 H. K. Hardy and J. M. Silcock scrutinized the intermetallic compounds in equilibrium with the aluminium solid solution in the ternary Al-Li-Cu system by using a Debye-Sherrer power diffraction method. At 773 K they found several compounds corresponding to hexagonal and cubic structures, in addition to a phase they called T2, with composition close to Al6Li3Cu, which exhibited an X-ray diffraction pattern escaping any periodic arrangement based indexation scheme [8]. This oddity remained dormant for more than three decades, until M. Audier and collaborators proved in 1986 that this phase actually belongs to the iQC class, and they were able to grow large grains up to the millimeter size, exhibiting the growth morphology of a multi-faceted rhombic triacontahedron, by conventional solidification techniques in close to equilibrium conditions [9]. The observed dodecahedral and triacontahedral morphologies were a novelty in both crystallography and mineralogy.
These two examples clearly illustrate that QCs had been inadvertedly found quite before they were properly discovered. Two main reasons can be invoked to account for this fact; one reason is related to experimental techniques, the other one has to do with conceptual aspects:
  • For one thing, QCs discovery required the use of a suitable experimental technique, namely, electron microscopy, because ”while X-ray diffraction is great for studying many aspects of crystals, it cannot show you rotational symmetry" in an explicit manner 1. The importance of the electron diffraction method was further illustrated during the decade-long systematic search for naturally formed (rather than artificially synthesized) QCs performed by P. Steinhard, L. Bindi, and co-workers, ultimately leading to the discovery of icosahedrite (2009) and decagonite (2015) mineral samples [10] 2.
  • On the other hand, during more than two centuries the mineralogical, crystallographical, and solid state communities had generally assumed that all crystals must be periodic regular arrays on a lattice, and this conceptual framework became a paradigm that arose from experience, rather than from fundamental principles [15]. What about the possible existence of regular distributions of atoms in the space beyond the periodic order realm? By all indications, such a possibility was essentially ignored 3, probably due to the cogent influence deriving from the so-called crystallographical restriction theorem, stating that the only rotation axes compatible with translation symmetry are the 2-fold, 3-fold, 4-fold, and 6-fold ones [16]. In this regard, it is important to note that structures which do not preserve the translation symmetry in 3D lattices can satisfy a properly generalized crystallographic restriction theorem in the case of higher dimension lattices. Thus, a 6D hypercubic lattice is invariant under the icosahedral group and so is its 3D image resulting from a suitable projection [17].
In this regard, QCs discovery provides an illustrative example of an actual discovery which was not preceded by a compelling enough theoretical discovery [18], albeit Alan Mackay had properly anticipated in 1982 the existence of 5-fold symmetry in solid state [19], on the basis of optical diffraction patterns in Penrose related lattices [20] 4.

2. A provisional definition

To date the existence of aperiodic crystals has been reported in three broad classes of materials, namely, incommensurate composites, incommensurately modulated phases, and quasicrystalline compounds [21,22,23]. In all of these structures the atomic arrangements exhibit well defined long-range order, which gives rise to high quality discrete diffraction patterns, in spite of the absence of lattice periodicity. An important distinction can be made between incommensurate structures and QCs by attending to their X-ray, electron or neutron diffraction patterns, namely: for incommensurate structures one can always find a sub-pattern of high intensity spots (the so-called main reflections), related to an average periodic structure in physical space. Along with these high intensity reflections, there is a set of lower intensity peaks grouped around them (the so-called satellite spots). The satellite reflections stem from the presence of structural modulations characterized by a periodicity which is incommensurate with that of the average structure. Usually the amplitude of this modulation is relatively small, so that the overall structure can be confidently described in terms of a perturbed averaged periodic structure. On the contrary, there is no periodic reference structure in QCs, and their structure determination is more demanding in this case.
In April 1991 the International Union of Crystallography (IUCr) approved the establishment of an ad interim Commission on Aperiodic Crystals to promote the development of common methods and nomenclature for the crystallographic investigation of both incommensurate phases and QCs. According to the terms of reference introduced by this Commission by "crystal" is meant any solid having an essentially discrete diffraction diagram, and by "aperiodic crystal" is meant any crystal in which three dimensional lattice periodicity can be considered to be absent [24]. The revamped crystal definition highlights that periodicity at the atomic scale is a sufficient but not necessary condition for crystallinity. Instead, the presence of a long-range atomic order able to diffract must be regarded as the essential attribute of crystalline matter. Consequently, among crystals we can now distinguish between periodic crystals, which display periodic arrangements of atoms, and aperiodic crystals, lacking such a periodicity, which is generally replaced by other kinds of ordering principles, such as scale invariance (inflation symmetry) or long-range repetitiveness.
Therefore, the existence of a mathematically well defined long-range atomic order, which gives rise to high quality discrete diffraction patterns, despite the absence of lattice translation symmetry, should be properly regarded as the generic attribute of ordered solid state matter.
Currently, the IUCr Commission on Aperiodic Crystals defines QCs in the following terms 5:
1.
A quasicrystal is an aperiodic crystal that is not an incommensurate modulated structure, nor an aperiodic composite crystal. Often, quasicrystals have crystallographically ’forbidden’ symmetries. These are rotations of order different from 1, 2, 3, 4 and 6. In three dimensions a lattice periodic structure may only have rotation symmetry of an order equal to one of these numbers. However, the presence of such a forbidden symmetry is not required for a quasicrystal. A system with crystallographically allowed rotation symmetry that is locally similar to one with forbidden symmetries is also a quasicrystal.
2.
The term quasicrystal stems from the property of quasiperiodicity observed for the first alloys found with forbidden symmetries. Therefore, the alternative definition is: a quasicrystal is an aperiodic crystal with diffraction peaks that may be indexed by n integer indices, where n is a finite number, larger than the dimension of the space (in general). This definition is similar to that of aperiodic crystal.
By inspecting the IUCr definitions of QCs we can appreciate some inconvenient features, namely:
  • It is a negative definition, stating what a QC is not as compared to other atomic structures ("A quasicrystal is an aperiodic crystal that is not an incommensurate modulated structure, nor an aperiodic composite crystal").
  • The second definition merely states that "QC definition is similar to that of aperiodic crystal", but does not clearly precise what are the differences between QCs and aperiodic crystals (a broader class of materials including them).
Thus, at the time being we are still lacking a clear, concise, and definitive definition of what a QC is. For instance, according to the first definition above the existence of axes of symmetry forbidden in periodic crystals is not actually required, although such a requirement is very frequently mentioned in the literature. In fact, during the last two decades some authors have argued that the current IUCr QC definition is too restrictive, since it excludes an interesting collection of structures that exhibit the scale invariant symmetry properties of QCs without displaying any forbidden symmetry [25]. Indeed, several examples of QCs exhibiting 2-, 3-, and 4-fold symmetry axes along with scale invariance symmetry characterized by irrational scale factors have been reported, being referred to as cubic QCs. This important feature is illustrated by the quasicrystalline phase of Al69Pd22Mn9, corresponding to an aperiodic structure just exhibiting cubic symmetry [26], or by non-periodic square-triangle tilings of the plane showing an overall 6-fold symmetry [27]. These findings support the view that QC definition should not include the requirement that they must display a classically forbidden axis of symmetry.
This unsatisfactory situation urges the crystallographic community to reconsider the provisional definitions introduced more than 30 years before. To this end, I recommend a careful reading of the insightful thoughts discussed by R. Lifshitz some time ago [28]. In particular, it may be pertinent to take a closer look at the originally proposed QC notion: according to D. Levine and P. Steinhardt "A quasicrystal is the natural extension of the notion of a crystal to structures withquasiperiodic, rather than periodic, translational order" [4]. Therefore, we may better define QCs as long-range ordered solids whose diffraction pattern exhibits symmetries that are incompatible with translational symmetry, with the proviso that this long-range order stems from the underlying quasiperiodic distribution of atoms throughout the space. Otherwise, they should be regarded as periodic or almost periodic crystals representatives, respectively.
In my opinion such a tentative definition has two convenient pros:
1.
It is a positive definition stating what QCs are by indicating a specific atomic property: quasiperiodic order (QPO), which distinguishes them from both periodic crystals and incommensurate phases.
2.
It allows for a systematic classification of the broad aperiodic crystals realm on the basis of the mathematical nested sets involving periodic, quasiperiodic, and almost-periodic functions.
A simple one-dimensional example of a QP function is given by f ( x ) = A 1 cos ( x ) + A 2 cos ( α x ) , where α is an irrational number and A 1 and A 2 are real numbers. Remarkably enough this QP function can be written as a one-dimensional projection of the periodic function in two dimensions f ( x , y ) = A 1 cos x + A 2 cos y , through the restriction y = α x . Since any QP function can be thought of as deriving from a periodic function in a space of higher dimension, the so-called cut-and-project method, which is widely used in the study of QCs, ultimately relies on this mathematical property. In this way, most of the basic notions of classical crystallography can be properly extended to the study of QCs by considering suitable lattices in appropriate hyperspaces.
Other QC definition proposals focus on their spectral properties instead:
"A quasi-crystal is a distribution of discrete point masses whose Fourier transform is a distribution of discrete point frequencies. Or to say it more briefly, a quasi-crystal is a pure point distribution that has a pure point spectrum. This definition includes as a special case the ordinary crystals, which are periodic distributions with periodic spectra" [29].
This definition nicely highlights the conceptual primacy of QPO over that of periodic (P) order, which just reduces to a particular case, within the even larger set of almost periodic functions. In this regard, it is interesting to note that, to the best of my knowledge, almost periodic (AP) crystals have not yet been found in Nature.

3. Novel symmetries and long-range order

The three classes of aperiodic crystals identified up to now share a common feature, namely, all of them exhibit order without translational symmetry [22]. The QP long-range order in QCs can be envisioned by sitting their building blocks on the nodes of a QP tiling in physical space, which can be properly described in terms of a systematic application of inflation symmetry operations. This means that if all the vectors of the reciprocal quasi-lattice in a QC are multiplied by a constant factor greater than one (the so-called inflation parameter) the reciprocal lattice remains unchanged. Indeed, the presence of the scale invariance symmetry is essential to obtain a QP translation order [21,23,30]. This symmetry had not been previously considered in classical crystallography, and it is directly related to the emergence of self-similar, hierarchical patterns embodying atomic cluster aggregates. Therefore, from a structural viewpoint QCs can be regarded as self-similar arrays of atoms, where the translation symmetry, characteristic of periodic crystals, is replaced by a scale invariance one, with scale factors given by irrational numbers. Accordingly, QCs exhibit a novel crystallographic symmetry: scale invariance [23,31,32].
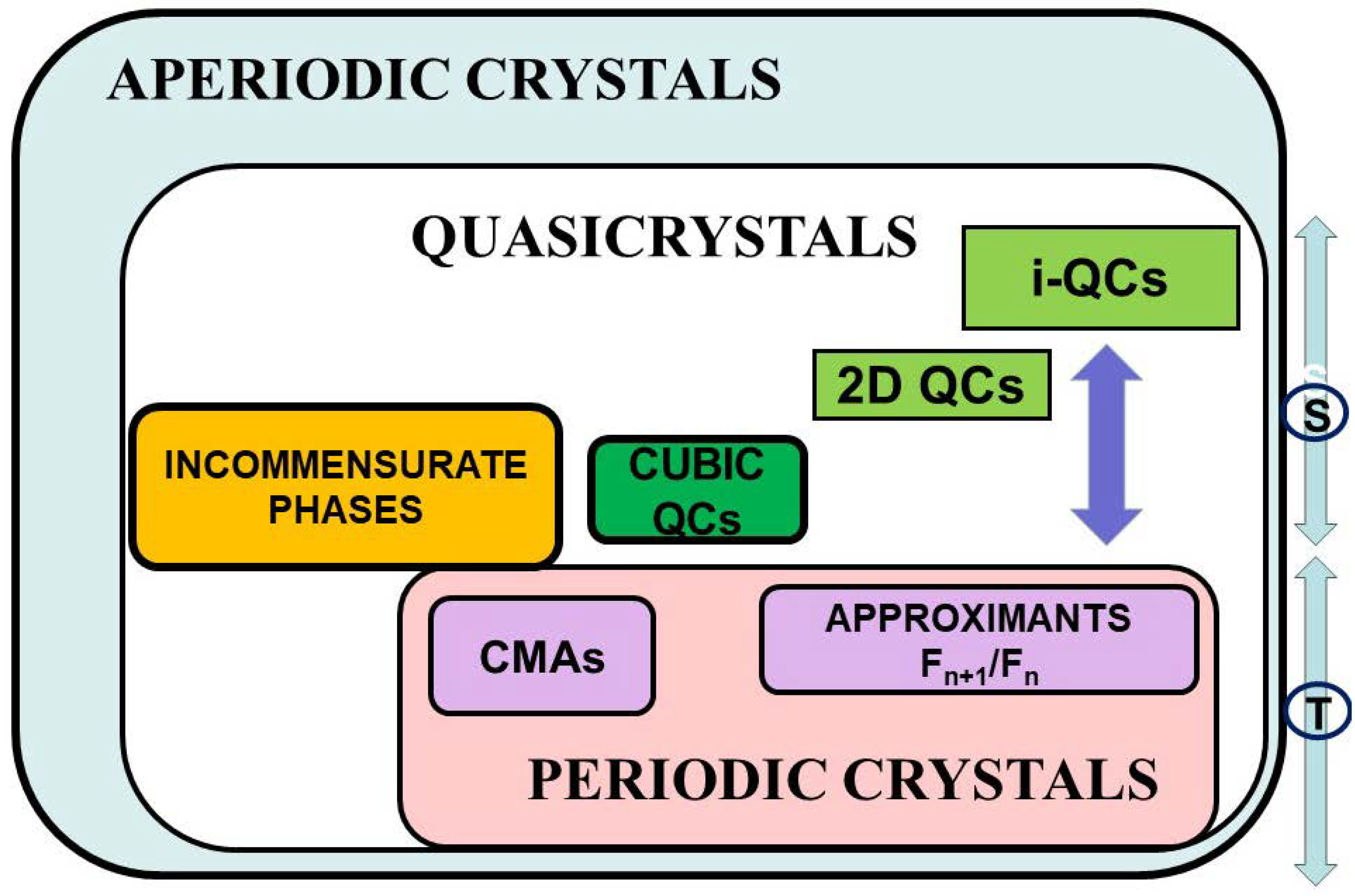
In Figure 1 I display a tentative classification scheme of the aperiodic crystals realm, which is based on two guiding principles. On the one hand, we consider the mathematical nature of the atomic density distribution function ρ ( r → ) , according to the nested hierarchy P ⊂ Q P ⊂ A P functions, respectively defining periodic, quasiperiodic and almost periodic crystals. On the other hand, we take into account the long-range order symmetries underlying the atomic density distribution function ρ ( r → ) of the considered solid, namely, translation (T) or scale invariance (S) symmetries, along with their point group rotational symmetries of finite order.
Periodic crystals having translation symmetry, as well as 2-fold, 3-fold, 4-fold, and 6-fold rotations axes, are located at the lower zone, and they include compounds with relatively large unit cells, such as the so-called complex metallic alloys (CMA), and the approximant crystals (AC) which are closely related to QCs.
Indeed, in most quasicrystalline forming alloy systems the true QC phase diagram region is surrounded by a number of compositionally related periodic crystals having very similar compositions, which are called AC phases, because they exhibit huge unit cell sizes which periodically repeat through the three directions of space. The AC unit cells show atomic structures closely resembling those of the true QC, from which they can nevertheless be distinguished. Within the superspace framework these periodic structures can be derived by projection from a parent hyperlattice onto the 3D physical space, as it occurs in the case of QCs. However, whereas for QCs the projection involves irrational numbers, in the case of ACs the projection is expressed in terms of rational approximants to the former irrational quantities. Accordingly, approximant cubic crystals can be classified by a rational number, which, in the case of iQCs and dQCs, is a ratio of two consecutive terms F n + 1 / F n in the Fibonacci sequence F n = { 1 , 1 , 2 , 3 , 5 , 8 , … } . Up to now, the cubic 2 / 1 approximants are the highest order cases reported with structural details 6.
Approximant phases should not be confused with giant-unit-cell intermetallics exhibiting complex structures that contain some hundred up to several thousand atoms in the unit cell. A representative example is provided by the Mg32(Al,Zn)49 compound, first described by Pauling and co-workers in 1952, with 162 atoms in the unit cell [34]. These giant unit cells, with lattice parameters of several nanometers, strikingly contrast with the unit cells of elementary metals and simple intermetallics, which in general comprise from single up to a few tens atoms only. In addition, all these giant unit cells have a substructure based on polyhedral atom arrangements or clusters that partially overlap or are linked by bridging elements. Accordingly, they exhibit translational periodicity on the scale of many interatomic distances, whereas on the few nm scale the atoms are arranged in clusters, where icosahedrally-coordinated environments play a prominent role. According to the classification scheme shown in Figure 1 the role played by the local symmetry of the structural clusters progressively increases from the non-QC related CMAs (on the left) to the QC-related AC ones (on the right).
Incommensurate phases are the simplest structures exhibiting long-range scale invariance symmetry [35] and, consequently, they are located at the borderline separating translation based from inflation based structures in Figure 1. The next step in increasing hierarchical order is provided by the cubic QCs we previously described, followed by the 2D QCs (including octagonal, decagonal, and dodecagonal rotational symmetries). These materials exhibit QPO within planes which are periodically stacked along the perpendicular direction. Finally, on the right hand of the upper region of the QCs set we find the iQCs, which are full-fledged QP structures along the three directions of the space. Including both periodic and QP crystals sets we find the vast region of purely aperiodic crystals (i.e., neither P nor QP ones), probably including many structures of biological interest [36,37].

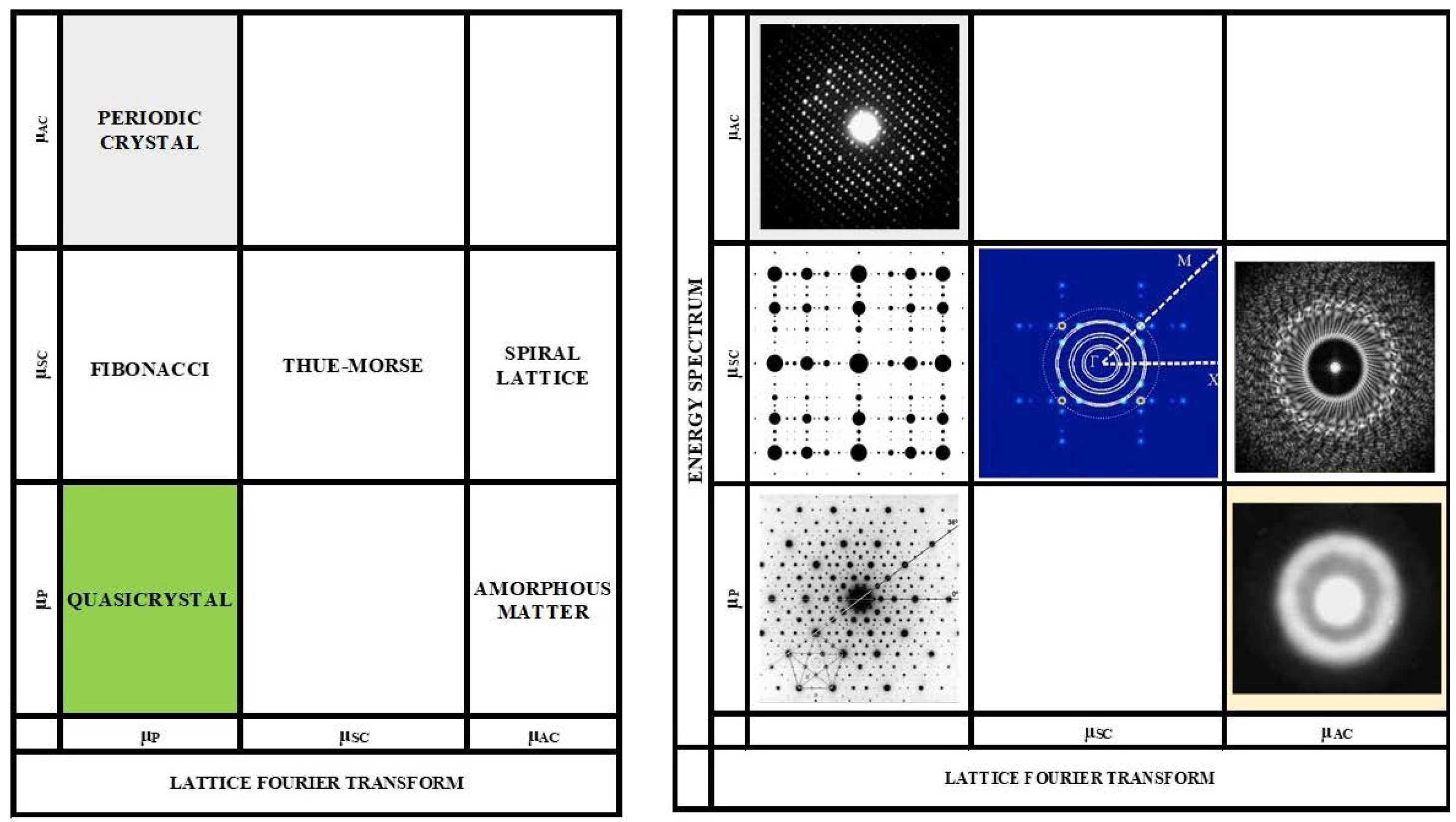
4. Aperiodic crystals spectral classification scheme

A mathematically convenient way to describe both the structure and the energy (or frequency) related properties of solids is provided by the use of measures, which are linear maps that associate a number to an appropriate function. A well known and widely used measure is the Lebesgue measure μ ( f ) ≡ ∫ f ( x ) d x , which is commonly used in integration of functions f ( x ) on the real numbers R [38]. From the view point of condensed matter physics there are two important measures one can consider when studying the properties of solid materials. For one thing, we have a measure related to the atomic density distribution Fourier transform, which discloses the main features of X-ray, electron or neutron diffraction patterns resulting from the spatial structure of the solid. On the other hand, we have a measure related to the energy (frequency) spectra of the system, respectively describing its electronic structure or the frequency distribution of the atomic vibrations in the case of the phonon spectrum.
In order to gain a deeper insight on the relationship between the structural order present in an aperiodic solid (as determined by its diffraction pattern) and its related transport properties, stemming from its energy and frequency spectra main features and the nature of its eigenstates, we will exploit the Lebesgue’s decomposition theorem, which states that any measure μ can be uniquely decomposed in terms of three kinds of spectral components (and mixtures of them), namely: pure point ( μ P ), absolutely continuous ( μ A C ) and singularly continuous ( μ S C ) spectra, in the form μ = μ P ∪ μ A C ∪ μ S C [3]. To this end, we introduce the spectral charts depicted in Figure 2, where we provide a graphical classification scheme of aperiodic systems based on the Lebesgue’s spectral components of their diffraction spectra (in abscissas) and their energy spectra (in ordinates), respectively. In this way, the old-fashioned classification scheme of solids based on the periodic-amorphous dichotomy is replaced by a much richer one [39,40].
In its upper left corner we have the periodic crystals exhibiting pure point Fourier spectra (discrete Bragg diffraction peaks) and an absolutely continuous energy spectrum (Bloch wave functions in allowed bands). In the lower right corner we have amorphous matter representatives, described in terms of uncorrelated random lattices, exhibiting an absolutely continuous Fourier spectrum (diffuse spectra) and a pure point energy spectrum (exponentially localized wave functions). In this context it is convenient to highlight that, although both random structures and aperiodically ordered arrangements lack strict translational symmetry, the absence of periodicity characteristic of aperiodic systems is not the same in nature as the complete lack of long-range order characteristic of amorphous matter. In fact, in aperiodic systems translational symmetry is usually replaced by other symmetry operations which amorphous matter does not possess. In the left lower corner of Figure 2 we locate QCs, and in its middle right panel we locate the cubic QCs, blending scale invariant global symmetry and classical 2-, 3-, 4-, or 6-fold rotation axes. For the sake of illustration, in the right panel of Figure 2 we display suitable examples of experimental diffraction patterns for several representatives; in its upper left corner we can see the typical pattern for a periodic crystal; in the middle left panel the calculated diffraction spectrum of a square Fibonacci lattice; in the left lower corner we show the electron diffraction pattern typical iQC along its 5-fold axis; in its lower right corner we have an amorphous matter representative exhibiting an absolutely continuous Fourier spectrum (diffuse spectra); and finally, in the middle right panel we show a representative diffraction image of a Vogel spiral [44].

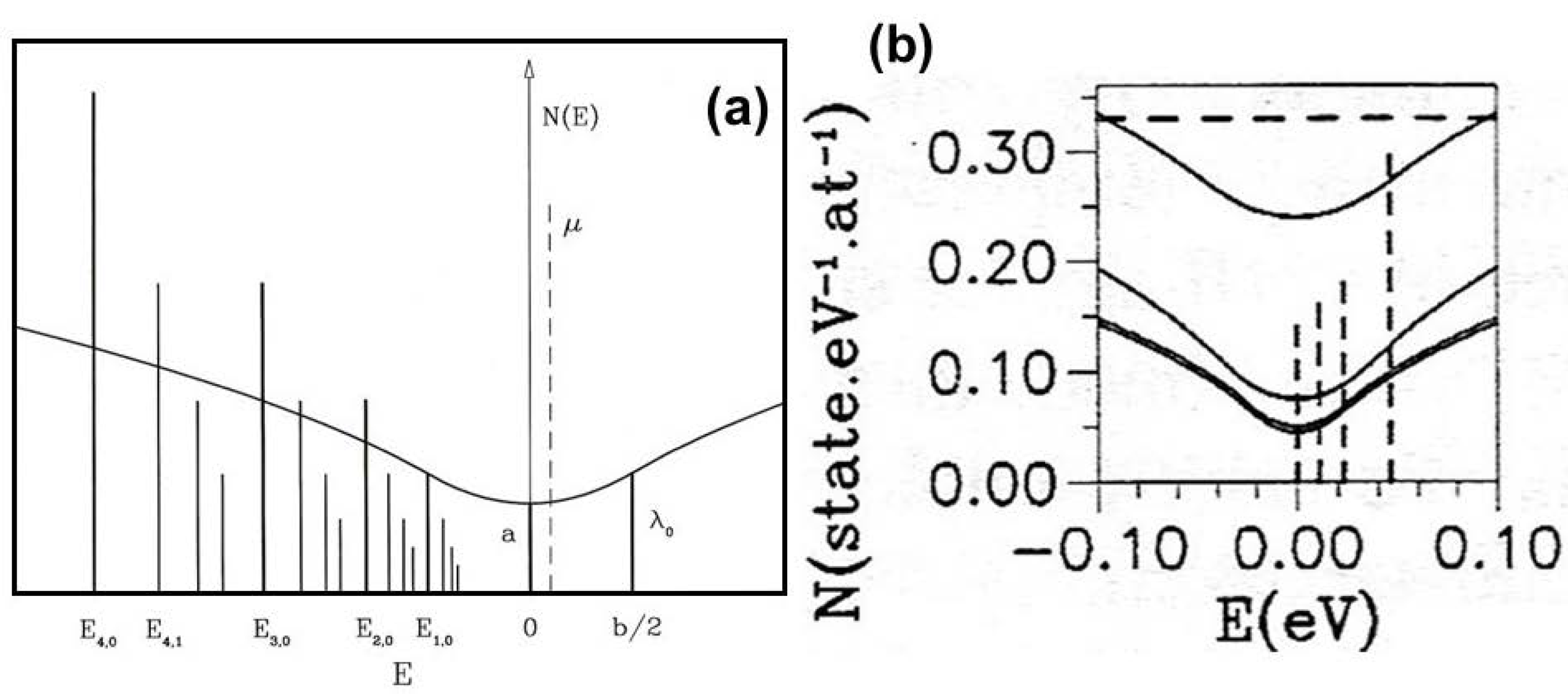
5. Intrinsic physical properties

In Table 1 we list a series of physical properties of both typical metallic compounds and iQCs. By comparing both columns we readily realize that iQCs have attributes which are quite different from those of common intermetallic compounds. These differences can be particularly appreciated by studying some basic transport properties, such as the electrical and thermal conductivity vs temperature curves (respectively shown in Figure 3 and Figure 5).
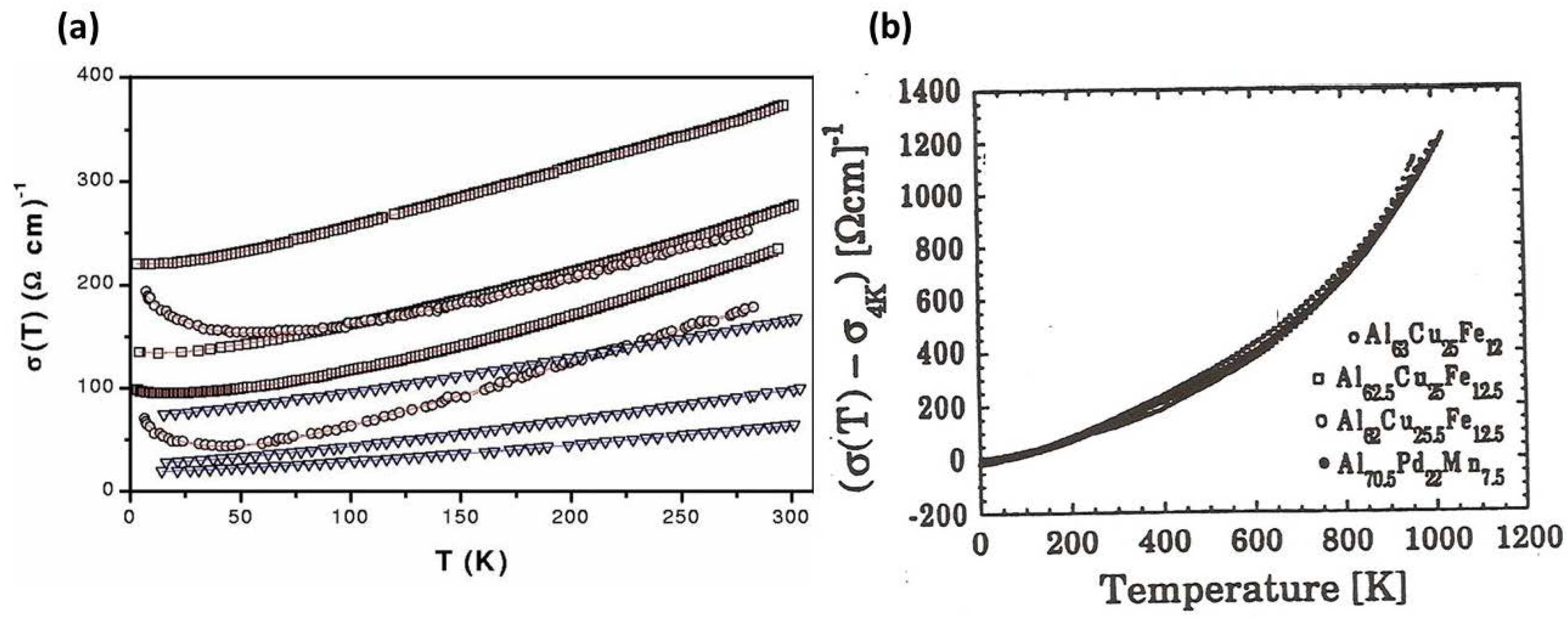
In Figure 3 we see the electrical conductivity σ ( T ) starts by taking low values which progressively increase with the temperature. In addition we observe several general trends in the σ ( T ) curves, namely:
  • Electrical conductivities [45] take unusually low values for alloys made of good metals (Figure 3a).
  • In most samples σ ( T ) steadily increases as the temperature increases up to the melting point (Figure 3b), at variance with usual metals.
  • The σ ( T ) curves are extremely sensitive to minor variations in the sample stoichiometry (Figure 3b).
  • The electrical residual resistivity at low temperatures increases when the structural order of the sample is improved by annealing, in contrast to the decrease in resistivity that usually accompanies removal of defects in common alloys (Matthiessen rule).
Most of these characteristic properties can be accounted for in terms of the expression (1) [47]:
σ ( T ) = ∫ 0 ∞ σ ( E ) − ∂ f ∂ E d E = e 2 V ∫ 0 ∞ N ( E ) D ( E ) − ∂ f ∂ E d E ,
where e is the elementary charge, V is the sample’s volume, N ( E ) measures the density of electronic states (DOS) close to the Fermi level, D ( E ) gives the diffusivity of these states, and f ( E , T ) is the Fermi-Dirac distribution function. The σ ( T ) curve is then determined by both the number of available electronic states close to the Fermi level and their diffusivity value, both magnitudes generally taking on quite small values in the case of iQCs. The low N ( E ) value can be explained by the high symmetry related to the icosahedral geometry, which leads to an enhancement of the diffraction effect by the atomic planes spatial distribution, which shifts the conduction electrons energies towards higher energy levels from the Fermi energy value, hence depleting the number of available electrons for electrical propagation, a process referred to as the opening of a QPO-related pseudogap (see Figure 4). In this regard, one realizes that the depth of the observed pseudogap clearly correlates with the quality of the long-range QPO present in the considered sample, being generally broader for ACs and systematically getting deeper and narrower with the structural perfection of QCs (see Figure 4b). Along with the small number of available states, most of them have also significantly low values of their transmission coefficients, which significantly reduce the resulting diffusivity coefficient values [48].
On the other hand, as we increase the temperature, both the available states in the DOS as well as their transmission coefficient values slightly enhance, leading to a progressive increment of the resulting electrical conductivity, mediated by the partial derivative factor in Eq.(1):
− ∂ f ∂ E = s e c h 2 x 2 ,
with x ≡ ( E − E F ) / k B T , where k B is the Boltzmann constant.
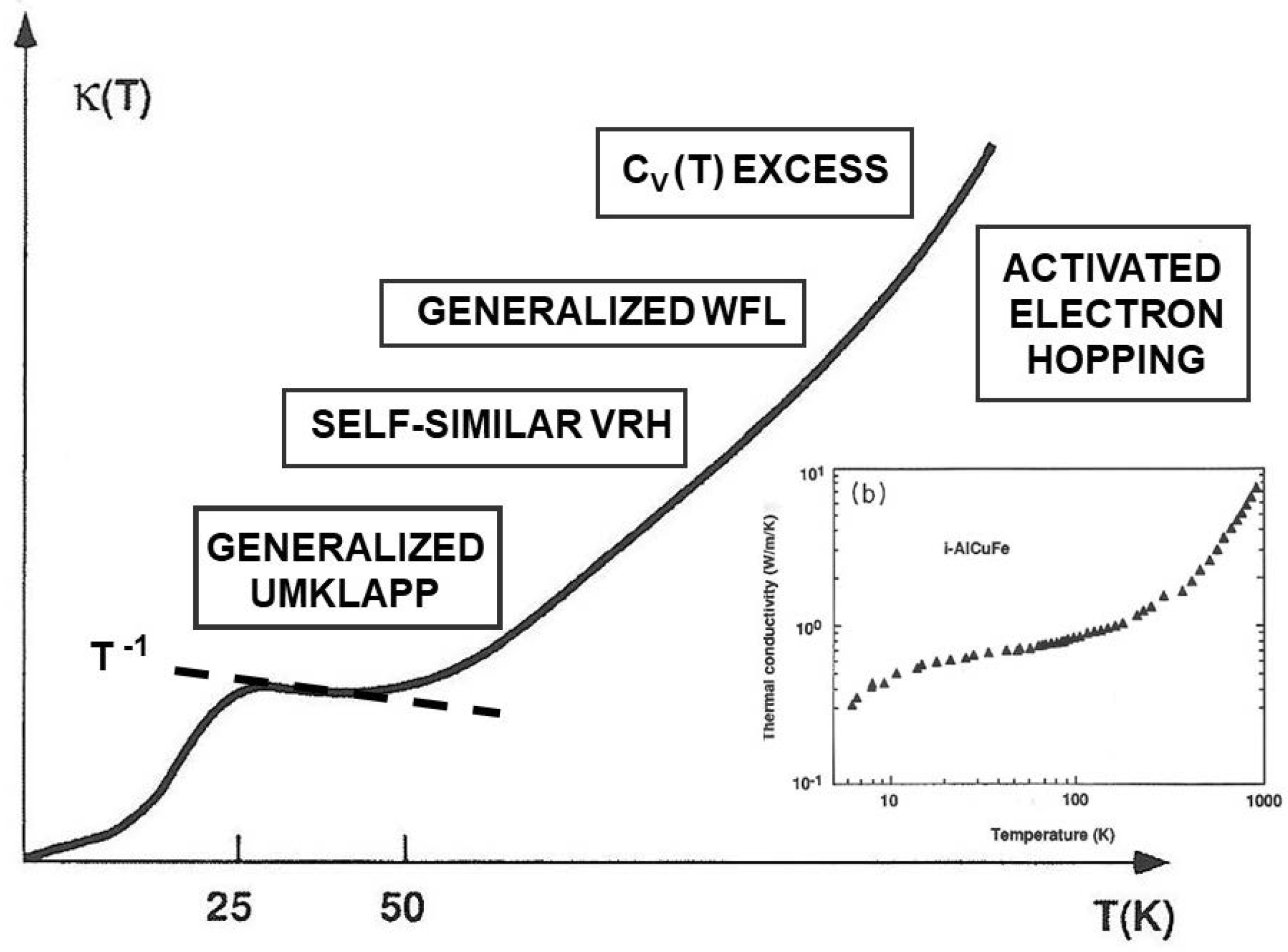
Preprints 87876 g005
Figure 5. (Main frame) Sketch depicting the main features of the thermal conductivity in iQCs over a broad temperature interval. Different physical processes taking place at different temperature ranges are indicated. (Inset) Measured thermal coefficient curve for an i-AlCuFe QC.[49]. (Reprinted figure with permission from Janot C, Conductivity in quasicrystals via hierarchically variable-range hopping, Phys. Rev. B 53 181-191 (1996) Copyright (1996) by the American Physical Society).
Figure 5. (Main frame) Sketch depicting the main features of the thermal conductivity in iQCs over a broad temperature interval. Different physical processes taking place at different temperature ranges are indicated. (Inset) Measured thermal coefficient curve for an i-AlCuFe QC.[49]. (Reprinted figure with permission from Janot C, Conductivity in quasicrystals via hierarchically variable-range hopping, Phys. Rev. B 53 181-191 (1996) Copyright (1996) by the American Physical Society).
Preprints 87876 g005
The thermal conductivity curve shown in Figure 5 also starts taking on extraordinarily small values at low temperature, comparable to those reported for typical thermal insulator materials of industrial interest. The main features of the κ ( T ) curve shown in Figure 5 can be explained in term of the expression [50]:
κ ( T ) = L 0 T σ ( T ) + v 2 τ 3 V ∫ 0 ω D ℏ ω D ( ω ) ∂ p ∂ T d ω ,
The first term in Eq.2, referred to as the Wiedemann-Franz’s law, expresses the contribution to the thermal conductivity due to the electrons, which is in turn proportional to the Lorenz’s number ( 1.5 − 2.4 × 10 − 8 V 2 K − 2 ) and to their electrical conductivity. As we saw σ ( T ) is really small in the regime of low temperatures, accounting for the remarkably low κ values plotted in Figure 5. The second term in Eq.2 gives the contribution due to lattice phonons oscillations in terms of the vibrational DOS D ( ω ) and the Planck distribution function p ( ω , T ) , where v is the sound velocity of the considered material, and τ ( ω , T ) is the average time between heat current degrading collisions involving phonons at a given temperature (the so-called phonon relaxation-time). In the low frequency regime, the specific heat contribution due to the phonon propagation is also reduced by the high fragmentation of the phonon spectrum due to the hierarchical structure of the quasiperiodic lattice, leading to a dense folding of the Brillouin zone [51].
The low thermal conductivity of QCs can be understood in terms of two main facts. For one thing, heat propagates mainly by means of phonons, since the charge carrier concentration is severely reduced due to the presence of a pseudogap around the Fermi level. On the other hand, reciprocal space has a nearly fractal pattern in QCs, so that the transfer of momentum to the lattice is not bounded below, and the thermal current intensity is strongly reduced due to an enhancement of phonon-phonon scattering processes occurring at all scales in the reciprocal space.
The magnetism of iQCs has been extensively studied during the past quarter-century to discover the first QP arrangement of magnetic moments. To this end, iQCs containing rare-earth (R) elements such as ZnMgR, CdMgR, and CdR have arisen a lot of attention, and recently the metastable golden-based Au65Ga20(Gd, Tb)15 iQCs have been reported to exhibit a ferromagnetic transition at T T C =23K (16K) [52,53], though the results could not be regarded as conclusive due to the presence of a considerable amount of magnetic secondary 1/1 AC phase. Indeed, their magnetic susceptibilities commonly display spin-freezing phenomena. Quite remarkably, the discovery of ferromagnetic AuGaDy iQCs with high phase purity and tunable composition has been recently reported [54,55].
To gain further insight into the ferromagnetic transitions of i-Au65Ga20Tb15 and i-Au65Ga20Gd15, R. Tamura and co-workers have additionally performed neutron diffraction experiments on both iQCs, achieving the first direct observation of long-range magnetic order in QCs via this experimental technique. Therefore, Au-Ga-R IQCs (with R = Gd, Tb) are the most isotropically ordered magnets among all materials discovered to date.
Superconductivity had never been reported for QCs, except for one example of a metastable iQC phase of Al-Zn-Mg, which demonstrated bulk superconductivity at T T C ≃ 0.05 K [56]. Some theoretical studies suggested that the quasicrystalline superconductivity exhibits unconventional behavior such as the nonzero sum of the momenta of Cooper pair electrons [57] and intrinsic vortex pinning not by impurities and defects [58]. Recently, it has been reported that some rare-earth bearing iQCs exhibit an unconventional form of superconductivity with critical temperatures in the range 10-20K.
An abrupt change in certain physical properties in a series of compounds may indicate an abrupt change in the bond type (e.g., from mainly metallic to mainly covalent). For the sake of illustration, broadly speaking one would expect relatively low melting points in molecular solids. Thus, when studying the melting temperatures of several i-QCs based on the three known cluster types (Bergman, Mackay and Tsai), the relatively high melting points observed in Al-based QCs may be indicating stronger than expected bonds among neighboring clusters. Alternatively, one may also think of the hierarchical spatial arrangement of clusters as precluding an easy separation from each other, even if they interact weakly among them. In this regard, it is interesting to note that the melting point of the Al65Cu20Fe15 cubic approximant alloy is Tm = 1281 K, about 12 % higher than that of the related icosahedral phase. This may be indicative of long-range QPO effects in QCs.

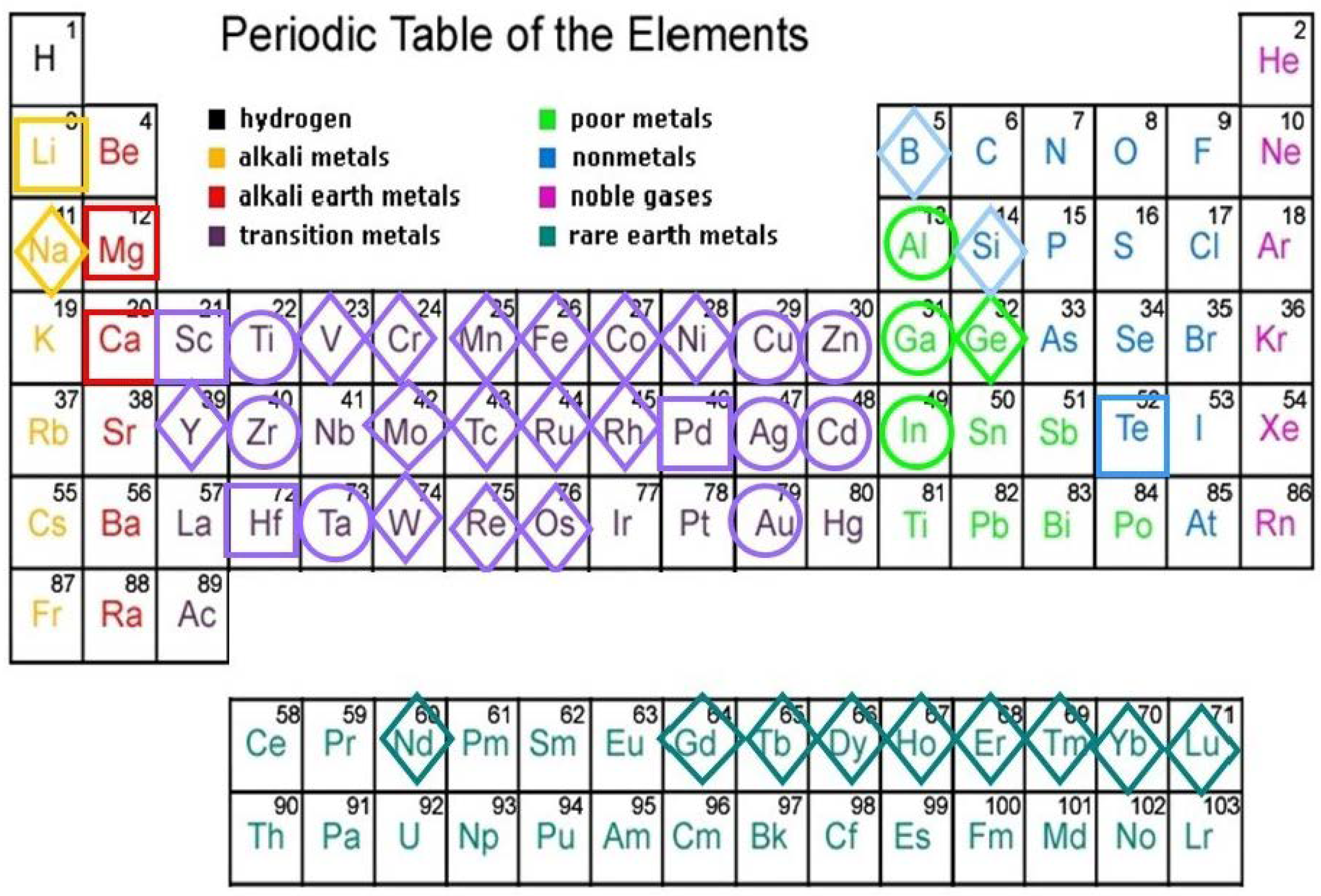
6. Chemical bonding in QCs

Elements composing thermodynamically stable QCs found to date belong to the broad chemical family of metals, including representatives from alkali, alkaline earth, transition metals, or rare-earth blocks (see Figure 6). By inspecting Figure 6 we also see that most main forming elements cluster in groups 11-13 and 4, whereas minority elements are mainly found among transition metals or rare-earth elements. Thus, most metallic atoms are able to participate in the formation of quasicrystalline phases when one adopts the proper stoichiometric ratios. Indeed, as a matter of fact all of the stable QCs discovered to date have very narrow composition ranges in their respective phase diagrams, indicating that the alloy chemistry strongly affects the stability of these compounds.
In fact, whenever there are wave functions overlapping among contiguous atoms in a solid lattice, the possibility of charge delocalization (i.e., extended character of the electrons) naturally emerges. In turn, the electronic itineracy in a long-range ordered potential is at the basis of the Brillouin zone concept in solid state physics, which arises from diffraction and interference processes of electronic wave functions with arrangements of atomic planes (either periodically or quasiperiodically stacked). Indeed, it is the long-range order (not exclusively periodic one) which allows for a truly extended nature of charge carriers throughout a solid via resonant band formation. Accordingly, it seems reasonable to expect that the very nature of chemical bonding in QCs could play a significant role in the onset of most of their distinctive physical properties, which ultimately will depend on fine details of the electronic structure, including the relative positions of the atomic levels, the size of the atoms, the crystal structure, and the number of valence electrons. These results inspired the search for semiconducting QCs in Al-TM i-QCs. In this way, the possible existence of semiconducting approximants and even band insulators in Al-based QCs was put forward. These phases should exhibit a QP chemical bond network extending over long distances, which could only be established on an underlying high structural QP arrangement of atoms throughout the space. Now, since the main building blocks of i-QCs are assumed to be hierarchically arranged atomic clusters one must consider bonds among atoms inside clusters along with cluster-cluster interactions giving rise to the extended chemical network.
Alternatively, the non-metallic behavior of QCs could also be understood as due to the QP arrangement of atoms throughout the space, which naturally leads to the formation of a deep pseudogap near the Fermi energy along with the existence of a significant number of electronic states exhibiting very low diffusion coefficients. To this end, one must take into account the existence of a richer behavior for electronic states in QCs: on the one hand, we have extended electronic wave functions able to open a pseudogap close to the Fermi level via diffraction and interference processes with quasiperiodically stacked arrangements of atomic planes; on the other hand, we have localized electronic states as well, stemming from resonant effects involving nested atomic clusters exhibiting self-similar geometries at different scales. This polyvalent transmission characteristic of electronic states in solids endowed with self-similar invariance symmetry is at the root of the so-called critical nature of these wave functions, which belong to fractal-like energy (vibration) spectra in the ideal case. Thus, critical electronic states embrace a diverse set of wave functions exhibiting a broad palette of possible diffusivity values, ranging from highly conductive transparent states to highly resistive, almost localized ones [45].

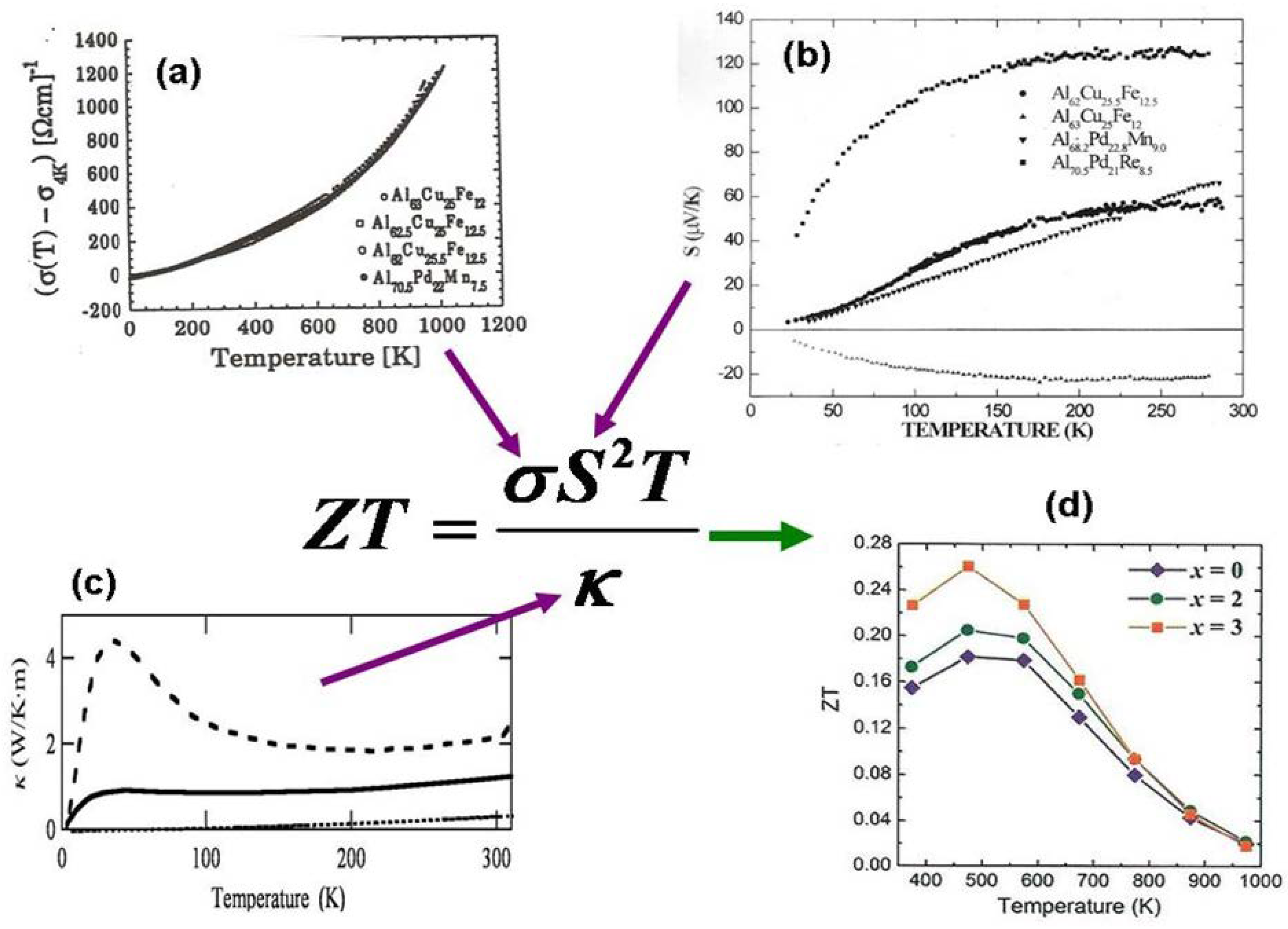
7. Potential and marketed applications

In order to be of technological relevance a material must be easy to produce in the desired shape (say, bulk, powder or coating), stable in working conditions, environmentally friendly, low cost and non-toxic. In addition, a novel material must benchmark already existing competitive materials for any given specific application. It is certainly difficult to fulfil all these criteria at once and, consequently, only a few new materials ultimately find a successful route to the market.
Quasicrystals were discovered when technology was attaining very important progress in many significant fields. Accordingly, it is easy to understand that it is not a simple task to readily identify a relatively important application for these compounds. Notwithstanding this, as early as 1993 several tribological properties were successfully implemented on the basis of several specific properties of QCs which are amenable to be properly combined to devise smart materials blending properties that usually exclude each other in more usual materials of industrial interest. For instance, QCs’ low κ ( T ) and relatively high melting temperature might make them useful as thermal barriers, and combined with their relatively high S(T) might make them useful as thermoelectric materials, although their low σ ( T ) represents a disadvantage (see Figure 7). In addition, QCs’ high corrosion resistance makes them useful as coatings, reinforcement precipitates in combination with marging steels or light alloys (Al and Mg based), and composites manufacture with QC powder grains (3D printing). In addition, the absence of Drude peak favours their possible use as solar energy absorbers or for energy harvesting.
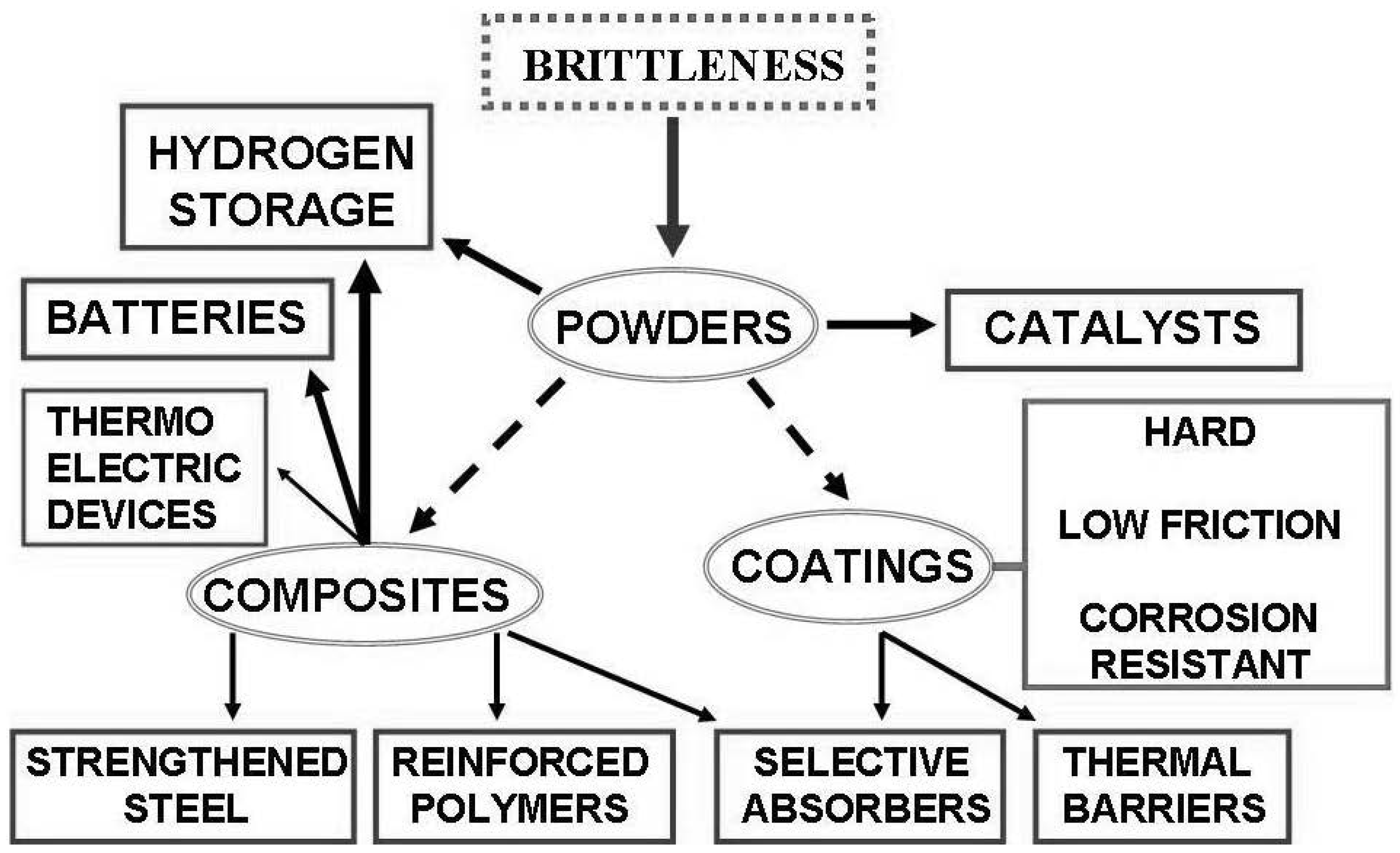
Even though a major drawback of macroscopically sized QCs is they brittleness at low and intermediate temperatures, a brittle-to-ductile transition, driven by a sample size reduction, was recently reported for i-AlPdMn QCs at room temperature, the critical size being located around 500 − 350 nm [59]. This finding certainly opens up the possible application of nano-sized QCs in the design of small scale devices. Conversely, QCs are not very useful as bulk materials at macroscopic scale due to their characteristic brittleness, which restricts their use as structural materials. Instead, they can be easily crashed into powders in order to fruitfully be employed as surface coatings or as composites. In such a case, the mechanical integrity is supplied by the substrate or the matrix, respectively, while the QC can be used to improve required functions by exploiting their specific properties, hence promoting their applications as functional materials. The brittle nature of QCs can also be exploited to get fine-grained particles of interest for surface catalysis or hydrogen storage. The related technological niches are sketched in Figure 8. These applications, which include hard-low-friction-corrosion-resistant coatings, thermal barriers, solar selective absorbers, composites, catalysts, and hydrogen storage materials, have been systematically demonstrated in laboratories, and some of them have even reached marketplace. Also, the potential applications of QCs include rechargeable batteries, photovoltaic solar cells, thermal emission control, and thermophotovoltaic devices.
Despite their enhanced performance, QCs and ACs did not reach so far an outstanding level of performance that would justify their substitution to conventional catalysts that are in use in chemistry plants. The same holds true for precipitation-hardened alloys, with the major exception of maraging steels [60]. It seems still too early to know if the discovery of long range ferromagnetism in AuGaDy QCs will lead to magnets with very low coercitivity as can be expected from the very high symmetry of the lattice. As well, the occurrence of superconductivity in AlZnMg iQCs opens an avenue for another type of potential high-tech applications.

8. Conclusions

What is the role of long-range QPO in the emergence of specific properties of QCs? A number of physico-chemical properties of QCs and their related approximant phases exhibit similar features (low adhesion energy, corrosion resistance, surface hardness, temperature dependence of the electrical and thermal transport coefficients, low electrical and thermal conductivity values) as compared to their neighboring compounds in the phase diagrams displaying typically metallic physical and chemical properties (see Table 1). Most of these peculiar features can be traced back to a significantly low value of the electronic density of states (DOS) near the Fermi level in both QCs and ACs, along with the characteristic spatial distribution of the electronic states in these materials, which are referred to as critical eigenstates. In particular, regarding their magnetic properties, unconventional spatially extended Cooper pairs have been recently observed to form under weak-coupling conditions; the sum of the momenta of the Cooper pair electrons was nonzero, in contrast to the zero total momenta of the Cooper pair in conventional BCS superconductivity. Unlike any other known superconductors in periodic systems, this finding opens up a new research field to investigate unprecedented unique superconducting states, spatially inhomogeneous on any length scale reflecting the self-similarity of the quasiperiodic structure [61].
Forty years after the initial publication by Shechtman and his colleagues, and a Nobel Prize bestowed on him, it turns out that QCs have made a huge impact on fundamental science, but not yet in technology. They not only forced the scientific community to revise its paradigm about order in condensed matter, but also shed new light on many aspects of metal physics: this is where their real usefulness has to be looked upon [62]. Regarding practical applications, only three, at most four, inventions using them came successfully to the market. All of them are in the area of composites or in association with other materials: steelss, polymers, and oil. Per se, QCs made of metals have not yet demonstrated economic usefulness because they form in a very narrow composition range and they are brittle. Yet, once associated with another material, or if (at least one of) the dimensions is sufficiently reduced, they may prove some utility.
We have found just four different symmetry classes among quasicrystals to date, namely, icosahedral, decagonal, dodecagonal and octagonal ones. Is that all? Certainly, one can think of many more possible arrangements of matter giving rise to purely discrete diffraction patterns and exhibiting beautiful and subtle spatial symmetries [17,31].
QCs display long-range orderings of atoms through the space which can be properly described in terms of a systematic application of inflation symmetry operations. Indeed, the presence of the scale invariance symmetry is essential to obtain a QP translation order [21,23]. This symmetry had not been previously considered in classical crystallography, and it is directly related to the emergence of self-similar, hierarchical patterns embodying atomic cluster aggregates. Therefore, from a structural viewpoint QCs can be regarded as self-similar arrays of atoms, where the translation symmetry, characteristic of periodic crystals, is replaced by a scale invariance one, with scale factors given by irrational numbers. In summary, the three classes of aperiodic crystals identified up to now share a common feature, namely, all of them exhibit order without translational symmetry [22].
A growing number of experimental and numerical simulation evidences now suggest that a main factor determining the remarkable properties of QCs is related to physical-chemical aspects involving nearest and next-nearest atomic neighbors, thereby highlighting the important role played by the chemical bonding in the emergence of the characteristic physical properties of QCs.
Thus, rather than trying to explain the specific properties of QCs in terms of the conceptual schemes originally introduced to describe classical periodic solids (e.g., in terms of metallic, semimetallic, semiconductor, or insulator behaviors), it may be advisable to introduce broader perspectives able to properly account for the main features appearing in their electronic structure.

Acknowledgments

This article is dedicated to the memory of Profs. Esther Belin-Ferré, Patricia A. Thiel, An Pang Tsai, and Manuel Torres, with my heartfelt gratitude for the continued interest in my research activities, valuable advice and motivating support they provided me during the time I had the fortune to share with them. I am gratefully indebted to Professors Jose Luis Aragón, Marc de Boissieu, Jean Marie Dubois, Kaoru Kimura, Uichiro Mizutani, Gerardo G. Naumis, Juan M. Pérez-Mato, Luis Elcoro, and Victor R. Velasco for their interest in my research work during the last 25 years. Their illuminating advice has significantly contributed to guide my scientific work in the science of QCs. It is a pleasure to thank Profs. Luca Bindi, Luca Dal Negro, Didier Mayou, and Tsunehiro Takeuchi for inspiring conversations, and to Profs. Claire Berger and Luigi Moretti for sharing with me very useful materials. I warmly thank M. Victoria Hernández for a critical reading of the manuscript.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Shechtman D, Blech I, Gratias D, Cahn J W, Metallic phase with long-range orientational order and no translation symmetry, 1984 Phys. Rev. Lett. 53, 1951-1954. [CrossRef]
  2. Steurer W, Deloudi S, Crystallography of Quasicrystals - Concepts, Methods and Structures, Springer Series in Materials Science 126 (Springer Verlag, Berlin, 2009).
  3. Baake M, Grimm U, Aperiodic Order I: A Mathematical Invitation, Encyclopedia of Mathematics and Its Applications 149 (Cambridge University Press, Cambridge, 2013).
  4. Levine D, Steinhardt P J, Quasicrystals: A new class of ordered structures, 1984 Phys. Rev. Lett. 53, 2477-2480. [CrossRef]
  5. Bradley A J, Goldschmidt H J, An X-ray study of slowly cooled iron-copper-aluminum alloy: Part II. Alloys rich in aluminum, 1939 J. Inst. Metals 65, 403-418.
  6. Raghavan V, Al-Cu-Fe (Iron-Copper-Aluminum), 2005 J. Phase Eq. Diffusion 26, 59-64. [CrossRef]
  7. Tsai A P, Inoue A, Masumoto T, A stable quasicrystal in Al-Cu-Fe system, 1987 Jpn. J. Appl. Phys. 26, L1505-L1507. [CrossRef]
  8. Hardy H K, Silcock J M, The phase sections at 500 C and 350 C of aluminium-rich aluminium-copper-lithium alloys, 1956 J. Inst. Metals 84, 423.
  9. Dubost B, Lang J M, Tanaka M, Sainfort P, Audier M, Large AlCuLi single quasicrystals with triacontahedral solidification morphology, 1986 Nature (London) 324, 48-50. [CrossRef]
  10. Bindi L, Parisi G, Quasicrystals: fragments of history and future outlooks, 2023 Rend. Fis. Acc. Lincei 31, 9-17. [CrossRef]
  11. Bindi L, Steinhardt P J, Yao N, Lu P J, Natural quasicrystals, 2009 Science 324, 1306-1309. [CrossRef]
  12. Bindi L, Steinhardt P J, Yao N, Lu P J, Icosahedrite, Al63Cu24Fe13, the first natural quasicrystal, 2011Am. Mineral. 96, 928-931. Am. Mineral. [CrossRef]
  13. Bindi L, Yao N, Lin C, Hollister L S, Andronicos C L, Distler V V, Eddy M P, Kostin A, Kryachko V, MacPherson G J, et al., Natural quasicrystal with decagonal symmetry, 2015 Sci. Rep. 9111; 5. [CrossRef]
  14. Bindi L, Yao N, Lin C, Hollister L S, Andronicos C L, Distler V V, Eddy M P, Kostin A, Kryachko V, MacPherson G J, Decagonite, Al71Ni24Fe5, a quasicrystal with decagonal symmetry from the Khatyrka CV3 carbonaceous chondrite, 2015 Am. Mineral.100, 2340-2343. Am. Mineral. [CrossRef]
  15. Cahn J W, A celebration of the pioneering work on quasicrystals in France and the expansion of crystallography, 2014 C. R. Physique 15, e1-e5. [CrossRef]
  16. Structure of Materials: An Introduction to Crystallography, Diffraction, and Symmetry de Graef M, McHenry M E, 2nd Ed. (Cambridge University Press, 2012).
  17. Steurer W and Deloudi S, Fascinating quasicrystals, 2008 Acta Cryst. A64, 1.
  18. Gilead A, The philosophical significance of Alan Mackay’s theoretical discovery of quasicrystals, 2017 Struct. Chem. 28, 249-256. [CrossRef]
  19. Hargittai I, Forty years of quasicrystals: a bumpy road to triumph, 2022 Struct. Chem. 33, 311-314. [CrossRef]
  20. Mackay A L, Crystallography and the Penrose pattern, 1982 Physica A 114, 609-613. [CrossRef]
  21. Janssen T, Chapuis G, de Boissieu M, Aperiodic Crystals: From Modulated Phases to Quasicrystals (Oxford University Press, 2nd. Ed., Oxford, 2018).
  22. van Smaalen S, Modulated Crystal Structures, in Handbook of Solid State Chemistry (Dronskowski R, S. Kikkawa S, Stein A, 2017).
  23. Maciá-Barber E, Quasicrystals: Fundamentals and Applications (CRC Taylor & Francis, Boca Raton, 2021).
  24. International Union of Crystallography Report of the Executive Committee for 1991, 1992 Acta Cryst. A 48, 922. Available online: https://www.iucr.org/iucr/commissions/aperiodic-crystals (accessed on 11 May 2023).
  25. Lifshitz R, Quasicrystals: A matter of definition, 2003 Foundations of Physics 33, 1703-17011. [CrossRef]
  26. de Boissieu M, Boudard M, Ishimasa T, Elkaim E, Laurait J P, Letoublon A, Audier M, Duneau M, Reversible transformation between an icosahedral Al-Pd-Mn phase and a modulated structure of cubic symmetry, 1998 Philos. Mag. A78, 305-326.
  27. Paredes R, Aragón J L, Barrio R A, Nonperiodic hexagonal square-triangle tilings, 1998 Phys. Rev. B58, 11990-11995. [CrossRef]
  28. Liftshitz R, What is a crystal?, 2007 Z Kristallogr. 222, 313-317. [CrossRef]
  29. Dyson F, Birds and frogs, 2009 Notices of AMS 56 (2), 212-223.
  30. Elcoro L, Pérez-Mato J M, Cubic superspace symmetry and inflation rules in metastable MgAl alloy, 1999 Eur. J. Phys. B 7, 85-89. [CrossRef]
  31. Janner A, Which symmetry will an ideal quasicrystal admit?, 1991 Acta Cryst. A 47, 577-590. [CrossRef]
  32. Janner A, Towards a classification of icosahedral viruses in terms of indexed polyhedra, 2006 Acta Cryst. A 62, 319-330. [CrossRef]
  33. Bindi L, Pham J, Steinhardt P J, Previously unknown quasicrystal periodic approximant found in space, 2018 Sci. Rep. 8, 16271. [CrossRef]
  34. Bergman G, Waugh J L T, Pauling L, Crystal structure of the intermetallic compound Mg32(Al,Zn)49 and related phases, 1952 Nature (London)169, 1057; The crystal structure of the metallic phase Mg32(Al, Zn)49, 1957 Acta Cryst. 10, 254. Acta Cryst. [CrossRef]
  35. Elcoro L, Etxebarria I, Pérez-Mato J M, Modulation parameters in incommensurate modulated structures with inflation symmetry, 2000 J. Phys.: Condens. Matter 12, 841-848. [CrossRef]
  36. Maciá E, Aperiodic crystals in biology, 2022 J. Phys.: Condens. Matter 34, 123001 24pp.
  37. Maciá E, Biological hypercrystals, 2023 J. Phys.: Conf. Ser. 2461, 012006. [CrossRef]
  38. Grimm U, Aperiodic crystals and beyond, 2015 Acta Cryst. B71, 258-274. [CrossRef]
  39. Maciá E, The role of aperiodic order in science and technlogy, 2006 Rep. Prog. Phys. 69, 397-441. [CrossRef]
  40. Maciá-Barber E, Aperiodic Structures in Condensed Matter (CRC Taylor & Francis, Boca Raton, 2009).
  41. Lifshitz R, The square Fibonacci tiling, 2002 J. Alloys Comp. 342, 186-190. [CrossRef]
  42. Calvayrac Y, Quivy A, Bessière M, Lefebvre S, Cornier-Quinquandon M, Gratias D, Icosahedral AlCuFe alloys: towards ideal quasicrystals, 1990 J. de Physique 51, 417-431.
  43. Moretti L, Mocella V, Two-dimensional photonic aperiodic crystals based on Thue-Morse sequence, 2007 Opt. Express 15, 15314-23. [CrossRef]
  44. Dal Negro L, Lawrence J, Trevino J, Analytical light scattering and orbital angular momentum spectra of arbitrary Vogel spirals, 2012 Opt. Express 20, 18209. [CrossRef]
  45. Maciá E, Universal features in the electrical conductivity of icosahedral Al-transition-metal quasicrystals, 2002 Phys. Rev. B 66, 174203. [CrossRef]
  46. Mayou D, Berger C, Cyrot-Lackmann F, Klein T, Lanco P, Evidence for unconventional electronic transport in quasicrystals, 1993 Phys. Rev. Lett. 70, 3915-3918. [CrossRef]
  47. Maciá E, Modeling the electrical conductivity of icosahedral quasicrystals, 2000 Phys. Rev. B 61, 8771-8777. [CrossRef]
  48. Maciá E, Spectral classification of one-dimensional binary aperiodic crystals: An algebraic approach, 2017 Ann. Phys. 529, 1700079 (17pp). [CrossRef]
  49. Perrot A, Dubois J M, Heat diffusivity in quasicrystals and related alloys, 1993 Ann. Chim. Fr. 18, 501-511.
  50. Maciá E, Thermal conductivity of one-dimensional Fibonacci quasicrystals, 2000 Phys. Rev. B 61, 6645-6654. [CrossRef]
  51. Maciá E, de Boissieu M, Properties of CMAs: theory and experiments, in Complex Metallic Alloys Fundamentals and Applications (Wiley-VCH Verlag, Weinheim 2011).
  52. Tamura R, Ishikawa A, Suzuki S, Kotajima T, Tanaka Y, Seki T, Shibata N, Yamada T, Fujii T, Wang Ch W, Avdeev M, Nawa K, Okuyama D, Sato T J, Experimental Observation of Long-Range Magnetic Order in Icosahedral Quasicrystals, 2021 J. Am. Chem. Soc. 143, 19938-19944. [CrossRef]
  53. Shiino T, Gebresenbut G H, Pay Gómez C, Häusermann U, Nordblad P, Rydh A, Mathieu R, Examination of the critical behavior and magnetocaloric effect of the ferromagnetic Gd-Au-Si quasicrystal approximants, 2022 Phys. Rev. B 106, 174405. [CrossRef]
  54. Takeuchi R, Labib F, Tsugawa T, Akai Y, Ishikawa A, Suzuki S, Fujii T, Tamura R, High Phase-Purity and Composition-Tunable Ferromagnetic Icosahedral Quasicrystal, 2023 Phys. Rev. Lett. 130, 176701. [CrossRef]
  55. Sato N K, Ishimasa T, Deguchi K, Imura K, Effects of Electron Correlation and Geometrical Frustration on Magnetism of Icosahedral Quasicrystals and Approximants - An Attempt to Bridge the Gap between Quasicrystals and Heavy Fermions, 2022 JPSJ 91, 072001. [CrossRef]
  56. Kamiya K, Takeuchi T, Kabeya N, Wada N, Ishimasa T, Ochiai A, Deguchi K, Imura K, Sato N K, Discovery of superconductivity in quasicrystal, 2018 Nat. Comm. 9, 154. [CrossRef]
  57. Sakai S, Takemori N, Koga A, Arita R, Superconductivity on a quasiperiodic lattice: extended-to-localized crossover of Cooper pairs, 2017 Phys. Rev. B 95, 024509.
  58. Nagai Y, Intrinsic vortex pinning in superconducting quasicrystals, 2022 Phys. Rev. B 106, 064506. [CrossRef]
  59. Zou Y, Kuczera P, Sologubenko A, Sumigawa T, Kitamura T, Steurer W, Spolenak R, Superior room-temperature ductility of typically brittle quasicrystals at small sizes, 2016 Nature Commun. 7, 12261 (7pp). [CrossRef]
  60. Dubois J M, Potential and marketed applications of quasicrystalline alloys at room temperature or above, 2023 Rendiconti Lincei. Scienze Fisiche e Naturali 34 Issue 3, 689-702. [CrossRef]
  61. Tokumoto Y, Hamano K, Nakagawa S, Kamimura Y, Suzuki S, Tamura R, Edagawa K. [CrossRef]
  62. Dubois J M, Useful Quasicrystals (World Scientific, Singapore 2005).
1
Daniel Shechtman, 70th Birthday Celebration Symposium, 27 July 2011, Iowa State University, Ames (USA).
2
Icosahedrite was found in a rock within a meteorite collected from Khatyrka region of the Koryak mountains in the Chukotka oblast in the northeastern part of the Kamchatka peninsula (Russia), and deposited in the Mineralogical Collection of the Museo di Storia Naturale, Università di Firenze, Italy (catalogue number 46407/G) [11,12]. Decagonite was also identified in ∼ 60 μ m sized grains belonging to the Khatyrka meteorite, and named by the IMA (No. 2015-017) [13,14].
3
With the notable exception of A. Mackay, see below.
4
Alan L. Mackay was awarded the 2010 Oliver E. Buckley Condensed Matter Prize from the American Physical Society for his "pioneering contributions to the theory of quasicrystals, including the prediction of their diffraction pattern".
5
https://dictionary.iucr.org/Quasicrystal, last accessed 6 September 2023.
6
The first known mineral AC to decagonite was found in fragments from Khatyrka meteorite. This approximant, with chemical formula Al59Ni34Fe7, does not correspond to any previously recognized synthetic or natural phase. This mineral was approved by the IMA (No. 2018-038) and officially named proxidecagonite [33].
Preprints 87876 g001
Figure 1. Aperiodic crystals tentative classification attending to their underlying translational (T) or scale invariance (S) symmetries, along with their point group rotational symmetries. See details in the text.
Figure 1. Aperiodic crystals tentative classification attending to their underlying translational (T) or scale invariance (S) symmetries, along with their point group rotational symmetries. See details in the text.
Preprints 87876 g001
Preprints 87876 g002
Figure 2. (Left panel) Spectral classification chart showing the location of QCs in the aperiodic crystals landscape. (Right panel) Illustrative diffraction patterns in the spectral classification chart. (a) a typical periodic crystal, (b) square Fibonacci lattice (representative of the cubic QCs class) [41], (c) AlMn iQC [42], (d) Thue-Morse square lattice [43], (e) a Vogel spiral [44], (f) a representative amorphous sample.
Figure 2. (Left panel) Spectral classification chart showing the location of QCs in the aperiodic crystals landscape. (Right panel) Illustrative diffraction patterns in the spectral classification chart. (a) a typical periodic crystal, (b) square Fibonacci lattice (representative of the cubic QCs class) [41], (c) AlMn iQC [42], (d) Thue-Morse square lattice [43], (e) a Vogel spiral [44], (f) a representative amorphous sample.
Preprints 87876 g002
Preprints 87876 g003
Figure 3. (a) Room temperature electrical resistivity σ ( T ) values of QCs belonging to different alloy systems [45]. (b) The temperature dependence of electrical resistivity of representative Al-based iQCs is compared up to their respective melting points [46]. (Data files courtesy of Claire Berger).
Figure 3. (a) Room temperature electrical resistivity σ ( T ) values of QCs belonging to different alloy systems [45]. (b) The temperature dependence of electrical resistivity of representative Al-based iQCs is compared up to their respective melting points [46]. (Data files courtesy of Claire Berger).
Preprints 87876 g003
Preprints 87876 g004
Figure 4. (a) Diagram showing the main contributions to the electronic structure of iQCs close to the Fermi energy μ . (b) DOS structure around the Fermi energy. (Reprinted figures with permission from Maciá E, Modeling the electrical conductivity of icosahedral quasicrystals, Phys. Rev. B 618771-8777 (2000). Copyright (2000) by the American Physical Society) [47].
Figure 4. (a) Diagram showing the main contributions to the electronic structure of iQCs close to the Fermi energy μ . (b) DOS structure around the Fermi energy. (Reprinted figures with permission from Maciá E, Modeling the electrical conductivity of icosahedral quasicrystals, Phys. Rev. B 618771-8777 (2000). Copyright (2000) by the American Physical Society) [47].
Preprints 87876 g004
Preprints 87876 g006
Figure 6. Chemical elements found in thermodynamically stable QC alloys. Main forming elements ( A l , I n , T i , Z r , Z n , C d , C u , A g , A u ) are circled. The second major constituents are squared. Minor constituents are framed within a diamond.
Figure 6. Chemical elements found in thermodynamically stable QC alloys. Main forming elements ( A l , I n , T i , Z r , Z n , C d , C u , A g , A u ) are circled. The second major constituents are squared. Minor constituents are framed within a diamond.
Preprints 87876 g006
Preprints 87876 g007
Figure 7. Sketch showing the role of the different transport coefficients in the thermoelectric figure of merit (ZT) for diverse iQCs.
Figure 7. Sketch showing the role of the different transport coefficients in the thermoelectric figure of merit (ZT) for diverse iQCs.
Preprints 87876 g007
Preprints 87876 g008
Figure 8. Diagram showing the possible niches of application (boxes) of materials based on quasicrystalline powders, composites and coatings (ovals).
Figure 8. Diagram showing the possible niches of application (boxes) of materials based on quasicrystalline powders, composites and coatings (ovals).
Preprints 87876 g008
Table 1. Comparison between the physical properties of intermetallic QCs versus typical metallic materials. I (S) stands for ionic (semiconducting) materials typical properties.
Table 1. Comparison between the physical properties of intermetallic QCs versus typical metallic materials. I (S) stands for ionic (semiconducting) materials typical properties.
PROPERTY METALS QUASICRYSTALS
MECHANICAL ductility, malleability brittle (I)
TRIBOLOGICAL relatively soft very hard (I)
moderate friction low friction coefficient
easy corrosion corrosion resistant
ELECTRICAL high conductivity low conductivity (S)
resistivity increases with T resistivity decreases with T (S)
small thermopower moderate thermopower (S)
MAGNETIC paramagnetic diamagnetic, spin-glass
ferromagnetic unconventional ferromagnetic
THERMAL high conductivity very low conductivity (I)
large specific heat small specific heat
OPTICAL Drude peak no Drude peak, IR absorption (S)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated