Exposure to quasi-electrostatic field induced currents is a hazard of live-line transmission work. These steady-state induced currents are typically less than 1 mA, and their sensory effects range from imperceptible to painful depending on the person and conditions such as contact area and duration. Permanent injury from these currents is unlikely but they can distract workers, increasing the risk of injury from falls or other dangers. Identifying contact current severity and training workers can help reduce risk of accidents. Measuring induced currents along a climbing route is time consuming and simulation is challenging because of geometric complexity of the worker, transmission structure, conductor bundles, and electric fields in the climbing space. This research explores calculation of worker contact current using a recently developed adaptation of the charge simulation method. The method uses Fourier principles to improve computational efficiency when explicitly modeling all bundle subconductors. The research also examines reasonable simplifications for modeling lattice structures and human geometry. Calculated results compare well to measured currents for a worker climbing a 400 kV lattice structure. This indicates the method is a practical option for calculating the severity of steady-state contact currents. A simple calculation is suggested for estimating these currents.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

One of the hazards of high voltage live-line work is exposure to currents caused by capacitive effects between energized conductors, the worker, and the grounded structures supporting the conductors. Data in [1] indicates that about one percent of the population can perceive currents between 0.1 mA and 0.7 mA and that the mean perception level for a 180-lb person is about 1.0 mA. A steady-state current limit of 1.0 mA at frequencies below 2.5 kHz is listed as a guideline in [2] to avoid painful shocks in adults and children. However, linemen have reported varying levels of annoyance and pain when the steady-state currents are below 1.0 mA [3], [4]. The initial transient discharge currents can be higher than the steady-state currents but are very short in duration. These transient and steady-state currents will not normally cause direct injury but can be a distraction which increases risk of mistakes and injury from more prominent hazards such as falls or inadvertent contact with energized equipment.

The National Electric Safety Code in the United States requires that transmission line conductor height be sufficient to limit steady-state capacitive current to 5 mA if the largest anticipated vehicle or object under the line is short-circuited to ground [5]. In these situations, the object size dominates and the charge collecting area of the person is negligible. However, electrical workers must often operate relatively close to energized conductors. When positioned inside these regions of high electric field the human body has enough charge collecting surface area to allow capacitive currents above worker perception thresholds. The induced current experienced by a line worker during live-line maintenance has three dominant states listed in Table 1.

The term “microshock” does not have an industry standard definition, but generally refers to discharges that result in unpleasant sensation [9]. Much of the literature focuses on microshocks related to the transient condition. However, previous studies do not control well for point of contact surface area (including arc channel area in the case of the transient state). Medical research has shown that current density and hence contact surface area play a role in sensory severity [10]. This is consistent with the apparent lack of painful sensation reported for the insulated steady-state condition which has essentially the same current magnitude as the grounded steady-state condition, but which is not concentrated at any one part of the body. For a given lineman and location on a tower, the conditions corresponding to discomfort or pain seem to occur mostly in the transient condition or the grounded steady-state condition when contact area is small. Also, previous studies don’t thoroughly address impulse duration and neurological sensory limitations. For example, the dynamics associated with cell membrane action potential characteristics lead to an inverse relationship between current perception threshold and pulse length [11]. Consequently, if contact area is the same, it is not clear whether reported sensations are worse for the transient condition with its higher magnitude but very short duration pulses or for the grounded steady-state condition. This is an area for future research. Regardless, the capacitance values associated with the worker are critical factors in both the transient and steady-state conditions. These capacitances are directly related to the steady-state short-circuit current. Consequently, characterizing the steady-state short-circuit current is key to developing models suitable for both the transient and steady-state conditions.

Determining circuit characteristics and corresponding induced currents of the worker-transmission line system can be done with experiments or 3D simulation. Experiments in the literature were performed using metallic human surrogates and simulations were done with software such as CDEGS^® (full wave model), COMSOL Multiphysics^® (finite element method), PSCAD/EMTDC^® (circuit model), and early variations of the charge simulation method [6], [12], [13], [14], [15]. Measurements and simulations published in the literature focused mainly on electric potential of the workers when insulated from the tower.

The goal of the present research was to use simulation to calculate the steady-state capacitive currents experienced by a line worker when grounded on a tower, as these can be more directly related to medical research data regarding human response to electrical stimuli. Simulations are validated using previously unpublished data from the UK of line worker capacitive currents measured while climbing an in-service 400 kV transmission structure.

The research proposes use of a recently developed adaptation of the charge simulation method which uses Fourier principles to improve computational efficiency when explicitly modeling all transmission line subconductors [16]. This leaves more computing resources available for detailed modeling of the worker and for assessing geometric iterations such as variation of worker position within the climbing space. As an extension of this capability, the research examines reasonableness of simplifications for human geometry. Finally, simplifications of lattice tower modeling are assessed.

The Method section addresses the theoretical background of the problem and provides an overview of the charge simulation approach used to implement computations. This section also discusses the strategy for modeling lattice towers for 3D analysis. The Results section compares measured data to the calculated data. Results include sensitivity cases involving worker size and variation in the level of detail used to model the worker. The Discussion section summarizes the work and includes a simple method for estimating steady-state short-circuit current.

2. Method

Methods for calculating electrostatically induced short-circuit currents include empirical formulas [17] or electromagnetic modeling with numerical techniques. Recently, a method rooted in fundamental physics has been developed that can be used to both understand the influence of different parameters on and to calculate the severity of induced currents due to capacitive effects [18]. The method allows direct application of Thevenin’s theorem to determine an equivalent circuit from which the currents can be calculated.

2.1. Application of Thevenin’s Theorem to the Case of High Voltage Workers

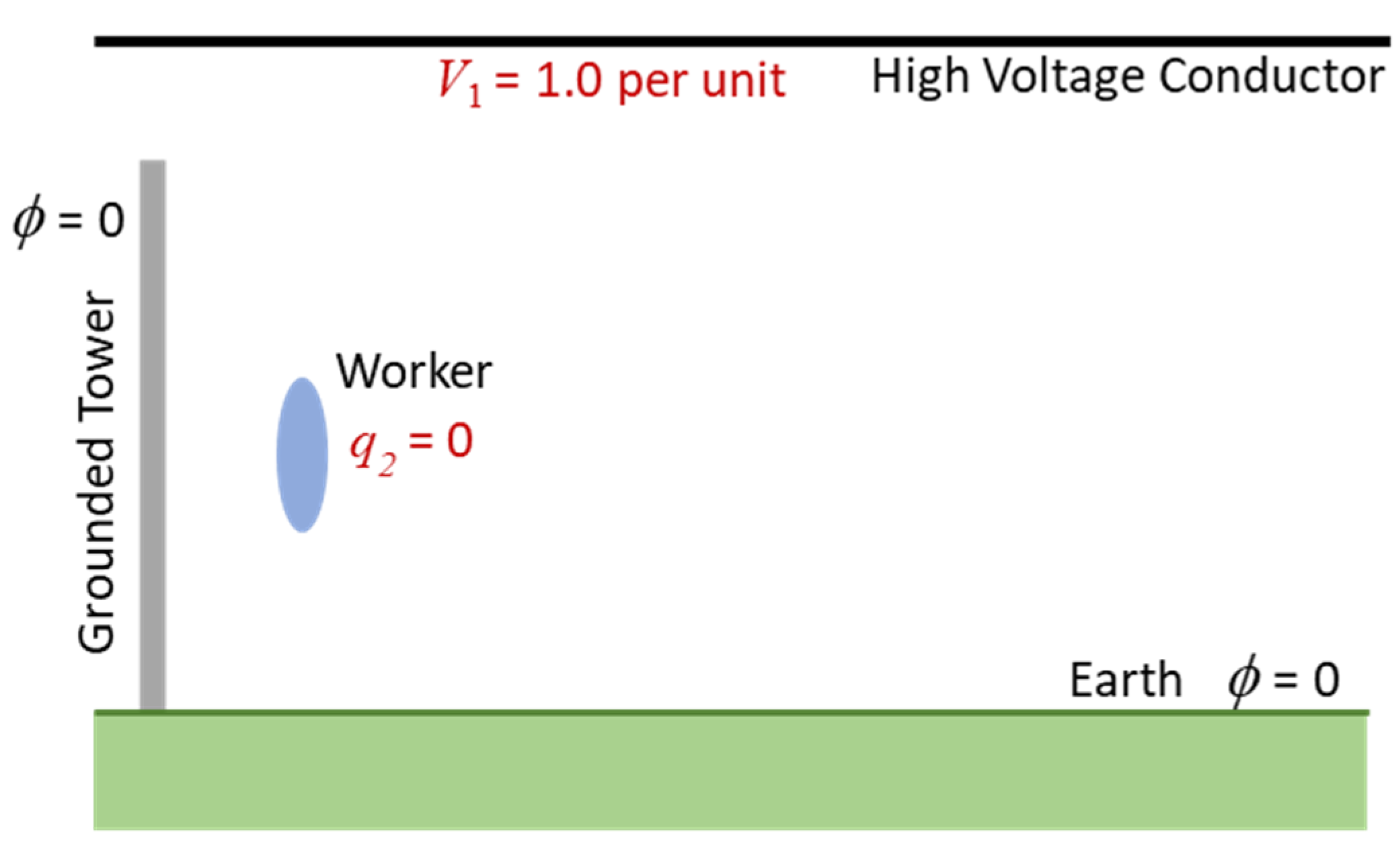
The geometry of the problem is illustrated in Figure 1. Here, a worker (represented by a spheroid and assumed insulated from the tower) is climbing a tower near a high voltage conductor energized to an ac voltage. As a result, there is a difference in voltage between the worker and tower that can lead to a microshock when the worker makes non-insulated contact with the tower. It will be assumed here that the high voltage conductor, the tower, the earth and the worker are perfect conductors and that the fields can be analyzed using quasi-electrostatics. The goal is to develop a Thevenin equivalant circuit for the entire system at the terminals indicated in Figure 1. The current calculated for a short-circuit across these terminals is both the current for the grounded condition and the driving force behind microshocks for the transient condition.

The background for the analysis that follows can be found in [19]. First, it will be assumed that the tower and the earth are held at zero potential (i.e.,

ϕ = 0

). Given this, the charge on the high voltage conductor (conductor #1) or the worker (conductor #2) can be found by splitting the problem into two (since the problem is linear and superposition holds) and solving Laplace’s equation for each problem. These equations are:

∇²ϕ_i = 0, ϕ_i regular at infinity, i = 1 or 2

(1)

ϕ_i = 1, on conductor i

(2)

ϕ_i = 0, on all other conductors

(3)

Given the solutions to these problems, the total potential at any point in space is:

ϕ = V_{1} ϕ_{1} + V_{2} ϕ_{2}

(4)

where V₁ and V₂ are the voltages assigned to conductors 1 and 2 respectively. Given (4), the total charge carried by conductor i is:

q_{i} = - ε_{0} \int_{S_{i}} \frac{\partial ϕ}{\partial n} d S = V_{1} (- ε_{0} \int_{S_{i}} \frac{\partial ϕ_{1}}{\partial n} d S) + V_{2} (- ε_{0} \int_{S_{i}} \frac{\partial ϕ_{2}}{\partial n} d S)

(5)

This result holds since the boundary condition on a perfect conductor is:

\bar{D} \cdot {\bar{a}}_{n} = ε_{0} \bar{E} \cdot {\bar{a}}_{n} = - ε_{0} \frac{\partial ϕ}{\partial n} = ρ_{s}

(6)

where

{\bar{a}}_{n}

is the outward normal to the surface of the conductor and

ρ_{s}

is the surface charge density on the conductor. Given the result in (5), the total charge on each conductor can be written as a set of capacitance values as:

q_{1} = c_{11} V_{1} + c_{12} V_{2}

(7)

q_{2} = c_{21} V_{1} + c_{22} V_{2}

(8)

where c₂₁ = c₁₂ by reciprocity. The mutual capacitance terms represent the ratio of charge induced on one conductor due to the voltage on another conductor and are negative since charges of opposite polarity are induced [20]. The negative sign inherent in the mutual capacitance terms is not explicitly shown in (7) and (8), nor is it explicitly shown in subsequent equations. Similarly, image terms are not explicitly shown but calculated charges and capacitances must include them due to the presence of earth and the grounded tower. Defined in integral form, the above capacitances are:

c_{11} = - ε_{0} \int_{S_{1}} \frac{\partial ϕ_{1}}{\partial n} d S

(9)

c_{12} = c_{21} = - ε_{0} \int_{S_{12}} \frac{\partial ϕ_{1}}{\partial n} d S = - ε_{0} \int_{S_{21}} \frac{\partial ϕ_{2}}{\partial n} d S

(10)

c_{22} = - ε_{0} \int_{S_{2}} \frac{\partial ϕ_{2}}{\partial n} d S

(11)

Next, consider two special cases of Figure 1. The first is illustrated in Figure 2. Here, the high voltage conductor (conductor #1) is held at a voltage V₁ = 1.0 per unit and the worker (conductor #2) is floating with an unknown potential V₂ and a total charge of zero.

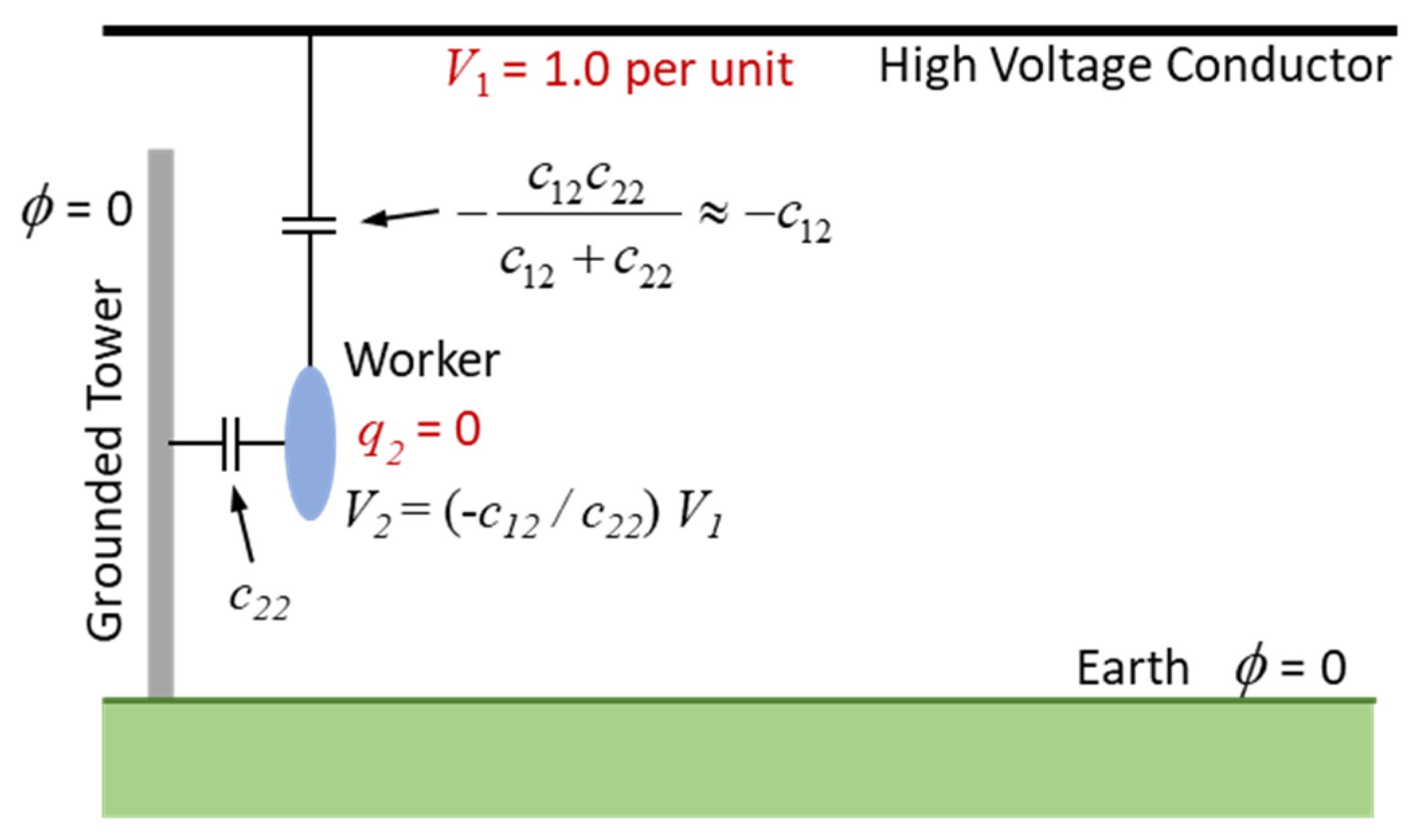
The purpose of this problem is to determine the unknown potential of the worker which (since the potential of the tower is 0) is then the open circuit voltage of the Thevenin equivalent circuit. This can be done by solving Laplace’s equation for the problem of Figure 2 with the total charge on the worker set to zero. However, it is also illustrative to consider how (8) can be used. Since

q_{2}

= 0, (8) reduces to:

0 = c_{12} V_{1} + c_{22} V_{2}

(12)

so that

V_{2} = (- c_{12} / c_{22}) V_{1}

(13)

This suggests that a capacitive voltage divider can be used to calculate the open circuit voltage if the capacitances are known. c₂₂ and -c₂₁ are respectively the capacitance between the worker and the tower/earth combination and the approximate capacitance between the high voltage conductor and the worker. Such a circuit is shown in Figure 3.

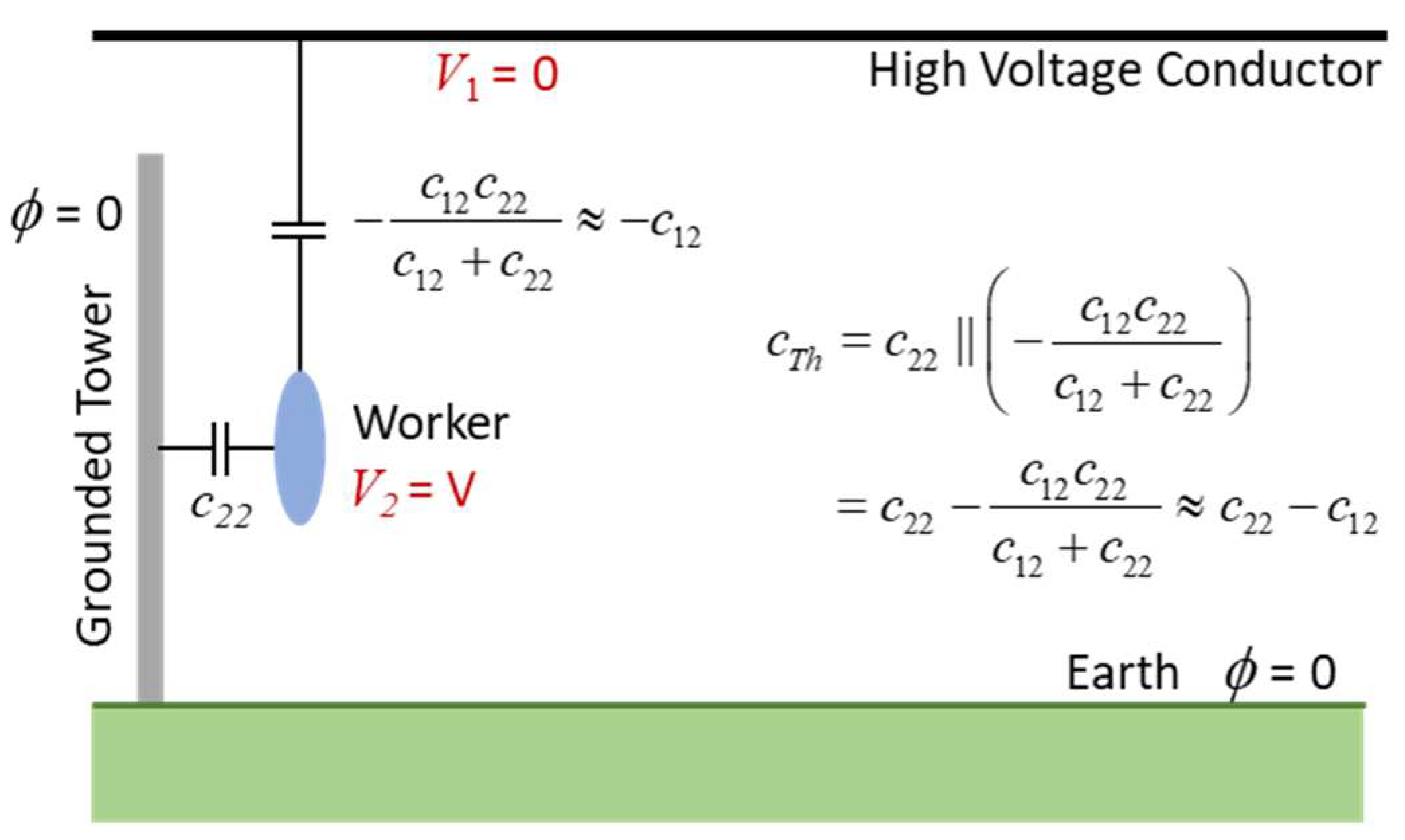
A second special case of Figure 1 is illustrated in Figure 4. Here, the potential of the high voltage conductor is set to zero and the potential of the worker is set to an arbitrary voltage V. The worker’s charge in this problem can be solved directly using Laplace’s equation. Again, insight can be gained by applying (8) to the result. More specifically:

q_{2} = c_{22} V

(14)

Hence,

c_{22} = q_{2} / V

(15)

By examination of Figure 4, the Thevenin impedance can be determined by setting the source voltage to zero (V₁ = 0) and calculating the impedance to the set of grounded conductors. The result is:

c_{t h} \approx c_{22} ∥ (- c_{12}) \approx c_{22} - c_{12}

(16)

where (c₂₂ - c₁₂) > c₂₂ because c₁₂ is negative and c₂₂ >> |c₁₂| because of the worker’s proximity to the tower.

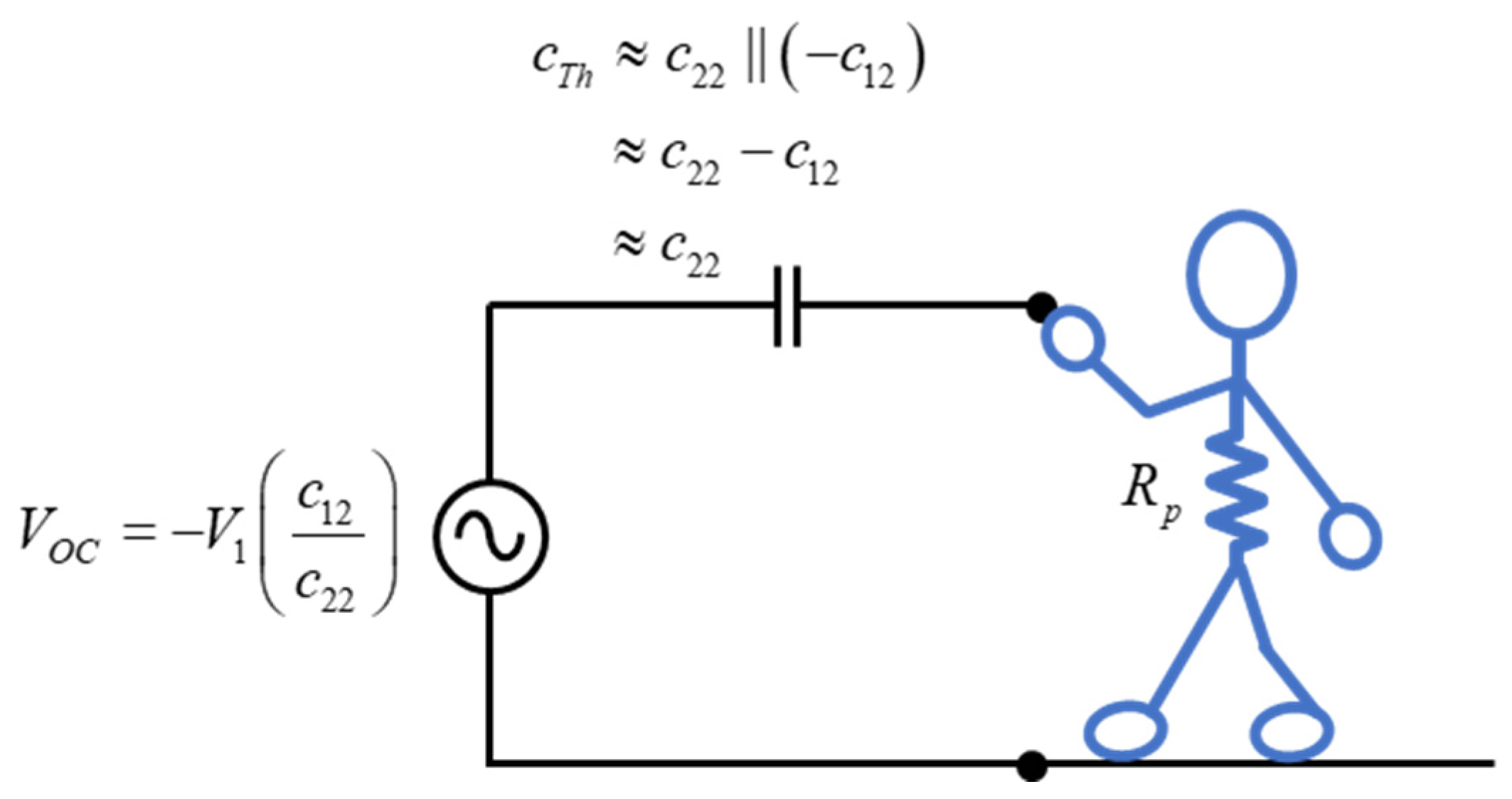
Note that c₂₂ is now known and the value V₂ was calculated by solving Laplace’s equation for the geometry of Figure 2. Further the value of c₁₂ is available from (13) since V₁ = 1 for the calculation. These results are summarized in the Thevenin Equivalent circuit shown in Figure 5. Note that R_p is the resistance of the person (roughly 1500 Ohms) and can generally be neglected compared to the Thevenin impedance (i.e.,

1 / (j ω (c_{22} - c_{12}))

) at the frequencies of interest. Finally, note that since

|c_{12}| < < c_{22}

, the open circuit voltage is much less than the voltage on the high voltage conductor.

2.2. Numerical Approach for Realistic Systems

Simplified cases such as that in the previous subsection serve to illustrate the theory and sometimes allow direct computation with analytical methods. Computations for more realistic situations involving complex worker or object models, tower geometry, and bundled, multi-phase conductors normally require numerical methods. The Fourier Enhanced Charge Simulation Method [16] was selected as the primary computation method for this analysis. This is an efficient adaptation of the standard charge simulation method for three-dimensional electrostatic calculations involving infinitely long parallel conductors near finite shaped conducting objects. While phase conductors are not actually infinite in length, modeling them as such is a very good approximation for local electric field calculations. The axial line charge densities that represent phase subconductors are each decomposed into a uniform charge density component and a nonuniform charge density component. The nonuniform components consist of line charge density segments, each with a linearly varying charge density. The finite conducting objects are modeled with a group of point charges offset from surface potential points. A typical problem involves solving for the line charge densities and point charge values given the system geometry and voltage boundary conditions. The method applies Fourier principles to reduce computational burden by moving the portions of the problem relating to conductor nonuniform line charge density to the spatial frequency domain using a discrete Fourier transform. Computation time can be significantly reduced relative to the standard all-spatial charge simulation, boundary element, or finite element methods. The overall simulation approach involves the following steps:

Discretize the surface of finite conducting objects by selecting a set of distributed points on their surfaces. Known voltages are enforced at these points. Higher point density allows greater accuracy but at the cost of greater computational burden.
Place point charges strategically at locations inside the object (offset from the surface points). The extent of the offset depends on the voltage point density at the surface. Generally, the number of charge points and the number of voltage points are the same, which allows for a direct solution. Otherwise, iterative optimization-based solution methods are needed.
Select Fourier parameters that control spatial discretization of the conductor line charge density segments.
Compute the line charge densities of each subconductor and the point charge values at each charge point that will satisfy the electric potential boundary conditions defined at the surfaces of the objects and phase conductors. Floating potential conditions require a zero net charge limit be enforced on the applicable object(s).
Once the point charge values are identified, the electric potential can be accurately calculated anywhere in the insulating medium external to the conductors.

The above steps were applied to find line worker charge and voltage which are necessary for calculation of the Thevenin equivalent circuit components. About 6,000 line charge density segments were used to model the conductors and about 10,000 points were used to model the steel pole and worker. Each simulation solved in about one minute on a computer with a CORE i7 intel^® processor and 32 GB of RAM.

2.3. High Voltage System Selected for Analysis

Figure 6 shows the double circuit tower used for detailed analysis and comparison to measurement. The structure is an L6 Standard D tower used in the United Kingdon. Dimensions of this and similar towers can be found in [21]. The phase conductors are located at heights of 20, 28, and 36 meters respectively above the earth and at distances (from top to bottom) from the center of the tower of +/- 6.5, +/- 10, and +/- 8.5 meters. Each conductor is a quad bundle with subconductors of 28.63 mm diameter and 305 mm spacing. For each calculation, the conductors were set to a voltage of 400 kV rms line-to-line with reverse phasing on the two sides (i.e., ABC or RST on the left and CBA or TSR on the right).

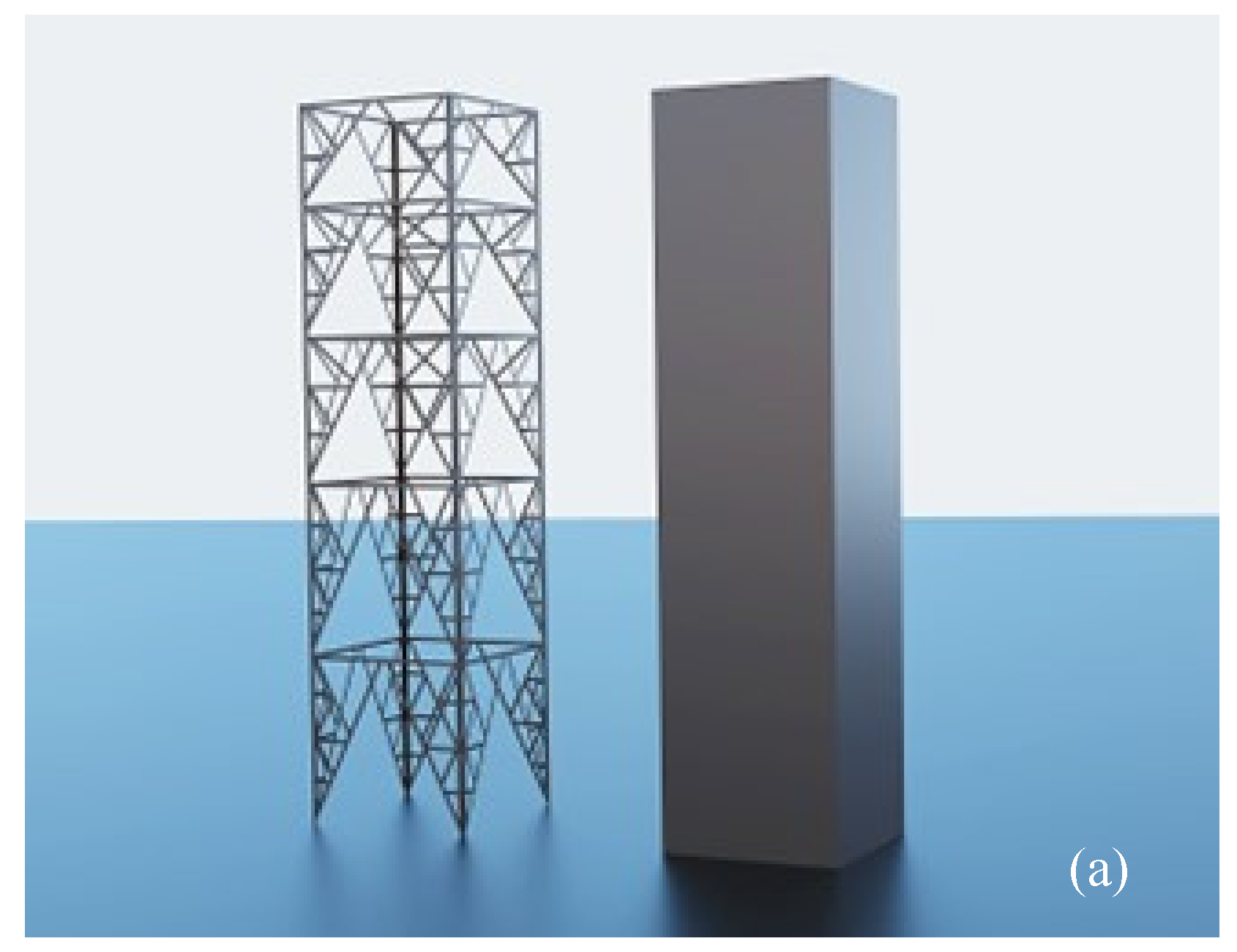
Even with the capabilities of modern numerical methods, modeling a detailed lattice tower is difficult and time consuming. As a preliminary step for microshock computations, finite element analysis (FEA) was conducted to determine if lattice towers could be reasonably simplified to planar geometries. Figure 7 shows the two geometries analyzed. Figure 7(a) is a detailed lattice tower representation using flat conducting members arranged in a pattern similar to that of the L6 Standard D lattice tower, but without the taper. The model in Figure 7(b) has the same outer dimensions but consists of conducting planar surfaces. Both models include a single tubular conductor (not shown) with radius equal to the geometric mean radius of the L6 Standard D condcutor bundle. This equivalent conductor was placed at a height and horizontal position similar to that of the lowest bundle of the L6 Standard D tower. Modeling many small diameter conductors adds significant computational burden to the finite element model and the equivalent single conductor provides an adequate representation of the driving electric field in the region of the climbing space at the tower corner.

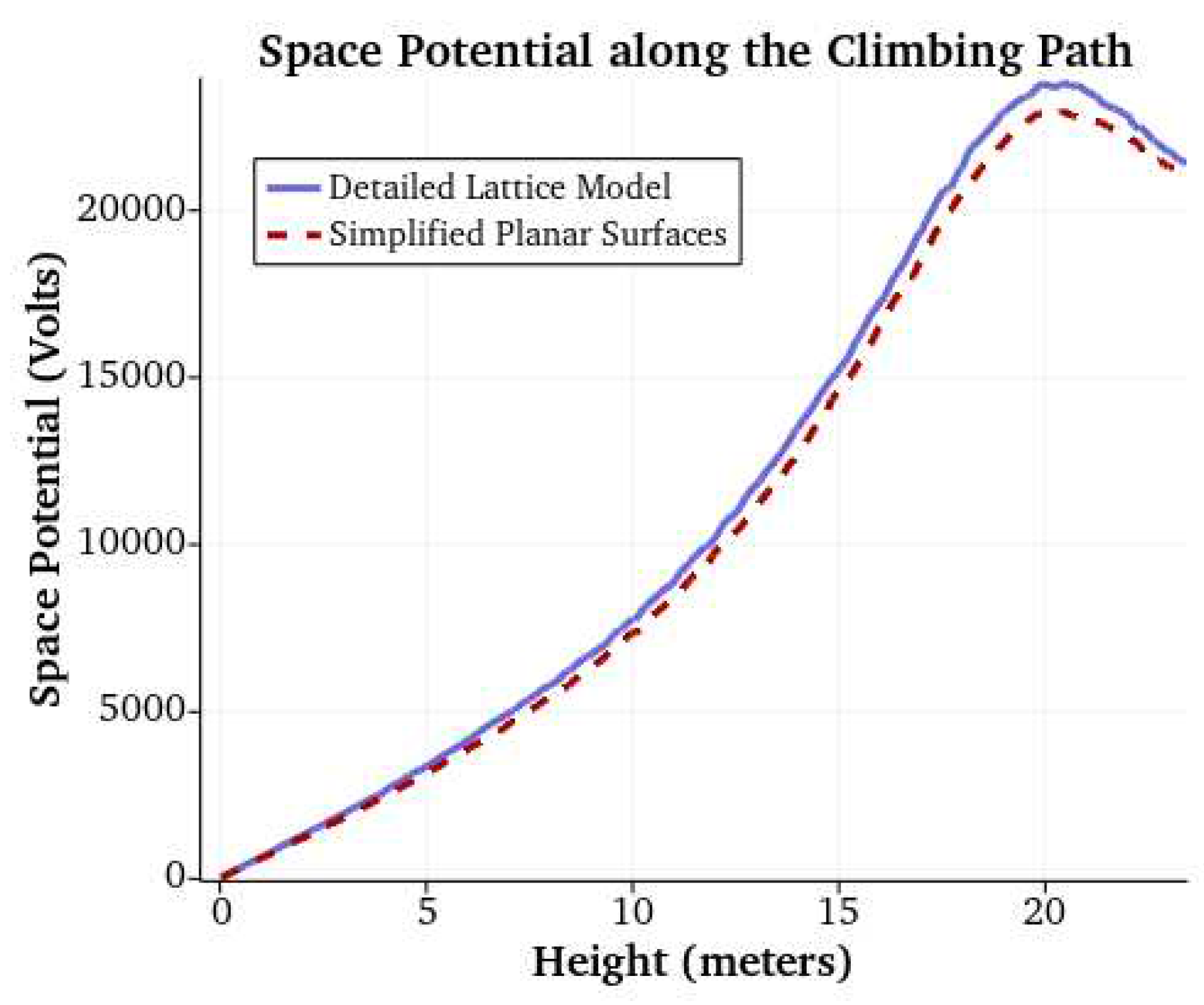
The tower models and earth plane were set to zero volts and the surface of the conductor was assigned a voltage of 230.9 kVrms line-to-ground. The space potential was then calculated in the region of the climbing space. Results in Figure 8 indicate that the planar model can be used without sacrificing significant accuracy. Figure 9 shows the final tower model used for the microshock calculations.

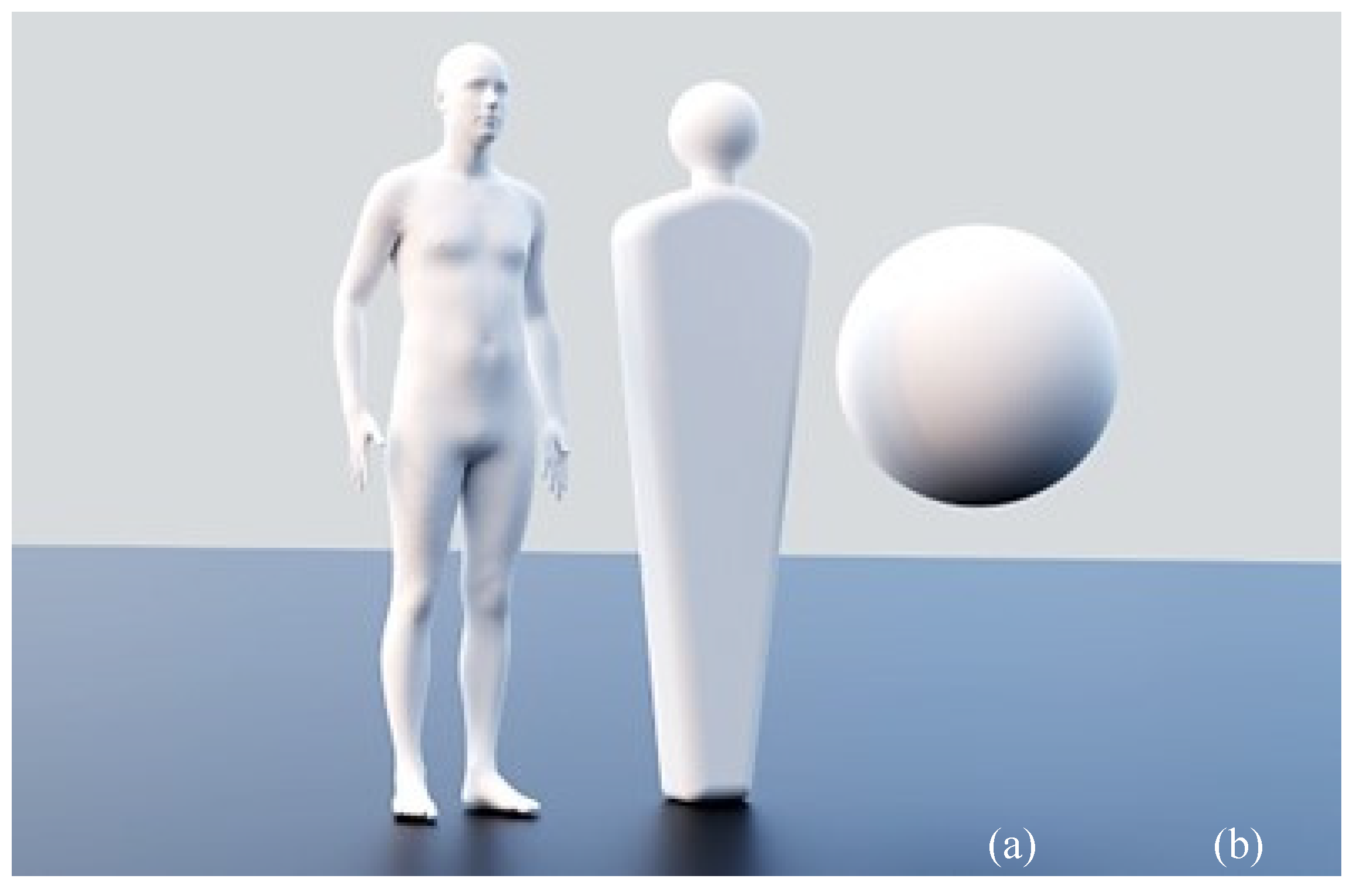
2.5. Human Model

Figure 10 shows the human models used for the analysis. An anatomically correct average sized human model was adapted from [22] and has a nominal height of about 1.8 meters and a surface area of about 1.9 m². Various cases were run with model sizes ranging between ± 20% of nominal based on surface area. Two other simplified shapes were used to assess the sensitivity of the method to the geometry of the line worker. These included a sphere and another shape that was simple to construct but which has proportions similar to the detailed model. The two simplified models were sized to have the same surface area as the detailed model.

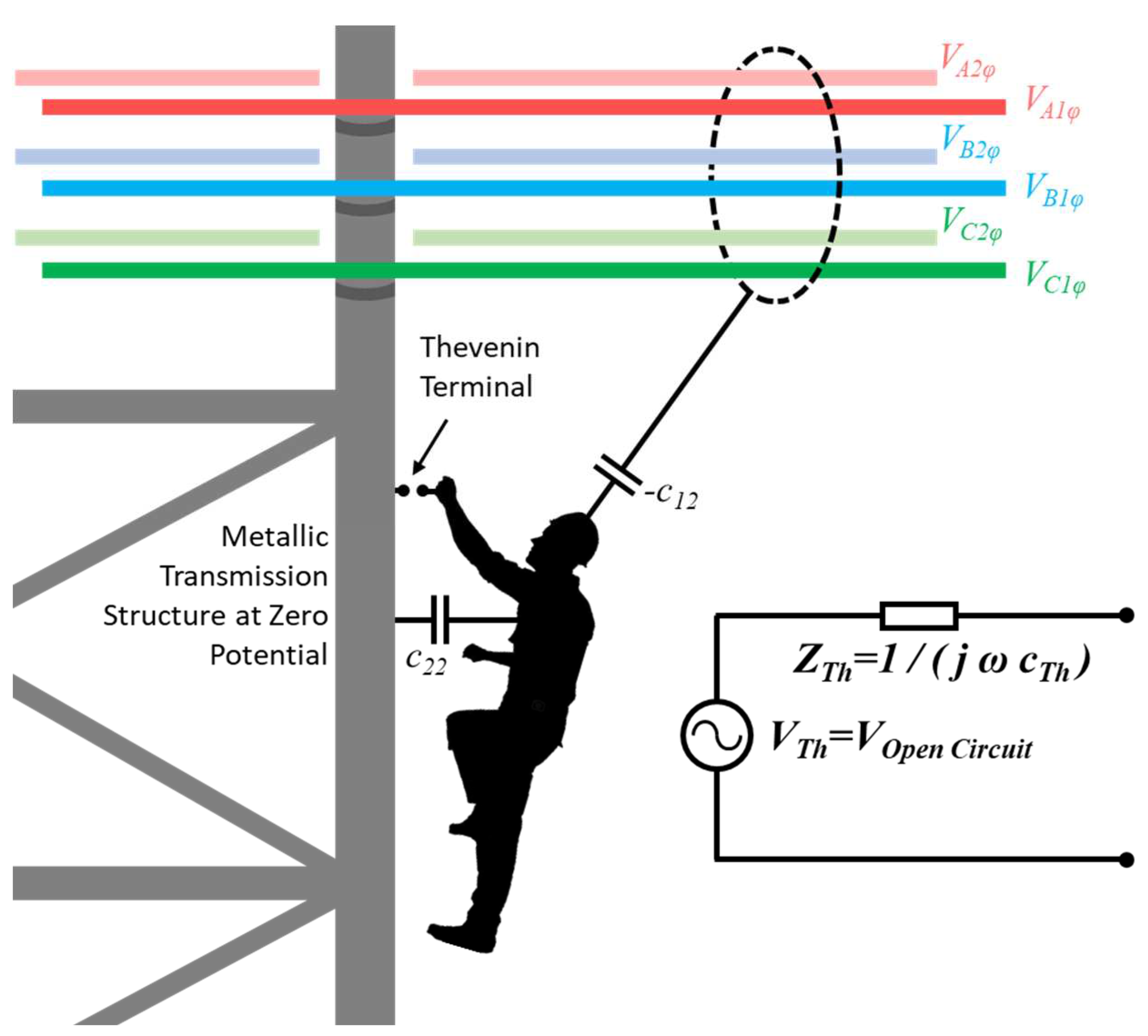
2.5. Simulation Process

Figure 11 shows the overall model used in the simulation process. The worker is assumed insulated from the phase conductors, from the grounded structure, and from reference earth by air and clothing. A Thevenin terminal is assumed at a point on the worker that could come directly into contact with a grounded tool or the structure. Conduction currents through air are neglected due to air’s high resistivity. Displacement current will exist due to capacitance between the worker and the other conductors in the system; namely the structure and ground plane, and the energized conductors. The influence of each phase conductor or phase bundle could be represented by a separate capacitance, but for illustration simplicity -c₁₂ is assumed to represent the net field effect of all phase conductors at the location of the worker. The structure is at ground potential but is modeled explicitly whereas the impact of the earth plane is accounted for through image theory assuming earth is a perfect conducting half space.

2.5.1. Analysis Steps

Determination of steady-state short-circuit currents involves application of Thevenin’s theorem. First, the open circuit voltage of the worker is determined, then the applicable Thevenin equivalent impedance is calculated, and finally the Thevenin circuit is used to calculate the short-circuit current. The first two steps are performed via electric field theory using the Fourier Enhanced Charge Simulation Method.

Step 1: calculate the open circuit voltage.

The open circuit voltage (V_OC) of the worker is determined by applying a floating potential condition to the worker model when situated at a location of interest and not contacting the structure or a grounded tool. Phase conductors are energized to the desired voltage (typically the nominal voltage or the maximum operating voltage). The worker is insulated from the grounded structure and energized phase conductors but since the worker is in a relatively strong electric field, they will be at some non-zero potential.

Considered from the circuit perspective, the worker open circuit voltage is based on a voltage divider between -c₁₂ and c₂₂. In this configuration current is through the capacitances, however it is limited by the very small value of -c₁₂.

Step 2: calculate the Thevenin impedance.

The next step is to find the equivalent impedance looking back into the Thevenin terminals. Following the standard Thevenin approach, voltage sources are set to zero volts. This places the capacitances in parallel which means the equivalent impedance is due to the summation of c₂₂ (between the worker and ground) and -c₁₂ (between the worker and the conductors).

Therefore, total capacitance can be obtained by setting the conductor voltages to zero, assigning an arbitrary voltage to the worker (V_worker), calculating the corresponding total charge (Q_worker) on the worker using charge simulation, then calculating total capacitance as C_Th = Q_worker / V_worker. The Thevenin equivalent impedance is then calculated as Z_Th = 1 / (j ω c_Th), where ω is the system frequency in radians per second.

Step 3: calculate the short-circuit current.

The short-circuit current magnitude (I_SC) is calculated as |I_SC| = |V_OC / Z_Th |= |V_OC ω c_Th|. Use a root-mean-square (rms) voltage input to obtain an rms value for the short-circuit current. Likewise, using an ac peak voltage will give the ac peak short-circuit current.

2.6. Measurement Method

A comprehensive set of measurements performed in the UK have been provided by EPRI. The measurements covered how the short-circuit currents between a grounded line worker (linesman) and the tower vary within the normally accessed climbing space on a tower for a range of tower designs from two different tower families. The measurements were conducted on three variants of the L6 tower family (including that of Figure 6) and two variants of the L2 tower family. These variants were a tangent suspension tower (with no angle deviation of the line), a tower for line angle deviations of between 30° and 60°, and a tower for line angle deviations of between 0° and 30° for one of the tower families.

Two line workers were equipped with a logging current-measuring meter that was capable of recording event markers. This meter was used to record steady-state currents (see State 2 in Table 1). Typical accuracy of the meters is ±5%. One side of the meter was connected to the linesman’s arm by a wrist strap, tightened to ensure good contact. The other side was connected to a clamp for making electrical connections to the tower. The linesmen wore boots with resistance sufficient to make short-circuit current in paths outside the measurement strap negligible.

The two line workers climbed each tower along two climbing legs on opposite corners of the tower starting immediately above the anti-climbing guard and climbing all the way to the very top, stopping every 5 feet (1.52 meters) to make a measurement.

Step bolts are 1 foot 3 inches apart (0.38 meters), located alternately on the two sides of the angle girder of the climbing leg. The meter was recording current continuously and the linesmen were asked to stop at every second pair of step-bolts, (that is, every 5 feet or 1.52 meters), fasten a non-conductive work position strap around the tower leg, lean back into it with no other contact with the tower, and take a current reading by recording an event mark on the current-logging meter. Two observers on the ground, one for each linesman, recorded the locations of their feet for each event number. The height and body mass index of each line worker was within 10% of a reference height of 5.77 feet (1.76 meters) and surface area of 20.5 square feet (1.90 square meters), similar to the size of the nominal human model used in simulation.

Only the results for the L6 D Standard tower are included in this paper for comparison to calculated values. A full set of measured data for the other tower families will be incorporated in a forthcoming EPRI report.

3. Results

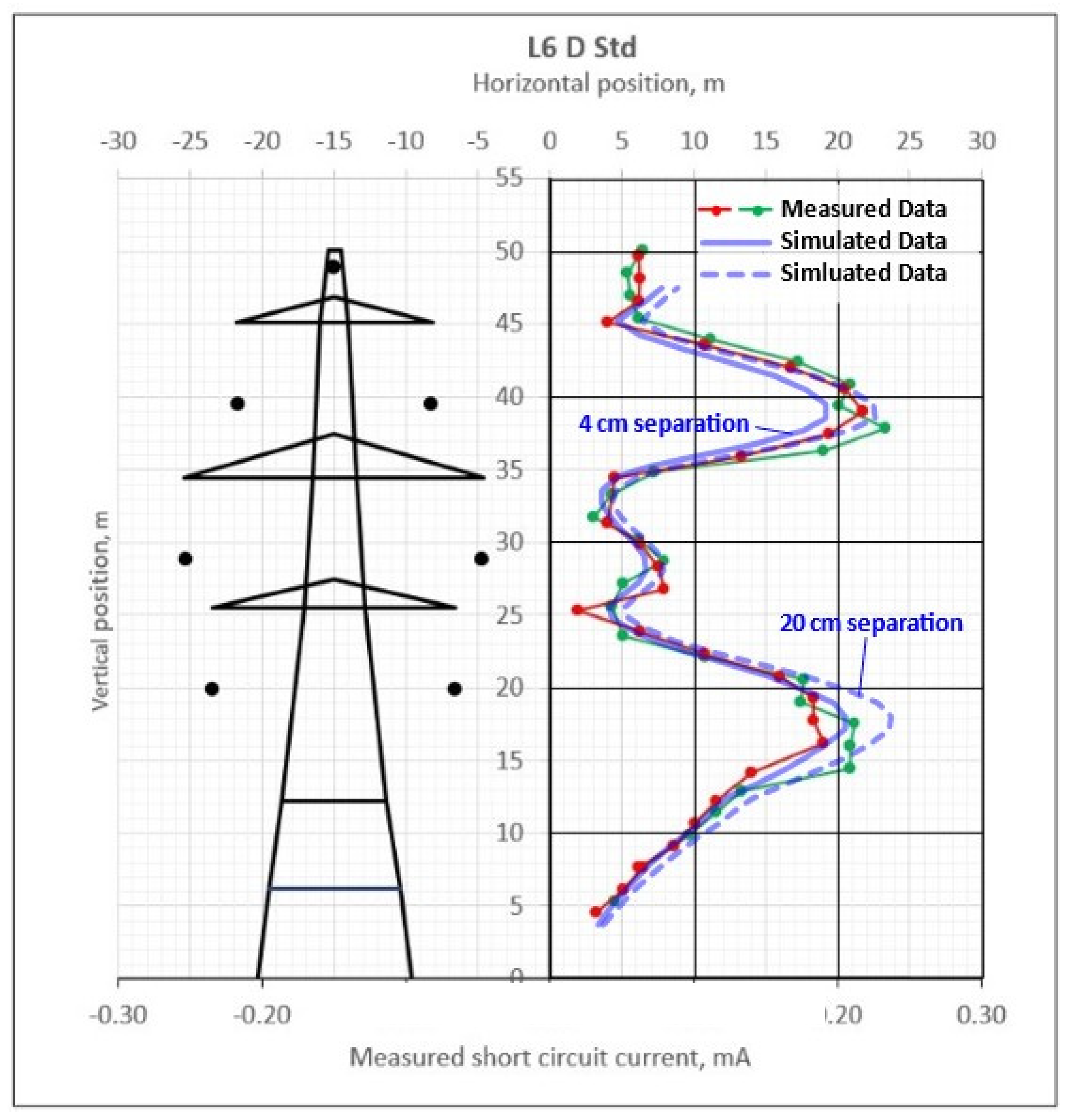
Results for the short-circuit current between the insulated worker and the tower as a function of the worker vertical position on the L6 D Standard tower are given in Figure 12. One measured data set is shown for each of the two workers who climbed the tower with the current meters. The two simulated data sets are both for the same detailed human model in Figure 10(a) but one has a 4 cm gap between the tower surface and the closest part of the model (the feet) and the other has the model placed at a distance of 20 cm from the tower surface.

Table 2 lists results of simulations to analyze impact of line worker size on short-circuit currents. Models were placed 4 cm from the surface of the tower corner at a vertical location corresponding to worst-case short-circuit current. Table 3 compares results for the three model shapes. The last column in both tables shows the space potential calculated at approximately the volumetric center of the human model, but without the model present (i.e., only the structure, ground, and energized conductors are in the model). This is for comparison to the open circuit voltage.

Results for open circuit voltage, model capacitance, and short-circuit current each vary approximately linearly with model surface area. Changes in capacitance and short-circuit current are not drastic for any of the cases in Table 2 and Table 3. Also, the space potential calculated in the absence of the model is close to the Open Circuit Voltage. These suggest that a reasonable rule-of-thumb estimate of short-circuit could be obtained by assuming a typical value of capacitance and estimating the space potential in the climbing space. The fact that there is little difference in the results for the three models with the same surface area indicates that results are not sensitive to shape of the line worker.

4. Discussion

The Fourier Enhanced Charge Simulation Method was well suited for analysis of the line worker microshock problem. The key assumptions or simplifications are the use of horizontal conductors, discretization of the geometry, and the size and placement of the human model. These are typical concessions for most numerical based methods. The proposed method has the advantage of easily accommodating a detailed human model and explicitly modeling each of the subconductors in the phase bundles. Results compare well with measured values indicating the simulation method could be used by utilities to calculate short-circuit current, which is one key determinant of microshock severity.

Compared to the detailed human model, relatively little error was introduced using the simplified human shape or the spherical human analog. This suggests that certain sensitivity studies could be performed using very simplified worker geometry with equivalent surface area. This makes sense given that the electric field does not change drastically in the climbing space within volumes that would be occupied by a worker.

While detailed simulation and measurement tend to produce the most accurate results, a quick estimate of maximum worker microshock can be obtained through reasonable assumptions regarding Thevenin capacitance (c_Th) and the open circuit voltage (V_OC). The short-circuit current can then be estimated as I_sc = V_OC ω c_Th, where ω is the system frequency in radians per second. Note that worker size and distance to the surface of the grounded structure being climbed will generally vary over relatively narrow ranges. Therefore, c_Th will also fall in a relatively narrow range. Also, as previously mentioned, the high voltage conductors have a relatively minor impact on worker Thevenin capacitance. 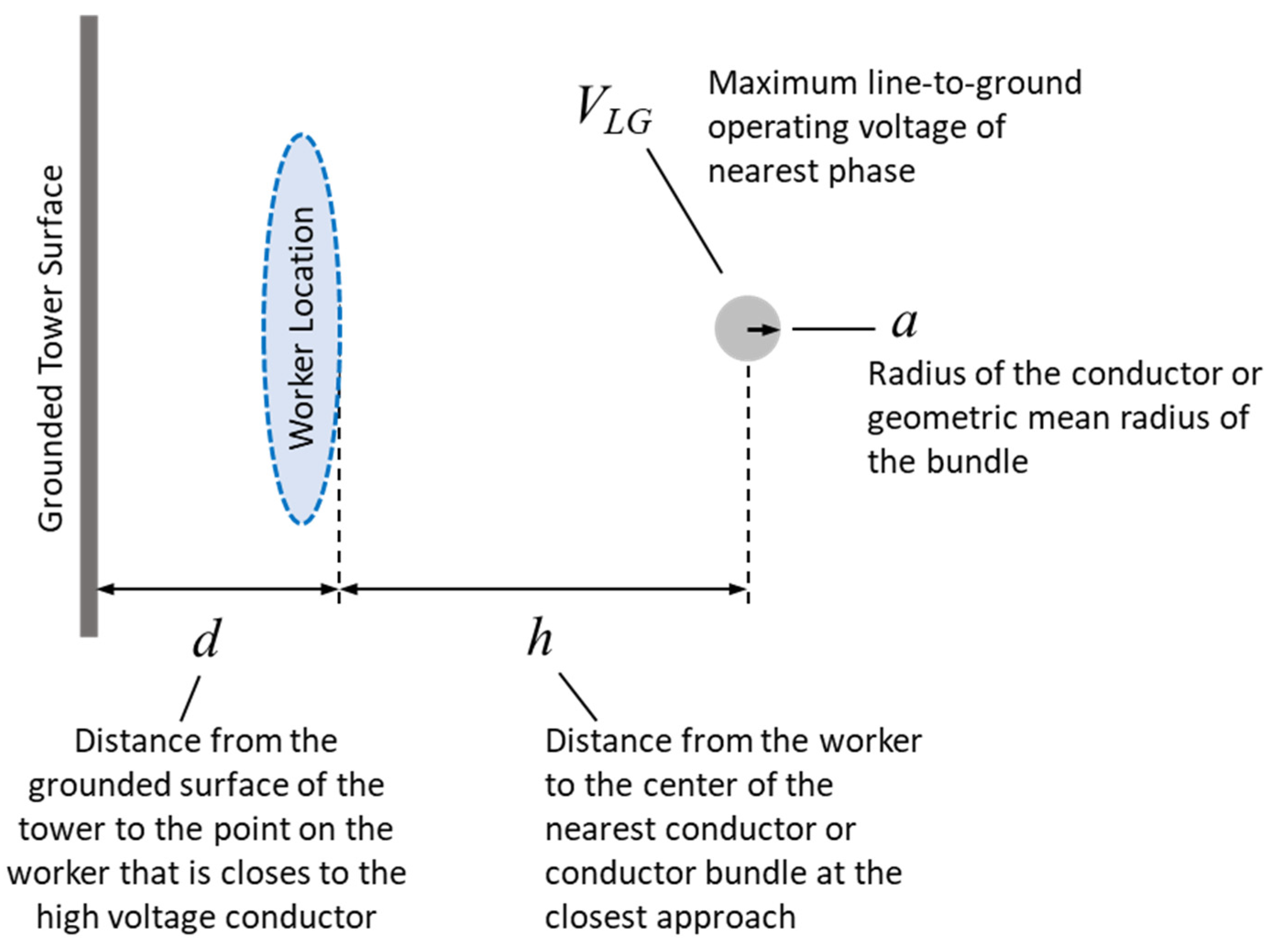Therefore, based on the data in Table 2 and Table 3 and the results in the example of Figure 12, the Thevenin capacitance of the average sized worker can be estimated to be between about 65 pF and 80 pF depending on proximity to the surface of the structure. Use of the higher end of the range would typically be best for estimating purposes. The open circuit voltage without the worker present can then be estimated using (19) from [23]. This is the equation for space potential at some distance from an energized conductor near a perfect conducting ground plane which replaces the lattice tower structure. The parameters of the equation are illustrated in Figure 13. Note that the approach neglects two of the phases. Under balanced operating conditions, inclusion of the other phases introduces some level of field cancellation which would reduce the open circuit voltage. Table 4 lists parameters and results of applying (19) to estimate the maximum short-circuit current for the example illustrated in Figure 12. The accuracy of the estimate in this case is somewhat coincidental but would typically be within 10 or 15% of simulated.

V_{O C} = \frac{V_{L G}}{\ln (2 (h + d) / a)} \ln (\frac{h + 2 d}{h})

(17)

Funding

Robert Olsen and David Renew were funded by EPRI for parts of this project and the measurement data are included by permission of EPRI.

Conflicts of Interest

The authors declare no conflict of interest.

References

J. C. Keesey and F. S. Letcher, “Minimum thresholds for physiological responses to flow of alternating electric current flow through the human body at power-transmission frequencies, Project MR005.8-0030B,” Naval Medical Research Institute, Bethesda, MD, 1969.
International Commission on Non-Ionizing Radiation Protection, “ICNIRP guidelines for limiting exposure to time-varying electric and magnetic fields (1Hz-100 kHZ),” Health Physics Society, vol. 99, no. 6, pp. 818-836, 2010.
D. W. Swanson, Private Communication, 2023.
Y. Ahmed and S. M. Rowland, “U.K. Linesmen’s Experience of Microshocks on HV Overhead Lines,” Journal of Occupational and Environmental Hygiene, vol. 6, no. 8, pp. 475-482, August 2009. [CrossRef]
IEEE, 2023 National Electrical Safety Code® (NESC®), 2022.
W. Pan, X. Li and Y. Li, “Calculation and Analysis of Micro-Shock Energy of Line Maintenance Personnel in High Electric Field,” in 5th Asia Conference on Power and Electrical Engineering (ACPEE), Chengdu, China, 220.
T. Lu and X. Li, “Measurement of Electrostatic Discharge Through Human Body Contacting Metallic Objects Under HVAC Transmission Lines,” in 41st Annual EOS/ESD Symposium (EOS/ESD), Riverside, CA, 2019.
W. He and et al., “Experimental Study on the Transient Electric Shock Characteristics Between Metal Sheds and the Human Body Near Ultrahigh Voltage Alternating Current Transmission Lines,” IEEE Transactions on Electromagnetic Compatibility, vol. 65, no. 3, pp. 679-688, 2023. [CrossRef]
Ø. G. Martinsen, S. Grimnes and H. Piltan, “Cutaneous Perception of Electrical Direct Durrent,” ITBM-RBM, vol. 25, no. 4, pp. 240-243, 2004. [CrossRef]
M. R. Prausnitz, “The Effects of Electric Current Applied to Skin: A Review for Transdermal Drug Delivery,” Advanced Drug Delivery Reviews, vol. 18, no. 3, pp. 395-425, 1996. [CrossRef]
Y. Ahmed, S. M. Rowland, G. Burnett and N. Pammenter, “Avoidance of Microshocks for HV Overhead Line Workers,” in International Conf on Electric and Magnetic Fields at Extremely Low Frequencies, Paris, 2011.
A. Gunatilake, Y. Ahmed and S. M. Rowland, “Modelling of Microshocks Associated With High-Voltage Equipment,” IEEE Transactions on Power Delivery, vol. 24, no. 1, pp. 202-207, January 2009. [CrossRef]
Y. Ahmed and S. M. Rowland, “Modelling Linesmen’s Potentials in Proximity to Overhead Lines,” IEEE Transactions on Power Delivery, vol. 24, no. 4, pp. 2270-2275, October 2009. [CrossRef]
C. J. Lin, R. Chuang and M. Chen, “Steady-state and Shock Currents Induced by ELF Electric Fields in a Human Body and a Nearby Vehicle,” IEEE Transactions on Electromagnetic Compatibility, vol. 32, no. 1, pp. 59-65, February 1990. [CrossRef]
M. Abdel-Salam and H. M. Abdallah, “Transmission-Line Electric Field Induction in Humans Using Charge Simulation Method,” IEEE Transactions on Biomedical Engineering, vol. 42, no. 11, pp. 1105-1109, November 1995. [CrossRef]
J. T. Leman and R. G. Olsen, “Fourier Enhanced Charge Simulation Method for Electrostatic Analysis of Overhead Transmission Lines,” IEEE Transactions on Power Delivery, vol. 37, no. 2, pp. 1078-1087, April 2022. [CrossRef]
General Electric, Co., Transmission Line Reference Book - 345 kV and Above, 2nd ed., Palo Alto, CA: Electric Power Research Institute, 1982.
R. G. Olsen and J. T. Leman, “On Calculating Contact Current for Objects Insulated from the Earth and Immersed in Quasi-static Electric Fields,” IEEE Power and Energy Technology Systems Journal, vol. 4, no. 1, pp. 16-23, March 2017. [CrossRef]
J. V. Bladel, Electromagnetic Fields, 2nd ed., Wiley-IEEE Press, 2007.
R. Morrison, Digital Circuit Boards: Mach 1 GHz, Hoboken, NJ: John Wiley & Sons, 2012.
D. Beardsmore, “L6 – Telcontar.net,” [Online]. Available: https://telcontar.net/Power/pylons/L6. [Accessed 31 August 2023].
T. Huysmans and J. Molenbroek, “DINED / Anthropometry in Design,” 2023. [Online]. Available: https://dined.nl/en. [Accessed 21 May 2023].
R. G. Olsen, High Voltage Overhead Transmission Line Electromagnetics - Volume I, 2nd ed., CreateSpace, 2018.

Figure 1. Geometry of the Problem.

Figure 2. Determining the open circuit voltage of the Thevenin equivalent.

Figure 3. Determination of open circuit voltage for the Thevenin equivalent circuit.

Figure 4. Determination of Thevenin impedance.

Figure 5. Final Thevenin equivalent.

Figure 6. UK L6 Standard D Tower (The tower in the photo has a 20 foot extension).

Figure 7. Models used to assess required tower detail; (a) detailed lattice tower model, (b) simplified planar surface model. Outer dimensions of both are 6.2 meters x 6.2 meters x 25 meters.

Figure 8. Comparison of space potential along the climbing path for the models in Figure 7.

Figure 9. Simplified UK L6 Standard D tower model.

Figure 10. Human models used to calculate the Thevenin equivalent circuit; (a) detailed model, (b) simple shape with overall proportions similar to the detailed model, (c) spherical model. All models have the same surface area.

Figure 11. Illustration of model used for the simulation process.

Figure 12. Measured and simulated steady-state short-circuit current as a function of worker position on the tower. Currents are in milliamps rms.

Figure 13. Simplified geometry for short-circuit current estimate using (19).

Table 1. Different states associated with induced current in line-workers.

Worker State	Description
Steady-state condition in which the worker is insulated from, but positioned on the grounded structure	Based on the electric field, the worker is at some floating potential and has approximately zero net charge. Conduction currents through air and insulated clothing are negligible. A displacement current (i.e., capacitive current) which causes fundamental frequency redistribution of surface charge on the worker which may or may not be perceived but is not painful because it is distributed over the whole body.
Steady-state condition in which the worker is in contact with the grounded structure	Worker is a grounded electrode that extends into the space between the tower and conductors. Charge is transferred between the tower (ground) and the worker to counter electric fields and maintain zero-potential. The current is effectively the same in magnitude to that of the insulated condition because in both cases the current is limited by the capacitance between the energized conductors and the worker. However, in this case the current is concentrated at the location of contact. The sensation will depend in part on the actual surface area of that contact location. A larger contact area will reduce sensation severity.
Transient condition representing the transition period between the worker being insulated and in-contact.	In this state the worker is either in the process of making or breaking contact with the grounded structure. Small transient impulses occur as arcs develop over very short distances between the structure and the point of contact on the worker. The amplitude of these impulse currents can be orders of magnitude higher that the steady state currents, but the duration of the current pulses tend to be less than one microsecond [6], [7], [8]. The transient currents are concentrated on a small area of the skin due to the small diameter of the arc channel between the skin and the tower.

Table 2. Comparison of short-circuit currents for varying human model size.

Human Model Size* (Percent of Surface Area Relative to the Nominal Case)	Open Circuit Voltage (Volts rms)	Model Capacitance (picofarads)	Short-circuit Current (milliamperes)	Space Potential without Model (Volts rms)
80%	7,900	67.1	0.167	8,085
90%	8,239	71.1	0.184	8,449
100%	8,562	74.7	0.201	8,808
110%	8,841	78.4	0.218	9,156
120%	9,118	81.9	0.235	9,486

*Models were placed 4 cm from the tower surface. The detailed model from Figure 10(a) was used.

Table 3. Comparison of simulation results for three human model shapes (refer to Figure 10(a)).

Model*	Open Circuit Voltage (Volts rms)	Model Capacitance (picofarads)	Short-circuit Current (milliamperes)	Space Potential without Model (Volts rms)
Sphere	11,538	64.2	0.233	12,817
Human Analog	11,881	64.2	0.240	12,358
Detailed Human	11,916	63.0	0.236	11,937

*Models were placed 20 cm from the tower surface. As expected, this results in higher open circuit voltages than the cases in Table 2 which were placed closer to the tower.

Table 4. Estimate of short-circuit current calculated by applying (19) to the example of Figure 12.

Parameter	Value	Comment
a	0.137 m	GMR for a quad bundle with spacing of 0.305 m and subconductor diameter of 2.861 cm, calculated using standard equations in [2].
d	0.44 m	Human model is about 0.3m in depth. Average distance from the front of the person to the tower surface is about 14 cm (4 cm at the feet with a tower surface slope of about 8:1 at the height of the lowest conductor).
h	5.26 m	Approximately 5.7 meters from the center of the lowest bundle to the surface of the tower.
V_LG	230.94 kV	400 kV line-to-line nominal voltage (rms) at a frequency of 50 Hz.
V_OC	8075 Volts	Volts rms calculated using (19).
c_Th	80 pF	The high end of the suggested range.
I_microshock	0.203 mA rms	Compare to the maximum simulated result of 0.204 mA rms.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Submitted:

11 October 2023

Posted: