Two Interference Mechanisms of Identical Particles in Quantum Mechanics

Huai-Yu Wang

doi:10.20944/preprints202310.0711.v1

Submitted:

10 October 2023

Posted:

11 October 2023

You are already at the latest version

Abstract

The phenomenon of interference is a characteristic of all waves. This paper reviews the interference of classical waves and of matter waves in quantum mechanics. In quantum mechanics, there are two interference mechanisms between identical particles. One is that the de Broglie wavelengths of two interference waves are the same, which is called the equal wavelength interference mechanism. The other is that the wavelengths of interference waves can also be different, in which case there should be an exchange term in additional to the direction term in the wave function. There is a fixed phase difference between the two terms, which causes interference. This is called exchange effect interference mechanism. We propose an experiment, which is simpler to what has been done, to show the exchange effect interference. There is a special case where two interference waves can satisfy both the two mechanisms. We propose an experiment to discriminate that in this case which mechanism plays a role on earth.

Keywords:

interference in quantum mechanics

;

identical particle

;

equal wavelength interference mechanism

;

exchange effect interference mechanism

Subject:

Physical Sciences - Quantum Science and Technology

I. Introduction

It is well known that when two waves meet, interference may occur. The occurrence of the interference needs certain conditions. Let us examine waves in classical mechanics and matter waves in quantum mechanics.

In the wave theory of classical mechanics, if there are two point vibration sources with the same vibration direction, their positions being at

r_{10}

and

r_{20}

, respectively. The waves they emit can be written as follows

F_{1} = A e^{i (2 π | r - r_{10} | / λ_{1} - ω_{1} t)}, F_{2} = B e^{i (2 π | r - r_{20} | / λ_{2} - ω_{2} t)} .

(1)

In the area they encounter, the two waves superimpose.

F = F_{1} + F_{2} = A e^{i (2 π | r - r_{10} | / λ_{1} - ω_{1} t)} + B e^{i (2 π | r - r_{20} | / λ_{2} - ω_{2} t)} .

(2)

After the superposition, the total wave intensity becomes

| F |^{2} = | A |^{2} + | B |^{2} + 2 Re (A^{*} B e^{- i 2 π (| r - r_{10} | / λ_{1} - | r - r_{20} | / λ_{2}) + i (ω_{1} - ω_{2}) t}) .

(3)

The in tensity at every position varies with time. Suppose that the two sources have the same vibration frequency:

ω_{1} = ω_{2} = ω

(4)

In a medium, there is a relationship between frequency and wavelength. When two waves’ frequencies are the same, their wavelengths are same either:

λ_{1} = λ_{2} = λ .

(5)

Under the conditions (4) and (5), Eq. (3) is reduced to be

| F |^{2} = | A |^{2} + | B |^{2} + 2 Re (A^{*} B e^{- i 2 π (| r - r_{10} | - | r - r_{20} |) / λ}) .

(6)

At any time, there is a fixed phase difference

2 π (| r - r_{10} | - | r - r_{20} |) / λ

between the two waves at every position. The strength varies with spatial coordinates but not with time. A stable interference pattern is formed, which is the interference of waves [1].

There are three conditions for two waves to interference: their vibration directions are the same; their vibration frequencies are the same, and there is a fixed phase difference at each point in space. Note that the same frequency can also be said to be the same wavelength.

In quantum mechanics, microscopic particles are of wave-particle duality. The famous de Broglie relations link the physical quantities describing the properties of particles with those describing the properties of waves. When a particle has a momentum p, it has a corresponding wavelength,

λ = h / p

; When it has an energy E, it has a corresponding frequency

ν = E / h

.

Due to the characteristics of wave, material waves can also interfere [2−21]. We examine if the three conditions for wave interference in classical mechanics apply to quantum mechanics. Matter waves do not have the concept of the vibration direction, so the condition of same vibration direction disappears for wave interfence in quantum mechanics. If two matter waves have the same de Broglie wavelength, interference will occur between two beams of particles.

In order to meet this condition, usually, a particle beam is separated into two or more partial beams. Then, the partial beams have the same wavelength and there is a fixed phase differences between them. After the partial beams go through some different paths, they encounter interference. There have been experiments showing this kind of interference. The simplest examples are the double-slit and multi-slit interference of electrons [2,3,4,5,6,7,8,9], double-slit interference of large molecules [10], and interference of cold neutrons [11]. The Davisson-Germer experiment [12] was to let electrons incident on a crystal to yield diffraction. In verifying the Aharonov-Bohm effect [13], an electron current was separated into two. The two currents bypassed a region where there was a magnetic field and then encountered interference [14,15,16]. A further experiment was that each of the two separated electronic currents went through a Josephson junction [17,18], and then the two currents encountered interference, which could lead to an interference pattern similar to that of double-slit interference [19,20].

In fact, the key to forming a stable interference pattern is that at each space point, there is a phase difference between interference waves that does not change over time.

The quantum interference listed above has two features. One is that the interference waves are separated from a beam of particles emitted from source, which ensures that they have a fixed phase difference in every space point, so that a stable interference pattern can be formed. If two identical particle waves are from different sources, they can also encounter interference. There has been an exquisited experiment in this regard [21]. Another feature is that interference quantum waves are identical particles. If two particles are distinguishable, can they interfere? No such experiment has been seen.

We believe that although there have been many quantum interference experiments, a comprehensive discussion of the interference mechanisms is desirable. It is necessary to explicitly write down the mathematical expressions for the interference mechanisms of matter waves in quantum mechanics. In this paper, we do not take into accout of spin. We point out that for two beams of particles of different masses, there is no interference; For idential particles, there are two interference mechanisms, one is called equal wavelength interference mechanism and the other is exchange effect interference mechanism. A special case is that when the both the mechanisms are met, which mechanism would actually work. We propose an experiment for making the distinction.

II. Two-particle interference in quantum mechanics

A wave function ψ obeys the Schrödinger equation,

i ℏ \frac{\partial}{\partial t} ψ = H ψ .

(7)

The particle density is defined by

ρ = ψ^{*} ψ .

(8)

The density’s derivative with respect to time is deduced from the Schrödinger equation,

\frac{\partial ρ}{\partial t} = \frac{1}{i ℏ} (ψ^{*} H ψ - ψ H ψ^{*}) .

(9)

For a single particle, the Hamiltonian is

H = - \frac{ℏ^{2}}{2 m} \nabla^{2} + V （ r) .

(10)

When it is substituted into (9), one obtains the continuity equation,

\frac{\partial ρ}{\partial t} = - \nabla \cdot j,

(11)

where the current density is expressed by

j = \frac{ℏ}{2 i m} (ψ^{*} \nabla ψ - ψ \nabla ψ^{*}) .

(12)

In this paper, we always consider time-independent Hamiltonian, so that the time factor in the wave function can be separated

ψ (r, t) = φ_{k} (r) e^{- i E t / ℏ} .

(13)

Hereafter, the time factor

e^{- i E t / ℏ}

is dropped when we write the wave function.

The simplest case is that there is only kinetic energy in the Hamiltonian (10) and no potential energy. This is a free particle with momentum p. Its wave function is

φ_{k} (r) = \frac{1}{{(2 π)}^{3 / 2}} e^{i k \cdot r},

(14)

where the wave vector is

k = p / ℏ

. The particle’s energy is

E = \frac{ℏ^{2} k^{2}}{2 m}

. By Eqs. (12) and (13), the current density is expressed by

j = \frac{ℏ k}{{(2 π)}^{3} m} .

(15)

The above are fundamental knowledges introduced in quantum mechanics textbooks.

Let us consider a two-particles system. The Hamiltonian is

H = - \frac{ℏ^{2}}{2 m_{1}} \nabla_{1}^{2} - \frac{ℏ^{2}}{2 m_{2}} \nabla_{2}^{2} + V (r_{1}, r_{2}) .

(16)

This is substituted into (9) to get

\frac{\partial ρ}{\partial t} = - \nabla_{1} \cdot j_{1} - \nabla_{2} \cdot j_{2},

(17)

where

j_{i} = \frac{ℏ}{2 i m_{i}} (ψ^{*} \nabla_{i} ψ - ψ \nabla_{i} ψ^{*}), i = 1, 2 .

(18)

Each momentum has a current density. The total current density is the sum of the

j_{1}

and

j_{2}

,

j = j_{1} + j_{2} .

(19)

We merely consider the cases where the interaction between the particles can be neglected, such that the Hamiltonian is simplified to be

H = - \frac{ℏ^{2}}{2 m_{1}} \nabla_{1}^{2} - \frac{ℏ^{2}}{2 m_{2}} \nabla_{2}^{2} .

(20)

The Hamiltonian is time-independent. The stationary wave function follows the eigenequation

H φ (r_{1}, r_{2}) = E φ (r_{1}, r_{2}),

(21)

where E is eigenenergy. We consider three cases.

A.: Two distinguishable particles

The wave function can be written as the product of the two single-particle wave functions:

φ = φ_{k 1} (r_{1}) φ_{k 2} (r_{2}) = \frac{1}{{(2 π)}^{3}} e^{i (k_{1} \cdot r_{1} + k_{2} \cdot r_{2})} .

(22)

The equation is substituted into (21) to get the energy

E = \frac{ℏ^{2} k_{1}^{2}}{2 m_{1}} + \frac{ℏ^{2} k_{2}^{2}}{2 m_{2}} .

(23)

By Eqs. (22) and (9), the current densities of the two momenta are respectively

j_{1} = \frac{ℏ k_{1}}{{(2 π)}^{3} m_{1}}, j_{2} = \frac{ℏ k_{2}}{{(2 π)}^{3} m_{2}} .

(24a)

The total current density is

j = \frac{ℏ}{{(2 π)}^{3}} (\frac{k_{1}}{m_{1}} + \frac{k_{2}}{m_{2}}) .

(24b)

When there are N free particles, the total wave function is the product of the N free-particle wave functions,

φ = φ_{k 1} (1) φ_{k 2} (2) \dots φ_{k N} (N)

. Then, from the Hamiltonian of the N free particles, one obtaines that on the right hand side of (24b), there are N terms. It is natural that the total current is

j = j_{1} + j_{2} + \dots + j_{N}

.

Equation (24) shows that the current in space is a constant. The density calculated from the wave function (22) by Eq. (8) is also a constant everywhere. Therefore, when two particle waves of different masses encounter, no interference occurs.

B.: Two identical particles with $| k_{1} | = | k_{2} |$ and with no exchange effect

In the case of identical particles, the two masses in Eqs. (16)-(19) are the same

m_{1} = m_{2} = m .

(25)

When their de Broglie wave vectors are the same,

| k_{1} | = | k_{2} | = k,

(26)

the total wave function can be written as the linear superposition of the two single-particle wace functions,

φ = A φ_{k 1} (r_{1}) + B φ_{k 2} (r_{2}) = \frac{1}{{(2 π)}^{3}} (A e^{i k_{1} \cdot r_{1}} + B e^{i k_{2} \cdot r_{2}}) .

(27)

Using (27) in (21), we chieve the energy:

E = \frac{ℏ^{2} k^{2}}{2 m} .

(28)

By eqs. (27) and (8), the particle density is

| ψ |^{2} = | A |^{2} + | B |^{2} + 2 Re (A B^{*} e^{i (k_{1} \cdot r_{1} - k_{2} \cdot r_{2})}) .

(29)

It varies in space but independent of time. So, a stationary interference pattern is formed. Equation (29) seems formally similar to (6), but their expressions of phase difference are not the same. In (29), the fixed phase difference is

k_{1} \cdot r_{1} - k_{2} \cdot r_{2}

, which is just the difference of the phases in the two terms in the wave function (27). When (27) is substituted into (18), the expression of the total current density has also this phase difference.

Thus, interference occurs between two beams of identical particles, provided that their de Broglie wavelengths are equal, see (26). This interference mechanism can be called equal wavelength interference mechanism. The experiments [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20] mentioned above belong to this mechanism.

Suppose that three particle beams with the same de Broglie wave length encounter. The Hamiltonian is

H = - \frac{ℏ^{2}}{2 m} (\nabla_{1}^{2} + \nabla_{2}^{2} + \nabla_{3}^{2})

and the wave functions contains three terms,

A e^{i k_{1} \cdot r_{1}} + B e^{i k_{2} \cdot r_{2}} + C e^{i k_{3} \cdot r_{3}}

,

| k_{1} | = | k_{2} | = | k_{3} |

. The corresponding energy is still (28). In the superposition area, the expression of the particle density

| ψ |^{2}

has three fixed phase differences:

k_{1} \cdot r_{1} - k_{2} \cdot r_{2}

,

k_{2} \cdot r_{2} - k_{3} \cdot r_{3}

, and

k_{3} \cdot r_{3} - k_{1} \cdot r_{1}

. The interference pattern is the superposition of those with three periods. If there are N particles with differenct momenta, the total wave function of the linear combination of N sinlge-particle wave functions. The corresponding energy is still (28), and the number of fixed phase difference is

C_{n}^{2} = \frac{N!}{2! (N - 2)!}

.

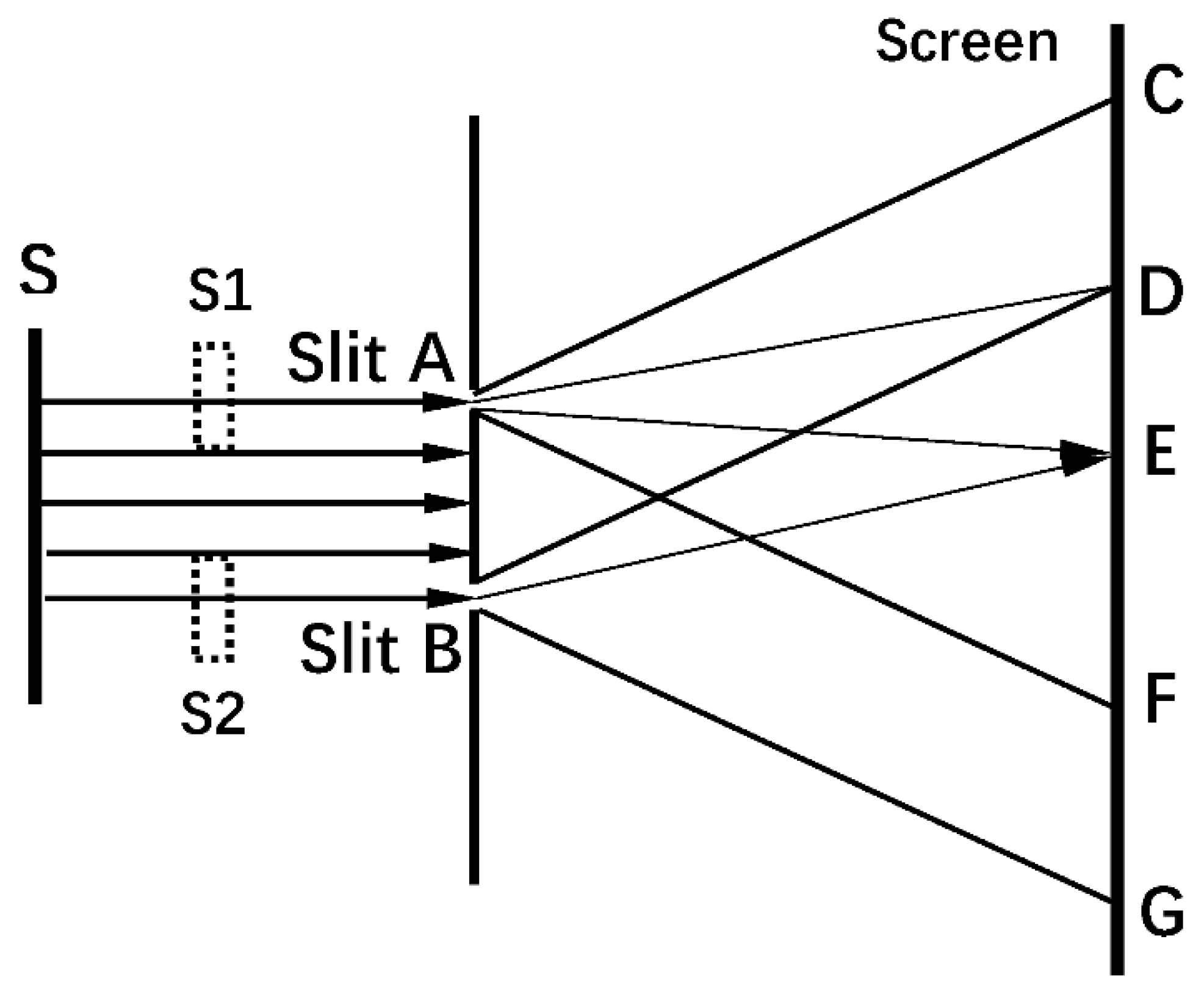
Figure 1 illustrates the interference of two particle beams of this kind of interference mechanism. In every point on the screen in Figure 1, say, point E, the wave vectors of the paarticles coming from the slits A and B are different, while their de Broglie wavelengths are equal.

The construction of the wave function (27) actually does not require that two particle waves come from the same particle source. They can come from different particle sources. In Figure 1, we draw two small dotted rectangles that represent two imagined particle sources, S1 and S2, independent of each other. The particles passing through the two slits A and B can respectively come from these two sources with the same de Broglie wavelength. When the single source S is replaced by the sources S1 and S2, the interference pattern in the screen will remain unchanged.

C.: Two identical particles with exchange effect

If the de Broglie wavelengths of the two beams of particles are not equal, the wave function (27) does not satisfy equation (21). Oppenheimer [22] first noted that the wave function of two identical particles should be written in the form of symmetry or antisymmetry with respect to particle exchange. Their wave functions are constructed as follows:

φ = \frac{1}{\sqrt{2}} [φ_{k 1} (r_{1}) φ_{k 2} (r_{2}) \pm φ_{k 1} (r_{2}) φ_{k 2} (r_{1})] = \frac{1}{\sqrt{2} {(2 π)}^{3}} {(e}^{i (k_{1} \cdot r_{1} + k_{2} \cdot r_{2})} \pm e^{i (k_{1} \cdot r_{2} + k_{2} \cdot r_{1})}) .

(30)

In this wave function, the first (second) term is called direct (exchange) term, and the upper (lower) sign stands for Bosons (Fermions). Substituting (30) into (21), we get the energy of this wave function to be the summation of the two individual particles.

E = \frac{ℏ^{2} k_{1}^{2}}{2 m} + \frac{ℏ^{2} k_{2}^{2}}{2 m} .

(31)

By Eqs. (30) and (8), we have the particle density:

| ψ |^{2} = \frac{1}{{(2 π)}^{3}} (1 \pm \cos (k_{1} - k_{2}) \cdot (r_{1} - r_{2})) .

(32)

Particle density varies with spatial coordinates but not over time. This results in a stable interference pattern. The phase difference at every space point is

(k_{1} - k_{2}) \cdot (r_{1} - r_{2})

. If (30) is substituted into (17), there is the same phase difference in the expression of the current density. The particle density varies periodically in space, the minimum value being 0.

Note that the wave vectors of the two interference waves are not the same. Therefore, they come from different particle sources. See [21] for such experiments.

In the wave function (30), the phase differenc between the direct and exchange terms is

k_{1} \cdot r_{1} + k_{2} \cdot r_{2} - (k_{1} \cdot r_{2} + k_{2} \cdot r_{1}) = (k_{1} - k_{2}) \cdot (r_{1} - r_{2}) .

(33)

This is just the phase difference in Eq. (32). It is not the direct interference between the two particle beams as the case of (27). In stead, when they encounter, they first mix to a wave function containing an exchange term, and then, interference occurs between the direct and exchange terms. This is called exchange effect interference mechanism.

Compared with the conditions of classical wave interference, it is seen that in this case even the condition of equal wavelength can be discarded. The reason is that the exchange term provides the required term participating the interference.

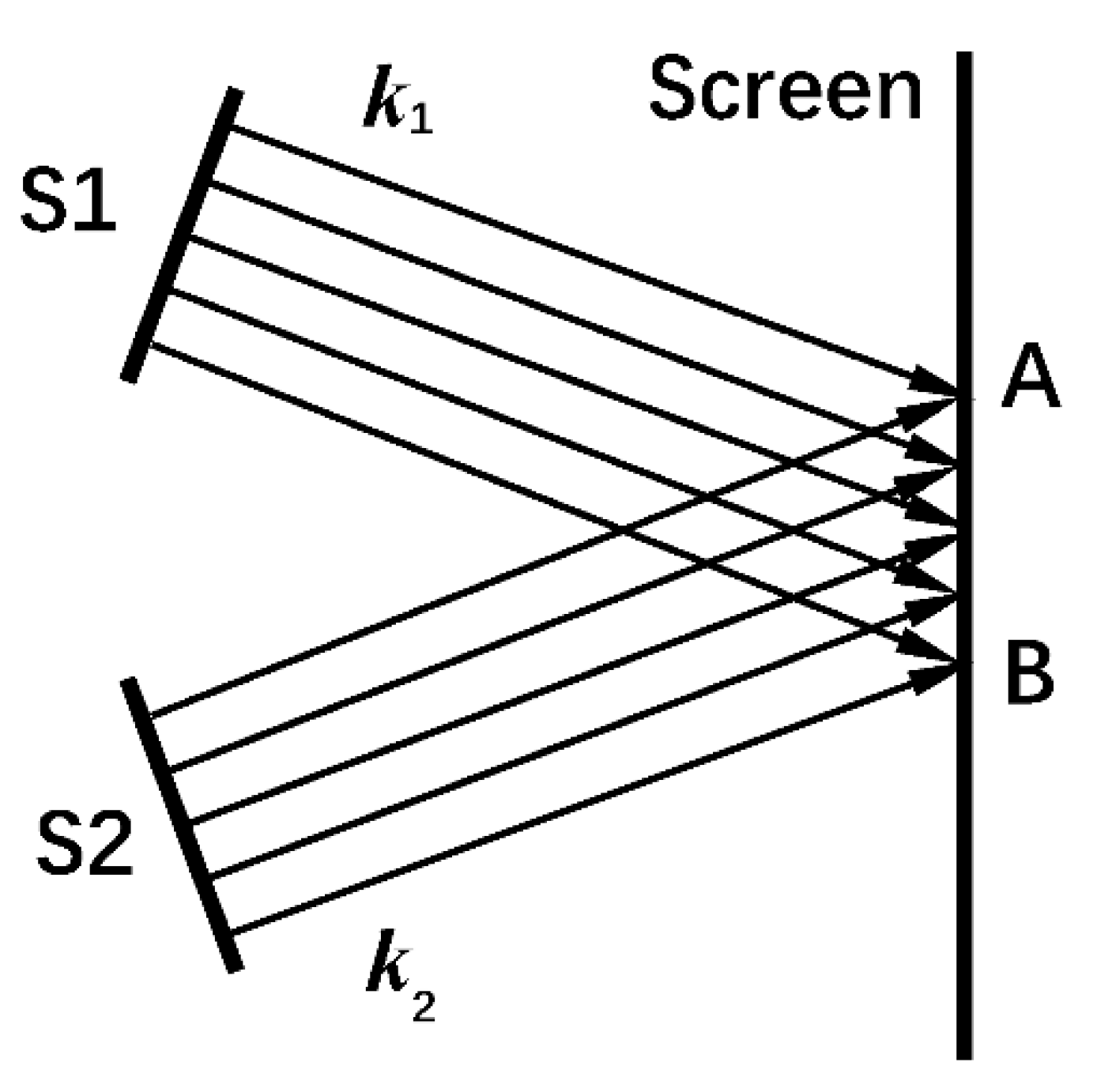
We illustrate this kind of interference in Figure 2. The particles come from two sources independent of each other. At every point on the screen, the wave vectors of particles from the two sources are always fixed. Although the interference mechanism of the experiment in [21] is the same as Figure 2, the setup in Figure 2 is much simpler. We suggest doing the experiment shown by Figure 2. This experiment is quite similar to double-slit interference.

Equation (33) applies in one-, two-, and three-dimensional spaces. In the following, we take electrons as an example.

We inspect the spatial periodicity of the interference pattern. Equation (33) helps us to make a numerical estimate. Assuming that the electron is accelerated by a voltage V to obtain the kinetic energy eV, its wave vector is

k \approx 5.129 \sqrt{V} {nm}^{- 1}

. If two electron beams move in the same direction and are subjected to voltages of 10 V and 9.5 V, respectively, then the interfering period is

2 π / | k_{1} - k_{2} | = 15.36 nm

. The smaller the absolute value of the wave-vector difference, the greater the space period. In this view, the interference period is artificially adjustable.

Table 1 lists the three interference mechanisms and corresponding expressions of spatial phase difference.

When there are two identical particles with respective wave vectors

k_{1}

and

k_{2}

, the wave function (30) has only one direct term and one exchange term, and these two terms interfere, as shown by Eq. (32). For identical particles with more wave vectors, there are more exchange terms in the multiparticle wave function. Thus, in the expression of particle density, there will be more interference terms. For example, we consider the case of three wave vectors

k_{1}

,

k_{2}

, and

k_{3}

. The three-particle wave function contains one direct term and five exchange terms. The energy is

E = - \frac{ℏ^{2}}{2 m} (k_{1}^{2} + k_{2}^{2} + k_{3}^{2})

. There are three wave vector difference,

k_{1} - k_{2}

,

k_{2} - k_{3}

, and

k_{3} - k_{1}

, so that the expression of the particle density contains three interference terms, and the interference patter is the superposition of those of three interference periods. In general, if there are N wave vectors,

k_{1}, k_{2}, \dots, k_{n}

, in a beam of identical particles, the N-particle wave function contains

N!

terms, where one is the direct term and all others are exchange terms. The number of wave vector difference,

k_{1} - k_{2}, k_{1} - k_{3}, \dots, k_{n - 1} - k_{n}

, is

C_{n}^{2} = \frac{N!}{2! (N - 2)!}

. The particle density contains

C_{n}^{2}

interference terms and the interference pattern is the superposition of

C_{n}^{2}

interference periods.

For the case of two wave interference, the two independent sources can be arbitrarily placed. They can be linear sources or planar sources. It follows that interference can be formed in one-, two, and three-dimensional space.

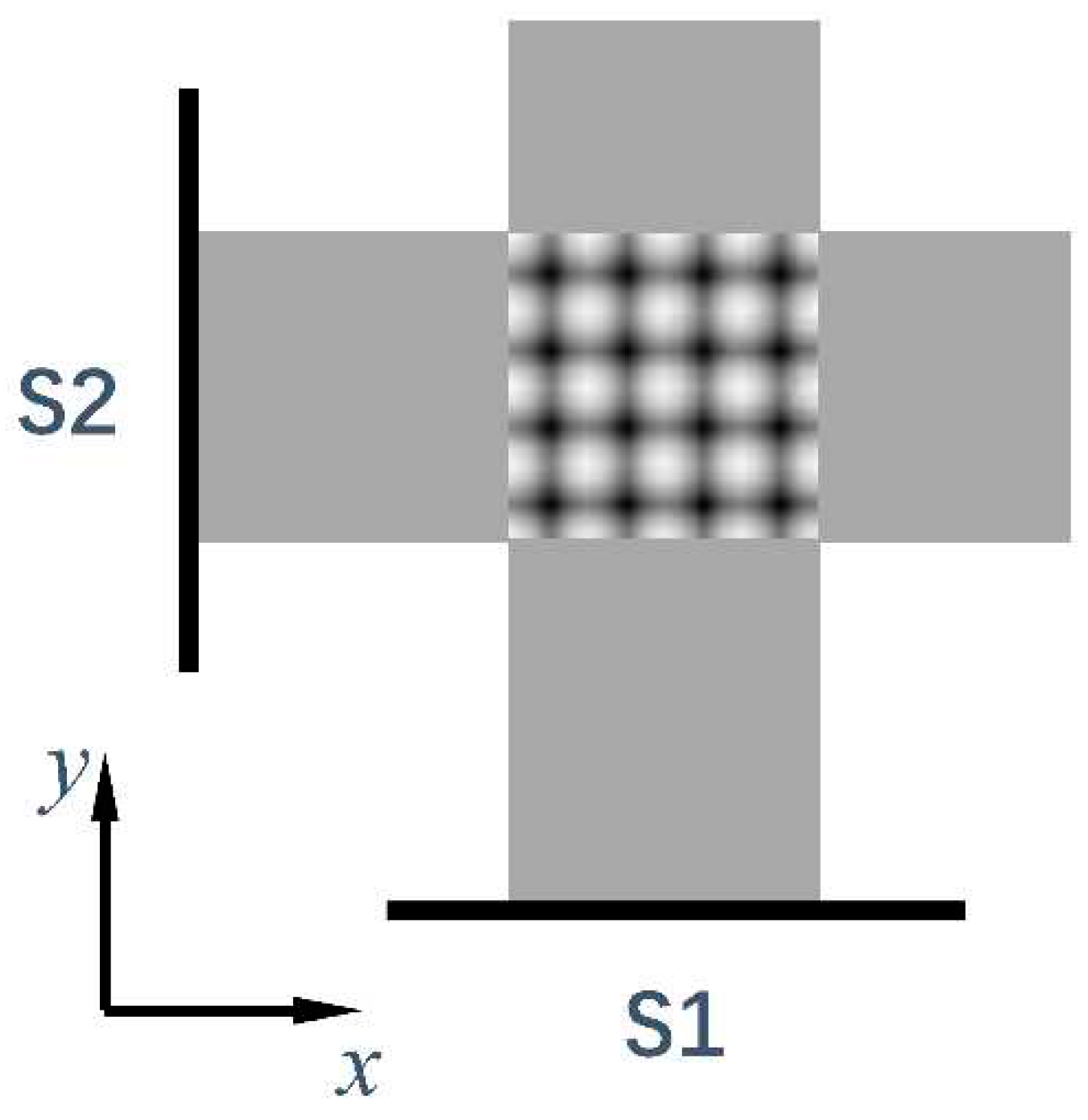
In Figure 2, the two electron berms form one-dimensional interference pattern on the screen. If the two sources are placed in the way of Figure 3, such that the two wave vectors

k_{1}

and

k_{2}

of the emitted electron beams are respectively along the x and y directions, the interference pattern is formed in two-dimensional space. If the sources in Figure 3 have widths along the z directions, i.e., planar sources, and

k_{1}

and

k_{2}

have z components, then, the interference pattern can be formed in three-dimensional space.

In Figure 3, an interference maximum, a black ball, can be regarded as a “density particle”. The interference pattern can be regarded as a “density crystal” formed by the periodic arrangement of density particles. Note that such a density crystal is suspended in the air.

Suppose that the two electron current densities emitted by the sources are the same. From Eq. (32), we know that each density particle contains twice the physical quantity of an electron, such as the mass m and charge e. Therefore, the electrons behave as being paired.

D.: A special case

In Figure 2, the two beams of electrons can have equal de Broglie wavelength, although their wave vectors are not he same. In that case, the two electron beams also meet equal wavelength interference mechanism besides the exchange effect interference mechanism. Then, which mechanism do the two electron waves interfere by on earth? In other words, is the total wave function in the interference region Eq. (27) or (30)? It is not easy to give an answer.

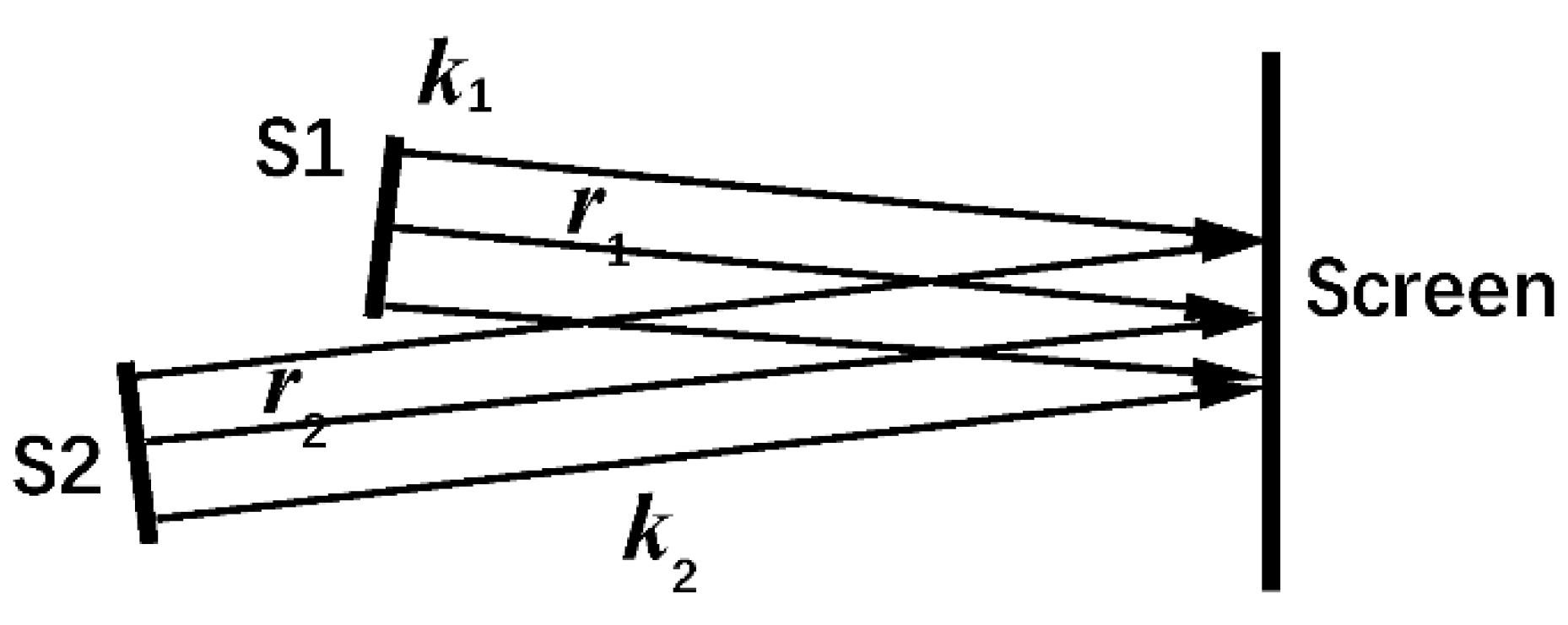
We suggest an experiment to make a distinction. Let the two sources emit electrons with equal de Broglie wavelength,

| k_{1} | = | k_{2} |

. The two sources are placed such that the two emitted beams are almost parallel, i.e.,

k_{1} \approx k_{2}

, see Figure 4. Then,

(k_{1} - k_{2}) \cdot (r_{1} - r_{2}) \approx 0 .

(34)

This phase difference is nearly zero. Hence, for exchange effect interference mechanism, the interference fringes are hardly to see. While for equal wavelength interference mechanism, the fixed phase difference is

k_{1} \cdot r_{1} - k_{2} \cdot r_{2} = k_{1} \cdot (r_{1} - r_{2}) + (k_{1} - k_{2}) \cdot r_{2} \approx k_{1} \cdot (r_{1} - r_{2}) .

(35)

This phase difference depends on the position vector difference

r_{1} - r_{2}

.

Let the electron source S2 in Figure 4 be arranged such that it can move in the direction of the

k_{2}

. Then, when S2 moves,

r_{2}

varies while

r_{1}

does not. The phase difference (34) is always about zero, while the phase difference (35) varies with the

r_{2}

. Therefore, when S2 moves, if the pattern on the screen does not change, it is an exchange effect interference mechanism, while if the pattern changes, it is the equal wavelength interference mechanism.

III. CONCLUSION

This paper reviews the interferences in classical mechanics and in quantum mechanics. In quantum mechanics, there is no interference between distinguishable particles. In the case identical particles, interference can occur. There are two interference mechanisms. One is the equal wavelength interference mechanism. That is, the de Broglie wavelengths of the particles participating in the interference are equal. The exchange effect does not play a role. The other is the exchange effect interference mechanism. That is, the two-particle wave function contains an exchnange term in addition to the direct term, and the two terms interfere. These two interference mechanisms have different expressions for phase differences.

A special case is that when the wavelengths of two beams of identical particles are just equal and exchange effect is also taken into account, it conforms both the two mechanisms. So, which interference mechanism will the two participating partilce beams follow? We propose an experiment to make a ddistinction.

Acknowledgments

This work is supported by the National Natural Science Foundation of China under Grant No. 12234013 and the National Key Research and Development Program of China under Nos. 2018YFB0704304 and 2016YFB0700102.

References

F. S. Crawford, Waves Berkeley physics course (McGraw-Hill Book Co., New York, 1968).
O. Donati, G. P. Missiroli, G. Pozzi, “An Experiment on Electron Interference,” Am. J. Phys. 41, 639–644 (1973). [CrossRef]
C. Jönsson, “Electron Diffraction at Multiple Slits” Am. J. Phys. 42, 4−12 (1974). [CrossRef]
P. G. Merli, G. F. Missiroli, and P. Pozzi P, “On the statistical aspect of electron interference phenomena,” Am. J. Phys. 44, 306−307 (1976). [CrossRef]
G. Matteucci; G. Pozzi, “Two further experiments on electron interference,” Am. J. Phys. 46, 619–623 (1978). [CrossRef]
A. Tonomura, J. Endo, T. Matsuda, T. Kawasaki, and H. Ezawa, “Demonstration of single-electron buildup of an interference pattern,” Am. J. Phys. 57, 117−120 (1989). [CrossRef]
S. Frabboni, G. C. Gazzadi, and G. Pozzi, “Young’s double-slit interference experiment with electrons,” Am. J. Phys. 75, 1053−1055 (2007). [CrossRef]
S. Frabboni, C. Frigeri, G. C. Gazzadi, G. Pozzi, “Two and three slit electron interference and diffraction experiments,” Am. J. Phys. 79, 615–618 (2011). [CrossRef]
E. Salançon, A. Degiovanni, L. Lapena, R. Morin, “From measuring electron charge to exploring particle-wave duality: A new didactic experimental approach,” Am. J. Phys. 87, 194−199 (2019). [CrossRef]
O. Nairz, M. Arndt, and A. Zeilinger, “Quantum interference experiments with large molecules,” Am. J. Phys. 71, 319−325 (2003). [CrossRef]
R. Gähler and A. Zeilinger, “Wave-optical experiments with very cold neutrons,” Am. J. Phys. 59, 316−324 (1991). [CrossRef]
C. Davisson and L., H. Germer, “The scattering of electron by a single crystal of nickel,” Nature 119(2998), 558−560 (1927). [CrossRef]
Y. Aharonov and D. Bohm, “Significance of electromagnetic potentials in quantum theory,” Phys. Rev. 115, 485−491 (1959). [CrossRef]
R. G. Chambers, “Shift of an Electron Interference Pattern by Enclosed Magnetic Flux,” Phys. Rev. Lett. 5, 3−5 (1960). [CrossRef]
A. Tonomura, N. Osakabe, T. Matsuda, T. Kawasaki, J. Endo, S. Yano, and H. Yamada, “Evidence for Aharonov-Bohm effect with magnetic field completely shielded from electron wave,” Phys. Rev. Lett. 56, 792−795 (1986). [CrossRef]
A. Tonomura, “Applications of electron holography,” Rev. Mod. Phys. 59, 639−669 (1987). [CrossRef]
B. D. Josephson, “Possible new effects in superconductive tunneling,” Physics Letters 1(7), 251−253 (1962). [CrossRef]
J. M. Rowell, “Magnetic Field Dependence of the Josephson Tunnel Current,” Phys. Rev. Lett. 11, 200−202 (1963). [CrossRef]
R. C. Jaklevic, J. Lambe, A. H. Silver, and J. E. Mercereau, “Quantum Interference Effects in Josephson Tunneling,” Phys. Rev. Lett. 12, 159−160 (1964). [CrossRef]
R. C. Jaklevic, J. J. Lambe, A. H. Silver, and J. E. Mercereau, “Quantum Interference from a Static Vector Potential in a Field-Free Region,” Phys. Rev. Lett. 12, 274−275 (1964). [CrossRef]
I. Neder, N. Ofek, Y. Chung, M. Heiblum, D. Mahalu, and V. Umansky, Interference between two indistinguishable electrons from independent sources. Nature 448, 333−337 (19 July, 2007). [CrossRef]
J. R. Oppenheimer, “On the quantum theory of electronic impact,” Phys. Rev. 32, 361−376 (1928). [CrossRef]

Figure 1. Illustration of the interference with equal wavelength interference mechanism. Since the particles passing through the two slits A and B come from one particle source S, their de Broglie wavelengths are equal. Two small dashed rectangles representing hypothetical independent particle sources S1 and S2 respectively emit particles with the same de Broglie wavelength.

Figure 2. Illustration of the interference with exchange effect interference mechanism. At every point on the screen, the wave vectors

k_{1}

and

k_{2}

of particles from the two sources are always fixed.

Figure 2. Illustration of the interference with exchange effect interference mechanism. At every point on the screen, the wave vectors

k_{1}

and

k_{2}

of particles from the two sources are always fixed.

Figure 3. The sources S1 and S2 are placed such that the wave vectors k₁ and k₂ of the emitted electrons are perpendicular to each other. In the region the two electon beams encounter, the interference pattern have a perion 2π/k₂ in the x direction and 2π/k₁ in the y direction.

Figure 4. The wave vectors of the electrons emitted by the two sources are almost parallel, and the two de Broglie wavelengths are equal. The electron source S1 is fixed. The electron source S2 can move in the direction of k₂.

Table 1. Three interference mechanisms. The

| r - r_{01}

and

r - r_{02}

in classical interference correspond to

r_{1}

and

r_{2}

in quantum interference, respectively.

Table 1. Three interference mechanisms. The

| r - r_{01}

and

r - r_{02}

in classical interference correspond to

r_{1}

and

r_{2}

in quantum interference, respectively.

Interference mechanism		Spatial phase difference
Classical wave interference		$2 π (\| r - r_{01} \| + \| r - r_{02} \|) / λ$
Quantum interference	Equal wavelength interference	$k_{1} \cdot r_{1} - k_{2} \cdot r_{2}, \| k_{1} \| = \| k_{2} \|$
	Exchange effect interference	$(k_{1} - k_{2}) \cdot (r_{1} - r_{2})$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Two Interference Mechanisms of Identical Particles in Quantum Mechanics

Abstract

Keywords:

Subject:

I. Introduction

II. Two-particle interference in quantum mechanics

III. CONCLUSION

Acknowledgments

References

MDPI Initiatives

Important Links

Subscribe