Submitted:
05 October 2023
Posted:
06 October 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
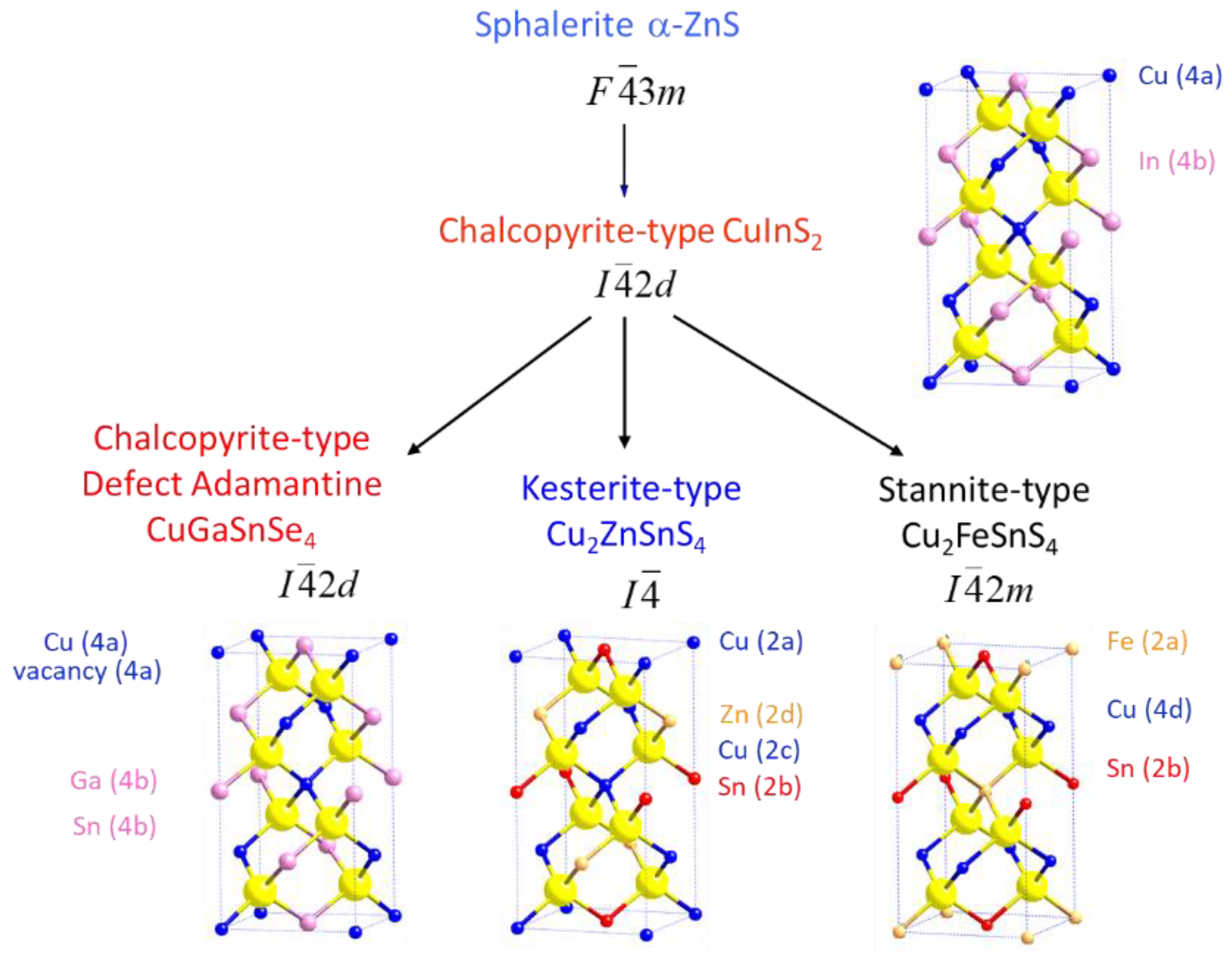
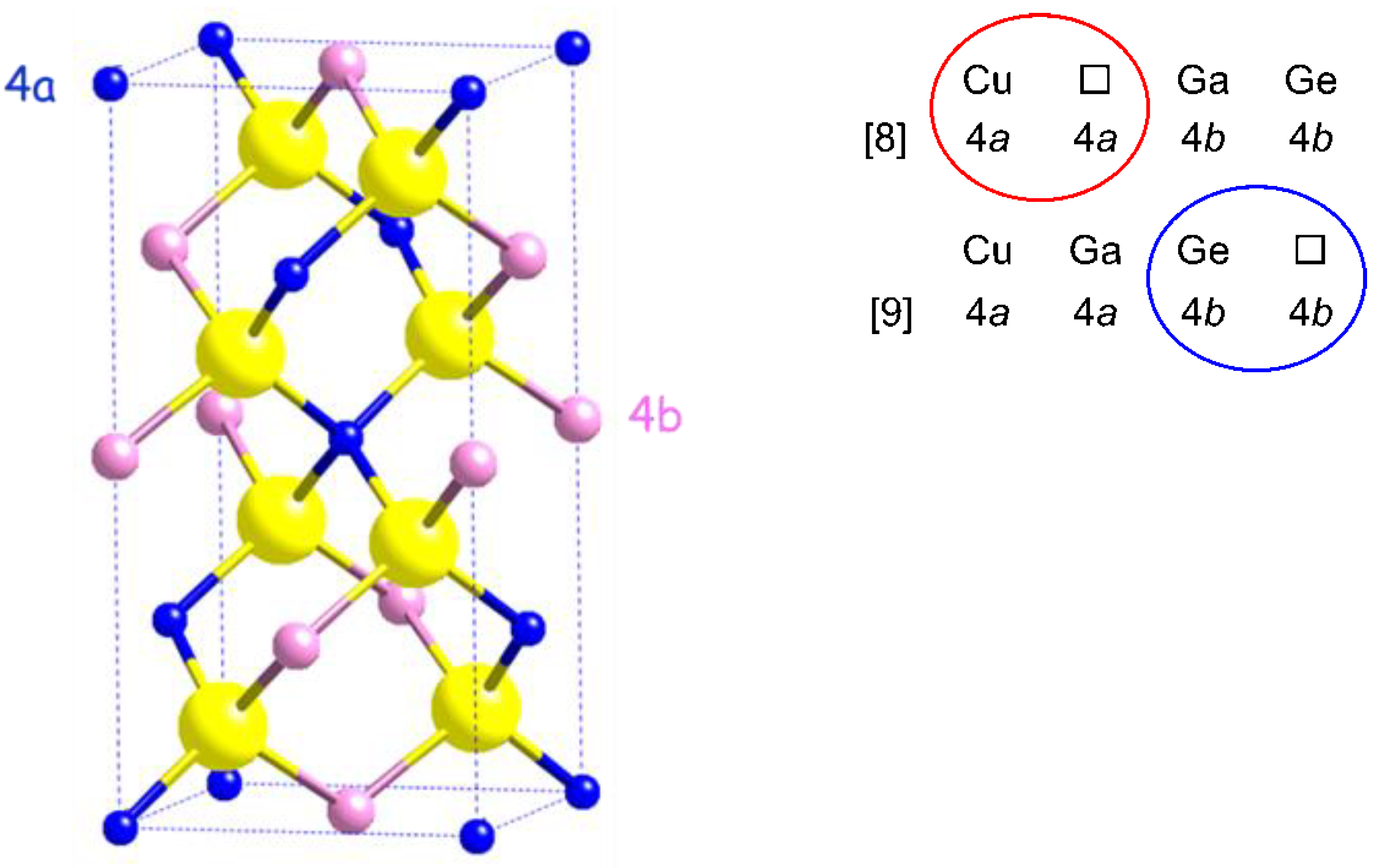
Structural considerations
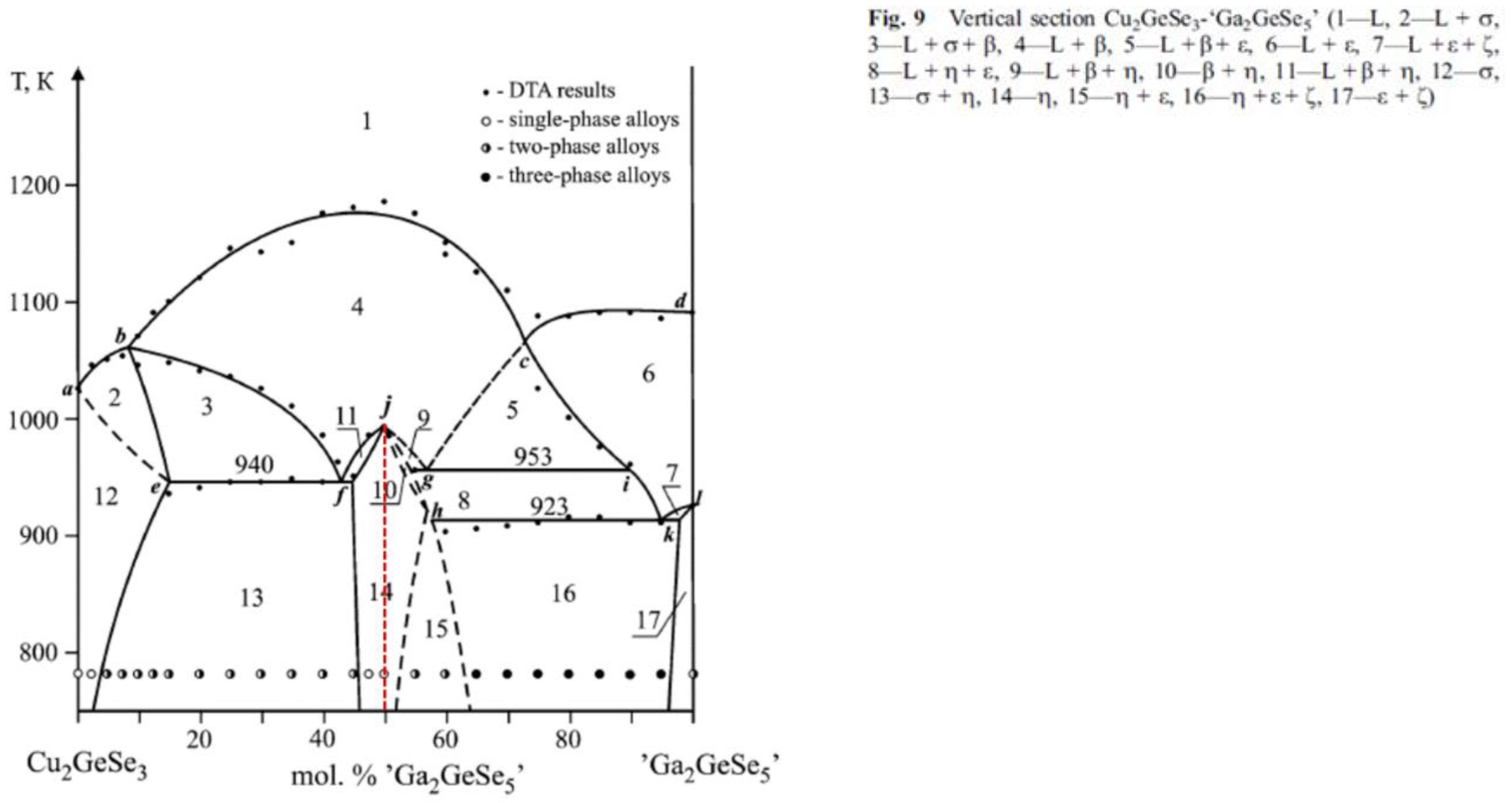
Thermodynamic properties
2. Materials and Methods
Crystal growth
Chemical characterization
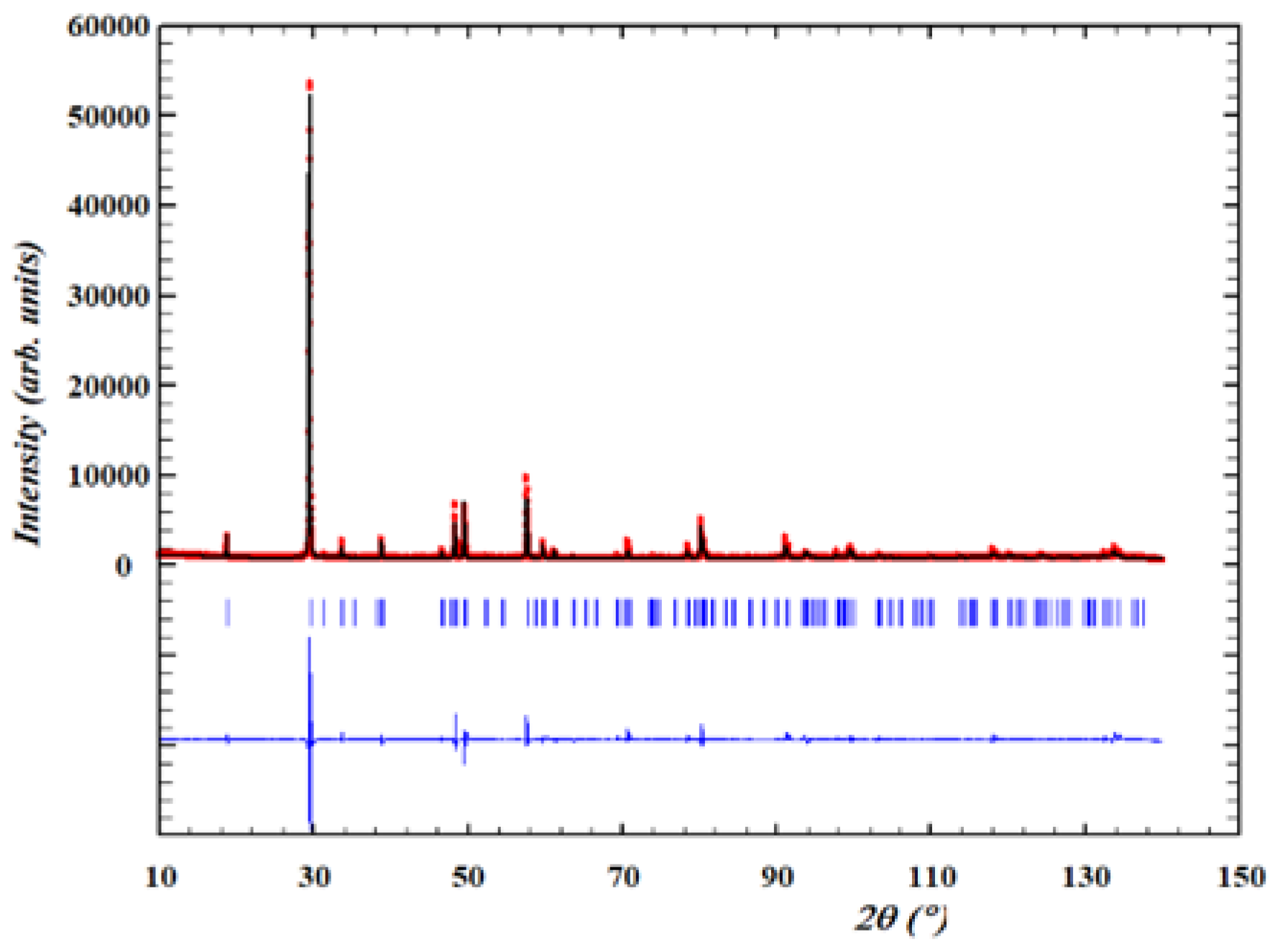
Structural characterization
Optical characterization
3. Results and Discussion
Crystal growth
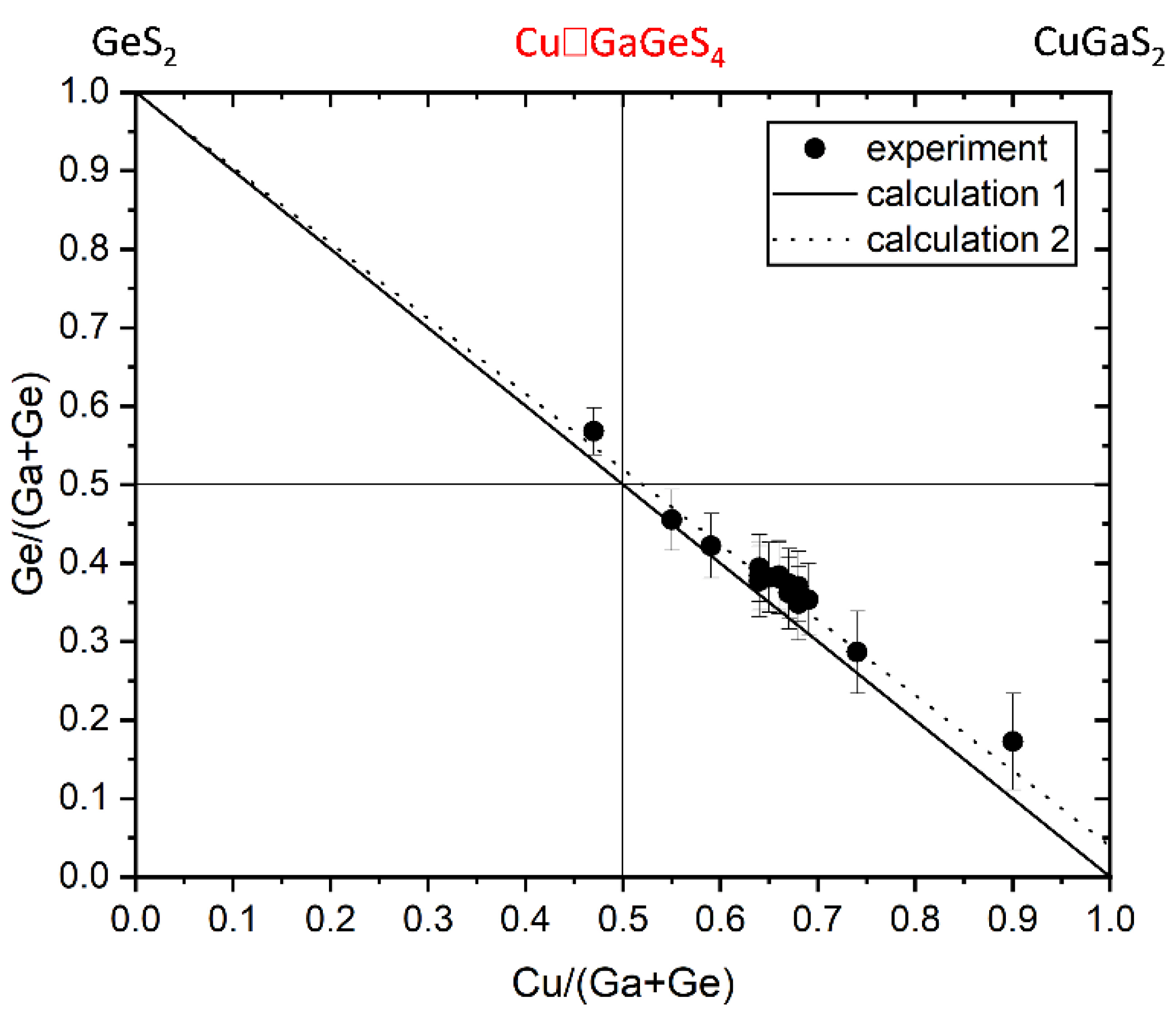
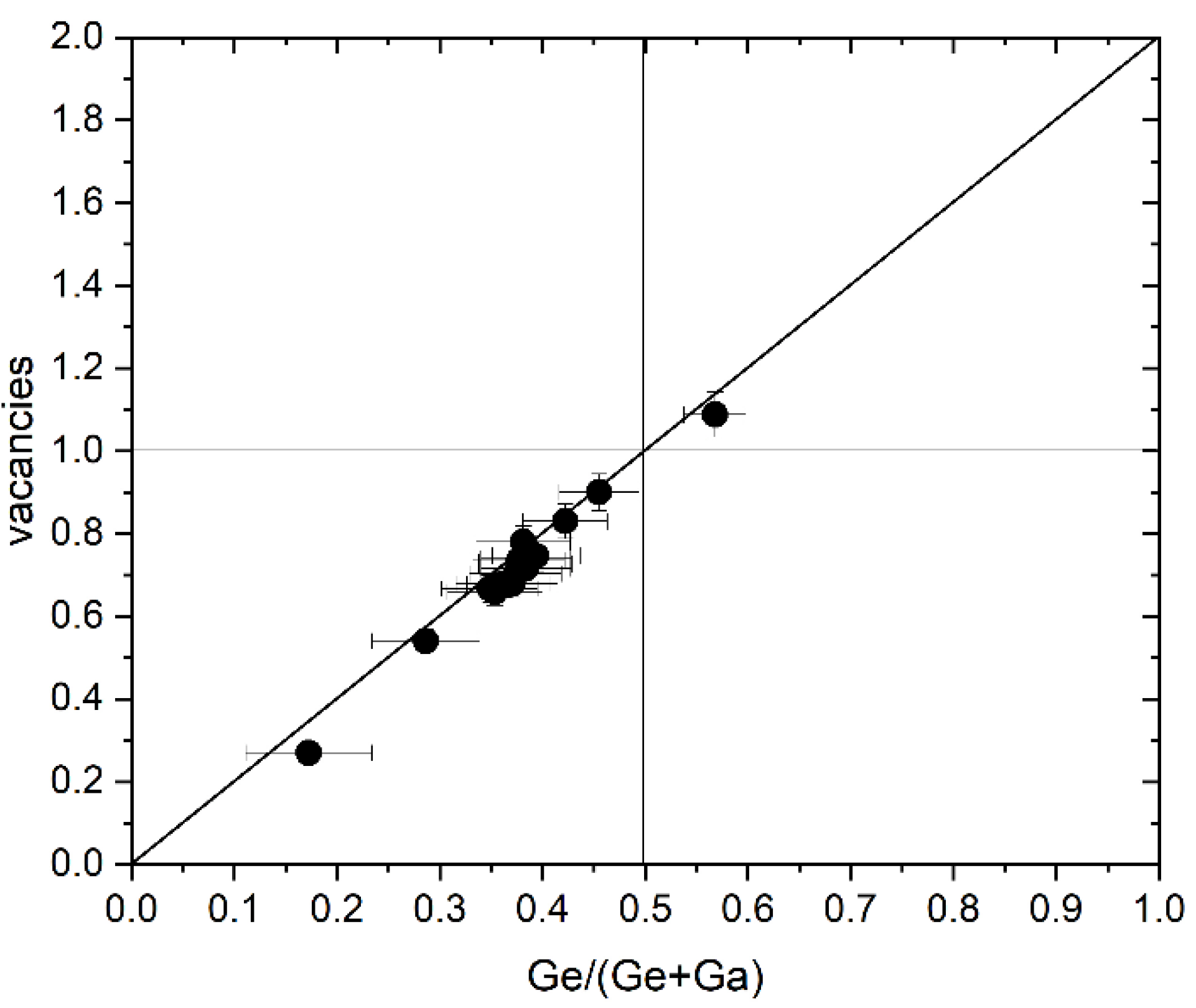
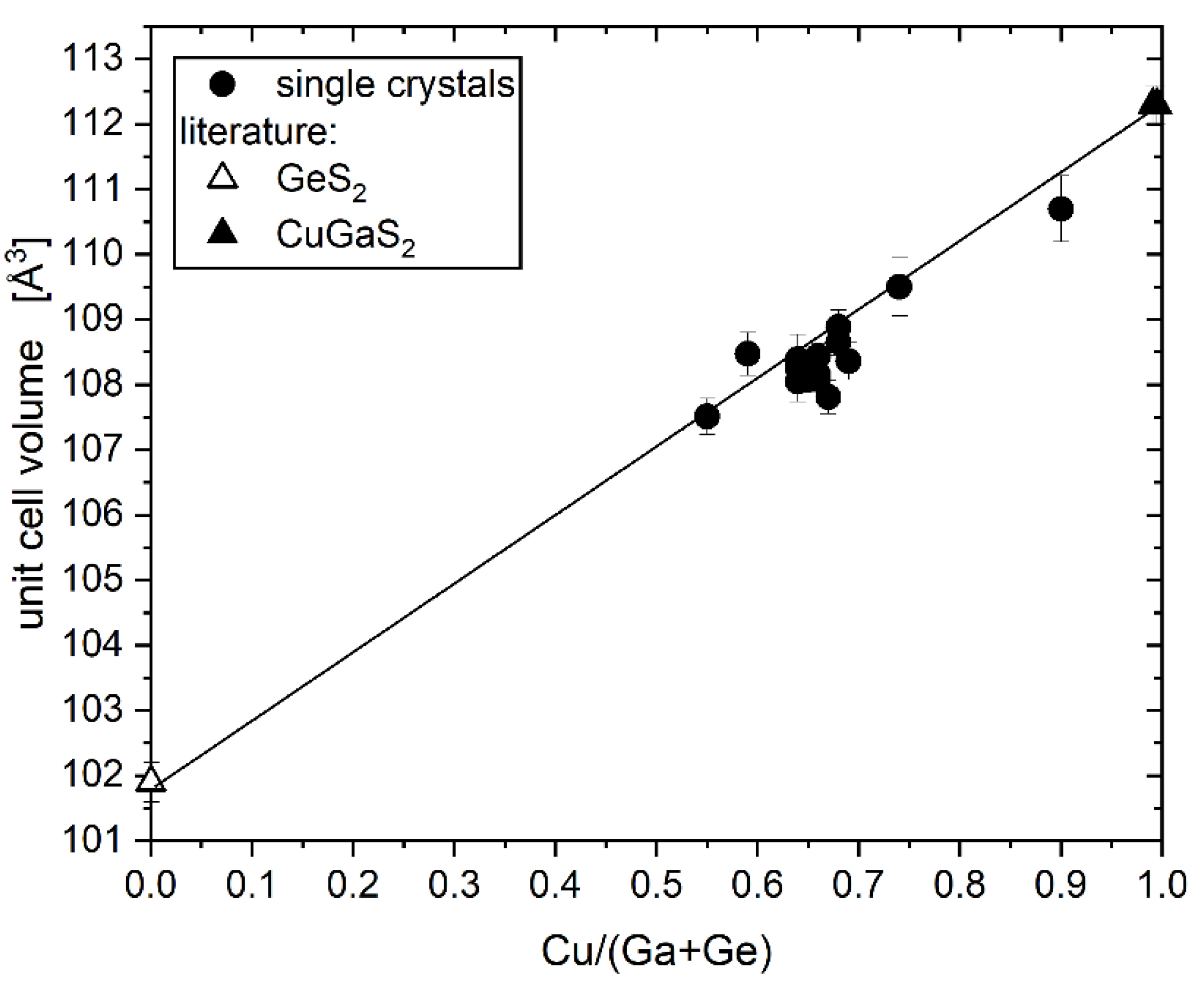
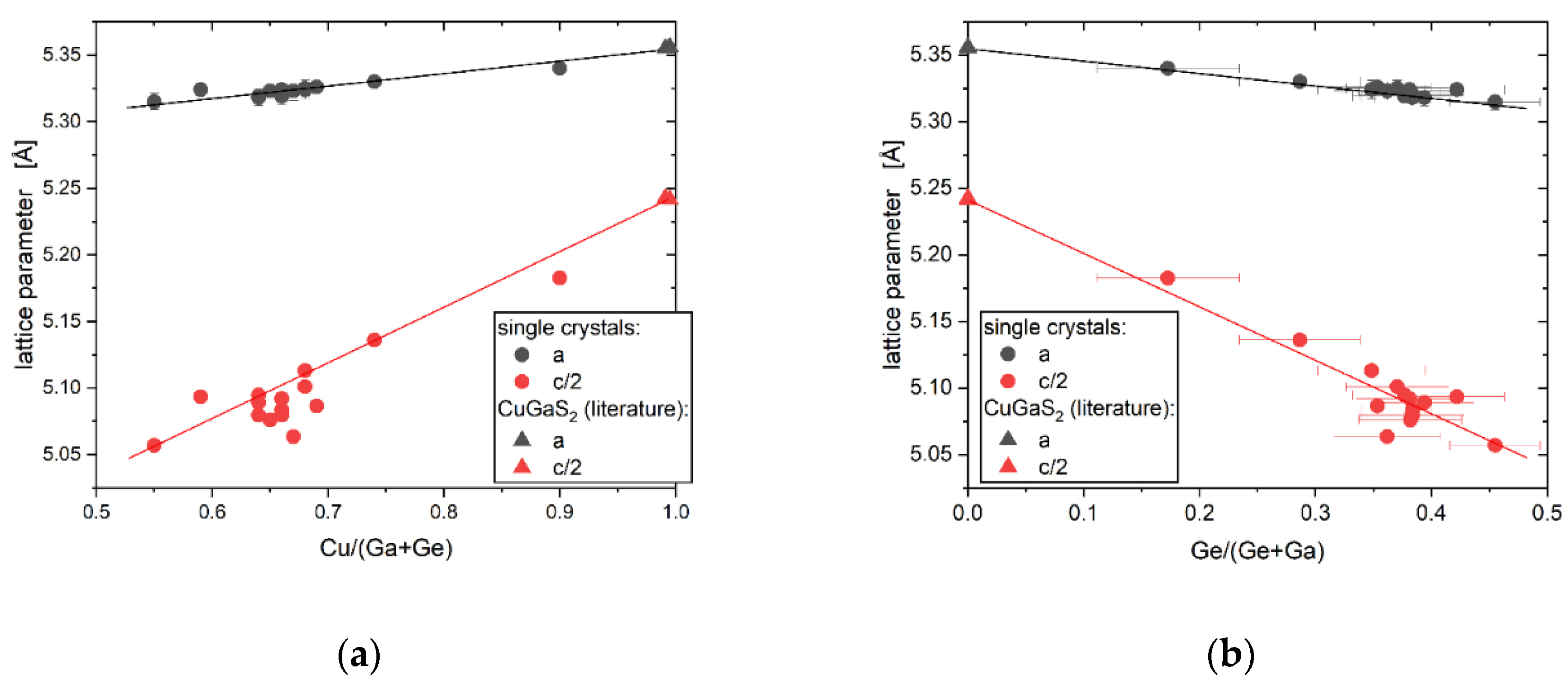
Chemical composition and off-stoichiometry relations
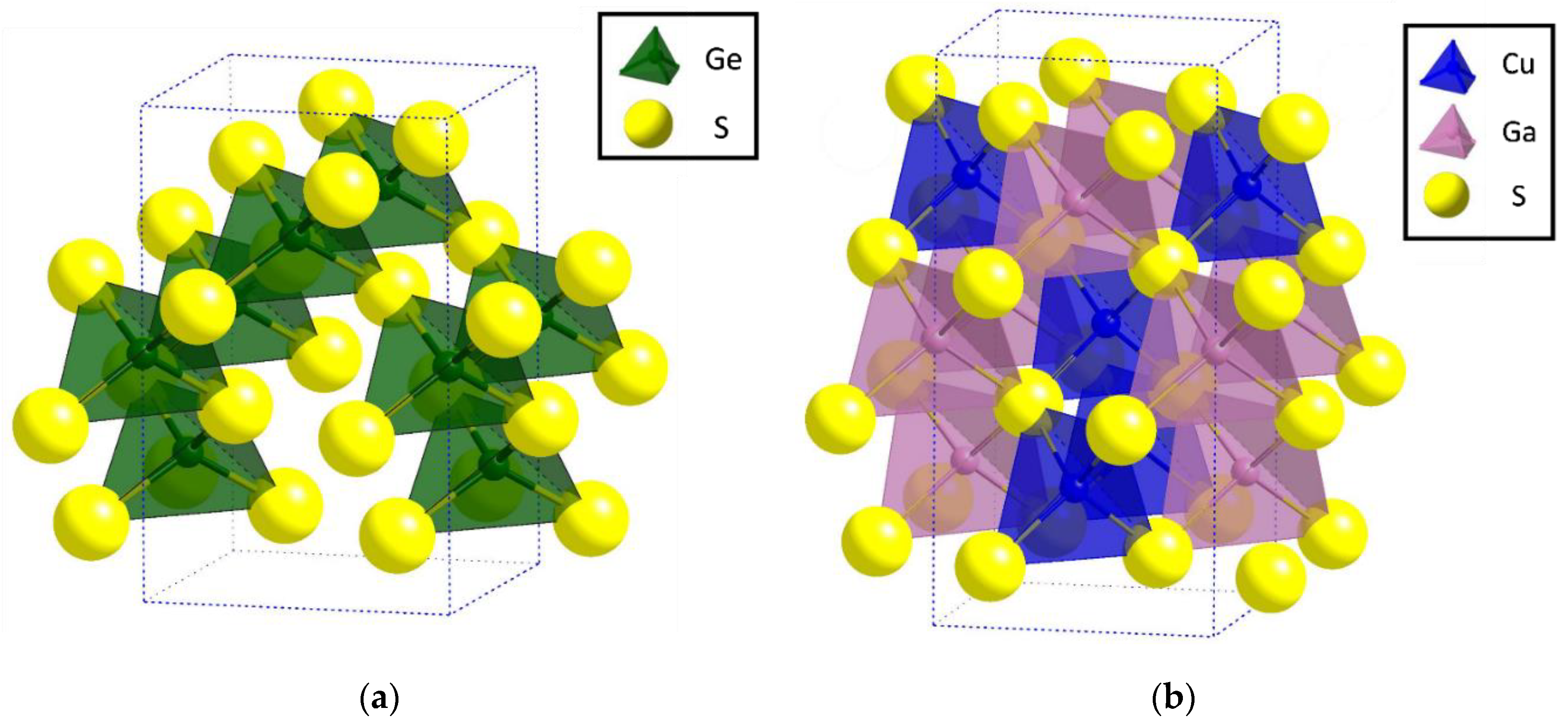
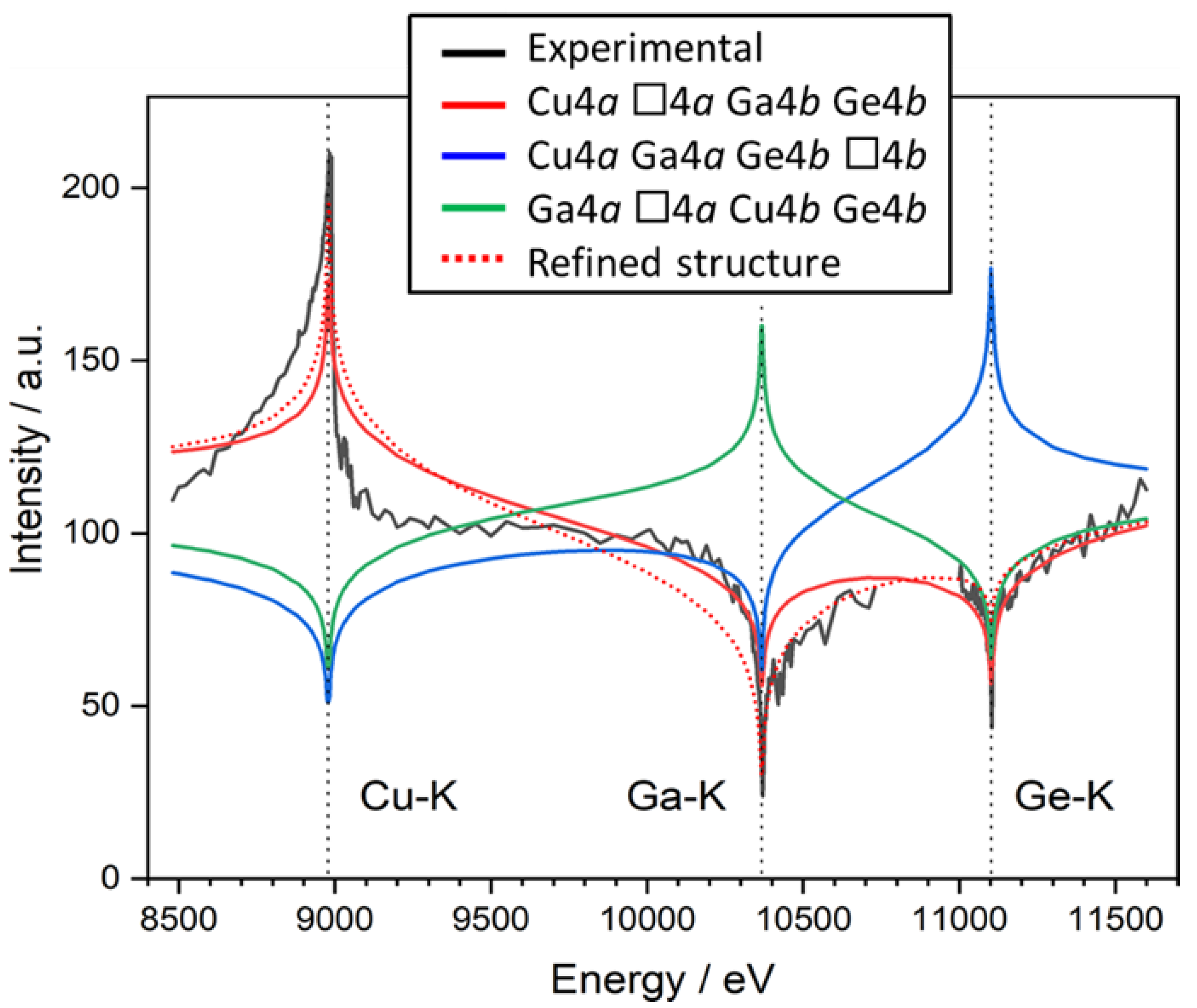
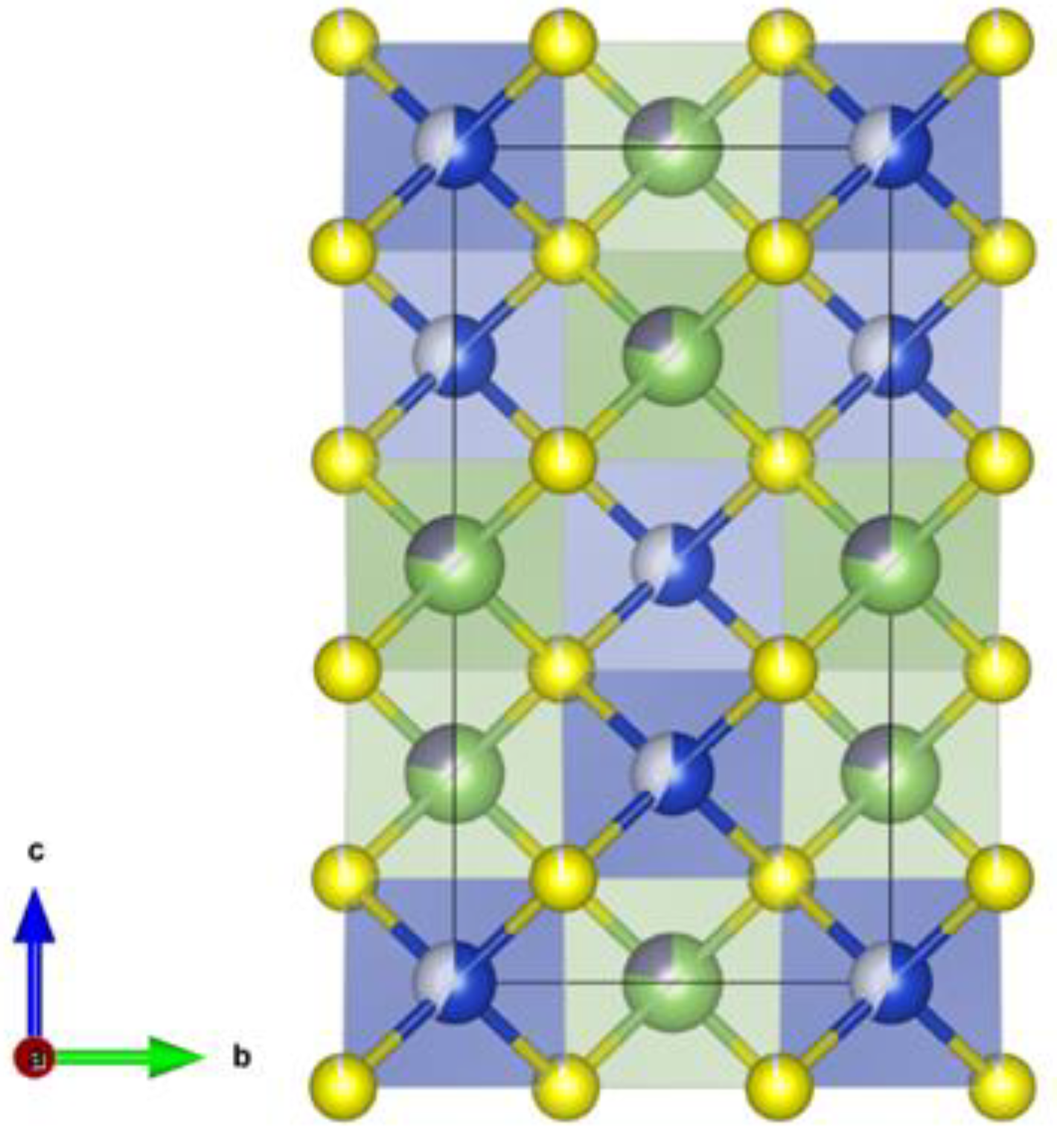
Crystal structure of Cu2(1-x)☐2(1-x)Ga2(1-x)Ge2xS4 defect adamantines
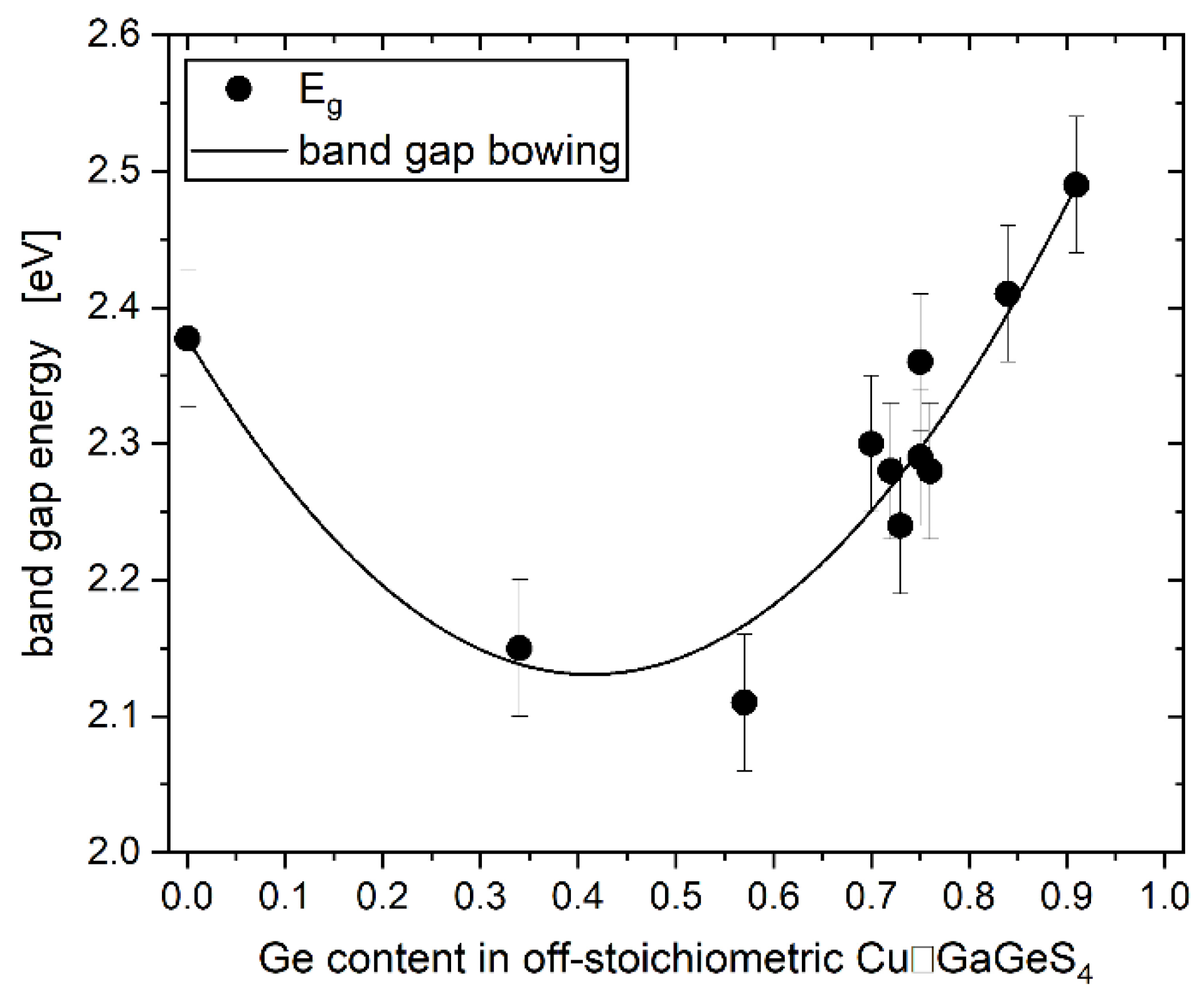
Band Gap Energy
5. Conclusions
Author Contributions
Acknowledgements
Conflicts of Interest
References
- Pamplin, B. The Adamantine Family of Compounds. Prog. Cryst. Growth Charact. 1981, 3, 179-192. [CrossRef]
- Matsushita, H.; Katsui, A. Materials design for Cu-based quaternary compounds derived from chalcopyrite-rule. J. Phys. Chem. Solids 2005, 66, 1933-1936. [CrossRef]
- Maeda, T.; Matsushita, H.; Katsui, A. Crystal growth of Cu-III-Ge-Se4 Quaternary compounds (III = Ga, In) by vertical Bridgman methods. Jpn. J. Appl. Phys. 2000, 39, (39-1), 41-43. [CrossRef]
- Lopez-Rivera, S. A.; Pamplin, B. R.; Woolley, J. C. High-Temperature lattice parameters and DTA of the quaternary compound CuGaSn☐Se4. Il Nuovo Cimento 1983, 2, (6), 1728-1735. [CrossRef]
- Garbato, L.; Geddo-Lehmann, A.; Ledda, F. Growth and structural properties of quaternary copper thiostannates. J. Crystal Growth 1991, 114, 299-306. [CrossRef]
- Hahn, H.; Strick, G. Über quaternäre Chalkogenide zinkblendeähnlicher Struktur. Naturwiss. 1967, 54, (9), 225-226. [CrossRef]
- Pamplin, B. R.; Ohachi, T.; Maeda, S.; Negrete, P.; Elworthy, T. P.; Sanderson, R.; Whitlow, H. J. Solubility of the group IV chalcogenides in I-III-VI2 compounds. In Ternary Compounds Holah, G. D. Institute of Physics 1977, pp 35-42.
- Woolley, J. C.; Goodchild, R. G.; Hughes, O. H.; Lopez-Rivera, S. A.; Pamplin, B. R. Quaternary Defect Chalcopyrite Compounds I III IV VI4. Jpn. J. Appl. Phys. 1980, 19, (suppl. 19-3), 145-148. [CrossRef]
- Kistaiah, P.; Vishnuvardhan Reddy, C.; Satyanarayana Murthy, K, Thermal-expansion anisotropy in the quaternary semiconductor CuGaGe1-x(VGe)xSe4 at elevated temperatures. Phys. Rev. B 1990, 42, (11), 7186-7192. [CrossRef]
- Lopez Rivera, A. Quaternary defect adamantine compounds of the type I-III-IV-☐2-VI4. University of Bath, 1981.
- Panyutin, V. L.; Ponedelnikov, B. E.; Chizhikov, V. I. Energy band spectra of mercury selenogermanate and copper thiogermanogallate. Sov. Phys. Semicond. 1983, 17, (9), 1061-1062.
- Strok, O. M.; Olekseyuk, I. D.; Zmiy, O. F.; Ivashchenko, I. A.; Gulay, L. D. The Quasi-ternary system Cu2Se-Ga2Se3-GeSe2. Journal of Phase Equilibria and Diffusion 2013, 34, (2), 94-103. [CrossRef]
- 13. Nitsche, R, Kristallzucht aus der Gasphase durch chemische Transportreaktionen. Fortschr. Miner. 1967, 44, (2), 231-287.
- KMC-2, H.-Z. B. f. M. u. E., X-ray beamline with dedicated diffraction and XAS endstations at BESSY II. Journal of large-scale research facilities 2016, 2, A49.
- Többens, D. M.; Gurieva, G.; Niedenzu, S.; Schuck, G.; Zizak, I.; Schorr, S. Cation distribution in Cu2ZnSnSe4, Cu2FeSnS4 and Cu2ZnSiSe4 by multiple-edge anomalous diffraction. Acta Cryst. B 2020, B76, 1027-1035. [CrossRef]
- Merritt, E. A. X-ray Anomalous Scattering. Biomolecular Structure Center the University of Washington 2014.
- Tauc, J.; Grigorovici, R.; Vancu, A. Optical properties and electronic structure of amorphous Germanium. Phys. stat. sol. 1966, 15, 627-637. [CrossRef]
- Stephan, C. Structural trends in off-stoichiometric chalcopyrite type compound semiconductors. Freie Universität Berlin, Berlin, 2011.
- Materials Project (next-gen.materialsproject.org), mp-7582.
- Dittmar, G.; Schäfer, H. Die Kristallstruktur von L.T.-GeS2. Acta Crystallogr. 1976, B32, 1188-1192. [CrossRef]
- Shannon, R. D, Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Cryst. A 1976, 32, (5), 751-767. [CrossRef]
- Bérar, J.-F.; Lelann, P. E.S.D.'s and estimated probable error obtained in Rietveld refinements with local correlations. J. Appl. Cryst. 1991, 24, (1), 1-5. [CrossRef]
- Kubelka, P.; Munk, F. Ein Beitrag zur Optik der Farbanstriche. Z.Techn.Physik 1931, 12, 593-601.
- Kubelka, P. New contributions to the optics of intensely light-scattering materials. Part I. J.Opt.Soc.Am. 1948, 38, 448-457. [CrossRef]

| Cu☐GaGeS4 | Cu☐GaGeSe4 | |||
| tetragonal [6] | tetragonal [7] |
tetragonal [8] |
tetragonal [9] |
|
|
a (Å) c (Å) |
5.334 [6] 10.050 |
5.302 [7] 10.212 |
5.568 [8] 10.841 |
5.5617 [9] 10.9238 |
| Tmelting (°C) | 1000 [2] | 1000 [10] | 836 [2] | |
| Tdecomposition (°C) | 710 [10] | |||
| Eg (eV) | 2.73 [11] | 1.85 [8] | 1.38 [3] | |
| Sample no. | Chemical formular | Cu/(Ga+Ge) | Ge/(Ge+Ga) | Iodine concentration (mg/cm3) |
a (Å) | c (Å) |
|---|---|---|---|---|---|---|
| To589 | Cu0.93☐1.08Ga0.86Ge1.13S4 | 0.467 | 0.568 | 0* | 5.330(5) | 10.203(6) |
| To557 | Cu1.10☐0.90Ga1.09Ge0.91S4 | 0.550 | 0.455 | 4.9 | 5.315(6) | 10.114(4) |
| To569 | Cu1.18☐0.83Ga1.15Ge0.84S4 | 0.593 | 0.422 | 5.0 | 5.324(1) | 10.187(6) |
| To597 | Cu1.27☐0.74Ga1.24Ge0.75S4 | 0.638 | 0.377 | 4.7 | 5.319(3) | 10.189(3) |
| To555 | Cu1.27☐0.75Ga1.22Ge0.76S4 | 0.641 | 0.384 | 4.9 | 5.318(2) | 10.159(2) |
| To329 | Cu1.27☐0.75Ga1.20Ge0.78S4 | 0.641 | 0.394 | 5.0 | 5.318(6) | 10.178(9) |
| To556 | Cu1.30☐0.69Ga1.24Ge0.77S4 | 0.647 | 0.383 | 4.9 | 5.320(4) | 10.159(3) |
| To581 | Cu1.29☐0.72Ga1.23Ge0.76S4 | 0.648 | 0.382 | 5.0 | 5.323(3) | 10.152(3) |
| To585 | Cu1.30☐0.72Ga1.23Ge0.75S4 | 0.656 | 0.384 | 8.1 | 5.324(3) | 10.184(3) |
| To583 | Cu1.30☐0.72Ga1.22Ge0.76S4 | 0.657 | 0.384 | 5.0 | 5.319(6) | 10.167(2) |
| To531 | Cu1.33☐0.68Ga1.27Ge0.72S4 | 0.668 | 0.379 | 5.0 | 5.323(7) | 10.127(3) |
| To591 | Cu1.35☐0.67Ga1.29Ge0.69S4 | 0.682 | 0.348 | 1.1 | 5.324(7) | 10.226(3) |
| To599 | Cu1.35☐0.68Ga1.24Ge0.73S4 | 0.685 | 0.371 | 3.1 | 5.330(3) | 10.272(8) |
| To580 | Cu1.36☐0.66Ga1.28Ge0.70S4 | 0.687 | 0.353 | 5.0 | 5.362(3) | 10.173(5) |
| To596 | Cu1.47☐0.54Ga1.42Ge0.57S4 | 0.739 | 0.286 | 4.7 | 5.330(3) | 10.272(8) |
| To588 | Cu1.76☐0.27Ga1.63Ge0.34S4 | 0.893 | 0.213 | 1.1 | 5.340(3) | 10.365(9) |
| literature | ||||||
| CuGaS2 [18] | 0.991 | 0 | 5.355(1) | 10.485(2) | ||
| CuGaS2 [18] | 0.995 | 0 | 5.356(1) | 10.483(2) | ||
| GeS2 [19] | 0 | 1 | 5.68 | 8.97 | ||
| Composition (refined): Cu1.152(3) Ga1.554(26) Ge0.446(26) S3.799(13) | ||||||
| Space group: | ||||||
| Atom | Wyckoff | x | y | z | Biso [Å2] | s.o.f. |
| Cu | 4a | 0 | 0 | 0 | 0.830(36) | 0.576(2) |
| Ga | 4b | 0 | 0 | 0.5 | 0.909(15) | 0.777(13) |
| Ge | 4b | 0 | 0 | 0.5 | 0.909(15) | 0.223(13) |
| S | 8g | 0.25518(20) | 0.25 | 0.125 | 0.804 | 0.950(3) |
| S anisotropic |
U11 = 0.010(2), U22 = 0.0029(19), U33 = 0.0179(7), U12 = 0, U13 = 0, U23 = 0.0041(7) | |||||
| Lattice parameter |
a = 5.321383(10) Å | c = 10.18642(3) Å | V = 288.4500(12) Å3 | |||
| overall fit indicators (referring to the combined four diffraction patterns): | ||||||
| Rwp = 0.067 | Chi2 = 11.7 | Bérar SCOR 822] = 4.42 | ||||
| Sample no. | Composition | Band gap energy Eg (eV) |
|---|---|---|
| To557 | Cu1.10☐0.90Ga1.09Ge0.91S4 | 2.49(5) |
| To569 | Cu1.18☐0.83Ga1.15Ge0.84S4 | 2.41(5) |
| To597 | Cu1.27☐0.74Ga1.24Ge0.75S4 | 2.29(5) |
| To581 | Cu1.29☐0.72Ga1.23Ge0.76S4 | 2.28(5) |
| To585 | Cu1.30☐0.72Ga1.23Ge0.75S4 | 2.36(5) |
| To531 | Cu1.33☐0.68Ga1.27Ge0.72S4 | 2.28(5) |
| To599 | Cu1.35☐0.68Ga1.24Ge0.73S4 | 2.24(5) |
| To580 | Cu1.36☐0.66Ga1.28Ge0.70S4 | 2.30(5) |
| To596 | Cu1.47☐0.54Ga1.42Ge0.57S4 | 2.11(5) |
| To588 | Cu1.76☐0.27Ga1.63Ge0.34S4 | 2.15(5) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





