Schrödinger’s Cat May Be Dead All Along

1. Introduction

The thought experiment popularly known as ‘Schrödinger’s Cat’ [1] is a widely known paradox in quantum mechanics used to frame the question of when exactly quantum superposition ends [2]. For years, this thought experiment has been debated and has been considered as a paradox that has no definite answer – the cat is dead and alive at the same time [3,4]. The current work confronts this conclusion of the paradox.

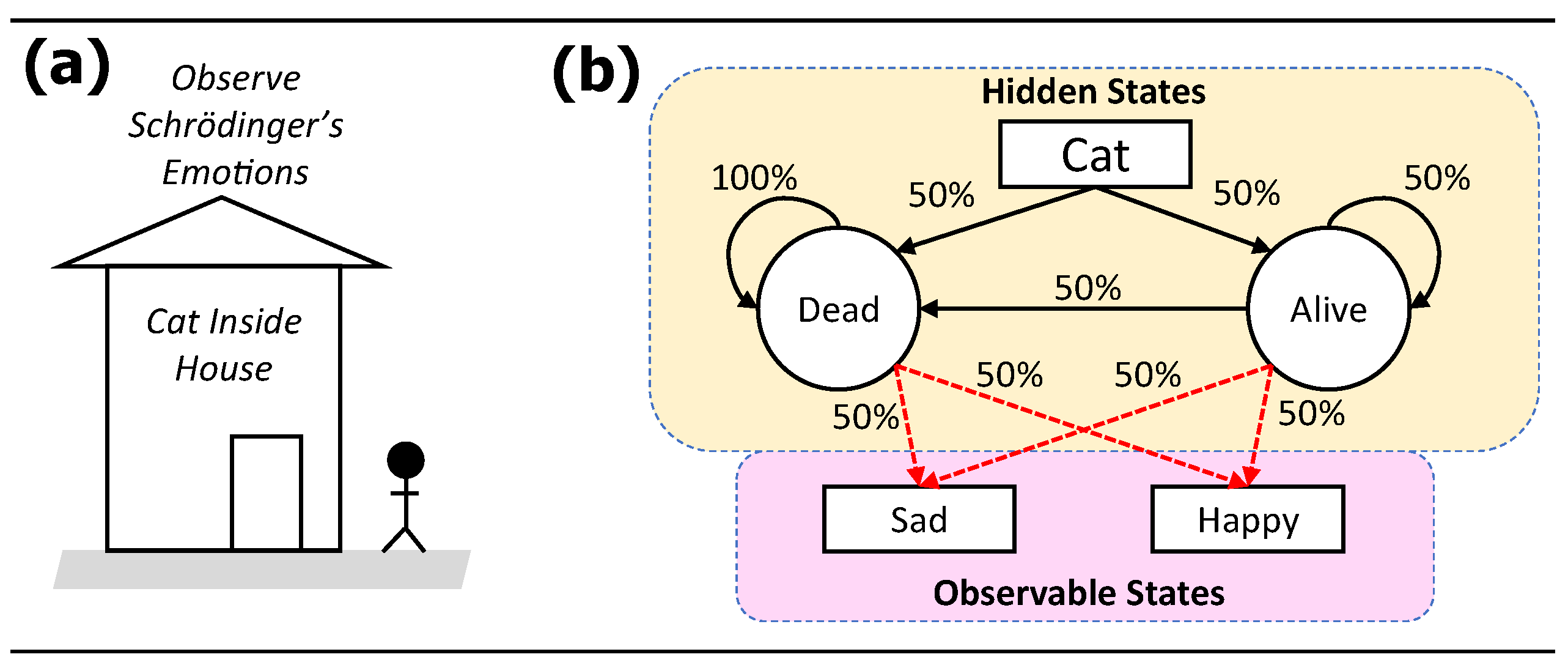
This current work shows that the probability of the cat being alive is not equal to the probability of the cat being dead amid making inference based on equally random observable states. This is done by framing the problem as a search for the Hidden Markov Model (HMM) [5,6] of the states of the cat. The problem model is schematically shown in Figure 1. With HMM, the states of the cat are hidden and must be computed using observable states that are affected by the hidden states. In this problem model, the observable states are the emotions of Schrödinger who directly observes the cat and shows two emotions – sad or happy – at equal prior probabilities (50% each) from each hidden state. We are the observers of these emotional states of Schrödinger, and we want to use these observations to estimate probabilities of the unknown states of the cat. The hidden state – cat being dead or cat being alive – has the following prior probabilities: if the cat is alive then it has equal chances of being alive (50%) or dead (50%), and if the cat is dead then it will remain dead (100%).

To estimate the posterior probabilities of the HMM states, a sequence of observations must be collected and used as inputs into the training of the network leading to a convergence of the probabilities of the hidden states. This set of observations can be synthetically generated from a random process. Because there are just two observable states, the sample generation process is a Bernoulli (p=0.50) process.

2. Methodology

The workflow in this work was implemented using the Python programming language. The Python codes in Jupyter Notebook files used in this work are curated in the online GitHub repository of the work: https://github.com/dhanfort/HMM_Schrod_cat.git.

2.1. Mathematical Formulation

The prior probabilities based on Figure 1 constitute the initial probabilities of the transition matrix $T=\left[\begin{array}{cc}1& 0\\ 0.5& 0.5\end{array}\right]$ and emission matrix $E=\left[\begin{array}{cc}0.5& 0.5\\ 0.5& 0.5\end{array}\right]$. Matrices $T$ and $E$ would then be trained on the observable states to determine their posterior. The starting state matrix probability is fixed at equal probabilities $s=\left[\begin{array}{cc}0.5& 0.5\end{array}\right]$. Rigorous mathematical derivations and explanations of the forward algorithm and updating algorithm in the training of HMM to learn $T$ and $E$ from observable states can be found in these references: [6,7].

2.2. Model Traning and Inference

The Python module ‘hmmlearn’ [8] was used to train the HMM. Datasets of observable states consisted of varying samples sizes and batch sizes were generated from a Bernoulli(p=0.5) implemented using the ‘random’ function in Numpy module [9]. The observable states were coded as follows: 0 = Sad, and 1 = Happy. The hidden states were coded as follows: 0 = Dead, and 1 = Alive. The ‘hmmlearn.CategoricalHMM’ function was used to model the HMM. After training the HMM, the model was then used to compute the stationary probabilities of the hidden states to determine the chances of the cat being Dead or Alive.

3. Results and Discussion

3.1. Observation-based Model Training

The results of the observation-based training of the network are shown in Figure 2, where the summarized results are the values of the updated transition matrix $T$. The transition matrix $T$ models the changes of hidden states in HMM. Determining how observable states affect the transition probabilities would elucidate how the estimates of hidden state probabilities change. Based on our preliminary computations, the number of batches of observations and the size observation samples per batch significantly affect the updating of matrix $T$. As can be seen in Figure 2, matrix $T$ converged to varying distribution of posterior transition probabilities.

3.2. Stationary Probabilities

For each of the trained transition matrix $T$ (Figure 2), the stationary probabilities of the hidden states (Cat = Dead, or Cat = Alive) were computed using the ‘get_stationary_distribution()’ function in the HMM model. The resulting stationary probabilities were consistently P(Cat = Dead) = 1.0 and P(Cat = Alive) = 0 in all the observation-based model training of the HMM. These probabilities indicate that Schrödinger’s cat may be dead all along.