Prerpints.org logo
Preprint
Article

Sound of Sirens, Echoes of Trauma: Unpacking Socioeconomic Vulnerabilities in the Israel-Hamas Conflict

This is a preprint, it has not been peer-reviewed.

Submitted:

09 December 2023

Posted:

12 December 2023

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
This study investigates the socio-economic determinants correlated with Post-Traumatic Stress Disorder (PTSD) symptoms amid the 'Guardian of the Walls' operation, in the Israel-Hamas conflict. Our investigation primarily focused on assessing the effects of missile strikes on Israeli civilians. By conducting an in-depth statistical analysis of individual experiences, we sought to unravel the correlation between socioeconomic status and PTSD susceptibility.Our findings reveal a stark disparity in PTSD risks across different socio-economic groups. Individuals from lower socio-economic backgrounds exhibited a notably higher propensity for PTSD symptoms, suggesting that socio-economic adversity intensifies the psychological toll of conflict exposure. Conversely, higher education and stable family environments appeared to mitigate PTSD risks, underscoring the protective role of certain socio-economic factors.The study's implications extend far beyond the immediate context of the Israel-Hamas conflict. By elucidating the heightened vulnerability of lower socio-economic groups to PTSD, it calls for a nuanced approach to mental health intervention in conflict zones. This approach should not only address the direct psychological impact of conflict but also consider the broader socio-economic fabric that shapes individual experiences of trauma.This research contributes to a growing body of knowledge on PTSD in conflict settings, offering valuable insights for policymakers, mental health professionals, and humanitarian organizations. By highlighting the socio-economic dimensions of PTSD, it advocates for more comprehensive, context-sensitive mental health strategies. Such strategies are crucial for addressing the complex array of factors influencing mental health in conflict zones, ultimately paving the way for more resilient and supportive communities.
Keywords: 
  -  

1. Introduction

The notion of mental trauma encompasses psychological damage inflicted by an event that the individual perceives as jeopardizing fundamental needs, such as self-esteem, personal safety, socio-economic standing, or physical health (Ehlers & Clark, 2000). The psychological toll of war-related violence can have enduring ramifications on the emotional and mental well-being of both victims and witnesses. Individuals exposed to such traumatic incidents may experience a spectrum of psychological challenges, including Post-Traumatic Stress Disorder (PTSD), major depressive disorder, pervasive feelings of helplessness, heightened anxiety, and chronic fear (WHO, 2001). Individuals' responses to trauma can vary significantly, with some showing a quick and lasting natural recovery, while others may develop persistent trauma-related psychologic disorders. The specific nature and extent of the trauma experienced are key factors influencing these outcomes. Research indicates that exposure to different types of traumatic events, as well as varying levels of exposure, can lead to distinct psychiatric and neurobiological consequences. This suggests that the qualitative differences in traumatic experiences, along with their intensity and duration, play a crucial role in determining the psychological and biological impact on individuals (Amir et al. 1996; Benjet et al., 2016; Contractor et al., 2018; Ford et al., 2006; Smith et al., 2016).
The enduring impact of war violence extends beyond immediate harm, leaving a lasting imprint on the mental health of communities residing in conflict-affected areas. The long-term psychological consequences of mass violence are predominantly attributable to the trauma it engenders (MacDermid Wadsworth, 2010; Murthy and Lakshminarayana, 2006). Consequently, instances of military conflict and associated stressors can be classified as traumatic events, capable of eliciting a range of PTSD symptoms (Blevins et al., 2015; Paryente, 2021).
The ramifications of psychological stress are not only distressing in their immediate effects on mental well-being but also have far-reaching consequences. Elevated levels of trauma, fear, depression, and anxiety can culminate in emotional exhaustion, impair social interactions, and pose significant obstacles to daily functioning. Such psychological states frequently precipitate alterations in the behavior and decision-making patterns of affected individuals (Bayer, 2023; Bayer et al., 2019; Bayer and Shtudiner, 2023; Solomon and Bayer, 2022).
This study delves into how socioeconomic status is correlated with the emergence of Post-Traumatic Stress Disorder (PTSD) symptoms in Israeli civilians following the 'Guardian of the Walls' operation during the Israel-Hamas conflict. It additionally investigates the extent to which exposure to rocket attacks, quantified by the number of missile alert alarms, affects the likelihood of developing PTSD.
In our study, we specifically focus on post-traumatic stress disorder (PTSD) because of its explicit classification in the DSM-5, compared to other related mental health conditions. While traumatic experiences such as exposure to warfare or acts of terror can lead to a variety of psychological issues including depression and other psychological disorders, not all of these issues are necessarily a direct result of the traumatic experience. In contrast, PTSD is uniquely defined in the DSM-5 as being directly related to traumatic events. Given the scope of our research and the complexities involved in analyzing all mental health outcomes and their origins, we chose to concentrate on PTSD, a disorder inherently connected to experiencing traumatic events.s

Post-traumatic stress disorder (PTSD) risk factors

Post-traumatic stress disorder (PTSD) is a multifaceted mental health issue, significantly influenced by the level and nature of exposure to traumatic events. The likelihood of developing PTSD is closely linked to the intensity of exposure to disasters, which can vary greatly. This variance in exposure levels provides a basis for comparative studies, underscoring the critical role of the nature and degree of disaster exposure in the onset of PTSD (Amir et al. 1996; Benjet et al., 2016; Contractor et al., 2018; Ford et al., 2006; Smith et al., 2016). Similarly, research consistently indicates that proximity to a disaster site is a key factor, with higher PTSD prevalence rates found among individuals living closer to the site compared to those residing further away (Havenaar, et al.,1997; Schlenger et al., 2002).
The risk of Post-Traumatic Stress Disorder (PTSD) is significantly influenced by personal characteristics, including educational level, income, and broader socioeconomic factors. Socioeconomic status, in particular, is a critical determinant in both understanding and managing PTSD risks, with lower socioeconomic status consistently correlated with higher PTSD risks (Brewin et al., 2000; DiGrande et al., 2008). Research extensively supports the association between lower levels of education and an increased likelihood of developing PTSD (Brewin et al., 2000; DiGrande et al., 2008; Iversen et al., 2008; Johnson et al., 2002; Schnur et al., 2004). Additionally, income level plays a pivotal role in PTSD prevalence. Studies have found that individuals with lower income or without a regular income face higher rates of PTSD following disasters (Cheng et al., 2014; DiGrande et al., 2008).
Other factors such as age (Brewin et al., 2000; Kongshøj & Berntsen, 2022), gender, race/ethnicity, previous trauma exposure, general childhood adversity (Brewin et al., 2000), marital status (Li et al., 2022), and cultural value orientation (Burri et al., 2014) have also been identified as significant correlates of PTSD post-disasters.
Given that previous literature addresses a range of traumatic events with varying characteristics, there is a need for focused research on the unique Israeli context, particularly concerning exposure to missile attacks in populated areas. These attacks are characterized by their random nature and can lead to distinct psychological impacts. The diversity in the types of disasters, populations affected, and contexts covered in existing studies makes it difficult to apply their conclusions directly to the Israeli scenario. Therefore, a specific investigation into the Israeli case is essential to understand the unique psychological consequences of these types of traumatic events, which differ in nature from those typically discussed in the broader PTSD literature. This underscores the importance of conducting context-specific research to understand the nuances and specific impacts of trauma in different scenarios.

"Guardian of the Walls" operation

During the 12-day conflict between Israel and Hamas in Gaza in May 2021, Hamas and other militant organizations launched a total of 4,360 rockets and mortar shells, primarily targeting densely populated areas within Israel. Of these, 3,573 rockets landed within Israeli territory, while the remainder either misfired, landed within the Gaza Strip, or fell into the Mediterranean Sea.
Israel's Iron Dome missile defense system successfully intercepted approximately 90% of the rockets aimed at populated areas. The rocket attacks directly resulted in 11 fatalities, including one soldier killed by an anti-tank missile strike. Additionally, 357 individuals sustained injuries. According to a 2022 report by The Meir Amit Intelligence and Terrorism Information Center, the rocket attacks caused substantial damage to residential buildings, educational facilities, factories, and agricultural structures. Figure 1 offers a geographical representation of the areas where rocket alerts were activated during the "Guardian of the Walls" military operation.
The enduring conflict between Israel and Hamas has resulted in considerable human suffering and loss for both parties. While there has been extensive research into the conflict's dynamics, there remains a notable dearth of information concerning the psychological repercussions of rocket attacks on residents in the affected areas. This study seeks to fill this knowledge gap by examining the relationship between socioeconomic status and the prevalence of Post-Traumatic Stress Disorder (PTSD) among Israelis residing in regions impacted by the Israel-Hamas hostilities1. Specifically, we investigate the association between PTSD symptoms and various factors, including the degree of exposure to rocket attacks, individual characteristics, and socio-economic variables. Our focus is on Israeli civilians who lived through the intense period of the Israeli military's "Guardian of the Walls" operation in May 2021. The objective is to elucidate the extent to which PTSD correlates with these diverse factors, thereby providing a more nuanced understanding of the psychological toll that armed conflict exacts on civilian populations.

2. Methodology

Questionnaires

To assess the prevalence and severity of Post-Traumatic Stress Disorder (PTSD)2 symptoms among participants, we employed the Post-Traumatic Checklist for DSM-5 (PCL-5). This self-report questionnaire is a widely recognized tool for evaluating the intensity of PTSD symptoms, aligning with the 20 diagnostic criteria specified in the DSM-5 (Blevins et al., 2015). The PCL-5 consists of 20 multiple-choice questions, each scored on a 5-point Likert scale ranging from 0 to 4, which participants complete to indicate the extent to which they have been troubled by each symptom over the past month.
The questionnaire has demonstrated high internal reliability, boasting an alpha coefficient of 0.96 (Bovin et al., 2016; Wortmann et al., 2016). The cumulative scores from all items yield a total severity score, which can vary between 0 and 80. Following previous research (Bovin et al., 2016; Wortmann et al., 2016), the PCL-5 was also utilized to offer a provisional PTSD diagnosis. A symptom was acknowledged if any item was rated as 2, denoting "Moderately," or higher. To align with the DSM-5 diagnostic criteria, which necessitate at least one item from Criterion B (questions 1-5), one item from Criterion C (questions 6-7), two items from Criterion D (questions 8-14), and two items from Criterion E (questions 15-20), we created a dichotomous variable termed 'PTSD Binary.' This variable was assigned a value of 1 for participants meeting the diagnostic criteria and 0 for those who did not. For the scope of this study, participants who did not exhibit any PTSD symptoms were classified as "healthy," regardless of any other existing physical health conditions.
Participants were asked to provide demographic information, including gender, age, income, education level, and number of children, as well as specific experiences related to Operation "Guardian of the Walls." In this context, participants were queried about their residential locations. This data was used to create a variable that quantified the frequency of missile alarms activated in their respective localities. This variable was generated by cross-referencing the residential information supplied by participants with data from the Israeli Home Front Command, which tracks the number of alarms triggered in each settlement. Given that the Israeli defense system activates a missile alarm for each incoming missile aimed at a specific residential area, the frequency of these alarms serves as a proxy for the number of missile strikes targeting a given locality.
Additionally, we employed a categorical variable to delineate various regions within Israel, categorizing them based on the time residents have to seek shelter following a rocket alarm. These time-based regions were divided into seven categories, ranging from "Immediate" to "3 minutes," as illustrated in Figure 2.

Research population

The study utilized an online survey distributed across multiple social media platforms, initially attracting 395 respondents. After eliminating thirteen entries due to either incomplete or irrelevant information, the final sample consisted of 382 participants. Of these, 78.8% were female, with an average age of 38.72 years. Participation was voluntary and free of charge. Importantly, the participants came from various regions of Israel, each affected to varying degrees by rocket attacks during the "Guardian of the Walls" operation—ranging from heavily impacted areas to those with minimal exposure. Our data collection includes a wide range of demographic variables, ensuring a comprehensive representation of the population, and allowing for a deeper exploration of not only the presence of PTSD but also its intensity and variability across different socioeconomic strata. Based on the established diagnostic criteria, 62 participants exhibited PCL-5 scores indicative of significant PTSD symptoms. The distribution of these scores is graphically represented in Figure 3.

Data Processing

We investigated the association between the frequency of missile alarm events, as an indicator of exposure level, and the incidence of post-traumatic stress disorder (PTSD). This involved conducting variance tests on a dichotomous variable, alongside evaluating the PTSD Checklist for DSM-5 (PCL-5) scores. Our analysis extended to examining the correlation between PCL-5 scores and the number of rocket siren occurrences in the participants' residential areas, using a variety of statistical models, encompassing both linear and non-linear approaches.
In the subsequent phase of our study, we focused on exploring the relationship between socioeconomic factors and the emergence of PTSD. Our attention was particularly drawn to the dichotomous variable consistent with DSM diagnostic criteria. We employed multivariable probit models, chosen for their proficiency in managing binary outcome variables. This approach enabled a more nuanced understanding of how socioeconomic status influences PTSD risk. Additionally, we applied Ordinary Least Squares (OLS) linear regression models to further examine the PCL-5 test scores concerning socioeconomic factors.

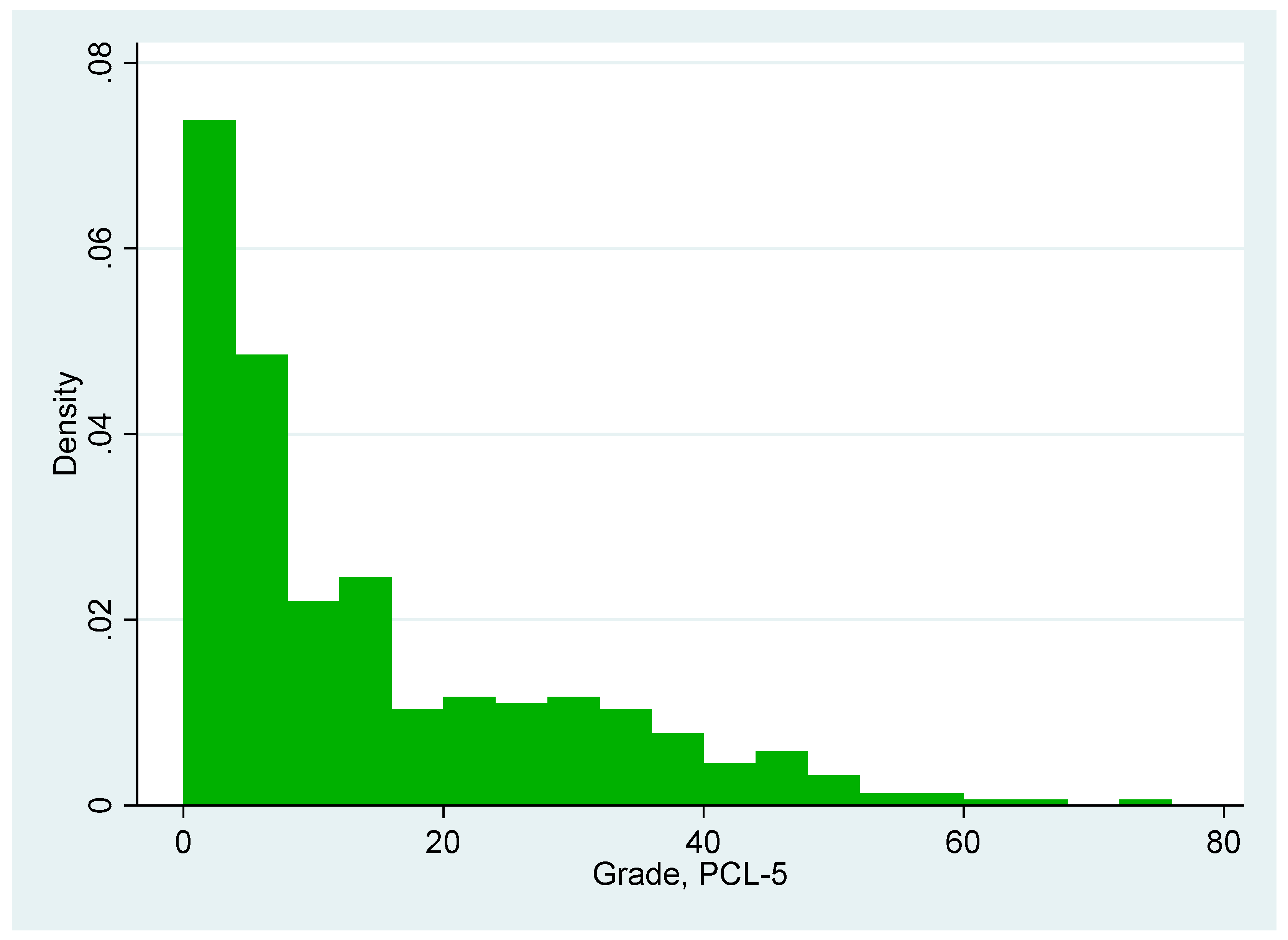
3. Results

Table 1 provides Descriptive Statistics for Our 382-participant Sample, categorized by the PTSD Binary Variable According to DSM-5 Post-Trauma Criteria. The participants are categorized into two groups based on a binary PTSD variable, which serves as a dichotomous indicator for meeting the DSM-5 diagnostic criteria for post-traumatic stress disorder.
Figure 4 displays the distribution of rocket alarm exposure in relation to PTSD symptom status among respondents. This violin plot reveals variances in rocket alarm frequencies between those with clinical-level presence and absence of PTSD symptoms. A noticeable spread and density of alarm counts is evident, suggesting a potential correlation between the frequency of rocket alarms and the manifestation of PTSD symptoms. The wider sections of the plot indicate where data points are more concentrated, providing insights into common alarm frequencies experienced by each group.

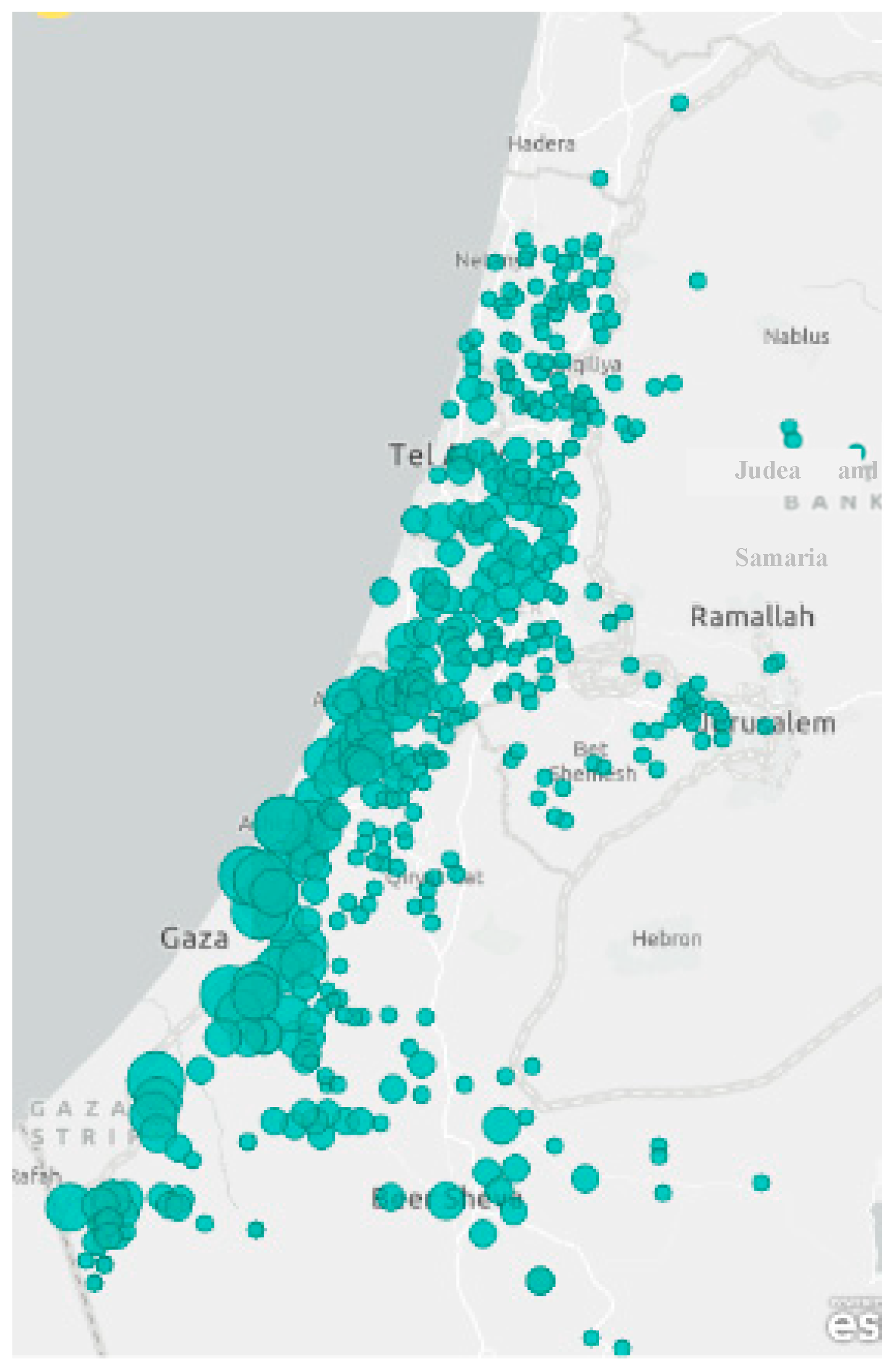
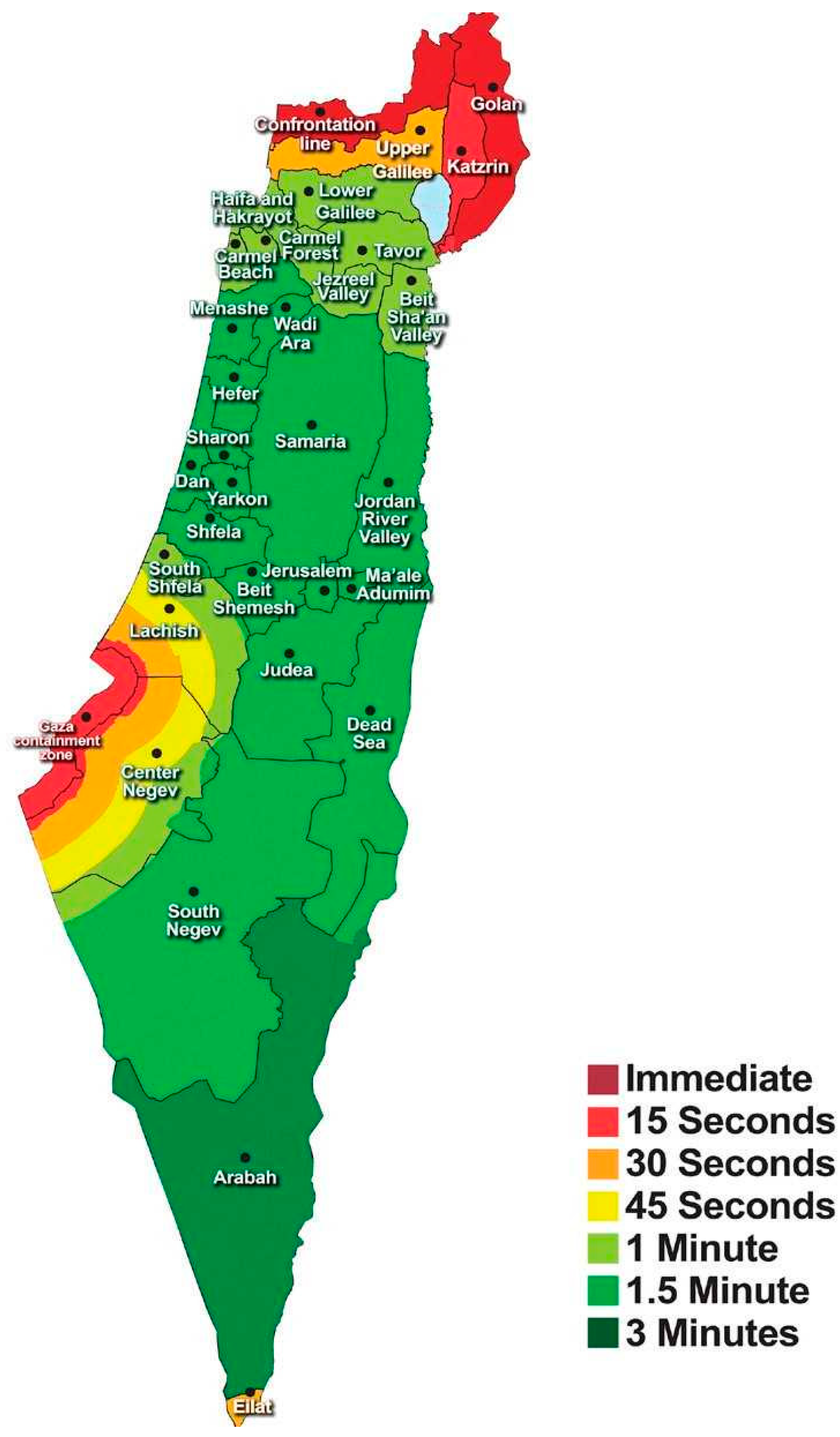
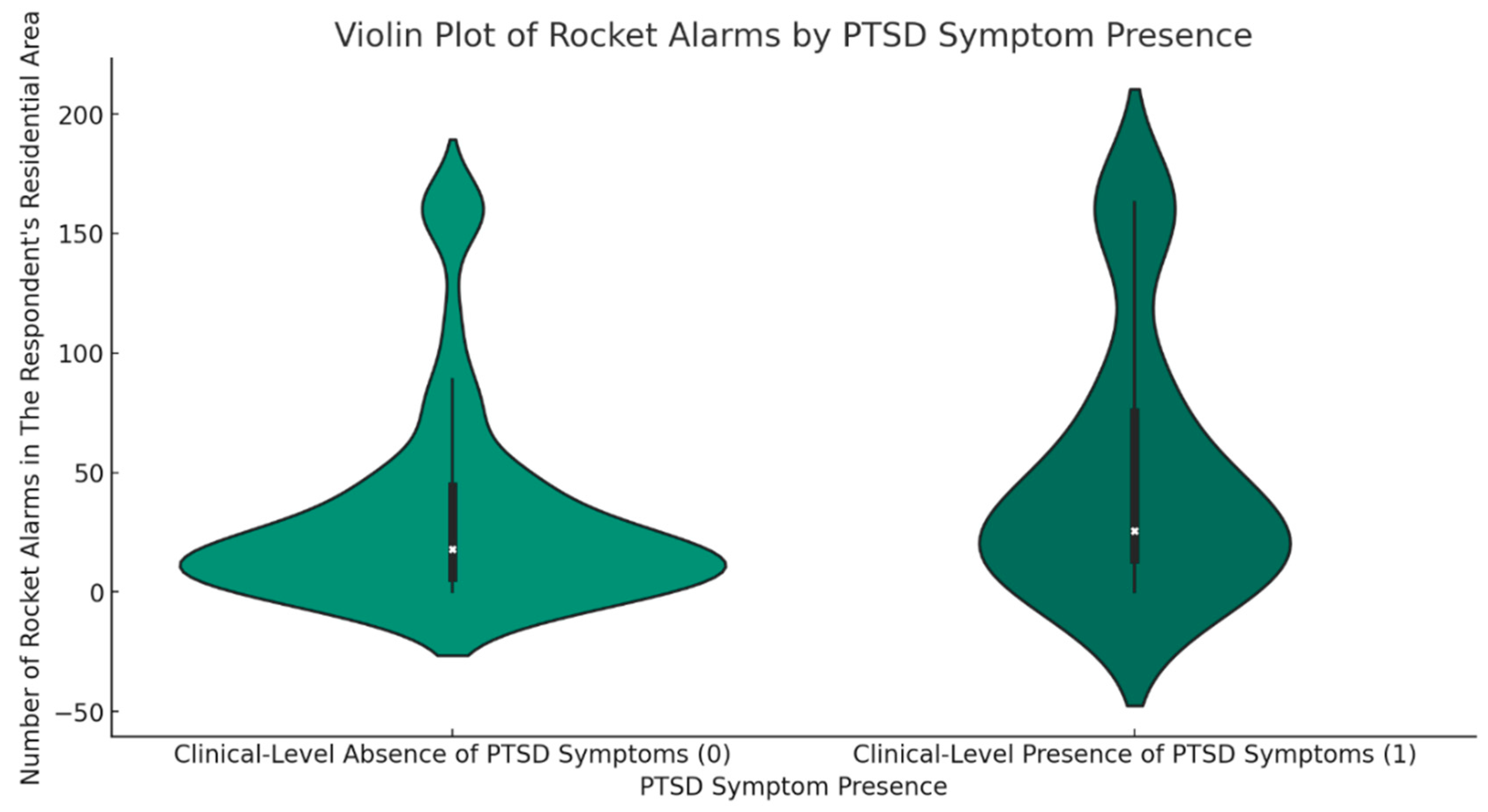
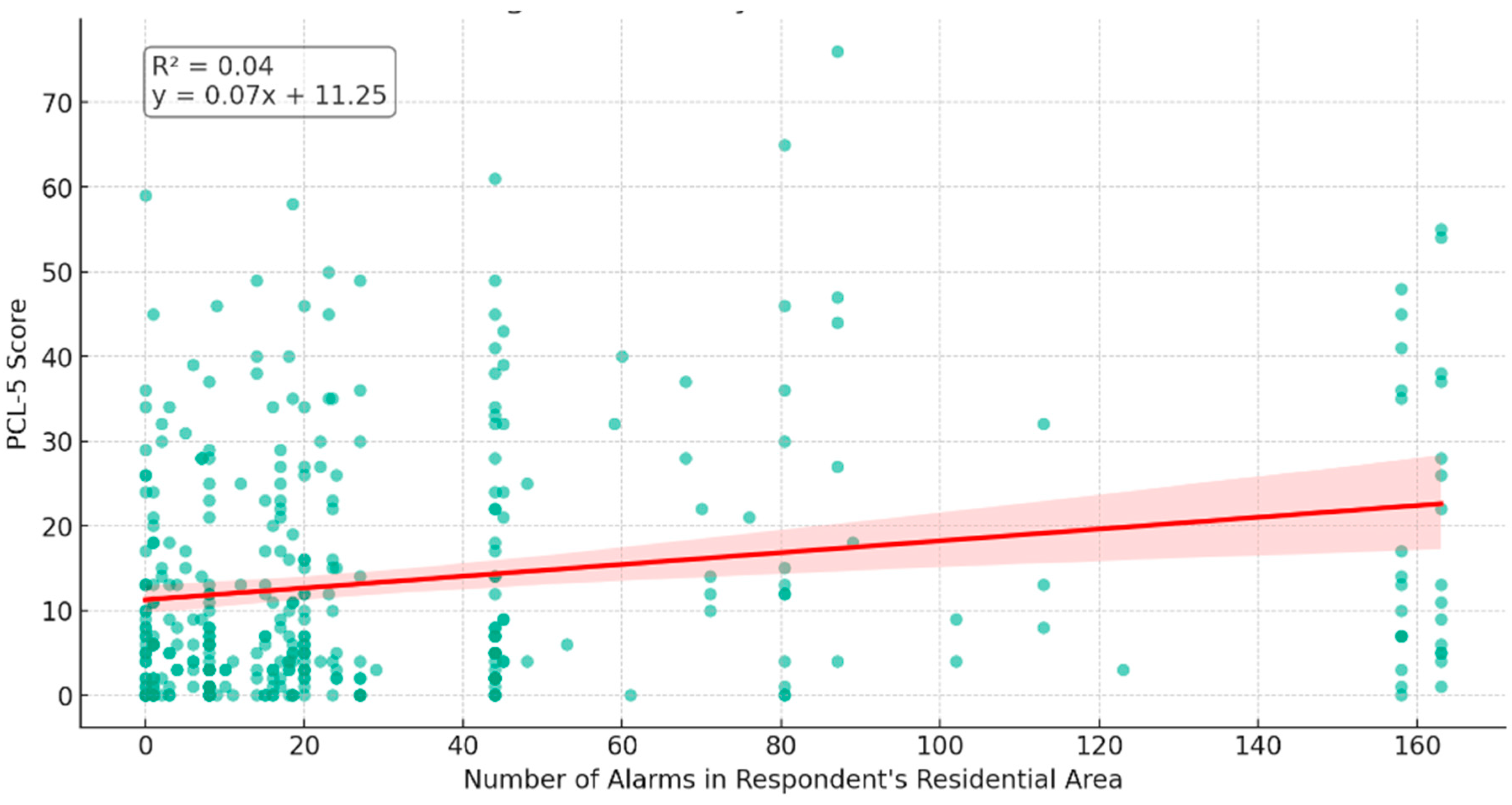
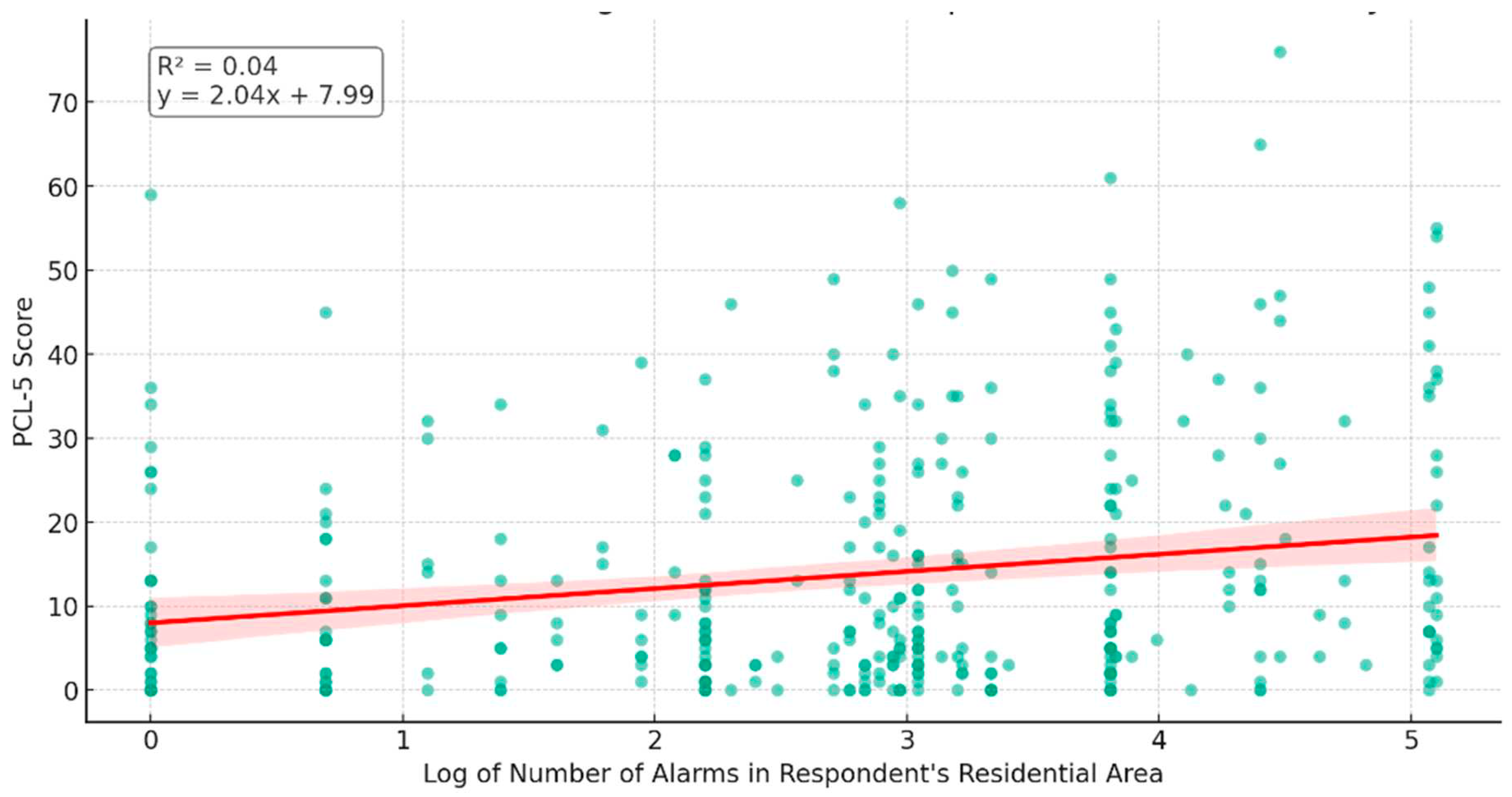
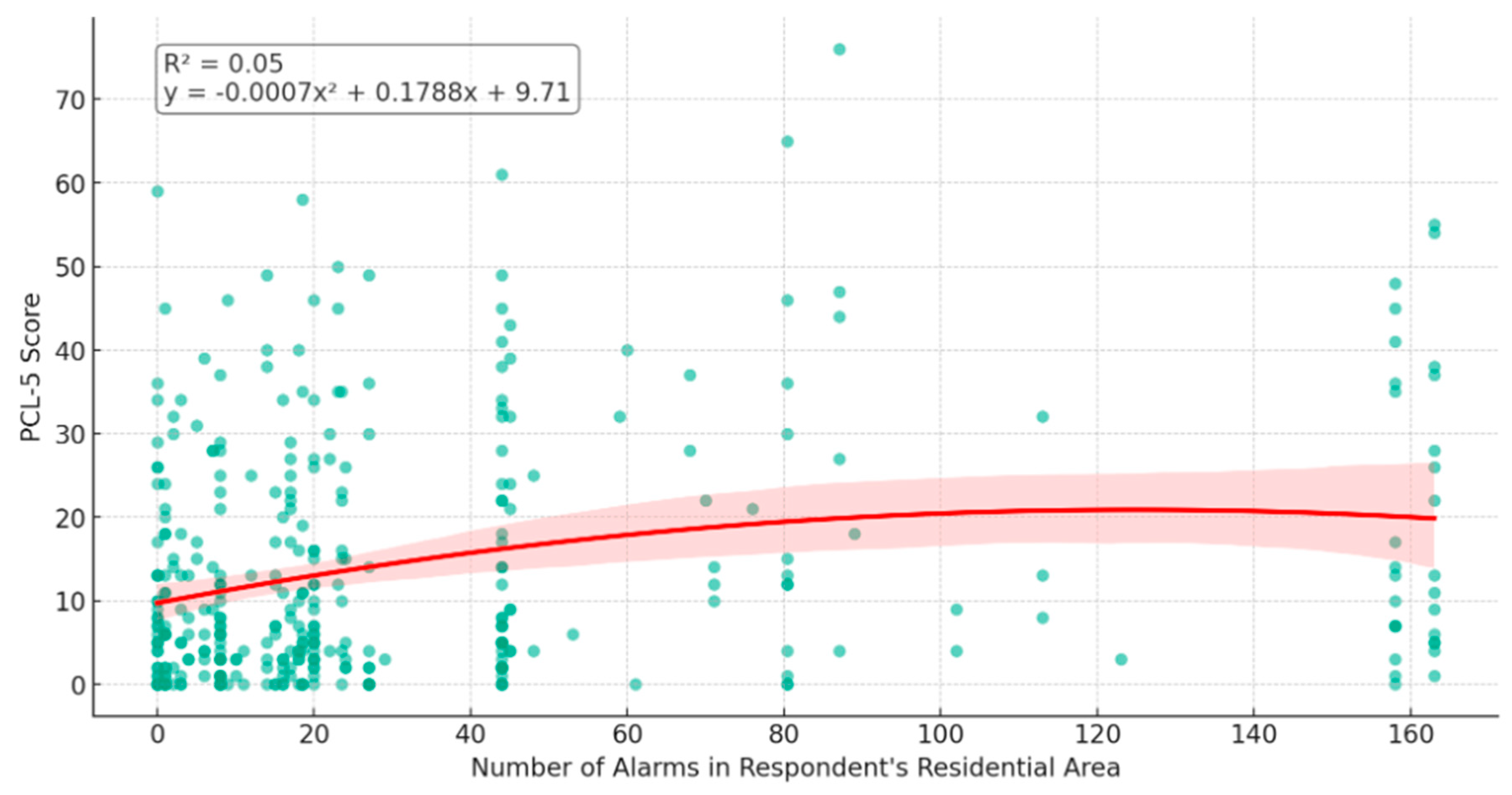
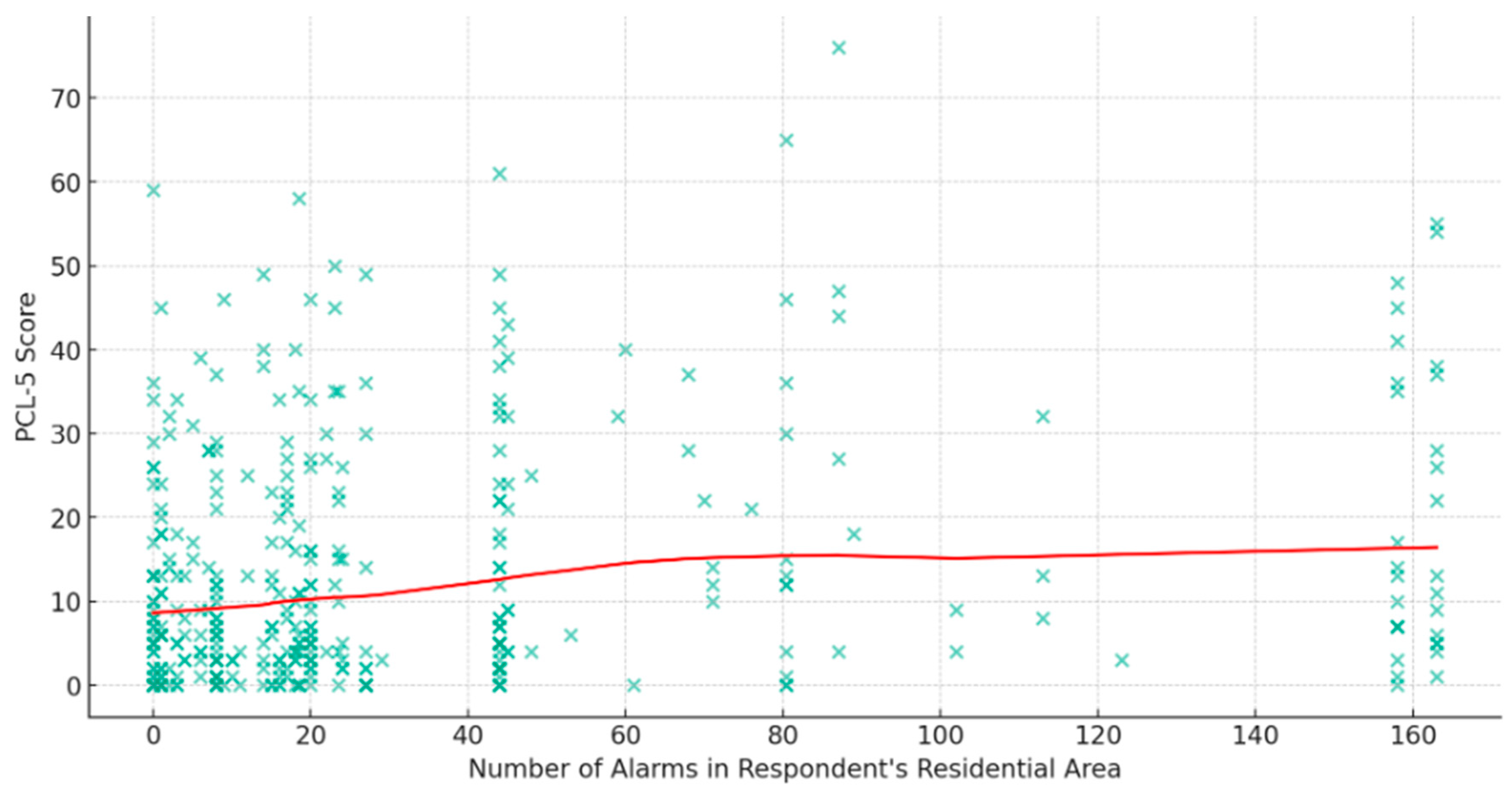
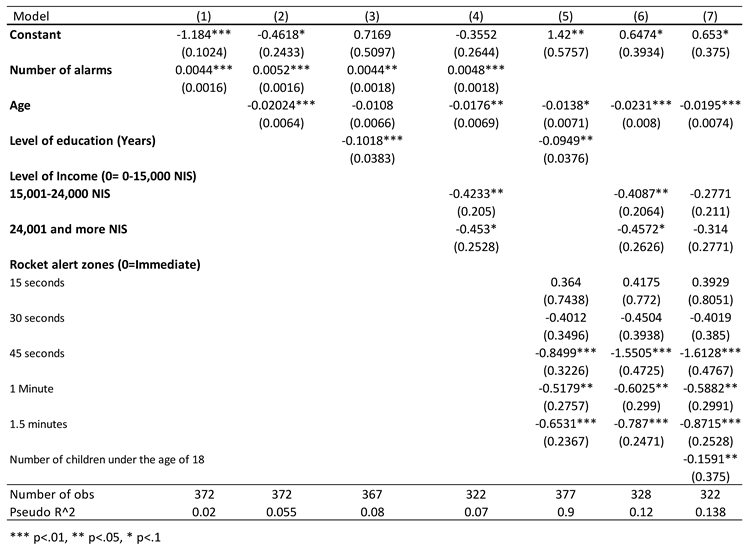
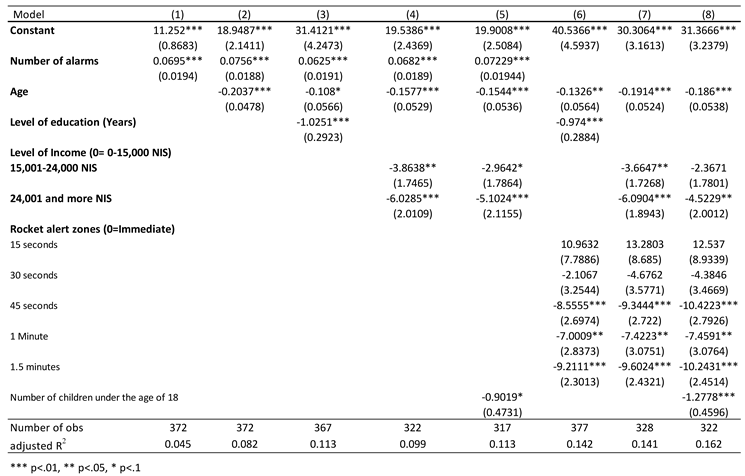
Exposure to Missile Alarms as a Measure of Missile Attacks and PTSD Symptoms

The ANOVA analysis, focusing on a dichotomous variable labelled 'PTSD Binary' concerning the number of missile alarms, provides significant insights into the correlation between missile alarm exposure and the likelihood of PTSD. The analysis revealed an F-statistic of approximately 8.12 and a p-value of 0.0046. This F-statistic indicates notable variance in the number of missile alarms experienced by individuals across different groups, signifying varied exposure levels to potentially traumatic events. Importantly, the precise p-value, which is significantly less than the conventional threshold of 0.05, robustly suggests that these differences are statistically significant.
This finding is pivotal as it implies that individuals exposed to a higher frequency of missile alarms are more likely to be classified as suffering from PTSD. In essence, there appears to be a stronger correlation between a higher exposure to missile alarms, as a proxy to the number of missile attacks in the residential area, and the likelihood of developing PTSD.
In order to try and estimate as accurately as possible the relationship between the number of missile alarms in the respondent's place of residence, as a measure of the intensity of exposure to missile attack events, and the score in the PCL-5 test as a measure of the severity of PTSD symptoms, various models were examined. Both linear and non-linear models were tested for their fit in describing the findings.
In the presented analysis in Figure 5, a linear regression model is employed to elucidate the relationship between the frequency of missile alarm exposure in a respondent's residential area and the severity of post-traumatic stress disorder (PTSD) symptoms, as quantified by the PCL-5 test scores. The PCL-5 score, serving as the dependent variable, is a recognized metric for evaluating the intensity of PTSD symptoms, with higher scores indicative of greater symptom severity. The independent variable, the number of missile alarms, is utilized as a surrogate measure for the respondent's exposure level to missile attacks. The resultant regression plot, accentuated with a red trend line, delineates a discernible linear association between these two variables. The R-squared value, prominently displayed on the plot, conveys the extent of variance in PTSD symptomatology that can be ascribed to variations in missile alarm exposure.
The statistical findings from the simple linear regression analysis revealed a notable relationship between the number of missile alarms in a respondent's residential area and their PCL-5 test score, which assesses the severity of post-traumatic stress disorder (PTSD) symptoms. The regression model, based on observational data, demonstrates a linear correlation, where an increase in the number of alarms is associated with a higher PCL-5 score. This suggests that greater exposure to missile alarms, indicative of potential exposure to traumatic events, corresponds to more severe PTSD symptoms. The R-squared value indicates the proportion of variance in the PCL-5 scores that can be explained by the number of alarms. While this correlation is statistically significant, it is important to note that it does not imply causation. Other factors not accounted for in this model might also influence PTSD severity.
In the conducted analysis presented in Figure 6, a logarithmic transformation was applied to the variable representing the number of missile alarms to examine its correlation with the severity of post-traumatic stress disorder (PTSD) symptoms, as measured by the PCL-5 score. This methodological approach, diverging from the standard linear regression analysis, addresses potential non-linear relationships and skewness in the data. Logarithmic transformations are particularly beneficial when variables exhibit a broad range or when the relationship between variables is multiplicative.
The application of this transformation yielded a linear correlation between the log-transformed missile alarm counts and PCL-5 scores, suggesting a significant proportion of the variance in PTSD symptom severity is explainable by these transformed alarm counts. This indicates a potentially more robust relationship than what might be inferred from the untransformed data. The analysis reveals two key insights: firstly, the persistence of a statistical correlation between missile alarm exposure and PTSD severity, consistent with initial linear observations. Secondly, and perhaps more critically, the relationship appears to exhibit a logarithmic pattern. This implies that increments in alarm exposure, particularly at lower ranges, are associated with a more pronounced impact on PTSD symptom severity compared to higher ranges.
Moving beyond linear models, we explored a variety of non-linear modeling approaches in an effort to best describe the relationship between the variables. Ultimately, we implemented a quadratic polynomial regression model, which emerged as the most suitable for capturing the potential non-linear dynamics, as depicted in Figure 7. This model, a deviation from previous linear approaches, revealed an increased explanatory power, as demonstrated by a higher R-squared value. The quadratic model suggests a positive correlation between the frequency of missile alarms and the severity of PTSD symptoms up to a certain point, beyond which the impact of additional alarms appears to plateau or diminish significantly.
The model indicates that initially, as the number of missile alarms increases, there is a corresponding increase in PTSD symptom severity. However, this trend reaches a threshold, beyond which further exposure to missile alarms does not continue to escalate PTSD symptoms at the same rate. This point of inflection, where the rate of change in PTSD severity begins to level off, is a critical finding of the analysis. It suggests a possible saturation effect or a coping mechanism, where individuals exposed to a high number of alarms might not experience a proportional increase in symptom severity.
The exact point of this transition, as identified by the model, occurs at the vertex of the quadratic curve (124.88 rocket alarms at 20.88 PCL-5 points). This vertex represents the number of alarms beyond which additional exposures have a markedly reduced impact on PTSD severity. The quadratic model has the lowest Mean Squared Error (MSE) and the highest R-squared (R²) value, suggesting it provides the best fit among the three for explaining the relationship between the Total PCL-5 Score and the number of rocket alarms.
Non-parametric models, such as the Locally Weighted Scatterplot Smoothing (LOWESS) model, are valuable analytical tools in statistics, especially when the relationship between variables does not conform to a specific parametric form. Unlike parametric models that presuppose a certain functional relationship (like linear or polynomial), non-parametric models are more flexible and can adapt to the shape of the data, making them ideal for exploring complex and nuanced relationships.
The LOWESS model I initially presented is a prime example of a non-parametric approach. It creates a smooth curve through the dataset, allowing for the visualization of potential patterns and trends that might not be apparent or accurately captured by traditional parametric models. In the context of our analysis, the LOWESS model was applied to explore the relationship between the number of missile alarms in a respondent's residential area and the severity of their PTSD symptoms, as measured by PCL-5 scores.
The results of the LOWESS analysis (Figure 8) revealed a nuanced, possibly non-linear relationship between these two variables. The smoothed curve indicated an initial increase in PTSD symptom severity with an increasing number of alarms, followed by a leveling off or potential decrease beyond a certain point. This pattern suggests a complex dynamic where initial exposure to missile alarms might significantly impact PTSD symptoms, but this impact might plateau or change beyond a certain level of exposure. These findings highlight the utility of non-parametric models in capturing the subtleties inherent in real-world data.
The subsequent sections of the article will investigate additional socioeconomic factors that correlate with PTSD, aiming to provide a more holistic understanding of the factors contributing to its development.

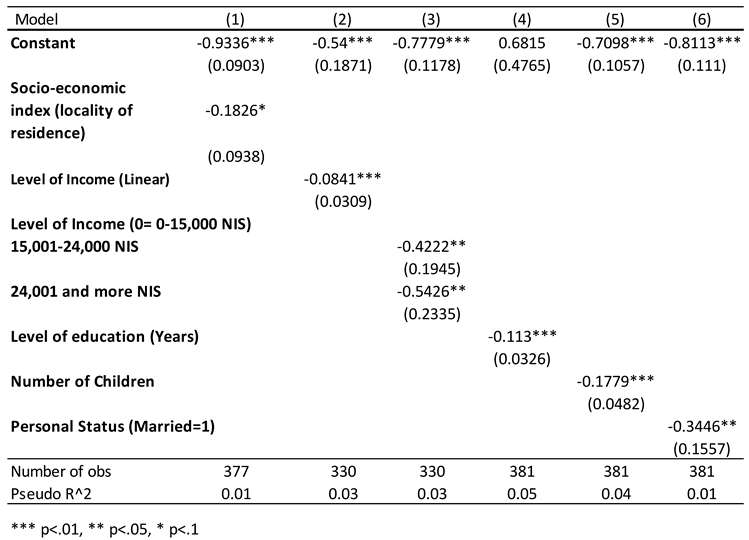
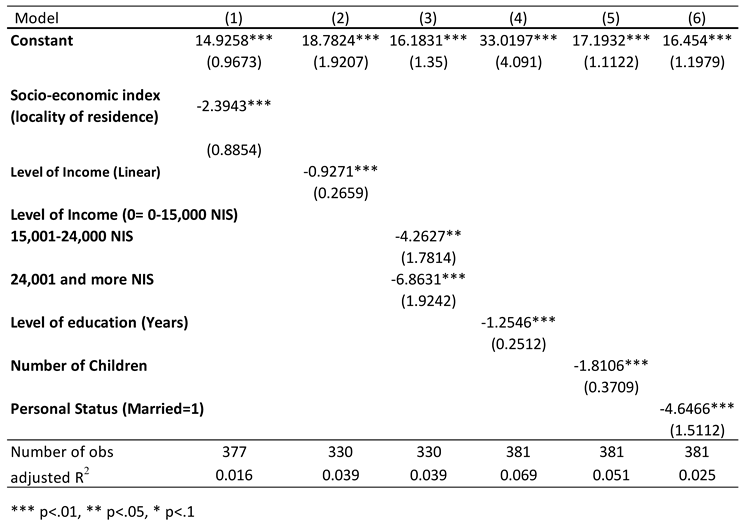
Socioeconomic Status and PTSD Symptoms

To examine the relationship between socio-economic factors and the prevalence of PTSD symptoms, we applied both simple probit and OLS models. The probit models use a binary dependent variable to classify individuals as either exhibiting PTSD symptoms (1) or not (0), thereby assessing the likelihood of clinical-level manifestation of PTSD symptoms based on socio-economic factors. Furthermore, our OLS models, which utilize the PCL-5 Score Variable, delve deeper into this relationship. These models collectively aim to explore how socio-economic status correlation with the probability of experiencing PTSD symptoms. The results of these models are presented in Table 2 and Table 3.
By employing single-variable models, we could isolate each socioeconomic factor to determine its specific impact on PTSD symptoms likelihood. Our analysis indicates that individuals with higher levels of education and income, as well as those who are married and those with more children, have a significantly lower probability of experiencing PTSD symptoms. Moreover, there's a negative correlation—statistically significant—between the socio-economic status of an individual's residence area and the probability of developing PTSD symptoms. Both probit and OLS models corroborate these findings, with the OLS models demonstrating greater robustness.
Analysis of Table 1 reveals marked differences in age, income, education, and number of children between the two studied groups. To explore how these demographics, along with the frequency of missile alarms, relate to PTSD symptoms, we employed multivariate probit models. These models use a binary dependent variable based on DSM-5 criteria, representing clinical (1) or non-clinical (0) levels of PTSD symptoms, where '0' indicates symptoms below the clinical threshold. This dichotomous approach, detailed in Table 4, aligns with professional clinical standards for accurately identifying clinical PTSD, as measured by the PCL-5 test. The models aim to rigorously analyze the interplay between PCL-5 test outcomes and various factors, including missile alarm frequency, age, education, and other relevant controls. The primary objective is to discern and comprehend the variables most strongly correlated with the PCL-5 test results.
Our analysis demonstrated a statistically significant positive correlation between the frequency of rocket alarms in a residential area and the probability of manifesting PTSD symptoms (p<0.01 across all tested models, models 1-4). When employing the categorical area variable as a substitute for the number of alarms (models 5 and 6), it became evident that regions situated at greater distances from the Gaza Strip were less likely to fall into the PTSD category. Although the distance from the Gaza Strip and the number of missile attacks are inversely related, in most cases, the frequency of sirens serves as a more precise predictor of missile attacks than mere geographical proximity to the Gaza Strip. This is likely due to the variable intensity of rocket fire targeting different areas, making siren activations a more reliable gauge of missile threat.
In the majority of the models where age was included as a variable, except model 3, we observed a statistically significant negative correlation between age and the probability of developing PTSD symptoms. This implies that the likelihood of experiencing PTSD symptoms diminishes as age increases. This finding is in congruence with existing academic literature, notably, the study conducted by Kongshøj and Berntsen (2022), which similarly identified a decrease in the propensity for PTSD symptoms with advancing age.
Our data also underscore the influential roles of education and income in determining an individual's risk of falling into the PTSD category. According to our models, individuals with higher educational attainment (models 3 and 5) and greater income levels (models 4 and 6) were generally less prone to PTSD symptoms. These findings are consistent with what is described in the literature review. Due to the high correlation between education and income, it was not feasible to include both variables in a single model without affecting its accuracy. The inclusion of additional variables did not improve the model's predictive power. These findings correspond to previous research on the subject, particularly in the context of the impact of education level on the tendency to develop PTSD and the income effect on the subject.
The number of children under 18 years of age per respondent demonstrates a statistically significant inverse correlation with the likelihood of experiencing post-traumatic stress symptoms that surpass diagnostic levels. Specifically, a higher number of children is associated with a reduced probability of exhibiting symptoms at a clinically significant level. When this analysis was broadened to include all children, regardless of their age, similar trends were observed. However, this more inclusive count of children slightly improved the variable's explanatory strength, thereby augmenting the overall diagnostic robustness of the model.
Table 5 introduces a Multivariate Ordinary Least Squares (OLS) Regression Analysis, aimed at delving into the factors that influence the severity of PTSD, as quantified by the PCL-5 scores. This approach extends beyond the scope of the probit models, employing the overall PCL-5 test score as the dependent variable. Although the PCL-5 test is not the principal diagnostic tool, it is recognized in the literature as a valid metric for assessing PTSD severity. The strength of using the PCL-5 score lies in its continuous nature, offering a nuanced range of scores instead of a binary categorization. This feature brings a higher level of specificity and granularity to the assessment, thereby enhancing the explanatory capability of the analysis, which is observed to be more substantial than that of the probit models.
The results of the OLS model were consistent with those from the probit model, exhibiting similar directional trends. However, the OLS model displayed greater strength, particularly in terms of the statistical significance of its explanatory variables and a higher R^2, indicating a greater proportion of variance explained.

Conclusions

Our comprehensive investigation into the prevalence of Post-Traumatic Stress Disorder (PTSD) among Israeli civilians amidst the Israel-Hamas conflict has yielded significant insights, particularly in the context of rocket alarm frequency, socio-economic factors, age, and family structure.
A crucial finding is the substantial impact of rocket alarm frequency in residential areas on PTSD likelihood and severity. This correlation highlights the psychological toll of missile attacks, with areas closer to the Gaza Strip experiencing more frequent alarms and consequently a higher risk of PTSD. Importantly, our analysis indicates that beyond a certain exposure level, further increases in alarm frequency do not significantly exacerbate PTSD symptoms. This finding suggests a complex relationship between exposure and symptom severity, possibly indicating a saturation point where the impact of additional alarms diminishes, potentially due to desensitization or the activation of coping mechanisms after repeated exposure.
Additionally, our study emphasizes the significant influence of socioeconomic variables, such as education and income, on PTSD prevalence. Higher levels of education and income are associated with a decreased likelihood of PTSD, underlining the role of socioeconomic status in mental health outcomes. This aspect of our research adds depth to the understanding of conflict psychology and underscores the importance of socio-economic factors in determining vulnerability to PTSD.
Our findings reveal a negative correlation between age and the development of PTSD symptoms, indicating that younger individuals may be more susceptible in conflict settings. This aligns with existing academic literature and underscores the need for age-specific mental health support.
The inverse relationship between the number of children under 18 and PTSD severity suggests a protective effect of family structure in traumatic contexts. This trend persists even when considering children of all ages, highlighting the importance of support networks in mitigating PTSD impacts.
Our research offers critical insights for policymakers and mental health professionals in developing effective mental health strategies for populations affected by conflict. Tailoring these strategies to address the diverse needs of different socio-economic groups can significantly enhance their effectiveness. Comprehensive and inclusive mental health care in post-conflict settings is crucial, especially for economically challenged groups.
In summary, this study contributes to the field of mental health in conflict zones by highlighting the complexity of PTSD and underscoring the need for multi-dimensional approaches in addressing its impact. Our findings also suggest the potential effectiveness of policies facilitating civilian evacuation to minimize exposure to missile alerts, although the trauma from such evacuations requires further exploration.
While advancing the understanding of PTSD in conflict contexts, our research's limitations, including its cross-sectional design and reliance on self-reported assessments, suggest the need for further studies employing longitudinal designs and exploring various conflict environments. Future research should also include clinical diagnostics and focus on the impact of missile alerts on children to provide a more comprehensive understanding of PTSD in conflict settings.

Declarations

The authors of this article declare that the article is the original work of the authors, has not been published or submitted elsewhere, and that all sources used in the preparation of this article have been properly cited and referenced. Furthermore, no financial support was received for the writing of this article, and there is no direct or indirect financial involvement with any of the organizations or individuals mentioned. Additionally, no conflicts of interest exist with regard to the authorship or publication of this academic article. Before conducting any research described in this article, the authors obtained approval from the relevant institutional ethics committee and ensured that the research was conducted ethically by relevant ethical guidelines. Research data is available on OSF.io, a platform for storing, sharing, and managing research data.

Acknowledgment

The authors extend their heartfelt gratitude to the participants who took the time to complete the research questionnaire. A significant number of these participants hail from the areas surrounding the Gaza Strip. These individuals have endured devastating acts of merciless and cruel violence against their family members and friends within their communities by terrorists from the Hamas organization, particularly on October 7, 2023. You are in our thoughts, and our most fervent prayers and deepest sympathies are unreservedly with you. We extend our heartfelt wishes for a full and speedy recovery to those who have been injured. We fervently hope for the immediate and safe return of those who are being held hostage. Additionally, we pray for those who have been tragically murdered.

Notes

1
This research is part of a study focused on the effects of rocket attacks on the Israeli population during a specific military operation. The study was conducted by Dr. Yaakov Bayer from Ben Gurion University and Dr. Solon Solomon from Brunel University London School of Law. Comprising multiple perspectives and disciplines, the research aims to provide a comprehensive understanding of the issue. The legal conclusions extracted from the research are published in Solon Solomon & Yaakov Bayer (2023) Is All Mental Harm Equal? The Importance of Discussing Civilian War Trauma from a Socio-Economic Legal Framework's Perspective. Nordic Journal of International Law, Volume 93 (2023), Pages: 1-20.
2
It is important to note that the questionnaire is one of the diagnostic tools for people with PTSD. A complete diagnosis of PTSD includes a clinical diagnosis that was not included in our study. Therefore, this is not a clinical diagnosis but a general and partial evaluation and assessment according to the validated questionnaire.

References

  1. American Psychiatric Association (1994). Diagnostic and statistical manual of mental disorders.
  2. American Psychiatric Association (2000) DSM-IV-TR, 4th ed.
  3. Amir, M., Kaplan, Z., & Kotler, M. (1996). Type of trauma, severity of posttraumatic stress disorder core symptoms, and associated features. The Journal of General Psychology, 123(4), 341-351. [CrossRef]
  4. Anderhub, V., Güth, W., Gneezy, U., & Sonsino, D. (2001). On the interaction of risk and time preferences: An experimental study. German Economic Review, 2(3), 239-253. [CrossRef]
  5. Bayer, Y.M. (2023) Challenges in Autonomous Financial Management Among Patients with Serious Mental Illness During Long-Term Hospitalization: Insights from Israel. Preprints 2023.
  6. Bayer, Y.M., Ruffle Bradely, Zultan Ro'i, Dwolazky Tzvi (2018) Time preferences in patients with mild cognitive impairment (MCI). Laurier Centre for Economic Research and Policy Analysis: Toronto.
  7. Bayer, Y.M. Shtudiner, Z., Suhorukov, O., & Grisaru, N. (2019). Time and risk preferences, and consumption decisions of patients with clinical depression. Journal of Behavioral and Experimental Economics, 78, 138-145. [CrossRef]
  8. Bayer Y.M., & Shtudiner, Z. Sirens of stress: Financial risk, time preferences, and post-traumatic stress disorder: Evidence from the Israel-Hamas Conflict. Journal of Health Psychology, 13591053231207693. [CrossRef]
  9. Benjet, C., Bromet, E., Karam, E. G., Kessler, R. C., McLaughlin, K. A., Ruscio, A. M., ... & Koenen, K. C. (2016). The epidemiology of traumatic event exposure worldwide: results from the World Mental Health Survey Consortium. Psychological medicine, 46(2), 327-343. [CrossRef]
  10. Blevins, C. A., Weathers, F. W., Davis, M. T., Witte, T. K., & Domino, J. L. (2015). The post-traumatic stress disorder checklist for DSM-5 (PCL-5): Development and initial psychometric evaluation. Journal of traumatic stress, 28(6), 489-498. [CrossRef]
  11. Bovin, M. J., Marx, B. P., Weathers, F. W., Gallagher, M. W., Rodriguez, P., Schnurr, P. P., & Keane, T. M. (2016). Psychometric properties of the PTSD checklist for diagnostic and statistical manual of mental disorders–fifth edition (PCL-5) in veterans. Psychological assessment, 28(11), 1379. [CrossRef]
  12. Brewin, C. R., Andrews, B., & Valentine, J. D. (2000). Meta-analysis of risk factors for posttraumatic stress disorder in trauma-exposed adults. Journal of consulting and clinical psychology, 68(5), 748. [CrossRef]
  13. Burri, A., & Maercker, A. (2014). Differences in prevalence rates of PTSD in various European countries explained by war exposure, other trauma and cultural value orientation. BMC research notes, 7, 1-11. [CrossRef]
  14. Cheng, Y., Wang, F., Wen, J., & Shi, Y. (2014). Risk factors of post-traumatic stress disorder (PTSD) after Wenchuan earthquake: a case control study. PLoS One, 9(5), e96644. [CrossRef]
  15. Contractor, A. A., Caldas, S. V., Dolan, M., Lagdon, S., & Armour, C. (2018). PTSD's factor structure and measurement invariance across subgroups with differing count of trauma types. Psychiatry Research, 264, 76-84. [CrossRef]
  16. Ehlers, A., & Clark, D. M. (2000). A cognitive model of posttraumatic stress disorder. Behavior research and therapy, 38(4), 319-345. [CrossRef]
  17. DiGrande, L., Perrin, M. A., Thorpe, L. E., Thalji, L., Murphy, J., Wu, D., ... & Brackbill, R. M. (2008). Posttraumatic stress symptoms, PTSD, and risk factors among lower Manhattan residents 2–3 years after the September 11, 2001 terrorist attacks. Journal of Traumatic Stress: Official Publication of The International Society for Traumatic Stress Studies, 21(3), 264-273. [CrossRef]
  18. Ford, J. D., Stockton, P., Kaltman, S., & Green, B. L. (2006). Disorders of extreme stress (DESNOS) symptoms are associated with type and severity of interpersonal trauma exposure in a sample of healthy young women. Journal of interpersonal violence, 21(11), 1399-1416. [CrossRef]
  19. Havenaar, J. M., Rumyantzeva, G. M., van den Brink, W., Poelijoe, N. W., Van den Bout, J., van Engeland, H., & Koeter, M. W. (1997). Long-term mental health effects of the Chernobyl disaster: an epidemiologic survey in two former Soviet regions. American Journal of Psychiatry, 154(11), 1605-1607. [CrossRef]
  20. Iversen, A. C., Fear, N. T., Ehlers, A., Hughes, J. H., Hull, L., Earnshaw, M., ... & Hotopf, M. (2008). Risk factors for post-traumatic stress disorder among UK Armed Forces personnel. Psychological medicine, 38(4), 511-522. [CrossRef]
  21. Israel Central Bureau of Statistics (2012), Financial Literacy Survey: Knowledge, Opinions, and Behavior in Financial Issues, Jerusalem: Central Bureau of Statistics [Hebrew].
  22. Johnson, S. D., North, C. S., & Smith, E. M. (2002). Psychiatric disorders among victims of a courthouse shooting spree: A three-year follow-up study. Community mental health journal, 38, 181-194. [CrossRef]
  23. Kessler, R. C., & Frank, R. G. (1997). The impact of psychiatric disorders on work loss days. Psychological medicine, 27(4), 861-873. [CrossRef]
  24. Kongshøj, I. L. L., & Berntsen, D. (2022). Is young age a risk factor for PTSD? Age differences in PTSD-symptoms after Hurricane Florence. Traumatology. [CrossRef]
  25. Langner, T. S., & Michael, S. T. (1963). Life stress and mental health: II. The midtown Manhattan study.
  26. Li, S., Guo, C., & Chan, S. S. (2022). ICD-11 posttraumatic stress disorder and complex PTSD among hospital medical workers in China: impacts of Wenchuan Earthquake exposure, workplaces, and sociodemographic factors. Frontiers in psychiatry, 12, 735861. [CrossRef]
  27. MacDermid Wadsworth, S. M. (2010). Family risk and resilience in the context of war and terrorism. Journal of Marriage and Family, 72(3), 537-556. [CrossRef]
  28. Mollica, R. F., Wyshak, G., & Lavelle, J. (1987). The psychosocial impact of war trauma and torture on Southeast Asian refugees. The American journal of psychiatry. [CrossRef]
  29. Murthy, R. S., & Lakshminarayana, R. (2006). Mental health consequences of war: a brief review of research findings. World psychiatry, 5(1), 25.
  30. Paryente, B. (2021). Parenting Experiences under Ongoing Life-threatening Conditions of Missile Attacks. Journal of Child and Family Studies, 30(7), 1685-1696. [CrossRef]
  31. Schnurr, P. P., Lunney, C. A., & Sengupta, A. (2004). Risk factors for the development versus maintenance of posttraumatic stress disorder. Journal of Traumatic Stress: Official Publication of The International Society for Traumatic Stress Studies, 17(2), 85-95. [CrossRef]
  32. Schlenger, W. E., Caddell, J. M., Ebert, L., Jordan, B. K., Rourke, K. M., Wilson, D., ... & Kulka, R. A. (2002). Psychological reactions to terrorist attacks: findings from the National Study of Americans' Reactions to September 11. Jama, 288(5), 581-588. [CrossRef]
  33. Smith, H. L., Summers, B. J., Dillon, K. H., & Cougle, J. R. (2016). Is worst-event trauma type related to PTSD symptom presentation and associated features?. Journal of Anxiety Disorders, 38, 55-61. [CrossRef]
  34. Solomon, S., & Bayer, Y. M. (2022). Reading mental harm through the lens of socio-economic rights: An empirical study of the impact of education, family, and income on the notion of civilian mental harm in warfare. Brunel University London, Ben Gurion University of the Negev.
  35. The Meir Amit Intelligence and Terrorism Information Center, https://www.terrorism-info.org.il/, Retrived:06/04/2022.
  36. Vinck, P., Pham, P. N., Stover, E., & Weinstein, H. M. (2007). Exposure to war crimes and implications for peace building in northern Uganda. Jama, 298(5), 543-554. [CrossRef]
  37. World Health Organization. (2001). The World Health Report 2001: Mental health: new understanding, new hope.
  38. Wortmann, J. H., Jordan, A. H., Weathers, F. W., Resick, P. A., Dondanville, K. A., Hall-Clark, B., ... & Litz, B. T. (2016). Psychometric analysis of the PTSD Checklist-5 (PCL-5) among treatment-seeking military service members. Psychological assessment, 28(11), 1392. [CrossRef]
Preprints 92838 g001
Figure 1. Geographic Distribution of Rocket Alarm Activations During Operation "Guardian of the Walls." Data was obtained from the Home Front Command of the Israel Defense Forces (IDF) via a Freedom of Information Law request.
Figure 1. Geographic Distribution of Rocket Alarm Activations During Operation "Guardian of the Walls." Data was obtained from the Home Front Command of the Israel Defense Forces (IDF) via a Freedom of Information Law request.
Preprints 92838 g001
Preprints 92838 g002
Figure 2. Geographic Distribution of Rocket Alert Timings, Sourced from the Israeli Home Front Command.
Figure 2. Geographic Distribution of Rocket Alert Timings, Sourced from the Israeli Home Front Command.
Preprints 92838 g002
Preprints 92838 g003
Figure 3. Distribution of PCL-5 Test Scores Among Participants.
Figure 3. Distribution of PCL-5 Test Scores Among Participants.
Preprints 92838 g003
Preprints 92838 g004
Figure 4. Distribution of Rocket Alarm Exposure by PTSD Symptom Status.
Figure 4. Distribution of Rocket Alarm Exposure by PTSD Symptom Status.
Preprints 92838 g004
Preprints 92838 g005
Figure 5. Simple Linear Regression Model of the Correlation between the Number of Rocket Alarms and PCL-5 Test Score.
Figure 5. Simple Linear Regression Model of the Correlation between the Number of Rocket Alarms and PCL-5 Test Score.
Preprints 92838 g005
Preprints 92838 g006
Figure 6. Simple Linear Regression Model of the Correlation between the Log of Number of Rocket Alarms and PCL-5 Test Score.
Figure 6. Simple Linear Regression Model of the Correlation between the Log of Number of Rocket Alarms and PCL-5 Test Score.
Preprints 92838 g006
Preprints 92838 g007
Figure 7. Quadratic polynomial regression Model of the Correlation between the Number of Rocket Alarms and PCL-5 Test Score.
Figure 7. Quadratic polynomial regression Model of the Correlation between the Number of Rocket Alarms and PCL-5 Test Score.
Preprints 92838 g007
Preprints 92838 g008
Figure 8. LOWESS analysis Correlation between the Number of Rocket Alarms and PCL-5 Test Score.
Figure 8. LOWESS analysis Correlation between the Number of Rocket Alarms and PCL-5 Test Score.
Preprints 92838 g008
Table 1. Subjects' Descriptive Statistics.
Table 1. Subjects' Descriptive Statistics.
PTSD Healthy T Test
Age 34.23
(12.36)		 39.81
(13.98)		 T=-2.900
p=0.004
Male 0.16
(0.37)		 0.22
(0.41)		 T=-0.995
p=0.321
Income 4.88
(3.15)		 6.27
(2.97)		 T=-2.914
p=0.005
Education 13.83
(3.11)		 15.61
(2.95)		 T=-4.274
P<0.001
Children 1.13
(1.45)		 2.01
(1.85)		 T=-3.525
P<0.001
N 62 320
Note: Standard deviations appear in parentheses.
Table 2. Outcomes of the Simple Probit Estimation Model, featuring a Binary Variable to Indicate Clinical-Level Presence (1) or Absence (0) of PTSD Symptoms. The model explores the association between socio-economic factors and the probability of manifesting symptoms of post-trauma.
Table 2. Outcomes of the Simple Probit Estimation Model, featuring a Binary Variable to Indicate Clinical-Level Presence (1) or Absence (0) of PTSD Symptoms. The model explores the association between socio-economic factors and the probability of manifesting symptoms of post-trauma.
Preprints 92838 i001
Table 3. Outcomes of the Simple OLS Model, featuring the PCL-5 Score Variable. The model explores the association between socio-economic factors and the probability of manifesting symptoms of post-trauma.
Table 3. Outcomes of the Simple OLS Model, featuring the PCL-5 Score Variable. The model explores the association between socio-economic factors and the probability of manifesting symptoms of post-trauma.
Preprints 92838 i002
Table 4. Multivariate Probit Estimation Model with a Binary Variable Indicating Clinical-Level Presence (1) or Absence (0) of PTSD Symptoms.
Table 4. Multivariate Probit Estimation Model with a Binary Variable Indicating Clinical-Level Presence (1) or Absence (0) of PTSD Symptoms.
Preprints 92838 i003
Table 5. Multivariate Ordinary Least Squares (OLS) Regression Analysis Using the PCL-5 Score as the Dependent Variable.
Table 5. Multivariate Ordinary Least Squares (OLS) Regression Analysis Using the PCL-5 Score as the Dependent Variable.
Preprints 92838 i004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated