Enhancing Security of BB84 Quantum key Distribution Protocol against Detector Blinding Attacks by Use of an Active Quantuam Entropy Source in the Receiving Station

1. Introduction

Randomness is the key ingredient of security of any cryptographic protocol, including quantum key distribution (QKD) protocols. To understand the role of randomness in the security of QKD, here we study so-called detector blinding attack (DBA) [1,2,3,4,5,6,7,8,9] which injects strong light into the quantum channel and exploit technological weaknesses/features of the single-photon detectors used within, with the purpose of controlling the internal entropy source and thus break the security. This particularly successful attack strategy makes possible not only a completely undetectable eavesdropping, but also a full recovery of the secret key, thus defying two most notable strengths of QKD: 1) the ability to detect eavesdropping, and 2) the information-theoretic unconditional security of the generated secret key. Various adaptations of the DBA have been mounted on a range of scientific and commercial bipartite QKD systems [1,2] rendering them completely unusable even though their manufacturers have previously claimed them provable and unbreakably secure for years before the blinding attack has become publicly known.

Each instance of DBA is specifically tailored for a detector feature that is being exploited, for example: passive quenching [5], active quenching [4], superlinearity [5], thermal effects [1,2,5] etc. as well as specific architecture of the receiving station, such as passive or semi-active base control. In the demonstrated attacks the optical power of the incoming blinding light ranges from up to 28 mW one-time pulse [3], 8 mW continuous [4], all the way down to a few pW continuous [5] or even less than 120 photons per pulse [6], which is a power span of over 15 decades! Most of scientific and research works propose to defend against a detector blinding attack by upgrading hardware so as to be able to detect strong light incoming from the quantum channel [10,11,12,13,14]. Apart from being technologically challenging, the main problem with that approach is that while it may prevent a particular attack, it does not guarantee restoring of provable security, as noted in Ref. [4] and experimentally demonstrated in [14]. Repelling the attack by "brute force", i.e., without a deeper understanding of how and why it works, leaves a metallic aftertaste that a clever modification of the attack could make it work again.

In this paper we investigate the information-theoretic background of this devastating attack strategy on so called "discrete variable QKD" that is, QKD protocols which communicate single qubits. We show that success of a blinding attack relies on the attacker's ability to obtain information on the receiver’s choice of detection base. In a detector blinding attack it is done by active sending a multi-qubit messages with a purpose to take control over the internal entropy source which selects the base. Based on this insight, an elegant defense strategy is developed for preventing the whole family of multi-qubit attacks on receiver's entropy source, which restores the unconditional security of a QKD protocol. On top of that, by monitoring an additional parameter of the communication over the quantum channel, it is possible to detect a general entropy source attack at no further cost in hardware.

Even though blinding attack works well on virtually any QKD protocol [8], for the sake of simplicity and without the loss of generality, we will study attacks on two implementations of the BB84 protocol [15,16], which were broken in Refs. [4] and [5].

2. BB84 Protocol in a Nutshell

In the BB84 QKD protocol, two legitimate parties who wish to establish a secure communication, usually named Alice and Bob, are linked by one quantum channel and one authenticated (but not necessarily encrypted) classical channel, while an eavesdropper Eve has a physical access to both channels, as shown in Figure 1.

It is assumed that classical communication channel is bidirectional and information-theoretic authenticated: Alice can be sure that she is talking to Bob, and vice versa. The messages exchanged between Alice and Bob over this channel need not be encrypted, which means that Eve can read them but cannot change them. The quantum channel is unidirectional: Alice uses it to send qubits to Bob.

In the first phase of the BB84 protocol, Alice sends to Bob, over the quantum channel, a random classical bit equiprobably valued 0 or 1, encoded in a linearly polarized qubit as follows: bit value 0 is randomly and equiprobably encoded as either 0^o or 45^o polarization, while bit value 1 is randomly and equiprobably encoded as either 90^o or 135^o. Alice typically uses an electronic quantum random number generator (QRNG) [17,18,19,20,21,22] in order to generate a qubit. Bob randomly selects one out of the two orthogonal bases in which the qubit is measured: (0^o, 90^o) or (45^o, 135^o). With probability of 1/2, namely when his base happens to match the polarization of the qubit, Bob obtains the exact bit value that Alice sent, while in the other case Bob obtains a random bit. To figure out which is the case, Bob discloses his base to Alice over the authenticated classical channel. Knowing which qubit she sent, Alice replies either "keep" in which case they keep the bit, or "discard" in which case they both discard their bits. This communication is repeated until Alice and Bob collect a sufficiently long raw key, for example until the length of $L$ bits, agreed beforehand, is reached. The repeated communication is performed periodically with frequency $f_G$, which technically allows Bob to define a short period of time $t_G$ (henceforth gate time) around the expected time of arrival of qubits and in that manner reduce the effect of noise (dark counts). Note that, by listening to the communication over the classical channel alone, Eve is not able to figure out the value of the bit that is kept. Furthermore, she cannot fake any of the communication over the classical channel because it is authenticated. All she can do is to intervene in the quantum channel and listen to the classical channel. Ideally, after this initial phase, Alice and Bob end up with the same stream of bits, namely their secret common key. However, due to inevitable hardware imperfections such as: noise (dark counts and afterpulses in single-photon detectors), losses, bases misalignment, etc. as well as Eve's tampering with the quantum channel, there will be some differences (errors). In order to correct them, they need two further classical communication phases, namely information reconciliation and privacy amplification, which are performed over the authenticated classical channel.

The blinding attack is performed entirely in the initial phase in which the quantum channel is used, so we do not need to analyze the leftover two classical phases of the BB84 protocol. Furthermore, in a DBA Alice is never under attack, so her setup will not be discussed either.

3. Detector Blinding Attack on BB84 with Passive Base Selection

In the receiving station (Bob) which has been broken in Ref. [4], random selection of bases is performed passively, by help of a non-polarizing beam splitter (BS), as shown in Fig 2. Note that the sender (Alice) needs an equivalent of 2 random bits to generate the qubit state (namely to choose 1 out of 4 possible qubit states), while Bob needs an equivalent of 1 bit of entropy per received qubit to randomly choose its measurement basis (1 out of 2 possible bases), which mandates that each station must have a private random number generator or something equivalent of it. In the Bob setup, show in Figure 2, the random selection of the receiving base is obtained through the use of the beam splitter BS.

The detector blinding attack (DBA), on this setup, works as follows. Eve cuts the quantum channel between Alice and Bob (e.g., an optic fiber or aerial link) and blinds simultaneously all four detectors in Bob by shining strong pulsed circularly polarized light of high enough intensity, as explained in Ref. [4]. Each detector in Bob receives ¼ of the incident power of the blinding light. Pulses are powerful and frequent enough (~70 kHz repetition rate, 8 mW per pulse) to keep the detectors thermally blinded at all times during the qubit exchange. This blinding strategy generates a four-fold coincidence among all detectors upon every blinding pulse.

In that state, detectors are sensitive only to strong pulses of light brighter than some threshold power$P_{thr}$, superimposed on top of the blinding light, so called "fake states". For example, Eve can shoot a pulse polarized at 45^o and of power just over ${2P}_{thr}$. Half of the power would end up in the 45^o detector making it click. The 135^o detector will receive a negligible power while detectors in the other base will receive ${2P}_{thr}$ each, thus none of the other detectors will click. Note that the success of the attack is not very sensitive to the pulse power as it can be anywhere between just above ${2P}_{thr}$ and just below ${4P}_{thr}$, leaving quite a wide range for the attack to work on all 4 detectors which, for other security reasons, should be well matched in their specs anyway.

Eve measures Alice's qubit in a randomly selected base (either (0^o, 90^o) or (45^o, 135^o)) using a receiving station which is a close copy of Bob. Note that Eve is receiving Alice's qubits using the close copy of Bob's station and using the same protocol as Bob would. After the measurement, Eve sends to Bob a fake state matching her measurement, effectively copying her measurement result to Bob who then measures the same as Alice.

Finally, Eve passively listens to the classical channel between Alice and Bob and does whatever they do in the next two classical phases, namely information reconciliation and privacy amplification, in order to arrive to exactly the same "secret" key. Note that the attack does not introduce any extra bit error rate (BER). Since blinded detectors do not produce dark counts, a prudent Eve may send to Bob random "noise" pulses targeting each detector separately (at an individual dark count rate), thus not taking chances in case that Bob is monitoring dark count rates of the detectors. Note that, by Kerchoff's principle of cryptography [23], Eve knows the dark count rates of Bob's detectors. She could, for example, in quite a realistic scenario, be the vendor of Bob's station and could have measured dark count rates (and all other relevant parameters) prior to selling it.

While it is deemed in Ref. [4] that detector blindability is what makes the DBA viable, in this work we go a step further and seek for an insight at the level of information theory.

First we note that, in order for the DBA to work, Eve must make sure that Bob's and hers detection bases match, before sending him a light signal that contains an information. In the attack described above, fake states contain the information Eve wants Bob to receive, while continuous circularly polarized blinding light does not contain any.

Next we note that a fake state pulse is split deterministically at the beamsplitter BS such that exactly one-half of its power hits each detection base. This is in stark contrast with BB84 where Bob receives a single qubit from Alice and where the BS serves as an internal and private entropy source which randomly selects one of the two Bob's detection bases. Apparently, due to deterministic splitting of a fake state under DBA, entropy of this internal randomness generator is zero - the entropy source it effectively disabled. But, without the random selection of bases, Bob is unable to run BB84. Whatever Bob is actually running, it is not the BB84. But he does not know that because he does not realize his entropy source has been compromised.

In the BB84 protocol, random base selection of the receiving station is a pivotal and indispensable ingredient of the security. Let us investigate this in more detail. As explained above, as per original BB84, Bob must calculate his reception base in order to be able send this information to Alice. He does that from the detections. Namely, if either detector 0^o or 90^o fires then Bob concludes that his random base is 0, if any the other two detectors fire then the base is 1, and finally if no detector fires or more than two detectors fire (e.g., due to the noise) then the communication instance is inconclusive and must be discarded. If Bob is monitoring randomness of the sequence of bases (even though this is not a part of BB84), he would notice a perfect randomness. But how can this be when his own entropy source is incapacitated? Obviously, the randomness of his detection bases can be traced back to the beampslitter BS in Eve's station, which is still functioning in the quantum regime because it is receiving single qubits from Alice. This means that Eve and Bob are now logically united into one receiving station, "Eve-Bob", which performs a correct BB84 protocol with Alice. In effect, Eve has sneak into Bob's station (even though she might be physically far away) and is able to obtain enough information to arrive to the exact same key as Alice and Bob.

What information Eve obtains? The DBA allows Eve to directly set the detection outcome of any of the four detectors in Bob thus she knows everything that Bob knows. Indirectly, she also gains knowledge of Bob's bases. It is tempting to conjecture that if Bob is monitoring proper operation of his detectors, e.g., by making sure they are not blinded and are sensitive to single photons, then devastating attacks like DBA are impossible.

But, could Eve mount a successful attack without blinding the detectors? To answer that, we consider two scenarios.

In the first scenario let us suppose Eve is able to set Bob's receiving base by some means other than detector blinding. Then, her best strategy would be to set Bob's base so as to match hers, but this time she would send to Bob a single qubit matching her measurement. Bob would detect the same bit as Eve, without any increased loss or error with respect to when Eve is absent. Thus, Eve would obtain all the information as in the DBA and would stay invisible.

In the second scenario Eve succeeds without having a control over Bob's bases. Let us suppose that Bob himself is choosing his reception base randomly (e.g., by help of a true random number generator or equivalent), but that Eve somehow gets the information about the base before receiving Alice's qubit. Now, Eve may set her base to match Bob's, receive Alice's qubit and send to Bob a qubit that matches her measurement. Eve would again obtain the key and would stay invisible. Note that in both of those scenarios, communication is performed via single qubits and thus Bob's BS will operate in the quantum regime and will introduce a 3 dB loss of useful signal. However, this amount of loss is not a problem for Eve, as will be clarified later.

From this discussion one can see that if Eve has information on Bob's bases on time, the whole QKD protocol is doomed—it would give no security whatsoever with or without blinding of detectors. We conclude that Eve's success relies in DBA solely on the fact that her mutual information with Bob's choice of bases is maximal:

$$I\left(E, B\right)=1$$

(1)

where $E=\left(e_1,{\dots e}_L\right)$is a random variable describing Eve's knowledge on Bob's receiving bases during all $L$ rounds of the initial phase of BB84, and $B=\left(b_1,{\dots b}_L\right)$is a random variable describing Bob's knowledge on his receiving bases. The base codes $e_i$ and $b_i$ have a value 0 for (0, 90) base and 1 for (45, 135) base.

The DBA is just a technique by which Eve obtains the mutual information of Equation (1) in full.

4. Detector Blinding Attack on BB84 with Semi-Active Base Selection

In the receiving station (Bob) which has been broken in Ref. [5], random choice of detection bases is performed actively by means of a phase electro modulator (PEM) driven by an explicit electronic QRNG, as shown in Figure 3. The state of the QRNG (0 or 1) determines the receiving base. According to the above discussion, we assume that the QRNG is private meaning that it cannot be manipulated nor predicted by Eve. This base choice technique functions exactly as required by BB84 for single qubits. It also diverts all the incoming power of a strong fake state to the selected base.

The version of DBA used against this setup works as follows. Eve again cuts the quantum channel between Alice and Bob. She blinds simultaneously all four detectors in Bob by shining strong continuous (CW) circularly polarized light of a carefully tailored intensity, as explained in Ref. [5]. Note that circularly polarized light distributes evenly among the detectors regardless of the state of the PEM, and thus Eve is able to simultaneously blind, and keep blinded forever (or at least during the qubit exchange phase) both detectors, and thus both bases. Note that while the active control of PEM works correctly for qubits and fake states, it has no effect on the blinding light. Therefore, we name the setup in Figure 3 "semi-active". As in the previous DBA, blinded detectors are sensitive only to fake states pulses brighter than a threshold power$P_{thr}$, superimposed on top of the blinding CW light, which confines the fake state power to the range between slightly above ${2P}_{thr}$ and slightly below ${4P}_{thr}$.

The difference to the previous setup (shown in Figure 2) is that, here, Eve is able to copy her measurement to Bob with only 50% success, namely in those instances where her base coincides with Bob's by a chance. In the other 50% Bob's blinded detectors receive nothing and the bit is lost. Next, by passively listening to the classical communication between Alice and Bob in the next phases of the BB84 protocol, Eve is able to figure out which bits were lost, sift the same bits as Alice and Bob do and recover 100% of the key. While this attack reduces the key rate by a factor of 2 (equivalent of channel loss of 3 dB) with respect to when Eve is not there, the security situation is not satisfactory because Eve still obtains the full key and, in the presence of other losses or a strongly varying loss, she might just get away undetected. In fact, Eve might place her away from Bob, such that the channel loss between them is at least 3 dB, in which case the loss would be compensated because her fake states Bob detects with no loss. In fact, if the channel loss between Eve and Bob is greater than 3 dB, Eve will have to fake an additional loss, not to raise suspicion, which is technically quite easy. On top of that, note that Alice and Bob have no secure way of calibrating the key rate because Eve might decide to be present all the time and introduce the 3 dB loss when not eavesdropping and remove it when she does. This architecture of receiving station (Figure 3) has also been shown vulnerable to the weak pulse (~120 photons) attack with an early test prototype of superconducting nanowire single-photon detectors exploiting their superlinear behavior and/or their great sensitivity to thermal effects [6].

The reason for this relative success of Eve even with the "active" control of bases is that this setup is still not satisfying assumptions under which the BB84 protocol has been proven secure (e.g., [16,24]) namely that a light received by Bob's station must hit not more than one base at a time, which is an implicit assumption of a single-qubit communication. This assumption is violated in the setup in Figure 3.

5. Improved Setup with a Fully-Active Base Selection

Following the discussion above, we propose an improved receiving station, shown in Figure 4. It consists of two physically distinct detection bases and a mirror which directs all incoming light to one and only one base under control of a local and private QRNG. Such a switching mechanism is allowed by laws of quantum mechanics and can be implemented for example by a motorized mirror, a MEMS router [25] or a mechanical switch inside optical fibers [26]. We will now analyze how this setup operates under a DBA attack.

The DBA attack requires careful tailoring of characteristics of the blinding light (e.g., its power, polarization, whether it should be a CW or a pulsed light, etc.) as well as precise modeling of single-photon detectors, in order to arrive to a reliable blinding technique for a particular receiving station. The difference of the proposed receiver (shown in Figure 4), with respect to the two previous receivers (shown in Figs. 2 and 3), is that here only one (randomly selected) base receives light, while the other base is in darkness. Following the previous discussion we will differ two cases: the continuous blinding light and the pulsed blinding light.

In case of the continuous blinding light attack on the new receiver Eve cannot keep blinded both bases at all times nor is her attack invisible. Namely, whenever the QRNG changes the receiving base, the two detectors that were previously in dark get both simultaneously hit by a strong blinding light. One is able to predict what happens then without any modeling of a particular detector. When a single-photon sensitive detector, which was previously in the dark and ready to detect, gets hit by a strong light, it will detect, that is produce a "click", an output pulse signifying a detection, at least once. This is because the sensor will do exactly what it is supposed to do when a single photon is detected: for example, an avalanche photodiode will become highly conductive while a superconductive nanowire will become highly resistant. Such transitions will necessarily generate a detection signal. The detector(s) in question may become blinded, but that will happen only after that initial detection. As explained before, because not being able to decide which state was sent, Bob will have to announce such events discarded: this will happen in 50% of gates. In the other 50% of gates Eve is able to send her measurement to Bob with probability of 1/2 (in total 25% of gates) namely in those instances where her base coincides with Bob's randomly selected base by a chance, while in the remaining 25% gates Bob will receive nothing (his detectors will remain silent), resulting in 4-fold drop of the effective key rate with respect to no eavesdropper. Even though this higher loss, equivalent of 6 dB, introduced by Eve, is in principle easier to detect by Alice and Bob, this is still not satisfactory because: a) Eve may be able to compensate for the loss (as explained before); and b) Eve can obtain a complete knowledge of the key without being detected.

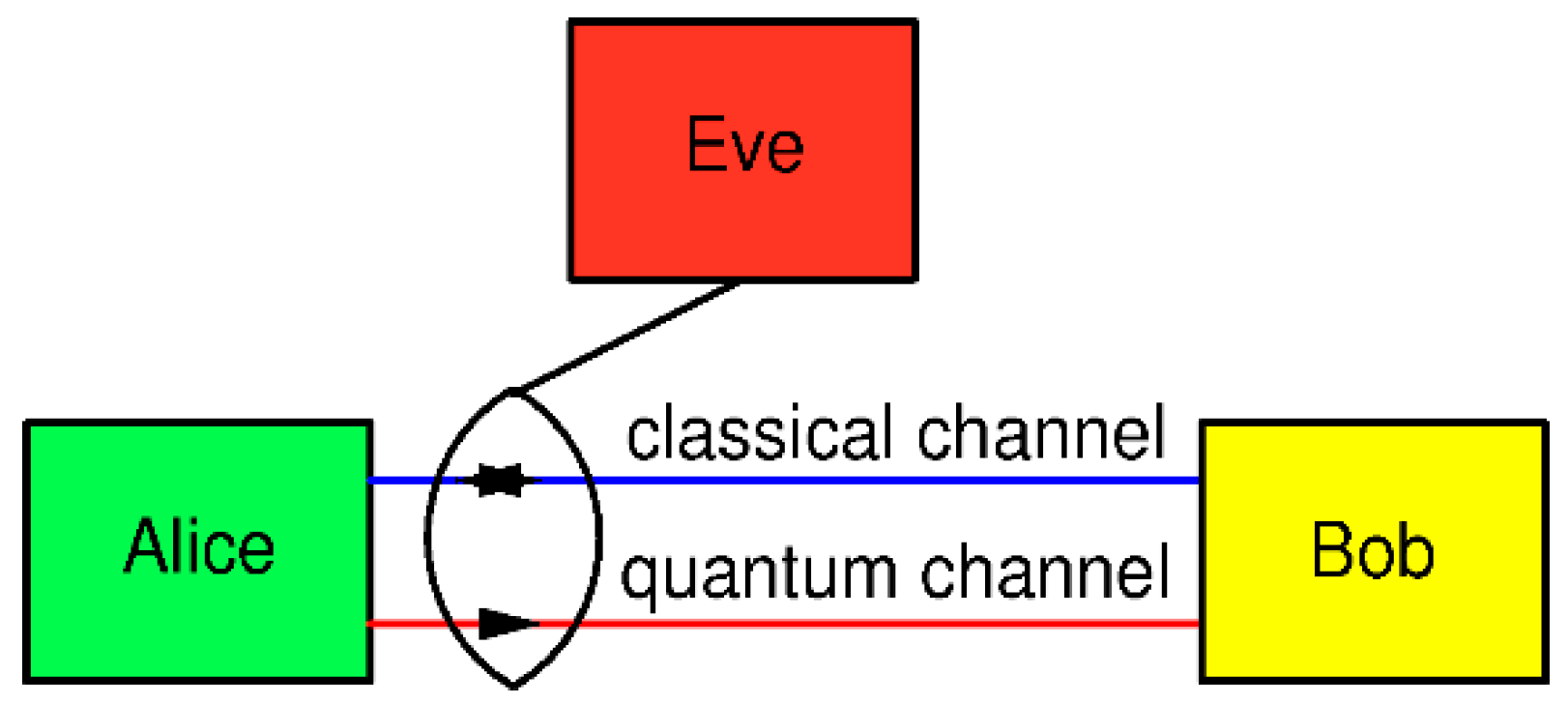
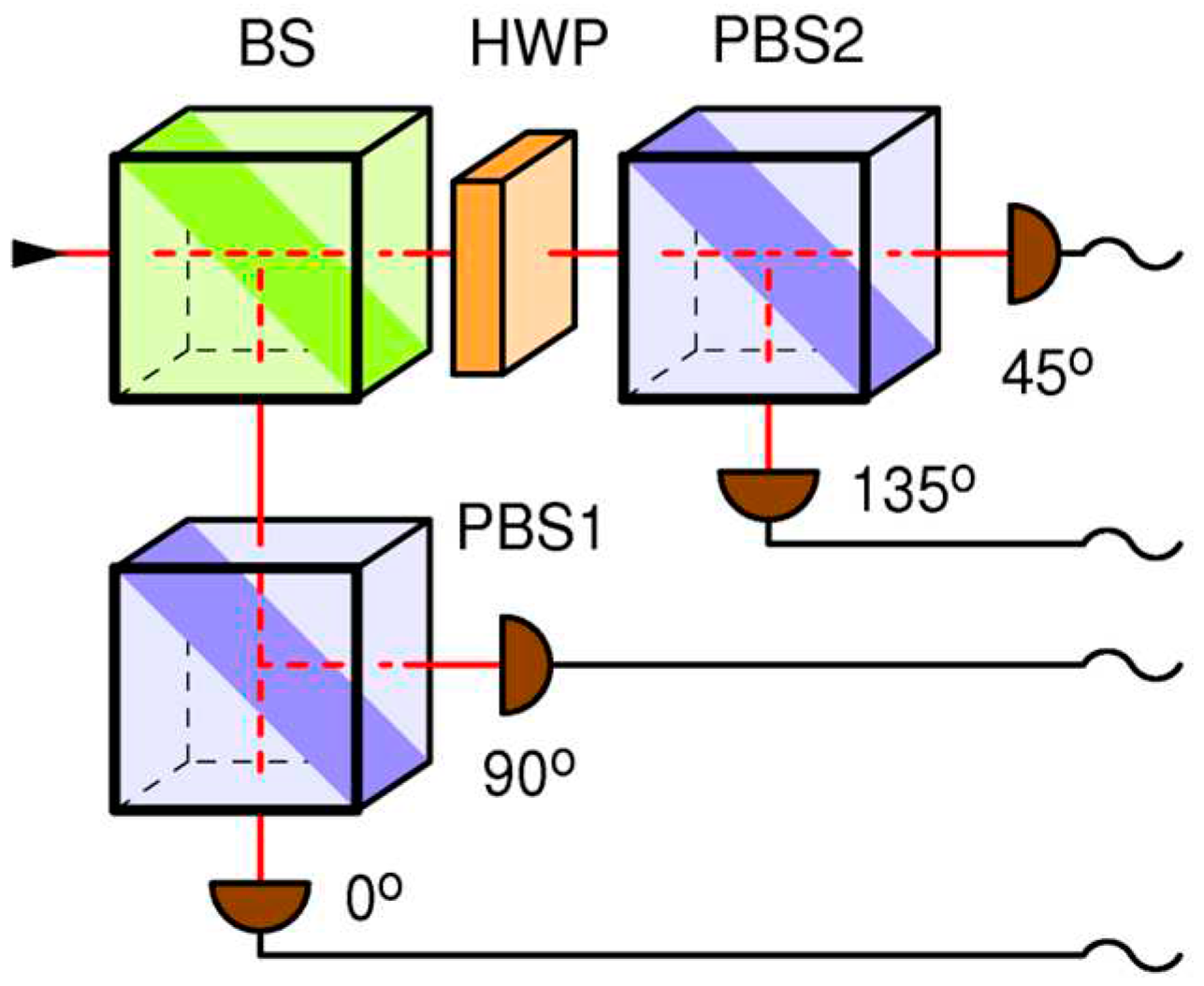
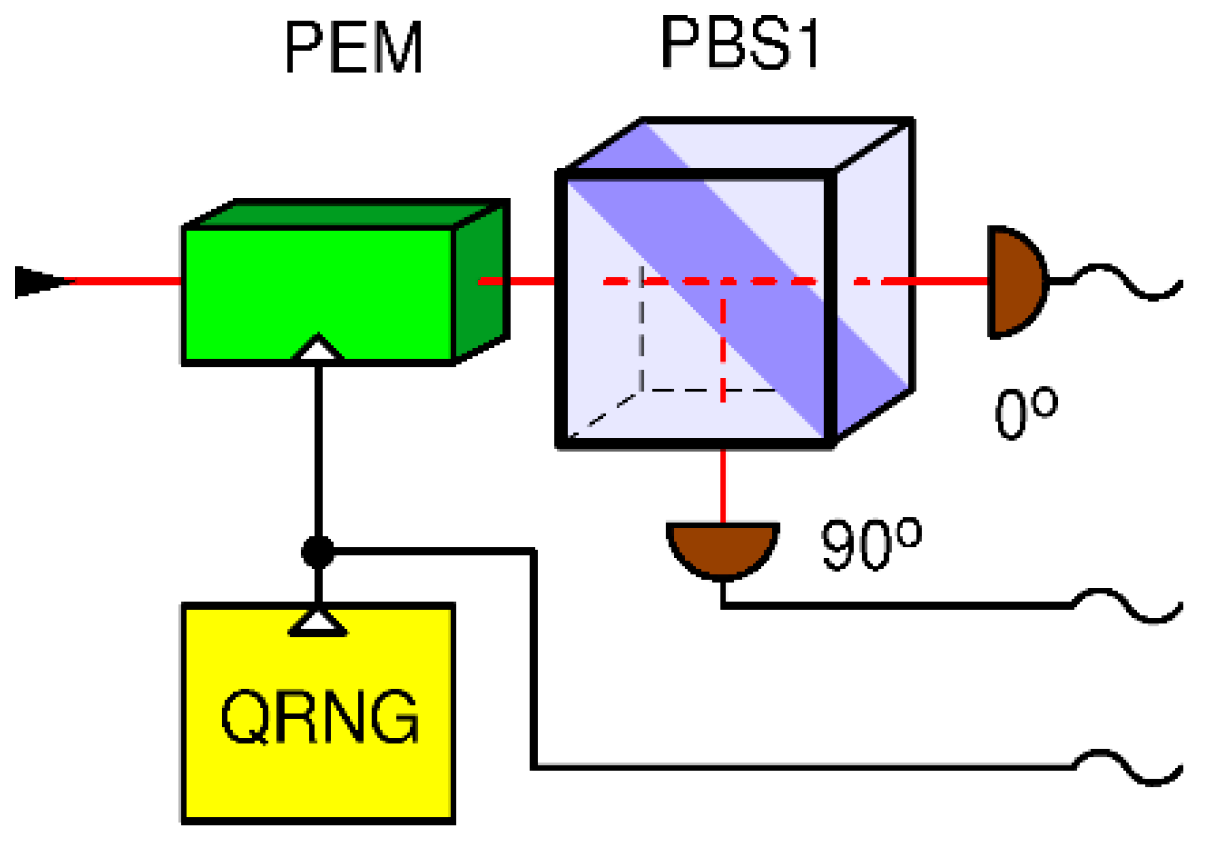
In case of the pulsed blinding light, very strong laser pulses keep detectors thermally blinded. In the original DBA described in Refs. [4,7], performed on the setup shown in Figure 2, it is noted that such strong pulses will cause simultaneous detection in all affected detectors. Because of that, Eve keeps the blinding pulses outside of gate so that they do not generate extra in-gate coincidences, and shoots them frequent enough to keep all the detectors blinded at all times. However, when this attack is applied to the setup in Figure 4, Eve is not sure which base gets blinded, because bases are selected at random with probability 1/2, therefore she needs to rise the blinding rate by at least twice. Even so, because of the binomial statistics of base selection, occasionally a base might get out of blinding and generate an extra in-gate coincidence when hit by a fake state. While details of this behavior would have to be investigated further, it is safe to assume that, in her best scenario, Eve will be able to achieve blinding and retrieve the full key, albeit at the expense of 6 dB loss caused merely by the random base choice. The un-avoidable price paid for the pulsed blinding is causing the out-of-gate coincidences between two detectors in the active (selected) base.

5.1. Attack Analysis

It would naively seem that Eve can successfully eavesdrop on the receiver in Figure 4 using blinding techniques. However, this particular setup enables yet another lever arm available for Alice and Bob to defeat Eve, which relies on monitoring in-gate and out-of-gate coincidences.

Let us first discuss a regular quantum communication with single qubits, in which Bob knows the arrival time of Alice's qubit and opens a short detection time window $t_G$, named "gate", around it, to detect the qubit. In order to have a non-zero secret key rate of the BB84 protocol, the bit error rate of the first phase must be $<11.5$% [27]. The dark count occurrence probability during the gate for a single detector is:

$$p_{DCR}={\left(1-e^{-t_G{f}_{DCR}}\right)\cong t}_G{f}_{DCR}$$

(2)

where $f_{DCR}$ is the dark count rate (DCR) of the detector and $t_G$ is duration of the gate. The right-hand approximation is valid for $t_G{f}_{DCR}\ll 1$, which is often the case. Bob can confidently determine the dark count rates for all four detectors by disconnecting the receiver from the quantum channel and performing measurements in the dark. To simplify calculation, we will henceforth assume equal DCR for all detectors. DCR-caused "accidental" coincident detection between a pair of detectors belonging to the same base is a Poissonian random event. Its probability during the gate-open period $t_G$, or "in gate" probability, is given by:

$$p_{AIn}=p_{DCR}^2\cong t_G^2{f}_{DCR}^2$$

(3)

When receiving qubits, the coincidence rate between two detectors forming a base, is described by the Hong-Ou-Mandel (HOM) effect, which characterizes the probability of simultaneous photon detection at the two outputs of a beamsplitter [28]. By considering a coherent input state qubit, emitted from Alice with an average photon number $〈n〉$ within a gate-open period $t_G$, the per-gate-coincidence-probability measured by Bob in any of its two bases is given by [29]:

$$p_{QIn}=\frac{1}{2}{\left(1-e^{-\frac{〈n〉{ϵ}_B{ϵ}_{QCh}}{2}}\right)}^2\cong \frac{{〈n〉}^2{ϵ}_B^2{ϵ}_{QCh}^2}{8}$$

(4)

where${ϵ}_B$ is Bob's system quantum efficiency, which includes effects of finite detector quantum efficiency, optics imperfections and other losses in Bob, while quantum channel efficiency ${ϵ}_{QCh}$ is a fraction of qubits that survive through the quantum channel connecting Alice and Bob. The right-hand approximation is valid for $\left({〈n〉ϵ}_B{ϵ}_{QCh}\right)/2\ll 1$, which holds true in a practical QKD where typically $〈n〉 ~ 0.1$ and ${ϵ}_{S }~ 0.1-0.5$ while loses can be anywhere between a few dB and few tens of dB. The overall factor $1/2$ equals probability that the qubit is in a "wrong" base. In the case that the base is "right" for the given qubit, there will be no coincidence in principle because photon will end up in only one detector. Here we neglect a possible imperfection in Bob's polarizers, which in may allow for a small probability of coincidence (typically less than 0.01). The coincidence probability is composed of both the accidental coincidences and qubit-related coincidences. Both being Poisson random processes, the total in-gate coincidence probability $p_{Cin}$, for the regular BB84 protocol in setup in Figure 4, is given by:

$$p_{CIn}=p_{AIn}+p_{QIn}-{p_{AIn}p}_{QIn}\cong t_G^2{f}_{DCR}^2+\frac{{〈n〉}^2{ϵ}_B^2{ϵ}_{QCh}^2}{8}$$

(5)

As an example, assuming the following realistic values: gate time $t_G=5$ ns, the dark count rate $f_{DCR}=1000$ cps, average photon number in a qubit $〈n〉=0.1$, Bob's system quantum efficiency ${ϵ}_B=0.25$, and the quantum channel transfer efficiency ${ϵ}_{QCh}=0.16$ (-8 dB), one arrives to $p_{CIn}={2·10}^{-6}$.

Using the same approach, we can calculate out-of-gate coincidence rate for DCR:

$$p_{AOut}={\left({ \frac{1}{f_G}-t}_G\right)}^2{f}_{DCR}^2$$

(6)

The qubits do not fall outside of gate and therefore do not cause out-of-gate coincidences:

$$p_{QOut}=0.$$

(7)

The total out-of-gate coincidence probability, for the regular BB84 protocol in setup in Figure 4, equals:

$$p_{COut}=p_{AOut}+p_{QOut}-p_{AOut}{p}_{QOut}={\left({ \frac{1}{f_G}-t}_G\right)}^2{f}_{DCR}^2$$

(8)

where $f_G$ is rate at which Alice emits qubits. Using the same set of communication parameters as in the previous example and $f_G=10$ MHz, one arrives to $p_{COut}=9.0·{10}^{-9}$.

Our defense strategy relies on the fact that both in-gate and out-of-gate coincidence probabilities, described by Equation (5) and Equation (8), are dramatically enhanced under a strong-light attack, as will be shown below.

The case of the CW DBA. Let $N$ be the number of photons arriving during a gate onto a detector. Then the probability $p_N$ that the detector, having a quantum efficiency $ϵ$, will detect at least once is given by [29]:a = 1,

$$p_N=1-{\left(1-ϵ\right)}^N$$

(9)

or even closer to unity in case of superlinear detectors [6]. Considering a coherent blinding light, with an average photon number $\langle m\rangle$ arriving on Bob during a gate, the overall coincidence probability, according to Equation (9), is:

$$p_{DBAIn}={\left(1-{\left(1-{ϵ}_B\right)}^{\frac{〈m〉}{2}}\right)}^2$$

(10)

Assuming an attack using as few as $〈m〉=20$ photons incident on Bob per gate, and assuming that ${ϵ}_B=0.25$, then the coincidence probability $p_{DBAIn}$ is about $0.94$ and it would quickly approach theoretical maximum of $1$ for a larger $〈m〉$. This is about 6 orders of magnitude higher than in-gate coincidence probability of the regular BB84 protocol $p_{CIn}={2·10}^{-6}$, as calculated above, even though the incident optical power considered in this example is much smaller than required for an actual detector blinding attack.

In the case of the pulsed DBA, which operates upon the principle of thermal blinding with strong out-of-gate pulses, such an attack will not enlarge in-gate coincidences between detectors in the same base. However, as explained above, each blinding light pulse will create one out-of-gate coincident pair of detections in two detectors belonging to the base which is currently selected by the QRNG. The coincidence probability for either detection base, per gate, is given by:

$$p_{DBAOut}=\frac{f_{BPR}}{f_G}$$

(11)

where $f_{BPR}$ is a minimum required blinding pulse rate, being 70 kHz according to [4] and, as explained above, this needs to be at least doubled by Eve because of the active base selection in this setup. As justified above, we do not add dark counts to that rate.

Assuming $f_{BPR}=140$ kHz and other parameters the same as in the previous examples, we obtain $p_{DBAOut}=1.4·{10}^{-2}$. On the other hand, the coincidence probability of the undisturbed QKD $p_{COut}=9.6·{10}^{-9}$, as calculated above, is more than 6 orders of magnitude smaller.

This demonstrates that, both in the in-gate and in the out-of-gate DBA, the corresponding coincidence rates will be strongly enhanced with respect to the undisturbed BB84, when using the setup shown in Figure 4. This fact is the basis for our defense strategy, which should work for any type of strong light attack, DBA included.

5.2. Proposed Defense Strategy against Strong-Light Attacks

To defend from strong light attacks, we focus on two pairs of equations: on one hand Equation (5) and Equation (8) which model in- and out- of-gate coincidence probabilities during execution of a pristine BB84 QKD protocol, and on the other hand Equation (10) and Equation (11) which model the same coincidence probabilities, but under a strong-light attack. The huge rise in coincidence probabilities under a strong light attack, even for injected light level far less than required to mount an actual blinding attack, present a robust figure of merit for discerning undisturbed quantum communication from an attack condition. In modern QKD systems, output of each detector is connected to a dedicated channel of a time-tagger and time stamps are recorded, thus the above probabilities can be evaluated by a simple data analysis.

The defense strategy, valid for the receiver in Figure 4, is outlined below.

In the first step, one collects information about Bob's system quantum efficiency ${ϵ}_B$, dark count rates $f_{DCR}^{\left(k\right)}$ of all four detectors, where index $k\in \left\{\mathrm{0,1},\mathrm{2,3}\right\}$ marks the detector dedicated for measuring of the k-th polarization (namely linear polarization of angle $\frac{\pi }{4}k$), and estimate their respective statistical uncertainties ${\sigma }_{DCR}^{\left(k\right)}$. As before, in order to simplify treatment, but with an obvious extension to the general case, we henceforth assume that all detectors exhibit the same dark count parameters:$f_{DCR}$ and ${\sigma }_{DCR}$. All these parameters may be known in advance. Alternatively, one may disconnect Bob from the quantum channel and perform an appropriate set of measurements (calibration) to obtain them. We also assume that parameters $〈n〉$, $f_G$, $t_G$ are known or negotiated before the start of QKD protocol. While Eve may know all of these parameters (by Kerchoff's principle), she may not influence them.

In the second step, during the quantum communication session (namely the first phase of BB84), one measures Bob's in-gate and out-of-gate coincidence probabilities related to reception of qubits, namely $p_{CIn}^{\text{'}}$ and $p_{COut}^{\text{'}}$. For example, $p_{CIn}^{\text{'}}$ is evaluated as the sum of rates of coincidences between pairs of detectors (0, 2) and (1, 3) that happen only during gates, divided by the rate of gates $f_G$. Similarly is evaluated $p_{COut}^{\text{'}}$ except that said coincidences are now counted out of gates. Furthermore, if the quantum channel transmissivity ${ϵ}_{QCh}$ is not known/calibrated beforehand, it should be estimated. To that end, one measures the total rate of detections of all four detectors within coincidence windows, $f_{QInTot}$ and estimates its variance ${\sigma }_{QInTot}^2$. The qubit reception probability is then equal to:

$$p_{QInTot}=\frac{f_{QInTot}-f_G{t}_G\sum _{k=0}^3{f}_{DCR}^{\left(k\right)}}{f_G}=\frac{f_{QInTot}}{f_G}-4t_G{f}_{DCR}.$$

(12)

According to Equation (10), for undisturbed BB84, it should be equal to:

$$p_{QInTot}=1-{\left(1-{ϵ}_B{ϵ}_{QCh}\right)}^{〈n〉}.$$

(13)

Solving for ${ϵ}_{QCh}$ gives:

$${ϵ}_{QCh}=\frac{1}{{ϵ}_B}\left(1-{\left(1-p_{QInTot}\right)}^{\frac{1}{〈n〉}}\right).$$

(14)

Note that Eve does not control ${ϵ}_B$ nor $〈n〉$, but she can manipulate apparent $p_{QInTot}$ to a certain extent. On one hand, she could make $p_{QInTot}$ lower by randomly omitting qubits from Alice, but that would not enable her to increase her information on the resulting key, while the key would only get shorter for all three parties. On top of that, communication-induced coincidence probabilities would became smaller, thus ratio of probability of blinding-induced coincidences would rise in comparison to ones from communication. That would make Eve's attack more easily discoverable. On the other hand, she could make $p_{QInTot}$ higher, by removing a (part of) loss she induced beforehand, as explained before, if any. In that case, she must "invent" new qubits for Bob that would cause rising of BER, causing Alice and Bob to remove this extra information in the privacy amplification so Eve will not gain any new knowledge on the key nor would the effective key length change. By doing so, her discoverability would get smaller by a factor she enlarged $p_{QInTot}$, but that is not a significant gain, as will be shown below.

Before going to the final step, one needs to estimate the statistical uncertainty of ${ϵ}_{QCh}$. To that end we assume that predominant uncertainty of $p_{QInTot}$ comes from statistical uncertainties of $f_{QInTot}$ and dark count rates. We further assume that qubit detection and dark counts are Poissonian events. It is then straightforward to show, using standard statistical theory of propagation of uncertainty, that its variance is given by:

$${\sigma }_{QCh}^2=\left(\frac{{\sigma }_{QInTot}^2}{f_G^2}+16t_G^2{\sigma }_{DCR}^2\right){\left(\frac{{\left(1-p_{QInTot}\right)}^{\frac{1}{〈n〉}-1}}{〈n〉{ϵ}_B}\right)}^2.$$

(15)

At the end of this step, following parameters, pertaining to the hardware and the quantum communication, are known: $〈n〉$, $f_G$, $t_G$, ${ϵ}_B$, $f_{DCR}$, ${\sigma }_{DCR}$, $p_{QIn}^{\text{'}}$, $p_{QOut}^{\text{'}}$, ${ϵ}_{QCh}$, and ${\sigma }_{QCh}$. These are input to the final step.

In the third and final step, one calculates upper limits on probabilities of in- and out- of gate coincidence probabilities for undisturbed QKD communication ($p_{CInTHR}$ and $p_{COutTHR})$, and compares them to the directly measured probabilities of in- and out- of gate coincidence ($p_{QIn}^{\text{'}}$ and $p_{QOut}^{\text{'}}$) in order to detect whether the QKD system is under attack, at a desired (arbitrary) level of confidence.

The in- and out- of gate undisturbed coincidence probabilities $p_{CIn}$ and $p_{COut}$ can be estimated using Equations (5) and (8) respectively and parameters available from the previous step. Their respective variances are:

$${\sigma }_{CIn}^2=4t_G^4{f}_{DCR}^4+\frac{{〈n〉}^4{ϵ}_B^4{ϵ}_{QCh}^4}{16}{\left(\frac{{\sigma }_{QCh}}{{ϵ}_{QCh}}\right)}^2$$

(16)

$${\sigma }_{COut}^2=4{\left({ \frac{1}{f_G}-t}_G\right)}^4{f}_{DCR}^4{\left(\frac{{\sigma }_{DCR}}{f_{DCR}}\right)}^2$$

(17)

Next, without any assumption on the statistical distribution(s) governing their values, one can find the respective upper limits on those probabilities, using Chebyshev's inequality [30]:

$$p\left(p_{CIn}\ge p_{CInTHR}\right)\le \frac{{\sigma }_{CIn}^2}{p_{CInTHR}^2}$$

(18)

Having in mind that all variables in the above equation are positive, an upper limit on ${ϵ}_{QCh}^{\prime }$ is given by:

$$p_{CInTHR}\le \frac{{\sigma }_{CIn}}{\sqrt{p\left(p_{CIn}\ge p_{CInTHR}\right)}}$$

(19)

which can be interpreted as:

$$p_{CInTHR}=\frac{{\sigma }_{CIn}}{\sqrt{{1-p}_{CONF}}}$$

(20)

where $p_{CONF}$ is an arbitrarily chosen probability (confidence level) that inequality $p_{CIn}<p_{CInTHR}$ holds. Equivalently we obtain:

$$p_{COutTHR}=\frac{{\sigma }_{COut}}{\sqrt{1-p_{CONF}}}$$

(21)

Finally, we define the following security criterion. If both inequalities below hold, for coincidence probabilities measured for a QKD session:

$$p_{CIn}^{\prime }<p_{CInTHR}$$

$$p_{COut}^{\prime }<p_{COutTHR}$$

(22)

one concludes that the QKD session is not under a DBA with confidentiality level of $p_{CONF}$. On the other hand, if any of the two inequalities fail, the session is insecure and should be aborted.

Let us now work out one numerical example. We assume the same realistic parameters as above for easier comparison, namely: $〈n〉=0.1$, $f_G=10$ MHz, $t_G=5$ ns, ${ϵ}_B=0.25$, $f_{DCR}=1$ kcps, on top of that ${\sigma }_{DCR}=100$ cps, total in-gate detection rate $f_{QInTot}=4·{10}^4$ cps, and ${\sigma }_{QInTot}=1$ kcps. From Equarions (12), (14) and (15) we obtain: $p_{QInTot}=3.98·{10}^{-3}$, ${ϵ}_{QCh}=0.156$ and ${\sigma }_{QCh}=3.86·{10}^{-3}$. Then, Equarions (16) and (17) yield: ${\sigma }_{CIn}=9.4·{10}^{-6}$ and ${\sigma }_{COut}=1.8·{10}^{-9}$. Finally, even requiring a very high confidence level of 99.9999% $(p_{CONF}=0.999999)$, Eqs.(20) and (21) give a rather small/strict threshold values on coincidence probabilities: $p_{CInTHR}=9.4·{10}^{-3}$ and $p_{COutTHR}=$ $1.8·{10}^{-6}$.

The criterion in Equation (22) tells us that as soon as $p_{CIn}^{\prime }\ge 9.4·{10}^{-3}$ or $p_{COut}^{\prime }\ge 1.8·{10}^{-6}$ one concludes, with 99.9999% confidence, that the session has been compromised. To appreciate the discerning capability of this defense, we should remember that for the DBA attacks described in the previous section, using the same values of communication parameters, we got $p_{CIn}^{\prime }\approx 0.94$ and $p_{COut}^{\prime }\approx 1.4·{10}^{-2}$ which is several orders of magnitude higher than their respective thresholds $p_{CInTHR}$ and $p_{COutTHR}$. We conclude that it is very unlikely that any multi-photon attack strategy would pass the criterion Equation (22) in conjunction with the setup of Figure 4.