Submitted:
28 September 2023
Posted:
29 September 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
2.1. Studied Material
2.2. Mechanical Testing
2.3. Determination of SRS
3. Results
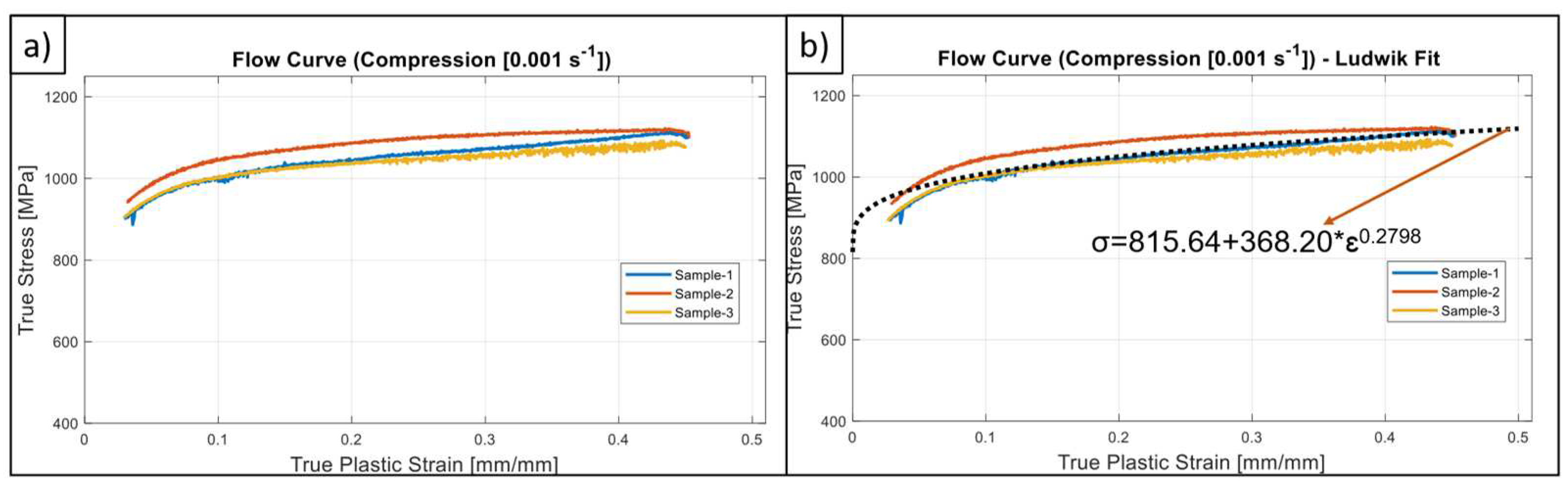
3.1. Basic Formulation
3.2. Time Integration Procedure
- Initialization: Uptake the material parameters, state variables and the deformation gradient (F) at beginning of the time increment.
- Computation of strain tensor: Compute the Hencky strain tensor by use of F (Our code was constructed as finite-strain basis in such a way that free body translations were eliminated by means of Hencky strain measure [28], however Kroner decomposition [28] was discarded for the present study). Hencky strain measure is one of the most appropriate ways to deal with moderate deformations [30].
- Check the plasticity criterion: Compute the trial stress (Equation (21)) and check for the yield locus definition (Equation (23)).
-
Update state variables:If ≤ 0 → step is elastic (∆λ = 0) thus, conserve the state variables.If > 0 → step is plastic, solve for ∆λ (Equation (20)). Update , , , .
- Finalization: Deliver the state variables and tangent modulus to Abaqus solver for the convergence check.
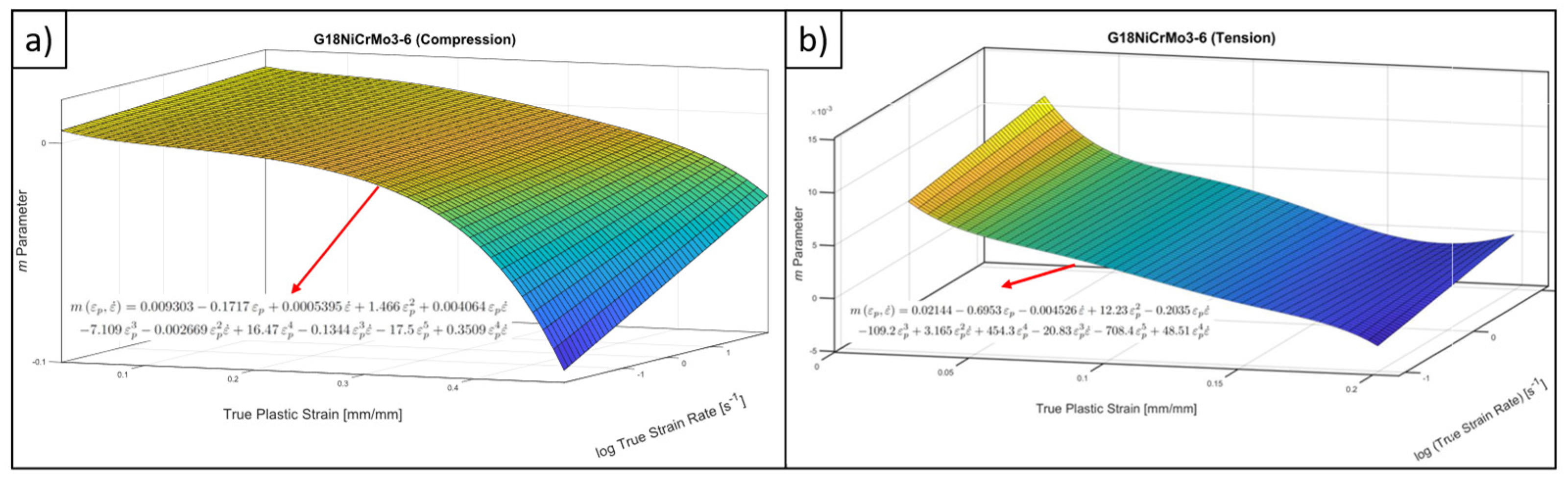
3.3. Imposing the Asymmetry and Rate Dependence
4. Results and Discussion
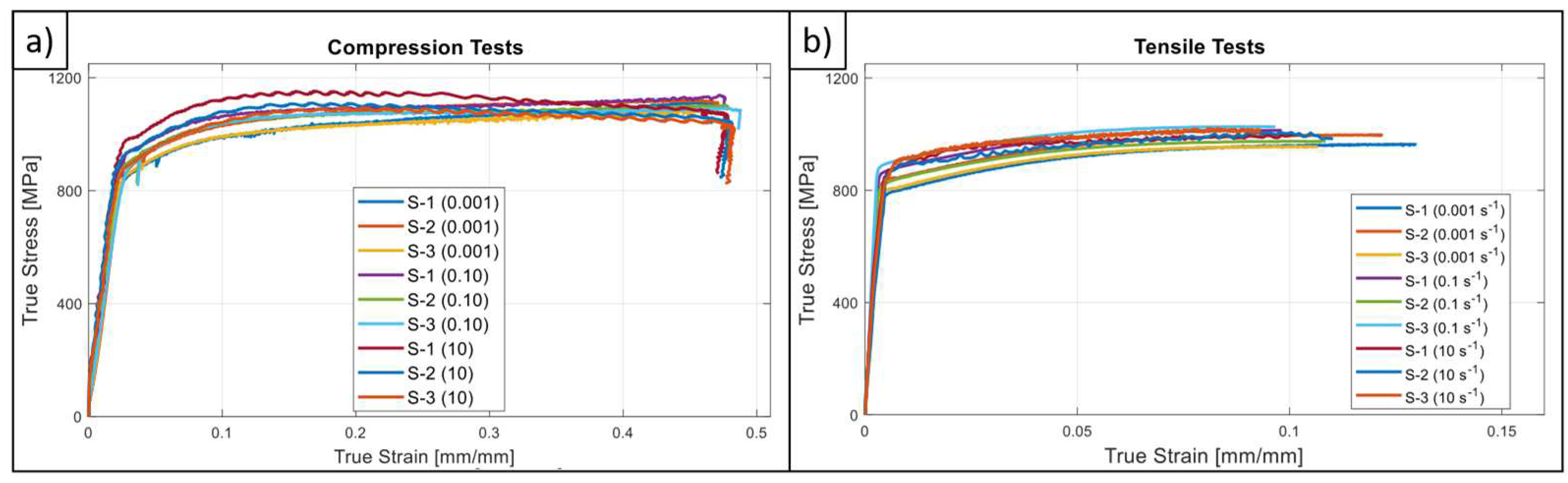
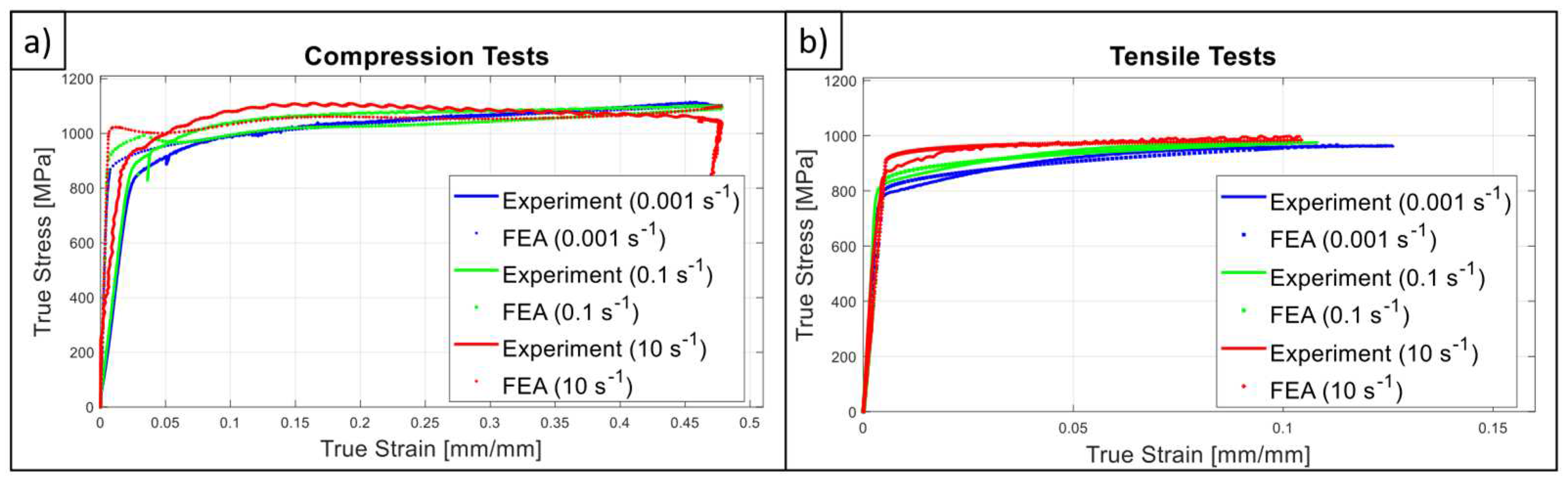
4.1. Mechanical Testing
4.2. Determination of SRS
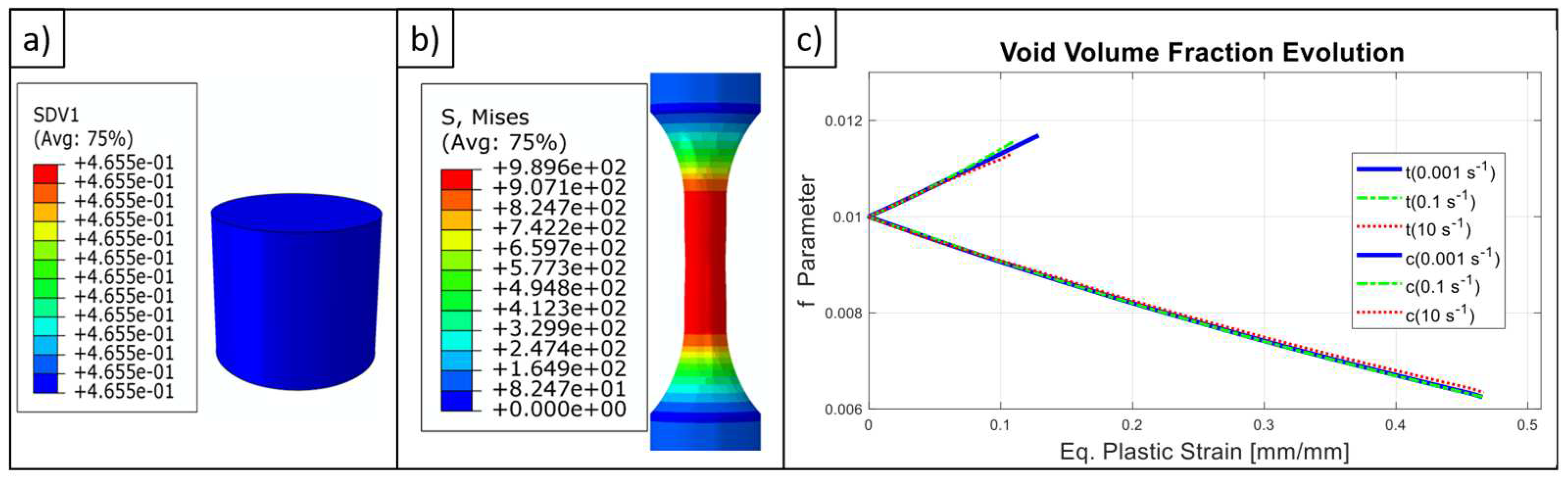
4.3. FEA Models
5. Conclusions
- G18NiCrMo3-6 material possess an asymmetric yielding character, in other words, yields stress in compression in 4% bigger than the tensile one.
- Indeed, the strain hardening and SRS character is also quite asymmetric for the studied material. This fact was quantified with the help of power law-based flow stress formulation and determination of m parameter. From a general point-of-view, SRS is more dominant on tensile direction however, it has a decreasing tendency with increasing strain as like the compressive stress states. In the view of authors’, the shared material data within this study provides an important resource for the upcoming research activities on G18NiCrMo3-6 about which the existing literature data is extremely limited.
- Unlike the tensile test in medium strain rate regime, strain softening phenomena was observed in compression tests which was interpreted as the effect of adiabatic heating. Owing to this finding in compression side the material exhibits rate sensitivity character up to certain strain value but then strain softening effect contributes to the plastic response. This fact can be handled by defining SRS parameters as a function of strain as in the proposed constitutive model. On the contrary, a conventional Johnson-Cook type formalism cannot catch up this phenomenon where the effect of rate contribution is formulated through a constant multiplier term.
- The created constitutive model (UMAT file) run without any problem which was formulated on finite strain basis and uses implicit time integration scheme. This UMAT file could easily serve in inspecting the effect of material parameters (like initial void volume fraction and etc.) on the macro-mechanical performance of any design which is made up of G18NiCrMo3-6.
- Our efforts will focus on creating proper coupling between the estimated void volume fraction and any appropriate damage rule to improve the proposed model which would account for both damage, void coalescence, and localization phenomena.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FEA | Finite element analysis |
| SRS | Strain rate sensitivity |
| UMAT | User subroutine to define a material’s mechanical behavior |
| UTS | Ultimate tensile strength |
References
- Drucker, D.C.; Prager, W. Soil mechanics and plastic analysis or limit design. Quarterly of Applied Mathematics 1952, 10, 157–165. [Google Scholar] [CrossRef]
- Gurson, A.L. Continuum Theory of Ductile Rupture by Void Nucleation and Growth: Part I—Yield Criteria and Flow Rules for Porous Ductile Media. Journal of Engineering Materials and Technology 1977, 99, 2–15. [Google Scholar] [CrossRef]
- Trillat, M.; Pastor, J. Limit analysis and Gurson’s model. European Journal of Mechanics - A/Solids 2005, 24, 800–819. [Google Scholar] [CrossRef]
- Coffin, L. F., J. The Flow and Fracture of a Brittle Material. Journal of Applied Mechanics 2021, 17, 233–248. [Google Scholar] [CrossRef]
- WIESE, J.W.; DANTZIG, J.A. Modeling stress development during the solidification of gray iron castings. Metallurgical Transactions A 1990, 21, 489–497. [Google Scholar] [CrossRef]
- Hjelm, H.E. Yield Surface for Grey Cast Iron Under Biaxial Stress. Journal of Engineering Materials and Technology 1994, 116, 148–154. [Google Scholar] [CrossRef]
- Altenbach, H.; Stoychev, G.; Tushtev, K. On elastoplastic deformation of grey cast iron. International Journal of Plasticity 2001, 17, 719–736. [Google Scholar] [CrossRef]
- Hosseini, E.; Holdsworth, S.R.; Flueeler, U. A temperature-dependent asymmetric constitutive model for cast irons under cyclic loading conditions. The Journal of Strain Analysis for Engineering Design 2018, 53, 106–114. [Google Scholar] [CrossRef]
- Smith, M. ABAQUS/Standard User’s Manual, Version 6.9; Dassault Systèmes Simulia Corp: United States, 2009. [Google Scholar]
- Josefson, B.L.; Hjelm, H.E. Modelling Elastoplastic Deformations in Grey Cast Iron. In Low Cycle Fatigue and Elasto-Plastic Behaviour of Materials—3; Springer Netherlands: Dordrecht, 1992; pp. 465–472. [Google Scholar] [CrossRef]
- Metzger, M.; Seifert, T. Computational assessment of the microstructure-dependent plasticity of lamellar gray cast iron – Part II: initial yield surfaces and directions. International Journal of Solids and Structures 2015, 66, 194–206. [Google Scholar] [CrossRef]
- Andriollo, T.; Thorborg, J.; Tiedje, N.S.; Hattel, J. Modeling of damage in ductile cast iron - The effect of including plasticity in the graphite nodules. IOP Conference Series: Materials Science and Engineering 2015, 84, 012027. [Google Scholar] [CrossRef]
- Pina, J.; Shafqat, S.; Kouznetsova, V.; Hoefnagels, J.; Geers, M. Microstructural study of the mechanical response of compacted graphite iron: An experimental and numerical approach. Materials Science and Engineering: A 2016, 658, 439–449. [Google Scholar] [CrossRef]
- Fernandino, D.O.; Cisilino, A.P.; Boeri, R.E. Determination of effective elastic properties of ferritic ductile cast iron by computational homogenization, micrographs, and microindentation tests. Mechanics of Materials 2015, 83, 110–121. [Google Scholar] [CrossRef]
- Brauer, S.A.; Whittington, W.R.; Johnson, K.L.; Li, B.; Rhee, H.; Allison, P.G.; Crane, C.K.; Horstemeyer, M.F. Strain Rate and Stress-State Dependence of Gray Cast Iron. Journal of Engineering Materials and Technology 2017, 139. [Google Scholar] [CrossRef]
- Cocks, A. Inelastic deformation of porous materials. Journal of the Mechanics and Physics of Solids 1989, 37, 693–715. [Google Scholar] [CrossRef]
- Yalçinkaya, T.; Erdoğan, C.; Tandoğan, I.T.; Cocks, A. Formulation and Implementation of a New Porous Plasticity Model. Procedia Structural Integrity 2019, 21, 46–51. [Google Scholar] [CrossRef]
- Erdoğan, Can. Numerical Implementation and Analysis of a Porousplasticity Model for Ductile Damage Prediciton, PhD., Middle East Technical University, Turkey, January 2021.
- Gul, A.; Aslan, O.; Kayali, E.S.; Bayraktar, E. Assessing Cast Aluminum Alloys with Computed Tomography Defect Metrics: A Gurson Porous Plasticity Approach. Metals 2023, 13. [Google Scholar] [CrossRef]
- Maier, V.; Durst, K.; Mueller, J.; Backes, B.; Höppel, H.W.; Göken, M. Nanoindentation strain-rate jump tests for determining the local strain-rate sensitivity in nanocrystalline Ni and ultrafine-grained Al. Journal of Materials Research 2011, 26, 1421–1430. [Google Scholar] [CrossRef]
- Ghosh, A. On the measurement of strain-rate sensitivity for deformation mechanism in conventional and ultra-fine grain alloys. Materials Science and Engineering: A 2007, 463, 36–40. [Google Scholar] [CrossRef]
- Acharya, S.; Gupta, R.; Ghosh, J.; Bysakh, S.; Ghosh, K.; Mondal, D.; Mukhopadhyay, A. High strain rate dynamic compressive behavior of Al6061-T6 alloys. Materials Characterization 2017, 127, 185–197. [Google Scholar] [CrossRef]
- Kumaresan, G.; Kalaichelvan, K. Multi-dome forming test for determining the strain rate sensitivity index of a superplastic 7075Al alloy sheet. Journal of Alloys and Compounds 2014, 583, 226–230. [Google Scholar] [CrossRef]
- Nemes, J.A.; Eftis, J.; Randles, P.W. Viscoplastic Constitutive Modeling of High Strain-Rate Deformation, Material Damage, and Spall Fracture. Journal of Applied Mechanics 1990, 57, 282–291. [Google Scholar] [CrossRef]
- Hao, S.; Brocks, W. The Gurson-Tvergaard-Needleman-model for rate and temperature-dependent materials with isotropic and kinematic hardening. Computational Mechanics 1997, 20, 34–40. [Google Scholar] [CrossRef]
- Fan, H.; Li, Y.; Jin, X.; Chen, B. Effect of tempering temperature on microstructure and mechanical properties of G18NiMoCr3-6. Jinshu Rechuli/Heat Treatment of Metals 2017, 42, 163–165. [Google Scholar] [CrossRef]
- Salemi, A.; Abdollah-zadeh, A. The effect of tempering temperature on the mechanical properties and fracture morphology of a NiCrMoV steel. Materials Characterization 2008, 59, 484–487. [Google Scholar] [CrossRef]
- Hencky, H. The Elastic Behavior of Vulcanized Rubber. Journal of Applied Mechanics 2021, 1, 45–48. [Google Scholar] [CrossRef]
- Kröner, E. Allgemeine Kontinuumstheorie der Versetzungen und Eigenspannungen. Archive for Rational Mechanics and Analysis 1959, 4, 273–334. [Google Scholar] [CrossRef]
- Anand, L. On H. Hencky’s Approximate Strain-Energy Function for Moderate Deformations. Journal of Applied Mechanics 1979, 46, 78–82. [Google Scholar] [CrossRef]
- Ludwik, P. Elemente der technologischen Mechanik; Springer Berlin, Heidelberg, 1909. [CrossRef]
- Sorini, C.; Chattopadhyay, A.; Goldberg, R.K. Micromechanical modeling of the effects of adiabatic heating on the high strain rate deformation of polymer matrix composites. Composite Structures 2019, 215, 377–384. [Google Scholar] [CrossRef]
- Soares, G.; Patnamsetty, M.; Peura, P.; Hokka, M. Effects of Adiabatic Heating and Strain Rate on the Dynamic Response of a CoCrFeMnNi High-Entropy Alloy. Journal of Dynamic Behavior of Materials 2019, 5. [Google Scholar] [CrossRef]
- Nasraoui, M.; Forquin, P.; Siad, L.; Rusinek, A. Influence of strain rate, temperature, and adiabatic heating on the mechanical behavior of poly-methyl-methacrylate: Experimental and modeling analyses. Materials and Design 2012, 37, 500–509. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. A constitutive model and data for metals subjected to large strains, high strain rates, and high temperatures. In Proceedings of the 7th International Symposium on Ballistics. The Netherlands, 1983, Vol. 21 (1), pp. 541–547.
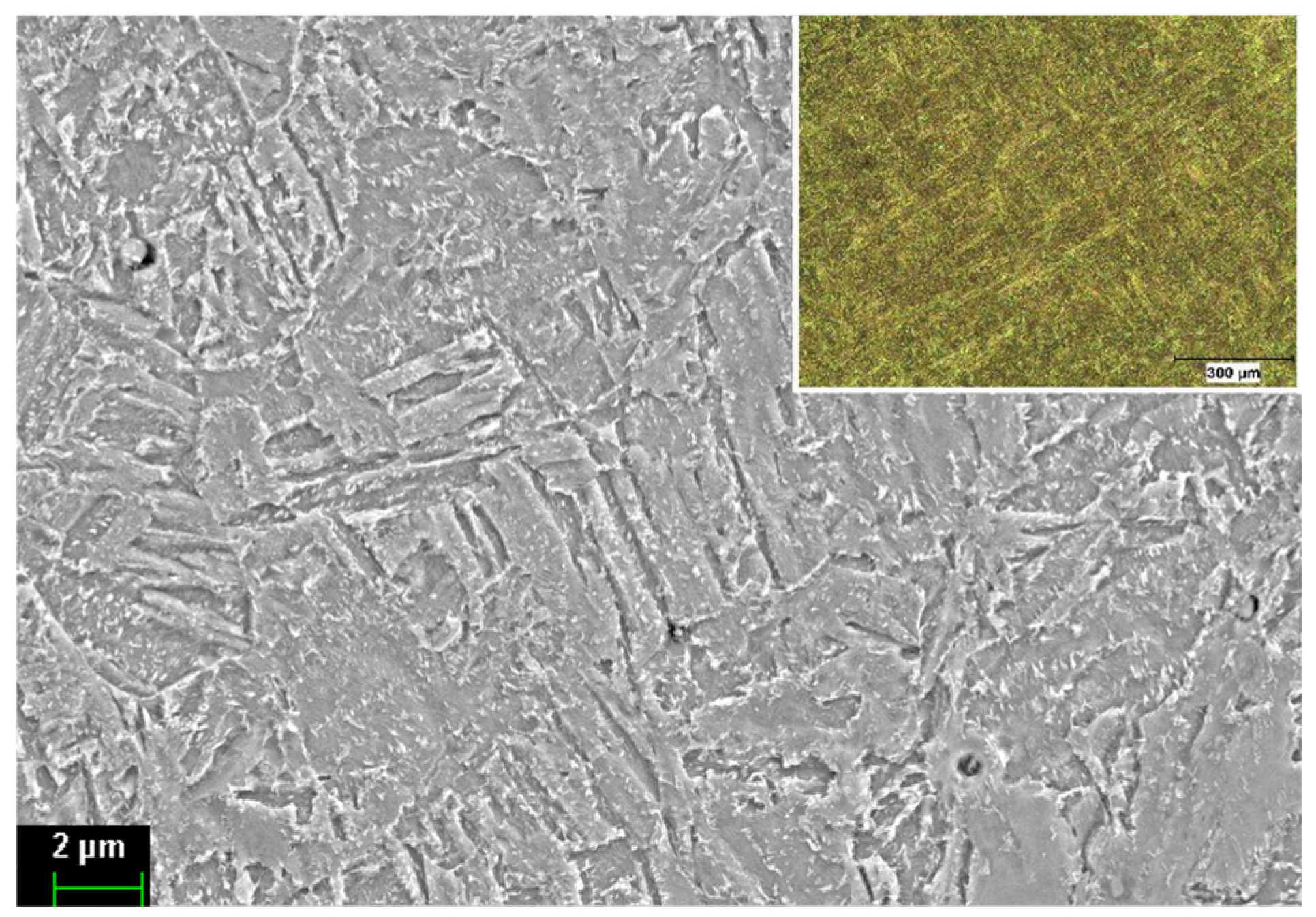

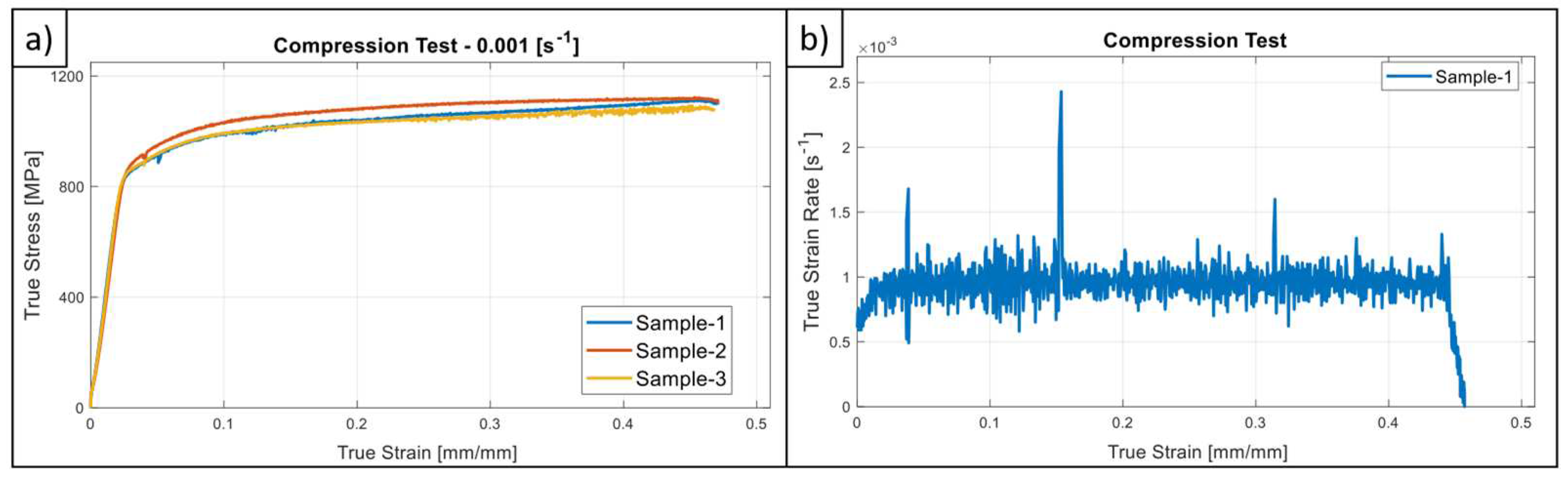
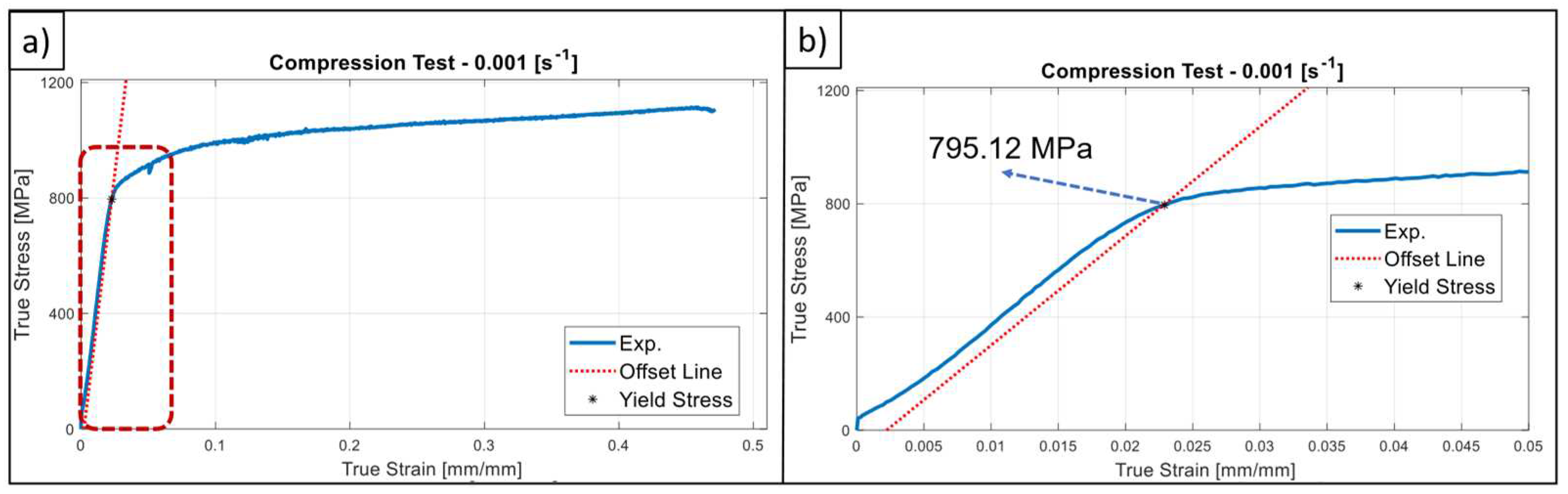
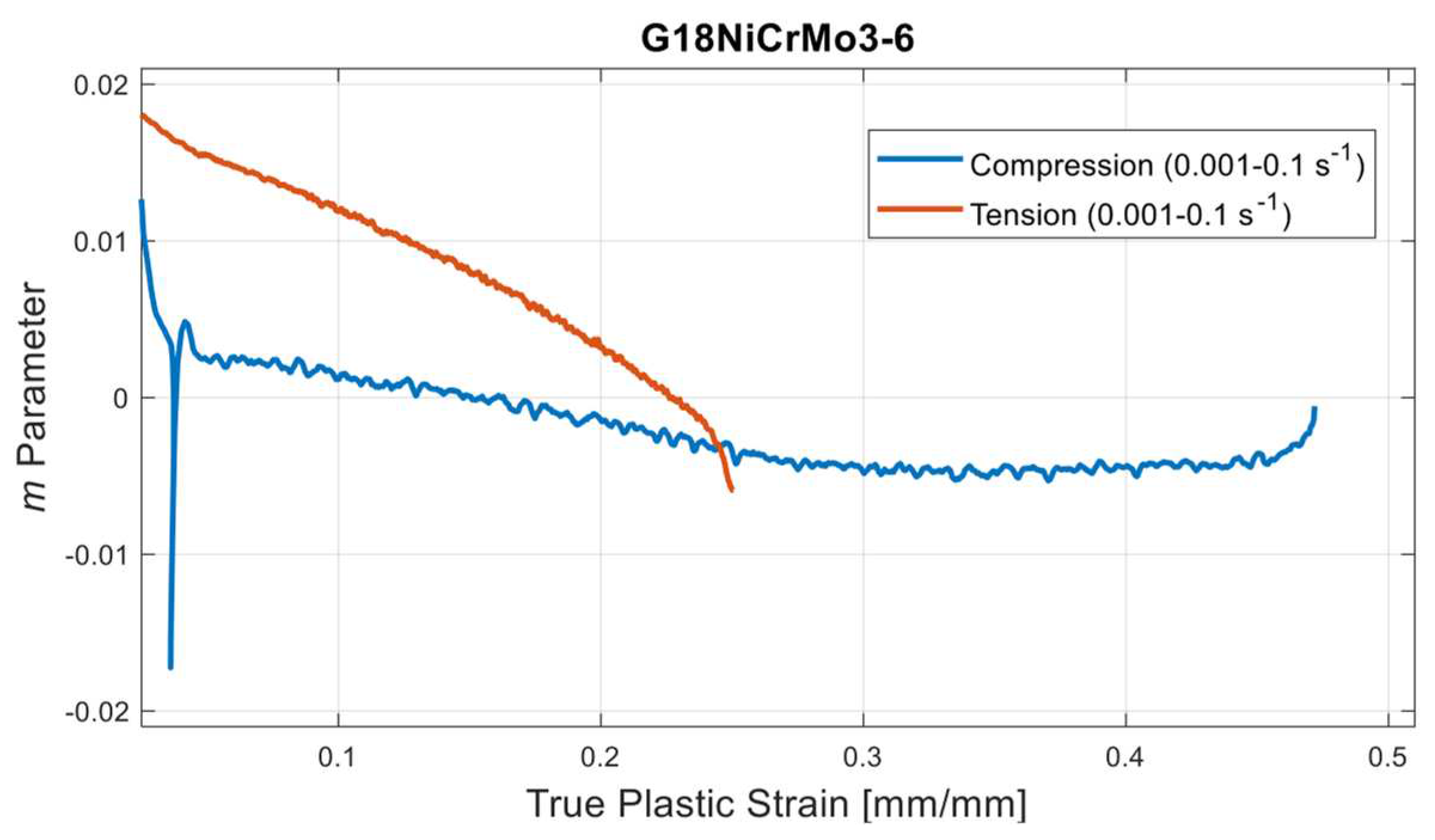

| C | Si | Mn | Ni | Cr | Mo | Cu | Fe |
|---|---|---|---|---|---|---|---|
| 0.20 | 0.50 | 0.90 | 0.80 | 0.50 | 0.45 | 0.15 | Balance |
| B | n | ||||
| Compression | 815.64 (±1.93%) | 862.79 (±1.89%) | 882.18 (±2.89%) | 368.20 | 0.2798 |
| Tension | 808.65 (±2.70%) | 858.73 (±2.84%) | 876.80 (±1.36%) | 551.30 | 0.5075 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





