Submitted:
25 September 2023
Posted:
28 September 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
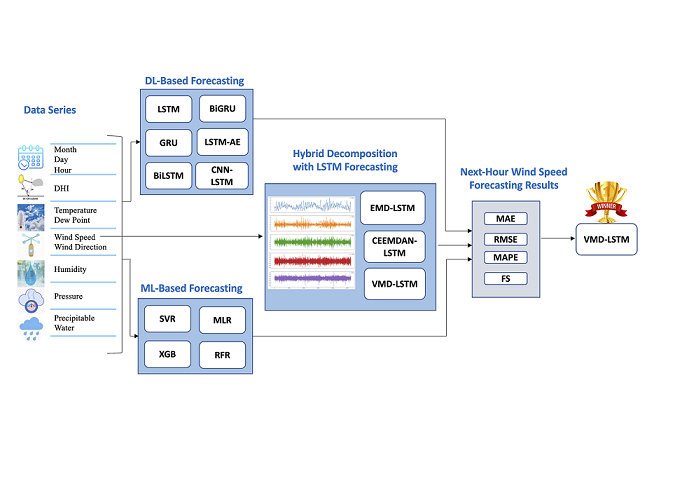
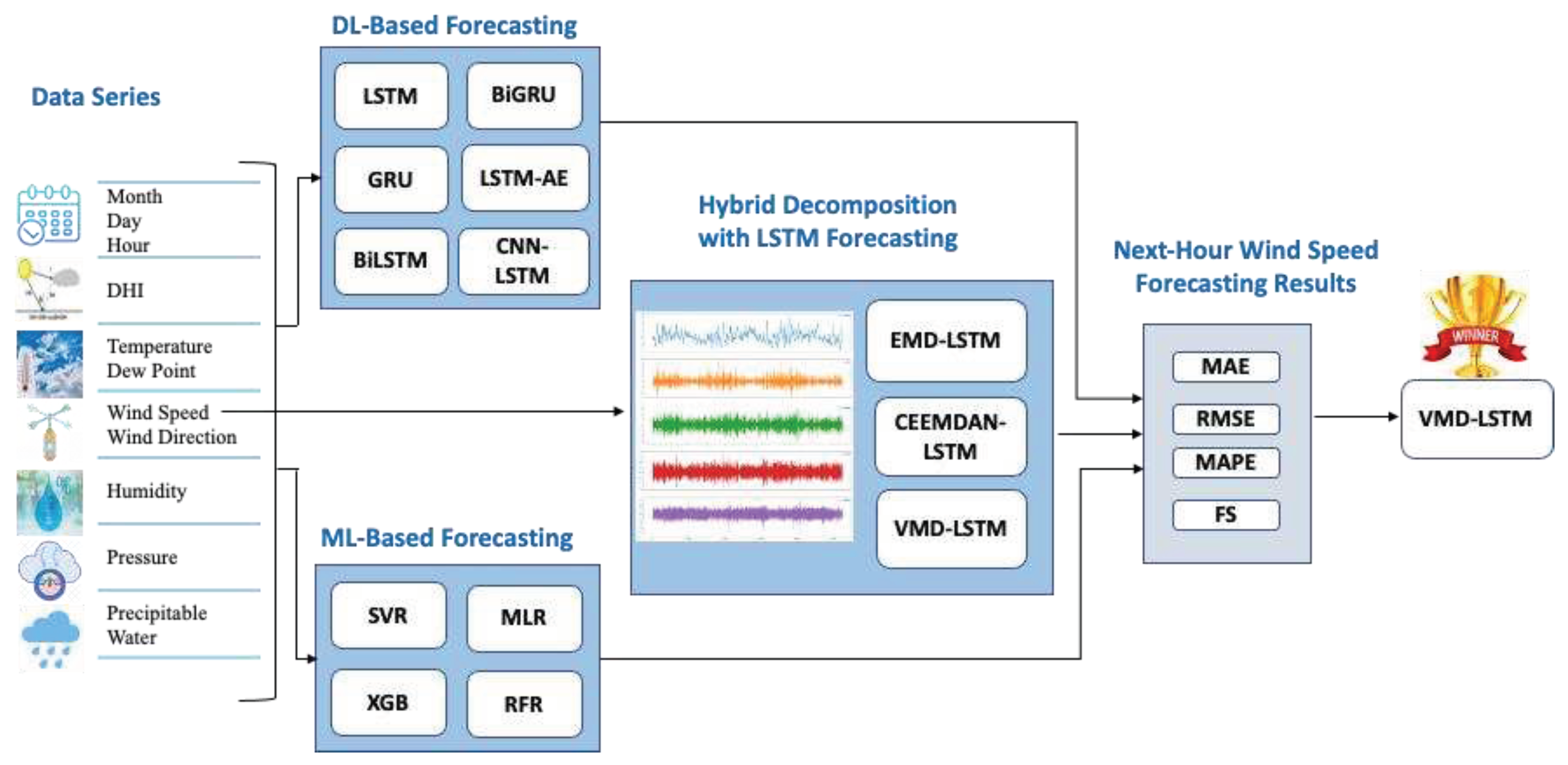
- We propose a novel hybrid model of the VMD method and LSTM model for next-hour wind speed prediction in a hot desert climate, such as the climate in Saudi Arabia. This is the first work, to our knowledge, proposing a hybrid model for this combination of task and weather.
- We provide a performance comparison of the proposed model and two hybrid models of data decomposition techniques and the LSTM model, six DL-based models, and four ML-based models, using previous hours’ wind speed values only versus using weather variables besides wind speed values to show the effect of including weather variables on the forecasting performance.
- Model performance comparisons are provided using data from four different locations in Saudi Arabia and two international locations, Caracas and Toronto. We present the results using visualization and several performance metrics, including mean absolute error (MAE), root mean square error (RMSE), mean absolute percentage error (MAPE), and forecast skills (FS).
2. Related Work
3. Methodology
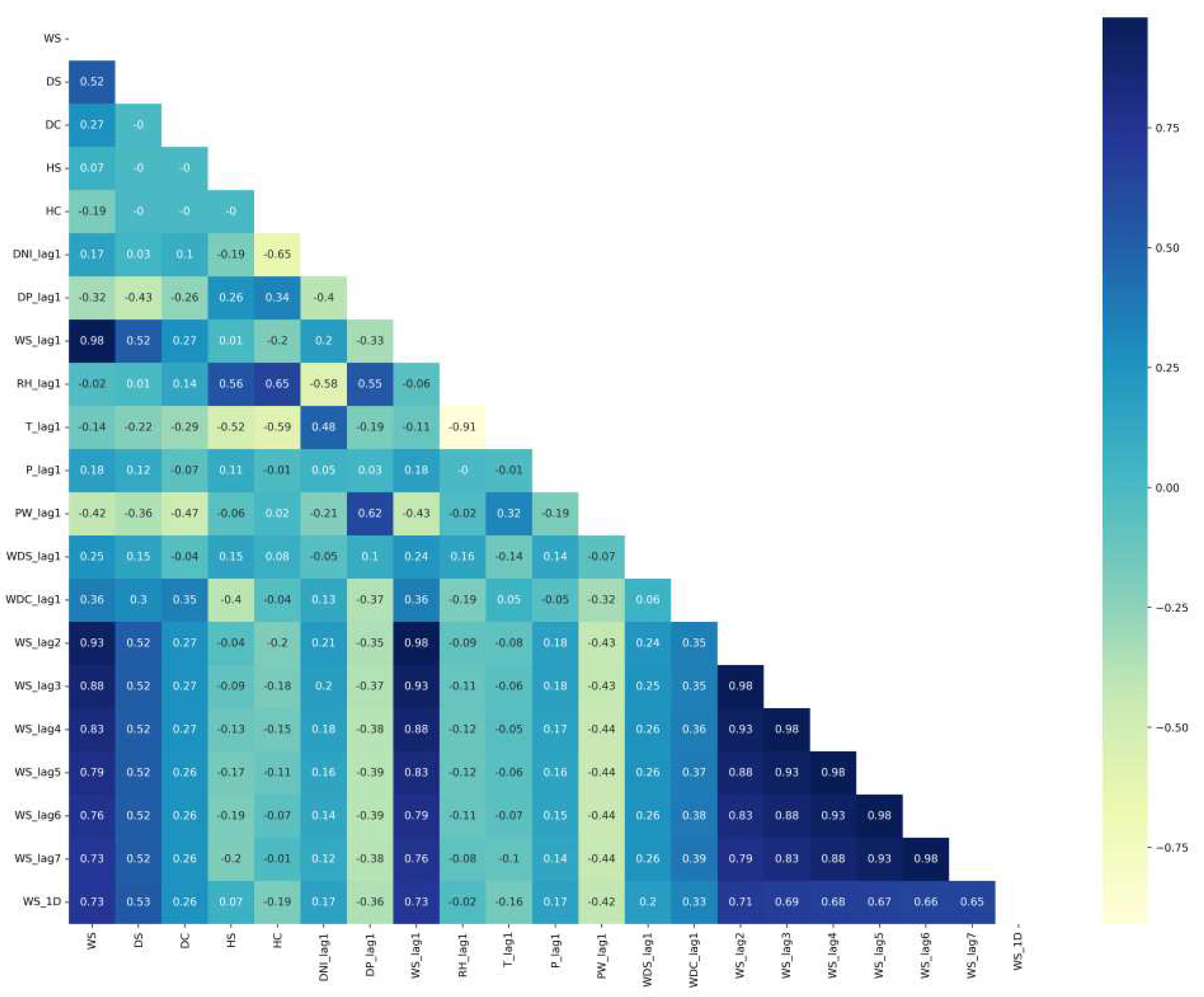
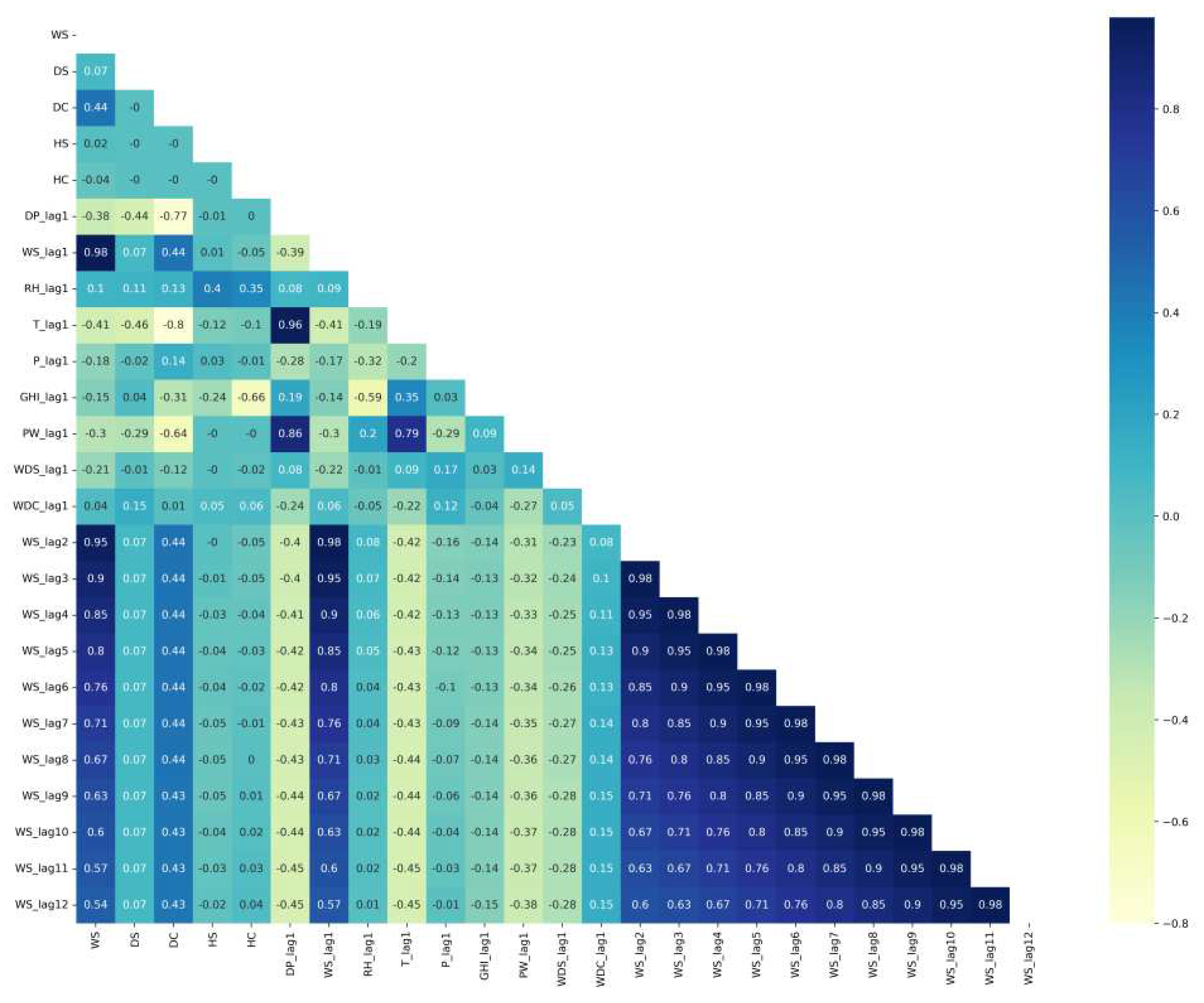
3.1. Data Preprocessing
3.1.1. Data Collection
3.1.2. Feature Engineering
- Output: Wind Speed as a meter per second (m/s)
- Wind Direction as degree (°)
- Clear sky Global Horizontal Irradiance as watt per square meter (w/m2)
- Clear sky Diffuse Horizontal Irradiance as w/m2
- Clear sky Direct Normal Irradiance as w/m2
- Precipitable Water (PW) as Millimeter
- Temperature (T) as Celsius (°C)
- Dew Point (DP) as Celsius (°C)
- Pressure (P) as Millibar
- Relative Humidity as a percentage (%)
3.1.3. Data Normalization and Portioning
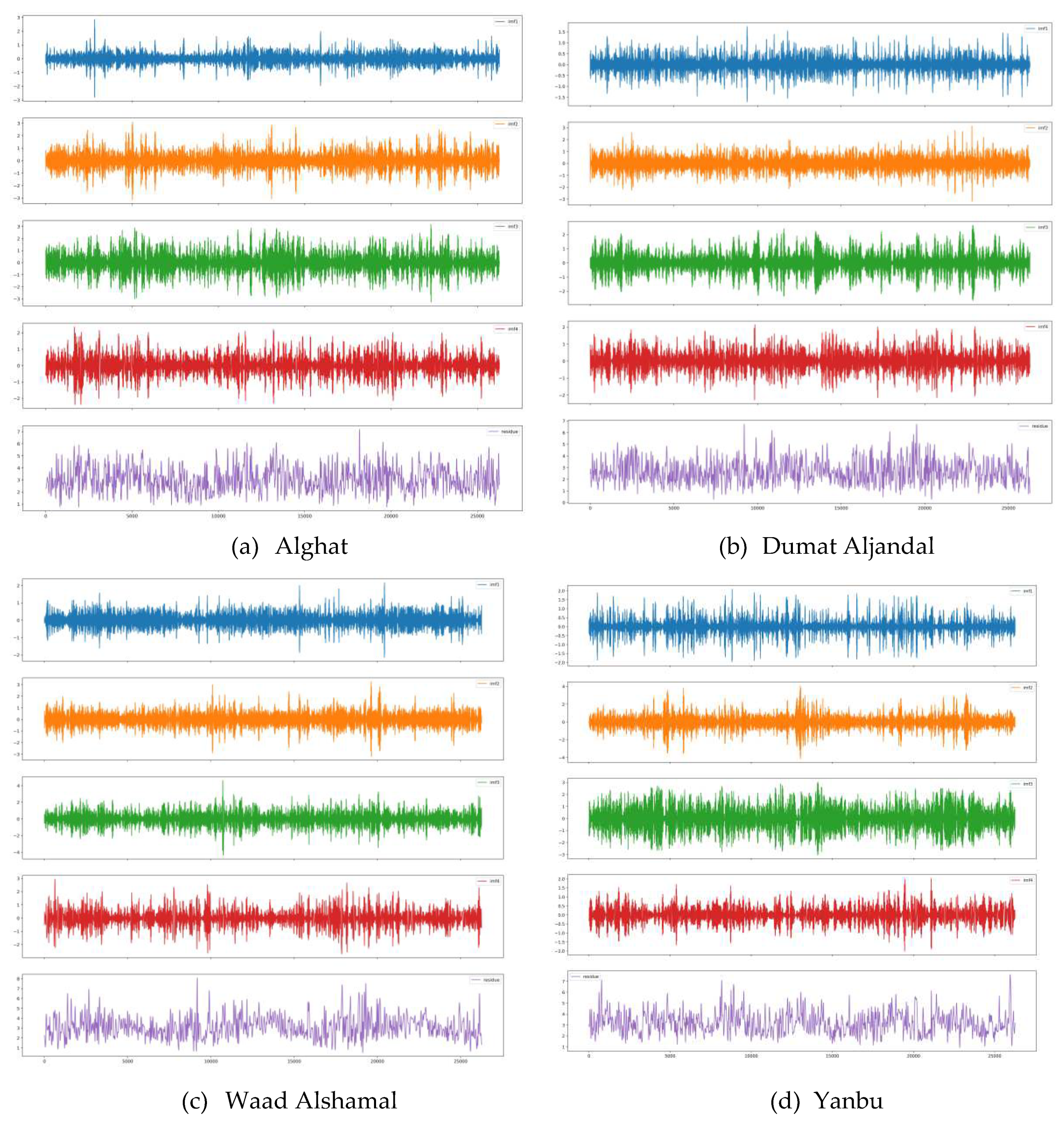
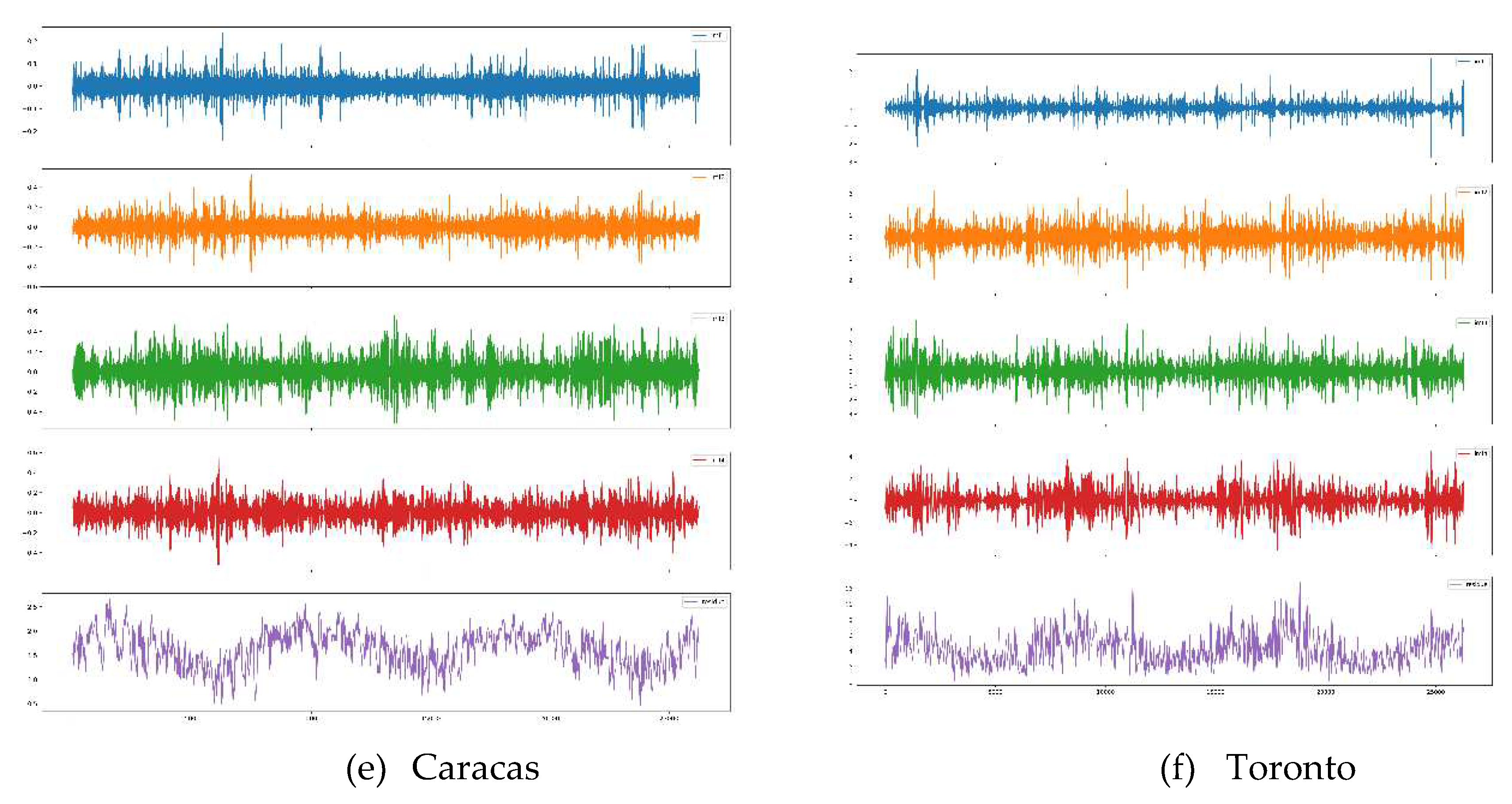
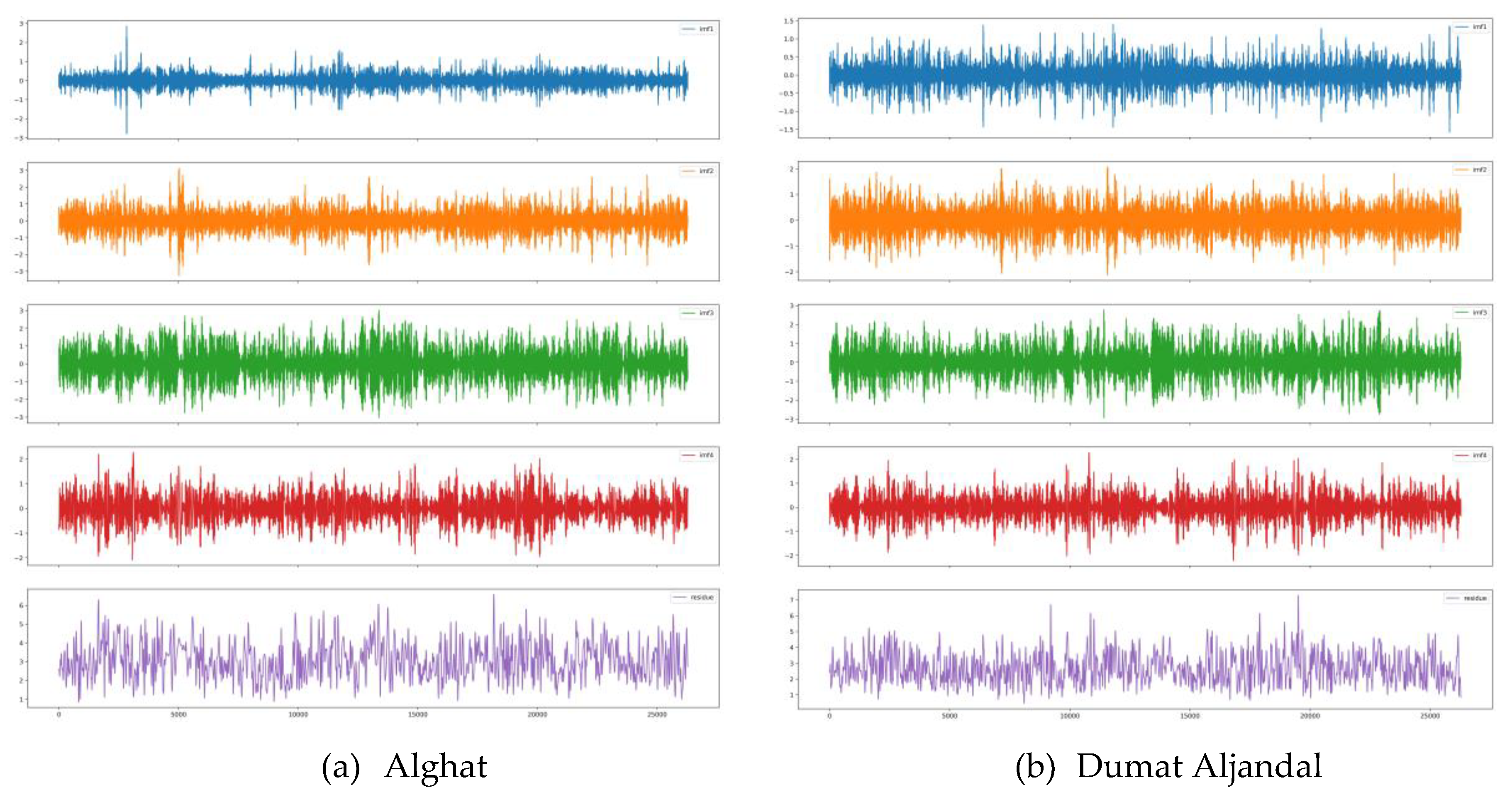
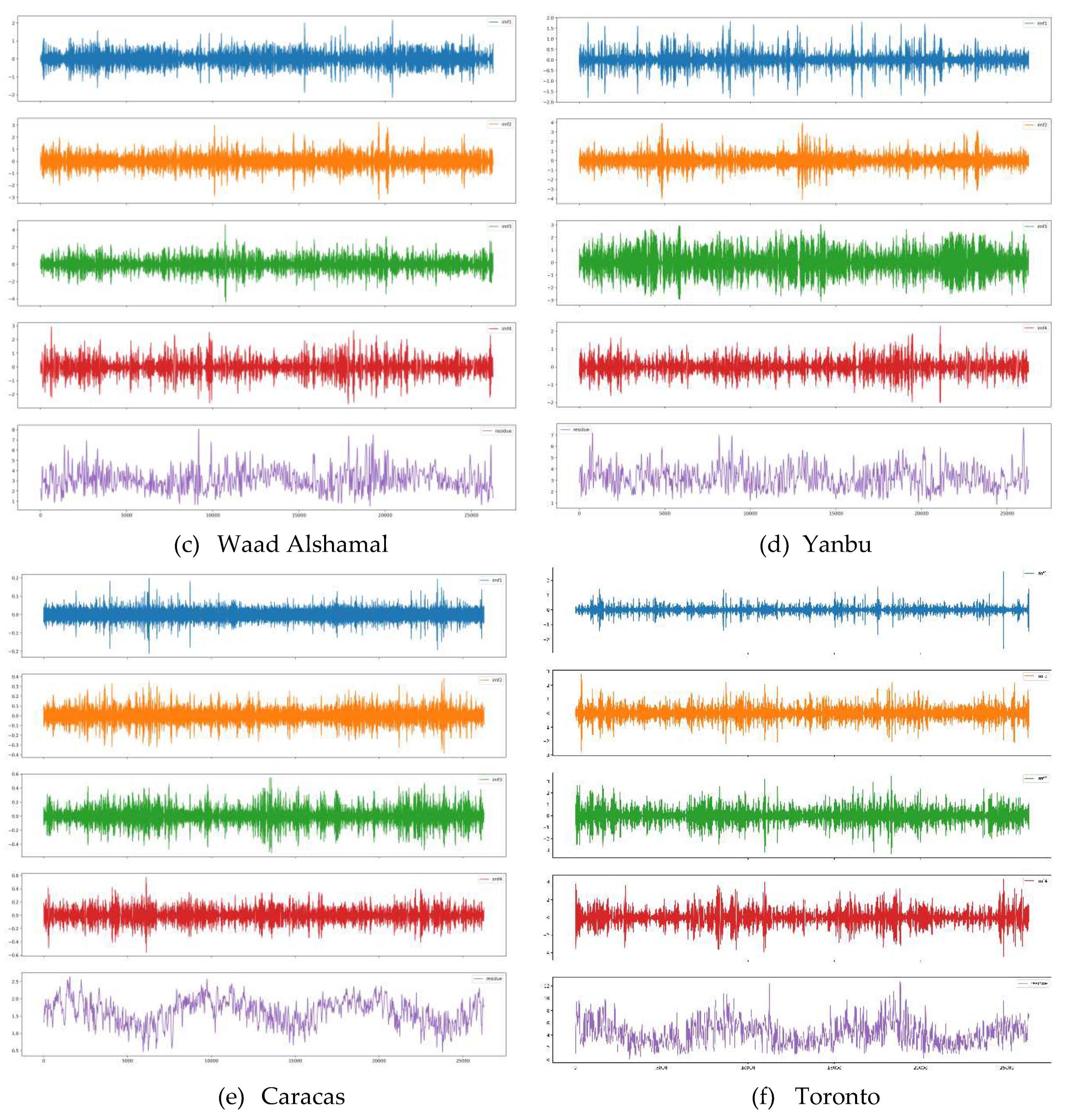
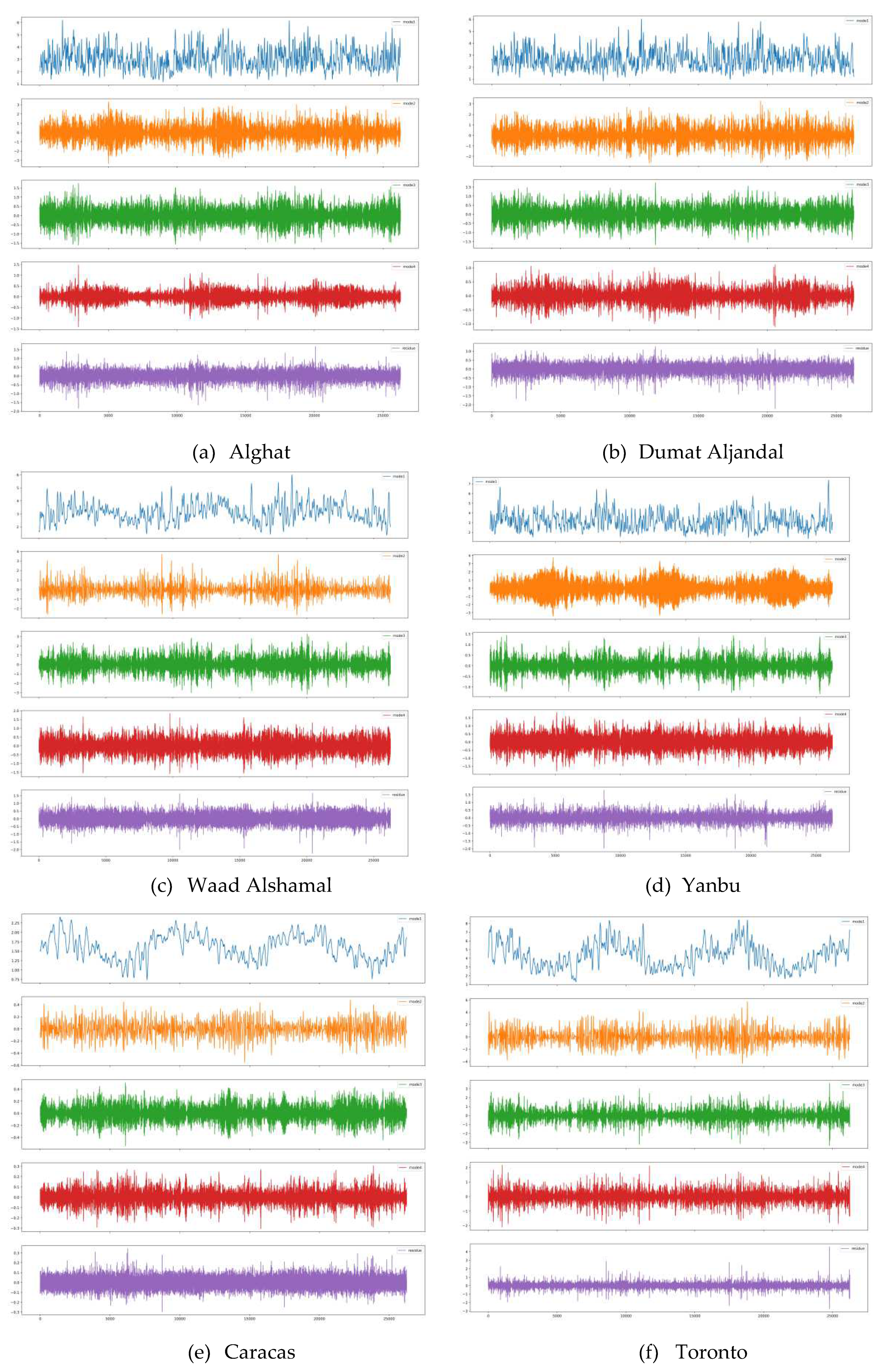
3.1.4. Data Decomposition Methods
3.1.4.1. EMD
3.1.4.2. CEEMDAN
3.1.4.3. VMD
3.2. Models’ Development
3.2.1. DL-Based Models
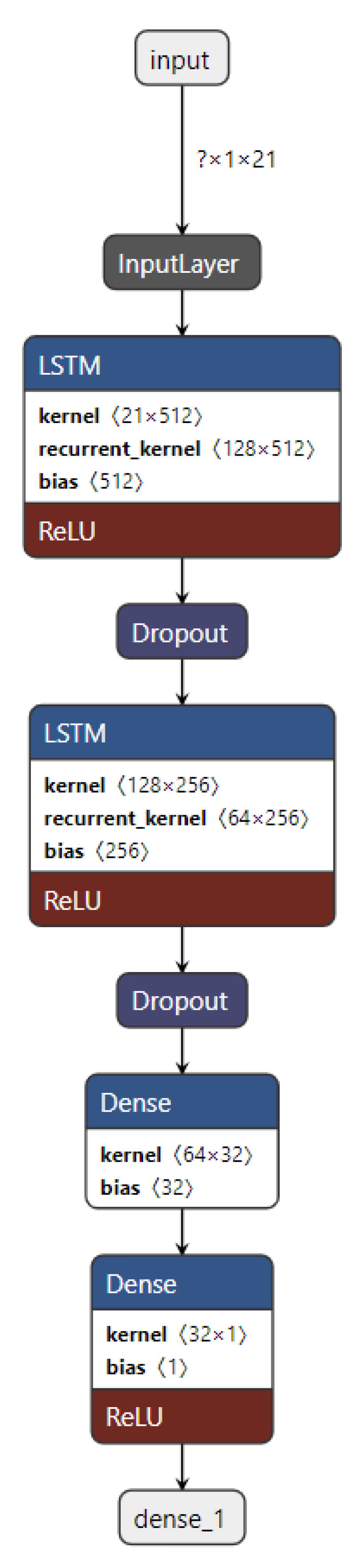
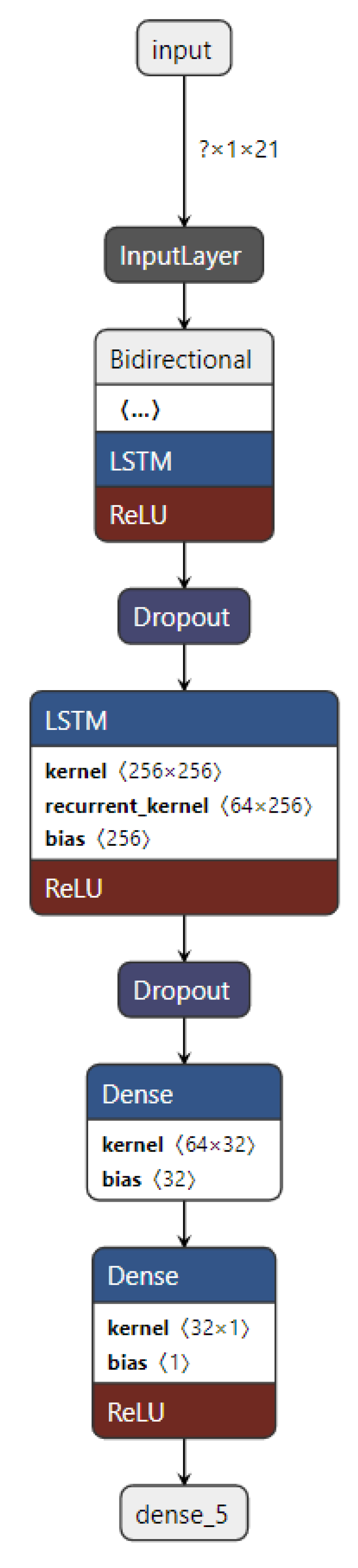
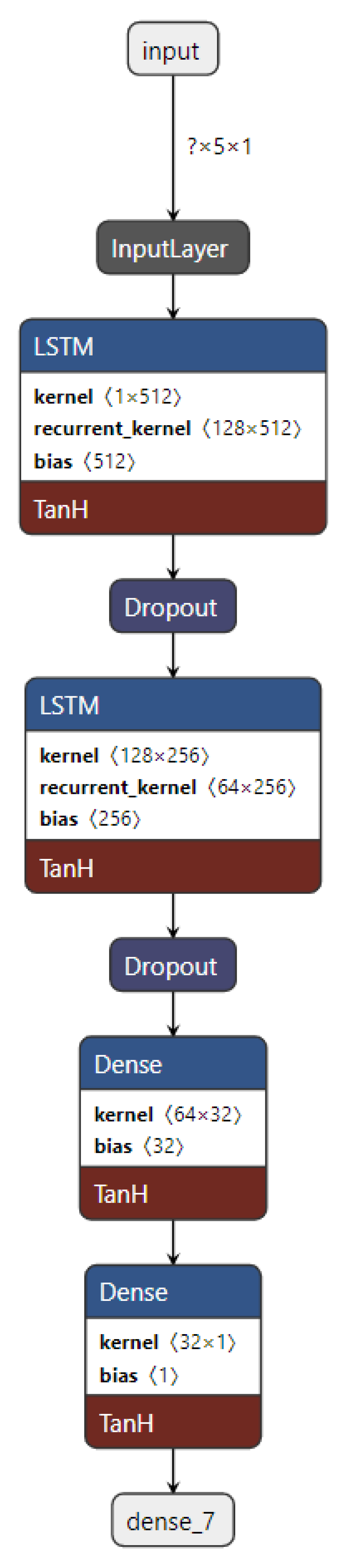
3.2.1.1. LSTM
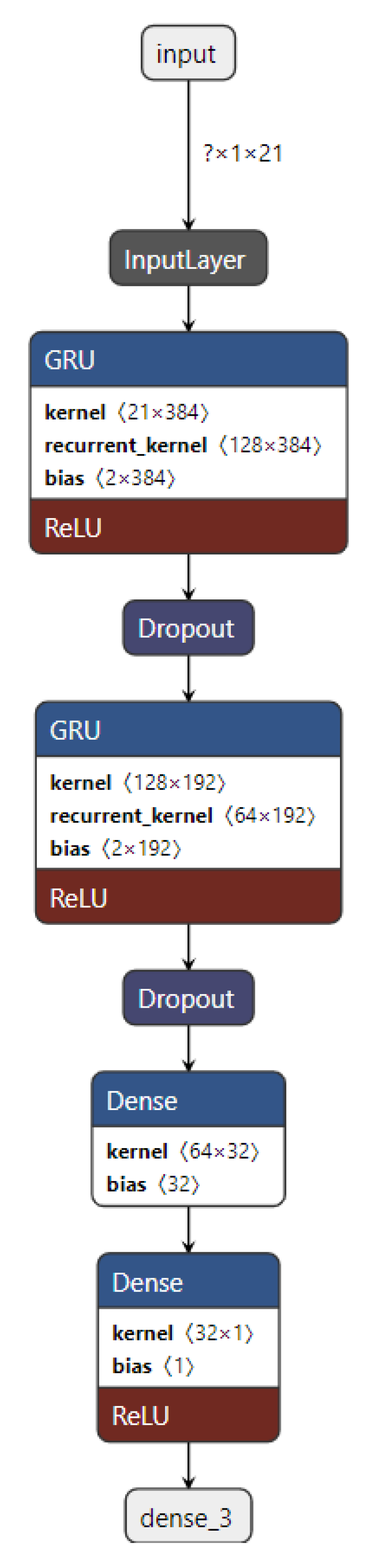
3.2.1.2. GRU
3.2.1.3. BiLSTM
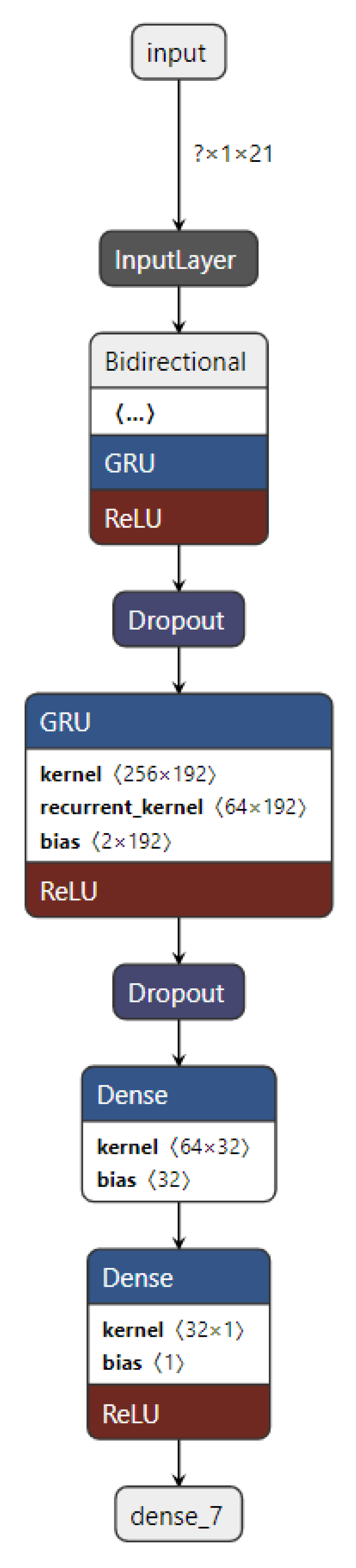
3.2.1.4. BiGRU
3.2.1.5. LSTM-AE
3.2.1.6. CNN-LSTM
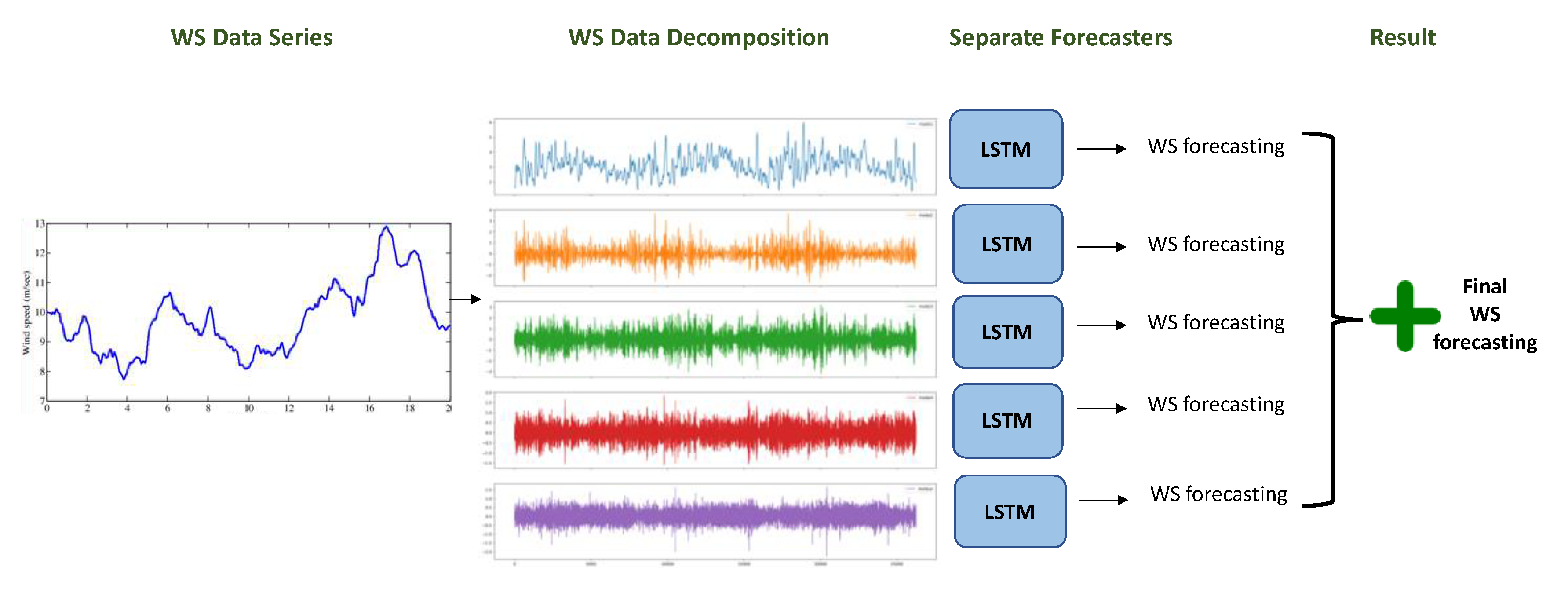
3.2.1.7. Hybrid Model of Decomposition Methods and LSTM
3.2.2. ML-Based Models
3.2.1.1. SVR
3.2.1.2. RFR
3.2.1.3. XGB
3.2.1.4. MLR
3.3. Implementation
3.4. Evaluation Metrics
4. Results and Discussion
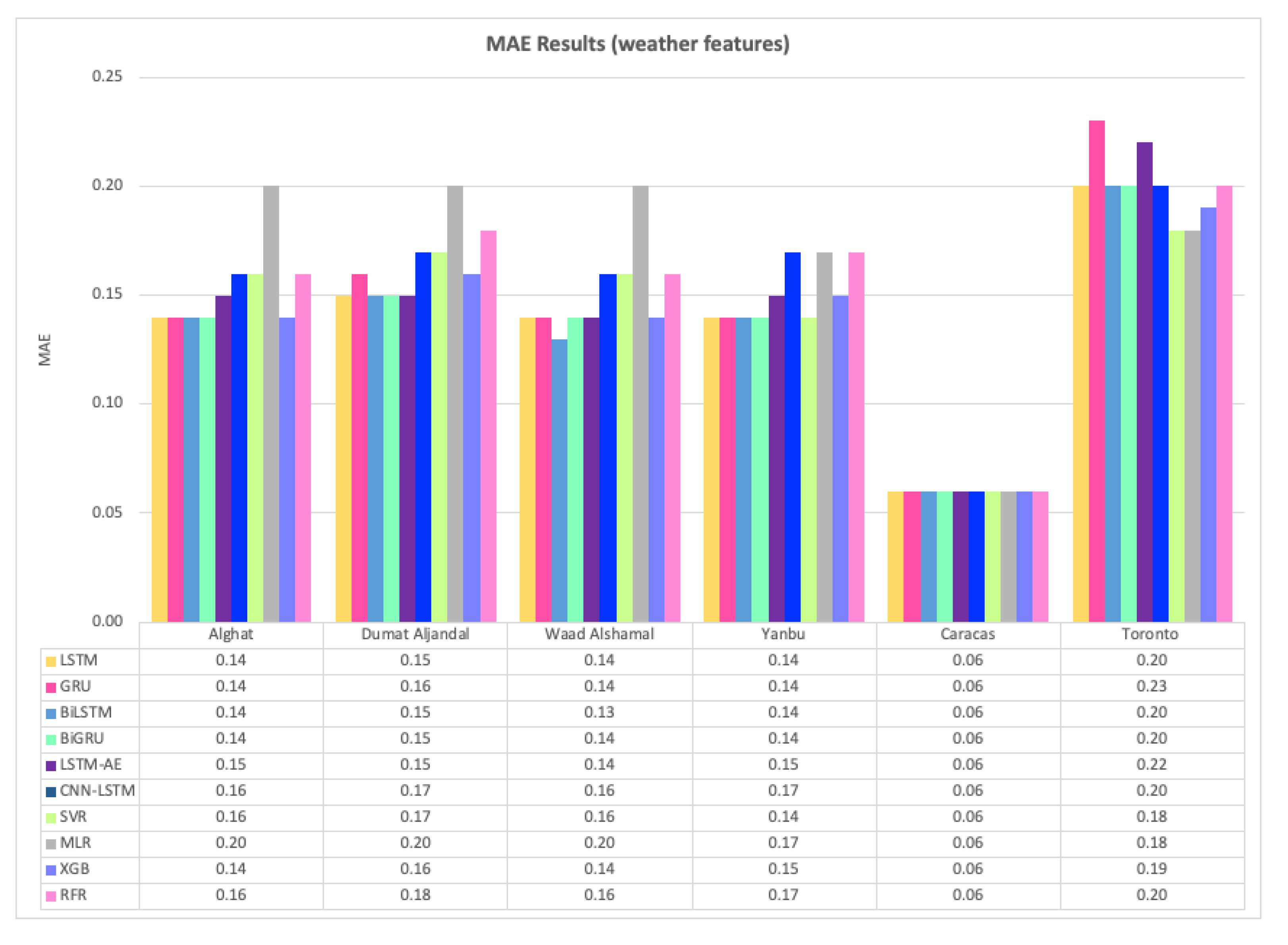
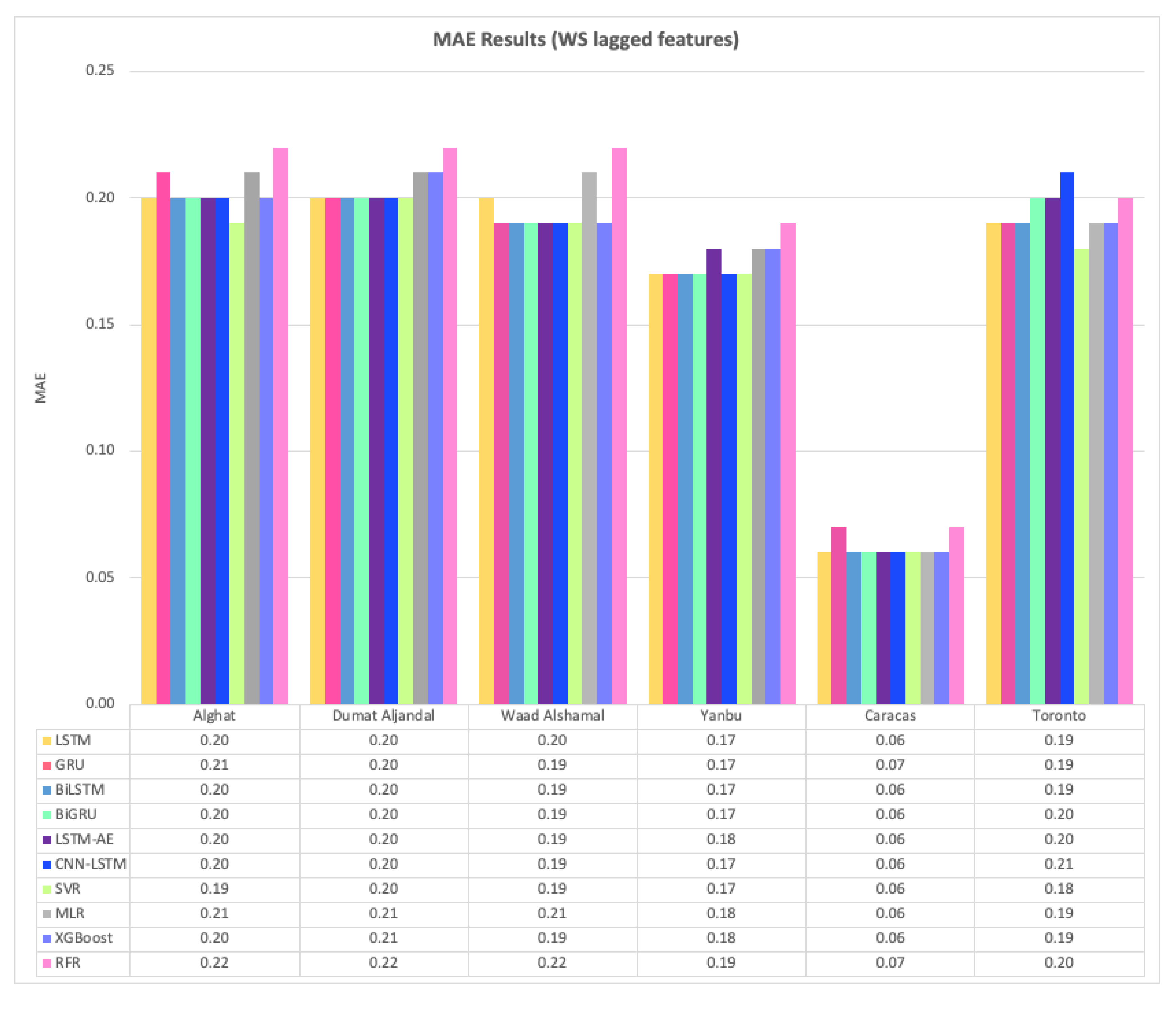
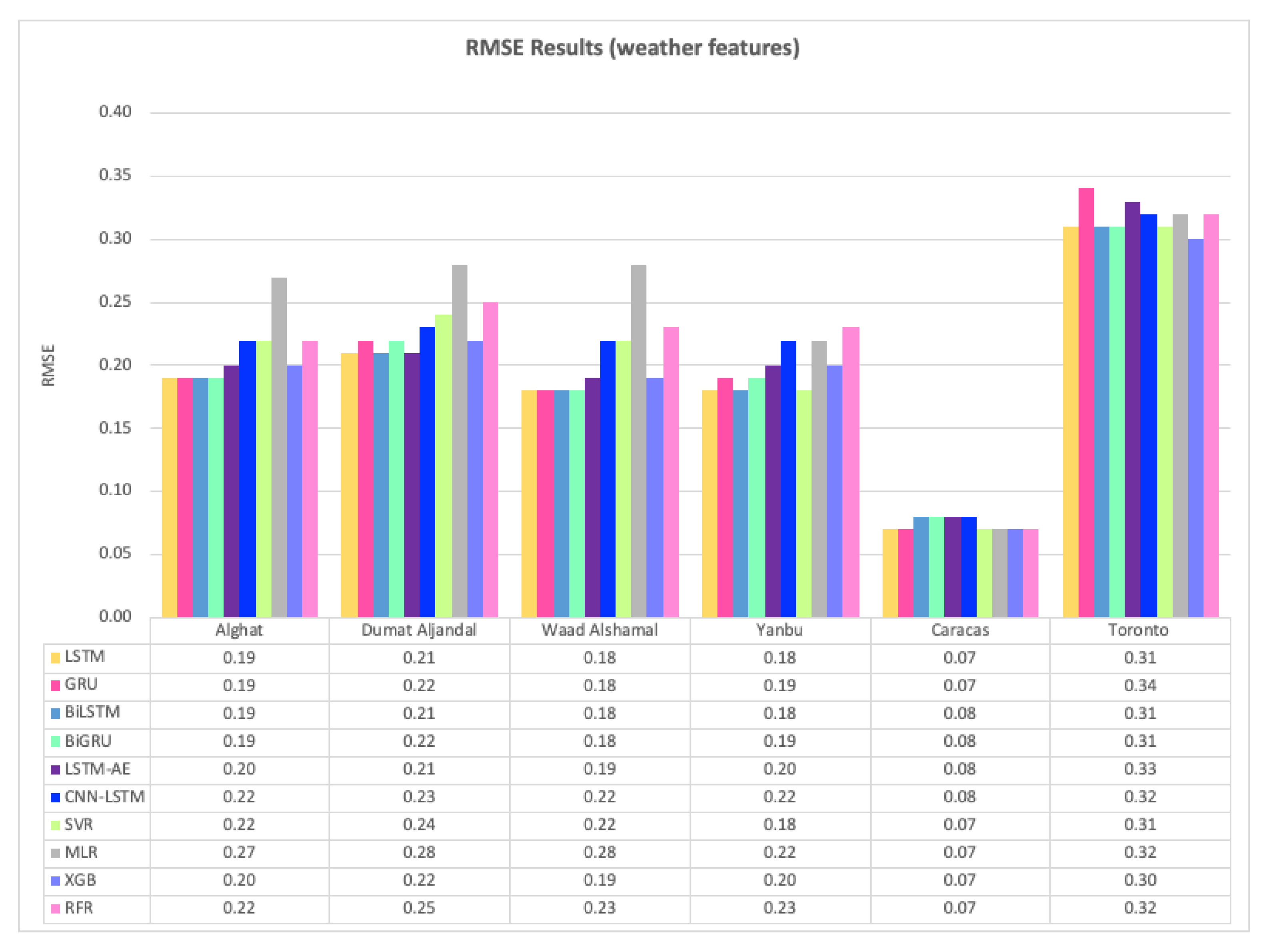
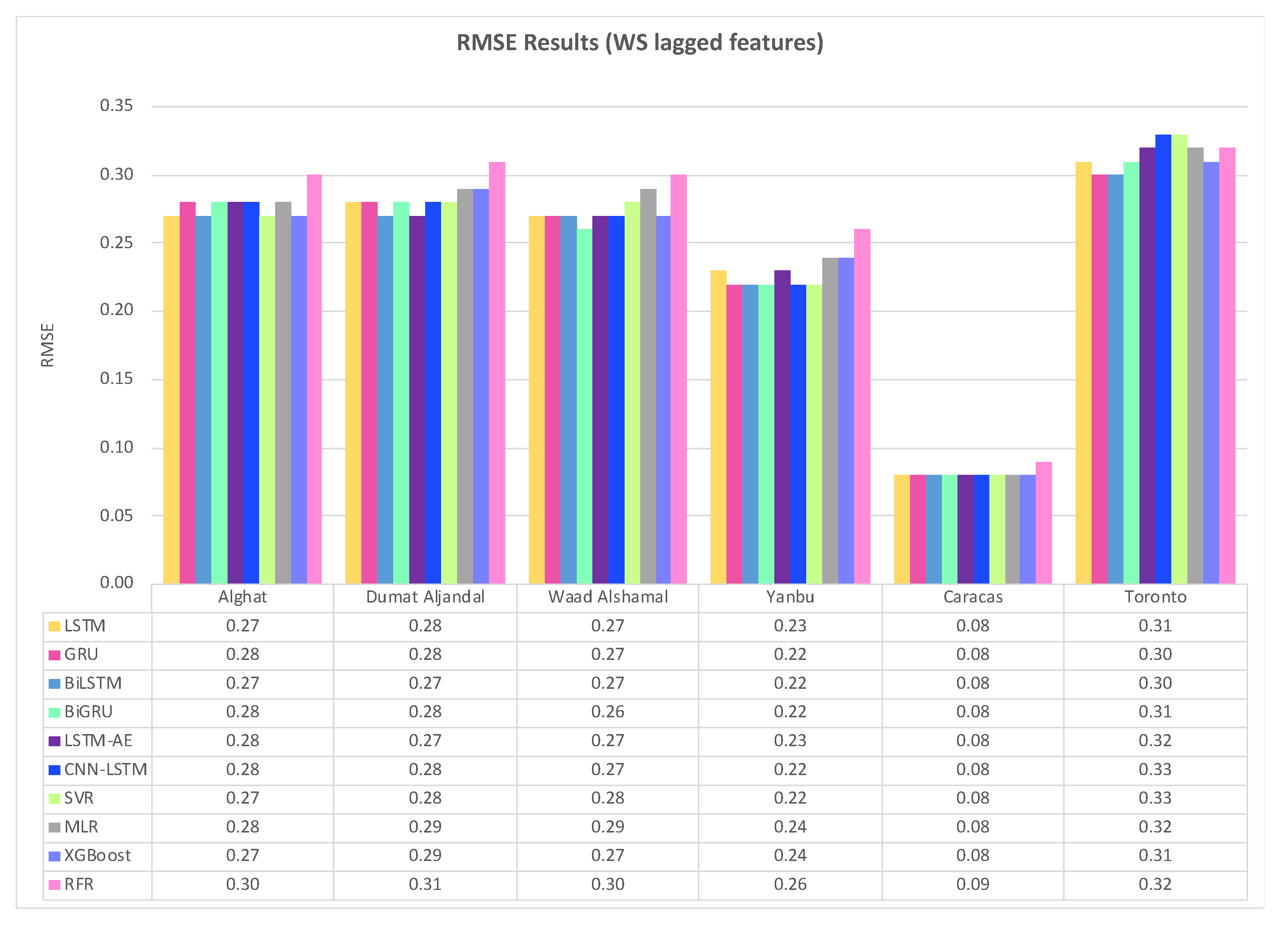
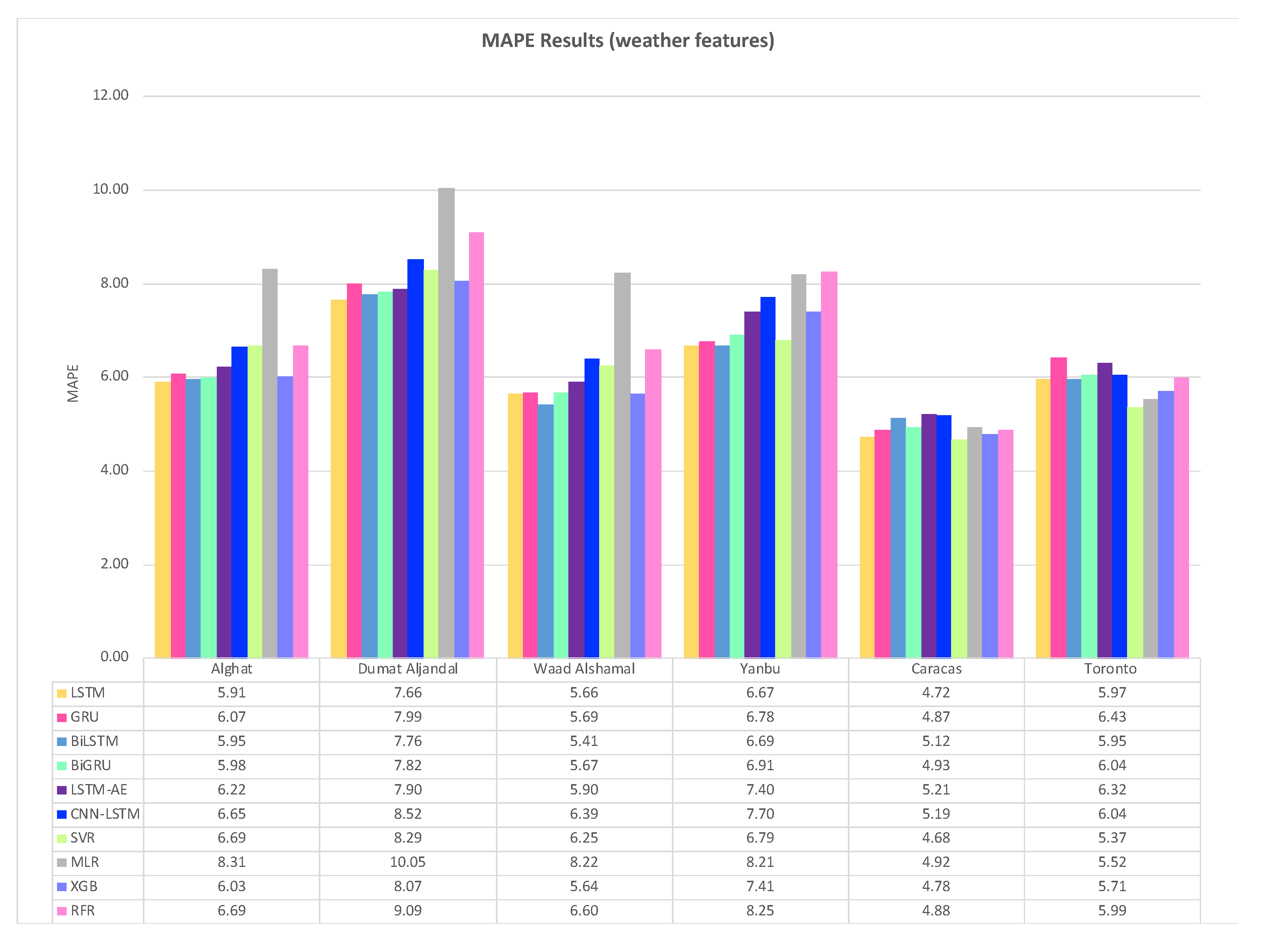
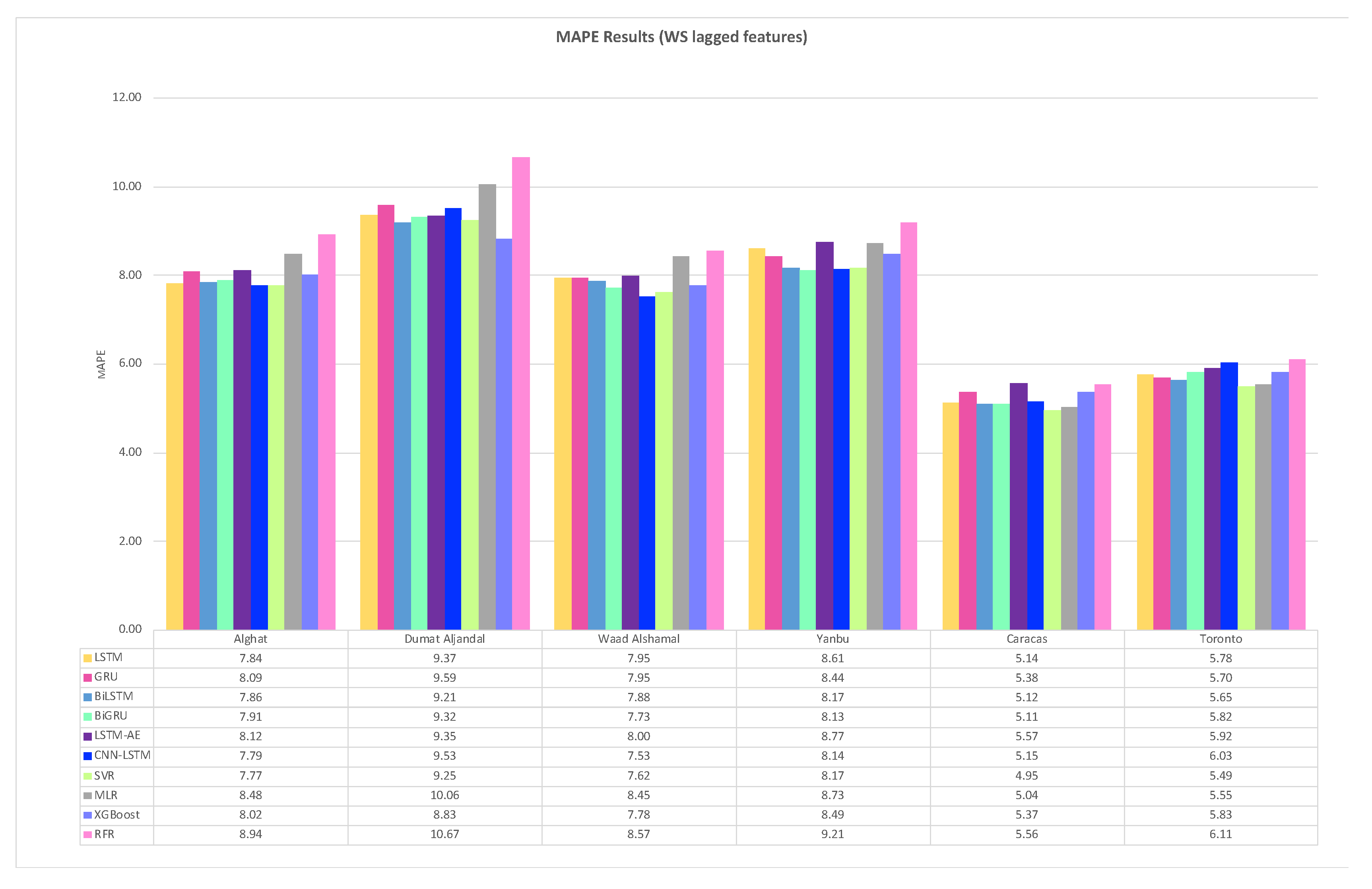
4.1. Effect of Using Last Hour’s Weather Variables on Forecasting
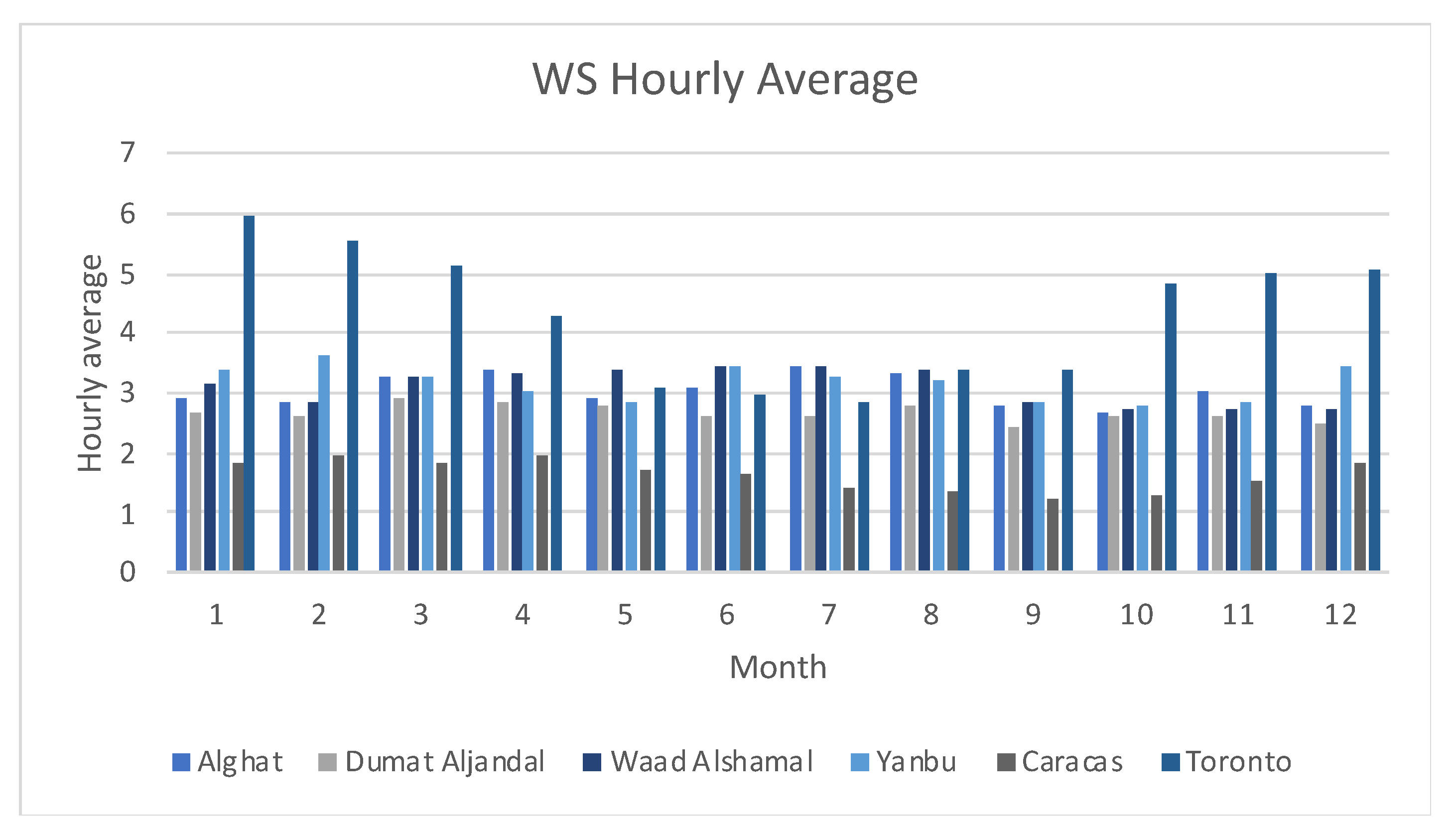
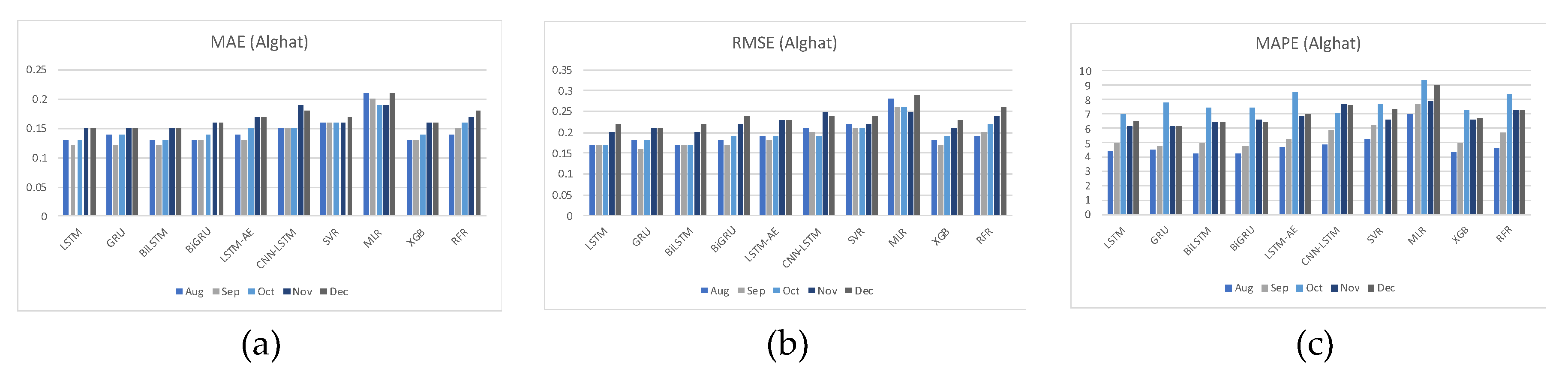
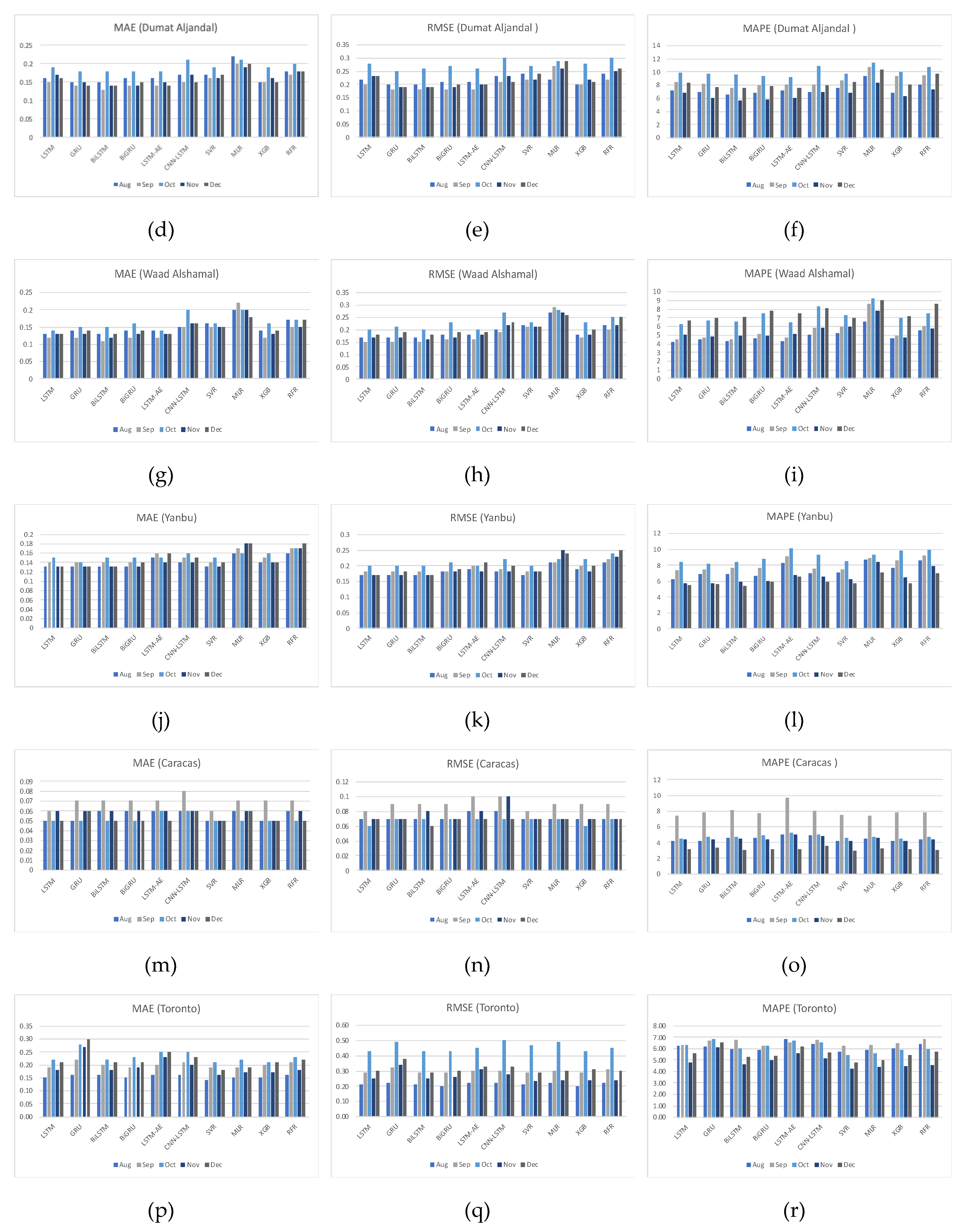
4.2. Effect of Seasonality on Forecasting
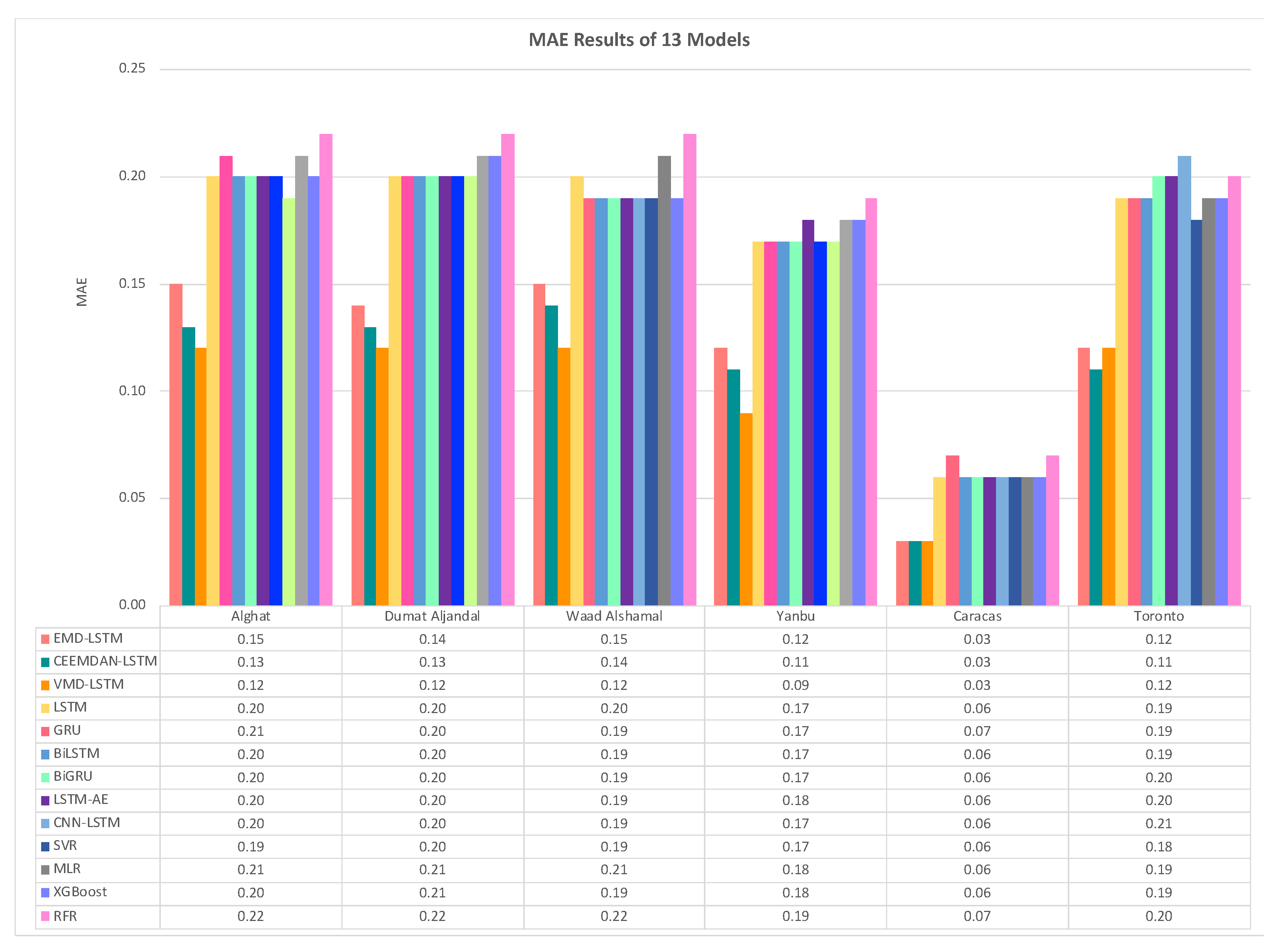
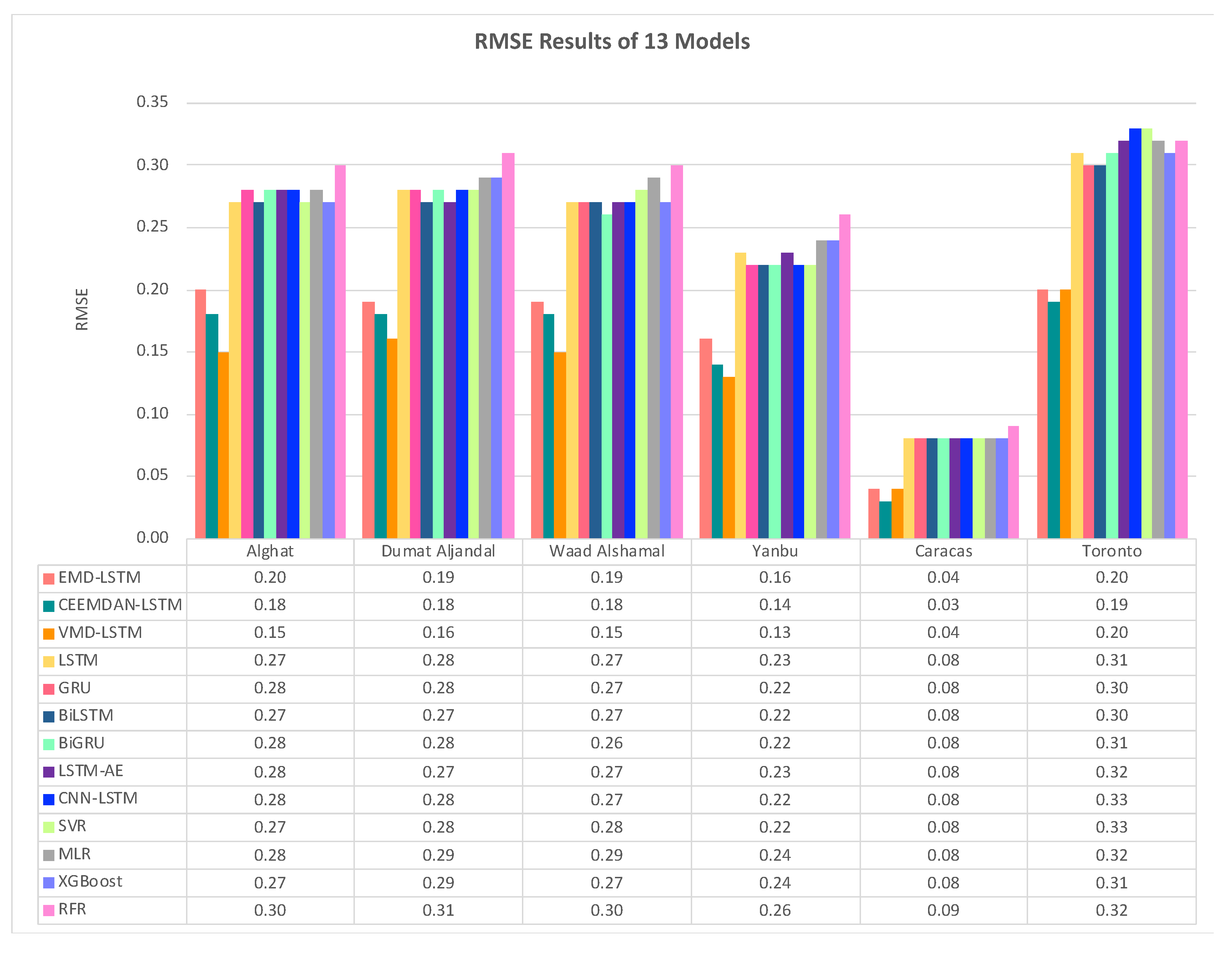
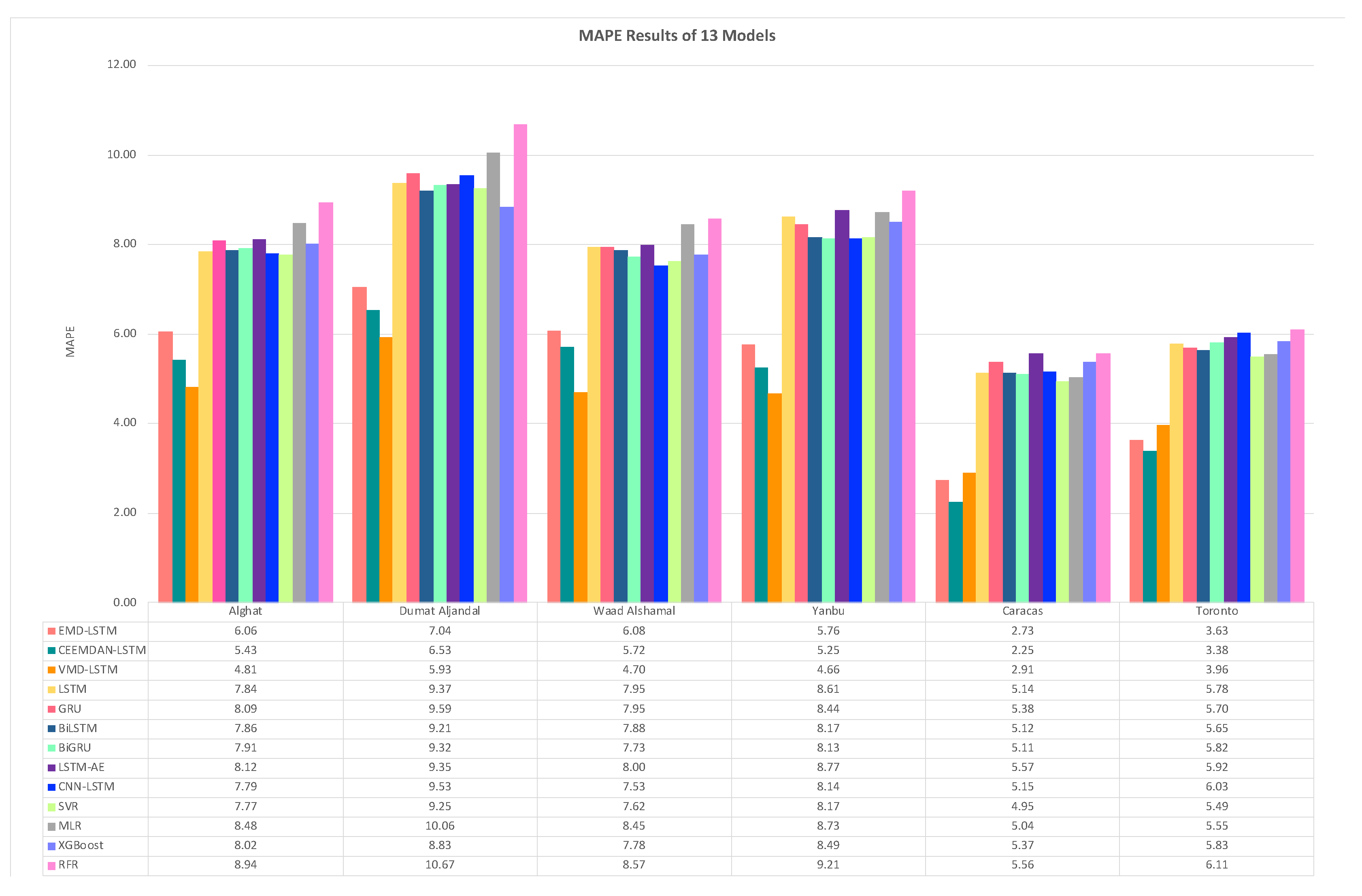
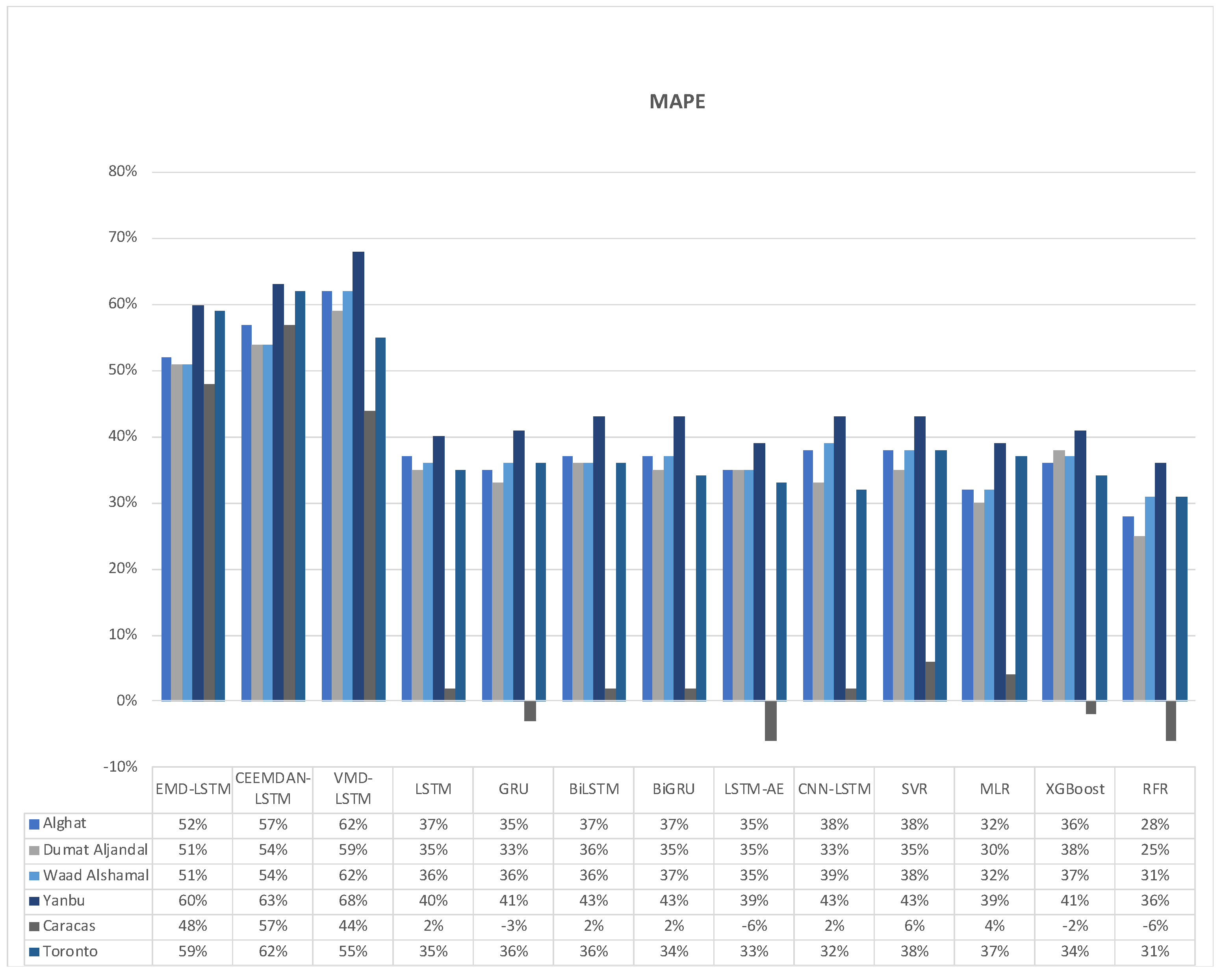
4.3. Effect of Using Decomposition Methods on Forecasting
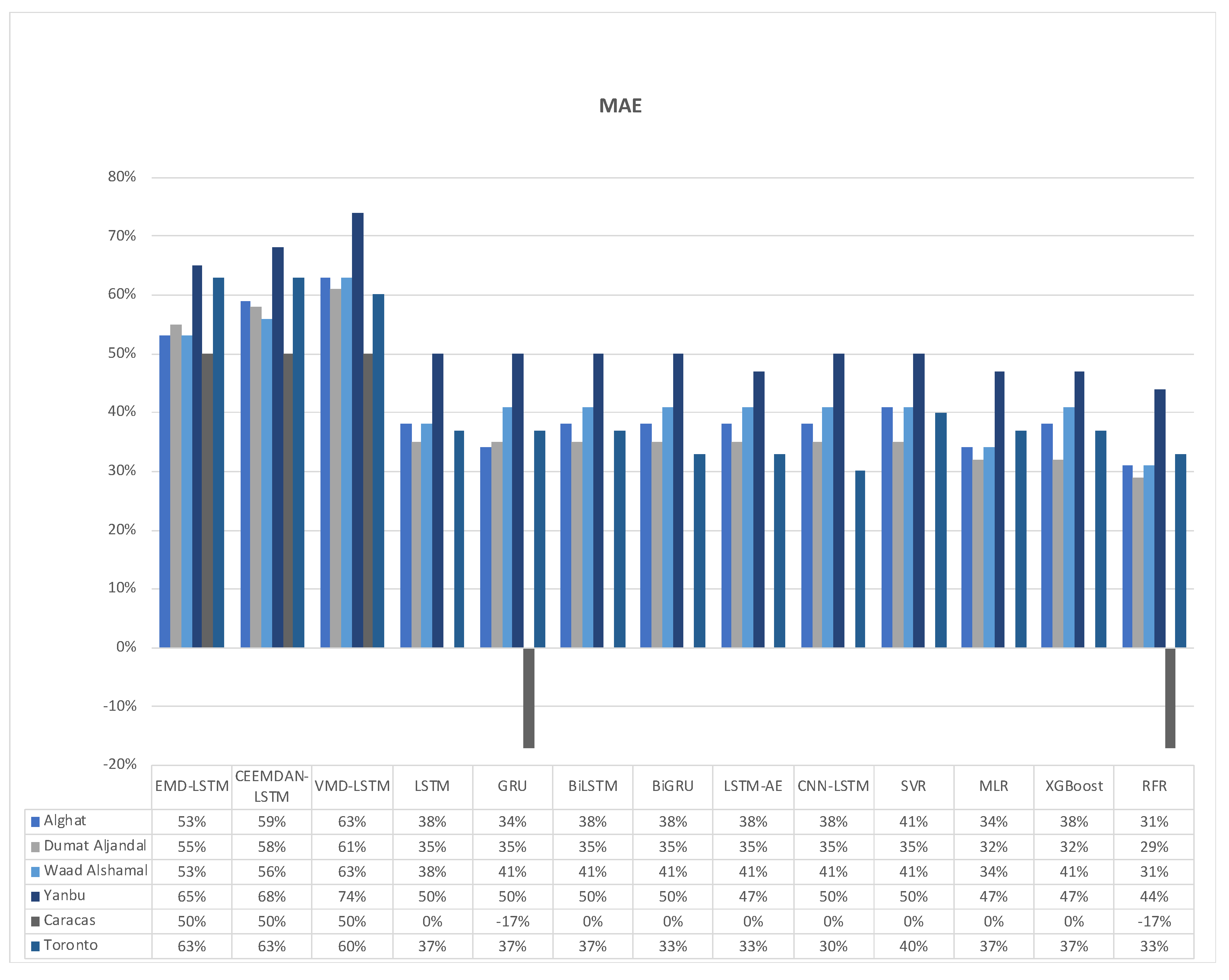
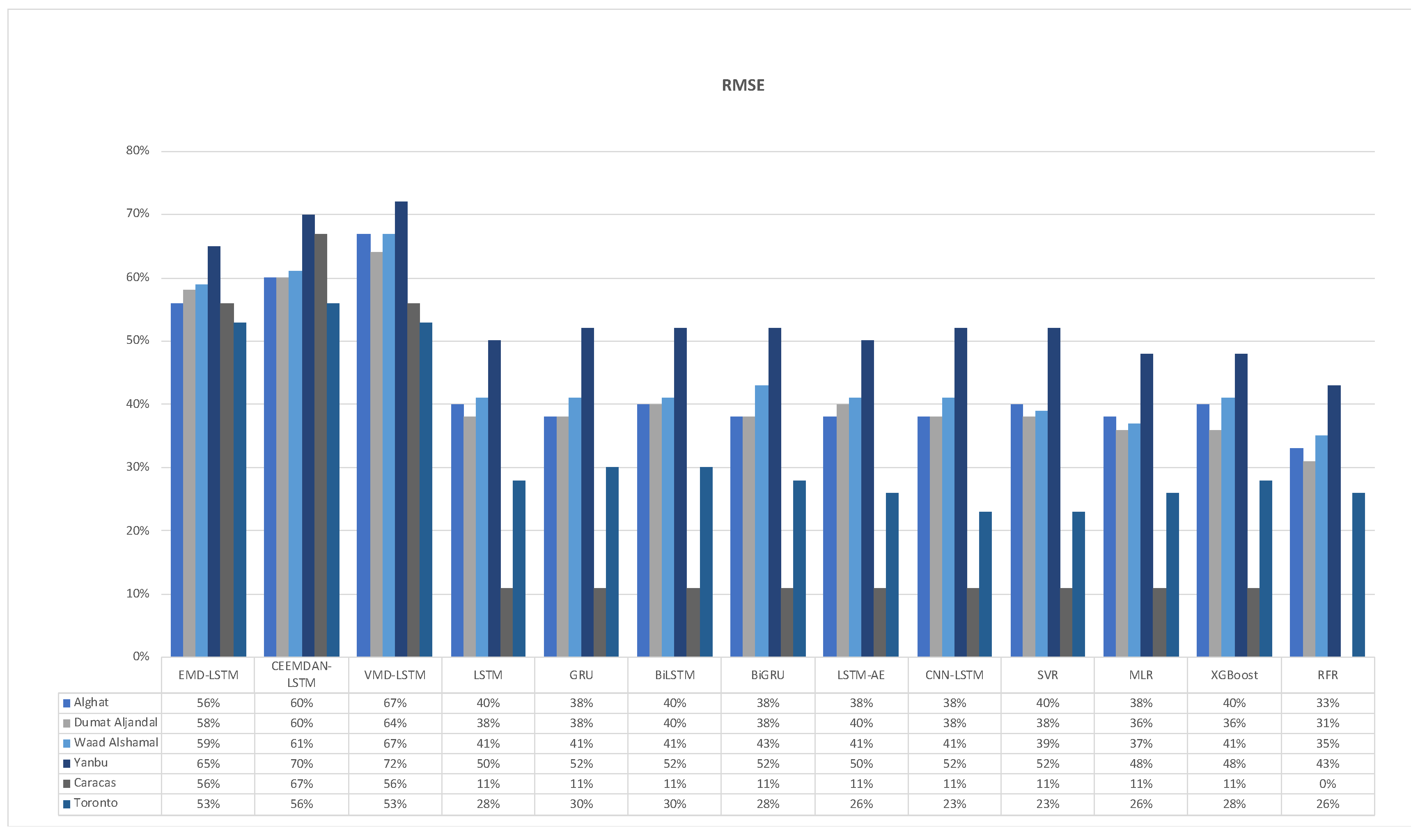
4.4. Forecast Skills of all Models
5. Conclusion
- The best forecasting model for the Saudi locations, according to MAE, RMSE, MAPE, and FS, is the hybrid model of VMD and LSTM model.
- The best forecasting model for Caracas and Toronto, according to MAE, RMSE, MAPE, and FS, is the hybrid model of CEEMDAN and the LSTM model.
- All DL-based models have similar performance, but complex structures like the LSTM-AE and CNN-LSTM models have higher errors.
- Using the last hour’s weather variables besides the last values of WS has improved the forecasting results for all models. However, the hybrid models with decomposition methods achieved better forecasting results.
- If seasons do not affect the hourly average of WS at the data source location, forecasting results would not show a big variance either. Here, it is unnecessary to partition the datasets according to seasons and train separate forecasters.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SA | Saudi Arabia |
| NWP | Numerical Weather Prediction |
| RNN | Recurrent Neural Network |
| kNN | K-Nearest Neighbors |
| AE | Autoencoder |
| LSTM | Long Short-Term Memory |
| CNN | Convolutional Neural Network |
| GRU | Gated Recurrent Unit |
| BiLSTM | Bidirectional LSTM |
| BiGRU | Bidirectional GRU |
| RFR | Random Forest Regression |
| MLR | Multiple Linear Regression |
| MLP | Multilayer Perceptron Network |
| VMD | Variational Mode Decomposition |
| EMD | Empirical Mode Decomposition |
| CEEMDAN | Complete Ensemble Empirical Mode Decomposition with Adaptive Noise |
| SVR | Support Vector Regression |
| RMSE | Root Mean Square Error |
| MAPE | Mean Absolute Percentage Error |
| MAE | Mean Absolute Error |
| MSE | Mean Squared Error loss |
| WS | Wind Speed |
| WD | Wind Direction |
| WP | Wind Power |
| T | Temperature |
| P | Pressure |
| RH | Relative Humidity |
| ZA | Zenith Angle |
| PW | Precipitable Water |
| DP | Dew Point |
| HS | Hour Sine |
| HC | Hour Cosine |
| DS | Day Sine |
| DC | Day Cosine |
| WDS | Wind Direction Sine |
| WDC | Wind Direction Cosine |
| ML | Machine Learning |
| DL | Deep Learning |
| FFNN | Feed Forward Neural Network |
| GHI | Global Horizontal Irradiation |
| DHI | Diffuse Horizontal Irradiation |
| DNI | Direct Normal Irradiance |
| WSTD | Wavelet Soft Threshold Denoising |
| ReLU | Rectified Linear Unit |
| RR | Ridge Regression |
| ESN | Echo State Network |
| PE | Permutation Entropy |
| RBFNN | Radial Basis Function Neural Network |
| IBA | Improved Bat Algorithm |
| FS | Forecast Skill |
| XGB | eXtreme Gradient Boosting |
| ACF | Autocorrelation Function |
| GA | Genetic Algorithm |
| LN | Linear-Nonlinear |
| MOBBSA | Multi-Objective Binary Back-tracking Search Algorithm |
| DE | Differential Evolution algorithm |
| SIRAE | Stacked Independently Recurrent Auto Encoder |
| NSRDB | National Solar Radiation Data Base |
| NREL | National Renewable Energy Laboratory |
| PSM | Physical Solar Model |
| SD | Standard Deviation |
| VAR | Variance |
| IMFs | Intrinsic Mode Functions |
| ARIMA | Auto Regressive Integrated Moving Average |
References
- International Renewable Energy Agency (IRENA), “Future of Wind - Executive Summary,” 2019.
- Dumat Al Jandal wind farm in Saudi Arabia starts production. Available online: https://www.power-technology.com/news/dumat-al-jandal-wind/ (accessed on 24 February 2023).
- Giani, P.; Tagle, F.; Genton, M.G.; Castruccio, S.; Crippa, P. Closing the gap between wind energy targets and implementation for emerging countries. Appl. Energy 2020, 269, 115085. [Google Scholar] [CrossRef]
- Alharbi, F.; Csala, D. Saudi Arabia’s Solar and Wind Energy Penetration: Future Performance and Requirements. Energies 2020, 13, 588. [Google Scholar] [CrossRef]
- Saudi press agency, “Saudi Arabia Announces Floating Five Projects to Produce Electricity with Use of Renewable Energy with Total Capacity of 3,300mw,” 25/09/2022. Available online: https://www.spa.gov.sa/viewfullstory.php?lang=en&newsid=2386966 (accessed on 1 April 2023).
- Mohandes, M.A.; Rehman, S. Wind Speed Extrapolation Using Machine Learning Methods and LiDAR Measurements. IEEE Access 2018, 6, 77634–77642. [Google Scholar] [CrossRef]
- Abualigah, L.; Abu Zitar, R.; Almotairi, K.H.; Hussein, A.M.; Elaziz, M.A.; Nikoo, M.R.; Gandomi, A.H. Wind, Solar, and Photovoltaic Renewable Energy Systems with and without Energy Storage Optimization: A Survey of Advanced Machine Learning and Deep Learning Techniques. Energies 2022, 15, 578. [Google Scholar] [CrossRef]
- V. Bali, A. Kumar, and S. Gangwar, “Deep learning based wind speed forecasting-A review,” in 2019 9th International Conference on Cloud Computing, Data Science & Engineering (Confluence), 2019, pp. 426–431.
- Deng, X.; Shao, H.; Hu, C.; Jiang, D.; Jiang, Y. Wind Power Forecasting Methods Based on Deep Learning: A Survey. Comput. Model. Eng. Sci. 2020, 122, 273–301. [Google Scholar] [CrossRef]
- Liu, H.; Chen, C.; Lv, X.; Wu, X.; Liu, M. Deterministic wind energy forecasting: A review of intelligent predictors and auxiliary methods. Energy Convers. Manag. 2019, 195, 328–345. [Google Scholar] [CrossRef]
- Alkhayat, G.; Mehmood, R. A review and taxonomy of wind and solar energy forecasting methods based on deep learning. Energy AI 2021, 4, 100060. [Google Scholar] [CrossRef]
- Manero, J.; Béjar, J.; Cortés, U. “Dust in the Wind...”, Deep Learning Application to Wind Energy Time Series Forecasting. Energies 2019, 12, 2385. [Google Scholar] [CrossRef]
- Peng, Z.; Peng, S.; Fu, L.; Lu, B.; Tang, J.; Wang, K.; Li, W. A novel deep learning ensemble model with data denoising for short-term wind speed forecasting. Energy Convers. Manag. 2020, 207, 112524. [Google Scholar] [CrossRef]
- Alhussein, M.; Haider, S.I.; Aurangzeb, K. Microgrid-Level Energy Management Approach Based on Short-Term Forecasting of Wind Speed and Solar Irradiance. Energies 2019, 12, 1487. [Google Scholar] [CrossRef]
- Lawal, A.; Rehman, S.; Alhems, L.M.; Alam, M. Wind Speed Prediction Using Hybrid 1D CNN and BLSTM Network. IEEE Access 2021, 9, 156672–156679. [Google Scholar] [CrossRef]
- Faniband, Y.P.; Shaahid, S.M. Univariate Time Series Prediction of Wind speed with a case study of Yanbu, Saudi Arabia. Int. J. 2021, 10, 257–264. [Google Scholar]
- Zheng, Y.; Ge, Y.; Muhsen, S.; Wang, S.; Elkamchouchi, D.H.; Ali, E.; Ali, H.E. New ridge regression, artificial neural networks and support vector machine for wind speed prediction. Adv. Eng. Softw. 2023, 179, 103426. [Google Scholar] [CrossRef]
- Salman, U.T.; Rehman, S.; Alawode, B.; Alhems, L.M. Short term prediction of wind speed based on long-short term memory networks. FME Trans. 2021, 49, 643–652. [Google Scholar] [CrossRef]
- Huang, H.; Castruccio, S.; Genton, M.G. Forecasting High-Frequency Spatio-Temporal Wind Power with Dimensionally Reduced Echo State Networks. J. R. Stat. Soc. Ser. C (Applied Stat. 2022, 71, 449–466. [Google Scholar] [CrossRef]
- Alharbi, F.R.; Csala, D. Wind Speed and Solar Irradiance Prediction Using a Bidirectional Long Short-Term Memory Model Based on Neural Networks. Energies 2021, 14, 6501. [Google Scholar] [CrossRef]
- F. R. Alharbi and D. Csala, “Short-Term Wind Speed and Temperature Forecasting Model Based on Gated Recurrent Unit Neural Networks,” in 2021 3rd Global Power, Energy and Communication Conference (GPECOM), 2021, pp. 142–147.
- Brahimi, T. Using Artificial Intelligence to Predict Wind Speed for Energy Application in Saudi Arabia. Energies 2019, 12, 4669. [Google Scholar] [CrossRef]
- Y. P. Faniband and S. M. Shaahid, “Forecasting Wind Speed using Artificial Neural Networks–A Case Study of a Potential Location of Saudi Arabia,” in E3S Web of Conferences, 2020, vol. 173, p. 1004.
- Liang, T.; Xie, G.; Fan, S.; Meng, Z. A Combined Model Based on CEEMDAN, Permutation Entropy, Gated Recurrent Unit Network, and an Improved Bat Algorithm for Wind Speed Forecasting. IEEE Access 2020, 8, 165612–165630. [Google Scholar] [CrossRef]
- Jiang, Z.; Che, J.; He, M.; Yuan, F. A CGRU multi-step wind speed forecasting model based on multi-label specific XGBoost feature selection and secondary decomposition. Renew. Energy 2023, 203, 802–827. [Google Scholar] [CrossRef]
- Lv, S.-X.; Wang, L. Deep learning combined wind speed forecasting with hybrid time series decomposition and multi-objective parameter optimization. Appl. Energy 2022, 311, 118674. [Google Scholar] [CrossRef]
- Yildiz, C.; Acikgoz, H.; Korkmaz, D.; Budak, U. An improved residual-based convolutional neural network for very short-term wind power forecasting. Energy Convers. Manag. 2020, 228, 113731. [Google Scholar] [CrossRef]
- Wang, L.; Tao, R.; Hu, H.; Zeng, Y.-R. Effective wind power prediction using novel deep learning network: Stacked independently recurrent autoencoder. Renew. Energy 2020, 164, 642–655. [Google Scholar] [CrossRef]
- Hu, H.; Wang, L.; Tao, R. Wind speed forecasting based on variational mode decomposition and improved echo state network. Renew. Energy 2020, 164, 729–751. [Google Scholar] [CrossRef]
- M. Sengupta, A. Habte, Y. Xie, A. Lopez, and G. Buster, “National Solar Radiation Database (NSRDB).” United States, 2018. [CrossRef]
- Petneházi, G. Recurrent neural networks for time series forecasting. arXiv 2019, arXiv:1901.00069. [Google Scholar]
- Qian, Z.; Pei, Y.; Zareipour, H.; Chen, N. A review and discussion of decomposition-based hybrid models for wind energy forecasting applications. Appl. Energy 2018, 235, 939–953. [Google Scholar] [CrossRef]
- Liu, H.; Chen, C. Data processing strategies in wind energy forecasting models and applications: A comprehensive review. Appl. Energy 2019, 249, 392–408. [Google Scholar] [CrossRef]
- Peng, T.; Zhang, C.; Zhou, J.; Nazir, M.S. An integrated framework of Bi-directional long-short term memory (BiLSTM) based on sine cosine algorithm for hourly solar radiation forecasting. Energy 2021, 221, 119887. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, Y.; Yang, L.; Liu, Q.; Yan, K.; Du, Y. Short-Term Photovoltaic Power Forecasting Based on Long Short Term Memory Neural Network and Attention Mechanism. IEEE Access 2019, 7, 78063–78074. [Google Scholar] [CrossRef]
- M. C. Sorkun, C. Paoli, and Ö. D. Incel, “Time series forecasting on solar irradiation using deep learning,” in 2017 10th International Conference on Electrical and Electronics Engineering (ELECO), 2017, pp. 151–155.
- Lynn, H.M.; Pan, S.B.; Kim, P. A Deep Bidirectional GRU Network Model for Biometric Electrocardiogram Classification Based on Recurrent Neural Networks. IEEE Access 2019, 7, 145395–145405. [Google Scholar] [CrossRef]
- Nguyen, H.; Tran, K.; Thomassey, S.; Hamad, M. Forecasting and Anomaly Detection approaches using LSTM and LSTM Autoencoder techniques with the applications in supply chain management. Int. J. Inf. Manag. 2020, 57, 102282. [Google Scholar] [CrossRef]
- Sagheer, A.; Kotb, M. Unsupervised Pre-training of a Deep LSTM-based Stacked Autoencoder for Multivariate Time Series Forecasting Problems. Sci. Rep. 2019, 9, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.H.T.; Phan, Q.B. Hourly day ahead wind speed forecasting based on a hybrid model of EEMD, CNN-Bi-LSTM embedded with GA optimization. Energy Reports 2022, 8, 53–60. [Google Scholar] [CrossRef]
- Caraka, R.E.; et al. Employing best input SVR robust lost function with nature-inspired metaheuristics in wind speed energy forecasting. IAENG Int. J. Comput. Sci. 2020, 47, 572–584. [Google Scholar]
- Drisya, G.V.; Asokan, K.; Kumar, K.S. Wind speed forecast using random forest learning method. arXiv 2022, arXiv:2203.14909. [Google Scholar]
- Barhmi, S.; Elfatni, O.; Belhaj, I. Forecasting of wind speed using multiple linear regression and artificial neural networks. Energy Syst. 2019, 11, 935–946. [Google Scholar] [CrossRef]
- Li, G.; Xie, S.; Wang, B.; Xin, J.; Li, Y.; Du, S. Photovoltaic Power Forecasting With a Hybrid Deep Learning Approach. IEEE Access 2020, 8, 175871–175880. [Google Scholar] [CrossRef]
- Hossain, M.S.; Mahmood, H. Short-Term Photovoltaic Power Forecasting Using an LSTM Neural Network and Synthetic Weather Forecast. IEEE Access 2020, 8, 172524–172533. [Google Scholar] [CrossRef]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.-L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Ramli, M.A.; Twaha, S.; Al-Hamouz, Z. Analyzing the potential and progress of distributed generation applications in Saudi Arabia: The case of solar and wind resources. Renew. Sustain. Energy Rev. 2017, 70, 287–297. [Google Scholar] [CrossRef]
- Yan, X.; Liu, Y.; Xu, Y.; Jia, M. Multistep forecasting for diurnal wind speed based on hybrid deep learning model with improved singular spectrum decomposition. Energy Convers. Manag. 2020, 225, 113456. [Google Scholar] [CrossRef]
- Wang, D.; Luo, H.; Grunder, O.; Lin, Y. Multi-step ahead wind speed forecasting using an improved wavelet neural network combining variational mode decomposition and phase space reconstruction. Renew. Energy 2017, 113, 1345–1358. [Google Scholar] [CrossRef]
- Liu, H.; Mi, X.; Li, Y. Smart multi-step deep learning model for wind speed forecasting based on variational mode decomposition, singular spectrum analysis, LSTM network and ELM. Energy Convers. Manag. 2018, 159, 54–64. [Google Scholar] [CrossRef]
- Wang, X.; Yu, Q.; Yang, Y. Short-term wind speed forecasting using variational mode decomposition and support vector regression. J. Intell. Fuzzy Syst. 2018, 34, 3811–3820. [Google Scholar] [CrossRef]
- Alkhayat, G.; Hasan, S.H.; Mehmood, R. SENERGY: A Novel Deep Learning-Based Auto-Selective Approach and Tool for Solar Energy Forecasting. Energies 2022, 15, 6659. [Google Scholar] [CrossRef]
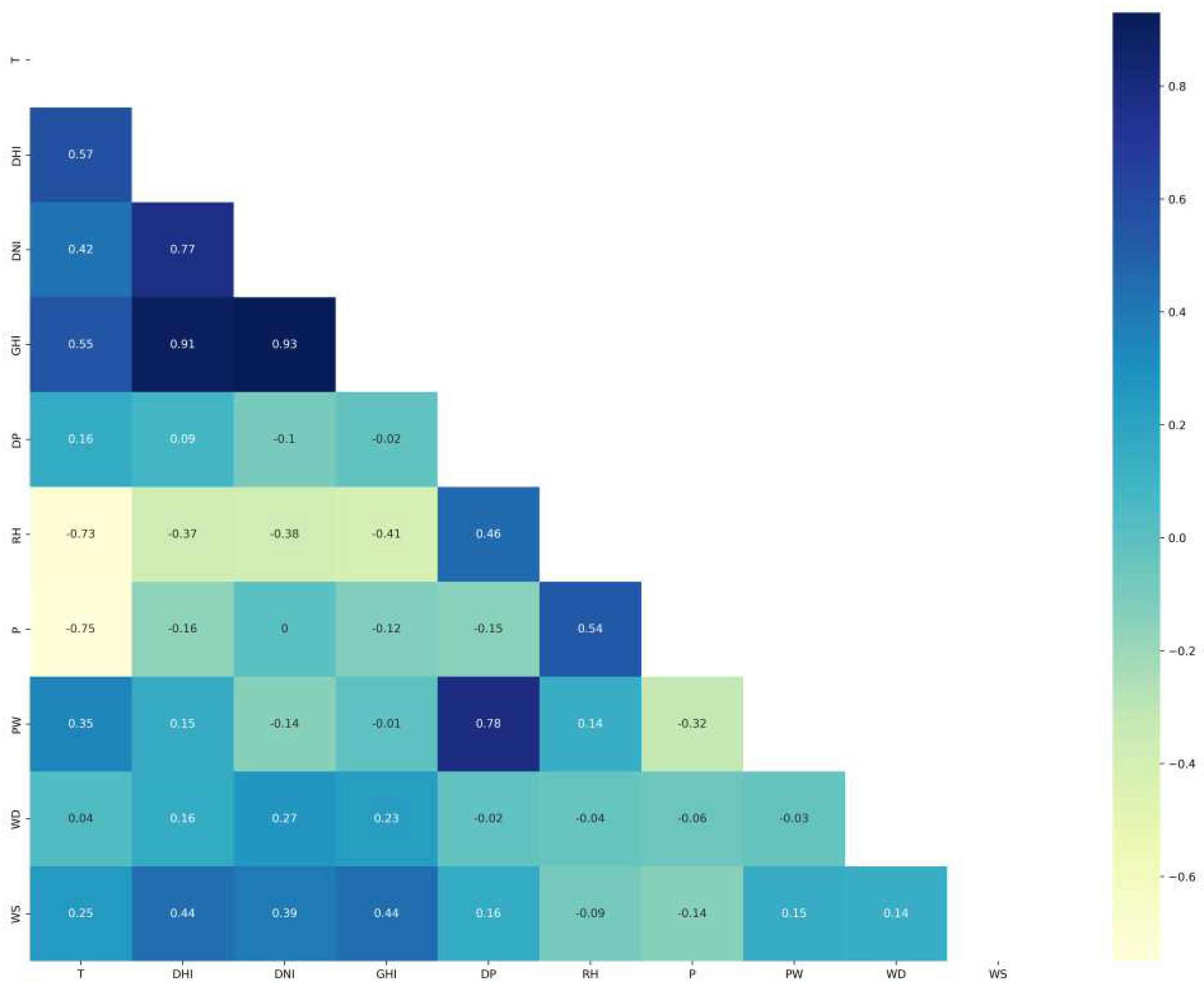
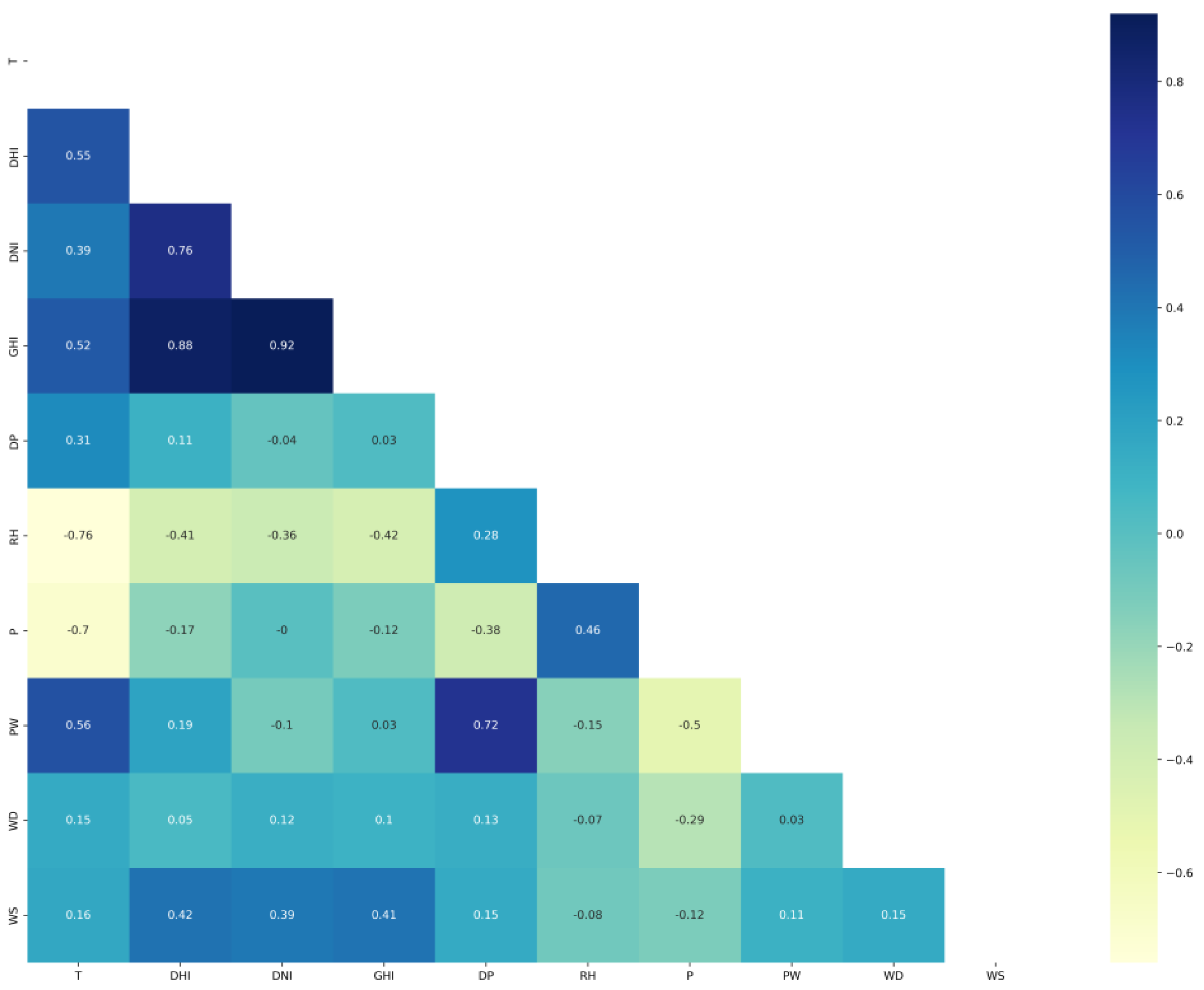
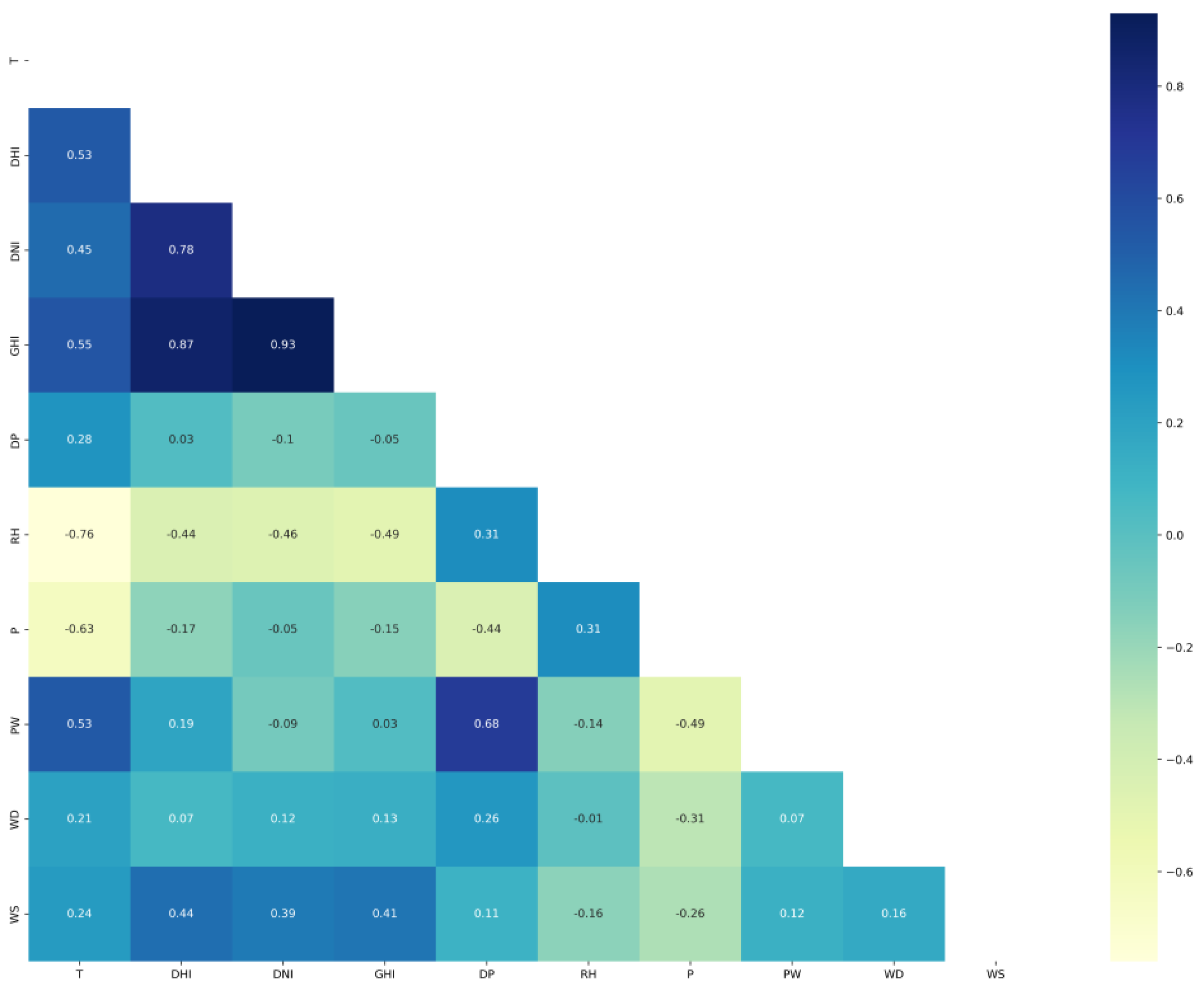
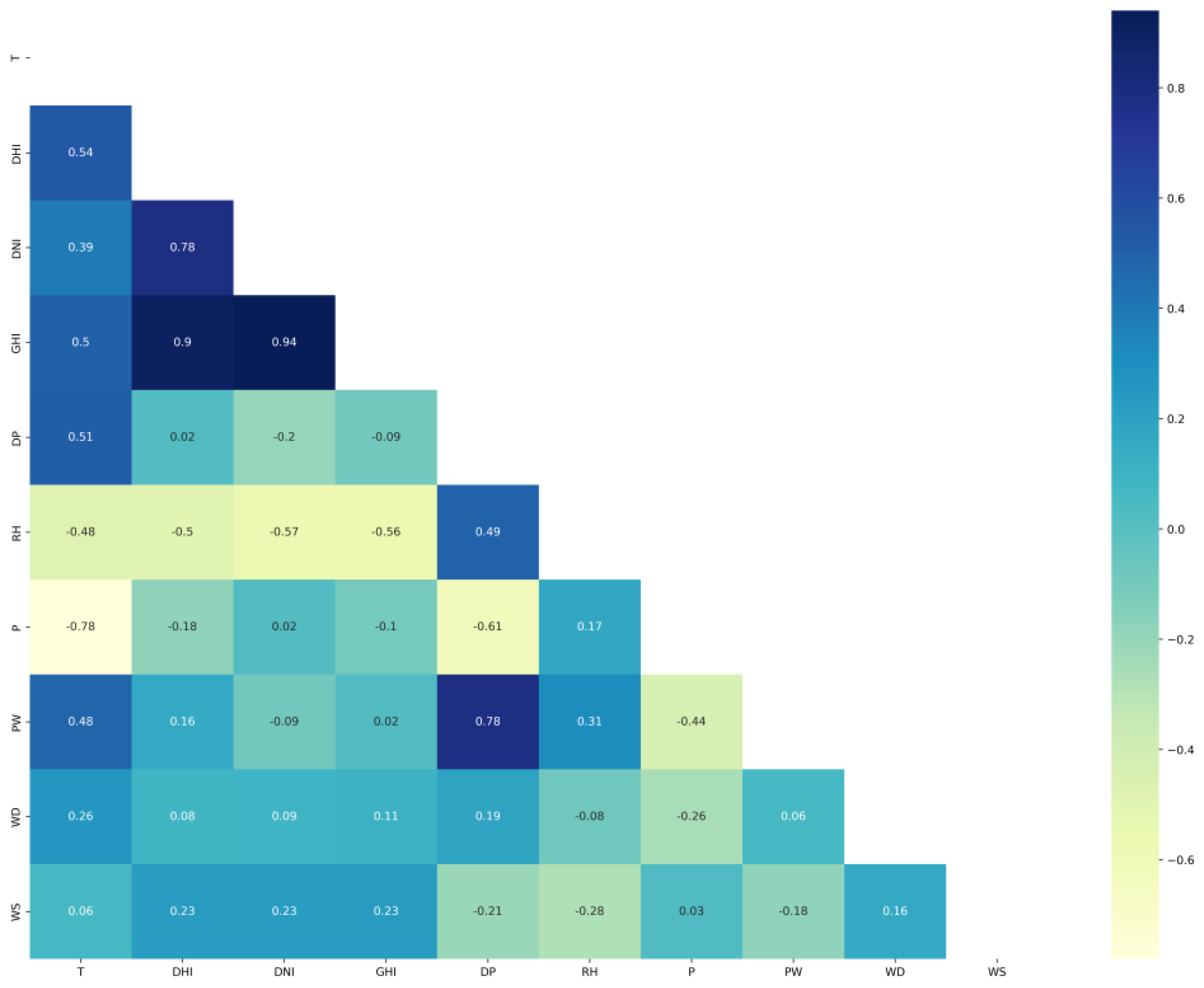
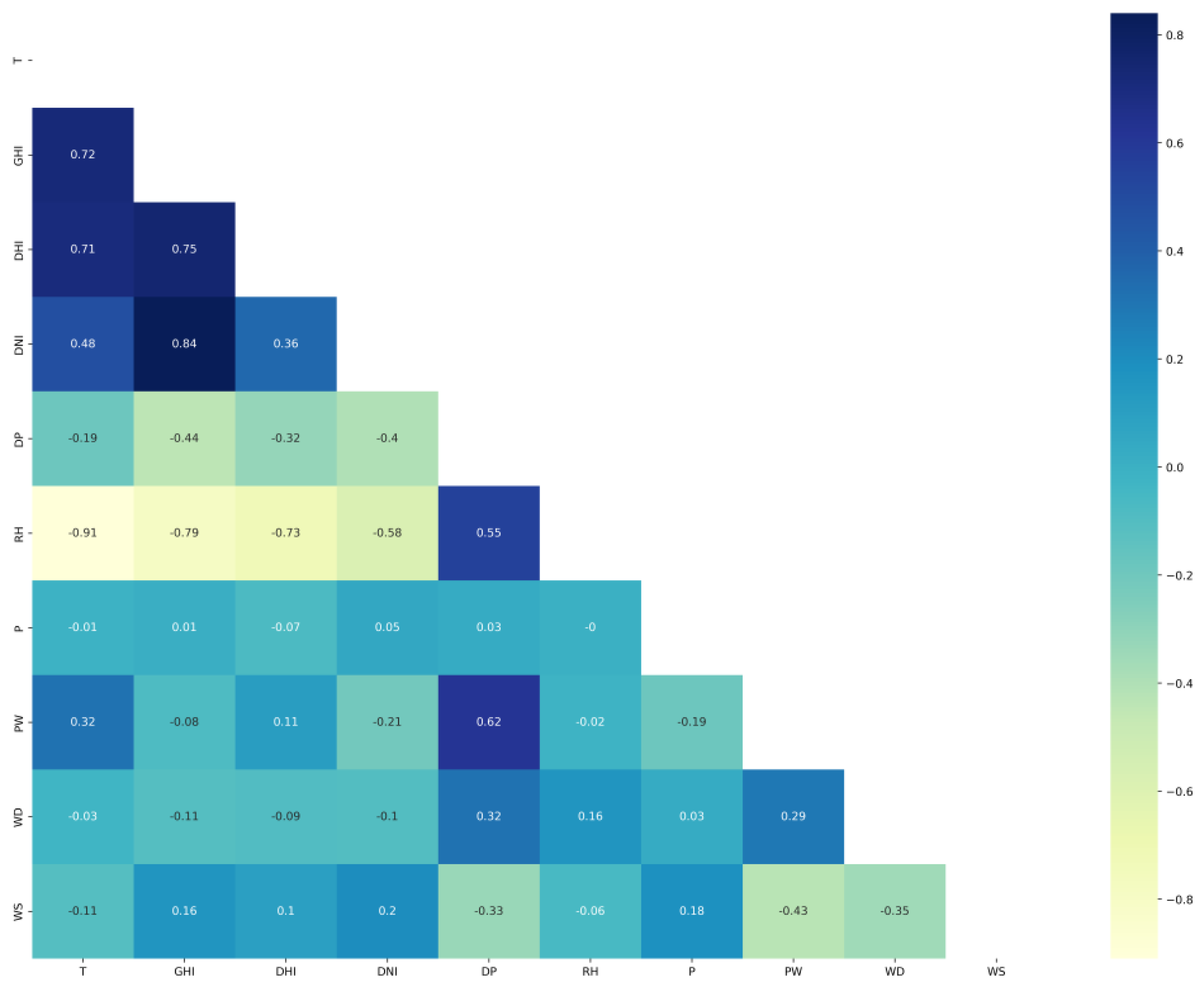
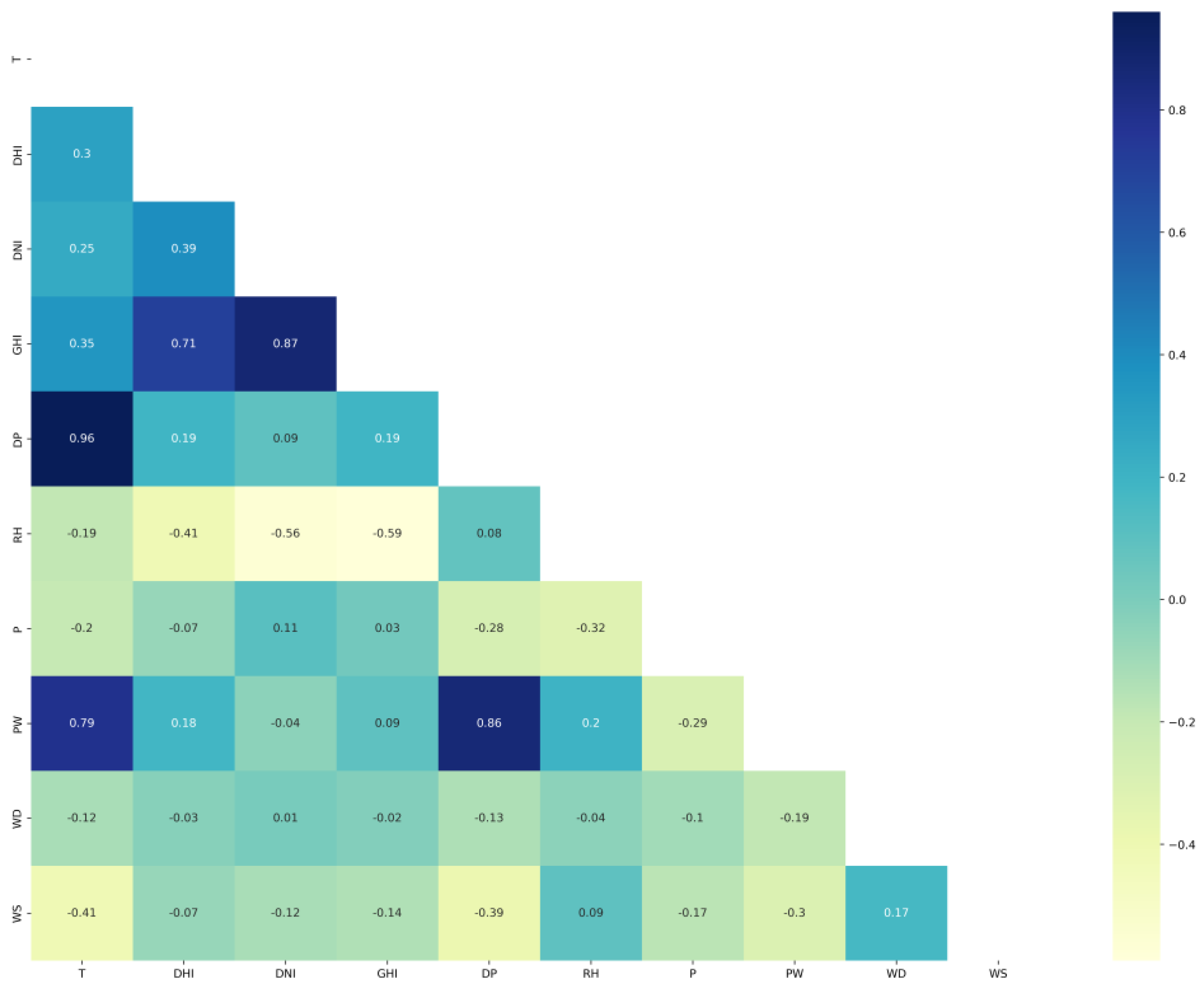
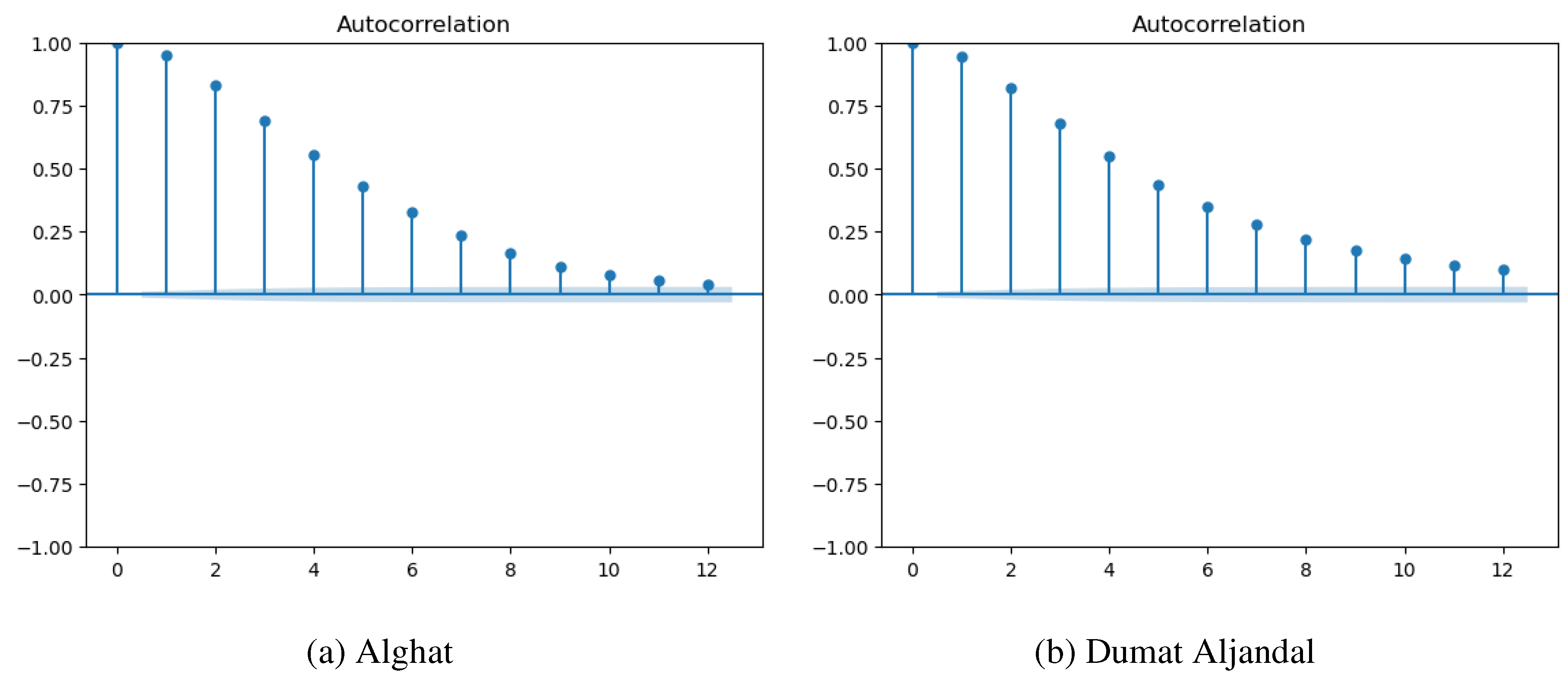
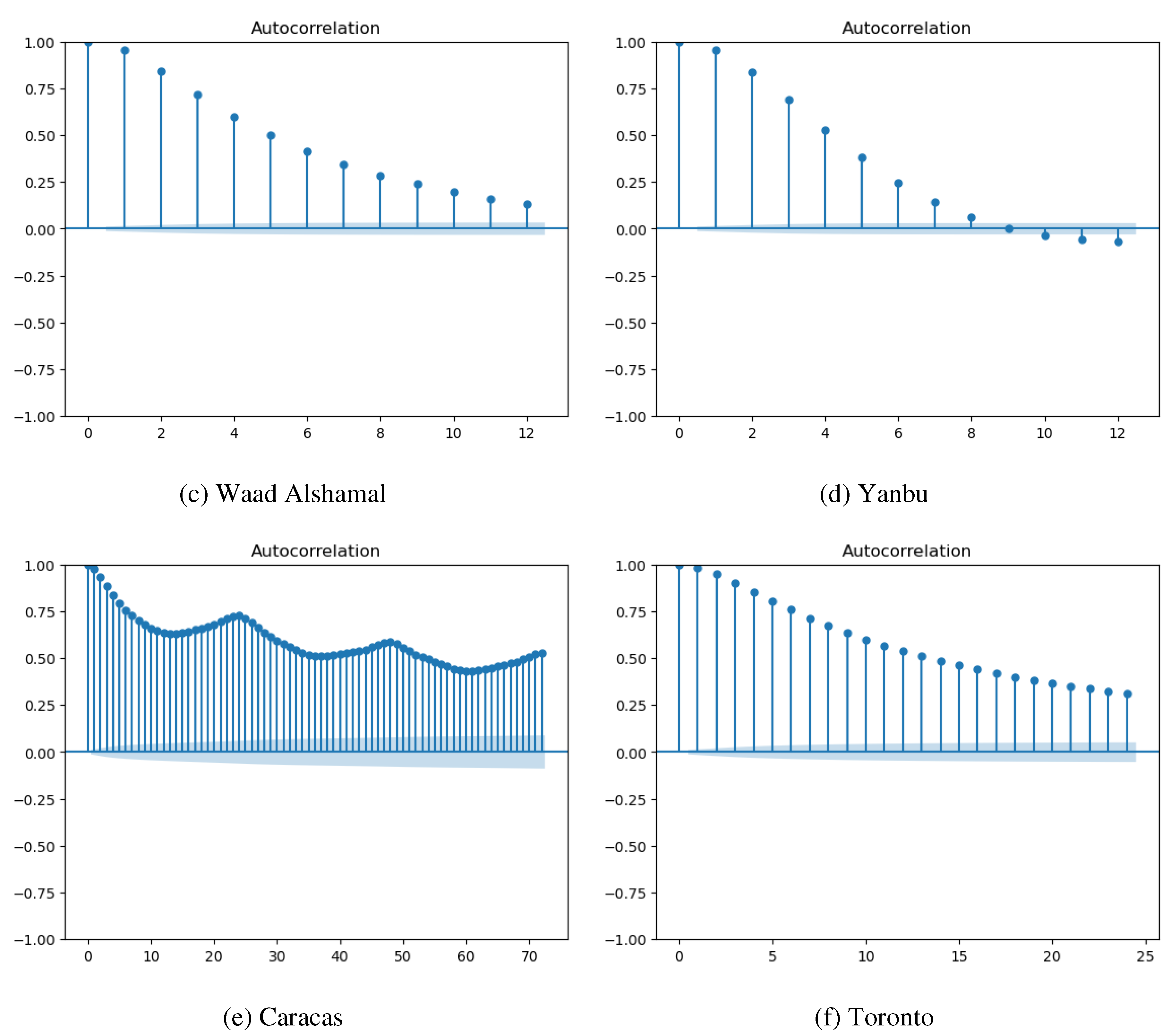
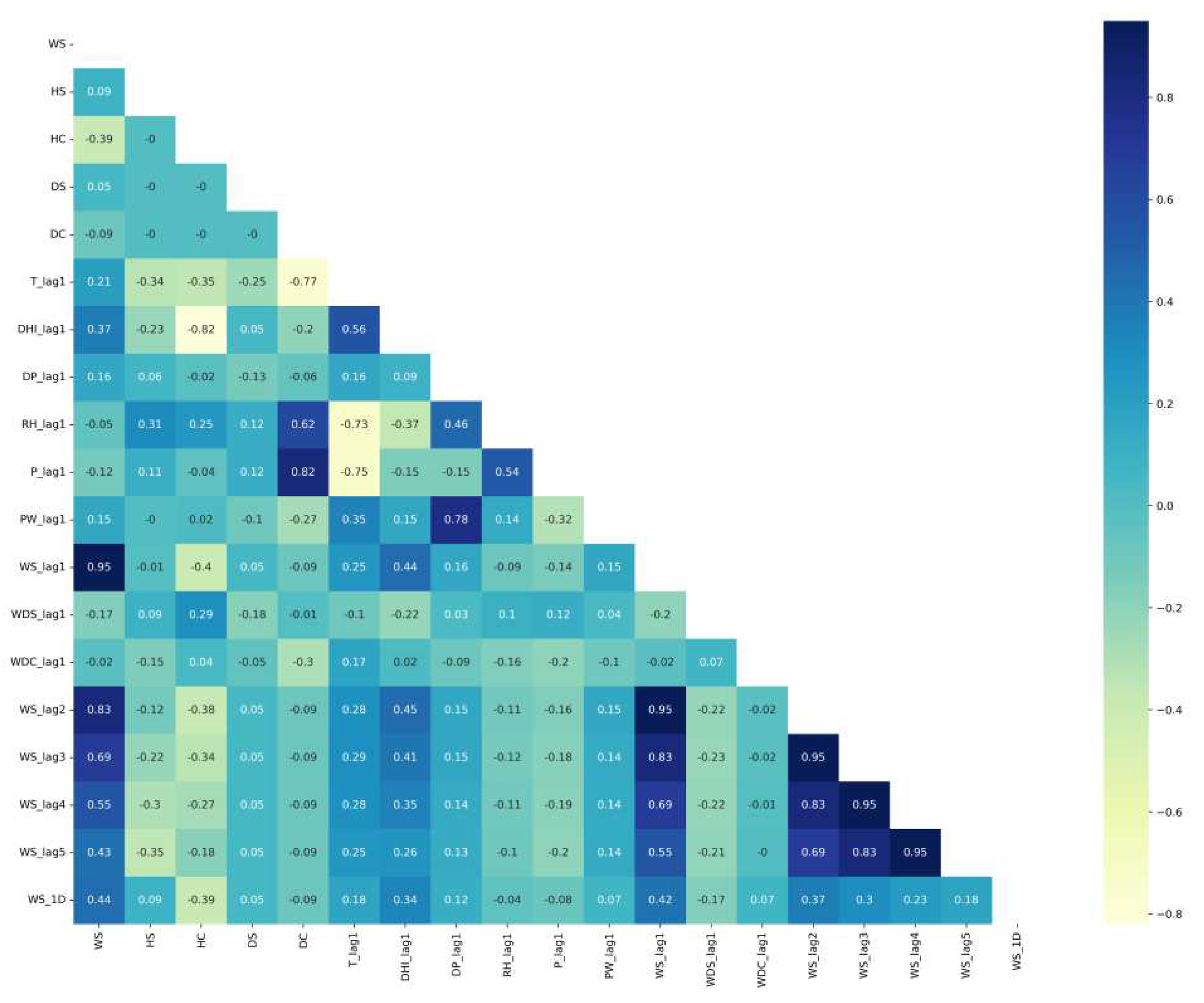
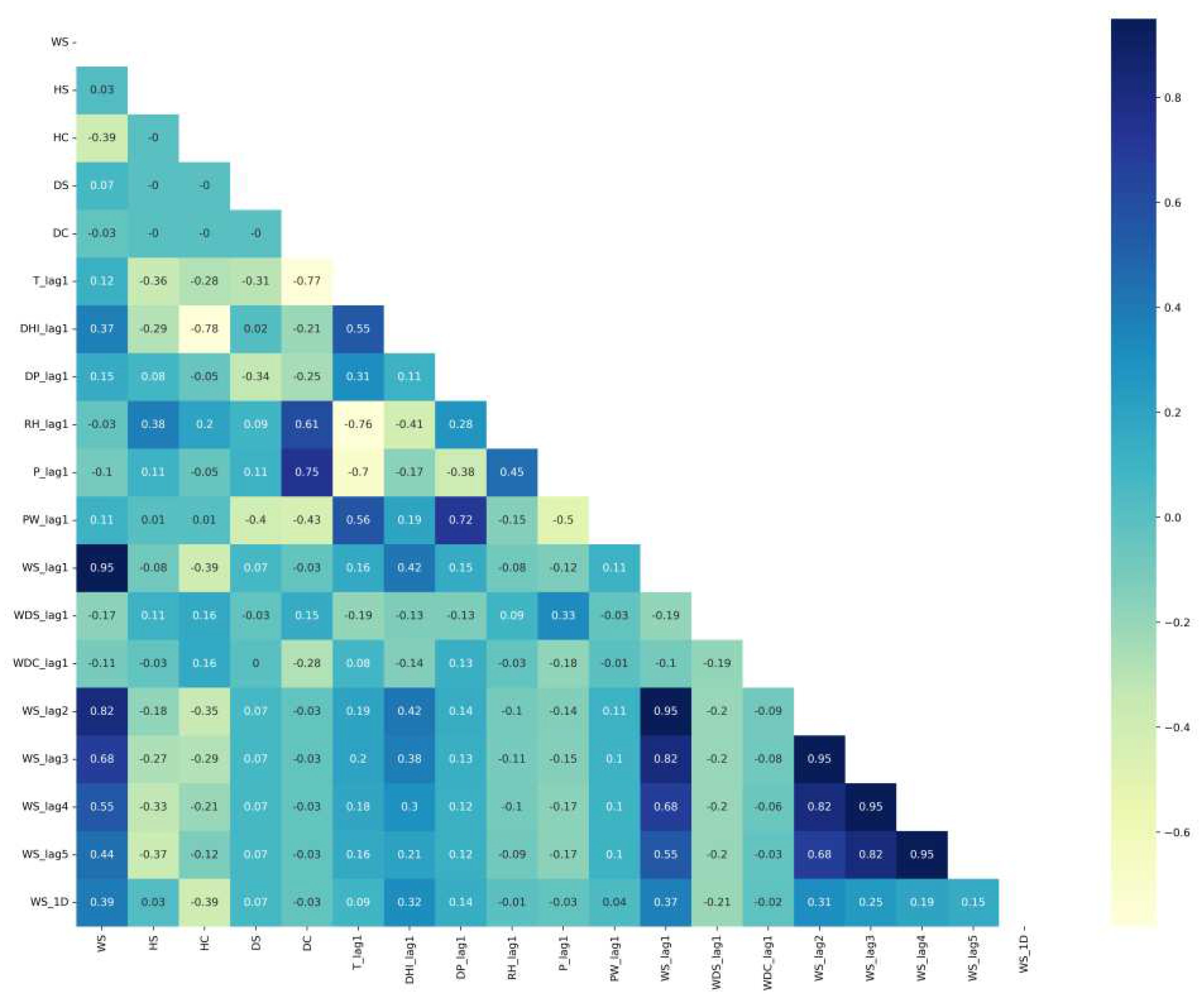
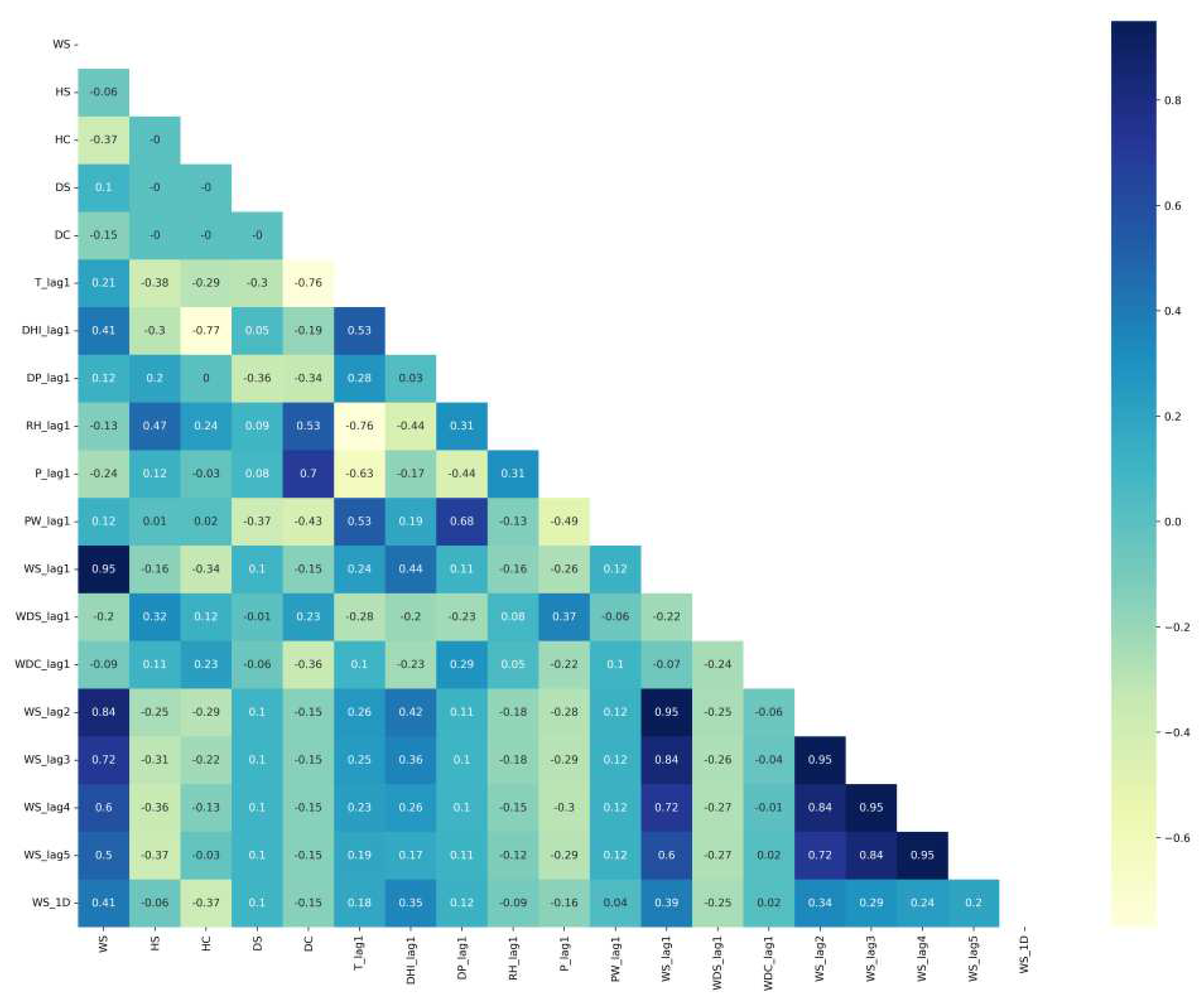
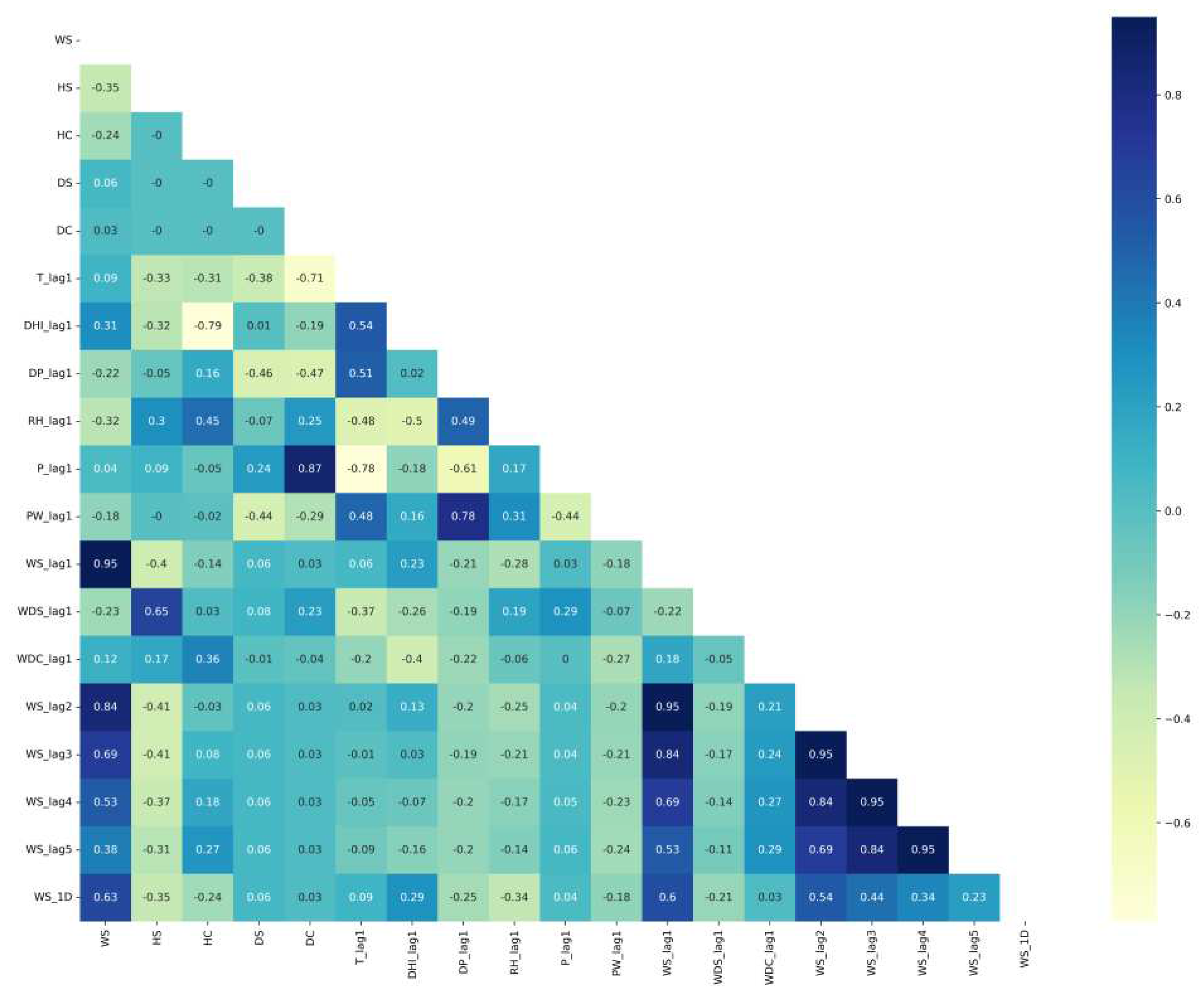


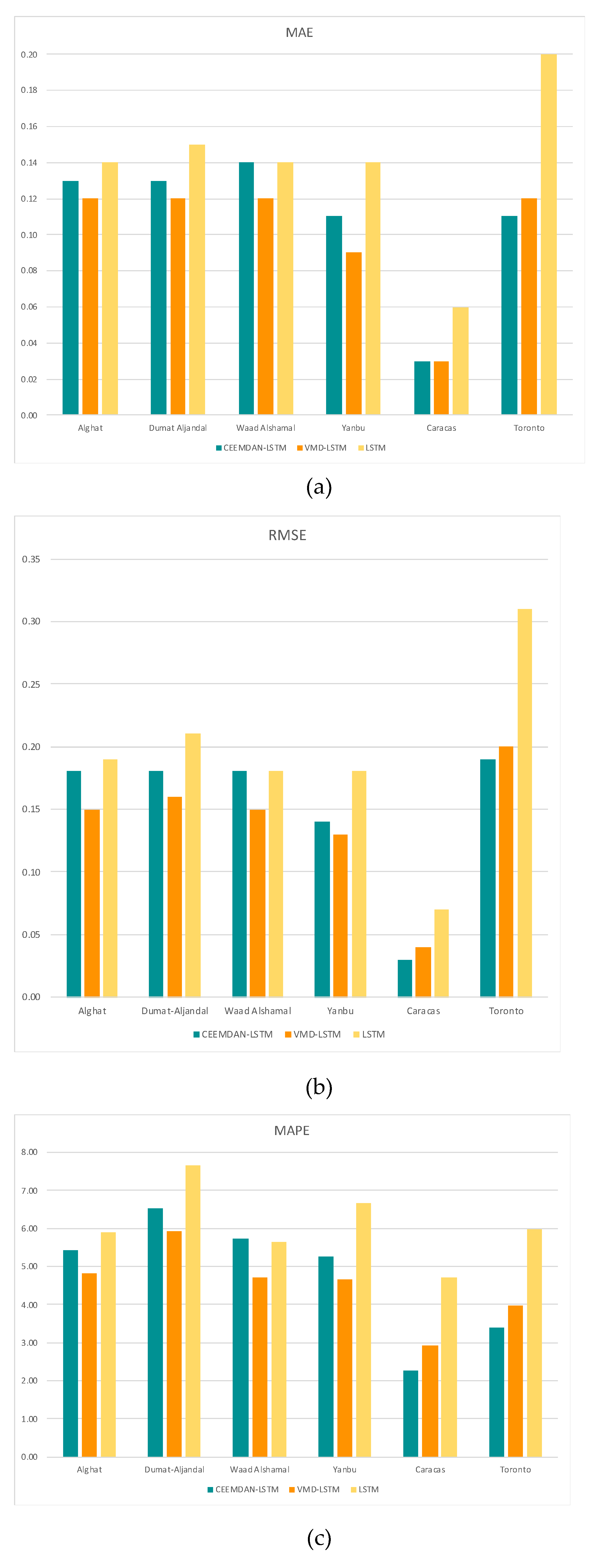
| Ref No. | Objective | Method | Features | Data source | Results |
|---|---|---|---|---|---|
| [15] | WS | CNN-BiLSTM | WS, Maximum WS, SD of WS | Ground-based | MAE=0.30, RMSE=0.43, MAPE=115 for a location in SA |
| [16] | WS | SVR | WS | Ground-based | MAE=2.37, MAPE= 206.80 for Yanbu, SA |
| [17] | WS | RR | WS, WD, PWS, T, P, RH | Mesoscale atmospheric model | MAE=1.22, RMSE=0.26, R2=0.9 for a city in SA |
| [18] | WS | LSTM | WS, T, P | Ground-based | MAE=0.28, R2=0.97 for Dhahran, SA |
| [19] | WS | ESN | WS | Simulated data by WRF | MSE= 0.24 for a location in SA |
| [20] | WS | BiLSTM | WS, GHI, DNI, DHI, T | Simulated data | MAE=0.4, RMSE=0.6, MAPE=15, R2=0.93 for Dumat Aljandal, SA |
| [21] | WS | GRU | WS, T | Simulated data | MAE=0.48, RMSE=0.66, MAPE=5, R2=0.93 for Dumat Aljandal, SA |
| [22] | WS | FFNN | T, WD, GHI, PWS, RH, P | Ground-based | RMSE =0.81, R=0.92, MAE=0.61 for Jeddah, SA RMSE =0.54, R=0.87 for Riyadh, SA RMSE =0.86, R=0.90, for Taif, SA RMSE =1.12, R=0.90, for Afif, SA |
| [23] | WS | FFNN | WS, T, RH | Ground-based | MAPE =6.65%, MSE = 0.09 for Qaisumah village, SA |
| [12] | WS | MLP, CNN, RNN | WS | Simulated data by WRF | R2 for CNN and RNN model is higher than MLP in USA |
| [14] | WS | CNN | T, RH, P, WS, season, month, day, hour | Simulated data by PSM | MAE=0.09, RMSE=0.23, sMAPE=4.92 for USA |
| [13] | WS | Hybrid model of WSTD+ GRU | WS | Ground-based | MAE=0.23, RMSE=0.38, MAPE=0.01 for Bondvill, USA MAE=0.17, RMSE=0.26, MAPE=0.07 for Penn State University, USA MAE=0.40, RMSE=0.53, MAPE=0.03 for Boulder, USA MAE=1.26, RMSE=1.86, MAPE=0.19 for Desert Rock, USA |
| [24] | WS | Hybrid model of CEEMDAN+ PE+ GRU+RBFNN +IBA | WS | Ground-based | MAE=0.45, RMSE=0.59, MAPE=4.79% for Zhangjiakou, China |
| [25] | WS | Hybrid model of EMD+VMD+ XGB+ CGRU+ GA | WS | Ground-based | RMSE=0.57, MAE=0.41, MAPE=8.36% for Shandong Province of China |
| [26] | WS | Hybrid model of VMD+LN+ MOBBSA+ LSTM-AE | WS | Ground-based | MAE= 0.08, RMSE=0.11, MAPE=2.95% for Rocky Mountains, USA |
| [27] | WP | Hybrid model of VMD+ residual-based CNN | WP, WS, WD | Ground-based | R= 0.97, RMSE=0.05, MAE=0.04 for a location in Turkey |
| [28] | WP & WS | Hybrid model of VMD+ SIRAE | WP, WS | Ground-based | RMSE= 1.23% for Galicia, Spain MAE= 2.45%, RMSE=3.16% for Dodge City, USA |
| [29] | WS | Hybrid model of VMD+ ESN+DE | WS, WD, T, P, RH, | Ground-based | RMSE= 0.12, MAE= 0.10, MAPE= 2.6% for Galicia, Spain |
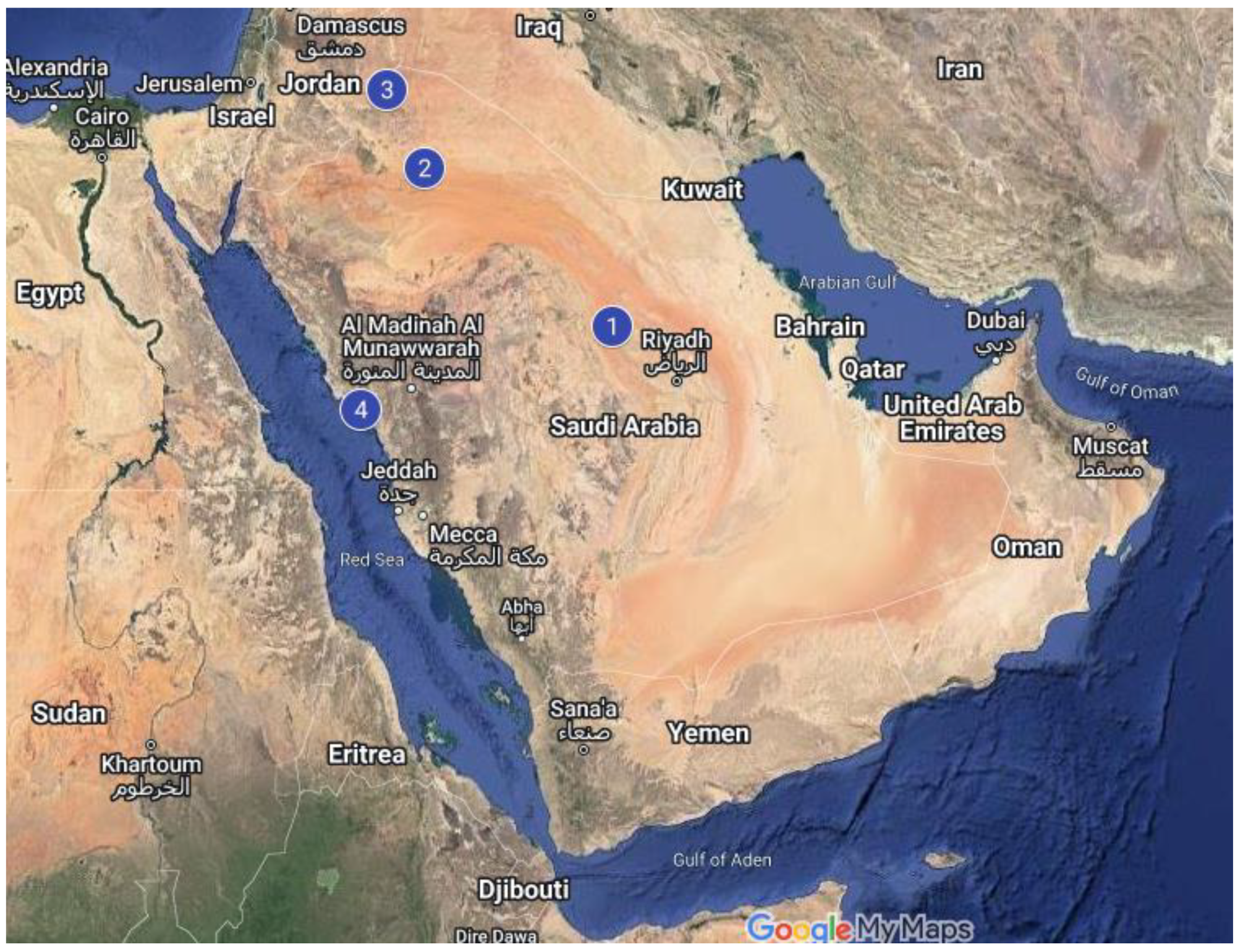
| Location No. | Location Name | Latitude (N) | Longitude (E) | Elevation (m) |
|---|---|---|---|---|
| 1 | Alghat | 26.32 | 43.45 | 674 |
| 2 | Dumat Aljandal | 29.52 | 39.58 | 618 |
| 3 | Waad Alshamal | 31.37 | 38.46 | 747 |
| 4 | Yanbu | 23.59 | 38.13 | 10 |
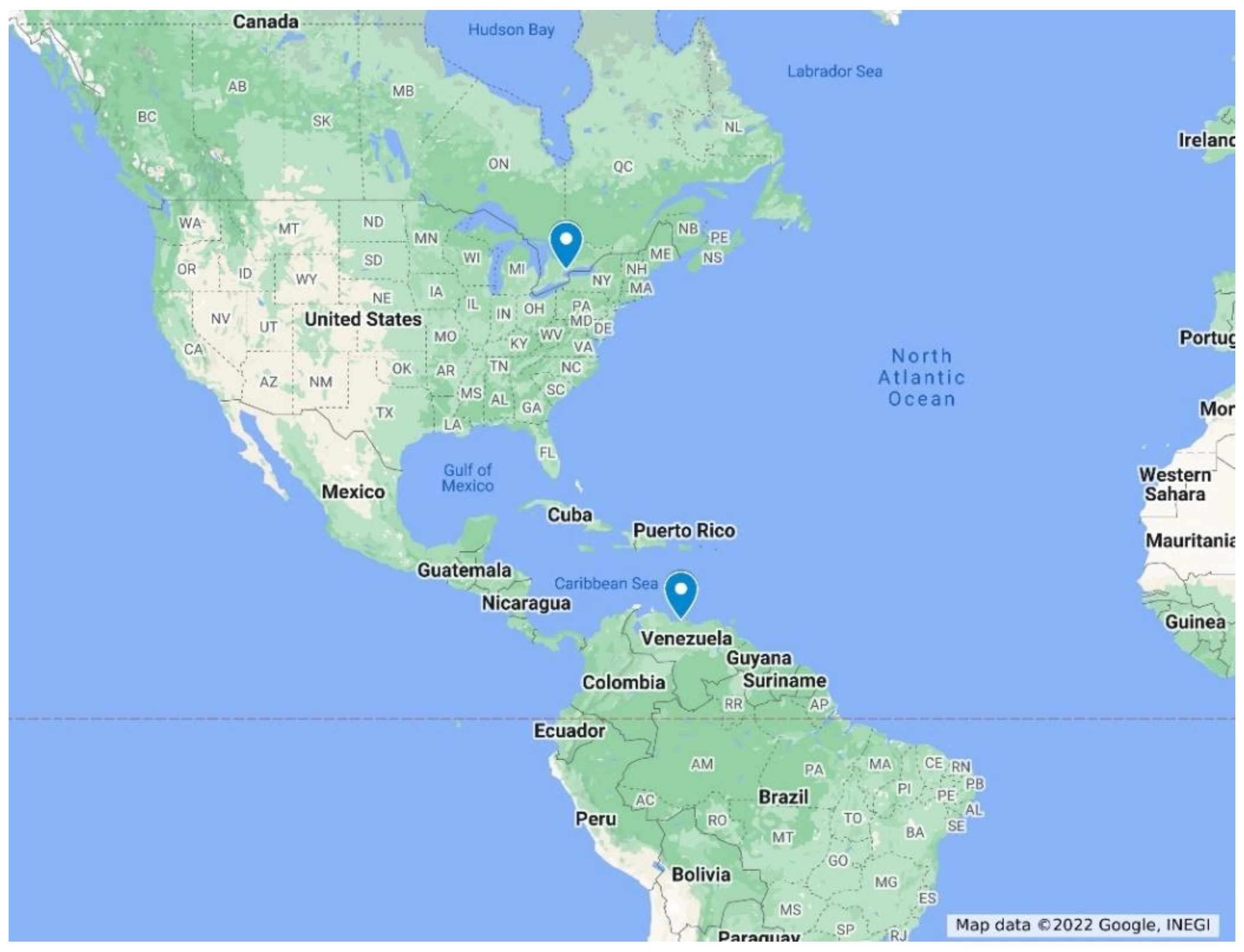
| Location Name | Latitude (N) | Longitude (E) | Elevation (m) |
|---|---|---|---|
| Caracas, Venezuela | 10.49 | -66.9 | 942 |
| Toronto, Canada | 43.65 | -79.38 | 93 |
| Time t features | Time t1 features | WS lagged features |
|---|---|---|
| WS (output) | T_lag1 | WS_lag1 |
| DHI_lag1 | WS_lag2 | |
| HS | DP_lag1 | WS_lag3 |
| HC | RH_ lag1 | WS_lag4 |
| DS | P_lag1 | WS_lag5 |
| DC | PW_lag1 | WS_1D |
| WDS_lag1 | ||
| WDC_lag1 |
| Common features | Caracas only | Toronto only | ||
|---|---|---|---|---|
| WS (output) | T_lag1 | WS_lag1 | WS_1D | WS_lag8 |
| DP_lag1 | WS_lag2 | DNI_lag1 | WS_lag9 | |
| HS | RH_ lag1 | WS_lag3 | WS_lag10 | |
| HC | P_lag1 | WS_lag4 | WS_lag11 | |
| DS | PW_lag1 | WS_lag5 | WS_lag12 | |
| DC | WDS_lag1 | WS_lag6 | GHI_lag1 | |
| WDC_lag1 | WS_lag7 | |||
| Dataset | WS mean | WS SD | WS VAR | WS MIN | WS MAX | |
|---|---|---|---|---|---|---|
| Alghat | Train: | 3.03 | 1.53 | 2.33 | 0.1 | 10 |
| Val: | 3.13 | 1.58 | 2.50 | 0.2 | 8.6 | |
| Test: | 3.01 | 1.43 | 2.04 | 0.2 | 9.2 | |
| All: | 3.04 | 1.52 | 2.31 | 0.1 | 10 | |
| Dumat Aljandal | Train: | 2.65 | 1.40 | 1.97 | 0.1 | 9.8 |
| Val: | 2.79 | 1.55 | 2.39 | 0.1 | 10.3 | |
| Test: | 2.62 | 1.37 | 1.87 | 0.1 | 7.3 | |
| All: | 2.66 | 1.42 | 2.02 | 0.1 | 10.3 | |
| Waad Alshamal | Train: | 3.08 | 1.56 | 2.44 | 0.2 | 10.6 |
| Val: | 3.40 | 1.69 | 2.86 | 0.4 | 11.1 | |
| Test: | 2.97 | 1.39 | 1.93 | 0.2 | 9.3 | |
| All: | 3.12 | 1.56 | 2.44 | 0.2 | 11.1 | |
| Yanbu | Train: | 3.17 | 1.61 | 2.58 | 0.1 | 11.2 |
| Val: | 3.31 | 1.70 | 2.89 | 0.1 | 9.9 | |
| Test: | 3.06 | 1.58 | 2.50 | 0.2 | 9.6 | |
| All: | 3.17 | 1.62 | 2.62 | 0.1 | 11.2 | |
| Caracas | Train: | 1.63 | 0.42 | 0.17 | 0.1 | 2.9 |
| Val: | 1.76 | 0.34 | 0.12 | 0.8 | 2.7 | |
| Test: | 1.39 | 0.39 | 0.15 | 0.1 | 2.6 | |
| All: | 1.62 | 0.42 | 0.17 | 0.1 | 2.9 | |
| Toronto | Train: | 4.38 | 2.37 | 5.60 | 0.1 | 14.7 |
| Val: | 3.85 | 2.49 | 6.17 | 0.3 | 15.6 | |
| Test: | 4.28 | 2.07 | 4.29 | 0.3 | 14.1 | |
| All: | 4.28 | 2.35 | 5.52 | 0.1 | 15.6 | |
| Hyperparameter | Value | Optimization |
|---|---|---|
| Learning Rate | 0.001 | Adam Optimizer |
| Number of Epochs | 100 | Activation Function= ReLU, Tanh* |
| Dropout | 0.1 | Loss Function= MSE |
| Batch Size | 500 | Early Stopping |
| Weight Decay | 0.000001 | Kernel Initializer= glorot uniform |
| Time t features | Time t-1 features | WS features |
|---|---|---|
| WS (output) | T_lag1 | WS_lag1 |
| DHI_lag1 | WS_lag2 | |
| HS | DP_lag1 | WS_lag3 |
| HC | RH_ lag1 | WS_lag4 |
| DS | P_lag1 | WS_lag5 |
| DC | PW_lag1 | WS_1D |
| WDS_lag1 | ||
| WDC_lag1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





