Uncertainty Quantification Based on Residual Tsallis Entropy of Order Statistics

1. Introduction

Information theory plays a crucial role in quantifying the uncertainty inherent in random phenomena. Its applications span a variety of areas, as detailed in Shannon’s influential work [1]. Considering a non-negative random variable X with an absolutely continuous cumulative distribution function (cdf) $F\left(x\right)$ and a probability density function (pdf) $f\left(x\right)$, the Tsallis entropy of order $\alpha$ becomes a relevant measure as defined in [2], given by

$$\begin{array}{ccc}\hfill H_{\alpha }\left(X\right)& =& \frac{1}{1-\alpha }\left[{\int }_0^{\infty }{f}^{\alpha }\left(x\right)dx-1\right],\hfill \\ & =& \frac{1}{1-\alpha }[E\left(f^{\alpha -1}\left(F^{-1}\left(U\right)\right)\right)-1],\hfill \end{array}$$

(1)

for all $\alpha >0,\alpha \ne 1,$ where $E(·)$ denotes the expectation and $F^{-1}\left(u\right)=inf\{x;F\left(x\right)\ge u\},$ for $u\in [0,1],$ denotes the quantile function. In general, the Tsallis entropy can take negative values, but it can be made non-negative by choosing appropriate values of $\alpha$. An important observation is that $H\left(X\right)={lim}_{\alpha \to 1}{H}_{\alpha }\left(X\right)$, which illustrates the convergence of Tsallis entropy to Shannon differential entropy. Unlike the Shannon entropy, which exhibits additivity, the Tsallis entropy exhibits non-additivity. In particular, for two independent random variables X and Y in the Shannon framework $H(X,Y)=H\left(X\right)+H\left(Y\right)$ holds, while in the Tsallis framework we find $H_{\alpha }(X,Y)=H_{\alpha }\left(X\right)+H_{\alpha }\left(Y\right)+(1-\alpha )H_{\alpha }\left(X\right)H_{\alpha }\left(Y\right)$. The non-additive nature of the Tsallis entropy provides greater flexibility compared to the Shannon entropy, making it applicable in various areas of information theory, physics, chemistry, and technology.

Considering the lifetime of a newly introduced system denoted by X, the tsallis entropy $H_{\alpha }\left(X\right)$ serves as a measure of the inherent uncertainty of the system. However, there are cases where the actors have knowledge about the current age of the system. For example, they know that the system is operational at time t and want to evaluate the uncertainty in the remaining lifetime given by $X_t=X-t\mid X>t$. In such scenarios, the conventional Tsallis entropy $H_{\alpha }\left(X\right)$ no longer provides the desired insight. Therefore, a new measure, the residual Tsallis entropy (RTE), is introduced, defined as follows:

$$\begin{array}{ccc}\hfill H_{\alpha }(X;t)& =& \frac{1}{1-\alpha }\left[{\int }_0^{\infty }{f}_t^{\alpha }\left(x\right)dx-1\right]\hfill \\ & =& \frac{1}{1-\alpha }\left[{\int }_t^{\infty }{\left(\frac{f\left(x\right)}{S\left(t\right)}\right)}^{\alpha }dx-1\right],\hfill \end{array}$$

(2)

where

$$f_t\left(x\right)=\frac{f(x+t)}{S\left(t\right)},x,t>0,$$

is the pdf of $X_t$ and $S\left(t\right)=P(X>t)$ is the survival function of X.

Extensive research has been done in the literature to explore various properties and statistical applications of Tsallis entropy. For detailed insights, we recommend the work of Asadi et al. [3], Nanda and Paul [4], Zhang [5], Maasoumi [6], Abe [7], Asadi et al. [8], and the references cited in these works. These sources provide comprehensive discussions on this topic and allow for a deeper understanding of Tsallis entropy in various contexts.

The aim of this paper is to study the properties of RTE in terms of order statistics. We consider a random sample of size n from a distribution F denoted by $X_1,X_2,\dots ,X_n$. The order statistic represents the ordering of these sample values from smallest to largest, denoted $X_{1:n}\le X_{2:n}\le \dots \le X_{n:n}$. Order statistics are very important in many areas of probability and statistics because they can be used to describe probability distributions, to test how well a data set fits a particular model, to control the quality of a product or process, to analyze the reliability of a system or component, and for many other applications.

Moreover, they are indispensable in reliability theory, especially for studying the lifetime properties of coherent systems and performing lifetime tests on data obtained by various censoring methods. For a thorough understanding of the theory and applications of order statistics, we recommend the comprehensive review by David and Nagaraja [9]. This source covers the topic in depth and provides useful insights into the theoretical and practical aspects of order statistics. Many researchers have studied the information properties of order statistics and have gained useful insights, which can be found in [10,11,12] and the references therein. Zarezadeh and Asadi [13] studied properties of residual Renyi entropy of order statistics and record values; see also [14]. Continuing this line of research, our study aims to contribute to the field by investigating the properties of residual Tsallis entropy in terms of order statistics. More recently, Alomani and Kayid [15] have studied the properties of the Tsallis entropy of a coherent and mixed system.

The results of this work is structured as follows: In Section 2, we present the representation of RTE for order statistics denoted as $X_{i:n},$ from a sample drawn from an arbitrary continuous distribution function $F.$ We express these RTE in terms of RTE for order statistics from a sample drawn from a uniform distribution. Since closed-form expressions for the RTE of order statistics are often not available for many statistical models, we derive upper and lower bounds to approximate the RTE. We provide several illustrative examples to demonstrate the practicality and usefulness of these bounds. In addition, we study the monotonicity properties of RTE for the extremum of a sample under mild conditions. We find that the RTEs of the extremum of a random sample exhibit monotonic behavior as the number of observations in the sample increases. However, we counter this observation by presenting a counterexample that demonstrates the non-monotonic behavior of RTE for other order statistics $X_{i:n}$ with respect to sample size. To further analyze the monotonic behavior, we examine the RTE of order statistics $X_{i:n}$ with respect to the index of order statistics $i.$ Our results show that the RTE of $X_{i:n}$ is not a monotonic function of i over the entire support of $F.$

Throughout the paper, “${\le }_{st}$" and “${\le }_{lr}$" stand for usual stochastic and likelihood ratio orders, respectively, for more details on these orderings, we refer the reader to Shaked and Shanthikumar [16].

2. Residual Tsallis Entropy of Order Statistics

Hereafter, we present an expression for the RTE of order statistics in relation to the RTE of order statistics from a uniform distribution. Let us consider the pdf and the survival function of $X_{i:n}$ denoted by $f_{i:n}\left(x\right)$ and $S_{i:n}\left(x\right)$, respectively, where $i=1,\dots ,n$. It holds that

$$f_{i:n}\left(x\right)=\frac{1}{B(i,n-i+1)}{\left(F\left(x\right)\right)}^{i-1}{\left(S\left(x\right)\right)}^{n-i}f\left(x\right),x>0,$$

(3)

$$S_{i:n}\left(x\right)=\sum _{k=0}^{i-1}\left(\genfrac{}{}{0pt}{}{n}{k}\right){\left(1-S\left(x\right)\right)}^k{\left(S\left(x\right)\right)}^{n-k},x>0,$$

(4)

where

$$B(a,b)={\int }_0^1{x}^{a-1}{(1-x)}^{b-1}dx,a>0,b>0,$$

is known as the complete beta function; see e.g., David and Nagaraja [9]. Furthermore, we can express the survival function $S_{i:n}\left(x\right)$ as follows:

$$S_{i:n}\left(x\right)=\frac{{\overline{B}}_{F\left(x\right)}(i,n-i+1)}{B(i,n-i+1)},$$

(5)

where

$${\overline{B}}_x(a,b)={\int }_x^1{u}^{a-1}{(1-u)}^{b-1}du,0<x<1,$$

is known as the incomplete beta functions. In this section, we adopt the notation $Y\sim {\overline{B}}_t(a,b)$ to denote that the random variable Y follows a truncated beta distribution with pdf given by:

$$f_Y\left(y\right)=\frac{1}{{\overline{B}}_t(a,b)}{y}^{a-1}{(1-y)}^{b-1},t\le y\le 1.$$

(6)

The paper is concerned with the study of the residual tsallis entropy of the random variable $X_{i:n}$, which measures the degree of uncertainty about the predictability of the residual lifetime of the system contained in the density of $[X_{i:n}-t|X_{i:n}>t]$. In reliability engineering, $(n-i+1)$-out-of-n systems are an important type of structure. In this case, an $(n-i+1)$-out-of-n system functions if and only if at least $(n-i+1)$ components of n components function. We consider a system consisting of independent and identically distributed components whose lifetimes are represented by $X_1,X_2,\cdots ,X_n$. The lifetime of the whole system is determined by the order statistic $X_{i:n}$, where i denotes the position of the order statistic. When $i=1$, this corresponds to a serial system, while $i=n$ represents a parallel system. In the context of $(n-i+1)$-out-of-n systems operating at time t, the RTE of $X_{i:n}$ serves as a measure of entropy associated with the remaining lifetime of the system. This dynamic entropy measure provides system designers with valuable information about the entropy of $(n-i+1)$-out-of-n systems in operation at a given time t.

To increase computational efficiency, we introduce a lemma that establishes a relationship between the RTE of order statistics from a uniform distribution and the incomplete beta function. This relation is crucial from a practical point of view and allows for a more convenient computation of RTE. The proof of this lemma, which follows directly from the definition of RTE, is omitted here because it involves simple computations.

Lemma 1. 

Suppose we have a random sample of size n from a uniform distribution on (0,1) and we arrange the sample values in ascending order where $U_{i:n}$ the i-th order statistic. Then

$$H_{\alpha }(U_{i:n};t)=\frac{1}{1-\alpha }\left[\frac{{\overline{B}}_t(\alpha (i-1)+1,\alpha (n-i)+1)}{{\overline{B}}_t^{\alpha }(i,n-i+1)}-1\right],0<t<1,$$

for all $\alpha >0,\alpha \ne 1.$

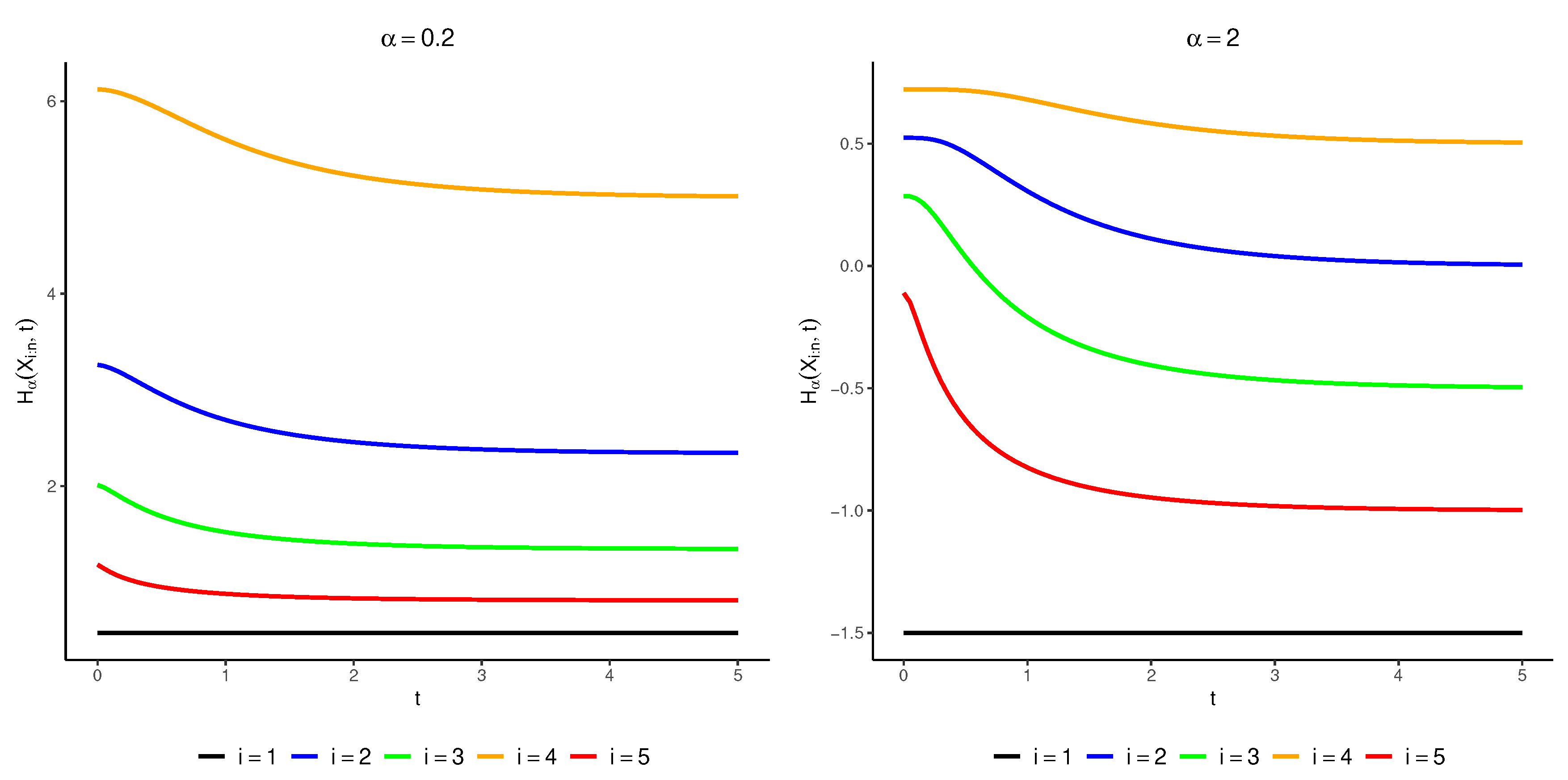
Using this lemma, researchers and practitioners can easily compute the RTE of order statistics from a uniform distribution using the well-known incomplete beta function. This computational simplification improves the applicability and usability of RTE in various contexts. In Figure 1, we show the plot of $H_{\alpha }(U_{i:n};t)$ for different values of $\alpha$ and $i=1,2,\cdots ,5$ when the total number of observations is $n=5$. The figure shows that there is no inherent monotonicity between the order statistics. However, in the following analysis (Lemma 3), we establish conditions under which a monotonic relationship can be established between the index i and the number of components in the system. This lemma will provide valuable insight into the arrangement of the system components and the resulting effect on the reliability of the system.

The upcoming theorem establishes a relationship between the RTE of order statistics $X_{i:n}$ and the RTE of order statistics from a uniform distribution.

Theorem 1. 

The residual Tsallis entropy of $X_{i:n},$ for all $\alpha >0,\alpha \ne 1,$ can be expressed as follows:

$$H_{\alpha }(X_{i:n};t)=\frac{1}{1-\alpha }\left[((1-\alpha )H_{\alpha }(U_{i:n};F\left(t\right))+1)\mathbb{E}\left[f^{\alpha -1}\left(F^{-1}\left(Y_i\right)\right)\right]-1\right],t>0,$$

(7)

where $Y_i\sim {\overline{B}}_{F\left(t\right)}(\alpha (i-1)+1,\alpha (n-i)+1).$

Proof. 

By using the change of $u=F\left(x\right),$ from (2),(3) and (5), we get

$$\begin{array}{ccc}\hfill H_{\alpha }(X_{i:n};t)& =& \frac{1}{1-\alpha }\left[{\int }_t^{\infty }{\left(\frac{f_{i:n}\left(x\right)}{S_{i:n}\left(t\right)}\right)}^{\alpha }dx-1\right]\hfill \\ & =& \frac{1}{1-\alpha }\left[{\int }_t^{\infty }{\left(\frac{F^{i-1}\left(x\right)S^{n-i}\left(x\right)f\left(x\right)}{{\overline{B}}_{F\left(t\right)}(i,n-i+1)}\right)}^{\alpha }dx-1\right]\hfill \\ & =& \frac{1}{1-\alpha }\left[\frac{{\overline{B}}_{F\left(t\right)}(\alpha (i-1)+1,\alpha (n-i)+1)}{{\overline{B}}_{F\left(t\right)}^{\alpha }(i,n-i+1)}{\int }_t^{\infty }\frac{F^{\alpha (i-1)}\left(x\right)S^{\alpha (n-i)}\left(x\right)f^{\alpha }\left(x\right)}{{\overline{B}}_{F\left(t\right)}(\alpha (i-1)+1,\alpha (n-i)+1)}dx-1\right]\hfill \\ & =& \frac{1}{1-\alpha }\left[\frac{{\overline{B}}_{F\left(t\right)}(\alpha (i-1)+1,\alpha (n-i)+1)}{{\overline{B}}_{F\left(t\right)}^{\alpha }(i,n-i+1)}{\int }_{F\left(t\right)}^1\frac{u^{\alpha (i-1)}{(1-u)}^{\alpha (n-i)}{f}^{\alpha -1}\left(F^{-1}\left(u\right)\right)}{{\overline{B}}_{F\left(t\right)}(\alpha (i-1)+1,\alpha (n-i)+1)}du-1\right]\hfill \\ & =& \frac{1}{1-\alpha }\left[((1-\alpha )H_{\alpha }(U_{i:n};F\left(t\right))+1)\mathbb{E}\left[f^{\alpha -1}\left(F^{-1}\left(Y_i\right)\right)\right]-1\right],t>0.\hfill \end{array}$$

(8)

The last equality is obtained from Lemma 1 and this completes the proof. □

After some calculation, it can be seen that when in (7) the order $\alpha$ goes to unity, the Shannon entropy of i-th order statistic from a sample of F can be written as follows:

$$H(X_{i:n};t)=H(U_{i:n};F\left(t\right))-\mathbb{E}\left[f\left(F^{-1}\left(Y_i\right)\right)\right],$$

where $Y_i\sim {\overline{B}}_{F\left(t\right)}(i,n-i+1).$ The specialized version of this result for $t=0,$ was already obtained by Ebrahimi et al. [12]. Below, we provide an example for illustration.

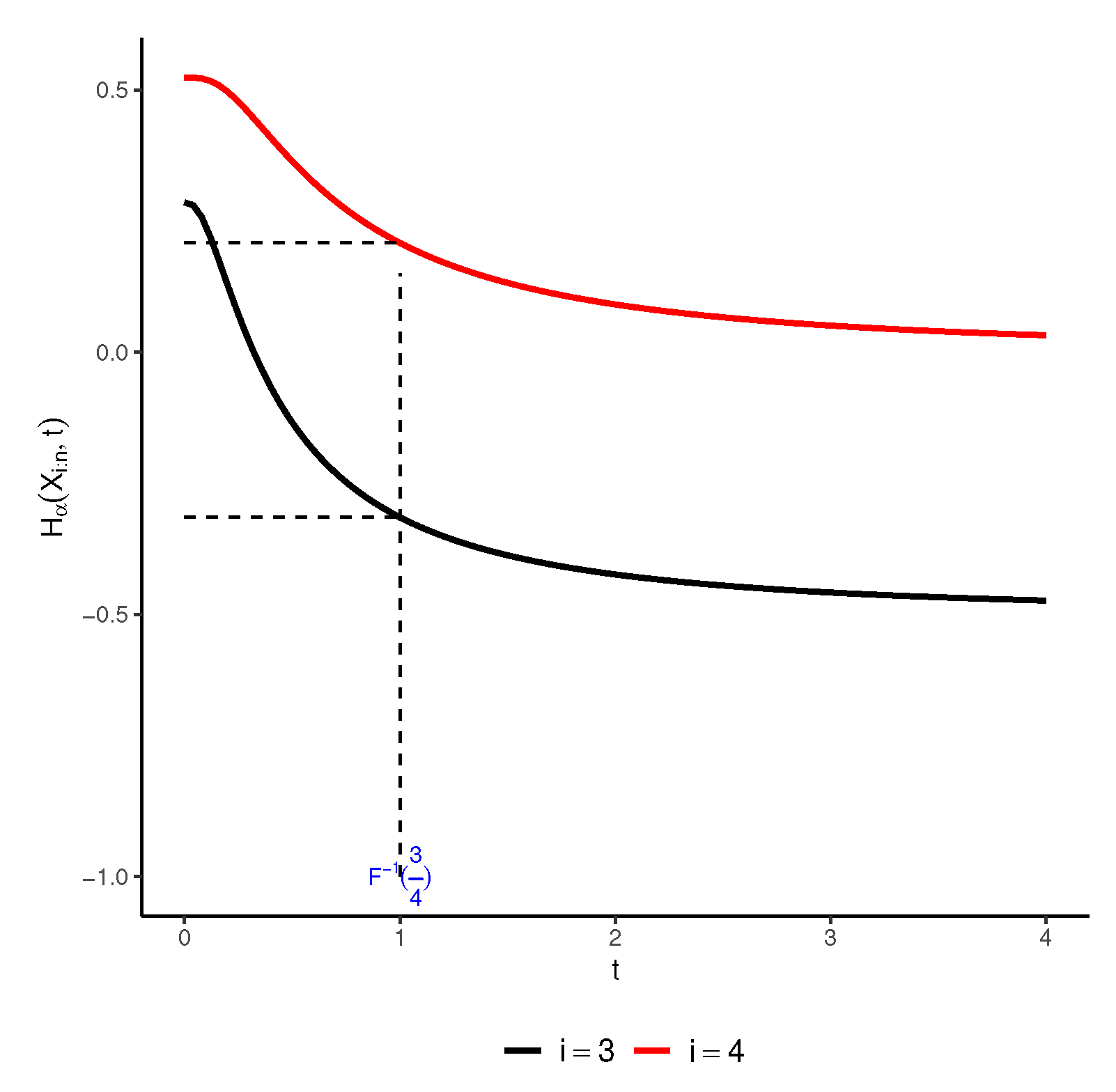
Example 1. 

Suppose that X is a standard exponential distribution with mean unity. Then $f\left(F^{-1}\left(u\right)\right)=1-u,0<u<1,$ and we have

$$\mathbb{E}\left[f^{\alpha -1}\left(F^{-1}\left(Y_i\right)\right)\right]=\frac{{\overline{B}}_{1-e^{-t}}(\alpha (i-1)+1,\alpha (n-i+1))}{{\overline{B}}_{1-e^{-t}}(\alpha (i-1)+1,\alpha (n-i)+1)}.$$

(9)

Thus, from (7), we obtain

$$H_{\alpha }(X_{i:n};t)=\frac{1}{1-\alpha }\left[\frac{{\overline{B}}_{1-e^{-t}}(\alpha (i-1)+1,\alpha (n-i+1))}{{\overline{B}}_{1-e^{-t}}^{\alpha }(i,n-i+1)}-1\right],i=1,2,\cdots ,n.$$

(10)

In Figure 2, we plotted $H_{\alpha }(X_{i:n};t)$ for some values of $\alpha$ and $i=1,2,\cdots ,5$ when $n=5.$ When $i=1$, we can use (10) to get

$$H_{\alpha }(X_{1:n};t)=\frac{n^{\alpha -1}-\alpha }{(1-\alpha )\alpha },t>0.$$

Also, we know that

$$H_{\alpha }(X;t)=\frac{1-\alpha }{(1-\alpha )\alpha },t>0.$$

Therefore, we have

$$H_{\alpha }(X_{1:n};t)-H_{\alpha }(X;t)=\frac{n^{\alpha -1}-1}{\alpha (1-\alpha )},t>0.$$

This finding reveals an intriguing characteristic: the discrepancy between the RTE of the lifetime of a series system and the RTE of each component is not influenced by time. Instead, it solely relies on two factors: the number of components within the system and the parameter $\alpha$ in the exponential case.

While we have successfully obtained a closed expression for the first order statistics of RTE in the exponential distribution, the task becomes significantly more difficult when we consider the higher order statistics in some other distributions. Unfortunately, closed-form expressions for the RTE of higher-order statistics in these distributions, as well as in many other distributions, are generally not available. Given this limitation, we are motivated to explore alternative approaches to characterizing the RTE of order statistics. We therefore propose to establish thresholds for the RTE of order statistics. To this end, we present the following theorem as a conclusive proof that provides valuable insight into the nature of these bounds and their applicability in practical scenarios.

Theorem 2. 

Consider a non-negative continuous random variable X with pdf f and cdf $F.$ Let us denote the RTEs of X and the i-th order statistic $X_{i:n}$ as $H_{\alpha }(X;t)$ and $H_{\alpha }(X_{i:n};t),$ respectively.

(a)

Let $M_i=f_{Y_i}\left(m_i\right)$ where $m_i=max\{F\left(t\right),\frac{i-1}{n-1}\}$ is the mode of the distribution of $Y_i$, then for $\alpha >1(0<\alpha <1),$ we have

$$H_{\alpha }(X_{i:n};t)\ge (\le )\frac{1}{1-\alpha }\left[((1-\alpha )H_{\alpha }(U_{i:n};F\left(t\right))+1)((1-\alpha )H_{\alpha }(X;t)+1)M_i{S}^{\alpha }\left(t\right)-1\right].$$

(b)

Suppose we have $M=f\left(m\right)<\infty ,$ where m is the mode of the pdf f, such that $f\left(x\right)\le M$. Then, for any $\alpha >0,$ we obtain

$$H_{\alpha }(X_{i:n};t)\ge \frac{1}{1-\alpha }\left[((1-\alpha )H_{\alpha }(U_{i:n};F\left(t\right))+1)M^{\alpha -1}-1\right].$$

Proof. 

(a) By applying Theorem 2.3, we only need to find a bound for $\mathbb{E}\left[f^{\alpha -1}\left(F^{-1}\left(Y_i\right)\right)\right].$ To this aim, for $\alpha >1(0<\alpha <1)$ we have

$$\begin{array}{ccc}\hfill \mathbb{E}\left[f^{\alpha -1}\left(F^{-1}\left(Y_i\right)\right)\right]& =& {\int }_{F\left(t\right)}^1\frac{u^{\alpha (i-1)}{(1-u)}^{\alpha (n-i)}}{{\overline{B}}_{F\left(t\right)}(\alpha (i-1)+1,\alpha (n-i)+1)}{f}^{\alpha -1}\left(F^{-1}\left(u\right)\right)du\hfill \\ & \ge (\le )& M_i{\int }_{F\left(t\right)}^1{f}^{\alpha -1}\left(F^{-1}\left(u\right)\right)du\hfill \\ & =& M_i{\int }_t^{\infty }{f}^{\alpha }\left(x\right)dx\hfill \\ & =& M_i[(1-\alpha )H_{\alpha }(X;t)+1]S^{\alpha }\left(t\right).\hfill \end{array}$$

The result now is easily obtained by recalling (7).

(b) Since for $\alpha >1(0<\alpha <1),$ it holds that

$$f^{\alpha -1}\left(F^{-1}\left(u\right)\right)\le (\ge )M^{\alpha -1},$$

one can write

$$\mathbb{E}\left[f^{\alpha -1}\left(F^{-1}\left(Y_i\right)\right)\right]M^{\alpha -1}.$$

The result now is easily obtained from relation (7) and this completes the proof. □

The given theorem branches into two elements. The first subdivision, denoted (i), establishes a lower bound for the RTE associated with $X_{i:n}$, denoted $H_{\alpha }(X_{i:n};t)$. It should be noted that the given lower bound can be transformed into an upper bound under certain conditions. This bound is formed by using the incomplete beta function together with the RTE of the original distribution. Conversely, in part (ii) of the theorem, a lower bound is introduced for the RTE of $X_{i:n}$, denoted as $H_{\alpha }(X_{i:n};t)$. This lower bound is expressed via the RTE of order statistics from a uniform distribution and the mode, represented by m, of the underlying distribution. This finding provides interesting insights into the information properties of $X_{i:n}$ and provides a quantifiable measure of the lower bound of RTE with respect to the mode of the distribution.

In the following lemma we deal with the monotonic behavior of the RTE of order statistics. To lay the groundwork for our subsequent findings, we first introduce a central lemma that plays a fundamental role in our analysis.

Lemma 2. 

Consider two non-negative functions, $q\left(x\right)$ and $s_{\beta }\left(x\right)$, where $q\left(x\right)$ is an increasing function. Let t and c be real numbers such that $0\le t<c<\infty$. Additionally, assume that the random variable $Z_{\beta }$ follows a pdf $f_{\beta }\left(z\right)$, where $\beta >0,$ as

$$f_{\beta }\left(z\right)=\frac{q^{r\beta }\left(z\right)s_{\beta }\left(z\right)}{{\int }_t^c{q}^{r\beta }\left(x\right)s_{\beta }\left(x\right)dx},z\in (t,c).$$

(11)

Let r be real valued and define function $g_{\alpha }$ as follows:

$$K_{\alpha }\left(r\right)=\frac{1}{1-\alpha }\left[\frac{{\int }_t^c{q}^{r\alpha }\left(x\right)s_{\alpha }\left(x\right)dx}{{\left({\int }_t^c{q}^r\left(x\right)s_1\left(x\right)dx\right)}^{\alpha }}-1\right],\alpha >0,\alpha \ne 1.$$

(12)

(i)

If for $\alpha >1(0<\alpha <1),$$Z_{\alpha }{\le }_{st}\left({\ge }_{st}\right)Z_1,$ then $K_{\alpha }\left(r\right)$ is an increasing function of $r.$

(ii)

If for $\alpha >1(0<\alpha <1),$$Z_{\alpha }{\ge }_{st}\left({\le }_{st}\right)Z_1,$ then $K_{\alpha }\left(r\right)$ is a decreasing function of $r.$

Proof. 

We just prove Part (i) since the proof for Part (ii) is similar. Assuming that $K_{\alpha }\left(r\right)$ is differentiable in terms of r, we can obtain

$$\frac{\partial K_{\alpha }\left(r\right)}{\partial r}=\frac{1}{1-\alpha }\frac{\partial g_{\alpha }\left(r\right)}{\partial r},$$

where

$$g_{\alpha }\left(r\right)=\frac{{\int }_t^c{q}^{r\alpha }\left(x\right)s_{\alpha }\left(x\right)dx}{{\left({\int }_t^c{q}^r\left(x\right)s_1\left(x\right)dx\right)}^{\alpha }}.$$

It is evident that

$$\begin{array}{ccc}\hfill \frac{\partial g_{\alpha }\left(r\right)}{\partial r}& =& \frac{\alpha }{{\left({\int }_t^c{q}^r\left(x\right)s_1\left(x\right)dx\right)}^{\alpha +1}}\hfill \\ & \times & \left[{\int }_t^{c}logq\left(x\right)q^{r\alpha }\left(x\right)s_{\alpha }\left(x\right)dx{\int }_t^c{q}^r\left(x\right)s_1\left(x\right)dx-{\int }_t^{c}logq\left(x\right)q^r\left(x\right)s_1\left(x\right)dx{\int }_t^c{q}^{r\alpha }\left(x\right)s_{\alpha }\left(x\right)dx\right]\hfill \\ & =& \frac{\alpha {\int }_t^c{q}^r\left(x\right)s_1\left(x\right)dx{\int }_t^c{q}^{r\alpha }\left(x\right)s_{\alpha }\left(x\right)dx}{{\left({\int }_t^c{q}^r\left(x\right)s_1\left(x\right)dx\right)}^{\alpha +1}}\left[\mathbb{E}[logq\left(Z_{\alpha }\right)]-\mathbb{E}[logq\left(Z_1\right)]\right]\le (\ge )0.\hfill \end{array}$$

(13)

Using the fact that $Z_{\alpha }{\le }_{st}\left({\ge }_{st}\right)Z_1$ and that $log(·)$ is an increasing function, one can show that $\mathbb{E}[logq\left(Z_{\alpha }\right)]\le (\ge )\mathbb{E}[logq\left(Z_1\right)]$. This implies that (13) is non-positive (non-negative), and hence $K_{\alpha }\left(r\right)$ is an increasing function of r. □

Corollary 1. 

Under the assumptions of Lemma 2, it can be proven that when $q\left(x\right)$ is decreasing, the following holds:

(i)

For $\alpha >1(0<\alpha <1),$$Z_{\alpha }{\le }_{st}\left({\ge }_{st}\right)Z_1,$ then $K_{\alpha }\left(r\right)$ is a decreasing function of $r.$

(ii)

If for $\alpha >1(0<\alpha <1),$$Z_{\alpha }{\ge }_{st}\left({\le }_{st}\right)Z_1,$ then $K_{\alpha }\left(r\right)$ is a increasing function of $r.$

Due to Lemma 2, we can prove the following corollary for $(n-i+1)$-out-of-n systems with components having uniform distributions.

Lemma 3. 

(i)

When considering a parallel (series) system consisting of n components with a uniform distribution over the unit interval, the RTE of the system lifetime decreases as the number of components increases.

(ii)

If $i_1\le i_2\le n,$ are integers, then $H_{\alpha }(U_{i_1:n};t)\le H_{\alpha }(U_{i_2:n};t)$ for $t\ge \frac{i_2-1}{n-1}.$

Proof. 

(i) The presumption is that the system operates in parallel. Analogous reasoning can be applied to a series system to authenticate the outcome via Remark 2.9. From Lemma 1, we get

$$H_{\alpha }(U_{n:n};t)=\frac{1}{1-\alpha }\left[\frac{{\int }_t^1{x}^{\alpha (n-1)}dx}{{\int }_t^1{x}^{n-1}dx}-1\right],0<t<1.$$

So, Lemma 2 readily reveals that $H_{\alpha }(U_{i:n};t)$ can be depicted as (12) where $q\left(x\right)=x$ and $s_{\alpha }\left(x\right)=x^{\alpha }$. We adopt the assumption, devoid of any generality loss, that $n\ge 1$ is a continuous variable. Considering $\alpha >1(0<\alpha <1),$ the ratio

$$\frac{{\int }_t^1{x}^{\alpha (n-1)}dx}{{\int }_t^1{x}^{n-1}dx},$$

is increasing (decreasing) in t and hence we can establish the inequality

$$Z_{\alpha }{\ge }_{st}\left({\le }_{st}\right)Z_1,$$

where the pdf of $Z_{\beta },\beta >0,$ is defined in equation (11). By applying Lemma 2, we can deduce that the RTE of the parallel system is a decreasing function as the number of components increases.

(ii) To begin, we observe that

$$\begin{array}{ccc}\hfill H_{\alpha }(U_{i:n};t)& =& \frac{1}{1-\alpha }\left[\frac{{\int }_t^1{x}^{\alpha (i-1)}{(1-x)}^{\alpha (n-i)}dx}{{\left({\int }_t^1{x}^{i-1}{(1-x)}^{n-i}dx\right)}^{\alpha }}-1\right]\hfill \\ & =& \frac{1}{1-\alpha }\left[\frac{{\int }_t^1{\left(\frac{x}{1-x}\right)}^{\alpha i}\frac{{(1-x)}^{n\alpha }}{x^{\alpha }}dx}{{\left({\int }_t^1{\left(\frac{x}{1-x}\right)}^i\frac{{(1-x)}^n}{x}dx\right)}^{\alpha }}-1\right],\hfill \end{array}$$

Furthermore, the pdf of $Z_{\alpha }$ as stated in (11) is expressed as

$$f_{\alpha }\left(z\right)=\frac{{\left(\frac{z}{1-z}\right)}^{\alpha i}\frac{{(1-z)}^{n\alpha }}{z^{\alpha }}}{{\int }_t^1{\left(\frac{x}{1-x}\right)}^{\alpha i}\frac{{(1-x)}^{n\alpha }}{x^{\alpha }}dx},z\in (t,1),$$

where in this context $q\left(x\right)=\frac{x}{1-x}$ and $s_{\alpha }\left(x\right)=\frac{{(1-x)}^{n\alpha }}{x^{\alpha }}.$ Hence, it is apparent that for $1\ge z\ge t\ge \frac{i_2-1}{n-1}$ and $\alpha >1$ (or $0<\alpha <1$), we can write

$$Z_{\alpha }{\le }_{st}\left({\ge }_{st}\right)Z_1.$$

In conclusion, it can be inferred for $i_1\le i_2\le n,$ that

$$H_{\alpha }(U_{i_1:n};t)\le H_{\alpha }(U_{i_2:n};t),t\ge \frac{i_2-1}{n-1},$$

and this signifies the end of the proof. □

Theorem 3. 

Consider a parallel (series) system consisting of n independent and identically distributed random variables $X_1,\dots ,X_n$ representing the lifetime of the components. Assume that the common distribution function F has a pdf f that is increasing (decreasing) in its support. Then, the RTE of the system lifetime is decreasing in $n.$

Proof. 

Assuming that $Y_n\sim {\overline{B}}_{F\left(t\right)}(\alpha (n-1)+1,1),$ then $f_{Y_n}\left(y\right)$ indicates the pdf of $Y_n.$ It is evident that

$$\frac{f_{Y_{n+1}}\left(y\right)}{f_{Y_n}\left(y\right)}=\frac{{\overline{B}}_{F\left(t\right)}(\alpha (n-1)+1,1)}{{\overline{B}}_{F\left(t\right)}(\alpha n+1,1)}{y}^{\alpha },F\left(t\right)<y<1,$$

is increasing in $y.$ This implies that $Y_n{\le }_{lr}{Y}_{n+1}$ and therefore $Y_n{\le }_{st}{Y}_{n+1}$. Moreover, for $\alpha >1(0<\alpha <1),$$f^{\alpha -1}\left(F^{-1}\left(x\right)\right)$ is an increasing (decreasing) function of $x.$ Therefore

$$\mathbb{E}\left[f^{\alpha -1}\left(F^{-1}\left(Y_n\right)\right)\right]\le (\ge )\mathbb{E}[f^{\alpha -1}\left(F^{-1}\left(Y_{n+1}\right)\right].$$

(14)

From Theorem 2.3, for $\alpha >1(0<\alpha <1),$ we have

$$\begin{array}{ccc}\hfill (1-\alpha )H_{\alpha }(X_{n:n};t)+1& =& [(1-\alpha )H_{\alpha }(U_{n:n};F\left(t\right))+1]\mathbb{E}\left[f^{\alpha -1}\left(F^{-1}\left(Y_n\right)\right)\right]\hfill \\ & \le (\ge )& [(1-\alpha )H_{\alpha }(U_{n:n};F\left(t\right))+1]\mathbb{E}\left[f^{\alpha -1}\left(F^{-1}\left(Y_{n+1}\right)\right)\right]\hfill \\ & \le (\ge )& [(1-\alpha )H_{\alpha }(U_{n+1:n+1};F\left(t\right))+1]\mathbb{E}\left[f^{\alpha -1}\left(F^{-1}\left(Y_{n+1}\right)\right)\right]\hfill \\ & =& (1-\alpha )H_{\alpha }(X_{n+1:n+1};t)+1.\hfill \end{array}$$

The first inequality is obtained by noting that $(1-\alpha )H_{\alpha }(U_{n:n};F\left(t\right))+1$ is non-negative. The last inequality is obtained from Part (i) of Lemma 3. Thus, one can conclude that $H_{\alpha }(X_{n:n};t)\ge H_{\alpha }(X_{n+1:n+1};t)$ for all $t>0.$ □

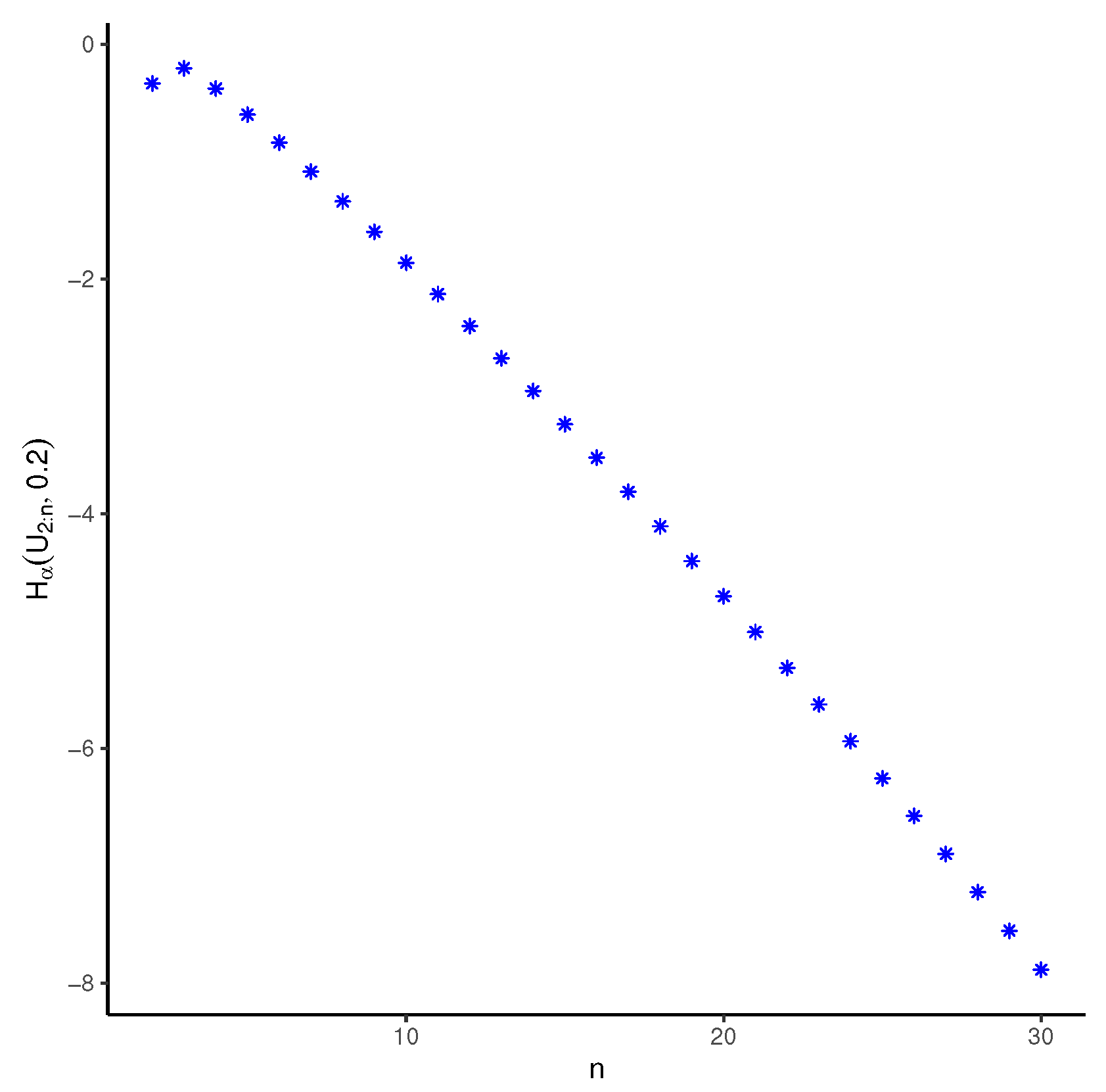
Many distributions have decreasing pdfs, such as the exponential distribution, the Pareto distribution, and mixtures of these two. On the other hand, some distributions have increasing pdfs, such as the power distribution with its density function. Using part (i) of the corollary 1, we can prove a theorem for distributions whose pdfs go up or down. But we have to be careful, because this theorem does not work for all kinds of $(n-i+1)$-out-of-n systems, as the next example shows.

Example 2. 

Let us consider the system works if at least $(n-1)$ of its n components work. Then, the system’s lifetime is the second smallest component lifetime, $X_{2:n}.$ The components have the same distribution, uniform on $(0,1).$ In Figure 3, we see how the RTE of $X_{2:n}$ changes with n when $a=2$ and $t=0.02.$ The graph shows that the RTE of the system does not always decrease as n increases. For example, it reveals that $H_{\alpha }(X_{2:2};0.02)$ is less than that of $H_{\alpha }(X_{2:3};0.02)$.

In reliability theory, we can imagine a case where the pdf decreases, and thus the RRE of a serial system decreases, when the system has more components. This happens when we have a lifetime model with a failure rate ($h\left(t\right)=f\left(t\right)/S\left(t\right)$) that decreases with time. Then the data distribution must have a density function that also decreases. Some lifetime distributions in the reliability domain have the property that their RTE decreases as their scale parameter increases. This is the case, for example, with the Weibull distribution with a shape parameter less than one and with the Gamma distribution with a shape parameter less than one. Therefore, the RTE of a series system with components following these distributions becomes smaller as the number of components increases.

Now, we want to see how the RTE of order statistics $X_{i:n}$ changes with $i.$ We use Part (ii) of Lemma 3, which gives us a formula for the RTE of $X_{i:n}$ in terms of $i.$

Theorem 4. 

Suppose X is a continuous random variable that is always positive. Its distribution function is F and its pdf is $f.$ The pdf f decreases over the range of possible values of $X.$ Let $i_1$ and $i_2$ be two whole numbers such that $i_1\le i_2\le n.$ Then the RTE of the $i_1$-th smallest value of X among n samples, $X_{i_1:n},$ is less than or equal to the RTE of the $i_2$-th smallest value, $X_{i_2:n},$ for all values of X that are greater than or equal to the $F^{-1}\left(\frac{i_2-1}{n-1}\right)$th percentile of $F.$

Proof. 

For $i_1\le i_2\le n,$ it is easy to verify that $Y_{i_1}{\le }_{lr}{Y}_{i_2}$ and hence $Y_{i_1}{\le }_{st}{Y}_{i_2}$. Now, we have

$$\begin{array}{ccc}\hfill (1-\alpha )H_{\alpha }(X_{i_1:n};t)+1& =& [(1-\alpha )H_{\alpha }(U_{i_1:n};t)+1]\mathbb{E}\left[f^{\alpha -1}\left(F^{-1}\left(Y_{i_1}\right)\right)\right]\hfill \\ & \ge (\le )& [(1-\alpha )H_{\alpha }(U_{i_1:n};t)+1]\mathbb{E}\left[f^{\alpha -1}\left(F^{-1}\left(Y_{i_2}\right)\right)\right]\hfill \\ & \ge (\le )& [(1-\alpha )H_{\alpha }(U_{i_1:n};t)+1]\mathbb{E}\left[f^{\alpha -1}\left(F^{-1}\left(Y_{i_2}\right)\right)\right]\hfill \\ & =& (1-\alpha )H_{\alpha }(X_{i_2:n};t)+1,\hfill \end{array}$$

Using Part (ii) of Lemma 3 and the same reasoning as in the proof of Theorem 3, we can obtain the result. □

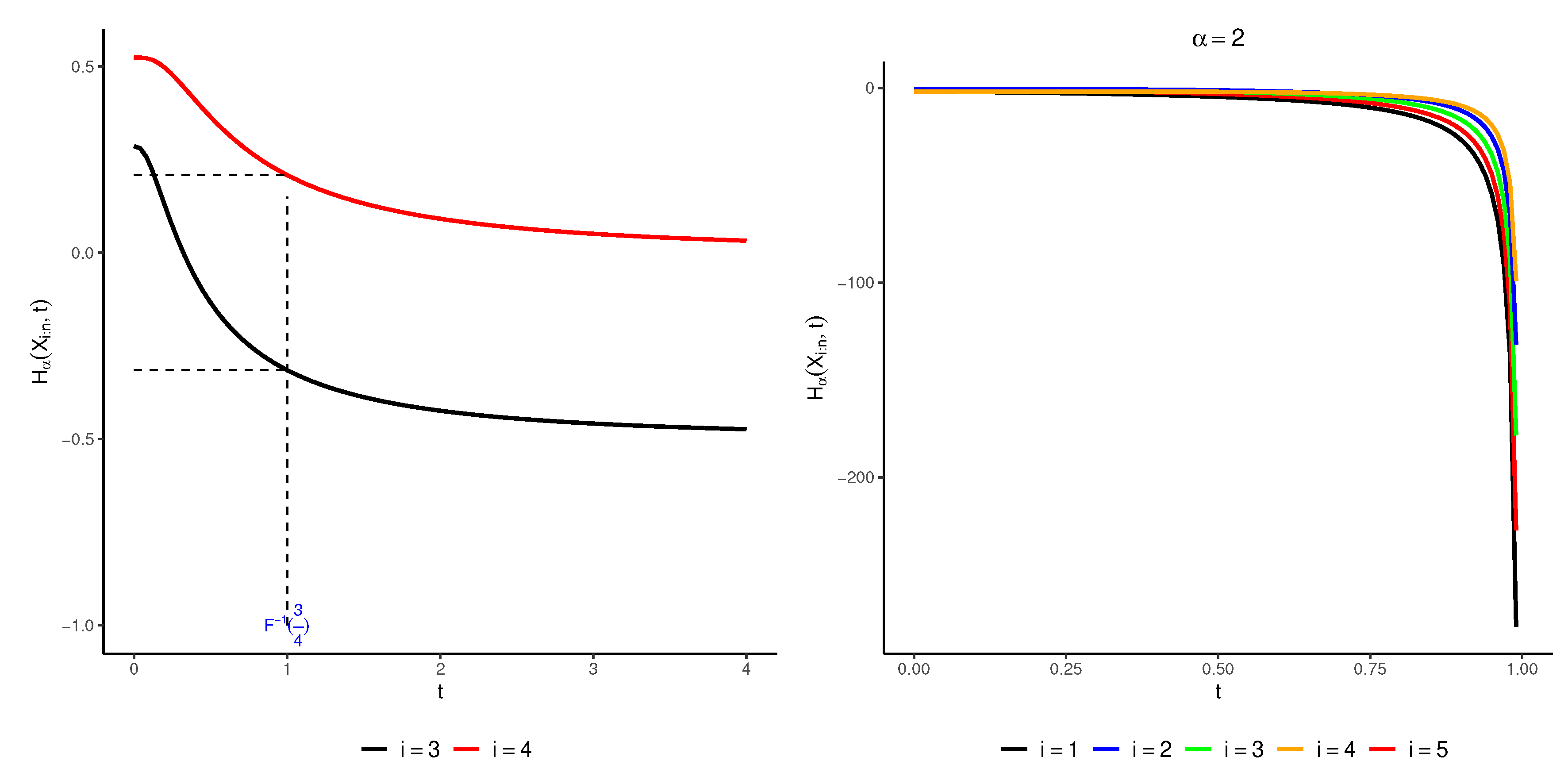
The following example shows that the condition $t\ge F^{-1}\left(\frac{i_2-1}{n-1}\right)$ cannot be dropped from the conditions of theorem.

Example 3. 

Assume the survival function of X as

$$S\left(x\right)=\frac{1}{{(1+x)}^2},x>0.$$

In Figure 4, we see how the RTE of order statistics $X_{i:5},$ for $i=3,4$ and $\alpha =2$, changes with $t,t\in (0,5).$ The plots show that the RTE of the order statistics does not always go up or down as i goes up for all values of $t.$ For example, for the values of $t<F^{-1}\left(\frac{3}{4}\right)$ the RTE is not monotonic in terms of $i.$

We can get a useful result from Theorem 4.

Corollary 2. 

Suppose X is a non-negative continuous random variable that is always positive with cdf F and pdf $f.$ The pdf f decreases over the range of possible values of $X.$ Let i be a whole number that is less than or equal to half of $n+1.$ Then, the RTE of $X_{i:n},$ is increasing in i for values of t greater than the median of distribution.

Proof. 

Suppose $i_1\le i_2\le \frac{n+1}{2}.$ This means that

$$m\ge F^{-1}\left(\frac{i_2-1}{n-1}\right),$$

where $m=F^{-1}\left(\frac{1}{2}\right)$ is the middle value of $F.$ By Theorem 4, we get for $t\ge m$ that $H_{\alpha }(X_{i_1:n};t)\le H_{\alpha }(X_{i_2:n};t).$ □

3. Conclusion

This article addresses the concept of RTE for order statistics. We have presented a new approach to express the RTE of order statistics from a continuous distribution in terms of the RTE of order statistics from a uniform distribution. This connection provides valuable insight into the properties and behavior of RTE for different distributions. Furthermore, due to the complexity of obtaining closed-form expressions for RTE of order statistics, we have derived bounds that provide practical approximations and allow a better understanding of their properties. These bounds serve as useful tools for analyzing and comparing RTE values in different scenarios. In addition, we examined the influence of the index of order statistics, denoted i, and the total number of observations, denoted n, on RTE. By examining the changes in RTE with respect to i and n, we gained a deeper understanding of the relationship between the position of the order statistic and the entropy of the overall distribution. To validate our results and demonstrate the applicability of our approach, we have provided illustrative examples. These examples demonstrate the practical implications of RTE for order statistics and illustrate the versatility of our methodology for different distributions. In summary, this study contributes to the understanding of RTE for order statistics by establishing relationships, deriving bounds, and investigating the influence of index and sample size. The results of this work provide valuable insights for researchers and practitioners working in the field of statistical inference and entropy-based analysis.