Submitted:
18 September 2023
Posted:
20 September 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Composite Scattering from Multiple Dielectric Targets using the MOM method
2.1. One-dimensional fractal sea surface
2.2. Composite scattering coefficient calculation
 where is the unit normal vector of the surface pointing to the free space or targets,, is the first derivative of the sea surface function . and denote the total fields in regionand; and are Green functions in and ; is the first kind zero order Hankel function . and () are the propagation vectors in and ; are the total fields at arbitrary location inner the class missile targets ; are the corresponding 2-D Green functions; are the corresponding propagation vectors; are the total fields at arbitrary location inner class ship targets ; The corresponding 2-D Green functions are and the propagation vectors are .
where is the unit normal vector of the surface pointing to the free space or targets,, is the first derivative of the sea surface function . and denote the total fields in regionand; and are Green functions in and ; is the first kind zero order Hankel function . and () are the propagation vectors in and ; are the total fields at arbitrary location inner the class missile targets ; are the corresponding 2-D Green functions; are the corresponding propagation vectors; are the total fields at arbitrary location inner class ship targets ; The corresponding 2-D Green functions are and the propagation vectors are .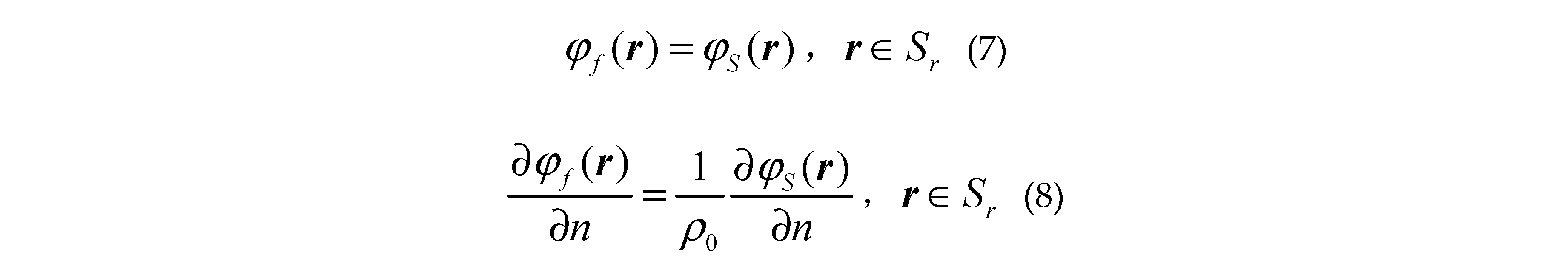
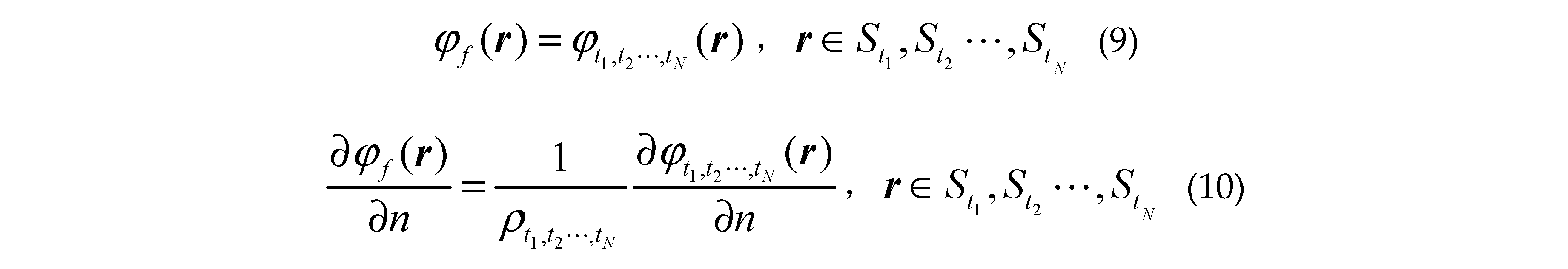
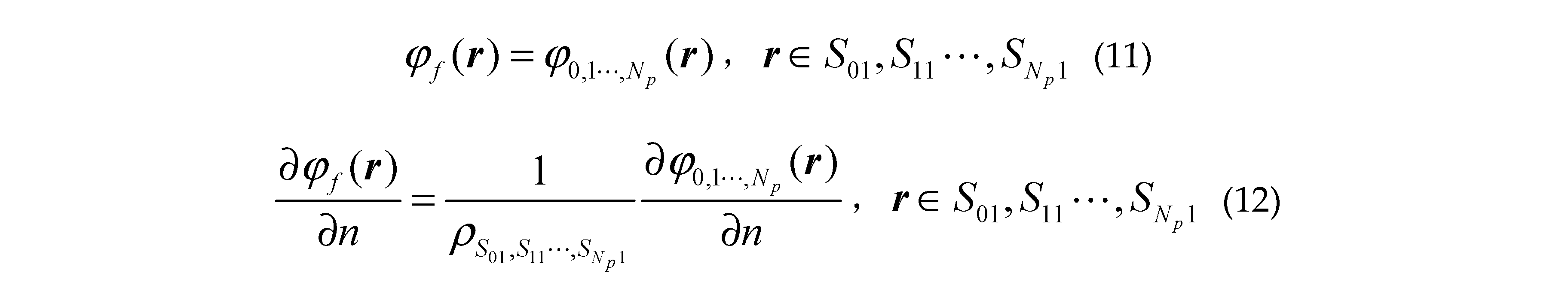
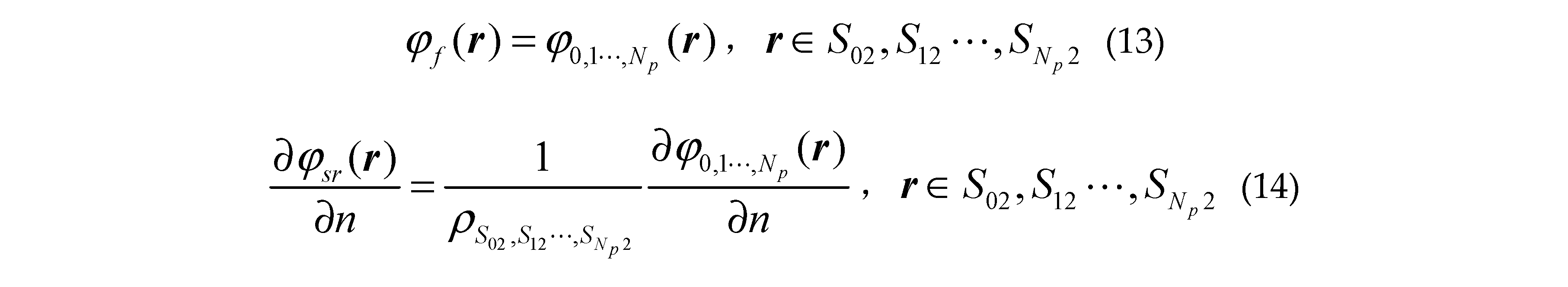
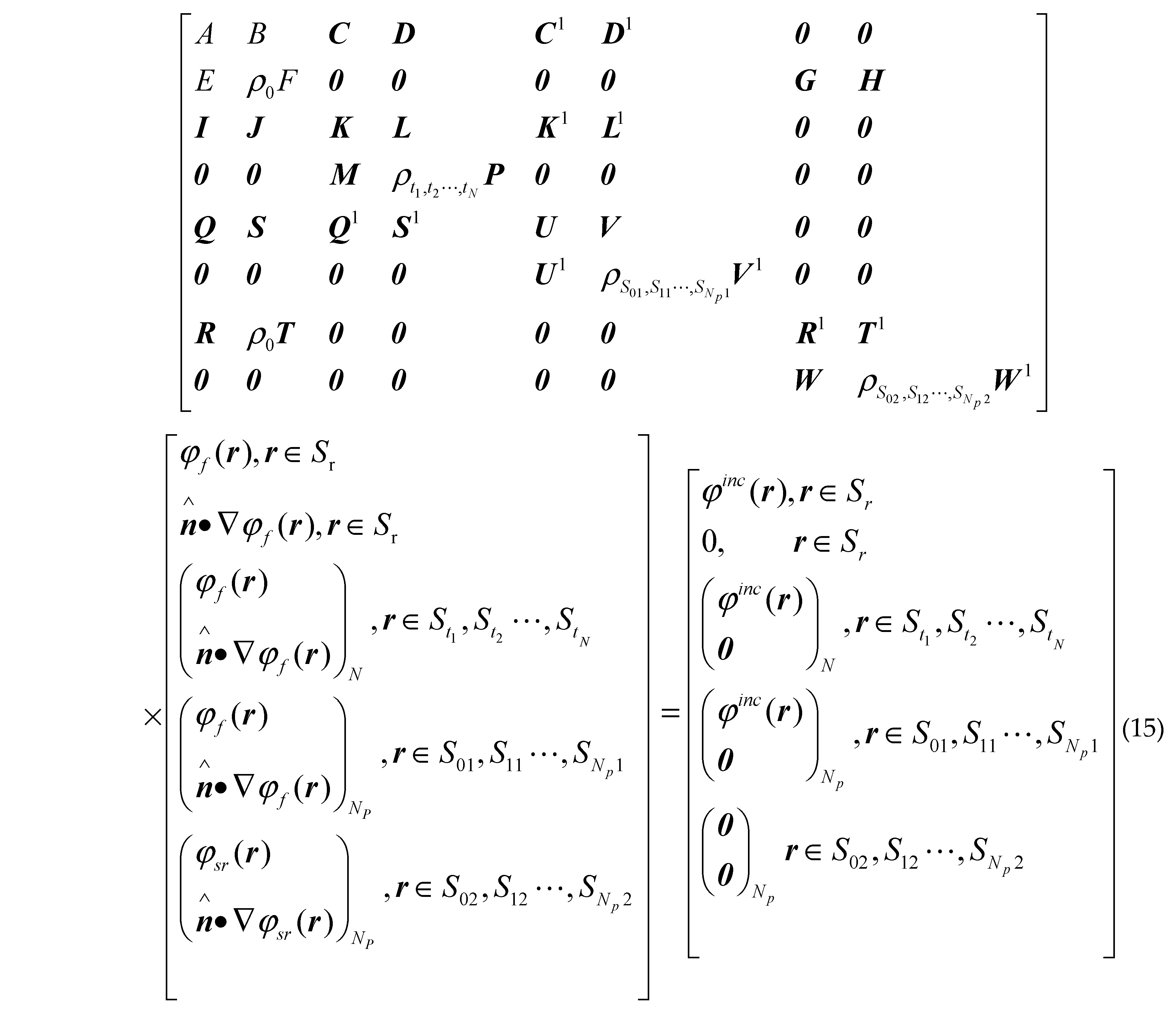
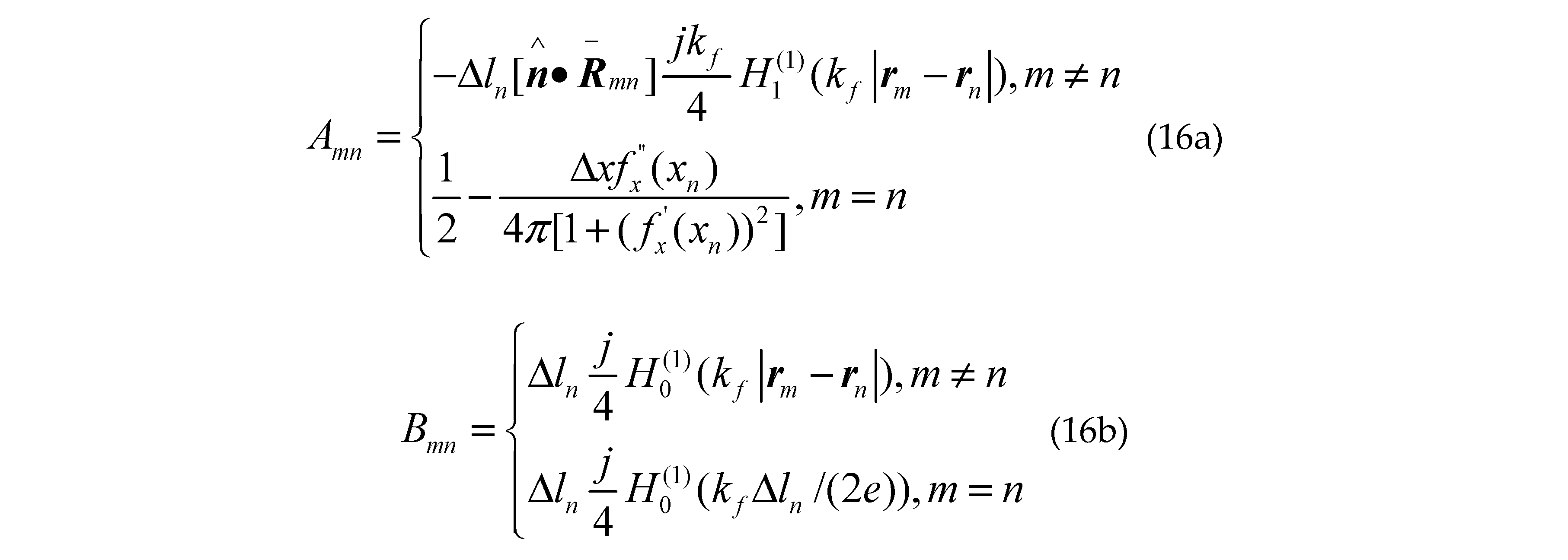 where denotes
where denotes
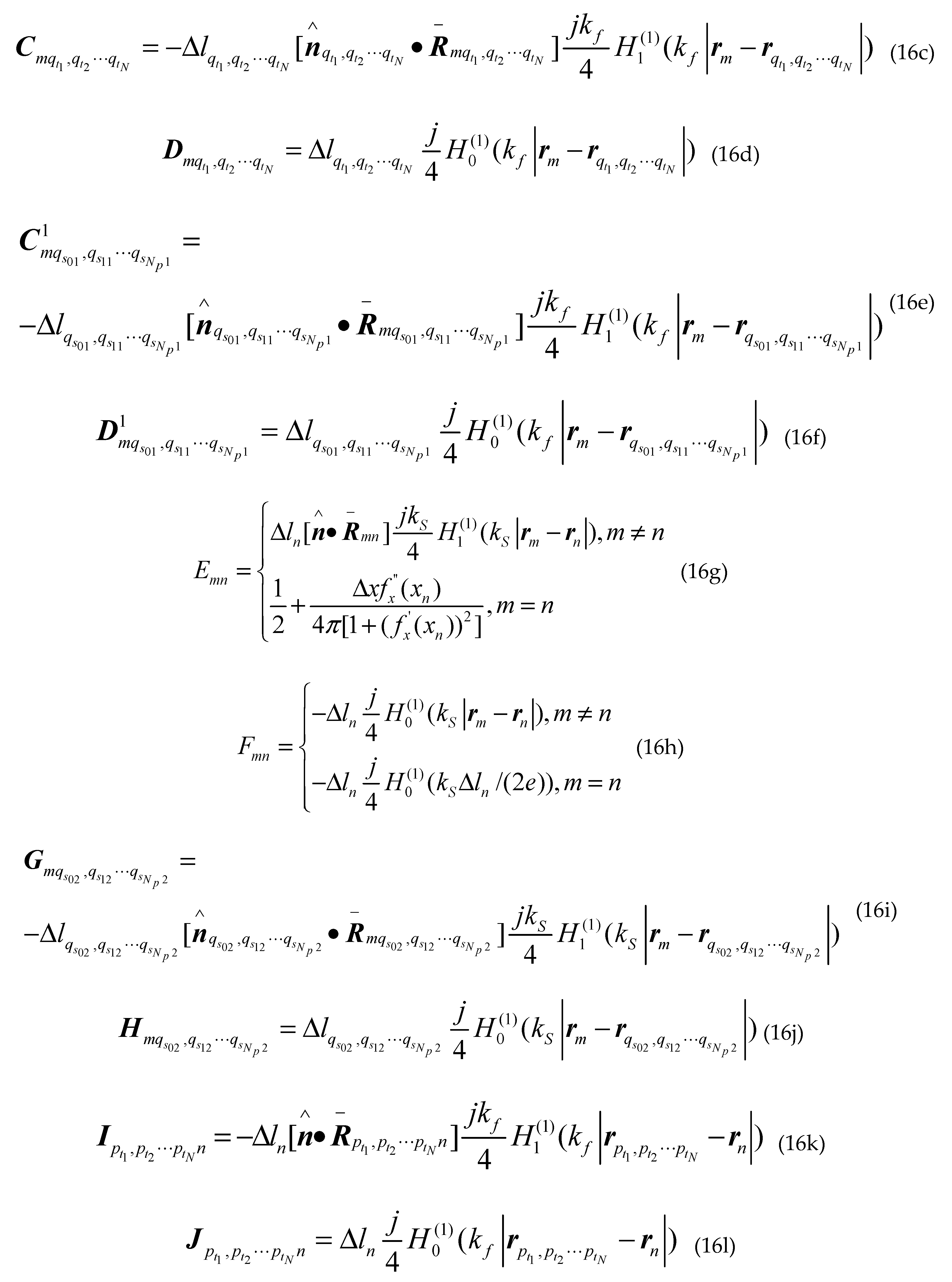
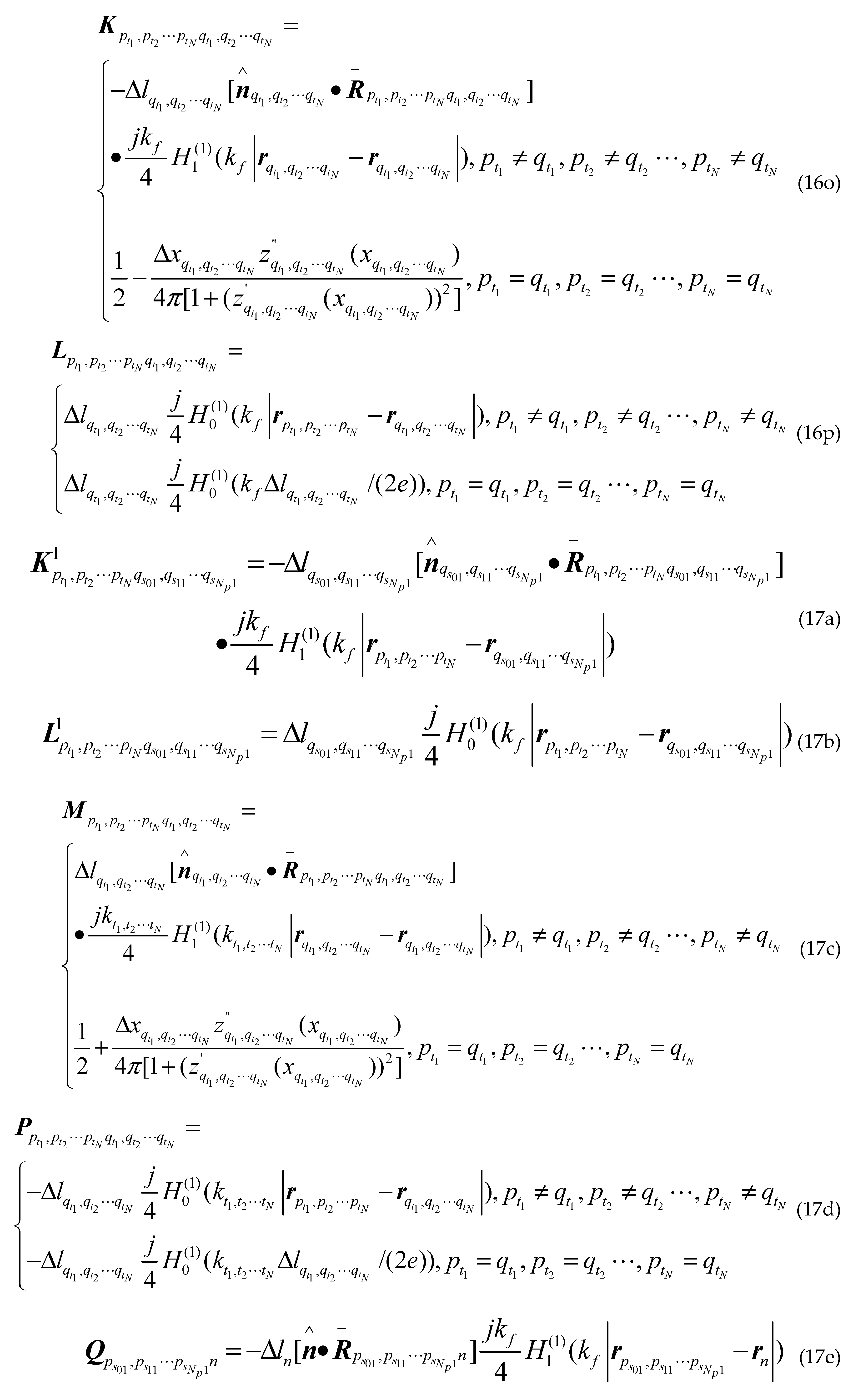
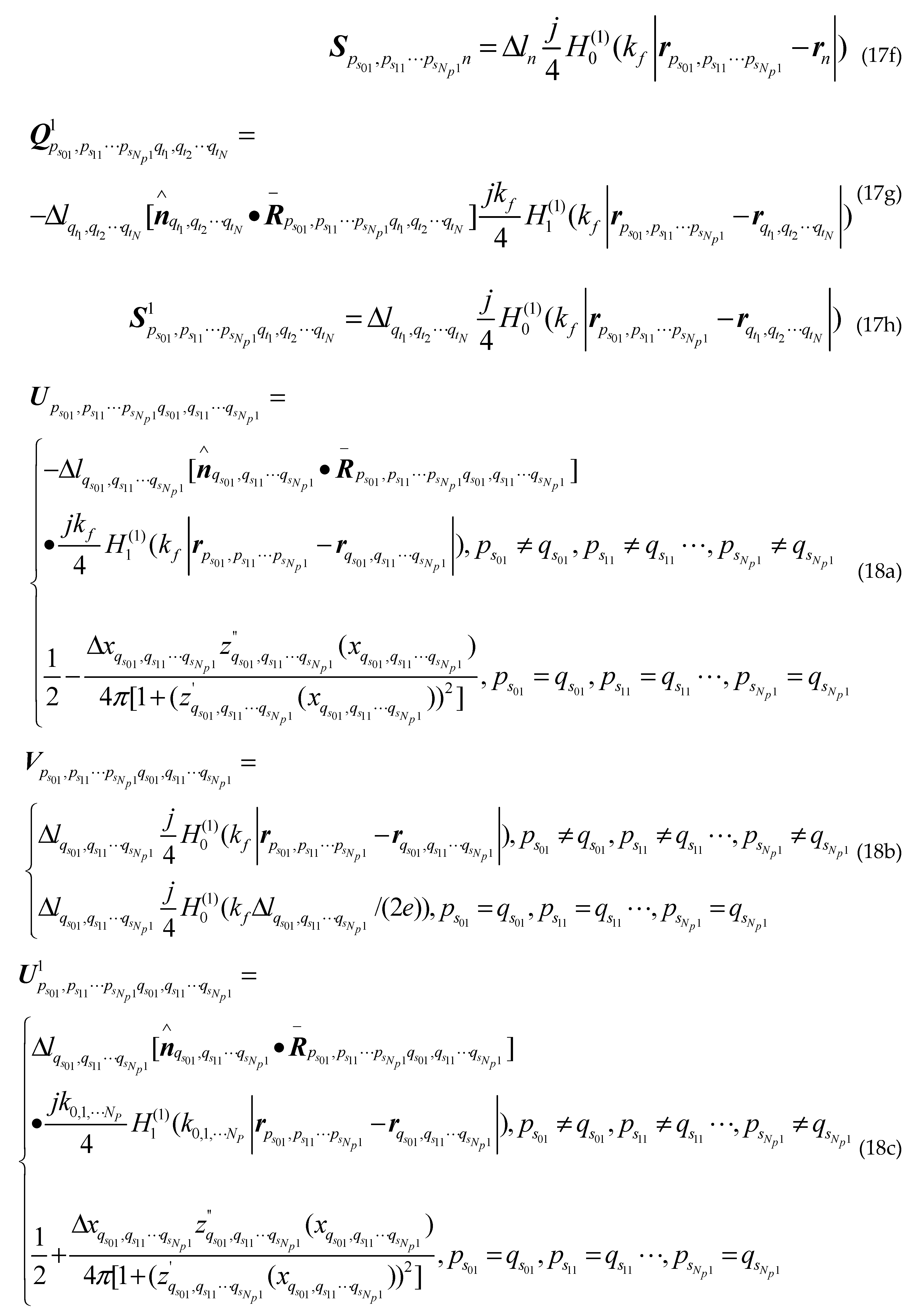
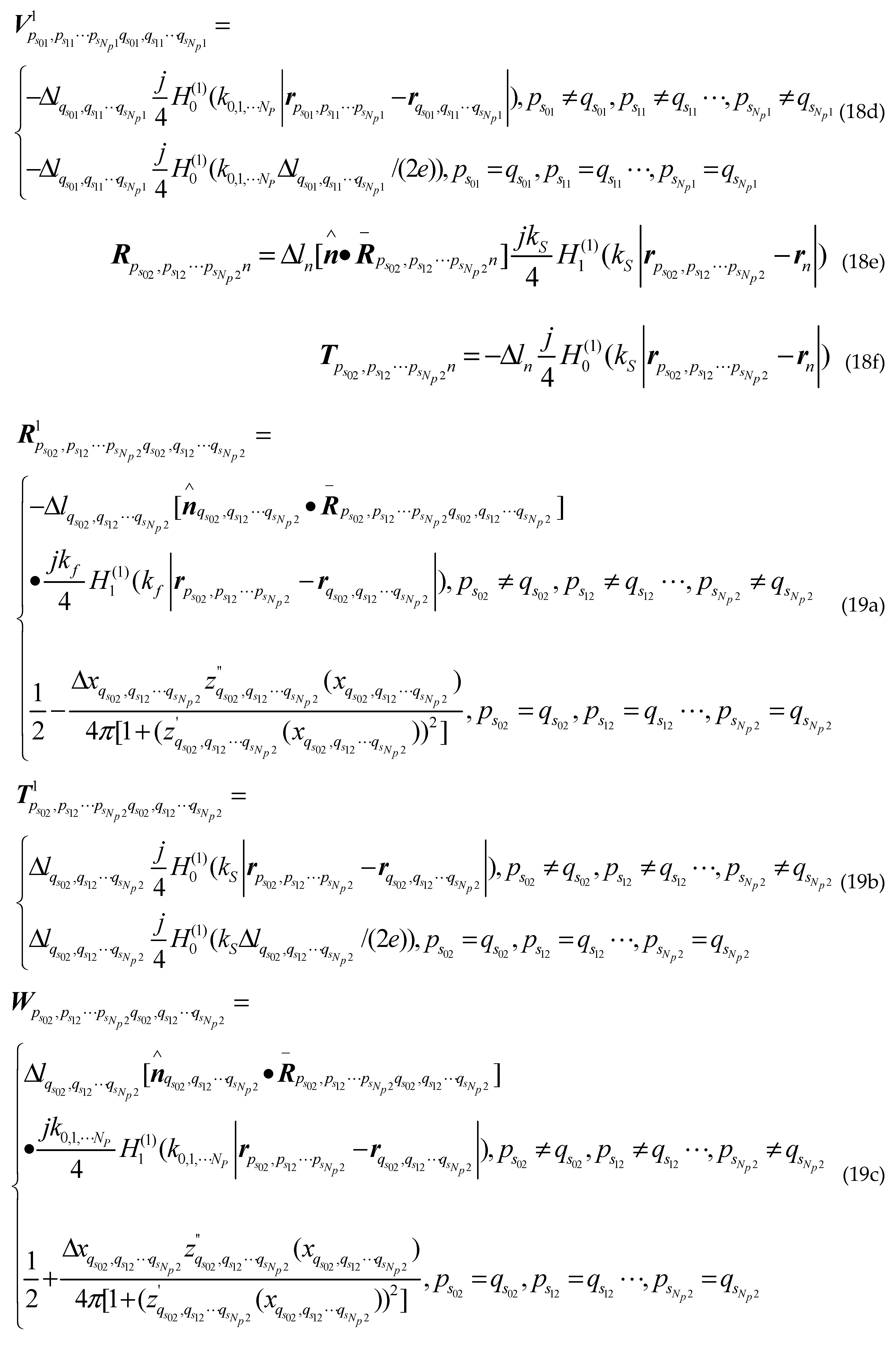
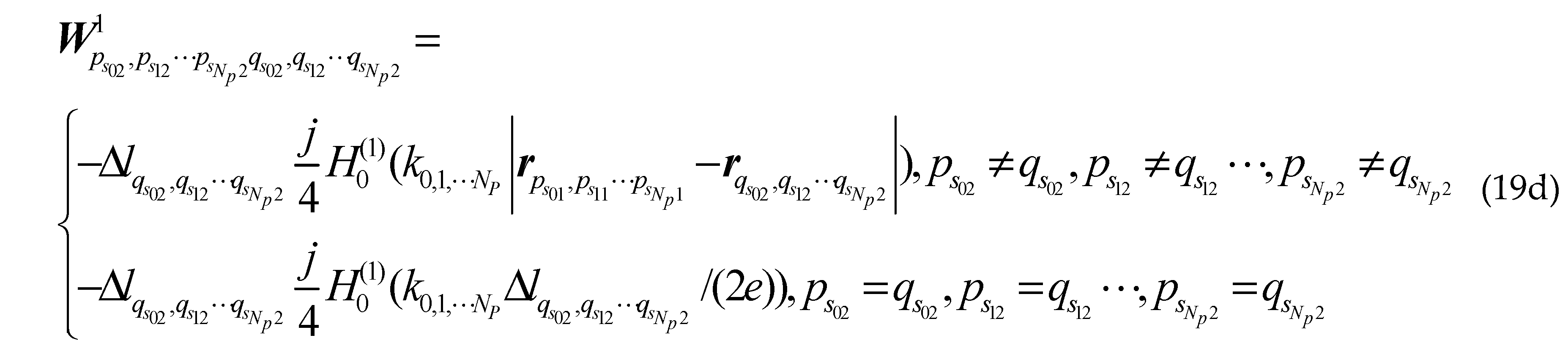
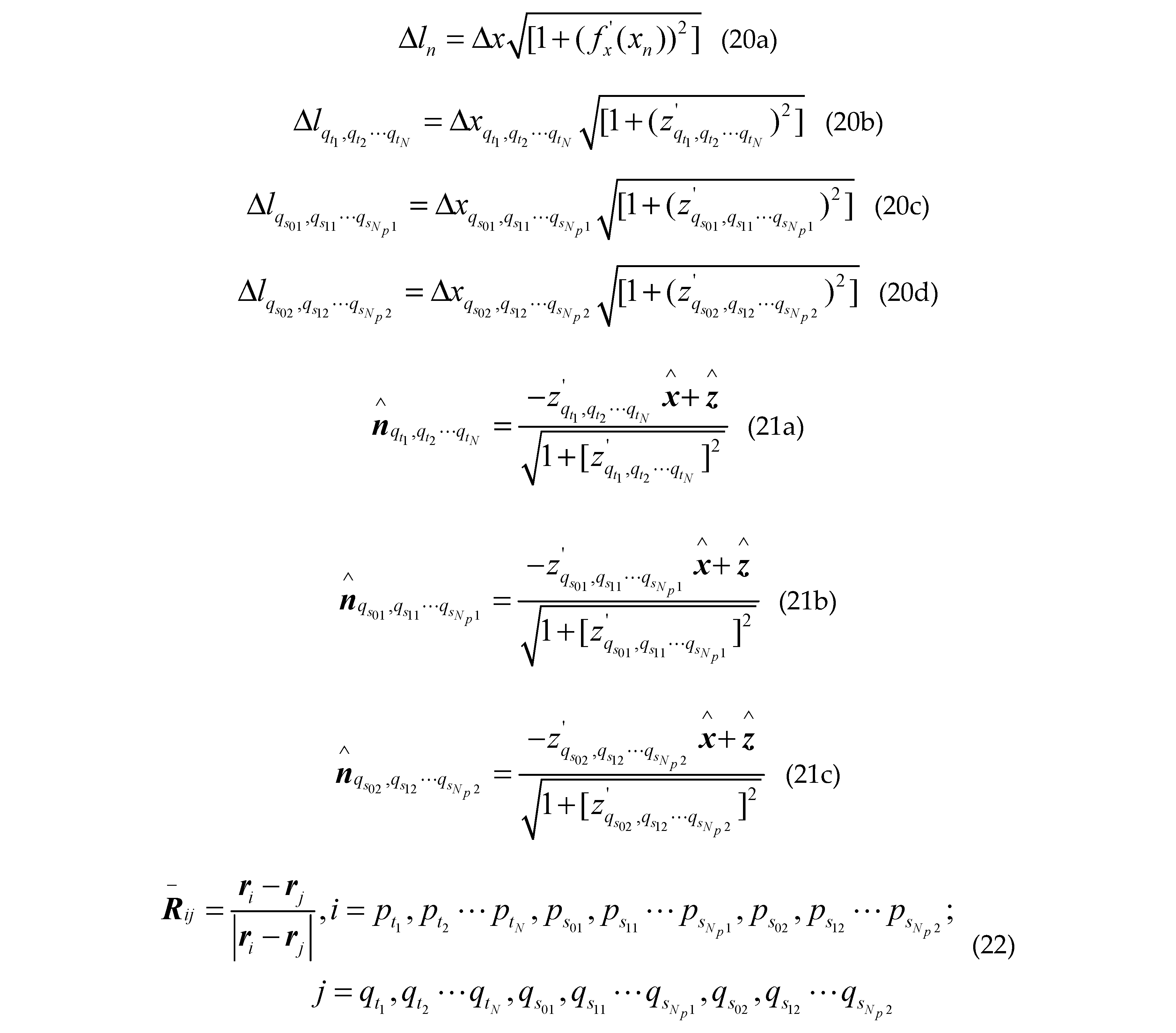 Where is the first kind first order Hankel function; is the second derivative of the sea surface function ; ,and are the first derivative of the class missile target surface contours, the class ship target surface contours upper and lower the sea surface; , and are the second derivative of the class missile target surface contours, the class ship target surface contours upper and lower the sea surface; are arbitrary two points on sea surface; are arbitrary two points on different class missile target surfaces; are arbitrary two points on upper surface of different class ship targets; are arbitrary two points on lower surface of different class ship targets; other groups are as follows:
Where is the first kind first order Hankel function; is the second derivative of the sea surface function ; ,and are the first derivative of the class missile target surface contours, the class ship target surface contours upper and lower the sea surface; , and are the second derivative of the class missile target surface contours, the class ship target surface contours upper and lower the sea surface; are arbitrary two points on sea surface; are arbitrary two points on different class missile target surfaces; are arbitrary two points on upper surface of different class ship targets; are arbitrary two points on lower surface of different class ship targets; other groups are as follows:
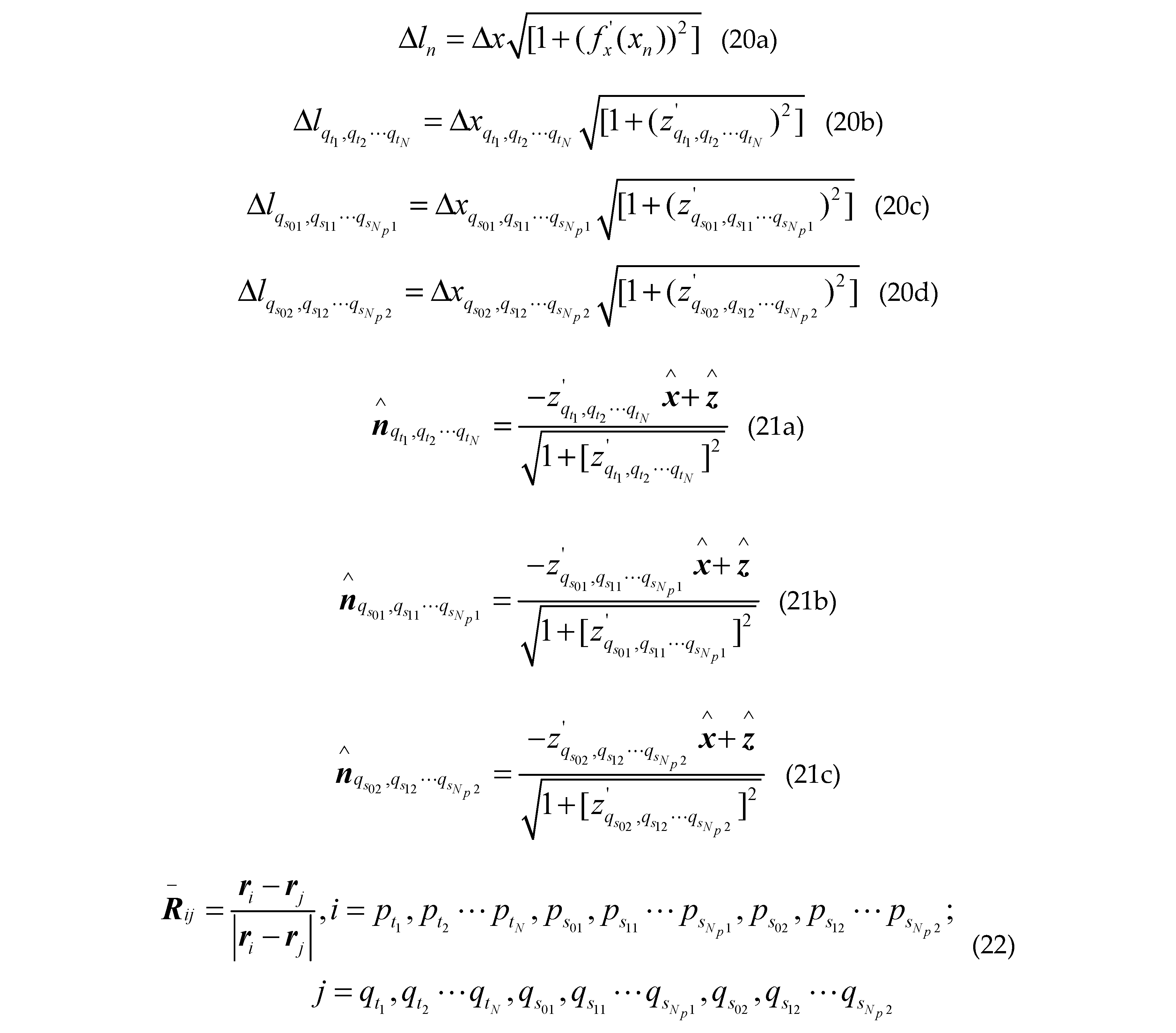

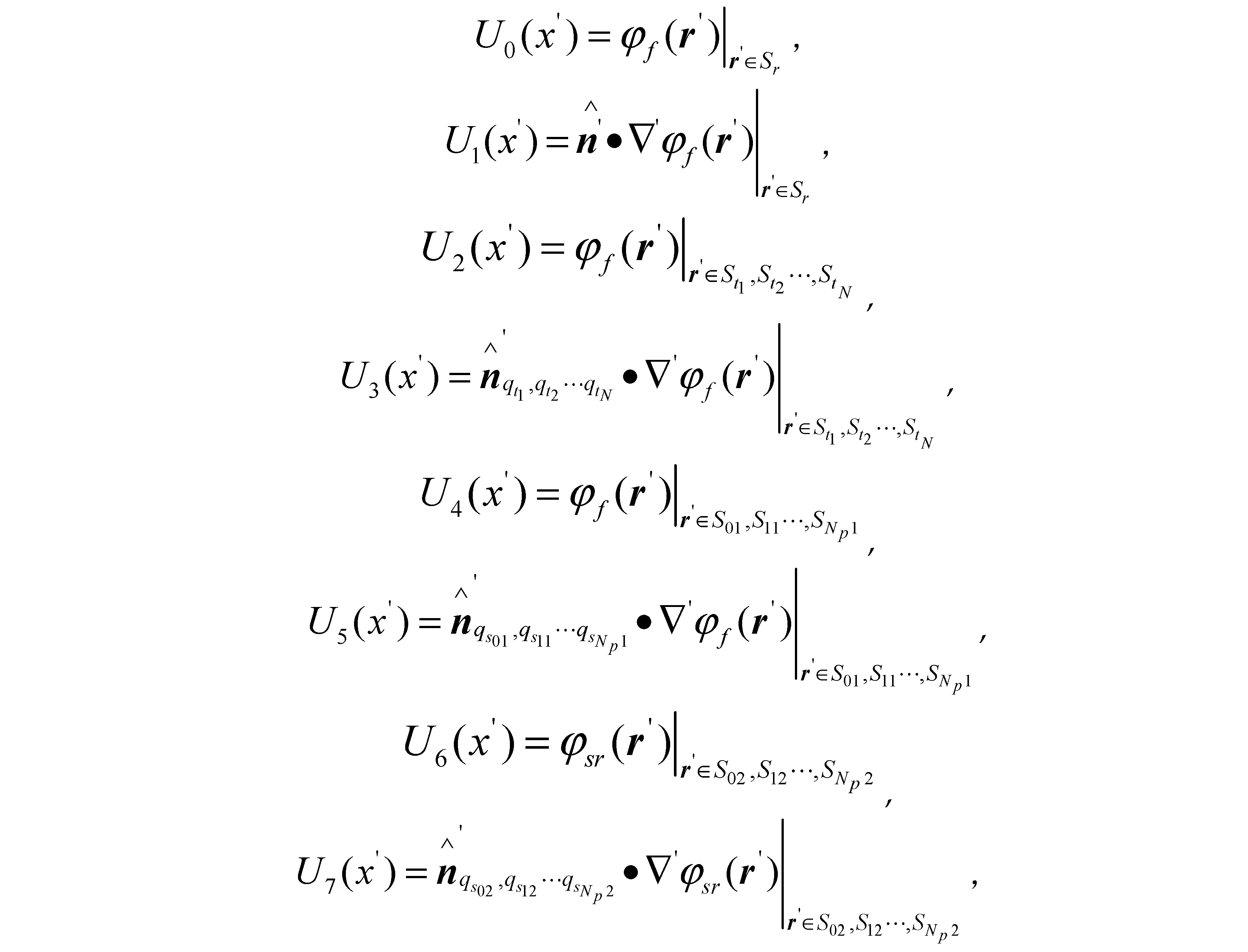 So the scattered field at any point in space can be obtained:
So the scattered field at any point in space can be obtained:
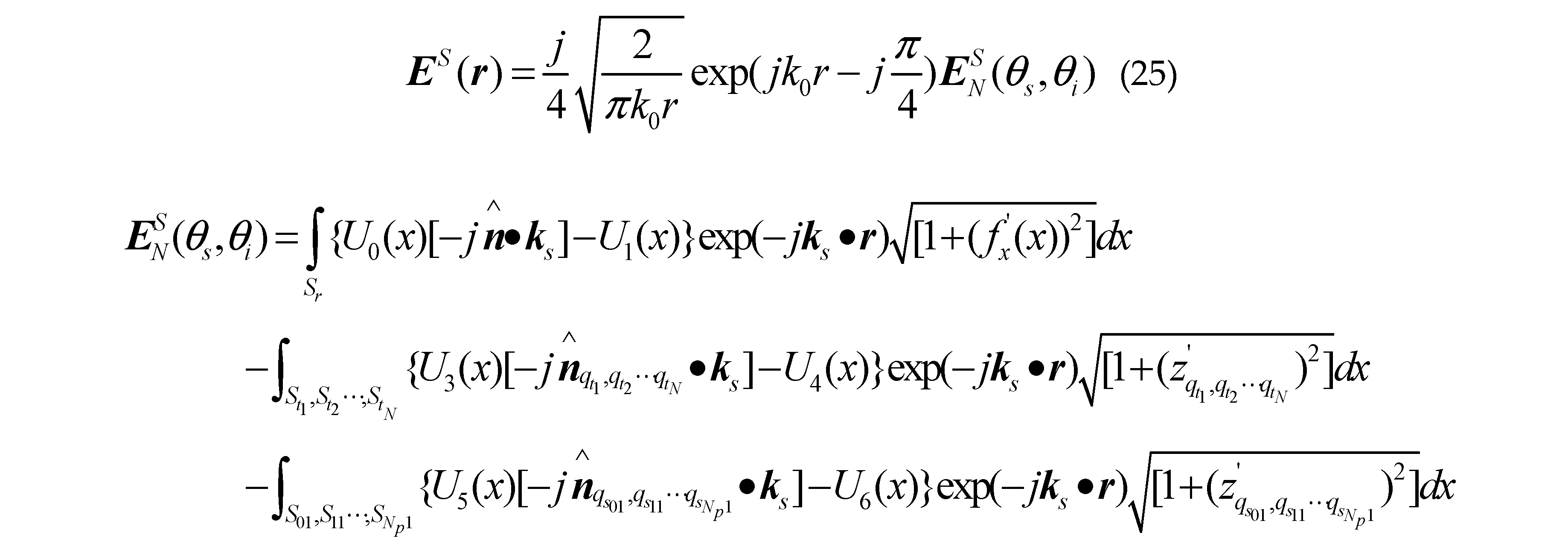 where , , , is the incident angle, is the scattering angle, is the incident azimuth, is the scattering azimuth.
where , , , is the incident angle, is the scattering angle, is the incident azimuth, is the scattering azimuth. Where is the tapered wave width factor,
Where is the tapered wave width factor,
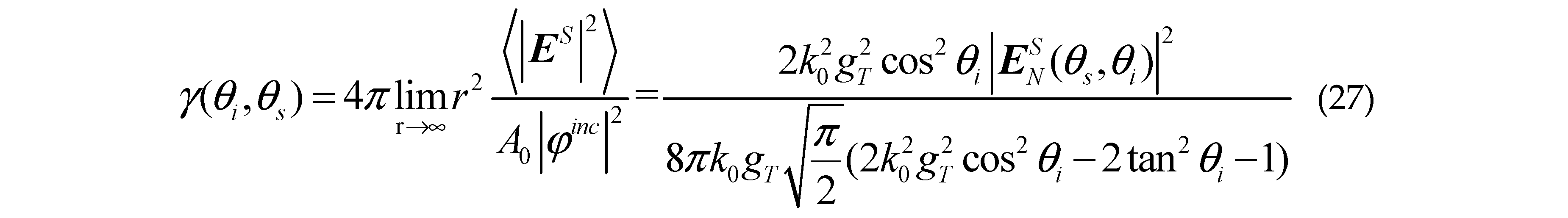
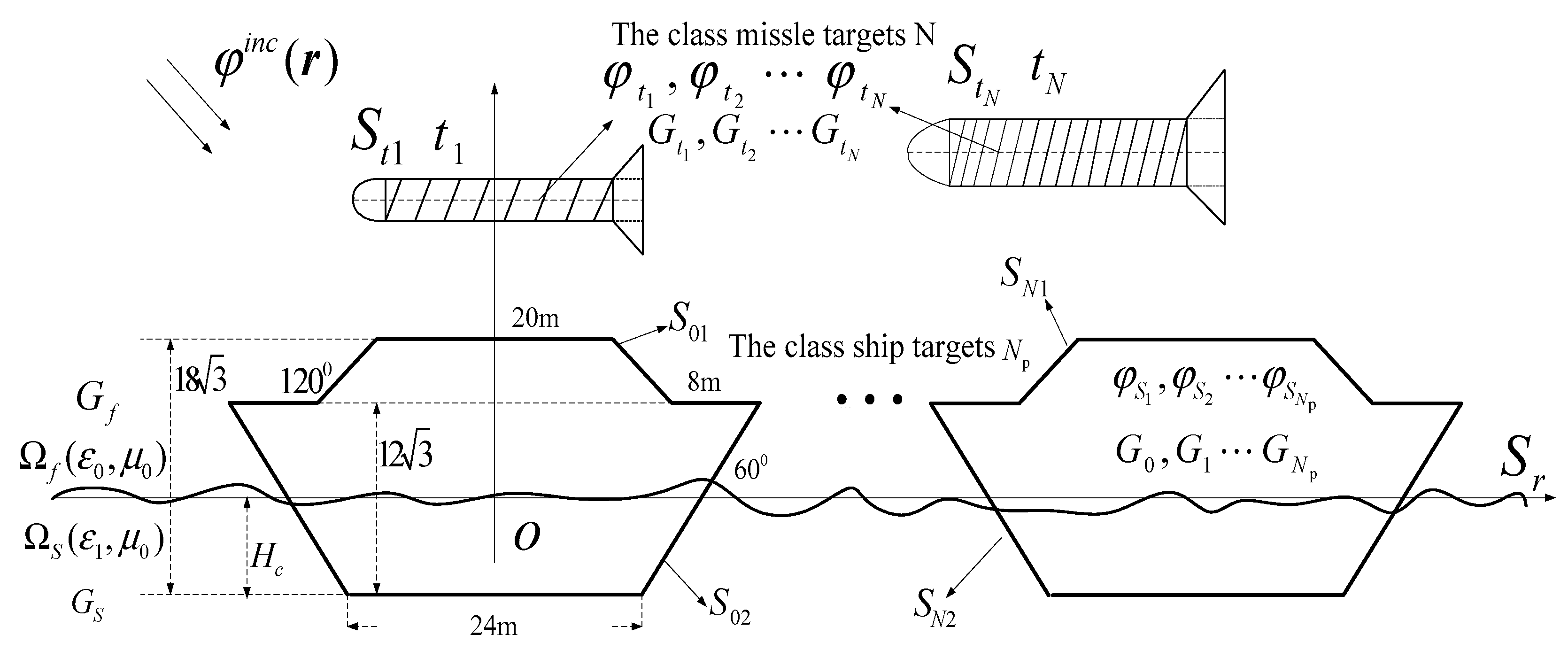
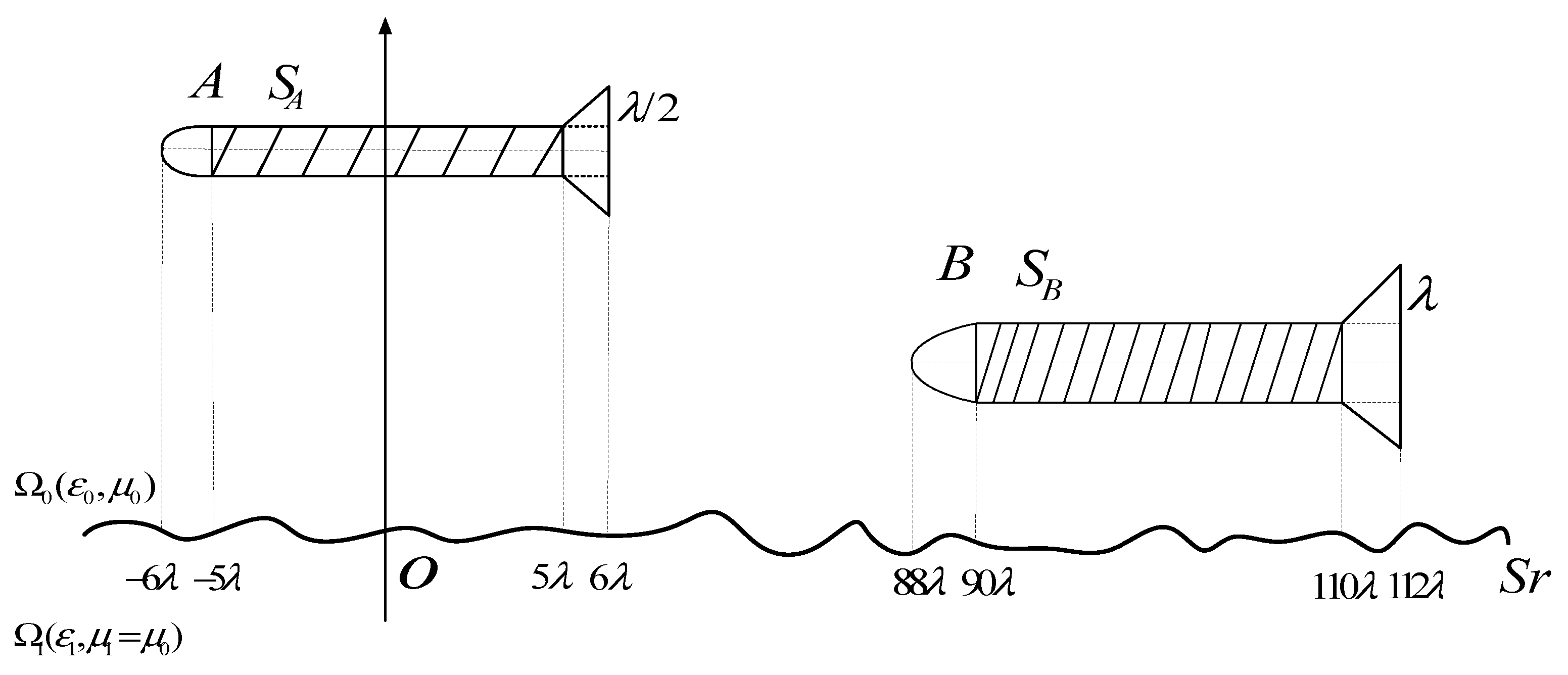
2.3. Establish the coordinates for targets above the sea
3. Numerical examples
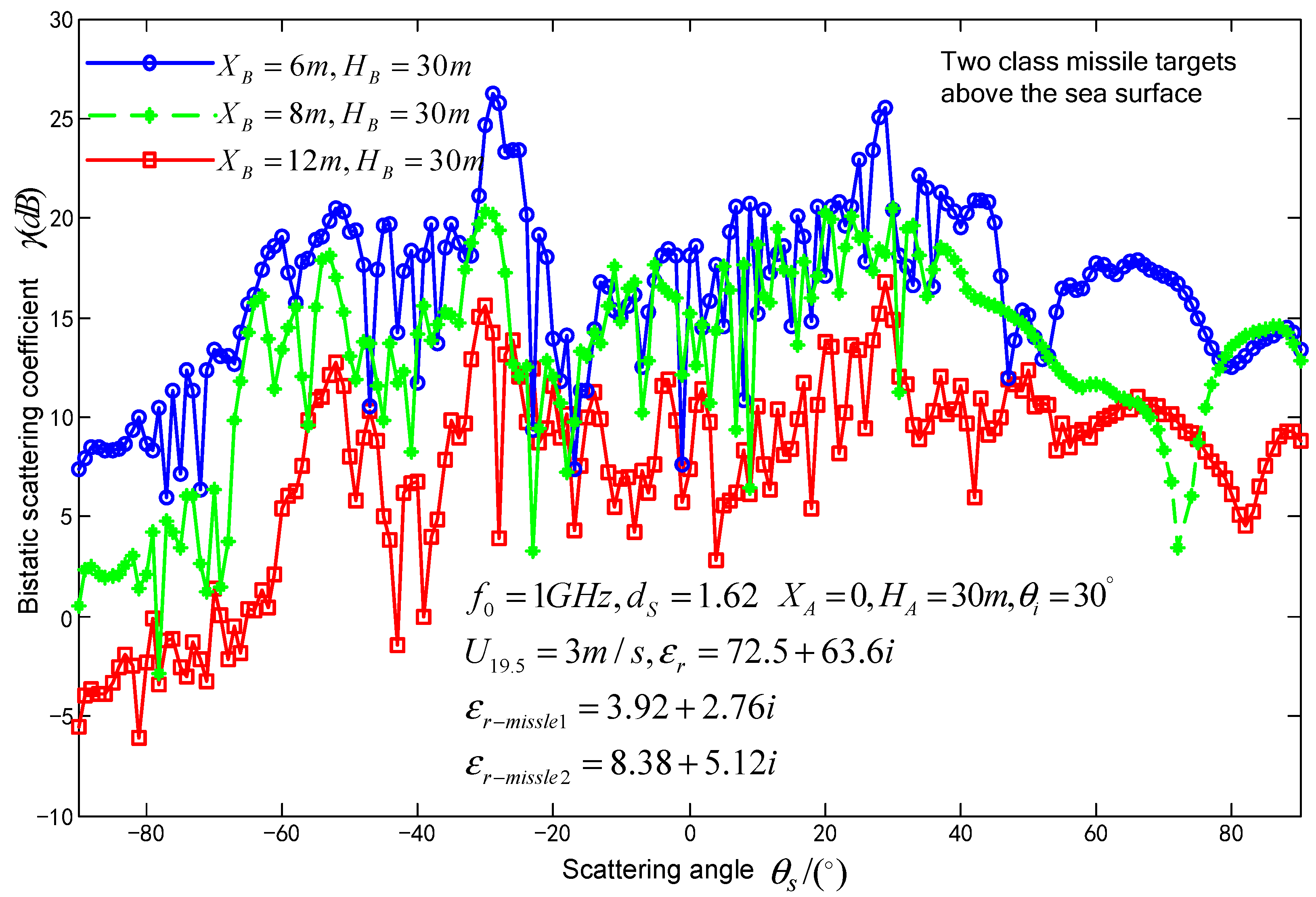
3.1. Effect of class missile target permittivity and spatial locations on composite scattering coefficient
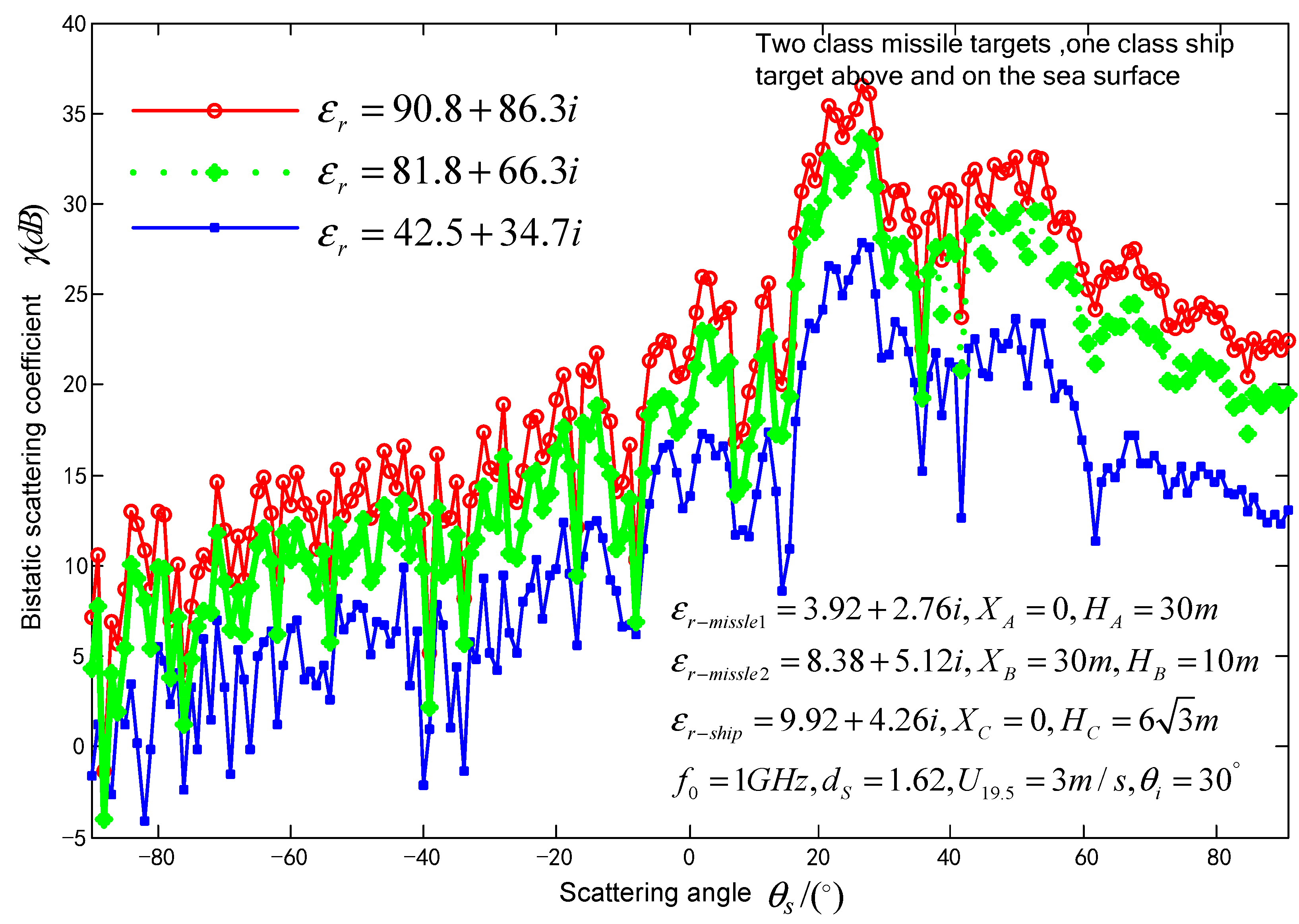
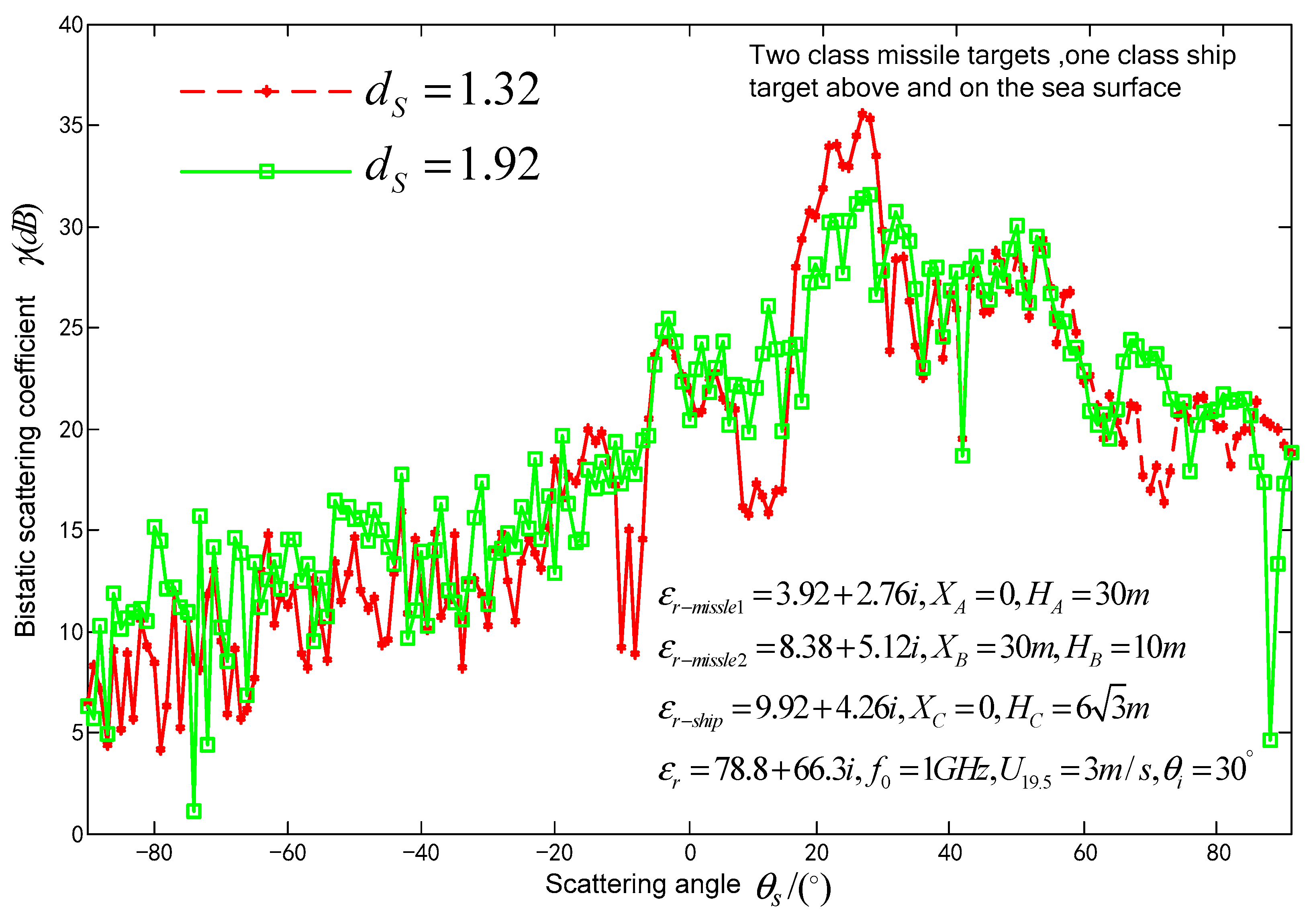
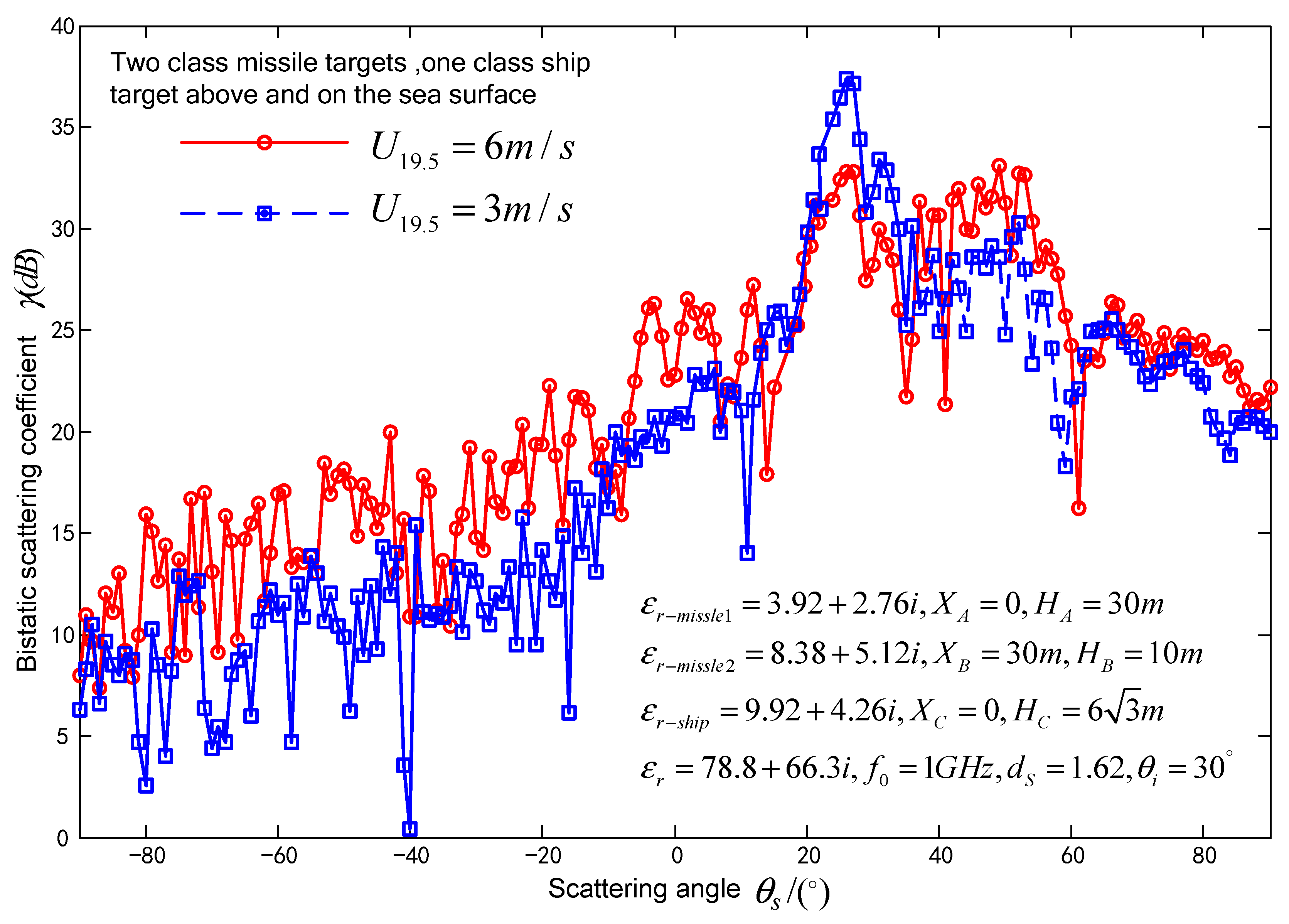
3.2. Impact of Seawater permittivity, fractal dimensions, wind speed at sea surface on composite scattering coefficient
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Niu, B.; Gu, L.; Gong, C. Measure the performance of cooperative detection of sea-skimming target. 2012 11th International Conference on Signal Processing (ICSP 2012). LOCATION OF CONFERENCE, ChinaDATE OF CONFERENCE; pp. 2262–2265. [CrossRef]
- Gini. F, Greco. M, “A suboptimum approach to adaptive coherent radar detection in compound- Gaussian clutter,” IEEE Trans on Aerospace and Electronic Systems. 35(3), 1095-1104(1999). [CrossRef]
- Conte. E Lops. M, “Asymptotically optimum radar detection in compound-Gaussian clutter,” IEEE Trans on Aerospace and Electronic Systems. 31(2), 617-625(1995). [CrossRef]
- Winebrenner, D.P.; Ishimaru, A. Application of the phase-perturbation technique to randomly rough surfaces. J. Opt. Soc. Am. A 1985, 2, 2285–2293. [Google Scholar] [CrossRef]
- Holliday, D. Resolution of a controversy surrounding the Kirchhoff approach and the small perturbation method in rough surface scattering theory. IEEE Trans. Antennas Propag. 1987, 35, 120–122. [Google Scholar] [CrossRef]
- Tian, G.; Tong, C.; Sun, H.; Zou, G.; Liu, H. Improved Hybrid Algorithm for Composite Scattering From Multiple 3D Objects Above a 2D Random Dielectric Rough Surface. IEEE Access 2020, 9, 4435–4446. [Google Scholar] [CrossRef]
- Tian, J.; Tong, J.; Shi, J.; Gui, L. A new approximate fast method of computing the scattering from multilayer rough surfaces based on the Kirchhoff approximation. Radio Sci. 2017, 52, 186–195. [Google Scholar] [CrossRef]
- Pinel, N.; Le Bastard, C.; Bourlier, C. Modeling of EM Wave Coherent Scattering From a Rough Multilayered Medium With the Scalar Kirchhoff Approximation for GPR Applications. IEEE Trans. Geosci. Remote. Sens. 2019, 58, 1654–1664. [Google Scholar] [CrossRef]
- Hira Lynn Broschat, “The phase perturbation approximation for rough surface scattering from a pierson-moskowitz sea surface”. IEEE Trans on Geoscience and Remote Sensing, 1993, 31(1): 278-279. [CrossRef]
- Afifi, S.; Dusseaux, R. Scattering From 2-D Perfect Electromagnetic Conductor Rough Surface: Analysis With the Small Perturbation Method and the Small-Slope Approximation. IEEE Trans. Antennas Propag. 2017, 66, 340–346. [Google Scholar] [CrossRef]
- Xu Xiaoyan, “The Forward-Backward IPO algorithm for Calculating Open-Ended Cavities,” Space Electronic Technology.(1), 72-75(2008).
- J. Ma, L. X. J. Ma, L. X. Guo and H. Zeng, “The FIT-MoM Hybrid Method for Analysis of Electromagnetic Scattering by Dielectric Bodies of Revolution” IEEE Transactions on Antennas and Propagation. 66(3), 1384-1388(2018). [CrossRef]
- Ozgun, O.; Kuzuoglu, M. A Domain Decomposition Finite-Element Method for Modeling Electromagnetic Scattering From Rough Sea Surfaces With Emphasis on Near-Forward Scattering. IEEE Trans. Antennas Propag. 2018, 67, 335–345. [Google Scholar] [CrossRef]
- Smith, D.R.; Burns, S.; Simpson, J.J.; Ferrone, S.M. FDTD Modeling of Scattered Ultra-Low Frequency Electromagnetic Waves From Objects Submerged in the Ocean. IEEE Trans. Antennas Propag. 2019, 67, 2534–2541. [Google Scholar] [CrossRef]
- Iodice, A. Forward-backward method for scattering from dielectric rough surfaces. 50. [CrossRef]
- Liang, Y.; Guo, L.; Wu, Z. The EPILE Combined With the Generalized-FBM for Analyzing the Scattering From Targets Above and on a Rough Surface. IEEE Antennas Wirel. Propag. Lett. 2010, 9, 809–813. [Google Scholar] [CrossRef]
- Li, Z.; Jin, Y.-Q. Bistatic scattering from a fractal dynamic rough sea surface with a ship presence at low grazing-angle incidence using the GFBM/SAA. Microw. Opt. Technol. Lett. 2001, 31, 146–151. [Google Scholar] [CrossRef]
- G. Kubicke, C. G. Kubicke, C. Bourlier, and J. Saillard. Scattering by an object above a randomly rough surface from a fast numerical method: Extended PILE method combined with FB-SA [J].Waves in Random and Complex Media. 2008, 18(3):495-519. [CrossRef]
- X.Ye, Y-Q.Jin. Fast iterative approach to difference scattering from the target above a rough surface [J]. IEEE Trans on Geoscience and Remote Sensing, 2006, 44(l):108-115. [CrossRef]
- H.X.YOU,” A hybrid KA-MOM algorithm for computation of scattering from a 3D PEC target above a dielectric rough surface,” Radio Sci. 43 (3), 3008-3018(2008). [CrossRef]
- Pham-Xuan, V.; Trinh, D.; De Gersem, H.; Brennan, C. Novel Iterative Algorithm for the Solution of Electromagnetic Scattering From Layered Random Rough Surfaces. IEEE Trans. Antennas Propag. 2018, 66, 3810–3815. [Google Scholar] [CrossRef]
- Zhang, M.; Zhao, Y.; Li, J.-X.; Wei, P.-B. Reliable Approach for Composite Scattering Calculation From Ship Over a Sea Surface Based on FBAM and GO-PO Models. 65. [CrossRef]
- Wang Yunhua,Guo Lixin,Wu Zhensen,” The application of an improved 2D fractal model for electromagnetic scattering from the sea surface,” Acta Physica Sinica, 55(10), 5193-5195(2006).
- F. Berizzi, D. M. F. Berizzi, D. M. Enzo, “Fractal analysis of the signal scattered from the sea surface,” IEEE Trans on Antennas and Propagation. 47(2), 325-327(1999). [CrossRef]
- Shay, N.R.; Weile, D.S.; Kastner, R. Balanced Electric-Magnetic Absorber Green’s Function Method for MoM Matrix Thinning and Conditioning. IEEE Trans. Antennas Propag. 2018, 66, 2996–3001. [Google Scholar] [CrossRef]
- B. Guan, J. F. B. Guan, J. F. Zhang, “Electromagnetic scattering from objects above a rough surface using the method of moments with half-space Green’s function,“ IEEE Trans on Geoscience and Remote Sensing, 47(10), 3399-3405(2009. [CrossRef]
- Guérin, C.-A.; Soriano, G.; Chapron, B. The weighted curvature approximation in scattering from sea surfaces. Waves Random Complex Media 2010, 20, 364–384. [Google Scholar] [CrossRef]

| Parameter items | Simulation value |
|---|---|
| Incident angle of the tapered wave | 30° |
| Incident frequency | |
| The wind speed at 19.5 above the sea surface | 3m/s |
| Observation time | 0.25s |
| Observation distance | 90m |
| Sample frequency | 6kHz |
| Gravity constant | 9.8 |
| Power-law factor | 2.9 |
| Correction factor | 1.65 |
| Fractal dimension | 1.62 |
| Scale factor | 0.985 |
| Scale factor | 1.015 |
| Number of resonant waves | 400 |
| Normalization constant | 0.152 |
| Relative Speed of target to sea surface | 360m/s |
| Relative dielectric of the sea water | 72.5+j63.6 |
| Angular propagation direction | 45° |
| Fundamental wavenumber | 0.84 |
| Standard deviation of the amplitude | 0.19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).




