On the interpretation of cosmic acceleration

1. Introduction

For over thirty years, cosmologists have built up conclusive evidence that cosmic expansion is accelerating. To explain such observation, we need to assume that there is a mysterious new component: Dark Energy (DE) or a Cosmological Constant, $\mathsf{\Lambda }$. This new term is usually interpreted as a repulsive force between galaxies that opposes gravity and dominates the expansion. Such strange behaviour is often flagged as one of the most important challenges to understand the laws of Physics today and could provide an observational window to understand Quantum Gravity ([1]).

Usually, cosmic acceleration is defined by the adimensional coefficient $q\equiv (\ddot{a}/a)H^{-2}$, where $H\equiv \dot{a}/a$. For a universe with an equation of state $p=\omega \rho$ this results in $q=-\frac{1}{2}(1+3\omega )$. For regular matter or radiation we have $\omega >0$ so we expect the expansion to decelerate ($q<0$) because of gravity. However, concordant measurements from galaxy clustering (e.g. [2,3,4]), Type Ia supernova ([5,6]) and CMB ([7,8]) all agree with an expansion that tends asymptotically to $q\simeq 1$ or $\omega \simeq -1$ (e.g. see [9] and references therein for a review of more recent results, including weak gravitational lensing). This behaviour is very consistent with a Cosmological Constant $\mathsf{\Lambda }$ (see [10,11,12]) where $H^2$ tends to $H^2=\mathsf{\Lambda }/3\equiv r_{\mathsf{\Lambda }}^{-2}$ and q tends to $q=1$. What does this all mean?

The term Dark Energy (DE) was introduced by [13] to refer for any component with $\omega <-1/3$. However, there is no fundamental understanding of what DE is or why we measure a term with $\omega \simeq -1$. A natural candidate for DE is $\mathsf{\Lambda }$ , which is equivalent to $\omega =-1$ and can also be thought of as the ground state of a field (the DE), similar to the Inflaton but with a much smaller ($\simeq {10}^{-50}-{10}^{-100}$) energy scale. $\mathsf{\Lambda }$ can also be a fundamental constant in GR, but this has some other complications ([10,11,12]).

2. Cosmic Acceleration

Current observations of the cosmos seem consistent with General Relativity (GR) with a flat FLRW (Friedmann–Lemaitre–Robertson–Walker) metric in comoving coordinates, corresponding to a homogeneous and isotropic space :

$$d{s}^2=-d{\tau }^2+a{\left(\tau \right)}^2\left[d{\chi }^2+{\chi }^{2}d\mathsf{\Omega }\right],$$

(1)

where we use units of $c=1$ and $a\left(\tau \right)$ is the scale factor. For a classical perfect fluid with matter and radiation density $\rho ={\rho }_m+{\rho }_R$, the solution to Einstein’s field equations (called LCDM) is well known:

$$H^2=\frac{8\pi G}{3}\rho +\frac{\mathsf{\Lambda }}{3}\equiv H_0^2\left[{\mathsf{\Omega }}_m{a}^{-3}+{\mathsf{\Omega }}_R{a}^{-4}+{\mathsf{\Omega }}_{\mathsf{\Lambda }}\right],$$

(2)

where ${\mathsf{\Omega }}_X\equiv \frac{{\rho }_X}{{\rho }_c}$, where ${\mathsf{\Omega }}_m$ and ${\mathsf{\Omega }}_R$ represents the current ($a=1$) matter and radiation density, ${\rho }_c\equiv \frac{3H_0^2}{8\pi G}$ and ${\mathsf{\Omega }}_m+{\mathsf{\Omega }}_R+{\mathsf{\Omega }}_{\mathsf{\Lambda }}=1$. The cosmological constant ($\mathsf{\Lambda }$) term corresponds to ${\mathsf{\Omega }}_{\mathsf{\Lambda }}=H_0^{-2}\mathsf{\Lambda }/3\simeq 0.7$ where $H_0\simeq 70$Km/s/Mpc. Given ${\mathsf{\Omega }}_m\simeq 0.3$ and ${\mathsf{\Omega }}_R\simeq 4\times {10}^{-5}$ we can use the above equations to find $a\left(\tau \right)$.

Cosmic acceleration is usually defined as $\ddot{a}/a$, where the dot represents a derivative with respect to proper time $\tau$. A derivative over Eq.2 shows that:

$$q\left(z\right)\equiv \frac{\ddot{a}}{a}\frac{1}{H^2}=\left({\mathsf{\Omega }}_{\mathsf{\Lambda }}-\frac{1}{2}{\mathsf{\Omega }}_M{a}^{-3}-{\mathsf{\Omega }}_R{a}^{-4}\right)\frac{H_0^2}{H^2}.$$

(3)

For $\mathsf{\Lambda }=0$ Eq.2-3 indicate that as time passes ($a\Rightarrow \infty$) we have that $H\Rightarrow 0$ and $q\Rightarrow -1/2$. This is because gravity opposes cosmic expansion and brings the expansion asymptotically to a halt. Including $\mathsf{\Lambda }$ brings the expansion to accelerate so that $H\Rightarrow r_{\mathsf{\Lambda }}^{-1}$ and $q\Rightarrow 1$. 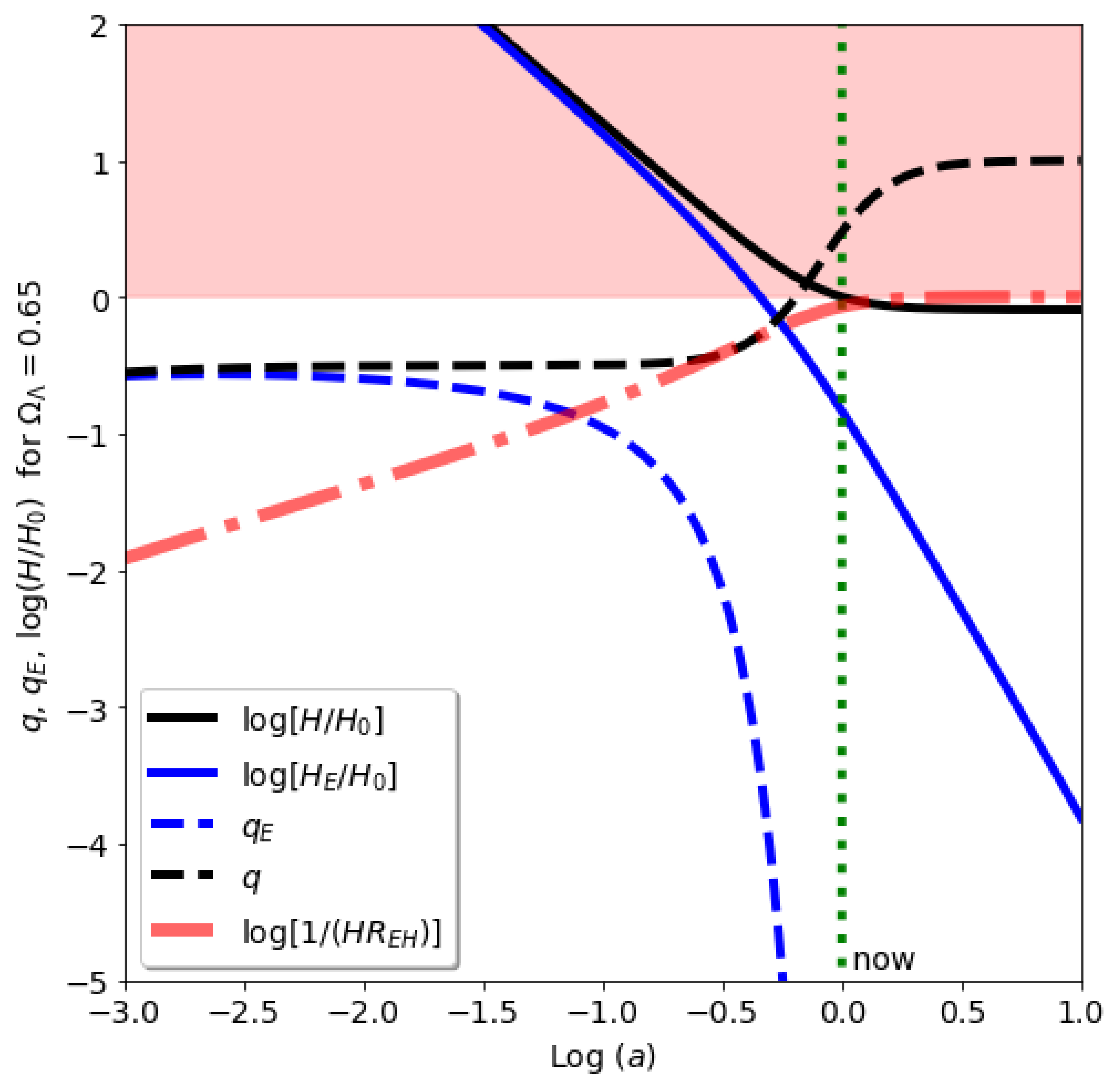This is illustrated as black lines in Figure 1 for ${\mathsf{\Omega }}_{\mathsf{\Lambda }}=0.7$. The effect of $\mathsf{\Lambda }$ is then interpreted as a mysterious new repulsive force (or Dark Energy) that opposes gravity.

But this interpretation of acceleration, based on $\ddot{a}/a$, corresponds to the acceleration of 3D space-like events, $d\tau =0$, of fixed comoving separation $\Delta \chi$:

$$d=a\left(\tau \right)\Delta \chi$$

(4)

so that $\dot{d}/d=\dot{a}/a$ and $\ddot{d}/d=\ddot{a}/a$. Such events are not causally connected and correspond to a non-local theory of Gravity or to the Newtonian approximation of action at a distance where the speed of light is infinite. We need a better definition of acceleration to identify the nature of its physical causes within GR.

3. Event Acceleration

To have a coordinate invariant measurement of cosmic acceleration we need to use the distance between the events that are causally connected. We introduce here the event expansion rate $H_E$ and acceleration $q_E$ to have an invariant measurement and to better interpret the effects of $\mathsf{\Lambda }$ in the cosmic expansion and therefore its possible mysterious meaning.

A photon emitted at time $\tau$ can travel following an outgoing radial null geodesic $ds=0$ which from Eq.1 implies $d\tau =a\left(\tau \right)d\chi$. The proper distance $R\left(\tau \right)$ traveled between the event at $\tau$ and the future event at ${\tau }_1>\tau$ is then (see e.g. [14]):

$$R(\tau ,{\tau }_1)=a\left(\tau \right){\int }_{\tau }^{{\tau }_1}d\chi =a\left(\tau \right){\int }_{\tau }^{{\tau }_1}\frac{d{\tau }^{\prime }}{a\left({\tau }^{\prime }\right)}$$

(5)

Thus, we argue that we should use R instead of d in Eq.4 as a measure of distance in cosmology to define cosmic acceleration and expansion rate. Such change is equivalent to a simple change of coordinates in the FLRW metric of Eq.1, from comoving coordinates $d\chi$ to physical coordinates $dR=ad\chi$:

$$d{s}^2=-d{\tau }^2+d{R}^2+R^2\left(\tau \right)d\mathsf{\Omega }.$$

(6)

We then have that $\dot{R}=HR-1$ (where, as before, the dot is a derivative with respect to $\tau$) and we can define the expansion rate between events as:

$$H_E\left(\tau \right)\equiv \frac{\dot{R}}{R}=H\left(1-\frac{1}{HR}\right)$$

(7)

where the additional term, $\frac{1}{HR}$ corresponds to a friction term. There is an ambiguity in this definition because R in Eq.5 depends also on the arbitrary time ${\tau }_1$ use to define R. To break this ambiguity we will fix here R to be the distance to ${\tau }_1\Rightarrow \infty$ (which corresponds to a possible Event Horizon):

$$H_E\left(\tau \right)\equiv \frac{\dot{R}}{R}=H\left(1-\frac{1}{H{R}_{EH}}\right)$$

(8)

where $R_{EH}\equiv R[\tau ,{\tau }_1=\infty ]$. As we will see in next section, this choice implies that $\frac{1}{H{R}_{EH}}$ is zero unless $\mathsf{\Lambda }\ne 0$. So this new invariant way to define cosmic expansion and acceleration reproduces the standard one when $\mathsf{\Lambda }=0$. But for $\mathsf{\Lambda }>0$ we have that the event expansion halts $H_E\Rightarrow 0$ (blue line in in Figure 1) due to the friction term (red line) for $a>1$, while the standard Hubble rate definition approaches a constant $H\Rightarrow \sqrt{\mathsf{\Lambda }/3}\equiv r_{\mathsf{\Lambda }}^{-1}$(black line). This might seem irrelevant at first look, but the physical interpretation is quite different. In the standard definition the expansion becomes asymptotically exponential (de-Sitter or inflationary expansion) while in our new definition it becomes static!

The event acceleration can then be measured as:

$$q_E\equiv \frac{\ddot{R}}{R}\frac{1}{H_E^2}=\left(q-\frac{1}{H{R}_{EH}}\right){\left[1-\frac{1}{H{R}_{EH}}\right]}^{-2}$$

(9)

As before, for $\mathsf{\Lambda }=0$ the friction term, $\frac{1}{H{R}_{EH}}$, makes little difference between q and $q_E$. For $\mathsf{\Lambda }>0$ the friction term asymptotically cancels the $\mathsf{\Lambda }$ term in $\frac{\ddot{a}}{a}$ (i.e. Eq.3) so that $\frac{\ddot{R}}{R}$ is always negative, no matter how large is $\mathsf{\Lambda }$ ($H{R}_{EH}\Rightarrow 1$ and $q_E=-\infty$). The net effect of the $\mathsf{\Lambda }$ term is to bring the expansion of events to a faster stop ($H_E\Rightarrow 0$) that in the case with gravity alone. This is illustrated in Figure 1. The $\mathsf{\Lambda }$ term produces a faster deceleration (than with gravity alone). This corresponds to an attracting (and not repulsive) force, as explained in more detail in the Appendix.

4. Event Horizon

But what is more relevant to understand the meaning of $\mathsf{\Lambda }$ is that the additional deceleration brings the expansion to a halt within a finite proper distance between the events, creating an Event Horizon (EH). This is the maximum distance that a photon emitted at time $\tau$ can travel following the outgoing radial null geodesic:

$$R_{EH}=a{\int }_a^{\infty }\frac{d{a}^{\prime }}{H\left(a^{\prime }\right)a^{\prime 2}}<\frac{1}{H[a=\infty ]}=r_{\mathsf{\Lambda }}$$

(10)

where $r_{\mathsf{\Lambda }}\equiv \sqrt{3/\mathsf{\Lambda }}$. For $\mathsf{\Lambda }=0$ we have $R_{EH}=\infty$, so there is no EH. But for $\mathsf{\Lambda }>0$ we have that $R_{EH}\Rightarrow r_{\mathsf{\Lambda }}$ (red line in Figure 1). We can then see that $\mathsf{\Lambda }$ corresponds to a causal horizon or boundary term. The analog force behaves like a rubber band between observed galaxies (events) that prevents them crossing some maximum stretch (i.e. the EH). We can interpret such force as a boundary term that just emerges from the finite speed of light (see the Appendix).

The FLRW metric with $\mathsf{\Lambda }$, asymptotically tends to the de-Sitter metric, which can be written as:

$$d{s}^2=-\left(1-r^2/r_{\mathsf{\Lambda }}^2\right)d{t}^2+\frac{d{r}^2}{1-r^2/r_{\mathsf{\Lambda }}^2}+r^{2}d{\mathsf{\Omega }}^2$$

(11)

This form corresponds to a static 4D hyper-sphere of radius $r_{\mathsf{\Lambda }}$. So in this (rest) frame, events can only travel a finite distance $r<r_{\mathsf{\Lambda }}$ within a static 3D surface of the imaginary 4D hyper-sphere. Thus there is a frame duality that allows us to equivalently describe de-Sitter space as either static (in proper or physical coordinates $r=a\left(\tau \right)\chi$ and t) or exponentially expanding (in comoving coordinates $\chi$ and $\tau$).

This frame duality can be understood as a Lorentz contraction $\gamma =1/\sqrt{1-{\dot{r}}^2}$, where $\dot{r}=Hr=r/r_H$. An observer in the rest frame, sees the moving fluid element $ad\chi$ contracted by the Lorentz factor $\gamma$. Therefore, the FLRW metric becomes de-Sitter:

$$a^2{d}^2\chi ={\gamma }^2{d}^{2}r=\frac{d^{2}r}{1-r^2/r_H^2},$$

(12)

This radial element corresponds to the metric of a hypersphere of radius $r_H\equiv 1/H$ that expands towards a constant event horizon $r_H\Rightarrow r_{\mathsf{\Lambda }}$ (see also [15] and the Appendix in [16]). This duality is better understand using our new measures for the expansion rate $H_E$ and cosmic deceleration $q_E$ based on the distance between causal events.

5. Comparison to Data

We show next how to estimate the new measure of cosmic acceleration, $q_E$, using direct astrophysical observations. As an example consider the Supernovae Ia (SNIa) data as given by the ’Pantheon Sample’ compilation ([17]) consisting on 1048 SNIas between $0.01<z<2.3$. Each SNIa provides a direct estimate of the luminosity distance $d_L\left(z\right)$ at a given measured redshift z. This corresponds to comoving look-back distance:

$$\chi \left(z\right)=a{d}_L\left(z\right)={\int }_0^z\frac{dz}{H\left(z\right)}$$

(13)

so that ${\chi }^{\prime }\equiv d\chi /dz$ gives us directly ${\chi }^{\prime }=r_H=H^{-1}$ , where the prime is a derivative respect to z. The second derivative gives us the acceleration:

$$q=1+\frac{{\chi }^{\prime \prime }}{a{\chi }^{\prime }};q_E=\frac{q-{\chi }^{\prime }/R_{EH}}{{(1-{\chi }^{\prime }/R_{EH})}^2}.$$

(14)

$R_{EH}$ is given by the model prediction in Eq.10 (arbitrarily fixed at ${\mathsf{\Omega }}_{\mathsf{\Lambda }}=0.85$ in both data and models). We adopt here the approach presented in [18], who used an empirical fit to the luminosity distance measurements, based on a third-order logarithmic polynomial:

$$\chi \left(a\right)=a{d}_L=a\left(x+A{x}^2+B{x}^3\right)H_0^{-1}ln10$$

(15)

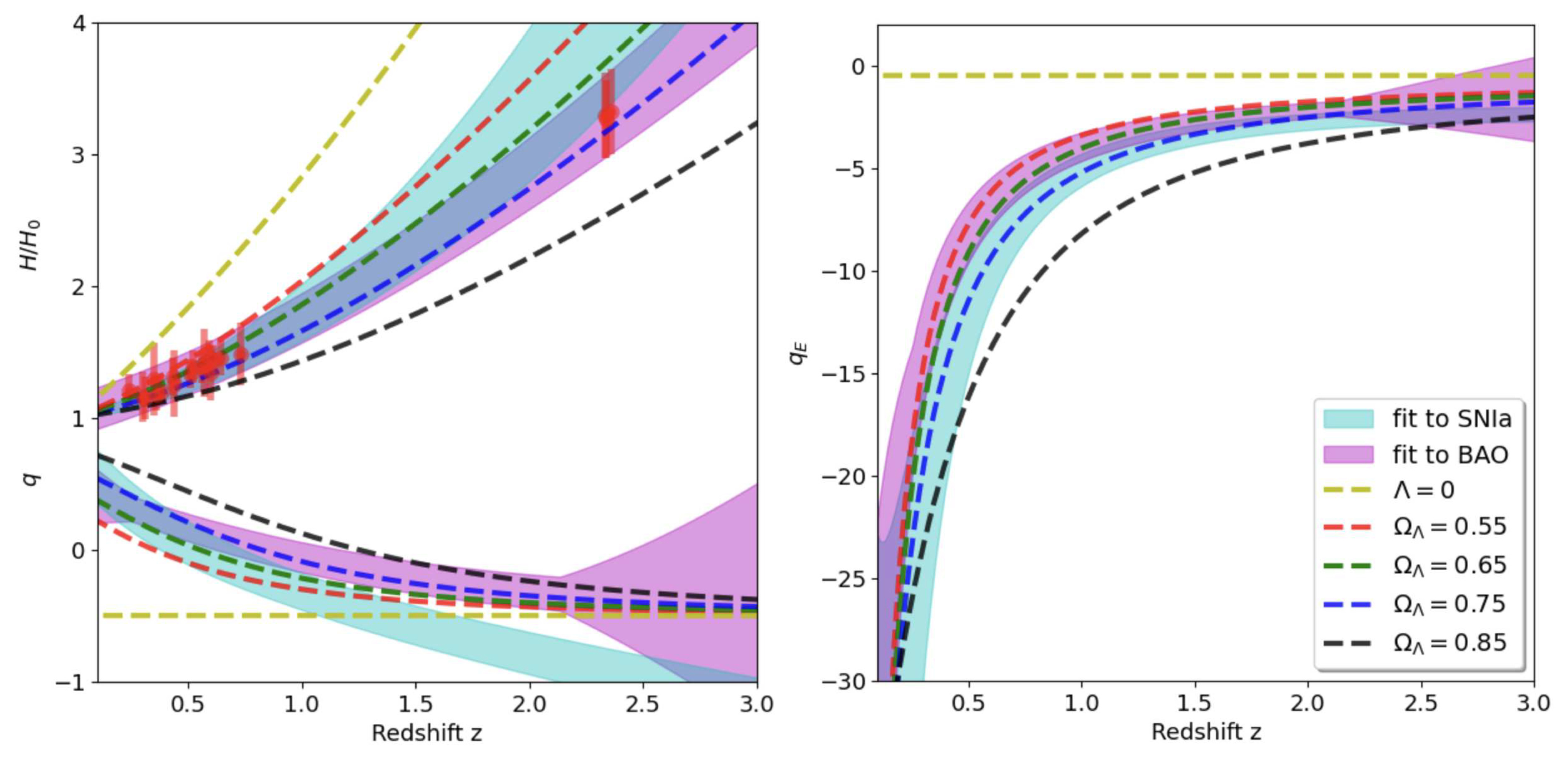
where $x=-{log}_{10}a$. [18] find a good fit to: $A=3.15\pm 0.12$ and $B=3.27\pm 0.41$ to the full SNIa ’Pantheon Sample’. We use these values of A and B and its corresponding errors to estimate H, q and $q_E$ using the above relations. Results for H and q are shown as shaded cyan regions in the left panel Figure 2. They are compared to the LCDM predictions in Eq.2 and 3.

There is a very good agreement in $H\left(z\right)$ for ${\mathsf{\Omega }}_{\mathsf{\Lambda }}\simeq 0.65$. At $z<1$, the $q\left(z\right)$ estimates are also consistent with the ${\mathsf{\Omega }}_{\mathsf{\Lambda }}\simeq 0.65$ predictions. But the detailed $q\left(z\right)$ evolution with redshift does not seem to follow any of the model predictions, specially for $z>1$. The $q\left(z\right)$ estimates are too steep compare to the different models predictions. If we compare instead the $q_E$ estimates (see right panel of Figure 2) we find a much better agreement with the model predictions. This seems to validate our $q_E$ approach, but it is not clear from this comparison alone if this is caused by the fitting function use in Eq.15.

To test this further we use measurements of the radial BAO data to estimate $q_E$. Such measurements give us a direct estimate of $H\left(z\right)$ (as first demonstrated by [19,20]) so they have the advantage over SNIa that we only need to do a first order derivative, to estimate q or $q_E$:

$$q=1+\frac{1}{aH}\frac{dH}{dz};q_E=\frac{q-r_H/R_{EH}}{{(1-r_H/R_{EH})}^2}.$$

(16)

As an illustration we use $H\left(z\right)$ measurements presented in Table 2 in [21]. This compilation of $H\left(z\right)$ is shown as red points with $2\sigma$ errorbars in the left panel Figure 2. The compilation include values from the clustering of galaxies ($z<1$) and Ly-alpha forest in QSO ($z>2$). The combination of two separated redshift ranges allows for a very good measurement of $dH/dz$ at the intermediate redshift ($1<z<2$), where we found (see above) the discrepancies in SNIa for q and $q_E$ model comparison. This provides a very good contraint on cosmic acceleration, indenpend of possible calibration errors in $H_0$ or sampling errors. This is something that we can not yet do with the current SNIa data, but will be very interesting to see in the near future with upcoming data. We fit a quadratic polynomial to the radial BAO data:

$$H\left(z\right)=H_0+H_{1}z+H_2{z}^2.$$

(17)

We have checked that the results presented here are very similar if we use a cubic polynomial. We find $H_0\simeq 68\pm 3$, $H_1\simeq 39\pm 8$ and $H_2\simeq 12\pm 3$ (in units of Km/s/Mpc) with strong covariance between the errors (the cross-correlation coefficient between $H_1$ and $H_2$ is $-0.99$). The value of $H_0$ is in good agreement with the Planck CMB fit ([8]) but in some tension with the SNIa local calibration: $H_0=73\pm 1$ (see [22]). This corresponds to either a local calibration problem (in SNIa, in radial BAO or in both) or a tension in the $\mathsf{\Lambda }$CDM model at different times or distances (see e.g. [23]). We ignore this normalization problem here and just focus on the evolution $H/H_0$ to measure cosmic acceleration q or $q_E$ (which are fairly independent of $H_0$).

In the right panel of Figure 2 we show (as shaded regions) the measurements for $q_E$ given by combining Eq.15 and Eq.17 with Eq.16. The measurements clearly favour models with large negative cosmic event acceleration $q_E<0$, which supports our interpretation of $\mathsf{\Lambda }$ as a friction term.

Comparing left and right panels in Figure 2 we see that both q and $q_E$ are rougthly consistent with models with ${\mathsf{\Omega }}_{\mathsf{\Lambda }}\simeq 0.7$ ( or $\mathsf{\Lambda }\simeq 2H_0^2$) in good concordance with $H\left(z\right)$ in the upper left panel of Figure 2.

Even when the underlying model for q and $q_E$ is the same, note how the measured q and $q_E$ data have different tensions with the model predictions as a function of redshift. In particular, the radial BAO and SNIa data sets show inconsistencies among them for q around $1.5<z<2.5$. This is a well known tension (see e.g. Fig.17 in [24]). This tension disappears when we use the corresponding estimates for $q_E$. Data is more consistent with the $q_E$ estimation.

One would expect that a perfect realizations of the LCDM model in Eq.2 would produce consistent results in both q and $q_E$. But deviations from LCDM and systematic effects can produce tensions in data, specially if we use a parametrization, like q, which refers to events we never observe. The q and $q_E$ parametrization of acceleration are more general than the particular LCDM model and the fact that data prefers $q_E$ is an important indication. Data lives in the light-cone, which corresponds to $q_E$ rather than q. At $z\simeq 2$ the difference between a light-cone and space-like separations is very significant and any discrepancies in the data or model will show more pronounced in the q modeling.

We conclude that the data shows some tensions with LCDM predictions (as indicated by q) but confirms that cosmic expansion is clearly decelerating (as indicated by $q_E$) so that events are trapped inside an Event Horizon ($R_{EH}$).

6. Discussion & Conclusion

We have shown here that the measured $\mathsf{\Lambda }$ term, which is usually interpreted as causing cosmic acceleration (see §Section 2), results in a faster cosmic deceleration of events (than that caused by gravity alone, see §Section 3). This explains the origin of the Event Horizon (EH, see §Section 4) that results from an expansion dominated by $\mathsf{\Lambda }$. It points in the direction that $\mathsf{\Lambda }$ is not a new form of vacuum energy ([10,11,12]) but a boundary or surface term in the field equations.

The EH measured in our cosmic expansion behaves like the interior of a Schwarzschild Black Hole (BH) and is identical to it if we assume that the space outside $R_{EH}$ is approximately empty (see [16]). We can also conjecture from this, that the interior dynamics of the Schwarzschild BH radius, $r_S=2GM$, could also have a similar $\mathsf{\Lambda }$ surface term $r_{\mathsf{\Lambda }}=r_S$, as part of its field equations, at least for expanding interior BH solutions. The $\mathsf{\Lambda }$ term becomes the actual mechanism that prevents anything from escaping the BH interior (see [25]).

The Event Horizon $R_{EH}$ measured with $q_E$ (i.e. Eq.10, which is equivalent to the presence of $\mathsf{\Lambda }$) also tell us that there is a finite mass $M_T$ trapped within $R_{EH}$. If we assume that the space outside $R_{EH}$ is approximately empty, such $M_T$ provides is in fact the explanation for the observed $R_{EH}$ and therefore for $\mathsf{\Lambda }$: $2G{M}_T=\sqrt{3/\mathsf{\Lambda }}$, as in the Schwarzschild BH (see [26]).

That $\mathsf{\Lambda }$ is fixed by the total mass $M_T$ of our universe is in good agreement with the physical interpretation presented here that $\mathsf{\Lambda }$ corresponds to a friction (attractive) force that decelerates cosmic events. In the Appendix we elaborate in this idea and revisit the Newtonian limit to show that $\mathsf{\Lambda }$ corresponds to an additional (attractive) Hooke’s term to the inverse square gravitational law.