Thus, the general procedure will be to use this system of equations to construct the function with an interesting cosmological behaviour. Since the constant C will change the possible solutions we will consider separately the two different scenarios, namely the case in which it can be eliminated, that is the non-projectable case and the case in which it has to be different from zero which is the projectable case.
4.1. Non-projectable case
Let us begin firstly with the non-projectable case in which
. We could start by proposing the simplest ansatz of cosmological interest, namely a constant Hubble parameter which describes a universe with an exponential acceleration ideal for an inflationary era. With this proposal in [
37] it was shown that these theories could result on a solution with two different periods of accelerated expansion. However with the reduced system of equations (that is after choosing the value of
) this proposal will lead us to a vanishing value for the
F function. Therefore we will propose instead an ansatz that describes an accelerated expanding universe but in the form of a power law with the time parameter, that is we propose that the scale factor in the Jordan frame has the form
where
n is a constant that will be considered as positive. Thus the Hubble parameter is
. With this ansatz using Eq. (
40) we obtain that
is related to the time variable as
We note from (
31) that we must always have
in order to have the scalar field properly defined. We will generally be interested on values of
n that describes accelerating expanding universes and therefore from the above we note that considering positive values for
we obtain the condition
. We note from this expression that
grows inversely with time with a behaviour similar to what we could expect of the curvature. In this scenario Eq. (
41) is written as
which leads to the solution
where
and
are integration constants and
The other equations on the system are immediately satisfied. Using (
43) we can find the form of
F as a function of
, we obtain in this way
where we have defined the positive constants
The last inequality follows from the condition
in both cases and we have also defined
We note that our general solution contains two terms of powers of
and thus we expect that it can fulfil the dS conjecture for any of the terms taken independently. The condition to have a non-negative potential for the scalar field in the Einstein frame (
36) in this case takes the form
Furthermore from (
48) we obtain that
Thus the condition (
50) can be easily fulfilled by taking positive values for the integration constants
and
. In this case we obtain
Since there is a minus sign in the first term the F function cannot have a definite sign for all values of , and thus we cannot fulfil the dS conjecture for all values of if we consider both terms at the same time as we anticipated. Thus let us consider each term separately.
First let us consider the positive power factor on
, that is we choose
and
, then the first dS conjecture (
35) leads to
In the other case if we consider the negative power factor on
by choosing
and
the conjecture leads to
In both cases the condition (
36) is satisfied. Thus the dS conjecture leads in both cases to an inequality for the HL parameter
. We also note that the faster we want the expansion to be, that is the bigger the value of
n, the closer we get to the value
. Thus in order to fulfil the conjecture independently of
and to have a fast expansion, we obtain that
must be bigger but close to
and thus away for its IR limit value. We also note that since in both cases the first dS conjecture leads to a region of validity for the
parameter and neither
nor
in (
47) depend on
, the form of the
function is not constrained by the conjecture, it only depends on
n, and thus we have the freedom to choose any positive values of interest for these terms, in contrast to the standard
case.
On the other hand, the second dS conjecture (
37) in this case is written in general as
Taking the positive powers of
, that is taking
this leads to
which can never be fulfilled because the term on the left hand side is always positive. Taking now the negative powers of
, that is taking
we obtain the condition
which again is never fulfilled. Thus we obtain that the second dS conjecture is never compatible with the obtained
function.
In summary, we have obtained that in these theories we can describe universes with a power law scale factor that describe expanding universes in the Jordan frame and this behaviour leads naturally to power law terms for the function. In the Einstein frame we obtain a scalar field in which we can apply the Swampland conjectures. The first one of the dS conjectures can be fulfilled for each term on the solution of F independently of leading to an inequality for the HL parameter which is in agreement with the difficulties of achieving this scenario in GR since it leads us to the opposite limit of GR that is it leads us to the UV limit for rapidly expanding universes. We also obtain that the second dS conjecture can never be valid for this form of the function.
Finally we would like to explore what is the behaviour described by these solutions on the Einstein frame where we have the scalar field coupled to gravity. For this we note that since both frames are related by the transformation (
27) in the Einstein frame we also have a flat FLRW metric, but now the scale factor is given by
Let us consider each term separately as previously done. For the negative powers of
we choose
and
. Thus the scale factor is
We note that
does not depend on
and therefore the result (
54) derived from the dS conjecture will not restrict the range of values that it can take. We obtain in this case that the exponent will always be positive, and thus the universe will always be expanding.
On the other hand, for the positive power term of
we choose
and
. Thus the scale factor is given by
Once again
is independent of
and always takes positive values describing expanding universes. It can be shown that in general
Thus, for negative powers of
in
F we have in the Einstein frame a more rapidly expanding universe than in the Jordan frame for
. On the contrary, for positive powers we have an slower expanding universe. For small time values
this behaviour is flipped and the fastest expanding universe corresponds to positive powers of
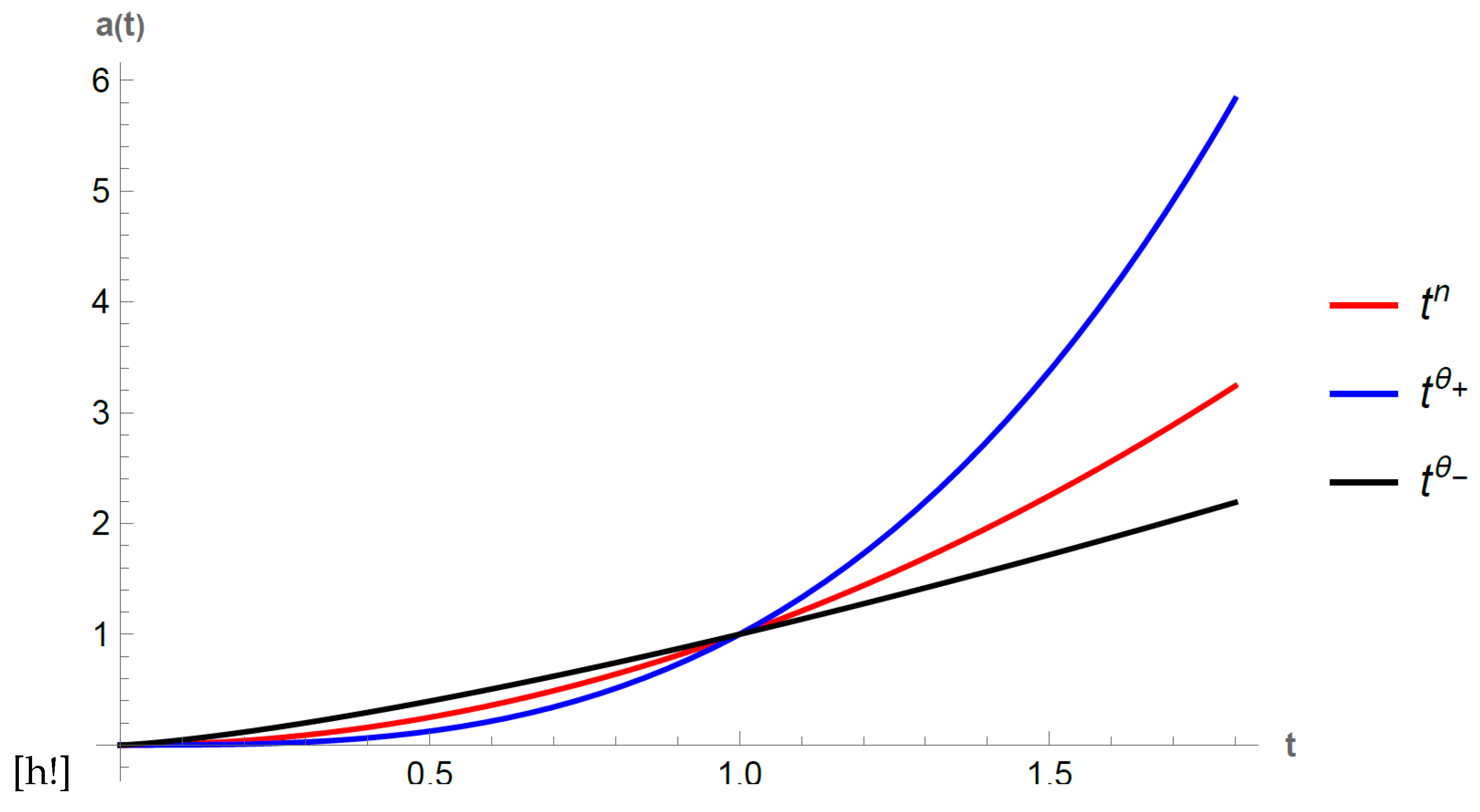
. We show the behaviour just described for
in
Figure 1.
4.2. Projectable case
Let us consider now the projectable case in which we take
in the system of equations (
38)-(
41). We are going to propose the same ansatz as before that is the scale factor as a power law on the time variable. Thus Eq. (
43) is still valid. In this case Eq. (
41) leads to
The solution of this equation consists of the homogeneous solution (the same as before with
) and a particular solution, in this form we obtain the solution
where we note that we must exclude the possible roots of the polynomial
, which are
. In this case the function
takes the form
where we have defined
The condition for the positivity of the scalar field potential (
36) leads in this case to
Since Eqs. (
51) hold we note that in order to fulfil this condition for all values of
we need
, thus
. Therefore we have two possibilities:
We note that in this case
Since the last term will always be present, if we take
the function
F will not have a definite sign for all values of
and thus it will not fulfil the dS conjecture for all values of
. Thus we will consider only the positive power and take
. In this case we could fulfil the dS conjecture for all positive values of
but not independently of it as we have stated before. The first dS conjecture in this case leads to
Moreover we note that in order to fulfil this inequality for all values of
we must ask each term within square brackets to be positive, in this form we obtain the two inequalities
We note that (
69) is the same as the one obtained in the non-projectable case (
53). However since both inequalities are on the same parameter, we only need to impose the stronger one. It turns out that (
69) is more restrictive than (
70) only if
. Thus for most of the values of
n the dS conjecture will be satisfied by (
70) for every value of
. Then, considering
leads us to a stronger condition for the parameter
for most cases.
From (
64) and taking
we note that in this case
Thus since
we have
for all
. However we have from these expressions that
which does not have a definite sign for all values of
. Therefore the second dS conjecture (
37) can not be studied in general for all values of
in this case.
In summary in the projectable case the first dS conjecture can still be fulfilled for all positive values of but not independently of it. The conjecture also leads to an inequality for the parameter and for most values of n this condition is more restrictive than the non-projectable case.
Once again the metric in the Einstein frame will also be a flat FLRW metric. In this case taking
the scale factor will be
Thus in the projectable case the scale factor has a dependence on
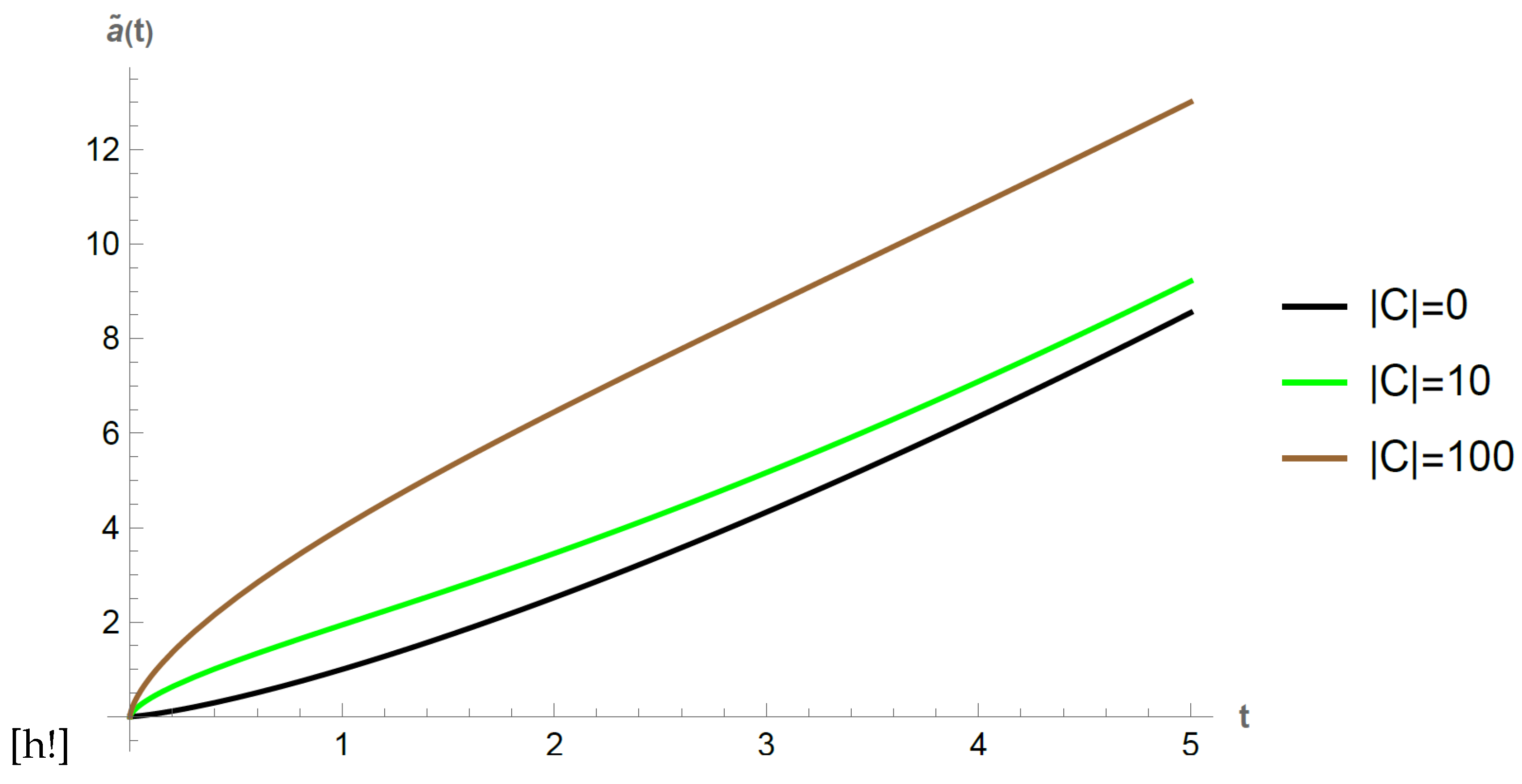
and the dS conjecture leads to a lower bound for it. Since both terms are positive, the universe is always expanding. In
Figure 2 we plot this scale factor choosing
,
and
for different values of
C. Since
in order to fulfil the conditions mentioned we need to take negative values for
C, thus we write
. We see that the effect of projectability, that is of values for
different than zero is that as
increases, the scale factor increases, making the expansion faster.
Finally let us note from (
64) that taking
and
we have two terms of positive powers of
. Thus we could hope to write this function in a form that resembles an approximation of an Einstein-Hilbert term plus corrections. We also note from the dS conjecture inequality (
69) that if
n is close to its limiting value
we can have access to the IR limit
. Thus let us study what form do our solutions take for
n close to
. We write
with
. In this case we can take
and the most restrictive inequality is (
69). From (
64) taking
,
and (
75) we obtain
For
we can make the approximation [
19]
Thus we obtain
with the correction term
Consequently the scale factor in the Einstein frame (
74) takes the form
In this case we can take values of
greater than 1 and the resulting universes are always expanding. However let us point out a subtle issue with this IR limit. From (
40) we obtain
We note that this value does not coincide with the GR value of
R (
23). Thus since we chose
the
IR limit does not correspond to GR. In order to perform a correct GR limit in Sub
Section 4.4 we are going to avoid this choice and consider the conjectures in the general case.
4.4. The general case
In the general scenario in which we consider
and
as independent parameters the action has the form (
28) and the scalar field is defined by (
31). We note that in general we do not have an action that can be divided into a sum of an action for gravity plus the action of a scalar field because of the third term in the action that combines the metric with the scalar field. However we do have an explicit definition for a scalar field with the correct form of the kinetic term in the action as before and we also have a definition for its corresponding potential. Thus we propose that the dS conjectures are still applicable for this action. A similar scenario was presented in [
24] were the conjectures were studied with an scalar field that is non canonically coupled to gravity as well.
In order to have a correct definition of the scalar field we need the parameter
defined in (
32) to be a real number which leads to
From the system of equations (
24) and (
25) we obtain
We are going to consider
and
, use the same ansatz for the scale factor in the Jordan frame as before, that is
and consider the non-projectable case (
). Thus the latter reduces to
With this ansatz from (
22) we obtain
with
. As a result, we can still interpret
as related to the curvature. In the particular case we considered only positive values for
which led us to a lower bound for
n compatible with expanding universes. For consistency and later convenience we will also ask in the general case for positive values of
, consequently we obtain the condition
which leads to
from where we obtain
. Thus, as a result of considering only a correct definition of the scalar field and positive values for
we have obtained upper bounds for
. Now let us proceed as in the particular case by solving (
84) and construct the
function. The general solution of (
84) is
with
where we have defined
Using (
85) we can integrate the latter expression to obtain
with
constants of integration and
The condition for the scalar field potential to be positive in this case takes the form
which is the same as in (
50) with
substituted by
. Therefore, in order to fulfil this condition for all values of
we ask each term to be positive. We choose
and
and we are left with the conditions
and
. The first condition is fulfilled with (
86) whereas the second leads to
From (
86) and (
93) it can be proven that we always have
and therefore the
function in the general case (
90) always consists of a negative power term of
and one with positive exponent. The negative power term has a negative coefficient whereas the posite power term has a positive coefficient as in the particular case studied before.
Thus, in the general case we have 3 inequalities (
82), (
86) and (
93) that constraint the values of
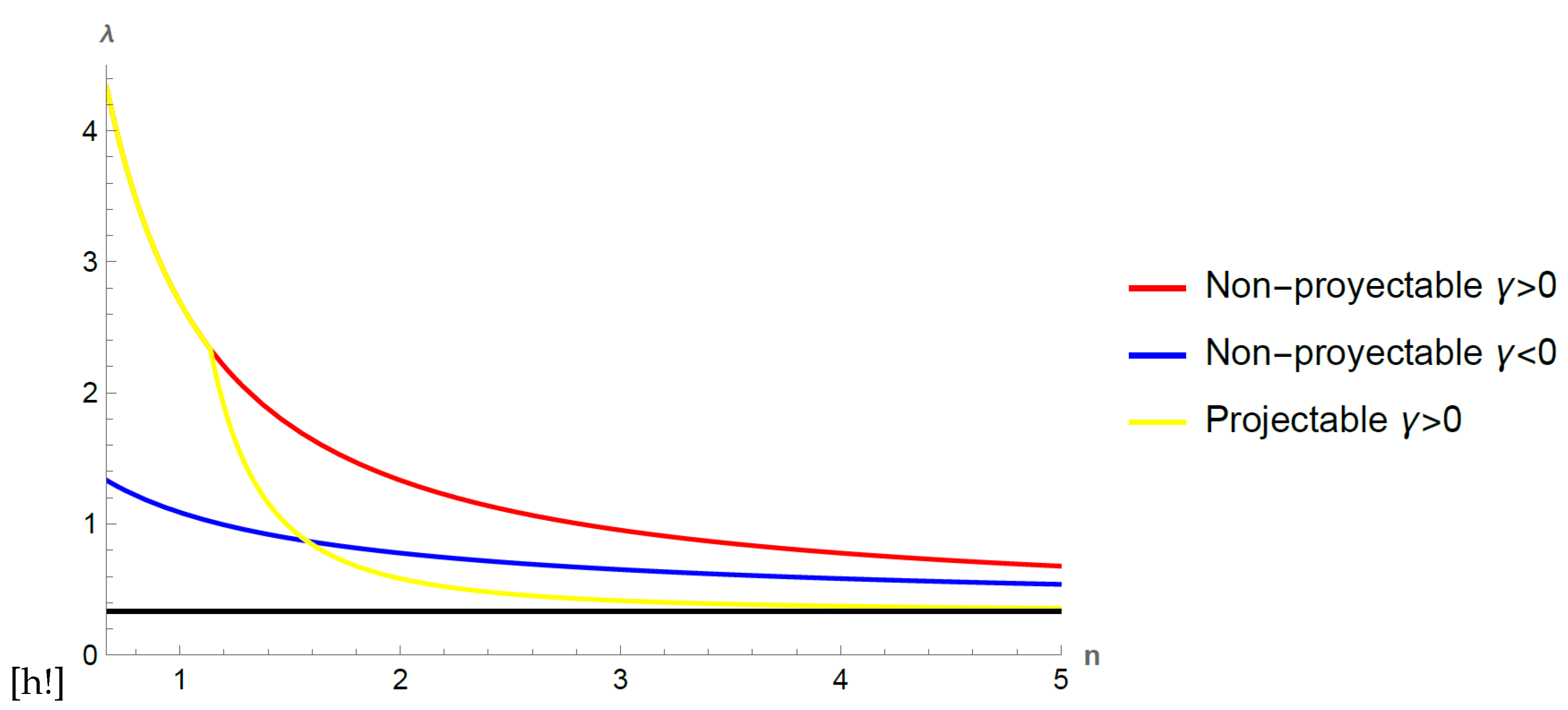
. Since the three are constraints on the same parameter it suffices to take the most restringent one, then these inequalities lead to
We note that the closer
is to zero, the closer
gets to its limiting value
. We also note that
in order to correctly fulfilled the inequalities and therefore the simpler version of
theories that do not take into account this term are inconsistent with this conformal transformation and thus the generalization of [
37] is needed.
The first dS conjecture has the form (
35) with the
function (
90). In order to fulfil this conjecture independently of
we take once again each term separately. For the negative power term we take
and the conjecture leads to
On the other hand for the positive power term we choose
and the conjecture leads to
In general both expressions (
95) and (
96) lead to a region of validity for the
parameter in terms of
and thus we can compare the resulting bounds with (
94) to investigate the region of compatibility. However the expression are complicated to solve analytically and thus we carry out a numerical analysis.
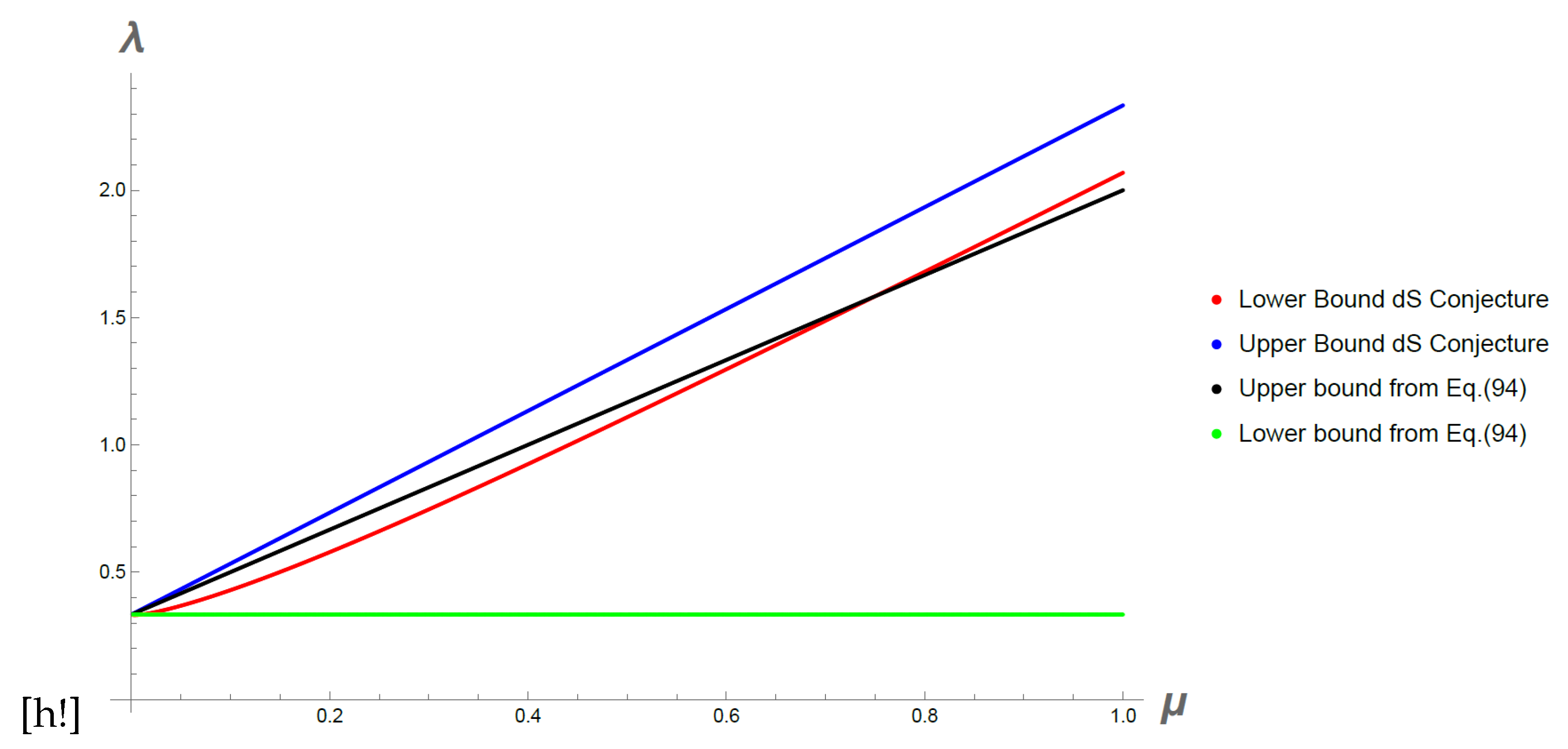
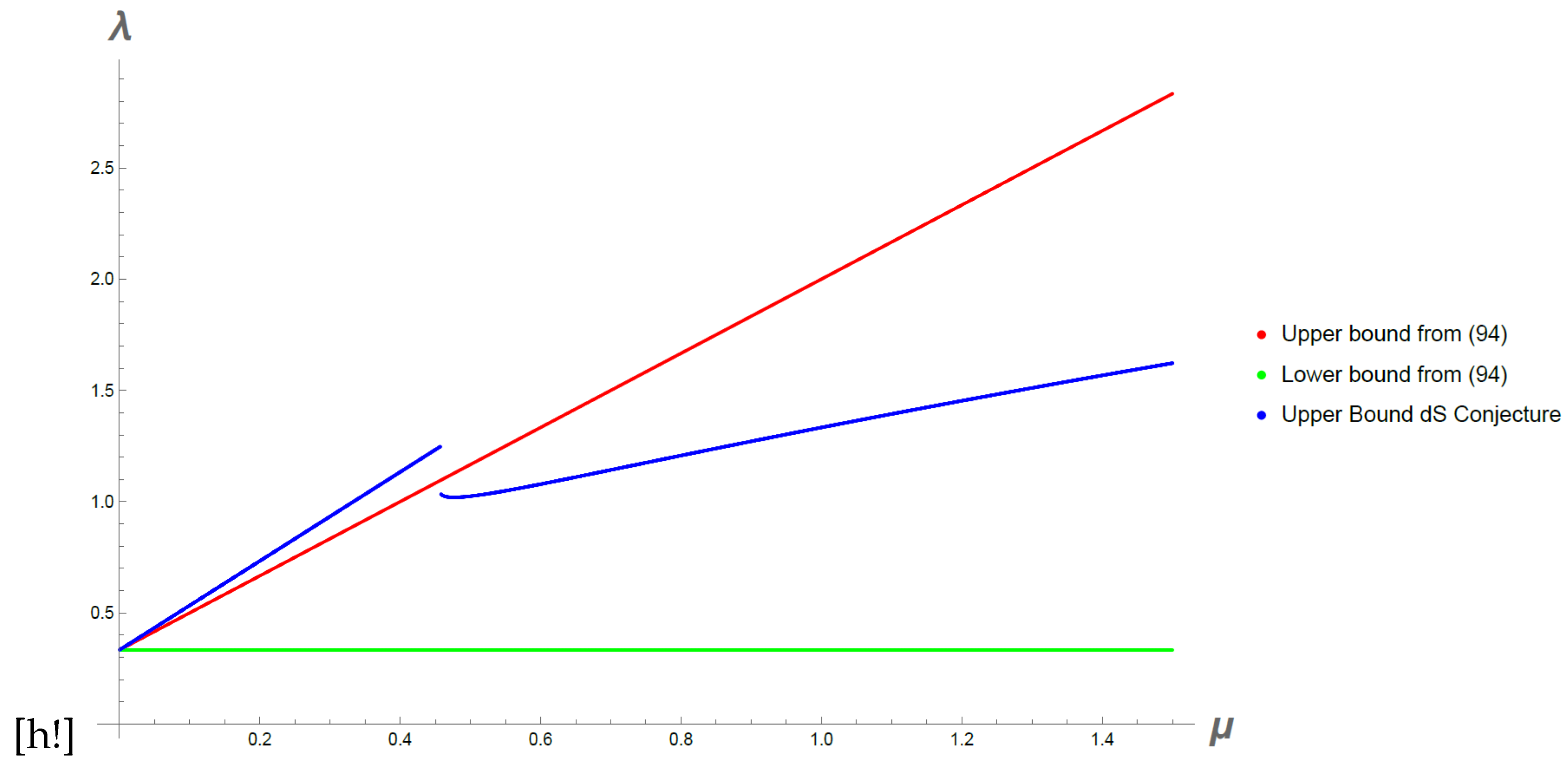
For the negative power term upper and lower bounds coming from (
95) are found numerically. In
Figure 4 these bounds are shown for
,
and varying the
parameter. We also show the upper and lower bounds coming from (
94). We note that in order to fulfil both expressions, we need the upper bound from (
94) to be bigger than the lower bound from (
95) and thus
is bounded from above and consequently the allowed values of
increase as
increases but not above a maximum value. For smaller values of
n or bigger values of
c the restriction on
is more severe and
gets closer to
.
For the positive power term in
we find with a numerical analysis that for small values of
(
96) leads to an upper bound for
that is bigger than the one coming from (
94) and thus the conjecture is satisfied as a consequence of (
94). On the other hand, for values of
big enough (
96) leads to two regions of validity, one is an upper bound which is smaller than (
94) and one is a region with an upper and lower bounds bigger than (
94) and therefore inconsistent. Thus, for big values of
the dS conjecture is more restrictive than (
94). In any case, both upper bounds grows with
and thus, in this scenario we can have access to bigger values of
. It only gets restricted to be close to
if
is small enough. In
Figure 5 we show this behaviour for
and
. For smaller values of
n or bigger values of
c the region where the dS conjecture is more restrictive than (
94) is found for smaller values of
.
The second dS conjecture leads to (
55) with
instead of
and thus for the positive power term we have (
56) with
and for the negative power term we have (
57) with
. Therefore, the second dS conjecture is never fulfilled in the general scenario as well.
In the general case the metric in the Einstein frame will also have the FLRW form with the scale factor given by
Thus, for the negative power term we choose
and
and the scale factor takes the form
with
Similarly for the positive power term we choose
and
and the scale factor takes the form
with
In the general scenario the scale factor will depend on
and
and therefore the inequalities (
94) and the region coming from the first dS conjecture will restrict it. Moreover it can be proven that we always have
and thus we always have expanding universes.
Thus, the general scenario is similar to the particular case, that is, in order to have a properly defined scalar field and to fulfil the first dS conjecture gets restricted in terms of around and the resulting description in the Einstein frame are expanding universes. For the positive power term however we can have access to bigger values of by increasing the values of which will be important to consider the limit of interest in the following. In this case we also obtain that the second dS conjecture is never fulfilled.
Furthermore, the general scenario allows us to correctly perform the limit
which as stated before should correspond to standard
. In this limit (
82) and (
93) are automatically satisfied whereas (
86) leads to
. The fist dS conjecture will correspond to upper bounds for
n.
For the negative power term (
95) leads to
which is inconsistent with
c being an order 1 constant. For the positive power term (
96) leads to
The biggest upper value is obtained in
and corresponds to approximately
. Using (
88) we obtain for the allowed values of the exponent in the
F function to be
The allowed region (
103) must be compared to the one obtained in the standard
case (
15). The lower bound from (
103) comes from the dependence of
on
n and the condition
coming from (
86). Since the system of equations (
24) and (
25) reduces to standard
in the limit
,
, after proposing the ansatz
, the same form of the
f function (
90) should emerge and thus, after imposing
in the standard
theories we will obtain the same lower bound. The upper bound in contrast is different. This comes from the fact that although in the Jordan frame the
theory recovers standard
in the mentioned limit, the transformation to the Einstein frame for
theories is only on the three-metric (
27) whereas in standard
the conformal transformation used is in the complete 4-metric (
5). Thus the resulting scalar field and scalar potential are different and therefore the first dS conjecture has a different form. It is interesting however that even though the analytic form of both upper bounds are different, their maximum value are not too far. In standard
we get approximately
whereas in
we get approximately
. Thus
theory allows a bigger region for the exponent although it is still not too far from 1. Therefore in the limit
the
theories lead to a consistent result with the standard
theories, that is, the power of
gets restricted to be bigger than 1 (actually bigger than
) but not too big, smaller than approximately
. From (
101) we obtain that in this limit the scale factor has the form (
100) with
Thus, there is enough room for accelerated expansion in the Einstein frame.
Finally, let us study the projectable case. Since the obtained form for the
F function has the same form as the one obtained in the particular case, it only changes the specific form of the exponents, the projectable case can be treated as it was done in Sub
Section 4.2. In this case the
F function is written as
The condition for a positive potential is written analogously to (
66) and it can also be fulfilled for all values of
by taking the coefficient for the new term to be positive and
. Once again we take
, then the first dS conjecture is written with two terms as in (
68) and thus in order to fulfil the conjecture for all values of
we obtain two inequalities. The first is the same as in (
96) whereas the second is
Thus we obtain an extra inequality that has to be taken at the same time with (
94) and (
96) but now it is a lower bound for
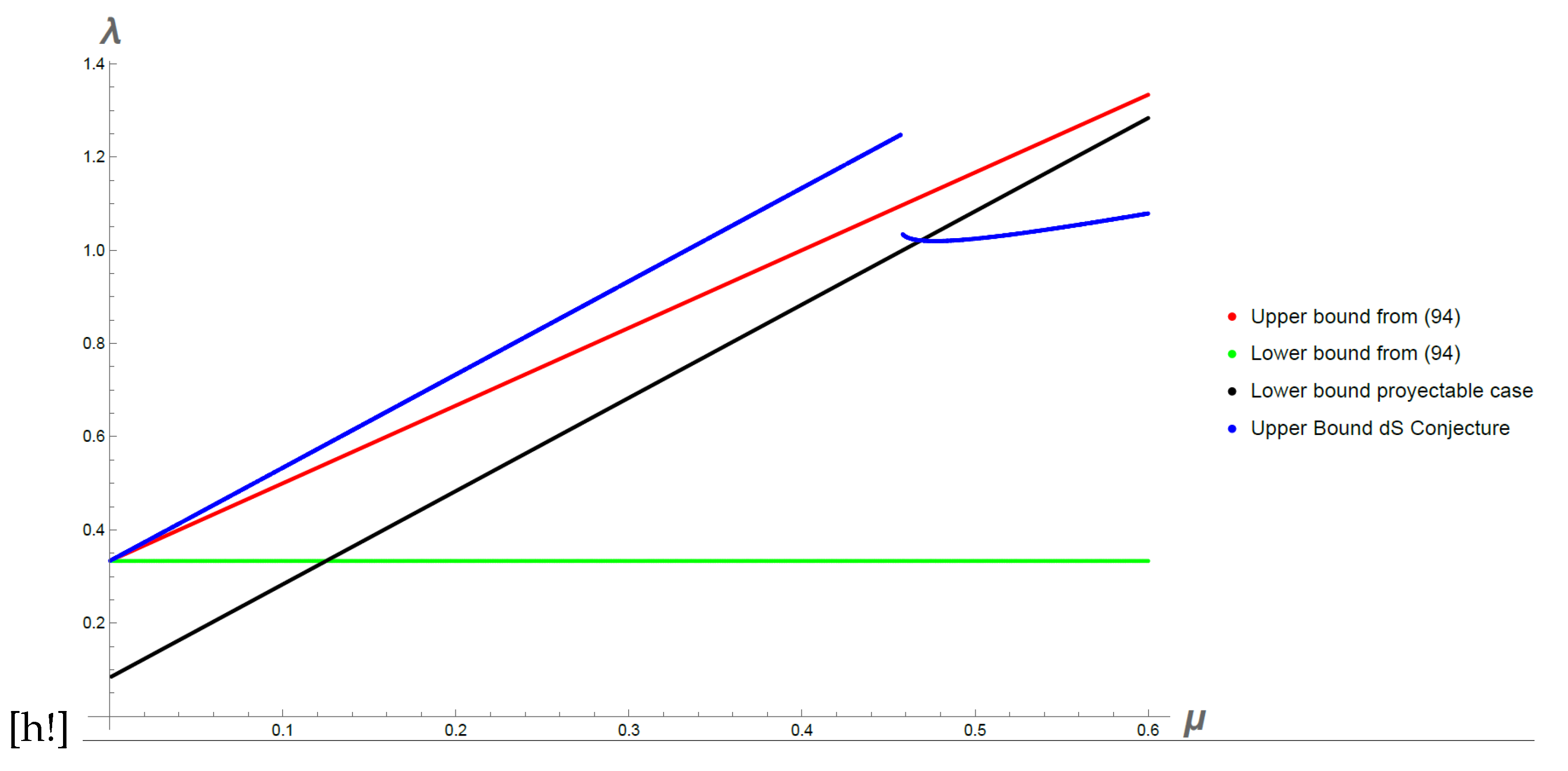
. In
Figure 6 we show the bounds shown earlier for (
94) and (
96) but we now add the bound coming from (
106) for
and
. We note that in order to fulfil the complete system of inequalities there is an upper bound for
and thus
gets restricted once again to be close to
.
In the
limit (
106) reduces to
the upper bound gets it maximum value at
and corresponds to approximately
. Thus in the proyectable case, the upper bound on
n is more restrictive than in the non-proyectable case, this leads to
Thus we get bounds that are even more restrictive than standard
in this case. However, the form of the
F function has an extra power term with a exponent of
. If we take small values of
n around
we can write this function as GR plus correction terms as in (
78) (the only difference will be the coefficients of each term and the exponent of the second term in (
79)) since in this case we can obtain consistently
in the mentioned limit.