Prerpints.org logo
Preprint
Article

Multiobjective Optimization of Weight Reduction Process Parameters of Micropolyester Woven Fabrics Using Taguchi-Grey Relational Analysis

Altmetrics

Downloads

109

Views

38

Comments

0

This version is not peer-reviewed

Submitted:

29 August 2023

Posted:

31 August 2023

You are already at the latest version

Alerts
Abstract
The weight loss process variables of alkali-treated micropolyester woven fabric were optimized and reported in this study. The grey relational analysis (GRA) with the help of the Taguchi technique was efficiently used to optimize the key variables of this process. The caustic soda concentration, treatment temperature, and weight loss machine speed were considered the control or design parameters. The weight reduction percentage, air permeability, tensile strength, and thermal resistance of alkali-treated woven polyester fabrics were also considered as responses in this study. The experiments were implemented according to a 33 full factorial design. The levels of the control parameters which yield the maximum weight reduction, tensile strength, air permeability, and minimum thermal resistance of the treated polyester fabrics were found to be NaOH concentration and treatment temperature with the highest levels, and machine speed with the lowest level. This means that a 27% caustic soda concentration, treatment temperature of 125 OC, and machine speed of 40 m/min exhibited the optimum properties of the treated micropolytester fabrics. It is also proved that the treatment temperature is the most influential factor affecting the micropolyester fabric’s properties. The confirmation test which was carried out in this study confirmed that the GRA improved the alkali-treated polyester fabric properties.
Keywords: 
Subject: Engineering  -   Other

1. Introduction

The production scale of polyester fabrics occupies the forefront of synthetic fibers around the globe. This is because of the excellent characteristics of this type of fabric, such as high strength, good elasticity, high chemical stability, good wear resistance, easy wear and wash, corrosion resistance, and good light and heat resistance [1,2,3,4,5,6,7]. Due to their prominent properties, polyester fabrics are widely used for clothing, home furnishing, medical textiles, technical applications, protective clothing, and sportswear [8,9,10,11].
Despite noteworthy properties, polyester fabrics have a waxy and clammy feel, are prone to forming high static charges, and tend to pill, especially with blends. Also, they have low moisture regain, are hydrophobic, and are flammable to a great extent [12,13,14,15,16]. These disadvantages adversely influence polyester fabrics' application in human daily life [17,18,19].
Many drawbacks of the polyester fabric have been enhanced through different pretreatments. One of the most popular techniques is the de-weighing (weight reduction process), or more precisely, the alkaline hydrolysis of polyethylene terephthalate (PET) fabric by a solution of sodium hydroxide with a specific concentration. The weight reduction of PET fabric is a finishing process that has long been recognized in the textile industry. This finishing process aimed to enhance the wettability, drape, and handling characteristics of polyester fabrics leading to a silky touch handle [20]. In this process, aqueous sodium hydroxide hydrolysis attacks the PET fibers. Over time, this hydrolysis attack starts at the fibers' outer layers and works through the center. As a result of this hydrolysis, the ester bonds in the PET polymer chains are broken down at ester linkage, leading to the hydroxyl and carboxyl groups, which enhance polarity and to form hydrogen bonds with water molecules, which in turn improve fabric wettability [21,22,23].
The key parameters of the weight loss process include caustic soda concentration, squeezing rollers’ pressure, and presence of an accelerator, the effect of pre-setting, fabric structure, time, and temperature of the treatment. The influence of the majority of these parameters on the physical, mechanical, handle, thermal, and electrical characteristics of polyester woven fabrics has been extensively investigated in numerous research papers.
To the best of my knowledge, despite the importance of the process of weight reduction of the PET fabrics, none of the researchers optimized its operational parameters. Therefore, the overarching objective of this study is to conduct a multiobjective optimization of the weight loss process parameters in terms of PET fabric properties. The key parameters of the weight loss process to be optimized were sodium hydroxide concentration, treatment temperature, and machine speed. The optimization technique was conducted using the Taguchi technique and grey relational analysis in terms of alkaline-treated woven polyester fabric properties such as weight reduction percentage, thermal resistance, air permeability, and tensile strength.

2. Experimental work

2.1. Materials

Throughout this study, 100% bleached polyester woven fabrics with plain weave structure, warp yarn density of 32 ends/cm, weft yarn density of 25 picks/cm, and mass per unit area of 198m g/m2 were used accordingly. These types of fabrics were produced on a Picanol Rapier (GamMax 6- R-190) weaving machine from drawn-textured yarns DTY with counts of 135d/150f for both warp and weft yarns. This means that the woven types of yarns are made from micro polyester filaments with a linear density of 0.9 denier per filament. After bleaching, the undertaken micro polyester filament woven fabric has undergone alkaline hydrolysis with caustic soda under different conditions.
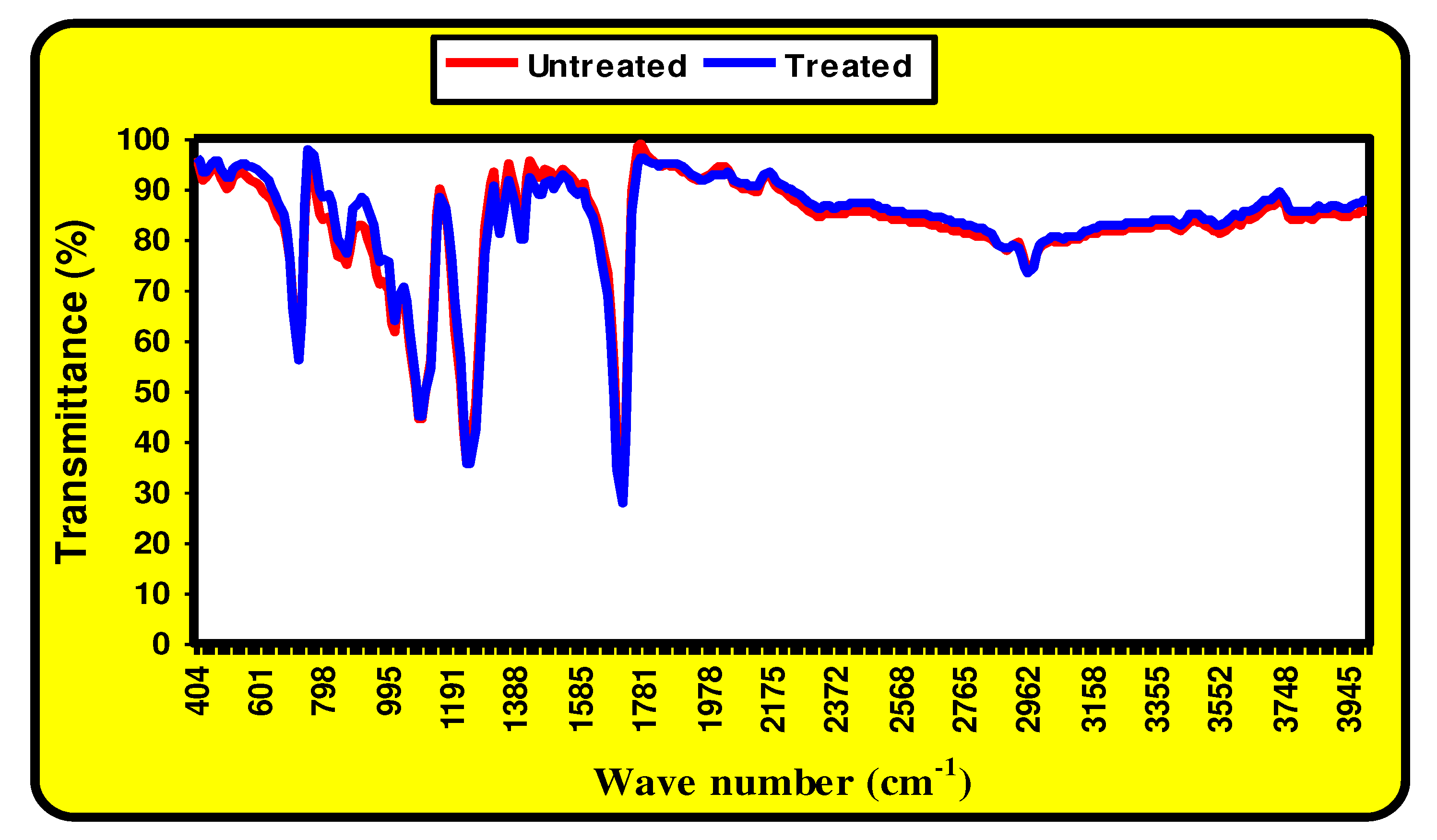
The scanning electron microscope of treated and untreated (blank) microplyester woven fabric samples was displayed in Figure 1. It can be shown from this figure that the alkaline hydrolysis polyester fabric has elliptical and elongated pits or cavities toward the polyester filament axis. It was reported that the cavities become wider and deeper with the increase in caustic soda concentration. In comparison to untreated fabric, the treated one is thinner and rougher. The FTIR of the untreated (blank) and treated polyester fabric was also presented in Figure 2.

2.2. Weight reduction process

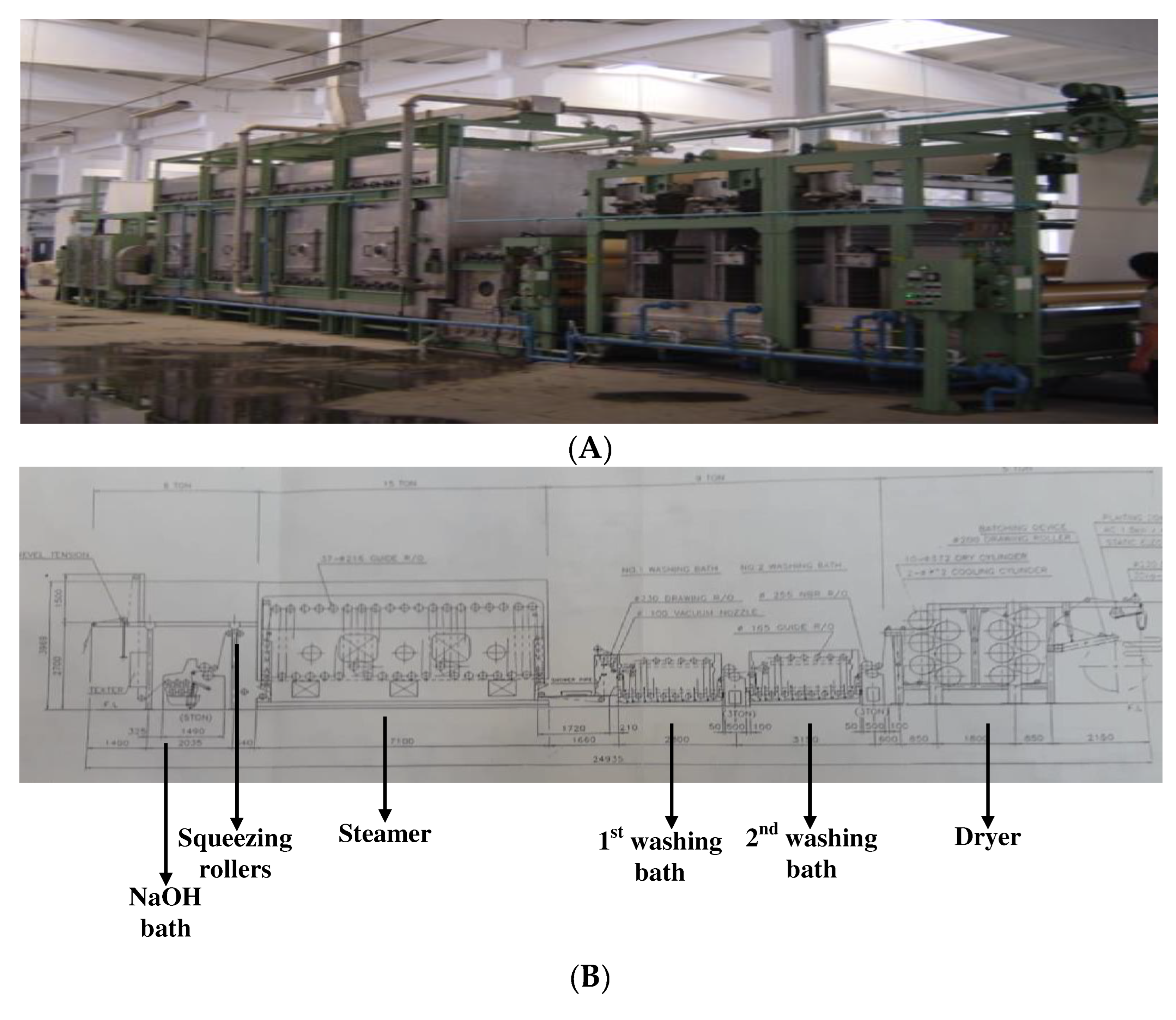
In the course of this study, alkaline hydrolysis of drawn textured polyester fabric was carried out using JSSR-AW/2W continuous weight reduction machine. Figure 3A and 3B respectively depict the general view and sketch diagram of the used weight reduction machine.
Alkaline treatment with NaOH, heat treatment (steaming), washing, and drying are the four key stages in the alkaline hydrolysis of polyester woven fabrics. Micropoltyester fabrics woven from drawn texture yarns (DTY) were treated with sodium hydroxide (NaOH) in an aqueous solution at the ambient temperature (25–30 oC) and with three different levels of concentrations, i.e. 19%, 23%, and 27%. Following the soda bath, the polyester fabrics are squeezed between two rollers to remove any excess soda from the fabric. Squeezing rollers are subjected to pressures of 2 bar. The alkali-treated woven fabrics were then moved to the steaming chamber, in which the primary interaction between the polyester microfilament and NaOH takes place. The steamer in this investigation has three different temperatures, namely, 90 OC, 110 oC, and 125 OC. The alkali-treated polyester fabrics are then washed twice, with the final rinse taking place at room temperature with running water. Finally, the treated woven fabrics are dried using twelve heated cylinders by superheated steam. It is worth noting that the operating widths of cylinders in this machine are 160 cm although their actual widths are about 180 cm.
The levels of control parameters of the weight loss process were tabulated in the following Table 1.
As the steamer is the main and substantial reaction chamber in the weight reduction machine, the staying time of the treated polyester in this room is the main factor upon which different properties of the fabrics depend. The steaming chamber contains approximately thirty-seven heated rollers around which the treated polyester fabrics are wrapped tightly. Of these, 18 cylinders are at the top of the steamer, 17 cylinders at the bottom, and two floating cylinders. The floating cylinders stop the weight reduction machine when the treated fabrics are torn or any problem occurs. It is worth mentioning that the treated fabrics move vertically between the top and bottom cylinders. The diameter of each cylinder in the steamer is around 216 mm (21.6 cm), and the distance between the top and bottom cylinders is approximately 1.8 m, therefore, the treated fabrics move about 80 meters in the steaming chamber. As the speed of the weight reduction machine is varied with three levels, namely 20, 30, and 40 m/min, therefore, the staying times of the treated polyester fabrics in the steamer are about 4 min, 2.7 min, and 2 min respectively.
Polyester filaments are mostly subjected to alkaline hydrolysis in the steamer at high temperatures. During the hydrolysis process between NaOH and polyester filament, PET will be divided into its monomers, Ethylene Glycol (EG), and Terephthalic Acid (TA), as shown in Figure 4. It has been confirmed that caustic soda only affects the surface of the filament, and not the filament core. Because of the cross-linking and degree of crystallinity of polyester, the hydrolysis reaction with caustic soda is not violent and occurs slowly at the filament surface. It was found that the treatment temperature has a huge influence on the hydrolysis reaction rate and its degree as well [31].

2.3. Laboratory testing

Before the measurement, the treated and untreated (blank) fabric samples were placed in standard conditions for a full day to be dried and to prepare them for measuring their intended properties. Each fabric's property has examined ten times in the warp direction, and the average of individual readings was calculated.
The mass per unit area of the blank and treated polyester fabrics was measured in accordance with ASTM D3766/D3776M-20. Fabric samples with a surface area of 100 cm2 were accurately cut and their weights were precisely measured on an electronic balance. The results of fabric weight were converted into g/m2.
The weight reduction percentages of all treated polyester fabrics were determined according to the following formula:
Weight   reduction   ( % ) = m 1 − m 2 m 1 × 100
where m1 and m2 are the masses per unit area of the blank and the treated fabric samples respectively.
Thermal resistance refers to the ability of a substance to withstand heat flow through it. As the thermal resistance increases, the heat loss through the fabric decreases. The air that is trapped within and between individual fibers is the main cause to give the fabric heat resistance. The thermal resistance equals the reciprocal of thermal conductivity times the fabric thickness. The following formulas can be used to calculate the fabric's thermal resistance [20,32].
R = t λ
where R indicates the fabric's thermal resistance (W-1m2K), λ denotes the thermal conductivity, and t is the fabric thickness in centimeters.
The effective thermal fabric conductivity can also be measured and calculated using the following equation:
λ = W × h A Δ T ( W / cm . ° C )
(W/cm.oC)
(3)
where W is the heat loss (Watt), h is the fabric thickness (cm), A is the area of the B.T-heat plate (cm2), and ΔT is the temperature difference across the sample (oC).
Air permeability is a measure of air flow in cubic centimeters perpendicularly through the fabric surface area of one square centimeter per second at a differential pressure of 12.5 cm of water head. In addition to fabric comfort, air permeability is most influential property for different applications, such as tents, industrial filters, parachutes, sail fabrics, raincoat materials, airbags, etc. In this paper, the air permeability of the blank and de-weighted fabrics was evaluated according to the standard test method ASTM D737 using an air permeability tester. The tensile strength of the fabric samples under study was also investigated according to ASTM D5034 using the Instron tensile strength instrument of model 4411.

2.4. Experimental design

According to the chosen control factors and their intended levels, a 33 full factorial design was implemented to address these variables. Therefore, twenty-seven fabric samples were produced and treated with different conditions. Besides, one fabric sample (blank sample) will not be undergone any treatment. As a result, the final total number of the produced fabric samples is 28 samples.
The experimental arrangement using 33 factorial design which shows how the treated fabric samples were produced throughout this investigation was tabulated in Table 2. According to this table, the sequences of experiments were carried out in this study.
The results of the statistical analysis will concentrate on the main effects and their interaction effects will be excluded. For each trial, the analysis was conducted using the average of ten individual readings. Table 3 shows the intended control factors, their levels, and their respective fabric properties, namely the percentage of fabric weight reduction, tensile strength, air permeability, and thermal resistance. The untreated fabric properties were also listed in Table 4.

2.5. Optimization technique using Taguchi

The optimization of any process parameters is the primary step in the Taguchi approach to obtain excellent quality without raising the cost. It should be noted that the Taguchi approach is originally used to optimize single performance characteristics [33].
In this sophisticated technique, the optimal parameters can be obtained using the signal-to-noise ratios (S/N ratios). In general, there are three different modes of S/N ratios; these are the nominal-the-best, the higher-the-better, and the smaller-the-better. The following equations can be used to evaluate each mode.
- The nominal- the- best
η = 10 log [ y 2 − S 2 ]
- The higher, the better
η = − 10 log [ 1 n ∑ i = 1 n 1 y i j 2 ]
- The smaller, the better
η = − 10 log [ 1 n ∑ i = 1 n y i j 2 ]
where η is the S/N ratio, yij is the ith result of the experiment for jth factor, S 2 , and y _ denote the sample variance and mean respectively, and n is the number of replications of the ith experiment.
Since the aim of this study is to establish alkali-treated micropolyester woven fabrics with high weight reduction, high tensile strength, high air permeability, and low thermal resistance, thus it is interested in achieving larger values for weight reduction, tensile strength, and air permeability and a smaller value for thermal resistance.

2.6. Grey relational analysis (GRA)

The term grey refers to information that is either undetermined or incomplete. The GRA technique is used effectively to solve complex relationships between many performance characteristics. Using this technique, the multi-response characteristics are transformed into single-response characteristics. To perform this analysis, the following stages should be completed in order: normalization step, obtaining the grey relational coefficient (GRC), and getting the grey relational grade (GRG).
To reduce the variability and overcome the impact of using diverse units for the response characteristics, the S/N ratio of each response characteristic is normalized to be in the range between zero and one. Generally speaking, in accordance with the kind of performance characteristics, the normalization is accomplished and an appropriate equation is used. For the higher-the- better and the smaller-the- better, the following equations can be used.
y i * ( k ) = y i 0 ( k ) − min y i 0 ( k ) max y i 0 ( k ) − min y i 0 ( k ) For higher the-betterk
y i * ( k ) = max y i 0 ( k ) − y i 0 ( k ) max y i 0 ( k ) − min y i 0 ( k ) For smaller the-better
where min y i 0 ( k ) , and max y i 0 ( k ) denote the smallest and largest values of the original experimental data for the kth response respectively. Also, y i 0 ( k ) denotes the original experimental value in the ith experiment for the kth response. The value of y i * ( k ) indicates the normalized data in the ith experiment and kth response. Typically, the greatest value of the normalized data, which is equal to one, was depicted as a superior performance property [34].
The normalized data were then used to calculate the grey relational coefficient (GRC), which represents the relationship between the optimal and actual normalized experimental data. Typically, the following equation is used to calculate the GRC:
ζ i ( k ) = Δ min + ζ Δ max Δ o i ( k ) + ζ Δ max
where Δoi(k) refers to the deviation sequence of the reference and comparability sequences, and it can be calculated using the equation 10.
Δ o i ( k ) = ‖ y 0 * ( k ) − y i * ( k ) ‖
where ζ is referred to as the distinguishing coefficient, which can take any value ranging between zero and one. In this study, ζ is equal to one. The y 0 * ( k ) , and y i * ( k ) are the sequence and comparability sequence respectively.
The GRC for each performance characteristic is averaged to evaluate the grey relational grade. The following equation is used to calculate the grey relational grade:
γ i = 1 n ∑ k = 1 n w i ξ i ( k )
where γi indicates the final grey relational grade for the ith experiment and n refers to the number of response variables. Also, wi denotes the weighting factor for the ith experiment.
The calculation of the weight factor for each performance characteristic plays a vital role in determining the final grey relational grade. It is worth noting that the impacts of responses on the multiple performance characteristics for any engineering system are not equal. However, to calculate the final grey relational grade of multiple characteristics, most researchers utilize equal weight which yields imprecise results. Therefore, it is very important to use an applicable approach to calculate the weight factor for each response variable according to its importance and effect degree. This means that the weight factors for weight reduction, tensile strength, air permeability, and thermal conductivity of alkali-treated fabrics will differ from each other.
In general, the weight factor for each response variable can be calculated using the following formula [35,36]:
W i = ∑ j = 1 p D e l t a i . j ∑ i = 1 m ∑ j = 1 p D e l t a i . j
In this equation, delta refers to the S/N ratio ranges. P denotes the number of responses and m is the number of parameters.
As the grey relational grade increases, the parameter approaches the optimum sequence. Typically, the best multi-performance characteristic is that has the highest value of the grey relational grade. Consequently, the grey relational grade can be utilized to determine the best level of each control factor as well as each factor effect [37,38,39].

2.7. Analysis of variance

To identify the significant influence of each control factor on the grey relational grade the analysis of variance was implemented using Minitab version 18 statistical software. In this statistical analysis, the variability of the grey relational grade was separated into two different components. After that, the sum of squares of the deviation of each component from the overall average of the grey relational grade was then calculated
Using this statistical analysis, the importance of the effect of each control parameter on the multi-performance characteristics was also evaluated. The control parameter which has the greatest influence on the multi-performance characteristics is one that has the highest contribution percentage. It should be noted that the significance of each control variable is assessed according to the significance level 0 ≤ α ≤0.05.

3. Results and discussion

As previously disclosed in the experimental part, this study analyzes the various parameters involved in the alkaline hydrolysis of micropolyester woven fabrics to raise its quality. On the basis of the control parameters, namely caustic soda concentration, treatment temperature, and machine speed, some of the important responses such as percentage of weight reduction, air permeability, tensile strength, and thermal resistance were measured and then optimized. In order to get the best combination of the control factors that yield the optimum response variables, the grey relation analysis was carried out.
The best indicator of better performance of the treated woven fabrics lies in the high weight reduction percentage, tensile strength, air permeability values, and low thermal conductivity value. Therefore, weight reductions, tensile strength, and air permeability are considered as the higher-the-better criterion, and thermal resistance is considered as the smaller-the- better criterion.

3.1. S/N ratios and grey relational coefficients and their grades

The values of S/N ratios for the alkaline-treated micropolyester woven fabrics' properties and their normalized values were depicted in Table 5. These values were calculated for high weight reduction percentage, high air permeability, high tensile strength, and low thermal resistance values of the treated woven fabrics according to equations 4 through 8.
The normalized values of signal-to-noise ratios were transformed into grey relational coefficients in accordance with the different steps in the grey relation analysis especially using equations 7 through 10. In calculating the grey relational coefficients, the distinguishing coefficient has taken the value of one. After determining the grey relational coefficients, their grade values were evaluated using equation No. 11. It is worth mentioning that the weighting factor in determining grey relation grades has different values according to the importance of each response variable. The equation No. 12 was efficiently used to determine the different weighting factors corresponding to response variables. The weighting factors for the weight reduction percentage, tensile strength, air permeability, and thermal resistance of the treated woven fabrics were found to be 47%, 12%, 26%, and 15% respectively. According to the weight factors of responses under study, the grey relational grades were calculated using the following equation:
GRG = 0.47 GRCA+0.26 GRCB+0.12 GRCC+ GRCD
where GRCA, GRCB, GRCC, and GRCD are the grey relational coefficients of weight reduction, air permeability, tensile strength, and thermal resistance of alkaline-treated polyester fabrics.
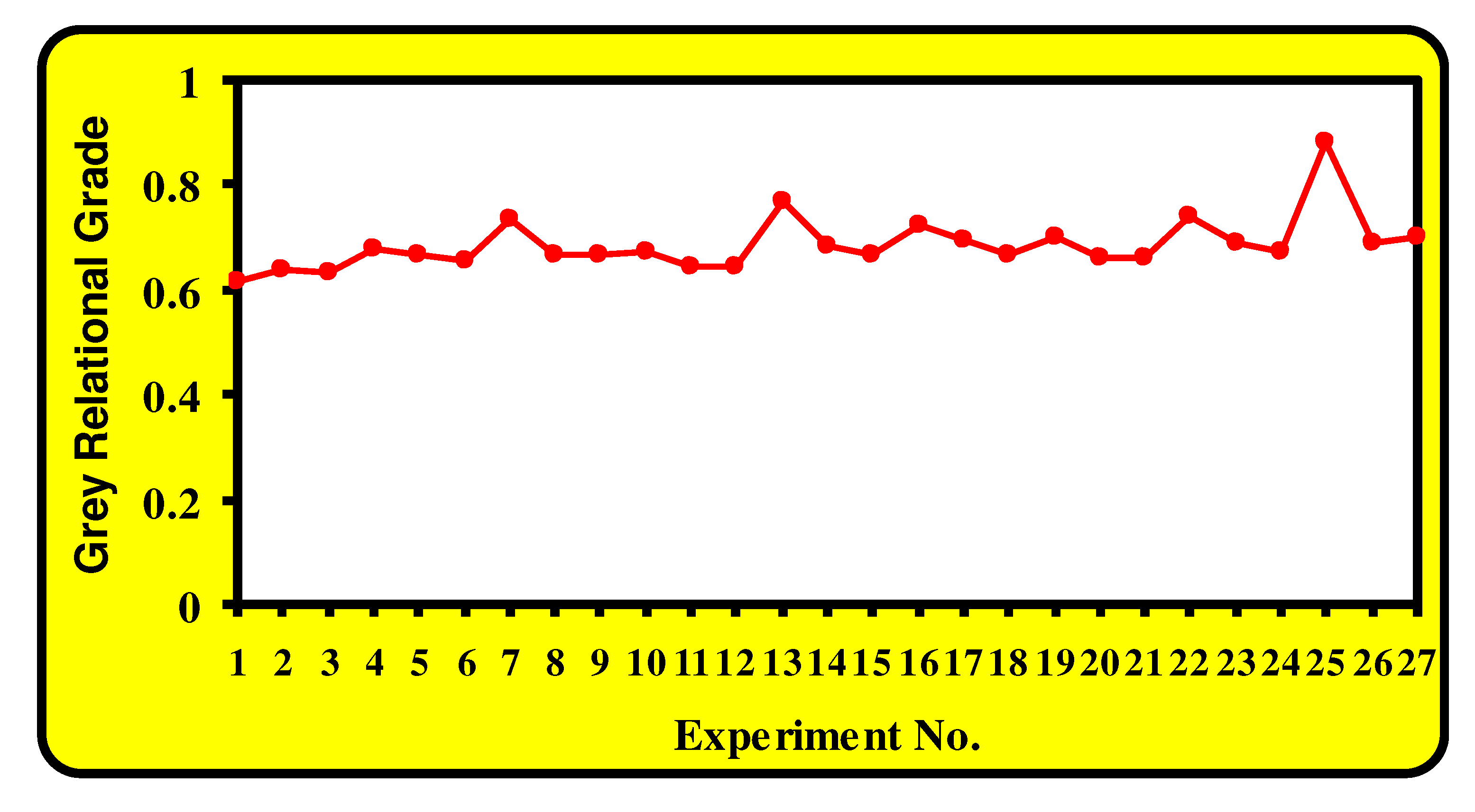
The GRC values, grade values (GRG) and their ranks were tabulated in Table 6. Generally, the highest value of the GRG corresponds to the optimum multi-response characteristics. Different grey relational grades versus the number of experiments were depicted in Figure 5.
From Figure 5 and Table 6, it can be noticed that the highest value of the grey relational grade was associated with the alkaline hydrolyzed polyester fabric with parameters stated in experiment number 25. Therefore, among the 27 experiments, experiment number 25 gave the best multi-performance characteristics. It is also observed that experiment number one has the lowest value of the grey relational grade among all cases. Response Table 7 shows the average values of GRG at different control factor levels. It should be noted that the grey relational grade refers to the degree of asociation between referential and comparative sequences. The higher the grey relational grade, the stronger correlation between the two sequences is. Consequently, the highest value of the grey relational grade yields the best result where maximum weight reduction, maximum air permeability, maximum tensile strength, and minimum thermal resistance are achieved for this study. From Table 7, it can be proved that the highest grey relational grade values for the different control factors, namely A, B, and C are A3, B3, and C1. 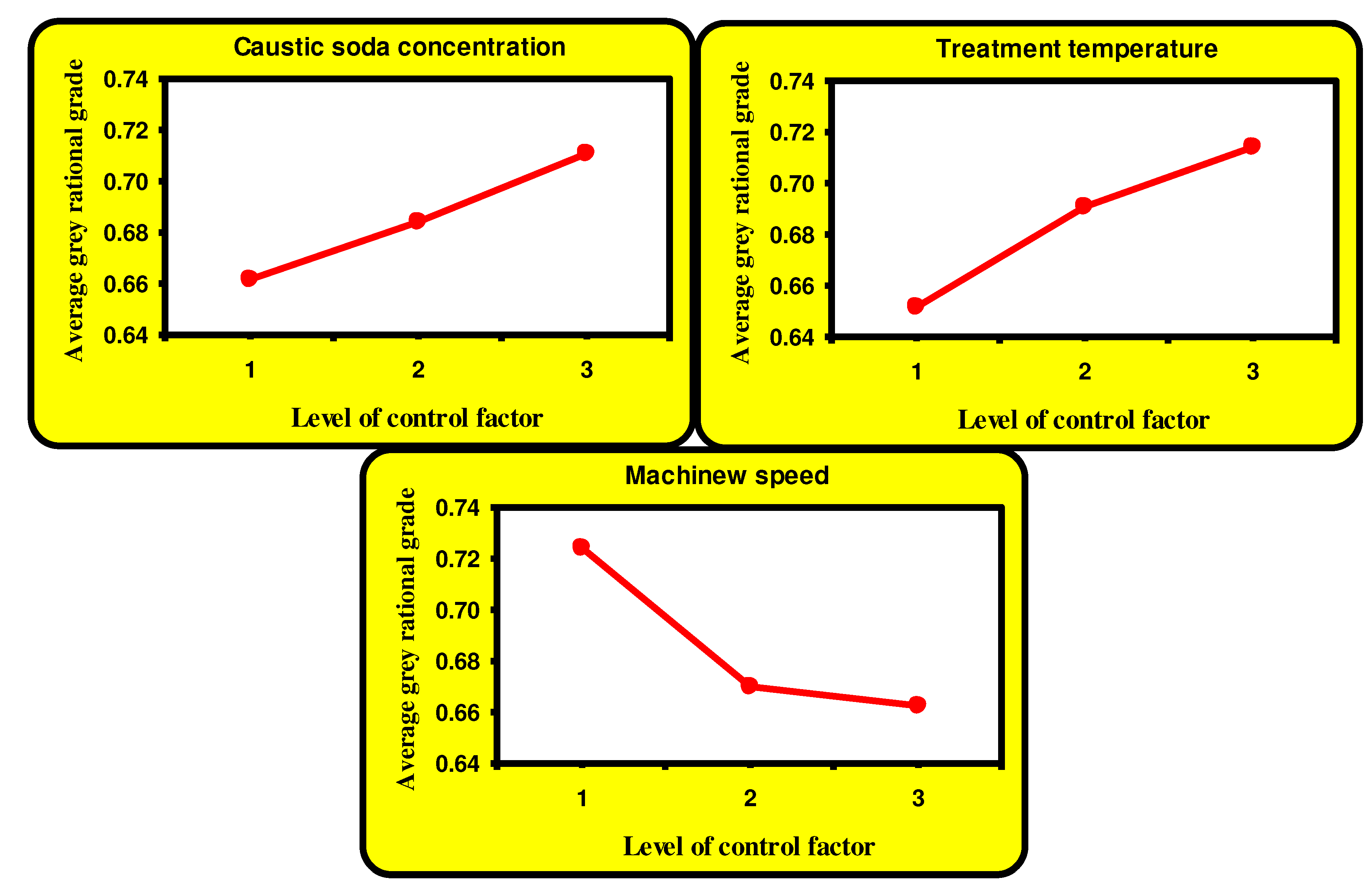Therefore, A3B3C1 expresses the optimum combination of alkaline-treated micropolyester fabric parameters to maximize weight reduction percentage, tensile strength, and air permeability and minimize their thermal resistance as well. Besides, it has been confirmed that the factor with the highest gain value has the most impact on the characteristic performance. Table 7 further shows that the most important factor influencing the performance qualities of treated polyester fabrics is the treatment temperature.
Figure 6 illustrates the effects of each control factor on the average grades of the grey relational analysis. This figure demonstrates that the third level of NaOH concentration and treatment temperature, along with the first level of weight reduction machine speed are the optimum levels to maximize tensile strength, air permeability, and weight reduction and minimize the thermal resistance of the treated micropolyester fabrics.

3.2. Results of the analysis of variance (ANOVA)

Using analysis of variance (ANOVA), the impact of each control factor on the grey relational grad was assessed, and the contribution of each factor was also shown in Table 8. From this table, it can be noticed that all control factors have a significant influence on the grey relational grade at a 0.01 significant level. It is also seen that the treatment temperature has the most influential effect on the multiple performance characteristics. It was estimated that the treatment temperature accounted for 29% of the effects on the grey relational grade, while caustic soda concentration and machine speed accounted for 15% and 26% respectively of the effects on the grey relational grade. This means that treatment temperature affects the alkaline-treated polyester fabric properties more than other control parameters. It is also seen that the contribution percentage of each control factor can be confirmed using the value of significant levels (p-values) in Table 8. As the percentage contribution of the control factor on the multi-performance characteristics increases, the p-value decreases. It is also noticed that the contibution percentage of each control factor is aggreing with the gain values listed in Table 7.

3.3. Confirmation test

After determining the optimal process control factors, the confirmation test is conducted to validate the analysis. The control factors are incorporated in the confirmation experiment at their optimal levels. The following equation can be used to forecast the grey relational analysis:
γ p r e d = γ t + ∑ ( γ i − γ t )
where γt represents the overall average of GRG values, γi denotes the average of GRG values at optimal levels as obtained from Table 9. From the above equation, it was estimated that the forecasted value of the GRG is about 0.778. The prediction of percentage error refers to the closeness of both experimental and predicted of GRG values to each other. It was determined that the prediction error percentage is about 11%. In comparison to the initial condition, the grey relational grade was improved by around 42%. Also, using the grey relational analysis, the weight reduction of the treated micropolyester fabrics increased from 8.7% to 36.8%, and air permeability also increased from 9.7 cm3/cm2.sec to 28.6 cm3/cm2.sec. Regarding the thermal resistance of the treated fabrics, it was found to be improved by approximately 5%. In the case of tensile resistance, it was decreased from 753 Newton to 493 Newton. This result is natural because the alkaline treatment of the polyester fabric makes the fabric becomes thinner, which in turn reduces its tensile strength.

4. Conclusion

In this study, a 33 full factorial design with the help of the Taguchi methodology and the grey relational analysis were effectively utilized to optimize the control parameters of the weight loss process of the alkaline–treated micropolyester woven fabrics. The essential design parameters of this process were NaOH concentration, treatment temperature, and weight loss machine speed. The weight reduction percentage, air permeability, tensile strength, and thermal resistance of alkali-treated polyester fabrics were taken as response variables. This study's findings reveal that all the control parameters significantly impact the properties of the treated polyester fabrics. It was found that the treatment temperature has the greatest impact on the treated fabric properties. The highest grey relational grade was found to be associated with the polyester fabrics treated with the highest NaOH concentration, highest treatment temperature, and lowest weight loss machine speed. The confirmation test detected and predicted the grey relational grade which was found to equal 0.778. It was estimated that the prediction error percentage of optimum GRG and the corresponding predicted one is about 11%. It was also found that the grey relational analysis improved the treated fabric properties with substantial values.

Funding

This research received no external funding.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

This paper is based upon work supported by Science, Technology & Innovation Funding Authority (STDF) under grant number 43342.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Fabia, J. , Gawlowski, A., Rom, M., Slusarczyk, C., Brzozowska-Stanuch, A., Sieradzka, M. PET fibers modified with cloisite nanoclay. Polymers (Basel), 2020; 12. [Google Scholar]
  2. Ni, Y.P. , Wu, W.S., Chen, L., Zhao, X., Qin, Z.H., Wang, X.L., Wang, Y.Z. How hydrogen bond interactions affect the flame retardancy and anti-dripping performances of PET. Macromol. Mater. Eng. 2019; 305. [Google Scholar]
  3. Zhao, H.B. , Wang, Y.Z. Design and synthesis of PET-based copolyesters with flame[1]retardant and antidripping performance. Macromol. Rapid Commun. 2017; 38. [Google Scholar]
  4. Chang, S. , Zhou, X., Xing, Z., Tu, T. Probing polarity of flame retardants and correlating with interaction between flame retardants and PET fiber. J. Colloid Interface Sci. 2017, 498, 343–350. [Google Scholar] [CrossRef] [PubMed]
  5. Qi, L. , Wang, B. , Zhang, W., Yu, B., Zhou, M., Hu, Y., Xingm W. Durable flame retardant and dip-resistant coating of polyester fabrics by plasma surface treatment and UV-curing., Progress in Organic Coatings 2022, 172, 107066. [Google Scholar]
  6. Fang Yinchun, Liu Xinhua, Wu Yarong, High efficient flame retardant finishing of PET fabric using eco-friendly DOPO[J], The Journal of The Textile Institute 2021, 5, 113–120.
  7. Jian, Li, Peng, Qi, Dan, M. et al. Eco-friendly flame retardant and smoke suppression coating containing boron compounds and phytic acids for nylon/ cotton blend fabrics. J. Ind. Crop. Prod. 2022, 15, 186–198. [Google Scholar]
  8. Liu, J. , He, H., Yu, Z., Suryawanshi, A., Li, Y., Lin, X., Sun, Z. Investigation of temperature-responsive and thermo-physiological comfort of modified polyester fabric with Sericin/PNIPAAm/Ag NPs interpenetrating polymer network hydrogel. Text. Res. J. 2020, 90, 2622–2638. [Google Scholar] [CrossRef]
  9. Wu, J.-N. , Qin, Z.-H., Chen, L., Liu, B.-W., Wang, X.-L., Wang, Y.-Z. Tailoring schiff base cross-linking by cyano group toward excellent flame retardancy, anti-dripping and smoke suppression of PET. Polymer 2018, 153, 78–85. [Google Scholar] [CrossRef]
  10. Brueckner, T. , Eberl, A., Heumann, S., Rabe, M., & Guebitz, G. Enzymatic and chemical hydrolysis of poly (ethylene terephthalate) fabrics. Journal of Polymer Science Part A: Polymer Chemistry 2008, 46, 6435–6443. [Google Scholar]
  11. Rakesh M. Musale and Sanjeev R. Shukla. Weight reduction of polyester fabric using sodium hydroxide solutions with additives cetyltrimethylammonium bromide and [BMIM] Cl. The Journal of The Textile Institute 2017, 108 4, 467-471.
  12. Petkovska, J. , Mladenovic, N., Markovi´c, D., Radoiˇci´c, M., Chiang, H., Bethany, C., et al. Environmentally benign few-bilayer intumescent nanocoating for flame retardant enzyme/plasma modified polyester fabric. Polymer Degradation and Stability 2023, 214, 110406. [Google Scholar] [CrossRef]
  13. Wu, J. N. , Chen, L., Fu, T., Zhao, H.B., Guo, D. M., Wang, X. L., Wang, Y. Z. New application for aromatic Schiff base: high efficient flame-retardant and anti[1]dripping action for polyesters. Chem. Eng. J. 2018, 336, 622–632. [Google Scholar] [CrossRef]
  14. Fang, Y. C. , Zhou, X., Xing, Z. Q., Wu, Y. R. Flame retardant performance of a carbon source containing DOPO derivative in PET and epoxy, J. Appl. Polym. Sci. 2017, 134, 44639. [Google Scholar] [CrossRef]
  15. Mousazadegan, F.; Saharkhiz, S.; Maroufi, M. , Weight reduction of microfibre polyester fabric and the effect on its physical and mechanical properties. The Journal of the Textile Institute 2010, 101, 716–728. [Google Scholar] [CrossRef]
  16. Natarajan, S.; Moses, J. , Surface modification of polyester fabric using polyvinyl alcohol in alkaline medium. Indian Journal of Fibre and Textile Research 2012, 37, 287–291. [Google Scholar]
  17. Zhang, A. -N., Zhao, H.-B., Cheng, J.-B., Li, M.-E., Li, S.-L., Cao, M., Wang, Y.-Z. Construction of durable eco-friendly biomass-based flame-retardant coating for cotton fabrics. Chem. Eng. J. 2021; 410. [Google Scholar]
  18. Carosio, F. , Di Pierro, A., Alongi, J., Fina, A., Saracco, G. Controlling the melt dripping of polyester fabrics by tuning the ionic strength of polyhedral oligomeric silsesquioxane and sodium montmorillonite coatings assembled through layer by layer. J. Colloid Interface Sci. 2018, 510, 142–151. [Google Scholar] [CrossRef] [PubMed]
  19. Wu, Y. , Zhou, X., Xing, Z., Ma, J. Metal compounds as catalysts in the intumescent flame retardant system for polyethylene terephthalate fabrics. Text. Res. J. 2018, 89, 2983–2997. [Google Scholar] [CrossRef]
  20. Alsaid Ahmed Almetwally. Alkaline hydrolysis of polyester woven fabrics and its influence on thermal comfort properties. Egyptian Journal of Chemistry 2022, 65, 259–274. [Google Scholar]
  21. Kanik, M.; Bayari, A. Effect of weight reduction process on printing properties of polyester fabrics. Coloration Technology 2006, 119, 264–268. [Google Scholar] [CrossRef]
  22. Tadesse, M.; Chavan, R. , Catalyzation of Alkaline Hydrolysis of Polyester by Oxidizing Agents for Surface Modification. International Journal of Sciences: Basic and Applied Research (IJSBAR) 2015, 22, 232–253. [Google Scholar]
  23. Tavanai, H. , Kaynak, A. Effect of weight reduction pre-treatment on the electrical and thermal properties of polypyrrole coated woven polyester fabrics. Synthetic Metals 2007, 157, 764–769. [Google Scholar] [CrossRef]
  24. Mousazadegan, F. , Saharkhiz, S., Maroufi, M. Weight reduction of microfibre polyester fabric and the effect on its physical and mechanical properties. The Journal of The Textile Institute 2010, 101, 716–728. [Google Scholar] [CrossRef]
  25. Nabil, A. Ibrahim, Basma M. Eid, Heba M. Khalil, Alsaid A. Almetwally. A new approach for durable multifunctional coating of PET fabric. Applied Surface Science 2018, 448, 95–103. [Google Scholar] [CrossRef]
  26. Tavanai, H. , Kaynak, A. Effect of weight reduction pre-treatment on the electrical and thermal properties of polypyrrole coated woven polyester fabrics. Synthetic Metals 2007, 157, 764–769. [Google Scholar] [CrossRef]
  27. Shahin M. F., A. R M. a. M. M. M. Optimizing the dyeing process of Alkali-treated polyester fabric with dolu natural dye. Journal of Engineering Research and Applications. 2014, 4, 35–40. [Google Scholar]
  28. Özdemir, H. , Thermal comfort properties of clothing fabrics woven with polyester/cotton blend yarns. AUTEX Research Journal 2017, 17, 135–141. [Google Scholar] [CrossRef]
  29. El Messiry, M. , El Ouffy, A., Issa, M. Microcellulose particles for surface modification to enhance moisture management properties of polyester, and polyester/cotton blend fabrics. Alexandria Engineering Journal 2015, 54, 127–140. [Google Scholar] [CrossRef]
  30. Natarajana, S. , and Moses J. J. Surface modification of polyester fabric using polyvinyl alcohol in alkaline medium. Indian Journal of Fibre & Textile Research 2012, 37, 287–291. [Google Scholar]
  31. Zhang, Xudong. Modifications of nonwoven polyethylene terephthalate fibrous matrices via NaOH hydrolysis: Effects on pore size, fiber diameter, cell seeding andproliferation. Process biochemistry (1991) (1359-5113), 44, 2009.
  32. Test Method for Thermal Resistance of Batting Systems Using a Hot Plate, ASTM D1518, 2014.
  33. Manimaran, G. , Kumar, M. P. Multiresponse optimization of grinding AISI 316 stainless steel using grey relational analysis. Materials and Manufacturing Processes 2013, 28, 418–423. [Google Scholar] [CrossRef]
  34. Zhipeng Xing, Haicong Dai, Jiong Zhang and Yufeng Li. Evaluation and improvement of greenness for milling AL6061 alloy through life cycle assessment and grey relational analysis. Materials 2022, 15, 8231.
  35. Yan, J, Li, L. Multi-objective optimization of milling parameters – the trade-offs between energy, production rate and cutting quality. J Clean Prod 2013, 52, 462–71. [Google Scholar] [CrossRef]
  36. Bademlioglu, A.H. , Canbolat A.S., Kaynakli O. Multi-objective optimization of parameters affecting Organic Rankine Cycle performance characteristics with Taguchi-Grey Relational Analysis. Renewable and Sustainable Energy Reviews 2020, 2020, 109483. [Google Scholar] [CrossRef]
  37. Mohammed Shakir Nahi, Saad Hameed Al-Shafaie, and Sundus Abbas Jasim. Multi-Objective optimization in electrical discharge machining of SiC and/ or B4C reinforced Al7075 using grey relational analysis. AIP Conference Proceedings 2023, 2830, 030021. [Google Scholar] [CrossRef]
  38. Yu Su, Guoyong Zhao, Yugang Zhao, Jianbing Meng and Chunxiao Li. Multi-Objective optimization of cutting parameters in turning AISI 304 austenitic stainless steel. Metals 2020, 10, 217. [CrossRef]
  39. Ajith Arul Daniel, S. , Pugazhenthi R., Kumar R., Vijayananth S. Multi objective prediction and optimization of control parameters in the milling of aluminium hybrid metal matrix composites using ANN and Taguchi -grey relational analysis. Defence Technology 2019, 15, 545–556. [Google Scholar] [CrossRef]
Preprints 83646 g001
Figure 1. Scanning Electron Microscope of treated and unreated micropolyetser woven fabrics.
Figure 1. Scanning Electron Microscope of treated and unreated micropolyetser woven fabrics.
Preprints 83646 g001
Preprints 83646 g002
Figure 2. FTIR of untreated and treated micropolyester woven fabric.
Figure 2. FTIR of untreated and treated micropolyester woven fabric.
Preprints 83646 g002
Preprints 83646 g003
Figure 3. General view (A) and sketch diagram (B) of the continuous weight reduction machine.
Figure 3. General view (A) and sketch diagram (B) of the continuous weight reduction machine.
Preprints 83646 g003
Preprints 83646 g004
Figure 4. A consequence of polyester hydrolysis by caustic soda.
Figure 4. A consequence of polyester hydrolysis by caustic soda.
Preprints 83646 g004
Preprints 83646 g005
Figure 5. Values of grey relational grades versus experiment numbers.
Figure 5. Values of grey relational grades versus experiment numbers.
Preprints 83646 g005
Preprints 83646 g006
Figure 6. Levels of control factors versus their corresponding average grey relational grades.
Figure 6. Levels of control factors versus their corresponding average grey relational grades.
Preprints 83646 g006
Table 1. Levels and cods of control parameters of alkaline hydrolysis process of micro polyester woven fabric.
Table 1. Levels and cods of control parameters of alkaline hydrolysis process of micro polyester woven fabric.
Independent factors Factor code Levels codes and values
-1 0 1
Caustic soda concentration (X1), % A 19 23 27
Machine speed (X3), m/min B 20 30 40
Treatment temperature (X4), oC C 90 110 125
Table 2. Arrangement of the experiments to treat the drawn textured polyester using a 33 full factorial design.
Table 2. Arrangement of the experiments to treat the drawn textured polyester using a 33 full factorial design.
Machine Speed
(m/min) - (C )		 Temperature
(OC) - (B )		 Caustic soda concentration (%) - (A ) Sample No.
20 90 19 1
30 90 19 2
40 90 19 3
20 110 19 4
30 110 19 5
40 110 19 6
20 125 19 7
30 125 19 8
40 125 19 9
20 90 23 10
30 90 23 11
40 90 23 12
20 110 23 13
30 110 23 14
40 110 23 15
20 125 23 16
30 125 23 17
40 125 23 18
20 90 27 19
30 90 27 20
40 90 27 21
20 110 27 22
30 110 27 23
40 110 27 24
20 125 27 25
30 125 27 26
40 125 27 27
Untreated ( Blank) sample 28
Table 3. Experimental layout using L9 orthogonal array for weight reduction process parameters and corresponding their fabric properties.
Table 3. Experimental layout using L9 orthogonal array for weight reduction process parameters and corresponding their fabric properties.
Experiment No. Levels of the control factors Fabric properties
A B C Weight reduction (%) Air permeability Tensile strength Thermal resistance
1 1 1 1 8.7 9.7 753.4 4.7
2 1 1 2 8.2 9.4 892.7 4.6
3 1 1 3 4.9 9.7 861.9 5.7
4 1 2 1 14.8 10.9 777.0 4.6
5 1 2 2 13.0 11.8 751.4 4.7
6 1 2 3 10.3 11.8 803.4 4.7
7 1 3 1 19.1 16.8 754.4 4.4
8 1 3 2 13.5 13.0 757.3 4.1
9 1 3 3 12.7 10.7 804.4 4.6
10 2 1 1 11.9 12.3 786.8 4.9
11 2 1 2 8.3 11.4 803.4 5.1
12 2 1 3 8.7 11.2 802.5 4.9
13 2 2 1 23.9 17.8 666.1 4.6
14 2 2 2 15.2 12.5 760.3 4.3
15 2 2 3 12.3 13.2 735.8 4.6
16 2 3 1 16.7 18.1 696.5 4.5
17 2 3 2 16.1 15.7 685.7 4.1
18 2 3 3 15.2 10.8 734.8 4.4
19 3 1 1 14.1 15.8 750.5 4.6
20 3 1 2 11.2 13.7 757.3 4.4
21 3 1 3 9.9 12.9 773.0 5.0
22 3 2 1 22.4 16.9 625.9 4.4
23 3 2 2 14.6 15.7 755.4 3.9
24 3 2 3 11.9 14.2 799.5 4.3
25 3 3 1 36.8 28.6 492.5 3.3
26 3 3 2 21.6 15.6 645.5 2.5
27 3 3 3 19.6 15.4 718.1 3.5
A: Concentration of caustic soda – B: Treatment temperature – C: Machine speed
Table 4. Properties of untreated micropolyester woven fabric.
Table 4. Properties of untreated micropolyester woven fabric.
Properties Value
Weight (g/m2 ) 198.3
Tensile strength (Newton ) 835
Air permeability (cm3/cm2.sec ) 6.796
Thermal resistance (W-1m2K ) 5.42
Table 5. S/N ratios and their normalized values for the treated polyester fabric properties.
Table 5. S/N ratios and their normalized values for the treated polyester fabric properties.
Experiment
No.		 Weight reduction Air permeability Tensile strength Thermal resistance
S/N
ratio		 Normalized
S/N		 S/N
ratio		 Normalized
S/N		 S/N
ratio		 Normalized
S/N		 S/N
ratio		 Normalized
S/N
1 18.78 0.29 19.73 0.04 57.25 0.66 -13.44 0.74
2 18.27 0.26 19.39 0.00 59.01 1.00 -13.23 0.71
3 13.75 0.00 19.69 0.03 58.70 0.94 -15.30 1.00
4 23.38 0.55 20.61 0.13 57.80 0.77 -13.29 0.72
5 22.27 0.49 21.42 0.21 57.49 0.71 -13.41 0.74
6 20.22 0.37 21.40 0.21 58.09 0.82 -13.44 0.74
7 25.62 0.68 24.40 0.52 57.55 0.72 -12.88 0.67
8 22.60 0.50 22.21 0.30 57.58 0.72 -12.32 0.59
9 22.07 0.47 20.58 0.12 58.11 0.83 -13.30 0.72
10 21.51 0.44 21.57 0.23 57.91 0.79 -13.90 0.81
11 18.33 0.26 21.10 0.18 58.10 0.82 -14.18 0.85
12 18.75 0.28 20.99 0.17 58.08 0.82 -13.83 0.80
13 27.57 0.79 24.89 0.58 56.44 0.51 -13.27 0.72
14 23.64 0.56 21.83 0.25 57.61 0.73 -12.71 0.64
15 21.78 0.46 22.31 0.31 57.32 0.67 -13.30 0.72
16 24.45 0.61 25.10 0.60 56.86 0.59 -13.03 0.69
17 24.13 0.59 23.87 0.47 56.72 0.56 -12.26 0.58
18 23.61 0.56 20.65 0.13 57.31 0.67 -12.91 0.67
19 22.98 0.53 23.94 0.48 57.50 0.71 -13.27 0.72
20 20.98 0.41 22.70 0.35 57.57 0.72 -12.88 0.67
21 19.83 0.35 22.18 0.29 57.75 0.76 -14.07 0.83
22 27.01 0.76 24.51 0.53 55.87 0.40 -12.88 0.67
23 23.26 0.54 23.89 0.47 57.56 0.72 -11.87 0.53
24 21.48 0.44 23.04 0.38 58.05 0.82 -12.78 0.65
25 31.30 1.00 28.96 1.00 53.81 0.00 -10.49 0.34
26 26.66 0.74 23.78 0.46 56.06 0.43 -8.05 0.00
27 25.83 0.69 23.15 0.39 57.12 0.63 -10.81 0.38
Table 6. Grey relational coefficients (GRC) and their grade values (GRG) for treated microplyester woven fabric properties.
Table 6. Grey relational coefficients (GRC) and their grade values (GRG) for treated microplyester woven fabric properties.
Experiment
No.		 Grey relational coefficients (GRC)
Grey Relational grade (GRG)		 Rank
Weight reduction Air permeability Tensile strength Thermal conductivity
1 0.5837 0.5091 0.7465 0.7962 0.615734 27
2 0.5739 0.5 1 0.7777 0.63639 25
3 0.5 0.5079 0.9429 1 0.630191 26
4 0.6891 0.534 0.8111 0.7833 0.677547 12
5 0.6604 0.5592 0.7733 0.7929 0.667542 16
6 0.613 0.5588 0.8493 0.7963 0.654749 22
7 0.7555 0.6773 0.78 0.7499 0.737271 4
8 0.6687 0.5865 0.7843 0.7086 0.667177 17
9 0.6553 0.5332 0.8518 0.7837 0.666397 18
10 0.6419 0.5642 0.8245 0.8387 0.673156 14
11 0.575 0.549 0.8502 0.8659 0.644931 23
12 0.583 0.5457 0.8482 0.832 0.642496 24
13 0.8247 0.7018 0.6692 0.7812 0.76759 2
14 0.6961 0.573 0.7874 0.7372 0.68124 11
15 0.6483 0.5901 0.7543 0.7838 0.666199 19
16 0.7193 0.7128 0.7069 0.7614 0.722451 5
17 0.7102 0.6527 0.6939 0.7046 0.692434 8
18 0.6955 0.5353 0.7537 0.7525 0.669392 15
19 0.6783 0.6558 0.7745 0.7816 0.699512 7
20 0.6298 0.6046 0.7825 0.7499 0.659573 21
21 0.6048 0.5853 0.8044 0.8551 0.661256 20
22 0.8038 0.6824 0.6233 0.7495 0.742429 3
23 0.6859 0.6535 0.7819 0.6788 0.687924 10
24 0.6412 0.6177 0.8439 0.7422 0.674562 13
25 1 1 0.5 0.6014 0.880208 1
26 0.7909 0.6487 0.6374 0.5 0.691882 9
27 0.7625 0.6224 0.7326 0.6178 0.700792 6
Table 7. Average values of grey relational grades at different factors levels.
Table 7. Average values of grey relational grades at different factors levels.
Control factors Level1 Level 2 Level 3 Gain
(Max-Min)
Caustic soda concentration 0.6614 0.6844 0.7109a 0.0495
Treatment temperature 0.6515 0.6911 0.7142a 0.0627
Machine speed 0.7240a 0.6699 0.6629 0.0611
Total mean grey relational grade= 0.6856 – a is the optimal level
Table 8. Analysis of variance ANOVA for the grey relational grades.
Table 8. Analysis of variance ANOVA for the grey relational grades.
Source of variation DF SS MS F P-value Contribution
%
Caustic soda concentration concentration 2 0.01103 0.0055 5.19 0.015 15
Treatment temperature 2 0.02012 0.1006 9.48 0.001 29
Machine sped 2 0.0183 0.0091 8.54 0.002 26
Error 20 0.02123 0.0011 30
Total 26 0.07051
Table 9. Confirmation experiment results for initial, experimental, and predicted grey relational grades.
Table 9. Confirmation experiment results for initial, experimental, and predicted grey relational grades.
Initial conditions Optima conditions
Predicted Experimental
Levels A1B1C1 A3B3C1 A3B3C1
Weight reduction 8.7 --- 36.8
Air permeability 9.7 ---- 28.6
Tensile strength 753.4 ---- 492.6
Thermal resistance 4.7 ----- 3.34
GRG 0.6157 0.778 0.88
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated