Dynamic Analysis of a Timoshenko-Ehrenfest SWCNT in the Presence of Surface Effects: The Truncated Theory

1. Introduction

Nanotubes due to their exceptional mechanical, physical and electrical properties have attracted great attention from researchers and have a wide range of applications. As a result, detailed studies on their mechanical properties have been conducted [1–3], and static and dynamic behavior of single-walled and multi-walled carbon nanotubes have been proposed using Euler-Bernoulli and Timoshenko beam models [4–10]. Atomistic and continuous modelling approaches were used to analyse the mechanical properties of nanotubes, depending on the level of investigation. Although the atomistic approach is more suitable for investigating nanometric structures [4], it has had little applicability as it is more time-consuming. Continuous approaches, on the other hand, have received more attention than the former and among them beam models have proven to be more convenient, although classical theories, such as the Euler-Bernoulli or Timoshenko beam model [5–8], or even higher-order theories have proven to be inadequate because they do not capture the influence of the nonlocal effect. To overcome this drawback, models incorporating non-local effects have been proposed, based on the theory of non-local elasticity [9–14] developed by Eringen (see, in particular, [15,16]). Numerous theoretical and numerical methods have been developed to investigate the influence of non-local effects on the free vibrations of structures and nanostructures. For a detailed discussion, the reader can refer to the following works [17–24].

Another important concept that has attracted considerable attention to researchers is the size-dependent mechanical behaviour of nanobeams due to surface stress. Unlike the classical continuum, in which the effect of surface energy is ignored because it is small compared to the mass energy, for nanoscale materials and nanostructures, the surface effects are significant due to the high surface-to-volume ratio. Consequently, by applying Euler-Bernoulli and Timoshenko beam theories, several theories have been developed to account for the effect of surfaces/interfaces on mechanical deformation [25–31]. For example, He and Lilley [25] studied the surface effects on the elastic behavior of static bending nanowires using the Euler-Bernoulli beam theory. By using the refined Timoshenko beam theory, Wang and Feng [26] examined surface effects on the axial buckling and the transverse vibration of nanowires, and applying the nonlocal Timoshenko beam theory, Lee and Chang [27] have studied the natural frequency of nanotubes with consideration of surface effects. Gurtin and Murdoch developed a linearized theory of surface elasticity, named "Gurtin-Murdoch model" [32,33], that attracted considerable attention and was widely used to study elastic behavior of solids at nano-scales.

This paper deals with the free vibration of a Timoshenko-Ehrenfest single-walled carbon nanotube based on the nonlocal theory and taking surface effects into account. To model these effects on frequency response of nanotubes, we use Eringen’s nonlocal elastic theory and surface elastic theory to modify the governing equations. A modified version of Timoshenko nonlocal elasticity theory - known as the nonlocal truncated Timoshenko beam theory - is put forth to investigate the free vibration behavior of single-walled carbon nanotubes (SWCNT), as indicated in [10,34]. Using the Hamilton’s principle, the governing equations and the corresponding boundary conditions are derived.

There are several studies in the literature that address the topic of free vibrations of nanotubes and nanostructures based on nonlocal and surface theory. The modelling of nonlocal and surface effects are investigated separately in most cases. The aim of this paper is the modelling of a single walled carbon nanotube for analysing the frequency response of the nanotubes, the combined surface and nonlocal effects. Furthermore, starting from Timoshenko truncated theory for the beam model, developed in [34], in the present paper the authors develop this theory for Timoshenko single-walled carbon nanotubes using the geometric and variational approach. The novelty of the proposed approach is that it shows a perfect analogy between variational and direct methods for the dynamic analysis of beams. Similarly the surface effect, which becomes dominant as surface to volume ratio increases in submicron or nanoscale structure, is modeled based on the surface elasticity theory as proposed by Gurtin and Murdoch [32,33]. Finally, to check the accuracy and validity of the suggested method, some numerical examples are carried out. The impacts of the nonlocal coefficient, surface effects and nanotube length on the free vibration of SWCNT are evaluated and the results are compared with those found in the literature. The findings indicate that the length of the nanotube, the nonlocal parameter and the surface effect all play important roles and should not be disregarded in the vibrational analysis of nanotubes.

This paper is structured as follows. In Sect. 2 Eringen nonlocal theory assumptions, stress resultants in nonlocal theory and surface theory for analysing the frequency response of the nanotubes are reported. Sect.3 provides the derivation of the motion equations for the nonlocal truncated Timoshenko beam theory by means the direct and variational approaches and the equations of motion of single-walled carbon nanotube are derived by using the truncated Timoshenko-Ehrenfest beam theory. Finally, solving the system of differentials equations of nonlocal truncated Timoshenko-Ehrenfest nanotube and the case of simply-supported nanotube solution is analyzed. The influence that small-scale parameter, surface effect and nanotube length have on the first natural, dimensionless frequency of SWCNT is investigated in Sect. 4, in order to assess the accuracy and validity of the proposed method. Finally, a summary of this investigation and main conclusions is provided in Sect. 5.

2. Eringen nonlocal theory and surface theory for nonlocal Timoshenko-Ehrenfest nanotube analysis

2.1. Eringen nonlocal theory assumptions and stress resultants in nonlocal theory

According to Eringen non local theory assumptions [15,16], the Cauchy stress state, at a given reference point x, is a function of the strain field at all points of the body. This observation is in accordance with the atomic theory of lattice dynamics and phonon dispersion, and this effect decreases as the space between the particles increases.

For isotropic and homogeneous elastic beam, the constitutive relation in an integral form for the nonlocal stress tensor at a point x is expressed as:

$$\mathit{\sigma }={\int }_V\mathit{\alpha }\left(\right|{\mathit{x}}^{\prime }-\mathit{x}|,\tau )\mathit{t}\left({\mathit{x}}^{\prime }\right)\mathrm{d}{\mathbf{x}}^{\prime }$$

(1)

where t(x) is the conventional stress tensor at point x, which is related to the strain tensor $\mathit{ϵ}$ by the following conventional constitutive relation:

$$\mathit{t}\left(\mathit{x}\right)=\mathit{C}\left(\mathit{x}\right)\otimes \mathit{ϵ}\left(\mathit{x}\right)$$

(2)

where C is the fourth-order elasticity tensor and ⊗ denotes the “double-dot product”. The following are also defined: $\alpha$(| x’-x|,$\tau$) is the nonlocal coefficient introducing into the constitutive equation the nonlocal effect at the reference point x produced by local strain at the source x’, |x’-x| is the Euclidean distance. $\tau$, which depends on the bulk’s material, is a constant defined as the scale parameter that incorporates the small-scale factor.

Since the integral form Eq. (1) is quite complicated, the following the nonlocal constitutive relations is often used:

$$\left(1-{\tau }^2{l}_e{}^2{\nabla }^2\right)\mathit{\sigma }=\mathit{t},\tau =\frac{e_0{l}_i}{l_e}$$

(3)

where $e_0$ is a material constant determined experimentally, $l_i$, $l_e$ are the internal and external characteristic lengths, respectively, and $\nabla {}^2$ is the Laplace operator.

Applying Eq. (3) and according to nonlocal elasticity theory for homogeneous and isotropic nanotube, the constitutive relation of the Cauchy stress tensor take the following form:

$${\sigma }_{\mathrm{zz}}-{\mu }^2\frac{{\partial }^2{\sigma }_{\mathrm{zz}}}{\partial z^2}=E{e}_{\mathrm{zz}},\mu =\left(e_0{l}_i\right)$$

(4)

$${\sigma }_{\mathrm{zy}}-{\mu }^2\frac{{\partial }^2{\sigma }_{\mathrm{zy}}}{\partial z^2}=2G{e}_{\mathrm{zy}}$$

(5)

where ${\sigma }_{\mathrm{zz}}$ and $e_{\mathrm{zz}}$ are the normal stress and normal strain, respectively, E is elasticity modulus, $\mu$ is the small scale parameter that incorporates the small scale effect and z is the coordinate measured from the mid-plane of the nanotube. Also, ${\sigma }_{\mathrm{zy}}$ and $e_{\mathrm{zy}}$ are the transverse shear stress and the transverse shear strain, respectively, G is shear modulus and y is the longitudinal coordinate measured from the left-end of the nanotube.

Using Eq. (4) the moment-curvature relation can be expressed as:

$$M-{\mu }^2\frac{{\partial }^{2}M}{\partial z^2}=\mathrm{EI}\frac{\partial \varphi }{\partial z}$$

(6)

where M is the bending moment, I is the moment of inertia and $\varphi$ is the rotation due to bending, and using Eq. (5), the relation among the internal moment, internal shear force and the external applied loads can be expressed as:

$$Q-{\mu }^2\frac{{\partial }^{2}Q}{\partial z^2}=\mathrm{GA}\kappa \left(\frac{\partial v}{\partial z}+\varphi \right)$$

(7)

where Q is the shear force, A is the area of the straight section, v the transverse displacement and $\kappa$ the shear corrector factor.

2.2. Surface effect theory for nanotubes analysis

In the present section, the analysis for the surface effects is considered to describe the vibrations nonlocal analysis of nanotubes. Unlike the classical continuum, in nanoscale materials and nanostructures, the surface effects are significant due to the high surface-to-volume ratio which the result is the higher elastic modulus and mechanical strength than classical continuous. Therefore the surface and induced surface forces cannot be ignored.

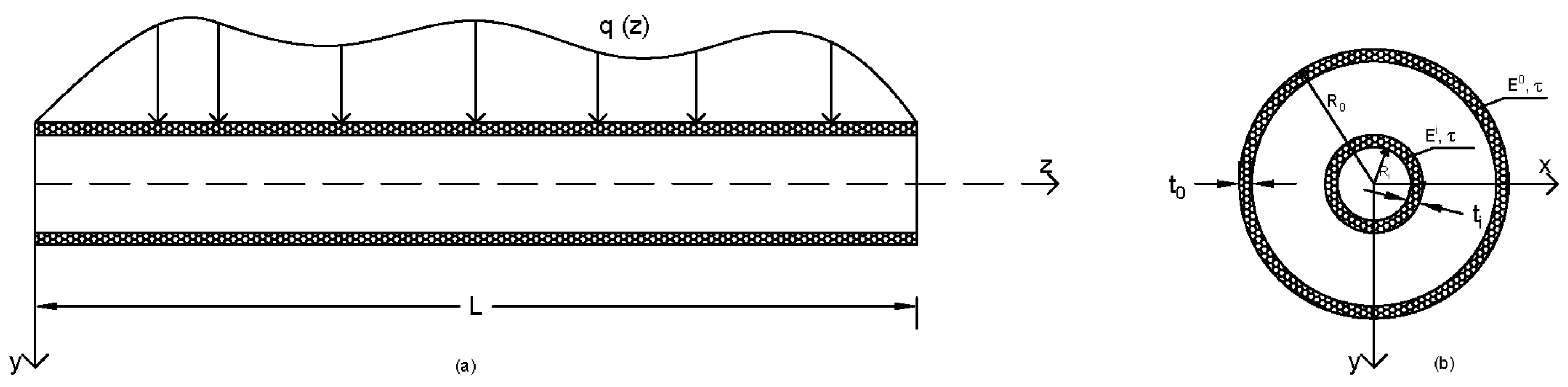
Consider a single-walled carbon nanotube (SWCNT) with length L. Figure 1 shows a schematic of nanotube with inner and outer thin surface layers, of circular cross-section with inner and outer radii $R_i$ and $R_o$ and thickness h. Also, the constitutive properties E, G and $\rho$ are Young’s modulus, shear modulus and mass density, respectively. Finally, the following geometrical properties are defined: moment of inertia I, cross-sectional area A and transverse displacement v which depends on the spatial coordinate z and time t. The thicknesses of the internal and external surface thin layers are assumed to be $t_i$ and $t_o$, respectively, and their surface elasticity modulus are $E^i$ and $E^0$, respectively.

For circular cross sections of a nanotube, the effective flexural rigidity ${\mathrm{EI}}^{*}$, which includes the surface bending elasticity on the nonotube and its flexural rigidity, is given by:

$${\mathrm{EI}}^{*}=\mathrm{EI}+\pi E^s\left(R_0^3+R_i^3\right)$$

(8)

where $E^s$ is the surface elastic modulus, which can be determined by experiments, is the effective flexural rigidity, and $R_i$ and $R_o$ are inner and outer radii, respectively. For the zero-thickness surface layers, an idealised model is used, represented by the following properties $E^0{t}_0$ and $E^i{t}_i$ which is constant magnitude and equal to $E^s$ as a material property.

Let be also q(z) the transverse distributed loading induced by residual surface tension of surface layers.

$$q\left(z\right)=H\frac{{\partial }^{2}v}{\partial z^2}$$

(9)

where H is the constant parameter and is equal to:

$$H=4\tau \left(R_i+R_0\right)$$

(10)

It is determined by the residual surface tension and depends on the shape of cross section.

In the following we write the differential equations for a Timoshenko nanotube with truncated theory in the presence of surface effects using both the geometric and variational methods.

3. Theoretical formulation: equations of motion for nonlocal truncated Timoshenko-Ehrenfest beam models for nanotubes analysis

3.1. Equation of motion for a truncated Timoshenko-Ehrenfest beam: Euler method

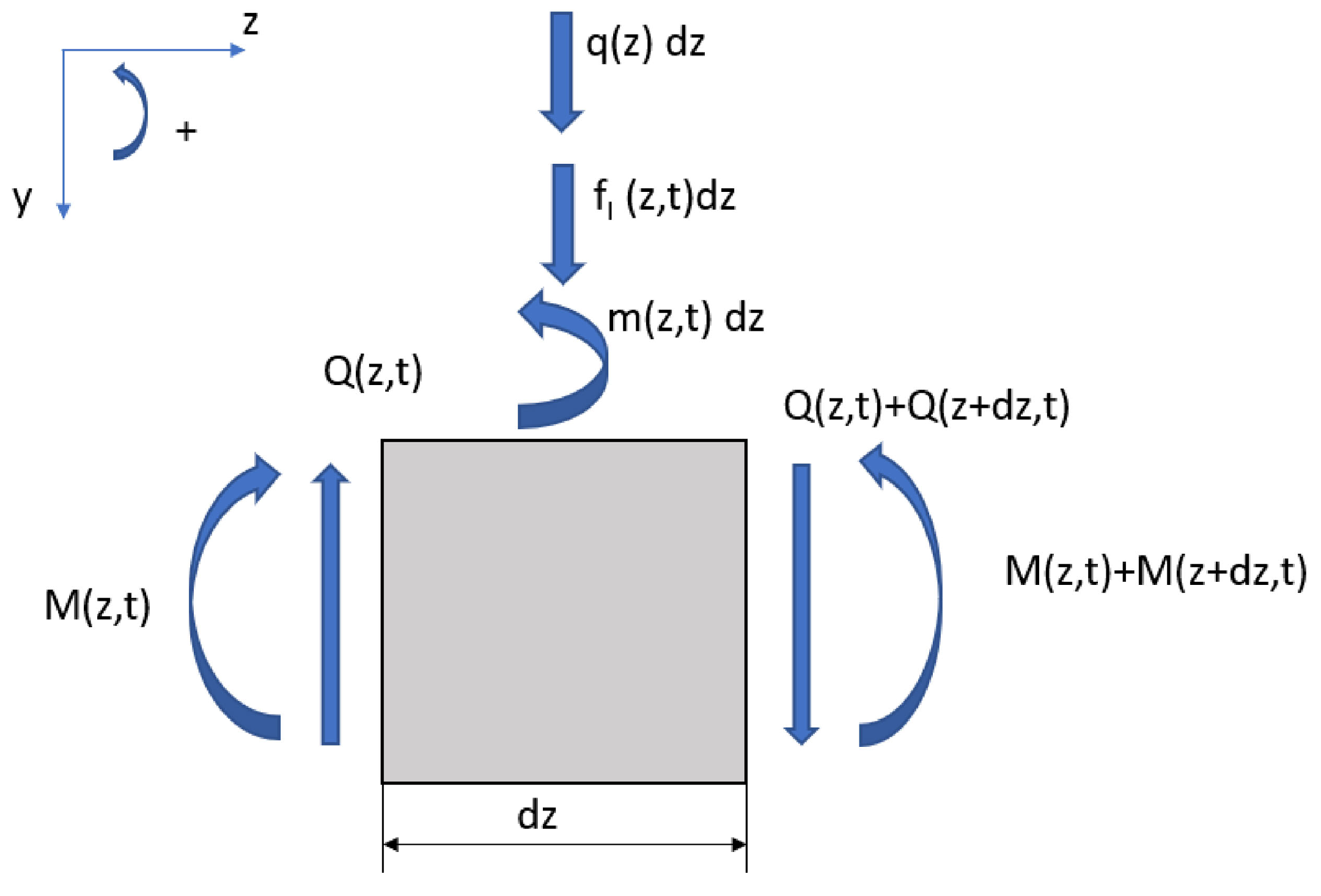
Consider the ashlar nanotube element in Figure 2 and according to the paper [10], the equilibrium of the the applied loads at the abscissa z-axis is imposed: equilibrium to the vertical translation and rotation around the centre of the right section of all the forces identified on the elementary ashlar, starting from its equilibrium.

Separate contributions are provided for the translational $f_{\mathrm{I}1}$ and rotational m inertias, taking into account the following formulas:

$$f_{\mathrm{I}1}=-\rho \mathrm{A}\frac{{\partial }^{2}v}{\partial t^2}$$

(11)

$$m=-\rho \mathrm{I}\frac{{\partial }^2{\varphi }_b}{\partial t^2}$$

(12)

where t denotes the time variable. Also, the rotational inertial term m depends only on the flexural rotation ${\varphi }_b=-\frac{\partial v}{\partial z}$, whereas the total rotation $\varphi$ is connected to ${\varphi }_b$ via the following expression:

$$\varphi ={\varphi }_b+\psi =-\frac{\partial v}{\partial z}+\psi$$

(13)

The equation for the vertical translation equilibrium is:

$$\frac{\partial Q}{\partial z}=\rho \mathrm{A}\frac{{\partial }^{2}v}{\partial t^2}-q\left(z\right)$$

(14)

whose first derivative, when substituted in Equation (7), yields:

$$Q=\mathrm{GA}\kappa \left(\frac{\partial v}{\partial z}+\varphi \right)+{\mu }^2\rho \mathrm{A}\frac{{\partial }^{3}v}{\partial t^2\partial z}-{\mu }^2\frac{\partial q\left(z\right)}{\partial z}$$

(15)

By substituting the value expressed by Equation (9) in place of $q\left(z\right)$, Equation (15) can be completed as follows:

$$\rho \mathrm{A}\frac{{\partial }^{2}v}{\partial t^2}-{\mu }^2\rho \mathrm{A}\frac{{\partial }^{4}v}{\partial t^2\partial z^2}+{\mu }^{2}H\frac{{\partial }^{4}v}{\partial z^4}-\mathrm{GA}\kappa \left(\frac{{\partial }^{2}v}{\partial z^2}+\frac{\partial \varphi }{\partial z}\right)-H\frac{{\partial }^{2}v}{\partial z^2}=0$$

(16)

The equilibrium at rotation with respect to the centre of gravity of the right face of the elementary ashlar, on the other hand, is given by the following expression

$$\frac{\partial M}{\partial z}=Q-\rho \mathrm{I}\frac{{\partial }^{3}v}{\partial t^2\partial z}$$

(17)

which when derived once and substituted in Equation (6) leads to

$$M={\mathrm{EI}}^{*}\frac{\partial \varphi }{\partial z}+{\mu }^2\left(-\rho \mathrm{I}\frac{{\partial }^{4}v}{\partial t^2\partial z^2}+\rho \mathrm{A}\frac{{\partial }^{2}v}{\partial t^2}-q\left(z\right)\frac{{\partial }^{3}v}{\partial t^2\partial z}\right)$$

(18)

The equilibrium of motion Eq. (17) can be written:

$${\mathrm{EI}}^{*}\frac{{\partial }^2\varphi }{\partial z^2}-{\mu }^2\rho \mathrm{I}\frac{{\partial }^{5}v}{\partial t^2\partial z^3}+\rho \mathrm{I}\frac{{\partial }^{3}v}{\partial t^2\partial z}-\mathrm{GA}\kappa \left(\frac{\partial v}{\partial z}+\varphi \right)=0$$

(19)

Equations (16) and (19) constitute the system of differential equations of motion of a Timoshenko-Ehrenfest nanotube model derived from the truncated Timoshenko beam theory and surface theory.

3.2. Equations of motion for a truncated Timoshenko-Ehrenfest beam: variational method

In this section, according to the Hamilton principle, the motion equations for a single-walled carbon nanotube are derived.

For the local theory, the strain energy ${\Pi }_e$ is represented as follows:

$${\Pi }_e=\frac{1}{2}\left({\int }_0^{L}M\frac{\partial \varphi }{\partial z}dz+{\int }_0^{L}Q\left(\frac{\partial v}{\partial z}+\varphi \right)dz\right)$$

(20)

Equations (15) and (18), used to calculate the shear stress Q and bending moment M for non-local elasticity, show that the terms defined here additional to the local theory are constant quantities that do not vary in terms of force, so they do not contribute to the strain energy but are potential energy of the loads P, (see Ref. [21]).

The strain energy can be written as:

$$\Pi =\frac{1}{2}{\int }_0^L\mathrm{EI}{\left(\frac{\partial \varphi }{\partial z}\right)}^2\mathrm{dz}+\frac{1}{2}{\int }_0^L\mathrm{GA}\kappa {\left(\frac{\partial v}{\partial z}+\varphi \right)}^2\mathrm{dz}$$

(21)

As can be seen, only the local terms are present in the formulation of the strain energy. The potential energy P is equal to the work performed by the forces of inertia, modified by the sign, for the corresponding displacement, and is expressed as follows:

$$\begin{array}{cc}\hfill P_{\mathrm{nl}}=& {\int }_0^L{\mu }^2\left(-\rho \mathrm{I}\frac{{\partial }^{4}v}{\partial t^2\partial z^2}+\rho \mathrm{A}\frac{{\partial }^{2}v}{\partial t^2}-H\frac{{\partial }^{2}v}{\partial z^2}\right)\frac{\partial \varphi }{\partial z}\mathrm{dz}+\hfill \\ & {\int }_0^L\left({\mu }^2\rho \mathrm{A}\frac{{\partial }^{3}v}{\partial t^2\partial z}-{\mu }^{2}H\frac{{\partial }^{3}v}{\partial z^3}\right)\left(\frac{\partial v}{\partial z}+\varphi \right)\mathrm{dz}\hfill \end{array}$$

(22)

The rotational component of the forces of inertia eq.(8), as done with the Timoshenko beam in the truncated theory, is introduced as potential energy:

$$P_m=-{\int }_0^{L}m\varphi \mathrm{dz}=-{\int }_0^L-\rho \mathrm{I}\frac{{\partial }^2{\varphi }_b}{\partial t^2}\varphi \mathrm{dz}=-{\int }_0^L-\rho \mathrm{I}\frac{{\partial }^2}{\partial t^2}\left(-\frac{\partial v}{\partial z}\right)\varphi \mathrm{dz}$$

(23)

Finally, the potential energy of the load q:

$$P_E=-{\int }_0^{L}qv\mathrm{dz}=-{\int }_0^{L}H\frac{{\partial }^{2}v}{\partial z^2}v\mathrm{dz}$$

(24)

and the kinetic energy T is:

$$T=\frac{1}{2}{\int }_0^L\rho \mathrm{A}{\left(\frac{\partial v}{\partial t}\right)}^2\mathrm{dz}$$

(25)

3.3. Equations of motion for nonlocal truncated Timoshenko-Ehrenfest nanotube

According to Hamilton principle and truncated Timoshenko-Ehrenfest theory, the equations of motion for a single-walled carbon nanotube are computed.

Summing the strain energy Eq.(21) and the potential energies Eq.(22) and Eq.(23), from which kinetic energy (24) is subtracted, we obtain:

$$\begin{array}{cc}\hfill & {\int }_{t_1}^{t_2}\delta \left(\Pi +P_{\mathrm{nl}}+P_m+P_E-T\right)\mathrm{dt}=\hfill \\ \hfill & {\int }_0^L{\mathrm{EI}}^{*}\frac{\partial \varphi }{\partial z}\delta \left(\frac{\partial \varphi }{\partial z}\right)\mathrm{dz}+{\int }_0^L\mathrm{GA}\kappa \left(\frac{\partial v}{\partial z}+\varphi \right)\delta \varphi \mathrm{dz}+{\int }_0^L\mathrm{GA}\kappa \left(\frac{\partial v}{\partial z}+\varphi \right)\delta \left(\frac{\partial v}{\partial z}\right)\mathrm{dz}+\hfill \\ \hfill & {\int }_0^L{\mu }^2\left(\rho \mathrm{A}\frac{{\partial }^{2}v}{\partial t^2}-\rho \mathrm{I}\frac{{\partial }^{4}v}{\partial t^2\partial z^2}-H\frac{{\partial }^{2}v}{\partial z^2}\right)\delta \left(\frac{\partial \varphi }{\partial z}\right)\mathrm{dz}+\hfill \\ \hfill & {\int }_0^L\left({\mu }^2\left(\rho \mathrm{A}\frac{{\partial }^{3}v}{\partial t^2\partial z}-H\frac{{\partial }^{3}v}{\partial z^3}\right)\right)\delta \varphi \mathrm{dz}+{\int }_0^L\left({\mu }^2\left(\rho \mathrm{A}\frac{{\partial }^{3}v}{\partial t^2\partial z}-H\frac{{\partial }^{3}v}{\partial z^3}\right)\right)\delta \left(\frac{\partial v}{\partial z}\right)\mathrm{dz}+\hfill \\ \hfill & -{\int }_0^L\rho \mathrm{I}\frac{{\partial }^{3}v}{\partial z\partial t^2}\delta \varphi \mathrm{dz}-{\int }_0^{L}H\frac{{\partial }^{2}v}{\partial z^2}\delta \mathrm{v}\mathrm{dz}-{\int }_0^L\rho \mathrm{A}\frac{\partial v}{\partial t}\delta \left(\frac{\partial v}{\partial t}\right)\mathrm{dz}=0\hfill \end{array}$$

(26)

Integrating by parts and collecting all the terms in the previous equations allows us to write:

$$\rho \mathrm{A}\frac{{\partial }^{2}v}{\partial t^2}-{\mu }^2\rho \mathrm{A}\frac{{\partial }^{4}v}{\partial t^2\partial z^2}+{\mu }^{2}H\frac{{\partial }^{4}v}{\partial z^4}-\mathrm{GA}\kappa \left(\frac{{\partial }^{2}v}{\partial z^2}+\frac{\partial \varphi }{\partial z}\right)-H\frac{{\partial }^{2}v}{\partial z^2}=0$$

(27)

$${\mathrm{EI}}^{*}\frac{{\partial }^2\varphi }{\partial z^2}-{\mu }^2\rho \mathrm{I}\frac{{\partial }^{5}v}{\partial t^2\partial z^3}+\rho \mathrm{I}\frac{{\partial }^{3}v}{\partial t^2\partial z}-\mathrm{GA}\kappa \left(\frac{\partial v}{\partial z}+\varphi \right)=0$$

(28)

As can be seen, the Equations (27-28) have the same form as the Equations (16,19) found by the Euler method and represent the set of differential equations of motion for a Timoshenko-Ehrenfest SWCNT.

Finally, the associated boundary conditions are given by:

$${\left.\left.\left[\left({\mu }^2\left(\rho \mathrm{A}\frac{{\partial }^{2}v}{\partial t^2}-\rho \mathrm{I}\frac{{\partial }^{4}v}{\partial t^2\partial z^2}-H\frac{{\partial }^{2}v}{\partial z^2}\right)+{\mathrm{EI}}^{*}\frac{\partial \varphi }{\partial z}\right)\right.\right)\delta \varphi \right]}_0^L=0$$

(29)

$${\left[\left(\left({\mu }^2\rho \mathrm{A}\frac{{\partial }^{3}v}{\partial t^2\partial z}-{\mu }^{2}H\frac{{\partial }^{3}v}{\partial z^3}\right)+\mathrm{GA}\kappa \left(\frac{\partial v}{\partial z}+\varphi \right)\right)\delta \mathrm{v}\right]}_0^L=0$$

(30)

3.4. Solving the system of differentials equations of nonlocal truncated Timoshenko-Ehrenfest nanotube

In order to find the differential equations solutions of nonlocal truncated Timoshenko-Ehrenfest nanotube, we look for periodic solutions of the form:

$$\begin{array}{c}\hfill v(z,t)=v\left(z\right)e^{\mathrm{i}\omega \mathrm{t}}\end{array}$$

$$\begin{array}{c}\hfill \varphi (z,t)=\varphi \left(z\right)e^{\mathrm{i}\omega \mathrm{t}}\end{array}$$

(31)

where $\omega$ is the frequency of natural vibration. On substituting Equations (31) into equations (27-28) we have:

$$\rho \mathrm{A}{\omega }^{2}v-{\mu }^2\rho \mathrm{A}{\omega }^2\frac{{\partial }^{2}v}{\partial z^2}+\mathrm{GA}\kappa \left(\frac{{\partial }^{2}v}{\partial z^2}+\frac{\partial \varphi }{\partial z}\right)-{\mu }^{2}H\frac{{\partial }^{4}v}{\partial z^4}+H\frac{{\partial }^{2}v}{\partial z^2}=0$$

(32)

$${\mathrm{EI}}^{*}\frac{{\partial }^2\varphi }{\partial z^2}+{\mu }^2\rho \mathrm{I}{\omega }^2\frac{{\partial }^{3}v}{\partial z^3}-\rho \mathrm{I}{\omega }^2\frac{\partial v}{\partial z}-\mathrm{GA}\kappa \left(\frac{\partial v}{\partial z}+\varphi \right)=0$$

(33)

From Equation (32) the following expression is derived:

$$\begin{array}{c}\hfill \frac{\partial \varphi }{\partial z}=\frac{{\mu }^2}{\mathrm{GA}\kappa }H\frac{{\partial }^{4}v}{\partial z^4}+\left(\frac{{\mu }^2\rho \mathrm{A}{\omega }^2}{\mathrm{GA}\kappa }-1-\frac{H}{\mathrm{GA}\kappa }\right)\frac{{\partial }^{2}v}{\partial z^2}-\frac{\rho \mathrm{A}{\omega }^2}{\mathrm{GA}\kappa }v\end{array}$$

(34)

which when derived twice and substituted into Equation (33) derived once gives:

$$\begin{array}{cc}\hfill & \frac{{\mu }^2{\mathrm{EI}}^{*}}{\mathrm{GA}\kappa }H\frac{{\partial }^{6}v}{\partial z^6}+\left(-{\mu }^{2}H+{\mu }^2\rho \mathrm{I}{\omega }^2+{\mathrm{EI}}^{*}\left(-1-\frac{H}{\mathrm{GA}\kappa }+\frac{{\mu }^2\rho \mathrm{A}{\omega }^2}{\mathrm{GA}\kappa }\right)\right)\frac{{\partial }^{4}v}{\partial z^4}+\hfill \\ \hfill & \left(-{\mathrm{EI}}^{*}\frac{\rho \mathrm{A}{\omega }^2}{\mathrm{GA}\kappa }-{\mu }^2\rho \mathrm{A}{\omega }^2-\rho \mathrm{I}{\omega }^2+H\right)\frac{{\partial }^{2}v}{\partial z^2}+\rho \mathrm{A}{\omega }^{2}v=0\hfill \end{array}$$

(35)

Equation (35) represents the differential equation of motion for a Timoshenko-Ehrenfest nanotube derived from the fourth order truncated theory in $v\left(z\right)$ and in the presence of surface effects.

On introducing the following non-dimensional coefficients:

$$\begin{array}{cc}\hfill & \zeta =\frac{z}{L};{\Omega }^2=\frac{\rho A{L}^4{\omega }^2}{\mathrm{EI}};{\eta }^2=\frac{{\mu }^2}{L^2};{\beta }^2=\frac{\mathrm{EI}}{\mathrm{GA}\kappa L^2};{\alpha }^2=\frac{I}{A{L}^2};\hfill \\ \hfill & u^2=\frac{\pi E^s\left(R_i^3+R_o^3\right)}{\mathrm{EI}};{\delta }^2=\frac{4\tau \left(R_i+R_o\right)L^2}{\mathrm{EI}};h=\left(R_o-R_i\right)\hfill \end{array}$$

(36)

with $\zeta \in [0,1]$ the dimensionless counterpart of $z\in [0,L],$ ${\Omega }^2$ the frequency parameter, ${\eta }^2$ scaling effect parameter, ${\beta }^2$ shear deformation parameter, ${\alpha }^2$ slenderness ratio, $u^2$ surface elasticity modulus and ${\delta }^2$ residual surface tension, the governing Eq.(35) may be rewritten as:

$$\begin{array}{cc}\hfill & \left(1+u^2\right){\eta }^2{\beta }^2{\delta }^2\frac{{\partial }^{6}v}{\partial {\zeta }^6}+\left(\left(1+u^2\right)\left(-1-{\beta }^2{\delta }^2+{\Omega }^2{\beta }^2{\eta }^2\right)+{\Omega }^2{\eta }^2{\alpha }^2-{\eta }^2{\delta }^2\right)\frac{{\partial }^{4}v}{\partial {\zeta }^4}+\hfill \\ \hfill & \left(-\left(1+u^2\right){\Omega }^2{\beta }^2-{\Omega }^2{\eta }^2-{\Omega }^2{\alpha }^2+{\delta }^2\right)\frac{{\partial }^{2}v}{\partial {\zeta }^2}+{\Omega }^{2}v=0\hfill \end{array}$$

(37)

The system of differential equations (32-33) by means the dimensionless coefficients assumes the following form:

$${\beta }^2{\Omega }^{2}v-{\beta }^2{\eta }^2{\Omega }^2\frac{{\partial }^{2}v}{\partial {\zeta }^2}+\left(\frac{{\partial }^{2}v}{\partial {\zeta }^2}+\frac{\partial \overline{\varphi }}{\partial \zeta }\right)-{\beta }^2{\eta }^2{\delta }^2\frac{{\partial }^{4}v}{\partial {\zeta }^4}+{\beta }^2{\delta }^2\frac{{\partial }^{2}v}{\partial {\zeta }^2}=0$$

(38)

$$\left(1+u^2\right)\frac{{\partial }^2\overline{\varphi }}{\partial {\zeta }^2}+{\eta }^2{\alpha }^2{\Omega }^2\frac{{\partial }^{3}v}{\partial {\zeta }^3}-{\Omega }^2{\alpha }^2\frac{\partial v}{\partial \zeta }-\frac{1}{{\beta }^2}\left(\frac{\partial v}{\partial \zeta }+\overline{\varphi }\right)=0$$

(39)

Setting $\overline{\varphi }$ = $\varphi$ L, it is possible to derive from Equation (39) the value of $\stackrel{\_}{\varphi }$ as a function of $v\left(\zeta \right)$:

$$\begin{array}{cc}\hfill & \overline{\varphi }={\beta }^4{\eta }^2{\delta }^2\left(1+u^2\right)\frac{{\partial }^{5}v}{\partial {\zeta }^5}+\left({\beta }^2\left(1+u^2\right)\left({\beta }^2{\eta }^2{\Omega }^2-1-{\beta }^2{\delta }^2\right)+{\beta }^2{\eta }^2{\alpha }^2{\Omega }^2\right)\frac{{\partial }^{3}v}{\partial {\zeta }^3}+\hfill \\ \hfill & -\left({\beta }^4\left(1+u^2\right){\Omega }^2+{\beta }^2{\Omega }^2{\alpha }^2+1\right)\frac{\partial v}{\partial \zeta }\hfill \end{array}$$

(40)

Also, the dimensionless boundary conditions (29-30) are given by:

$${\left[\left(-{\eta }^2{\Omega }^{2}v+\left({\eta }^2{r}^2{\Omega }^2-{\eta }^2{\delta }^2\right)\frac{{\partial }^{2}v}{\partial {\zeta }^2}+\left(1+u^2\right)\left(\frac{\partial \overline{\varphi }}{\partial \zeta }\right)\right)\delta \overline{\varphi }\right]}_0^1=0$$

(41)

$${\left[\left(\left(-{\eta }^2{\Omega }^2\frac{\partial v}{\partial \zeta }-{\eta }^2{\delta }^2\frac{{\partial }^{3}v}{\partial {\zeta }^3}\right)+\frac{1}{{\beta }^2}\left(\frac{\partial v}{\partial \zeta }+\overline{\varphi }\right)\right)\delta \mathrm{v}\right]}_0^1=0$$

(42)

3.4.1. The case of the simply-supported nanotube

In what follows, the case of a simply supported Timoshenko-Ehrenfest nanotube is analysed.

Consider the dimensionless vibration modes associated with the nanotube of the following form:

$$v\left(\zeta \right)=\mathrm{Sin}\left(m\pi \zeta \right)$$

(43)

where m=1,2,3,... is the m-th natural frequency of the transverse vibration of nanotube.

Substituting Equation (43), appropriately derived, into differential Equation (37), one gets:

$$\begin{array}{cc}\hfill & (-m^6{\pi }^6\left(1+u^2\right){\beta }^2{\delta }^2{\eta }^2+{\Omega }^2-m^2{\pi }^2\left({\delta }^2-\left({\alpha }^2+\left(1+u^2\right){\beta }^2+{\eta }^2\right){\Omega }^2\right)+\hfill \\ \hfill & m^4{\pi }^4\left(-{\delta }^2{\eta }^2+{\alpha }^2{\eta }^2{\Omega }^2+\left(1+u^2\right)\left(-1+{\beta }^2\left(-{\delta }^2+{\eta }^2{\Omega }^2\right)\right)\right))=0\hfill \end{array}$$

(44)

whose solution is:

$${\Omega }_m=\frac{\pi \sqrt{m^2\left({\delta }^2+m^4{\pi }^4\left(1+u^2\right){\beta }^2{\delta }^2{\eta }^2+m^2{\pi }^2\left(1+{\beta }^2{\delta }^2+u^2\left(1+{\beta }^2{\delta }^2\right)+{\delta }^2{\eta }^2\right)\right)}}{\sqrt{\left(1+m^2{\pi }^2\left({\alpha }^2+\left(1+u^2\right){\beta }^2\right)\right)\left(1+m^2{\pi }^2{\eta }^2\right)}}$$

(45)

from Eq. (45), the dimensionless natural frequency is given by:

$$\begin{array}{cc}\hfill & f_m=\frac{{\omega }_m}{2\pi }=\frac{1}{2\pi }\hfill \\ \hfill & \left(\frac{\pi \sqrt{L^4{m}^2{\delta }^2+m^6{\pi }^4\left(1+u^2\right){\beta }^2{\delta }^2{\eta }^2+L^2{m}^4{\pi }^2\left(1+{\beta }^2{\delta }^2+u^2\left(1+{\beta }^2{\delta }^2\right)+{\delta }^2{\eta }^2\right)}}{\sqrt{L^2\left(L^2+m^2{\pi }^2\left({\alpha }^2+\left(1+u^2\right){\beta }^2\right)\right)\left(L^2+m^2{\pi }^2{\eta }^2\right)}}\sqrt{\frac{\mathrm{EI}}{\rho A{L}^4}}\right)\hfill \end{array}$$

(46)

On setting $\beta$=0, $\alpha$=0 in Equation (44), the differential equation for the Euler-Bernoulli nanotube is obtained:

$$m^4{\pi }^4\left(-1-u^2-{\delta }^2{\eta }^2\right)+{\Omega }^2-m^2{\pi }^2\left({\delta }^2-{\eta }^2{\Omega }^2\right)=0$$

(47)

whose solution is given by:

$${\Omega }_m^{\mathrm{EU}}=\frac{\pi \sqrt{m^2\left({\delta }^2+m^2{\pi }^2\left(1+u^2+{\delta }^2{\eta }^2\right)\right)}}{\sqrt{1+m^2{\pi }^2{\eta }^2}}$$

(48)

From Equation (48) the natural frequency of the Euler-Bernoulli nanotube is derived as follows:

$$f_m^{\mathrm{EU}}=\frac{{\omega }_m^{\mathrm{EU}}}{2\pi }=\frac{1}{2\pi }\left(\sqrt{\frac{{\pi }^2\left(m^4{\pi }^2+m^4{\pi }^2{u}^2+m^2{\delta }^2+m^4{\pi }^2{\delta }^2{\eta }^2\right)}{1+m^2{\pi }^2{\eta }^2}}\sqrt{\frac{\mathrm{EI}}{\rho A{L}^4}}\right)$$

(49)

4. Numerical results and discussion

In order to evaluate the effects of the nonlocal parameter, surface effects and length of the nanotube on the natural frequency of nanotubes, the suggested analytical method is validated in this section. A few numerical examples have been carried out, and the findings with those of previous publications that have been published in the literature have been compared. The numerical computations have been carried out using in-house software created in the Mathematica language [33].

4.1. Effect of surface and nonlocal parameters on the frequency ratio of Timoshenko-Ehrenfest nanotube

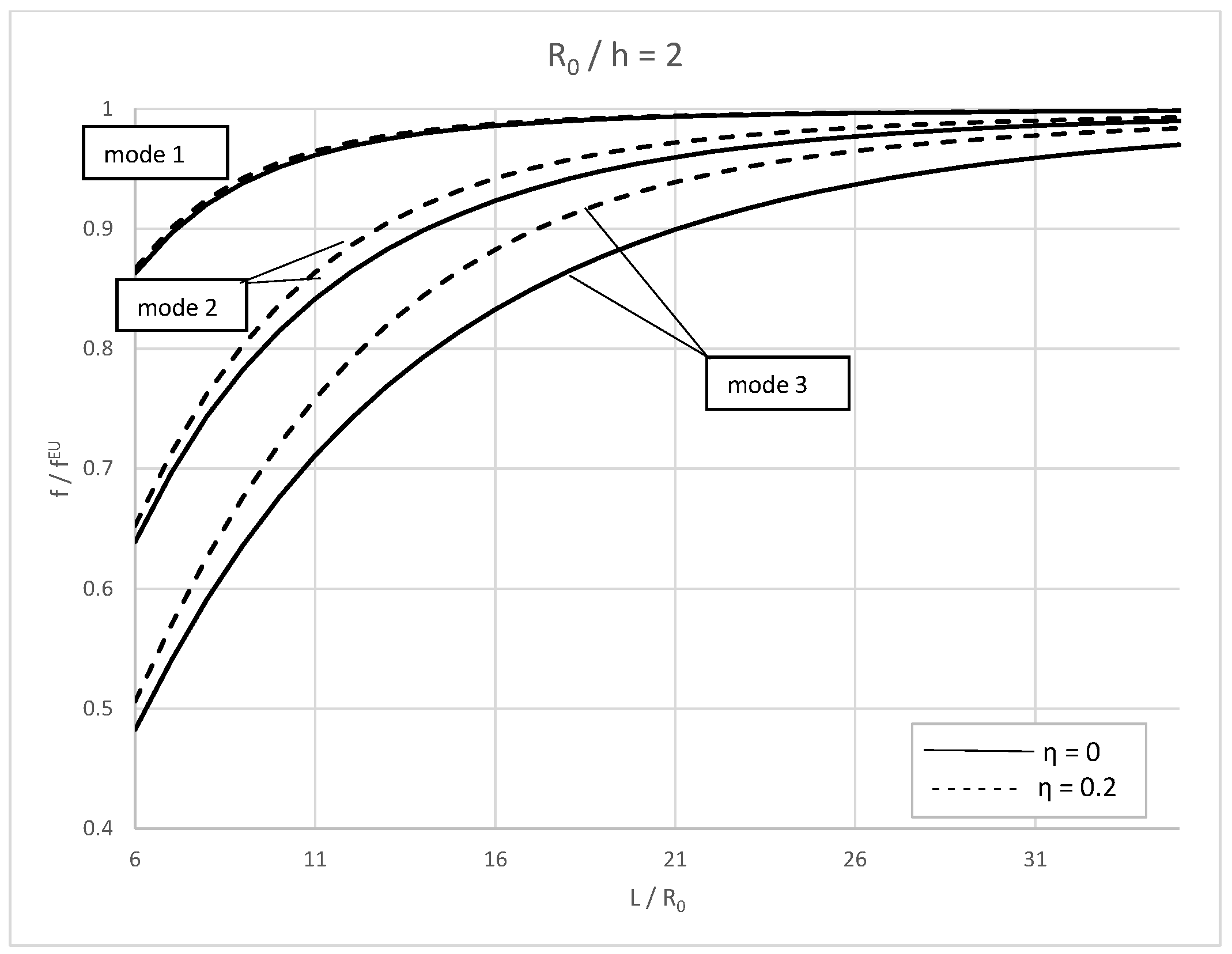
As a first numerical example, let us consider the material properties of an anodic alumina nanotube with crystallographic of [111] direction, as deduced in [28]: E=70 GPa, G =27 GPa, $\rho$ =2700 $\mathrm{kg}/m^3$, Es=5.1882 N/m, $\tau$ =0.9108 N/m, K=5/6. Setting $\alpha$=0 and $\beta$=0, the case of nanotube, which satisfying the boundary conditions between the nanotube and its surfaces, is analyzed. To investigate the influence of considering the nonlocal and surface effects, the first three natural frequencies of alumina Timoshenko-Ehrenfest nanotube, normalized with respect to the fundamental Euler-Bernoulli natural frequencies, versus the aspect ratios, $L/R_o$, are plotted. The effect of varying the aspect ratio $L/R_o$ nonlocal and surface parameters on the free frequencies of the nanotube is investigated for two cases of constant of $R_o$ /h =2 and $R_o$ /h=6 and for the first three vibration modes. The results are obtained for simply-supported (S-S) boundary condition.

In Figure 3, the variations of the normalized natural frequencies ratio with respect to the aspect ratios of nanotube are plotted for two nonlocal parameter values equal to $\eta$=0,$\eta$=0.2 and with a constant ratio value $R_o$ /h =2. According to the plotted curves in Figure 3, with the increase in local parameter, the normalized natural frequencies ratio increases and the first non-dimensional frequency ratio is more sensitive to the initial condition. The variations of the first frequency are more than the second and third one and for a constant value of aspect ratio $L/R$ and varying the nonlocal effect $\eta$ it is revealed that the difference between the values of the first and second modes slightly increase. On the other hand, for $\eta$=0 and $\eta$=0.2, one can see that the values of the frequency ratio of the second and third shape mode decrease respect to the first natural frequencies.

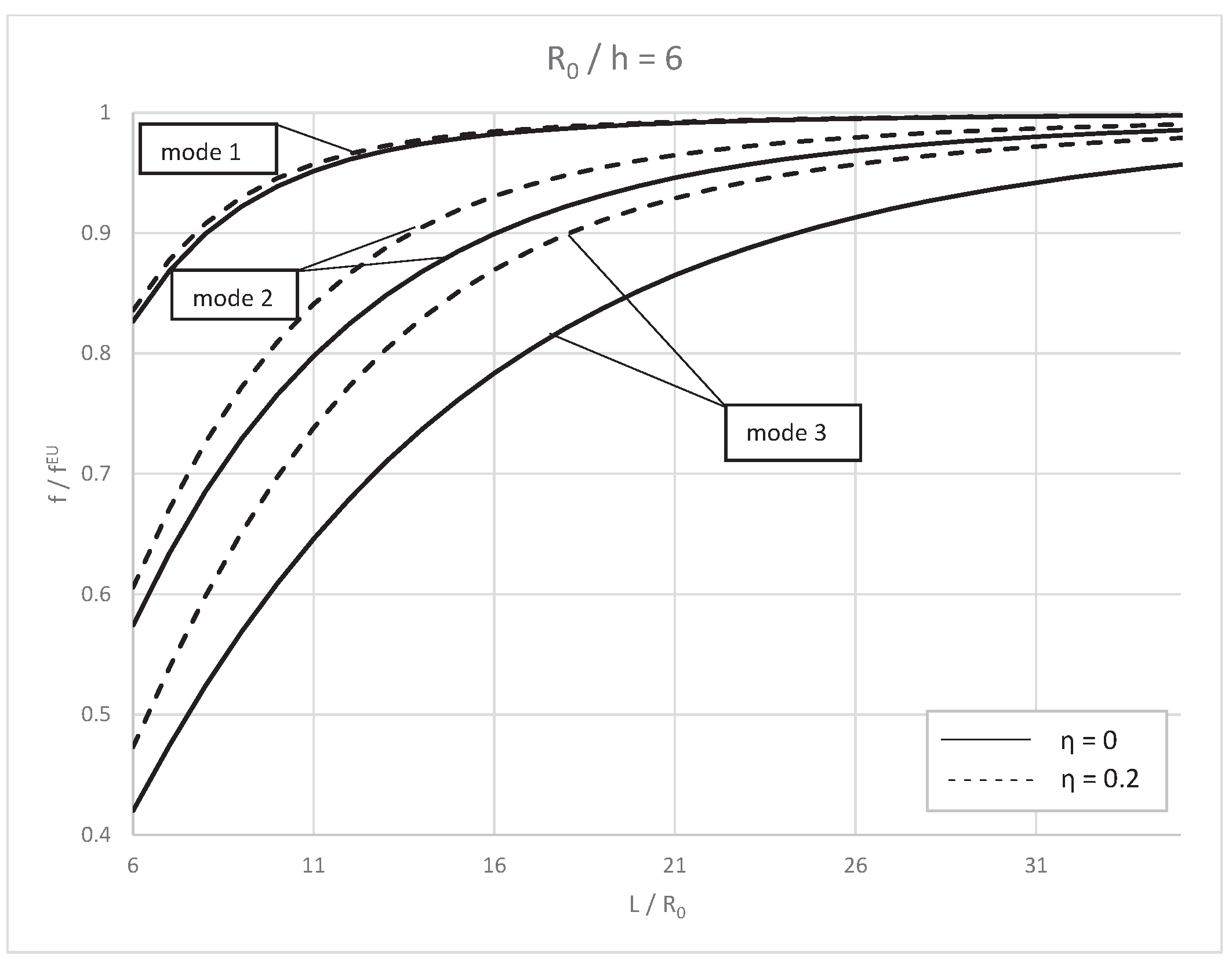
Similar findings as those found in Figure 3 can be observed in Figure 4 for the case of the nanotube with a constant ratio $R_o$ /h =6. It is observed from Figure 4 that in constant ratio $R_o$ /h of the nanotube with increase in the aspect ratio, the non-dimensional natural frequencies ratio increases. Also, the figure illustrates that increasing the nonlocal parameter cause increase of non-dimensional natural frequencies ratio.

The results show that the shape of the modes does not significantly change against the previous one in the first and second modes, however, it has a meaningful effect of the configuration of the third mode.

Comparison between the case of Figure 3 curves with those of Figure 4, in fact, indicates that there are significant differences between the results of two cases, especially in low lengths. It is also shown that by increasing the nonlocal parameter the second non-dimensional frequencies ratio increases respect to the first non-dimensional frequencies ratio, whereas the third one decreases. It is obviously inferred that the greater values of the nonlocal parameter have much more influence on the higher mode shapes of the nanotube.

4.2. Effect of surface and nonlocal parameters on the frequency ratio of Timoshenko-Ehrenfest nanotube varying the constant ratio $R_o$ /h

In the second numerical example, the case of single-walled carbon nanotube, with $L/R_o$=10 at different values of $R_o$ /h and nonlocal parameters, is investigated. Example is given to evaluate the effects of the non-local parameter, the surface parameter and the length of the nanotube on the free vibration frequencies ratio of mode 1 of a Timoshenko beam to a Bernoulli-Euler beam.

In Table 1, varying the constant ratio $R_o$ /h =0,10 and setting $L/R_o$=10, the first natural frequency of alumina Timoshenko-Ehrenfest nanotube, normalized with respect to the fundamental Euler-Bernoulli natural frequency, versus the constant ratio $L/R_o$=10, are calculated.

From Table 1, it can be seen that for different values of nonlocal parameter $\eta$ the increase in the constant ratio $R_o$ /h cause decrease in value of natural frequencies ratio. Also, when the value of $R_o$ /h is small, the ratio value is large because the nanotube is stiff. In addition, it can be seen that increasing the nonlocal parameter increases the frequency ratio. This is because the nonlocal effect is taken into account that makes the nanotube stiffer.

5. Concluding remarks

In present study the free vibration of a Timoshenko-Ehrenfest single-walled carbon nanotube, based on the nonlocal theory and taking surface effects into account, has been developed. A modified version of Timoshenko’s nonlocal elasticity theory - known as the nonlocal truncated Timoshenko beam theory - is put forth to investigate the free vibration behavior of single-walled carbon nanotubes, as indicated in [10,32]. Starting from Timoshenko truncated theory for the beam model and using the geometric and variational approach, the truncated Timoshenko-Ehrenfest single-walled carbon nanotube theory has been derived. Using the Hamilton’s principle, the governing equations and the corresponding boundary conditions have been derived.

As is well- know, it is not always possible to find analytical solutions for all sets of boundary conditions and varied geometries. This circumstance has motivated the present research. The novelty of the proposed approach has been devoted to finding solutions to the eigenvalue problem of single-walled carbon nanotube by employing the truncated theory in those cases for which, to the authors’ knowledge, no analytical solutions have been provided in the literature. Finally, a few numerical examples were proposed to show the effectiveness of the proposed approach, including a comparison with results in the literature. In particular, the results have showed that the present formulation is very efficient and capable of satisfactorily describing the behaviour of nanobeams. Finally, it was explained how the nanotube length, surface effect and non-local parameters influence the three initial SWCNT frequencies.

The results shown in Figure 3, Figure 4 and Table 1 allow the following considerations to be made:

-

the figure illustrates that increasing the nonlocal parameter cause increase of natural frequencies ratio;

-

by increasing the nonlocal parameter the second frequencies ratio increases respect to the first non-dimensional frequencies ratio, whereas the third one decreases;

-

for different values of nonlocal parameter $\eta$ the increase in the constant ratio $Ro/h$ cause decrease in value of natural frequencies ratio.