Submitted:
09 January 2024
Posted:
10 January 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Sanders‒Koiter Shell Theory for SWCNTs
3. Nonlocal Strain Gradient Anisotropic Elastic Shell Model
4. Force and Moment Resultants
5. Equations of Motion
6. Solution Method
7. Numeric Results
7.1. Validation of the Anisotropic Elastic Shell Model
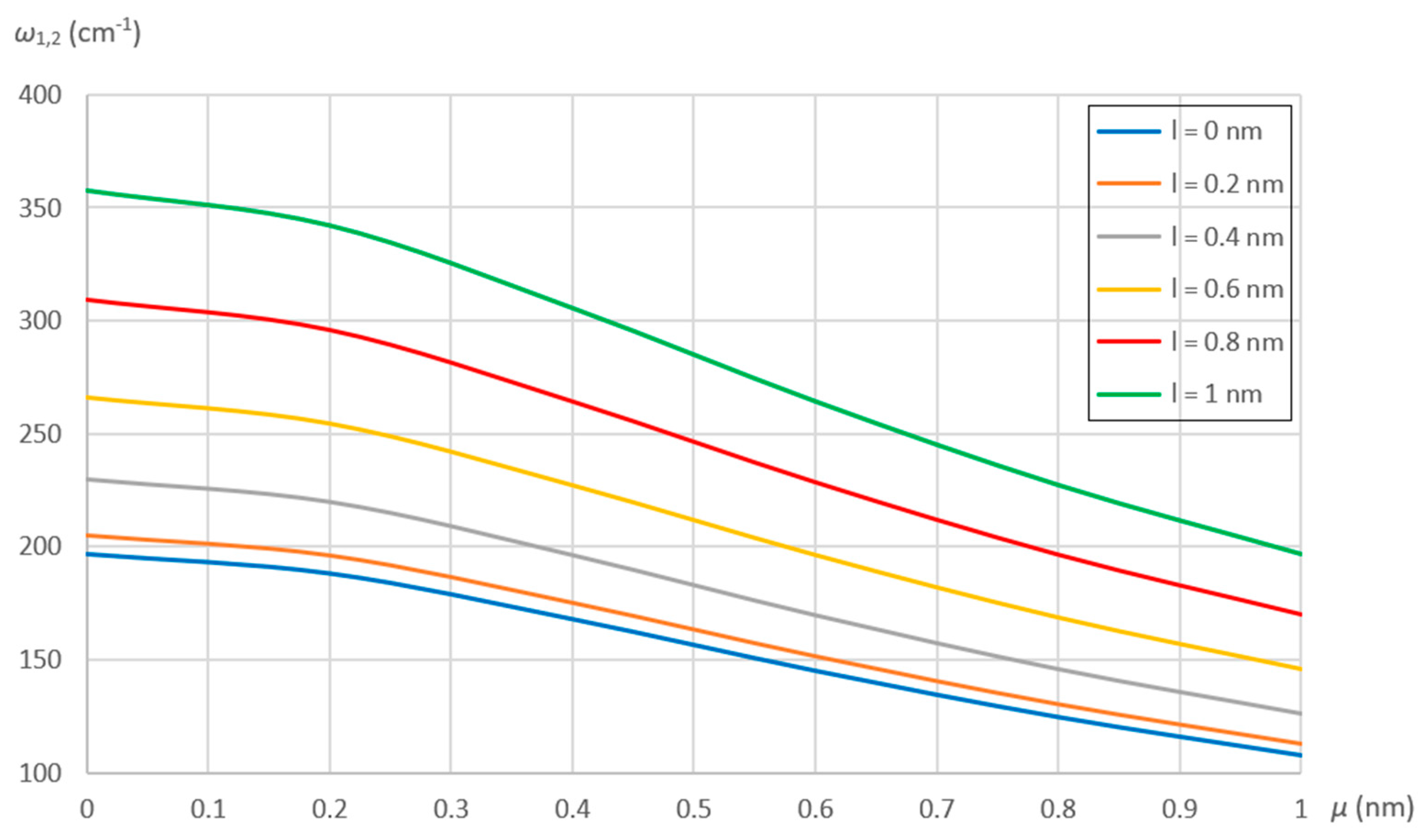
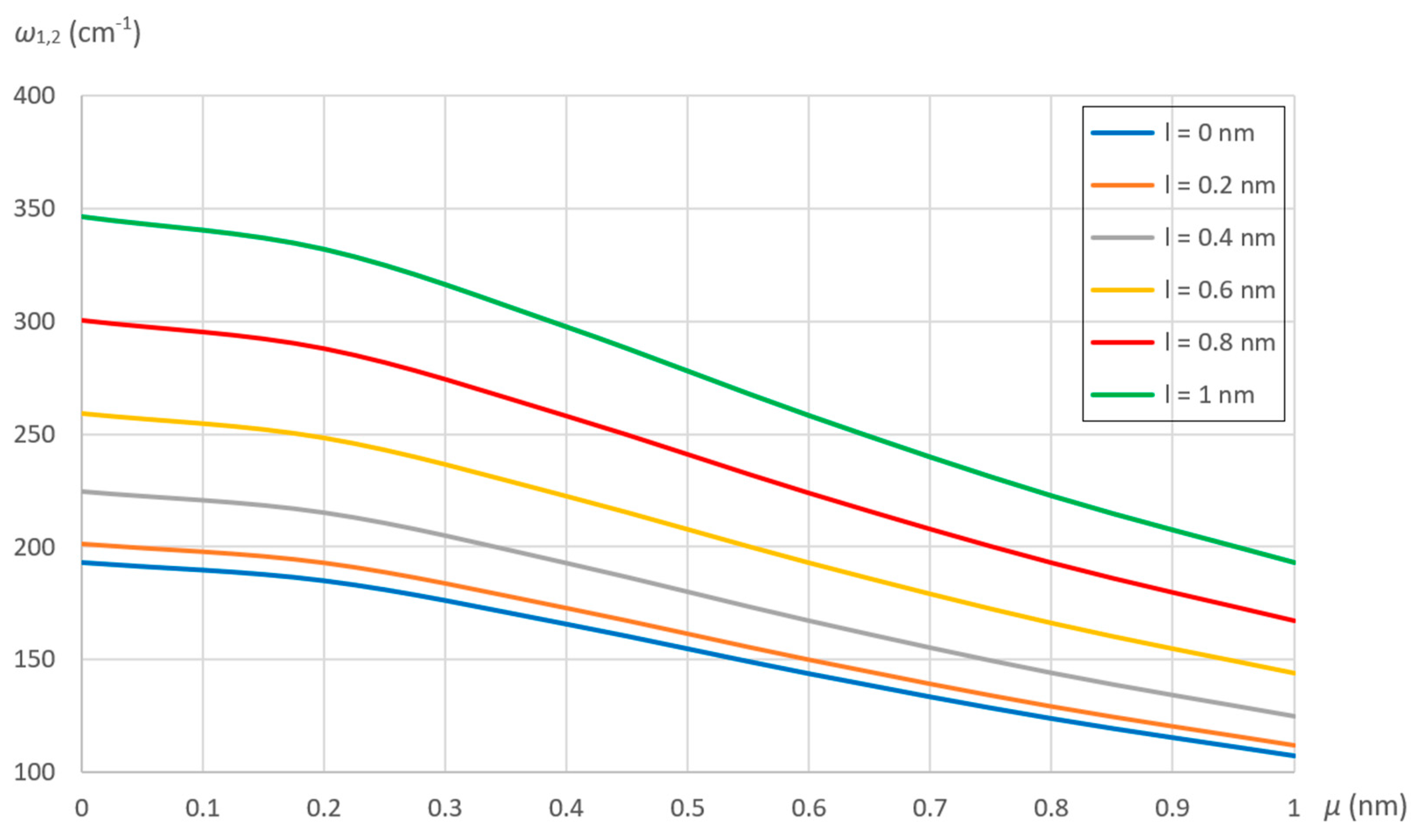
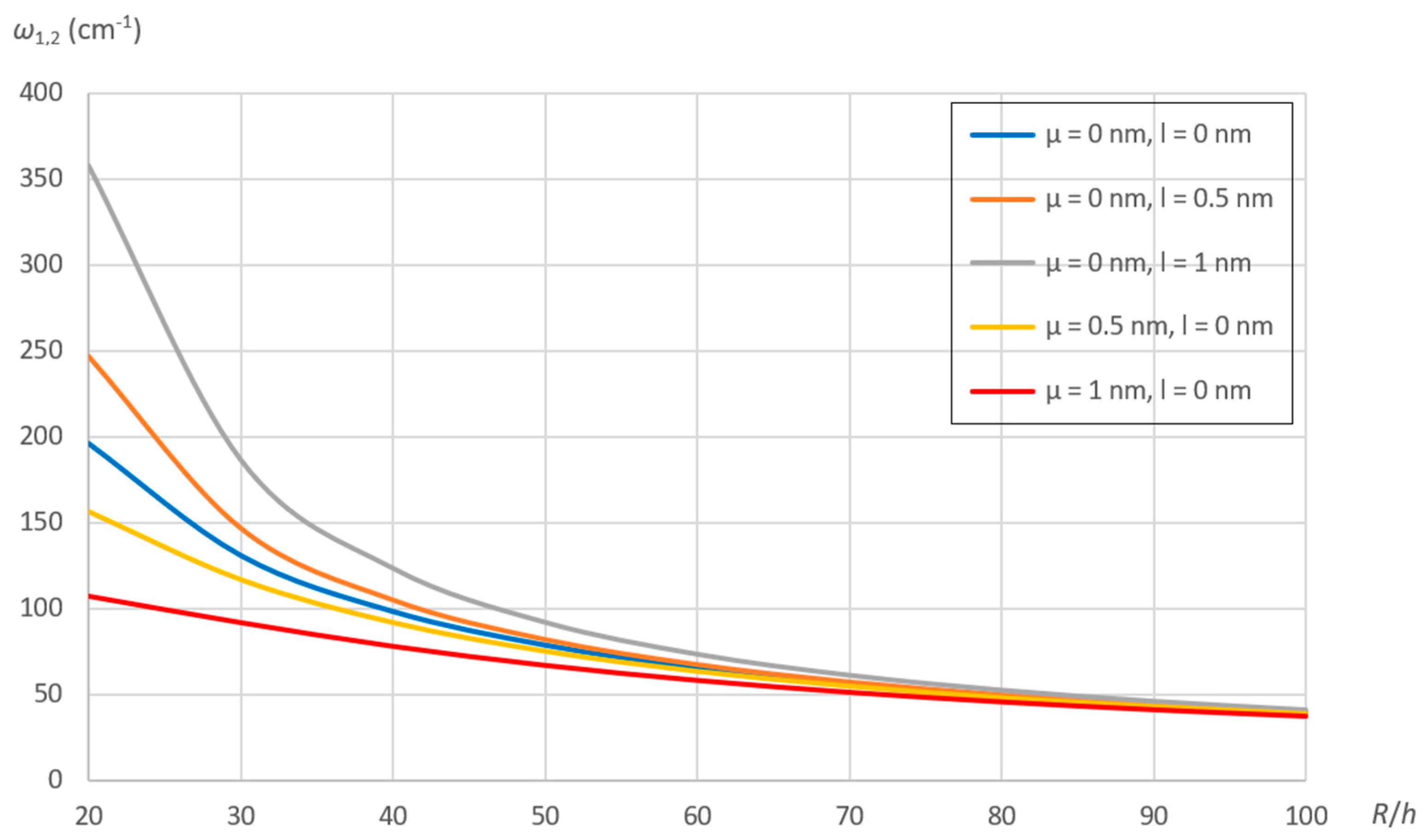
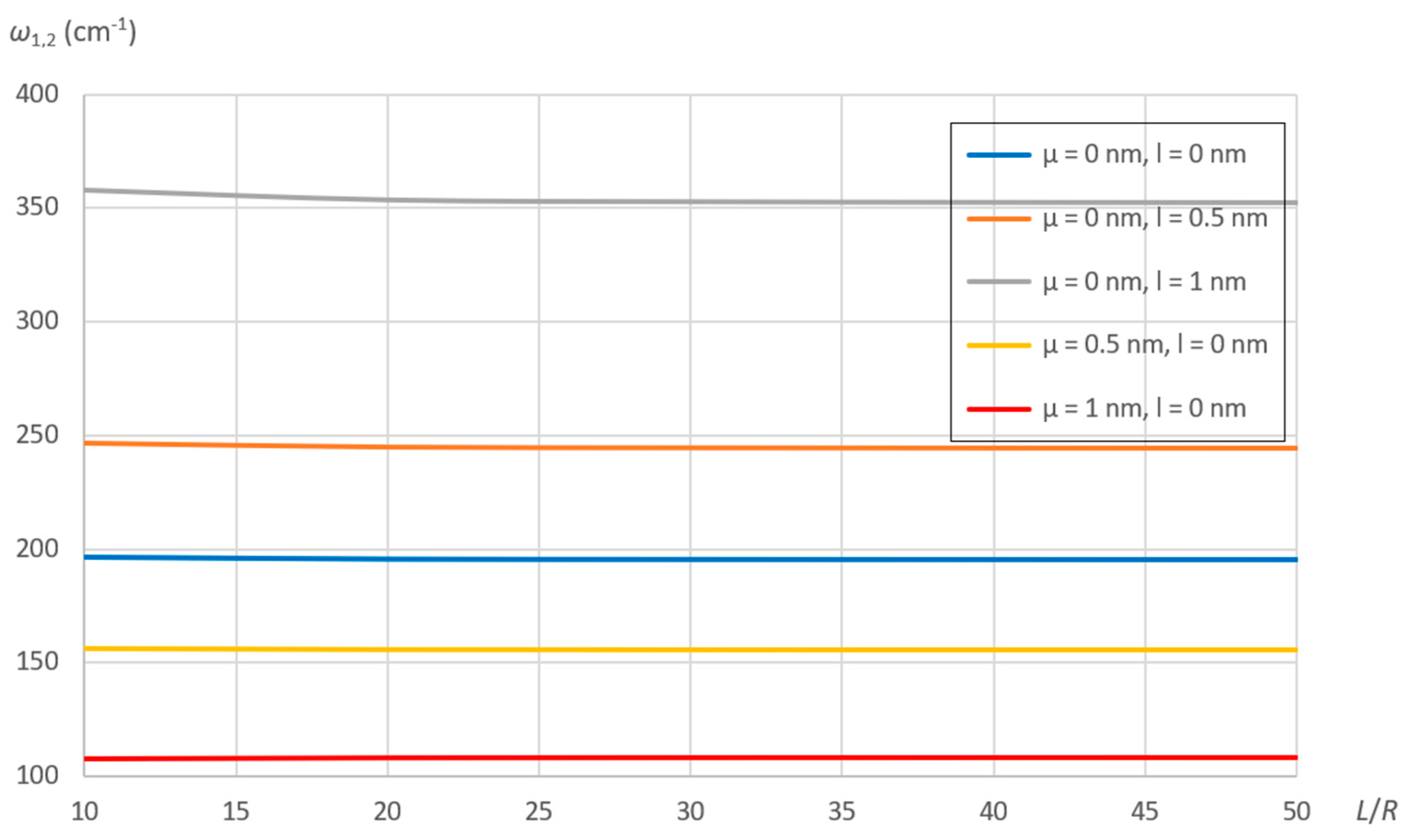
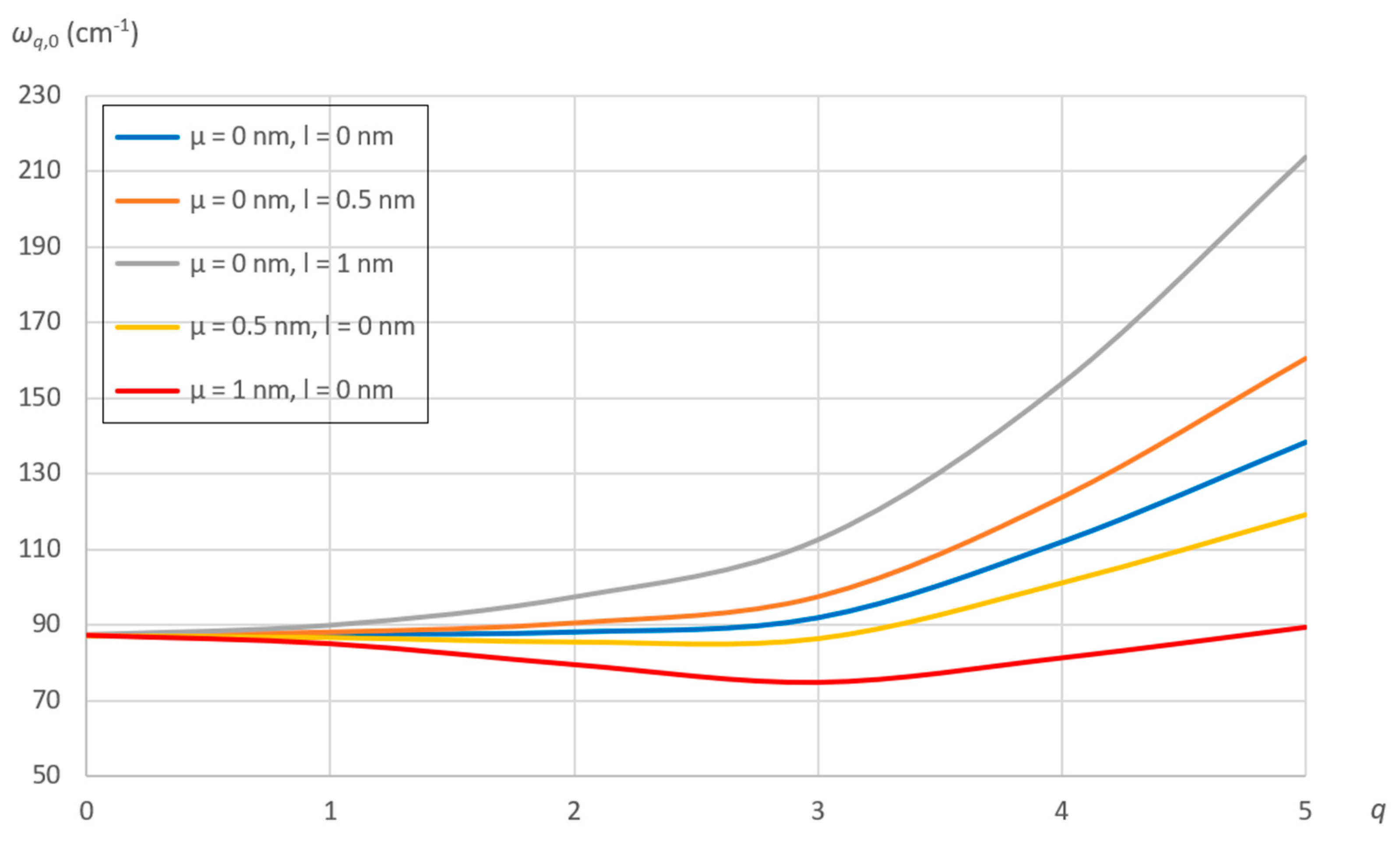
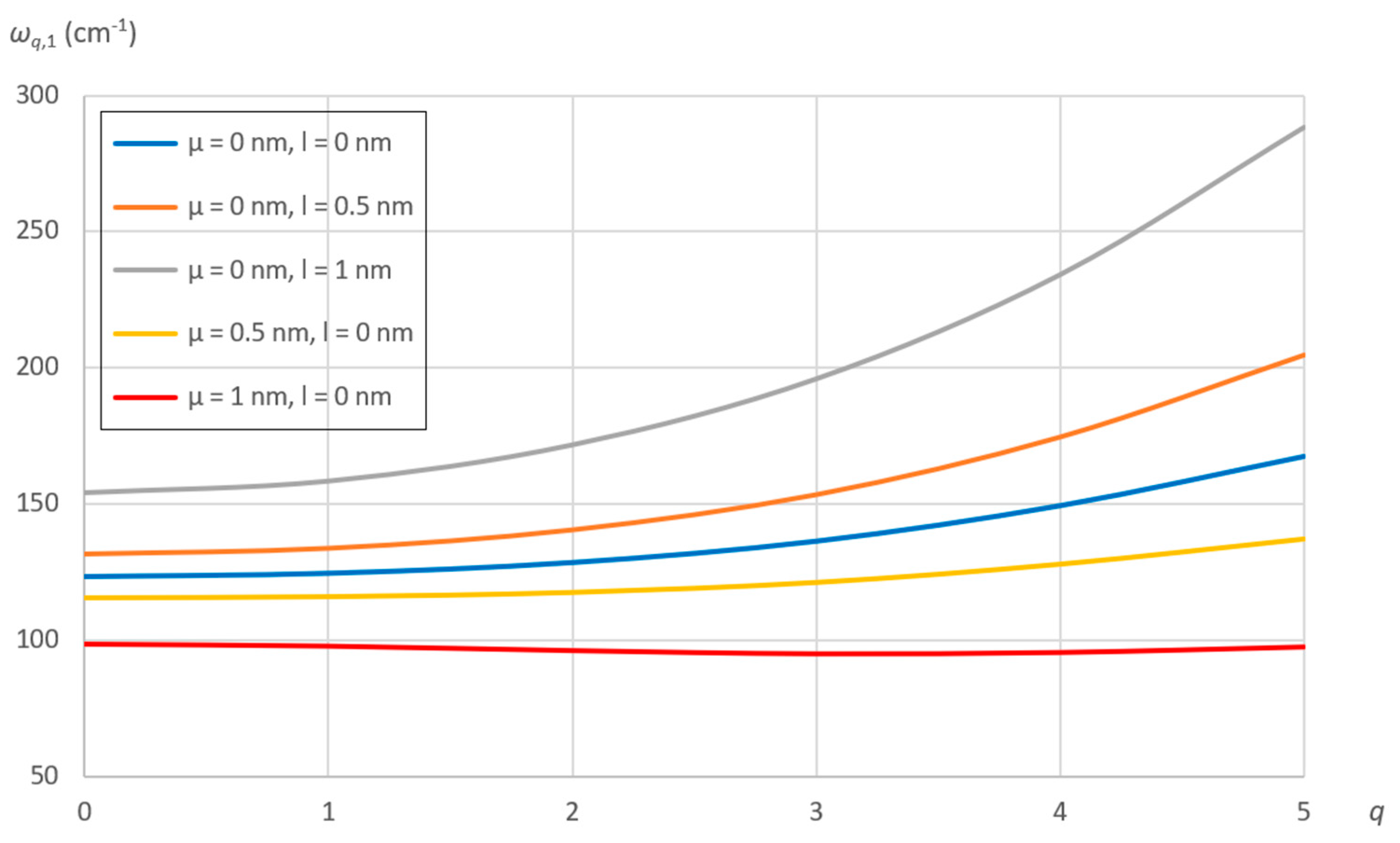
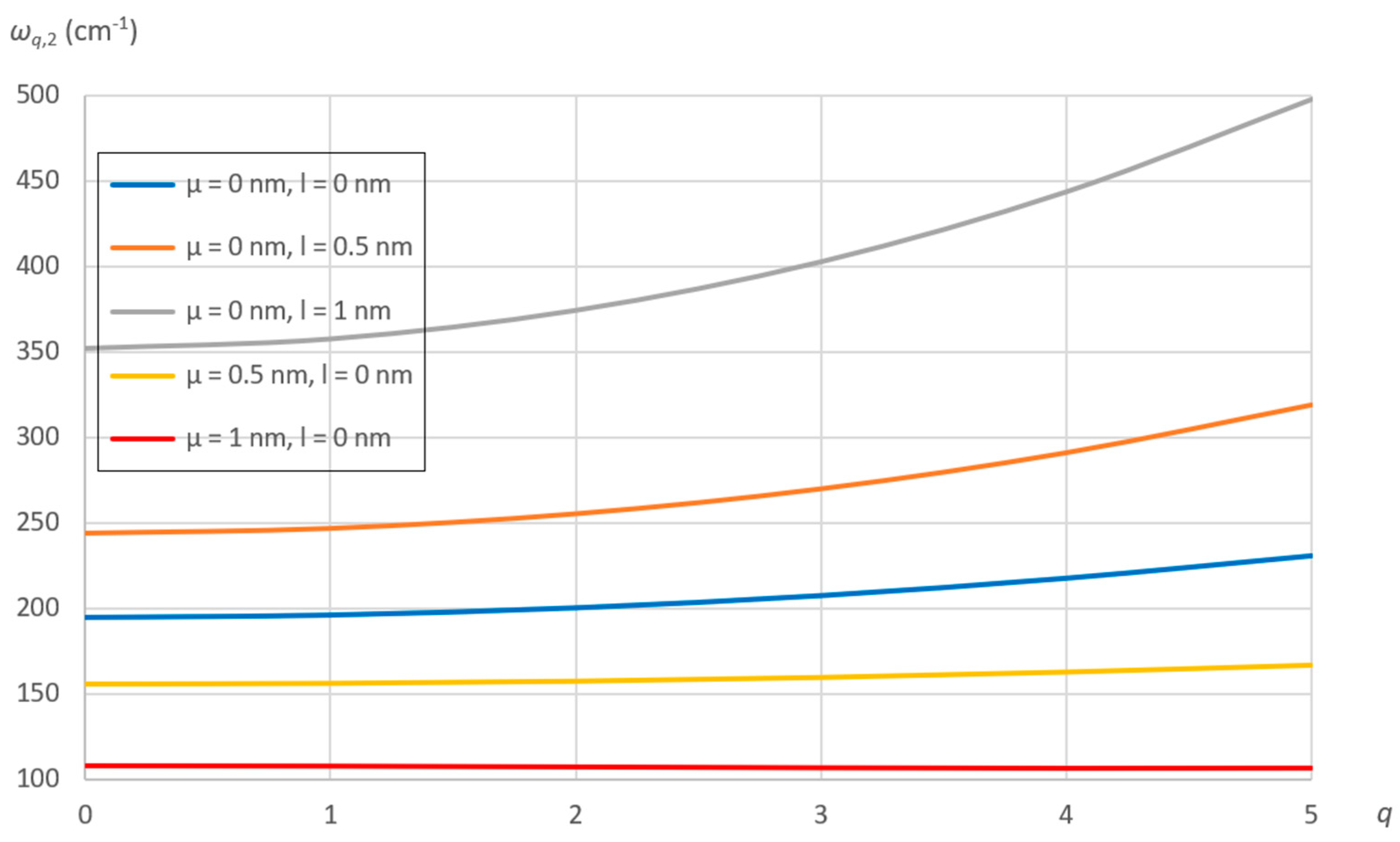
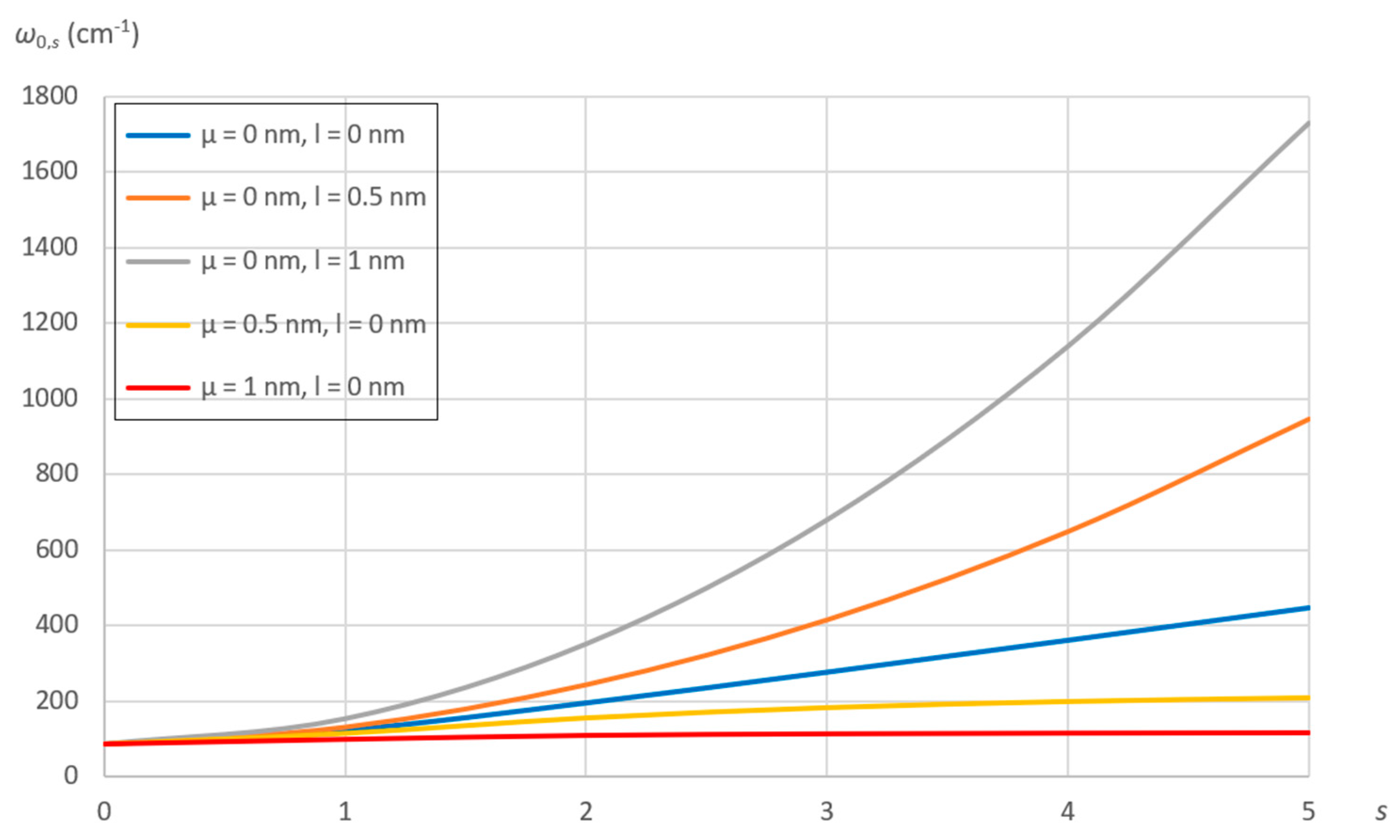
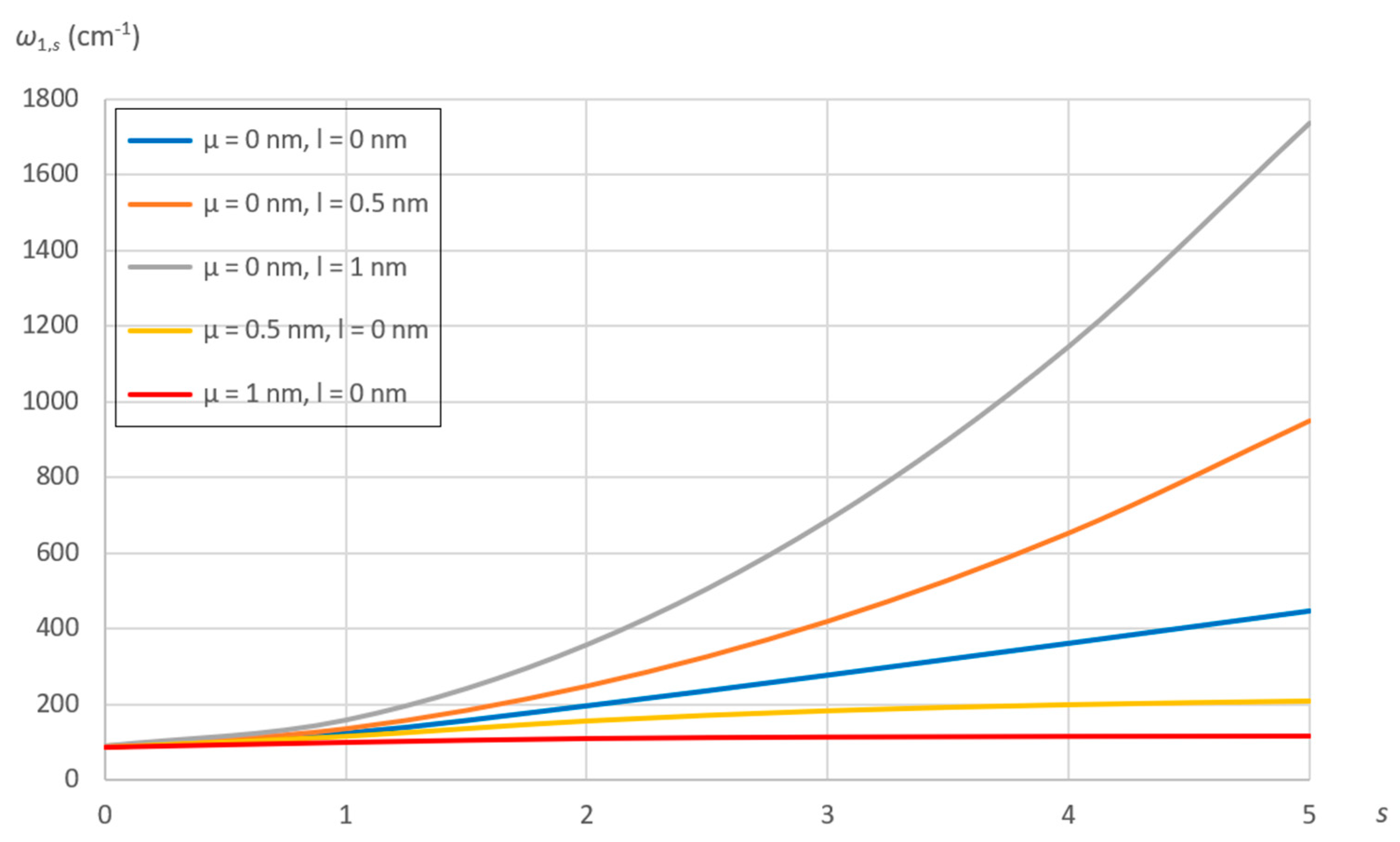
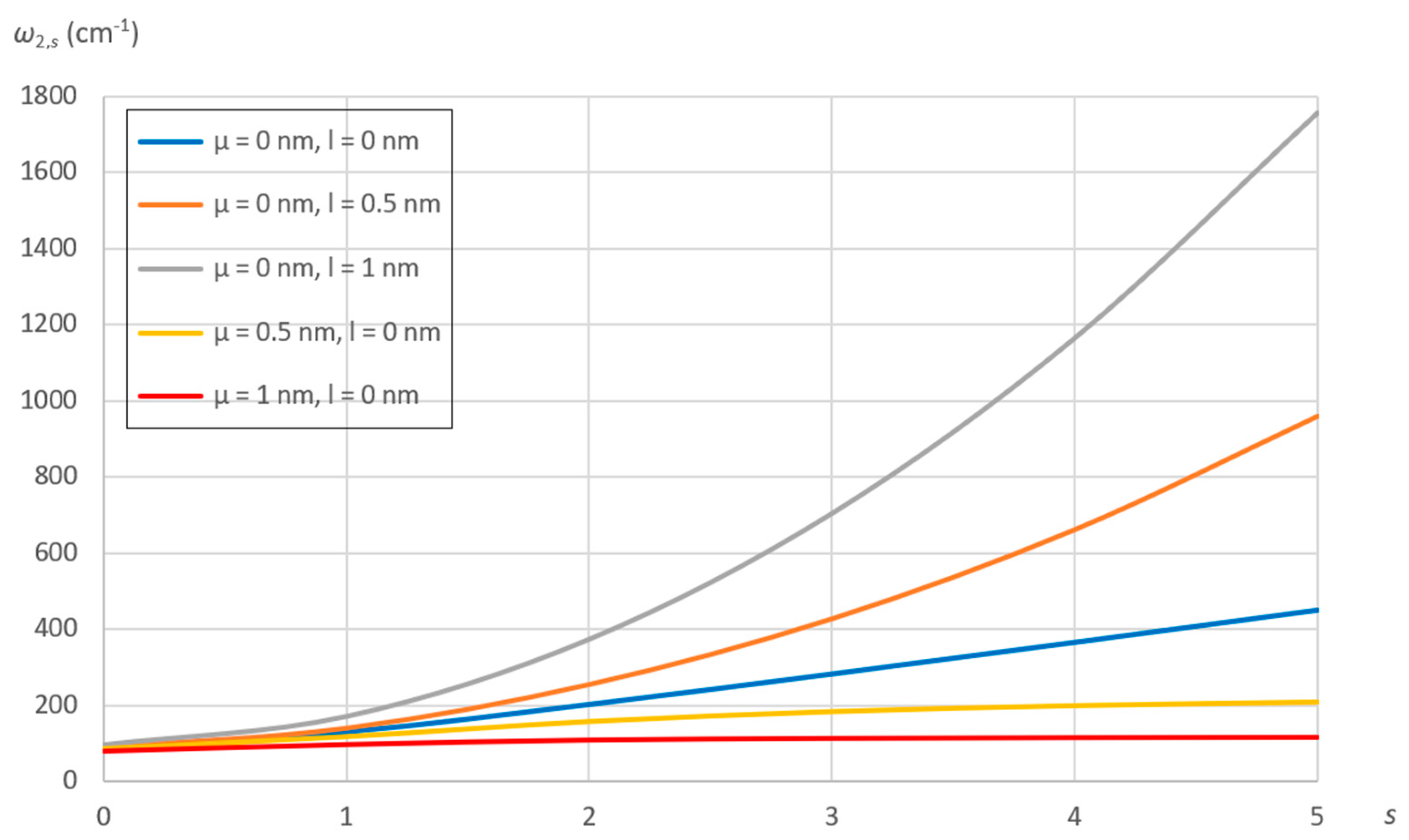
7.2. Effect of Nonlocal and Material Parameters
8. Conclusions
- The natural frequency of the undeformed vibration mode is independent of both nonlocal and material parameters.
- For a generic linear vibration mode, the natural frequencies decrease as the nonlocal parameter increases, while they increase as the material parameter increases.
- The decrease of the natural frequencies with increasing SWCNT radius is exponential as the material parameter increases, while it is linear as the nonlocal parameter increases.
- The effect of nonlocal and material parameters on the natural frequencies is independent of SWCNT chirality and length.
- As the number of longitudinal half‒waves increases, the natural frequencies linearly decrease with increasing the nonlocal parameter, while they exponentially increase with increasing the material parameter.
- As the number of circumferential waves increases, the natural frequencies little increase with increasing the nonlocal parameter, while they strongly exponentially increase with increasing the material parameter.
Author Contributions
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix
References
- Chang, T.; Geng, J.; Guo, X. “Prediction of chirality‒ and size‒dependent elastic properties of single‒walled carbon nanotubes via a molecular mechanics model”. Proceedings of the Royal Society A 2006, 462, 2523–2540. [Google Scholar] [CrossRef]
- Chang, T. “A molecular based anisotropic shell model for single‒walled carbon nanotubes”. Journal of the Mechanics and Physics of Solids 2010, 58, 1422–1433. [Google Scholar] [CrossRef]
- Ghavanloo, E.; Fazelzadeh, S.A. “Vibration characteristics of single‒walled carbon nanotubes based on an anisotropic elastic shell model including chirality effect”. Applied Mathematical Modelling 2012, 36, 4988–5000. [Google Scholar] [CrossRef]
- Strozzi, M.; Elishakoff, I.; Bochicchio, M.; Cocconcelli, M.; Rubini, R.; Radi, E. “A Comparison of Shell Theories for Vibration Analysis of Single‒Walled Carbon Nanotubes Based on an Anisotropic Elastic Shell Model”. Nanomaterials 2023, 13, 1390. [Google Scholar] [CrossRef] [PubMed]
- Eringen, A.C. “Linear theory of nonlocal elasticity and dispersion of plane waves”. International Journal of Engineering Sciences 1972, 10, 425–435. [Google Scholar] [CrossRef]
- Eringen, A.C. “On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves”. Journal of Applied Physics 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Fazelzadeh, S.A.; Ghavanloo, E. “Nonlocal anisotropic elastic shell model for vibrations of single‒walled carbon nanotubes with arbitrary chirality”. Composite Structures 2012, 94, 1016–1022. [Google Scholar] [CrossRef]
- Mindlin, R.D. “Micro‒structure in linear elasticity”. Archive for Rational Mechanics and Analysis 1964, 16, 51–78. [Google Scholar] [CrossRef]
- Mindlin, R.D.; Eshel, N.N. “On first strain‒gradient theories in linear elasticity”. International Journal of Solids and Structures 1968, 4, 109–124. [Google Scholar] [CrossRef]
- Lim, C.W.; Zhang, G.; Reddy, J.N. “A higher‒order nonlocal elasticity and strain gradient theory and its applications in the wave propagation”. Journal of the Mechanics and Physics of Solids 2015, 78, 298–313. [Google Scholar] [CrossRef]
- Li, L.; Li, X.; Hu, Y. “Free vibration analysis of nonlocal strain gradient beams made of functionally graded material”. International Journal of Engineering Science 2016, 102, 77–92. [Google Scholar] [CrossRef]
- Li, X.; Li, L.; Hu, Y.; Ding, Z.; Deng, W. “Bending, buckling and vibration of axially functionally graded beams based on nonlocal strain gradient theory”. Composite Structures 2017, 165, 250–265. [Google Scholar] [CrossRef]
- Li, L.; Hu, Y. “Nonlinear bending and free vibration analyses of nonlocal strain gradient beams made of functionally graded material”. International Journal of Engineering Science 2016, 107, 77–97. [Google Scholar] [CrossRef]
- Apuzzo, A.; Barretta, R.; Faghidian, S.A.; Luciano, R.; de Sciarra, F.M. “Free vibrations of elastic beams by modified nonlocal strain gradient theory”. International Journal of Engineering Science 2018, 133, 99–108. [Google Scholar] [CrossRef]
- Thai, H.T.; Vo, T.P.; Nguyen, T.K.; Kim, S.E. “A review of continuum mechanics models for size‒dependent analysis of beams and plates”. Composite Structures 2017, 177, 196–219. [Google Scholar] [CrossRef]
- Roudbari, M.A.; Jorshari, T.D.; Lü, C.; Ansari, R.; Kouzani, A.Z.; Amabili, M. “A review of size‒dependent continuum mechanics models for micro‒ and nano‒structures”. Thin‒Walled Structures 2022, 170, 108562. [Google Scholar] [CrossRef]
- Hosseini, M.; Hadi, A.; Malekshahi, A.; Shishesaz, M. “A review of size‒dependent elasticity for nanostructures”. Journal of Computational Applied Mechanics 2018, 49, 197–211. [Google Scholar] [CrossRef]
- Mehralian, F.; Beni, Y.T.; Zeverdejani, M.K. “Nonlocal strain gradient theory calibration using molecular dynamics simulation based on small scale vibration of nanotubes”. Physica B 2017, 514, 61–69. [Google Scholar] [CrossRef]
- Ru, C.Q. “Chirality‒Dependent Mechanical Behavior of Carbon Nanotubes Based on an Anisotropic Elastic Shell Model”. Mathematics and Mechanics of Solids 2009, 14, 88–101. [Google Scholar] [CrossRef]
- Chang, T.; Geng, J.; Guo, X. “Chirality‒ and size‒dependent elastic properties of single‒walled carbon nanotubes”. Applied Physics Letters 2005, 87, 251929. [Google Scholar] [CrossRef]
- Yakobson, B.I.; Brabec, C.J.; Bernholc, J. “Nanomechanics of Carbon Tubes: Instabilities beyond Linear Response”. Physical Review Letters, 1996; 76, 2511–2514. [Google Scholar]
- Gupta, S.S.; Bosco, F.G.; Batra, R.C. “Wall thickness and elastic moduli of single‒walled carbon nanotubes from frequencies of axial, torsional and inextensional modes of vibration”. Computational Materials Science 2010, 47, 1049–1059. [Google Scholar] [CrossRef]
- Cheng, H.C.; Liu, Y.L.; Wu, C.; Chen, W.H. “On radial breathing vibration of carbon nanotubes”. Computational Methods in Applied Mechanical Engineering 2010, 199, 2820–2827. [Google Scholar] [CrossRef]
- Gupta, S.; Bosco, F.G.; Batra, R.C. “Breakdown of structural models for vibrations of single‒wall zigzag carbon nanotubes”. Journal of Applied Physics 2009, 106, 063527. [Google Scholar] [CrossRef]
- Duan, W.H.; Wang, C.M.; Zhang, Y.Y. “Calibration of nonlocal scaling effect parameter for free vibration of carbon nanotubes by molecular dynamics simulations”. Journal of Applied Physics 2007, 101, 024305. [Google Scholar] [CrossRef]
- Ansari, R.; Ajori, S.; Arash, B. “Vibrations of single and double‒walled carbon nanotubes with layerwise boundary conditions: A molecular dynamics study”. Current Applied Physics 2012, 12, 707–711. [Google Scholar] [CrossRef]
- Leissa, A.W. “Vibrations of Shells”; Government Printing Office: Washington DC, 1973. [Google Scholar]
- Yamaki, N. “Elastic Stability of Circular Cylindrical Shells”. North‒Holland, Amsterdam, 1984.
- Ventsel, E. “Thin Plates and Shells. Theory, Analysis and Applications”; The Pennsylvania State University, Marcel Dekker: New York, NY, USA, 2001. [Google Scholar]
- Soedel, W. “Vibrations of Shells and Plates”, 3rd ed. The Pennsylvania State University, Marcel Dekker: New York, NY, USA, 2004.
- Calladine, C. “Theory of Shell Structures”; Cambridge University Press: New York, NY, USA, 1983. [Google Scholar]
- Amabili, M. “Nonlinear Vibrations and Stability of Shells and Plates”. Cambridge University Press: New York, NY, USA, 2008. [Google Scholar]
- Strozzi, M.; Smirnov, V.V.; Pellicano, F.; Kovaleva, M. “Nonlocal anisotropic elastic shell model for vibrations of double‒walled carbon nanotubes under nonlinear van der Waals interaction forces”. International Journal of Non‒Linear Mechanics 2022, 146, 104172. [Google Scholar] [CrossRef]
- Avramov, K.V. “Nonlinear vibrations characteristics of single‒walled carbon nanotubes by nonlocal elastic shell model”. International Journal of Non‒Linear Mechanics 2018, 107, 149–160. [Google Scholar] [CrossRef]
- Yang, J.; Ke, L.L.; Kitipornchai, S. “Nonlinear free vibration of single‒walled carbon nanotubes using nonlocal Timoshenko beam theory”. Physica E 2010, 42, 1727–1735. [Google Scholar] [CrossRef]
- Strozzi, M.; Smirnov, V.V.; Manevitch, L.I.; Pellicano, F. “Nonlinear normal modes, resonances and energy exchange in single‒walled carbon nanotubes”. International Journal of Non‒Linear Mechanics 2020, 120, 103398. [Google Scholar] [CrossRef]
- Fang, B.; Zhen, Y.X.; Zhang, C.P.; Tang, Y. “Nonlinear vibration analysis of double‒walled carbon nanotubes based on nonlocal elasticity theory”. Applied Mathematical Modelling 2013, 37, 1096–1107. [Google Scholar] [CrossRef]
- Soltani, P.; Farshidianfar, A. “Periodic solution for nonlinear vibration of a fluid‒conveying carbon nanotube based on the nonlocal continuum theory by energy balance method”. Applied Mathematical Modelling 2012, 36, 3712–3724. [Google Scholar] [CrossRef]
- Strozzi, M.; Pellicano, F. “Nonlinear Resonance Interaction between Conjugate Circumferential Flexural Modes in Single‒Walled Carbon Nanotubes”. Shock and Vibration, Volume 2019, Article ID 3241698, 33 pages. [CrossRef]
- Avramov, K.V.; Kabylbekova, B.; Seitkazenova, K.; Myrzaliyev, D.S.; Pecherskiy, V.N. “Nonlocal anisotropic shell model of linear vibrations of multi‒walled carbon nanotubes”. Journal of Mechanical Engineering, 23, 14–26. [CrossRef]
- Strozzi, M.; Smirnov, V.V.; Manevitch, L.I.; Pellicano, F. “Nonlinear vibrations and energy exchange of single‒walled carbon nanotubes. Radial breathing modes”. Composite Structures 2018, 184, 613–632. [Google Scholar] [CrossRef]
- Mikhasev, G.; Radi, E.; Misnik V, V. “Modeling pull-in instability of CNT nanotweezers under electrostatic and van der Waals attractions based on the nonlocal theory of elasticity”. International Journal of Engineering Science 2024, 195, 104012. [Google Scholar] [CrossRef]
- Mikhasev, G.; Radi, E.; Misnik, V. “Pull-in instability analysis of a nanocantilever based on the two-phase nonlocal theory of elasticity”. Journal of Applied Computational Mechanics 2022, 8, 1456–1466. [Google Scholar]
| Carbon‒carbon bond length a (nm) | 0.142 |
| Carbon‒carbon bond elongation Kρ (nN/nm) | 742 |
| Carbon‒carbon bond angle variance Kθ (nN·nm) | 1.42 |
| Equivalent thickness h (nm) | 0.0665 |
| Equivalent mass density ρ (kg/m3) | 11700 |
| SWCNT radius R (nm) | 1.34 |
| Natural frequency ωRBM (cm‒1) | Difference % | ||
|---|---|---|---|
| Chirality indices (n, m) | Anisotropic elastic model (Sanders shell theory) | Molecular dynamics simulations [22] | |
| (10, 0) | 294.310 | 290.810 | 1.20 |
| (6, 6) | 284.460 | 278.450 | 2.16 |
| (12, 0) | 245.868 | 242.576 | 1.36 |
| (7, 7) | 244.074 | 239.020 | 2.11 |
| (8, 8) | 213.709 | 209.323 | 2.10 |
| (14, 0) | 211.067 | 207.980 | 1.48 |
| (16, 0) | 184.870 | 181.960 | 1.60 |
| (10, 10) | 171.104 | 167.644 | 2.06 |
| (18, 0) | 164.443 | 161.773 | 1.65 |
| (20, 0) | 148.073 | 145.577 | 1.71 |
| (12, 12) | 142.650 | 139.778 | 2.05 |
| (25, 0) | 118.551 | 116.439 | 1.81 |
| (15, 15) | 114.161 | 111.878 | 2.04 |
| (30, 0) | 98.835 | 97.013 | 1.88 |
| (18, 18) | 95.153 | 93.253 | 2.04 |
| (33, 0) | 89.865 | 87.507 | 2.69 |
| (20, 20) | 85.645 | 83.935 | 2.04 |
| Natural frequency ωRBM (cm‒1) | Difference % | ||
|---|---|---|---|
| Chirality indices (n, m) | Isotropic elastic model (Sanders shell theory) | Molecular dynamics simulations [22] | |
| (10, 0) | 299.083 | 290.810 | 2.84 |
| (6, 6) | 288.075 | 278.450 | 3.46 |
| (12, 0) | 249.447 | 242.576 | 2.83 |
| (7, 7) | 246.812 | 239.020 | 3.26 |
| (8, 8) | 215.923 | 209.323 | 3.15 |
| (14, 0) | 213.955 | 207.980 | 2.87 |
| (16, 0) | 187.002 | 181.960 | 2.77 |
| (10, 10) | 172.925 | 167.644 | 3.15 |
| (18, 0) | 166.287 | 161.773 | 2.79 |
| (20, 0) | 149.741 | 145.577 | 2.86 |
| (12, 12) | 144.037 | 139.778 | 3.05 |
| (25, 0) | 119.753 | 116.439 | 2.85 |
| (15, 15) | 115.183 | 111.878 | 2.95 |
| (30, 0) | 99.772 | 97.013 | 2.84 |
| (18, 18) | 96.003 | 93.253 | 2.95 |
| (33, 0) | 90.665 | 87.507 | 3.61 |
| (20, 20) | 86.396 | 83.935 | 2.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





