Modelling the Symmetric Wave Structures of the Ion-Acoustic for the BBMPB Equation in the Fluid Ions Using Hirota Bilinear Technique

1. Introduction

The study of wave phenomena is an important aspect of modern physics and has been a subject of interest for many years. Waves can be observed in various physical systems such as fluids, plasmas, and solids, and their dynamics can be described by a variety of mathematical models. In particular, the behavior of waves in plasmas has been an active area of research due to its relevance for a wide range of applications, including space physics, fusion research, and plasma processing.

One of the most important wave phenomena in plasmas is the ion-acoustic wave [1], which is a compressional wave that is primarily driven by the motion of the ions in the plasma. The ion-acoustic wave is a fundamental mode of oscillation in plasmas and is characterized by its dispersion relation, which relates the wave frequency to the wave number. The study of ion-acoustic waves is of great importance in plasma physics because it provides insights into the basic plasma processes, such as energy transport, wave-particle interactions, and turbulence [2,3,4,5].

Benjamin-Bona-Mahony-Peregrine-Burgers (BBMPB) model is a nonlinear partial differential equation that can be used to explore nonlinear wave patterns. The equation is given by:

$$v_t-v_{xxt}-\alpha v_{xx}+\lambda v_x+\theta v{v}_x+\beta v_{xxx}=0,$$

where $v(x,t)$ is the unknown function, $\alpha$, $\beta$, $\lambda$, and $\theta$ are constants.

The BBMPB equation has been studied extensively by researchers in the field of nonlinear wave theory. In particular, there have been many studies on the existence and stability of solitary wave solutions for this equation. One of the earliest studies on the BBMPB equation was conducted by Benjamin and Peregrine [6], where they derived the BBMPB equation as a model for long waves in shallow water. They showed that the equation has solitary wave solutions that are stable under certain conditions. Some of the recent studies of this equation are, Yang et al., constructed the traveling wave solutions for the Zakhrov-Kuznetsov-Benjamin-Bona-Mahony equation [7], while Akcagil et al., founded the exact travelling wave solutions of nonlinear pseudoparabolic equations by using the $\frac{G^{\prime }}{G}$ expansion method [8], etc. Overall, the BBMPB equation has been studied extensively in the literature, and there have been many important results regarding its properties and solutions.

1.1. Discussion of Model and the Wave Structures

The Benjamin–Bona–Mahony–Peregrine–Burgers (BBMPB) equation is a mathematical model that can describes the dynamics of ion-acoustic wave structures in a plasma consisting of fluid ions. This equation is a modified version of the classical Burgers equation [8], which is a nonlinear partial differential equation that describing the propagation of shocks in a fluid. The BBMPB equation incorporates the effects of dispersion, diffusion, and nonlinearity, which are all important factors that affect the behavior of ion-acoustic waves in a plasma. The BBMPB equation is given by:

$$v_t-v_{xxt}-\alpha v_{xx}+\lambda v_x+\theta v{v}_x+\beta v_{xxx}=0,$$

(1)

where $v(x,t)$ is the ion-acoustic wave amplitude, t is time, x is position, and the constants $\alpha$, $\lambda$, $\theta$, and $\beta$ are parameters that depend on the properties of the plasma. The first term on the left-hand side of the equation represents the dispersive effects of the plasma, while the second term represents the diffusive effects. The third and fourth terms represent the linear damping and driving forces, respectively, while the fifth term represents the nonlinear effects that arise due to the interaction between the waves.

The BBMPB equation can be used to study a wide range of ion–acoustic wave phenomena in plasmas, including the formation of solitons, shock waves, and other nonlinear structures. In particular, the equation can be used to study the propagation of ion-acoustic waves in a plasma with a spatially varying ion density profile, which is a common feature of many plasma systems. The equation can also be used to study the effects of external forces, such as electric fields or magnetic fields, on the dynamics of ion–acoustic waves.

One of the most important features of ion-acoustic waves in plasmas is their ability to form coherent structures, such as solitons and shock waves, that can propagate over long distances without dissipating [1,9]. These structures arise due to the interplay between the dispersive, diffusive, and nonlinear effects in the plasma, and their properties can be studied using the BBMPB equation. Solitons are stable, localized wave packets that maintain their shape as they propagate through the plasma, while shock waves are characterized by a rapid increase in wave amplitude and are often associated with energy dissipation [9,10].

The BBMPB equation can be solved analytically in some special cases, such as when the plasma is homogeneous or when the nonlinearity is weak [11]. The BBMPB equation has been extensively studied in the literature due to its rich and diverse wave structures. In this context, analytical methods have been used to investigate different types of wave structures. In the following, we will briefly introduce some of the wave structures that are studied in this research for the BBMPB equation.

Three–wave hypothesis: The three-wave hypothesis is a well-known phenomenon in nonlinear science, which describes the interaction of three waves that satisfy certain resonance conditions [1,12,13].

Breather wave: A breather wave is a localized and oscillatory solution that maintains its shape over time [1,14,17].

Lump periodic waves: Lump periodic waves are periodic solutions that consist of a sequence of wave packets [1,14,17].

Mixed–type wave solutions: Mixed-type wave solutions are complex and diverse wave structures that have both soliton-like and oscillatory components [1,13,16].

Periodic cross kink: A periodic cross kink is a localized wave structure that exhibits a crossing behavior [1,16,17].

Cross–Kink Rational Wave Solution: The cross-kink rational wave solution is a type of nonlinear wave solution that is characterized by the presence of two perpendicular kinks in the wave profile, which cross each other at a single point [18,19].

M–Shaped Rational Wave Solution: The M-shaped rational wave solution is another type of nonlinear wave solution that is characterized by an "M" shaped profile [18,19].

M–Shaped Rational Wave Solution with One Kink Wave: The M-shaped rational wave solution with one kink wave is a variant of the M-shaped solution that includes a single kink in the wave profile [18,19].

M–Shaped Rational Wave Solution with Two Kink Waves: The M-shaped rational wave solution with two kink waves is a variant of the M-shaped solution that includes two kinks in the wave profile [18,19].

2. Glimpse of the Method

In this section, we use the method to gain the solutions of the ion-acoustic wave structures in the fluid ions, described by the nonlinear partial differential equation (NLPDE) in two variables, x and t given by

$$\mathsf{\Psi }(v,v_t,v_x,v_{xt},v_{tt},v_{xx},\cdots )=0,$$

(2)

where $v(x,t)$ is the ion-acoustic wave amplitude, t is time, x is position , $\mathsf{\Psi }$ is a polynomial in $v=v(x,t)$ with different partial derivatives, in which highest order derivatives and nonlinear terms are involved.

We use the transformation $v(x,t)=V\left(\eta \right)$, where $\eta =x-ct$, and $V={\displaystyle \frac{\frac{\partial f\left(\eta \right)}{\partial \eta }}{f\left(\eta \right)}}$ in (2), and get the ordinary differential equation as follows:

$$\mathsf{\Psi }(V,c{V}^{\prime },V^{{}^{\prime }},c{V}^{{}^{″}},c^2{V}^{{}^{″}},V^{{}^{‴}},\dots )=0,$$

(3)

where $\mathsf{\Psi }$ is polynomial function of V and we integrate (3) with respect to $\eta$ and letting the integral constants 0 for our convenience and simplifying the resulting equation, we get

$$\begin{array}{c}\hfill (c+\beta )V^{{}^{″}}-\alpha V^{{}^{\prime }}+(\lambda -c)V-\frac{\theta }{2}{V}^2=0.\end{array}$$

(4)

To find the different form of solutions to (1), we use the following transformation [1] as

$$V={\displaystyle \frac{\frac{\partial f}{\partial \eta }}{f}},$$

(5)

$$\begin{array}{ccc}& & 4(\beta -1)f^{\prime }{\left(\eta \right)}^3+f\left(\eta \right)f^{\prime }\left(\eta \right)\left((2\alpha +\theta )f^{\prime }\left(\eta \right)-(\beta -1)f^{″}\left(\eta \right)\right)\hfill \\ & & +2f{\left(\eta \right)}^2\left((\beta -1)f^{\left(3\right)}\left(\eta \right)-\alpha f^{″}\left(\eta \right)+(\lambda +1)f^{\prime }\left(\eta \right)\right)=0.\hfill \end{array}$$

(6)

In bilinear form we have

$$\begin{array}{ccc}\hfill & & 2f^2\left(-\alpha \frac{{\partial }^{2}f}{\partial {\eta }^2}+(\beta -1)\frac{{\partial }^{3}f}{\partial {\eta }^3}+(\lambda +1)\frac{\partial f}{\partial \eta }\right)+\hfill \\ & & f\frac{\partial f}{\partial \eta }\left((2\alpha +\theta )\frac{\partial f}{\partial \eta }-6(\beta -1)\frac{{\partial }^{2}f}{\partial {\eta }^2}\right)+4(\beta -1){\left(\frac{\partial f}{\partial \eta }\right)}^3=0.\hfill \end{array}$$

(7)

Our focus now is on eq. (7) which we will used to find the different solutions of the wave structures discussed for eq. (1).

3. Finding the Solutions of the Wave Structures

• Multiwave solutions: With the help of the following transformation [1], we are able to use the three wave hypothesis to generate different types of solutions:

  $$f=n_{2}cos\left(\eta {ϵ}_3+{ϵ}_4\right)+n_{1}cosh\left(\eta {ϵ}_1+{ϵ}_2\right)+n_{3}cosh\left(\eta {ϵ}_5+{ϵ}_6\right).$$

  (8)
  Substituting eq. (8) in eq. (7), simplifying and collecting like terms with trigonometric and hyperbolic functions and equating the coefficients of each obtained expressions to zero. So, we obtained the system of equation and simplified with the help of Mathematica to gain the different sets of unknown constants such as:
  Set 1:$n_3=0,{ϵ}_1=-\frac{\sqrt{\lambda +1}}{\sqrt{2}\sqrt{\beta -1}}and{ϵ}_3=\frac{\sqrt{-\lambda -1}}{\sqrt{2}\sqrt{\beta -1}},$ and putting them in eq. (8) and then to eq. (5) gives

  $$V_{1,1}\left(\eta \right)=\frac{\frac{\sqrt{\lambda +1}{n}_{1}sinh\left(\frac{\sqrt{\lambda +1}\eta }{\sqrt{2}\sqrt{\beta -1}}-{ϵ}_2\right)}{\sqrt{2}\sqrt{\beta -1}}-\frac{\sqrt{-\lambda -1}{n}_{2}sin\left(\frac{\sqrt{-\lambda -1}\eta }{\sqrt{2}\sqrt{\beta -1}}+{ϵ}_4\right)}{\sqrt{2}\sqrt{\beta -1}}}{n_{2}cos\left(\frac{\sqrt{-\lambda -1}\eta }{\sqrt{2}\sqrt{\beta -1}}+{ϵ}_4\right)+n_{1}cosh\left(\frac{\sqrt{\lambda +1}\eta }{\sqrt{2}\sqrt{\beta -1}}-{ϵ}_2\right)}.$$

  (9)
  The multiwave solution of eq. (1) is extracted as

  $$v_{1,1}(x,t)=\frac{\sqrt{\lambda +1}{n}_{1}sinh\left(\frac{\sqrt{\lambda +1}(x-ct)}{\sqrt{2}\sqrt{\beta -1}}-{ϵ}_2\right)-\sqrt{-\lambda -1}{n}_{2}sin\left(\frac{\sqrt{-\lambda -1}(x-ct)}{\sqrt{2}\sqrt{\beta -1}}+{ϵ}_4\right)}{\sqrt{2}\sqrt{\beta -1}\left(n_{2}cos\left(\frac{\sqrt{-\lambda -1}(x-ct)}{\sqrt{2}\sqrt{\beta -1}}+{ϵ}_4\right)+n_{1}cosh\left(\frac{\sqrt{\lambda +1}(x-ct)}{\sqrt{2}\sqrt{\beta -1}}-{ϵ}_2\right)\right)}.$$

  (10)
  Set 2:$n_1=0,{ϵ}_3=\frac{\sqrt{-\lambda -1}}{\sqrt{2}\sqrt{\beta -1}},{ϵ}_5=-\frac{\sqrt{\lambda +1}}{\sqrt{2}\sqrt{\beta -1}},$ and putting them in eq. (8) and then to eq. (5) gives

  $$V_{1,2}\left(\eta \right)=\frac{\frac{\sqrt{\lambda +1}{n}_{3}sinh\left(\frac{\sqrt{\lambda +1}\eta }{\sqrt{2}\sqrt{\beta -1}}-{ϵ}_6\right)}{\sqrt{2}\sqrt{\beta -1}}-\frac{\sqrt{-\lambda -1}{n}_{2}sin\left(\frac{\sqrt{-\lambda -1}\eta }{\sqrt{2}\sqrt{\beta -1}}+{ϵ}_4\right)}{\sqrt{2}\sqrt{\beta -1}}}{n_{2}cos\left(\frac{\sqrt{-\lambda -1}\eta }{\sqrt{2}\sqrt{\beta -1}}+{ϵ}_4\right)+n_{3}cosh\left(\frac{\sqrt{\lambda +1}\eta }{\sqrt{2}\sqrt{\beta -1}}-{ϵ}_6\right)}.$$

  (11)
  The multiwave solution of eq. (1) is extracted as

  $$v_{1,2}(x,t)=\frac{\sqrt{\lambda +1}{n}_{3}sinh\left(\frac{\sqrt{\lambda +1}(x-ct)}{\sqrt{2}\sqrt{\beta -1}}-{ϵ}_6\right)-\sqrt{-\lambda -1}{n}_{2}sin\left(\frac{\sqrt{-\lambda -1}(x-ct)}{\sqrt{2}\sqrt{\beta -1}}+{ϵ}_4\right)}{\sqrt{2}\sqrt{\beta -1}\left(n_{2}cos\left(\frac{\sqrt{-\lambda -1}(x-ct)}{\sqrt{2}\sqrt{\beta -1}}+{ϵ}_4\right)+n_{3}cosh\left(\frac{\sqrt{\lambda +1}(x-ct)}{\sqrt{2}\sqrt{\beta -1}}-{ϵ}_6\right)\right)}.$$

  (12)
• Interaction via double exponential form: With the help of the following transformation [1], we generate different types of solutions:

  $$f=n_{1}exp\left(\eta {ϵ}_1+{ϵ}_2\right)+n_{2}exp\left(\eta {ϵ}_3+{ϵ}_4\right).$$

  (13)
  Substituting eq. (13) in eq. (5), simplifying and collecting like terms with exponential functions and equating the coefficients of each obtained expressions to zero. So, we obtained the system of equation and simplified with the help of Mathematica to gain the different sets of unknown constants such as:
  Set 1:${ϵ}_1=-\frac{2(\lambda +1)}{\theta },{ϵ}_3=0,\alpha =-\frac{\theta }{2},\beta =1,$ and putting them in eq. (13) in eq. (5), we obtain

  $$V_{2,1}\left(\eta \right)=-\frac{2(\lambda +1)n_1{e}^{{ϵ}_2-\frac{2(\lambda +1)\eta }{\theta }}}{\theta \left(n_1{e}^{{ϵ}_2-\frac{2(\lambda +1)\eta }{\theta }}+n_2{e}^{{ϵ}_4}\right)}.$$

  (14)
  So the solution of eq. (1) extracted as

  $$v_{2,1}(x,t)=-\frac{2(\lambda +1)n_1{e}^{{ϵ}_2}}{\theta \left(n_2{e}^{\frac{2(\lambda +1)(x-ct)}{\theta }+{ϵ}_4}+n_1{e}^{{ϵ}_2}\right)}.$$

  (15)
  Set 2:${ϵ}_1=0,{ϵ}_3=-\frac{2(\lambda +1)}{\theta },\alpha =-\frac{\theta }{2},\beta =1,$ and putting them in (13) in eq. (5), we obtain

  $$V_{2,2}\left(\eta \right)=-\frac{2(\lambda +1)n_2{e}^{{ϵ}_4-\frac{2(\lambda +1)\eta }{\theta }}}{\theta \left(n_2{e}^{{ϵ}_4-\frac{2(\lambda +1)\eta }{\theta }}+n_1{e}^{{ϵ}_2}\right)}.$$

  (16)
  So the solution of eq. (1) extracted as

  $$v_{2,2}(x,t)=-\frac{2(\lambda +1)n_2{e}^{{ϵ}_4}}{\theta \left(n_1{e}^{\frac{2(\lambda +1)(x-ct)}{\theta }+{ϵ}_2}+n_2{e}^{{ϵ}_4}\right)}.$$

  (17)
  Set 3:${ϵ}_1=-\frac{2(\lambda +1)}{\theta },{ϵ}_3=-\frac{2(\lambda +1)}{\theta },$ and putting them in (13) in eq. (5), we obtain

  $$V_{2,3}\left(\eta \right)=\frac{-\frac{2(\lambda +1)n_1{e}^{{ϵ}_2-\frac{2(\lambda +1)\eta }{\theta }}}{\theta }-\frac{2(\lambda +1)n_2{e}^{{ϵ}_4-\frac{2(\lambda +1)\eta }{\theta }}}{\theta }}{n_1{e}^{{ϵ}_2-\frac{2(\lambda +1)\eta }{\theta }}+n_2{e}^{{ϵ}_4-\frac{2(\lambda +1)\eta }{\theta }}}.$$

  (18)
  So the solution of eq. (1) extracted as

  $$v_{2,3}(x,t)=\frac{-\frac{2(\lambda +1)n_1{e}^{{ϵ}_2-\frac{2(\lambda +1)(x-ct)}{\theta }}}{\theta }-\frac{2(\lambda +1)n_2{e}^{{ϵ}_4-\frac{2(\lambda +1)(x-ct)}{\theta }}}{\theta }}{n_1{e}^{{ϵ}_2-\frac{2(\lambda +1)(x-ct)}{\theta }}+n_2{e}^{{ϵ}_4-\frac{2(\lambda +1)(x-ct)}{\theta }}}.$$

  (19)
• Homoclinic breather approach: With the help of the following transformation [1], we generate different types of solutions:

  $$f=n_{1}exp\left(r\left(\eta {ϵ}_3+{ϵ}_4\right)\right)+exp\left(-r\left(\eta {ϵ}_1+{ϵ}_2\right)\right)+n_{2}cos\left(r\left(\eta {ϵ}_5+{ϵ}_6\right)\right).$$

  (20)
  Substituting eq. (20) in eq. (7), simplifying and collecting like terms with exponential, trigonometric and exponential-trigonometric functions and equating the coefficients of each obtained expressions to zero. So, we obtained the system of equation and simplified with the help of Mathematica to gain the different sets of unknown constants such as:
  Set 1:$n_1=0,{ϵ}_1=\frac{\sqrt{-{(\lambda +1)}^2}{ϵ}_5}{\lambda +1},\alpha =-\frac{\theta }{8},\beta =\frac{32\lambda +{\theta }^2+32}{32(\lambda +1)},r=-\frac{2\sqrt{-{\lambda }^2-2\lambda -1}}{\theta {ϵ}_5},$ and putting them in eq. (20) and then in eq. (5), we obtain

  $$V_{3,1}\left(\eta \right)=\frac{-\frac{2(\lambda +1)n_1{e}^{r\left({ϵ}_4-\frac{2(\lambda +1)\eta }{\theta r}\right)}}{\theta }-\frac{2(\lambda +1)e^{-r\left(\frac{2(\lambda +1)\eta }{\theta r}+{ϵ}_2\right)}}{\theta }}{n_1{e}^{r\left({ϵ}_4-\frac{2(\lambda +1)\eta }{\theta r}\right)}+n_{2}cos\left(r{ϵ}_6\right)+e^{-r\left(\frac{2(\lambda +1)\eta }{\theta r}+{ϵ}_2\right)}}.$$

  (21)
  So, the homoclinic breather solution of eq. (1) extracted as

  $$v_{3,1}(x,t)=-\frac{2(\lambda +1)\left(e^{\frac{2\sqrt{-{(\lambda +1)}^2}{ϵ}_2}{\theta {ϵ}_5}}-n_2{e}^{\frac{2(\lambda +1)(x-ct)}{\theta }}sinh\left(\frac{2(\lambda +1)\left({ϵ}_5(x-ct)+{ϵ}_6\right)}{\theta {ϵ}_5}\right)\right)}{\theta \left(n_2{e}^{\frac{2(\lambda +1)(x-ct)}{\theta }}cosh\left(\frac{2(\lambda +1)\left({ϵ}_5(x-ct)+{ϵ}_6\right)}{\theta {ϵ}_5}\right)+e^{\frac{2\sqrt{-{(\lambda +1)}^2}{ϵ}_2}{\theta {ϵ}_5}}\right)}.$$

  (22)
  Set 2:${ϵ}_1=\frac{\sqrt{-{(\lambda +1)}^2}{ϵ}_5}{\lambda +1},{ϵ}_3=\frac{\sqrt{-{(\lambda +1)}^2}{ϵ}_5}{-\lambda -1},\alpha =-\frac{\theta }{8},\beta =\frac{32\lambda +{\theta }^2+32}{32(\lambda +1)},r=-\frac{2\sqrt{-{\lambda }^2-2\lambda -1}}{\theta {ϵ}_5},$ and putting them in eq. (20) and then in eq. (5), we obtain

  $$V_{3,2}\left(\eta \right)=-\frac{2(\lambda +1)\left(e^{\frac{2\sqrt{-{(\lambda +1)}^2}\left({ϵ}_2+{ϵ}_4\right)}{\theta {ϵ}_5}}-n_2{e}^{\frac{2\left(\lambda \eta +\frac{\sqrt{-{(\lambda +1)}^2}{ϵ}_4}{{ϵ}_5}+\eta \right)}{\theta }}sinh\left(G\right)+n_1\right)}{\theta \left(e^{\frac{2\sqrt{-{(\lambda +1)}^2}\left({ϵ}_2+{ϵ}_4\right)}{\theta {ϵ}_5}}+n_2{e}^{\frac{2\left(\lambda \eta +\frac{\sqrt{-{(\lambda +1)}^2}{ϵ}_4}{{ϵ}_5}+\eta \right)}{\theta }}cosh\left(G\right)+n_1\right)},$$

  (23)

  where $G=\frac{2(\lambda +1)\left(\eta {ϵ}_5+{ϵ}_6\right)}{\theta {ϵ}_5}$. So, the Homoclinic breather solution of eq. (1) extracted as

  $$v_{3,2}(x,t)=-\frac{2(\lambda +1)\left(-n_{2}exp\left(R\right)sinh\left(\frac{2(\lambda +1)\left({ϵ}_5(x-ct)+{ϵ}_6\right)}{\theta {ϵ}_5}\right)+e^{\frac{2\sqrt{-{(\lambda +1)}^2}\left({ϵ}_2+{ϵ}_4\right)}{\theta {ϵ}_5}}+n_1\right)}{\theta \left(n_{2}exp\left(R\right)cosh\left(\frac{2(\lambda +1)\left({ϵ}_5(x-ct)+{ϵ}_6\right)}{\theta {ϵ}_5}\right)+e^{\frac{2\sqrt{-{(\lambda +1)}^2}\left({ϵ}_2+{ϵ}_4\right)}{\theta {ϵ}_5}}+n_1\right)},$$

  (24)

  where $R=\frac{2\left((\lambda +1)(x-ct)+\frac{\sqrt{-{(\lambda +1)}^2}{ϵ}_4}{{ϵ}_5}\right)}{\theta }$.
  Set 3:$n_1=0,{ϵ}_1=\frac{\sqrt{-{(\lambda +1)}^2}{ϵ}_5}{-\lambda -1},\alpha =-\frac{\theta }{8},\beta =\frac{32\lambda +{\theta }^2+32}{32(\gamma +1)},r=\frac{2\sqrt{-{\lambda }^2-2\lambda -1}}{\theta {ϵ}_5}$ and putting them in eq. (20) and then in eq. (5), we obtain

  $$V_{3,3}\left(\eta \right)=\frac{2(\lambda +1)\left(n_2{e}^{\frac{2\left(\lambda \eta +\frac{\sqrt{-{(\lambda +1)}^2}{ϵ}_2}{{ϵ}_5}+\eta \right)}{\theta }}sinh\left(\frac{2(\lambda +1)\left(\eta {ϵ}_5+{ϵ}_6\right)}{\theta {ϵ}_5}\right)-1\right)}{\theta +\theta n_2{e}^{\frac{2\left(\lambda \eta +\frac{\sqrt{-{(\lambda +1)}^2}{ϵ}_2}{{ϵ}_5}+\eta \right)}{\theta }}cosh\left(\frac{2(\lambda +1)\left(\eta {ϵ}_5+{ϵ}_6\right)}{\theta {ϵ}_5}\right)}.$$

  (25)
  So, the Homoclinic breather solution of eq. (1) extracted as

  $$v_{3,3}(x,t)=\frac{2(\lambda +1)\left(n_{2}exp\left(\frac{2\left((\lambda +1)(x-ct)+\frac{\sqrt{-{(\lambda +1)}^2}{ϵ}_2}{{ϵ}_5}\right)}{\theta }\right)sinh\left(\frac{2(\lambda +1)\left({ϵ}_5(x-ct)+{ϵ}_6\right)}{\theta {ϵ}_5}\right)-1\right)}{\theta n_{2}exp\left(\frac{2\left((\lambda +1)(x-ct)+\frac{\sqrt{-{(\lambda +1)}^2}{ϵ}_2}{{ϵ}_5}\right)}{\theta }\right)cosh\left(\frac{2(\lambda +1)\left({ϵ}_5(x-ct)+{ϵ}_6\right)}{\theta {ϵ}_5}\right)+\theta }.$$

  (26)
• Mixed type solutions: With the help of the following transformation [1], we generate different types of solutions:

  $$f=n_{1}exp\left(r\left(\eta {ϵ}_1+{ϵ}_2\right)\right)+n_{2}exp\left(-r\left(\eta {ϵ}_1+{ϵ}_2\right)\right)+n_{3}sin\left(r\left(\eta {ϵ}_3+{ϵ}_4\right)\right)+n_{4}sinh\left(r\left(\eta {ϵ}_5+{ϵ}_6\right)\right).$$

  (27)
  Substituting in eq. (27) and then in eq. (7), we obtain, simplifying and collecting like terms with exponential, trigonometric and exponential-trigonometric functions and equating the coefficients of each obtained expressions to zero. So, we obtained the system of equation and simplified with the help of Mathematica to gain the different sets of unknown constants such as:
  Set 1:$n_1=0,n_3=0,{ϵ}_1=\frac{\sqrt{{(\lambda +1)}^2}{ϵ}_5}{-\lambda -1},\alpha =-\frac{\theta }{8},\beta =\frac{32\lambda +{\theta }^2+32}{32(\lambda +1)},r=-\frac{2\sqrt{{\lambda }^2+2\lambda +1}}{\theta {ϵ}_5},$ and putting them in eq. (27) and then in eq. (5),

  $$V_{4,1}\left(\eta \right)=\frac{\frac{2\sqrt{{(\lambda +1)}^2}\sqrt{{\lambda }^2+2\lambda +1}{n}_{2}exp\left(Q\right)}{(-\lambda -1)\theta }-\frac{2\sqrt{{\lambda }^2+2\lambda +1}{n}_{4}cosh\left(\frac{2\sqrt{{\lambda }^2+2\lambda +1}\left(\eta {ϵ}_5+{ϵ}_6\right)}{\theta {ϵ}_5}\right)}{\theta }}{n_{2}exp\left(Q\right)-n_{4}sinh\left(\frac{2\sqrt{{\lambda }^2+2\lambda +1}\left(\eta {ϵ}_5+{ϵ}_6\right)}{\theta {ϵ}_5}\right)},$$

  (28)

  where $Q=\frac{2\sqrt{{\lambda }^2+2\lambda +1}\left(\frac{\sqrt{{(\lambda +1)}^2}\eta {ϵ}_5}{-\lambda -1}+{ϵ}_2\right)}{\theta {ϵ}_5}$.
  The mixed type solution of eq. (1) extracted as

  $$v_{4,1}(x,t)=\frac{-2(\lambda +1)n_{2}exp\left(W\right)-2\sqrt{{(\lambda +1)}^2}{n}_{4}cosh\left(\frac{2(\lambda +1)\left({ϵ}_5(x-ct)+{ϵ}_6\right)}{\theta {ϵ}_5}\right)}{\theta \left(n_{2}exp\left(W\right)-n_{4}sinh\left(\frac{2\sqrt{{(\lambda +1)}^2}\left({ϵ}_5(x-ct)+{ϵ}_6\right)}{\theta {ϵ}_5}\right)\right)},$$

  (29)

  where $W=\frac{2\left((\lambda +1)(ct-x)+\frac{\sqrt{{(\lambda +1)}^2}{ϵ}_2}{{ϵ}_5}\right)}{\theta }$.
  Set 2:$n_1=0,n_4=0,{ϵ}_1=\frac{2(\lambda +1)}{\theta r},{ϵ}_3=\frac{2\sqrt{-{\lambda }^2-2\lambda -1}}{\theta r},\alpha =-\frac{\theta }{8},\beta =\frac{32\lambda +{\theta }^2+32}{32(\lambda +1)},$ and putting them in eq. (27) and then in eq. (5),

  $$V_{4,2}\left(\eta \right)=\frac{\frac{2\sqrt{-{\lambda }^2-2\lambda -1}{n}_{3}cos\left(r\left(\frac{2\sqrt{-{\lambda }^2-2\lambda -1}\eta }{\theta r}+{ϵ}_4\right)\right)}{\theta }-\frac{2(\lambda +1)n_2{e}^{-r\left(\frac{2(\lambda +1)\eta }{\theta r}+{ϵ}_2\right)}}{\theta }}{n_{3}sin\left(r\left(\frac{2\sqrt{-{\lambda }^2-2\lambda -1}\eta }{\theta r}+{ϵ}_4\right)\right)+n_2{e}^{-r\left(\frac{2(\lambda +1)\eta }{\theta r}+{ϵ}_2\right)}}.$$

  (30)
  The mixed type solution of eq. (1) extracted as

  $$v_{4,2}(x,t)=\frac{2\sqrt{-{(\lambda +1)}^2}{n}_3{e}^{\frac{2(\lambda +1)(x-ct)}{\theta }+r{ϵ}_2}cos\left(\frac{2\sqrt{-{(\lambda +1)}^2}(x-ct)}{\theta }+r{ϵ}_4\right)-2(\lambda +1)n_2}{\theta \left(n_3{e}^{\frac{2(\lambda +1)(x-ct)}{\theta }+r{ϵ}_2}sin\left(\frac{2\sqrt{-{(\lambda +1)}^2}(x-ct)}{\theta }+r{ϵ}_4\right)+n_2\right)}.$$

  (31)
• Periodic Cross-kink: With the help of the following transformation [1], we generate different types of solutions:

  $$\begin{array}{ccc}\hfill f& =& n_{1}exp\left(r\left(\eta {ϵ}_3+{ϵ}_4\right)\right)+exp\left(-r\left(\eta {ϵ}_1+{ϵ}_2\right)\right)\hfill \\ & & +n_{2}cos\left(r\left(\eta {ϵ}_5+{ϵ}_6\right)\right)+n_{3}cosh\left(r\left(\eta {ϵ}_7+{ϵ}_8\right)\right)+{ϵ}_9.\hfill \end{array}$$

  (32)
  Substituting eq. (32) in eq. (7), simplifying and collecting like terms with exponential, trigonometric and exponential-trigonometric functions and equating the coefficients of each obtained expressions to zero. So, we obtained the system of equation and simplified with the help of Mathematica to gain the different sets of unknown constants such as:
  Set 1:$n_2=0,{ϵ}_1=\frac{\sqrt{{(\lambda +1)}^2}{ϵ}_7}{-\lambda -1},{ϵ}_3=\frac{\sqrt{{(\lambda +1)}^2}{ϵ}_7}{\lambda +1},{ϵ}_9=0,\alpha =-\frac{\theta }{8},\beta =\frac{32\lambda +{\theta }^2+32}{32(\lambda +1)},r=-\frac{2\sqrt{{\lambda }^2+2\lambda +1}}{\theta {ϵ}_7},$ and putting them in eq. (32) and then in eq. (5),

  $$V_{5,1}\left(\eta \right)=-\frac{2(\lambda +1)\left(e^{\frac{2\sqrt{{(\lambda +1)}^2}\left({ϵ}_2+{ϵ}_4\right)}{\theta {ϵ}_7}}-n_3{e}^{\frac{2\left(\lambda \eta +\frac{\sqrt{{(\lambda +1)}^2}{ϵ}_4}{{ϵ}_7}+\eta \right)}{\theta }}sinh\left(\frac{2(\lambda +1)\left(\eta {ϵ}_7+{ϵ}_8\right)}{\theta {ϵ}_7}\right)+n_1\right)}{\theta \left(e^{\frac{2\sqrt{{(\lambda +1)}^2}\left({ϵ}_2+{ϵ}_4\right)}{\theta {ϵ}_7}}+n_3{e}^{\frac{2\left(\lambda \eta +\frac{\sqrt{{(\lambda +1)}^2}{ϵ}_4}{{ϵ}_7}+\eta \right)}{\theta }}cosh\left(\frac{2(\lambda +1)\left(\eta {ϵ}_7+{ϵ}_8\right)}{\theta {ϵ}_7}\right)+n_1\right)}.$$

  (33)
  So the periodic Cross-kink solution of eq. (1) extracted as

  $$v_{5,1}(x,t)=-\frac{2(\lambda +1)\left(-n_{3}exp\left(L\right)sinh\left(\frac{2(\lambda +1)\left({ϵ}_7(x-ct)+{ϵ}_8\right)}{\theta {ϵ}_7}\right)+e^{\frac{2\sqrt{{(\lambda +1)}^2}\left({ϵ}_2+{ϵ}_4\right)}{\theta {ϵ}_7}}+n_1\right)}{\theta \left(n_{3}exp\left(L\right)cosh\left(\frac{2(\lambda +1)\left({ϵ}_7(x-ct)+{ϵ}_8\right)}{\theta {ϵ}_7}\right)+e^{\frac{2\sqrt{{(\lambda +1)}^2}\left({ϵ}_2+{ϵ}_4\right)}{\theta {ϵ}_7}}+n_1\right)},$$

  (34)

  where $L=\frac{2\left((\lambda +1)(x-ct)+\frac{\sqrt{{(\lambda +1)}^2}{ϵ}_4}{{ϵ}_7}\right)}{\theta }$.
  Set 2:$n_1=0,n_2=0,{ϵ}_1=\frac{\sqrt{{(\lambda +1)}^2}{ϵ}_7}{\lambda +1},{ϵ}_9=0,\alpha =-\frac{\theta }{8},\beta =\frac{32\lambda +{\theta }^2+32}{32(\lambda +1)},r=\frac{2\sqrt{{\lambda }^2+2\lambda +1}}{\theta {ϵ}_7},$ and putting them in eq. (32) and then in eq. (5),

  $$V_{5,2}\left(\eta \right)=\frac{2(\lambda +1)\left(n_3{e}^{\frac{2\left(\lambda \eta +\frac{\sqrt{{(\lambda +1)}^2}{ϵ}_2}{{ϵ}_7}+\eta \right)}{\theta }}sinh\left(\frac{2(\lambda +1)\left(\eta {ϵ}_7+{ϵ}_8\right)}{\theta {ϵ}_7}\right)-1\right)}{\theta +\theta n_3{e}^{\frac{2\left(\lambda \eta +\frac{\sqrt{{(\lambda +1)}^2}{ϵ}_2}{{ϵ}_7}+\eta \right)}{\theta }}cosh\left(\frac{2(\lambda +1)\left(\eta {ϵ}_7+{ϵ}_8\right)}{\theta {ϵ}_7}\right)}.$$

  (35)
  The periodic Cross-kink solution of eq. (1) extracted as

  $$v_{5,2}(x,t)=\frac{2(\lambda +1)\left(n_{3}exp\left(\frac{2\left((\lambda +1)(x-ct)+\frac{\sqrt{{(\lambda +1)}^2}{ϵ}_2}{{ϵ}_7}\right)}{\theta }\right)sinh\left(\frac{2(\lambda +1)\left({ϵ}_7(x-ct)+{ϵ}_8\right)}{\theta {ϵ}_7}\right)-1\right)}{\theta n_{3}exp\left(\frac{2\left((\lambda +1)(x-ct)+\frac{\sqrt{{(\lambda +1)}^2}{ϵ}_2}{{ϵ}_7}\right)}{\theta }\right)cosh\left(\frac{2(\lambda +1)\left({ϵ}_7(x-ct)+{ϵ}_8\right)}{\theta {ϵ}_7}\right)+\theta }.$$

  (36)
  Set 3:$n_1=0,n_2=0,{ϵ}_1=\frac{2(\lambda +1)}{\theta r},{ϵ}_7=\frac{2\sqrt{{\lambda }^2+2\lambda +1}}{\theta r},{ϵ}_9=0,\alpha =-\frac{\theta }{8},\beta =\frac{32\lambda +{\theta }^2+32}{32(\lambda +1)},$ and putting them in eq. (32) and then in eq. (5),

  $$V_{5,3}\left(\eta \right)=\frac{\frac{2\sqrt{{\lambda }^2+2\lambda +1}{n}_{3}sinh\left(r\left(\frac{2\sqrt{{\lambda }^2+2\lambda +1}\eta }{\theta r}+{ϵ}_8\right)\right)}{\theta }-\frac{2(\lambda +1)e^{-r\left(\frac{2(\lambda +1)\eta }{\theta r}+{ϵ}_2\right)}}{\theta }}{n_{3}cosh\left(r\left(\frac{2\sqrt{{\lambda }^2+2\lambda +1}\eta }{\theta r}+{ϵ}_8\right)\right)+e^{-r\left(\frac{2(\lambda +1)\eta }{\theta r}+{ϵ}_2\right)}}.$$

  (37)
  So the periodic Cross-kink solution of eq. (5) extracted as

  $$v_{5,3}(x,t)=-\frac{2\left(-\sqrt{{(\lambda +1)}^2}{n}_3{e}^{\frac{2(\lambda +1)(x-ct)}{\theta }+r{ϵ}_2}sinh\left(\frac{2\sqrt{{(\lambda +1)}^2}(x-ct)}{\theta }+r{ϵ}_8\right)+\lambda +1\right)}{\theta n_3{e}^{\frac{2(\lambda +1)(x-ct)}{\theta }+r{ϵ}_2}cosh\left(\frac{2\sqrt{{(\lambda +1)}^2}(x-ct)}{\theta }+r{ϵ}_8\right)+\theta }.$$

  (38)
• Cross-Kink Rational Wave Solution: With the help of the following transformation [18], we generate different types of solutions:

  $$f=n_{1}exp\left(\eta {ϵ}_1+{ϵ}_2\right)+exp\left(-\left(\eta {ϵ}_1+{ϵ}_2\right)\right)+\left(\eta r_1+r_2\right){}^2+\left(\eta r_3+r_4\right){}^2+r_5.$$

  (39)
  Substituting eq. (39) in eq. (7), simplifying and collecting like terms with exponential functions and equating the coefficients of each obtained expressions to zero. So, we obtained the system of equation and simplified with the help of Mathematica to gain the different sets of unknown constants such as:
  Set 1:$n_1=0,{ϵ}_1=\frac{2(\lambda +1)}{\theta },r_2=-\frac{r_1(2\lambda \eta +2\eta +\theta )}{2(\lambda +1)},r_3=0,\alpha =-\frac{\theta }{2},\beta =1,$ and putting them in eq. (39) in eq. (5) we obtain

  $$V_{6,1}\left(\eta \right)=-\frac{4{(\lambda +1)}^3}{2{(\lambda +1)}^2\theta +{\theta }^3{r}_1^2{e}^{\frac{2(\lambda +1)\eta }{\theta }+{ϵ}_2}}.$$

  (40)
  So the Cross-Kink rational wave solution of eq. (1) extracted as

  $$v_{6,1}(x,t)=\frac{4{(\lambda +1)}^3}{2{(\lambda +1)}^2\theta +{\theta }^3{r}_1^2{e}^{\frac{2(\lambda +1)(x-ct)}{\theta }+{ϵ}_2}}.$$

  (41)
  Set 2:${ϵ}_1=0,r_2=-\frac{r_1(2\lambda \eta +2\eta +\theta )}{2(\lambda +1)},r_3=0,\alpha =-\frac{\theta }{2},\beta =1,$ and putting them in eq. (39) in eq. (7), we obtain

  $$V_{6,2}\left(\eta \right)=\frac{2\left(r_1-\frac{(2\lambda +2)r_1}{2(\lambda +1)}\right)\left(\eta r_1-\frac{r_1(2\lambda \eta +2\eta +\theta )}{2(\lambda +1)}\right)}{n_1{e}^{{ϵ}_2}+\left(\eta r_1-\frac{r_1(2\lambda \eta +2\eta +\theta )}{2(\lambda +1)}\right){}^2+r_4^2+r_5+e^{-{ϵ}_2}}.$$

  (42)
  So, the Cross-Kink rational wave solution of eq. (1) extracted as

  $$v_{6,2}(x,t)=\frac{2\left(r_1-\frac{(2\lambda +2)r_1}{2(\lambda +1)}\right)\left(r_1(x-\mathrm{ct})-\frac{r_1(2\lambda (x-\mathrm{ct})+2(x-\mathrm{ct})+\theta )}{2(\lambda +1)}\right)}{\left(r_1(x-\mathrm{ct})-\frac{r_1(2\lambda (x-\mathrm{ct})+2(x-\mathrm{ct})+\theta )}{2(\lambda +1)}\right){}^2+n_1{e}^{{ϵ}_2}+r_4^2+r_5+e^{-{ϵ}_2}}.$$

  (43)
  Set 3:$n_1=0,{ϵ}_1=\frac{2(\lambda +1)}{\theta },r_1=-i{r}_3,r_4=i{r}_2,r_5=0,$ and putting them in eq. (39) in eq. (7), we obtain

  $$V_{6,3}\left(\eta \right)=\frac{-\frac{2(\lambda +1)e^{-\frac{2(\lambda +1)\eta }{\theta }-{ϵ}_2}}{\theta }+2r_3\left(\eta r_3+i{r}_2\right)-2i{r}_3\left(r_2-i\eta r_3\right)}{e^{-\frac{2(\lambda +1)\eta }{\theta }-{ϵ}_2}+\left(\eta r_3+i{r}_2\right){}^2+\left(r_2-i\eta r_3\right){}^2}.$$

  (44)
  So the Cross-Kink rational wave solution of eq. (1) extracted as

  $$v_{6,3}(x,t)=\frac{2r_3\left(r_3(x-ct)+i{r}_2\right)-2i{r}_3\left(r_2-i{r}_3(x-ct)\right)-\frac{2(\lambda +1)e^{-\frac{2(\lambda +1)(x-ct)}{\theta }-{ϵ}_2}}{\theta }}{\left(r_3(x-ct)+i{r}_2\right){}^2+\left(r_2-i{r}_3(x-ct)\right){}^2+e^{-\frac{2(\lambda +1)(x-ct)}{\theta }-{ϵ}_2}}.$$

  (45)
• M-Shaped Rational Wave Solution: With the help of the following transformation [18], we generate different types of solutions:

  $$f=\left(\eta r_1+r_2\right){}^2+\left(\eta r_3+r_4\right){}^2+r_5$$

  (46)
  Substituting eq. (46) in eq. (7), simplifying and like terms and equating the coefficients of each obtained expressions to zero. So, we obtained the system of equation and simplified with the help of Mathematica to gain the different sets of unknown constants such as:
  Set 1:$r_2=\frac{-\eta r_1^2-\eta r_3^2-r_3{r}_4}{r_1},r_5=-\frac{\left(r_1^2+r_3^2\right)\left(\eta r_3+r_4\right){}^2}{r_1^2},$ and putting them in eq. (46) in eq. (5), we obtain

  $$V_{7,1}\left(\eta \right)=\frac{2\left(r_1+\frac{-r_1^2-r_3^2}{r_1}\right)\left(\eta r_1+\frac{-\eta r_1^2-\eta r_3^2-r_3{r}_4}{r_1}\right)+2r_3\left(\eta r_3+r_4\right)-\frac{2r_3\left(r_1^2+r_3^2\right)\left(\eta r_3+r_4\right)}{r_1^2}}{{\left(\eta r_1+\frac{-\eta r_1^2-\eta r_3^2-r_3{r}_4}{r_1}\right)}^2+\left(\eta r_3+r_4\right){}^2-\frac{\left(r_1^2+r_3^2\right){\left(\eta r_3+r_4\right)}^2}{r_1^2}}.$$

  (47)
  So the M-Shaped rational wave solution of eq. (1) extracted as

  $$v_{7,1}(x,t)=\frac{2\left(r_1+\frac{-r_1^2-r_3^2}{r_1}\right)H+2r_3\left(r_3(x-ct)+r_4\right)-\frac{2r_3\left(r_1^2+r_3^2\right)\left(r_3(x-ct)+r_4\right)}{r_1^2}}{H^2+{\left(r_3(x-ct)+r_4\right)}^2-\frac{\left(r_1^2+r_3^2\right){\left(r_3(x-ct)+r_4\right)}^2}{r_1^2}},$$

  (48)

  where $H=\frac{r_1^2(-(x-ct))-\eta r_3^2-r_3{r}_4}{r_1}+r_1(x-ct)$.
  Set 2:$r_2=i{r}_4,r_3=-i{r}_1,$ and putting them in eq. (46) in eq. (5), we obtain

  $$V_{7,2}\left(\eta \right)=\frac{2r_1\left(\eta r_1+i{r}_4\right)-2i{r}_1\left(r_4-i\eta r_1\right)}{\left(r_4-i\eta r_1\right){}^2+\left(\eta r_1+i{r}_4\right){}^2+r_5}.$$

  (49)
  So the M-Shaped rational wave solution of eq. (1) extracted as

  $$v_{7,2}(x,t)=\frac{2r_1\left(r_1(x-\mathrm{ct})+i{r}_4\right)-2i{r}_1\left(r_4-i{r}_1(x-\mathrm{ct})\right)}{\left(r_4-i{r}_1(x-\mathrm{ct})\right){}^2+\left(r_1(x-\mathrm{ct})+i{r}_4\right){}^2+r_5}.$$

  (50)
  Set 3:$r_2=\frac{-\eta r_1^2-\eta r_3^2-r_3{r}_4}{r_1},\alpha =0,$ and putting them in eq. (46) in eq. (7), we obtain

  $${\mathsf{\Psi }}_{7,3}\left(\eta \right)=\frac{-\frac{2(\lambda +1)e^{-\frac{2(\lambda +1)\eta }{\theta }-{ϵ}_2}}{\theta }+2r_3\left(\eta r_3+i{r}_2\right)-2i{r}_3\left(r_2-i\eta r_3\right)}{e^{-\frac{2(\lambda +1)\eta }{\theta }-{ϵ}_2}+\left(\eta r_3+i{r}_2\right){}^2+\left(r_2-i\eta r_3\right){}^2}.$$

  (51)
  So the M-Shaped rational wave solution of eq. (1) extracted as

  $$v_{7,3}(x,t)=\frac{2r_3\left(r_3(x-ct)+i{r}_2\right)-2i{r}_3\left(r_2-i{r}_3(x-ct)\right)-\frac{2(\lambda +1)e^{-\frac{2(\lambda +1)(x-ct)}{\theta }-{ϵ}_2}}{\theta }}{\left(r_3(x-ct)+i{r}_2\right){}^2+\left(r_2-i{r}_3(x-ct)\right){}^2+e^{-\frac{2(\lambda +1)(x-ct)}{\theta }-{ϵ}_2}}.$$

  (52)
• M-Shaped Rational Wave Solution with One Kink Wave: With the help of the following transformation [18], we generate different types of solutions:

  $$f=n_{1}exp\left(\eta {ϵ}_1+{ϵ}_2\right)+\left(\eta r_1+r_2\right){}^2+\left(\eta r_3+r_4\right){}^2+r_5.$$

  (53)
  Substituting eq. (53) in eq. (7), simplifying and collecting like terms with exponential functions and equating the coefficients of each obtained expressions to zero. So, we obtained the system of equation and simplified with the help of Mathematica to gain the different sets of unknown constants such as:
  Set 1:$n_1=0,{ϵ}_1=\frac{2(\lambda +1)}{\theta },r_2=-\frac{r_1(2\lambda \eta +2\eta +\theta )}{2(\lambda +1)},r_3=0,\alpha =-\frac{\theta }{2},\beta =1,$ and putting them in eq. (53) in eq. (5), we obtain

  $$V_{8,1}\left(\eta \right)=-\frac{4{(\lambda +1)}^3}{2{(\lambda +1)}^2\theta +{\theta }^3{r}_1^2{e}^{\frac{2(\lambda +1)\eta }{\theta }+{ϵ}_2}}.$$

  (54)
  So the solution of eq. (1) extracted as

  $$v_{8,1}(x,t)=\frac{4{(\lambda +1)}^3}{2{(\lambda +1)}^2\theta +{\theta }^3{r}_1^2{e}^{\frac{2(\lambda +1)(x-ct)}{\theta }+{ϵ}_2}}.$$

  (55)
  Set 2:${ϵ}_1=0,r_2=-\frac{r_1(2\lambda \eta +2\eta +\theta )}{2(\lambda +1)},r_3=0,\alpha =-\frac{\theta }{2},\beta =1,$ and putting them in eq. (53) in eq. (7), we obtain

  $$V_{8,2}\left(\eta \right)=\frac{2\left(r_1-\frac{(2\lambda +2)r_1}{2(\lambda +1)}\right)\left(\eta r_1-\frac{r_1(2\lambda \eta +2\eta +\theta )}{2(\lambda +1)}\right)}{n_1{e}^{{ϵ}_2}+\left(\eta r_1-\frac{r_1(2\lambda \eta +2\eta +\theta )}{2(\lambda +1)}\right){}^2+r_4^2+r_5+e^{-{ϵ}_2}}.$$

  (56)
  So the solution of eq. (1) extracted as

  $$v_{8,2}(x,t)=\frac{2\left(r_1-\frac{(2\lambda +2)r_1}{2(\lambda +1)}\right)\left(r_1(x-\mathrm{ct})-\frac{r_1(2\lambda (x-\mathrm{ct})+2(x-\mathrm{ct})+\theta )}{2(\lambda +1)}\right)}{\left(r_1(x-\mathrm{ct})-\frac{r_1(2\lambda (x-\mathrm{ct})+2(x-\mathrm{ct})+\theta )}{2(\lambda +1)}\right){}^2+n_1{e}^{{ϵ}_2}+r_4^2+r_5+e^{-{ϵ}_2}}.$$

  (57)
  Set 3:$n_1=0,{ϵ}_1=\frac{2(\lambda +1)}{\theta },r_1=-i{r}_3,r_4=i{r}_2,r_5=0,$ and putting them in eq. (53) in eq. (7), we obtain

  $$V_{8,3}\left(\eta \right)=\frac{-\frac{2(\lambda +1)e^{-\frac{2(\lambda +1)\eta }{\theta }-{ϵ}_2}}{\theta }+2r_3\left(\eta r_3+i{r}_2\right)-2i{r}_3\left(r_2-i\eta r_3\right)}{e^{-\frac{2(\lambda +1)\eta }{\theta }-{ϵ}_2}+\left(\eta r_3+i{r}_2\right){}^2+\left(r_2-i\eta r_3\right){}^2}.$$

  (58)
  So the solution of eq. (1) extracted as

  $$v_{8,3}(x,t)=\frac{2r_3\left(r_3(x-ct)+i{r}_2\right)-2i{r}_3\left(r_2-i{r}_3(x-ct)\right)-\frac{2(\lambda +1)e^{-\frac{2(\lambda +1)(x-ct)}{\theta }-{ϵ}_2}}{\theta }}{\left(r_3(x-ct)+i{r}_2\right){}^2+\left(r_2-i{r}_3(x-ct)\right){}^2+e^{-\frac{2(\lambda +1)(x-ct)}{\theta }-{ϵ}_2}}.$$

  (59)
• M-Shaped Rational Wave Solution with Two Kink Waves: With the help of the following transformation [18], we generate different types of solutions:

  $$f=n_{1}exp\left(\eta {ϵ}_1+{ϵ}_2\right)+n_{2}exp\left(\eta {ϵ}_3+{ϵ}_4\right)+\left(\eta r_1+r_2\right){}^2+\left(\eta r_3+r_4\right){}^2+r_5.$$

  (60)
  Substituting eq. (60) in eq. (7), simplifying and collecting like terms with exponential functions and equating the coefficients of each obtained expressions to zero. So, we obtained the system of equation and simplified with the help of Mathematica to gain the different sets of unknown constants such as:
  Set 1:${ϵ}_1=-\frac{2(\lambda +1)}{\theta },{ϵ}_3=-\frac{2(\lambda +1)}{\theta },r_1=0,r_3=0,r_5=-r_2^2-r_4^2,$ and putting them in eq. (60) in eq. (5), we obtain

  $$V_{9,1}\left(\eta \right)=\frac{-\frac{2(\lambda +1)n_1{e}^{{ϵ}_2-\frac{2(\lambda +1)\eta }{\theta }}}{\theta }-\frac{2(\lambda +1)n_2{e}^{{ϵ}_4-\frac{2(\lambda +1)\eta }{\theta }}}{\theta }}{n_1{e}^{{ϵ}_2-\frac{2(\lambda +1)\eta }{\theta }}+n_2{e}^{{ϵ}_4-\frac{2(\lambda +1)\eta }{\theta }}}.$$

  (61)
  So the solution of eq. (1) extracted as

  $$v_{9,1}(x,t)=\frac{-\frac{2(\lambda +1)n_1{e}^{{ϵ}_2-\frac{2(\lambda +1)(x-ct)}{\theta }}}{\theta }-\frac{2(\lambda +1)n_2{e}^{{ϵ}_4-\frac{2(\lambda +1)(x-ct)}{\theta }}}{\theta }}{n_1{e}^{{ϵ}_2-\frac{2(\lambda +1)(x-ct)}{\theta }}+n_2{e}^{{ϵ}_4-\frac{2(\lambda +1)(x-ct)}{\theta }}}.$$

  (62)
  Set 2:${ϵ}_1=-\frac{2(\lambda +1)}{\theta },{ϵ}_3=-\frac{2(\lambda +1)}{\theta },r_2=-i{r}_4,r_3=i{r}_1,r_5=0,$ and putting them in eq. (60) in eq. (5), we obtain

  $$V_{9,2}\left(\eta \right)=\frac{-\frac{2(\lambda +1)n_1{e}^{{ϵ}_2-\frac{2(\lambda +1)\eta }{\theta }}}{\theta }-\frac{2(\lambda +1)n_2{e}^{{ϵ}_4-\frac{2(\lambda +1)\eta }{\theta }}}{\theta }+2i{r}_1\left(r_4+i\eta r_1\right)+2r_1\left(\eta r_1-i{r}_4\right)}{n_1{e}^{{ϵ}_2-\frac{2(\lambda +1)\eta }{\theta }}+n_2{e}^{{ϵ}_4-\frac{2(\lambda +1)\eta }{\theta }}+{\left(r_4+i\eta r_1\right)}^2+{\left(\eta r_1-i{r}_4\right)}^2}.$$

  (63)
  So the solution of eq. (1) extracted as

  $$v_{9,2}(x,t)=\frac{-\frac{2(\lambda +1)n_1{e}^{{ϵ}_2-A}}{\theta }-\frac{2(\lambda +1)n_2{e}^{{ϵ}_4-A}}{\theta }+2i{r}_1\left(r_4+i{r}_1(x-\mathrm{ct})\right)+2r_1\left(r_1(x-\mathrm{ct})-i{r}_4\right)}{n_1{e}^{{ϵ}_2-A}+n_2{e}^{{ϵ}_4-A}+{\left(r_4+i{r}_1(x-\mathrm{ct})\right)}^2+{\left(r_1(x-\mathrm{ct})-i{r}_4\right)}^2},$$

  (64)

  where $A=\frac{2(\lambda +1)(x-\mathrm{ct})}{\theta }$.
  Set 3:$n_1=0,{ϵ}_3=-\frac{2(\lambda +1)}{\theta },r_1=-i{r}_3,r_4=i{r}_2,r_5=0,$ and putting them in eq. (60) in eq. (5), we obtain

  $$V_{9,3}\left(\eta \right)=\frac{-\frac{2(\lambda +1)n_2{e}^{{ϵ}_4-\frac{2(\lambda +1)\eta }{\theta }}}{\theta }+2r_3\left(\eta r_3+i{r}_2\right)-2i{r}_3\left(r_2-i\eta r_3\right)}{n_2{e}^{{ϵ}_4-\frac{2(\lambda +1)\eta }{\theta }}+\left(\eta r_3+i{r}_2\right){}^2+\left(r_2-i\eta r_3\right){}^2}.$$

  (65)
  So the solution of eq. (1) extracted as

  $$v_{9,3}(x,t)=\frac{-\frac{2(\lambda +1)n_2{e}^{{ϵ}_4-\frac{2(\lambda +1)(x-ct)}{\theta }}}{\theta }+2r_3\left(r_3(x-ct)+i{r}_2\right)-2i{r}_3\left(r_2-i{r}_3(x-ct)\right)}{\left(r_3(x-ct)+i{r}_2\right){}^2+\left(r_2-i{r}_3(x-ct)\right){}^2+e^{{ϵ}_4-\frac{2(\lambda +1)(x-ct)}{\theta }}}.$$

  (66)

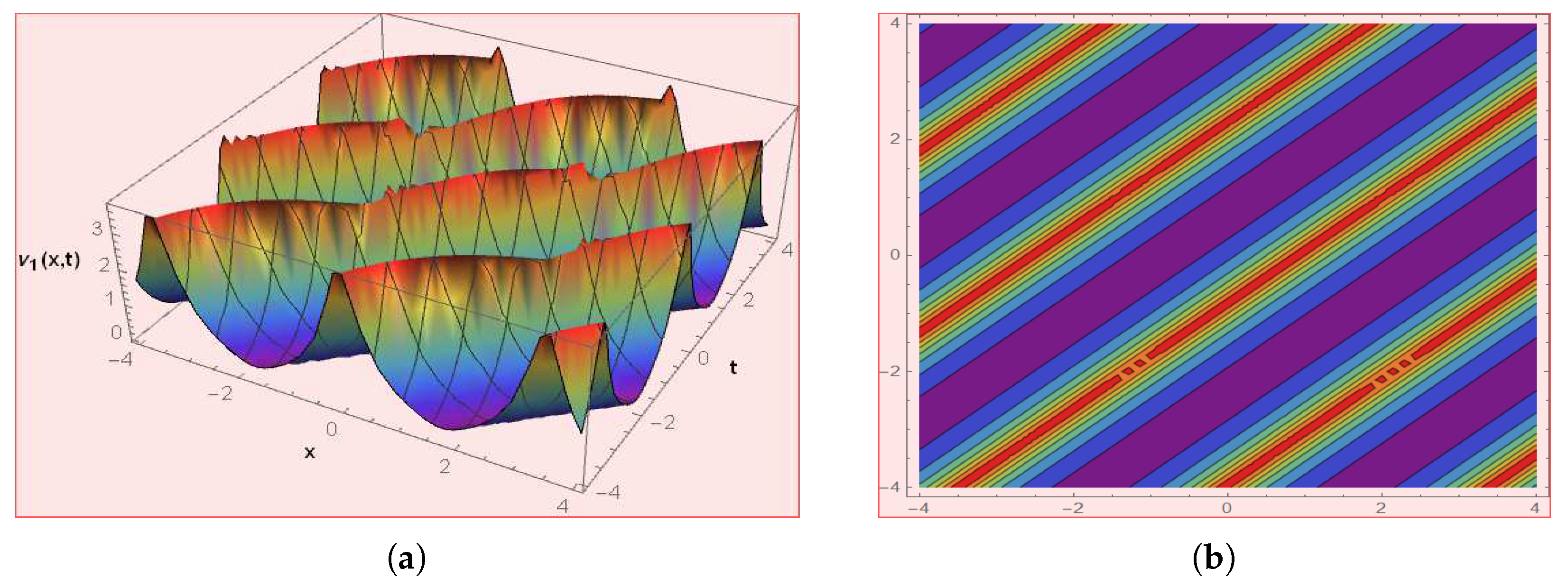
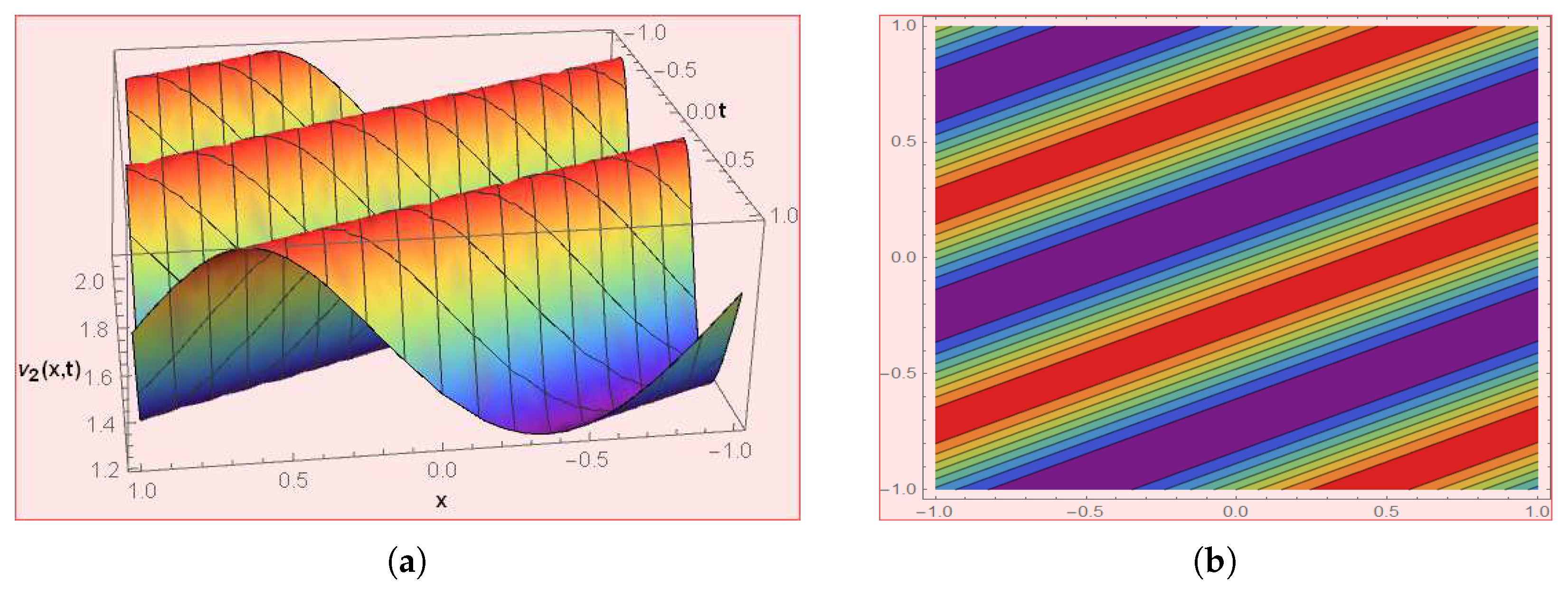
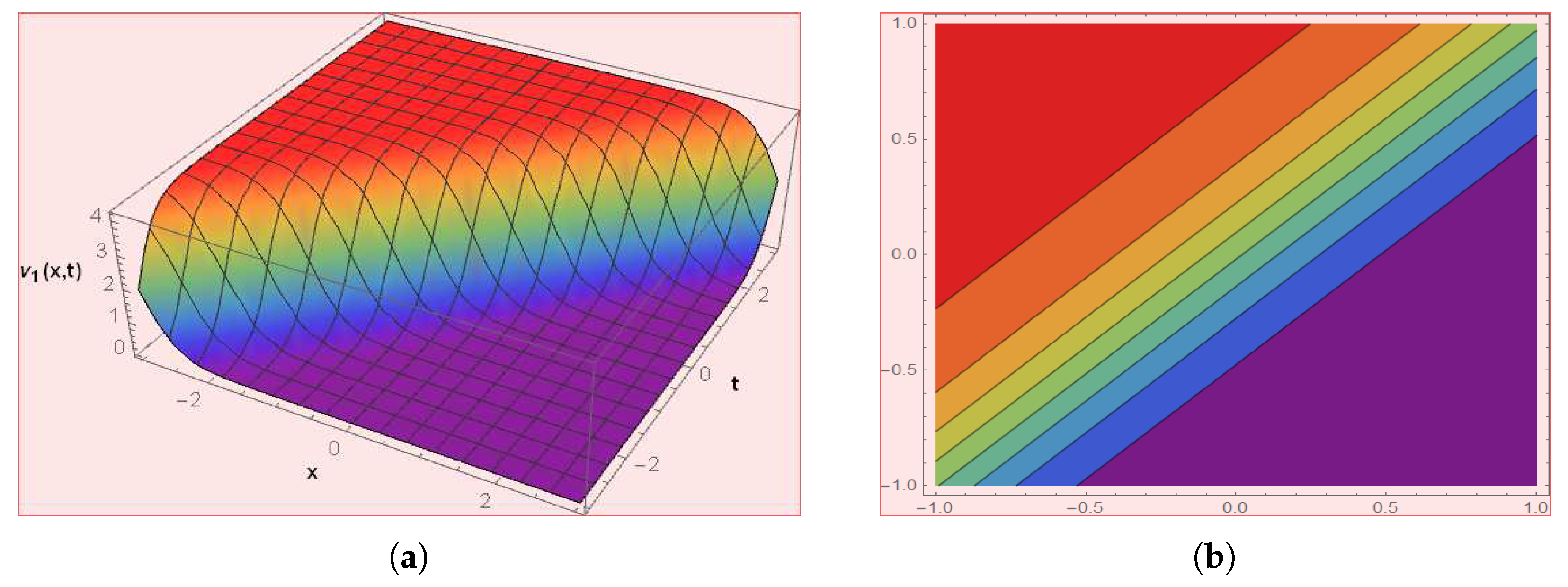
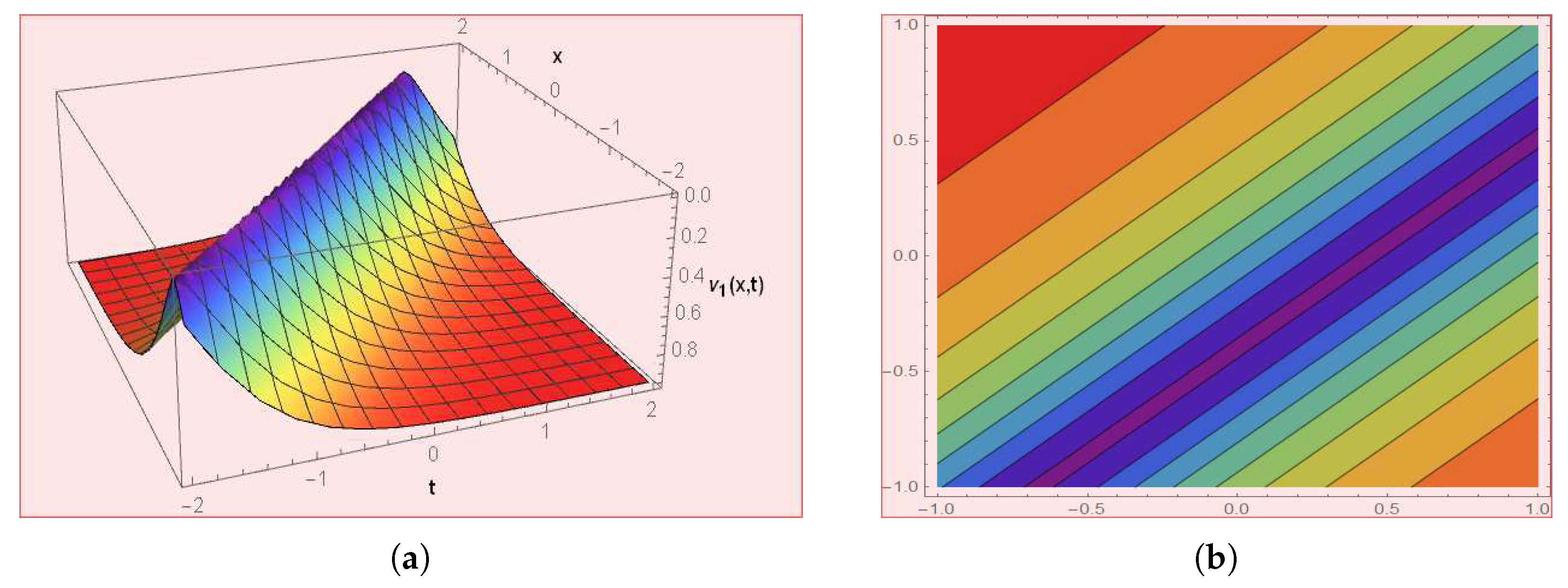
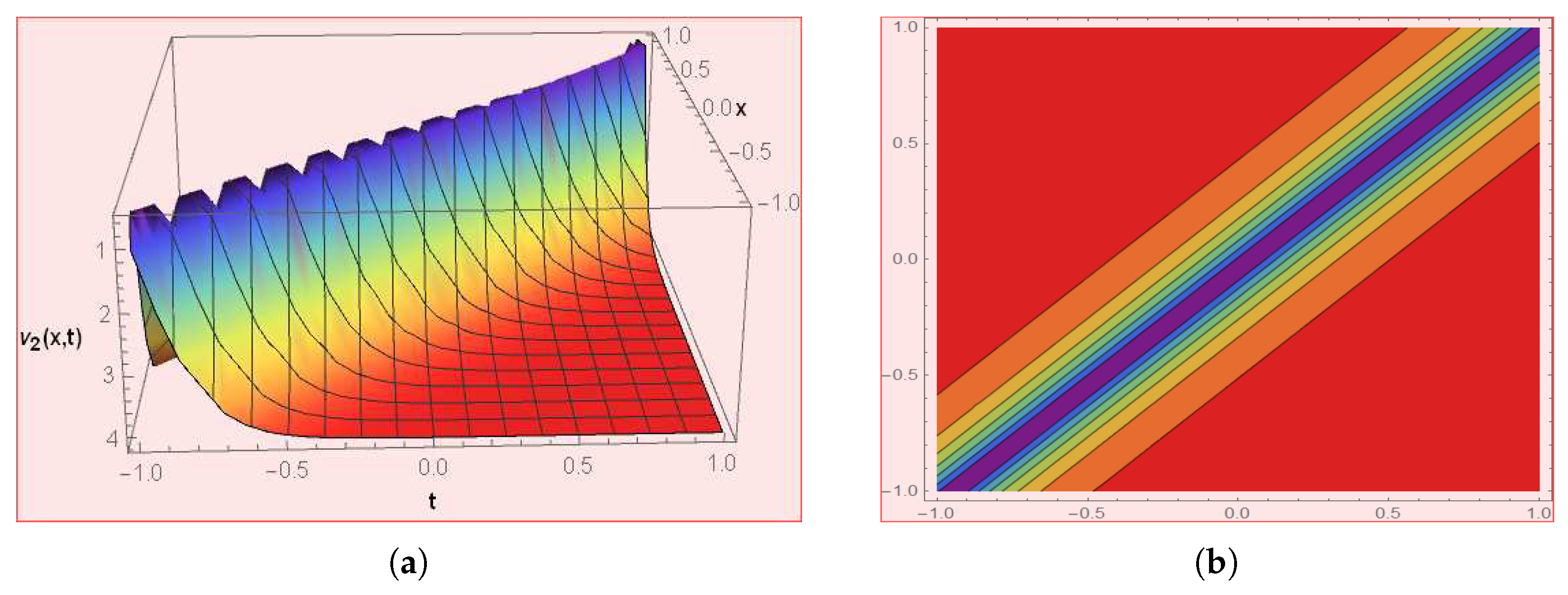
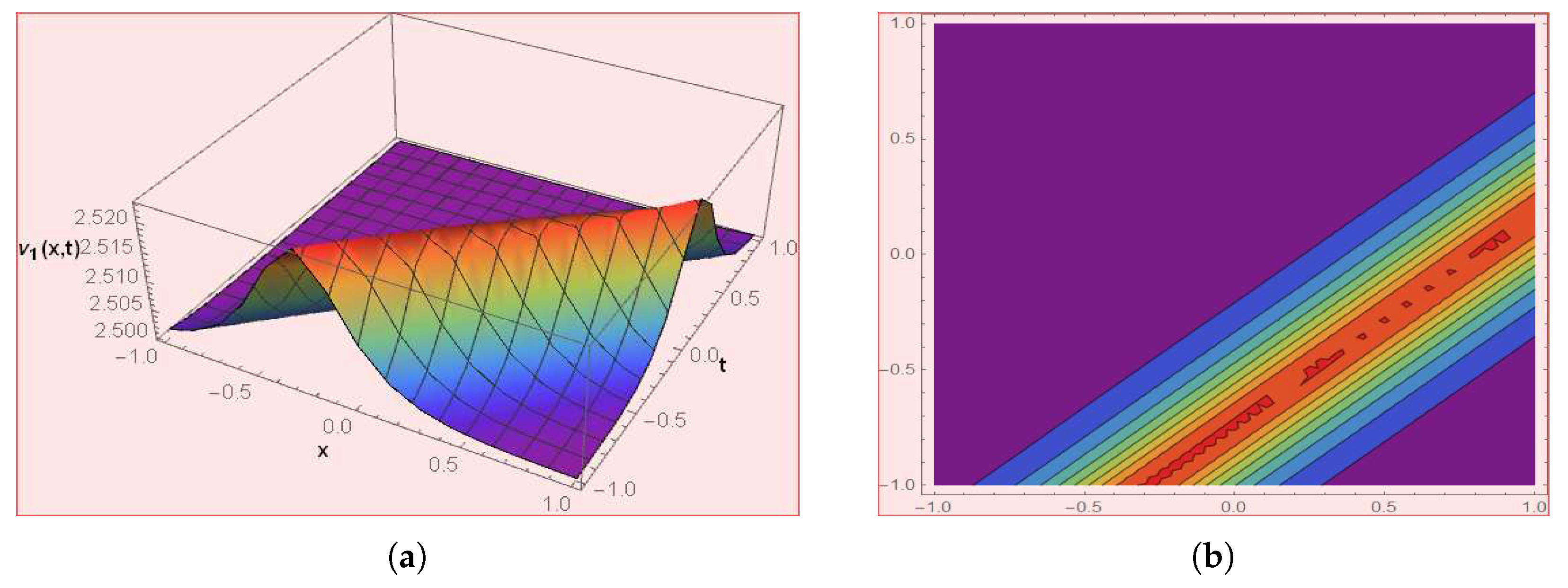
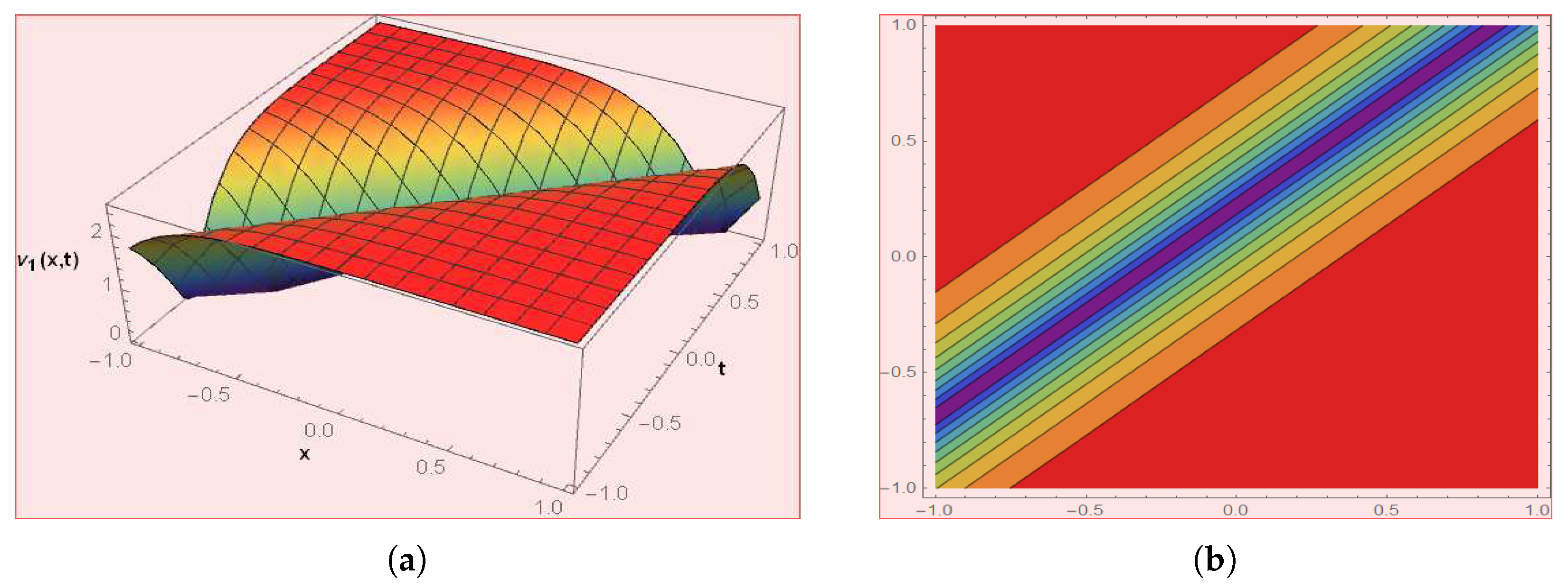
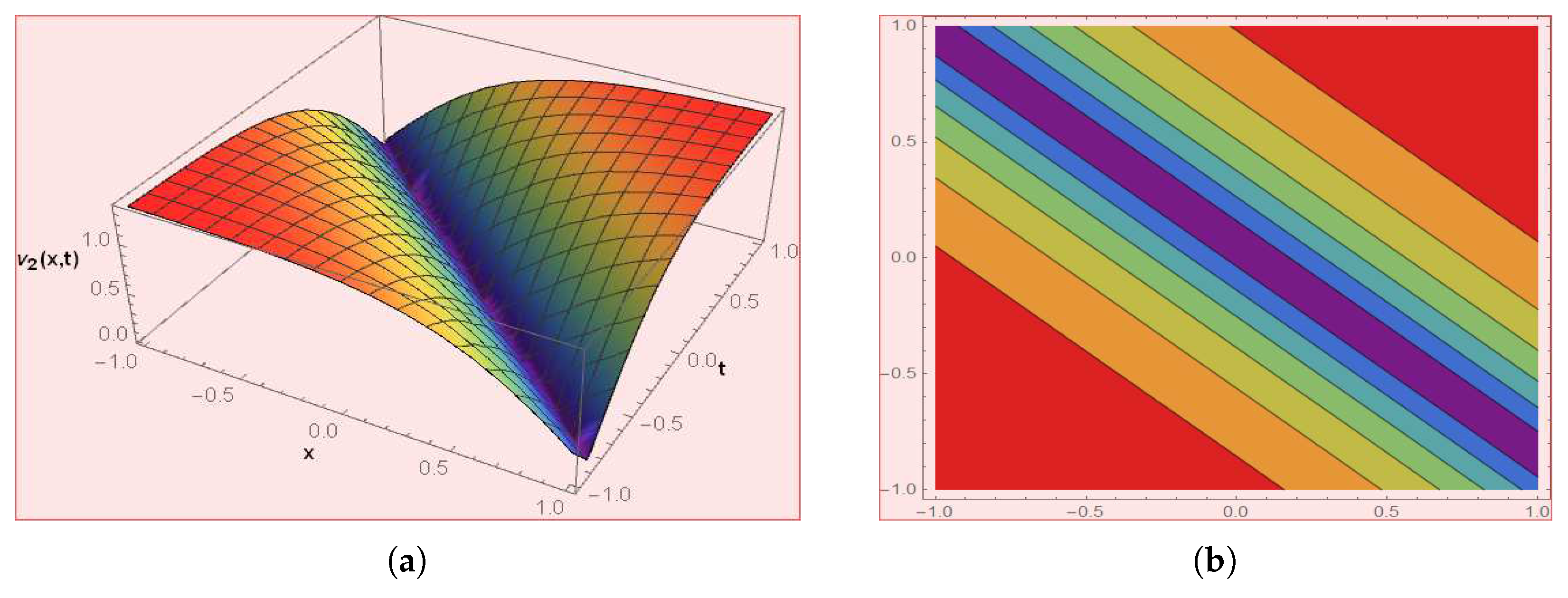
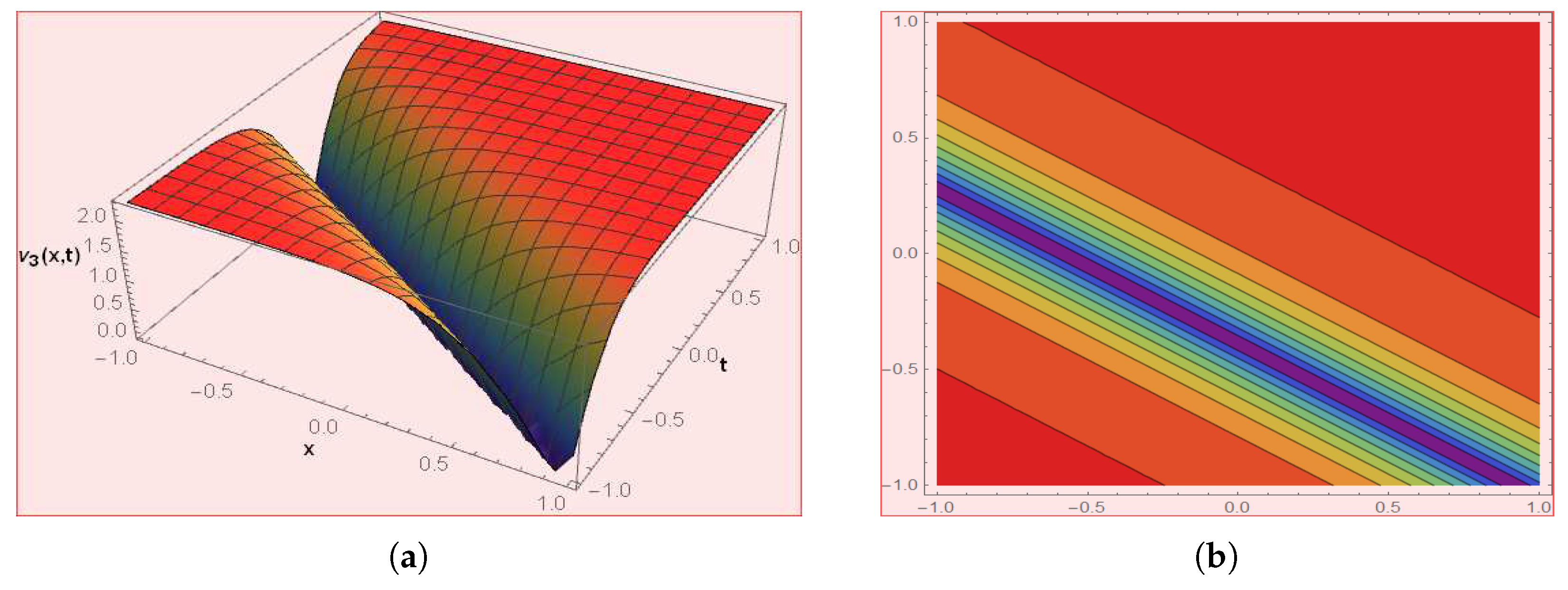
4. Graphical Presentations

Let us look at some of the graphical representations of the aforesaid solutions. The various wave structures below demonstrate graphical depictions of some of the solutions as obtained above. Graphs have been extensively utilized to explain the dynamics and distinctive appearance of solutions generated from the BBMPB equation. The results obtained here show that the system has a very diversified wave shape for use in fluid ion applications. Figure 1 and Figure 2 are drawn for the multiwave solutions while Figure 3 shows the kink type solution for the double rational form solution. Figure 4 and Figure 5 show the breather waves and Figure 6 corresponds to the mixed type solution. Figure 7, Figure 8 and Figure 9 represent the physical behavior for the periodic cross kink solutions. These solutions are effective in the further study of dynamical systems.

5. Conclusion

The Benjamin-Bona-Mahony-Peregrine-Burgers (BBMPB) equation is a useful model for understanding the behavior of ion-acoustic waves in fluid ions. The ion-acoustic wave is a fundamental mode of oscillation in plasmas and is characterized by its dispersion relation, which relates the wave frequency to the wave number. The study of ion-acoustic waves is of great importance in plasma physics because it provides insights into the basic plasma processes, such as energy transport, wave-particle interactions, and turbulence. The Hirota bilinear transformation technique is used to construct different types of the solutions and this method gives us the exact Ionic wave structures. The different types of the wave structures are constructed successfully in the forms of breather waves, lump periodic waves, mixed-type wave solutions, cross-kink rational wave solutions, M-shaped rational wave solutions, and M-shaped rational wave solutions with one or two kink waves. Overall, the study of ion-acoustic wave structures using the BBMPB equation provides valuable insights into the behavior of plasma waves and the underlying physics of ion-acoustic wave phenomena. The different types of wave solutions studied through this equation gives us a clear understanding of the complex dynamics of these wave structures, and may have important implications for the design of plasma-based technologies and experiments.