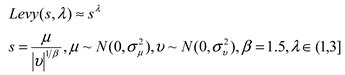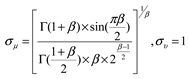1. Introduction
The multiobjective optimization problem is a key research direction in the field of optimization. In scientific research and engineering application, most practical optimization problems involve the need of simultaneously optimizing multiple objective functions in the design process. To make the problem even complex, these multiple objectives may be mutually constraining. Therefore, it is imperative to study multiobjective optimization algorithms. Over the recent years, a variety of swarm intelligence optimization algorithms have sprung up in an endless stream, and quite a few of them have demonstrated excellent performance in solving multiobjective optimization problems. Against large-scale multiobjective optimization problems with complicated backgrounds, literature [
1] proposes a competition-based swarm optimization (CSO) algorithm, which adopts a two-stage update strategy to boost the search efficiency to an enormous extent. Literature [
2] proposes a new-type multiobjective sine cosine algorithm (MOSCA) for the prediction of a wind speed hybrid prediction system. Domestic and foreign scholars have achieved good results by introducing some new mechanisms and evolution strategies into the multiobjective optimization field. Literature [
3] introduces the Levy disturbance and the niched optimization technology to improve the effectiveness of the multiobjective sparrow algorithm and applies this algorithm to optimize the capacity configuration of wind-sunlight diesel batteries. Literature [
4] proposes a novel congestion strategy to improve the multiobjective sparrow algorithm and adopts multiple test functions and a disc brake design to test the algorithm performance. Literature [
5] proposes an evolution algorithm (DMOES) based on a new-type evolution strategy, which involves a simulated niche of codirectional magnetic particles to approximate the Pareto front and adopts two strategies, the non-dominated solution and the dominated solution, to accelerate convergence, hence can obtain a good Pareto front at low computational cost.
Multivariant optimization algorithm (MOA) [
6] is a swarm intelligence optimization algorithm proposed in 2013. Taking full advantage of the characteristic of sufficiently large modern compute memory, the algorithm establishes a computer data structure based structural body, which manages searching atoms in the form of multiple linked lists and employs search individuals to alternate between global and local searches to implement the procedure of optimization. This algorithm is compact-structured, with low computational complexity, process memory, high convergence and computational accuracy [
7]. As proven by literatures [
8,
9,
10], this algorithm has good asymptotic property, convergence, and reachability. Later, some scholars applied it in dynamic route optimization [
11], data clustering [
12], three-dimensional container loading problem [
13] and other practical applications and achieved good results.
Based on MOA, this paper proposes a multiobjective multivariant optimization algorithm (MMOA). The algorithm has improved the global and local searching mechanisms by adopting a good point set [
14] for initialization, increasing the population diversity and avoiding its dependence on the initial solutions. A nonlinear adaptive search radius is introduced to supersede, and avoid the blindness due to, the random radius in the primitive MOA, and the search range is narrowed by enabling the search radius to decrease gradually with the increase of the number of iterations. The way the search radius is processed balances the global and local searches of the algorithm and increases the convergence precision of the algorithm. Levy Flight [
15] and Sine chaotic mapping [
16] are introduced to disturb the local search and increase the population diversity. What is boosted is not just the optimization efficiency and convergence rate but also the optimization accuracy of the algorithm.
2. MOA
MOA is a multivariant search swarm intelligence optimization algorithm. Its basic thought is to construct a structural body composed of a horizontal linked list that saves global optimal solutions in order and a vertical linked list that saves local optimal solutions in order. Individuals with different functions are arranged in the structural body in a certain pattern, each performing its own functions and sharing information. The searching individuals are updated continually during iterations, and the search range is gradually narrowed until the global optimal solution and multiple local optimal solutions are found ultimately. The structural body is shown in
Figure 1. By function of the searching individuals in the algorithm, the individuals responsible for global search are called global atoms (Ga’s), whereas the individuals responsible for local search are called local atoms (La’s). Ga’s are arranged in a queue pattern, whereas La’s are arranged in a stack pattern, composing an upper triangular structural body. The global optimal solution and multiple local optimal solutions are to be found in the end through alternate iterations between global search and local search.
Ga’s are generated by Equation (1):
where
represents the dimension of the problem;
and
are the upper and lower limits of the
th dimension of the solution space;
is a function that generates a random number uniformly distributed between
and
. La’s are generated by equation (2):
where
is the search radius, and
is a function that generates a random number uniformly distributed between -1 and 1.
3. MMOA
To implement the MMOA, fast non-dominated sorting [
14] and novel crowding distance are adopted to adjust the external archiving strategy, with searching atoms randomly selected as Ga’s from external archives. The good point set is adopted for population initialization and to ensure population diversity and avoid the dependence of the algorithm on the initial solutions. The nonlinear adaptive search radius is introduced to decrease gradually with the increase of the number of iterations and narrow the search range, thus balancing the global and local searches and enhances the convergence precision of the algorithm. To improve the update formula for local atoms, Levy Flight and chaotic mapping are introduced to increase population diversity and optimization efficiency.
3.1. Good Point Set Initialization
Given that there are multiple mutually constraining objective functions in a multiobjective optimization problem, the problem-solving process is even complex. To avoid the dependence of the algorithm on the initial solutions, the good point set [
15] theory proposed by Loo-keng Hua et al. is adopted to construct the solution space of initialized searching atoms. The basic theory of good point set is introduced below: Assuming
is a unit cube in
-dimensional Euclidean space, and
, if
with its deviation
, where
is a constant depending only on
and arbitrary positive number
, then
is called a good point set, with
being the good point(s).
denotes taking the decimal part, and
denotes the number of points. Take
, where
is the smallest prime number satisfying
. Map the good points into the search space to get:
From
Figure 2 , one can find that the points in the good point set are more uniformly distributed in the 2D space. Adopting the good point set for initialization favors the searching atoms finding the global optimal solution while avoiding premature convergence.
3.2. Nonlinear Search Radius
In single-objective MOA, the search radius decreases linearly with the gradual increase in the number of iterations. The search radius determines the size of the search space of the algorithm. However, most problems with the need for optimization are nonlinear and noncontinuous. Therefore, a linear search space is to the disadvantage of searching for optimal solutions. Here a nonlinear adaptive search radius is adopted as shown in equation (5):
where α = 0.1825, t denotes the current number of iterations, and T denotes the maximum number of iterations. The search radius decreases nonlinearly with the increase of the number of iterations. At the initial stage of iterations, the radius is relatively large, which favors global search; with the increase of the number of iterations, the search radius decreases nonlinearly, and the local search predominates progressively.
3.3. Global Search
In multiobjective optimization, for two arbitrary solutions and of objective functions , if , then dominates , denoted as . If there exist and such that and , then neither nor is dominated. A set of solutions are non-dominated, i.e., Pareto optimal solutions, if none of the solutions is dominated by any solution. The essence of multiobjective optimization is to find a set of Pareto optimal solutions such that the values of the objective functions are minimized.
MMOA adopts fast non-dominated sorting, an external archiving strategy , and a novel crowding distance to obtain Ga’s. The Ga’s are generated by randomly drawing individuals from external archives. Assume
is the set of solutions,
is the number of solutions dominated by solution
in the population, and
is the set of dominated solutions. Fast non-dominated sorting is in essence a cyclic classification process. It begins by finding all solutions sets for
that cannot be dominated by any other solution, denoted as class
-1, and removes these solutions from
. Next, this process is looped by continuing to search for non-dominated solution sets in
, denoted as class
-2. The classification continues until all solutions have been classified. To ensure diversity, a certain distance should be kept between one solution and another in a same class, which requires calculating the crowding distance for each solution by the concrete formula of equation (6).
where
is the distance ratio of searching atom
at the
th objective function. The total crowding distance of searching atom
at multiobjective functions is
, where
is the number of objective functions. As
approaches
, the uniformity of solution distribution is better.
3.4. Local Search
To enhance the local search capacity of MMOA, this paper improves the update formula for La’s by introducing Levy Flight to control La’s. Levy Flight [
16] was proposed by French mathematician Paul Levy. It provides a random walk mechanism to control local search, increase the diversity of searching atoms in the algorithm, and avoid the algorithm from running into the local optima in the later phase. Levy Flight is formulated by equations (7) and (8):
The update formula for the La’s in the local linked list is given by equation (9):
where
denotes Levy Flight,
denotes the dimension in the problem,
, and
denotes Sine chaotic mapping. Sine chaotic mapping [
17] is a classical one-dimensional unimodal mapping, mathematically expressed by equation (10):
where
. A chaotic phenomenon occurs for
.
denotes the historical optimal solution, and denotes the global optimal solution. , decreasing nonlinearly with the increase of the number of iterations.
3.5. Algorithm Flow
According to the foregoing presented strategy, the algorithm flow of the MMOA proposed in this paper is detailed as below:
Initialize the population Np using the good point set; set the maximum size Nr of external archives and maximum number of iterations T; perform non-dominated sorting among the initial solutions, update the external archives, and record the global optimum and local optima;
While (t < T)
Select Np individuals randomly as the current global atoms from external archives;
for i = 1: Np
for j = 1: Np - i+1
Using formula (9), locally develop each local atom based on the upper triangular structural body, update the positions of current local atoms, and calculate their fitness;
Perform non-dominated sorting among all current atoms and add non-dominated individuals into the external archives;
end for
end for
Update the local optimal solutions and the global optimal solution;
Update the parameters R and C2;
t = t + 1;
end while;
Output all solutions in the set of external archives
4. Simulation experiment
4.1. Experiment Setup
To verify the performance of MMOA, this paper compares MMOA with NSGA-II [
14], multiobjective evolutionary algorithm based on decomposition (MOEA/D) [
18], non-dominated sorting whale optimization algorithm (NSWOA) [
19], multiobjective Grey Wolf Optimizer (MOGWO) [
20], and non-dominated sorting Moth-Flame Optimization (NDSMFO) [
21]. To ensure objectivity, the main parameters in all algorithms are set as: individual number in or size of the largest set of external archives = 150, population size = 30, maximum number of iterations = 200. The parameters in all comparative algorithms are set in accord with the corresponding literatures.
There are many performance evaluation indexes for MOA, which are divided into three major classes: convergence, diversity, and composite indexes evaluating convergence and diversity. This paper selects one diversity index and two composite indexes to evaluate the algorithm performance [
22].
A composite index evaluating the algorithm performance, it calculates the mean value of the minimum distances from real Pareto individuals to the approximate solution set work out by the algorithm. It is mathematically expressed by equation (11).
where
is the Euclidean distance from individual
to the closest solution in
, and
is the
-base. The smaller the value of IGD, the better the convergence and diversity of
, which is more capable to approximate to the ensemble of real Pareto individuals. When
.
- 2.
Spatial Index (SP)
This evaluates the distribution of the individuals in the approximate solution set of Pareto in the objective space. It is mathematically expressed by equation (12):
where
represents the known real Pareto,
is the Manhattan distance between two closest solution vectors on the non-dominated boundary, and
is the average distance. The smaller the value of SP, the better the spatial distribution of solution set
.
- 3.
Hypervolume (HV)
A composite index evaluating the algorithm, it measures the volume of the dominated objective space bounded by
. It is mathematically expressed by equation (13).
where
is a set of reference points preset to be distributed in the objective space, and
is Lebesgue measure. The higher the value of
, the more approximate
is to the ensemble of real Pareto individuals, and the better the diversity in the objective space.
To verify the validity of this algorithm, this paper selects four ZDT series dual-objective test functions and two DTLZ series triple-objective test functions to examine the solving performance of the algorithm. The selected test functions are shown in
Table 1.
4.2. Experimental Results and Analysis
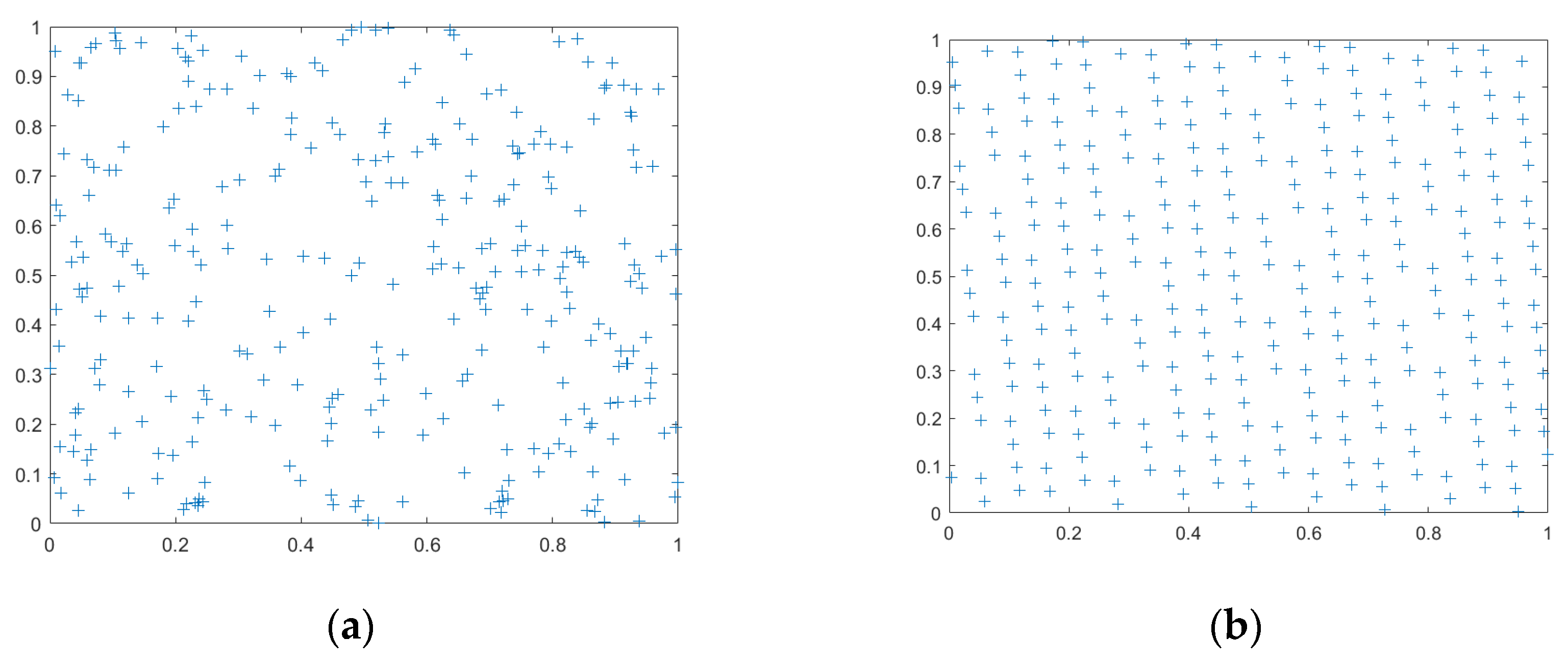
To avoid randomness, each of the test functions runs independently 10 times, and the listed test data are averages of the 10 times. The average runtimes are shown in
Figure 3. MMOA achieves superior results on most of the test functions to the other comparing functions. During the algorithm iteration process, the environment is time-varying, and yet the algorithm adopts the nonlinear adaptive search radius
, avoiding the blind search and shortening its runtime.
Tabels 2–4 correspond respectively to the means and mean square errors of IGD, SP and HV on the six test functions achieved by MMOA versus the other five comparing algorithms. The boldface terms highlight the optimal IGD and SP values for each test function.
From
Table 2, the MMOA in this paper achieves five optimal IGD means over the six test functions, while NSWOA achieves one optimal value. The convergence effect on DTLZ6 is next only to NSWOA. Moreover, the results of both algorithms have the same order of magnitude. MMOA introduces Levy Flight and Sine chaotic mapping for disturbance purposes and to improve the local atoms, conduct full local search, and improve the convergence precision.
A comparative analysis of the SP performance indexes of the six algorithms via
Table 3 reveals that MMOA achieves four optimal values and MOGWO achieves two on the six test functions, while none of the other comparing algorithms achieves an optimal value on the distributive performance index. MMOA adopts fast non-dominated sorting, the external archiving strategy and the novel crowding distance to acquire global atoms, giving full consideration to the spatiality of solutions, which endows it with a good distributive performance in Pareto solution sets of multiobjective optimization problems, as indicated by the small SP means.
The data presented in
Table 4 show that, despite the three optimal values achieved by MMOA and NSWOA each, the gap between them is quite narrow. In MMOA, the good point set is adopted for the initialization of searching atoms, increasing the population diversity, further guaranteeing the spatial diversity of solutions, and making the HV values of MMOA relatively high.
To further compare the performances of MMOA and the other comparing algorithms, this paper conducts a t-test with the results of the two performance indexes, IGD and SP. In terms of 5% level of significance, a comparative analysis is made between MMOA and the other five algorithms. The analysis results are shown in TABLEs III and IV, where “+”, “-” and “=” signify the performance of MMOA is superior, inferior, and approximate to the corresponding comparing algorithm, respectively. From the two tables, one can find the performance indexes of MMOA are significantly superior to NSGAII, MOEA/D and NSMFO amid most of the test functions, except that it is approximate or inferior to MOGWO and NSWOA on only a few of the functions. From the above experiments, MMOA demonstrates superior convergence precision and distributive performance.
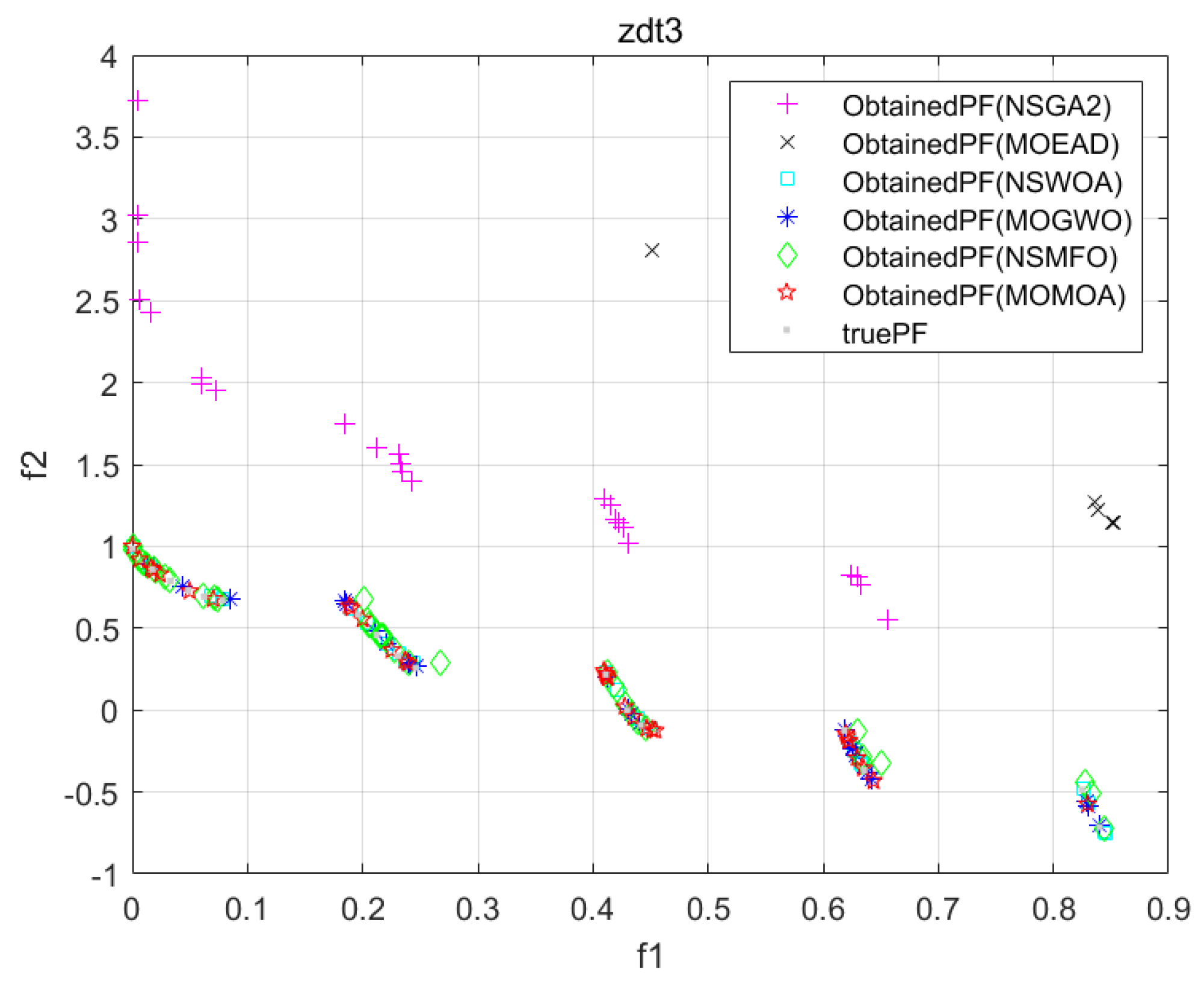
To intuitively display the convergency and distributivity of the solution set derived by each algorithm,
Figure 4 present the Pareto fronts of the six algorithms on some of the test problems.
4.3. Engineering Application
To test the validity of MMOA in solving practical engineering problems, this paper applies it to the problem of a disc brake design [
23]. The disc brake design is a typical multiobjective engineering design problem. The problem involves two objective functions: the braking time
and the braking mass
of the disc brake, subject to five constraints
, which denote the minimum distance between radii, the maximum length of the brake, pressure, temperature, and torque, respectively. The problem is formulated as equation (14):
where the four design variables
represent the disc’s outer radius, inner radius, joint force, and number of friction surfaces, respectively.
In the algorithm the population size is set as 50, the individual number in or size of the largest set of external archives as 200, and the maximum number of iterations as 500, with the same settings for the rest of the parameters.
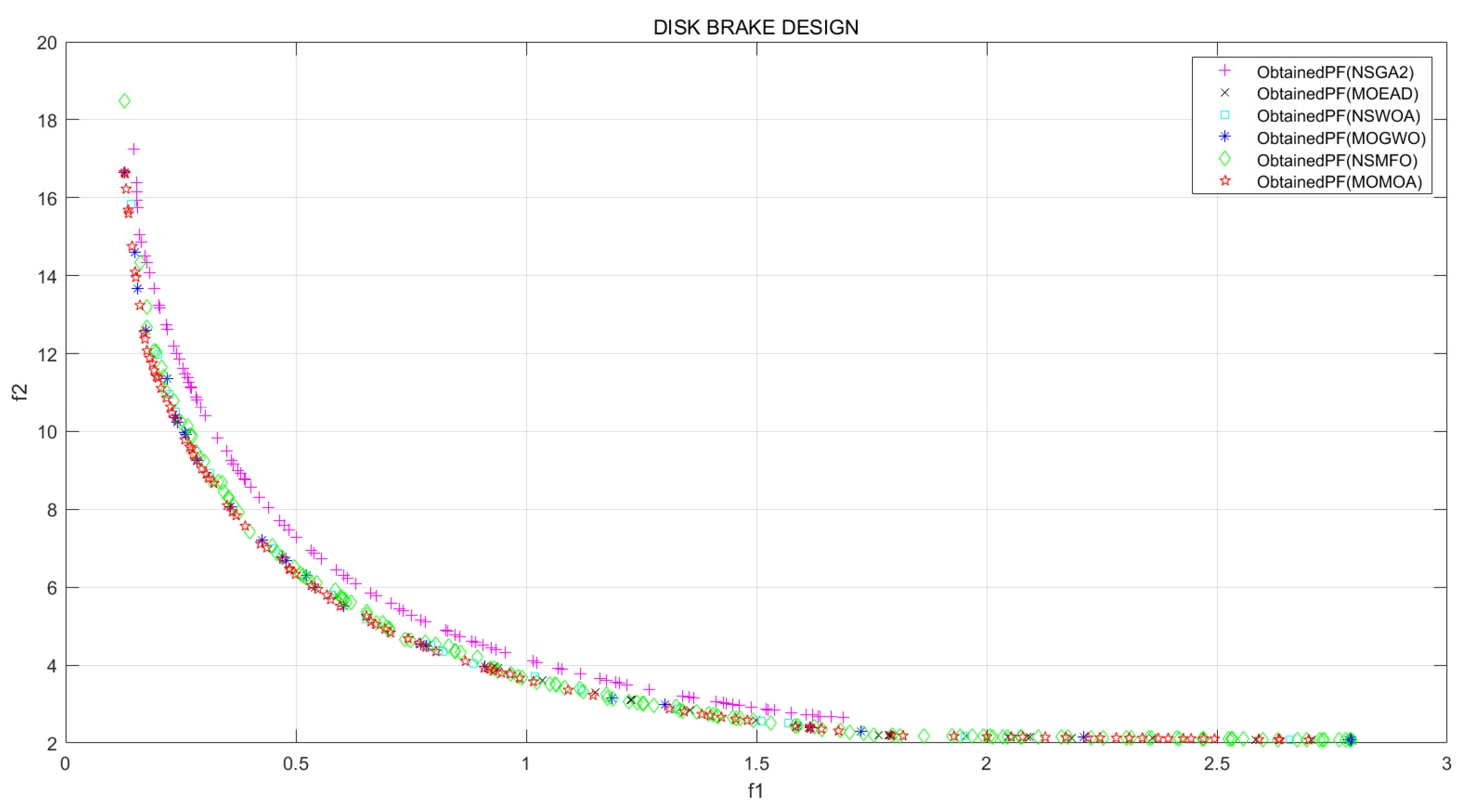
Figure 5 shows the results of optimization by MMOA and by the five algorithms selected in this paper. From Figure 7, MMOA renders a smoother result.
Table 5 presents the spatial evaluator SP and runtime. The SP value of MMOA is the smallest, showing that MMOA has the optimal distributivity of solutions. The runtime, although not the shortest, and slightly inferior to NSWOA, is at the same order of magnitude as NSWOA. Therefore, MMOA can be applied to solve multiobjective engineering problems.
5. Conclusions
At present, various new-type swarm intelligence algorithms have emerged in an endless stream. Their use in combination with novel mechanisms in solving multiobjective optimization problems has become a new research hot spot. Based on MOA, this paper has proposed the multiobjective MOA (MMOA), adopted the test functions and the disc braker design model to test the algorithm, and compared it with five optimization algorithms. The experimental results have shown that the solution set of MMOA demonstrates excellent convergence, spatial distributivity, and scalability. The innovation points achieved by the algorithm in this paper include:
adopting the good point set for initialization of searching atoms, which is conducive to increasing population diversity and avoiding the dependence of the algorithm on the initial solutions;
implementing the nonlinear adaptive search radius, which has the capacity of balancing global search avoiding blind search and accelerating optimization with effectiveness;
improving the global atom setting method in the single-objective MOA, configuring external archives through fast non-dominated sorting and novel crowding distance, and randomly selecting from external archives searching atoms as global atoms for global search;
improving the formula for local atoms in the single-objective MOA, and introducing Levy Flight and Sine chaotic mapping, by which to impose perturbation as the search radius decreases to increase population diversity and boost the algorithm’s optimization efficiency and convergence rate of the algorithm.
Future research will focus on the practical application of MMOA. In recent years, despite the wide attention to the data privacy issue paid by both the industrial and academic communities, data sharing remains hard to implement due to isolated data islands and privacy protection in practical application. Federated learning is an effective approach to break isolated data islands and protect data privacy by building a swarm intelligence model. However, how to address the communication overhead while ensuring accuracy is a problem expected to be resolved by federated learning. With the focus on such practical application problems in the future, MMOA will be employed to optimize the model structure of federated learning, reduce the communication cost, and enhance accuracy.
Author Contributions
Conceptualization, Q.T., X.S.; Methodology, Q.T.; Software, Q.T., X.L.; Writing—original draft, Q.T.; Writing—review & editing, Q.T.; Supervision, Q.T. and F.L.; Project administration, Q.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We would like to thank KetengEdit (
www.Ketengedit.com) for its linguistic assistance during the preparation of this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- T, Y.; Z, X.; Z, X.; J, Y. Efficient Large-Scale Multiobjective Optimization Based on a Competitive Swarm Optimizer. IEEE T. Cybern. 2020, 50, 3696–3708. [Google Scholar] [CrossRef]
- Wang, J.; Yang, W.; Du, P.; Niu, T. A novel hybrid forecasting system of wind speed based on a newly developed multi-objective sine cosine algorithm. Energy Conv. Manag. 2018, 163, 134–150. [Google Scholar] [CrossRef]
- Dong, J.; Dou, Z.; Si, S.; Wang, Z.; Liu, L. Optimization of Capacity Configuration of Wind–Solar–Diesel–Storage Using Improved Sparrow Search Algorithm. J. Electr. Eng. Technol. 2022, 17, 1–14. [Google Scholar] [CrossRef]
- Z, Wen. ; J, Xie.; G, Xie.; et al. Multi-objective Sparrow Search Algorithm Based on New Crowding Distance. Computer Engineering and Applications 2021, 57, 102–109. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, K.; Shen, C.N.; Liu, X.M.; Yen, G.G. Multiobjective Evolution Strategy for Dynamic Multiobjective Optimization. IEEE Trans. Evol. Comput. 2020, 24, 974–988. [Google Scholar] [CrossRef]
- Gou, C.; Shi, X.; Li, B.; Li, T.; Liu, L.; Zhang, Q.; Liu, Y. A novel multivariant optimization algorithm for multimodal optimization. in 2013 6th International Congress on Image and Signal Processing (CISP 2013), 2013, 3, 1623–1627. [Google Scholar] [CrossRef]
- Li, B. The study on the multivariant optimization process memorise algorithm and multimodal optimization under the dynamic and static condition. Doctor thesis, Yunnan University Kunmming, 2015. (In Chinese)
- Li, B.; Lv, D.; Zhang, Q. et al. On asymptotic property of multivariant optimization algorithm. Control Theory & Applications, 2015, 32, 169–177. (In Chinese) [Google Scholar] [CrossRef]
- Li, B.; Shi, X.; Gou, C. et al. On the convergence of multivariant optimization algorithm. Applied Soft Computing 2016, 48, 230–239. [Google Scholar] [CrossRef]
- B, Li.; D, Lv.; L, Liu. ; X, Shi.; J, Chen.; Y, Zhang. On accessibility of multivariant optimization algorithm. Systems Engineering and Electronics 2015, 37, 1670–1675. (In Chinese) [Google Scholar] [CrossRef]
- Li, B.; Lv, D.; Q, Zhang. ; X, Shi.; J, Chen.; Y, Zhang. A Path Planner Based on Multivariant Optimization Algorithm. Acta Electronica Sinica 2016, 44, 2242–2247. (In Chinese) [Google Scholar] [CrossRef]
- Zhang,Q. ; Li,B.; Liu, Y. et al. Data clustering using multivariant optimization algorithm. Int. J. Mach. Learn. Cybern. 2016, 7, 773–782. [Google Scholar] [CrossRef]
- S, Li.; X, Shi. ; S, Zhang.; Y, Dong.; L, Gao. Multi-variant Optimization Algorithm for Three Dimensional Container Loading Problem. ACTA AUTOMATICA SINICA 2018, 44, 106–115. (In Chinese) [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Yan, S.; Yang, P.; Zhu, D. et al. Improved sparrow search algorithm based on good point set. Journal of Beijing University of Aeronautics and Astronautics 2021. (In Chinese). [CrossRef]
- MA, W.; Zhu, X. Sparrow Search Algorithm Based on Levy Flight Disturbance Strategy. JOURNAL OF APPLIED SCIENCES — Electronics and Information Engineering 2022, 40, 116–130. [Google Scholar] [CrossRef]
- Zhao, X. Research on optimization performance compasion of different one-dimensional chaotic maps. Application Research of Computers 2012, 29, 913–915. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Islam, Q.N.U.; Ahmed, A.; Abdullah, S.M. Optimized controller design for islanded microgrid using non-dominated sorting whale optimization algorithm (NSWOA). Ain Shams Eng J 2021, 12, 3677–3689. [Google Scholar] [CrossRef]
- Mirjalili, S.; Saremi, S.; Mirjalili, S.M.; Coelho, L.D.S. Multi-objective grey wolf optimizer: A novel algorithm for multi-criterion optimization. Expert Syst. Appl. 2016, 47, 106–119. [Google Scholar] [CrossRef]
- Jangir, P.; Trivedi, I.N. Non-Dominated Sorting Moth Flame Optimizer: A Novel Multi-Objective Optimization Algorithm for Solving Engineering Design Problems. Engineering Technology Open Access Journal 2018, 2. [Google Scholar] [CrossRef]
- Audet, C.; Bigeon, J.; Cartier, D.; Le Digabel, S.; Salomon, L. Performance indicators in multiobjective optimization. Eur. J. Oper. Res. 2021, 292, 397–422. [Google Scholar] [CrossRef]
- Khodadadi, M.; Azizi, S. Talatahari.; P, Sareh. Multi-Objective Crystal Structure Algorithm (MOCryStAl): Introduction and Performance Evaluation. IEEE Access 2021, 9, 117795–117812. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).